APLICACIONES DE ESTADÍSTICA CIRCULAR A PROBLEMAS DE

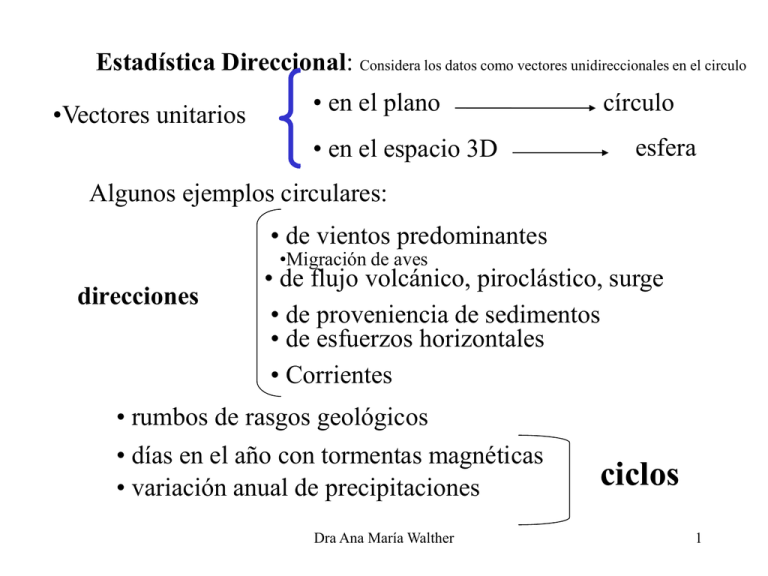
Estadística Direccional: Considera los datos como vectores unidireccionales en el circulo
•Vectores unitarios
• en el plano
• en el espacio 3D
círculo
esfera
Algunos ejemplos circulares:
• de vientos predominantes
•Migración de aves
direcciones
• de flujo volcánico, piroclástico, surge
• de proveniencia de sedimentos
• de esfuerzos horizontales
• Corrientes
• rumbos de rasgos geológicos
• días en el año con tormentas magnéticas
• variación anual de precipitaciones
Dra Ana María Walther
ciclos
1
Representación
Determino un punto de inicio y un sentido de giro para marcar cada dato
0
q
r=1
Más de un dato en la misma dirección
Lo marco con más de un punto
Dra Ana María Walther
2
Datos agrupados en clases
Histogramas lineales
Histogramas circulares
30
25
20
15
10
5
0
0
60
120
180
240
300
360
30
25
20
15
10
5
0
-180
-120
-60
0
60
120
180
240
Dra Ana María Walther
300
360
420
480
540
3
Histograma circular:
• área de cada barra proporcional a la frecuencia de la clase
•cambio barras por sectores == Diagrama de Rosas
• área de cada sector proporcional
a la frecuencia de la clase
• si las clases tienen anchos
iguales, el radio de cada sector es
proporcional a
f
Una manera de hacer la roseta es calcular el intervalo mayor como el 100% y se calculan los
Dra Ana María Walther
4
demás con respecto a estos
Diagramas de rosas
N
100
Con clases de igual
ancho cambio sectores
por radios en centro de
cada clase
== representación
lineal
50
100
50
El problema de
emplear clases es que
influye el
agrupamiento usado
50
100
50
100
Dra Ana María Walther
5
Distribuciones
Distribución unimodal
Distribución bimodal
Dra Ana Maríamultimodal
Walther
Distribución
6
Variables Axiales
Si cada dirección es equivalente a la opuesta
Para todo datos axiales:
0
N
q=q+p
0
N
30
60º
30
Duplico
ángulos
90º
q
2q
120º
180º
Dra Ana María Walther
7
Parámetros y Estadísticos
Circulares
cantidades que sirven para resumir los datos
población
muestra
estadísticos escalares
• desenrollar los datos
• elegir un punto de corte
Dra Ana María Walther
8
Cada dirección en el plano = vector unitario v.
Elegimos una dirección inicial (norte =0)
y una orientación (horaria)
0
x
y
• ángulo q , en radianes
y con módulo 2p
v
• v = (cos q, sen q )
Dra Ana María Walther
9
Describir una muestra por características del conjunto
• de posición
- media
- mediana
• de concentración (o de dispersión)
- Longitud de la resultante
Medidas
- Varianza
- Rango circular
• de asimetría
• de curtosis
Dra Ana María Walther
10
Medidas de posición
0
C
R
dirección Media
q
= resultante de la suma vectorial
S
n
C   cosq i
i 1
n
S   senq i
i 1
módulo R2 = C2 + S2
 
 
tg 1 S
q  1 C
tg S + p
C
Dra Ana María Walther
si C  0
si C  0
11
dirección media
= dirección del centro de masa de los vi
v  (C ; S )
R
; R
n
C
S
con C 
; S
n
n
R=0, q no queda definido
q minimiza la dispersión
Dra Ana María Walther
12
Dirección Media para datos axiales
dirección media estará influenciada por la ubicación de los
datos respecto al arco de 180° considerado.
0
N
0
N
30
Duplico
ángulos
q
30
2q
Hay diferencias entre la media calculada con 2q y la
hallada empleando las direcciones contenidas en el
menor arco que abarque todos los datos.
ambas medias solo coinciden en distribuciones
simétricas,
Dra Ana María Walther
13
distribución simétrica = medias coincidentes
Distribución de frecuencias y medias calculadas con ángulos o con
ángulos duplicados
A
B
C
tita
2tita
0
10
20
30
40
grados
50
60
70
Figura 23
distribuciones asimétricas con distintas curtosis
las medias(2q) desplazadas hacia las modas
Dra Ana María Walther
14
La dirección Mediana
•mitad de datos en
arco (qmd; qmd +p)
Md
fig. 3.3
•mayoría de datos +cerca
de qmd que de (qmd +p)
50%
50%
•n impar, qmd coincide
con un dato
•n par, qmd =punto medio
del arco entre los 2 datos
ubicados en la mitad
Md + p
Dra Ana María Walther
15
Medidas de concentración (o de dispersión)
• Longitud de la resultante media
R2 = C2 + S2
R/n  1 ... qi bien agrupados
R/n  0 ... qi muy dispersos
R/n da medida de concentración del conjunto de los datos,
pero no es un valor eficaz:
datos concentrados en sitios opuestos también dan R/n 0
Dra Ana María Walther
16
Varianza circular
V  1 R
con 0  V  1
presenta los mismos inconvenientes que R
Desviación estándar circular
(SD , v) (en radianes)
Desviación
estándar angular
v   2 ln R

1 n
D(q )   p  p  q i  q
n i 1

dispersión en ángulos alrededor de la media
Rango Circular 
Longitud del arco mínimo que
contenga
todas las observaciones.
Dra Ana María Walther
17
Medidas de Asimetría (skewness o sesgo)
sˆ 
R2 . sen(q 2  2q )
1  R 
3
2
R2=resultante media de ángulos 2qi.
q2= dirección media de ángulos 2qi.
Distribución asimétrica Mo y q no coinciden,
la q tiende a situarse corrida respecto de la Mo para el lado de
la cola más larga.
Medidas de Curtosis (o elevación)
R2 . cos(q 2  2q )  R
ˆ
K
2
1  R 
Dra Ana María Walther
4
18
Caracterizar una distribución en el
círculo unitario
•de cada valor
•de un intervalo
Frecuencias:
f(q) = función de la curva
de probabilidad = fdp.
fdp
F(q)
0
q
Dra Ana María Walther
2p
19
fdp
Frecuencias:
F(q)
q
0
•de cada valor
•de un intervalo
[0;q]
2p
F (x)= Prob(0  X  q), con 0 ≤ x ≤ 2p
( depende del punto elegido como 0)
Función de distribución acumulada
F(q) = Prob(0  X  q),
F(x)
F(q)
1
con 0  q  2p
F(0)=0
0
0
Dra Ana María Walther
2p
F(2p)=1 20
Distribución simétrica con media en 180°
1
0.8
0.6
0.4
0.2
0
F(q)= área bajo la curva de
probabilidad entre 0
y un punto (q) dado
f(q) = la curva representa la
función densidad de probabilidad
= fdp
0
0
1
0
270
270
90
90
180
Dra Ana María Walther
180
21
Modelos Circulares
Distribución Uniforme
1
2p
Básica
0
fdp
Para Ho
1
2p
La fdp de una dist uniforme es 1/2p
No hay concentración en ninguna dirección
0.2
1
2p
0.15
fdp
1
f q  
2p
0.1
r=0
Dra Ana María Walther
0.05
0
-180
-90
0
90
180
22
Función Distribución Acumulada
F x   Pr ob0  q  x 
Con, 0 ≤ x ≤ 2p
1
x
F x   

0 2p
2p
 
Pr ob(  q   ) 
2p
x
para      + 2p
Propiedad Aditiva:
qi ~ Uc
,
i=1,...,n
Dra Ana María Walther
Sn=Sqi ~ Uc
23
Modelos Circulares
Distribución von Mises
• unimodal
Mo
• media m  parámetro
m
• simétrica en m
• moda en qm
antimoda
• antimoda en qm+p
• parámetro de concentración
k
Dra Ana María Walther
24
parámetro de concentración k
Distribución von Mises
Prob. Mo
= exp[2k]
Prob. antiMo
a > k > agrupamiento
k=0 :distribución uniforme.
Mo
k=4, 99% en (mp/2, m+p/2
k=0
k= 8
k=1
k= 4
k=2
k=4
k=8
k= 2
Serie5
k= 1
-180
-90
0
90
180
Dra Ana María Walther
antiMo
25
Distribución von Mises
1
. exp[k . cos(q  m )]
fdp: f (q , m , k ) 
2p .I 0 (k )
I0= función de Bessel modificada
de primer tipo y de orden cero
fdp
Aproximación de
Abramowitz yStegun,
1965:
1 k 
I 0 (k )  

2
r  0 r!  2 

0
m
Dra Ana María Walther
2r
26
Estimar el parámetro de concentración
k
Para una distriubción von Mises VM(m,k)
aproximaciones
 A1 R
 
5 5
k  2R + R + R
6
3
R<0.53
0.43
k  0.4 + 1.39 R +
1 R
0.53  R<0.85
R>0.85
R>0.90
Mardia y Jupp, 2000
k
Fisher 1993
1
21  R   1  R   1  R 
2
3
N
k
2N  R 
1
k
21  R 
Dra Ana María Walther
27
Problema 1:
En una roca conglomerádica se efectuó un análisis de
imbricación de clastos midiéndose 15 direcciones. Calcular:
a) la dirección media (en grados) y la longitud de la resultante (R);
b) la varianza circular (V) ;
c) la desviación estándar circular (v);
d) la desviación estándar angular (CSD);
e) el rango circular  .
61°
358°
349°
77°
141°
42°
91°
356°
71°
48°
83°
Dra Ana María Walther
104°
11°
95°
81°
28
•Calculamos:
a) xi=cosqi , yi=senqi
C= 5.5624 ;
q=60.1°;
i=1,...15
S= 9.6780 ;
R=0.744
b) varianza circular : V =1-R= 0,256
c) SD :
v   2 ln R
v= 0,769
.180/p =44.06°
Dra Ana María Walther
29
ASD = 36.6°
d) desviación estándar angular
e)
=152°

1 n
D(q )   p  p  q i  q
n i 1

rango circular =arco (349°, 141°).
Dra Ana María Walther
30