Todo y más

El infinito ¿es una propiedad
matemática válida o es una
abstracción desprovista de sentido?
La ambición intelectual de David
Foster Wallace le permite contarnos
la historia de los matemáticos que
se esforzaron en entender el
infinito, desde la Antigua Grecia
hasta
el
contraintuitivo
descubrimiento
del
genio
matemático Georg Cantor, según el
cual existían diversos tipos de
infinito. El autor aborda un conjunto
de
logros
matemáticos
extremadamente
abstractos
y
técnicos, aunque muy profundos,
interesantes
y
hermosos.
El
objetivo es hablar de esos logros de
tal manera que resulten atractivos y
comprensibles para lectores que no
tengan preparación técnica ni sean
expertos en la materia.
El resultado es una obra inteligente,
sugestiva y gratificante, que nos
ofrece una profunda comprensión
inmediata del mundo de las
matemáticas. David Foster Wallace
ha hecho comprensibles por fin
algunos
aspectos
de
las
matemáticas difíciles de entender y
que
pocos
sospechaban
que
pudieran poseer: las matemáticas
son asombrosas y de una belleza
impresionante.
David Foster Wallace
Todo y más
Breve historia del infinito
ePub r1.0
koothrapali 01.09.15
Título original: Everything and More. A
Compact History of ∞
David Foster Wallace, 2003
Traducción: Joan Vilaltella Catanyer
Editor digital: koothrapali
ePub base r1.2
PRÓLOGO BREVE PERO
NECESARIO
Desafortunadamente este es un
prólogo que hay que leer —y en primer
lugar—
para
entender
ciertas
características estructurales del texto
principal y algunas partes que casi
parecen un código. De estas, la más
frecuente es la abreviatura SEI en
negrita. Para su información, no se
trata de un tic o un error tipográfico,
sino que sustituye la expresión «Si está
interesado», que, de tanto usarla en los
primeros borradores, finalmente, por
pura repetición, evolucionó de ser una
frase normal, utilizada para introducir
algún párrafo, hasta convertirse en un
signo abstracto extratextual —SEI—
que ahora sirve para clasificar ciertos
fragmentos de texto de un modo
particular. De qué modo lo hace es algo
que ahora quedará justificado y
explicado.
Todo y más es una obra de
divulgación científica. Aborda un
conjunto de logros matemáticos
extremadamente abstractos y técnicos,
aunque enormemente profundos e
interesantes, y también hermosos. El
objetivo es hablar de esos logros de tal
manera que resulten atractivos y
comprensibles para lectores que no
tengan preparación técnica de nivel
profesional ni sean expertos en la
materia. Hacer las matemáticas
bonitas, o por lo menos conseguir que
el lector entienda que alguien pueda
considerarlas así. Todo esto, por
supuesto, suena muy bien, pero hay una
pega: ¿cómo de técnica puede llegar a
ser la presentación sin que el lector se
pierda o sin enterrarle en un sinfín de
pequeñas definiciones y aclaraciones
aparte? Además, si se asume, como
parece plausible, que algunos lectores
tienen mucha más preparación técnica
que otros, ¿qué tono debe tener la
explicación para que sea accesible al
neófito sin ser aburrida o irritante para
alguien que ha practicado muchas
matemáticas en el instituto?
A partir de este punto, SEI en
negrita señala partes del material a las
que se puede echar un vistazo, leerlas
por encima u omitirlas por completo si
el lector lo desea. Es decir, se pueden
ignorar sin perderse nada importante.
Probablemente, más de la mitad de las
notas son SEI, así como varios párrafos,
e incluso un par de subsecciones del
texto principal. Algunos de los
fragmentos
opcionales
son
divagaciones
o
efemérides
históricas;[0.1] algunos son definiciones
o explicaciones en los que un lector
ducho en matemáticas no tendrá que
perder el tiempo. Pero la mayoría de
los fragmentos SEI están pensados para
lectores con gran preparación técnica, o
un interés poco usual en las verdaderas
matemáticas,
o
una
paciencia
sobrenatural, o las tres cosas; dichos
fragmentos proporcionan una mirada
más detallada a asuntos que la
explicación principal pasa por alto o
deja de lado.
Hay otras abreviaturas en el libro.
Algunas solo están para ahorrar
espacio. Otras son consecuencia de un
peculiar problema de estilo que se da
en la escritura técnica, que consiste es
que con frecuencia tenemos que
utilizar las mismas palabras una y otra
vez de un modo que se hace
terriblemente pesado —la cuestión es
que algunas palabras técnicas tienen
significados muy específicos que
ningún sinónimo puede captar—. Así,
especialmente en el caso de ciertos
términos de alta tecnología, la
abreviatura es el único modo de
conseguir un poco de variedad. En
realidad, nada de esto es un problema.
Todas las abreviaturas del libro están
contextualizadas de tal modo que
debería quedar totalmente claro qué
significan. Sin embargo, por si hubiera
errores del autor o confusiones
innecesarias, aquí presentamos una
lista de las principales abreviaturas que
puede consultar en caso de necesidad:
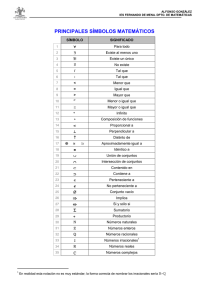
A. C. P. = Axioma del conjunto potencia
A. E.
= Axioma de elección
C1-1
= Correspondencia uno a uno
«C y n. = «Continuidad y números
i.»
irracionales» de Dedekind
CV
= Círculo vicioso
D. en
D.
= Demostración en diagonal
D. Η. P. = Divina Hermandad de Pitágoras
DNC
= Dos nuevas ciencias de Galileo
E. D.
= Ecuación diferencial
E. O.
= Ecuación de onda
G. E.
= GLOSARIO DE EMERGENCIA
H. C.
= Hipótesis del continuo
LTE
= Ley del tercero excluido
N. & L. = Newton y Leibniz
P. A. I. = Principio de abstracción
ilimitada
P. A. L. = Principio de abstracción
limitada
P. C.
= Producto cartesiano
P. C. G. = Problema de convergencia
S. F.
general de las series de Fourier
P. C. V. = Problema de la cuerda vibrante
P. del I. = Paradojas del infinito de
Bolzano
P. I.
= Principio de inducción
P. Z.
= Paradojas de Zenón
RIV
= Regresión infinita viciosa
R. N.
= Recta numérica
R. R.
= Recta real
T. A. C. = Teoría axiomática de conjuntos
TAC
= Teoría analítica del calor de
Fourier
T. B.
= Teorema del binomio
Τ. Β.
W.
= Teorema de BolzanoWeierstrass
Τ. Ε C. = Teorema fundamental del
cálculo
Τ. I. C. = Teoría informal de conjuntos
Τ. Ρ.
= Teorema de Pitágoras
T. U.
= Teorema de unicidad
Τ. V. Ε. = Teorema de los valores
extremos de Weierstrass
U. S.
Μ.
= Argumento Uno Sobre Muchos
de Platón
VNB
= Sistema de axiomas para la
teoría de conjuntos de Von
Neumann y Bernays
ZFS
= Sistema de axiomas para la
teoría de conjuntos de ZermeloFraenkel-Skolem
1
§1a.
Existe algo así como un historiador de
las matemáticas. Aquí está, a modo de
apertura, una cita de tal historiador en
la década de 1930:
Una conclusión parece ser
ineludible: sin una teoría
consistente
del
infinito
matemático no hay teoría de los
irracionales. Sin una teoría de
los irracionales no hay análisis
matemático de ninguna forma
remotamente parecida a lo que
tenemos ahora. Y finalmente,
sin el análisis, la mayor parte de
las matemáticas —incluyendo
la geometría y la mayor parte
de las matemáticas aplicadas—
tal como existe actualmente,
dejaría de existir. Por lo tanto,
la tarea más importante a la que
tienen que hacer frente los
matemáticos debería ser la
construcción de una teoría
satisfactoria del infinito. Cantor
lo intentó; con qué éxito es algo
que se verá después (Bell, págs.
521-522).
Los
excitantes
términos
matemáticos no importan por ahora. El
Cantor de la última línea es el profesor
Georg F. L. P. Cantor, nacido en 1845,
naturalizado alemán, perteneciente a
una familia de comerciantes y
reconocido padre de la teoría abstracta
de conjuntos y de las matemáticas
transfinitas. Algunos historiadores han
debatido en un tira y afloja la cuestión
de si era judío. Cantor en latín
significa «cantante».
Georg F. L. P. Cantor es el
matemático más importante del
siglo XIX y una figura de gran
complejidad y sufrimiento. Estuvo
entrando y saliendo de hospitales
mentales buena parte de su madurez
tardía y murió en un sanatorio en
Halle[1.1] en 1918. Curiosamente, Kurt
Gödel, el matemático más importante
del siglo XX, también murió como
resultado de una enfermedad mental.
Ludwig
Boltzmann,
el
físico
matemático más importante del
siglo XIX, se suicidó. Y así
sucesivamente. Los historiadores y los
estudiosos de la cultura pop tienden a
dedicar mucho tiempo a los problemas
psiquiátricos de Cantor y a si estaban
relacionados, y de qué modo, con su
trabajo sobre las matemáticas del ∞.
En el año 1900 se celebró en París
el 2.º Congreso Internacional de
Matemáticos. El profesor David
Hilbert, por aquel entonces el
matemático n.º 1 del mundo, describió
los números transfinitos de Georg
Cantor como «el mejor producto del
genio matemático» y «una de las más
bellas realizaciones de la actividad
humana en el dominio de lo puramente
inteligible» (Hilbert, «Über das
Unendliche» [«Sobre el infinito»], pág.
197).
He aquí una cita de Gilbert K.
Chesterton: «Los poetas no enloquecen,
pero los jugadores de ajedrez sí. Los
matemáticos se vuelven locos, y los
cajeros, pero los artistas creativos no
suelen hacerlo. No estoy atacando la
lógica: solo digo que este peligro yace
en la lógica, no en la imaginación»
(Chesterton, citado por Barrow, pág.
171). Y aquí está un fragmento del
texto de la solapa de una reciente
biografía divulgativa de Cantor: «A
finales del siglo XIX, un matemático
extraordinario languidecía en un
sanatorio […] Cuanto más se acercaba
a las respuestas que buscaba, más
lejanas parecían. A la larga, ello le
condujo a la locura, igual que a otros
matemáticos antes que a él» (Amir D.
Aczel, The Mystery of the Aleph:
Mathematics, the Kabbalah, and the
Search for Infinity, Four Walls Eight
Windows, 2000).
Los casos de grandes matemáticos
con enfermedades mentales tienen
enorme resonancia para los escritores y
cineastas de la época pop. Esto tiene
que ver principalmente con las ideas
preconcebidas y las sensibilidades de
esos mismos escritores/cineastas, y a
su vez dichas ideas están en función de
lo que se podría llamar el molde
arquetípico particular de nuestra época.
No hace falta decir que dichos moldes
cambian con el tiempo. Hoy, el
Matemático Mentalmente Enfermo
parece ser de algún modo lo que el
Caballero
Errante,
el
Santo
Mortificado, el Artista Atormentado y
el Científico Loco fueron en otras
épocas: algo así como nuestro
Prometeo, el que va a lugares
prohibidos y vuelve con regalos que
todos podemos aprovechar pero cuyo
precio solo paga él. Esto es
probablemente un poco exagerado, por
lo menos en la mayoría de los
casos.[1.2] Pero Cantor encaja en el
molde mejor que la mayoría. Y las
razones para ello son mucho más
interesantes que cualesquiera fueran
sus problemas y síntomas.[1.3]
Pero saber algo sobre los logros de
Cantor no es lo mismo que valorarlos,
lo cual constituye nuestro objetivo e
implica
ver
las
matemáticas
transfinitas como una especie de árbol,
con sus raíces en las paradojas de la
Antigua Grecia acerca de la
continuidad y la inconmensurabilidad,
y sus ramas enredadas en la crisis
moderna sobre los fundamentos de las
matemáticas: Brouwer y Hilbert y
Russell y Frege y Zermelo y Gödel y
Cohen y sus colegas. Los nombres
ahora mismo son menos importantes
que el árbol, siendo este una especie de
esquema
general
que
conviene
recordar.
§1b.
Pero
Chesterton se equivocaba
respecto a una cosa. O era por lo menos
impreciso. El peligro que intentaba
concretar no es la lógica. La lógica es
solo un método, y los métodos no
pueden desquiciar a las personas. De lo
que en realidad intenta hablar
Chesterton es de una de las principales
características de la lógica, y de las
matemáticas. Su cualidad de abstractas.
La abstracción.
Vale la pena esclarecer el
significado de abstracción. Puede que
sea el término más importante para
apreciar el trabajo de Cantor y el
contexto que lo hizo posible.
Gramáticamente, la raíz viene de un
adjetivo,
del
latín
abstractus
(«apartado»). El Oxford English
Dictionary contiene nueve definiciones
importantes del adjetivo, de las cuales
la más pertinente es la 4.a.: «Apartado
o separado de la materia, de la
corporeidad material, de la práctica, o
de los ejemplos particulares. Opuesto a
concreto». También resultan de interés
las definiciones 4.b., «Ideal, destilado
hasta su esencia», y 4.c., «Abstruso».
He aquí una cita de Carl B. Boyer,
que es más o menos el Gibbon de la
historia de las matemáticas:[1.4] «Pero
¿qué son, después de todo, los enteros?
Todo el mundo cree saber qué es el
número tres, hasta que intenta definirlo
o explicarlo» (Boyer, pág. 596). Por
ello, resulta instructivo hablar con los
profesores
de
matemáticas
de
preescolar e informarse acerca de cómo
se enseñan realmente los números
enteros a los niños. Cómo se les
enseña, por ejemplo, lo que es el
número cinco. Primero se les dan, por
ejemplo, cinco naranjas. Algo que
puedan tocar o sostener. Se les pide que
las cuenten. Luego se les da una foto de
cinco naranjas. Después, una foto que
combina las cinco naranjas con el
numeral «5», de modo que asocien
ambas cosas. Luego, una imagen con
solo el numeral «5» y sin las naranjas.
Entonces los niños comienzan con
ejercicios verbales en los que empiezan
a hablar sobre el entero 5 per se, como
un objeto en sí mismo, aparte de las
cinco naranjas. En otras palabras, son
sistemáticamente
engañados,
o
inducidos, para que traten a los
números como cosas en lugar de como
símbolos de las cosas. Entonces se les
puede enseñar aritmética, la cual
contiene relaciones elementales entre
números. (El lector notará el
paralelismo con el modo en que se nos
enseña a usar el lenguaje. Pronto
aprendemos que el nombre «cinco»
significa, simboliza, el entero 5, etc.).
A veces
un
chaval
tiene
dificultades, dicen los profesores.
Algunos niños entienden que la palabra
«cinco» significa 5, pero siguen
queriendo saber ¿5 qué? ¿5 naranjas?
¿5 céntimos? ¿5 puntos? Esos niños,
que no tienen ningún problema para
sumar o restar naranjas o monedas, a
pesar de todo tendrán malos resultados
en las pruebas de aritmética. No
pueden tratar el 5 como un objeto per
se. A menudo son enviados a grupos de
Educación Matemática Especial, donde
todo se enseña en términos de grupos o
conjuntos de objetos reales en lugar de
números «separados de ejemplos
particulares».[1.5]
La cuestión clave es que la
definición básica de «abstracto» para
nuestros propósitos va a ser algo
combinada: «apartado o más allá de la
particularidad
concreta,
de
la
experiencia sensorial». Usado solo de
este modo, «abstracto» es un término
de la metafísica. De hecho, en todas las
teorías matemáticas está implícito
algún tipo de postura metafísica. El
padre de la abstracción en las
matemáticas fue Pitágoras. El padre de
la abstracción en la metafísica, Platón.
Pero las otras definiciones del
Oxford English Dictionary no son
irrelevantes. No solo porque las
matemáticas modernas son abstractas
en el sentido de ser extremadamente
abstrusas. Para las matemáticas
también es esencial abstraer en el
sentido de reducir algo a su esencia
absoluta, a su esqueleto, como en el
resumen de un artículo o de un libro.[*]
Como tal, su significado puede ser
pensar profundamente en cosas en las
que la mayoría de la gente no puede
pensar profundamente, porque se pone
como loca.
Todo esto es solo una especie de
calentamiento. No será todo igual.
Aquí están dos citas más de figuras
prominentes. Morris Kline: «Una de las
grandes contribuciones griegas al
concepto mismo de matemáticas fue el
reconocimiento consciente y el énfasis
en el hecho de que las entidades
matemáticas son abstracciones, ideas
sostenidas por la mente y claramente
diferenciadas de los objetos físicos o
las imágenes» (Kline, pág. 29).
Ferdinand de Saussure: «Lo que se les
ha pasado por alto a los filósofos y a
los lógicos es que desde el momento en
que un sistema de símbolos se vuelve
independiente
de
los
objetos
designados, él mismo está sujeto a
sufrir cambios que son incalculables
para el lógico» (Saussure, pág. 23).
La abstracción lleva incluidos todo
tipo de problemas y quebraderos de
cabeza, eso lo sabemos todos. Parte del
riesgo es cómo usamos los nombres.
Pensamos en los significados de los
nombres en términos de denotaciones.
Los nombres sustituyen cosas: hombre,
mesa, pluma, David, cabeza, aspirina.
Se da un tipo especial de comicidad
cuando hay confusión respecto a lo que
es un nombre de verdad, como en
«¿Quién va primero?» o en aquellas
bromas de Alicia en el país de las
maravillas: «¿Qué puedes ver en el
camino?». «Nada». «¡Qué vista más
buena! ¿Qué aspecto tiene nada?». Pero
la comicidad tiende a desvanecerse
cuando
los
nombres
denotan
abstracciones, en el sentido de
conceptos generales divorciados de
ejemplos concretos. Muchas de estas
abstracciones-nombres tienen su raíz
en un verbo. «Movimiento» es un
nombre, y también «existencia».
Usamos
palabras
como
estas
continuamente. La confusión viene
cuando intentamos pensar en qué
significan exactamente. Es como la
observación de Boyer acerca de los
enteros. ¿Qué denotan exactamente
«movimiento»
y
«existencia»?
Sabemos que existen cosas concretas y
particulares, y que a veces se mueven.
¿Existe el movimiento per se? ¿De qué
manera? ¿De qué manera existen las
abstracciones?
Por supuesto, esta última cuestión
es en sí misma muy abstracta. Ahora
probablemente usted comienza a sentir
dolor de cabeza. Hay una especie de
incomodidad o impaciencia ante este
tipo de cosas. Surgen preguntas como:
«¿Qué es exactamente la existencia?» o
«¿Qué queremos decir exactamente
cuando hablamos del movimiento?».
La incomodidad es muy distintiva y
aparece solo en cierto nivel del proceso
de abstracción, porque la abstracción
funciona por niveles, igual que los
exponentes
o
las
dimensiones.
Digamos que «hombre» refiriéndose a
un hombre en particular es el Nivel
Uno. «Hombre» refiriéndose a la
especie es el Nivel Dos. Algo así como
«humanidad» es el Nivel Tres: ahora
estamos hablando de los criterios
abstractos para que algo pueda ser
calificado de humano. Y así
sucesivamente. Pero pensar de ese
modo puede ser peligroso, extraño.
Pensar con suficiente abstracción sobre
cualquier cosa… Seguramente todos
hemos tenido la experiencia de pensar
en una palabra, por ejemplo, «pluma»,
y en algo así como repetirla para
nuestros adentros una y otra vez, hasta
que deja de significar nada. La misma
extrañeza de llamar «pluma» a algo
empieza a meterse en la conciencia de
un modo inquietante, como los
síntomas de un inminente ataque
epiléptico.
Como probablemente sabe el lector,
buena parte de lo que ahora llamamos
filosofía analítica está relacionado con
cuestiones como estas, del Nivel Tres o
incluso del Cuatro. Como en la
epistemología = «¿Qué es exactamente
el conocimiento?»; la metafísica =
«¿Cuáles
son
exactamente
las
relaciones entre los constructos
mentales y los objetos del mundo
real?», etc.[1.6] Podría ser que los
filósofos y los matemáticos, que pasan
mucho tiempo pensando (a) en
abstracto (b) sobre abstracciones o (c)
ambas cosas, tengan eo ipso propensión
a las enfermedades mentales. O podría
ser simplemente que las personas
susceptibles
de
padecer
una
enfermedad mental tengan mayor
propensión a pensar en este tipo de
cosas. Es como la cuestión del huevo y
la gallina. Pero algo es seguro. Es un
mito total que el hombre sea curioso
por naturaleza y que esté ávido de la
verdad, y que desee, por encima de
todo, conocer.[1.7] Admitiendo ciertos
significados de «conocer», hay en
realidad una gran cantidad de cosas que
no queremos conocer. Evidencia de
ello son los abundantes asuntos y
problemas acerca de los cuales no nos
gusta pensar en abstracto.
Veamos un poco de teoría. Los
temores y peligros del pensamiento
abstracto constituyen grandes motivos
para que ahora a todos nos guste estar
todo el día muy ocupados y
bombardeados por estímulos. El
pensamiento abstracto tiende más bien
a asaltarnos en momentos de tranquilo
reposo. Por ejemplo, a primera hora de
la mañana, especialmente si usted se
despierta antes de que suene el
despertador, de repente y sin ningún
motivo puede comenzar a pensar que
ha estado levantándose de la cama cada
mañana sin la más mínima duda de que
el suelo le sostendría. Mientras yace
ahí considerando el asunto, parece por
lo menos teóricamente posible que
algún defecto en la construcción del
suelo o en su integridad molecular
podría hacer que este se combara, o
incluso que usted lo atravesara
limpiamente por algún aberrante
fenómeno cuántico o algo parecido. En
cierto sentido, no es algo que parezca
una imposibilidad lógica o algo así. No
es que usted tenga realmente miedo de
que el suelo se venga abajo justo en el
momento en que se levante. Es solo
que ciertos estados mentales y líneas
de pensamiento son más abstractos, y
no están centrados en ninguna
necesidad u obligación que vaya usted
a atender cuando se levante. Esto es
solo un ejemplo. La cuestión abstracta
que está usted considerando desde la
cama es si su confianza en el suelo está
verdaderamente
justificada.
La
respuesta inicial, que es afirmativa, se
basa en el hecho de que usted se ha
levantado por la mañana miles, en
realidad bastante más de diez mil veces
hasta ahora, y el suelo le ha sostenido
cada vez. Es la misma manera de
justificar que saldrá el sol, que su
esposa recordará cómo se llama usted,
que cuando tiene ciertas sensaciones
eso significa que está a punto de
estornudar, etc. Porque han sucedido
una y otra vez anteriormente. El
principio involucrado es realmente el
único modo de predecir cualquiera de
los fenómenos con los que contamos
automáticamente sin tener que pensar
en ellos. Y la inmensa mayoría de los
hechos cotidianos son fenómenos de
este tipo, y sin esta confianza basada en
experiencias
anteriores
nos
volveríamos todos locos, o por lo
menos seríamos incapaces de hacer
nada porque tendríamos que detenernos
y deliberar acerca de la más mínima
cosa. Es un hecho: la vida tal como la
conocemos sería imposible sin esta
confianza. Pero aun así, esta confianza
¿está verdaderamente justificada o es
solo extremadamente conveniente?
Esto es pensar en abstracto, con su
característico perfil escalonado, y
ahora usted se encuentra varios
escalones hacia arriba. Ya no está
pensando solo en el suelo y en su peso,
ni en su confianza ni en cuán necesaria
parece ser ese tipo de confianza para la
supervivencia básica. Ahora está usted
pensando en una regla, ley o principio
mucho más general por el que esta
confianza rutinaria, con toda su
miríada de formas e intensidades, está
de hecho justificada en lugar de ser
solo una serie de extraños reflejos
clónicos que le impulsan a lo largo del
día. Otra señal clara de que se trata de
pensamiento abstracto: usted todavía
está quieto. Parece que está gastando
una tremenda energía y aún no se ha
movido. Todo está ocurriendo en su
mente. Es extremadamente raro. No es
nada sorprendente que a la mayoría de
la gente no le guste. De repente tiene
sentido que a menudo se represente a
los locos poniéndose las manos en la
cabeza o golpeándola contra algo. Pero
si recibió buenas lecciones en la
escuela, puede que ahora recuerde que
la regla o principio que usted intuye ya
existe: su nombre oficial es principio
de inducción (P. I.). Es el precepto
fundamental de la ciencia moderna. Sin
el principio de inducción, los
experimentos no podrían confirmar las
hipótesis, y nada en el universo físico
podría predecirse con un mínimo de
confianza. No podría haber leyes
naturales o verdades científicas. El P. I.
afirma que si algo, x, ha sucedido en
ciertas circunstancias particulares n
veces en el pasado, tenemos
justificación para creer que las mismas
circunstancias darán lugar a x en la
ocasión n + 1. El P. I. es totalmente
respetable y fidedigno, y parece una
salida inteligente para librarse del
problema. Es decir, hasta que le asalte
(como solo puede suceder en estados
mentales muy abstractos o cuando falta
más de la cuenta para que suene el
despertador) la idea de que el propio
P. I. no es más que una abstracción a
partir de la experiencia… Así que,
ahora ¿qué justifica exactamente
nuestra confianza en el P. I.? Este
último pensamiento puede estar o no
acompañado de cierto recuerdo de la
infancia, por ejemplo, de varias
semanas pasadas en la granja de un
pariente (es una larga historia).
Veamos, en un corral con alambrada, al
lado del garaje, había cuatro pollos, el
más listo de los cuales se llamaba
señor Pollo. Cada mañana, cuando el
empleado de la granja llegaba al corral
con cierto saco de arpillera, el señor
Pollo se excitaba y empezaba a dar
picotazos anticipados en el suelo,
porque sabía que era la hora de comer.
Era cada mañana a la misma hora h, y
el señor Pollo se había dado cuenta de
que h(empleado + saco) = comida, y
así estaba confiadamente dando sus
picotazos por adelantado aquella
última mañana de domingo cuando el
empleado de repente extendió el brazo,
cogió al señor Pollo estrujándole el
cuello, lo metió en el saco de arpillera
y se lo llevó a la cocina. Recuerdos
como este tienden a mantenerse
bastante vivos, si se tienen. Pero la idea
que sale de aquí es que de acuerdo con
el principio de inducción parece que el
señor Pollo estuviera en lo cierto, al no
esperar otra cosa que la comida tras la
aparición (n + 1) del empleado + el
saco a la hora h. Pero el hecho de que
el señor Pollo no solo no sospechara
nada sino que su falta de desconfianza
parece completamente justificada,
resulta sin duda inquietante. Hallar
alguna justificación a un nivel más alto
para nuestra confianza en el P. I. parece
mucho más urgente cuando nos damos
cuenta de que, sin dicha justificación,
nuestra
propia
situación
es
indistinguible de la del señor Pollo.
Pero la conclusión, por abstracta que
sea, parece ineludible: lo que justifica
nuestra confianza en el principio de
inducción es que haya funcionado tan
bien en el pasado, por lo menos hasta
ahora. Eso significa que nuestra única
verdadera
justificación
para
el
principio de inducción es el principio
de inducción, lo cual parece poco firme
y cuestionable en extremo.
Tras esta última conclusión, la
única alternativa a la posibilidad de
quedarse paralizado en la cama de por
vida es hacer más indagaciones
abstractas acerca de lo que significa
exactamente
«justificación»
y
averiguar si es verdad que las únicas
justificaciones válidas para ciertas
creencias y principios son racionales y
no circulares. Por ejemplo, sabemos
que en cierto número de casos cada año
hay coches que de repente invaden el
carril contrario y chocan frontalmente,
matando a personas que conducían sin
esperar un accidente. Y así también
sabemos, en cierta medida, que sea
cual sea la confianza que nos permite
conducir en carreteras de doble sentido,
esta confianza no está en un 100%
justificada racionalmente por las leyes
de la probabilidad y la estadística. Y
aun así, «justificación racional» podría
no ser aplicable en este caso. Podría
tratarse más bien de que si usted no
pudiera creer que su coche no va a
chocar de repente, simplemente no
sería capaz de conducir, y así su
necesidad o deseo de conducir funciona
como una especie de «justificación» de
su confianza.[1.8] Entonces sería mejor
no empezar a analizar las diversas
«justificaciones» aparentes para su
necesidad o deseo de conducir un
coche: en algún punto usted se da
cuenta de que el proceso de
justificación abstracta puede, por lo
menos en principio, seguir para
siempre. La capacidad para detener una
línea de pensamiento abstracto tan
pronto como se ve que no termina
nunca es parte de lo que habitualmente
distingue a las personas sanas y
funcionales, las que cuando finalmente
suena el despertador pueden pisar el
suelo sin inquietudes y entrar en los
asuntos concretos del mundo real, de
las personas desquiciadas.
INTERPOLACIÓN
La razón táctica para usar a veces el
símbolo ∞ en lugar de «infinito» en
este libro es que la parpadeante
extrañeza
de
∞
sirve
como
recordatorio de que no está nada claro
de qué hablamos siquiera. Todavía no.
Por ejemplo, evite pensar que ∞ es
solo un número increíblemente,
inverosímilmente
enorme.
Por
supuesto, hay muchos números como
esos, especialmente en la física y la
astronomía, por ejemplo, si en la física
un ultranano-instante de 5 × 10−44
segundos se admite generalmente como
el intervalo de tiempo más pequeño al
que se puede aplicar el concepto
normal de tiempo continuo (que lo es),
los datos astronómicos indican que ha
habido aproximadamente 6 × 1060
ultranano-instantes de esos desde el
Big Bang. O sea, un 6 seguido de 60
ceros. Todos hemos oído hablar de
tales números, y habitualmente
imaginamos que solo se pueden tratar y
manipular mediante ordenadores muy
avanzados y super-refrigerados o algo
así. La verdad es que hay muchos
números demasiado grandes para que
los procese un ordenador real o incluso
teórico. El límite de Bremermann es el
término relevante en este caso. Dados
los límites impuestos por la teoría
cuántica básica, un tal Hans-Joachim
Bremermann demostró en 1962 que
«Ningún sistema de procesamiento de
datos, artificial o viviente, puede
procesar más de 2 × 1047 bits por
segundo por cada gramo de su masa»
(Klir y Yuan, págs. 2-3), lo que
significa que un superordenador
hipotético del tamaño de la tierra
(= 6 × 1027 gramos aproximadamente)
funcionando durante tanto tiempo
como la tierra ha existido (= 1010 años
aproximadamente, con cerca de
3,14 × 107 segundos/año) puede haber
procesado a lo sumo 2,56 × 1092 bits,
número que se conoce como límite de
Bremermann. Los cálculos que
involucran números mayores que
2,56 × 1092 se llaman problemas
transcomputacionales, en el sentido de
que no son teóricamente viables
siquiera. Y hay abundantes problemas
de este tipo en la física estadística, la
teoría de la complejidad, la teoría de
fractales, etc. Todo esto resulta
excitante pero no muy pertinente. Lo
pertinente es esto: considere algún
número transcomputacional, imagínese
que es un grano de arena, piense en una
playa entera, o en un desierto, o en un
planeta, o incluso en una galaxia llena
de esa arena, y no solo un 1 seguido de
ese número de ceros será < ∞, sino
que su cuadrado será < ∞, y si
10x
llamamos x al número, 10x será < ∞,
y así sucesivamente. Y en realidad ni
siquiera es correcto comparar 10x e ∞
aritméticamente de ese modo porque ni
siquiera están en la misma área de
codificación matemática ni incluso, de
algún modo, en la misma dimensión.
Y, sin embargo, también es verdad que
algunos ∞ son mayores que otros,
como
en
las
comparaciones
aritméticas. Hablaremos de todo esto.
Por ahora la cuestión es que solo
después de Richard Dedekind y George
Cantor ha sido posible hablar de
cantidades infinitas y su aritmética de
un modo coherente y significativo. De
ahí el uso del símbolo ∞.
SEI
El propio símbolo ∞ tiene el nombre
técnico lemniscata (al parecer viene de
«cinta» en griego) y fue introducido en
las matemáticas por John Wallis en su
obra de 1655 Arithmetica Infinitorum,
que fue uno de los antecedentes
importantes del cálculo de Newton.[1.9]
Thomas Hobbes, contemporáneo de
Wallis y algo así como un matemático
excéntrico, se quejó en una reseña de
que la Arithmetica Infinitorum tenía un
grado de abstracción demasiado
exagerado como para intentar leerla,
definiéndola como «una costra de
símbolos», hablando así en nombre de
futuras generaciones de estudiantes.
Entre otras denominaciones de la
lemniscata están «el nudo del amor» y
«la curva del plano cartesiano que
satisface la ecuación (x2 + y2)2 =
a2(x2 − y2)». Por otro lado, si se trata
trigonométricamente, se define como
«la curva que satisface la ecuación en
coordenadas polares r2 = a cos 2θ», y
se conoce también como lemniscata de
Bernoulli.
FIN DE LA INTERPOLACIÓN
§1c.
Respecto
a todo el asunto de la
abstracción y los significados de los
términos, hay un síndrome que es o
bien una abstracción de alto nivel o
algún tipo de extraña mutación
nominal. «Caballo» puede significar
este caballo de aquí, o puede significar
el concepto abstracto, como al decir
«Caballo: mamífero con pezuñas de la
familia Equidae». Lo mismo ocurre
con la palabra «cuerno», y con
«frente». Todos los términos pueden
abstraerse de entes particulares, pero
aun así sabemos que provienen de
ellos. Pero ¿qué pasa con un unicornio,
el cual parece resultar de la
combinación
de
los
conceptos
«caballo», «cuerno» y «frente», de
forma que se origina completamente
por la concatenación de abstracciones?
O sea, podemos juntar y manipular
abstracciones para formar entes con un
nombre que no denota nada en
absoluto. Aquí el gran problema resulta
ser: ¿cómo podemos decir que un
unicornio existe, y que sea de una
manera fundamentalmente diferente,
menos real, de la manera en que
existen abstracciones como humanidad,
cuerno o número entero? O dicho de
otra forma: ¿de qué modo existen las
entidades abstractas?, ¿existen solo
como ideas en la mente humana, es
decir, son ficciones metafísicas? Este
tipo de cuestión también puede
mantenerle todo el día en la cama. Y
pende sobre las matemáticas desde el
principio: ¿cuál es el estatus ontológico
de las entidades y relaciones
matemáticas?
Las
realidades
matemáticas, ¿son descubiertas o
meramente creadas, o de algún modo
ambas cosas? He aquí de nuevo a
Morris
Kline:
«Las
doctrinas
filosóficas de los griegos limitaron las
matemáticas de otro modo. Durante el
período clásico creían que el hombre
no crea los hechos matemáticos: estos
son preexistentes. El hombre se limita
a establecerlos y registrarlos» (Kline,
pág. 175).
Y aquí está otra cita de David
Hilbert, el gran primer defensor de los
transfinitos de Cantor:
El infinito no se halla en
ninguna parte de la realidad, sin
importar qué experiencias,
observaciones o conocimientos
se
invoquen.
¿Puede
el
pensamiento acerca de las cosas
ser tan diferente de las cosas?
¿Pueden los procesos de
pensamiento ser tan distintos
del proceso real de las cosas?
En definitiva, ¿puede el
pensamiento estar tan apartado
de la realidad? (Hilbert, pág.
191).
Y es verdad, no hay nada más
abstracto que el infinito. Por lo menos
en el sentido de nuestro concepto de ∞
difuso, intuitivo y expresado en
«lenguaje natural». Es algo así como el
más definitivo alejamiento de la
experiencia real. Considérese la
característica única más ubicua y
opresiva del mundo de lo concreto, es
decir, que todo llega a un fin, es
limitado, termina, y luego concíbase,
en abstracto, algo sin esa característica.
Son obvias las analogías con ciertas
ideas de Dios. La abstracción de todas
las limitaciones es una manera de
explicar el impulso religioso en
términos laicos, lo cual también se
conoce como antropología de la
religión. Un ser perfecto puede
entenderse como uno desprovisto de
todas
las
imperfecciones
que
percibimos en nosotros mismos y en el
mundo, uno omnipotente, es decir sin
limitaciones a su voluntad, etc. El
hecho de que sea una manera bastante
seca y triste de hablar de la religión no
tiene importancia. La cuestión es que
exactamente el mismo tipo de
explicación puede darse acerca de
cómo llegamos al concepto de ∞ y qué
queremos decir en definitiva con todas
las formas de la palabra «infinito» que
barajamos. Pero si se trata realmente
de la explicación correcta es algo
relacionado con los compromisos que
adquirimos. En un sentido metafísico.
¿Queremos decir realmente que el ∞
existe solo del modo en que existen los
unicornios, que todo es cuestión de
manipular abstracciones hasta que la
palabra «infinito» no tenga ningún
referente real? ¿Qué hay del conjunto
de todos los números enteros? Empiece
a contar 1, 2, 3, y así sucesivamente, y
dese cuenta de que nunca se detendrá,
ni sus hijos cuando usted muera, ni los
hijos de sus hijos, etc. Los enteros
nunca se detienen. No hay fin. El
conjunto de todos los enteros,
¿constituye un ∞ real? ¿O los enteros
mismos no son reales sino solo
abstracciones? Además, ¿qué es
exactamente un conjunto?, y ¿los
conjuntos
son
reales
o
solo
instrumentos conceptuales, etc.? O
¿son quizá los enteros y/o los conjuntos
solo «matemáticamente reales» y no
«realmente reales»?, y ¿cuál es
exactamente
la
diferencia?,
y
¿podríamos desear conceder al ∞
cierta realidad matemática pero no del
otro tipo (suponiendo que no haya
todavía más tipos)? Y ¿en qué punto
las cuestiones se vuelven tan abstractas
y las distinciones tan sutiles y el dolor
de cabeza tan terrible que simplemente
ya no podemos pensar más en nada de
ello?
Es en áreas como las matemáticas y
la metafísica donde encontramos una
de las cualidades más extrañas de la
mente humana media. Es la habilidad
de concebir cosas que, estrictamente
hablando, no podemos concebir.
Podemos concebir de un modo
aproximado qué es la omnipotencia,
por ejemplo. Por lo menos podemos
usar la palabra «omnipotencia» con
bastante seguridad de saber de qué
estamos hablando. Y, aun así, incluso
la antinomia de un escolar como
«¿Puede un ser omnipotente crear algo
tan pesado que ni él mismo podría
levantarlo?» pone de relieve serios
fallos
en
nuestra
comprensión
cotidiana de la omnipotencia. Así que
hay más de un tipo de abstracción que
resulta relevante aquí. Este tipo es más
psicológico, y muy moderno.
Un dato evidente: nunca antes ha
habido tantos abismos entre lo que el
mundo parece ser y lo que la ciencia
nos dice que es. Para nosotros, la gente
de la calle, es como si un millón de
revoluciones copernicanas tuvieran
lugar al mismo tiempo. Es decir, por
ejemplo, sabemos, como alumnos de
instituto y lectores de Newsweek que
somos, que el tiempo es relativo, que
las partículas cuánticas pueden estar
ahí y a la vez no estarlo, que el espacio
es curvo, que los colores no son
inherentes a los objetos mismos, que
las singularidades astronómicas tienen
densidad infinita, que nuestro amor por
nuestros hijos está preprogramado por
la evolución, que hay un punto ciego en
el centro de nuestra visión que nuestro
cerebro
rellena
automáticamente.
Sabemos también que nuestros
pensamientos y sentimientos en
realidad solo son transferencias
químicas en 1,5 kg
de
masa
electrificada. Que estamos hechos en
nuestra mayor parte de agua, que el
agua es fundamentalmente hidrógeno,
y el hidrógeno es inflamable, y, sin
embargo,
nosotros
no
somos
inflamables. «Sabemos» una casi
infinidad de verdades que contradicen
nuestra experiencia inmediata y de
sentido común acerca del mundo. Y
aun así tenemos que vivir y funcionar
en el mundo. Así que abstraemos,
compartimentamos: hay cosas que
sabemos, y cosas que «sabemos». «Sé»
que mi amor por mi hijo está en
función de la selección natural, pero sé
que le quiero, y siento y actúo según lo
que sé. Vista objetivamente, toda esta
cuestión es bastante esquizoide, pero el
hecho importante es que, como gente
subjetiva de la calle, raramente
notamos
el
conflicto.
Porque,
naturalmente, nuestra vida es en un
99,99% concretamente operativa, y
operamos en concreto según lo que
sabemos, no según lo que «sabemos».
De nuevo, hablamos de gente de la
calle como usted y yo, no de los
gigantes de la filosofía y las
matemáticas, muchos de los cuales
tuvieron famosas dificultades para
navegar por el mundo real. Einstein
saliendo de su casa en pijama, Gödel
incapaz de alimentarse, etc. Para
valorar cómo es la vida interior de los
grandes
científicos/matemáticos/metafísicos,
solo necesitamos tumbarnos e intentar
formarnos una idea verdaderamente
rigurosa y coherente, en contraste con
una idea difusa como las que se
exponen en Newsweek, acerca de qué
significa en realidad «omnipotente»,
«número entero» o «ilimitable», o
«finito pero ilimitado». Intentar llevar
a cabo un poco de pensamiento
abstracto disciplinado o dirigido.[1.10]
Hay una tensión, como la de una fuga
musical,
muy
definida
pero
inarticulable involucrada en este tipo
de pensamiento, una sensación de la
que aquella repetición epiléptica de
«pluma, pluma» una y otra vez es solo
un pálido reflejo. Uno de los caminos
más rápidos hacia esa sensación (por
experiencia personal madrugadora) es
intentar pensar profundamente en la
dimensión. Hay algo que «sé», y es que
las dimensiones espaciales más allá del
Gran 3 existen. Incluso puedo construir
un teseracto o hipercubo con cartón. Un
teseracto, un extraño tipo de cubo
dentro de un cubo es una proyección
3D de un objeto 4D, del mismo modo
en que « » es una proyección 2D de
un objeto 3D. El truco es imaginar que
las líneas y planos relevantes del
teseracto forman ángulos de 90o (es lo
mismo con « » y un cubo real),
porque la 4.ª dimensión espacial es una
que
de
algún
modo
existe
perpendicularmente a la longitud,
anchura y profundidad de nuestro
campo visual normal. Yo «sé» todo
esto, como probablemente lo «sabe»
usted…, pero ahora intente imaginarlo
realmente. Concretamente. Casi de
forma inmediata, puede sentir una
tensión en la raíz misma de su yo, las
primeras hebras deshilachadas de una
mente cuyas costuras empiezan a
ceder.
Con respecto a «saber» en contraste
con saber de un modo concreto y
material, el segundo tipo es lo que
Descartes quería decir con «una clara y
distinta aprehensión» y lo que en
lenguaje moderno se llama «entender»
o «captar». Es de nuevo el estado
epistoesquizoide de la mente moderna
media: sentimos que «sabemos» cosas
que el aparato conceptual de nuestra
mente en realidad no puede captar. A
menudo son objetos y conceptos en los
más lejanos límites de la abstracción,
cosas que literalmente no podemos
imaginar: espacios con D > 3,
coreografía
cuántica,
conjuntos
fractales, materia oscura, raíces
cuadradas de números negativos,
botellas de Klein y cajas de Freemish y
escalinatas de Penrose. E ∞. A
menudo, este tipo de cosas se
caracterizan como dotadas de una
existencia únicamente «intelectual» o
«matemática». De nuevo, están muy
lejos de tener un significado claro,
aunque usar estos términos constituye
un juego de niños.
Obsérvese, por favor, que esta
habilidad común de dividir nuestra
atención y «saber» cosas que no
podemos captar es un rasgo distintivo
moderno. Los antiguos griegos, por
ejemplo, no podían hacerlo. O no
querían. Necesitaban las cosas claras, y
creían que no se puede saber algo a
menos que se entienda realmente.[1.11]
No es un accidente que sus
matemáticas no incluyeran ni el 0 ni el
∞. Su palabra para infinito también
significaba «lío».
El espíritu griego ha dado forma a
la filosofía y a la práctica de las
matemáticas desde el principio. Las
verdades matemáticas se establecen
mediante demostraciones lógicas y son
extremadamente claras y nítidas. Es
precisamente esto lo que exime a las
matemáticas de problemas laberínticos
al estilo de cómo justificar con
exactitud el principio de inducción: las
relaciones
y
demostraciones
matemáticas no son inductivas sino
deductivas, formales. Las matemáticas,
en otras palabras, son un sistema
formal, donde «formal» significa
forma pura, 100% abstracta. La idea
central
es
que
las
verdades
matemáticas son ciertas y universales
precisamente porque no tienen nada
que ver con el mundo. Si esto resulta
algo opaco, he aquí un pasaje de
Godfrey H. Hardy en su Apología de un
matemático, la obra inglesa en prosa
más lúcida jamás escrita sobre
matemáticas:
«La
certidumbre
de
las
matemáticas —dice [Alfred N.]
Whitehead— depende de su
completa
generalidad
abstracta». Cuando afirmamos
que 2 + 3 = 5, afirmamos una
relación entre tres grupos de
«cosas», y esas cosas no son
manzanas ni peniques, o cosas
de uno u otro tipo en particular,
sino solamente cosas, «cosas
cualesquiera». El significado de
la afirmación es completamente
independiente
de
las
individualidades
de
los
miembros de los grupos. Todos
los «objetos» matemáticos o
«entidades» o «relaciones»,
como «2», «3», «5», «+» o «=»,
y todas las proposiciones
matemáticas en las que
aparecen, son completamente
generales en el sentido de ser
completamente
abstractas.
Realmente una de las palabras
de Whitehead es superflua,
porque la generalidad, en este
sentido, es abstracción (Hardy,
Apology, pág. 106).
Observe el lector que en esta cita
«generalidad» se refiere no solo a la
abstracción de términos y referentes
individuales, sino a la universalidad
completamente abstracta de las
verdades afirmadas. Esta es la
diferencia entre una mera curiosidad
matemática y un teorema matemático.
Un famoso ejemplo de esa diferencia
(famoso para los alumnos del doctor
Goris, en cualquier caso) es que (1)
«La suma de la serie (1 + 3 + 5 + 7 +
9) = 52» es una curiosidad, mientras
que (2) «Para cualquier x, la suma de
los primeros x enteros impares = x2» es
un teorema, es decir, matemáticas de
verdad.
Lo que viene a continuación está
pensado
principalmente
como
recordatorio de cosas que usted ya
conoce por encima o vio en la escuela.
Si su familiaridad con los sistemas
formales es menos superficial,
reconocerá los siguientes tres párrafos
como extremadamente burdos y
simplistas y está invitado a tratarlos
como SEI y omitirlos o echarles una
ojeada. Un sistema formal de
demostración requiere axiomas y
reglas de inferencia. Los axiomas son
proposiciones básicas tan obvias que
pueden afirmarse sin demostración.
Recuerde, por ejemplo, los axiomas de
Euclides o los postulados de Peano. Las
reglas de inferencia, a veces llamadas
leyes del pensamiento, son los
principios lógicos que justifican la
obtención de verdades a partir de otras
verdades.[1.12] Algunas de las reglas de
inferencia son tan simples como la ley
de identidad, la cual básicamente
sostiene que si algo es P, entonces es P.
Otras son más elaboradas. Para
nuestros propósitos son especialmente
importantes dos reglas de inferencia.
La primera es conocida como ley del
tercero excluido (LTE). Por la LTE,
una proposición matemática tiene que
ser o bien verdadera o bien, si no lo es,
falsa.[1.13] La otra gran regla de
inferencia involucra la relación lógica
de implicación, con el significado
«Si… entonces» y se representa a
menudo con el símbolo «→». La regla
de implicación más obvia es que
(1) «P → Q» y (2) «P es verdadera»
permiten obtener la conclusión «Q es
verdadera». La que vamos a usar con
frecuencia es la complementaria de
esta regla, llamada habitualmente
modus tollens. Puede sostenerse que
(1) «P → Q» y (2) «Q es falsa»
permiten afirmar que (3) «P es
falsa».[1.14]
Una razón por la que la LTE y el
modus tollens son importantes para las
matemáticas es que hacen posible el
método de demostración indirecta,
también conocido como demostración
por reductio ad absurdum o a veces
solo reductio. He aquí cómo funciona.
Supongamos que quiere demostrar P.
Lo que hace es suponer lo contrario,
no-P, y entonces demostrar que no-P
implica lógicamente una contradicción
como, por ejemplo, «Q y no-Q». (Por la
LTE, nada puede ser verdadero y falso
a la vez, de modo que la conjunción
«Q y no-Q» será siempre falsa). Por el
modus tollens, si (1) no-P →
(Q y no-Q) y (2) (Q y no-Q) es falsa,
entonces (3) no-P es falsa. Y, por la
LTE,[1.15] si no-P es falsa, entonces P
tiene que ser verdadera.
Muchas de las demostraciones más
importantes y conocidas de la historia
de las matemáticas han sido de este
tipo. Aquí está un ejemplo. Es la
demostración de Euclides de la
Proposición 20 en el Libro IX de los
Elementos. La Proposición 20 trata de
los números primos, es decir —como
probablemente recuerda de la escuela
—, de los números enteros que no
pueden dividirse por enteros más
pequeños sin que quede resto. La
Proposición 20 afirma básicamente que
no existe un último número primo. (Lo
que esto significa, por supuesto, es que
la cantidad de números primos es en
realidad infinita, pero Euclides le da
vueltas a la cuestión, y con toda
seguridad nunca dice «infinito»). Aquí
está la demostración. Supóngase que de
hecho existe el último número primo.
Llamémosle Pn. Esto significa que la
secuencia de números primos (2, 3, 5,
7, 11, …, Pn) es exhaustiva y finita: (2,
3, 5, 7, 11, …, Pn) son todos los primos
que existen.[1.16] Ahora considérese el
número R, que definimos como el
número que se obtiene multiplicando
todos los primos hasta Pn y sumando 1
al resultado. R es obviamente mayor
que Pn. Pero ¿es R primo? Si lo es,
tenemos una contradicción inmediata,
porque ya habíamos supuesto que Pn
era el mayor número primo posible.
Pero si R no es primo, ¿por qué número
se puede dividir? Obviamente no se
puede dividir por ninguno de los
números primos de la secuencia (2, 3,
5,…, Pn), porque dividir R por
cualquiera de ellos daría resto 1. Pero
dicha secuencia contiene todos los
números primos que existen, y estos
son en definitiva los únicos números
por los que se puede dividir un número
que no sea primo. Así que si R no es
primo, y si ninguno de los primos (2, 3,
5,…, Pn) puede ser divisor suyo, tiene
que haber algún otro primo por el que
R se pueda dividir. Pero esto contradice
la suposición de que (2, 3, 5, …, Pn) es
una lista exhaustiva de todos los
números primos. De uno u otro modo,
tenemos una contradicción clara. Y
como la suposición de que hay un
último número primo implica una
contradicción, el modus tollens dicta
que la suposición es necesariamente
falsa, lo cual por la LTE[1.17] significa
que la negación de la suposición es
necesariamente verdadera, es decir, que
ningún número primo es el último. Q.
E. D.
Observe, por favor, que la
primalidad no tiene nada que ver con el
mundo. Concierne solo a relaciones
entre números. Los griegos fueron los
verdaderos inventores de lo que
llamamos matemáticas, porque —en
eso también— fueron los primeros en
tratar los números y sus relaciones
como abstracciones más que como
propiedades de colecciones de objetos
reales. Es importante ver hasta qué
punto esto fue un salto. Ya desde
registros muy antiguos, es fácil ver que
las matemáticas tuvieron su matriz en
lo concreto. En lo inmediatamente
concreto. Considérense hechos como
que las cifras también se llaman
«dígitos» y que la mayoría de los
sistemas de numeración —no solo el
nuestro en base 10 sino también los de
base 5 y base 20 de la Europa
prehistórica—
están
claramente
pensados a partir de los dedos de la
mano y los dedos de los pies. O que
aún hablamos de «cuerdas» de círculos
o de «caras» de poliedros, o que
«cálculo» proviene de la palabra griega
que significa «piedrecita», etc. Es bien
conocido que hubo civilizaciones
anteriores a la griega, como los
babilonios y los egipcios, con un grado
considerable
de
sofisticación
matemática, pero las suyas eran unas
matemáticas
extremadamente
prácticas, usadas para la agrimensura,
el comercio y las finanzas, la
navegación, etc. Los babilonios y los
egipcios, en otras palabras, estaban
más interesados en las cinco naranjas
que en el 5. Fueron los griegos los que
convirtieron las matemáticas en un
sistema
abstracto,
un
lenguaje
simbólico especial que permite a las
personas no solo describir el mundo,
sino explicar sus más profundas leyes y
pautas. Se lo debemos todo.[1.18] Hasta
el punto de que los logros de
Weierstrass, Cantor y Dedekind en la
teoría de conjuntos y la teoría de
números modernas son imposibles de
valorar sin entender el salto
hiperdimensional
entre
las
matemáticas como una abstracción
práctica de propiedades del mundo real
y las matemáticas, como diría
Ferdinand de Saussure, como un
«sistema
de
símbolos
[…]
independiente
de
los
objetos
designados». Ni tampoco se pueden
valorar verdaderamente sin considerar
también los consiguientes «cambios
incalculables…»,
porque
las
matemáticas abstractas que han
desterrado la superstición y la
ignorancia y la sinrazón y han dado a
luz al mundo moderno son también las
matemáticas abstractas atravesadas por
la sinrazón y la paradoja y el enigma, y
que han estado intentando, en cierto
modo, atarse los zapatos sobre la
marcha desde el momento mismo en
que adquirieron el estatus de lenguaje
verdadero. Por favor, tenga presente
que un lenguaje es a la vez un mapa del
mundo y su propio mundo, con sus
propias zonas de penumbra y sus
grietas, lugares donde enunciados que
parecen obedecer todas las reglas del
lenguaje son, a pesar de todo,
imposibles de tratar.
Podemos suponer que el «lenguaje
natural» es un territorio familiar, pero
solo como recordatorio considere la
distancia y la diferencia entre usar
«árbol» y «roca» para designar
auténticos árboles y rocas y la
vergonzosa semántica de Clinton
hablando de «inhalar» o «contacto
sexual». O explore la conocida
paradoja «Estoy mintiendo» (también
un invento griego). O medite sobre
frases como «“‘No tiene sentido’ no
tiene sentido” no tiene sentido» o
«“Produce
falsedad
cuando
es
precedida por su cita” produce falsedad
cuando es precedida por su cita». Se
dará cuenta de que estas tres últimas,
como la mayoría de las fisuras
paradójicas,
involucran
la
autorreferencia o la regresión, dos
demonios que han afligido el lenguaje
desde hace tanto tiempo como
queramos retroceder.
Las matemáticas no están exentas.
Y, por supuesto, como las matemáticas
son un lenguaje totalmente abstracto, y
se supone que extremadamente
«higiénico» debido a su falta de
referentes específicos del mundo real,
sus paradojas y enigmas son mucho
más problemáticos. Es decir, que las
matemáticas tienen que afrontarlos
realmente en lugar de ponerlos sin más
en la trastienda del pensamiento
cuando suena el despertador. Algunos
dilemas pueden tratarse con un enfoque
«legalista», por así decirlo, mediante
definiciones y estipulaciones.[1.19]
Analicemos un ejemplo fácil del
álgebra escolar: a partir del hecho
indiscutible de que en una igualdad
entre dos fracciones los denominadores
son iguales si los numeradores lo son,
es decir, si
entonces y = z,
podría parecer que si
,
entonces (x − 4) = (x − 3), o sea 4 = 3,
lo que evidentemente no tiene sentido,
ya que presenta una «fisura». Esto se
resuelve decretando que la única
solución posible de
es
x = 5 (pues 0 dividido por cualquier
cosa da otra vez 0, lo cual, obviamente,
no implica 4 = 3) y estipulando que el
teorema
solo es
válido si x ≠ 0.
Veamos un caso difícil. Todos
conocemos los decimales periódicos,
como 2/3 = 0,666… Resulta posible
demostrar que 0,999… es igual a 1,0
con solo un par de movimientos
totalmente «legales»: si x = 0,999…,
entonces 10x = 9,999…, y ahora
restemos x de 10x:
9,999… − 0,999…
y obtenemos 9x = 9,0 y por lo tanto
x = 1. ¿Es engañoso o no? Depende de
cómo tratemos la secuencia infinita
«0,999…» y de si decidimos postular la
existencia de algún número mayor que
0,999… pero menor que 1,0. Un
número
así
involucraría
un
infinitésimo, es decir, un ente
matemático de pequeñez literalmente
infinita. Puede que recuerde los
infinitésimos de las matemáticas del
instituto. Pero puede que no recuerde
—probablemente porque no se lo
explicaron— que a causa de los
infinitésimos los fundamentos del
cálculo
fueron
extremadamente
controvertibles y poco firmes durante
doscientos años, ni que más o menos
por el mismo motivo las matemáticas
transfinitas de Cantor fueron recibidas
con acalorado escepticismo a finales
del siglo XIX: nada ha causado más
problemas
—históricamente,
metodológicamente, metafísicamente
— que las cantidades infinitas. En
muchos sentidos, la historia de esos
problemas relacionados con el ∞ es la
propia historia de las matemáticas.
§1d.
Esta
introducción es muy rápida e
imprecisa, por supuesto. Ahora
tenemos que hacer algunas distinciones
al aproximarnos al ∞ como tema
histórico. La primera es la distinción
obvia entre lo infinitamente grande
(= transfinito) y lo infinitamente
pequeño (= infinitesimal, = ). La
segunda gran diferencia es entre el ∞
como característica del mundo físico
—por ejemplo, al preguntarnos si el
universo es infinito, si la materia es
infinitamente divisible, si el tiempo
tiene un principio y un fin— y el ∞
como ente matemático abstracto o
concepto, en la misma línea que las
funciones, los números, la primalidad,
y demás. También ha habido algo de
introducción a la ontología de las
abstracciones analizando si existen
realmente los objetos matemáticos y
cómo existen, cuestiones acerca de las
cuales, por supuesto, aún quedan
cavilaciones para llenar una biblioteca.
Lo que debe quedar claro es que los
problemas y controversias sobre el ∞
de los que nos vamos a ocupar aquí se
centran en la cuestión de si las
cantidades infinitas pueden existir
realmente como entes matemáticos.
La tercera distinción puede
empezar pareciendo nimia. Concierne a
palabras relacionadas con el ∞ como
«cantidad» y «número». Estas tienen
un extraño y confuso doble sentido, del
mismo modo en que lo tienen
«longitud» o «gramo». Un trozo de
cuerda tiene cierta longitud, por
ejemplo, en metros, pero también
decimos cosas como «unos metros de
cuerda» o «longitud de onda». Una
cierta cantidad de fármaco que pesa un
gramo también se llama «un gramo de
fármaco». Asimismo, «cantidad» o
«número»
pueden
funcionar
predicativamente
—es
decir,
respondiendo
a
las
preguntas
«¿cuántas?» o «¿cuánto?» de algo— y
también como nombres comunes que
denotan el ente descrito. Por lo tanto,
puede resultar ambiguo, cuando se usa
un término como «número infinito», si
se está usando predicativamente («Hay
una cantidad infinita de números
primos») o nominativamente («El
primer número infinito de Cantor es
ℵ0»). Y la diferencia es importante,
porque el uso predicativo de «∞»
puede ser difuso y puede significar solo
«indefinidamente grande» o «muy muy
grande», mientras que, tras Dedekind y
Cantor, el uso nominativo tiene una
denotación muy específica, aunque
abstracta.
En cierto sentido, el poder y quizás
incluso toda la raison d’être del
lenguaje de las matemáticas es que está
diseñado para ser tan claro y sin
connotaciones que evite justamente
este tipo de ambigüedades. Intentar
expresar cantidades y relaciones
numéricas en lenguaje natural, como
traducir proposiciones matemáticas al
castellano y viceversa, a menudo causa
problemas.[1.20] Un ejemplo favorito
del doctor Goris era la vieja historia
sobre tres hombres que llegan a un
motel tarde por la noche. Solo queda
una habitación libre, y cuesta 30€. Los
huéspedes deciden poner 10€ cada uno
y compartirla, pero cuando llegan a la
habitación se dan cuenta de que está
hecha un desastre —parece que, por
alguna confusión, nadie había hecho la
limpieza tras irse los anteriores
ocupantes— y comprensiblemente los
tres hombres llaman al recepcionista
para quejarse. Aquí pueden omitirse
unos cuantos detalles y florituras. La
cuestión es que se hace tarde, las
personas de la limpieza ya no están, y
no hay ninguna habitación más, de
modo que, tras un poco de regateo, el
recepcionista acepta rebajar 5€ el
precio de la habitación y repartir
sábanas limpias. Manda al botones a la
habitación con sábanas, toallas y el
reintegro de 5€ en forma de cinco
monedas de 1€. Etc., etc., donde lo
importante es que hay cinco monedas
de 1€ y tres individuos, de modo que
estos (misteriosamente ablandados) se
quedan 1€ cada uno y dejan que el
botones se quede los 2€ restantes como
propina. Así, cada hombre ha
empezado pagando 10€ y ha
recuperado 1€, de modo que cada uno
ha pagado 9€, y los tres juntos, 27€. El
botones tiene los otros 2€, lo que suma
29€, así que ¿dónde está el euro
restante? En este problema, la cuestión
es que la verborrea (de la que había
considerablemente más en la versión
del doctor Goris: incluía un relato
épico que duraba todo el curso sobre
esos tres hombres y sus diversas
biografías y peripecias y los diferentes
enigmas matemáticos con que se
topaban siempre) le confunde para que
intente calcular (30 − 3) + 2 en lugar
de la pertinente (30 − 5) + (3 + 2),
dando como resultado mayor confusión
y diversión y posibles puntos extra.
Existen
varios
tipos
de
provocaciones interlingüísticas como
esta. Las que no se pueden resolver se
convierten en verdaderas paradojas,
algunas de las cuales son profundas. No
debería sorprender, dado que el ∞ es la
abstracción definitiva y a la vez
arraigadamente difuso, que este figure
en muchas de esas paradojas. Tome,
por ejemplo, la idea de que no hay un
último entero, o un entero mayor que
todos los demás, y de que el tiempo se
extiende hacia adelante infinitamente.
Ahora imagine una lámpara de larga
duración perfectamente construida con
un
gran
botón
rojo
de
Apagada/Encendida, e imagine que esta
mañana la lámpara está apagada pero a
las 16:30 alguien la encenderá, a la
misma hora del día siguiente alguien la
apagará, a la misma hora del día
siguiente alguien la encenderá de
nuevo, y así sucesivamente, cada día,
por el resto del tiempo. Y ahora
considere si, tras un número infinito de
días, la lámpara estará apagada o
encendida. Puede que recuerde de las
matemáticas del instituto[1.21] que en
realidad este problema está relacionado
con algo llamado una serie infinita
divergente, más específicamente la
serie de Grandi, 1 − 1 + 1 − 1 + 1 − 1
+ 1…, serie que suma 0 si la
calculamos según (1 − 1) + (1 − 1) +
(1 − 1) +… pero que suma 1 si la
calculamos según 1 + (−1 + 1) +
(−1 + 1) + (−1 + 1)…, y la traca final
es que, como ambos cálculos son
matemáticamente lícitos, la suma
«real» de la serie parece ser a la vez 1 y
no-1, lo cual por la LTE es imposible.
Sin embargo, tal vez recuerde[1.22] que
la serie de Grandi resulta ser de un
subtipo particular de serie infinita
divergente conocida como serie
oscilante, y que como tal es un ejemplo
aleccionador de estipulación de sumas
parciales (denotadas por sn), siendo el
simbolismo relevante algo parecido a
«1 + ∑(−1)n donde sn = 0 para n par y
sn = −1 para n impar», simbolismo que
parece tan legislativamente críptico y
pesado precisamente porque tiene que
estar diseñado para evitar fisuras como
la paradoja de la lámpara.
También hay antinomias que giran
alrededor del ∞ no como un concepto
del lenguaje natural o un terrain vague
numérico sino simplemente como un
rasgo de la geometría, de tal forma que
pueden representarse mediante figuras
simples, y no basta con meras
estipulaciones. Considérense los puntos
y las rectas. Está claro que cualquier
recta contiene una infinidad de puntos.
Un punto, recuerde, es «un elemento de
la geometría que tiene posición pero no
extensión» (Nelson, pág. 330), en el
sentido de que un punto es una
abstracción, pura posición. Pero si una
recta se compone únicamente de
puntos, y los puntos no tienen
extensión,
¿cómo
puede
tener
extensión una recta? Por definición,
todas las rectas la tienen. La respuesta
parece tener algo que ver con el ∞,
pero ¿cómo puede ∞ × 0 ser igual a
algo que no sea 0?
Aquí está otra peor. Todo lo que
necesita es a Euclides y una regla.
Dibuje una línea como esta:
donde el segmento de recta PQ es tres
veces más largo que el segmento QR.
Como los segmentos de recta están
compuestos por puntos, parece
razonable la idea de que debería haber
tres veces más puntos en PQ que en
QR. Pero resulta que hay exactamente
la misma cantidad en ambos. Puede
verlo. Convierta los segmentos en el
triángulo recto QPR girando PQ hacia
arriba y continuando la rotación hasta
que P esté justo encima de R, y después
dibuje el segmento PR:
Después recuerde que, por el axioma de
las paralelas de Euclides,[1.23] por cada
punto del segmento PQ pasará
exactamente una recta paralela al
segmento PR:
y que esta recta cortará al segmento QR
exactamente en un punto. Lo mismo es
cierto para cada punto individual de
PQ; simplemente dibuje una recta
paralela a PR que corte a PQ en dicho
punto, y la recta cortará a QR en un
único punto:
sin duplicaciones y sin que falten
puntos, de modo que a cada punto de
PQ le corresponde un punto de QR, es
decir, que hay exactamente tantos
puntos en QR como en PQ, aunque
PQ = 3(QR).
Puede usted generar una paradoja
similar creando un par de círculos
concéntricos tales que el radio del
círculo mayor mida el doble que el
radio del círculo interior.[1.24] Como la
circunferencia de cualquier círculo es
una función directa de su radio, la
circunferencia del círculo mayor mide
el doble que la del círculo menor. Y
una circunferencia también es una línea
(curva), de modo que debería haber dos
veces más puntos en la circunferencia
del círculo mayor. Pero no: como
ambos círculos tienen un centro
común, el simple trazo de algunos
radios permite establecer que cualquier
radio que corte al círculo grande en un
punto N cortará al círculo pequeño en
un único punto correspondiente N1, sin
redundancias ni ausencias:
demostrando así que el número de
puntos en las circunferencias de ambos
círculos es el mismo.
Estos son verdaderos problemas, no
solo tediosos o antiintuitivos sino
matemáticamente profundos. Georg F.
L. P. Cantor los resolvió todos, más o
menos. Pero, por supuesto, la expresión
coloquial «resolver» puede significar
distintas
cosas.
Como
se
ha
mencionado, en matemáticas un modo
de
tratar
con
los
problemas
desestabilizantes es decretar su
inexistencia, desterrando ciertos tipos
de entes matemáticos y/o cargando los
teoremas
de
estipulaciones
y
exclusiones diseñadas para evitar
resultados extraños. Antes de la
invención
de
las
matemáticas
transfinitas, esta era la manera de tratar
la mayor parte de las paradojas del ∞.
Se «resolvían» empezando por
difuminar la distinción entre una
paradoja y una contradicción, y luego
aplicando una especie de reducción al
absurdo
metafísica:
si
admitir
cantidades infinitas, como el número
de puntos de una recta o el conjunto de
todos los enteros, conduce a
conclusiones paradójicas, tiene que
haber algo inherentemente erróneo o
sin sentido en las cantidades infinitas,
y así las entidades relacionadas con el
∞ no podrían «existir» realmente en un
sentido
matemático.
Este
fue
esencialmente
el
argumento
desplegado, por ejemplo, contra la
famosa paradoja de Galileo en el
siglo XVII. Aquí está la paradoja de
Galileo. El quinto axioma de Euclides
dicta que «el todo es siempre mayor
que la parte», lo cual parece bastante
irrefutable. También resulta obvio que
todo cuadrado perfecto (por ejemplo, 1,
4, 9, 16, 25…) es un número entero,
mientras que no todo número entero es
un cuadrado perfecto. En otras
palabras, el conjunto de todos los
cuadrados perfectos no es más que una
parte del conjunto de todos los
números enteros, por lo que en virtud
del quinto axioma de Euclides es más
pequeño. El problema es que el mismo
tipo
de
igualdad-mediantecorrespondencia que vimos con PQ/QR
y los dos círculos también se puede
establecer en este caso. Porque aunque
no es cierto que cada número entero
sea un cuadrado perfecto, sí es cierto
que cada número entero es la raíz
cuadrada de un cuadrado perfecto: 2 de
4, 3 de 9, 4 de 16, 912 de 831.744, y así
sucesivamente. Visualmente, se pueden
alinear los dos conjuntos y demostrar
una
perfecta
e
inagotable
correspondencia de uno a uno entre sus
miembros:[1.25]
Así pues, la conclusión de la
paradoja de Galileo es que el quinto
axioma de Euclides, una parte
indispensable de las matemáticas
básicas, y una verdad obvia que
podemos comprobar con cualquier tipo
de conjunto que seamos capaces de ver
o contar, queda contradicho por los
conjuntos infinitos de todos los
números enteros y todos los cuadrados
perfectos. Ante esta situación, hay dos
caminos posibles. El estándar, como se
ha mencionado, es declarar que los
conjuntos infinitos son el equivalente
matemático de los unicornios o la
«nada» que Alicia ve en el camino.[1.26]
El otro, que es revolucionario tanto
intelectual como psicológicamente, es
tratar la equivalencia paradójica de
Galileo no como una contradicción
sino como la descripción de cierto
nuevo tipo de ente matemático que es
tan abstracto y extraño que no se ciñe a
las reglas normales de las matemáticas
y requiere un tratamiento especial. Es
decir, consiste en indicar (como hizo
adivine quién) que «El fallo
fundamental de todas las así llamadas
demostraciones de la imposibilidad de
los números infinitos es que atribuyen
a dichos números todas las propiedades
de los números finitos, mientras que
los números infinitos […] constituyen
una clase completamente nueva de
número, un tipo cuya naturaleza
debería ser objeto de investigación y no
de prejuicios arbitrarios» (Cantor,
«Über die verschiedenen Standpunkte
in bezug auf das aktuelle Unendliche»,
en
Gessamelte
Abhandlungen.
Traducción editada de un extracto de
Dauben, Georg Cantor, pág. 125).
Pero, por otro lado, dicha actitud
podría no ser revolucionaria, sino
sencillamente una locura.[1.27] Como
considerar el hecho de que nunca nadie
ha visto un unicornio ni una sola vez y
afirmar que esto no es una indicación
de que los unicornios no existen
realmente, sino más bien un indicio de
que los unicornios constituyen un
nuevo tipo de animal con la singular
propiedad de ser invisibles. Está claro
que aquí encontramos la sutil
diferencia entre genio y locura de la
que se alimentan escritores y cineastas
modernos. La verdad es que toda clase
de entes extraños y no directamente
observables como el 0, los enteros
negativos, los números irracionales,
etc., se introdujeron originalmente en
las matemáticas con el mismo tipo de
aura de locura/incoherencia pero, a día
de hoy, están totalmente aceptados y
son incluso esenciales. Al mismo
tiempo, ha habido muchas otras
innovaciones que eran realmente
insensatas o intratables y fueron
expulsadas entre risas de la ciudad,
matemáticamente hablando, y nosotros,
la gente de la calle, jamás oímos hablar
de ellas.
Sin embargo, que algo sea una sutil
distinción no significa que no sea una
distinción. El pensamiento matemático
es abstracto, pero también minucioso y
pragmático y muy enfocado a la
obtención de resultados. La diferencia
entre
una
teoría
matemática
revolucionaria y brillante y otra
«chiflada» está, por lo tanto, en lo que
se pueda hacer con ella, en si da o no
da resultados significativos. He aquí a
Hardy explicando lo que considera
«resultados significativos»:
Podríamos decir, en cierto
modo, que una idea matemática
es «significativa» si se puede
relacionar, de una manera
natural y reveladora, con un
gran complejo de otras ideas
matemáticas. Así, un teorema
matemático serio, un teorema
que conecte ideas significativas,
es probable que conduzca a
importantes avances en las
propias matemáticas e incluso
en otras ciencias (Hardy,
Apology, pág. 89).
Las teorías de Cantor sobre los
conjuntos infinitos y los números
transfinitos
acaban
resultando
significativas precisamente de esta
manera. La razón de ello es, en parte,
que Cantor era un excelente
matemático profesional y aportó
demostraciones ingeniosas de las
características formales importantes,
que hicieron de sus ideas verdaderas
teorías y no solo hipótesis atrevidas.
Pero también hay otras razones. El
mismo Galileo había planteado la
hipótesis de que la verdadera
conclusión de su paradoja era que «los
atributos “igual”, “mayor” y “menor”
no son aplicables al infinito, sino solo a
cantidades finitas» (Galileo Galilei,
pág. 32). Pero nadie se tomó esto en
serio, y no por estupidez: las
matemáticas no tienden a estar llenas
de gente estúpida o de mente cerrada.
Realmente, el momento no era el
adecuado para la sugerencia de Galileo,
ni existían todavía las herramientas
matemáticas
adecuadas
para
convertirla en una verdadera teoría
incluso si Galileo hubiera querido… lo
cual no fue así, hecho del que sería
equivocado concluir que él no era tan
perspicaz o brillante como Georg
Cantor. Como la mayoría de los
gigantes
que
revolucionan
las
matemáticas o la ciencia, Cantor era en
un 100% un hombre de su tiempo y
lugar, y sus logros fueron la habitual
conjunción de un talento personal y un
coraje extraordinarios[1.28] con el
contexto adecuado de problemas y
condiciones
generales
que,
en
retrospectiva, tienden a hacer que los
avances
intelectuales
parezcan
inevitables, y sus autores, casi
incidentales.
Para expresarlo de otro modo, las
matemáticas son piramidales. Cantor
no surgió súbitamente de la nada. Por
lo tanto, una verdadera valoración
requiere una comprensión de los
conceptos y problemas que dieron
lugar a la teoría de conjuntos e hicieron
que las matemáticas transfinitas fueran
significativas en el sentido de Hardy.
Esto necesita tiempo, pero como la
explicación es también piramidal
podemos proceder de un modo más o
menos ordenado, y no será todo tan
abstracto y discursivo como esta
introducción.
2
§2a.
Ahora
estamos empezando de verdad.
Hay dos maneras de investigar el
contexto de la teoría de conjuntos
cantoriana. La primera es hablar de la
intrincada y abstracta danza del infinito
y los límites a lo largo de la evolución
de las matemáticas. La segunda es
examinar el esfuerzo histórico de las
matemáticas para representar la
continuidad, es decir, el suave fluir y/o
los aspectos densamente sucesivos del
movimiento y los procesos del mundo
real. Cualquiera que tenga incluso los
más
vagos
recuerdos
de
las
matemáticas del instituto recordará que
la continuidad y el ∞/límite son
esencialmente el fundamento del
cálculo, y podría recordar también que,
en términos generales, tienen su origen
en la metafísica de los antiguos griegos
y su matriz particular en Zenón de Elea
(hacia 490-435 a. C., quien murió con
sus dientes literalmente aún en la oreja
del despótico gobernante de Elea,
Nearco I; es una larga historia), cuyas
epónimas paradojas lo desencadenaron
todo.
Unos cuantos hechos procedentes
de Ática, para empezar. En primer
lugar, las matemáticas griegas eran
abstractas, ciertamente, pero estaban
profundamente arraigadas en los
métodos de los babilonios y los
egipcios. Para los griegos no hay una
diferencia real entre los entes
aritméticos y las figuras geométricas,
por ejemplo, entre el número 5 y un
segmento de cinco unidades de
longitud. En segundo lugar, para ellos
tampoco hay unas distinciones claras
entre las matemáticas, la metafísica y
la religión: en muchos sentidos eran
todas la misma cosa. En tercer lugar, el
desagrado propio de nuestra época y
cultura respecto a los límites —por
ejemplo, al decir «un hombre limitado»
o «SI SU VOCABULARIO ES LIMITADO,
SUS POSIBILIDADES DE ÉXITO SON
LIMITADAS»,
etc.— habría sido
incomprensible para los antiguos
griegos. Baste decir que los límites les
gustaban mucho, y una consecuencia
directa
de
ello
es
su
antipatía/desconfianza respecto al ∞.
El término helénico to apeiron
significa no solo infinitamente
largo/grande, sino también indefinible,
complejo sin remedio, aquello-que-nopuede-ser-tratado.[2.1]
To
apeiron
también
hacía
referencia al caos ilimitado y sin
naturaleza propia del que surgió la
creación. Anaximandro (610-545 a. C.),
el primero de los presocráticos que usó
el término en su metafísica, lo define
esencialmente como «el sustrato
ilimitado del que provino el mundo»
(Edwards, v. 3, p. 190). Y aquí
«ilimitado» significa no solo sin fin e
inagotable, sino informe, desprovisto
de cualquier frontera, distinción o
cualidad específica. Algo así como el
vacío, pero de lo que está desprovisto
inicialmente es de forma.[2.2] Y esto,
para los griegos, no es nada bueno.
Aquí está una cita definitiva de
Aristóteles, esa fuente de citas
definitivas: «La esencia del infinito es
la privación, no la perfección sino la
ausencia de límite» (Física, III, 7,
208a). La cuestión es que al abstraer
todas las limitaciones para obtener el
∞, también se elimina lo más
importante: sin límite implica sin
forma, y eso significa el caos, la
fealdad, un lío. Téngase, pues, presente
el hecho ático cuatro: el ubicuo y
esencial esteticismo del intelecto
griego. El desorden y la fealdad eran el
malum in se definitivo, la señal segura
de que algo iba mal con un concepto,
del mismo modo en que la
desproporción y el desorden eran
inaceptables en el arte griego.[2.3]
Pitágoras de Samos (570-500 a. C.)
es crucial en todos los sentidos para la
historia del ∞. (En realidad, es más
exacto decir «la Divina Hermandad de
Pitágoras» o por lo menos «los
pitagóricos», porque en relación con el
∞ no es tan importante el hombre
como la secta). Fue la metafísica
pitagórica
la
que
combinó
explícitamente el to apeiron de
Anaximandro con el principio de límite
(peras en griego) que otorga estructura
y orden —la posibilidad de forma— al
vacío
primigenio.
La
Divina
Hermandad de Pitágoras (D. H. P.),
que, como es bien sabido, fundó una
religión entera del número, postuló este
límite como matemático, geométrico.
Es la acción del peras sobre to apeiron
la que da lugar a las dimensiones
geométricas del mundo concreto: to
apeiron limitado una vez da lugar al
punto geométrico, limitado dos veces
da lugar a la recta, tres veces da lugar
al plano, y así sucesivamente. Por
extraño o primitivo que esto pueda
parecer,
era
extremadamente
importante, y también lo eran los
pitagóricos. Su cosmología basada en
el peras implicaba que la génesis de los
números era la génesis del mundo. Sí,
la excentricidad de la D. H. P. es
legendaria, igual que sus reglas
estacionales para el sexo o el odio
patológico de Pitágoras hacia las
legumbres. Pero fueron las primeras
personas que consideraron, y adoraron,
los números como abstracciones. El
puesto central del número 10 en su
religión, por ejemplo, no estaba
relacionado con los dedos, sino con el
estatus del número 10 como la suma
perfecta de 1 + 2 + 3 + 4.
Los miembros de la D. H. P. fueron
también los primeros filósofos que
trataron de forma explícita la relación
metafísica
entre
las
realidades
matemáticas abstractas y las realidades
empíricas concretas. Su postura
fundamental era que la realidad
matemática y el mundo concreto eran
lo mismo, o más bien que la realidad
empírica era una especie de sombra o
proyección de las matemáticas
abstractas.[2.4] Además, muchos de sus
argumentos a favor de la primacía del
número se basaban en el hecho
observado de que las relaciones
matemáticas
puramente
formales
tenían sorprendentes consecuencias
para los fenómenos del mundo real. Un
famoso ejemplo es cómo la D. H. P.
obtuvo la razón áurea (
,
cuya solución es aproximadamente
)
de las conchas marinas y los troncos de
algunos árboles y estableció su uso en
la
arquitectura.
Como
se
ha
mencionado,
algunas
de
estas
conexiones fueron conocidas por
culturas anteriores como los egipcios, o
quizás «usadas» sería mejor, pues los
egipcios tenían un interés nulo en
conocer cuáles eran realmente las
conexiones, o en qué significaban. Un
par más de ejemplos. En la práctica, los
egipcios habían usado lo que ahora
llamamos el teorema de Pitágoras en
ingeniería y agrimensura a lo largo del
Nilo, pero fue Pitágoras quien lo
convirtió en un auténtico teorema, y lo
demostró. Muchas culturas pregriegas
también tocaban música, pero fue la
D. Η. P. la que descubrió los conceptos
de octava, de quinta perfecta, etc.,
observando que ciertos intervalos
musicales siempre se correspondían
con ciertas razones entre las longitudes
de las cuerdas pulsadas: de 2 a 1, de 3 a
2, y así sucesivamente. Como las
cuerdas eran rectas y las rectas eran
entes geométricos/matemáticos,[2.5] las
razones entre las longitudes de las
cuerdas eran lo mismo que razones
entre números enteros, o sea números
racionales, que resultan ser los entes
fundamentales de la metafísica
pitagórica.
Etcétera, siendo lo importante que
los intentos de la D. Η. P. para articular
las conexiones entre la realidad
matemática y el mundo físico eran
parte del proyecto, más amplio, de la
filosofía presocrática, el cual era
básicamente dar una explicación
racional, no mitopoiética, de lo que era
real y de su origen. Quizás incluso más
importante que la D. Η. P., en relación
con el ∞, es el protomístico
Parménides de Elea (hacia el 515-?
a. C.), no solo porque su distinción
entre «Vía de Verdad» y «Vía de
Apariencia» delimitó los términos de la
metafísica griega y (también) influyó
en Platón, sino porque el discípulo y
defensor n.º 1 de Parménides fue el
antes mencionado Zenón, el más
endiabladamente listo e irritante de
todos los filósofos griegos (al que se
puede ver dándole un palizón a
Sócrates,
argumentativamente
hablando, en el Parménides de Platón).
Los argumentos de Zenón a favor de la
metafísica de Parménides tomaron la
forma —como también se ha
mencionado— de algunas de las más
profundas y enrevesadas paradojas de
la historia del mundo. A favor de la
relevancia de estos rompecabezas para
nuestro propósito general, he aquí otra
bonita cita de Bertrand Russell:
En este mundo caprichoso, nada
es más caprichoso que la fama
póstuma. Uno de los más
notables ejemplos de la falta de
juicio de la posteridad es el
eleático Zenón […], que puede
ser considerado el fundador de
la filosofía del infinito. Inventó
cuatro argumentaciones, todas
inconmensurablemente sutiles y
profundas, para demostrar que
el movimiento es imposible,
que Aquiles nunca puede
alcanzar a la tortuga, y que una
flecha en pleno vuelo está
realmente en reposo. Tras ser
refutadas por Aristóteles, y por
todos los filósofos posteriores
desde entonces hasta nuestros
días, dichas argumentaciones
fueron
reformuladas,
y
constituyeron la base de un
renacimiento matemático, por
parte de un profesor alemán,
quien probablemente nunca
soñó en ninguna conexión entre
él mismo y Zenón (Russell,
Mysticism and Logic, pág. 76).
Dicho sea de paso, la metafísica de
Parménides —que es incluso más
aventurada que la de la D. H. P., y que
en retrospectiva se parece más a la
religión oriental que a la filosofía
occidental— se puede describir como
una especie de monismo estático,[2.6] y
las paradojas de Zenón (que en realidad
son más de cuatro) están, conforme a
ello, dirigidas contra la realidad de (1)
la pluralidad y (2) la continuidad. Por
ahora nos interesa (2), que para Zenón
toma la forma, como menciona
Russell, del movimiento físico tal
como lo conocemos habitualmente.
El argumento básico de Zenón
contra la realidad del movimiento se
conoce como la dicotomía. Parece muy
simple y se desarrolla en dos de sus
más famosas paradojas: «El Estadio» y
«Aquiles contra la Tortuga». La
dicotomía es usada y analizada
posteriormente, con todo tipo de
presentaciones e intenciones, por
Platón, Aristóteles, Agripa, Plotino,
santo Tomás de Aquino, Leibniz, John
Stuart Mill, Francis Herbert Bradley y
William James (sin olvidar a Douglas
Hofstadter en Gödel, Escher, Bach).
Veamos cómo funciona.[2.7] Usted está
en una esquina, el semáforo cambia e
intenta cruzar la calle. Observe la
maniobra al usar el término «intenta».
Porque antes de que usted pueda cruzar
toda la calle, obviamente tiene que
hacer la mitad del recorrido. Y antes de
hacer la mitad del recorrido, debe hacer
la mitad de la mitad del recorrido. Esto
no es más que sentido común. Y antes
de hacer la mitad de la mitad del
recorrido, debe hacer la mitad de la
mitad de la mitad del recorrido, y así
sucesivamente. Y más. Expresado de
un modo más excitante, la paradoja es
que un peatón no puede desplazarse del
punto A al punto B sin cruzar todos los
subintervalos sucesivos de AB, cada
uno de los cuales tiene una longitud
, donde los valores de n forman la
secuencia (1, 2, 3, 4, 5, 6, …), y donde
los puntos suspensivos significan, por
supuesto, que la secuencia no termina
nunca. Continúa para siempre. Este es
el temido regressus in infinitum,
también conocido como regresión
infinita viciosa o RIV. Lo que la
convierte en «viciosa» en este caso es
que le pide a usted que realice un
número infinito de acciones antes de
alcanzar su objetivo, lo cual —como
«infinito» consiste precisamente en que
la cantidad de dichas acciones no tiene
fin— convierte al objetivo en algo
lógicamente imposible. O sea, que
usted no puede cruzar la calle.
La
manera
estándar
de
esquematizar
la
dicotomía
es
habitualmente:
(1) Para cruzar el intervalo AB
primero tiene que cruzar todos
los subintervalos
, siendo n
= 1, 2, 3, 4, 5, 6, …
(2) Hay una cantidad infinita de
tales subintervalos.
(3) Es imposible cruzar una
cantidad
infinita
de
subintervalos en una cantidad
finita de tiempo.
(4) Por lo tanto, es imposible
cruzar AB.
No hace falta decir que el intervalo
AB no tiene por qué ser una calle muy
ancha, ni siquiera una calle. La
dicotomía se aplica a cualquier tipo de
movimiento continuo. En clase, al
doctor Goris le gustaba presentar la
argumentación en términos del
movimiento del dedo desde la falda
hasta la punta de la nariz. Y, por
supuesto, como sabe cualquiera que
haya logrado alguna vez cruzar una
calle o tocarse la nariz, tiene que haber
algo sospechoso en el argumento de
Zenón. Hallar y articular esa sospecha
es un asunto muy distinto. Tenemos
que ir con cuidado, también: hay más
de una manera de equivocarse. Si
estudió usted algo de matemáticas de
bachillerato, por ejemplo, puede ser
tentador decir que el paso (2) de la
dicotomía esconde una simple falacia,
concretamente la de suponer que la
suma de una serie infinita tiene que ser
a su vez infinita. Posiblemente
recuerde que el
del paso (1) es
simplemente
otra
manera
de
representar la serie geométrica
,
y
que
la
fórmula correcta para hallar la suma de
esta serie geométrica es
, donde
a es el primer término de la serie y r es
su razón, y que aquí ambos valen , y
que
, por lo que en este caso
parece que las calles se pueden cruzar y
las narices se pueden tocar sin ningún
problema, así que la dicotomía en
realidad es solo un truco con las
palabras y no una paradoja en absoluto,
excepto tal vez para civilizaciones
demasiado primitivas y poco ilustradas
como para conocer la fórmula de la
suma de una serie geométrica.
Solo que esta respuesta no servirá.
De momento dejemos a un lado la
cuestión de si es técnicamente correcta.
Lo que importa es que es trivial:
representa lo que los filósofos
llamarían una visión empobrecida del
problema de Zenón.
Pues ¿de dónde sale exactamente
como fórmula para sumar esta
serie geométrica? Es decir, dicha
fórmula ¿es solo un poco de palabreo
«legalista» para evitar que existan
ciertas
paradojas,
o
es
matemáticamente «significativa» en el
sentido de Hardy? Y ¿cómo
determinamos cuál es?
Curiosamente, cuanto más estándar
fuera la lección de matemáticas que
recibió, más difícil será evitar
responder de una manera demasiado
pobre. Como, por ejemplo, justificar
indicando,
en
la
mejor
tradición del 2.º curso de cálculo,[2.8]
que la serie geométrica relevante en
este caso es un subtipo particular de
serie infinita convergente, y que la
suma de tal serie se define como el
límite de la sucesión de sus sumas
parciales (es decir, si la sucesión s1, s2,
s3, …, sn, … de las sumas parciales de
una serie tiende a un límite S, entonces
S es la suma de la serie), y que
podemos afirmar con seguridad,
respecto a dicha serie, que
,
así
que
funciona
perfectamente… en cuyo caso usted
habrá respondido una vez más a la
dicotomía de Zenón de un modo que es
complejo, formalmente excitante,
técnicamente correcto y profundamente
trivial. En la línea de responder
«Porque es ilegal» como respuesta a
«¿Por qué está mal matar?».
El problema con las clases de
matemáticas de bachillerato —las
cuales consisten casi completamente en
la ingestión y la regurgitación rítmicas
de información abstracta, y cuyo ritmo
es tal que maximiza este flujo de datos
recíproco— es que su misma dificultad
superficial puede hacernos creer que
realmente sabemos algo cuando todo lo
que «sabemos» realmente son fórmulas
abstractas y reglas para su aplicación.
En las clases de matemáticas raramente
aprendemos si cierta fórmula es
verdaderamente significativa, o por
qué, o de dónde salió, o qué dependía
de ella.[2.9] Hay claramente una
diferencia entre ser capaz de usar una
fórmula de forma correcta y saber
realmente cómo resolver un problema,
saber por qué un problema es un
problema matemático de verdad y no
un simple ejercicio. Respecto a esto
véase un pasaje más de Russell sobre
Zenón,[2.10] esta vez destacando
algunas partes:
Zenón se preocupó, de hecho,
acerca de tres problemas, cada
uno
planteado
por
el
movimiento pero cada uno más
abstracto que el movimiento, y
susceptible de un tratamiento
puramente aritmético. Esos son
los
problemas
de
lo
infinitesimal, lo infinito y la
continuidad.
Enunciar
claramente las dificultades
involucradas quizás era lograr
la parte más dura de la tarea
del filósofo (Russell, Mysticism
and Logic, pág. 77).
Además, «
» no consigue
aclarar las dificultades en vueltas, pues
le falta contexto y no aporta
motivación. Poner en claro dichas
dificultades es, de hecho, la verdadera
dificultad con la que nos encontramos
aquí (y si usted empieza a sentir cierta
incomodidad/dolor de cabeza, sabrá
que estamos en el auténtico territorio
de Zenón).
En primer lugar, para ahorrarnos
por lo menos 103 palabras, eche un
vistazo de tipo recordatorio a las dos
siguientes gráficas esquemáticas, una
de
la
sucesión
divergente[2.11]
correspondiente a 2n y la otra de la
sucesión convergente expresada por
:
Una de las auténticas dificultades
contextuales que rodeaban la dicotomía
era que los griegos no tenían ni usaban
el 0 en sus matemáticas (el 0 había sido
una invención babilonia muy tardía,
puramente práctica y actuarial, hacia el
año 300 a. C.). Por lo tanto, se podría
decir que al no haber número/cantidad
reconocido/a hacia donde pueda
converger la sucesión convergente
(véase la Figura 2a(2)), las
matemáticas griegas carecían de
equipamiento
conceptual
para
comprender la convergencia, los
límites, las sumas parciales, etc. Esto
sería verdad en cierto sentido,[2.12] y no
completamente trivial.
Aún menos trivial es el mencionado
temor griego de to apeiron. Zenón fue
el primer filósofo en usar ese agujero
negro de la lógica que viene a ser el ∞
como una auténtica herramienta
argumentativa, es decir, la regresión
infinita viciosa (RIV), que incluso
actualmente se usa en argumentaciones
lógicas
como
un
método
de
demostración en la línea de la
reducción al absurdo. Ejemplo: en
epistemología, la RIV es la manera
más fácil de refutar la afirmación
habitual de que para saber realmente
algo hay que saber que se sabe. Como
en la mayoría de las demostraciones
por RIV hay algo maliciosamente
divertido en esta. Sea x una variable
con la cual denotaremos cualquier
hecho o estado de cosas que pueda ser
precedido por el término «que» y
reformulemos la afirmación original
como (1) «Para saber que x, tiene que
saber que sabe que x». Como la frase
entera «que sabe que x» también es un
hecho o estado de cosas, en el siguiente
paso de la demostración puede
simplemente sustituir x por [sabe que
x] dentro de la afirmación original y,
mutatis mutandis, el resultado es (2)
«Para saber que [sabe que x], tiene que
saber que sabe que [sabe que x]», la
siguiente y totalmente válida extensión
de la cual es (3) «Para saber que [sabe
que sabe que x], tiene que saber que
sabe que [sabe que sabe que x]», y así
sucesivamente,
ad
infinitum,
exigiéndole que satisfaga una cantidad
sin fin de precondiciones para saber
cualquier cosa.
[SEI La RIV es una herramienta tan
poderosa que puede usted usarla
fácilmente para irritar competidores
profesionales o enfurecer a su pareja en
conflictos domésticos, o (aún peor)
para volverse loco usted mismo en la
cama por la mañana pensando, por
decir algo, en cualquier tipo de relación
entre dos cosas o términos, como
cuando decimos que 2 y 4 están
relacionados por la función y = x2, o
que si las nubes provocan la lluvia,
entonces las nubes y la lluvia tienen
una relación causal. Si usted considera
la idea en abstracto y pregunta,
respecto a cualquier relación, si dicha
relación está ella misma relacionada
con los dos términos que relaciona, la
respuesta es ineludiblemente sí (pues
es imposible ver cómo una relación
puede conectar dos términos a menos
que tenga su propia relación con cada
uno, del modo en que un puente entre
dos orillas tiene que estar conectado
con cada orilla), en cuyo caso la
relación entre, digamos, las nubes y la
lluvia en realidad implica dos
relaciones más —o sea, aquellas entre
(1) las nubes y la relación y (2) la
lluvia y la relación—, cada una de las
cuales obviamente implica dos más, y
así sucesivamente, ad infinitum…, lo
cual no resulta ser en absoluto un
camino
abstracto
divertido
ni
productivo para seguir a tempranas
horas de la mañana, especialmente
porque la serie geométrica de
relaciones en este caso es más bien
divergente y no convergente, y como
tal está relacionada con todo tipo de
series
divergentes
modernas
y
especialmente temibles, como el
aumento exponencial del cáncer, la
fisión nuclear, la epidemiología, etc.
También vale la pena observar que las
horribles RIV divergentes, como las
que acabamos de ver, siempre
involucran la metafísica de las
abstracciones, tales como «relación» o
«conocimiento». Es como si siempre se
abriera algún tipo de rendija o fisura en
el desplazamiento de los casos
particulares de conocimiento/relación
al
conocimiento/relación
in
abstractus].
Zenón
mismo
está
casi
fetichísticamente atado a la RIV
divergente y la usa en varias de sus
paradojas menos conocidas. Aquí está
una
P.
Z.[2.13]
específicamente
antipitagórica contra la idea de que
cualquier cosa puede estar en algún
sitio en particular, lo que se puede
esquematizar de la siguiente forma
simplificada:
(1) Todo lo que existe está en
alguna ubicación.
(2) Por lo tanto, la ubicación existe.
(3) Pero por (1) y (2), la ubicación
tiene que estar en una
ubicación, y
(4) Por (1)-(3), la ubicación de la
ubicación tiene que estar ella
misma en una ubicación, y…
(5) así sucesivamente ad infinitum.
A esta es fácil verle los engranajes,
pues aquí la verdadera dificultad
russelliana es cierta imprecisión
respecto a «existir». En realidad, como
los antiguos griegos ni siquiera tenían
un verbo específico para la existencia,
el infinitivo relevante es el aún más
impreciso «estar». Desde un punto de
vista
puramente
gramatical,
el
argumento de Zenón puede ser acusado
de la clásica falacia de la
equivocación,[2.14] pues «estar» puede
tener todo tipo de significados
distintos,
por
ejemplo,
«Estoy
asustado» en comparación con «Está
lloviendo» o «Estar ahí». Pero puede
usted ver que continuar en esta línea
conducirá (una vez más) a las
cuestiones más profundas de la
paradoja, las cuales son (otra vez de
nuevo) metafísicas: ¿qué significan
exactamente estos diferentes sentidos
de «estar»?, y en particular, ¿qué
significa el sentido más especializado
de «existir»?, es decir, ¿qué tipo de
cosas existen realmente?, y ¿de qué
maneras?, y ¿hay diferentes tipos de
existencia para diferentes tipos de
cosas?, y entonces, ¿algunos tipos de
existencia son más básicos o
sustanciales que otros? Etcétera.
Se habrá dado cuenta de que ya nos
hemos topado con este tipo de
cuestiones una docena de veces y
todavía estamos a más de dos mil años
de Georg Cantor. Son la verdadera
oveja negra en la historia del ∞ y no
hay manera de evitarlas si queremos
algo más que un montón de clases
vomitadas de matemáticas abstractas
sobre teoría de conjuntos transfinita.
Trato hecho. Ahora es el momento de
trazar un esbozo del argumento de
Platón del Uno Sobre Muchos
(U. S. M.), que es precisamente el
tratamiento clásico de este tipo de
cuestiones al aplicarlas al asunto de la
predicación.
Puede que también recuerde el
U. S. M. del instituto. En ese caso
relájese porque esto no durará mucho.
Para Platón, si dos individuos tienen
algún atributo común y, por lo tanto,
pueden ser descritos[2.15] por el mismo
predicado —«Tom es un hombre»,
«Dick es un hombre»—, entonces hay
algo en virtud de lo cual Tom y Dick
(junto a todos los demás referentes del
predicado
nominativo
«hombre»)
tienen ese atributo en común. Ese algo
es la «forma» ideal hombre, forma que
es lo que realmente, definitivamente
existe, mientras que los hombres
individuales son solo manifestaciones
temporales de la forma, con una
especie de existencia prestada o
derivada, como las sombras o las
imágenes proyectadas. Esta es una
versión muy simplificada, pero no
distorsionada, del U. S. M., e incluso a
este nivel no debería ser difícil ver las
influencias de Pitágoras y Parménides
en la teoría ontológica de Platón sobre
las «formas», de la cual el U. S. M. es
obviamente una parte.
Aquí es donde la verdad se vuelve
un poco complicada. Como parece
suceder a menudo, la complicación
involucra a Aristóteles. Es cierto que la
primera mención del U. S. M. está en el
Parménides de Platón, pero de hecho lo
que hizo famoso al argumento fue la
Metafísica de Aristóteles,[2.16] que
intenta demolerlo en una extensa
discusión. El contexto podría llenar
varias estanterías pero podemos omitir
la mayor parte.[2.17] Lo extraño (por
razones que están al caer) es que el
argumento más conocido de Aristóteles
contra la teoría de las formas de Platón
es virtualmente el Zenón de los libros
de texto. Ese argumento, habitualmente
llamado del Tercer Hombre, es a todos
los efectos una reducción al absurdo de
tipo RIV divergente aplicada al
U. S. M. Tras observar que tanto los
hombres individuales como la forma
hombre obviamente comparten alguna
cualidad o atributo predicativo,
Aristóteles indica que entonces tiene
que haber otra forma metafísica —
digamos hombre'— que incluye ese
atributo común, lo cual implica aún
otra forma, hombre'', para incluir lo
predicativamente común a hombre' y
[hombre + hombre], etc., ad infinitum.
Le parezca o no válido el
argumento del Tercer Hombre como
refutación del U. S. M. puede muy bien
haberse dado cuenta de que la teoría de
las formas de Platón[2.18] tiene sus
propios problemas, como, por ejemplo,
una conspicua ridiculez cuando el
U. S. M. se aplica a ciertos predicados:
¿hay una forma ideal del hecho de ser
zurdo?, ¿de la estupidez?, ¿de la
porquería? Pero observe que la teoría
de Platón tiene mucha más potencia y
plausibilidad cuando se aplica a
cualquier tipo de sistema que depende
de
relaciones
formales
entre
abstracciones. Como, por ejemplo, a
las matemáticas. El desplazamiento
conceptual de «cinco naranjas» y
«cinco céntimos» a la cantidad cinco y
el número entero 5 es precisamente el
desplazamiento de Platón de «hombre»
y «hombres» a Hombre. Recuerde,
después de todo, la conclusión de
Hardy en §1c: cuando usamos una
expresión como «2 + 3 = 5», lo que
estamos expresando es una verdad
general cuya generalidad depende de la
abstracción total de los términos
involucrados. En realidad estamos
diciendo que dos cosas cualesquiera
más tres cosas cualesquiera son igual a
cinco cosas cualesquiera.
Solo que realmente nunca decimos
eso. En cambio, hablamos del número 2
y del número 5, y sobre relaciones
entre esos números. Vale la pena «una
vez más» indicar que esto podría ser
solo una maniobra semántica, o
metafísica, o ambas cosas. Y vale la
pena recordar aquellas dos cosas del
§1d sobre los sentidos predicativo y
nominativo de «longitud» y «gramo», y
los diferentes tipos de afirmaciones de
existencia envueltas en «No veo nada
en el camino» y «El hombre es curioso
por naturaleza» y «Está lloviendo». Y
entonces considerar, cuidadosamente,
las afirmaciones de existencia que
suscribimos cuando hablamos de
números. ¿Es el «5» solo algún tipo de
abreviatura intelectual para todos los
conjuntos quíntuples del mundo
real?[2.19] Parece bastante claro que no
lo es, o por lo menos que esto no es
todo lo que «5» es, pues hay montones
de cosas acerca del 5 (por ejemplo, que
5 es primo, que la raíz cuadrada de 5 es
2,236…) que no tienen nada que ver
con conjuntos de objetos reales, pero sí
tienen que ver con cierto tipo de
entidad llamada números y con sus
cualidades y relaciones. La existencia
real, aunque extraña, de los números es
también sugerida por el modo en que
muchas de esas cualidades y relaciones
—como, por ejemplo, que √5 no se
puede expresar ni como un decimal
finito ni como una razón de números
enteros— parece que en realidad son
descubiertas en lugar de ser inventadas
o propuestas y después defendidas. La
mayoría de nosotros nos sentiríamos
inclinados a decir que √5 es un
número irracional incluso si nunca
nadie demostrara realmente que lo es, o
por lo menos resulta que para negarlo
habría que comprometerse con una
teoría muy compleja y de aspecto
extraño acerca de qué son los números.
Todo este asunto es, por supuesto,
increíblemente complejo (lo cual es
una de las razones por las que
hablamos de él solo a pequeños
pedazos contextuales), porque no solo
la cuestión es abstracta, sino que todo a
lo que se refiere es una abstracción:
existencia, realidad, número… Pero
considere también por un momento
cuántos
niveles
de
abstracción
intervienen en las propias matemáticas.
En la aritmética está la abstracción del
número. Y luego está el álgebra, donde
una variable es un símbolo aún más
abstracto de algún número o números y
una función es una precisa pero
abstracta relación entre dominios de
variables. Y luego, por supuesto, están
las matemáticas de bachillerato y sus
derivadas e integrales de funciones, y
luego, ecuaciones integrales que
involucran funciones desconocidas, y
familias de funciones en el caso de las
ecuaciones diferenciales, y funciones
compuestas (que son funciones de
funciones), e integrales definidas
calculadas como la diferencia entre dos
integrales, y así sucesivamente hacia
arriba a través de la topología y el
análisis tensorial y los números
complejos y el plano complejo y los
complejos conjugados de matrices,
etc., con lo que toda la aventura se
convierte en una especie de torre de
pasteles
con
abstracciones
de
abstracciones de abstracciones que bien
vale la pena suponer que todo lo que se
está manipulando es algo real y
tangible, o si no uno se queda tan
abstraído que no puede ni sacar punta
al lápiz y mucho menos hacer cálculos.
Los aspectos más relevantes
respecto a todo esto son que la cuestión
de la realidad última de los entes
matemáticos no es solo enojosa, sino
también controvertida, y que, de hecho,
fueron las teorías de Cantor sobre el ∞
las que pusieron dicha controversia en
primer plano dentro de las matemáticas
modernas. Y que en esta controversia,
los matemáticos que tienden a
considerar las cantidades y relaciones
matemáticas como metafísicamente
reales se llaman platónicos,[2.20] y por
lo menos ahora está claro el porqué, y
el término podrá reaparecer más
adelante.
§2b.
El primer no platónico realmente serio
es Aristóteles. Sin embargo, lo que
resulta extraño e irónico de la RIV al
estilo de Zenón que Aristóteles usa
contra la metafísica de Platón es que
Aristóteles también realiza el primer y
más importante intento griego de
refutar las paradojas de Zenón. Esto
está principalmente en los Libros III, V
y VIII de la Física y en el Libro IX de
la Metafísica, cuyas discusiones sobre
Zenón acabarán teniendo un efecto
pernicioso sobre la manera en que las
matemáticas tratarán el ∞ durante los
dos milenios siguientes. Al mismo
tiempo, Aristóteles sí logra articular
las dificultades clave en por lo menos
algunas de las paradojas de Zenón, así
como plantear claramente y por
primera vez algunas cuestiones
realmente vitales relacionadas con el
∞ que nadie intentará siquiera
responder de un modo riguroso hasta el
siglo XIX. Por ejemplo: «¿Qué significa
exactamente decir que algo es
infinito?» y «¿De qué tipo de cosa
podemos
siquiera
preguntar
coherentemente si es infinita o no?»
(semiextractado de Edwards, v. 3, pág.
183).
Respecto
a
esas
cuestiones
centrales, puede que recuerde la
famosa predilección de Aristóteles por
la división y la clasificación;
literalmente le puso «analítica» a la
filosofía analítica. Véase, por ejemplo,
este fragmento de la discusión de la
dicotomía en el Libro VI de la Física:
«Pues hay dos sentidos en los que la
longitud y el tiempo y en general
cualquier cosa continua se llaman
“infinitos”: se llaman así o bien
respecto a su divisibilidad, o bien
respecto a sus extremidades [=
tamaño]» (VI, 2, 233a), la cual resulta
ser la primera ocasión en la que alguien
indica que «infinito» tiene más de un
significado.
Aristóteles
quiere
principalmente distinguir entre un
sentido fuerte o cuantitativo, al
significar literalmente infinito en
tamaño, longitud o duración, y un
sentido más débil correspondiente a la
divisibilidad infinita de una longitud
finita. La distinción realmente crucial,
afirma, involucra el tiempo: «Así,
mientras que en un tiempo finito una
cosa no puede entrar en contacto con
cosas
cuantitativamente
infinitas,
puede entrar en contacto con cosas
infinitas respecto a la divisibilidad:
pues en este sentido el tiempo mismo
es infinito» (ibíd.).
Ambas citas precedentes provienen
de dos de los principales argumentos
de Aristóteles contra la dicotomía de
Zenón, tal como se ha esquematizado
en las págs. 57-58. El objetivo de este
argumento en particular es la expresión
de la premisa (3) «en una cantidad
finita de tiempo». La conclusión de
Aristóteles es que si Zenón puede
representar el intervalo AB como la
suma de un número infinito de
subintervalos, el tiempo adjudicado
para cruzar AB debería representarse
del mismo modo: digamos
para recorrer
para
recorrer
,
,
para
recorrer
, etc. Pero este argumento
no es de gran ayuda, pues tener una
cantidad infinita de tiempo para cruzar
la calle no es menos contradictorio que
la propia dicotomía original respecto a
nuestra experiencia cuando cruzamos
la calle en diez segundos. Además, es
fácil construir versiones de las P. Z.
que no requieren explícitamente acción
o tiempo transcurrido. (Por ejemplo,
imagine un queso cuya primera porción
es = a la mitad del queso entero, y la
siguiente porción, = la mitad de la
primera porción y puntos suspensivos
ad infinitum: ¿hay una última porción
de queso o no?). La cuestión: los
contraargumentos relacionados con el
tiempo secuencial o con subintervalos
o incluso movimientos humanos reales
siempre acabarán empobreciendo la
dicotomía y no lograrán subrayar las
verdaderas dificultades involucradas.
Porque Zenón puede corregir su
presentación y simplemente decir que
estar en A y luego estar en B requiere
que usted ocupe los infinitos puntos
correspondientes a la secuencia
, o, peor, que
llegar a B en absoluto implica que
usted haya ocupado ya una secuencia
infinita de puntos. Y esto parece
contradecir bastante claramente la idea
de una secuencia infinita: si «∞»
significa realmente «sin fin», entonces
una secuencia infinita es una secuencia
donde, sin importar cuántos términos
se tomen, todavía quedan términos
restantes. O sea, que podemos
olvidarnos de cruzar calles o tocarnos
la nariz. Zenón puede hacer girar su
molinillo en términos de secuencias
abstractas y de que hay algo
inherentemente
contradictorio
o
paradójico en la idea de que una
secuencia infinita jamás pueda
completarse.
Contra esta segunda versión más
abstracta y dañina de la dicotomía,
Aristóteles lanza su argumento más
influyente. Este depende de la
semántica de «infinito», también, pero
es diferente, y se centra en el mismo
tipo de cuestiones predicativas que
surgen en el U. S. M. y en la paradoja
de la ubicación de Zenón. Tanto en la
Física como en la Metafísica,
Aristóteles traza una distinción entre
dos cosas distintas que podemos querer
decir en realidad cuando usamos
«haber» + ∞ en una oración
predicativa como «Hay un número
infinito de puntos que deben ser
ocupados entre A y B». La distinción es
solo superficialmente gramatical; en
realidad, es una distinción metafísica
entre dos afirmaciones de existencia
radicalmente diferentes implícitos en
el «hay» de la oración. La dicotomía
parece depender de que no veamos
esto. La distinción es entre realidad y
potencialidad
como
cualidades
predicativas, y la argumentación
general de Aristóteles es que el ∞ es
un tipo especial de cosa que existe
potencialmente pero no realmente, y
que los predicados con la palabra
«infinito» deben aplicarse a las cosas
de un modo correspondiente, como
demuestra la confusión de la
dicotomía. De manera específica,
Aristóteles afirma que ninguna
extensión espacial (por ejemplo, el
intervalo AB) es «realmente infinita»,
pero que cualquiera de tales
extensiones
es
«potencialmente
infinita» en el sentido de ser
infinitamente divisible.
Todo esto se vuelve muy elaborado
y complejo, por supuesto: se dedican
carreras enteras a estudiar de manera
sesuda las definiciones de Aristóteles.
Baste decir aquí que la cuestión de la
existencia-real-o-potencial-del-∞ es
vital para nuestro relato general aunque
reconozcamos su dificultad. No ayuda
mucho que las propias explicaciones y
ejemplos de Aristóteles…
Es
como
el
que
está
construyendo respecto al que
tiene la capacidad de construir,
o el despierto respecto al
dormido, o el que está viendo
respecto al que tiene los ojos
cerrados pero puede ver.
Definamos la realidad mediante
uno de los miembros de esta
antítesis, y la potencialidad
mediante el otro. Pero no
afirmamos que todas las cosas
tengan existencia real en el
mismo sentido, sino solo por
analogía, como A en B o
respecto a B, C en D o respecto
a D, pues algunas son como el
movimiento respecto a la
potencia, y las otras como la
sustancia respecto a algún tipo
de materia… (Metafísica, IX, 6,
1048a-b)
… no son exactamente prodigios de
claridad. Lo que quiere decir con
«potencial» es, póngase énfasis en esto,
no el tipo de potencialidad por el cual
una niña es potencialmente una mujer o
una bellota es un roble en potencia. Es
más bien como el extraño y abstracto
tipo de potencialidad por el cual una
copia perfecta de la Pietà[2.21] de
Miguel Ángel existe potencialmente en
un bloque de mármol intacto. O,
hablando del ∞, el modo en que
cualquier cosa que suceda cíclicamente
(o,
en
términos
de
A.,
«sucesivamente»)
—como,
por
ejemplo, que sean las 6:54, lo cual
ocurre cada día puntualmente— para
Aristóteles es potencialmente infinita
en el sentido de que es posible una
recurrencia periódica sin fin de que
sean las 6:54, aunque el conjunto de
todos los momentos 6:54 no puede ser
realmente infinito porque nunca
coexistirán todos los 6:54: el ciclo
periódico
nunca
será
«completado».[2.22]
Probablemente pueda usted ver
cómo va a desarrollarse todo esto en
relación con la dicotomía. Pero
también tiene su truco. Las analogías
de la estatua y de las 6:54 aquí no van a
funcionar demasiado bien. Cierto, el
intervalo AB y/o el conjunto de todos
los subintervalos o puntos entre A y B
no es «realmente infinito» sino solo
«potencialmente infinito». Pero aquí el
sentido en el que Aristóteles quiere
decir que «AB es potencialmente
infinito» es más cercano a la idea,
digamos, de precisión infinita en la
medición. Lo cual se puede ilustrar del
siguiente modo. La altura actual de mi
sobrina mayor, que es de unos 97,9 cm,
puede precisarse hasta 97,87 cm, y con
un entorno más controlado y
equipamiento sofisticado sin duda
alguna podría precisarse todavía más y
más, hasta tres, once o n decimales,
donde n es, potencialmente, ∞; pero
solo potencialmente ∞, porque es
obvio que en el mundo real nunca
habrá ninguna manera de lograr una
precisión verdaderamente infinita,
aunque sea posible «en principio». De
esta manera, para Aristóteles, AB es
«en principio» infinitamente divisible,
aunque esta división infinita nunca se
puede llevar a cabo con toda verdad en
el mundo real.
SEI Un poco de complicación final:
En su mayor parte, lo que Aristóteles
llama «número» (en el sentido de las
cantidades matemáticas en general)
aparentemente
es
potencialmente
infinito no en el modo en que la
medición es potencialmente infinita,
sino en el modo en que el conjunto de
todos
los
instantes
6:54
es
potencialmente infinito. Por ejemplo,
el conjunto de todos los enteros es
potencialmente infinito en el sentido de
que no hay un número entero mayor
que los demás («En la dirección del
tamaño siempre es posible pensar en un
número
de
tamaño
mayor»
[Aristóteles, Física, III, 6, 207b]), pero
no es realmente infinito porque el
conjunto no existe como una entidad
completa. En otras palabras, para
Aristóteles los números forman un
continuo sucesivo: hay una cantidad
infinita pero nunca coexisten («Se
puede tomar una cosa tras otra sin fin»
[ibíd., 206b]).
Como refutación de la dicotomía de
Zenón, la distinción ∞-potencialrespecto-a-∞-real no es demasiado
persuasiva, evidentemente ni siquiera
para Aristóteles, cuya regresión del
Tercer Hombre parece que se podría
descartar como solo potencialmente
infinita. Pero la distinción acaba
resultando enormemente importante
para la teoría y la práctica de las
matemáticas. En resumen, relegar el ∞
al estatus de potencialidad permitió
que las matemáticas occidentales, o
bien descartaran las cantidades
infinitas, o bien justificaran su uso, o a
veces ambas cosas, dependiendo de las
intenciones. Es todo muy extraño. Por
un lado, el argumento de Aristóteles
dio credibilidad al rechazo griego del
∞ y de la «realidad» de las series
infinitas, y fue una razón importante
por la que los griegos no desarrollaron
lo que ahora conocemos como cálculo.
Por otro lado, otorgar a las cantidades
infinitas por lo menos una existencia
abstracta o teórica permitió que
algunos matemáticos griegos las usaran
en
técnicas
que
eran
extraordinariamente
parecidas
al
cálculo diferencial e integral; tan
parecidas que, en retrospectiva, es
sorprendente que el cálculo tardara mil
setecientos años en ser inventado. Pero,
volviendo al primer punto, una gran
razón por la que tardó tantos años fue
la penumbra metafísica a la que
Aristóteles, con su concepto de
potencialidad, había desterrado el ∞, y
que servía para legitimar la alergia de
las matemáticas a un concepto que de
todos modos nunca podría tratar.
Excepto que —volviendo al
segundo punto o ya en un tercer punto
—[2.23] cuando Leibniz y Newton
introducen realmente el cálculo hacia
1700, es esencialmente la metafísica de
Aristóteles la que justifica su
despliegue de infinitesimales, o sea dx
en la infame
de las
matemáticas de primer año en la
universidad. Recuerde, por favor, o
sepa, que una cantidad infinitesimal de
algún modo está lo bastante cerca de 0
para ser despreciable en una suma, es
decir x + dx = x, y lo bastante lejos de
0 para servir como divisor en fórmulas
como la que acabamos de ver. De
nuevo, muy brevemente, tratar los
infinitesimales
como
cantidades
potencialmente/teóricamente existentes
permitió que los matemáticos las
usaran en cálculos que tenían
extraordinarias aplicaciones en el
mundo real, pues eran capaces de
abstraer y describir justamente los
tipos de fenómenos suavemente
continuos que el mundo contenía. Estos
infinitesimales resultan ser muy
importantes. Sin ellos puede usted caer
en grietas como la cuestión de
0,999… = 1,0 a la que hemos echado
un vistazo en §1c. Como prometimos
entonces, la salida más rápida en este
caso es permitir que x represente no
0,999…, sino 1 menos cierto
infinitesimal, al que llamaremos , tal
que 1 >
> 0,999… Entonces
se pueden hacer
operaciones que antes:
las
mismas
10x =
,
− x, que es =
da 9x =
en cuyo caso x todavía da
,
,
y
no hay ninguna fea confabulación con
1,0.
Excepto, claro está, que la cuestión
es si tiene sentido metafísico o
matemático postular la existencia, ya
sea real o potencial, de cierta cantidad
que es < 1 pero a la vez excede el
decimal infinito 0,999… El problema
es doblemente abstracto, porque no
solo 0,999… no es una cantidad del
tipo de las del mundo real, sino que es
algo que ni siquiera podemos concebir
como un ente matemático: sea cual sea
la relación entre 0,999… y
existe[2.24] más allá del decimal
n-ésimo, un lugar al que nada ni nadie
puede llegar nunca, ni siquiera en
teoría. Así que no queda claro si no
estamos simplemente cambiando un
tipo de grieta paradójica por otro. Este
es un tipo más de cuestión de las que
fueron totalmente polémicas hasta que
llegaron Weierstrass, Dedekind y
Cantor en el siglo XIX.
Piense lo que piense usted de la
ontología de tipo potencial de
Aristóteles para el ∞, observe que por
lo menos estuvo muy acertado en el
uso de palabras como «punto» y
«existen» en la oración no predicativa
«Hay [= existen] un número infinito de
puntos intermedios entre A y B». Igual
que en la paradoja de la ubicación de
Zenón, obviamente aquí hay alguna
imprecisión semántica. En la dicotomía
revisada, la imprecisión se halla en la
correspondencia implícita entre un ente
matemático abstracto —en este caso
una serie geométrica— y el espacio
físico real. Pero no está claro que
«existir» sea el blanco más vulnerable:
hay una ambigüedad bastante más
obvia en la semántica de «punto». Si A
y B son los dos lados de una calle del
mundo real, entonces la expresión «el
número infinito de puntos entre A y B»
está usando «punto» para denotar una
ubicación precisa en el espacio físico.
Pero en la expresión «el número
infinito
de
puntos
intermedios
designado por
», «punto» se refiere
a una abstracción matemática, un ente
sin dimensión, con «posición pero no
magnitud». Para ahorrarnos varias
páginas de concienzudo análisis que
puede usted hacer en su tiempo
libre,[2.25]
aquí
observaremos
simplemente que cruzar un número
infinito de puntos matemáticos sin
dimensión no es obviamente paradójico
del modo en que lo es cruzar un
número infinito de puntos del espacio
físico. Respecto a esto, el argumento de
Zenón puede parecerse más bien al
rompecabezas de los tres-hombres-enun-motel del §1: la traducción de una
situación esencialmente matemática al
lenguaje natural nos lleva a olvidar que
las palabras normales pueden tener
significados y referentes enormemente
distintos. Observe, una vez más, que el
simbolismo
abstracto
y
el
esquematismo de las matemáticas
puras están diseñados para evitar
precisamente este problema, y que este
es el motivo por el que las definiciones
matemáticas técnicas a menudo son tan
soporíferamente densas y complejas.
No debe caber ninguna ambigüedad o
equivocación. Las matemáticas, como
medir la altura de los niños, son una
actividad consagrada al ideal de la
precisión.
Lo cual suena todo muy bien,
excepto que resulta que también hay
una inmensa ambigüedad —formal,
lógica, metafísica— en muchos de los
términos y conceptos básicos de las
matemáticas mismas. De hecho, los
conceptos
matemáticos
más
fundamentales habitualmente son los
más difíciles de definir. Esto en sí
mismo es una característica de los
sistemas formales. La mayor parte de
las definiciones matemáticas están
construidas a partir de otras
definiciones. Son las cosas realmente
básicas las que tienen que definirse a
partir de casi nada. Con un poco de
suerte, y por razones que ya se han
analizado, esas cosas básicas tendrán
algo que ver con el mundo en el que
realmente vivimos todos.
§2c.
Volvamos por un momento al tema de
Zenón-y-la-semántica-de-«punto». La
relación entre un ente matemático (por
ejemplo, una serie, un punto
geométrico) y el espacio físico real es
también la relación de lo discreto con
lo continuo. Piense en un camino
adoquinado en contraste con una
carretera recién asfaltada. Como lo que
la dicotomía intenta hacer es
descomponer un proceso físico
continuo en una serie infinita de pasos
discretos, puede verse como el primer
intento en la historia de representar la
continuidad matemáticamente. No
importa que Zenón en realidad
estuviera intentando demostrar que la
continuidad era imposible; igualmente
fue el primero. También fue el primero
en reconocer[2.26] que hay más de un
tipo de ∞. El to apeiron de la
cosmología griega es pura extensión,
tamaño infinito, y la serie de enteros 1,
2, 3… asciende y se aleja hacia ese
mismo tipo de Gran ∞. Mientras que
por otro lado el Pequeño ∞ de Zenón
parece estar como anidado, en medio
de los enteros ordinarios, y esto último
es naturalmente difícil de concebir.
Resulta que la manera más clara de
representar estos dos tipos diferentes
de ∞ es con la buena y vieja recta
numérica (R. N.), componente habitual
de las aulas escolares.[2.27] La recta
numérica es otro legado de los griegos,
que, como recordará, trataban los
números y las formas geométricas casi
del mismo modo. (Euclides, por
ejemplo,
rechazaba
cualquier
razonamiento matemático que no
pudiera ser «construido», es decir,
demostrado conforme a la geometría.)
[2.28] Lo que debemos valorar de la
recta numérica y su modesto
matrimonio
de
matemáticas
y
geometría es que también se trata de la
perfecta unión entre forma y contenido.
Porque cada número corresponde a un
punto, y como la recta numérica a la
vez contiene todos los puntos y
determina su orden, los números
pueden definirse completamente según
su posición en la R. N. en relación con
las posiciones de otros números. Por
ejemplo, 5 es el entero inmediatamente
a la derecha de 4 y a la izquierda de 6,
y decir que 5 + 2 = 7 es como decir
que 7 está dos posiciones a la izquierda
de 5; es decir, la «distancia»
matemática entre dos números
distintos puede ser representada e
incluso calculada de forma gráfica.
Incluso sin el cero o enteros
negativos[2.29], y con la definición más
bien difusa de «punto» dada por
Euclides como «aquello que no tiene
parte», la recta numérica es una
herramienta inmensamente poderosa.
También resulta ser la perfecta
esquematización de un continuo, en el
sentido de «ente o sustancia cuya
estructura o distribución es continua e
ininterrumpida», y como tal la R. N.
encarna perfectamente la antinomia de
la continuidad que Zenón propuso y
nadie hasta Dedekind pudo resolver.
Pues en la R. N. se cumplen las dos
cosas siguientes: (1) Cada punto está
próximo a otro punto, (2) Entre dos
puntos cualesquiera siempre hay otro
punto.
Aunque todo el mundo sabe qué
aspecto tiene, la recta numérica[2.30] se
reproduce aquí, empezando por el 0
que los griegos, por motivos que ahora
no importan, no tenían:
Si el Gran ∞, el infinito en
extensión,
está
a
la
derecha
interminable de la recta numérica, el
Pequeño ∞ que Zenón explota se halla
en el intervalo de aspecto totalmente
finito entre 0 y 1. Zenón revela que
dicho intervalo contiene un número
infinito de puntos intermedios, como la
secuencia
Lo que es más (por
decirlo así), está claro que este infinito
de
no agota realmente los puntos
entre 0 y 1, pues omite no solo
sucesiones infinitas convergentes como
,
,
,
, …,
,
,
,
, …,
etc., sino otro conjunto infinito de
fracciones
donde x es un número
impar. Y al considerar que cada una de
dichas fracciones corresponderá a su
propia sucesión geométrica infinita a
través del desarrollo de
ejemplo, , ,
,
, …, ,
—por
,
,
…, etc.— parece que el
intervalo finito 0-1 de la R. N. en
realidad aloja una infinidad de
infinitos. Lo cual es, por decirlo con
suavidad, metafísicamente confuso y a
la vez matemáticamente ambiguo:
¿será ∞2, ∞∞, o qué?
Solo que la cosa empeora, o
mejora. Porque todos los números
recién mencionados son racionales.
Probablemente ya sabe que ese adjetivo
proviene de «razón» y que la expresión
«los números racionales» se refiere a
todos los números expresables como
enteros o como razones de dos enteros
(o sea, fracciones). Esto es solo un
recordatorio, pero es importante. El
descubrimiento de que no todos los
números son racionales fue por lo
menos tan duro para la visión griega
del mundo como las paradojas de
Zenón. Y fue especialmente enojoso
para la Divina Hermandad de
Pitágoras. Recuerde las convicciones
pitagóricas de que todo es una cantidad
o razón matemática y de que nada
infinito puede existir realmente en el
mundo (pues «peras → forma» es lo
que hace posible la existencia para
empezar).
Luego recuerde el teorema de
Pitágoras. Como se ha mencionado,
una curiosidad interesante es que los de
la D. Η. P. no fueron los verdaderos
descubridores de ese teorema. En
realidad aparece en tablillas de la
Antigua Babilonia tan tempranas como
del 2000 a. C. Una razón por la que se
llama teorema de Pitágoras es que
permitió que la D. Η. P. descubriera las
«magnitudes
inconmensurables»,
también
llamadas
números
irracionales.[2.31] Dichos números, que
resultan ser inexpresables como
cantidades finitas, eran tan letales para
la metafísica pitagórica que su
descubrimiento fue como la versión
griega del caso Watergate. Recordará
de la infancia que el teorema de
Pitágoras no causa problemas con
figuras como el triángulo rectángulo de
lados 3, 4 y 5 que aparece en las
introducciones a la geometría, donde la
suma de los cuadrados de 3 y 4 es un
número cuya propia raíz cuadrada es
racional. Pero comprenda que eso de
los «cuadrados» era literal para los
griegos. Es decir, en un triángulo de
lados 3, 4 y 5 trataban cada lado
también como el lado de un cuadrado:
y entonces sumaban las áreas de los
cuadrados. Hay dos razones por las que
esto merece comentarse. La primera ya
se ha mencionado antes: aunque ahora
jugamos con exponentes y raíces in
abstractus, para los griegos los
problemas de matemáticas siempre se
formulaban,
y
resolvían,
geométricamente. Un número racional
era una razón literal de las longitudes
de dos segmentos. Elevar al cuadrado
era construir un cuadrado y tomar su
área. La otra razón es que según la
mayoría de los relatos fue un simple y
humilde cuadrado el que empezó todo
el
embrollo.
Considérese
específicamente el familiar cuadrado
unidad, de lado 1, e incluso más en
concreto el triángulo rectángulo
isósceles cuya hipotenusa es la
diagonal del cuadrado unidad:
De lo que se dio cuenta la D. Η. P.
(probablemente a través de mediciones
reales y cada vez más frenéticas) es
que por pequeña que sea la unidad de
medida usada, el lado del cuadrado
unidad es inconmensurable con la
diagonal, es decir, no es medible con la
diagonal. Esto significa que no hay
ningún número racional
= . La cantidad
tal que
era algo que la
D. Η. P. acabó llamando arratos, «lo
que no tiene razón», o —como logos
podía significar a la vez palabra y
proporción— alogos, que por lo tanto
significaba a la vez «lo que no tiene
proporción» y «lo que no puede ser
dicho».
La
demostración
de
la
inconmensurabilidad de
es otro
famoso caso de demostración por
reducción
al
absurdo,
y
una
especialmente bonita porque es muy
simple y solo requiere matemáticas
elementales. Veamos. En primer lugar,
para los propósitos de la reducción al
absurdo, supóngase que D y S son
conmensurables. Esto significa que
es igual a alguna razón
donde p y q
son enteros sin ningún factor común
aparte de 1. Sabemos por el teorema de
Pitágoras
que
D2 = S2 + S2,
o
D2 = 2S2, lo cual si
=
significa que
p2 = 2q2. También sabemos que el
cuadrado de cualquier número impar
será impar y el cuadrado de cualquier
número
par
será
par
(puede
comprobarlo usted mismo). Además,
sabemos que el doble de cualquier
número entero es un número par. Esa
es toda la artillería que necesitamos.
Por la LTE, o bien p es impar, o bien p
es par. Si (1) p es impar, hay una
contradicción inmediata, pues 2q2 tiene
que ser impar. Pero si (2) p es par, eso
significa que es igual al doble de algún
número, digamos 2r, así que
introduciendo dicha equivalencia en la
ecuación original p2 = 2q2 se obtiene
4r2 = 2q2, lo cual se reduce a 2r2 = q2,
lo que significa que q2 es par, lo que
evidencia que q es par, lo cual quiere
decir que p y q son ambos pares, en
cuyo caso tienen un factor común
distinto de 1, lo cual de nuevo es una
contradicción,
(1)
Arroja
una
contradicción,
(2)
arroja
una
contradicción, y no hay (3). Así que D
y S son inconmensurables. Fin de la
demostración.[2.32]
El hecho de que los números
racionales no pudieran expresar algo
tan cotidiano como la diagonal de un
cuadrado —por no mencionar otros
irracionales hipotenoides fáciles de
construir como √5, √8, etc.—
obviamente era desestabilizante para
toda la cosmogonía de los pitagóricos.
Al parecer, el golpe de gracia fue el
descubrimiento de que su amada razón
áurea
era
también
irracional,
resultando
ser
(1 + √5)
o
1,618034… Hay todo tipo de
espeluznantes relatos apócrifos acerca
de los extremos a los que llegó la
D. Η. P. para mantener en secreto la
existencia[2.33] de los irracionales, algo
que nos podemos saltar porque son
mucho más importantes, histórica y
matemáticamente, los propios números
irracionales. Son importantes por lo
menos
por
tres
razones.
(1)
Matemáticamente,
los
números
irracionales son una consecuencia
directa de la abstracción. Están un
nivel entero por encima de las 5
naranjas o el
queso. No se encuentran
números irracionales hasta que se
empiezan
a
generar
teoremas
abstractos como el T. P. Y observe, por
favor, que en realidad solo son una
grieta para las matemáticas puras. Los
egipcios y otros pueblos se habían
encontrado con números irracionales
en la agrimensura y la ingeniería, pero
como solo les importaban las
aplicaciones prácticas no tenían ningún
problema en tratar la √2 como 1,4 o .
(2) El descubrimiento
irracionales
señaló
la
de los
primera
verdadera divergencia entre las
matemáticas y la geometría, pues los
matemáticos podían entonces crear
números que los geómetras no podían
medir realmente. (3) Resulta que los
irracionales, como los
de Zenón, son
una consecuencia de intentar expresar y
explicar la continuidad con respecto a
la recta numérica. Los números
irracionales son el motivo por el que la
recta numérica no es técnicamente
continua. Como la RIV de la
dicotomía, los irracionales representan
huecos o agujeros en la recta numérica,
intersticios a través de los cuales el
caos ilimitado del ∞ podía entrar y
provocar un lío en las pulcras
matemáticas de la Ática.
Y no es solo un problema griego.
Porque lo importante de los números
irracionales es que no pueden ser
representados por fracciones; y,
además, si usted intenta expresar
irracionales en notación decimal,[2.34]
entonces la secuencia de dígitos tras la
coma no será ni finita (como en el caso
de los decimales racionales 2,0 o 5,74)
ni periódica (lo que significa una
repetición según alguna pauta, como en
el caso de los racionales 0,333… = ,
1,181818… =
, etc.).[2.35]
Esto significa que, por ejemplo, la
expresión decimal de √3 puede
desarrollarse hasta 1,732, o 1,73205, o
1,7320508, o, literalmente, hasta donde
usted quiera… o más lejos. Y a su vez
esto significa que cierto punto definido
de la recta numérica —o sea, el punto
correspondiente al intervalo que,
multiplicado
por
sí
mismo,
corresponde al punto-entero 3— no
puede ser nombrado ni expresado de
modo finito.[2.36]
Así, el intervalo finito 0-1 de la
recta numérica está aún más
inconcebiblemente poblado. No solo
hay una cantidad infinita de secuencias
infinitas de fracciones, sino también
una
cantidad
infinita
de
irracionales,[2.37] cada uno de los
cuales es a su vez numéricamente
inexpresable excepto como una
secuencia infinita de decimales no
periódicos. Hagamos una pausa para
considerar los vertiginosos grados de
abstracción involucrados en esto. Si la
CPU humana no puede aprehender o
incluso concebir siquiera el ∞, parece
que ahora se le pide dar cuenta de una
infinidad de ∞, de la cual una cantidad
infinita de miembros individuales son a
su vez inexpresables con finitud, y
todos en un intervalo tan finito y de
aspecto tan inocente que se usa en la
clase de los niños pequeños. Todo lo
cual suena muy extraño.
Desde luego, hay tantas maneras de
tratar
esa
extrañeza
como
connotaciones tiene «tratar». Los
griegos,* por ejemplo, simplemente
rehusaron tratar los irracionales como
números. O bien los incluían en la
categoría
de
longitudes/áreas
puramente geométricas y no los usaban
nunca en sus matemáticas per se, o
bien racionalizaban literalmente el uso
de irracionales manipulando su
aritmética (ejemplo: los pitagóricos
usaron el truco de escribir 2 como
de modo que pudieran tratar la √2
como ).[2.38] Si su rechazo a reconocer
la existencia de números dados por su
propio
razonamiento
matemático
parece algo peculiar, sepa que hasta el
siglo XVIII prácticamente todos los
grandes matemáticos europeos hicieron
lo mismo,[2.39] incluso cuando la
legendaria revolución científica estaba
empezando a dar todo tipo de
resultados que requerían una aritmética
de los irracionales. Hasta finales del
siglo XIX,* de hecho, nadie* daría con
una teoría rigurosa o incluso una
definición de los irracionales. La mejor
definición
vendría
de
Richard
Dedekind,* mientras que el tratado más
exhaustivo del estatus de los números
reales en la recta sería el de Georg
Cantor.
§2d.
* INTERPOLACIÓN INEVITABLE
PERO AL FIN Y AL CABO DE TIPO
SEI
Omita las siguientes páginas si lo
desea, pero los asteriscos en el párrafo
precedente
marcan
cosas
que
históricamente hablando no son 100%
verdad. A saber: un estudiante y
protegido de Platón conocido como
Eudoxo de Cnidos (408-354 a. C.) en
realidad se aproximó mucho a una
definición rigurosa de los irracionales,
que luego Euclides incluyó como
Definición 5 en el Libro V de los
Elementos. La definición de Eudoxo
incluye proporciones y razones
geométricas, lo cual no es nada
sorprendente dado que las matemáticas
griegas se habían visto confrontadas
con los irracionales en forma de ciertas
proporciones geométricas que no
podían expresarse como razones. Tras
la debacle de la D. Η. P., esas
magnitudes inconmensurables parecían
estar por todas partes. Por ejemplo,
considérese un rectángulo en el que dos
de los lados son iguales a la diagonal
del cuadrado unidad: ¿cómo se supone
que debe calcularse su área? Y lo que
es más importante: ¿cómo podían los
griegos distinguir los casos de
inconmensurabilidad de tipo irracional
de los casos donde simplemente se
tienen
magnitudes
de
especies
diferentes que no se pueden comparar
mediante razones, como una longitud
respecto a un área, o un área respecto a
un volumen 3D? En realidad, Eudoxo
fue el primer griego que intentó definir
«razón» de forma matemática:
Se dice que unas magnitudes
tienen la misma razón, la
primera respecto a la segunda y
la tercera respecto a la cuarta,
cuando,
si
cualesquiera
equimúltiples se tomen de la
primera y de la tercera, y
cualesquiera equimúltiples de la
segunda y de la cuarta, los
primeros equimúltiples a la vez
exceden, a la vez igualan, o a la
vez son inferiores a los
segundos
equimúltiples
tomados
en
el
orden
correspondiente (Euclides en
Heath, v. 2, pág. 114).
… la opacidad de lo cual puede
mitigarse traduciendo algunas partes
del teorema de lenguaje natural a
símbolos matemáticos básicos. La
definición de Eudoxo afirma que,
dados , , y los enteros a y b,
=
si
y solo si (ap < bq) → (ar < bs) y
(ap = bq) → (ar = bs) y (ap > bq) →
(ar > bs). A primera vista, esto puede
parecer obvio o trivial;[2.40] véase, por
ejemplo, cuánto se parece a la regla
que aprendimos en la escuela para
multiplicar fracciones en cruz. Pero en
realidad no es nada trivial. Aunque
Eudoxo solo pretendía aplicarla a
magnitudes geométricas más que a
números per se, la definición funciona
perfectamente para identificar y
distinguir números racionales de
números irracionales y de cantidades
geométricas
inmisciblemente
diferentes, etc. Además, observe, por
favor, el modo en que la definición de
Eudoxo resulta efectiva para operar en
un conjunto infinito completo, por
ejemplo, el
de los números
racionales.[2.41] Lo que Eudoxo hace es
usar enteros arbitrarios para especificar
una división[2.42] del conjunto de todos
los racionales en dos subconjuntos: el
conjunto de todos los racionales para
los cuales ap ≤ bq y el conjunto de
todos los racionales para los cuales
ap > bq. El suyo es, pues, el primer
teorema capaz de referirse, exhaustiva
y específicamente,[2.43] a una colección
infinita completa. Desde este punto de
vista se le podría llamar el primer
resultado significativo en teoría de
conjuntos, unos dos mil trescientos
años antes de la invención de la teoría
de conjuntos.
También vale la pena señalar que
en las matemáticas probablemente no
hay mejores ejemplos del dicho de
Russell sobre los caprichos de la fama
intelectual que Eudoxo y su
colaborador póstumo Arquímedes
(287-212 a. C.). El segundo, está claro,
es famoso anecdóticamente por su
«¡Eureka!», pero a la vista de nuestros
propósitos generales sería injusto no
reconocer que él y Eudoxo, en cierta
medida, inventaron las matemáticas
modernas, las cuales tuvieron que ser
reinventadas varios siglos después
porque nadie se había preocupado de
prestar atención a las consecuencias de
sus resultados.
Probablemente, su invento más
importante es la conocida propiedad de
exhaustación, que Eudoxo descubrió y
Arquímedes refinó. Era un modo de
calcular las áreas y volúmenes de
superficies y figuras curvadas, algo con
lo que la geometría griega, obviamente,
tenía muchos problemas (pues es
respecto a las curvas donde se
encuentran la mayor parte de los
problemas de la continuidad y los
irracionales). Los geómetras anteriores
a Eudoxo habían tenido la idea de
aproximar el área de una figura curva
comparándola
con
polígonos
regulares[2.44] cuyas áreas podían
calcular con exactitud. Como ejemplo,
véase cómo el mayor cuadrado que
puede caber dentro de un círculo
funciona como una burda aproximación
del área del círculo:
mientras que, digamos, el mayor
octágono que cabe dentro será una
aproximación algo mejor:
y así sucesivamente, siendo lo
importante que cuantos más lados
tenga el polígono inscrito, más
próxima será su área a la del propio
círculo. La razón por la que el método
nunca funcionó realmente es que se
necesitaría un polígono de ∞ número
de lados para acertar el área del
círculo, e incluso si este ∞ era solo
uno de los ∞ potenciales de
Aristóteles, los griegos todavía estaban
estancados, por la misma razón
mencionada respecto a la dicotomía: no
tenían el concepto de convergencia
hacia un límite. Eudoxo dio a las
matemáticas justamente este concepto
con su introducción de la propiedad de
exhaustación, que aparece como la
Propiedad 1 en el Libro X de los
Elementos:
Si de cualquier magnitud se
sustrae una parte no menor que
su mitad, y si del resto se
sustrae otra vez no menos que
su mitad, y si este proceso de
sustracción
se
continúa,
finalmente
quedará
una
magnitud menor que cualquier
magnitud
preasignada
del
mismo tipo (Euclides en Boyer,
pág. 91).
En notación moderna, esto es
equivalente a decir que si p es una
magnitud dada y r una razón tal que
≤ r < 1,
entonces
el
límite
de
p(1 − r)n es 0 cuando n tiende a ∞; es
decir,
p(1 − r)n = 0. Esto permite
aproximar de forma arbitraria un
polígono de una infinidad de lados, o
un número infinito de rectángulos bajo
una curva, siendo cada lado/rectángulo
arbitrariamente (= infinitesimalmente)
pequeño, y luego sumar los lados o las
áreas mediante la inversa del mismo
proceso por el que se han obtenido. El
método de exhaustación es, a todos los
efectos, el bueno y antiguo cálculo
integral. Con él, Eudoxo fue capaz de
demostrar, por ejemplo, que la razón de
las áreas de dos círculos cualesquiera
es igual a la razón de los cuadrados de
sus radios, que el volumen de un cono
es
del volumen del cilindro con la
misma base y altura, etc. Y la obra de
Arquímedes Medición de un círculo
usa la exhaustación para obtener una
aproximación sin precedentes de π,
según
<π<
.
Obsérvese también la precaución
metafísica de las entidades abstractas
de la exhaustación. El método de
Eudoxo para conseguir que lados o
figuras infinitamente pequeños entren
en las ecuaciones no hace afirmaciones
acerca de la existencia de magnitudes
infinitamente pequeñas. Fíjese en el
lenguaje
suave
de
la
citada
Proposición 1 de los Elementos. El
«menor que cualquier magnitud
preasignada»
es
particularmente
brillante y sorprendentemente similar
al «arbitrariamente grande/pequeño»
del
análisis
moderno.[2.45]
Básicamente, supone decir que, para
propósitos matemáticos, se pueden
alcanzar magnitudes tan pequeñas
como se quiera, y trabajar con ellas. Es
esta preocupación por el método y los
resultados más que por la ontología lo
que hace a Eudoxo y a Arquímedes tan
misteriosamente modernos. El modo en
que sus «magnitudes menores que
cualesquiera magnitudes preasignadas»
son creadas y desplegadas en la
exhaustación viene a ser idéntico al
modo en que los infinitesimales serán
tratados en el cálculo temprano.
Por qué, entonces, Europa tuvo que
esperar diecinueve siglos hasta el
verdadero cálculo, la geometría
diferencial y el análisis constituye una
muy larga historia, que esencialmente
explica el mencionado dicho de
Russell. Una causa es la misma razón
por la que nadie pensó en aplicar la
exhaustación a la dicotomía de Zenón:
a los griegos solo les importaba la
geometría, y entonces nadie pensaba en
el movimiento y la continuidad como
abstraíbles en la geometría de la recta
numérica. Otra razón es Roma, la
Imperial, cuyo saqueo de Siracusa y
asesinato de Arquímedes hacia el 212
a. C. puso fin bruscamente a la
matemática helénica,[2.46] y cuya
hegemonía
durante
los
siglos
posteriores conllevó que gran parte de
la sustancia y el impulso de las
matemáticas griegas se perdiera
durante mucho tiempo. La causa más
eficiente, sin embargo, fue Aristóteles,
cuya influencia, por supuesto, no solo
sobrevivió a Roma sino que alcanzó
nuevas cimas con la expansión del
cristianismo y la Iglesia en el período
500-1300 d. C., aproximadamente.
Resumiendo: la doctrina aristotélica se
convirtió en dogma de la Iglesia, y
parte de la doctrina aristotélica era la
consideración del ∞ como solo
potencial, una ficción abstracta y
origen de confusión, to apeiron,
territorio reservado solo a Dios, etc.
Esta
visión
predominó
fundamentalmente hasta la era
isabelina.
FIN DE LA INTERPOLACIÓN
§2e.
(Continuación de §2c desde el párrafo
de la pág. 84 con asteriscos de
interpolación).
Aquí
están, a modo de aperitivo,
algunas de las cosas que Cantor[2.47]
acabó descubriendo sobre los ∞
anidados de Zenón y Eudoxo. Aquí
«descubierto»
no
quiere
decir
simplemente
encontrado,
sino
realmente demostrado. La recta
numérica es, obviamente, infinitamente
larga y contiene una infinidad de
puntos. Incluso hay tantos puntos en el
intervalo 0-1 como en la recta
numérica entera. De hecho, hay tantos
puntos en el intervalo 0,00000000010,0000000002 como en toda la R. N.
También resulta que hay tantos puntos
en el mencionado microintervalo (o en
uno un cuatrillón de veces más
pequeño, si usted quiere) como en el
plano 2D —incluso si este plano es
infinitamente grande— o en cualquier
forma 3D, o en la totalidad del propio
espacio 3D infinito.
Es más, sabemos que hay una
infinidad de números racionales en la
recta numérica infinita, y (por cortesía
de Zenón) que dichos racionales son
tan infinitamente densos en la recta que
literalmente ningún número racional
dado tiene un siguiente; es decir, entre
dos números racionales cualesquiera de
la R. N. siempre se puede encontrar un
tercero. Un hecho del cual aquí
tenemos una breve demostración.
Tomemos dos racionales distintos p y
q. Como son diferentes, p ≠ q, lo cual
implica que uno es mayor que el otro.
Digamos que es p > q. Esto significa
que en la recta numérica hay por lo
menos alguna distancia medible, por
pequeña que sea, entre q y p. Tomemos
esa distancia, dividámosla por algún
número (2 es el más fácil), y añadamos
el cociente al número más pequeño q.
Tenemos un nuevo número racional,
, entre p y q. Y como el
número de números simplemente
enteros por los cuales podemos dividir
(p − q) antes de añadir el cociente a q
es infinito, en realidad hay una
infinidad de puntos racionales entre
cualesquiera p y q. Dejemos que esto
vaya calando, y entonces tengamos en
cuenta que incluso dada la densidad
infinita de la cantidad infinita de
números racionales en la recta
numérica, puede demostrarse que el
porcentaje total de espacio de la R. N.
ocupado por la totalidad de los
infinitamente
infinitos
números
racionales es: ninguno. Es decir, o,
nulo, nada. La versión técnica de la
demostración es de Cantor, y observe
qué espíritu más eudoxiano-exhaustivo
tiene, incluso en la siguiente forma en
lenguaje natural, que requiere un poco
de visualización creativa.
Imagine que puede ver la recta
numérica entera y cada uno de los
infinitos puntos individuales que
contiene. Imagine que quiere una
manera rápida y fácil de distinguir los
puntos correspondientes a números
racionales de los correspondientes a
irracionales. Lo que va a hacer es
identificar los puntos racionales
envolviendo cada uno de ellos en un
pañuelo rojo.[2.48] De este modo
destacarán. Como técnicamente los
puntos geométricos carecen de
dimensión, no sabemos qué aspecto
tienen, pero lo que sí sabemos es que
no se necesitará un pañuelo muy
grande para cubrir uno de ellos. En este
caso, el pañuelo rojo puede ser
arbitrariamente pequeño, por ejemplo
de 0,00000001 unidades, o la mitad de
ese tamaño, o la mitad de la mitad, …,
etc. En realidad, incluso el más
pequeño de los pañuelos será
innecesariamente grande, pero para
nuestros propósitos podemos decir que
el
pañuelo
es
básicamente
infinitamente pequeño: llamemos φ a
ese tamaño. Así, un pañuelo de tamaño
φ cubre el primer punto racional de la
R. N. Entonces, como, por supuesto, el
pañuelo puede ser tan pequeño como
queramos, digamos que usted usa solo
un pañuelo de tamaño para envolver
el siguiente punto racional. Y digamos
que usted continúa de ese modo, siendo
el tamaño de cada pañuelo rojo
exactamente
del tamaño del anterior,
para todos los números racionales,
hasta que todos están envueltos y
cubiertos. Ahora, para hallar el
porcentaje total de espacio que todos
los números racionales ocupan en la
recta numérica, todo lo que tiene que
hacer es sumar los tamaños de todos
los pañuelos rojos. Por supuesto, hay
una infinidad de pañuelos, pero
respecto al tamaño se traducen como
términos de una serie infinita,
específicamente la serie geométrica al
estilo de Zenón
+
+
+
+
+ …; y, dada la buena y vieja fórmula
para sumar tal serie, la suma
del tamaño total de los infinitos
pañuelos resulta ser 2φ. Pero φ es
infinitesimalmente pequeño, siendo los
infinitesimales (como se mencionó en
§2b) tan increíblemente próximos a o
que al multiplicarlos por cualquier cosa
el
resultado
es
también
un
infinitesimal, por lo cual 2φ es también
infinitesimalmente pequeño, lo que
significa que todos los infinitos
números
racionales
combinados
ocupan
solo
una
porción
infinitesimalmente pequeña de la R. N.
—o sea, básicamente ninguna en
absoluto—,[2.49] lo que a su vez es
como decir que la inmensa, inmensa
mayoría de los puntos en cualquier tipo
de recta continua corresponderán a
números irracionales, y así, a pesar de
que la antes mencionada recta real es
realmente una recta, la recta numérica
formada solo por racionales, aunque
pueda parecer infinitamente densa, en
realidad es en un 99,999…% espacio
vacío, como un helado muy poroso o el
universo mismo.
Dejemos que cada uno haga una
pausa en privado para intentar imaginar
por un momento qué aspecto podía
tener el interior de la cabeza del
profesor Georg F. L. P. Cantor cuando
está demostrando este tipo de cosas.
Un lector atento puede objetar aquí
que hay algún truco como los de Zenón
en la anterior demostración, y
preguntar por qué no se podría aplicar
un procedimiento similar con pañuelos
y series a los números irracionales para
demostrar que el % total de espacio
recto ocupado por los irracionales es
también 2φ. La razón de que tal
demostración no pueda funcionar es
que, por infinitamente o incluso
∞∞mente numerosos que sean los
pañuelos rojos, siempre habrá más
números irracionales que pañuelos.
Como siempre, esto también lo
demostró Cantor.
3
§3a.
Llegados
a
este punto resulta
justificado
ahorrarse
cualquier
pretensión de continuidad narrativa y
hacer un barrido de varios siglos en una
especie de cronología esquemática que
va de, digamos, el 476 d. C. (caída de
Roma) hasta la década de 1660
(preliminares del
cálculo). Por
supuesto, en la cronología destaca lo
relacionado con el ∞ y/o la situación
general de las matemáticas cuando
Dedekind y Cantor entraron en escena.
Y quedando las desventajas de la
abstracción esquemática en cierto
modo superadas por las ventajas del
ahorro de espacio, pues por lo menos
uno de nosotros está empezando a
darse cuenta que el espacio disponible
va a ser un problema. Así pues, aquí en
§3, el objetivo es simplemente resumir
ciertos desarrollos que ayudan a sacar a
la luz las eventuales condiciones
necesarias/suficientes
para
las
matemáticas transfinitas.[3.1]
Aproximadamente del 500 al 1200
d. C. Sin demasiados progresos en las
matemáticas occidentales gracias a
Roma, Aristóteles, el neoplatonismo, la
Iglesia, etc., la verdadera actividad está
ahora en Asia y el mundo islámico.
Como muy tarde hacia el 900 d. C., las
matemáticas de la India han
introducido el cero como «décimo
numeral» y lo representan mediante el
símbolo con el que estamos
familiarizados,[3.2] han desarrollado un
sistema decimal de notación posicional
que es básicamente el nuestro, y han
codificado los fundamentos de cómo
funciona el 0 en aritmética (0 + x = x,
= 0, no es válido dividir por 0, etc.)·
Los matemáticos indios y árabes, libres
de cualquier geomefilia griega, son
capaces de trabajar y lograr resultados
significativos
con
los
enteros
negativos, el antes mencionado o, las
raíces irracionales, y variables para
representar números arbitrarios y así
enunciar propiedades generales.[3.3] La
mayoría de las innovaciones indoárabes regresaron a Europa más tarde,
gracias principalmente a las conquistas
islámicas (p. ej., de la India, cuyas
matemáticas los árabes asimilaron, en
el siglo VII, llegando incluso a España
en 711, etc.).
Hacia 1260. Los argumentos quia
de santo Tomás de Aquino a favor de la
existencia de Dios[3.4] constituyen la
fusión oficial de la metafísica de
Aristóteles y la doctrina de la Iglesia.
La base de la argumentación de santo
Tomás es que, como en el mundo todo
tiene una causa y esas causas, a su vez,
tienen causas, y así sucesivamente, en
algún punto de la cadena tiene que
haber una «causa original» sin causa,
es decir, Dios. Observe que este es
esencialmente el mismo argumento que
el famoso «primer motor», al que nada
mueve, de Aristóteles en el Libro VIII
de su Metafísica. El argumento del
primer motor es adoptado tanto por san
Agustín como por Maimónides
también en demostraciones de Dios. Lo
que es más importante, véase que para
que el argumento de santo Tomás
funcione tiene que aceptarse la premisa
tácita de que una cadena transitiva
infinita de causas y efectos es
imposible o incoherente. En otras
palabras, tiene que considerarse como
axiomática la imposibilidad del ∞
como característica real del tiempo o
del universo, lo cual básicamente
significa
aceptar
el
destierro
aristotélico del ∞ al mismo extraño
estatus puramente potencial de El
pensador de Rodin en todas las masas
de bronce.
Sin embargo, en otra parte de la
Summa Theologiae, santo Tomás
introduce un argumento más original:
La existencia de una multitud
infinita real es imposible. Pues
cualquier conjunto de cosas que
uno considere tiene que ser un
conjunto específico. Y los
conjuntos de cosas están
especificados por el número de
cosas en ellos. Ahora, ningún
número es infinito, pues el
número resulta de contar a lo
largo de un conjunto en
unidades. Así, ningún conjunto
de
cosas
puede
ser
inherentemente ilimitado, ni
puede ocurrir que sea ilimitado
(Summa Theologiae, I.a., 7.4.
Traducción semiextractada, y
editada, de Rucker, Infinity and
the Mind, pág. 52).
Este pasaje es citado por el propio
Cantor en su «Mitteilungen zur Lehre
vom Transfiniten»,[3.5] donde lo
califica de la única objeción realmente
significativa, en toda la historia, a la
existencia de un ∞ real. Para nuestros
propósitos, hay dos cosas significativas
acerca del argumento de santo Tomás:
(1) Trata el ∞ en términos de
«conjuntos de cosas», que es lo que
Cantor y Dedekind harán seiscientos
años después (además, la tercera frase
de santo Tomás es casi exactamente la
manera en que Cantor definirá el
cardinal de un conjunto). (2) Todavía
más importante, reduce todas las
distinciones
y
complicaciones
metafísicas de Aristóteles a la cuestión
de si existen números infinitos. Es fácil
ver que aquí lo que realmente le gusta a
Cantor es el punto (2), que convierte el
argumento en una especie de reto a
medida,
pues
la
única
y
verdaderamente plausible refutación a
santo Tomás consistirá en que alguien
dé una teoría rigurosa y coherente de
los
números
infinitos
y
sus
propiedades.
Hacia 1350 + Breve salto temporal.
Tres
personajes
de
mediana
importancia respecto a la continuidad y
las series infinitas: Nicole Oresme,
Ricardus «el Calculador» Suiseth y
Francesco Luigi Grandi. Oresme
inventa
en
1350
un
método
«latitudinal» para representar de forma
gráfica el movimiento y la aceleración
uniforme.[3.6] Entre otras cosas, ello
permite la primera indicación de que la
velocidad relativa (= recta inclinada) y
el área relativa (= área bajo la recta
inclinada) son dos aspectos de la
misma cosa. Coincidiendo más o
menos en el tiempo, Suiseth resuelve
un problema latitudinal particular que
equivale a demostrar que la serie
infinita
+
+
+
+…+
tiene
una suma finita, concretamente 2.
(N. B.: nadie piensa todavía en aplicar
este método a la dicotomía). Entonces,
Oresme responde demostrando que otra
serie infinita,
+
+
+
+
+
+
… + , alias la «serie armónica», no da
una suma finita a pesar de que la
sucesión de términos individuales
parece aproximarse claramente a o.
(SEI La demostración de Oresme es
ingeniosamente simple. Agrupando los
términos de la serie de tal modo que el
primer término = el primer grupo, el
segundo y tercer términos = el segundo
grupo, los términos del cuarto al
séptimo = el tercer grupo, etc., de
manera que el grupo n-ésimo contenga
2n−1 términos, demuestra que al final
tenemos un número infinito de grupos
cada uno de los cuales tiene una suma
parcial ≥ , dando lugar a una suma
infinita para la serie).
Las series de Suiseth y de Oresme
son, por supuesto, ejemplos respectivos
de convergencia y divergencia, pero
durante siglos nadie sabrá cómo
nombrar o tratar los distintos tipos de
series infinitas.[3.7] Incluso en la era
poscálculo, cuando las series se
convirtieron en la manera obvia de
representar funciones complicadas para
la diferenciación y la integración,
algunos avatares de Zenón continuaron
reapareciendo con paradojas que
confundieron varios intentos de
sistematizar la convergencia y la
divergencia. Una de las más diabólicas
era la buena y vieja serie oscilante 1 −
1 + 1− 1 + 1 − 1 + 1… de §1d, que el
matemático católico Grandi gustaba de
usar para atormentar a los hermanos
Bernoulli, famosos colegas de Leibniz
que habían demostrado la divergencia
de la serie armónica de Oresme en la
década de 1690. Recuerde que el truco
de la serie de Grandi es que según
cómo se agrupen los términos acaba
resultando igual a 0 y a 1 a la vez…; o,
poniendo x = 1 en la fórmula
protologarítmica
= 1 − x + x2 −
x3 + …, se obtiene la igualdad
=1−
1 + 1 − 1 + 1 − 1 + 1 …, la cual,
jocosamente Grandi, sugirió que era la
forma en que Dios había creado algo
del vacío (0).
[SEI Si recuerda usted algo del
álgebra del instituto, también vale la
pena echar un vistazo a una horrible
pequeña serie divergente que en la
década de 1730 puso en apuros a
Leonhard Euler (1707-1783, icono del
análisis temprano). Recordará que
según las reglas de división de
polinomios,
= 1 − x + x2 − x3 +
…, que, sustituyendo x = 2 se convierte
en la desafortunada igualdad −1 = 1 +
2 + 4 + 8 + … O puede obtenerse de
nuevo la serie de Grandi sustituyendo
x = −1 en la misma expansión.
O, si su formación matemática es
sólida, puede divertirse expandiendo
mediante el teorema del binomio
para obtener log(1 + x) = x − x2 +
x3 + … y viendo (al igual que
Newton, Mercator y Wallis) que
cuando x = 2, la serie tiene una suma
infinita pero también debería ser igual
a log 3. Hay un sinfín de rompecabezas
de este tipo].
Hacia 1425-1435. El arquitecto
florentino Filippo Brunelleschi inventa
la técnica de la perspectiva lineal en la
pintura. La obra de Leon B. Alberti
Della pictura es el primer tratado
publicado sobre cómo funciona.
Probablemente todos sabemos que
antes del Renacimiento los cuadros
parecían planos y muertos y
extrañamente
desproporcionados.
Brunelleschi aplica la geometría al
espacio pictórico, hallando un modo de
representar un «plano-base» horizontal
3D en un «plano-pintura» vertical 2D.
La técnica se ve muy fácilmente en las
representaciones
de
cuadrados
horizontales
(por
ejemplo,
el
embaldosado del Baptisterio de
Florencia) como paralelogramos (en
numerosos cuadros del mismo) que se
vuelven más estrechos y agudos a
medida que el suelo se desliza hacia el
fondo del cuadro. Brunelleschi/Alberti
consideran a todos los efectos una
pintura como una ventana abierta
interpuesta entre una escena y el
espectador, y observan que todas y
cada una de las «ortogonales», o rectas
paralelas que se alejan en el espacio a
90° respecto a dicha ventana, parecerán
converger hacia un punto de fuga a la
altura de los ojos del espectador
(Honour y Fleming, págs. 319-320).
Este punto de fuga se concibe,
geométricamente, como un punto a
distancia infinita del espectador. Casi
todo el mundo sabe lo que Masaccio,
Durero, Da Vinci y otros colegas
fueron capaces de hacer con este
descubrimiento.
Matemáticamente, el concepto de
punto-en-el-∞ es usado más tarde por
Johannes Kepler en el principio de
continuidad que establece para
secciones cónicas y que luego emplea
para sus leyes del movimiento
planetario (véase más adelante), y
también es de importancia central para
Gérard Desargues y su invención, hacia
1640, de la geometría proyectiva, e
incluso más adelante para la topología,
la geometría riemanniana, el análisis
tensorial (sin el cual, a su vez, no
habría relatividad general), etc.
Año 1593. La obra Varia Responsa
de
Franç0is
Viète
(un
abogado/criptógrafo francés) incluye la
primera fórmula para sumar una serie
geométrica
infinita,[3.8]
que
es
terriblemente parecida a la antes
mencionada
de las matemáticas
elementales. Aunque no es demasiado
bonita, Viète es también el primero en
dar una expresión numérica precisa de
π, concretamente como un producto
infinito expresable así
[SEI La finalidad de destacar puntos
como los dos últimos es establecer que
el ∞, en varias manifestaciones y
contextos, está adquiriendo cada vez
más interés en aplicaciones fructíferas
incluso aunque continúe siendo
metafísicamente sospechoso y nadie
tenga ni idea de cómo tratarlo
matemáticamente].
Año 1637. La géometrie de René
Descartes
introduce
el
ahora
omnipresente
plano
coordenado
cartesiano, el cual permite que las
figuras geométricas se representen
aritmética/algebraicamente.
Aproximadamente entre 1585 y
1638. Tres personajes importantes, de
los cuales dos son extremadamente
famosos: Simon Stevin, Johannes
Kepler y Galileo Galilei.
En la década de 1580, Stevin (un
ingeniero flamenco) resucita la
propiedad de exhaustación de Eudoxo
al derivar fórmulas para características
relacionadas con el peso de diferentes
figuras geométricas. Por ejemplo, en su
obra Estática (1586), Stevin demuestra
que el centro de gravedad de un
triángulo se halla sobre su mediana, y
lo hace inscribiendo un número
ilimitado
de
paralelogramos
arbitrariamente pequeños en el
triángulo y demostrando cosas acerca
de los centros de gravedad de las
figuras inscritas resultantes. Stevin,
también conocido como el Arquímedes
holandés, merece más fama de la que
consiguió. Aquí está una cita
descontextualizada pero pertinente de
Carl Boyer: «Fueron en gran manera
las modificaciones resultantes de los
antiguos métodos infinitesimales las
que acabaron conduciendo al cálculo, y
Stevin fue uno de los primeros en
sugerir tales cambios» (Boyer, pág.
322).
Tal como se explica en la obra de
Kepler Astronomia nova (1609), la 2.ª
ley del movimiento planetario depende
de que se conciba el área circunscrita
por un vector radial que une un planeta
orbitando con el Sol como compuesta
(es decir, el área está compuesta) de
infinitos
triángulos
infinitamente
delgados, cada uno con el vértice A en
el Sol y los vértices B y C
infinitesimalmente próximos a lo largo
de la trayectoria orbital. La suma
efectuada por Kepler de las áreas de
esta infinidad de infinitesimales era,
setenta años antes de Leibniz, cálculo
aplicado.[3.9]
Años 1636-1638. Galileo Galilei,
puesto por la Inquisición bajo arresto
domiciliario en Florencia, escribe Dos
nuevas ciencias, un diálogo al estilo de
Platón sobre la mecánica/dinámica. En
este libro hay un montón de cosas
relacionadas con el ∞. Un ejemplo es
el modo en que Galileo aplica las
técnicas de representación latitudinal
de Oresme al movimiento de
proyectiles y demuestra que la curva
descrita por la trayectoria de un
proyectil es una parábola. Tras dos mil
años de estudio matemático de las
secciones cónicas, la elipse orbital de
Kepler y la parábola de los proyectiles
de
Galileo
son
las
primeras
aplicaciones reales de las cónicas a las
ciencias físicas. La obra menos
conocida de Kepler, Ad Vitellionem
paralipomena,[3.10]
ya
había
demostrado que las elipses, las
hipérbolas, las parábolas y las
circunferencias son todas productos de
una extraña y armónica danza entre dos
focos. La parábola se explica como lo
que le ocurre a una hipérbola cuando la
posición de un foco respecto al otro
alcanza el ∞. De un modo nada
accidental, toda la teoría de Kepler
sobre las interrelaciones de las cónicas
se conoce como el principio de
continuidad.
La obra Dos nuevas ciencias de
Galileo era en cierto sentido una larga
«pedorreta» a la Inquisición, que lo
trató de forma infame. Parte de su
proyecto era que el hombre normal del
diálogo actuara como portavoz de la
metafísica aristotélica y del credo de la
Iglesia, y que su compañero algo más
ilustrado le fuera dando bofetones
intelectuales. Una de las dianas
principales es la división ontológica
por Aristóteles del ∞ en real y
potencial, que la Iglesia básicamente
había transformado en la doctrina de
que solo Dios es realmente infinito y
nada más en su creación puede serlo.
Ejemplo: Galileo ridiculiza la idea de
que el número de partes en el que se
puede dividir cualquier segmento sea
solo «potencialmente» (o sea, no
realmente) infinito demostrando que si
usted dobla el segmento hasta que sea
una circunferencia —el cual, según
Nicolás de Cusa,[3.11] se define como
un polígono regular con un ∞ número
de lados—, usted ha «reducido a
realidad ese número infinito de partes
que pretendía, mientras era recto, que
estaban contenidas en él solo
potencialmente» (ibíd., pág. 329).
El portavoz de Galileo también
dedica
mucho
tiempo
a
los
infinitesimales, principalmente por su
utilidad en los resultados de Stevin y
Kepler. Galileo es el primero en
distinguir entre diferentes «órdenes» de
infinitesimales, principalmente a través
de un elaborado argumento sobre por
qué, si la Tierra gira, los objetos no son
arrojados hacia fuera según varias
tangentes a la curva de giro, lo cual es
una larga historia, pero lo importante
es que dos infinitesimales son de
distinto orden si su razón tiende o bien
a 0, o bien a ∞ y son del mismo orden
si su razón es finita. Esto es relevante
porque (1) la idea de que los
infinitesimales de orden más alto son
tan
increíblemente
pequeños
y
evanescentes que se pueden descartar
de una ecuación porque no tendrán
ningún efecto sobre el resultado
acabaría siendo vital para el cálculo
clásico, y (2) la distinción de Galileo
anticipa algunos de los propios
descubrimientos de Cantor sobre la
extraña aritmética de las cantidades
infinitas, es decir, que no todos los ∞
tienen el mismo tamaño pero que las
diferencias entre ellos no son
realmente aritméticas (por ejemplo,
sumar n a ∞ no lo incrementa, ni
sumar ∞ a ∞ o multiplicar ∞ por ∞)
sino, en cierto modo, geométricas.[3.12]
La
extremada
extrañeza
matemática del ∞, que Galileo dedica
mucho tiempo a ejemplificar en las
DNC, es bastante lúcidamente atribuida
a la epistemología y no a la metafísica.
Las paradojas surgen, según el
portavoz de Galileo, solo «cuando
intentamos, con nuestra mente finita,
discutir el infinito, asignándole
aquellas propiedades que otorgamos a
lo finito y limitado» (Galileo Galilei,
pág. 31). La gran ilustración de ello es
la paradoja de Galileo que hemos visto
en §1, en la cual recuerde que podía
establecer una correspondencia de uno
a uno entre todos los enteros y todos
los cuadrados perfectos incluso aunque
sea evidente que hay muchos más
enteros que cuadrados perfectos.[3.13]
De este rompecabezas, Galileo
concluye que «debemos decir que hay
tantos cuadrados como números», y así
(otra vez) que «los atributos “igual”,
“mayor” y “menor” no son aplicables a
las cantidades infinitas, sino solo a las
finitas» (ibíd., pág. 32). Aunque esta
última conclusión acabe resultando
equivocada, las de DNC todavía es la
primera
actitud
verdaderamente
moderna hacia los infinitos reales
como entes matemáticos. Obsérvese,
por ejemplo, que Galileo no recurre a
la vieja reducción al absurdo
aristotélica para concluir, a partir del
comportamiento paradójico de los
conjuntos infinitos, que no se puede
razonar acerca del ∞. En cambio, se
las arregla de algún modo para
anticiparse tanto a Kant (atribuyendo
las paradojas del ∞ a las arraigadas
restricciones de las «mentes finitas» y
no a cualquier realidad exterior a la
mente) como a Cantor (usando la
correspondencia de uno a uno como
medida comparativa de los conjuntos,
argumentando que las cantidades
infinitas obedecen a un tipo de
aritmética diferente al de las
cantidades finitas, etc.).
Hechos conocidos: el siglo XVII,
con su Contra-Contra-Reforma y su
revolución científica, vio la primera
auténtica explosión de progreso filomatemático
desde
el
apogeo
helenístico. Este es el siglo en el que
Descartes inventa la geometría con
coordenadas (así como la duda radical),
Desargues inventa la geometría
proyectiva; Locke, el empirismo;
Newton y Leibniz, las matemáticas
superiores. Nada de eso habría sido
posible sin aflojar el estrangulamiento
aristotélico
del
pensamiento
occidental. Las DNC de Galileo están
al mismo nivel que el Discurso del
método de Descartes y el Novum
Organum de Bacon en términos de
ruptura liberadora, y no es en absoluto
accidental que dedique tanto tiempo al
De
entre
montones
de
citas
pertinentemente favorables, véase la
del profesor Danzig: «Cuando, tras un
estupor de mil años, el pensamiento
europeo se deshizo del efecto de las
pócimas adormecedoras tan hábilmente
administradas
por
los
Padres
Cristianos, el problema del infinito fue
uno de los primeros en ser revivido»
(Tobías Danzig, Number: the Language
of Science, extractado de Seife, pág.
106).
El otro motivo por el que Dos
nuevas ciencias es importante es por su
sostenido y original uso de la función.
Sin duda recordará usted lo que es una
función matemática y por qué es difícil
definirla claramente (como, por
ejemplo,
«Una
relación
entre
variables», «Una regla para establecer
la imagen de un dominio», «Una
correspondencia»). Una función está
por lo menos un nivel de abstracción
por encima de las variables, siendo
básicamente una regla para emparejar
elementos de un conjunto con
elementos de otro conjunto. Por ahora
supongamos que todos sabemos
bastante bien qué es una función, o más
bien qué hace, pues una función en
realidad
es
una
especie
de
procedimiento, aunque un simbolismo
como «f(x) = » tiende a hacer que
parezca una cosa. Por lo menos
gráficamente, la idea de una función
había estado ahí desde Oresme en el
siglo XIV, aunque este había usado
terminología escolástica y llamaba a
esa técnica una latitud de formas,
siendo «forma» el término aristotélico
para características o calidades, de las
que se consideraba que incluían cosas
como la velocidad de un cuerpo en
movimiento. No fue hasta Galileo que
la gente entendió que la velocidad no
es una cualidad de la cosa que se
mueve, sino más bien un proceso
abstracto representable por la función
elemental r = , igual que (un nivel de
abstracción más hacia arriba) fue
Galileo quien determinó que la
aceleración actúa como la función
s = at2.
Dos nuevas ciencias es el primer
libro de matemáticas en usar funciones
de forma extensiva y no gráfica,
aunque estas son descritas verbalmente
y a menudo (como los griegos) en
términos de proporciones y razones. Lo
que es sorprendente es la velocidad con
que la noción/teoría de las funciones
ganó aceptación una vez alcanzada
cierta masa crítica de necesidades y
permisos.[3.14] La mayor parte de esas
necesidades
involucraban
la
continuidad. Lo principal aquí es que la
astronomía de Kepler y los estudios del
movimiento de Galileo —motivados en
gran parte por la necesidad de mejorar
la medición del tiempo en la
navegación (otra vez, una larga
historia)— generaron el impulso para
un estudio riguroso de las curvas, que
el plano coordenado cartesiano
permitía expresar de forma algebraica,
es decir, en términos de funciones
como y = x2, y = sen x, y así
sucesivamente.
Las
importantes
distinciones
entre
funciones
polinómicas,
algebraicas
y
trascendentes[3.15]
se
obtenían
fácilmente a partir de la clasificación
de las curvas por Descartes, y también
a partir de las representaciones
explícitas como funciones mediante
diferentes tipos de series algo más
tarde (1670 aprox.). La propia palabra
«función», a propósito, viene de
Gottfried W. Leibniz.[3.16] Lo cual, por
supuesto, no es para nada un accidente,
pues Leibniz ayudó a inventar el
cálculo, y una de sus características
más poderosas es el uso de funciones
para representar procesos. Tras
Leibniz, el concepto plagado de fisuras
de
«fenómeno
continuo»
es
reemplazado en las matemáticas por la
función continua y la serie infinita… y,
de hecho, las exploraciones del ∞ por
Cantor acabarán surgiendo de una
aplicación particular
de dichas
herramientas a cierto conjunto de
problemas acerca del calor. Lo cual es
obviamente una historia muy larga que
ahora no vamos a desarrollar.
Aquí, dicho sea de paso, está una
cita de David Berlinski: «Es el
contraste entre lo continuo y lo discreto
lo que constituye el gran motor
generador por el cual los números
reales son construidos y el cálculo
creado» (Berlinski, pág. 130). Para
recordar dónde estamos en el bosque
general, esta sección es solo de árboles.
Aproximadamente 1647-1665. Tres
personajes medianamente importantes,
que si esto hubiera sido doscientos
años antes ahora serían todos
extremadamente famosos: Gregory de
St. Vincent, John Wallis y James
Gregory.
Hacia 1647: Gregory de St. Vincent
propone una solución a la dicotomía de
Zenón que menciona de manera
explícita la suma de una serie
geométrica.[3.17] Es también el primer
matemático en postular que una serie
infinita representa una verdadera
magnitud o suma, la cual también es el
primero en postular cómo el límite de
la serie, que él llama el «terminus de la
progresión» y describe en términos
bastante eudoxianos como un extremo
«al que la progresión no llega, aunque
continúe hacia el infinito, pero al que
puede acercarse más próximamente
que por cualquier intervalo dado»
(Gregory of St. Vincent, Opus
Geometricum, extractado de Kline, pág.
437).
Año 1655: Wallis, el segundo
matemático británico más grande del
siglo, publica su antes mencionada
obra Arithmetica infinitorum, cuyo
título es 0% casual. Este es el primer
trabajo importante sobre la aplicación
de las series infinitas a la
aritmetización de la geometría, y será
indispensable
para
la
versión
newtoniana del cálculo[3.18] un par de
décadas después. Entre los resultados
importantes
de
la
Arithmetica
infinitorum: las primeras definiciones
generales correctas del límite de una
sucesión infinita y de la suma de una
serie infinita, el uso de un producto
infinito para representar el seno y el
coseno, la demostración de que
×
con la
×
=1−
=
× … (compárese
+
−
+
−
…
de Leibniz unos cuantos años después),
y, por supuesto, el primer uso de «∞»
como símbolo para ∞.
Año 1665: James Gregory (un
escocés) define «función», insta a que
se considere la aproximación a un
límite como la sexta función básica del
álgebra, y expande varias funciones
trigonométricas y trigonométricas
inversas como series infinitas, por
ejemplo, demostrando que «arcan x = x
−
+
−
+ …» se cumple para
−1 ≤ x ≤ 1. En esta época se llevó a
cabo mucho trabajo sobre expansiones
en serie, principalmente porque los
navegantes,
ingenieros,
etc.,
necesitaban una trigonometría mucho
más detallada y precisa, y tablas de
logaritmos, y las expansiones de
funciones en serie infinita eran la
mejor manera de interpolar los valores
de las tablas.
[SEI también en 1665 aprox. El
teorema del binomio, es decir, la
fórmula para desarrollar (p + q)n, es
liberado de la dependencia de
(p + q)n−1 y del triángulo de Pascal por
Newton. Se cree que la expansión es
infinita para n fraccionarias o
negativas, pero nadie puede demostrar
nada realmente sobre el T. B. o la
convergencia/divergencia de las series
en general hasta Jean-Baptiste Fourier
hacia 1820.]
§3b.
Tal como, por lo menos, se ha sugerido
y ahora será explicado, el consenso
histórico-matemático es que el
siglo XVII tardío marca el inicio de una
Edad de Oro moderna en la cual hay
muchos más avances matemáticos
significativos que en cualquier otra
época de la historia mundial. Ahora las
cosas empiezan a moverse realmente
deprisa, y no podemos hacer mucho
más que intentar construir una especie
de camino señalizado desde los
primeros trabajos sobre funciones hasta
Cantor y su «infinicopia».
Subrayemos
rápidamente
dos
cambios a gran escala en el mundo
matemático. El primero tiene que ver
con la abstracción. La mayor parte de
las matemáticas desde los griegos hasta
Galileo tiene una base empírica: los
conceptos
matemáticos
son
abstracciones directas a partir de la
experiencia del mundo real. Esta es una
razón por la que la geometría (junto a
Aristóteles) dominó el razonamiento
matemático durante tanto tiempo. La
moderna transición del razonamiento
geométrico
al
algebraico[3.19]
constituye un síntoma en sí mismo de
un cambio mayor. Hacia 1600,
entidades como el cero, los enteros
negativos y los irracionales se usan de
forma rutinaria. Ahora empiece a
añadir en las décadas subsiguientes las
introducciones
de
los
números
complejos, los logaritmos neperianos,
los polinomios de grado alto y los
coeficientes literales en el álgebra —y
también más adelante, por supuesto, las
derivadas 1.ª y 2.ª y la integral— y está
claro que desde la pre-Ilustración hasta
aquí las matemáticas se han alejado
tanto de cualquier tipo de observación
del mundo real que podemos decir
junto a Saussure que ahora son, como
sistema de símbolos, «independientes
de los objetos designados», es decir,
que ahora las matemáticas se ocupan
mucho más de las relaciones lógicas
entre conceptos abstractos que de
cualquier correspondencia particular
entre esos conceptos y la realidad
física. La cuestión es que en el siglo
XVII las matemáticas se convierten
principalmente en un sistema de
abstracciones a partir de otras
abstracciones y no a partir del mundo.
Lo cual hace que el segundo gran
cambio parezca paradójico: la nueva
hiperabstracción de las matemáticas
resulta funcionar increíblemente bien
en las aplicaciones al mundo real. En la
ciencia, la ingeniería, la física, etc.
Tome, como ejemplo obvio, el cálculo,
que es exponencialmente más abstracto
que cualquier tipo de matemáticas
«prácticas» anteriores (por ejemplo, ¿a
partir de qué observación del mundo
real sueña uno la idea de que la
velocidad de un objeto y el área bajo
una curva tienen algo que ver entre
sí?), y a pesar de todo tienen un acierto
sin precedentes al representar/explicar
el movimiento y la aceleración, la
gravedad, los movimientos planetarios,
el calor: todo lo que la ciencia nos dice
que es real del mundo real. No es por
nada que David Berlinski llamara al
cálculo «el primer relato que este
mundo se contó a sí mismo al
convertirse en el mundo moderno»
(Berlinski, pág. xi). Porque de lo que
va el mundo moderno, lo que es, es la
ciencia. Y es en el siglo XVII cuando se
consuma el matrimonio entre las
matemáticas y la ciencia, siendo la
revolución científica a la vez la causa y
el efecto de la «explosión matemática»
porque la ciencia —cada vez más
liberada de sus encuentros aristotélicos
con la sustancia respecto a materia y
potencialidad respecto a realidad—
ahora se convierte esencialmente en
una actividad matemática[3.20] en la
que la fuerza, el movimiento, la masa,
y la ley-como-fórmula constituyen la
nueva plantilla para entender cómo
funciona la realidad. Hacia finales del
siglo XVII, las matemáticas serias son
parte de la astronomía, la mecánica, la
geografía, la ingeniería civil, la
planificación urbana, la marmolería, la
carpintería, la metalurgia, la química,
la hidráulica, la hidrostática, la óptica,
el pulido de lentes, la estrategia
militar, el diseño de pistolas y cañones,
la elaboración de vinos, la arquitectura,
la música, la construcción de barcos, la
medición del tiempo, los calendarios,
todo.
Y la influencia práctica actúa en
ambos sentidos. Aquí está una cita
definitiva de Kline: «A la vez que la
ciencia empezó a apoyarse más y más
en las matemáticas para obtener sus
conclusiones físicas, las matemáticas
empezaron a apoyarse más y más en
los resultados científicos para justificar
sus propios procedimientos» (Kline,
pág. 395). Y, como se verá de sobras en
los § 4 y 5, esta unión resulta fructífera
pero también está llena de riesgos. En
pocas palabras, todo tipo de cantidades
y procedimientos antes dudosos ahora
son aceptados en las matemáticas por
su eficacia práctica, lo que significa
que si las matemáticas quieren
mantener su rigor deductivo tendrán
que ser rigurosamente «teorizadas» y
basadas en el esquema axiomático de
las matemáticas. Adivine en qué
ejemplos
de
estos
conceptos
largamente cuestionables estamos
interesados aquí. Eche otro vistazo al
translúcido Kline, ahora en un capítulo
de su Pensamiento matemático titulado
«Las matemáticas en 1700»: «Las
cantidades infinitamente grandes, que
los
griegos
habían
evitado
estudiadamente, y las infinitamente
pequeñas, que los griegos habían
esquivado hábilmente, [ahora] tenían
que ser afrontadas» (Ibíd., pág. 393).
§3c.
Así
pues, una vez la historia del ∞
llega a finales del siglo XVII, ahora
vamos disparados a una velocidad
irreversible hacia Cantor y sus colegas,
y las matemáticas se vuelven mucho
más abstractas y técnicas. Y el «Alto
Mando» ha decidido que en puntos
seleccionados deberá usted someterse a
pequeños y rápidos glosarios de
emergencia (G. E.) en los cuales ciertos
términos/conceptos inevitables se
definen de modo que luego puedan
usarse
sin
tener
que
parar
constantemente y hacer sesudas
búsquedas in medias acerca de lo que
significan. Algunos serán nuevos, otros
ya han sido mencionados o pueden
parecer algo obvios, pero son lo
bastante importantes para que ellos y
algunos de sus subtérminos asociados
se aseguren al 100%.
N. B.: El siguiente primer
GLOSARIO DE EMERGENCIA puede
resultar un poco seco debido
simplemente a la compresión. Y
aunque era tentador designarlo como
SEI para lectores con fuerte formación
matemática, el hecho es que muchas de
las definiciones están tan radicalmente
reducidas
y
simplificadas
que
probablemente le valga la pena dedicar
algo de su tiempo por lo menos a
hojear este G. E. I para tener claras las
maneras específicas en las que vamos a
utilizar los términos. Para los lectores
que no sepan demasiadas matemáticas
superiores, por otro lado, lo que sigue
es todo lo que necesitan para continuar
por lo menos durante unos cuantos §
más.
GLOSARIO DE EMERGENCIA I,
CON UN SALTO TEMPORAL
NARRATIVO ASOCIADO
— Recta
real.
Como
se
ha
mencionado, es esencialmente una
recta numérica ampliada, en el
sentido de una recta geométrica con
una graduación fija y densa de
modo que cada número real
corresponde a un único punto en la
recta. Para nuestros propósitos, la
recta real es un «espacio
topológico», lo cual aquí significa
que la recta y el conjunto de todos
los números reales que representa
pueden usarse sin distinción para
referirse a la misma cosa
abstracta,[3.21] la cual, también se
ha mencionado, se llama de manera
habitual «el continuo», donde este
término significa exactamente lo
que aparenta significar: el origen y
la manifestación de la continuidad
combinados.
— Función. Ya bastante tratado en
§3a, o eche un vistazo a esta
maravillosa definición directa de
una clase de matemáticas escolares:
«Una relación entre dos cosas
donde el valor de una está
determinado por el valor de la
otra». Recordará del álgebra básica
que en una función típica como
y = f(x), x es la variable
independiente e y es la variable
dependiente, en el sentido de que
los cambios en x producen cambios
en y según las reglas de f. El
conjunto[3.22] de todos los valores
posibles
que
la
variable
independiente puede adquirir se
llama el dominio de la función. El
conjunto de todos los valores
posibles de y es el recorrido de la
función.
— Función real. Una función cuyos
dominio y recorrido son conjuntos
de números reales.
— Función continua (a). La función
y = f(x) es continua si cambios muy
pequeños en x dan solo cambios
muy pequeños en y: no hay grandes
saltos ni interrupciones ni cosas
extrañas. Si una función es
discontinua,
habitualmente
es
discontinua para cierto valor de la
variable
independiente,
por
ejemplo,
es
discontinua en x = 1.[3.23] (Para su
información, resulta que hay todo
tipo de discontinuidades, cada una
con su comportamiento, gráfica y
nombre técnico característicos,
«discontinuidad
de
salto»,
«discontinuidad
evitable»,
«discontinuidad asintótica», pero
mejor no nos vamos a liar con esas
distinciones).
— Intervalo. El espacio en la recta
real entre dos puntos, digamos p y
q, que es equivalente al conjunto de
todos los números reales entre p y
q. Aquí, p y q se llaman los
extremos del intervalo. El intervalo
cerrado
[p, q]
contiene
los
extremos, el intervalo abierto (p, q)
no. Observe los corchetes en el caso
de los intervalos cerrados y los
paréntesis en el caso de los
intervalos abiertos; así es como se
simboliza la diferencia.
— Entorno. En la recta real, el entorno
de un punto p es el intervalo abierto
(p − a, p + a) donde a > 0. Otra
manera de expresar eso es decir que
el a-entorno de p es el conjunto de
todos los puntos cuya distancia a p
es menor que a.
— Función
continua
(b).
Las
funciones se califican a menudo de
continuas/discontinuas en o sobre
ciertos intervalos. Una función f(x)
es continua en el intervalo abierto
(p, q) si es continua en cada punto
de (p, q). Para que sea continua en
el intervalo cerrado [p, q], tiene que
cumplirse lo siguiente:
f(x) = f(p) y
f(x) = f(q)
que, por supuesto, solo tendrán
sentido si está usted familiarizado
con los límites.
— Límites. O quizá más bien límites y
cotas, pues estos están relacionados
pero también son crucialmente
diferentes. La distinción es
probablemente más fácil de ver
respecto a las sucesiones. ¡Uy!
— Sucesión. Cualquier secuencia de
términos formada mediante alguna
regla, por ejemplo, la sucesión
geométrica 1, 2, 4, 8, 16, …, 2n−1,
…
— Límites y cotas (a-d). La técnica
memorística informal que el doctor
G. siempre sugería era que límite
involucra las expresiones «tiende
a» o «se aproxima a», mientras que
cota se califica de «superior» o
«inferior», (a) El límite de una
sucesión es el gran concepto tácito
tras la dicotomía de Zenón y está
implícito en la exhaustación de
Eudoxo, la volumétrica de Kepler,
etc. Respecto a las sucesiones,
«límite» se refiere al número al que
nunca llegamos realmente pero al
que nos aproximamos más y más y
más, a medida que aumenta el
número de términos de la sucesión.
Expresado de un modo algo más
excitante, el límite L de una
sucesión infinita p1, p2, p3, …, pn,
… es el número al que la sucesión
se aproxima (o al que «tiende»)
cuando n se aproxima a donde esta
última aproximación se simboliza
mediante una pequeña «→» bajo la
línea de texto, siendo la expresión
completa:
pn = L. (b) El límite
de una función es básicamente el
valor al que se aproxima la variable
dependiente cuando la variable
independiente se aproxima a algún
otro valor. Un ejemplo frecuente de
las clases de cálculo es f(x) = ,
donde f(x) se aproxima a 0 cuando x
tiende a ∞, expresado según
= 0.[3.24] (c) Una cota de
una función es un «espécimen»
totalmente
distinto.
Es
una
restricción de algún tipo (o de
algunos tipos) sobre el recorrido de
la función. Un ejemplo clásico de la
trigonometría es f(x) = sen x, donde
todos los valores de f(x) van a estar
entre −1 y 1. Más importante para
nuestros propósitos es que las
funciones pueden tener cotas
superiores (M) y/o cotas inferiores
(L) tales que f(x) ≤ M y/o f(x) ≥ L,
para toda x del dominio de la
función. Incluso más importantes
son las todavía más restringidas
mínima cota superior y máxima
cota inferior de una función, donde
M1 es la mínima cota superior de
f(x) si cualquier otra cota superior
Mn es ≥ M1, y L1 es la máxima
cota inferior de f(x) si es ≥ que
cualquier otra cota inferior Ln. (d)
Las sucesiones pueden tener cotas
de modo muy parecido al de las
funciones. La sucesión infinita de
enteros positivos 1, 2, 3,…
obviamente tiene una cota inferior
en o, que también será la cota
superior de −1, −2, −3,… Una
sucesión acotada es una que tiene
cota superior y cota inferior: por
ejemplo, si x ≥ 1, es fácil ver que la
secuencia
generada
al
desarrollar[3.25]
será
acotada.[3.26] [3.27]
— Series. Definibles como sucesiones
cuyos términos están sumados los
unos a los otros, como en la serie
geométrica 1 + 2 + 4 + 8 + 16 +
… + 2n−1 + … La relación íntima
de las series con las sucesiones
significa que comparten la mayoría
de las cualidades y predicados
asociados, con una gran excepción:
donde las sucesiones tienen límites,
las series tienen límites y sumas.
Puede que recuerde la infame sigma
mayúscula de las matemáticas
superiores, que le permite designar
la suma incluso de series con un
número infinito de términos:
porque resulta que todas las series
interesantes son infinitas. La suma
de la serie infinita p1 + p2 + p3 +
… + pn … se escribe
pn, donde
los pequeños y antipodales «∞» y
«n = 1» indican los límites (en el
sentido del intervalo de posibles
valores de n) de la serie.[3.28] Las
series infinitas son convergentes si
convergen hacia una suma finita
(véase, por ejemplo, cómo la
zenoide 1 +
+
+
+ …
converge hacia la suma 2) y
divergentes si no lo hacen (como la
serie 1 + 2 + 3 + 4 + …). Pero
ambos tipos de series tienen por lo
menos sumas abstractas[3.29] que se
pueden simbolizar mediante ∑ y
tratadas como cantidades en
cálculos posteriores.
— Producto infinito. Algo así como
una serie infinita excepto que los
términos
se
multiplican.[3.30]
Muchas cosas en trigonometría, de
π a las funciones seno y coseno,
pueden
representarse
como
productos infinitos, dependiendo de
cómo se traten los desarrollos.
— Desarrollo o expansión. Esto
significa expresar algo matemático
en
forma
de
sucesión/serie/producto (estamos
especialmente
interesados
en
desarrollos
en
serie).
Su
funcionamiento depende de lo que
esté usted desarrollando. El
desarrollo de una expresión
matemática
habitualmente
es
bastante directo. Recuerde todas las
operaciones mecánicas de las
matemáticas de bachillerato, como
(x + y)2 → x2 + 2xy + y2 (respecto
a las cuales recordará también que
cualesquiera
constantes
haya
delante de las variables de los
términos se conocen como los
coeficientes de la serie). Las
funciones, por otro lado, son más
interesantes y, por lo tanto, más
complicadas. Ni siquiera todas son
desarrollables, para empezar. Para
que una función sea representable
como una serie, el desarrollo en
serie de la función, o bien (1) tiene
que ser finito, o bien (2) si es
infinito tiene que converger hacia
la función para todos los valores de
las variables. Ejemplo: la función
trigonométrica
eos
x
es
representable por la serie de
potencias convergente 1 −
−
+
+
− …[3.31]
— Serie de potencias. Un tipo
particular de serie que incluye
exponentes (o sea, potencias),
siendo la forma genérica de una
serie de potencias p0 + p1x + p2x2
+ p3x3 + … + pnxn + … donde los
valores de x son números reales y
las p son coeficientes. Curiosidad:
el desarrollo de todas las funciones
básicas (seno, coseno, elípticas,
hiperbólicas,
logarítmicas
y
exponenciales) son todas series de
potencias (como también lo es la
dicotomía de Zenón).
— Series de Fourier, que son algo así
como la suma de dos series de
potencias;
se
estudian
en
matemáticas superiores[3.32] y
pueden
constituir
verdaderos
quebraderos de cabeza, pero son
vitales para el contexto de la
matemática transfinita y merecen
por lo menos una explicación
general. Para nuestros propósitos,
las series de Fourier se pueden ver
como desarrollos de funciones
periódicas, respecto a las cuales
todo lo que necesita saber es que
son maneras de representar varios
tipos de ondas, por lo que a veces
también se llaman funciones de
onda. Las funciones de onda
fundamentales
son
las
trigonométricas sen x y cos x, y la
serie de Fourier elemental es el
desarrollo de una función periódica
f(x)
como
—prepárese—
an cos (nx)
+
bn sen (nx),[3.33] donde a y b
son lo que se conoce como
coeficientes de Fourier, los cuales
son
tan
peliagudos
conceptualmente que nuestro plan
es evitarlos casi a cualquier precio.
— Cuadratura. Este es el término del
siglo XVII para cierto tipo de
problema que condujo al cálculo
integral. Técnicamente, se refiere a
construir un cuadrado cuya área =
el área delimitada por una curva
cerrada. Una versión moderna
temprana del viejo problema de la
cuadratura del círculo, en otras
palabras. Nos preocupamos de
definir la «cuadratura» porque se
usa más adelante en ciertos
contextos históricos donde sería
erróneo decir «integración» en su
lugar, porque la integración,
estrictamente hablando, no existía
todavía.
— Derivada (n.). El McGuffin del
cálculo
diferencial.
Es
una
expresión del ritmo de variación de
una función respecto a su variable
independiente.[3.34] Como puede
traer recuerdos de las clases de
matemáticas, añadamos que la
derivada de una función f(x) en
cierto punto p puede entenderse
como la pendiente de la tangente a
la curva dada por y = f(x) en p,
aunque esto no nos va a resultar
demasiado útil. Una curiosidad
importante como propina: el
proceso de hallar la derivada de una
función
dada
se
llama
diferenciación.
— Integral (n.). Esta es la inversa de
la derivada, es decir, la función que
tiene una derivada dada, esto es, la
función de la que se deriva la
derivada, es decir, si f(x) es la
derivada de g(x), entonces g(x) es la
integral de f(x). Encontraremos
mucho más sobre esto, en un
contexto moderno, en §4. (N. B. El
proceso de hallar la integral de una
función dada se llama integración,
que es lo que los matemáticos
hacen a menudo cuando están
atascados en un problema y no
saben cómo continuar. De ahí el
eslogan que puede verse en las
habitaciones de muchos estudiantes
universitarios: NO TE SIENTES A
ESPERAR: INTEGRA).
— Análisis. Otro término altamente
abstracto que no podemos ni
embellecer ni evitar. Hay una
definición muy formal que incluye
el modo en que ciertos tipos de
funciones varían en el entorno de
un punto en una superficie, que
dados nuestros objetivos generales
podemos omitir en favor de la idea
de que el análisis es la rama de las
matemáticas que estudia cualquier
cosa relacionada con los límites o
los «procesos límite», o sea, el
cálculo, las funciones de variables
reales o complejas, la topología de
la recta real, las sucesiones y las
series infinitas, etc. En los libros y
las
clases
suelen
hallarse
referencias al análisis como «las
matemáticas de la continuidad». Lo
cual puede despistar un poco,
porque a la mayoría nos enseñan
que
la
continuidad
es
la
jurisdicción del cálculo, y hay
algunas áreas completamente fuera
del cálculo que siguen siendo
análisis, y de las cuales un par son
especialmente
relevantes.
El
álgebra, de algún modo, se mezcla
con el análisis a través del teorema
del binomio[3.35] cuando n es < o y
el desarrollo de (p + q)n se
convierte en la infame serie
binomial. De modo parecido,
trigonometría → análisis cuando,
por ejemplo, las funciones seno y
coseno se desarrollan en sus
respectivas series de potencias.
Una complicación adicional es que
para las matemáticas modernas
«análisis» también puede tener como
connotación un tipo particular de
espíritu metodológico propio de las
disciplinas recién mencionadas. Véase,
por ejemplo, lo siguiente, del Oxford
Concise Dictionary of Mathematics:
«El término “análisis” ha llegado a
usarse para indicar un enfoque bastante
más riguroso de los temas del cálculo y
de los fundamentos del sistema de los
números reales» (Clapham, pág. 6),
donde la última frase = el ámbito de
Dedekind y Cantor, y las razones por
las que los temas del cálculo debían
haber necesitado «un enfoque más
riguroso» constituyen la verdadera
causa motivadora de su trabajo. En
pocas palabras, toda la cuestión de
rigor-y-fundamentos era parte de la
gran emergencia filosófica de las
matemáticas poscálculo, una profunda
división acerca del modo en que los
entes
matemáticos
debían
ser
considerados,
y
los
teoremas,
demostrados. Y esta división es a su
vez el contexto profundo tras las
controversias
respecto
a
las
matemáticas transfinitas de Cantor.
Todo lo cual será analizado mientras
avancemos.
Otro aspecto implícito en la cita del
diccionario Oxford son las viejas
oposiciones entre discreto y continuo y
entre geometría y matemáticas puras.
Resulta que todos los grandes nombres
tras el cálculo temprano estaban
preocupados
por
las
funciones
continuas y magnitudes que eran o bien
directamente geométricas (rectas,
curvas,
áreas,
volúmenes)
o
representables
geométricamente
(fuerza, velocidad, aceleración). Pero
ahora tenga en cuenta que una de las
mayores preocupaciones de las
matemáticas en el siglo anterior a
Cantor
y
Dedekind
será
la
aritmetización del análisis, que
esencialmente
significa
obtener
teoremas sobre funciones continuas
usando solo números, no curvas o
áreas. Esa aritmetización acaba
llevando el análisis más hacia los
territorios del álgebra y la teoría de
números, campos que hasta entonces se
habían dedicado a entes matemáticos y
fenómenos 100% discretos. Lo que
ocurre en el análisis del siglo XIX será
una separación de la geometría similar
a la de las matemáticas griegas tras el
descubrimiento de los irracionales por
la D. H. P.
Estamos de nuevo algo adelantados,
cronológicamente
hablando.
La
principal cuestión relacionada con el ∞
que debe tenerse en cuenta a lo largo
del siguiente par de §s será por qué
exactamente el cálculo debía haber
requerido
el
rigor
adicional
mencionado antes en el GLOSARIO DE
EMERGENCIA (en el cual más o menos
ya no estamos). También vale la pena
subrayar, de nuevo para su futuro uso,
que la distinción más importante entre
los fenómenos discretos y continuos en
las matemáticas es que los primeros se
pueden
caracterizar
simplemente
mediante números racionales, mientras
que la continuidad requiere todos los
números reales, incluyendo los
irracionales.
Resulta que una figura importante
tanto en la aritmetización del análisis
como en las matemáticas del ∞
Bernard P. Bolzano (1781-1848) de la
Universidad de Praga. Por diversas
razones este es el lugar adecuado para
hablar de él, aunque para hacerlo
tendremos que entrar brevemente en el
siglo XIX y luego saltar de nuevo hacia
atrás en el próximo §. En términos de
aritmetización, el padre Bolzano es el
menos conocido de un cuarteto de
matemáticos que fueron pioneros de lo
que se acabó conociendo como
«análisis riguroso» a principios del
siglo XIX, siendo los otros tres
Augustin-Louis Cauchy, Niels Abel, y
Peter Gustav Lojeune Dirichlet.
Cauchy tiende a recibir mayor
reconocimiento
gracias,
principalmente, a su Cours d’Analyse
(1821), que durante ciento cincuenta
años fue el libro de texto estándar de
matemáticas superiores en Europa. A
grandes rasgos, el proyecto de Cauchy
implica intentar rescatar el cálculo de
sus
dificultades
metafísicas[3.36]
definiendo
los
infinitesimales
rigurosamente en términos de límites,
pero buena parte del análisis de Cauchy
todavía está ligado a la geometría de
modos
que
acaban
causando
problemas. Es en realidad Bolzano, en
su obra de 1817 Rein analytischer
Beweis des Lehrsatzes…,[3.37] quien da
la primera demostración puramente
aritmética de un teorema que involucra
funciones continuas.[3.38] En este
mismo libro proporciona lo que ahora
se considera la definición matemática
correcta de la continuidad: f(x) es
continua en el intervalo A si en
cualquier punto a de A la diferencia
f(a + δ) − f(a) puede hacerse tan
pequeña como se quiera haciendo que δ
sea arbitrariamente pequeña. En
realidad, Bolzano representa otra clara
manifestación de los caprichos de la
fama matemática. Algo de esto
resultará aquí descontextualizado y
ante rem, pero para su información, por
ejemplo, su método para determinar si
una serie es continua todavía se usa
hoy, y se atribuye a Cauchy. O que
Bolzano fue el primer matemático en
obtener una función que es continua
pero no diferenciable (es decir, sin
derivada), un resultado que derribó la
suposición del cálculo temprano de que
la continuidad y la diferenciación iban
de la mano, y fue completamente
ignorado. La construcción por Karl
Weierstrass de una función similar,
treinta años más tarde, fue celebrada
como su «descubrimiento».[3.39]
Todo esto acabará siendo más
importante de lo que parece ahora
mismo, en particular la idea de la
continuidad como una propiedad
aritmética. Pero es el trabajo posterior
de
Bolzano
sobre
cantidades
infinitas[3.40] lo que resulta pertinente
aquí, aunque solo sea porque es la
conexión histórica más importante
entre las Dos nuevas ciencias de
Galileo
y
el
trabajo
de
Dedekind/Cantor. Por lo menos,
Bolzano, que era una especie de hereje,
tanto matemática como religiosamente
(por ejemplo, fue finalmente expulsado
de la Universidad de Praga por sus
sermones contra la guerra), es el
primer matemático desde Galileo en
tratar de manera explícita la distinción
entre los infinitos real y potencial de
Aristóteles. Como las DNC, la obra de
Bolzano Las paradojas del infinito es
profundamente
anti-aristotélica,
aunque también hay diferencias
importantes: los argumentos de
Bolzano son mucho más matemáticos
que los de Galileo, y también su
motivación. Para mencionar otra vez
algunas cosas que después se
desarrollarán con más detalle, lo que
impulsa las P. del I. tiene que ver con
ciertas
dificultades
metafísicas
relacionadas con el despliegue de
cantidades e incrementos de tipo ∞ en
el cálculo. Prácticamente, todos los
matemáticos
poscálculo
habían
intentado esquivar u ofuscar esas
dificultades invocando vagamente a
Aristóteles y suponiendo que todos los
∞ que estaban manejando eran solo
potenciales o «incompletos» (esta era
la idea básica tras los límites
cauchianos). Que Bolzano intentara
abrir grandes hendiduras en dicha
suposición es una razón por la que su
trabajo recibió tan poca atención.
También por ello, el profesor Cantor,
que tiende a ser uniformemente
vitriólico hacia la mayor parte de los
tratamientos históricos del ∞, a
menudo destaca a Bolzano con especial
aprovación.[3.41]
P. del I. es la consecuencia de los
intereses combinados de Bolzano por
las funciones, las colecciones infinitas
y la recta real. Resulta que a este libro
solo le faltan algunos conceptos para
inventar la teoría de conjuntos
moderna: «moderna» en el sentido de
ser capaz de tratar conjuntos infinitos.
[3.42] Una de las importantes maneras
en que anticipa el trabajo de Cantor es
que expresa abiertamente algo que solo
estaba implícito en la paradoja de
Galileo, es decir, la idea de la
correspondencia uno a uno como un
modo de establecer la equivalencia de
dos conjuntos. El enfoque de Bolzano
respecto a la paradoja de Galileo es
puramente abstracto, y cantoriano.
Consiste en tomar algo que Galileo
había atribuido a las limitaciones de la
mente humana y considerarlo como
una propiedad intrínseca de los
conjuntos infinitos; o sea, el hecho de
que un subconjunto de un conjunto
infinito puede tener tantos elementos
como el conjunto mismo. Como vamos
a ver, tras Georg Cantor (cuyo propio
trabajo fue controvertido pero para
nada ignorado), los matemáticos
entendieron que esa propiedad era, de
hecho, la característica distintiva de los
conjuntos infinitos, y la definición
matemática formal de conjunto infinito
se basa ahora en esta extraña
equivalencia.
Observe también que la versión de
Galileo de la equivalencia implicaba
solo los grandes ∞ de todos los enteros
y todos los cuadrados perfectos. Es
Bolzano quien formula por primera vez
la equivalencia entre los densos,
zenoicos pequeños ∞ de la recta real.
Lo hace en P. del I. examinando el
conjunto de todos los números reales
entre 0 y 1, es decir, el conjunto de
todos los puntos en el intervalo cerrado
[0, 1] de la recta real. Bolzano
considera la función elemental[3.43]
y = 2x y observa que si los valores de x
de su dominio son todos los puntos de
[0, 1], la función asignará a cada x un
único valor de y en el intervalo cerrado
más largo [0, 2]. De modo que 0,26
corresponderá a 0,52; 0,74, a 1,48;
0,624134021…, a 1,248268042…, y así
sucesivamente. En otras palabras, una
perfecta correspondencia uno a uno:
hay exactamente tantos puntos de la
recta real en [0, 1] como los hay en
[0, 2]. Y (como ahora parece obvio,
pero Bolzano fue el primero en señalar)
simplemente cambiando el coeficiente
de x en la función por cualquier otro
entero —y = 5x, y = 6,517x— puede
usted demostrar que hay exactamente
tantos números reales entre 0 y 1 como
entre 0 y cualquier otro número finito
en el que pueda pensar.*
*INTERPOLACIÓN DE TIPO SEI
En realidad, como ya vimos en §2e,
el número de puntos en [0, 1] es igual a
la de puntos en toda la recta real
extendiéndose infinitamente en ambas
direcciones. Aunque la demostración
formal
de
esto
es
bastante
elaborada,[3.44] una demostración de la
equivalencia está dentro de las
capacidades del escolar medio. Tome
el segmento de la recta real
correspondiente a [0, 1] y suspéndalo
por encima de la recta real entera,
luego sitúe la punta de un compás en el
punto medio exacto del segmento y
trace la mitad inferior de un círculo C
cuyo diámetro es 1,[3.45] y dispóngalo
de ese modo:
Tome cualquier punto de la recta
real y trace una recta L desde este
punto hasta el centro de C, es decir,
hasta el punto medio del diámetro. Sea
cual sea el punto de intersección con la
semicircunferencia inferior, trace una
recta vertical desde dicho punto hasta
que corte al diámetro [0, 1], de nuevo
como se indica:
Así, cualquier punto de la recta real
puede, mediante una L1, L2, L3, …, Ln,
ser puesto en correspondencia uno a
uno con un punto de [0, 1]. Q .E. D.
FIN DE LA INTERPOLACIÓN
Premoniciones técnicas aparte, Las
paradojas del infinito es también
notable
por
sus
intenciones
metafísicas. En esto, también, se
parece a las DNC y a parte del trabajo
posterior de Cantor. La postura básica
de Bolzano es desautorizar la cadena
aristo-escolástica del ser. Cree que el
universo creado es a la vez infinito en
extensión e infinitamente divisible. La
«Eternidad» es simplemente un ∞
temporal. Como la mayoría de los
matemáticos religiosos desde Pitágoras
hasta Gödel,[3.46] Bolzano cree que las
matemáticas son el lenguaje de Dios y
que se pueden obtener y demostrar
matemáticamente profundas verdades
metafísicas. Lo que le falta, en
términos de ampliar sus inspiraciones
sobre tamaños ∞, densidades y
equivalencias a verdaderos teoremas,
son los conceptos de teoría de
conjuntos acerca de la cardinalidad,
ordinalidad y potencia tal como se
aplican a colecciones de puntos.[3.47]
Puede establecer y demostrar la extraña
equivalencia
de
conjuntos/subconjuntos infinitos, y
puede vislumbrar que su relación no es
contradictoria, sino paradigmática.
Pero no tiene manera de convertir sus
demostraciones en una auténtica teoría
de los conjuntos infinitos y sus
relaciones, comportamientos, etc. La
principal razón de ello —por extraño
que pueda parecer ahora— es que en la
era de Bolzano todavía no hay ninguna
teoría coherente del sistema de los
números reales, ninguna definición
rigurosa de número irracional.
4
§4a.
El
consenso académico es que ha
habido tres grandes períodos de crisis
en los fundamentos de las matemáticas
occidentales. El primero fueron los
inconmensurables
pitagóricos.
El
tercero es la era (en la que se puede
argumentar que estamos todavía) tras
las demostraciones de incompletitud de
Gödel y el derrumbe de la teoría de
conjuntos cantoriana.[4.1] La segunda
gran crisis envolvió el desarrollo del
cálculo.
Ahora la idea va a ser trazar de
forma resumida cómo las matemáticas
transfinitas evolucionan gradualmente
a partir de ciertas técnicas y problemas
asociados con el cálculo/análisis. En
otras palabras, construir un andamiaje
conceptual para contemplar y valorar
los logros de Georg Cantor.[4.2] Como
se ha mencionado, esto significa ir
diacrónicamente hacia atrás, hacia
donde estaba la línea temporal original
al final de §3a.
O sea, que ahora estamos cerca del
fin del siglo XVII, la época de la
Restauración y el sitio de Viena, de
pelucas altas como torres y pañuelos
perfumados, etc. Sin duda, ya sabe que
el cálculo fue el descubrimiento
matemático más importante desde
Euclides. Un avance fundamental en la
capacidad de las matemáticas para
representar la continuidad y el cambio
y los procesos del mundo real. Ya se ha
hablado de algo de esto. Probablemente
también sabe que a Isaac Newton y/o
Gottfried Wilhelm Leibniz se les suele
atribuir
su
descubrimiento.[4.3]
También podría saber —o por lo menos
ser capaz de anticipar a partir de la
cronología de §3a— que la idea de una
atribución exclusiva o incluso dual es
absurda, como lo es la noción de que lo
que
ahora
llamamos
cálculo
corresponda a cualquier invención
individual. Incluso, según el más
simple de los recuentos, la autoría
tendría que ser compartida por al
menos una docena de matemáticos en
Inglaterra, Francia, Italia y Alemania
que estaban todos ocupadísimos
ramificando el trabajo de Kepler y de
Galileo sobre funciones, series infinitas
y las propiedades de las curvas,
motivados (es decir que lo estaban,
como ya se ha mencionado) por ciertos
problemas científicos urgentes que
también eran, o bien problemas
matemáticos, o abordables como tales.
Estos eran algunos de los
problemas motivadores más urgentes:
calcular la velocidad y la aceleración
instantáneas (física, dinámica), hallar
la tangente a una curva (óptica,
astronomía), hallar la longitud de una
curva, el área delimitada por una curva,
el volumen delimitado por una
superficie (astronomía, ingeniería),
hallar el valor máximo/mínimo de una
función (ciencia militar, esp. artillería).
Probablemente había algunas más.
Ahora sabemos que todos estos
problemas
están
estrechamente
relacionados: todos son aspectos del
cálculo. Pero los matemáticos que
trabajaban en ellos en el siglo XVII no
lo sabían, y Newton y Leibniz sí
merecen un enorme reconocimiento
por ver y conceptualizar las relaciones
entre, por ejemplo, la velocidad
instantánea de un punto y el área
delimitada por la curva que describe su
movimiento, o la tasa de variación de
una función y el área dada por una
función cuya tasa de variación
conocemos. Fueron Newton y Leibniz
los primeros en ver el bosque —o sea,
el teorema fundamental de que la
diferenciación y la integración son
inversas mutuas— y fueron capaces de
obtener un método general que
funcionaba con todos los problemas de
los tipos mencionados. Sobre el propio
misterio de la continuidad. Aunque no
sin tener que dar rodeos para evitar
algunas horribles grietas en este
bosque, y ciertamente no sin todo tipo
de árboles preliminares en forma de
resultados y descubrimientos de otras
personas. Además de los ya
mencionados en la cronología, están,
por ejemplo: 1629 - Pierre de Fermat y
su método para hallar los valores
máximo y mínimo de una curva
polinómica; hacia 1635 - Gilles
Personne
de
Roberval
y
su
descubrimiento de que la tangente a
una curva se podía expresar como una
función de la velocidad de un punto
móvil cuya trayectoria da la curva;[4.4]
1635
Francesco
Bonaventura
Cavalieri y su método de los
indivisibles para calcular áreas bajo
curvas; 1644 - Isaac Barrow y su
método de las tangentes geométrico.
Además, hacia 1668, hay un párrafo
muy premonitorio en el prefacio a la
obra de James Gregory Geometriae
Pars Universalis cuyo punto destacado
es que la división realmente importante
de las matemáticas no es en
geométricas y aritméticas, sino en
universales y particulares. Motivo por
el que es premonitorio: varios
matemáticos desde Eudoxo hasta
Fermat habían inventado y puesto en
práctica métodos propios del cálculo,
pero siempre geométricamente y
siempre en relación con problemas
específicos. Son Newton y Leibniz
quienes combinan los diversos métodos
de las latitudes y los indivisibles y
demás en una única técnica aritmética
cuya amplitud y generalidad (es decir,
su abstracción) son su gran fuerza.[4.5]
Pero sus formaciones y enfoques son
diferentes. Newton llega al cálculo a
través del método de las tangentes de
Barrow, el teorema del binomio y el
trabajo de Wallis sobre series infinitas.
La ruta de Leibniz incluye funciones,
pautas numéricas llamadas «sucesiones
de sumas y sucesiones de diferencias»,
y una distintiva metafísica[4.6] según la
cual una curva podía ser tratada como
una sucesión ordenada de puntos
separados
por
una
distancia
literalmente infinitesimal. (En pocas
palabras, para Leibniz las curvas son
generadas por ecuaciones, mientras que
las cantidades que varían a lo largo de
una curva son dadas por funciones;
seguramente hemos mencionado que
tiene derechos de autor sobre el
término «función»).
No vamos a entrar demasiado en el
asunto de Newton contra Leibniz, pero
las diferencias metafísicas en su
manera de contemplar las cantidades
infinitesimales son muy relevantes.[4.7]
Newton, en el fondo un físico que
pensaba en términos de velocidad y
tasa de variación, usó incrementos
infinitamente pequeños en los valores
de sus variables como herramientas
desechables al llegar a la derivada de
una función. La derivada de Newton
era básicamente un límite de tipo
eudoxiano de las razones de dichos
incrementos cuando se volvían
arbitrariamente pequeños. Leibniz, un
abogado/diplomático/cortesano/filósofo
para quien las matemáticas eran una
especie de pasatiempo colateral,[4.8]
tenía una ya mencionada metafísica
idiosincrática que involucraba ciertos
extraños, fundamentales, infinitamente
pequeños constituyentes de toda la
realidad,[4.9] y se puede decir que
construyó su cálculo alrededor de las
relaciones entre ellos. Esas diferencias
tenían implicaciones metodológicas,
obviamente, con Newton viéndolo todo
en términos de tasas de cambio y el
teorema del binomio, y, por lo tanto,
tendiendo
a
representar
las
funciones[4.10] como series infinitas, y
Leibniz prefiriendo lo que se conoce
como «formas cerradas», evitando las
series y usando sumas y funciones tal
cual,
incluyendo
funciones
trascendentes cuando las algebraicas no
daban resultado. Algunas de esas
diferencias eran solo de gusto: por
ejemplo, los dos usaron notaciones y
vocabularios totalmente diferentes,
aunque Leibniz era mejor y en
términos generales ganó.[4.11] Para
nosotros, lo importante es que las
versiones del cálculo de ambos
hombres causaron serios problemas a
las matemáticas como disciplina
deductiva, lógicamente rigurosa, y
fueron vigorosamente atacadas al
mismo tiempo que hacían posible todo
tipo de resultados increíbles en las
matemáticas y la ciencia. La causa de
la debilidad en los fundamentos
debería ser fácil de ver, tanto si el
problema es metodológico (en el caso
de Newton) como metafísico (caso de
Leibniz). Como se ha mencionado en
§2b y probablemente en alguna otra
parte (y es de todos modos bien
conocido), el problema concierne a los
infinitesimales, que una vez más a
finales del siglo XVII obligan a todos a
intentar tratar con las matemáticas del
∞.
La mejor manera de hablar de esos
problemas es resumir de qué modo
funciona el cálculo temprano. Vamos a
hacer una deducción no muy estándar
de tipo cuadratura que consigue ilustrar
varios aspectos de la técnica de una
sola vez, de manera que no tenga usted
que aburrirse con un montón de casos
distintos. También vamos a mezclar en
cierto modo los diferentes métodos y
terminologías de Newton y Leibniz,
pues la finalidad aquí no es la exactitud
histórica, sino la claridad en la
ilustración. Por la misma razón, vamos
a evitar los casos de cómo-hallar-latangente
y
cómo-llegar-de-lavelocidad-media-a-la-velocidadinstantánea que usan la mayoría de los
libros de texto.[4.12]
Primero, tome como referencia la
que vamos a llamar Figura 4a, la cual,
por favor, observe que ni siquiera está
remotamente a escala, pero tiene la
ventaja de hacer que las cosas resulten
fáciles de ver. Por la misma razón, la
«curva» relevante en la Figura 4a es
una recta, el tipo más simple de curva,
respecto a la cual los cálculos no son
nada complejos.[4.13] La curva de la
Figura 4a puede contemplarse, o bien
como un conjunto de puntos dado por
una función continua en un intervalo
cerrado, o bien como la trayectoria de
un punto en movimiento en el espacio
2D. Para este último caso, el
newtoniano (que parece ser el preferido
en la mayoría de las clases de
matemáticas superiores), observe que
aquí el eje vertical indica la posición y
el eje horizontal es el tiempo (por una
larga historia y buenas razones, podrían
estar intercambia dos, o no estarlo,
respecto a los ejes de las gráficas de
movimiento que usted debió de ver en
la escuela). Por lo tanto:
En primer lugar, pongamos que A,
el área bajo la curva, es igual a x2.
(Esto puede parecer extraño porque la
curva de la Figura es una línea recta,
así que parece como si A en realidad
debiera ser , pero para la mayoría de
las curvas dibujadas exactamente a
escala x2 funcionará; o sea, que aquí
sígame la corriente y suponga que y es
exactamente igual a x). Esto significa
que formalmente suponemos lo
siguiente:
(1) A = x2. Luego pongamos que x se
incrementa en una cantidad
infinitesimalmente pequeña t,[4.14]
con el área bajo la curva
incrementándose
consecuentemente en tz. Dado esto,
y dada la igualdad en (1),
obtenemos:
(2) A + tz = (x + t)2. Desarrollando el
binomio, obtenemos:
(3) A + tz − x2 + 2xt + t2. Y, como,
por (1), A = x2 podemos reducir (3)
a:
(4) tz = 2xt + t2.
Ahora
mire
atentamente. Tomamos (4) y
dividimos por t obteniendo:
(5) z = 2x + t. Mire de nuevo: al estar
t definida como infinitesimalmente
pequeña, 2x + t es equivalente, en
términos finitos, a 2x, de modo que
la ecuación relevante se convierte
en:
(6) z = 2x. Y punto final. En un
momento veremos qué demuestra
esto (Lavine, págs. 16-17).
Probablemente se habrá dado
cuenta de algún cambio serio en el
tratamiento que hace esta deducción de
la cantidad infinitesimal t. En el paso
de (4) a (5), t es suficientemente > 0
para ser un divisor válido. En el paso
de (5) a (6), sin embargo, t parece ser =
0, pues t sumada a 2x da 2x. En otras
palabras, t se trata como o cuando
conviene y como > o cuando
conviene,[4.15] lo cual parece dar lugar
a la contradicción (t = 0) & (t ≠ 0), lo
cual —como recordará de la anterior
discusión sobre demostraciones por
reducción al absurdo— parece una
amplia base argumental para volver
atrás y decir que debe de haber algún
error en el uso de cantidades
infinitesimales como t. Por lo menos,
esa t parece un truco de notación,
alguna versión matemática de la
«contabilidad
creativa»
en
economía.[4.16]
Excepto por lo siguiente. Si pasa
usted por alto la contradicción
aparente, o por lo menos aplaza la
reducción al absurdo, una deducción
como la de la Figura 4a (la cual, a
pesar de su parecido con el triángulo
característico de Leibniz, es en
realidad una versión simplificada del
proceso que Newton usa en De Analysi)
[4.17] resulta ser una pieza de artillería
matemática realmente notable, que
arroja por lo menos dos resultados
cruciales. El resultado n.º 1 es que se
puede demostrar que la tasa de cambio
de x2 es 2x si se acepta el cálculo
como representación del
cambio de x durante el «instante»
t.[4.18] El resultado n.º 2 es que se
puede demostrar que la tasa de cambio
del área A es la «curva» (o sea, la y de
la Figura 4a; recuerde que una recta es
un tipo de curva) que delimita A. Para
verlo,
calcule
simplifique para obtener
y
, luego
divida por
la sospechosamente
conveniente t para obtener z, la cual,
recuerde, es solo «infinitesimalmente
mayor» que y, y por lo tanto aquí se
puede considerar como = y.[4.19] Acaba
usted obteniendo y = 2x, la que resulta
ser la función que da la curva de la
Figura 4a. Lo cual significa que el
resultado y = 2x lleva empaquetado el
principio básico del cálculo integral: la
tasa de cambio del área delimitada por
una curva no es más que esa misma
curva. Lo que, a su vez, significa que la
integral de una función que tiene una
derivada dada es la propia función, lo
cual resulta ser el teorema fundamental
del cálculo (T. F. C.);[4.20] o sea, que la
diferenciación y la integración son
recíprocas[4.21] del mismo modo en que
lo son la multiplicación y la división o
las potencias y las raíces, lo cual es el
motivo de que el cálculo sea tan
poderoso y de que Newton y Leibniz
merezcan tanto reconocimiento: el
T. F. C. combina ambas técnicas en un
paquete de gran calibre (… mientras se
acepten los posibles malentendidos
acerca de si t = 0).
Sin embargo, la mayoría de
nosotros no aprendimos esto así en la
escuela. Si estudió usted un primer
curso de cálculo es probable que
aprendiera, mediante gráficos de
velocidad-y-aceleración, a tomar el
límite de Δx, o que
, donde
es la notación de Leibniz y el
concepto de límite es el modo en que el
análisis poscálculo embelleció a
posteriori todo el problema de los
infinitesimales. Puede que recuerde o
que sepa, por ejemplo, que en la
mayoría de los libros de texto
modernos un infinitesimal se define
como «una cantidad que da o tras la
aplicación de un proceso límite». Si
usted es un auténtico superviviente de
primer curso de cálculo, seguramente
también
puede
recordar
cuán
brutalmente abstracto y antiintuitivo
resulta intentar aprender esa cosa de
los límites: casi nadie explica a los
estudiantes de carrera los porqués del
método,[4.22] ni menciona que hay una
manera más fácil o por lo menos más
intuitiva de entender dx y Δx y t,
concretamente como órdenes de . La
mayoría de los profesores, en cambio,
intentan distraer a los estudiantes con
vistosos ejemplos de la capacidad del
cálculo para resolver todo tipo de
complejos problemas del mundo real:
desde la velocidad y aceleración
instantáneas como la 1.ª y la 2.ª
derivadas, a las órbitas elípticas de
Kepler y la
de Newton, los
movimientos de muelles disparados y
bolas rebotando, las penumbras de los
eclipses, o la intensidad de un sonido
como función de la rotación del
regulador de volumen, sin olvidar el
panorama trigonométrico que se abre al
aprender que d(sen x) = cos x y
d(cos x) = − sen x, que la tangente es
el límite de la secante, etc. Todo esto
se presenta de manera habitual como
preparación para dominar el concepto
de límite, un concepto que en realidad
no es menos abstracto o doloroso que
intentar solo concebir dx o t como
cantidades
increíblemente,
alucinantemente pequeñas.
A partir de todo lo dicho, queda
claro que el verdadero motivo tras el
enfoque del cálculo basado en los
límites era que las cantidades
infinitesimales de Newton y Leibniz, y
sus juegos de manos con la notación,
habían abierto algunas horribles
hendiduras en los fundamentos de las
matemáticas, dado que la proposición
«(x = 0) & (x ≠ 0)» viola todo tipo de
axiomas básicos de tipo LTE. Dado
nuestro relato hasta ahora, lo más fácil
de decir parece ser que la mayoría de
dichos presuntos problemas en realidad
estaban causados por la incapacidad de
las matemáticas para tratar con
cantidades infinitas, es decir, que,
como en el caso de la dicotomía de
Zenón y la paradoja de Galileo, la
auténtica dificultad era que nadie
entendía todavía la aritmética del ∞.
No sería exactamente un error decir
esto, pero para nuestros propósitos
resultaría por lo menos algo pobre.[4.23]
Como todo lo demás acerca de las
matemáticas tras el cálculo, las
verdaderas dificultades y las cosas que
están en juego aquí son más complejas.
§4b.
Recapitulemos
y reformulemos un
poco las cosas. La propia potencia del
cálculo y su relevancia provocaron en
las matemáticas de la modernidad
temprana el mismo tipo de crisis que la
dicotomía de Zenón había planteado a
los griegos. Solo que de algún modo
era peor. Las paradojas de Zenón no
habían resuelto ningún problema
matemático existente, mientras que las
herramientas del cálculo sí lo habían
hecho. La panoplia de resultados acerca
del mundo real que permitió el cálculo
ya se ha detallado, así como su
extraordinaria pertinencia en aquel
momento: todas las ciencias aplicadas
se estaban dando de bruces con los
problemas de los fenómenos continuos
justamente cuando Newton y Leibniz y
sus respectivas teorías dieron con una
explicación
matemática
de
la
continuidad.[4.24] Una que funcionaba.
Una que condujo directamente a la gran
decodificación moderna de las leyes
físicas como ecuaciones diferenciales.
Solo que desde el punto de vista de
los fundamentos es un desastre. Es todo
un castillo en el aire. Los
leibnizianos[4.25] no podían explicar u
obtener
cantidades
que
fueran
verdaderamente distintas de o pero a la
vez infinitamente próximas a o. Los
newtonianos,[4.26] que afirmaban que el
cálculo no dependía realmente de
cantidades infinitesimales sino más
bien de las «fluxiones» —donde
fluxión significa la tasa de cambio de
una variable dependiente del tiempo—,
se basaban en el requisito de que los
cocientes de dichas fluxiones se tomen
justo cuando se desvanecen o surgen de
o, en el sentido del primer o último
instante infinitesimal en el que son >
0, lo cual, por supuesto, no es más que
sustituir
cantidades
infinitamente
pequeñas por instantes infinitamente
breves. Y los newtonianos no tenían
una explicación mejor de esos
cocientes instantáneos que la que
tenían los leibnizianos de las
cantidades infinitesimales.[4.27] La
única verdadera ventaja de la versión
de Newton (para todo el mundo
excepto para los estudiantes de primer
curso de cálculo) es que ya tiene el
concepto de límite implícito de algún
modo en la idea de un primer/último
instante que se desvanece de tan
pequeño:
serían
principalmente
Agustin-Louis Cauchy y luego Karl
Weierstrass quienes desarrollaron todo
esto. (Weierstrass, dicho sea de paso,
fue profesor de Cantor).
A propósito de la continuidad, los
infinitesimales y el cálculo, vale la
pena echar un rápido vistazo a otra de
las paradojas de Zenón contra el
movimiento.
Esta
se
llama
habitualmente la paradoja de la flecha,
porque analiza el intervalo de tiempo
durante el cual una flecha está viajando
desde su arco hasta la diana.[4.28]
Zenón observa que en cualquier
instante específico de ese intervalo, la
flecha ocupa «un espacio igual a sí
misma», y dice que esto es lo mismo
que estar «en reposo». La cuestión es
que la flecha no puede estar realmente
moviéndose en un instante, porque el
movimiento requiere un intervalo de
tiempo, y aquí un instante no es un
intervalo: es la unidad de tiempo más
pequeña imaginable, y no tiene
duración, del mismo modo en que un
punto geométrico no tiene dimensión.
Y si en todos y cada uno de los
instantes la flecha está en reposo,
entonces la flecha no se mueve jamás.
De hecho, nada se mueve en ningún
caso, realmente, pues en cualquier
instante dado todo está en reposo.
Hay por lo menos una premisa
implícita en el argumento de Zenón,
que puede ponerse en evidencia
mediante un esquema:
(1) En todos y cada uno de los
instantes, la flecha está en
reposo.
(2) Cualquier intervalo de tiempo
está compuesto de instantes.
(3) Por lo tanto, durante cualquier
intervalo de tiempo la flecha no
se está moviendo.
La premisa encubierta es (2), que es
justamente lo que Aristóteles ataca en
la Física, descartando todas las P. Z.
sobre la base de que «… el tiempo no
está
compuesto
de
instantes
indivisibles»,[4.29] es decir, que la
misma noción de que algo esté o bien
en movimiento o bien en reposo en un
instante es incoherente. Obsérvese, sin
embargo, que es precisamente a esa
idea del movimiento en un instante a la
que el cálculo de Newton y Leibniz es
capaz
de
hallarle
sentido
matemáticamente, y no solo el
movimiento en general sino la precisa
velocidad instantánea, sin olvidar la
tasa-de-cambio-de-la-velocidad
instantánea
(=
aceleración,
2.ª
derivada), la tasa-de-cambio-de-laaceleración
instantánea
(=
3.ª
derivada), etc.
En relación con la paradoja de la
flecha, el hecho de que el cálculo
clásico
sea
capaz
de
tratar
precisamente lo que Aristóteles dice
que no puede ser tratado no es una
coincidencia. Para empezar, eche otro
vistazo a lo del instante «sin duración»
de hace dos párrafos, y observe que
este término es algo ambiguo. Resulta
que el tipo de instante del que habla
Zenón
es,
por
lo
menos
matemáticamente, no algo de duración
o, sino un infinitésimo. Tiene que
serlo. Considere de nuevo la vieja
fórmula escolar para el movimiento,
Velocidad × Tiempo = Distancia, o
v = . Una flecha en reposo tiene una v
de 0 y cubre una distancia 0d,
obviamente. Pero si en términos de
tiempo un instante = 0, entonces desde
el punto de vista de Zenón se acaba
postulando que o es el divisor en v = ,
lo
cual
es
matemáticamente
ilegal/falaz del mismo modo que todo
el asunto de «0 = » es ilegal/falaz.
Solo que aquí tenemos que ir de
nuevo con cuidado, y también con las
demás P. Z. Como ya se ha mencionado
en todo tipo de diferentes contextos, no
es lo mismo «tratar» algo que tratarlo
realmente. Incluso si admitimos que el
instante de Zenón es infinitesimal y,
por lo tanto, apto para el tratamiento
mediante fluxiones de Newton o el dx
de Leibniz, probablemente ya puede
ver que una «solución», al estilo del
cálculo clásico, de la flecha de Zenón
puede resultar trivial en el mismo
sentido en que «
» es trivial
respecto a la dicotomía. Es decir, la
flecha es realmente una paradoja
metafísica, y es precisamente una
explicación
metafísica
de
los
infinitesimales lo que el cálculo no
tiene. Sin tal explicación, todo lo que
podemos hacer es aplicar a la flecha
alguna fórmula de aspecto excitante
que dependerá de los mismos
infinitesimales misteriosos y de
aspecto paradójico que Zenón usa
desde el principio. Además, aún
quedará la inquietante cuestión de
cómo llega realmente una flecha a la
diana tras un intervalo que contiene
una infinidad de instantes de
tamaño .[4.30]
El problema es que, siendo la
flecha
metafísica,
también
es
extremadamente sutil y abstracta.
Considere por ejemplo otra premisa
encubierta, o quizás un tipo de
subpremisa que está implícita en la
parte (1) del argumento de Zenón: ¿es
realmente verdad que algo tiene que
estar o bien en movimiento o bien en
reposo?
Al
principio
parece
ciertamente verdadero, suponiendo que
tomemos «en reposo» como sinónimo
de «no moviéndose». Recuerde la LTE,
después de todo. Es seguro que, en
cualquier instante dado t, algo o bien se
está moviendo o bien no se está
moviendo, en el sentido de que en el
instante t tiene o bien una velocidad >
0 o una velocidad = 0. Que en realidad
esta disyuntiva no es válida —que aquí
la LTE no se puede aplicar realmente—
puede verse examinando la diferencia
entre el número 0 y la palabra abstracta
«nada». Es una diferencia sutil, pero
importante. La incapacidad de los
griegos para verla fue probablemente
lo que les impidió ser capaces de usar
el 0 en sus matemáticas, lo cual fue un
gran inconveniente. Pero 0 o nada es
una de esas distinciones abstractas de
las que es casi imposible hablar
directamente: más bien tiene que
hacerse mediante ejemplos. Imagine
una clase de matemáticas, y que en esa
clase hay un examen diabólicamente
difícil que se puntúa sobre 100, e
imagine que ni usted ni yo obtenemos
ni un solo punto. Pero hay una
diferencia: usted no está en la clase y
ni siquiera hizo el examen, mientras
que yo sí estoy, y lo hice. El hecho de
que usted obtuviera o puntos de ese
examen es, pues, irrelevante —su 0
significa Información No Disponible,
nada—, mientras que mi 0 es un cero
de verdad. O, si no le gusta esta,
imagine que usted y yo somos,
respectivamente, mujer y hombre,
ambos sanos y con una edad de entre
veinte y cuarenta años, y que ambos
estamos en la consulta de un médico, y
que ninguno de los dos ha tenido la
regla en las últimas diez semanas, en
cuyo caso mi número total de reglas no
es nada, mientras que el suyo es 0, y,
por lo tanto, significativo. Fin de los
ejemplos.
Así que simplemente no es verdad
que algo siempre tenga que ser o bien 0
o bien no-0: también podría ser nada,
Información No Disponible.[4.31] En
cuyo caso hay una respuesta no trivial a
la premisa de Zenón (1), a saber: el
hecho de que la flecha no se esté
moviendo en t no significa que su v en t
sea o, sino más bien que su v en t no es
nada. Que esta imprecisión en la
premisa (1) no se capte enseguida se
debe en parte a la cuestión del 0 o nada
y en parte a la vertiginosa abstracción,
de Cuarto Nivel, de palabras como
«desplazamiento» y «movimiento». El
término «movimiento», por ejemplo, es
especialmente engañoso porque no
parece para nada abstracto: parece
denotar llanamente algo o algún
proceso, mientras que, si piensa usted
en ello,[4.32] incluso el tipo más simple
de movimiento es en realidad una
complicada relación entre (a) un
objeto, (b) más de un lugar, y (c) más
de un instante. Punto a destacar: la
falacia de la flecha está en la
suposición que Zenón hace de que la
pregunta «¿Está o no está en
movimiento la flecha en el instante t?»
es más coherente que «¿Qué nota
obtuvo usted en ese curso que no
hizo?» o «Un punto geométrico, ¿es
curvo o recto?». La respuesta correcta a
las tres es: Información No Disponible.
[4.33]
Admitámoslo, esta respuesta al
problema de la flecha es, estrictamente
hablando,
más
filosófica
que
matemática. Del mismo modo que una
solución como la dada por el cálculo
clásico será filosófica, también, en el
sentido de que tiene que hacer
afirmaciones metafísicas sobre los
infinitesimales. La manera que tiene el
análisis moderno de tratar esta P. Z. es
muy diferente, y puramente técnica. Si
alguna vez estudió el problema de la
flecha en las matemáticas de
bachillerato, probablemente aprendió
que la premisa engañosa de Zenón es
(1), pero no oyó nada[4.34] sobre los
instantes como infinitesimales. Esto
(de nuevo) es porque el análisis ha
hallado el modo de esquivar tanto los
infinitesimales como el problema del
o-como-divisor en sus representaciones
de la continuidad. Así, en una clase
moderna de matemáticas, la premisa (i)
es declarada falsa porque la v-en-elinstante-t de la flecha se puede calcular
como «el límite de v medias respecto a
una sucesión de intervalos anidados
que convergen a 0 y siempre contienen
t», o algo muy parecido. Para su
información, el lenguaje de esta
solución[4.35] es weierstrassiano: es su
refinado concepto de límite[4.36] lo que
permitirá que el cálculo trate con los
problemas, relacionados entre sí, de los
infinitesimales y la divisibilidad
infinita al estilo de Zenón.
Las relaciones específicas entre
estos problemas son intrincadas y
abstractas, pero para nosotros son
totalmente oportunas. Por muy
extraños o corrosivos para los
fundamentos
que
sean
los
infinitesimales,
resulta
que
su
descalificación matemática/metafísica
también da lugar a algunas pequeñas y
perversas grietas. Ejemplo: sin los
infinitesimales, aparentemente no tiene
sentido hablar del «siguiente instante»
o de la «fracción de segundo
inmediatamente posterior», pues dos
instantes no pueden ser sucesivos.
Explicación:
sin
infinitesimales,
admitiendo cualesquiera dos instantes
supuestamente sucesivos t, y t2, hay
solo dos opciones: o bien no hay
ningún (o sea, 0) intervalo de tiempo
entre t1 y t2, o hay algún intervalo de
tiempo > 0 entre ellos. Si el intervalo
es 0, entonces t1 y t2 son claramente no
sucesivos, porque entonces son
exactamente el mismo instante. Pero si
hay algún intervalo de tiempo entre
ellos, entonces siempre hay otros
instantes, a intervalos más pequeños,
entre t1 y t2, porque cualquier intervalo
de tiempo finito siempre se puede
subdividir más y más, igual que las
distancias en la recta numérica.[4.37] Es
decir, que nunca va a haber un t2
inmediatamente después de t1. De
hecho, mientras los infinitesimales
sean non grata, siempre tiene que
haber un número infinito de instantes
entre t1 y t2. Esto es así porque si solo
hubiera un número finito de tales casos
intermedios, entonces uno de ellos, tx,
sería por definición el primero, lo cual
implicaría que tx es el instante más
próximo a t1,es decir, que tx es el
instante inmediatamente posterior a t1,
lo cual ya hemos visto que es
imposible (porque, claro, ¿qué pasa con
el instante
?).
Si ahora está usted notando cierto
parecido familiar entre estos problemas
de instantes no sucesivos, las paradojas
de Zenón, y algunos de los
rompecabezas de la recta real descritos
en §2c y e, sepa que no es ninguna
coincidencia. Todos son aspectos del
gran enigma de la continuidad en
matemáticas, el cual es que los entes
relacionados con el aparentemente no
pueden manejarse ni eliminarse. En
ningún caso resulta esto más evidente
que en el de los
. Están llenos de
paradojas y es imposible definirlos,
pero si se destierran de las matemáticas
al final hay que postular que cualquier
intervalo tiene una densidad infinita,
[4.38] por lo cual la idea de sucesión no
tiene sentido y ninguna ordenación de
los puntos del intervalo puede
completarse jamás, pues entre dos
puntos cualesquiera habrá no solo
algunos puntos más, sino toda una
infinidad de ellos.
Conclusión general: por muy bueno
que sea el cálculo para cuantificar el
movimiento y el cambio, no puede
hacer nada para resolver las verdaderas
paradojas de la continuidad. En
cualquier caso, no sin una teoría
coherente del ∞.
5
§5a.
La
tarea de las dos secciones
siguientes es mostrar cómo las
innovaciones de Dedekind y de Cantor
surgieron más o menos del mismo
modo que el cálculo; a saber, como
maneras de tratar ciertos problemas
que se habían hecho tan urgentes que
las matemáticas no podían avanzar
realmente sin afrontarlos. La idea de §5
es trazar un esquema de los
particulares desarrollos y controversias
poscálculo que crearon un entorno en el
cual las matemáticas transfinitas se
hicieron posibles, lo cual es también
decir necesarias. Por favor, obsérvese
también el uso de la expresión «trazar
un esquema». No hay modo de hacer
una cronología, incluso burda, del
período
1700-1850.
Ocurren
demasiadas cosas demasiado rápido.
En general, la situación de las
matemáticas tras el año 1700 resulta
enormemente extraña, y gran parte de
esta extrañeza tiene que ver de nuevo
con las relaciones entre la realidad
empírica y la abstracción conceptual.
[5.1]
Como puede atestiguar cualquiera
que haya pasado de las matemáticas de
bachillerato a las de primer curso de
carrera,
el
análisis
es
exponencialmente más abstracto y
difícil que cualquier otra cosa anterior.
[5.2] Al mismo tiempo, su poder
explicativo no tiene precedentes y sus
aplicaciones prácticas se disparan. Esto
se debe principalmente a la capacidad
del análisis para cuantificar el
movimiento y el proceso y el cambio, y
por el gran aumento en la generalidad
de las leyes físicas expresadas como
ecuaciones diferenciales y/o series
trigonométricas. Al mismo mismo
tiempo, igual que con el desarrollo del
cálculo clásico, buena parte del
progreso matemático desde 1700 hasta
por lo menos 1830 responde a
problemas científicos: de nuevo,
algunos de ellos ya han sido
mencionados. La cuestión es aquí
todavía más empática que en §3b: en
cualquier campo, desde la astronomía
hasta la ingeniería, la navegación, la
tecnología de guerra, etc., las
herramientas del análisis funcionaban
realmente. El resultado fue lo que el
bueno y viejo Morris Kline llama «una
fusión virtual de las matemáticas y
vastas áreas de la ciencia» (Kline, pág.
395).
Las ventajas de esa fusión son más
obvias que sus peligros. Recuérdese
una vez más que, supuestamente, una
característica de incalculable valor que
tienen las matemáticas es la verdad a
priori, y deductiva, de sus teoremas.
Las verdades científicas se establecen
empíricamente.
Son
verdades
inductivas, y como tales están sujetas a
todas las incertidumbres abstractas de
madrugada detalladas en §1. La
inducción, desde un punto de vista
lógico, no tiene fundamento, mientras
que las verdades matemáticas están
construidas sobre el granito de los
axiomas y las reglas de inferencia.
Todo esto se ha analizado ya, así como
las conexiones entre fundamentos y
rigor, además de la parte del glosario
de emergencia en §3c acerca del
análisis y su (eventual) intento de
inyectar más rigor en el cálculo.
Conclusión: no es suficiente que las
teorías
matemáticas
funcionen.
También se supone que deben estar
rigurosamente definidas y demostradas
de un modo que se ajuste al gran
estándar deductivo griego. Pero esto no
es lo que ocurrió durante la mayor
parte del siglo XVIII. Fue más bien
como una burbuja financiera. Y durante
un tiempo pareció estupenda. La
«fusión virtual» por la que los
descubrimientos matemáticos hicieron
posible avances científicos que a su vez
motivaron
más
descubrimientos
matemáticos[5.3] dio lugar a una
situación parecida a la de un árbol[5.4]
de espectaculares ramas y abundantes
hojas pero sin auténticas raíces.
Todavía no existían definiciones
rigurosas y fundamentadas de la
diferencial, la derivada, la integral, el
límite,
o
las
series
convergentes/divergentes. Ni siquiera
de la función. Había constantes
controversias, y, sin embargo, al
mismo tiempo parecía que no le
importaba a nadie.[5.5] El hecho de que
los infinitesimales del cálculo (y/o
ahora los límites de tipo ∞ hacia los
que las cantidades podían «tender» sin
llegar nunca realmente) funcionaran
tan bien sin ninguna fundamentación
coherente, de algún modo infectó todo
el espíritu del análisis. Sin que nadie lo
dijera de forma explícita, las
matemáticas empezaron a operar
inductivamente.
Fue en los terrenos de las
funciones, las ecuaciones diferenciales
y las series trigonométricas donde
surgieron muchos de los avances más
significativos del siglo XVIII y muchas
de sus más abominables confusiones.
En relación con nuestro relato, va a ser
importante examinar algunos de los
problemas matemáticos y científicos
específicos en los que se usaron dichos
conceptos. Esto a su vez requerirá otro
glosario de emergencia relevante
(aunque algo más duro)[5.6], al cual está
usted de nuevo invitado a dedicar
exactamente el tiempo o la atención
que sus conocimientos o su interés
merezcan (pero que probablemente
debería por lo menos hojear y dejar a
punto para consultas posteriores si las
dificultades in situ lo requieren), etc.
GLOSARIO DE EMERGENCIA II
— Derivada (n.) y Diferencial (n.).
Deben distinguirse aunque están tan
estrechamente relacionadas que una
derivada a veces se llama un
«coeficiente diferencial». Recuerde
del G. E. I que una derivada es la
tasa de cambio de una función
respecto
a
la
variable
independiente. En el caso de una
simple función como y = f(x),[5.7]
la derivada es
. Pero aquí los dx
y dy individuales son diferenciales.
En algo como y = f(x), donde x es
la variable independiente, la
diferencial de x (es decir, dx) es
cualquier cambio arbitrario en el
valor de x, en cuyo caso dy se puede
dy = f'(x)dx,
definir
mediante
donde f'(x) es la derivada de f(x).
(¿Le parece que tiene sentido? Si
f'(x) =
, entonces dy es bastante
claramente f'(x)dx).
Una manera fácil de aclarar ambos
términos es recordar que una
derivada es literalmente el cociente
de dos diferenciales, que es como
muchos leibnizianos definían en
realidad la derivada para empezar.
— Derivada parcial y diferencial total
es la distinción correspondiente en
el caso de «funciones de varias
variables»,[5.8] es decir, las que
tienen más de una variable
independiente.
Una
derivada
parcial es la tasa de cambio de una
función multivariable respecto a
una de las variables relevantes,
tomando
las
demás
como
constantes. Así, en general una
función tendrá tantas derivadas
parciales
como
variables
independientes. Para las derivadas
parciales se usa un símbolo
especial que el doctor Goris
llamaba el «6 disléxico». Por
ejemplo, las derivadas parciales de
la función que da el volumen de un
cilindro recto, V = πr2h, son
= 2πrh y
= πr2. Una
diferencial total, por otro lado, es
la diferencial de una función con
más de una variable independiente,
lo cual habitualmente equivale a
decir que es la diferencial de la
variable dependiente. Los ∂s
también se usan en las diferenciales
totales. En el caso de una función
multivariable como z = f(x, y), la
diferencial total de z, dz, será
.
Estas dos primeras definiciones
pueden parecer excesivamente
sutiles pero, de hecho, son
necesarias para entender las
— Ecuaciones
diferenciales
(a-c
[siendo (b) bastante extensa]), que
son la herramienta matemática n.º 1
para resolver problemas de física,
ingeniería, telemetría, automática y
todo tipo de disciplinas científicas.
Habitualmente se empieza a flirtear
con las E. D. al final de las
matemáticas de primer curso de
carrera. Y en el tercer curso de
cálculo se empieza a descubrir cuán
ubicuas y difíciles son realmente.
(a) En un sentido amplio, las
ecuaciones diferenciales involucran
relaciones
entre
una
x
independiente, una y dependiente, y
por lo menos una de las derivadas
de y respecto a x. Las E. D. pueden
considerarse o bien cálculo integral
combinado con algún tipo de
alucinógeno de clase IV o bien
(mejor[5.9]) como «metafunciones»,
en el sentido de hallarse un nivel de
abstracción por encima de las
funciones normales; a su vez esto
significa que si una función
ordinaria es una especie de
máquina en la que se introducen
ciertos números y de la que salen
otros números,[5.10] una ecuación
diferencial es otra especie de
máquina en la que se introducen
ciertas funciones y de la que salen
otras funciones. Entonces, la
solución
de
una
ecuación
diferencial concreta es siempre
alguna función, específicamente
una que se puede poner en el lugar
de la variable dependiente de la
E. D. para dar lugar a lo que se
conoce como una «identidad», que
es básicamente una tautología
matemática.
Puede que esto no haya sido de
mucha ayuda. En términos más
concretos,[5.11] una simple ecuación
diferencial
como
= 3x2 − 1
tiene como solución aquella
función cuya derivada es 3x2 − 1.
Esto significa que ahora se necesita
la integración, es decir, hallar por
lo menos una función equivalente a
∫(3x2 − 1)dx. Si recuerda algo de
las matemáticas de primero de
carrera, probablemente verá que
∫(3x2 − 1) dx
equivale
a
f(x) = x3 − x + C (donde C es la
infame constante de integración),
[5.12] ecuación que es lo mismo que
y = x3 − x + C, que al fin resulta
ser la solución general de la
ecuación diferencial
= 3x2 − 1.
Las soluciones particulares de
dicha E. D. serán aquellas
funciones en las que C toma algún
valor específico, como, por
ejemplo,
y = x3 − x + 2
(semisemiextractado a partir de
Berlinski, págs. 230-231).
(b) Gráficamente, a causa de C y la
cuestión de lo particular/general,
las ecuaciones diferenciales tienden
a dar «familias de curvas» como
soluciones. Los desarrollos de las
ecuaciones,
por
otro
lado,
normalmente dan secuencias de
funciones, y sepa que el cambio en
el análisis de las sucesiones/series
de
cantidades
a
las
sucesiones/series de funciones
acaba resultando crucial para la
historia del ∞. Desde el punto de
vista histórico, este cambio
caracteriza la transición de las
matemáticas desde el análisis del
siglo XVIII al estilo de Euler al de
principios y mediados del siglo XIX
más al estilo de Cauchy. Como se
mencionó brevemente en §3, al
barón Agustin-Louis Cauchy se le
atribuye el primer intento real de
dar rigor al análisis. Propuso un
concepto de límite más sofisticado,
basado en la convergencia, y fue
capaz de definir la continuidad, los
infinitesimales, e incluso del ∞ en
términos de dicho concepto.[5.13]
También fue Cauchy el primero que
trabajó seriamente en las series de
funciones, en las cuales los
problemas realmente cruciales
también
involucran
la
convergencia.
INTERPOLACIÓN RÁPIDA
INCRUSTADA EN (b)
Las E. D. de (b) van a complicarse.
Además de estar invitado a
consultar el G. E. I cuando sea
apropiado, debe usted conocer dos
hechos relacionados: (1) La
convergencia es (o por lo menos
parece) muy diferente en el caso de
las sucesiones/series de funciones
que
en
el
caso
de
las
sucesiones/series de cantidades. Por
ejemplo, una serie convergente de
funciones tiende hacia una cierta
función… o más bien es más
preciso decir que la suma de una
serie convergente de funciones
siempre
convergerá
a
una
función.[5.14] (2) Hay un montón de
conexiones entre los conceptos de
continuidad para funciones y de
convergencia para series de
funciones. Afortunadamente, solo
unas pocas de ellas nos importan,
pero en conjunto dichas conexiones
llegan hasta el mismo agitado
corazón del análisis del siglo XIX, y
algunas
cosas
se
hacen
extremadamente complicadas. Un
ejemplo es un famoso error que
cometió Cauchy, que se presenta
aquí solo como una indicación de lo
estrechamente ligadas que están la
continuidad y la convergencia
respecto a las funciones. Cauchy
sostenía que si la suma de una
sucesión de funciones continuas c0,
c1, c2, … converge en todas partes
de un cierto intervalo hacia una
función C, entonces la propia
función C es continua en ese
intervalo. Por qué eso era
importante, y erróneo, quedará
claro, con un poco de suerte, en un
par de §.
FIN DE LA INTERPOLACIÓN. REGRESO
AL PÁRRAFO 2 DE (b), EN CURSO
Como no podemos hacer sumas
parciales con las series de
funciones,
resulta
importante
pensar
en
comprobaciones
generales de la convergencia de
dichas
series/sucesiones.
Una
comprobación general pionera
llamada condición de convergencia
de Cauchy (o «3C») de la década de
1820 sostiene que una secuencia
infinita a0, a1, a2, …, an, …
converge (es decir, tiene límite) si
y solo si el valor absoluto de
(an+r − an) es inferior a cualquier
cantidad especificada para todo
valor de r, suponiendo que n sea
suficientemente grande.[5.15]
Un hecho final respecto a las
funciones y la convergencia (que
probablemente se tendría que haber
incluido
en
la
anterior
interpolación): para demostrar que
una función F es representable (=
desarrollable) como una serie
infinita, debe ser posible verificar
que la serie converge en todos los
puntos hacia F. Lo cual,
obviamente, no puede hacerse
sumando un número infinito de
términos:
se
necesita
una
demostración
abstracta.
Esto
también será importante cuando
lleguemos a los primeros trabajos
de Cantor sobre análisis.
(c) Una de las razones por las que
las ecuaciones diferenciales son tan
difíciles para los estudiantes es que
existen muchos tipos y subtipos
distintos, especificados por toda
clase de nomenclatura sofisticada:
«orden», «grado», «separabilidad»,
«homogeneidad»,
«linealidad»,
«factor de crecimiento», «factor de
decrecimiento», etc. Para nosotros,
la distinción más importante es
entre una ecuación diferencial
ordinaria
y
una
ecuación
diferencial parcial. Una E. D.
parcial involucra más de una
variable independiente, y, por lo
tanto, derivadas parciales (de aquí
el nombre), mientras que una E. D.
ordinaria no contiene derivadas
parciales. Como la mayoría de los
fenómenos físicos son lo bastante
complicados
para
requerir
funciones multivariable y derivadas
parciales, no es sorprendente que
las
ecuaciones
diferenciales
verdaderamente
útiles
y
significativas sean las parciales. Un
par más de términos sobre E. D.
que debe conocer son condiciones
de frontera y condiciones iniciales,
los cuales tienen que ver con
especificar valores permitidos de la
función y/o cualesquiera constantes
que intervengan en la ecuación.
Esos términos son pertinentes
porque hay importantes conexiones
entre dichas condiciones y la
especificación de ciertos intervalos
de la recta real en los cuales una
función puede adquirir valores, lo
cual después resultará crítico para
el análisis weierstrassiano de
mediados del siglo XIX del que
hablaremos en §5e.
— La ecuación de onda. Se trata de
una E. D. parcial especialmente
famosa y poderosa. De enorme
influencia tanto en las matemáticas
puras como en las aplicadas, sobre
todo en la física y en la ingeniería.
[5.16] Para nuestros propósitos, la
forma relevante de la ecuación de
onda es la iD o «no laplaciana», la
cual (SEI) tiene este aspecto:
— Series
trigonométricas,
que
probablemente tendrían que haber
sido tratadas en el G. E. I, son
básicamente series cuyos términos
se escriben como los senos y los
cosenos[5.17] de varios ángulos. La
forma genérica es habitualmente
algo parecido a
+
(ak cos kx
+ bk sen kx + …). Las series
trigonométricas tienen un papel
importante en nuestro relato, no
solo porque contienen las series de
Fourier como subtipo,[5.18] sino
también porque ciertas funciones
muy
importantes
pueden
representarse a la vez mediante
series trigonométricas y mediante
ecuaciones diferenciales parciales.
Resulta que las conexiones entre
E.
D.
parciales
y
series
trigonométricas
llegan
directamente a la raíz de lo que es
una función. Y, de hecho, la
definición matemática moderna de
función —que difiere de la
definición ad hoc del G. E. I pues
especifica que la asociación entre
cada x y su f(x) puede ser 100%
arbitraria, sin requerir ninguna
regla ni siquiera explicación[5.19]—
es el resultado de un trabajo
exhaustivo sobre las relaciones
entre las funciones y sus
representaciones como series.
— Convergencia uniforme & secretos
asociados (a-e). Estos términos
incluyen las definiciones del G. E. I
de intervalo y función continua así
como el material sobre la
convergencia de series y funciones
según Cauchy en el apartado
anterior Ecuaciones diferenciales
(b). Además de ser necesaria para
entender
ciertos
resultados
precantorianos importantes en
posteriores §, esta definición le
dará alguna idea de la abstracción
realmente vertiginosa del análisis
del siglo XIX.
(a) Definición central: una serie de
funciones continuas de x en un
intervalo (p, q) es uniformemente
convergente si converge para cada
valor de x entre p y q. También hay
detalles que podemos omitir sobre
la pequeñez arbitraria de los
«residuos»[5.20] de las series. Lo
crucial es que la suma de una serie
uniformemente convergente será
también una función continua de x
en el intervalo (p, q).
(b) Así como no todas las series son
convergentes, no todas las series
convergentes son uniformemente
convergentes. Ni todas las series
convergentes son monótonas, lo
cual esencialmente significa que
cambian siempre en el mismo
sentido. Ejemplo de serie monótona
decreciente: la dicotómica
+
+
+
+ …[5.21]
(c) Algo que tiene relación con la
convergencia de las series en un
intervalo dado (p, q) es el asunto de
si
una
función
f(x)
es
seccionalmente continua en un
intervalo dado (p, q), lo que ocurre
cuando (p, q) se puede dividir en un
número finito de subintervalos,
siendo f(x) continua en cada
subintervalo y teniendo un límite
finito en cada extremo inferior
(= p) y superior (= q). (Observe
aquí que «seccional» también
puede modificar/especificar la
monotonía,[5.22] es decir, que
algunas series son seccionalmente
monótonas,
un
pequeño
recordatorio que necesitará tener a
mano en algún punto de §5d).
(d) Por razones complicadas, si una
función
es
seccionalmente
continua, tendrá solo un número
finito de discontinuidades en su
intervalo (p, q) relevante. He aquí
un término fácil de entender: una
discontinuidad es simplemente un
punto[5.23] en el cual la función f(x)
no es continua. Ejemplo: la
semifourieriana
tendrá
claramente discontinuidades en los
valores de x que hagan cos(x − α)
igual a 1. Hay muchas subespecies
diferentes de discontinuidades,
hecho que en su mayor parte vamos
a pasar por alto. Gráficamente, una
discontinuidad es un punto en el
cual una curva no es suave, es
decir, donde salta, o cae
bruscamente, o incluso tiene un
agujero. Véase también un poco de
sutileza semántica: como la palabra
discontinuidad también puede
referirse, con abstracción de
2.º nivel, a la condición general de
que algo sea no continuo, el
término punto excepcional se usa a
veces para referirse a un punto
específico en el cual hay una
discontinuidad. Aquí el meollo de
la cuestión es que el análisis tiende
a usar «discontinuidad» y «punto
excepcional»
de
modo
intercambiable.
(e) Finalmente: un término
engañosamente
parecido
a
«convergencia
uniforme»
es
convergencia
absoluta,
que
matemáticamente
es
algo
totalmente diferente. Una serie
convergente infinita S puede tener
términos negativos (por ejemplo, la
serie de Grandi de §3a). Si todos
los términos negativos de S se
convierten en positivos (es decir, si
solo se admiten los valores
absolutos de los términos) y S
converge todavía, entonces es
absolutamente convergente. Si no,
es condicionalmente convergente.
FIN DEL G. E. II
§5b.
Lo
principal de §5 hasta ahora:
desprovistas de amarre durante el
siglo XVIII, pero cruciales, flotan en el
ambiente ideas sobre funciones,
funciones
continuas,
funciones
convergentes, etc., con todas sus
distintas definiciones respectivas y
propiedades en constante evolución y
refinamiento al abordar el análisis
varios problemas. Como se ha
mencionado, e igual que en el
siglo XVII, muchos de esos problemas
eran científicos/físicos. He aquí
algunos de los grandes problemas del
siglo XVIII: el comportamiento de
cadenas flexibles suspendidas de dos
puntos (también conocidos como
«problemas de catenarias»), los
movimientos de un punto a lo largo de
curvas
descendientes
(=«la
braquistócrona»), las barras elásticas
bajo tensión, los movimientos de un
péndulo en medios que presentan
resistencia, las formas adquiridas por
una vela bajo la presión del viento
(=«velaria»), las órbitas de los planetas
los unos respecto a los otros, las curvas
cáusticas en óptica, y los movimientos
de rumbo fijo (respecto a la brújula) en
una esfera (la Tierra) o problema de la
«loxodrómica».
Para
nuestros
propósitos, el más importante de todos
es el infame problema de la cuerda
vibrante (P. C. V.), que en algunos
sentidos
se
remonta
a
los
descubrimientos de Pitágoras acerca de
la escala diatónica en §2a. El P. C. V.
general es: dadas la longitud, la
posición inicial y tensión de una cuerda
de la que se tira verticalmente, calcular
sus movimientos cuando se la libera y
empieza a vibrar. Esos movimientos
serán curvas, lo cual es decir lo mismo
que funciones.
La razón por la que el P. C. V. es, a
menudo, un pilar de las matemáticas de
segundo curso de carrera es que marca
la primera aplicación real de las
ecuaciones diferenciales parciales a un
problema físico. He aquí un poco de
historia. En la década de 1740, Jean le
Rond d’Alembert propone lo que es
básicamente la ecuación de onda 1D
como la representación correcta del
P. C. V., dando[5.24] la solución general
y = f(x + ct) + g(x − ct) donde x es un
punto de una cuerda de longitud π, y es
el desplazamiento transversal de x en el
tiempo t, c es una constante,[5.25] y f y
g son funciones determinadas por las
condiciones iniciales. Donde las cosas
se ponen controvertidas es en el
alcance que se puede permitir a f y g.
Resulta que la solución de D’Alembert
solo funciona si la «curva inicial» de la
cuerda (es decir, el modo en que se la
tensa al principio) es ella misma una
función periódica. Esto impone una
gran restricción al modo de tensarla,
mientras que, por supuesto, en las
matemáticas y en la ciencia se desean
soluciones lo más generales posible. Y
así, jugadores de primera línea como
Leonard Euler, Daniel Bernoulli,
Joseph Louis LaGrange, Pierre Simon
de
LaPlace
y
D’Alembert[5.26]
empiezan a discutir acaloradamente
unos con otros sobre si dejar que la
tensión inicial de la cuerda sea
cualquier tipo de curva/función, sobre
cómo hacerlo y conseguir que la
ecuación de onda siga siendo aplicable.
En pocas palabras, el consenso que al
final sale de todo ello es que
independientemente de la forma inicial
de la cuerda, sus curvas vibracionales
van a ser funciones periódicas,
específicamente ondas senoidales. De
lo cual, por complicadas razones, se
sigue que sin importar cómo se tense la
cuerda al principio —es decir, que
puede seguir cualquier curva continua
—, la curva vibracional se podrá
representar
mediante una serie
trigonométrica.
En pocas palabras, muchísimos
descubrimientos importantes sobre la
naturaleza y las relaciones de las
funciones, las ecuaciones diferenciales
y las series trigonométricas surgen de
la ópera del desacuerdo acerca del
P. C. V. Lo que resulta crucial para
nuestro relato es esa idea de que
cualquier función continua[5.27] puede
ser representada como una serie
trigonométrica. En primer lugar, Euler,
luego D’Alembert, LaGrange, y el ya
mencionado y quijotesco Clairaut
empiezan a desarrollar métodos para
representar «funciones arbitrarias»
como series trigonométricas. El
problema es que esos métodos siempre
se obtienen y aplican con respecto a
algún problema físico particular, y
luego se afirma que la solución de
dicho problema es la justificación del
método. Nadie es capaz de zanjar el
asunto de la función → serie
trigonométrica mediante un teorema
abstracto. Eso es todo lo que está
ocurriendo hacia finales del siglo XVIII.
Ahora es el principio del siglo XIX,
tiempo durante el cual Cauchy y el
noruego Niels Henrik Abel[5.28]
empiezan a hacer un trabajo
significativo sobre la convergencia de
las series, trabajo que acaba resultando
incluso más significativo en 1822. Ese
año, el barón francés Jean-Baptiste
Joseph
Fourier[5.29]
(1768-1830),
trabajando en problemas sobre la
conducción del calor en metales,
demuestra en su obra Teoría analítica
del
calor
(TAC)
que
la
representabilidad mediante una serie
trigonométrica en realidad podía
establecerse tanto para funciones
continuas como para funciones
discontinuas,[5.30] incluso para curvas
«libremente dibujadas» (Lavine, pág.
30). La demostración de Fourier en la
TAC es demasiado técnica para entrar
mucho en ella, pero básicamente lo que
hace es explotar la relación entre la
suma de una serie y la integral de una
función: se da cuenta de que la
representabilidad mediante una serie
para
funciones
completamente
arbitrarias requiere ignorar el T. F. C. y
definir
la
integración
geométricamente[5.31]
y
no
simplemente como la recíproca de la
diferenciación.
Como en muchas clases se enseñan
las series de Fourier sin explicar de
dónde vienen las matemáticas, vale la
pena por lo menos mencionar que
Fourier empieza con una ecuación
diferencial parcial de 2.º orden para la
difusión del calor en un cuerpo 1D,
,[5.32]
donde
y
es
la
temperatura de un punto x en el
instante t, tras lo cual usa una técnica
estándar de E. D. llamada «separación
de variables», y la condición inicial de
que y = f(x), para obtener esa muy
especial serie trigonométrica conocida
actualmente como serie de Fourier,
cuya forma relevante se muestra aquí
como Figura 5b:
Figura 5b
f(x) =
a0 +
(an cos nx +
bn sen nx) donde 0 ≤ x ≤ 2π
Resulta que esta serie de Fourier es
en realidad muy parecida a lo que
Bernoulli había propuesto como
solución al P. C. V. hacia 1750, excepto
que Fourier es capaz de calcular los
coeficientes de la serie[5.33] para cada
valor entre 0 y 2π. En el caso de bn, por
ejemplo,
, es
decir, si se integra término a término,
los coeficientes bn serán
veces el
área bajo la curva (f(u) sen nu) en el
intervalo entre u = 0 y u = 2π. Los
cálculos para a0 y an son similares.
Se canse o no su vista, la cuestión
es que, mediante la fórmula de esos
coeficientes de Fourier, toda función de
una variable que se pueda concebir —
algebraica, trascendente, continua e
incluso discontinua—[5.34] se vuelve
representable
según
una
serie
trigonométrica de tipo Fourier en el
intervalo [0, 2π]. Hay todo tipo de
maravillosos puntos fuertes y ventajas
en esa técnica (la cual Fourier
desarrolló principalmente para dar una
solución general a la ecuación de
difusión; y en verdad lo logró). Un
ejemplo: entender la integración
geométricamente, y concebir una
función en términos de sus valores y no
como una mera expresión analítica,
[5.35] le permite a Fourier considerar la
posibilidad de representar como series
funciones sobre intervalos finitos, lo
que para el análisis del siglo XIX
constituye un importante avance en
flexibilidad.
Sin embargo, al mismo tiempo, las
series de Fourier son como una
repetición del cálculo temprano en
términos del contraste entre eficacia
práctica
y
rigor
deductivo.
Especialmente con el refinamiento por
Siméon Denis Poisson hacia 1820, las
series de Fourier se convierten en la
manera n.º 1 de resolver ecuaciones
diferenciales parciales —que son,
como se ha mencionado, las llaves de
oro para la física matemática, la
dinámica, la astronomía, etc.— y como
tales se puede decir que revolucionan
las matemáticas y la ciencia una vez
más. Pero también carecen de
fundamento: no hay nada parecido a
una teoría rigurosa de las series de
Fourier. En palabras de un historiador
de las matemáticas, las técnicas de
Fourier «suscitaron más preguntas de
las que él estaba interesado en
contestar o era capaz de resolver»
(Dauben, Georg Cantor, pág. 7). Lo
cual es a la vez delicado y cierto: la
TAC de Fourier afirma que una función
«completamente arbitraria» puede ser
representada por una serie como la de
la Figura 5b, pero no lo demuestra.
Tampoco detalla qué condiciones
específicas debe satisfacer una función
para ser representable de ese modo.
Aún más importante, Fourier afirma
que sus epónimas series son siempre
convergentes
en
un
intervalo
independientemente de cuál sea la
función o incluso de que sea expresable
como una única «y = f(x)», y aunque
esto tiene implicaciones importantes
para la teoría de las funciones, la
afirmación acerca del 100% de
convergencia no está demostrada ni
comprobada siquiera.
[SEI Había un problema parecido
que involucraba las integrales de
Fourier, sobre las cuales todo lo que
debemos saber es que son tipos
especiales de expresiones «cerradas»
que dan soluciones de ecuaciones
diferenciales parciales, las cuales, una
vez más, Fourier afirma que funcionan
para cualesquiera funciones arbitrarias,
y que ciertamente parecen hacerlo —es
decir,
funcionar—
siendo
especialmente buenas para problemas
de física. Pero ni Fourier ni nadie más
a principios de la década de 1820 puede
demostrar que las integrales de Fourier
funcionen para todas las f(x), en parte
porque todavía hay una profunda
confusión en las matemáticas acerca de
cómo definir la integral…, pero, de
todos modos, la razón por la que
estamos mencionando el problema de
las integrales de Fourier es que el
trabajo de Augustin-Louis Cauchy
sobre él le conduce a la mayor parte de
la «rigorización» del análisis por la que
se le da reconocimiento. Parte de ese
rigor incluye definir la integral como
«el límite de una suma», pero la mayor
parte (= la mayor parte del rigor)
concierne a los problemas de
convergencia mencionados en (b) y en
su pequeña interpolación del apartado
Ecuaciones diferenciales del G. E. II,
específicamente al pertenecer dichos
problemas al ámbito de las series de
Fourier].[5.36]
Hay otra manera de enunciar la
dificultad general. Fourier (en la línea
de Leibniz y Bolzano) tiene un modo
esencialmente geométrico de entender
las cosas, y una inclinación hacia las
demostraciones geométricas más que
hacia las demostraciones formales. En
muchos aspectos, esto es un remanente
del cálculo clásico y de la mentalidad
los-resultados-importan-más-que-lasdemostraciones del siglo XVIII. Pero tal
enfoque ahora es cada vez más
insostenible. También en la década de
1820 se descubren las primeras
geometrías no euclidianas (basadas
principalmente en el descubrimiento de
que el axioma de las paralelas de los
elementos[5.37] era prescindible), y la
idea de que la geometría podría ser
cualquier tipo de fundamento fijo e
inequívoco para cualquier cosa se
convierte en oficialmente absurda. Un
problema relacionado es que los
matemáticos desde Newton a Euler y
siguiendo hasta Gauss se habían
encontrado con muchos problemas de
paradojas al usar series sin considerar
su convergencia o divergencia,[5.38] y
el énfasis de Fourier y Cauchy en la
convergencia a intervalos ahora ayuda
a revelar cuán impreciso había sido el
análisis respecto a las series. El
resultado general es el arranque de una
rectificación en la «burbuja financiera»
del análisis o, tal como lo expresa
Morris Kline, «[Los] matemáticos
empezaron a preocuparse de las
imprecisiones en los conceptos y
demostraciones de vastas ramas del
análisis» (Kline, pág. 947). Es en la
década de 1820 cuando empezamos a
ver pronunciamientos como el de
Cauchy: «Sería un serio error pensar
que uno solo puede hallar la
certidumbre
en
demostraciones
geométricas o en el testimonio de los
sentidos» (Cauchy, Introducción al
Cours, traducción extractada de Kline,
ibíd. algo editada) y el de Abel: «Hay
muy pocos teoremas en el análisis
avanzado que hayan sido demostrados
de un modo lógicamente sensato. En
todas partes uno se encuentra con ese
precario método de concluir lo general
a partir de lo especial» (Abel, págs.
263-264),[5.39] convirtiéndose este
último en tan representativo del
atrincheramiento del siglo XIX como el
«Simplemente siga adelante» de
D’Alembert lo había sido del laissez
faire del siglo XVIII.
Conclusión general: junto a la caída
de Euclides, son las series de Fourier y
sus problemas de convergencia y de
representación de funciones arbitrarias
lo que provoca que los matemáticos de
la época se den cuenta de que los
conceptos atómicos como «derivada»,
«integral»,
«límite»,
«función»,
«continuo»
y
«convergente»
necesitaban definiciones rigurosas,
donde «riguroso» significa basar el
análisis en demostraciones formales y
el razonamiento aritmético y no en la
geometría, la intuición o la inducción a
partir de problemas específicos.
Excepto que a su vez «aritmético»
significaba el sistema de los números
reales, que en ese momento también
era todavía un lío sin fundamentar. Por
ejemplo, había terribles problemas con
los números negativos: Euler estaba
convencido de que en realidad eran >
∞, es decir, que deberían estar muy
lejos hacia la derecha en la recta
numérica, y tan tardíamente como en la
década de 1840, Augustus De Morgan
sostenía que los números negativos
eran simplemente tan «imaginarios»
como √−1. Y no olvidemos el caos
respecto a los números complejos. Sin
embargo, el peor problema era que el
concepto raíz de «número real» a su
vez no estaba claro porque los
irracionales aún estaban indefinidos. Si
no se pueden definir de manera
coherente números como √2 o √3, no
se puede demostrar ninguna de las
leyes aritméticas básicas acerca de
ellos, por ejemplo, que √2 × √3 =
√2 × 3.[5.40] Esto no es bueno, en
términos de rigor. En este período hay
cierta cantidad de valioso trabajo
colateral sobre los irracionales
trascendentes y algebraicos,[5.41] pero
en su mayor parte el propio sistema de
los números reales, sobre el cual está
trabajando todo el mundo para
fundamentar el análisis, está colgando
en el aire, lógicamente hablando.
§5c.
INTERPOLACIÓN DE TONO
LIGERO, SITUADA AQUÍ ANTE
REM PORQUE ESTE ES EL ÚLTIMO
LUGAR DONDE HACERLO SIN
PERTURBAR EL IMPARABLE
IMPULSO DEL CONTEXTO
MATEMÁTICO PRECANTOR
Se conservan varias fotos de Georg F.
L. P. Cantor en los libros, una de las
cuales, con un poco de suerte, será
apropiada y se podrá reproducir aquí en
alguna parte. Es un burgués alemán de
aspecto completamente corriente de la
era de los cuellos almidonados y las
barbas inflamables. (Observe, en las
fotos de familia, el chaleco de cuero y
el reloj de bolsillo con una muy visible
leontina, las trenzas y el miriñaque de
su mujer, la expresión austeramente
serena o abstraída del hombre
victoriano estándar. En Estados Unidos
habría llevado sombrero).
Hacia 1940, ciertos historiadores de
las matemáticas nacionalsocialistas
«descubrieron» que Cantor había sido
encontrado, poco después de nacer y
sin que se supiera nada de sus padres,
en un barco alemán rumbo al puerto de
San Petersburgo. Lo cual es pura
ficción. Aparentemente, el Reich
estaba preocupado por la posibilidad de
que Cantor hubiera sido judío: por
aquel entonces era considerado uno de
los más grandes intelectuales alemanes
de todos los tiempos. La historia del
barco todavía circula a veces; también
se ajusta a algunos de nuestros moldes,
no solo al de los nazis. Otra mentira de
las gordas es que Cantor dedujo varias
de sus más famosas demostraciones
sobre el ∞ estando en un sanatorio, lo
cual también es una tontería. La
primera hospitalización de Cantor fue
en 1884, cuando tenía treinta y nueve
años; la mayor parte de su importante
obra ya estaba hecha por aquel
entonces. No volvió a ser hospitalizado
hasta el año 1899. Fue en los últimos
veinte años de su vida cuando le
estuvieron dando de alta y de baja
constantemente.
Murió
en
la
Nervenklinik de Halle el 6 de enero de
1918.
En esta foto faltan las trenzas y el
reloj de bolsillo con leontina, pero
puede hacerse la idea.
El hogar de la familia Cantor en
Handelstrasse fue, por lo menos,
brevemente ocupado durante la
Segunda Guerra Mundial. No hay
indicios de que los nazis supieran de
quién había sido la casa. En todo caso,
parece evidente que la mayor parte del
patrimonio literario de Cantor se
perdió o se quemó. La mayor parte de
lo que se conserva está en la Akademie
der Wissenschaften en Gotinga y puede
examinarse tras un cristal. Cartas
familiares, árboles genealógicos, etc.
También se conservan todavía algunos
de los cuadernos que Cantor utilizaba,
como era habitual en aquella época
entre las personas instruidas, para
hacer borradores de cartas antes de
pasarlas a limpio y enviarlas. Además
había otros matemáticos a los que
escribía y que conservaron sus cartas.
Estas son las fuentes principales.
He aquí una cita de Joseph W.
Dauben, que en Estados Unidos es el
decano de los eruditos cantorianos: «Se
ha conservado demasiado poca
información para que se pueda hacer
una valoración detallada de la
personalidad de Cantor, lo que deja al
historiador en la situación o bien de no
decir nada sobre el tema, o bien de
hacer conjeturas tan bien como pueda»
(Dauben, GC, pág. 288). Buena parte de
las conjeturas publicadas son acerca
del padre de Cantor, el señor Georg W.
Cantor, siendo la gran cuestión
moderna si «Georg Woldemar tuvo un
efecto completamente nocivo y ruinoso
sobre la salud psicológica de su hijo»
(Bell, parafraseado por Dauben [que
aborrece absolutamente a Bell], GC,
pág. 278)[5.42] o si Georg W. Cantor fue
en realidad «un hombre dotado y
sensible, que amaba profundamente a
sus hijos y quería que vivieran vidas
felices, exitosas y gratificantes»
(Dauben, ibíd.). De uno u otro modo, es
seguro que hubo exactamente dos
hombres de negocios que tuvieron un
profundo efecto en la vida de Georg F.
L. P. Cantor, siendo uno de ellos su
padre, y el otro, el profesor Leopold
Kronecker, que empieza a estar muy
presente en §6.
Aquí está el esbozo a lápiz al que
nos referimos en el siguiente
párrafo.
El señor y la señora Georg W.
tienen seis hijos. Georg Jr. es el
primero. Toda la familia, en sentido
amplio, es artística y muestra mucho
talento: varios parientes son violinistas
clásicos o pintores que realizan
exposiciones. Un tataratío había sido
director del Conservatorio de Viena y
profesor del virtuoso Joseph Joachim,
un tío abuelo había sido el profesor de
derecho de Tolstoi en la Universidad de
Kazan. La fecha de nacimiento de
Georg F. L. P. Cantor es el 3 de marzo
de 1845. Un piscis. Algo parecido a un
prodigio del violín en su infancia.
Nadie sabe por qué lo dejó, pero tras un
cuarteto clásico en el instituto no hay
más mención del violín. También era
un buen dibujante naturalista. Un
dibujo a lápiz de su niñez, bastante
extraordinario, ha sobrevivido. Es
famoso por una «proclama» escrita con
doble sentido e indiscutiblemente
escalofriante que Georg W. puso en él.
La proclama misma ha sobrevivido
porque
(también
de
modo
escalofriante) Georg Jr. la guardó
consigo toda su vida:
Aunque Georg Ferd. Louis Phil.
Cantor no ha dedicado años al
estudio del dibujo según los
antiguos cánones, y aunque este
es su primer trabajo y en este
difícil
arte
una
técnica
perfeccionada solo se consigue
tras una gran diligencia, y
aunque además hasta ahora él
ha descuidado mucho este bello
arte, la gratitud de la nación —
quiero decir de la familia— es
unánimemente acordada para él
por este primer esfuerzo, el cual
da muestras ya de una gran
promesa (Dauben, GC, pág.
278).
Todas las fuentes están de acuerdo
en que Georg W. supervisaba
personalmente el desarrollo religioso
de sus hijos de un modo bastante
autoritario. Dese cuenta de lo fácil que
es, desde un punto de vista moderno,
ver esto como algo opresivo o
neurogénico cuando en realidad podría
haber sido simplemente lo habitual en
su tiempo y lugar. Es difícil de decir.
Lo mismo ocurre con el hecho de que
Cantor padre «se tomaba un interés
especial en la educación [de Georg] y
se preocupaba de dirigir su desarrollo
personal e intelectual» (ibíd., pág.
277).
La familia se muda de San
Petersburgo a Alemania occidental
cuando Georg tiene once años. La
razón, según los historiadores, es la
«mala
salud»
(Grattan-Guinness,
«Towards a Biography» pág. 352) de
Georg W., lo cual en 1850 era otra
manera de decir tuberculosis. Viven
principalmente en Fráncfort, en el Rin.
Georg asiste a escuelas preparatorias
en Darmstadt y en Wiesbaden. Como
parece ocurrir con la mayoría de los
grandes matemáticos, el genio analítico
de Cantor es descubierto en su
adolescencia
temprana.
En
la
Akademie aún pueden verse cartas
extasiadas de sus profesores de
matemáticas. La versión estándar de la
historia es que Georg. W. quiere que
los dones de Georg Jr. se dediquen a
usos prácticos e intenta obligar al chico
a hacer ingeniería, que Georg desea
ardientemente estudiar matemáticas
puras y tiene que insistir y suplicar,
etc., y que cuando finalmente Georg W.
accede, lo hace presionando mucho a
su frágil hijo para que alcance el éxito
y la excelencia. Tampoco está muy
claro si esto era cierto o hasta que
punto se trataba de algo singular en su
gestalt padre-hijo.[5.43]
Cantor estudia la carrera en Zúrich
y luego obtiene un título superior en
ciencias y el equivalente alemán de un
doctorado en la Universidad de Berlín,
que en aquella época es la vanguardia
europea de la ciencia (algo así como lo
que representa hoy el Massachusetts
Institute of Technology en Estados
Unidos). Entre sus profesores están
Ernest Eduard Kummer, Leopold
Kronecker
y
Karl
Weierstrass.
Kronecker es el director de tesis de
Cantor y su verdadero mentor y
defensor en el departamento. La ironía
de esto también empezará a aparecer en
§6.
§5d.
Ahora
hemos vuelto a 1820 con
Fourier y las series trigonométricas y
todos los retos y oportunidades que allí
aguardan. Si la discusión de §5b acerca
de las series de Fourier y el apartado
Ecuaciones diferenciales del G. E. II
con su material interpolado sobre las
conexiones entre la continuidad y la
convergencia resultaron medianamente
claros, no le sorprenderá saber que en
la TAC Fourier proporciona la primera
definición moderna de convergencia, y
también introduce la vital idea de
convergencia en un intervalo. Pero que
(de nuevo) Fourier no llega a dar una
demostración rigurosa, o incluso a
especificar criterios de convergencia
que
hicieran
posible
dicha
demostración. Así, de lo que estamos
hablando ahora es de la convergencia.
Fueron Bolzano[5.44] y, más
célebremente, Cauchy quienes hicieron
el primer trabajo destacado sobre
condiciones/pruebas de convergencia.
Como se ha mencionado ya en un par
de ocasiones, muchos de los resultados
de Cauchy eran valiosos, pero también
cometió errores extraños que causaron
más problemas. Aunque gran parte de
su trabajo era sobre series de
funciones, por ejemplo, Cauchy optó
por definir «límite» en términos de
variables y no de funciones. O un
ejemplo incluso mejor en este caso es
el modo en que intentó establecer una
identidad total entre la convergencia y
la continuidad en términos de
sucesiones/series
de
funciones.
Recuerde[5.45] que la afirmación de
Cauchy es que si una sucesión de
funciones continuas converge en el
intervalo I hacia una función C,
entonces la propia C es continua en I,
lo cual resulta que no es cierto a menos
que la sucesión convergente sea
uniformemente convergente. Lo que
ocurre en este caso es que Niels Abel,
al
demostrar
que Cauchy se
equivoca[5.46] y refinar el teorema,
desarrolla lo que ahora se conoce como
prueba de convergencia uniforme de
Abel,[5.47] a la vez que toda clase de
criterios y condiciones para varios
tipos de convergencia de varios tipos
de
series
trigonométricas
y
polinómicas también están siendo
desarrollados por varios matemáticos
del siglo XIX al esforzarse estos en
enmendar los errores de otros
matemáticos
y/o
resolver
los
problemas con mejores métodos.
Uno de los más importantes
matemáticos enmendadores de la época
fue Peter Gustav Lejeune Dirichlet
(1805-1859), un amigo de Fourier cuya
obra de 1829 «Sur la convergence des
séries trigonométriques» hizo mucho
para clarificar y rigorizar lo que llegó a
conocerse como el problema de la
convergencia general de las series de
Fourier (P. C. G. S. F). Hay varios
avances importantes en este artículo,
por ejemplo, que Dirichlet es el
primero en descubrir y distinguir la
convergencia
absoluta
y
la
convergencia condicional. Además,
desmiente la afirmación de Cauchy de
que una serie monótona decreciente es
lo mismo que una serie convergente.
Pero más importante es que en «Sur la
convergence» Dirichlet establece y
demuestra la validez del primer
conjunto
de
condiciones
suficientes[5.48] para que una serie de
Fourier converja hacia su f(x) original.
Este último resultado es pertinente
y merece algo de detalle. Dirichlet usa
una f(x) periódica en el intervalo [−π,
π] y básicamente demuestra que si (1)
su serie de Fourier es seccionalmente
continua y, por lo tanto, solo tiene un
número finito de discontinuidades[5.49]
en el intervalo, y si (2) la serie es
seccionalmente monótona, entonces (3)
la serie convergerá siempre hacia la
función f(x), incluso si esa función
requiere más de una expresión de tipo
«y = f(x)» para representarla en el
intervalo.
Hay un requisito adicional, que
Dirichlet demuestra también. La
función f(x) tiene que ser integrable, es
decir,
tiene que ser finita,
básicamente porque los coeficientes
relevantes de la serie de Fourier se
calculan como integrales y estas tienen
que estar «bien definidas» (larga
historia). Como ejemplo de una
función que no es integrable y, por lo
tanto, no puede ser representada por
una serie de Fourier bien definida,
Dirichlet se inventa una f(x) patológica
cuyos valores son iguales a una
constante c cuando x es racional pero
iguales a una constante d (con d ≠ c)
cuando x es irracional, función que
ciertamente no es integrable. A grandes
rasgos, es esa f(x) patológica lo que
conduce a Dirichlet, ocho años más
tarde,[5.50] a dar la definición de
«función» que se usa todavía en las
matemáticas modernas: «y es una
función de x cuando a cada valor de x
en un intervalo dado le corresponde un
único valor de y» (Dirichlet, «Über die
Darstellung…», traducción extractada
de Kline, pág. 950). Lo importante es
que la correspondencia puede ser
completamente arbitraria. No importa
si la dependencia de y respecto a x
sigue alguna regla en particular, o
incluso
si
puede
expresarse
matemáticamente.[5.51] Por extraño que
pueda sonar, en realidad es 100%
rigurosa para propósitos matemáticos,
pues la arbitrariedad da máxima
generalidad, o sea abstracción. (La
definición de Dirichlet también resulta
estar muy próxima a la idea bolzanocantoriana de la correspondencia uno a
uno entre dos conjuntos de números
reales, excepto que por supuesto ni
«conjunto» ni «número real» han sido
definidos aún en las matemáticas).
En su artículo de 1837, Dirichlet es
también capaz de demostrar que se
puede prescindir del requisito acerca de
la monotonía (2) e incluso permitir un
número mayor de discontinuidades (1)
en su demostración de 1829 y aun así
garantizar la convergencia de la serie
de Fourier hacia su f(x) integrable…
siempre
que
el
número
de
discontinuidades en (1) permanezca
finito. Sin embargo, esto todavía no es
lo
mismo
que
demostrar
la
convergencia de las series de Fourier
para
cualquier
f(x)
arbitraria,
especialmente si se intenta fourierizar
las complejas funciones y a menudo
salvajemente discontinuas del análisis
puro y la teoría de números.[5.52]
Respecto a esas funciones complejas,
la cuestión que Dirichlet no llega a
responder es si el criterio (1) de su
demostración se podría debilitar para
permitir
una
infinidad[5.53]
de
discontinuidades en el intervalo y
constituir aún una condición suficiente
de convergencia.
Ahora entra en escena Georg
Friederich Bernhard Riemann (18261866, ese coloso de las matemáticas
puras que lo revolucionó todo desde las
funciones y la teoría de números hasta
la geometría,[5.54] y es el único rival
serio de Cantor para el título de
Matemático del Siglo), aunque la
intervención de Riemann es breve y
con un papel de transición. Veinte años
mayor que Cantor, Riemann es alumno
de Dirichlet en la Universidad de
Berlín, y también amigo de Dedekind.
[5.55] En un artículo fundacional de
1854,[5.56] Riemann ataca el problema
de la convergencia general de las series
de Fourier de un modo completamente
nuevo. Centrándose en la suposición de
que una f(x) tiene que ser integrable
para ser representable como una serie
de Fourier, deduce condiciones
generales que cualquier función debe
satisfacer para tener una integral,
condiciones que acaban resultando
importantes tanto para la teoría de la
integración en análisis como para la
convergencia
de
las
series.
Esencialmente,
las
«condiciones
generales que cualquier función debe
satisfacer»
significa
condiciones
necesarias, mientras que recordará
usted que la demostración de Dirichlet
de 1829 había involucrado condiciones
suficientes. Entonces, al darle la vuelta
al enfoque de su profesor y al
concentrarse en las condiciones
necesarias de convergencia, Riemann
resuelve el gran problema de Dirichlet:
construye una función que tiene una
infinidad de discontinuidades en cada
intervalo pero a pesar de todo es
integrable y 100% convergente en cada
punto.[5.57] Una consecuencia de este
resultado es algo conocido como
teorema de localización de Riemann, el
cual afirma que la convergencia de una
serie trigonométrica en un punto
depende completa y exclusivamente
del comportamiento de su f(x)
relevante en un entorno arbitrariamente
pequeño[5.58] de dicho punto. Y lo del
«entorno arbitrariamente pequeño» es
lo que finalmente da validez a las
afirmaciones de Fourier y Dirichlet
acerca de las series que representan
funciones completamente arbitrarias:
mediante el teorema de localización,
incluso
funciones
altamente
discontinuas y patológicas pueden ser
representadas
por
series
trigonométricas, y, si son integrables,
por series de Fourier.
Sin embargo, como es ya habitual,
a la vez que el trabajo de Riemann está
resolviendo antiguas preguntas también
está planteando otras nuevas. Y en
definitiva son esas cuestiones las que
dan tanta importancia a su artículo de
1854. Ejemplo: una consecuencia del
teorema de localización es que dos
funciones integrables diferentes pueden
representarse mediante la misma serie
trigonométrica incluso aunque difieran
en una cantidad grande pero finita de
puntos. ¿Hay alguna manera de obtener
el mismo resultado para dos funciones
que difieran en una infinidad de
puntos? Otros ejemplos importantes:
¿Exactamente qué propiedades de las
series trigonométricas les permiten ser
convergentes incluso con ∞ puntos
excepcionales en cada intervalo?, y
¿Cómo están relacionados exactamente
los conceptos de f(x)-continuidad,
intervalos y entornos con la teoría de
las series trigonométricas?, y ¿Es toda
serie trigonométrica una serie de
Fourier? (es decir, ¿converge toda serie
trigonométrica hacia una función
integrable?), y ¿Si más de una función
puede ser representada por la misma
serie trigonométrica, es cierto el
recíproco, o cada f(x) única tiene una
sola y única representación como serie
trigonométrica?[5.59]
Tras el artículo de Riemann, el
siguiente gran asunto en las
matemáticas puras es afrontar las
técnicas necesarias para resolver los
problemas que este había planteado,
siendo especialmente desafiante la
cuestión de basar dichas técnicas en
fundamentos rigurosos en lugar de la
intuición inductiva o basada en la fe
que había marcado buena parte del
análisis en el pasado. N. B. el énfasis
en el rigor/fundamento se debe en parte
a que las funciones totalmente
abstractas de Riemann finalmente han
desplazado las series de Fourier del
reino de la física y las matemáticas
aplicadas al de las matemáticas puras
per se. Pero además, por supuesto,
ahora estamos en 1850, y la necesidad
de rigor (tal como se ha discutido en
relación con la década de 1820 en §5b)
es todavía más urgente y general. En
tiempo real ha tardado varias décadas,
pero el boom de la justificación-porresultados ahora está dando paso
completamente a la economía más
contraccionista,
del
demuestremientra-avanza, de lo que los
historiadores de las matemáticas
llamarán la aritmetización del análisis.
§5e.
La figura crucial en este punto es Karl
Weierstrass (1815-1897), a quien ahora
podemos revelar dramáticamente como
uno de los héroes de lo referido en §2a
acerca de Bertrand Russell y las
paradojas de Zenón. Aquí está el resto
de aquella cita:[5.60]
Desde Zenón hasta nuestros
días, los mejores intelectos de
cada generación han atacado
por turnos los problemas, pero a
grandes
rasgos
no
han
conseguido nada. En nuestro
propio tiempo, sin embargo,
tres hombres —Weierstrass,
Dedekind y Cantor— no solo
han logrado avances en los
problemas, sino que los han
resuelto completamente. Las
soluciones,
para
aquellos
familiarizados
con
las
matemáticas, son tan claras que
ya no cabe la menor duda o
dificultad […] De los tres
problemas,
el
de
los
infinitesimales fue resuelto por
Weierstrass; la solución de los
otros dos fue empezada por
Dedekind y definitivamente
conseguida por Cantor (Russell,
Mysticism and Logic, pág. 77).
Weierstrass no está directamente en
la fila de eruditos formada por FourierCauchy-Dirichlet-Riemann: hasta sus
cuarenta años, es un desconocido en el
mismo sentido en que lo fue Bolzano.
Su carrera temprana está dedicada a dar
clases de bachillerato en Prusia
Oriental (no exactamente un centro de
poder),[5.61] y se dice que era
literalmente demasiado pobre para
pagar el envío de sus trabajos a las
revistas. Finalmente, empieza a
publicar a finales de la década de 1850,
y causa un revuelo en las matemáticas,
y es contratado como profesor por la
prestigiosa Universidad de Berlín: es
toda una historia, larga y algo
romántica. (SEI Weierstrass es también
conocido entre los matemáticos por ser
físicamente corpulento, un atleta
dotado, un fiestero empedernido que se
escaqueaba en el instituto, indiferente a
la música —los matemáticos suelen ser
fanáticos de la música—, y un
compañero jovial, gregario, nada
neurótico, buenazo y muy querido.
También es generalmente considerado
el mejor profesor de matemáticas del
siglo, aunque nunca publicó sus
lecciones y ni siquiera dejaba que sus
alumnos tomaran apuntes).[5.62]
La razón específica por la que
estamos hablando de Weierstrass es
que
son
principalmente
sus
descubrimientos los que permiten a las
matemáticas atacar las cuestiones
planteadas por los trabajos de Dirichlet
y Riemann acerca del P. C. G. S. F.
Véase en este sentido la siguiente cita
del historiador de las matemáticas I.
Grattan-Guinness: «[L]a historia del
análisis matemático durante el último
tercio del siglo XIX es en notable
medida la historia de los matemáticos
aplicando técnicas weierstrassianas a
problemas riemannianos» (GrattanGuinness, From the Calculus to Set
Theory [«Del cálculo a la teoría de
conjuntos»], pág. 132). La verdadera
inspiración tras esas técnicas no es
Fourier o de Riemann, sino el
tangencialmente mencionado Niels
Henrik Abel (siendo Weierstrass un
enorme fan de Abel), específicamente
una innovación llamada funciones
elípticas que Abel había obtenido hacia
1825 a partir de la integrales elípticas,
las cuales, más tarde, para abreviar,
surgen al calcular la longitud de arco
de una elipse y son un asunto
importante tanto en las matemáticas
puras como en las aplicadas.[5.63] El
primer
trabajo significativo de
Weierstrass (aún en Prusia, a la luz de
una vela, entre cuestionarios de
examen) incluye los desarrollos en
serie de potencias de las funciones
elípticas, lo cual le conduce a
problemas acerca de la convergencia de
las series de potencias,[5.64] y luego a la
convergencia, la continuidad y las
funciones en general.
La razón por la que Russell le alaba
respecto
al
problema
de
los
infinitesimales es la misma razón por
la que Weierstrass recibe el máximo
reconocimiento por la aritmetización
del análisis. Es el primero en dar una
teoría de los límites totalmente
rigurosa y metafísicamente impoluta.
Como es importante, y está detrás del
modo en que ahora la mayoría de
nosotros aprendemos cálculo en el
instituto, por lo menos observemos
rápidamente que la definición de los
límites de Weierstrass sustituye los
términos en lenguaje natural usados
por Abel/Bolzano/Cauchy, expresiones
como «se aproxima a un límite» y «se
hace menor que cualquier cantidad
dada», por las épsilon y delta
minúsculas y los delimitadores «| |» del
valor absoluto. Un gran beneficio
colateral de la teoría de Weierstrass es
que caracteriza el límite y la
continuidad de tal modo que cualquiera
de los dos puede ser definido en
términos del otro. Véase, por ejemplo,
esta definición de función continua,
que ciento cincuenta años después
sigue siendo todavía el «estándar de la
industria»:[5.65] f(x) es continua en un
punto xn si y solo si, para cualquier
número positivo ε, existe un δ positivo
tal que para cualquier x del intervalo
|x − xn| < δ,
|f(x) − f(xn)| < ε*
(semiextractado de Kline, pág. 952).
*INTERPOLACIÓN RÁPIDA
INCRUSTADA SEMI-SEI
Por favor, omita los siguientes tres
párrafos si y solo si la definición de
Weierstrass ya le parece perfectamente
clara.
Como
la
definición
recién
mencionada no es SEI, debemos
considerar la posibilidad de que quizás
esté < 100% claro por qué es tan
importante. Podríamos hablar de cómo
la definición es específicamente una
rigorización de la que aparece en el
Cours d’Analyse de Cauchy, «f(x) será
una función continua de la variable si
el valor numérico de la diferencia
f(x + α) − f(x) decrece indefinidamente
con el de a» (Cauchy, Cours, pág. 35):
el gran acierto de Weierstrass es que da
con un sustituto riguroso, totalmente
aritmético, del nebuloso «decrece
indefinidamente». Pero nada de eso va
a significar mucho si no podemos ver
cómo funciona realmente la nueva
definición de Weierstrass, lo cual a su
vez requiere examinar la densa sintaxis
técnica en la que está expresada para
los
matemáticos.
Su
lenguaje
hiperabstracto puede hacer que la
definición parezca o bien totalmente
trivial (por ejemplo, como ε y δ no
tienen relación entre sí en la definición,
¿no es obvio que se puede tomar una δ
por cada ε que se quiera?), o bien
totalmente
incomprensible
(por
ejemplo, ¿cómo se puede determinar a
qué equivale |x − xn| si no se sabe qué
es x?). O por lo menos estas eran las
quejas iniciales de nuestra clase al
doctor Goris, quien las trataba a su
manera habitual e inolvidable, más o
menos como sigue:[5.66]
En primer lugar, recordemos del
G. E. I que función continua significa
que cambios muy pequeños en la
variable independiente de la función
(x) producen solo cambios muy
pequeños en la variable dependiente
(f(x), alias y). Lo de los «cambios muy
pequeños» es lo que realmente importa
aquí: nos da la pista de que diferencias
como |x − xn| de la definición se van a
considerar
realmente
pequeñas.
Respecto a xn y x: xn es un punto en
particular, concretamente el punto para
el cual vamos a evaluar la continuidad
de la función, y x es, técnicamente,
cualquier punto en el intervalo de la
función, aunque dado lo que función
continua significa es mejor pensar en x
como cualquier punto que sea
«suficientemente próximo» a xn. Esto
es así porque lo más importante de la
definición de Weierstrass es que nos
permita verificar que una diminuta
diferencia entre x y xn dará solo una
diminuta diferencia entre f(x) y f(xn).
El motor de esa verificación son los
números positivos ε y δ, y la manera
fácil de entender esos dos números y su
relación es en términos de un juego.
Aquí está el juego: usted escoge
cualquier positivo que desee, no
importa lo pequeño que sea, y yo
intento encontrar un positivo que haga
verdadera la conjunción (|x − xn| < δ)
& (|f(x) − f(xn)| < ε):[5.67] y si puedo
encontrar tal para cada positivo que
usted escoja, entonces la f(x) es
continua, mientras que si no puedo,
entonces no lo es.
Como hacía el doctor Goris,
veamos un ejemplo con una función
que no sea continua, de modo que
podamos ver que no cualquier δ servirá
para un ε dado. La función se define
así: f(x) = 1 si x ≠ 0, y f(x) = 0 si
x = 0. Vamos a evaluar la continuidad
de esa f(x) en el punto xn donde xn = 0.
El juego es que usted puede escoger
cualquier valor positivo que desee para
ε, y supongamos que escoge ε = . Así
que ahora yo tengo que encontrar un
positivo tal que (|x − xn| < δ) &
(|f(x) − f(xn)| < )
sea
cierto.
Pero
ahora, por favor, retroceda hasta, o
recuerde, la nota 14 de §1c y su regla
de que una conjunción lógica es
verdadera solo cuando sus dos
términos, tanto el pre-«&» como el
post-«&», son verdaderos. Y ahora
mire
nuestro
término
«post»,
«|f(x) − f(xn)| < |». Por la definición
de nuestra función, sabemos que
f(xn) = 0, y por la misma definición,
sabemos que cualquier otro x que no
sea xn da un f(x) igual a 1 (porque xn es
el único punto en el cual x = 0). Por lo
tanto, si xn = 0, |f(x) − f(xn)| siempre
será igual a 1, el cual es obviamente
mayor que . No importa qué pueda yo
escoger para que |x − xn| sea menor que
él, |f(x) − f(xn)| jamás será <
cuando
xn = 0. Como el segundo término será
siempre
falso,
la
conjunción
(|x − xn| < δ) & (|f(x) − f(xn)| < ) será
falsa independientemente del valor de
δ. Aquí lo importante es que no hay un
δ positivo para ε = , de modo que el
criterio de la definición, «para
cualquier número positivo, existe un
positivo tal que…» no se satisface. Por
lo tanto, la función no es continua en xn
(cosa que ya sabíamos para empezar,
pero aquí se trataba de aplicar la
definición de Weierstrass a un caso
claro). El juego ha terminado.
FIN DE LA INTERPOLACIÓN SEMI-SEI.
REGRESO A LA DISCUSIÓN PRINCIPAL
DE §5E, EN CURSO
Un retazo de posible perplejidad no
cubierto en la interpolación: lo que
Weierstrass ha definido aquí arriba es
solo la continuidad en un punto, pero
como usted puede escoger cualquier
punto en un intervalo dado para que sea
xn, una f(x) puede obviamente definirse
como continua en un intervalo si es
continua en todos y cada uno de los xn
del intervalo. Así, una definición
general de continuidad para funciones
sale directamente de la definición
inicial. Y —eso es lo que sacudió el
mundo matemático— también sale la
definición de límite: si se toma la
definición original de Weierstrass,
entonces se puede decir que f(x) tiene
límite L en si se sustituye f(xn) por L y
todavía se puede encontrar un δ para
cada ε de modo que (|x − xn| < δ) &
(|f(x) − L| < ε) sea cierto.
Hay una razón por la que todo esto
parece tan horriblemente abstracto: es
horriblemente abstracto. Sin embargo,
por esa misma abstracción, la de
Weierstrass es la teoría más limpia y
clara que se ha formulado jamás sobre
los límites y la continuidad.[5.68] No
hay líos con el lenguaje natural: la
definición no usa nada más que
números
reales
y
operadores
elementales como − y <. Como es tan
limpia y abstracta y aritmética, la
teoría también permite a Weierstrass
definir
la
convergencia,
la
convergencia
uniforme
y
la
convergencia absoluta rigurosamente,
proporcionar pruebas fiables para todas
ellas,[5.69] y demostrar una serie de
cosas acerca de la continuidad y la
convergencia
de
las
series
trigonométricas que nadie había sido
capaz de esclarecer. Los ejemplos
relevantes aquí incluyen (1) su
demostración de que una serie de
funciones
continuas[5.70]
puede
converger
hacia
una
función
discontinua, y (2) su ya mencionado
desmentido de la teoría según la cual
continuidad = diferenciabilidad, lo
cual desmiente dando una función de la
que demuestra que es 100% continua
pero no tiene derivada en ningún punto.
Si tiene usted curiosidad, esta es la f(x)
dada por
br cos (arπx) donde a es
impar, 0 < b < 1, y 2ab > 2 + 3π, y,
dicho sea de paso, si usted representa
gráficamente esta f(x) obtiene una
curva sin ninguna tangente. Recordará
de §3c que Bernhard P. Bolzano ya
había dado una función parecida (de la
que no hay indicios que Weierstrass
supiera nada), pero hay una diferencia
crucial. Bolzano simplemente había
presentado su ejemplo, mientras que
gracias a sus definiciones puramente
formales Weierstrass tiene munición
para demostrar realmente que su propia
f(x) es a la vez continua y no
diferenciable. Otro avance importante:
en el análisis weierstrassiano, el
ejemplo
concreto
siempre
es
coincidente con la demostración
general abstracta.
Como también se ha mencionado
en §3c, a Bolzano y a Weierstrass
conjuntamente se les reconoce un gran
teorema sobre los límites de una
función continua,[5.71] un teorema que
es pertinente aquí en parte porque
considera una sucesión/serie infinita de
números reales como un conjunto
infinito de puntos de la recta real (y los
primeros tipos de conjuntos infinitos
que interesarán a Georg Cantor serán
esos conjuntos de puntos). Aquí
probablemente quiera usted recordar
las definiciones de intervalo, límites y
cotas del G. E. I. Formalmente
hablando, el teorema de BolzanoWeierstrass sostiene que todo conjunto
de puntos infinito y acotado contiene
por lo menos un punto límite, que es un
punto xn, tal que todo intervalo que lo
contiene
también
contiene
∞
miembros
del
conjunto
(semiextractado de Lavine, pág. 38).
[5.72] Puede no parecerlo de inmediato,
pero el T. B. W. es una auténtica
bomba. Por ejemplo, resulta que da un
potente antídoto, y sin infinitesimales,
a la paradoja del sin-instante-siguiente
de §4b (rompecabezas que en sí mismo
es consecuente con la alucinante
densidad de los ∞ puntos de la recta
real).
Si le interesa esto, he aquí cómo
funciona. El T. B. W. en realidad
contiene dos teoremas, uno de los
cuales es de Bolzano, hacia 1830, y
afirma que, dado un intervalo cerrado
[a, b], una función continua f(x) en
[a, b] que sea positiva para algún valor
de x y negativa para algún otro valor de
x tiene que ser igual a 0 para algún
valor de x.[5.73] Geométricamente,
podemos entender esto viendo que una
curva continua que vaya de algún lugar
por encima del eje x a algún lugar por
debajo del eje x en realidad tiene que
cortar el eje x en algún punto. En
términos de rigor, el problema de
Bolzano era que para demostrar este
teorema tenía que demostrar que todo
conjunto acotado de valores/puntos
debe tener una mínima cota superior,
[5.74] demostración que se iba a pique
por la ausencia de teorías coherentes
sobre los límites y los números reales.
De modo que, una vez más, en realidad
Bolzano solo pudo proponer su teorema
y demostrar geométricamente que era
cierto.
No
pudo
demostrarlo
formalmente. Sin embargo, veinte años
más tarde, Karl Weierstrass usa su
teoría rigurosa de los límites para
demostrar el «lema de la mínima cota
superior» de Bolzano como parte de su
propio teorema de los valores extremos
(T. V. E.), que es la otra gran parte del
T. B. W. Es este teorema de los valores
extremos (= si una f(x) es continua en
[a, b], entonces tiene que haber por lo
menos un punto en [a, b] donde f(x)
tiene su valor máximo, M, y otro punto
en [a, b] donde f(x) tiene su valor
mínimo, m), junto a la muy poderosa
definición
de
continuidad
de
Weierstrass, lo que proporciona una
salida matemática de la grieta del sininstante-siguiente. A saber: como el
tiempo es claramente una función que
fluye continuamente,[5.75] podemos
suponer que hay un intervalo finito
[t1, t2] de longitud > 0 entre dos
instantes cualesquiera t1 y t2, y ahora,
gracias al T. V. E., demostramos que
hay un punto en [t1, t2] donde la
función tiempo tiene su valor mínimo
m, y, por lo tanto, que ese tm será,
matemáticamente hablando, el instante
inmediatamente posterior a t1.
A partir de este resultado,
probablemente pueda usted ver cómo el
teorema de los valores extremos se
podría utilizar contra la dicotomía de
Zenón misma (pues
es una función
continua prototípica). En el análisis
weierstrassiano estricto, sin embargo,
el T. V. E. ni siquiera es necesario,
pues la teoría aritmética de los límites
nos permite explicar —con pleno
sentido— por qué la serie convergente
+
+
+…+
tiene suma 1.
§5e(1)
INTERPOLACIÓN SOBRE EL
ANÁLISIS WEIERSTRASSIANO Y
ZENÓN
Recordará
invocar
que ya hemos intentado
y
otras
diversas
soluciones predecibles de la dicotomía,
solo para descubrir que no «enuncian
claramente
las
dificultades
involucradas», y aún menos explican
cómo podemos llegar a cruzar la calle.
Ahora se pueden ignorar, más o menos,
todos esos intentos anteriores, aunque
no hará ningún daño recordar o revisar
la nota 35 de §2c y su explicación
acerca de cómo los decimales son
representaciones
de
series
convergentes.
Además
de,
por
supuesto, las últimas páginas del §5e
justo anterior. Así pues, aquí está una
respuesta a la dicotomía según el
análisis weierstrassiano.[5.76]
De lo que habla realmente la
dicotomía es de cierto número racional
s (= la anchura de la calle, la longitud
de arco desde la falda hasta la punta de
la nariz), número que Zenón nos invita
a aproximar mediante una serie de
potencias convergente de otros
números racionales sn, donde n
representa por sí mismo la sucesión
infinita 1, 2, 3,… Esto puede parecer
opaco en lo abstracto, pero muchos
números
racionales
se
pueden
aproximar del mismo modo. El
racional s , por ejemplo, se puede
aproximar mediante la siguiente serie
convergente sn:
+
+
+…+
. La dicotomía es solo un poco más
engañosa que lo de , y parte de ese
engaño se puede mitigar hablando de la
dicotomía «revisada» y más abstracta
de §2b, donde no hay tiempo ni
longitud, sino simplemente cierta
cantidad s de la que se toma la mitad,
de esta se toma la mitad, y de esta, la
mitad, etc., hasta que las porciones más
pequeñas empiezan a igualar
donde
n es arbitrariamente grande.[5.77]
Sumar las porciones obtenidas de este
modo nos da el sn de la dicotomía
como la siguiente serie de potencias
convergente: sn =
+
+
+…+
. Y lo que hay que ver aquí es que
ese sn es una aproximación de 1 del
mismo modo que 0,999… es una
aproximación de 1. Es decir, la suma
de sn difiere de 1 solo en
, y esa
diferencia se hará arbitrariamente
pequeña
al
aumentar
n
indefinidamente.
Se
admite
que
esos
«arbitrariamente» e «indefinidamente»
cauchyescos aquí parecen vagos e
insatisfactorios, y Zenón quiere que lo
sean: quiere que quedemos apabullados
por el hecho de que hay un número
infinito de términos en «
+
+
+
…» y que en el mundo real nunca
podemos acabar de sumarlos todos, en
cuyo caso ahora viene Weierstrass al
rescate.
Un par de preliminares harán más
fácil ver cómo funciona esto. En
primer lugar, sepa que el índice n
también funciona como un número
ordinal[5.78] de cualquier término dado
de la serie sn, es decir, que
es el 1.er
término,
es el 4.º término,
es el
47.º término, etc. Observe, también,
que la diferencia entre dos términos
sucesivos cualesquiera de sn se hace
más y más pequeña al alejarnos cada
vez más en la serie. Donde la
«diferencia» de esta última frase se
puede representar como una distancia
en la recta numérica. Es decir, que
estamos hablando de intervalos.
O sea, que allá vamos. Sabemos
que la suma de la sn de la dicotomía
diferirá de 1 solo en
donde n = 1, 2,
3,… Para demostrar que 1 es realmente
la suma de sn, tenemos que demostrar
que 1 es el límite de la función
donde n = 1, 2, 3, …[5.79] Lo
demostramos
mediante
el
planteamiento de Weierstrass «f(x)
tiene límite L en un punto xn si y solo
si, para cualquier número positivo ε,
existe un número positivo δ tal que
para cualquier x del intervalo
|x − xn| < δ, |f(x) − f(xn)| < ε». Aquí L
y xn son ambas 1, f(x) es
,yx
puede ser cualquiera: la manera más
simple de hacer la demostración es
dejar que x = el punto
. Y recuerde
(suponiendo que leyó la interpolación
de §5e) que la extraña sintaxis de la
definición en realidad significa que
tenemos que ser capaces de hallar un δ
para cada ε de modo que la conjunción
lógica (|x − xn| < δ) & (|f(x) − L| < ε)
sea cierta. Luego, el único otro
preliminar es asegurarnos de que
recordamos qué significan los símbolos
de valor absoluto: |1 − 10| y |10 − 1|,
ambos = 9, y que |f(x) − L| y |L − f(x)|
también son equivalentes. Weierstrass
usa valores absolutos porque hablamos
de intervalos en la recta numérica, es
decir, de la distancia numérica entre
diferentes puntos, que es la misma
desde cualquier dirección. Aquí, lo que
los «| |» nos permiten hacer es, a
efectos prácticos, intercambiar ambos
términos de sustracción, lo cual hará
que los auténticos intervalos de la R. N.
de los que estamos hablando sean más
fáciles de representar claramente.
Perdón por toda la verborrea:
estamos haciendo que suene menos
fácil de lo que es realmente. Así, para
demostrar que 1 es el límite de la
función
dicotómica
,
tenemos que hallar, para cualquier
número positivo ε tal que el intervalo
entre 1 y
es < ε, un positivo
δ
tal
que
&
sea cierta. Lo
cual resulta que no es difícil de hacer.
Respecto a ε y al segundo término de la
conjunción, la situación es de algún
modo la contraria que en el ejemplo de
la interpolación:
nunca será falso, sin importar qué valor
positivo escoja usted para ε. Por
ejemplo, supongamos que decide que
ε = 0,001. Entonces puede hacer que
sea
cierto
haciendo que n sea igual a 10 (tal como
lo será en el décimo término de sn), en
cuyo caso
=
, en cuyo caso
=
, en cuyo caso
=
−
=
, lo cual es lo mismo que
0,0009765, que es ciertamente < 0,001.
La cuestión es que sin importar qué
diminuto ε se escoja, se puede ajustar
el valor de n de tal modo que
acabe
siendo
inferior a ε.
Así, el segundo término de la
conjunción siempre va a ser cierto.
Ahora todo de lo que debemos
preocuparnos es el primer término y
encontrar
un
δ
que
haga
cierto para un ε
dado. Obviamente, no tenemos la
misma carte blanche para escoger δ
que teníamos para escoger ε, porque
nuestra elección de ε determina el
valor que asignamos a n y, por lo tanto,
a
, y es
que δ tiene que
superar. Pero resulta que la relación de
dependencia entre escoger δ y ε
simplifica la tarea de hallar una δ
relevante. Veamos de nuevo el ejemplo
donde ε = 0,001 y así n = 10 y
=
. Aquí necesitamos un δ
positivo tal que
< δ. En
este caso particular, δ = 1 funcionará
perfectamente… y, de hecho, resulta
que δ = 1 funcionará para cualquier
valor posible de ε. Probablemente
puede ver por qué. Es porque todos los
valores posibles de los ε deben, por
definición, ser positivos. Aunque ε se
puede hacer más y más pequeño, y
cuanto más pequeño, mayor tiene que
ser n para hacer que
sea inferior a ε, y cuanto mayor sea n,
más próximo a 1 será
. De
todos modos, el requisito de que ε sea
> o asegura que
será
siempre < 1. Y como, sin importar que
ε escoja usted, δ = 1 asegura que la
conjunción
&
será
cierta,
entonces el criterio principal de la
definición: «para cualquier número
positivo ε, existe un positivo δ», se
satisface.
Por lo tanto,
= 1,
por consiguiente, 1 es la suma de sn.
Por lo tanto, usted puede realmente
cruzar la calle.
La confusión central de la
dicotomía queda ahora al desnudo: la
tarea de desplazarse del punto A al
punto B no involucra subtareas
necesarias, sino más bien una sola tarea
cuyo «1» puede ser aproximado con
validez mediante una serie infinita
convergente. Es la mecánica de esa
aproximación lo que el análisis
weierstrassiano es capaz de explicar, es
decir, explicar realmente, 100%
aritméticamente, sin infinitesimales,
analogías,
o
cualesquiera
ambigüedades del lenguaje natural de
las que buscaba Zenón. No resulta nada
pobre decir que, tras Weierstrass, la
dicotomía se convierte simplemente en
un problema de definición más.
Pero
hay
algo
más.
La
demostración que acabamos de ver es
inusualmente detallada. En una clase
de
nivel
intermedio,
las
demostraciones
de
que
=1
o
de
que
= 0 raramente entran en los
intervalos de Weierstrass o los ε/δ. Han
pasado a ser de algún modo los
cimientos ocultos de los conceptos de
límite, su justificación deductiva. El
concepto
mismo
sigue
siendo
expresado en términos del lenguaje
natural como «indefinidamente» y
«tiende a». Lo cual probablemente es
bueno. En lugar de un tocho más acerca
de respuestas técnicas o genuinas,
observemos simplemente que en una
clase de matemáticas estándar una
solución de la dicotomía se detendrá
básicamente tras el 2.º párrafo de
§5e(1). Es decir, en una clase de
matemáticas se expondrá la serie
convergente sn =
+
+
+…+
, se indicará que la diferencia entre
sn y 1 es
, se demostrará que esta
diferencia se vuelve arbitrariamente
pequeña
al
aumentar
n
indefinidamente, y se enseñará que el
modo adecuado de manejar una serie
como esta es «diciendo que la suma sn
se aproxima al límite i cuando n tiende
a infinito, y escribiendo 1 =
+
+
+
+ …» (Courant y Robbins, pág.
64). Lo que está entre comillas es de un
auténtico libro de texto, edición
revisada © 1996, cursiva sic. El mismo
texto continúa:
Esta «ecuación» no significa
que realmente tengamos que
sumar infinitos términos; es
solo una expresión abreviada
del hecho de que 1 es el límite
de la suma finita sn cuando n
tiende a infinito (en ningún caso
es infinito). El infinito aparece
solo en el procedimiento sin fin
y no como una cantidad real
(ibíd).
Dejemos claro, de una manera muy
calmada y discreta, que si usted piensa
que puede detectar un tufillo
aristotélico en todas esas urgentes
garantías de que el ∞ no tiene que ser
tratado «como una cantidad real» en
problemas como la dicotomía, no está
imaginando cosas. Ni tampoco es
cuestión del modo prefabricado en que
las matemáticas se enseñan hoy a los
estudiantes universitarios. Es más
profundo que todo eso, y más antiguo.
Algo notable acerca del análisis y la
teoría de funciones del siglo XIX es que
cuanto más sofisticados se volvían,
más asombrosamente iba pareciéndose
su tratamiento del ∞ al viejo y canoso
concepto
aristotélico
de
«potencialidad». Y la cima de dicha
sofisticación, y de ese parecido, es el
análisis weierstrassiano.
Si, a pesar de todo, por algún azar
adicional se ha dado usted cuenta de
que la dicotomía y sus pretendidas
soluciones de aula y pizarra involucran
solo números racionales y la recta
numérica —sin olvidar que los ε y δ
ejemplarizantes de nuestra propia
demostración en §5e también han sido
todos racionales— entonces está usted
en situación de valorar una especie de
encantadora ironía.
6
§6a.
En
definitiva, más importante que
cualquier resultado específico es el
espíritu según el cual Weierstrass
redefine los límites y las funciones
continuas. Es decir, su compromiso con
el rigor fundacional, la higiene
apodíctica,
etc.
Su
propia
aritmetización del análisis es 100%
literal. Apunta no solo a eliminar los
conceptos geométricos y la intuición
inductiva de las demostraciones, sino
también a basar todas las matemáticas
poscálculo en el sistema de los
números reales del mismo modo en que
lo está la aritmética. Pero el sistema de
los números reales significa la recta
real, que como hemos visto no está
exactamente desprovista de grietas de
tipo ∞.
Los
historiadores
de
las
matemáticas expresan esto de varias
maneras, por ejemplo, Kline: «Fue
Weierstrass el primero en indicar que
para establecer cuidadosamente las
propiedades de las funciones continuas
necesitaba la teoría del continuo
aritmético» (Kline, pág. 979), o Bell:
«Los irracionales que nos dan los
conceptos de los límites y la
continuidad, de los cuales surge el
análisis, deben referirse de nuevo a los
enteros
mediante
un
firme
razonamiento» (Bell, pág. 419). Lo
destacado es la ironía prometida al
final de §5: el concepto riguroso de
límite dado por Weierstrass, que
parecía final y coherentemente haber
eliminado del análisis la necesidad de
cantidades de tipo y , resulta que a su
vez necesita una teoría rigurosa y clara
de los números reales, es decir, de los
irracionales y el continuo de la recta
real. Con respecto a lo cual véase la
frase
del
filósofo
matemático
Shaughan Lavine: «Y esa teoría
prontamente reintrodujo el infinito en
el análisis. El viejo infinito de las
cantidades infinitesimales e infinitas
fue simplemente sustituido por el
nuevo infinito de las colecciones
infinitamente grandes» (Lavine, pág.
38).
La verdad es que hay varias razones
diferentes e interrelacionadas por las
que los números irracionales/reales se
convierten ahora en un problema
puntero y apremiante. Uno de ellos,
como se acaba de mencionar, es
fundacional. Otro tiene que ver con las
aplicaciones: resulta que los ε y δ
weierstrassianos que aparecen en los
límites de problemas del mundo real
son a menudo irracionales, haciendo
que la cuestión de los ε y δ sea mucho
más difícil de establecer. Además,
están
el
antes
mencionado
P. C. G. S. F., la pérdida de fe en los
axiomas de Euclides, etc. También está
el hecho de que el nuevo énfasis de las
matemáticas en el rigor y la coherencia
formal pone de relieve un problema
lógico en el modo de tratar los
irracionales ya desde que la Divina
Hermandad los descubriera por primera
vez en §2c. Ese descubrimiento, como
vimos, fue geométrico —lo cual
significa
magnitudes
inconmensurables,
√2,
cocientes
eudoxianos, etc.— y las definiciones de
los
irracionales
utilizadas
en
matemáticas han sido geométricas
desde entonces. Esa práctica era, en los
translúcidos términos de Bertrand
Russell,
altamente ilógica, pues si la
aplicación de números al
espacio [geométrico] debe dar
algo más que tautologías, los
números
aplicados
deben
definirse independientemente, y
si no fuera posible nada más
que una definición geométrica,
no habría, hablando con
propiedad,
tales
entes
aritméticos como la definición
pretende
definir
(Russell,
Principles of Mathematics, pág.
278).
Argumento que costaría demasiado
tiempo examinar en detalle, pero puede
verse la tendencia general.
Así que lo que ocurre es que en las
décadas de 1860 y 1870 varios
matemáticos empiezan a intentar
obtener teorías rigurosas de los
irracionales/reales. Aquí los grandes
nombres incluyen a William Rowan
Hamilton, H. Kossak, Karl Weierstrass,
Ferdinand Lindemann, H. C. R. Méray,
Georg Cantor, Η. E. Heine, y Richard
Dedekind. Adivine en cuáles estamos
interesados.
En primer lugar, trabajando
aparentemente a partir de ideas que
había bosquejado en sus clases en la
Universidad de Berlín, algunos de los
alumnos y seguidores de Weierstrass
intentan usar sus definiciones clave
para intentar definir un número
irracional como, esencialmente, el
límite de un tipo particular de series
infinitas de números racionales. La
técnica de las definiciones es
convulsivamente técnica, pero por
fortuna ni siquiera tenemos que entrar
en ello porque resulta que la teoría no
funciona: es circular.[6.1] Esto es así
porque el límite irracional de
Weierstrass
no
puede
existir,
lógicamente hablando, hasta que haya
una definición de los números
irracionales. Aquí «existir» significa
precisamente lo que Russell quiere
decir justo antes cuando dice que «no
habría tales entes geométricos como la
definición
[geométrica]
pretende
definir».
No
se
puede
usar
coherentemente el concepto de número
irracional en la definición de «número
irracional» como no se puede definir
coherentemente «negro» como «el
color de un perro negro». Así, en pocas
palabras, los esfuerzos de los
weierstrassianos en realidad nunca
llegaron a ninguna parte.
La teoría del propio Cantor acerca
de los números reales surge en el
contexto de su trabajo sobre algo
llamado el teorema de unicidad (T. U.)
para series trigonométricas, y hay
buenas razones para esperar un poco a
hablar de él.
El plan más potente, significativo y
extraño para definir los irracionales es
el de Julius W. R. «Richard» Dedekind,
1831-1916, que es una docena de años
más joven que Weierstrass pero muy
parecido a él. Una persona afable y
equilibrada que dedica su vida
principalmente a dar clases en
Hochschulen, técnicas en Brunswick y
Zurich. Un soltero empedernido[6.2]
que vive con su hermana. Dedekind
vive hasta una edad tan avanzada y es
tan apreciado por los demás que
aparece en todas las matemáticas
modernas: alumno de Dirichlet y Gauss
en
Göttingen,
editor
de
la
Zahlentheorie de Dirichlet, amigo de
toda
la
vida
de
Riemann,
semiweierstrassiano,
colaborador
temprano con Leopold Kronecker en
geometría algebraica, colaborador y
amigo de Georg Cantor; y no era fácil
ser amigo de Cantor. Una historia
favorita entre los matemáticos es que
Dedekind fue tan increíblemente
longevo que en el famoso Calendario
Matemático de Teubner figuró durante
un tiempo que había muerto cierto día
de 1899, hasta que, finalmente, un año
Dedekind le escribió al editor que
estaba vivo y que además había pasado
el día en cuestión «en estimulante
conversación sobre “sistema y teoría”
con mi invitado del almuerzo y
honrado amigo Georg Cantor de Halle»
(traducción extractada, y algo editada,
de Bell, pág. 519).
La fecha de publicación de la
famosa obra de Dedekind «Continuidad
y números irracionales»[6.3] es 1872.
En parte es una respuesta a la propia
definición
de
Cantor
de
los
irracionales, que había aparecido como
parte de un extenso artículo sobre el
teorema de unicidad ese mismo año.
Pero resulta evidente que Dedekind
tenía su teoría básica a punto tan
tempranamente como en 1860. Como
Weierstrass (y a diferencia de Cantor),
no es muy ambicioso respecto a
publicar sus materiales. La motivación
de Dedekind, de nuevo como la de
Weierstrass, venía de enseñar cálculo
en la universidad: se había sentido cada
vez más incómodo con el uso de
conceptos geométricos indefinidos para
definir los límites y la continuidad.
Pero en vez de centrarse en la
aritmetización de los límites, Dedekind
en cierto modo profundiza más, va al
problema raíz que había preocupado a
Zenón, la D. H. P., Eudoxo, Aristóteles
y Bolzano, y había acechado al análisis
desde el teorema fundamental. El
problema: cómo obtener una teoría
100% aritmética de lo que se supone
que el cálculo se ocupa —continuidad
pura, como la del movimiento y
constructos geométricos continuos
como líneas y áreas y volúmenes—[6.4]
pero nunca había definido con
suficiente claridad y rigor para hacer
que sus demostraciones tuvieran
realmente sentido.
La entidad que Dedekind elige
como emblema de la continuidad
aritmética es la buena y vieja recta
real, la cual técnicamente aún
deberíamos llamar la recta numérica,
pues solo tras el establecimiento de lo
que se llama el axioma de CantorDedekind
se
convierte
en
rigurosamente correcto hablar de la
recta real. Llamémosla, pues, la recta
numérica (Dedekind simplemente la
llama L), y recuérdese de §2c que es
ordenada e infinitamente densa y
extensa, y que puede usarse para
representar los números racionales
asignando a cada número racional un
punto único de la recta. Y, sin
embargo, que toda la razón por la que
el análisis necesita algo más que los
números racionales es que la recta
numérica, como todas las rectas, es
continua de un modo en que el
conjunto de todos los racionales no lo
es. La manera que tiene Dedekind de
expresar esto se remonta directamente
a los griegos: «Sin embargo, es de la
máxima importancia el hecho de que
en la recta L hay infinitos puntos que
no corresponden a ningún número
racional» (Dedekind, pág. 8), y cita
como ejemplo la buena y vieja
diagonal del cuadrado unidad. De modo
que su estrategia es simplemente
explicar qué tiene L que la haga
continua y sin huecos mientras que el
conjunto infinitamente denso de los
números racionales no lo es. Por
supuesto, sabemos, como él y todos los
demás por aquel entonces, que son los
números irracionales, pero nadie ha
sido capaz de definirlos directamente.
Así que Dedekind aquí va a hacer de
Sócrates y a actuar como si nunca
hubiera oído hablar siquiera de los
irracionales y simplemente preguntara:
¿En qué reside exactamente la
continuidad de L?[6.5] Es su respuesta a
esta cuestión lo que convierte a la recta
real en una realidad matemática y
establece, junto a Cantor, que el
conjunto de todos los números reales
compone el continuo.
§6b.
INTERPOLACIÓN
Conocido
hoy como corte de
Dedekind, el recurso de R. D. para
construir
la
recta
real
es
extremadamente ingenioso y extraño, y
antes de que sucumbamos a sus
complejidades vale la pena indicar que
en un sentido profundo es la voluntad
de Dedekind de tratar el infinito real lo
que permite que su demostración siga
adelante. Como se ha mencionado en
§5 y en otras partes, una de las razones
por las que el concepto de límite fue
tan bien recibido en el análisis era que
se ajustaba bien a la vieja idea del
infinito potencial: la idea de que el ∞
es algo a lo que nos podemos
«aproximar» sin tener que llegar nunca
realmente hasta él parece sacada
directamente de la Metafísica. La
aceptación tácita por las matemáticas
de la distinción aristotélica se hace
explícita en una frase muy citada de
Karl Friedrich Gauss (sí: el Gauss de
Dedekind) hacia 1830:
Protesto por el uso de una
cantidad infinita como un ente
real; esto no se admite nunca en
matemáticas. El infinito es solo
una manera de hablar, en la cual
uno habla propiamente de
límites hacia los cuales ciertas
razones pueden aproximarse
tanto como se desee, mientras
que a otras se les permite
aumentar sin restricciones
(Gauss, extractado por Kline,
pág. 993).
Y así, por supuesto, es irónico que
solo un par de décadas después de que
Weierstrass despoje a los límites de las
últimas sombras del ∞ empecemos a
ver matemáticos de primera fila que no
solo aceptan el infinito real, sino que lo
usan en las demostraciones. Dedekind
es uno de ellos. Y no es que quede
persuadido por Cantor o por Bolzano o
por nadie más de la coherencia de los
conjuntos infinitos. Dedekind es, tal
como se definió el término en §2a, un
platónico. Cree claramente que la
realidad matemática no es tan empírica
como cognitiva:
Al hablar de la aritmética (el
álgebra, el análisis) como una
parte de la lógica, mi intención
es dar a entender que considero
el
concepto
de
número
completamente independiente
de las nociones o intuiciones
del espacio y el tiempo, que lo
considero
un
resultado
inmediato de las leyes del
pensamiento (Dedekind, pág.
31).
O quizá sea mejor llamarle un
fenomenólogo, pues la distinción
acerca de si las realidades matemáticas
son creaciones o descubrimientos no
parece importarle mucho a Dedekind:
«Los números son creaciones libres de
la mente humana; sirven como medio
para aprehender más fácilmente y más
nítidamente la diferencia entre las
cosas» (ibíd.).
O mire esto. En un ensayo
complementario a «Continuidad y
números irracionales» que se traduce
habitualmente como «El significado y
la naturaleza de los números»,[6.6]
Dedekind desarrolla una notable
demostración de su «Teorema 66.
Existen sistemas infinitos» que
consiste en lo siguiente: «Mi propio
reino de pensamientos,[6.7] es decir, la
totalidad S de todas las cosas que
pueden ser objetos de mi pensamiento,
es infinito. Pues si s significa un
elemento de S, entonces el pensamiento
s', que s puede ser un objeto de mi
pensamiento, es él mismo un elemento
de S,…» (ibíd., pág. 64, ligeramente
editado) y así sucesivamente, de modo
que la serie infinita ([s] + [s es un
objeto del pensamiento] + [«s es un
objeto del pensamiento» es un objeto
del pensamiento] + …) existe en el
Gedankenwelt, lo cual implica que el
Gedankenwelt mismo es infinito.
Respecto a esta demostración, observe
(a) su gran parecido con varias RIV al
estilo de Zenón que habíamos visto en
§2a, y (b) cuán fácilmente podríamos
objetar que la demostración solo
establece que el Gedankenwelt de
Dedekind es «potencialmente infinito»
(y en el preciso sentido aristotélico del
término), pues nadie podrá jamás
sentarse y pensar realmente en una
serie
infinita
completa
de
pensamientos del tipo (s + s' + s''), es
decir, la serie es una abstracción total.
La cuestión es que la demostración
de Dedekind en «El significado y
naturaleza de los números» no va a
convencer a nadie que no esté ya
dispuesto a admitir la existencia[6.8] de
sistemas/series/conjuntos… realmente
infinitos, y tanto Dedekind como
Cantor lo están. Al 100%. Sin embargo,
a diferencia de Dedekind, Cantor tiende
a representarse a sí mismo como si le
hubieran
arrastrado
gritando
y
pataleando hacia el ∞ real. Por
ejemplo:
La idea de considerar lo
infinitamente grande no solo en
la forma de la magnitud
ilimitadamente creciente y en la
forma
estrechamente
relacionada de las series
infinitas convergentes […] sino
también
fijarla
matemáticamente
mediante
números en la forma definida
del infinito completado me
sobrevino como una obligación
lógica, casi contra mi voluntad,
pues era contraria a unas
tradiciones que había llegado a
considerar muy valiosas en el
curso de varios años de esfuerzo
científico e investigaciones
(Cantor, «Foundations of the
Theory of Manifolds», págs. 7576).
Una parte de esa diferencia en la
presentación es que Georg Cantor era
un retórico más hábil que Richard
Dedekind, y otra parte es que tenía que
serlo: Cantor estaba en el frente de la
guerra por el ∞ de un modo en que
Dedekind nunca lo estuvo.
Otra cosa a tener en cuenta, sin
embargo, es que las matemáticas
transfinitas de Cantor acabarán
socavando totalmente las objeciones
aristotélicas, como la anterior (b), a la
demostración de Dedekind, pues la
teoría de Cantor constituirá una
evidencia directa de que los conjuntos
realmente
infinitos
pueden
ser
entendidos
y
manipulados,
verdaderamente tratados por el
intelecto humano, igual que la
velocidad y la aceleración son tratados
por el cálculo. Así, algo a valorar desde
el principio es que, por muy abstractos
que puedan ser los sistemas infinitos,
después de Cantor está claro que no son
abstractos del modo real/irreal en que
lo son los unicornios.
FIN DE LA INTERPOLACIÓN
§6c.
Volvamos
a la táctica inicial de
Dedekind de preguntar qué distingue la
continuidad de la recta numérica L.
Resulta que tanto Galileo como Leibniz
y Bolzano habían intentado postular
que la continuidad de L se basaba
realmente en la densidad infinita de sus
puntos constituyentes, es decir, en el
hecho de que entre dos puntos
cualesquiera de la R. N. siempre se
puede hallar un tercer punto. Como
hemos visto, sin embargo, la misma
característica vale para todos los
racionales de la forma ,[6.9] y como
(1) todo número racional se puede
expresar en la forma ,[6.10] y (2) ya
sabemos que el conjunto de todos los
racionales no es continuo, Dedekind
descarta la idea de que la continuidad
de L resida en algún tipo de densidad o
«estrecha vecindad»: «Mediante vagos
comentarios acerca de la conexión
ininterrumpida de las más pequeñas
partes [de L] obviamente no se gana
nada; el problema es indicar una
característica precisa de la continuidad
que pueda servir como base para
deducciones válidas» (Dedekind, págs.
10-11).
El golpe de efecto de Dedekind es
situar esta «característica precisa» no
en la densidad o la cohesión de L, sino
más bien en una propiedad contraria, la
separabilidad,
a
su
vez
una
consecuencia del hecho de que la recta
numérica sea ordenada y sucesiva, es
decir, que cada punto de la R. N. está a
la derecha de todos los puntos
correspondientes a números inferiores
y a la izquierda de todos los puntos
correspondientes a números superiores.
Esto significa que en cualquier punto
en particular podemos, en cierto modo,
cortar[6.11] la recta numérica en dos
partes,
dos
conjuntos
infinitos
mutuamente exclusivos,[6.12] A a la
derecha y B a la izquierda, donde todo
número racional de B es mayor que
todo número racional de A. Respecto a
esto,
«Continuidad
y
números
irracionales» (que es, como se ha
mencionado, el nombre informal para
un artículo matemático técnico) tiene
un aparte del tamaño de un párrafo
donde Dedekind en cierto modo da un
puntapié en el suelo y pretende
disculparse por lo poco convincente y
obvio que lo del schnitt debe de
parecer, por ejemplo: «[L]a mayoría de
mis
lectores
quedarán
muy
decepcionados al saber que es mediante
ese comentario banal que el secreto de
la continuidad será revelado» (ibíd.,
pág. 11). El comentario al que se
refiere es el recíproco lógico de la
afirmación anterior acerca de la
separabilidad, es decir:
Si todos los puntos de la recta
caben en dos categorías tales
que todo punto de la primera
categoría se halla a la izquierda
de todo punto de la segunda
categoría, entonces existe un
punto, y solo uno, que da lugar
a esta división de todos los
puntos en dos categorías,
dividiendo la recta en dos
porciones (ibíd.).
Lo que esto significa es que al
definir los miembros y las cotas de los
conjuntos A y B, se puede definir el
valor del punto en el cual se corta L en
las partes A y B. Y, como usted
recordará de §2c, definir un punto es
definir un número.
Solo que, como la recta en cuestión
es la recta numérica y representa solo
los números racionales, es justo
preguntar cómo va a ser posible que el
schnitt ayude a definir los números
irracionales, los cuales, por supuesto,
son el verdadero «secreto de la
continuidad». Que cada número
racional corresponderá a un schnitt
pero no cada schnitt corresponderá a un
número racional podría parecer
simplemente otro modo de formular la
aseveración según la cual no podemos
definir irracionales en términos de
racionales. La respuesta es que
Dedekind puede construir literalmente
la definición de cada número irracional
a partir de las características de los dos
conjuntos en los que divide la recta. El
método funciona como sigue.
Considere un schnitt en la R. N. que
divide toda la ∞ de números racionales
en dos conjuntos A y B tales que todos
los elementos b de B son mayores que
todos los elementos a de A. De forma
más específica, considere si estos A y B
pueden
tener
elementos
máximos/mínimos.[6.13] Dependiendo
de dónde y de cómo se defina el
schnitt, hay solo tres posibilidades, de
las cuales solo una puede ser cierta.
Posibilidad 1 = El conjunto A tiene un
elemento máximo a' (como en el caso,
por ejemplo, en que el corte A contiene
todos los números racionales ≤ 2 y B
contiene todos los números racionales
> 2). Posibilidad 2 = El conjunto B
tiene un elemento mínimo b' (como en
el caso, por ejemplo, en que el corte A
contiene todos los números racionales
< 2). Posibilidad 3 = No hay un
elemento máximo de A ni un elemento
mínimo de B.*
*MINIINTERPOLACIÓN
Respecto a que estas sean las únicas
tres opciones, probablemente ya puede
usted ver que no hay ningún modo en
que el conjunto B pueda tener jamás un
elemento máximo, porque B lo
contiene todo desde el schnitt hasta el
∞. Y la L de Dedekind es la recta real
y también incluye todos los racionales
extendiéndose hacia la izquierda desde
0, así que A lo contiene todo desde −∞
hasta el schnitt y no puede tener un
miembro mínimo. Pero en caso de que
se esté preguntando por qué no puede
haber una Posibilidad 4 en la cual haya
a la vez un miembro máximo a' de A y
un miembro mínimo b' de B, hay una
manera fácil de demostrar que esto no
es posible. Es una demostración por
reducción al absurdo, así que vamos a
suponer que existe un a' máximo y
también un b' mínimo. Pero esto
significa que existirá cierto número
racional, igual a
, que es a la vez
mayor que a' y menor que b', y, por lo
tanto, no puede ser miembro ni de A ni
de B. Pero A y B han sido definidos de
tal modo que juntos contienen todos los
números racionales. Por lo tanto, la
Posibilidad 4 es contradictoria.
Pero entonces, ¿por qué la
Posibilidad 3 no es contradictoria de la
misma manera?
DRAMÁTICO FINAL DE LA
MINIINTERPOLACIÓN
Enunciado
informalmente,
el
ejemplo de Dedekind para la
Posibilidad 3 es un schnitt cuyo
conjunto A contiene todos los números
racionales negativos y todos los
racionales positivos x tales que x2 < 2,
y cuyo conjunto B contiene todos los
racionales positivos x tales que x2 > 2.
Si se puede demostrar que ningún
número racional corresponde a este
schnitt, habremos definido cierto
número irracional, en este caso el
milenariamente
inconmensurable
√2.[6.14]
Ya hemos visto, en §2c, una
demostración de que √2 no es
racional.[6.15] Podríamos dormirnos en
estos laureles. Pero Dedekind no lo
hace, y proporciona su propia
demostración específica de que el
schnitt del ejemplo de la Posibilidad 3
no corresponde a ningún número
racional. Vamos a verla. Puede que
todos queramos respirar a fondo un
momento y relajarnos y estar muy
atentos. La de Dedekind es una
demostración por reducción al absurdo
y, por lo tanto, empieza suponiendo
que sí existe un racional x
correspondiente al schnitt de la
Posibilidad 3. Si ese x existe, entonces,
por la definición del conjunto A, o bien
x es el elemento máximo de A, o bien
es mayor que cualquier elemento de A
(o sea, que está en B). En todo caso,
cualquier número que sea mayor que x
(llamémosle x+) por definición va a
pertenecer con absoluta seguridad a B,
lo cual significa que (x+)2 debe ser > 2.
Entonces, si para cierto x podemos dar
un x+ mayor que x de tal modo que
(x+)2 < 2, la suposición inicial de que x
es racional quedará contradicha.
De modo que aceptemos las
anteriores especificaciones de x y x+, y
definamos cierto número positivo p
como igual a (2 − x2), y definamos x+
como igual a
. Esta última
definición puede parecer un poco
extraña, pero puede usted verificar
fácilmente
que
dadas
las
especificaciones originales y el valor
de p,
será mayor que x, de
modo que se mantiene la crucial
relación x+ > x. Ahora lo que queda de
la demostración son solo buenos y
viejos cálculos escolares:
(1) (x+)2 =
(2)
=
.
Como x es por definición mayor
que 1, x2 > x, de modo que
, y así
(3)
. Haciendo que 16 sea el
denominador común, se obtiene
(4)
. Como, por
definición,
p = (2 − x2),
entonces
claramente
x2 = (2 − p); así que por
sustitución la cantidad de (4) se
convierte en
(5)
, que
tras multiplicar constantes se
convierte en
(6)
, que
tras desarrollar el paréntesis del
2.º término da
(7)
,
lo
cual bastante obviamente se
reduce a
(8)
, lo cual es lo mismo
que
(9)
, cantidad que, al
ser
p>0
por
definición,
siempre va a ser < 2. Así,
mediante los pasos (1)-(9)
(destacando en particular los
pasos (1), (3) y (9)), hemos
determinado que
(10) (x+)2 <
< 2,
lo
cual, por la ley básica de la
transitividad, significa que
(11) (x+)2 < 2, que es precisamente
lo que necesitábamos para
contradecir la suposición inicial
de que el schnitt correspondía a
un racional x. Y esto quiere
decir que no corresponde a
ningún racional x. Q. E. D.
Dedekind,
justo
tras
la
demostración: «En esa propiedad de
que no todos los cortes son producidos
por números racionales consiste lo
incompleto o la discontinuidad del
dominio de todos los números
racionales» (ibíd., pág. 15, editado).
Pero esto no es ni la mitad del
asunto. El truco del schnitt permite que
los números irracionales se definan
completamente en términos de los
racionales, que es el único modo de
elaborar una teoría deductiva y 100%
rigurosa de los números reales. La
definición, en lenguaje asequible, es
que un número irracional es el valor de
un punto en el cual un schnitt divide la
R. N. en dos conjuntos A y B
bilateralmente
exhaustivos
que
respectivamente no tienen elemento
máximo o elemento mínimo.[6.16] Es
esta definición la que crea el continuo
—es decir, el conjunto de todos los
números reales— y transforma la recta
numérica en la recta real.[6.17] Lo que
es especialmente genial e ingenioso es
que la técnica de Dedekind usa
justamente lo que había hecho tan
misteriosos a los irracionales —su
correspondencia a puntos innominables
de la recta numérica— como parte de
su definición rigurosa.
§6d.
Por
supuesto, la teoría de Dedekind
también presupone la existencia de
conjuntos realmente infinitos. Más que
presuponer: mediante el truco del
schnitt, la definición formal de un
número real se convierte en «Cierto par
de conjuntos infinitos con ciertas
características particulares». Hay cierto
número de potenciales rarezas de las
que nos podemos dar cuenta en este
punto. En primer lugar, dada la larga y
muy documentada alergia de las
matemáticas a los ∞ reales, la teoría
de Dedekind bien podría verse
simplemente como la sustitución de
una cantidad de tipo indefinible por
otra, es decir, como invocar, para
fundamentar y definir los irracionales,
la idea oculta de no uno sino dos
conjuntos inimaginablemente enormes
y, aun así, precisamente ordenados,
cada uno de ellos infinito de algún
modo pero a la vez limitado muy
específicamente. Lo cual podría
chocarle una vez más como algo
demasiado parecido a Zenón. Si es así,
guárdese esa idea.
Segunda rareza: Si es usted
inusualmente atento e inmune al
aburrimiento, puede que ya haya
notado un sorprendente parecido entre
la teoría de Dedekind y lo de la
conmensurabilidad geométrica de
Eudoxo de Cnidos que vimos en §2d.
Con respecto a lo cual, por favor,
recuerde o revise §2d y vea que el
concepto de schnitt ahora ayuda a hacer
más claro cómo la definición por
Eudoxo de «razón» funciona para
designar números irracionales: el
número expresado por la razón
es
irracional (o sea, p y q son
inconmensurables) justo cuando, para
cualquier
número
racional
,
la
disyunción (ap < bq) o (ap > bq) es
cierta,[6.18] o sea ap ≠ bq. No hay aquí
acusación alguna de que Dedekind
plagiara a Eudoxo o ni siquiera de que
necesariamente supiera algo de él.
Véase, por ejemplo, el prefacio de «La
naturaleza y significado de los
números», en el cual Dedekind cita la
eudoxiana Definición 5 de los
Elementos sin ningún conocimiento
evidente de dónde la obtuvo Euclides.
Esta cita subraya la gran diferencia
entre Dedekind y Eudoxo, así como
entre las matemáticas griegas y el
análisis moderno:
[S]i uno contempla el número
irracional como la razón de dos
cantidades
mensurables,[6.19]
entonces esta manera [= la del
mismo
Dedekind]
de
determinarlo está ya descrita de
la
manera
más
clara
[6.20]
posible
en la celebrada
definición que da Euclides de la
igualdad de dos razones
(Elementos, V, 5) (ibíd.,
editado).
La diferencia está en la condición
inicial «Si… cantidades mensurables».
Eudoxo y Euclides eran (otra vez)
geómetras, y para ellos el problema de
los irracionales incluía magnitudes
geométricas
como
rectas/
áreas/volúmenes. Mientras que el
proyecto general de Dedekind (como,
de nuevo, el de Weierstrass mismo) es
huir de la geometría y fundamentar el
análisis totalmente en la aritmética.
[6.21]
Por esto, Dedekind dice una y otra
vez que la R. N. y los puntos
geométricos en su teoría del schnitt son
solo para entretenimiento. En realidad,
su antes mencionado prefacio contiene
una de las declaraciones más
conmovedoras jamás escritas sobre la
estética de la aritmetización, a saber:
«Aún me parece más bello que sin
ninguna
noción
de
cantidades
mensurables y simplemente mediante
un sistema finito de sencillos pasos del
pensamiento el hombre pueda avanzar
hacia la creación del dominio numérico
continuo puro» (ibíd., pág. 38
[puntuación sic]).
Por otro lado, si resulta correcto
decir que la intervención de conjuntos
realmente infinitos en una definición
matemática involucra solo «un sistema
finito de pasos del pensamiento» es una
cuestión justa, esto nos lleva de nuevo
al asunto que pusimos sobre la mesa
hace dos párrafos. Si resulta que usted
presenta objeciones al uso de conjuntos
infinitos en una definición rigurosa
porque le parece que tales conjuntos de
tipo
realmente
∞
son
matemáticamente
irreales/ilícitos,
entonces usted es, por supuesto, un
aristotélico/gaussiano y contará como
su defensor n.º 1 al profesor Leopold
Kronecker (1823-1891), que como se
ha mencionado fue una vez el mentor
de Georg Cantor y después su
archienemigo y la persona que algunos
historiadores piensan que más o menos
por sí sola le condujo a la locura, y
quien (= Kronecker) fue básicamente
el primer intuicionista de las
matemáticas, y que creía que solo los
enteros eran matemáticamente reales
porque solo ellos eran «claros a la
intuición», lo cual significaba que los
decimales,
los
irracionales
y
ciertamente los conjuntos infinitos eran
todos unicornios matemáticos. En la
historia de las matemáticas, la figura
de Kronecker a menudo se resume
mediante su máxima «Solo los enteros
son una creación de Dios; todo lo
demás es obra del hombre», del mismo
modo en que la figura de D’Alembert
queda resumida por «Siga adelante y la
fe vendrá», y la de Arquímedes, por
«¡Eureka!».[6.22] Veremos más de lo
que probablemente quiere usted oír
acerca de Leopold Kronecker y el
intuicionismo dentro de unos §. Por
ahora basta saber que así como
Weierstrass, Dedekind y algunos
colegas quieren eliminar la geometría
del análisis y basarlo todo en el sistema
de los números reales, Kronecker va
incluso más allá y quiere basar el
análisis solo en los enteros y en los
racionales expresados como razones de
enteros.
Así que volviendo ahora a la
objeción específica no-se-pueden-usarconjuntos-infinitos-en-una-definición a
la teoría de Dedekind de los números
reales. Hay por lo menos dos maneras
no triviales de responder a esto. La
primera es decir (de acuerdo con la
nota 21) que la teoría de Dedekind en
realidad no nos exige tratar conjuntos
infinitos en el sentido especial de
«tratar» descrito en §1. Estrictamente
hablando, la técnica del schnitt no
presupone ∞ reales más de lo que lo
hace
«
».
Lo
cual
equivale a decir que los conjuntos
infinitos A y B de la teoría de Dedekind
son
completamente
abstractos,
hipotéticos: no tenemos que contarlos
ni representarlos o ni siquiera pensar
en ellos más allá de saber que B > A y
decidir si existe un a' máximo, un b'
mínimo o ninguno.
Si esta respuesta no le emociona
demasiado y todavía le parece que todo
lo que la definición supuestamente
rigurosa de Dedekind está haciendo es
sustituir la imprecisión matemática de
los números irracionales por la de los
conjuntos infinitos, entonces es
oportuno indicar que coincidiendo con
la aparición de «Continuidad y
números irracionales», Cantor está
empezando a publicar trabajos que dan
precisión justo al tipo de conjuntos
realmente infinitos que Dedekind está
postulando. Como se insinuó en los § 1
y 4, la aparición casi simultánea de
Cantor y Dedekind en las matemáticas
es más o menos como lo de Newton y
Leibniz, una señal segura de que era el
«momento
adecuado»
para
los
conjuntos de tipo ∞. Igual de
impresionante es la manera escheriana
en que se superpone la obra de ambos
hombres.[6.23] Cantor es capaz de
definir y fundamentar los conceptos de
«conjunto infinito» y «número
transfinito», y de establecer técnicas
rigurosas para combinar y comparar
diferentes tipos de ∞, que es
justamente donde la definición de
Dedekind de los irracionales necesita
apuntalarse. Recíprocamente, la técnica
del schnitt demuestra que los conjuntos
realmente infinitos pueden tener
verdadera utilidad en el análisis. En
otras palabras, que por muy sensitiva y
cognitivamente abstractos que deban
permanecer, los ∞ a pesar de todo
pueden funcionar en las matemáticas
como abstracciones prácticas y no solo
como
extraños
divertimentos
paradójicos.[6.24]
También la coincidencia en el
tiempo es casi inquietante. Dedekind se
entera por primera vez de la existencia
de Georg Cantor el mes de marzo de
1872, cuando lee su obra «Über die
Ausdehnung eines Satzes aus der
Theorie
der
trigonometrischen
Reihen»[6.25] en una importante revista
mientras está dando los toques finales a
«Continuidad y números irracionales»,
en el último borrador del cual añade
una cita de Cantor y un «gracias de
corazón» a «este ingenioso autor» cuyo
artículo contiene una teoría de los
irracionales* que «… está de acuerdo,
aparte de la forma de la presentación,
con lo que designo como la esencia de
la continuidad» (Dedekind, pág. 3,
editado). Luego, más tarde ese mismo
año se conocen, por casualidad, cuando
están de vacaciones en Suiza. Chocan
el uno con el otro, literalmente. Cantor
es privatdozent en la Universidad de
Halle, y Dedekind da clases de
bachillerato
en
Brunswick.[6.26]
Congenian inmediatamente y empiezan
a cartearse, y muchos de los resultados
más significativos de Cantor se
desarrollan en esas cartas. Pero nunca
son auténticos colaboradores, y
aparentemente
tienen
un
gran
desacuerdo en 1880, cuando Cantor se
las arregla para conseguirle a Dedekind
una plaza de profesor en Halle y este la
rechaza (aunque deben de haberlo
resuelto con el tiempo si en 1899
tienen largas sobremesas tras comer
juntos). De nuevo, nos saltamos la
mayor parte de esas cosas personales.
§6e.
*INTERPOLACIÓN SEMI-SEI
La teoría de los irracionales de Georg
Cantor, que como se ha mencionado
está principalmente en el «Über […]
Reihen» de 1872, es a la vez
técnicamente compleja y, en definitiva,
menos relevante que el trabajo sobre
teoría de conjuntos del que forma
parte,[6.27] y dependiendo de su
cociente general
puede que
usted no quiera hacer más que echarle
una ojeada a la siguiente explicación,
que ocupa un complicado nicho
retórico y ha sido clasificada como
SEMI-SEI.
Cantor no está tan interesado en
definir los irracionales per se como en
desarrollar una técnica mediante la
cual pueda definir todos los números
reales, racionales e irracionales, del
mismo modo. En realidad, Cantor es el
primero que introduce en las
matemáticas la idea de un conjunto de
todos los números reales que
comprenda tanto a los racionales como
a los irracionales (a lo cual Dedekind,
por complicadas razones, se opone).
Obviamente, la teoría del propio
Cantor también depende de los
conjuntos infinitos, pero en este punto
para Cantor estos son más como
conjuntos infinitos de sucesiones
infinitas de números racionales. De
aquí viene, en parte, lo complejo de su
teoría. Otra parte es que Cantor quiere
usar la idea weierstrassiana de los
irracionales-como-límites
sin
el
problema de circularidad mencionado
en §6a, lo cual le conduce a usar
sucesiones convergentes en lugar de
series.
En concreto, para evitar la
circularidad de la definición de
Weierstrass, Cantor explota los hechos
de que (1) todos los números reales
pueden ser representados por decimales
infinitos (y los racionales tienen
decimales que o bien repiten
infinitamente su período básico (como
en la nota 10 de §6c), o bien acaban
con una infinidad de o seguidos o 9
seguidos (los cuales, recuperando el
rastro de la nota 35 de §2c, son
equivalentes, como cuando veíamos
que 0,999… = 1,000…), y que (2) los
decimales infinitos funcionan como
límites de fracciones decimales. (En la
escuela aprendió las fracciones
decimales: son la manera de hacer que
los chavales entiendan los decimales en
términos de fracciones, por ejemplo
0,15 =
+
+
. Aquí, pues,
tenemos otro caso en el cual el análisis
superior resulta estar en el fundamento
de la aritmética infantil: la regla
general es que cualquier decimal
infinito puede ser representado como la
serie infinita convergente a0100 +
a110−1 + a210−2 + a310−3 + … +
an10−n + …, serie que converge hacia
el decimal original, es decir, el decimal
es el límite/suma de la serie).[6.28]
Entonces, mediante un ingenioso
ejercicio de semántica matemática,
Cantor puede conseguir todo el botín
de los decimales observando, en la
línea de §5d, que el hecho de que una
sucesión cualquiera[6.29] de números
racionales converja equivale a que sea
representable mediante un decimal
infinito, el cual está, pues, definido
matemáticamente por la sucesión.
[SEI Si el anterior párrafo parece
sospechoso o enrevesado, podemos
reducir el argumento a un simple
silogismo: «Como (1) todos los
números son definibles mediante
decimales y (2) todos los decimales
son definibles mediante sucesiones, (3)
todos los números son definibles
mediante secuencias», lo cual resulta
ser 100% válido].
En definitiva, la idea básica de
Cantor es que una sucesión infinita de
números racionales define un número
real si la sucesión converge en el
sentido de que
(an+m − an) = 0
para
cualquier
m
arbitraria
(semiextractado de Kline, págs. 984985),[6.30] es decir, si la diferencia
entre
dos
términos
sucesivos
cualesquiera tiende a 0[6.31] al alejarnos
más y más por la sucesión (que por
supuesto es justo el modo en que los
decimales funcionan: en la posición
decimal n-ésima, valores sucesivos
pueden diferir a lo sumo en 10−n).
Cantor llama a las sucesiones que se
comportan de ese modo sucesiones
fundamentales, y lo que se conoce
como teoría de los números reales de
Cantor es que cada número real queda
definido mediante por lo menos una
secuencia fundamental.
Un par de potenciales objeciones en
este punto. Si a usted tal vez le choca
como algo circular o cuestionable que
Cantor defina «número real» como elque-es-definido-por-una-sucesiónfundamental —algo parecido a definir
«perro» como el-que-es-definido-porla-definición-de-«perro»—
entonces
tenemos que aclarar qué significa
exactamente «definir» en relación con
la teoría de Cantor. Básicamente
significa «es» o «es igual a». Es decir,
lo que permite que la teoría evite la
circularidad es que la sucesión
fundamental relevante es el número
real, del mismo modo que 0,15 es
Lim(0(100), 1(10−1), 5(10−2)) y una
función trigonométrica es su desarrollo
en serie convergente. Por otro lado,
como los números reales incluyen tanto
los irracionales como los racionales,
podría estar preguntándose si, y cómo,
las sucesiones fundamentales de
racionales de Cantor también pueden
definir números racionales, o si la idea
tiene sentido siquiera. La respuesta es
que tiene sentido y pueden hacerlo: la
estipulación de Cantor es que cuando
una sucesión fundamental a0, …, an, …
tiene todos los términos posteriores a
an iguales a x, la sucesión define (= es)
el número racional x.[6.32]
Para hacer verdaderamente viable
su teoría, Cantor todavía tiene que
demostrar cómo deducir propiedades
aritméticas y realizar operaciones
básicas
con
sus
sucesiones
fundamentales y los números reales
que estas definen. A continuación,
veremos un par de ejemplos de las
demostraciones de su artículo, donde
nuestros números reales relevantes son
aquí x e y:
(A) Como resulta que se puede
definir el mismo número real x
mediante más de una sucesión
fundamental,[6.33] la regla de
Cantor es que dos sucesiones
fundamentales a0, a1, a2, … y
b0, b1, b2, … definen el mismo
x si y solo si |an − bn| se
aproxima[6.34] a 0 cuando n
tiende a ∞.
(B) Para demostrar que se pueden
hacer
las
operaciones
aritméticas
básicas,
supongamos que an y bn son
sucesiones fundamentales que
definen x e y, respectivamente.
Cantor demuestra (en una orgía
de simbolismo ultratecnificado
que estamos omitiendo) que
(an ± bn) y (an × bn) son
también
sucesiones
fundamentales, definiendo así
los números reales x ± y y
x × y. En su demostración de
que
es
una
sucesión
fundamental que define
, la
única restricción es que x
obviamente no puede ser 0.
Por último, puede que haya visto
usted otra objeción potencial. Una
bastante fea. Y quizás el aspecto más
impresionante de la teoría de Cantor de
los
reales-mediante-sucesionesfundamentales —y por lo que
Dedekind le llama ingenioso— es el
modo en que Cantor evita esa objeción,
del tipo de las RIV letales, ante la cual
su teoría parece vulnerable al principio.
Pues si sucesiones fundamentales de
números racionales definen números
reales, ¿qué hay de las sucesiones
fundamentales de números reales (=
tanto racionales como irracionales)? Se
pueden construir fácilmente sucesiones
de números reales que convergen según
las especificaciones de Cantor: varios
tipos de series trigonométricas ya lo
hacen. ¿Necesitamos crear toda una
clase completamente nueva de números
para que funcionen como límites de
esas sucesiones de números reales? Si
es así, entonces necesitaremos otra
clase más para los límites de
sucesiones fundamentales de esos
nuevos números, y luego otra más… y
allá vamos: será el Tercer Hombre de
Aristóteles otra vez. Solo que Cantor lo
elude demostrando[6.35] el siguiente
teorema: si rn es una secuencia de
números
reales
tal
que
(rn+m − rn) = 0 para un m
arbitrario —es decir, si rn es una
sucesión fundamental de números
reales bona fide— entonces existe un
número real único r, definido por una
secuencia fundamental an de números
racionales, tal que
rn = r. En otras
palabras, Cantor es capaz de demostrar
que los propios números reales pueden
servir como límites de las sucesiones
fundamentales de números reales, de
modo que su sistema de definiciones es
autocontenido y a prueba de RIV.
§6f.
Como
se insinuó vagamente en §6d,
las teorías de Dedekind y Cantor entran
en conflicto con una más de las
doctrinas kroneckerianas, a menudo
conocida como constructivismo, que se
convertirá en una parte muy importante
del
intuicionismo
y
de
las
controversias
acerca
de
los
fundamentos filosóficos de las
matemáticas desatadas por la teoría de
conjuntos.[6.36] Todo esto se vuelve
muy pesado y complicado, pero es
importante. Aquí están los principios
básicos del constructivismo tal como
los practicó Kronecker y los
codificaron Jules-Henri Poincaré y
Luitzen Egbertus Jan Brouwer y otras
figuras destacadas del intuicionismo:
(1) Cualquier enunciado o teorema
matemático que sea más complicado o
abstracto que la aritmética de los
enteros de toda la vida debe ser
explícitamente derivado (es decir,
«construido») de la aritmética de los
enteros mediante un número finito de
pasos puramente deductivos. (2) Las
únicas demostraciones válidas en
matemáticas son las constructivas, y
aquí el adjetivo significa que la
demostración proporciona un método
para encontrar (es decir, «construir»)
cualesquiera
entes
matemáticos
involucrados en ella.[6.37]
Respecto a la metafísica de las
matemáticas, el constructivismo es, por
lo tanto, directamente opuesto al
platonismo: con la excepción quizá de
los enteros, las verdades matemáticas
no existen fuera de la mente humana.
De hecho, desde el punto de vista de
Kronecker y sus seguidores, decir que
cierto ente matemático «existe» es
decir literalmente que puede ser
construido con lápiz y papel por seres
humanos reales durante el tiempo del
que, siendo mortales, pueden disponer.
Puede usted ver, entonces, que los
constructivistas van a tener serios
problemas con los teoremas y las
demostraciones que involucran el ∞,
los conjuntos infinitos, las sucesiones
infinitas, etc., particularmente cuando
esas
cantidades
infinitas
son
explícitamente
presentadas
como
reales. Respecto a los schnitts de
Dedekind,
por
ejemplo,
los
constructivistas obviamente van a
ponerse nerviosos desde el principio.
No solo los irracionales no existen
realmente, y no solo Dedekind usa la
reducción al absurdo para demostrar
que algunos schnitts no corresponden a
números racionales. También está todo
el problema de definir un número en
términos de conjuntos infinitos de
otros números. Por ejemplo, Dedekind
ni siquiera especifica nunca las reglas
matemáticas mediante las cuales
obtiene los conjuntos A y B.
Simplemente dice que si la recta
numérica se puede dividir en A y B…,
sin dar ningún método o procedimiento
mediante el cual uno pueda construir
realmente estos conjuntos (conjuntos
que de todos modos no pueden
construirse o verificarse realmente),
estonces son infinitos. Y ya que
estamos, ¿qué es exactamente un
«conjunto», técnicamente hablando, y
cuál es el procedimiento para construir
uno? Y así sucesivamente.
Esta última pregunta compuesta de
los constructivistas (y admitamos que
Dedekind no la puede contestar)[6.38]
nos muestra un buen ejemplo del genio
particular de Georg Cantor Jr. y de por
qué merece el título de padre de la
teoría de conjuntos. Recuerde la
mención en §3c de cómo Cantor tomó
lo que se había considerado como una
característica paradójica y totalmente
intratable del ∞ —concretamente que
un conjunto/clase/agregado infinito
puede ponerse en correspondencia uno
a uno con su propio subconjunto— y la
transformó en la definición técnica de
conjunto infinito. Observe cómo hace
lo mismo aquí, convirtiendo lo que
parecían devastadoras objeciones en
criterios rigurosos, al definir un
conjunto S como cualquier agregado o
colección de entes discretos que
satisfaga dos condiciones: (1) S puede
ser considerado por la mente como un
agregado, y (2) Hay alguna regla o
condición enunciada mediante la cual
uno puede determinar, para una entidad
x cualquiera, si x es 0 no es un
elemento de S.[6.39]
Esta definición no aparece de
repente de la nada, está claro. Ahora
resulta apropiado recuperar cosas de
§5d sobre la convergencia y la
representabilidad
de
las
series
trigonométricas, el
teorema de
localización de Riemann, etc., para ver
de dónde sale realmente el trabajo de
Cantor sobre los irracionales y los
conjuntos.
7
§7a.
Esta sección incluso tiene epígrafes:
La teoría moderna del infinito
evolucionó de un modo contiguo
a partir de las matemáticas que la
precedieron.
SHAUGHAN LAVINE, pág. 41
Pero los no iniciados pueden
preguntarse cómo es posible
tratar con un número que no
puede contarse.
BERTRAND RUSSELL,
Mysticism and Logic, pág. 82
Pónganse todos los cinturones
por favor, porque estamos a punto
de subir por una pendiente muy
pronunciada.
E. ROBERT GORIS
Por
razones que a estas alturas
resultarán familiares, gran parte de lo
que sigue va a ir realmente rápido.
También es algo duro al principio,
pero, como ocurre con buena parte de
las matemáticas puras, se vuelve más
fácil al profundizar. Como ya se ha
mencionado, Cantor estudia en Berlín
bajo la responsabilidad de Weierstrass
y de Kronecker; sus primeros artículos
publicados son trabajos bastante
estándares sobre ciertos problemas en
teoría de números.[7.1] Obtenido el
doctorado, Cantor consigue un modesto
trabajo como privatdozent (lo cual
parece ser un extraño tipo de asistente
académico por libre)[7.2] en la
Universidad de Halle, y allí conoce a
un tal Eduard Heinrich Heine (18211881), un especialista en análisis
aplicado que había hecho importantes
trabajos sobre el calor, particularmente
sobre la ecuación de potencial.[7.3] En
todo caso, hacia 1870, Heine pertenece
al gran grupo de matemáticos que
trabajan en las series de Fourier y los
problemas planteados por el artículo de
Riemann
«Sobre
la
representabilidad…», y aparentemente
él (= Heine) consigue que Cantor se
interese por lo que se había llegado a
conocer como el problema de la
unicidad: si cualquier f(x) dada puede
ser representada por una serie
trigonométrica,
¿es
dicha
representación única, es decir, hay una
sola serie trigonométrica que puede
hacerlo? El propio Heine había sido
capaz de demostrar la unicidad solo
con la condición de que la serie
trigonométrica
relevante
fuera
uniformemente convergente.[7.4] Lo
cual,
claramente,
no
era
suficientemente bueno, pues hay
muchas series trigonométricas e
incluso series de Fourier que no son
uniformemente convergentes.
En 1872, el artículo de Cantor
«Sobre la extensión de una proposición
de
la
teoría
de
series
trigonométricas»[7.5]
define
y
demuestra un teorema de unicidad
mucho más general que no solo no
requiere la convergencia uniforme,
sino que permite excepciones a la
convergencia en una infinidad de
puntos, suponiendo que esos puntos
excepcionales[7.6] estén distribuidos de
un modo específico.
Como veremos, la forma precisa de
esta
distribución
es
bastante
complicada, como lo es el propio
teorema de 1872, que en realidad
Cantor ha desarrollado a lo largo de
varios artículos previos y apéndices
publicados a los mismos, pues su
criterio de unicidad evolucionó
gradualmente de requerir que la serie
trigonométrica dada fuera convergente
para todos los valores de x, a permitir
un
número
finito
de
puntos
excepcionales, hasta el teorema de
unicidad definitivo, en una forma 100%
general. Lo interesante es que es el
profesor Leopold Kronecker quien
ayuda a Cantor a refinar y simplificar
varios aspectos iniciales de su
demostración. Al mismo tiempo, el
enfoque de Cantor está profundamente
influido por el trabajo de Weierstrass
sobre la continuidad y la convergencia,
por ejemplo, la observación de que una
serie trigonométrica general de la
forma
f(x) = + ∑(an sen nx + bn cos nx)
debe ser uniformemente convergente
para ser integrable término a termino
(que era el modo en que Heine y todos
los demás habían intentado atacar el
problema de la unicidad). Los
historiadores han observado que las
relaciones
Cantor-Kronecker
se
enfriaron y que las cartas de Kronecker
se volvieron cada vez más críticas
cuando los refinamientos que hacía
Cantor del teorema de unicidad
empezaron a admitir infinitos puntos
en los cuales se podían permitir
excepciones a la representación de la
f(x) dada o a la convergencia de la
serie.[7.7] En cada sucesiva versión de
la
demostración,
Kronecker
básicamente veía a Cantor alejarse de
su
propia
postura
algebraica
constructivista de la teoría de
funciones
hacia
una
más
weierstrassiana. La apostasía fue
completa cuando el artículo definitivo
de 1872 fue publicado y toda su
primera parte estaba dedicada a la
teoría de los irracionales/reales
detallada en §6e.
Entender por qué precisamente
necesitaba una teoría coherente de los
irracionales es una manera tan buena
como cualquier otra de ver cómo el
trabajo de Cantor en el teorema de
unicidad le llevó a estudiar los
conjuntos infinitos per se. La
discusión, que se va complicando,
requiere que usted recuerde la regla del
teorema de Bolzano-Weierstrass según
la cual todo conjunto infinito y acotado
de puntos contiene por lo menos un
punto límite, y, por lo tanto, claro está,
también qué es un punto límite.[7.8]
Además, debe tener en cuenta que los
conceptos centrales de la demostración
de la unicidad se refieren todos a la
recta real (es decir, cuando se usan
términos como «conjunto de puntos» o
«punto excepcional» o «punto límite»,
en realidad se refieren a puntos
geométricos que corresponden a
números).[7.9] Por favor, observe
también que los «conjuntos infinitos
acotados de puntos» bajo consideración
tanto en el T. B. W. como en la
demostración de Cantor son en realidad
sucesiones, que son también las
entidades más sencillas respecto a las
cuales entender los puntos límite: por
ejemplo, el conjunto infinito de puntos
de la recta numérica {0, , ,
,
,
, …}[7.10] tiene como punto límite el
mismo
que es el límite de la sucesión
infinita 0, , ,
,
,
,…
O sea, que aquí vemos cómo Cantor
consigue su resultado cada vez más
general. Al principio (1870) necesita
una serie trigonométrica que no sea
uniformemente convergente[7.11] pero
que sea convergente en cualquier
punto, o sea convergente para todos los
valores de x. En el siguiente paso
(1871)[7.12] es capaz de demostrar que
si
dos
series
trigonométricas
aparentemente distintas convergen
hacia la misma función (arbitraria) en
todas partes excepto en un número
finito de puntos, en realidad son la
misma serie. Vamos a omitir esta
demostración porque lo realmente
pertinente es lo siguiente, que es el
resultado de 1872 donde Cantor puede
permitir un número infinito de puntos
excepcionales y, aun así, consigue
demostrar que las dos series
trigonométricas representativas son en
definitiva idénticas.[7.13] Su manera de
hacerlo es mediante la introducción del
concepto de conjunto derivado, cuya
definición es básicamente: si P es un
conjunto de puntos (o sea, cualquier
conjunto de puntos-números reales,
aunque en lo que obviamente está
pensando Cantor es en el conjunto
infinito de puntos excepcionales entre
las dos series trigonométricas),
entonces el conjunto derivado de P,
llamado P', es el conjunto de todos los
puntos límite de P. O más bien
deberíamos decir que P' es el primer
conjunto derivado de P, porque
mientras los conjuntos de puntos
relevantes sean infinitos, el proceso
entero
es,
en
principio,
indefinidamente iterable: P'' es el
conjunto derivado de P', P''' es el
conjunto derivado de P'', y así
sucesivamente, hasta que tras (n − 1)
iteraciones tendremos Pn como el
n-ésimo conjunto derivado de P. En la
explicación del teorema de unicidad
dada anteriormente, en lo que se centra
el criterio «suponiendo que estos
puntos excepcionales se distribuyen de
cierto modo específico» es en este
n-ésimo conjunto derivado Pn, siendo
la cuestión vital si Pn es infinito o no.
Las verdaderas matemáticas que
hay detrás de todo esto incluyen partes
extremadamente técnicas sobre el
comportamiento de los puntos límite,
pero esencialmente aquí estamos
viendo cómo funciona lo de la
distribución-de-puntos-excepcionales
en
el
teorema
de
unicidad.
Probablemente,
otra
inspiración
profunda no le vendría mal para
afrontar lo que viene.[7.14] Postulemos
un conjunto infinito de puntos P tal
que, para algún n finito, el
(n − 1)-ésimo conjunto derivado de P,
P(n−1) es infinito mientras que su nésimo conjunto derivado Pn es finito.
Entonces, si dos series trigonométricas
convergen a la misma f(x) excepto en
algunos o todos los puntos de P, son la
serie equivalente: así, la unicidad
queda demostrada. Probablemente, esto
no le ha resultado cegadoramente claro
y luminoso. La parte que resulta crucial
desarrollar es el requerimiento de que
Pn sea finito. Y para explicar eso
tenemos que introducir otra distinción:
cualquier conjunto P para el cual su
conjunto derivado Pn es finito para
algún n finito es lo que Cantor llama un
conjunto de primera especie, mientras
que, si Pn no es finito para ningún valor
finito de n, entonces P es un conjunto
de segunda especie. (Por eso el proceso
de obtener conjuntos derivados fue
descrito antes como «en principio»
indefinido; son solo los conjuntos de
segunda especie los que nunca dan
lugar a conjuntos derivados finitos y,
por lo tanto, permiten ∞ iteraciones
del proceso).
En definitiva, he aquí la razón por
la cual Cantor, en su demostración del
T. U., necesita que el conjunto infinito
de puntos excepcionales original P sea
un conjunto de primera especie, y, por
lo tanto, que Pn sea finito. Esto es así
porque, mediante el teorema de los
valores extremos de Weierstrass, se
puede demostrar con seguridad que si
cualquier conjunto derivado Pn es
finito, entonces en algún punto n + k
más adelante el conjunto derivado
P(n+k) va a tomar su valor mínimo
absoluto m, que en este caso será 0, o
ningún punto límite en absoluto. Lo
cual, en otras palabras, significa que
tan pronto como la progresión P', P'',
P''', …, Pn, … llega a un conjunto
derivado finito, sabemos que todo el
proceso iterativo va a detenerse en
algún lugar: acabará llegándose a un
P(n+k) sin elementos. Y, por supuesto,
sabemos que los elementos de todos
estos diversos P' y P'' son puntos
límite, y sabemos también, por el
teorema de Bolzano-Weierstrass, que
cualquier conjunto infinito acotado
tiene, por lo menos, un punto límite. Si
P(n+k) no tiene elementos, entonces el
conjunto del cual es el conjunto
derivado no tiene punto límite, y, por
lo tanto, según el T. B. W. él mismo
tiene que ser finito, y ahora por el
T. V. E. su número de elementos debe
tomar en algún punto su propio valor
mínimo de o elementos, y en ese
mismo punto el conjunto del cual este
es el conjunto derivado resulta que
debe ser finito, y así sucesivamente
hacia atrás pasando por los P(n+k) y Pn
y P(n−1) y P’…, lo cual significa —
simplificando mucho— que en algún
momento puede demostrarse que las
dos
series
trigonométricas
representativas se confunden en una
sola serie, estableciendo la unicidad.
Sin embargo, recordará de los §5e y
6e, que para funcionar al 100% en
todos los casos el teorema de los
valores extremos requiere una teoría de
los números reales, y que la versión
weierstrassiana de tal teoría era (como
Cantor mismo demostró) muy precaria.
Esta es una razón por la que la
demostración de Cantor de 1872
necesita su propia teoría de los
números reales. La segunda razón,
relacionada con la primera, es que para
usar el teorema de BolzanoWeierstrass más general para construir
su teoría de conjuntos derivados y
especies, Cantor necesita reconciliar
las propiedades geométricas de los
puntos en el continuo de una recta —en
el sentido de conceptos como «punto
límite», «intervalo», etc.— con el
continuo aritmético de los números
reales, ya que, por supuesto, las
entidades involucradas en el análisis
son en realidad números y no
puntos.[7.15]
Si observamos que los conjuntos
derivados de Cantor se parecen a la
idea general de un subconjunto y que el
hecho de que el valor mínimo del
número de elementos de P(n+k) = 0 es
esencialmente lo mismo que la
definición del conjunto vacío, es
posible distinguir las semillas de lo que
ahora se conoce como teoría de
conjuntos[7.16] en la demostración de la
unicidad de Cantor. Los conjuntos
derivados, el continuo de la recta
real/continuo de los números reales y
el teorema de unicidad son también los
«progenitores» de las matemáticas
transfinitas de Cantor, aunque de un
montón
de
maneras
bastante
complicadas. Acabamos de ver que el
P'' del teorema de unicidad requiere
que n sea finito, es decir, que Cantor
usa solo iteraciones finitas del proceso
conjunto-derivado-del-conjuntoderivado en su demostración. Sin
embargo, como ya hay tantos conjuntos
infinitos flotando alrededor de la
demostración (por ejemplo: el P
original es infinito, y todos los P' y P''
y así hasta P(n−1) pueden ser infinitos,
y
por
supuesto
las
series
trigonométricas relevantes son series
infinitas, sin olvidar que los puntos
límite involucran un número infinito de
puntos intraintervalo, y que dichos
intervalos pueden ser, ellos mismos,
infinitesimalmente
pequeños),
no
debería sorprendernos que Cantor
empiece a considerar más de cerca las
características de sus conjuntos
derivados bajo infinitas iteraciones
(descaradamente extractado de Lavine,
págs. 40-41).
En concreto, Cantor empieza a
preguntarse si la infinitud de un
conjunto derivado de segunda especie
infinitamente iterado P∞ podría diferir
de la infinitud del conjunto de primera
especie finitamente iterado o excederla
de algún modo. Más específicamente
aún, se da cuenta del gran parecido de
esas cuestiones con aquella otra acerca
de las relativas infinitudes de los
números racionales de la R. N. y de los
números reales de la R. R. Esta última
cuestión concierne al problema
discutido hace mucho en §2c. A saber:
mientras que los números racionales
son a la vez infinitos e infinitamente
densos, no son continuos (es decir, la
recta numérica está plagada de huecos),
mientras que, por supuesto, tanto
Dedekind como Cantor ahora han
demostrado la continuidad del conjunto
de todos los números reales tal como se
esquematizan en la R. R. Así, a Cantor
—quien para el T. U. ya ha
desarrollado técnicas para examinar
tanto los números reales como los
racionales y las propiedades de los
conjuntos infinitos— le parece
natural[7.17] preguntarse si el conjunto
infinito de todos los números reales es,
en cierto modo, mayor que el conjunto
infinito de todos los números
racionales. Pero ¿qué significaría aquí
«mayor»? Y lo mismo para «exceder»
en la anterior cuestión acerca de P∞ y
P(n−1), es decir, ¿cómo se pueden
describir y explicar matemáticamente
los tamaños comparativos de diferentes
∞? Llegados a este punto, en las
inmortales palabras de Gleason…
INTERPOLACIÓN
ADMINISTRATIVA
Ahora hay un par de cuestiones de
procedimiento que deben abordarse.
Varios volúmenes muy eruditos están
enteramente dedicados a los logros de
Cantor.[7.18] Puede usted asistir a un
curso de dos trimestres de teoría de
conjuntos en un departamento de
Lógica, Matemáticas, Filosofía o
Informática Teórica[7.19] y, aun así,
solo habrá rascado el barniz.
Históricamente,
las
teorías
y
demostraciones transfinitas de Cantor
se extienden a lo largo de veinte
años[7.20] y docenas de diferentes
artículos, a menudo con refinamientos
sucesivos y rectificaciones a materiales
anteriores, de modo que a veces hay
más de una versión de la misma
demostración. Está claro que aquí va a
ser
imposible
desarrollar
completamente
las
matemáticas
transfinitas o hacer verdadera justicia a
su evolución en las publicaciones de
Cantor.[7.21] Por otro lado, hay ciertos
libros populares recientes que dan
explicaciones tan superficiales y
reduccionistas de las demostraciones
de Cantor (explicaciones que, como se
ha
mencionado,
suelen
estar
subordinadas
a
una
narrativa
prometeica más amplia acerca de los
problemas psíquicos de Cantor o su
supuesta afiliación mística) que las
matemáticas quedan distorsionadas y
su belleza oscurecida, y obviamente
tampoco queremos hacer esto.
Así que el Alto Mando decide: el
compromiso de aquí en adelante será
sacrificar el orden cronológico y cierta
meticulosidad en el desarrollo a favor
de la meticulosidad conceptual y la
cohesión; es decir, presentar los
conceptos, teoremas y demostraciones
de Cantor de un modo que subraye sus
relaciones entre ellos y con las
matemáticas per se. Esto implicará no
solo omitir algunas cosas, sino a
menudo no decir que se están
omitiendo, o que a veces hay varias
versiones
diferentes
de
una
demostración dada y solo se explica la
mejor, o cuáles son las fechas exactas y
los títulos, traducidos o no, de todos los
artículos relevantes,[7.22] etc. También
implica
cierto
glosario
de
emergencia III especial de teoría de
conjuntos, aunque este G. E. tendrá que
administrarse gradualmente e in situ
porque parte del material es
simplemente demasiado abstracto para
introducirlo de entrada sin contexto.
FIN DE LA INTERPOLACIÓN
ADMINISTRATIVA
§7b.
Como
debería ser evidente, algunas
ideas muy importantes relacionadas
con el ∞ salen de la demostración del
T. U. general. Una de ellas concierne a
los tamaños relativos del conjunto de
todos los números racionales y del
conjunto de todos los números reales.
Otra es si la continuidad de la recta real
está relacionada de algún modo con el
tamaño/composición de este último. Y
otra idea es el concepto de número
transfinito, el cual Cantor obtiene a
partir de las mismas consideraciones
que le llevaron a distinguir conjuntos
infinitos de primera y de segunda
especie en la demostración de 1872.
Para ver cómo Cantor concibe y
genera sus números transfinitos, en
primer lugar necesitamos asegurarnos
de que algunos términos de teoría de
conjuntos que probablemente vio en la
escuela están claros por lo menos al
nivel de un G. E.[7.23] A saber: el
conjunto A es un subconjunto del
conjunto B si y solo si no hay ningún
elemento de A que no sea elemento de
B. La unión de dos conjuntos A y B es
el conjunto de todos los elementos de A
y todos los elementos de B, mientras
que la intersección de A y B es el
conjunto de solo aquellos elementos de
A que también son elementos de B. La
unión y la intersección se representan
normalmente mediante ∪ y ∩,
respectivamente. Por último, el
conjunto vacío de toda la vida, cuyo
símbolo habitual es ∅, es un conjunto
sin elementos. Y sepa que, en virtud de
lo que a primera vista parece solo una
rareza de la definición de subconjunto,
en cualquier circunstancia todo
conjunto siempre tendrá ∅ como
subconjunto. Fin del primer fragmento
in situ del G. E. III. Además, ahora
debe usted recordar lo de los conjuntos
de puntos de primera y segunda especie
del anterior §. En realidad también hay
algunos tecnicismos relacionados con
los criterios para distinguir conjuntos
«densos» y «densos en cualquier
punto» que estamos omitiendo, pero
esencialmente el modo en que Cantor
concibe y genera los números
transfinitos es este:[7.24]
Supongamos que P es un conjunto
de puntos infinito de segunda especie.
Cantor demuestra que el primer
conjunto
derivado,
P',
puede
«descomponerse»[7.25] en la unión de
dos subconjuntos diferentes, Q y R,
donde Q es el conjunto de todos los
puntos pertenecientes a conjuntos
derivados de P' de primera especie, y R
es el conjunto de los puntos que
pertenecen a todo conjunto derivado de
es decir, R es el conjunto de aquellos
puntos que todos los conjuntos
derivados de P' tienen en común. Por
qué no detenerse un segundo y leer esa
última frase de nuevo.[7.26] R es la
parte importante, y es en realidad como
Cantor define por primera vez la
«intersección» de conjuntos, aquí
mediante la sucesión infinita de
conjuntos derivados P', P'', P''', …
(siendo la sucesión infinita porque P es
un conjunto de segunda especie). A
diferencia de nuestro ∩, el símbolo de
Cantor para la intersección es un
extraño
ultracursivo. (De nuevo, no
vamos a hacerlo todo con tanto
detalle). Así, la definición oficial de R
es: R =
(P' P'', P''', …), que, junto a
la definición de «conjunto de segunda
especie», permite decir que las
siguientes dos afirmaciones son
ciertas:
(1) R =
(P(2), P(3), P(4), P(5), …)
…
(2) R =
(P(n), P(n+1), P(n+2),
P(n+3), …). [7.27]
MINIINTERPOLACIÓN
INCRUSTADA
Las afirmaciones (1) y (2) juntas
constituyen en realidad un tipo de
demostración, tan famosa como la
reducción al absurdo. Esta se llama
inducción matemática. Para demostrar
algún enunciado Cn para todos (n = ∞)
los
casos
mediante
inducción
matemática, primero (a) se demuestra
que C1 es cierto en el primer caso
n = 1, luego (b) se supone que Ck es
cierto en los primeros k casos (usted no
sabe qué número es k, pero a partir del
paso (a) sabe que existe: por lo menos
es 1), y entonces (c) se demuestra que
Ck+1 es cierto en los primeros (k + 1)
casos. Por extraño que parezca, los
pasos (a)-(c) nos aseguran que Cn será
cierto independientemente del valor de
n, es decir, que C es un auténtico
teorema.
FIN DE LA MINIINTERPOLACIÓN
Lo que las afirmaciones (1) y (2) de
Cantor le permiten hacer es definir R,
obtenido a partir de P, como: R = P∞;
es decir, R es el ∞-ésimo conjunto
derivado de P. Y como (otra vez) P es
un conjunto de segunda especie, no hay
ninguna posibilidad de que P∞ = ∅, lo
cual significa que el propio P∞ dará el
conjunto derivado P∞+1, este último
dará el conjunto derivado P∞+2, y así
sucesivamente, solo que aquí «y así
sucesivamente» significa que podemos
seguir generando conjuntos derivados
infinitos de la forma abstracta[7.28]
v
v−1
p(n0∞ + n1∞ + … + nv). Y como la n y
la v de esta fórmula son variables,
Cantor puede construir la siguiente
sucesión infinita de conjuntos infinitos:
∞
P(n∞ ),
∞n
P(∞
∞+1
∞∞
),
P(∞
∞+n
),
P(∞
n∞
),
P(∞ ), P(∞ ), … De esta sucesión
dice: «Vemos aquí una generación
dialéctica de conceptos, que lleva más
y más lejos, y así se mantiene necesaria
en
sí
misma
y
libre
de
arbitrariedades»… (Cantor, Gessamelte
Abhandlungen, pág. 148, traducción
extractada de Grattan-Guinness, From
Calc to S.T., pág. 191) mediante lo cual
quiere decir que dichos «conceptos»
son
entes
matemáticos
reales
—números
transfinitos—
rigurosamente establecidos por el
teorema de Bolzano-Weierstrass, las
propias definiciones de Cantor de
«número real», «conjunto derivado» e
«intersección»,
y
la
inducción
matemática.
Si objeta usted (como hicimos
algunos de nosotros al doctor Goris)
que los números transfinitos de Cantor
no son realmente números en absoluto
sino más bien conjuntos, entonces dese
∞+n
cuenta de que, por ejemplo, «P(∞ )»
es realmente un símbolo del número de
elementos de un conjunto dado, del
mismo modo en que «3» es un símbolo
del número de elementos del conjunto
{1, 2, 3}. Y como los transfinitos son
demostrablemente distintos e, igual
que los enteros, forman una sucesión
ordenada infinita,[7.29] son realmente
números, simbolizables (por ahora)
mediante el bien conocido sistema de
Cantor de los alephs o ℵ.[7.30] Y, como
verdaderos números, los transfinitos
resulta que están sujetos a los mismos
tipos de relaciones y operaciones
aritméticas que los números normales,
aunque, tal como ocurre con el 0, las
reglas de dichas operaciones son muy
diferentes en el caso de los ℵs y tienen
que establecerse y demostrarse
independientemente.
[SEI No haremos mucho con ellos,
pero si tiene usted curiosidad, aquí
están algunos de los teoremas estándar
para la suma, la multiplicación y la
exponenciación
de
números
transfinitos,
todos
obtenidos
o
sugeridos por Cantor. (Observe, por
favor, que las sumas y/o los productos
de una cantidad infinita de términos no
tienen nada que ver con las
sumas/límites de series infinitas en el
análisis, series ahora consideradas,
pos-Cantor,
cuasi-infinitas).
Supongamos que n es cualquier entero
finito, y que tenemos dos números
transfinitos distintos, designados por
ℵ0 y ℵ1, siendo ℵ1 > ℵ0,[7.31] en cuyo
caso las siguientes afirmaciones son
todas verdaderas:
(1) 1 + 2 + 3 + 4 + … + n + … =
ℵ0
(2) ℵ0 + n = ℵ0
(3) ℵ0 × n = ℵ0
(4) ℵ0 + ℵ0 + ℵ0 + … = ℵ0 × ℵ0
= (ℵ0)2 = ℵ0
(5) ℵ1 + n = ℵ1 + ℵ0 = ℵ1
(6) ℵ1 × n = ℵ1 × ℵ0 = ℵ1
(7) ℵ1 + ℵ1 + ℵ1 + … = ℵ1 × ℵ0
= ℵ1
(8) ℵ1 × ℵ1 = (ℵ1)2 = (ℵ1)n =
(ℵ1)ℵ0 = ℵ1 (semiextractado de
Edwards, ν. 7, pág. 422)
Ν. Β. La sustracción y la división solo
son posibles en ciertos casos híbridos,
por ejemplo, para un n finito,
ℵ0 − n = ℵ0 ;
= ℵ0, no entre los
transfinitos per se. [De nuevo, esto no
es muy diferente de lo que ocurre con
la aritmética del 0]. Observe también
que el caso de los exponentes
transfinitos como 2ℵ0, 2ℵ1, etc., es
especial y se discute en detalle más
adelante. FIN DE SEI).
En caso de que se esté preguntando
qué tiene que ver todo esto con las
otras grandes cuestiones relacionadas
con el ∞, concretamente los infinitos
comparativos
de
los
números
racionales y los números reales, y el
papel de los irracionales en la
continuidad de la recta real, sepa que
uno de los argumentos favoritos de
Cantor a favor de la realidad de los
números transfinitos[7.32] es su
similitud matemática/metafísica con
los irracionales, los cuales ya han sido
definidos con éxito por Dedekind en
términos de conjuntos infinitos. Como
dice Cantor:
Los
propios
números
transfinitos son en cierto
sentido nuevos irracionales, y
de hecho pienso que la mejor
manera de definir los números
irracionales
finitos
es
enteramente
similar;[7.33]
podría incluso decir que en
principio es lo mismo que mi
método para introducir los
números
transfinitos.
Uno
puede aseverar absolutamente:
los números transfinitos tienen
la misma aceptabilidad que los
números irracionales finitos;
son parecidos en su naturaleza
más intrínseca; pues tanto los
unos como los otros son formas
definidas y delineadas o
modificaciones del infinito real
(Cantor, Gessamelte Ab., págs.
395-396, traducción extractada
de Dauben, GC, pág. 128,
editado. Todas las cursivas sic).
Lo que resulta interesante es que
esta declaración clara e inequívoca
aparece en el mismo «Contribuciones
al estudio de los transfinitos» donde
hace mucho, en §3a, vimos que Cantor
citaba a santo Tomás de Aquino y le
atribuía la objeción a los números
infinitos en cuanto conjuntos infinitos.
Sin embargo, el argumento n.º 1 del
propio Cantor a favor de los números
transfinitos —un argumento repetido
en varias formas desde 1874 hasta
finales de la década de 1890— es que
«su
existencia
se
confirma
directamente mediante la abstracción a
partir de la existencia de conjuntos
infinitos» (Cantor resumido por
Dauben, GC, pág. 127).[7.34] Así, el
objetivo fundamental del trabajo de
Cantor entre 1874 y 1884 es desarrollar
una teoría coherente y consistente de
los conjuntos infinitos, y observe, por
favor, el plural «conjuntos», porque
para que tal teoría no sea trivial tiene
que haber más de un tipo de conjunto
(en el sentido de tipo matemático, que
se refiere básicamente al tamaño)[7.35]
y algún conjunto de reglas para
evaluarlos y compararlos.
§7c.
Esto
obviamente se confunde con la
cuestión de si la continuidad de la recta
real significa que el conjunto infinito
de todos los números reales es de algún
modo > el conjunto infinito de todos
los números racionales. Para abreviar
una historia muy larga, el trabajo de
Cantor en este problema avanza más o
menos simultáneamente a su desarrollo
del material acerca de los conjuntos
derivados y los números transfinitos.
[7.36]
Veamos. Al intentar hallar algún
modo de comparar los tamaños de dos
conjuntos que son ambos infinitamente
grandes, Cantor da con el mismo
concepto que ahora se utiliza en la
escuela para definir la igualdad entre
dos conjuntos, concretamente la
correspondencia uno a uno, o «C1-1».
(En realidad «da con» no es muy
correcto, pues hemos visto tanto a
Galileo como a Bolzano usar la
correspondencia uno a uno para
establecer sus respectivas paradojas;
aunque tras la teoría de Cantor ya no
serían paradojas). La correspondencia
uno a uno es, como puede que usted ya
sepa, el modo de establecer si dos
colecciones son iguales sin necesidad
de contarlas. Los libros de texto usan
todo tipo de diferentes situaciones para
ilustrar
cómo
funciona
el
emparejamiento C1-1, por ejemplo, los
dedos en su mano derecha y de su
mano izquierda, el número de
asistentes y de asientos en un teatro
lleno, los platillos y las tazas de café de
un restaurante. El doctor Goris tenía su
propia analogía (hecha claramente a
medida de su audiencia), que incluía el
número de chicos y de chicas en un
baile. Todos buscan pareja para bailar y
la cuestión es si alguien se queda solo y
afligido, de pie, apoyado en la pared.
Ya coge la idea. Un par de definiciones
formales: hay una correspondencia uno
a uno entre los conjuntos A y B si y
solo si existe un método (que, desde un
punto
de
vista
técnico,
no
necesariamente tenemos que conocer
explícitamente) para emparejar los
elementos de A con los elementos de B
de modo que cada elemento de A esté
emparejado con exactamente un
elemento de B, y viceversa. Entonces,
por definición, los conjuntos A y B
tienen el mismo número cardinal (o
cardinalidad) si y solo si hay
realmente una C1-1 entre ellos.[7.37]
Ahora, para la siguiente definición
recuerde, por favor, cómo Galileo
generó su epónima paradoja en §1d.
También
ayudaría
recordar
la
definición formal de subconjunto del §
anterior. Un conjunto A es un
subconjunto propio de B si y solo si A
es un subconjunto de B y existe por lo
menos un elemento de B que no es
elemento de A.[7.38] Así, por definición,
todo conjunto es subconjunto de sí
mismo, pero ningún conjunto es
subconjunto propio de sí mismo.
¿Tiene sentido? Debería tenerlo, por lo
menos para conjuntos con un número
finito de elementos.
Pero lo que Georg Cantor postula
como característica formal definitoria
de un conjunto infinito es que tal
conjunto se pueda poner en C1-1 con al
menos uno de sus subconjuntos
propios. Lo que equivale a decir que un
conjunto infinito puede tener el mismo
número cardinal que un subconjunto
propio suyo, como en el caso descrito
por Galileo del conjunto infinito de
todos los enteros positivos y el
conjunto de todos los cuadrados
perfectos, el cual es subconjunto propio
de aquel y también un conjunto
infinito.
Esta característica hace que toda la
idea de comparar los «tamaños» de
conjuntos infinitos parezca muy rara,
pues, por definición, un conjunto
infinito puede tener el mismo tamaño
(o cardinalidad) que un conjunto que
por definición es más pequeño. Lo que
Cantor hace aquí[7.39] es tomar otro
ingrediente distinto de la paradoja de
Galileo y convertirlo en una
herramienta extremadamente poderosa
e importante para comparar conjuntos
de tipo ∞. Este es, si quiere seguir la
pista, su primer golpe de increíble,
escalofriante genio, aunque al principio
pueda no parecer gran cosa. Es la idea
de correspondencia uno a uno con el
conjunto de todos los enteros positivos,
o sea {1, 2, 3, …}. La razón por la que
esto es crítico es que el conjunto de
todos los enteros positivos puede, en
principio, ser contado,[7.40] o sea que es
posible decir «Aquí está el primer
elemento 1, y el siguiente es 2, y …»,
etc., aunque en la práctica el proceso
nunca termine. En todo caso, de aquí el
concepto de Cantor de numerabilidad:
un conjunto infinito A es numerable si
y solo si hay una C1-1 entre A y el
conjunto de todos los enteros
positivos.[7.41]
El conjunto de todos los enteros
positivos también establece una
especie de número cardinal base para
conjuntos infinitos. Es la cardinalidad
de este conjunto lo que Cantor
simboliza con su famoso «ℵ0».[7.42] La
idea es que las cardinalidades de otros
conjuntos infinitos se pueden evaluar
mediante ese cardinal base, es decir, se
pueden comparar con ℵ0 viendo si se
pueden poner en correspondencia uno a
uno con los enteros positivos. Aquí está
un ejemplo (no es de Cantor per se,
pero es un buen precalentamiento):
Considérese si el conjunto C de
todos los enteros positivos y el
conjunto D de todos los enteros
(incluyendo el 0 y los negativos) tienen
la misma cardinalidad. El problema es
que hay una diferencia crucial entre
estos dos conjuntos: C tiene un
primerísimo elemento (es decir, uno
más pequeño que todos los demás),
concretamente 1, mientras que D (que
es básicamente el conjunto {…, −n, …,
0, …, n, …}) no lo tiene. E
inicialmente es difícil ver cómo
podemos comprobar si hay una C1-1
entre dos conjuntos si uno de ellos no
tiene
un
primer
elemento.
Afortunadamente, de lo que estamos
hablando aquí es de la cardinalidad, la
cual no tiene nada que ver con el orden
específico de los elementos del
conjunto.[7.43] Así que podemos jugar
un poco con el orden del conjunto D de
tal modo que a pesar de no tener un
elemento mínimo sí tenga un primer
elemento, pongamos por caso el o. Y
este pequeño juego nos permite
establecer,
y
representar
esquemáticamente,
una
perfecta
correspondencia C1-1
(Bunch, pág. 115, sustancialmente
editado) que demuestra que C y D
tienen la misma cardinalidad. Observe
que a pesar de que nunca pueda
finalizarse literalmente el proceso de
emparejamiento
con
conjuntos
infinitos, mientras se pueda establecer
un
procedimiento
para
una
correspondencia uno a uno que
funcione para los casos primeros,
n-ésimo y (n + 1)-ésimo, se habrá
demostrado por inducción matemática
que la correspondencia funcionará en
toda la extensión de ambos conjuntos.
En el ejemplo anterior hemos
demostrado que el conjunto de todos
los enteros es numerable aunque sea
imposible contar la totalidad de sus
elementos.[7.44]
El
método
de
demostración es © Cantor, y lo
importante que debe verse es que una
vez más es capaz de tomar una
característica implícita de algo, aquí la
capacidad de la inducción matemática
para abstraer un ∞ de posibles casos a
partir de un número finito de
resultados,
y
hacerla
explícita,
rigurosamente aplicable a conjuntos
infinitos.
Entonces, ahora está claro cómo
Cantor puede hacer una comparación
de tamaños de los conjuntos infinitos
de todos los números racionales y de
todos los números reales:[7.45] puede
mirar si uno de ellos es numerable, o si
lo son ambos. Lo que sigue es una serie
de demostraciones muy famosas, la
mayoría
desarrolladas
en
la
correspondencia
con
Richard
Dedekind, publicadas en la década de
1870, y luego revisadas y ampliadas a
principios de la década de 1890.
Primero los racionales.[7.46] Cuando se
considera la densidad infinita que
Zenón había explotado meramente en
los racionales geométricos entre 0 y 1,
parece como si el conjunto de todos los
números racionales jamás pudiera ser
numerado. No solo carece de un
elemento mínimo, sino que ni siquiera
hay un siguiente elemento tras ningún
racional dado (algo de lo que hemos
visto dos demostraciones distintas). Sin
embargo, de lo que se da cuenta Cantor
es de que ignorando las «relaciones de
magnitud» (extractada de Courant y
Robbins, pág. 79) entre miembros
sucesivos, en realidad podemos
disponer el conjunto de todos los
racionales en una fila, algo así como la
fila de todos los enteros positivos, y en
esa fila habrá un primer elemento r1,
un segundo elemento r2, y así
sucesivamente. Resulta que el término
técnico que denota esto, colocar un
conjunto en fila de ese modo, es dar
una numeración del conjunto, y la fila
misma se llama la numeración del
conjunto, en el sentido de que aquí la
construcción válida de una fila
ordenada constituirá una demostración
de que el conjunto de todos los
racionales realmente es numerable (es
decir, que se puede poner en C1-1 con
el conjunto de todos los enteros, y, por
lo tanto, tiene la misma cardinalidad
que este). La construcción de Cantor, a
veces llamada incorrectamente su
«demostración
en
diagonal»,[7.47]
funciona más o menos así:
Como vimos en §6c, todos los
números racionales se pueden escribir
como el cociente de dos enteros . Así
que creamos una tabla 2D de esos ,
donde la fila horizontal superior
contiene todos los racionales de la
forma
(es decir, los enteros), y la
primera columna vertical contiene
todos los racionales de la forma , y un
racional dado
estará situado en la
q-ésima fila y la p-ésima columna, del
siguiente modo:
Está claro que una tabla 2D no es lo
mismo que la sucesión/fila única y
ordenada de una verdadera numeración,
pero Cantor se las ingenia para hallar
un orden en los racionales de la tabla
mediante una única línea continua en
zigzag, del siguiente modo: empiece en
1 y vaya una posición hacia el este
hasta 2; luego en diagonal hacia el
sudoeste hasta
hasta
; luego, hacia el sur
; luego, otra vez en diagonal
hacia el nordeste a la primera fila de
nuevo hasta 3; luego, al este hasta 4;
luego, al sudoeste todo el camino hasta
; al sur hasta ; nordeste hasta 5, y así
sucesivamente, como en:
Los puntos en la línea anterior
formarán la secuencia 1, 2, , , , 3, 4,
, , , , , , , 5, 6, , , , , , , ,
…, de la que podemos eliminar con
legitimidad todos los cocientes donde p
y q tienen un factor común, de modo
que cada número racional diferente
aparezca solo una vez en su forma más
básica.
Este
proceso
de
eliminación/reducción entonces da la
sucesión lineal 1, 2, , 3, 4, , , , , 5,
6, , , , , , , …, , …, , sucesión
que constituye la fila ordenada
necesaria para la numeración,[7.48] lo
cual significa que el conjunto de todos
los racionales es, en efecto, numerable
y, por lo tanto, tiene la misma
cardinalidad que el conjunto de los
enteros, o sea, el bueno y viejo ℵ0.
La verdadera demostración en
diagonal aparece en la respuesta de
Cantor a la cuestión de si el conjunto
de todos los números reales es > el
conjunto de todos los racionales. Ahora
debería ser obvio que la demostración
de Cantor involucrará la numerabilidad
de los números reales, es decir, si los
reales son numerables, entonces su
cardinalidad = la de los racionales, y si
no lo son, entonces los reales son > los
racionales. A grandes rasgos, la
demostración es una reducción al
absurdo,
y
su
método
de
diagonalización se considera ahora
como una de las técnicas de
demostración más importantes en toda
la teoría de conjuntos. Aquí deben
observarse dos cuestiones preliminares.
(1) La primera demostración de Cantor,
en 1873-1874 y con influencia de
Dedekind, de la no numerabilidad de
los reales involucraba límites de
sucesiones respecto a «intervalos
anidados» en la recta real y resultaba
enormemente
compleja.
Las
demostraciones que estamos haciendo
aquí son las versiones revisadas de
Cantor, de hacia 1890: son a la vez más
simples y más significativas que la
primera. (2) Observe una vez más en la
siguiente explicación cómo Cantor usa
la forma decimal de los números reales
y explota el hecho, visto en §2c, de que
0,999… = 1 para representar no solo
los irracionales sino todos los números
reales como decimales que no terminan
nunca: por ejemplo, como en
0,5 = 0,4999…, 13,1 = 13,0999…, etc.
Esta estrategia (que en realidad sugirió
Dedekind) asegura que hay solo una
representación lícita de cada decimal;
enseguida veremos por qué Cantor
necesita disponer los números reales de
ese modo.
Veamos la demostración. Como es
una reducción al absurdo, empezamos
suponiendo que el conjunto de todos
los números reales es, de hecho,
numerable; es decir, que se puede
disponer como una sucesión o fila
ordenada.[7.49] Esta sucesión consistirá
en una tabla infinita de decimales
infinitos, de la cual podemos mostrar
por lo menos el principio del siguiente
modo:
1.º Real = X1, a1a2a3a4a5a6a7…
2.º Real = X2, b1b2b3b4b5b6b7…
3.º Real = X3, c1c2c3c4c5c6c7…
4.º Real = X4, d1d2d3d4dsd6d7…
5.º Real = X5, e1e2e3e4e5e6e7…
6.º Real = X6, f1f2f3f4f5f6f7…
…
Y así sucesivamente…
En esta tabla, las X denotan
cualesquiera partes enteras anteriores a
las comas decimales, y las a, b, etc.,
representan las infinitas sucesiones de
dígitos tras las comas decimales. Y la
suposición de la demostración es que la
versión infinita de tal tabla será
exhaustiva de todos los números reales.
Esto significa que la contradicción
deseada para conseguir la reducción al
absurdo requiere demostrar que dicha
tabla en realidad no agota el conjunto
de todos los reales, lo cual requiere
hallar un número real que no esté —no
pueda estar— en la tabla.
Lo que la demostración en diagonal
de Cantor hace es generar justamente
tal número, al que podemos llamar R.
La demostración es a la vez ingeniosa y
bella: una total confirmación de la
presencia del arte en las matemáticas
puras. En primer lugar, eche otro
vistazo a la tabla. Podemos dejar que la
parte entera de R sea cualquier X que
queramos, no tiene importancia. Pero
ahora mire la primerísima fila de la
tabla. Vamos a asegurarnos de que la
primera cifra decimal de R, a, es
diferente a la a1 de la tabla. Es fácil
hacerlo incluso sin saber qué número
particular es a1: especifiquemos que
a = (a1 − 1) a menos que a1 resulte ser
0, en cuyo caso a = 9. Ahora mire la
segunda fila de la tabla, porque vamos
a hacer lo mismo con la segunda cifra
de R, o sea b: b = (b2 − 1), o b = 9 si
b2 = 0. Así es como funciona.
Seguimos el mismo procedimiento con
la tercera cifra de R, c, y la cifra c3 de
la tabla, con d y d4, con e y e5, y así
sucesivamente, ad infinitum. Aunque
no podemos construir R en su totalidad
(del mismo modo que no podemos
finalizar toda la tabla infinita), aún
podemos ver que este número real
R = X,abcdefghi…
va
a
ser
demostrablemente
diferente
de
cualquier número real de la tabla.
Diferirá del 1.er número real en su
primera cifra decimal, del 2.0 número
real en su segunda cifra decimal, del
3.er número real en su tercera cifra…
y, dado el método diagonal,[7.50]
diferirá del n-ésimo número real de la
tabla en su n-ésima cifra. Ergo R no
está —no puede estar— incluido en la
tabla infinita anterior; ergo, la tabla
infinita no es exhaustiva de todos los
números reales; ergo (por las reglas de
la reducción al absurdo), la suposición
inicial es rebatida y el conjunto de
todos los números reales no es
numerable, es decir, no se puede poner
en C1-1 con el conjunto de los enteros.
Y como el conjunto de todos los
números racionales sí se puede poner
en C1-1 con los enteros, la cardinalidad
del conjunto de todos los reales tiene
que ser mayor que la cardinalidad del
conjunto de todos los racionales.
Q. E. D.*
*INTERPOLACIÓN RÁPIDA DE
BOSQUE Y ÁRBOL
Demos
un
paso
atrás
y
reflexionemos solo por un segundo
acerca de lo estratosféricamente
abstracto que es todo esto. Y de por qué
la teoría de conjuntos, de la que se
puede decir que es la parte más
fundamental de las matemáticas
modernas, es también la más
alucinante. La teoría de conjuntos es
100% trivial mientras tratemos con
conjuntos finitos, porque todas las
relaciones entre dichos conjuntos se
pueden determinar de manera empírica,
basta contar sus elementos. En la teoría
de conjuntos de números reales,
estamos tratando con agregados
abstractos de entes abstractos tan
numerosos que jamás podrán ser
contados
ni
completados
ni
comprendidos siquiera… y, sin
embargo,
estamos
demostrando,
deductivamente y, por lo tanto, de
forma definitiva, verdades sobre la
disposición y las relaciones de tales
cosas. En el fragor de todas estas
demostraciones y explicaciones, es
fácil perder de vista la absoluta rareza
de los conjuntos infinitos, una rareza
que no queda para nada disminuida por
el hecho de que Cantor y Dedekind
demostraran que esos ∞ yacen en la
misma raíz de las matemáticas y son
necesarios para tratar algo tan básico
como una recta. A propósito de dicha
rareza, he aquí una bonita cita de los
filósofos Benacerraf y Putnam:
Están los conjuntos; bellos,
perennes,
multitudinarios,
intrincadamente conectados. No
trabajan ni hilan. Ni tampoco, y
ahí
está
el
problema,
interaccionan con nosotros de
ningún modo. Así que, ¿cómo
se supone que debemos tener
acceso epistemológico a ellos?
Responder: «por intuición», es
difícilmente
satisfactorio.
Necesitamos alguna explicación
de cómo podemos tener
conocimiento de esas criaturas
(Benacerraf y Putnam, pág.
410).
y una del duro intuicionista Jules-Henri
Poincaré:
Una realidad completamente
independiente del espíritu que
la concibe, la ve, o la siente, es
una imposibilidad. Un mundo
tan externo como este, incluso
si
existiera,
nos
sería
inaccesible
para
siempre
(Poincaré
extractado
Barrow, pág. 276).
por
y una refutación bastante deliciosa del
platonista Kurt Gödel:
A pesar de su remota lejanía de
la experiencia de los sentidos,
tenemos algo parecido a una
percepción también de los
objetos de la teoría de
conjuntos, como se ve por el
hecho de que los axiomas nos
obligan a reconocerlos como
ciertos. No veo ninguna razón
por la que deberíamos tener
menos confianza en este tipo de
percepción, es decir, en la
intuición matemática, que en la
percepción sensorial, la cual
nos induce a construir teorías
físicas y a esperar que las
percepciones sensoriales futuras
se ajusten a ellas… (Gödel,
«What is Cantor’s Continuum
Problem?», pág. 270).
FIN DE LA INTERPOLACIÓN Y REGRESO
A §7C EN EL PÁRRAFO DE LA PÁG. 236
CON ASTERISCO AL FINAL
Algunas cosas más respecto a esas
dos primeras demostraciones. (1)
Como el número cardinal de los
conjuntos numerables es ℵ0, parece
como si tuviera sentido denotar la
cardinalidad del conjunto de todos los
números reales mediante «ℵ1», pero,
por complicadas razones, Cantor llama
al cardinal de este conjunto c, o
también «la potencia del continuo»,
pues resulta ser la no numerabilidad de
los reales lo que explica la continuidad
de la recta real. Lo que esto significa es
que la infinidad de puntos involucrados
en la continuidad es mayor que la
infinidad de puntos comprendidos por
cualquier tipo de sucesión discreta,
incluso una infinitamente densa. (2)
Mediante su demostración en diagonal
de que c > ℵ0, Cantor ha logrado
caracterizar la continuidad aritmética
íntegramente en términos de orden,
conjuntos, numerabilidad, etc. Es decir,
la ha caracterizado 100% de manera
abstracta, sin referencia alguna a
tiempo, movimiento, calles, narices,
quesos, o cualquier otra característica
del mundo físico, y por este motivo
Russell le atribuye el haber «resuelto
definitivamente»
los
profundos
problemas tras la dicotomía.[7.51] (3)
La D. en D. también explica, respecto a
la demostración del doctor Goris que
vimos en §2e, por qué habrá siempre
más números reales que pañuelos rojos.
Y nos ayuda a entender por qué los
números racionales en definitiva
ocupan un espacio o en la recta
real,[7.52] pues son obviamente los
números irracionales los que hacen que
el conjunto de todos los números reales
sea no numerable. (4) Una ampliación
de la demostración de Cantor ayuda a
confirmar la demostración de Joseph
Liouville, en 1851, de que hay un
número infinito de irracionales
trascendentales en cualquier intervalo
de la recta real. (Esto es bastante
interesante. Recordará de la nota 15 de
§3a que de los dos tipos de
irracionales, los transcendentes, como
π y e, son los que no pueden ser raíces
de polinomios con coeficientes enteros.
La demostración de Cantor de que el ∞
de los reales sobrepasa al de los
racionales se puede modificar para
demostrar que son en realidad los
irracionales trascendentes los que son
no numerables y que el conjunto de
todos los irracionales algebraicos tiene
la misma cardinalidad que los
racionales,[7.53] lo cual establece que,
en definitiva, son los realesirracionales-trascendentes los que
explican la continuidad de la R. R.). (5)
Dado que la D. en D. es una
demostración por reducción al absurdo
y que sus cantidades no se pueden
construir de ningún modo, no debería
sorprendernos que al profesor Leopold
Kronecker
y
a
otros
protoconstructivistas no les gustara en
absoluto (más respecto a esto en un par
de §). Según todos los testigos, la
campaña pública de Kronecker contra
Cantor empezó en serio con los
artículos acerca de c.
§7d.
Matemáticamente,
es probable que
pueda usted ver cuál es el siguiente
movimiento importante de Cantor. Una
vez demostrado mediante c que hay
una potencia de ∞ mayor que ℵ0,
empieza a buscar conjuntos infinitos
cuya cardinalidad podría ser mayor que
c. Su siguiente paso importante (que,
como podrá observar, todavía involucra
conjuntos de puntos) es un intento de
demostrar que el plano 2D contiene una
infinidad de puntos que es mayor que
el c de la recta real 1D, del mismo
modo en que c es mayor que el ℵ0 de la
recta numérica. Esta es la demostración
acerca de cuyo resultado final Cantor le
escribió la frase célebre a Dedekind
«Je le vois, mais je’n le crois pas» en
1877.[7.54] Se conoce a veces como su
demostración de la dimensión. La idea
general es demostrar que los números
reales no se pueden poner en C1-1 con
el conjunto de puntos en un espacio ndimensional, en este caso un plano, y,
por lo tanto, que la cardinalidad del
conjunto de puntos del plano es > la
cardinalidad del conjunto de todos los
reales. Los casos específicos de la
demostración son el cuadrado unidad
pitagórico de toda la vida y el intervalo
[0, 1] de la recta real. (Recordará de §3
que las P. del I. de Bolzano ya habían
sugerido en 1850 que [0, 1] contenía
tantos puntos como la recta real,
equivalencia
que
ahora
Cantor
demuestra formalmente en su artículo
de la dimensión. Como ya hemos visto
una demostración gráfica de la
equivalencia en §3c, omitiremos esta
demostración excepto para poner de
relieve lo que seguramente puede
anticipar: Cantor demuestra que
cualquier tipo de diagonalización que
se use para crear un nuevo número real
que sea > 1 puede duplicarse para crear
un nuevo número real en [0, 1]).
Para la demostración de la
dimensión, la principal del artículo,
tiene que visualizarse de algún modo el
cuadrado unidad como una cuadrícula o
malla cartesiana, con coordenadas
numéricas correspondientes a todos y
cada uno de los puntos del plano al que
pertenece. La estrategia de Cantor es
usar la diagonalización para demostrar
que hay números correspondientes a
esas coordenadas 2D que no se pueden
hallar en el conjunto de todos los
reales. Como resulta claro en sus cartas
a Dedekind, al principio Cantor está
seguro de que tales números se pueden
generar, pues todo geómetra desde
Riemann había trabajado bajo la
suposición de que la dimensión de
cualquier espacio (por ejemplo, 1D,
2D, 3D) estaba determinada de manera
única por el número de coordenadas
necesarias para identificar un punto en
dicho espacio (semiextractado de
Grattan-Guinness, From Calc to S.T.,
pág. 188).
Solo que la suposición resulta ser
errónea, tal como descubre Cantor en
su intento de construir sucesiones
decimales de coordenadas 2D que
permitan comparar puntos del plano
con decimales de números reales. Lo
peliagudo es, obviamente, que los
puntos del plano se especifican
mediante pares de números reales, y
los puntos de la recta, mediante
números reales solos, de modo que
(con ecos de Pitágoras y Eudoxo)
Cantor tiene que pensar una manera de
hacer conmensurables ambos conjuntos
de puntos. Le cuesta tres años imaginar
cómo hacerlo. Una vez más,
representemos todos los números
relevantes
mediante
sucesiones
infinitas de decimales. Tomemos
cualquier punto (x, y) del cuadrado
unidad. Estas coordenadas se pueden
escribir así:
x = 0,a1a2a3a4a5a6a7…
y = 0,b1b2b3b4b5b6b7…
las cuales se combinan para dar lugar a
la representación decimal única[7.55]
del punto (x, y):
0,a1b1a2b2a3b3a4b4a5b5a6b6a7b7…
Y a este punto le corresponderá
claramente un punto z único en el
intervalo [0, 1] de la R. R.,
concretamente el correspondiente al
número
real
0,a1b1a2b2a3b3a4b4a5b5a6b6a7b7…
[7.56]
Así,
mediante
ese
mismo
procedimiento y por extrapolación
directa a partir del cuadrado unidad y
[0, 1], cada punto de un plano 2D se
puede poner en C1-1 con un punto de la
R. R., y viceversa. Además, el método
(relativamente simple) de Cantor de
combinar las coordenadas en un único
número real implica que la misma
técnica general se puede usar para
demostrar que un cubo 3D, un
hipercubo 4D, o en realidad el conjunto
total de puntos de cualquier figura
n-dimensional
tiene
la
misma
cardinalidad que el conjunto de
números reales de la R. R.,
concretamente c. Este es un resultado
extraordinario, y por eso Cantor no
quedó decepcionado al no poder
demostrar su premisa original: había
descubierto una increíble profundidad
y riqueza en el continuo, y su
demostración revelaba (tal como le
escribió a Dedekind) «qué maravillosa
potencia albergan los números reales,
puesto que uno está en situación de
determinar de manera única, con una
sola coordenada, los elementos de un
espacio
continuo
n-dimensional»
(Cantor in Cavaillès, pág. 234.
Traducción editada semiextractada de
Dauben, GC, págs. 55-56, sustituyendo
la variable «ρ» original de Cantor por
«n»).
El descubrimiento de Cantor de que
las rectas, los planos, los cubos y los
politopos[7.57] eran todos equivalentes
como conjuntos de puntos llega
bastante lejos a la hora de explicar por
qué la teoría de conjuntos constituye un
desarrollo tan revolucionario para las
matemáticas: revolucionario en teoría
y también en la práctica. En parte, esto
se
remonta
al
problema
de
conmensurabilidad de los griegos y la
relación ambivalente del cálculo
clásico con la geometría. La
incomodidad acerca de utilizar
cantidades como x2 y x3 en la misma
ecuación
(pues
los
cuadrados
implicaban áreas 2D y los cubos →
volúmenes 3D) había persistido
durante siglos, y el énfasis del
siglo XIX en el rigor hacía que las
ambigüedades geométricas fueran
todavía más indigestas. Para abreviar
una larga historia, la teoría de
conjuntos cantoriana ayuda a unificar y
a clarificar las matemáticas en el
sentido de que todos los entes
matemáticos ahora se pueden entender
fundamentalmente como el mismo tipo
de cosa: un conjunto. Además, en las
nuevas geometrías no euclidianas,[7.58]
el descubrimiento de Cantor de que
todos los conjuntos de puntos
geométricos
son
transfinitamente
equivalentes (es decir, que todos tenían
la cardinalidad c) es de gran
importancia, en particular en la idea de
dimensión, tal como Cantor le comenta
también a Dedekind:
Esta visión [= la de G. C.]
parece opuesta a la que
prevalece generalmente, en
particular entre los defensores
de la nueva geometría, pues
hablan de dominios infinitos de
una, dos, tres,… n dimensiones.
A veces uno incluso encontrará
la idea de que la infinidad de
puntos de una superficie [2D] se
puede obtener, por así decirlo,
elevando al cuadrado la
infinidad de puntos de una
recta, y la de un sólido
elevándola al cubo (ibíd.).
No hace falta decir, sin embargo,
que nuestras expresiones «desarrollo
revolucionario»
y
«de
gran
importancia» son en retrospectiva.
Como ya se ha insinuado claramente,
no se dio el caso de que las
matemáticas predominantes en la
época se arrodillaran inmediatamente
para dar la bienvenida a las
demostraciones de Cantor posteorema
de unicidad. Particularmente, en
relación a la demostración de la
dimensión, matemáticos de casi todas
las tendencias se alinearon para
denostarla. Además de las objeciones
generales en §7c, los constructivistas
odiaban en especial la idea de crear, de
algún modo, irracionales 1D a partir de
combinaciones
2D
de
otros
irracionales,
así
como
la
«correspondencia no continua» que
daba la demostración de la dimensión
entre puntos de la recta y puntos del
plano.[7.59] Y fue en realidad el artículo
de
la
demostración
de
la
dimensión[7.60] el primero contra el que
Kronecker intrigó para conseguir que
fuera rechazado por una revista en cuyo
comité editorial estaba, algo acerca de
lo cual Cantor escribió muchas cartas
descargando su cólera. Pero no eran
solo los constructivistas o los
fundamentalistas. Véanse, para poner
solo un ejemplo, las siguientes líneas
de Paul Du Bois-Reymond, que no era
un kroneckeriano, sino un analista
destacado, en la tradición aristotélicogaussiana de los ∞ solo potenciales,
comentando la demostración de la
dimensión:
Parece
absolutamente
repugnante al sentido común. El
hecho simple es que este es el
resultado de un tipo de
razonamiento que permite a
ficciones
idealistas
[=
platónicas] asumir el papel de
genuinas cantidades aunque no
sean ni siquiera verdaderos
límites de representaciones de
cantidades (Du Bois-Reymond,
de la traducción al francés de
Die
allgemeine
Funktiontheorie,
fragmentos
semiextractados de Kline, pág.
998).[7.61]
§7e.
En
todo caso, hasta aquí hemos
establecido por lo menos y quizás a lo
sumo dos órdenes distintos de
conjuntos infinitos, ℵ0 y c,[7.62] y ahora
resulta apropiado preguntarse qué
tienen que ver exactamente esos
números cardinales con los números
transfinitos que vimos a Cantor
fabricar a partir de R y
y lo de los
conjuntos derivados de conjuntos
derivados en §7b. Siendo la gran
cuestión específica si se puede
demostrar que la sucesión infinita de
∞
conjuntos infinitos P(n∞ ), P(∞
∞+1)
,
∞+n
P(∞ ), etc., corresponde a una
jerarquía
infinita
de
números
cardinales cada vez mayores, o si ℵ0 y
c son los únicos cardinales infinitos y
no hay reales más allá de la potencia
transdimensional del continuo.
El siguiente gran descubrimiento de
Cantor es que se puede construir de
manera válida una sucesión infinita de
con juntos infinitos con números
cardinales cada vez mayores sin usar
nada más que las propiedades formales
de
los
conjuntos.[7.63]
Dichas
propiedades involucran los conceptos
de subconjunto y de conjunto potencia,
el segundo de los cuales se define aquí
mismo, para algún conjunto A, como
simplemente el conjunto de todos los
subconjuntos de A. Es decir, que todo
elemento de P(A) es algún subconjunto
de A. Esto resulta ser peor de lo que
parece. Todo conjunto, finito o no,
tiene un conjunto potencia,[7.64] pero lo
que Cantor es capaz de demostrar es
que incluso si el conjunto A es infinito,
su conjunto potencia P(A) siempre
tendrá un número cardinal mayor que
A. Más específicamente, puede
demostrar que el número cardinal de
P(A) siempre será igual a 2A.[7.65] Y esa
cosa de A → 2a acaba resultando
crucial para navegar por lo transfinito,
en cuyo reino resulta que uno en cierto
modo salta, como cuánticamente, de
una clase de números a la siguiente, sin
nada en medio: 2ℵ0 = ℵ1, 2ℵ1 = ℵ2, y
así sucesivamente (en cierto modo).
Las demostraciones de Cantor
acerca del conjunto potencia son
extremadamente intrincadas, y tenemos
que prepararnos para ellas de alguna
manera. Y como no hay duda de que
para todos nosotros la escuela
elemental queda muy lejana, conviene
que, por si no lo hemos dicho antes,
explicitemos que la manera formal de
designar un conjunto es poner a sus
elementos entre {llaves}, así, y que el
simbolismo para decir que «a es un
elemento de A»
es
«a ∈ A».
Recordemos
también
que
«subconjunto» es por definición más
inclusivo que «subconjunto propio», y
que entre los subconjuntos de cualquier
conjunto A estarán (1) el mismo A y (2)
el conjunto vacío, simbolizado por «∅»
o, a veces, por «{ }».[7.66] Por lo tanto,
como cualquier conjunto tiene por lo
menos algunos subconjuntos, se sigue
que cualquier conjunto tiene un
conjunto potencia. Para ver de manera
informal que el número de elementos
del conjunto potencia de A siempre es
igual a 2(Número de elementos de a), sea A el
conjunto de tres elementos {1, 2, 3}.
Los subconjuntos de A son: { }, {1},
{2}, {3}, {1, 2}, {1, 3}, {2, 3},
{1, 2, 3}, de los que hay exactamente 8
o 23. Una manera más rigurosa de
demostrar que P(A) = 2A es por
inducción
matemática,
que
técnicamente no es como lo hace
Cantor pero está por lo menos
implícito en su demostración. Además,
es comparativamente sencilla. Por
favor, repase o rememore lo visto en
§7b sobre los tres pasos de una
demostración
por
inducción
matemática, que aquí irán del siguiente
modo:
(a) Demostrar que la cardinalidad
de P(A) es igual a 2A para un
conjunto A con solo un
elemento. Tal A tiene como
subconjuntos los siguientes: ∅
y A mismo, lo que significa que
su P(A) tiene dos elementos, lo
cual es 21 elementos, es decir,
es 2A elementos, o sea que
¡bingo![7.67].
(b) Supongamos que es cierto que
si A tiene k elementos, el
número cardinal de P(A) = 2k.
(c) Demostrar que si A tiene (k + 1)
elementos, P(A) = 2(k+1).
A partir del paso (b) sabemos que
los primeros k elementos de A dan 2k
subconjuntos de A. Ahora tomamos
cada uno de esos 2k subconjuntos y
formamos un subconjunto nuevo que
también contiene el último de los
(k + 1) elementos de A (es decir, el
nuevo elemento extra designado por el
«+ 1»). Podemos formar exactamente
2k subconjuntos nuevos de ese tipo con
«1 elemento +»: uno para cada uno de
los subconjuntos originales. Así que
ahora tenemos los 2k subconjuntos
originales que no contienen al nuevo
elemento, y tenemos 2k nuevos
subconjuntos que sí lo contienen. Esto
son (2k + 2k) subconjuntos, lo cual es
equivalente a (2 × 2k) subconjuntos,
que es igual a 2(k+1) subconjuntos. Así
que (c) también está demostrado.
Podemos estar lo bastante seguros de
que P(A) = 2A.
Para nuestros propósitos, Cantor
tiene dos demostraciones principales
respecto al conjunto potencia. En
ninguna de las dos se preocupa todavía
por lo de 2A: su preocupación básica es
demostrar que incluso para un conjunto
infinito A, P(A) > A.[7.68] La primera
versión, hacia 1891, es importante
principalmente porque exhibe el poder
de la técnica de diagonalización como
arma de reducción al absurdo. Se puede
considerar una demostración de que el
conjunto de todos los subconjuntos del
conjunto de los enteros no es
numerable,[7.69] lo cual, como Cantor
ya ha demostrado que el conjunto de
los enteros es numerable, significará,
obviamente, que su conjunto potencia
tiene un número cardinal mayor que
ℵ0 .
Aquí
está
la
demostración.
Llamemos £ al conjunto de todos los
enteros, y P(E) a su conjunto potencia.
Sabemos de §7c que para que P(E) sea
numerable, debe ser posible establecer
una correspondencia uno a uno entre
P(E) y E. La presente demostración es
una reducción al absurdo, o sea que
supongamos que sí es posible tal C1-1
entre P(E) y E. Esto (como también
sabemos por las demostraciones en
diagonal de §7c) significa que la C1-1
se puede representar en una tabla como
en el siguiente ejemplo parcial, con los
elementos de E en la izquierda, y los
subconjuntos de E (que también son los
elementos de P(E), y pueden estar en
cualquier tipo de orden arbitrario que
queramos), en la derecha (parecido
razonable con Hunter, págs. 22-23):
Tabla n.º 2
E
0
1
2
3
4
5
6
↔
↔
↔
↔
↔
↔
↔
7
…
…
…
↔
↔
↔
↔
P(E)
{Todos los enteros}
{Conjunto vacío}
{Todos los enteros pares}
{Todos los enteros impares}
{Todos los primos}
{Todos los enteros > 3}
{Todos los cuadrados
perfectos}
{Todos los cubos perfectos}
…
…
…
Resulta que podemos modificar
esta tabla explotando una propiedad de
su C1-1 que quizás usted ya ha notado
si ha dedicado algún tiempo a pensar
por qué exactamente la relación entre
los conjuntos y sus conjuntos potencia
es siempre 2.ª y no 3.ª ni ningún otro
xA. La respuesta de fondo es que el «2»
de 2.ª refleja un tipo particular de
procedimiento de decisión. Para cada
subconjunto s de un conjunto A, hay
exactamente dos elecciones respecto a
cada elemento a de A: o bien a es un
elemento de s, o bien no lo es. Esta
última frase probablemente necesita
más de una lectura. Es difícil
expresarlo de manera clara en lenguaje
natural, pero la idea misma no es tan
complicada. A es un conjunto, a es
algún elemento en particular de A, s es
algún subconjunto en particular de A.
Preguntémonos si resulta que a es un
elemento de s. Pues, o bien lo es, o bien
no lo es. Agotamos todas las
posibilidades respecto a la pertenencia
de a al conjunto s si una vez incluimos
a en s y otra vez lo excluimos, dando
lugar así al dúo de subconjuntos s y s'
respecto a cada a.
(SEMI-SEI Este es uno de los puntos
de los que es simplemente imposible
saber si lo que se acaba de decir tendrá
sentido para el lector no experto. Si lo
del abstracto a-es-elemento-de-s-o-no
es lo bastante claro para que usted
entienda por qué explica por sí solo que
un conjunto A de tres elementos tenga
23
subconjuntos,
puede
omitir
libremente el resto de este párrafo. Por
si no lo es, vamos a ver un ejemplo
concreto. Pongamos que A es el mismo
conjunto {1, 2, 3} que hemos visto en
la pág. 246, donde hicimos la lista de
los subconjuntos de A: { }, {1}, {2},
{3}, {1, 2}, {1, 3}, {2, 3}, {1, 2, 3}.
Eche un vistazo a esos subconjuntos y
vea cuántas veces un elemento
particular de A —digamos el elemento
1— pertenece a alguno de los ocho
subconjuntos. Podrá ver que pertenece
a cuatro de ellos y está ausente de
cuatro. Si se fija en el elemento 2,
podrá ver que sucede lo mismo: 2 está
presente en cuatro y ausente de cuatro.
Lo mismo con el 3. ¿Puede ver por
qué? Hay ocho subconjuntos en total:
la mitad de ellos contienen cualquier
elemento en particular de A, y la otra
mitad no. En realidad, puede construir
el conjunto de todos los subconjuntos
de A de ese modo. Tome cualquier
elemento de A. Si su primer
subconjunto s no contiene el elemento,
su siguiente s' lo contendrá. O
recíprocamente. Es decir, para todo
elemento y subconjunto en particular,
hay dos elecciones, y en el conjunto de
todos los conjuntos estarán ambas. Dos
posibilidades para cada elemento. Por
lo tanto, el número de subconjuntos de
{1, 2, 3} será 2 × 2 × 2, o 23. Si esto
aún no consigue aclararle la idea
básica, le pedimos que simplemente se
la trague (la idea) porque no podemos
hacer nada mejor).
Bien, entonces esto significa que
podemos tomar la Tabla n.º 1 y
ampliarla por un lado preguntándonos,
para cada entero del conjunto E, si
realmente
es
parte
de
su
correspondiente subconjunto de la
columna P(E). Ponemos «Sí» si el
entero está en ese subconjunto en
particular, y «No» si no lo está. Así:
Tabla n.º 2
Y una vez hemos elaborado esta
Tabla n.º 2, podemos demostrar
fácilmente
que
la
supuesta
correspondencia entre E y P(E) no es
exhaustiva y, por lo tanto, no es una
C1-1 válida. Lo hacemos usando la
buena y vieja diagonalización para
construir un subconjunto de E que
nunca jamás aparecerá en la
correspondencia E ↔ P(E) de la tabla.
Es el subconjunto definido empezando
por la casilla que está completamente
al noroeste de la Tabla n.º 2 y
desplazándose diagonalmente hacia el
sudeste, cambiando «Sí» por «No» y
viceversa en todo el recorrido, así:
Tabla n.º 3
Todo lo que sabemos sobre este
nuevo subconjunto es que incluye 1, 4,
6 y 7, y que difiere por lo menos en un
elemento de cada subconjunto (o sea
cada elemento de P(E)) de la C1-1
original. Naturalmente, nuestra Tabla
n.º 3 es solo un fragmento, pero
continuando el simple proceso de
intercambio «Sí»-«No» a lo largo de la
diagonal podemos garantizar que el
nuevo subconjunto generado de ese
modo
diferirá
de
todos
los
subconjuntos de la C1-1 sin importar lo
lejos
que
lleguemos
en
los
emparejamientos. Por lo tanto, una
verdadera C1-1 entre E y P(E) es
imposible. Lo cual significa que P(E)
es no numerable,[7.70] y eso quiere
decir que su cardinalidad es mayor que
ℵ0. Q. E. D.
Aunque hay buenas razones por las
que hemos repasado esta demostración
tan gráfica y detalladamente, sepa que
no es así como lo hace Cantor. La
verdad es que nunca presenta de
manera explícita la demostración en
diagonal para P(E) > E y, por lo tanto,
para P(A) > A: simplemente hace
alusión a ella como una «extensión
natural» de su demostración en
diagonal de la no numerabilidad de los
números reales.[7.71] El argumento que
da para P(A) > A es un poco
rompecabezas, pero acaba jugando un
papel clave en el desenlace de nuestro
relato y, por lo tanto, es necesario
detallarlo. Esta demostración es
completamente
abstracta
y
no
específica,
diseñada
solo
para
demostrar que a partir de cualquier
conjunto infinito A se puede construir
algún conjunto infinito B cuyo número
cardinal supera al de A. Quizá sería
bueno que se preparase usted,
emocionalmente, para tener que leer lo
siguiente más de una vez.
A es un conjunto infinito. B es el
conjunto de todos los subconjuntos de
A[7.72]. Como todos los conjuntos son
por definición subconjuntos de sí
mismos, A es un subconjunto de A, es
decir que A es un elemento de B. Así
que, definitivamente, es posible
establecer una C1-1 entre todos los
elementos de A y, por lo menos, los de
un elemento de B. No es posible, sin
embargo, establecer una C1-1 entre
todos los elementos de A y todos los
elementos de B. Vamos a demostrar
esto mediante reducción al absurdo,
por lo que vamos a adoptar la postura
habitual y suponer que tal C1-1 está en
efecto construida y agota ambos
conjuntos infinitos. Ahora, sea a un
elemento cualquiera de A y b un
elemento cualquiera de B (o sea, que b
es un subconjunto cualquiera de A).
Como vimos antes con la Tabla n.º 2, la
C1-1 entre A y B puede ser
completamente aleatoria en el sentido
de que, en cualquier correspondencia
individual a ↔ b, a puede ser o no ser
un elemento del b con el que está
emparejado. Por ejemplo, allí el entero
3 estaba emparejado con {Todos los
enteros impares} y él mismo es un
entero impar, mientras que 6 estaba
emparejado con {Todos los cuadrados
perfectos} pero no es un cuadrado
perfecto. Será lo mismo con nuestra
C1-1
actual
y
sus
infinitos
emparejamientos a ↔ b: a veces a será
un elemento del subconjunto b con el
que está emparejado, y a veces no lo
será. Hasta aquí es todo bastante
sencillo y directo. Sin embargo, ahora
considere la totalidad de todos los a en
la C1-1 que no son elementos de los b
con los que están emparejados. Sea φ el
conjunto de todos los a con esa
característica. Por supuesto, φ es un
subconjunto de A, lo cual significa que
φ es un elemento de B, y aun así se
puede demostrar que φ no se puede
incluir en la C1-1 supuestamente
exhaustiva entre A y B. Pues si φ está
incluido, entonces está emparejado con
algún a, y como hemos visto solo hay
dos opciones: o bien este a es él mismo
un elemento de φ, o bien no lo es. Si a
es un elemento de φ… pero no puede
serlo, pues esto contradice la definición
de φ. Pero si a no es un elemento de φ,
entonces es, por definición, un
elemento de φ… lo cual no puede ser, o
sea que debe serlo, pero entonces no
puede serlo… y así, de un modo u otro,
ya tiene usted una contradicción de tipo
LTE. Por lo tanto, una verdadera C1-1
entre A y B no es posible; luego, la
cardinalidad de B es > la cardinalidad
de A. Quod erat dem*.
§7f
*SEMIINTERPOLATIVO
Por
favor, observe el parecido entre
esta última demostración y la paradoja
de los antiguos griegos «Estoy
mintiendo»,[7.73] donde si la afirmación
es verdadera entonces es falsa y si es
falsa entonces es verdadera. Lo cual
significa que ahora hemos entrado en el
territorio abismal de la autorreferencia.
Este es el verdadero motivo por el que
nos acabamos de arrastrar por la
demostración de Cantor de que B > A:
abre un tipo completamente nuevo de
grieta en las matemáticas modernas.
Aunque no es estrictamente nuestro
ámbito, sepa que en la década de 1930
el profesor Kurt Gödel[7.74] usará algo
muy parecido al truco de Cantor
«(a ∉ φ) → (a ∈ φ)» para demostrar
sus
devastadores
teoremas
de
incompletitud. (Dicho burdamente,
Gödel
demostrará
que
ciertas
proposiciones
matemáticas
bien
formadas son verdaderas, y aun así
indemostrables, mediante la deducción
de «Proposición P: la Proposición P es
indemostrable» como un teorema).
Más
importante
para
nuestros
propósitos es esta idea de que los
conjuntos pueden tener otros conjuntos
como elementos, que es esencial para
el concepto de conjuntos potencia y,
por
supuesto,
parece
bastante
inocente…,
solo
que
tras
la
demostración de Cantor resulta ser una
auténtica caída en picado por la grieta
de la autorreferencia. Ejemplo:
considere el teorema que Cantor acaba
de demostrar, que el conjunto de todos
los subconjuntos del conjunto A
siempre contendrá más elementos que
el mismo A. Pero ahora suponga que A
se define como «el conjunto de todos
los conjuntos». Por definición, este A
contendrá todos sus subconjuntos, pues
dichos subconjuntos son conjuntos, o
sea que en este caso P(A) > A no es
posible en modo alguno. Conclusión: el
mismo principio de los conjuntos-deconjuntos que Cantor necesita para
construir una jerarquía de conjuntos
infinitos da lugar a una paradoja casi
inmediatamente.
La evidencia histórica indica que
Cantor conocía la paradoja del
conjunto-de-todos-los-conjuntos hacia
1895,[7.75] aunque jamás la mencionó
ni una sola vez en sus trabajos
publicados. A pesar de todo ahora se la
conoce como la paradoja de Cantor.
También se considera como la base de
la paradoja más famosa de toda la
teoría de conjuntos, habitualmente
conocida como la antinomia de Russell
porque el ubicuo Bertrand Russell la
usó para torpedear la obra de Frege
Fundamentos de la aritmética en
1901.[7.76] Podemos esbozar
la
antinomia de Russell muy rápida y
fácilmente porque casi todo el mundo
ha oído hablar de ella en alguna
ocasión.
Aunque
se
desprende
directamente de la demostración
abstracta de Cantor sobre el conjunto
potencia, la antinomia también causa
estragos en el criterio principal de la
definición de «conjunto» que da
Cantor, que es (como recordará de la
nota 16 de §7a) que siempre hay un
procedimiento por el que dado un
elemento
cualquiera
se
puede
determinar si es un elemento de un
conjunto dado.[7.77] O sea, que aquí
está la antinomia de Russell. Como
hemos visto, algunos conjuntos son
elementos de sí mismos y algunos no
lo son. En realidad, la mayoría no lo
son; por ejemplo, el conjunto de todas
las sillas no es una silla, el conjunto de
todos los entes que pueden anudar el
pedúnculo de una cereza con su lengua
no puede hacer lo mismo, etc. Pero
algunos conjuntos sí se contienen a sí
mismos como elementos; por ejemplo,
el conjunto de todos los conjuntos, el
conjunto de todas las abstracciones, el
conjunto de todos los entes que no
pueden anudar el pedúnculo de una
cereza. Russell llama a los conjuntos
que no son elementos de sí mismos
conjuntos
normales,
y
a
los
autocontenidos, anormales. Así pues,
considere ahora el conjunto N de todos
los conjuntos normales: ¿es N un
conjunto normal?[7.78] Bien, si N es un
conjunto
normal,
entonces
por
definición no es un elemento de sí
mismo. Pero N es el conjunto de todos
los conjuntos que no son elementos de
sí mismos, de modo que N es un
elemento de sí mismo si no es un
elemento de sí mismo. Aunque
entonces si N realmente es un elemento
de sí mismo, entonces no puede ser un
elemento del conjunto de todos los
conjuntos que no son elementos de sí
mismos, de modo que en realidad N no
es un elemento de sí mismo, en cuyo
caso lo es… y así una y otra vez ad
infinitum.
Este tipo de paradoja, como el
rompecabezas «(a ∉ φ) → (a ∈ φ)» en
la reducción al absurdo de Cantor, se
conoce oficialmente como un círculo
vicioso (CV). Aquí «vicioso» significa
más o menos lo mismo que en la RIV
de §2a, es decir, que se convierte en
lógicamente imposible hacer algo que
estamos lógicamente obligados a hacer.
En las paradojas de tipo CV, como las
de Russell y Cantor, lo que no podemos
hacer es determinar si algo es o no es
un elemento de un conjunto, lo cual
viola tanto la definición formal de
«conjunto» como (mucho peor) la LTE.
O sea, que dichos problemas no son
minucias.
Llegados a este punto es casi
seguro que ha captado usted la
dinámica general de la historia del en
virtud de la cual ciertas paradojas dan
lugar a avances conceptuales que
pueden
abordar
esas
paradojas
originales, pero a su vez dan lugar a
nuevas paradojas, que entonces generan
otros avances conceptuales, y así
sucesivamente. Si es usted uno de los
lectores que se preocupan de las notas
al pie SEI, ya ha visto algo sobre un
tipo de solución técnica a la antinomia
de Russell, que es la sustitución por
Zermelo y otros colegas del principio
de abstracción ilimitada por el P. A.
Limitada. Otro tipo de solución es la
prohibición
de
definiciones
impredicativas, defendida por JulesHenri Poincaré (1854-1912), una figura
clave de la topología que además fue,
tras la muerte de Kronecker en 1891, el
oponente n.º 1 de las matemáticas
transfinitas.[7.79] La definición de
Poincaré de impredicativo es algo
sospechosa, pero en esencia implica
definir un objeto en términos de todo
un grupo de objetos del cual es parte.
Aún más esencialmente, una definición
impredicativa depende de propiedades
y descripciones autorreferentes, y «El
conjunto de todos los conjuntos que no
son elementos de sí mismos» es un
ejemplo perfecto de dicha definición
(como lo son «El conjunto de todos los
conjuntos» y la definición de Cantor
del conjunto φ en la anterior
demostración de B > A). Todo esto se
complica bastante, pero la táctica
general de Poincaré es caracterizar las
definiciones
impredicativas
en
términos de los resultados paradójicos
que pueden arrojar,[7.80] lo cual
entonces constituye el argumento
lógico para rechazarlas. Es algo así
como el modo en que la división por o
quedó proscrita. Desafortunadamente,
las definiciones formales de todo tipo
de términos y conceptos en el análisis,
desde «sucesión» y «serie» hasta
«punto límite» y «cota inferior»,
también son impredicativas —y
además se puede hacer que el mismo
concepto de impredicatividad genere
algunos CV muy feos—[7.81] de modo
que la solución de Poincaré nunca
cuajó realmente.
La propuesta de Russell para evitar
las epónimas paradojas de Cantor y de
él mismo es la teoría de los tipos, que,
para abreviar una muy larga historia, es
parte del programa fundacional de
Russell para intentar demostrar que
todas las matemáticas son reducibles a
lógica simbólica. La teoría de los tipos
es una especie de gramática de la
abstracción que rechaza ciertas clases
de proposiciones en las cuales
entidades de tipos diferentes se tratan
como equivalentes. En el sentido,
esencialmente, de metafísicamente
equivalentes.[7.82] La idea es que los
conjuntos de individuos no son el
mismo tipo de entidad que los
individuos mismos, y los conjuntos de
conjuntos no son del mismo tipo que
los conjuntos de individuos, y así
sucesivamente. Y el tipo de una entidad
en particular es función directamente
de cuán abstracta es dicha entidad, de
modo que se llega a una jerarquía de
conjuntos que se parece a los niveles de
abstracción informales de los que
hablamos en §1b: el tipo de Russell 1 =
individuos, tipo 2 = conjuntos, tipo 3 =
conjuntos de conjuntos, tipo 4 =
conjuntos de conjuntos de conjuntos,
etc.[7.83] Lo que permite que la teoría
evite los círculos viciosos es que la
misma clase de jerarquía se puede
aplicar a las proposiciones; por
ejemplo, tipo x; = alguna entidad de
algún tipo particular, tipo (x + 1) =
alguna proposición sobre esa entidad,
tipo (x + 2) = alguna proposición sobre
la proposición sobre la entidad, y así
sucesivamente. (N. B. Para Russell
«proposición» puede significar o bien
una frase en lenguaje natural o bien una
aseveración formal/matemática como
«a ∈ A»).[7.84] Y la gran regla es que,
suponiendo que m y n son enteros, una
proposición o conjunto de tipo n no se
puede aplicar a otra proposición u otro
conjunto de tipo n, sino solo a una
proposición o un conjunto de tipo m
donde m < n.
Por lo que respecta a nuestro relato,
la teoría de tipos viene a ser un
ejemplo perfecto de cómo se halla una
salida legal de una paradoja.
Ciertamente, la teoría ofrece una
«solución» a los rompecabezas de
Russell y Cantor —es decir, da una
explicación de cuál es el paso
«ilegítimo» de la paradoja— pero
también es increíblemente críptica e
inmanejable, y en definitiva tan dañina
para las matemáticas como lo de
Poincaré y la impredicatividad.
Veamos un rápido ejemplo: como los
números racionales se definen como
razones de enteros, y los irracionales
como
conjuntos/sucesiones
de
racionales, los tres tipos de números
son de diferentes tipos, y según las
reglas de la teoría no podríamos hacer
predicados en común acerca de los tres
sin
un
sinfín
de
diferentes
demostraciones y niveles y salvedades.
Para su información, Russell intentó
solventar algunas de esas dificultades
mediante lo que él llamó axiomas de
reducibilidad, pero estos eran incluso
más complicados y artificiosos y…
básicamente toda su tipología se vuelve
muy etérea y ahora solo es de interés
histórico.[7.85]
Si es necesario decir una vez más
que solo estamos echando una ojeada a
una superficie turbulenta, considérese
dicho.
Medidas
antiparadoja
específicas como las de Russell y
Poincaré son parte de una crisis mucho
más amplia y profunda, una que
precede a Cantor pero llega a hacerse
apremiante a través de sus teorías del
∞. Lo destacado, a grandes rasgos: las
paradojas de la teoría de conjuntos,
emparejadas con las preocupaciones
respecto a los fundamentos que
empiezan con Abel y Cauchy y llegan
al clímax con Frege y Peano, conducen
directamente
a
las
grandes
controversias
formalismo-contraintuicionismo de principios del
siglo XX. De nuevo, solo podemos
esbozarlas de manera esquemática.
Respecto a los conjuntos infinitos, por
ejemplo,
el
intuicionismo
es
rabiosamente
anti-Cantor,
y
el
formalismo, incondicionalmente proCantor, a pesar de que tanto el
formalismo como el intuicionismo son
anti-Platón y Cantor es un platónico
irreductible. Lo cual, con dolor de
cabeza o sin él, significa que volvemos
de nuevo a la metafísica: la riña
moderna respecto a los procedimientos
de las matemáticas es, en definitiva,
una disputa acerca del estatus
ontológico de los entes matemáticos.
Ya tuvimos una introducción al
intuicionismo en las discusiones de §6
acerca
del
constructivismo.
El
formalismo es harina de otro costal.
Quizá la mejor aproximación sea
volver a la cuestión en la que hemos
insistido anteriormente, a saber: las
paradojas de la teoría de conjuntos son
parte del problema más amplio de la
consistencia de las matemáticas, que
Hilbert propuso como Problema
Importante n.º 2[7.86] en el mismo
Congreso de París donde se le pudo ver
hablando de Cantor con entusiasmo en
§1a. El programa del propio Hilbert
para reconstruir las matemáticas de tal
modo que los teoremas no arrojen
paradojas es el formalismo, el cual
busca hacer que la abstracción de las
matemáticas sea a la vez total y
primaria. La idea básica del
formalismo es separar totalmente las
matemáticas del mundo y convertirlas
en un juego. Literalmente. Este juego
involucra la manipulación de ciertos
símbolos según ciertas reglas que
permiten construir secuencias de
símbolos a partir de otras secuencias de
símbolos. Es 100% formal: de aquí el
nombre. Lo que los símbolos de ese
juego matemático significan, o si
significan algo, no tiene nada que ver
con el juego. Y decir que un ente
matemático «existe» es simplemente
decir que no causa una contradicción.
[7.87] Lo que importa son las reglas, y el
proyecto entero del formalismo es una
teoría de la demostración: el objetivo
es construir un conjunto de axiomas y
reglas de inferencia[7.88] de donde se
puedan deducir todas las matemáticas,
de modo que todo sea deductivo y
riguroso y limpio, o sea, como un juego
autocontenido.
Si tiene usted algún tipo de
conocimientos de lógica o de filosofía
de las matemáticas, reconocerá que
esta es una descripción radicalmente
simplificada del formalismo. (Por decir
algo más, el programa de Hilbert
también implica descomponer las
matemáticas
en
niveles
de
razonamiento algo parecidos a los tipos
de Russell, de nuevo sin permitir
proposiciones
inter-nivel).
Probablemente, también sabrá que
dicho movimiento empieza a tener
serios problemas mucho antes de las ya
mencionadas demostraciones de Gödel
de que un sistema formal no puede ser
a la vez completo y consistente:[7.89]
por ejemplo, los formalistas ni siquiera
podían conseguir que la aritmética
básica fuera completa y consistente si
incluía la multiplicación como una
operación «legal», lo cual, obviamente,
es un serio problema. Así que no
necesitamos
hablar
del
empobrecimiento filosófico o de la
absoluta extrañeza de un juego
matemático sin referentes, porque el
formalismo ni siquiera podía tener
éxito según sus propias reglas.
Las respuestas más coherentes y
exitosas a las paradojas de tipo CV
vienen de dentro de la misma teoría de
conjuntos (la cual, hacia 1900, es un
campo en plena ebullición tanto en las
matemáticas como en la lógica, gracias
a adivine quién), y son encabezadas por
el seguidor y sistematizador n.º 1 de
Cantor, el profesor Zermelo.[7.90] Un
resultado de dichas respuestas es la
separación de la teoría de conjuntos
abstracta en dos subtipos, la teoría
informal de conjuntos y la teoría
axiomática de conjuntos. La T. I. C. es
simplemente la teoría de conjuntos de
Cantor normal con todas sus miserias y
grandezas,
incluyendo
su
susceptibilidad a las paradojas.[7.91] La
teoría axiomática de conjuntos es un
intento de obtener una versión más
rigurosa, fundacionalmente segura de
la teoría de conjuntos que tenga toda la
potencia conceptual de la T. I. C. pero
organizada de tal modo que evite
paradojas graves. El programa de la
T. A. C. es algo formalista en espíritu y
euclidiano: consiste en hacer que la
teoría de conjuntos sea un sistema
formal independiente[7.92] con un
conjunto propio de axiomas que
proporcione máxima consistencia y
completitud. Como ya se ha
mencionado en alguna parte, el sistema
axiomático más conocido se llama
habitualmente ZFS (de Zermelo,
Fraenkel, y Skolem). También hay el
sistema, más restrictivo, de von
Neumann-Bernays (VNB), y algunos
más, con varios embellecimientos
metateóricos,
diseñados
por
eminencias como Tarski, Quine,
Ramsey, y otros colegas.
Resulta que la teoría axiomática de
conjuntos y su correspondiente lógica
han tenido aplicaciones fructíferas en
muchos campos, como la teoría
matemática de las funciones reales, el
análisis y la topología, la gramática
generativa y los estudios sintácticos en
lingüística, y la teoría de la decisión,
algoritmos,
circuitería
lógica,
problemas de detención/«estudios-Ω»,
inteligencia artificial y procesamiento
combinatorio en ciencias de la
computación. Por lo tanto, a pesar de
tener cada vez menos espacio, vale la
pena incluir por lo menos un resumen
rápido de la axiomatización básica de
la que todos los sistemas principales
son variantes, con explicaciones
ajustadas y directamente relevantes
donde sea necesario, y por supuesto, en
este punto tardío, toda esta parte es
omitible/ojeable a su discreción SEI,
como sigue.
Concepto primitivo: la relación de
pertenencia ∈, donde «s ∈ S» significa
que el objeto s es un miembro o
elemento del conjunto S.
Αx. 1. Dos conjuntos son iguales si
contienen
los
mismos
elementos. (Observe que no es
«si y solo si…»; esto se debe a
que los conjuntos infinitos y sus
subconjuntos propios también
pueden ser iguales).
Αx. 2. Si a y b son objetos o conjuntos,
entonces {a, b} es un conjunto.
Αx. 3. Hay dos variantes en este caso.
1.ª variante: Para un conjunto S
y un «predicado definido»[7.93]
P, existe el conjunto Sp que
contiene solo aquellos x ∈ S[7.94]
que
tienen
la
propiedad
designada por P. 2.ª variante:
Existe un conjunto S con las
siguientes
características:
(a) ∅ ∈ S, y (b) Para cada x, si
x ∈ S, entonces {x} ∈ S. (Estas
son dos versiones técnicamente
distintas del principio de
abstracción
limitada
mencionado
antes.
Ambas
versiones hacen dos cosas
importantes. En primer lugar,
establecer que el conjunto vacío
existe. En segundo lugar, definir
y validar el método de la teoría
de conjuntos de la inducción
transfinita y, mediante dicho
método, establecer la existencia
de un conjunto S infinito
numerable cuyos elementos son
∅, {∅}, {{∅}}, {{{∅}}}, …
[7.95] Con lo cual si, en este
conjunto, ∅ se toma como 1 y,
para cada x, {x} es igual a
(x + 1), entonces S se convierte
en el conjunto ordenado de
todos los enteros positivos; lo
cual resulta ser muy parecido al
modo en que los postulados de
Peano[7.96] generan los enteros).
Αx. 4. La unión de un conjunto de
conjuntos es también un
conjunto. (Esto sirve como
definición técnica de «unión», a
partir de la cual «intersección»,
«producto cartesiano»,[7.97] etc.,
se pueden obtener mediante
manipulación lógica; algo no
muy
distinto
a
definir
completamente la conectiva
lógica «y» en términos de «no»
y «o»).
Αx. 5. El famoso axioma del conjunto
potencia:
Para
cualquier
conjunto S, existe el conjunto
potencia P(S) de S. (Aquí se
establece la jerarquía infinita de
los
conjuntos
infinitos.
Recuerde de §7b y siguientes
que toda la teoría de conjuntos
es trivial en el caso de los
conjuntos
finitos,
donde
«trivial» significa que se puede
comprobar la veracidad de
cualquier proposición de teoría
de
conjuntos
simplemente
mirando los elementos de los
conjuntos relevantes. Toda la
relevancia de estos axiomas está
en la posibilidad de demostrar
teoremas que sean transexperienciales, 100% abstractos:
como él mismo).
Αx. 6. El famoso e infame axioma de
elección (A. E.). En la
nomenclatura de la teoría de
conjuntos, el A. E. es: «Si S es
un conjunto de conjuntos no
vacíos disjuntos dos a dos, el
producto cartesiano de los
elementos de S[7.98] es no vacío;
cada elemento de este producto
cartesiano se designa como un
conjunto selección de S'»
(semiextractado de Edwards, v.
7, pág. 425, editado). En
lenguaje natural, es que a partir
de cualquier S se puede
construir un subconjunto S' con
alguna propiedad particular
incluso si no se puede
especificar un procedimiento
para elegir los elementos
individuales de S' [Zermelo
propuso el axioma de elección a
principios del siglo XX. Es
demasiado técnico para intentar
desarrollarlo aquí,[7.99] pero una
consecuencia importante del
A. E. es el principio del buen
orden, o sea que cualquier
subconjunto S' de cualquier
conjunto S se puede elegir y
disponer de tal modo que S'
tenga un primer elemento. Ya
hemos visto la importancia de
este
principio
en
las
demostraciones con C1-1, por
ejemplo, la primerísima acerca
de que {Todos los enteros} y
{Todos los enteros positivos}
tienen la misma cardinalidad. El
principio del buen orden es
también crucial para las
demostraciones de Cantor de
que c > ℵ0 y P(E) > E, pues las
diversas
tablas
de
esas
demostraciones
obviamente
debían tener todas un primer
elemento. Pero el axioma de
elección
fue
también
terriblemente controvertido (por
ejemplo, puede usted entender
por qué los intuicionistas y los
constructivistas odiaban la idea
de que se pudiera designar un
subconjunto sin ningún tipo de
procedimiento para elegir sus
elementos), y se mantuvo como
una de las grandes polémicas de
la teoría de conjuntos hasta que
(1) Kurt Gödel en 1940
demostró la consistencia lógica
del A. E. con los demás axiomas
de la teoría de conjuntos, y
luego (2) el profesor Paul
Cohen[7.100] en 1963 demostró
la independencia lógica del
A. E. (es decir, la consistencia
de su negación) respecto a los
demás axiomas de la teoría de
conjuntos, demostraciones que,
juntas, se puede decir que
resolvieron
el
lío
del
axioma].[7.101]
Αx. 7. Este suele conocerse como el
axioma de regularidad (A. R.).
También tiene varias versiones.
La más simple es que si x es un
objeto o un conjunto, x ∉ x. Una
formulación más subida de tono
es: «Todo conjunto no vacío S
contiene un elemento x tal que S
y x no tienen ningún elemento
en común» (semiextractado de
Edwards, v. 7, pág. 426,
editado).[7.102] (El axioma de
regularidad de algún modo
encierra las objeciones de
Poincaré y Russell a la
autorreferencia, o en todo caso
es este axioma el que elimina la
antinomia de Russell. También
evita formulaciones como «el
conjunto de todos los conjuntos»
y «el conjunto de todos los
números ordinales» y así evita
la paradoja de Cantor y la
paradoja, que explicaremos
enseguida, de Burali-Forti.
Observe que también rechaza la
demostración de Cantor, basada
en φ, de que P(A) > A en §7e.
Este es el motivo de que exista,
separadamente, el axioma del
conjunto potencia que hemos
visto antes, del cual se puede
deducir P(A) > A sin ningún tipo
de demostración que viole el
axioma de regularidad. Pero, por
favor, sepa que incluso con el
A. R., axiomáticas como la de
ZFS aún pueden estar sujetas a
ciertas paradojas de la teoría de
modelos,[7.103] de modo que
ahora, digamos en las cercanías
del año 2000, hay toda una
jerarquía de axiomatizaciones
de la teoría de conjuntos, cada
una con su propia inmunidad
especial a las paradojas,
conocida entre los especialistas
como fuerza de consistencia. Si
está interesado —y porque por
lo menos sus nombres son
divertidos—,
los
sistemas
principales de hoy, en orden
creciente
de
fuerza
de
consistencia, son: los postulados
de Peano, analítico, ZFS, Mahlo,
VNB, quiniano, débilmente
compacto,
hiper-Mahlo,
inefable,
Ramsey,
supercompacto, y n-enorme).
FIN DE §7F S.-1.
§7g
Sin
duda habrá notado que hace un
buen rato que Georg Cantor même no
ha sido mencionado y quizá se haya
preguntado dónde está en toda la
turbulencia fundacional de §7f. Las
profilaxis de Poincaré y de Russell, las
axiomatizaciones de Zermelo, etc., son
todas de principios del siglo XX,
tiempo en el cual Cantor ya ha
realizado sus mejores trabajos y casi ha
abandonado las matemáticas en favor
de las preocupaciones obsesivas que
consumieron sus últimos años.[7.104]
También es en esta época cuando entra
y sale de hospitales continuamente. La
dolorosa ironía es que es justamente
cuando la obra de Cantor está ganando
amplia aceptación y la teoría de
conjuntos está floreciendo en las
matemáticas y la lógica, cuando su
enfermedad se pone realmente fea, y
hay todo tipo de congresos especiales y
entregas de premios a las que no puede
asistir
porque
está
demasiado
indispuesto.
Más directamente relevante es que
incluso cuando Cantor se encontró por
primera vez con sus paradojas en la
década (probablemente) de 1880, no se
preocupó demasiado acerca de ellas, o
más bien no podía, porque tenía otros
problemas más apremiantes. De
matemáticas. Uno de los más
importantes es lo que ahora se conoce
como la hipótesis del continuo.[7.105]
La H. C. se caracteriza de toda clase de
formas —«¿Es la potencia del continuo
equivalente a la de la segunda clase de
números?»; «¿Son los números reales
el conjunto potencia de los números
racionales?»; «¿Es c lo mismo que
2ℵ0?»; «Es c = ℵ1?»— pero todas
ponen el dedo en la llaga. Cantor ya ha
demostrado que hay una jerarquía
infinita de conjuntos infinitos, así
como sus conjuntos potencia, y ha
demostrado que P(A) = 2A y 2A > A son
teoremas para conjuntos infinitos. Pero
todavía no ha demostrado cómo se
relacionan exactamente esos distintos
resultados. La cuestión central es si lo
de 2A > A constituye una ley
exhaustiva acerca de cómo se dispone
la jerarquía transfinita —es decir, si
para cada conjunto infinito A el
siguiente conjunto mayor es siempre
2A, sin ∞ intermedios entre ellos— y,
por lo tanto, si este proceso de —
exponenciación binaria— es la manera
de ir de un conjunto infinito al
siguiente, del mismo modo en que la
suma permite ir de un número entero al
siguiente. Un sí a esta larga pregunta es
la hipótesis del continuo. Lo que se
considera ahora como la forma general
de la H. C. es 2ℵn = ℵn+1,[7.106] pero la
versión original de Cantor es más
específica. Sabemos que ha demostrado
la existencia y cuáles son las
cardinalidades de dos conjuntos
infinitos distintos, concretamente el
conjunto
de
todos
los
enteros/racionales/algebraicos (= ℵ0) y
el de todos los reales/trascendentes,
equivalente también a los intervalos y
espacios continuos (= c); y ha
demostrado que c > ℵ0. Su propia
hipótesis del continuo es que c = 2ℵ0,
es decir, que c es en realidad ℵ1, el
conjunto
infinito
que
sigue
inmediatamente a ℵ0, sin nada en
medio.[7.107]
Los intentos
de
Cantor
de
demostrar la H. C. se produjeron a lo
largo de las décadas de 1880 y 1890, y
hay algunas conmovedoras cartas en
las que anunciaba con excitación a
Dedekind una demostración y entonces
un par de días más tarde descubría un
error y tenía que echarse atrás. Nunca
la demostró ni demostró que fuera
falsa, y algunos historiadores de la
tendencia pop piensan que la H. C. es
lo que realmente desquició a Cantor.
Matemáticamente hablando, la
verdad acerca de la hipótesis del
continuo es más complicada de lo que
los escritores pop dejan traslucir,
porque en realidad Cantor llega a los
diversos problemas de la H. C. a través
de su trabajo sobre números ordinales,
cuyas relaciones son más o menos
como la de «R =
(P', P'', P''', …)» en
§7b, y que, a pesar de nuestras mejores
intenciones, ahora tenemos que
esquematizar muy brevemente.[7.108]
En primer lugar, para ahorrar tiempo,
por favor recuerde o relea la nota 78 de
§5e(1) y su manual básico sobre
enteros ordinales y cardinales. Ahora
estamos interesados en los números
ordinales en la teoría de conjuntos, que
son un poco diferentes, e involucran el
concepto de tipos de orden de los
conjuntos.
Explicación
simple:
sabemos que si los conjuntos A y B
tienen el mismo número cardinal, se
pueden poner en C1-1. Si esta C1-1 se
puede hacer de tal modo que el orden
de los elementos de A y B quede sin
modificar, entonces A y B son del
mismo tipo de orden. (Un ejemplo
sencillo y directo de dos conjuntos con
la misma cardinalidad pero diferentes
tipos de orden era {Todos los enteros
positivos y Todos los enteros} en §7c.
Recuerde que tuvimos que apañar el
orden de este último para que tuviera
un primer elemento que se pudiera
emparejar con el 1 de los enteros
positivos).
Puede ver por qué esto va a ser más
complicado que los cardinales: ahora
nos preocupamos no solo de la cantidad
de elementos de un conjunto, sino
también de su disposición. O más bien
disposiciones, porque las posibles
permutaciones de dichas disposiciones
son buena parte del meollo de la teoría
de ordinales. Meollo al que vamos a
echar un vistazo, aunque debería usted
tener en cuenta que hay gran cantidad
de términos técnicos y distinciones
—«ordenado»,
«bien
ordenado»,
«parcialmente ordenado», «denso por
doquier», «número de relación»,
«teorema de numeración», y así
sucesivamente— de las que vamos a
ignorar la mayoría.[7.109] Algunos
hechos básicos: para conjuntos finitos,
cardinalidad = tipo de orden; es decir,
dos conjuntos finitos con el mismo
número cardinal tendrán de manera
automática el mismo tipo de orden.
Esto se debe a que hay exactamente un
tipo de orden para todos los conjuntos
de un elemento, un tipo de orden para
todos los conjuntos de dos elementos, y
así sucesivamente.[7.110] El número
total de posibles tipos de orden para
conjuntos finitos es, de hecho, lo
mismo que el número cardinal del
conjunto de los enteros positivos, o sea,
ℵ0. Pero con los conjuntos infinitos,
los tipos de orden se complican. Lo
cual no debería sorprendernos. Tómese
el recién mencionado conjunto infinito
numerable de todos los enteros
positivos: {1, 2, 3, 4, …} tiene más de
un tipo de orden. Esto no significa solo
intercambiar algunas tiras de números
en la sucesión infinita, pues el conjunto
todavía se podrá poner en C1-1 con el
conjunto original de los enteros
positivos, incluso si la correspondencia
es algo parecido a
Pero si toma usted uno de los
elementos del conjunto de los enteros y
lo pone en último lugar, como en {1, 3,
4, 5, 6, 7, …, 2}, ahora tiene un tipo de
orden totalmente diferente. El conjunto
{1, 3, 4, 5, 6, 7, …, 2} ya no se puede
poner en C1-1 con un conjunto ℵ0
normalmente ordenado que no tiene
último elemento y, por lo tanto, no le
da ningún modo de llegar a nada que se
pueda emparejar con el 2. Además,
observe que en el nuevo tipo de orden,
2 se convierte en un número ordinal
diferente: ya no es el 2.º elemento de
un conjunto sino ahora más bien el
último elemento, y no tiene ningún
número en concreto inmediatamente
antes que él. De aquí la definición de
número ordinal: es un número que
identifica dónde aparece cierto
elemento de un conjunto en cierto tipo
de orden.[7.111]
En la teoría de conjuntos cantoriana
hay dos reglas principales para generar
números ordinales, (1) Dado cualquier
número ordinal n, siempre se puede
obtener el siguiente ordinal, que es
n + 1. (2) Dado cualquier conjunto N
de n ordinales ordenado en sucesión
creciente (por ejemplo, el conjunto de
los enteros positivos), siempre se
puede obtener un último ordinal mayor
que todos los demás n. Este ordinal
final técnicamente funciona como el
límite de la sucesión de N y se puede
expresar como «Lim(N)».[7.112] Esas
reglas no tienen mal aspecto, pero las
cosas empiezan a complicarse cuando
consideramos no solo conjuntos de
números ordinales, sino números
ordinales como conjuntos, lo cual
podemos hacer porque un principio
básico de la teoría de conjuntos es que
todos los entes matemáticos se pueden
representar como conjuntos (por
ejemplo, el cardinal transfinito «ℵ0» es
el conjunto de números cardinales
{1, 2, 3, 4,…}; además, recuerde la
observación ante rem en §2a de que
«5» es literalmente el conjunto de
todos los quíntuplos). Pero así,
entonces, un número ordinal n, ¿qué
conjunto es? La respuesta es la tercera
gran regla de Cantor: para cada ordinal
n, n = el conjunto de todos los
ordinales menores que n; es decir, n se
identifica simplemente con el conjunto
de ordinales del cual es el límite.[7.113]
O, en términos formales,[7.114]
n = (∀x)x < n). Se puede generar toda
la secuencia de los enteros normales
(ya sea como cardinales o como
ordinales)
de
este
modo:
0 = (∀x)x < 0} = ∅;
1 = (∀x)x < 1} = {0};
2 = (∀x)x < 2} = {0,1};
y
así
sucesivamente. El número ordinal de
todo el conjunto infinito numerable
{0, 1, 2, 3, 4, …} es simbolizado por
omega minúscula, ω. Este ordinal
transfinito es el límite de la sucesión
de elementos del conjunto; es decir, es
el más pequeño de los números
mayores que todos los enteros finitos.
Otra manera, más común, de describir
ω es como el número ordinal de aquel
conjunto del cual ℵ0 es el número
cardinal.[7.115]
INTERPOLACIÓN SEI
Por duro que pudiera parecer el
último párrafo, casi todo lo que va más
lejos en la teoría de ordinales es tan
brutalmente abstruso y técnico que solo
podemos hacer algunas observaciones
generales. Una es que la aritmética de
los ordinales transfinitos es distinta a
la de los cardinales transfinitos, pero
no menos extraña; por ejemplo
(1 + ω) = ω, pero (ω + 1) > ω, ya que
por definición (ω + 1) es el ordinal
inmediatamente posterior a ω. Otra es
que, como en el caso de los ℵ
cardinales, se puede generar una
jerarquía
infinita
de
ordinales
transfinitos de conjuntos infinitos de
ordinales (puede que usted quiera leer
esta última frase otra vez), aunque en
este caso es un proceso muy diferente a
lo de 2ℵn = ℵn+1. La jerarquía
transfinita-ordinal está asociada con
entes abstractos llamados números
épsilon y con una operación aritmética
llamada tetración. No hablaremos de
los primeros excepto para decir que
esencialmente son una clase de
números tales que ωε= ε.[7.116] Pero la
tetración es más simple, y puede que ya
esté familiarizado con ella si estudió
muchas matemáticas en primeros
cursos de carrera o tuvo asignaturas
como teoría de cuerpos o combinatoria.
Básicamente es una exponenciación
delirante. La 4.ª tetración de 3 se
33
expresa como «43» y significa 33 , que
9
es = 33 , que es = 319.683, un valor
cuyo cálculo puede usted aceptar como
desafío. La relación técnica entre la
tetración, los ordinales transfinitos y
los números épsilon es el hecho de que
ε0 = ωω, que no es tan importante. Pero
si puede usted concebir, en abstracto,
una progresión como ω, ((ω + 1),
ω
(ω + 2), …, (ω + ω)), ω2, ωω, ωω, ωω,
…, entonces puede usted hacerse una
idea —o en todo caso una «idea»— de
la jerarquía y de las impensables
alturas de los números ordinales de
conjuntos infinitos de conjuntos
infinitos de ordinales de conjuntos
infinitos que involucra (sospechoso
parecido con Rucker, Infinity and the
Mind, págs. 74-75). Fin de las
observaciones generales.
FIN DE LA INTERPOLACIÓN SEI
Muy bien, o sea que el modo
específico en que Cantor se topa con la
hipótesis del continuo concierne a los
ordinales y los tipos de orden. Hemos
visto que hay más de un tipo de orden
para los conjuntos infinitos, como en el
caso de {1, 2, 3, 4, …} y {1, 3, 4, 5, 6,
7, …, 2}, no hace muchos párrafos.
Hay, de hecho, una infinidad de tipos
de orden distintos para cualquier
conjunto infinito, y lo que Cantor
demuestra[7.117] es que el conjunto de
posibles tipos de orden para un
conjunto infinito numerable es, en
cambio, no numerable. Esto significa
que hay una manera más de generar
una jerarquía infinita de conjuntos
infinitos: si S es un conjunto infinito
numerable, entonces Z es el conjunto
infinito no numerable de posibles tipos
de orden de S, y Z' será el conjunto de
posibles tipos de orden de Z, y…, y allá
vamos. (En realidad, decir que los
distintos procesos para obtener
jerarquías del ∞ son «distintos» es un
poco engañoso, porque la verdad es que
están relacionados de todo tipo de
formas. Las matemáticas de esas
relaciones están más allá del alcance
técnico de este libro y no las
trataremos aquí, pero puede por lo
menos hacerse una idea de ellas a partir
de la definición técnica que da Cantor
del conjunto Z [teniendo en cuenta que
«clase numérica» en realidad se refiere
a conjuntos de ordinales], a saber: «La
segunda clase numérica Z(ℵ0) es la
totalidad {α} de todos los tipos de
orden α de conjuntos bien ordenados de
cardinalidad ℵ0») (Cantor, pág. 44).
Pero no se necesita profundizar
tanto. Dejando fuera los ordinales
transfinitos como ω, todavía podemos
ver una marcada similitud, con
seguridad no casual, entre: (1) c como
conjunto de todos los números reales (y
no de todos los racionales, que es ℵ0);
(2) ℵ1 como conjunto potencia de ℵ0,
es decir, como 2ℵ0; (3) Z como el
conjunto de todos los tipos de orden de
ℵ0. El auténtico problema es que
Cantor no puede demostrar cierta
relación crucial entre estas tres
identidades. Recordará de hace un par
de páginas que la H. C. original de
Cantor es que (1) y (2) son lo mismo,
que c = 2ℵ0 = ℵ1, y que no hay ningún
tipo de ∞ intermedio entre ℵ0 y c.
Ahora estamos preparados para
entender por lo menos a grandes rasgos
cómo interviene aquí la relación (3).
En los últimos § de «Contribuciones…
Números» —a través de un proceso de
profundo
razonamiento
técnico,
imposible de resumir—, Cantor logra
deducir dos grandes cuestiones: (a) que
de ningún modo c puede ser > ℵ0, y (b)
que en caso de que sí exista algún
conjunto infinito que sea mayor que ℵ0
pero menor que c, este conjunto tiene
que ser el conjunto no numerable Z, o
sea la segunda clase numérica. Es la
cuestión (b) la que inspira su principal
ataque a la H. C., el cual consiste en un
intento de demostrar que las anteriores
relaciones (2) y (3) son en realidad la
misma; es decir, si Cantor puede
demostrar que Z = 2ℵ0, entonces por
(b) se podrá demostrar que no existe
ningún conjunto intermedio entre ℵ0 y
c, lo cual implicará que c = ℵ1.
Específicamente es Z = 2ℵ0 lo que no
pudo demostrar. Jamás. Pese a años de
estrujarse los sesos de manera
inimaginable. Si fue o no fue esto lo
que le desquició es una pregunta
imposible de contestar, pero es cierto
que su incapacidad de demostrar la
H. C. le dolió el resto de su vida: lo
consideraba su gran fracaso. Esto
también resulta triste en retrospectiva,
porque
ahora
los
matemáticos
profesionales saben exactamente por
qué Cantor no pudo ni demostrar ni
desmentir la H. C. Las razones son
profundas e importantes y llegan de
manera corrosiva hasta la raíz de la
consistencia formal de la teoría
axiomática de conjuntos, de modo
bastante parecido a como las
demostraciones de incompletitud de
Kurt Gödel desarraigan todas las
matemáticas como sistema formal. Una
vez
más,
los
problemas
correspondientes solo los podemos
esbozar o sintetizar.
La hipótesis del continuo y el antes
mencionado axioma de elección son los
dos grandes problemas acuciantes de la
teoría
de
conjuntos
temprana.
Particularmente respecto a la primera,
es importante distinguir entre dos
cuestiones diferentes. Una, metafísica,
es si la H. C. es verdadera o falsa. La
otra es si la H. C. se puede demostrar
formalmente, o desmentir, a partir de
los axiomas de la teoría de conjuntos
estándar.[7.118] Es la segunda cuestión
la
que
ha
sido
contestada
definitivamente, a lo largo de un
período de varias décadas, por Kurt
Gödel y Paul Cohen, a saber:
1938 Gödel demuestra formalmente
que la forma general de la
hipótesis del continuo es
consistente con los axiomas de
ZFS; es decir, que si la H. C.
misma se trata como un axioma
y se añade a los de la teoría de
conjuntos, entonces no puede
resultar ninguna contradicción
lógica.
1963 En uno de esos coups d’éclat
salidos de la nada que tanto
gustan a los eruditos de la
cultura pop y a los cineastas, un
joven profesor de Stanford
llamado
Paul
J.
Cohen
demuestra que la negación de la
H. C. general también se puede
añadir a los axiomas de ZFS sin
contradicción.[7.119]
Estos dos resultados juntos
establecen lo que ahora se conoce
como la independencia de la hipótesis
del continuo, lo cual significa que la
H. C. ocupa un lugar bastante parecido
al del axioma de las paralelas[7.120]
respecto al resto de la geometría de
Euclides: no se puede demostrar ni
contradecir a partir de los axiomas
estándar de la teoría de conjuntos.[7.121]
Además, recordará del § anterior que
Gödel y Cohen pueden obtener un
resultado parecido para el axioma de
elección, tan vital para las diversas
demostraciones en diagonal de Cantor;
Gödel demuestra que el axioma no se
puede contradecir dentro de ZFS/VNB;
Cohen, que no es demostrable en
ZFS/VNB.[7.122] Existen, como se ha
mencionado, sistemas axiomáticos
alternativos en los cuales la H. C. y el
A. E.: son demostrables/indemostrables
(por ejemplo, la teoría de conjuntos de
Quine está construida de tal modo que
el axioma de elección es contradictorio
prima facie), aunque muchos de esos
sistemas de consistencia enriquecida
usan el término «conjunto» de modos
que son terriblemente diferentes
respecto a las definiciones originales
de Cantor.
La
hipótesis
del
continuo
permanece viva de otras maneras. Es,
por ejemplo, la causa motivadora tras
varias axiomatizaciones teóricas y
extensiones de modelos de la teoría de
conjuntos en las cuales la H. C. y
diversos equivalentes se suponen[7.123]
demostradas o contradichas. Esos
sistemas especulativos están entre los
constructos más hiperabstractos de las
matemáticas modernas, e involucran
enrarecidos términos como «universos
cantónanos o de 1.er orden», «conjuntos
construibles o no construibles»,
«cardinales medibles», «ordinales
inaccesibles», «recursión transfinita»,
«super-completación» y muchos otros
cuya pronunciación resulta divertida
incluso si no se tiene una idea clara de
lo que se supone que significan.[7.124]
Para terminar, lo más importante que
debemos considerar es cómo repercute
la indemostrabilidad de la H. C. en la
otra gran cuestión: si la hipótesis es de
hecho verdadera. No es ninguna
sorpresa que haya n posibles visiones
diferentes acerca de esto. Un tipo de
enfoque formalista es que las distintas
axiomatizaciones
tienen
distintas
ventajas e inconvenientes, que la H. C.
será
demostrable/desmentible
en
algunas e indecidible en otras, y que el
sistema a adoptar dependerá del
propósito particular que se tenga. Otra
respuesta,
más
estrictamente
hilbertiana, será que, en realidad, en
este contexto, «verdadero» no puede
significar nada excepto «demostrable
en ZFS», y, por lo tanto, que la
independencia lógica de la H. C.
respecto a ZFS significa literalmente
que no es ni verdadera ni falsa.[7.125]
Un intuicionista puro será propenso a
ver todo el lío de la teoría de conjuntos
con
las
paradojas
y
la
indemostrabilidad
como
la
consecuencia natural de admitir dentro
de las matemáticas conceptos difusos y
no constructivos como los de conjunto,
subconjunto, ordinal, y, por supuesto,
∞ de tipo real.[7.126]
Pero
son
los
platónicos
matemáticos
(a
veces
también
conocidos como realistas, cantorianos
y/o
transfinitistas)
los
más
preocupados por la indecidibilidad, lo
cual es interesante, puesto que los dos
platónicos modernos más famosos son
Georg Cantor y Kurt Gödel, quienes
son conjuntamente responsables de, por
lo menos, dos tercios de todo el
desconcierto. La postura platónica en
este caso queda resumida con precisión
por Gödel, en un escrito acerca de su
demostración y la de Cohen respecto a
la independencia de la H. C.:
Solo alguien que (como el
intuicionista) niegue que los
conceptos y axiomas de la
teoría de conjuntos clásica
tengan
significado
alguno
podría estar satisfecho con tal
solución, no quien crea que
describen una realidad bien
determinada. Pues en realidad
la conjetura de Cantor debe de
ser o bien verdadera o bien
falsa, y su indecidibilidad a
partir de los axiomas tal como
se conocen hoy solo puede
significar que dichos axiomas
no contienen una descripción
completa de la realidad (Gödel,
«¿En qué […] Cantor?», pág.
268.
Versión
editada
semiextractada a partir de
Barrow, pág. 264).
Es decir, para un platónico
matemático, lo que las demostraciones
acerca de la H. C. demuestran
realmente es que la teoría de conjuntos
necesita hallar un conjunto mejor de
axiomas clave que el ZFS clásico, o por
lo menos necesitará añadir algunos
postulados más que sean —como el
axioma de elección— a la vez
«evidentes por sí mismos» y
consistentes con los axiomas clásicos.
Si está usted interesado, la visión
personal del propio Gödel era que la
hipótesis del continuo es falsa, que en
realidad hay toda una infinidad de ∞ al
estilo de Zenón anidados entre ℵ0 y c,
y que tarde o temprano debería hallarse
un principio que lo demostrara. Hasta
ahora no se ha hallado jamás tal
principio. Gödel y Cantor murieron
ambos en el confinamiento,[7.127] [7.128]
legándonos un mundo sin confines
finitos. Uno que gira, ahora, en una
nueva especie de vacío de lo formal.
Las
matemáticas
continúan
levantándose de la cama.
AGRADECIMIENTOS
Mi agradecido reconocimiento a las
siguientes personas por su ayuda:
Classena Bell, Jesse Cohen, Mimi
Bailey Davis, Jon Franzen, Bob Goris y
la jefa de departamento, Rochelle
Hartmann, Rich Morris, Erica Neely,
Joe Sears, Stephen Stern, John Tarter,
Jim Wallace, Sally Wallace y Bob
Wengert.
No hace falta decir que el autor es
el único responsable de cualesquiera
errores o imprecisiones que usted
pueda detectar en este manuscrito.
BIBLIOGRAFÍA
LIBROS
ABEL, NIELS H.,
Oeuvres complètes, v. 2,
Johnson reprint Corp., 1964.
ABIAN, ALEXANDER, The Theory of Sets
and Transfinite Arithmetic, W. B.
Saunders Co., 1965.
AULORN,
HOWARD,
Calculus with
Analyte Geometry, John Wiley &
Sons, 1980.
BARROW, JOHN D., Pi in the Sky:
Counting, Thinking and Being,
Clarendon/Oxford
University
Press, 1992.
BENACERRAF PAUL y PUTNAM HILARY
(eds.),
Philosophy
of
Mathematics: Selected Readings,
Prentice-Hall, 1964.
BENARDATE, J. A., Infinity: An Essay in
Metaphysics, Clarendon/Oxford
University Press, 1964.
BELL, ERIC T., Men of Mathematics,
Simon & Schuster, 1937.
BERLINSKI, DAVID, A Tour of the
Calculus, Pantheon Books, 1995.
BLACK, MAX, Problem of Analysis,
Cornell University Press, 1934.
BOYER, CARL,
A History of Mathematics,
2.ª ed. con Uta Merzbach, John
Wiley & Sons, 1991. [trad, cast.:
Historia de la matemáticas,
Alianza, Madrid, 2007.]
BROMWICH, T. J. L. y MACROBERT, T., An
Introduction to the Theory of
Infinite Series, 3.ª ed., Chelsea
Books, 1991.
BUNCH,
BRYAN
H.,
Mathematical
Fallacies and Paradoxes, Van
Nostrand Reinhold Co., 1982.
CANTOR, GEORG, Contributions to the
Founding of the Theory of
Transfinite Numbers, trad, de P. E.
B.
Jourdain,
Open
Court
Publishers, 1915; reimpresión =
Dover Books, 1960.
—, Transfinite Numbers: Three Papers
on Transfinite Numbers from the
Mathematische Annalen, G. A.
Bingley Publishers, 1941.
—,
Gessamelte
Abhandlungen
mathematischen
und
philosophischen Inhalts (= Obras
completas), Zermelo E. y Fraenkel
A. (eds.), 2.ª ed. G. Olms
Verlagsbuchhandlung, Hildesheim
FRG, 1966.
CAUCHY,
AUGUSTIN-LOUIS,
Cours
d’analyse algébrique = v. 3 de
Cauchy,
Oeuvres
completes,
2.ª ed., Gauthier-Villars, París,
1899.
Philosophie
mathématique, Hermann, París,
1962 (contiene versiones en
francés de toda la correspondencia
Cantor-Dedekind importante en
las págs. 179-251).
CHARRAUD,
NATHALIE,
Infini
et
Inconscient: Essai sur Georg
Cantor, Antrhropos, París, 1994.
CLAPHAM,
CHRISTOPHER
(ed.), The
Concise Oxford Dictionary of
Mathematics, 2.ª ed., Oxford
University Press, 1996.
COHEN, PAUL J., Set Theory and the
Continuum Hypothesis, W. A.
Benjamin, Inc., 1966.
CAVAILLÈS,
JEAN,
COPLESTON, FREDERICK,
A History of
Philosophy, v. I pt. II, Image
Books, 1962.
COURANT, RICHARD y HERBERT ROBBINS
(revisado por Ian Stewart), What
Is Mathematics? An Elementary
Approach to Ideas and Methods,
Oxford University Press, 1996.
[trad, cast.: ¿Qué son las
matemáticas?, Madrid]
DAUBEN, JOSEPH W. y GEORG CANTOR, His
Mathematics and Philosophy of
the Infinite, Princeton University
Press, 1979.
DEDEKIND, RICHARD, Essays on the
Theory of Numbers, trad, de
W. W. Beman, Open Court
Publishing Co., 1901; reimpresión
= Dover Books, 1963.
EDWARDS, PAUL (ed.), The Encyclopedia
of Philosophy, 1.ª ed., v. 1-8,
Collier MacMillan Publishers,
1967.
ERLICH, P. E. (ed.), Real Numbers,
Generalizations of the Reals, and
Theories of Continua, Kluwer
Academic Publishers, 1994.
FOURIER, J.-B. JOSEPH, Analytic Theory of
Heat, Dover Books, 1952.
FRAENKEL, ABRAHAM, Set Theory and
Logic,
Addison-Wesley
Publishing Co., 1966.
GALILEI,
GALILEO,
Dialogues
Concerning Two New Sciences,
Dover Books, 1952. [trad, cast.:
Diálogos acerca de dos nuevas
ciencias, Buenos Aires, Losada].
GLEASON, ALAN, Who Is Fourier?
Transnational
College
of
LEX/Language
Research
Foundation, 1995.
GÖDEL, KURT, The Consistency of the
Axiom of Choice and of the
Generalized
ContinuumHypothesis with the Axioms of Set
Theory, Princeton University
Press, 1940.
GRATTAN-GUINNESS, IVOR (ed.), From the
Calculus to Set Theory, Gerald
Duckworth & Co., Londres, 1980.
[Hay trad, cast.: Del cálculo a la
teoría de conjuntos, 1630-1910:
una
introducción
histórica,
Alianza, Madrid, 1984.]
HALBERG, LELAND r. y ZINK HOWARD,
Mathematics for Technicians, with
an Introduction to Calculus,
Wadsworth Publishing Co., 1972.
HALLETT,
MICHAEL,
Cantorian Set
Theory and Limitation of Size,
Oxford University Press, 1984.
HARDY, G. H., Divergent Series, Oxford
University/Clarendon Press, 1949.
—, A Mathematician's Apology,
Cambridge University Press,
1967/1992. [Hay trad, cast.:
Apología de un matemático,
Nivola, Madrid, 1999.]
HEATH, T. L., The Thirteen Books of
Euclid’s Elements, v. 1-3, Dover
Books, 1954.
HONOUR, HUGH y JOHN FLEMING, The
Visual Arts: A History, PrenticeHall, 1982.
HUNTER, GEOFFREY, Metalogic: An
Introduction to the Metatheory of
Standard First Order Logic,
University of California Press,
1971.
HUNTINGTON, E. V., The Continuum and
Other Types of Serial Order, with
an Introduction to Cantor’s
Transfinite Numbers, Harvard
University Press, 1929.
KLEENE, STEPHEN, C., Introduction to
Metamathematics, Van Nostrand,
1952.
KLINE, MORRIS, Mathematical Thought
from Ancient to Modern Times, v.
1-3, Oxford University Press,
1972. [Hay trad, cast.: El
pensamiento matemático de la
Antigüedad a nuestros días,
Alianza, Madrid.]
KLIR, GEORGE J. y BO YUAN, Fuzzy Sets
and Fuzzy Logic: Theory and
Applications, Prentice-Hall, 1955.
LAVINE, SHAUGHAN, Understanding the
Infinite, Harvard University Press,
1994.
MANCUSO, PAOLO (ed.), From Brouwer
to Hilbert: The Debate on the
Foundations of Mathematics in
the 1920s, Oxford University
Press, 1998.
McCALLUM, W. G., HUGHES-HALLETT D. y
A. M. GLEASON, Multivariable
Calculus (versión en borrador),
John Wiley & Sons, 1994.
McKEON, RICHARD (ed.), Basic Works of
Aristotle, Random House, 1941.
MENDELSON, ELLIOTT, Introduction to
Mathematical Logic, 2.ª ed., D.
Van Nostrand Co., 1979.
MILLER, ROBERT,
Bob Miller’s Calc I
Helper, McGraw-Hill, 1991.
NELSON, DAVID (ed.), The Penguin
Dictionary
of
Mathematics,
2.ª ed., Penguin Books, 1989.
PAPPAS,
THEONI,
Mathematical
Scandals, Wide World Publishing,
1997.
POINCARÉ, HENRI, Mathematics and
Science: Last Essays, trad, de J.
W. Boldue, Dover Books, 1963.
QUINE, W. V. O., Set Theory and Its
Logic,
Belknap/Harvard
University Press, 1963.
RIEMANN, GEORG F. B.,
Collected
Mathematical
Works,
Dover
Books, 1953.
RUCKER, RUDY, Infinity and the Mind,
Birkhäuser Boston, Inc., 1982.
RUSSELL, BERTRAND, Introduction to
Mathematical Philosophy, Allen
and Unwin, Londres, 1919.
—, Mysticism and Logic, Doubleday
Anchor Books, 1957.
—, Principles of Mathematics, 2.ª ed.,
W. W. Norton & Co., 1938.
RYLE, GILBERT, Dilemmas: The Tamer
Lectures
1953,
Cambridge
University Press, 1960.
SAINSBURY,
R.
M.,
Paradoxes,
Cambridge University Press,
1987.
Cours de
linguistique générale (R. Engler
[ed.]), Harrasowitz, Wiesbaden,
1974. [trad, cast.: Curso de
lingüística general, Buenos Aires,
Losada.]
SEIFE, CHARLES, Zero: The Biography of
a Dangerous Idea, Viking Press,
2000. [Hay trad, cast.: Cero. La
biografía de una idea peligrosa,
Castellón, Ellago].
SIERPINSKI, WACLAW, Hypothèse du
Continu,
Monografie
Matematyczne, Warsaw, 1934.
SUPPES, PATRICK, Axiomatic Set Theory,
D. Van Nostrand Co., 1965. [trad.
cast.: Teoría axiomática de
SAUSSURE,
FERDINAND
DE,
conjuntos, Norma, Barcelona].
University of St. Andrews, MacTutor
History of Mathematics, Web Site:
www.​groups.​dcs.​st-and.​ac.​uk/​
~history
VINOGRADOV,
I.
M.
(ed.), Soviet
Mathematical Encyclopedia, v. 9,
Kluwer Academic Publishers,
1993.
[Hay
trad,
cast.:
Enciclopedia de las matemáticas,
Mir, 1999].
WEISSTEIN, ERIC W., CRC Concise
Encyclopedia of Mathematics,
CRC Press, 1999.
WEYL,
HERMANN,
Philosophy
of
Mathematics and Natural Science,
Princeton University Press, 1949.
ARTÍCULOS Y ENSAYOS
BERKELEY, GEORGE,
«The Analyst, Or a
Discourse Addressed to an Infidel
Mathematician Wherein It is
Examined Whether the Object,
Principles, and Inferences of the
Modern Analysis are More
Distinctly Conceived, or More
Evidently Deduced, than Religious
Mysteries and Points of Faith.
“First Cast the Beam Out of Thine
Own Eye; and Then Shalt Thou
See Clearly to Cast Out the Mote
Out [sic] of Thy Brother’s Eye”»,
en Luce A. A. (ed.), The Works of
George Berkeley, Bishop of
Cloyne, Thomas Nelson & Sons,
1951.
BORGES, JORGE L., «Avatars of the
Tortoise», en Yates D. y Irby J.
(eds.),
Labyrinths,
New
Directions, 1962, págs. 202-208.
[Ed. orig.: «Avatares de la
tortuga», en Discusión, Obras
Completas, vol. 3, Sudamericana,
1932].
BROUWER, LUITZEN E. J., «Intuitionism
and Formalism», trad, de A.
Dresden, Bulletin of the American
Mathematical Society v. 30, 1913,
págs. 81-96.
CANTOR, GEORG, «Foundations of the
Theory of Manifolds», trad, de U.
R. Parpart, The Campaigner, n.º 9,
1976, págs. 69-97.
—, «Principien einer Theorie der
Ordnungstypen» (= «Principles of
a Theory of Order-Types»), mss.
1885, en Grattan-Guinness I., «An
Unpublished Paper by Georg
Cantor», Acta Mathematica v.
124, 1970, págs. 65-106.
DAUBEN JOSEPH W., «Denumerability
and Dimension: The Origins of
Georg Cantor’s Theory of Sets»,
Rete v. 2, 1974, págs. 105-135.
—, «Georg Cantor and Pope Leo XIII:
Mathematics, Theology, and the
Infinite», Journal of the History of
Ideas v. 38, 1977, págs. 85-108.
—, «The Trigonometric Background to
Georg Cantor’s Theory of Sets»,
Archive for the History of the
Exact Sciences, v. 7, 1971, pp·
181-216.
FREUDENTHAL, H. N., «Did Cauchy
Plagiarize Bolzano?», Archive for
the History of the Exact Sciences,
v. 7, 1971, págs. 375-392.
GÖDEL, KURT, «Russell’s Mathematical
Logic», en P. A. Schlipágs (ed.),
The Philosophy of Bertrand
Russell, Northwestern University
Press, 1944.
—, «What is Cantor’s Continuum
Problem?», en Benacerraf y
Putnam,
Philosophy
of
Mathematics, págs. 258-273.
GRATTAN-GUINNESS, IVOR, «Towards a
Biography of Georg Cantor»,
Annals of Science, v. 27 n.º 4,
1971, págs. 345-392.
HARDY, G. H., «Mathematical Proof»,
Mind, v. 30, 1929, págs. 1-26.
HILBERT,
DAVID,
«Uber
das
Unendliche», Acta Mathematica,
v. 48, 1926, págs. 91-122.
HILL, LEONARD, «Fraenkel’s Biography
of Georg Cantor», Scripta
Mathematica, n.º 2, 1933, págs.
41-47.
ROBINSON, ABRAHAM, «The Metaphysics
of the Calculus», en J. Hintikka
(ed.),
The
Philosophy
of
Mathematics, Oxford University
Press, 1969, págs. 153-163.
RUCKER, RUDOLF V. B., «One of Georg
Cantor’s Speculations on Physical
Infinities»,
Speculations
in
Science and Technology, 1978,
págs. 419-421.
—, «The Actual Infinite», Speculations
in Science and Technology, 1980,
págs. 63-76.
RUSSELL, BERTRAND,
«Mathematical
Logic as Based on the Theory of
Types», American Journal of
Mathematics, v. 30, 1908-09,
págs. 222-262.
SIERPINSKI,
WACLAW,
«L’Hypothèse
généralisé du continu et Paxiome
du
choix»,
Fundamenta
Mathematicae, v. 34, 1947, págs.
1-6.
WANG, H., «The Axiomatization of
Arithmetic», Journal of Symbolic
Logic, v. 22, 1957, págs. 145-158.
WILDER, R. L., «The Role of the
Axiomatic Method», American
Mathematical Monthly, v. 74,
1967, págs. 115-127.
WILL, FREDERICK,
«Will the Future Be
Like the Past?», en A. Flew (ed.),
Logic and Language, 2nd Series,
Basil Blackwell, Oxford UK,
1959, págs. 32-50.
DAVID FOSTER WALLACE. (21 de
febrero de 1962 - 12 de septiembre de
2008). Fue un autor estadounidense, que
escribió novelas, ensayos, y cuentos, y
trabajó como profesor en Pomona
College en Claremont. Fue extensamente
conocido por su novela Infinite Jest (La
broma infinita), que era considerada
por la revista Time como una de las 100
mejores novelas en lengua inglesa del
período comprendido entre 1923 y
2006.
David Ulin, un editor de libros para The
Los Angeles Times, llamó Wallace «uno
de los escritores más influyentes e
innovadoras de los últimos 20 años».
Una novela inacabada de Wallace, The
Pale King (El rey pálido), fue publicada
en 2011. Se prevé la publicación de una
biografía de Wallace escrita por D. T.
Max en 2012.
Notas
[0.1] SEI
Aquí tenemos un buen ejemplo
de curiosidad SEI. El autor, aquí
presente, es alguien con un interés de
aficionado
medio-alto
en
las
matemáticas y los sistemas formales.
También es alguien a quien se le
atravesaron las matemáticas en todos
los cursos a los que asistió, excepto
uno, que ni siquiera fue en la
universidad, pero que estaba impartido
por uno de esos raros especialistas que
pueden hacer que lo abstracto resulte
vivo y llamativo, y que te hablan
realmente cuando dan la lección, y de
quien todo lo que pueda ser bueno de
este librito es un pálido
bienintencionado reflejo. <<
y
[1.1] SEI
Halle, una mina de sal río
arriba cerca de Leipzig, más conocida
como el lugar de nacimiento de
Händel. <<
[1.2] SEI
aunque también lo es el otro
estereotipo, en las antípodas de este, de
los matemáticos como pequeñas
criaturas empollonas con pajarita. En la
arquetipología contemporánea, ambos
estereotipos parecen combinarse de
maneras importantes. <<
[1.3]
En términos médicos modernos,
resulta bastante claro que Georg F. L.
P. Cantor padecía un trastorno
maníaco-depresivo en una época en la
que nadie sabía lo que era, y que sus
ciclos bipolares se vieron agravados
por
tensiones
profesionales
y
decepciones, las cuales a Cantor no le
faltaron. Por supuesto, esto no da un
titular tan interesante como Genio
Enloquecido por Intentar Lidiar con el
∞. La verdad, sin embargo, es que el
trabajo de Cantor y su contexto son tan
interesantes y bellos que no hay
necesidad de convertir la vida de este
pobre tipo en una vacía alegoría
prometeica. La verdadera ironía es que
la visión del ∞ como una zona
prohibida o camino a la locura —visión
muy antigua y poderosa que acechó a
las matemáticas durante más de dos
mil años— es precisamente lo que la
obra de Cantor derribó. Decir que el ∞
enloqueció a Cantor es como lamentar
la derrota de san Jorge ante el dragón:
no solo es falso, sino insultante. <<
[1.4] SEI
Boyer comparte únicamente
con el profesor Morris Kline la cima de
la «cadena alimentaria» de los
historiadores de las matemáticas. Las
obras principales de Boyer y Kline son
respectivamente Historia de las
matemáticas
y
El
pensamiento
matemático de la Antigüedad a
nuestros días. Ambos libros son
excelentes
y
extraordinariamente
completos, por lo que los citaremos
con frecuencia. <<
[1.5]
Respecto a esto, Bertrand Russell
tiene un párrafo interesante sobre las
matemáticas de nivel intermedio,
donde suele darse el siguiente gran
salto de abstracción tras la aritmética:
«Al empezar álgebra, incluso el
muchacho
más
inteligente
se
encuentra, por regla general, con
grandes dificultades. El uso de letras es
un misterio, que parece no tener otro
propósito que la mistificación. Es casi
imposible, al principio, no pensar que
cada letra representa algún número en
particular, y que solamente el profesor
nos revelará qué número representa. El
hecho es que en el álgebra la mente
aprende por primera vez a considerar
verdades generales, verdades que no se
afirman solo de esta o aquella cosa en
particular, sino de cualquiera de un
grupo entero de cosas. Es en el poder
de entender y descubrir tales verdades
donde reside el dominio del intelecto
sobre todo el mundo de las cosas reales
y posibles; y la capacidad de tratar con
lo general en sí es uno de los dones que
una educación matemática debería
otorgar (Russell, Mysticism and Logic,
pág. 60)». <<
[*]
En inglés el resumen de un artículo
académico suele llamarse abstract. (N.
del t.) <<
[1.6]
SEI Según la mayoría de las
fuentes, Cantor no era únicamente un
matemático: tenía una auténtica
filosofía del infinito. Era extraña y casi
religiosa y, nada sorprendentemente,
abstracta. En cierto momento, Cantor
intentó cambiar su puesto de trabajo en
la
Universidad
de
Halle
del
Departamento de Matemáticas al de
Filosofía; la petición fue denegada.
Cabe reconocer que este no fue uno de
sus períodos más estables. <<
[1.7] SEI
La fuente de este pernicioso
mito es Aristóteles, quien desde cierto
punto de vista es el villano de todo
nuestro relato. <<
[1.8]
Una analogía aquí casi obligada es
el hecho de que la mayoría de nosotros
vamos en avión a pesar de saber que
cada año un determinado porcentaje de
aviones de pasajeros se estrellan. Pero
esto tiene que ver con las distintas
maneras de saber o «saber» (véase §1c
más
adelante).
También
está
relacionado con la urbanidad, pues los
viajes en avión son públicos y entra en
juego algo así como la confianza en el
grupo. Por ello, dirigirse a la persona
del asiento de al lado para informarle
de la probabilidad estadísticamente
calculada de que aquel avión se estrelle
no es incurrir en falsedad, sino en
crueldad: sería meterse con la delicada
infrastructura psicológica de su
justificación
para
volar.
SEI
Dependiendo del estado de ánimo o del
momento del día, podría resultarle a
usted curioso y parecerle interesante
que de las personas que no pueden
reunir esa extraña fe en principios que
no se pueden justificar racionalmente,
y, por lo tanto, no pueden volar, se diga
que tienen un «miedo irracional» a
volar. <<
[1.9] SEI
Resulta que lo único que
impidió a Wallis inventar el cálculo
diferencial en Arithmetica Infinitorum
fue su ignorancia del teorema del
binomio, el cual es esencial para
trabajar con infinitesimales. Véase esp.
§4 más adelante. <<
[1.10]
El singular e imponente doctor E.
Robert Goris, profesor de matemáticas
en el instituto, solía referirse a esto
como «mentalidad de sector privado»,
en el sentido de que se esperaban
resultados productivos reales. <<
[1.11] SEI
Por ello, la mayor parte de la
obra de Platón (y casi toda la de
Aristóteles)
es
acerca
de
la
conceptualización y la sistematización
de lo abstracto. <<
[1.12]
N. B. Independientemente del
significado, una verdad demostrada en
un sistema formal se conoce
técnicamente como un teorema, de aquí
el teorema de Pitágoras, etc. <<
[1.13]
Esta parte se requiere en la lógica
formal a causa de ciertas propiedades
del
operador
disyuntivo
«o».
Entraremos lo menos posible en esas
cosas tan crípticas. (Solo que, ya que
estamos, confesemos que estamos
usando la «LTE» de un modo informal
que también incluye el principio de
bivalencia. Dejar que la «LTE»
connote todo el edificio de la lógica
bivaluada está bien para nuestros
propósitos, pero sepa que no es 100%
riguroso). <<
[1.14]
Modus tollens (= «método de
negación» en latín) podría no parecer
una regla universal a menos que tenga
en cuenta que la implicación, como
relación lógica, no tiene que ver con la
causa sino con la certeza. En lógica
aplicada, los términos son condiciones
necesarias y suficientes. Si, por
ejemplo, P representa el enunciado
«mide 1,65 m de altura» y Q representa
«mide por lo menos 1,55 metros de
altura», entonces el significado
puramente lógico de «P → Q» se hace
evidente: en realidad significa que «Si
P es verdadera, Q no puede ser falsa en
modo alguno». Modus-tollenizar esto
como «no Q → no P» es simplemente
decir que si alguien no llega a los
1,55 m de altura, entonces no es
posible que mida 1,65 m. Dicho sea de
paso, otra relación lógica importante
que veremos bastante más adelante, en
§5e, podemos mencionarla ya aquí. Es
la relación de conjunción, que significa
«y» y se representa habitualmente
mediante «&» o «∧». La regla de oro es
que «P & Q» es verdadera solo cuando
P y Q son ambas verdaderas. Si
cualquiera de ellas es falsa, toda la
conjunción es falsa. <<
[1.15] SEI
Bueno, técnicamente, esto no
es tanto por la LTE como por la
definición de la conectiva lógica «no»,
cuya definición, sin embargo, o bien se
obtiene a partir de la LTE o (como
argumentan algunos) es lo mismo que
la LTE. N. B. Algunos sistemas
formales incluyen toda la transacción
de la reducción al absurdo como un
axioma, a veces llamado ley de
absurdidad. <<
[1.16]
Recordará del instituto que los
puntos suspensivos dentro de una
sucesión o serie significan «todos los
términos relevantes en medio». Si
están al final significan «y así
sucesivamente sin fin». Esta es una
abreviatura que se usa mucho en las
matemáticas puras. <<
[1.17]
De nuevo, estrictamente hablando
es algo más complicado pero, para
nuestros propósitos, la LTE servirá. <<
[1.18]
incluyendo
nuestra
esquizofrenia de la abstracción y, en
definitiva, el ser esclavos de la
tecnología y la razón científica. <<
SEI
[1.19]
Una de las razones por las que los
textos de matemáticas son tan
abstrusos y técnicos es por todas las
especificaciones y condiciones que
deben ponerse en los teoremas para
evitar las fisuras. En este sentido son
como documentos legales, y a menudo
su lectura es igual de divertida. <<
[1.20]
Recordará de las clases de
matemáticas
lo
especialmente
desagradables que resultaban las
dificultades para definir las cosas.
[Aquí
el
autor
se
refiere
específicamente a los problemas donde
un enunciado erróneamente formulado
induce a confusión. (N. del t.)]. <<
[1.21] SEI
Quede claro desde el principio
que «puede que recuerde usted» y «no
hace falta decir» y demás no son tics,
sino tácticas retóricas cuyo objetivo es
reducir las molestias de aquellos
lectores que ya están familiarizados
con lo que sea que se está discutiendo.
En realidad, no se necesita ninguna
experiencia en particular ni recordar
las matemáticas superiores para leer
este libro, pero parece por lo menos
razonable suponer que algunos lectores
tendrán una buena preparación
matemática, y simplemente lo educado
es admitirlo de vez en cuando. Como se
mencionó brevemente en el Prólogo, la
retórica de la escritura técnica está
cargada de incertidumbres acerca de
los niveles de experiencia de los
distintos lectores y sus curvas de
confusión-enojo. Nada de esto es su
problema, claro, por lo menos no
directamente. <<
[1.22]
Lo que viene a continuación no es
demasiado SEI, pero para seguirlo con
detalle probablemente necesitaría
haber estudiado algo de matemáticas
superiores, y si no es así no se
preocupe de nada más, excepto de
cómo el simbolismo tiene que cargarse
de salvedades. (SEI Y si estudió usted
los primeros cursos de cálculo y se da
cuenta de que nuestro simbolismo es
algo no estándar, tampoco se inquiete
por eso; más que nada porque todavía
no se ha definido ninguno de los
símbolos relevantes). <<
[1.23] SEI
= Definición 23 en el Libro I
de los Elementos. <<
[1.24] SEI
Esta está relacionada con una
cosa llamada la rueda de Aristóteles,
que es una historia en sí misma. <<
[1.25] SEI
Como veremos en §7, que
exista una correspondencia uno a uno
entre sus miembros en realidad ahora
es la definición de igualdad entre dos
conjuntos. <<
[1.26] SEI
Esto es un poco burdo. El
auténtico modo en que las matemáticas
neutralizaron el ∞ se basaba en cierta
distinción metafísica trazada por
Aristóteles para refutar a Zenón, a todo
lo cual llegaremos. <<
[1.27]
No es nada injusto mencionar que
Cantor se prodigó bastante en
declaraciones extravagantes durante la
controversia sobre los conjuntos
infinitos, muchas con un tono religioso
exageradamente grandilocuente, por
ejemplo: «No albergo duda alguna
respecto a la verdad de los transfinitos,
a los que he identificado con la ayuda
de Dios». (Cantor en la obra de Dauben
«Georg Cantor and Pope Leo XIII»,
pág. 106) o «El miedo al infinito es una
forma de miopía que destruye la
posibilidad de ver el infinito real, a
pesar de que este en su forma más alta
nos ha creado y nos sostiene» (Cantor,
Gessamelte Abhandlungen, pág. 374.
Traducción editada de un extracto de
Rucker, Infinity and the Mind, pág. 46).
<<
[1.28]
Naturalmente, se necesita tiempo
para
obtener
los
resultados
significativos que dan legitimidad a
una teoría matemática, e incluso más
tiempo para que sea plenamente
aceptada, y, por supuesto, durante ese
tiempo la cuestión locura-o-genio
permanece sin resolver, probablemente
incluso para el propio matemático, de
modo que este desarrolla su teoría y
elabora sus demostraciones en unas
condiciones de enormes tensiones y
dudas personales, y a veces ni siquiera
es reivindicado en vida, etc. <<
[2.1] SEI
Parece ser que el término to
apeiron se originó en la tragedia
griega, donde se refería a vestimentas o
ataduras «en las cuales uno se queda
enredado, sin escape». <<
[2.2] SEI
Probablemente valga la pena
destacar aquí que la descripción del
Génesis 1:2: «La tierra era caos y
confusión», es una manera plenamente
griega de caracterizar la pre-Creación.
<<
[2.3]
N. B. Este esteticismo helénico
nunca ha desaparecido de las
matemáticas, como se puede constatar
por el hecho de que una buena
demostración o un buen método se dice
que son «elegantes» o por la frase, muy
citada, de la Apología de Hardy: «La
belleza es la primera prueba; no hay
lugar permanente en el mundo para las
matemáticas feas» (Hardy, Apology,
pág. 85). <<
[2.4] SEI
En caso de que usted haya
notado que esta descripción suena
bastante platónica, sepa que, a pesar de
que Platón vivió un siglo más tarde que
Pitágoras, hay buenos indicios de que
entró en estrecho contacto con sus
sucesores, miembros de la D. Η. P.,
durante sus viajes por la Magna Grecia
(actualmente el sur de Italia, territorio
entonces colonizado por los griegos), y
que su metafísica de las matemáticas
subyace a la teoría de las «formas» del
propio Platón, respecto a lo cual véase
lo que sigue. <<
[2.5]
El concepto de «recta» de los
egipcios, por otro lado, era solo una
cuerda tensa, usada para delimitar el
terreno de alguien. <<
[2.6]
= a grandes rasgos «Todo es Uno»
+ «Nada cambia». <<
[2.7]
Lo que sigue no debería
clasificarse como SEI aunque usted ya
conozca la dicotomía, pues esta
discusión está hecha más bien a
medida. <<
[2.8]
Lo cual quiere decir, otra vez, que
lo siguiente solo tendrá sentido al
100% si ha estudiado usted las
matemáticas relevantes, y, una vez
más, no se preocupe si no lo hizo: lo
importante es la forma general del
razonamiento, que puede usted captar
sin conocer los símbolos/términos
específicos. (SEI De hecho, todos los
términos/símbolos
en
juego
se
definirán más adelante, pero no hasta
que los necesitemos). <<
[2.9]
Y, por supuesto, los estudiantes
raramente lo preguntan: las fórmulas
por sí solas son tan difíciles de
«entender» (es decir, de usar para
resolver problemas correctamente), que
a veces no nos damos cuenta de que no
las entendemos en absoluto. Que
acabemos sin saber siquiera todo lo que
ignoramos es la parte realmente
insidiosa de la mayoría de las clases de
matemáticas. <<
[2.10] SEI
Aquí se cita tanto a Russell
porque su prosa sobre todo esto es
extremadamente lúcida y acertada.
Además, observe el modo en que, como
los griegos, no hace ninguna distinción
real entre matemáticas y filosofía. <<
[2.11] SEI
en el sentido de que no tiene
un límite finito. Puede que la
convergencia y la divergencia no
adquieran pleno sentido hasta que
hablemos de los límites en §3c. Todo
lo que usted necesita en este punto es
una idea aproximada de la diferencia
entre la una y la otra, lo cual pretenden
ilustrar los gráficos. <<
[2.12] SEI
Los modos en los que eso no
es 100% cierto involucran a Eudoxo de
Cnidos, del cual tiende a hablarse
incluso menos que de Zenón. Véase
§2d más adelante. <<
[2.13] SEI
Todo lo que se sabe de las
paradojas de Zenón proviene de fuentes
secundarias, pues o bien Zenón no
escribió nada, o bien todo se perdió. La
paradoja anterior aparece célebremente
en el §209a de la Física de Aristóteles,
y observe cómo esta también gira
alrededor de cuestiones sobre la
ontología de las abstracciones,
particularmente en la transición del
paso (1) al paso (2). Además, si es
usted el tipo de persona que puede
mantener
cosas
aparentemente
irrelevantes en su cabeza durante varias
páginas, fíjese en que exactamente la
misma imprecisión metafísica de esta
P. Z. reaparecerá respecto a la
dicotomía en cuestiones acerca de qué
es exactamente un punto matemático,
como, por ejemplo, si un punto es una
abstracción geométrica, una ubicación
física real o ambas cosas. <<
[2.14]
Por ejemplo: 1) La curiosidad
mató al gato. 2) La bola de cordel más
grande del mundo es una curiosidad. 3)
Por lo tanto, la bola de cordel más
grande del mundo mató al gato. <<
[2.15]
Mediante la forma predicativa (o
«copulativa») de «ser», a causa de la
cual
aquí
la
predicación
es
problemática. <<
[2.16] SEI
en el Libro I, caps. 6 y 9.
Además, el
término metafísica
proviene del título de este libro, por
supuesto. Originalmente solo quería
decir que era el siguiente tratado de
Aristóteles tras la Física. <<
[2.17]
Una o dos curiosidades. Platón,
nacido Aristocles, vive entre el 427
a. C. y 347 a. C. aprox.; Aristóteles
vive entre el 384 a. C. y 322 a. C.
aprox. (compárese con Sócrates, 470
a. C.-399 a. C. aprox., y Zenón, 490
a. C.- 435 a. C. aprox.). Aristóteles
había sido un alumno estrella de la
Academia de Platón, encima de cuyo
portal curiosamente estaba inscrito el
lema QUE NO ENTRE AQUÍ NADIE QUE
SEA IGNORANTE EN GEOMETRÍA. <<
[2.18]
O por lo menos nuestra versión
simplificada de ella. <<
[2.19] SEI
Esto es un poco esotérico,
pero es para evitar posibles objeciones
a lo que sigue: Sí, en cierto sentido, si
«5» se entiende como una referencia o
indicación del conjunto de todos los
quíntuplos, entonces por los postulados
de Peano lo anterior es exactamente lo
que «5» es, aunque tanto «conjunto»
como los postulados de Peano son
dependientes de Cantor, o sea que nos
estamos adelantando literalmente dos
mil años. <<
[2.20]
SEI Véase, por ejemplo, esta
afirmación platónica clásica de Charles
Hermite (1822-1901, figura muy
destacada en teoría de números): «Creo
que los números y las funciones del
análisis no son el producto arbitrario de
nuestros espíritus: creo que existen
fuera de nosotros con el mismo
carácter de necesidad que los objetos
de la realidad objetiva; y los
descubrimos y los estudiamos como
hacen físicos, químicos y zoólogos
(Hermite en Barrow, pág. 259)». Como
irá saliendo probablemente en diversos
contextos a continuación, Bernhard P.
Bolzano, Richard Dedekind, y Kurt
Gödel son todos platónicos, y Georg F.
L. P. Cantor es por lo menos un
platónico en el armario. <<
[2.21]
Así como, claro está, cualquier
otra estatua jamás hecha, o imaginada,
o incluso no imaginada… <<
[2.22]
Como tantas cosas de
Aristóteles, esto no resulta fácil de
entender. La cuestión aquí es que
coexistir significa básicamente «existir
todos al mismo tiempo», lo cual es
imposible a causa del lapso de 23 horas
y 59 minutos entre cada repetición de
las 6:54 (estando dichos lapsos
incluidos en la misma definición de
«6:54»). En esencia, esta cuestión de la
Sucesión → No completación es
también el argumento de Aristóteles a
favor de que el Tiempo con mayúscula
es potencialmente pero no realmente
infinito, lo cual a su vez evita ciertas
SEI
paradojas de tipo Lámpara sobre la
eternidad y los momentos primero y
último. <<
[2.23] SEI
y para anticipar algunas cosas
que se discutirán en detalle en §4. <<
[2.24]
por así decirlo. <<
[2.25]
Solo como propuesta de reflexión:
no es trivial observar que los antiguos
griegos no tenían un verdadero
concepto de punto sin dimensión, algo
de extensión cero, pues no tenían 0. Y
quizá por lo tanto que, en cierto
sentido, la dicotomía era solo un
síntoma del verdadero problema de los
griegos, que era intentar hacer
matemáticas abstractas usando solo
cantidades concretas. <<
[2.26] SEI
en todo caso, el primero en la
práctica, el Libro VI de la Física se
lleva el mérito de hacerlo explícito. <<
[2.27]
En
las
escuelas
estadounidenses, la representación de
la recta numérica solía situarse encima
de la pizarra (o en la parte superior de
la pared de atrás en las aulas que tenían
retratos de los presidentes de EE. UU.
encima de la pizarra) y parecía algo así
como un termómetro tumbado. <<
SEI
[2.28] SEI
Más adelante, en §6f, veremos
la importancia de un criterio
completamente
diferente
de
«constructibilidad» para teoremas. <<
[2.29]
Los griegos también carecían de
estos últimos. <<
[2.30]
Por excitantes razones técnicas, a
las que llegaremos, la recta numérica
es más apropiadamente llamada recta
real si también representa los números
irracionales. Es decir, la «recta real» de
todos los números reales. Observe, por
cierto, que otro término matemático
para designar tanto el conjunto de los
números reales como a la recta real
resulta ser: el continuo. Probablemente
algo de todo esto será mencionado en
el texto, pero en algún punto deberá
resumirse la cuestión de la recta
numérica y la recta real, y este es un
lugar tan bueno como cualquier otro.
Sepa que las matemáticas y la
metafísica de ambos tipos de recta son
sin duda difíciles. Comparten tres
características cruciales, y la recta real
tiene una cuarta característica. Ambos
tipos de recta son por definición
infinitamente extensos, ambos son
infinitamente densos (= entre dos
puntos cualesquiera siempre hay otro
punto), y ambos son «sucesivos» u
«ordenados» (lo cual básicamente
significa que para cualquier punto n
(n − 1) < n < (n + 1)). La recta real,
además, tiene la propiedad de ser
continua, lo cual en este caso quiere
decir que no tiene huecos o agujeros.
Tenga en cuenta, para más adelante,
que es la continuidad de la recta real en
este sentido lo que acaba abriendo una
grieta en las matemáticas modernas.
Sin embargo, como se ha mencionado
justo antes en el texto principal, la
dicotomía de Zenón no necesita nada
más que la densidad de la recta
numérica para crear la paradoja. Por
esta razón, la dicotomía se puede
reformular tan fácilmente para
eliminar el tiempo/movimiento: su
RIV involucra cruzar no un espacio
real, sino solo el intervalo 0-1 de la
recta numérica. Es este segundo tipo en
particular de ∞, denso e inter-
numérico, que Aristóteles quiere
descartar calificándolo de meramente
«potencial». Finalmente, observe, por
favor, que en ciertos apartados a partir
de ahora y hasta §6 vamos a hablar
como si la recta numérica y la recta
real fueran la misma cosa, o como si la
recta numérica también pudiera
representar números irracionales. Esto
se debe a complicadas razones que
involucran la traducción de complejas
demostraciones al lenguaje natural,
pero no se preocupe por ello, solo le
conviene recordar el estatus especial de
la recta real hasta dentro de varios §s,
cuando resultará importante. <<
[2.31] SEI
El término anglosajón surd
era el preferido del doctor Goris porque
sostenía que su pronunciación era
mucho más divertida. Si alguien decía
«número irracional», él hacía como si
no pudiera oírle, lo cual, si conoce
usted la etimología de surd, verá que
también era una especie de broma entre
él y nosotros. [La etimología a la cual
se refiere el autor es la raíz latina
surdus, la misma de la cual proviene
«sordo». Hay una interesante relación
histórica, etimológica y conceptual
entre «irracional» y «sordo», que se
remonta al griego alogos, que podía
significar «sin razón» o «sin habla».
(N. del t.)]. <<
[2.32] SEI
Por supuesto, esto también
funciona como una demostración de
que la √2 es irracional, y así lo
presentó en clase por primera vez el
doctor Goris. <<
[2.33]
Por así decirlo. <<
[2.34] SEI
Lo cual es una invención del
siglo XVI. <<
[2.35]
También es importante recordar
que los decimales son solo numerales,
en el sentido de representaciones de
números y no números en sí mismos. Y
que los decimales también resultan ser
representaciones
de
series
por
convergentes, ejemplo 0,999… es
equivalente a
+
+
+
+
… Si puede usted ver por qué la suma
de esta serie infinita en particular es
1,0, probablemente se le ocurrirá que
en realidad la paradoja antes
mencionada de 0,999… = 1,0 no es una
paradoja en absoluto, sino una mera
consecuencia del hecho de que siempre
hay más de una manera de representar
cualquier número dado en notación
decimal. En este caso, la cantidad 1 se
puede expresar, o bien como
«1,000…», o bien como «0,999…».
Ambas representaciones son válidas,
aunque se necesita algo de matemáticas
superiores para ver el porqué. (SEI Una
vez más, si puede usted recordar las
cosas durante mucho tiempo y muchas
páginas, sepa ahora que en los § 6 y 7,
Georg Cantor va a hacer un uso
ingenioso de esa equivalencia técnica
entre 1,0 y 0,999… en un par de sus
más famosas demostraciones). <<
[2.36]
En todo caso, no
numéricamente. Otras maneras de decir
lo mismo: en la nomenclatura, digna de
un dentista, de las matemáticas de
bachillerato, no se puede extraer
completamente la raíz de 3; en
términos gráficos, una recta con una
pendiente irracional que parta del
origen nunca alcanzará ningún punto
correspondiente a unas coordenadas
cartesianas racionales. <<
SEI
[2.37]
Para ver de forma intuitiva que
hay (por lo menos) un número infinito
de puntos irracionales entre 0 y 1,
considere el conjunto de todos los
puntos correspondientes a 1/n, donde n
es irracional. <<
[2.38] SEI
En el fondo esto explica por
qué la trigonometría y la astronomía
griegas eran tan complejas: intentaban
cuantificar curvas continuas y áreas
bajo curvas solo con números
racionales. <<
[2.39]
Véase esta muy apropiada cita del
algebrista alemán Michael Stiefel,
hacia
1544:
«Pues,
al
hacer
demostraciones geométricas, cuando
los números racionales nos fallan, los
números irracionales se ponen en su
lugar y demuestran exactamente
aquellas cosas que los números
racionales no podían demostrar, nos
vemos obligados a aseverar que son
verdaderamente números. Por otro
lado, otras consideraciones nos obligan
a negar que los números irracionales
sean números en absoluto. A saber,
cuando buscamos someterlos a
[representación
decimal],
nos
encontramos con que se escabullen de
manera perpetua, de modo que ninguno
de ellos puede ser precisamente
aprehendido en sí mismo. Ahora, esto
no puede llamarse un verdadero
número, si es de tal naturaleza que
carece de precisión. Por lo tanto, así
como un número infinito no es un
número,
asimismo
un
número
irracional no es un verdadero número,
sino que permanece oculto en una
especie de nube de infinito (Michael
Stifel, Arithmetica Integra, 1544,
extractado a partir de Kline, pág.
251)». <<
[2.40]
Si no es así, entonces
sepa/recuerde que, según las reglas de
la lógica formal, una implicación como
«(ap < bq) → (ar < bs)» será falsa solo
cuando el primer término sea
verdadero, y el segundo, falso. A la
vista de esto, si quiere puede usted
asignar valores, por ejemplo, p = 1,
q = 2, r = 2, s = 4, a = 2, y b = 1, y
comprobar casos particulares de la
implicación. Verá que no hay ningún
caso en el cual el primer término sea
verdadero, y el segundo, falso; es decir,
que 1/2 realmente es igual a 2/4. <<
SEI
[2.41] SEI
Esto se hará mucho más
relevante cuando lleguemos a la teoría
de los números reales de Dedekind en
§6. <<
[2.42] SEI
Que en la teoría de Dedekind
se llamará un corte. <<
[2.43]
La especificidad reside en la
elección de los valores de a y b. <<
[2.44] SEI
= los que tienen todos los
lados de la misma longitud. <<
[2.45]
Es, en verdad, casi
increíblemente parecido al modo en
que Cauchy acabará definiendo los
infinitesimales en términos de límites
para evitar las varias fisuras asociadas
con las cantidades infinitamente
pequeñas, de todo lo cual se habla más
adelante en §5. <<
SEI
[2.46]
Una pequeña broma entre los
historiadores de las matemáticas es que
lo
único
matemáticamente
significativo que hicieron los romanos
fue matar a Arquímedes. <<
[2.47] SEI
Como veremos, tras unos
cuantos machetazos simplificadores
por parte de Bolzano y Dedekind. <<
[2.48]
Hay todo tipo de
procedimientos y objetos diferentes
para ilustrar esta demostración. Resulta
que el doctor Goris solía llevar/sonarse
con/desplegar de forma ilustrativa un
gran pañuelo rojo, al que durante más
de veinticinco años de clases se refirió
como al «pañuelito de la muerte». <<
SEI
[2.49] SEI
De hecho, se puede demostrar
matemáticamente que la probabilidad
de que alguien acierte un punto
racional de la recta numérica con un
dedo puesto al azar, un dardo o un
protón lanzados de manera aleatoria, o
lo que sea, es en todo caso: 0%. [El
autor omite aquí la observación de que
los susodichos dedo, dardo y protón
deberían tomarse como puntos
matemáticamente ideales para que la
afirmación tenga sentido. (N. del t.)].
<<
[3.1]
El único otro objetivo general de
§3 es lograr cierto grado de reducción y
simplificación que sea lógicamente <
absurdo. <<
[3.2]
Si en la escuela aprendió que el
símbolo viene de la letra griega
ómicron, le mintieron. <<
[3.3]
Reconocerá esto último como una
definición de álgebra, palabra que es en
realidad una deformación de Al-jabra,
un tratado del matemático de Bagdad
al-Khwarizmi (m. < 850 d. C.). <<
[3.4] SEI
en la Summa Theologiae y De
Potentia Dei (donde, SEI2, quia
significa «razonar retroactivamente de
los efectos a las causas»). <<
[3.5]
= «Contribuciones al estudio de lo
transfinito» (1887), que es uno de los
artículos más importantes de Cantor y
aparece en las págs. 378-440 de su
Gessamelte
Abhandlungen
mathematischen und philosophischen
Inhalts (= Obras completas). Lo
citamos de un modo tan horriblemente
detallado para que de ahora en adelante
entienda por qué no indicamos
detalladas
citas
polisilábicas
y
traducciones-de-citas de hasta el
último pequeño extracto relacionado
con Cantor. Prácticamente todo lo
cantoriano se puede encontrar en
Gessamelte Abhandlungen, obra que
recogemos en la Bibliografía. <<
[3.6]
= un cálculo primitivo,
precartesiano y prenewtoniano, de tipo
cien por cien geométrico. Las
epónimas latitudes del método son
pequeños segmentos verticales cuyas
longitudes representan la velocidad en
un instante (los instantes eran las
«longitudes» de la gráfica). No estoy
seguro de si todo esto explica el
nombre de la técnica o solo lo hace
más confuso. <<
SEI
[3.7]
Adivine quién lo consigue. <<
[3.8] SEI
Viète no usó las palabras
«suma», «serie» o «geométrica», pero
eso es lo que eran a todos los efectos.
<<
[3.9] SEI
Disculpas por la críptica prosa
matemática. Si puede soportarlo,
consulte también la obra de Kepler de
1615 Stereometria doliorum (=
Medición del volumen de barriles
[larga historia, donde intervienen el
emperador Rodolfo II y la industria
vinícola austriaca]). El método
«volumétrico»
del
libro
para
determinar áreas/volúmenes de figuras
creadas por curvas en rotación implica
tratar los sólidos como si estuvieran
compuestos
de
n
figuras
infinitesimales cuyas extensiones se
pueden sumar —de nuevo, mucho antes
que Newton y Leibniz—. <<
[3.10] SEI
Es verdad, todos los títulos
matemáticos de la modernidad
temprana suenan como horribles
enfermedades. <<
[3.11]
SEI hacia
1401-1464, aprox.,
matemático y cardenal de la Iglesia
católica; larga historia. <<
[3.12] SEI
Todo esto se desarrolla con
mucho más detalle más adelante, en el
clímax de §7. <<
[3.13] SEI
De hecho, la propia razón
tiende
a ∞ al alejarnos más y más por la
secuencia. <<
[3.14]
James Gregory (véase el texto
principal justo a continuación) da la
primera
definición
ampliamente
aceptada de función en un libro sobre
problemas de cuadratura solo treinta
años después de DNC. <<
[3.15]
De las diferencias entre estos
tipos de funciones expliquemos solo
que las trascendentes son las realmente
complejas:
trigonométricas,
exponenciales, logarítmicas, etc. Lo
que no podemos dejar sin aclarar es la
distinción entre números algebraicos y
trascendentes, que es parte de la amplia
taxonomía en la cual, por supuesto, los
enteros + las fracciones son los
números racionales, los racionales +
los irracionales son los números reales,
un número real más un número
imaginario como √−1 constituye un
número complejo, y así sucesivamente.
Dado nuestro objetivo general, no
necesitamos tratar con nada más que
números reales, afortunadamente. Pero
tenga en cuenta que el componente
irracional de los números reales se
compone, a su vez, de dos tipos de
números diferentes, o más bien la
distinción racional o irracional se
superpone en cierto modo con otra
distinción, entre números algebraicos y
trascendentes. La diferencia se vuelve
importante cuando llegamos a las
demostraciones de Cantor sobre los
diferentes tamaños de los ∞ de
diferentes «clases numéricas». Así
pues, un número es algebraico si es
raíz de un polinomio con coeficientes
enteros. Por ejemplo, √8 es un número
algebraico porque es la solución de la
ecuación 1x2 − 8 = 0. (En realidad, los
números enteros, los racionales, e
incluso los complejos también pueden
ser algebraicos, por ejemplo, las
respectivas soluciones de 2x − 14 = 0,
2x − 7 = 0, y 3x2 − 2x + 1 = 0, pero en
términos
de
Cantor/Dedekind/continuidad
solo
tenemos que esclarecer la cuestión de
los
irracionales).
Los
números
trascendentes, pues, son aquellos que
no son algebraicos, es decir, que no
pueden ser raíces de polinomios con
coeficientes enteros; π es un irracional
trascendente, y también el número e, la
base del logaritmo natural/hiperbólico
(no se preocupe si el término no le
resulta familiar). <<
[3.16] SEI
«Función» era la alternativa
de Leibniz al extraño «fluxión» de
Newton. Y, como ocurrió en muchos
otros casos con la terminología, el
término de Leibniz se convirtió en el
favorito. Curiosidad: Leibniz también
introdujo «constante» y «variable». <<
[3.17] SEI
La solución presentada es en
realidad para la paradoja de Aquiles y
la tortuga, pero viene a ser lo mismo.
<<
[3.18] SEI
Esta es la razón por la cual el
cálculo anglicano depende en gran
medida de las series infinitas y del
teorema del binomio. Véase §4a más
adelante. <<
[3.19]
Este cambio queda
simbolizado por la evolución de la
trigonometría, pasando de los grados y
las formas geométricas a los radianes y
las funciones trigonométricas. <<
SEI
[3.20] SEI
Aquí el coloso dominante es,
obviamente, Newton… <<
[3.21]
N. B. Tenga en cuenta,
especialmente para después, que las
teorías de Weierstrass, Dedekind y
Cantor sobre los números reales y la
continuidad suelen conocerse en los
libros de texto como la topología de la
recta real. <<
[3.22] SEI
por supuesto, estrictamente
hablando los conjuntos son entes
poscantorianos, pero qué le vamos a
hacer… <<
[3.23] SEI
Es decir, si usted representa
, verá que la curva
resultante
tiene
un
agujero
correspondiente a la posición del 1 en
el eje x, porque aquí es donde f(x) es
igual a
, que matemáticamente se
define
como
matemáticamente
indefinido. (SEI2 El lector con muchas
tablas podría darse cuenta de que aquí
hay cosas relacionadas con el valor
límite y el límite de una función, las
cuales no mencionamos porque todavía
no hemos hecho límites). <<
[3.24] SEI
Lo de la «aproximación» en
realidad es técnicamente erróneo, tal
como se explicará con algo de detalle
cuando empecemos a hablar del
análisis weierstrassiano en §5e. La
idea, aquí en G. E. I, es explicar los
límites de un modo intuitivamente
claro, no matemáticamente riguroso.
<<
[3.25]
¡Uy!2: véase Desarrollo más
adelante. <<
[3.26] SEI
o sea, por un 0 inferiormente
y por un 1 superiormente, para
comprobar lo cual está usted invitado a
dar valores a x. <<
[3.27]
N. B. Observe, por favor, que, a
grandes rasgos, las cotas y el ser no
acotado funcionan del mismo modo
para los conjuntos y para las
sucesiones. Esto empezará a ser
importante en §7, momento en el que
probablemente se le pedirá que
retroceda aquí y repase esta misma
nota. <<
[3.28] SEI
Más materiales para futura
recuperación: en caso de que se le haya
ocurrido preguntarse si el ∞ que
corona la suma denota un límite real o
un final o, de hecho, más bien la
ausencia de cualquier límite/final, sepa
que esta cuestión es altamente
significativa y llega hasta el corazón de
lo que Weierstrass/Dedekind/Cantor
fueron capaces de hacer por el análisis
(respecto a lo cual no se pierda el
apartado Análisis). Si, por otro lado, se
está preguntando qué visión tenían en
realidad los matemáticos anteriores a
Weierstrass de estos ∞ a los que sus x
y sus n se «aproximaban», la respuesta
básica es que relegaron esas cantidades
infinitamente grandes/pequeñas a la
misma existencia vaga, nebulosa, del
infinito potencial de Aristóteles. La
idea es que el verdadero estatus
matemático/metafísico de los infinitos
de los límites nunca tiene que
considerarse, porque en realidad nada
llega jamás allí. Si esto le choca como
algo sospechoso, entonces ya se
encuentra en situación de comprender
por qué Weierstrass pensaba que debía
ponerse rigor a todo el asunto. <<
[3.29]
Maldición. Muy bien. La verdad
estricta es más complicada que eso, e
involucra los límites de sucesiones de
sumas parciales, donde una suma
parcial = la suma de un número finito
de términos consecutivos de una serie.
La idea básica es que si la sucesión
infinita de sus sumas parciales tiende a
algún límite S, entonces una serie
infinita es convergente y su suma es S.
Y que una serie divergente es una cuya
sucesión de sumas parciales no se
aproxima a un límite, y por lo tanto no
tiene una suma finita. Todo lo cual
resulta demasiado abstracto en este
punto, pero con un poco de suerte
tendrá más sentido hacia el final de §5.
<<
[3.30] SEI
No nos vamos a preocupar de
términos asociados como producto
continuo y producto oscilante. <<
[3.31] SEI
donde el factorial 2! significa
2 × 1, 4! significa 4 × 3 × 2 × 1, etc.
<<
[3.32] SEI
estudiadas habitualmente con
la denominación de análisis armónico.
<<
[3.33] SEI
Si por casualidad está usted
volviendo a este apartado desde §5b y
dándose cuenta de que esta serie de
Fourier no se parece a la original de
Fourier vista en la presentación, sepa
que ambas son realmente la misma. Es
solo que la forma anterior clarifica
cómo la serie de Fourier contiene y
combina dos series trigonométricas
diferentes, las cuales —si no estaba
usted regresando— serán a su vez más
comprensibles cuando se definan las
series trigonométricas en G. E. II. Nos
disculpamos si esto resulta confuso: lo
estamos haciendo lo mejor que
podemos. <<
[3.34]
no tiene usted
conocimientos
de
matemáticas
superiores, esta definición tendrá más
sentido cuando veamos el cálculo
clásico en §4a. <<
SEI
Si
[3.35] SEI
Que fue definido de facto
justo al final de §3a. <<
[3.36] SEI
Respecto a lo cual, de nuevo,
véase lo que viene inmediatamente
después y §4 algo después. <<
[3.37] SEI
= «Demostración Puramente
Analítica…». El título entero tiene una
longitud de veintidós palabras y usted
no quiere verlo. <<
[3.38]
La demostración específica es que
los polinomios algebraicos son
continuos, lo cual es menos relevante
que las conexiones entre el hecho de
que una función sea continua en un
intervalo y que una serie/sucesión de
funciones sea convergente en un
intervalo. Estas conexiones empiezan a
volverse realmente importantes en §5.
<<
[3.39]
Para adelantarnos todavía más: en
§5e se analizará con cierta extensión
una importante hipótesis de Bolzano
acerca de sucesiones infinitas y puntos
límite, una hipótesis que Weierstrass
también redescubrió y demostró,
aunque respecto a esto la historia fue
amable con Bernard Bolzano y nombró
este resultado teorema de BolzanoWeierstrass, el cual resulta ser
importante para la teoría de Dedekind
de los números irracionales. (Para su
información,
no
hay
ninguna
indicación de que Weierstrass plagiara
a Bolzano ni nada parecido. Este tipo
de descubrimientos paralelos
producen
a
menudo
en
matemáticas). <<
se
las
[3.40]
concretamente su Paradoxien des
Unendlichen de 1851, que ni siquiera
estuvo disponible en inglés (como
Paradoxes of the Infinite) hasta 1950.
<<
[3.41] SEI
Véase, por ejemplo, la versión
inglesa de la obra de Cantor
«Foundations of the Theory of
Manifolds», que está en la Bibliografía
en el apartado de Artículos y Ensayos.
<<
[3.42]
Como veremos en §7, la mayor
parte de la teoría formal de conjuntos
es trivial si se supone que solo existen
los conjuntos finitos. <<
[3.43]
Como Cantor, Bolzano tiene un
don para elaborar demostraciones
simples, y con imágenes convincentes,
de proposiciones muy abstractas. <<
[3.44]
Véase §7d, o, si está
regresando desde §7d, ahora puede ver
por qué aquí entramos con tanto detalle
en esta equivalencia. <<
SEI
[3.45]
Es decir; que el diámetro es el
propio intervalo [0, 1]. (SEI La longitud
del arco hemisférico será obviamente
, pero esto no nos preocupa realmente).
<<
[3.46]
Esto incluye a Cantor en algunas
de sus declaraciones menos cautelosas
o equilibradas. <<
[3.47] SEI
Una vez más, todo eso se
define y analiza en §7. <<
[4.1]
Decisión del Alto Mando: vamos a
dejar de decir «véase más adelante»
todo el rato y a suponer simplemente
que de aquí en adelante resultará obvio
cuándo es oportuno. <<
[4.2] SEI
Como se ha mencionado, aquí
el objetivo retórico es preparar la
discusión
para
que
no
sea
grotescamente reduccionista pero a la
vez sea lo bastante clara y simple para
que se pueda seguir incluso si usted no
estudió matemáticas superiores. Es
cierto que estaría bien si las hubiera
estudiado, pero, por favor, tenga por
seguro que se han hecho considerables
esfuerzos y se ha pasado por muchas
fatigas para que no sea necesario. <<
[4.3]
De hecho hubo una gran disputa en
las matemáticas europeas acerca del
verdadero inventor; en concreto, acerca
de si Leibniz, cuyo primer artículo
relacionado con el cálculo es de 1674,
había plagiado a Newton, cuyo De
analysi per aequationes numero
terminorum
infinitas
circulaba
privadamente en 1669. <<
[4.4]
Disculpas por esta terrible sintaxis:
no hay una manera fina de comprimir a
Roberval. <<
[4.5]
Por ello, intentar resolver la
cuestión de la autoría diciendo que
Newton inventó el cálculo diferencial,
y Leibniz, el cálculo integral (como a
algunos profesores de matemáticas les
gusta hacer), lleva a confusión y es
erróneo. Lo importante es que Newton
y Leibniz entendieron que el problema
de las tangentes (= velocidad
instantánea) y el problema de las
cuadraturas (= áreas bajo curvas) eran
dos aspectos de un mismo problema
más amplio (= el de la continuidad) y,
por lo tanto, se podían tratar mediante
el mismo método general. La única
razón por la que Newton y Leibniz son
inmortales de las matemáticas es que
no separaron el cálculo del modo en
que lo hacen los cursos introductorios.
[Esta última afirmación del autor es
quizás exagerada, puesto que Newton y
Leibniz hicieron otras importantes
contribuciones a la ciencia, la técnica y
la filosofía, las cuales eran más que
suficientes
para
garantizar
la
inmortalidad a ambos. Véase sin ir más
lejos la nota siguiente. (N. del t.)]. <<
[4.6]
Siendo por supuesto Leibniz, como
Descartes, un importante filósofo, de
cuya ontología puede haber oído
términos como «sustancia individual»,
«transcreación»,
«identidad
de
indiscernibles»
y
«mónada
sin
ventanas». <<
[4.7] SEI
Algo de lo que sigue puede
enturbiar un poco la vista de tan
abstracto, pero será más fácil de
entender dentro de poco, cuando
veamos un ejemplo sencillo. <<
[4.8]
Seguramente todos detestamos ese
tipo de personas. <<
[4.9]
O sea, las mónadas
mencionadas tres notas al pie antes.
<<
SEI
[4.10]
Incluso
funciones
involucradas en problemas de áreas.
<<
SEI
[4.11] SEI
Entre otros leibnizismos están
«cálculo
diferencial»,
«cálculo
integral», «dx» y el signo integral de
toda la vida, «∫», del cual podemos
decir (curiosidad gorisiana) que
originalmente Leibniz quería que fuera
una S alargada para denotar «la suma
de las [coordenadas y] bajo una curva»
= (Boyer, pág. 403). <<
[4.12]
N. B. sobre posible SEI: si tiene
mucha preparación matemática, puede
omitir la siguiente presentación y sus
correspondientes comentarios, puede
que las simplificaciones no valgan la
pena. <<
[4.13]
SEI Para lectores con mucha
preparación que a pesar de todo no han
omitido todo esto pero ya se están
dando cuenta de que la Figura 4a se
parece a una ilustración muy
simplificada
del
«cociente
de
diferencias» de Leibniz, y quizá se
están preguntando por qué no seguimos
adelante sin más y hacemos su famoso
triángulo característico, la respuesta es
que usar el T. C. haría que la
explicación del problema se comiera
más de seis páginas y sometiera a todos
a un exceso de detalle de cálculo que al
final no resultaría importante. <<
[4.14]
De nuevo, si la Figura 4a se trata
como un problema de tasa de cambio, t
es un instante infinitesimal. (SEI Si se
ha encontrado usted con el término
algo pasado de moda cálculo
infinitesimal en relación con el cálculo
clásico, ahora puede ver que el término
proviene de la infinita pequeñez de
cantidades/duraciones como t). <<
[4.15]
N. B. Según Leibniz, eso es
precisamente lo que son los
infinitesimales: criaturas extrañas con
las que podemos hacer esto. Véase, por
ejemplo, este extracto de una carta a
John Wallis hacia 1690: «Es útil
considerar cantidades infinitamente
pequeñas tales que cuando se busca su
razón, puedan no ser consideradas cero
pero que sean despreciadas tan pronto
como se presenten acompañadas de
cantidades
incomparablemente
mayores. Así, si tenemos x + [t], [t] es
despreciado. Pero eso es distinto si
buscamos la diferencia entre x + [t] y
x…» (Leibniz extractado a partir de
Kline, pág. 384). <<
[4.16]
Una analogía incluso mejor
podría ser el caso de un científico
experimental que amañara sus datos
para confirmar la hipótesis que desea
confirmar. <<
[4.17] SEI
Los ejemplos de Newton en
D. A. eran más liosos y dependían más
del teorema del binomio, donde una
equivalencia como z = rxn (donde r es
una constante y la n puede ser una
fracción o incluso negativa) se puede
desarrollar para demostrar que la tasa
de cambio de rxn siempre será =
nrxn−1. Esto es lo que permite la
cadena teóricamente infinita de
derivadas sucesivas en las matemáticas
superiores. Por ejemplo, la 1.ª derivada
de, por ejemplo, y = x4 es 4x3; la 2.ª
derivada es 12x2, y así sucesivamente,
de modo que se puede hallar cualquier
derivada n-ésima mediante la razón
, aunque en el cálculo básico
habitualmente no se va mucho más allá
de la 2.ª derivada. <<
[4.18]
Observe, sin embargo, que se
tienen que usar el mismo tipo de
prácticas dudosas en este cálculo: (1)
= (2)
que es = (3)
,
, punto en el que
se supone que t ≠ 0 y se divide para
obtener: (4) 2x + t, donde se supone
que t = 0 y se desprecia para obtener:
(5) 2x. <<
[4.19]
O se puede obtener el mismo
resultado tratando z como equivalente a
todos los efectos a y en la ecuación (6)
de la deducción original. <<
[4.20] SEI
Tal como lo articuló Leibniz
por primera vez en 1686. <<
[4.21]
SEI Por
esto, los silabófilos
llaman
a
la
integración
antidiferenciación. <<
[4.22]
En este contexto, realmente el
método de los límites es un truco de
contabilidad metafísica que convierte
la infinitud/infinitesimalidad en una
característica del proceso de cálculo
más que de las cantidades calculadas.
Como debería ser evidente a estas
alturas, las leyes normales de la
aritmética no funcionan con cantidades
de tipo ∞ o infinitésimo, pero al
restringirse básicamente a sumas
parciales durante el 99% de las
operaciones, el cálculo basado en
límites permite aplicar esas reglas.
Luego, una vez el cálculo básico se ha
completado, se «toma el límite» y se
deja que t o dx o lo que sea «se
aproxime a 0», y se extrapola el
resultado. En términos pedagógicos, al
estudiante de matemáticas se le pide
que suponga que ciertas cantidades son
finitas y estables para los propósitos
del cálculo, pero luego transformables
y pequeñas hasta desvanecerse en la
etapa de los verdaderos resultados. Esta
contorsión intelectual hace que el
cálculo no solo parezca difícil, sino
extraña e innecesariamente difícil, lo
cual es una de las razones por las que el
cálculo es una asignatura tan temida.
<<
[4.23] SEI
(y quizá no sea buena idea
mencionarlo). Hay, de hecho, una
manera no trivial de decir lo mismo,
pero involucra el análisis no estándar,
inventado por un tal Abraham
Robinson en la década de 1970 y
pretende dar rigor a los infinitesimales
en el análisis mediante el uso de los
números hiperreales, los cuales a su
vez básicamente combinan los números
reales y los transfinitos cantónanos.
Esto
significa
que
es
todo
extremadamente teórico-conjuntista y
Cantor-dependiente,
además
de
controvertido, y salvajemente técnico,
y mucho más allá de los límites de esta
discusión… pero parece que para ser
rigurosos debemos por lo menos
mencionarlo, y quizá recomendar,
atendiendo a cualquier ardiente interés
por parte de usted, la obra del profesor
Abraham
Robinson
Nonstandard
Analysis, Princeton U. Press, 1996. <<
[4.24]
Esto probablemente necesita ser
explicado en lugar de solo repetido una
y otra vez. En el cálculo clásico, la
continuidad es tratada esencialmente
como una propiedad de las funciones:
una función es continua en algún punto
p si y solo si es diferenciable en p. Por
ello será tan importante el hallazgo de
Bolzano y Weierstrass en el siglo XIX
de aquellas funciones continuas pero
no diferenciables, y por esta razón la
teoría de la continuidad en el análisis
moderno es ahora mucho más
complicada. <<
[4.25]
Esto
quiere
decir
principalmente los dos J. Bernoulli y el
hijo de J. D., además de Guillaume
Fraçois Antoine, marqués de l’Hôpital,
que fue mecenas de uno de los J. (es
difícil no hacerse un lío con los
Bernoulli), todos los cuales florecieron
más o menos a principios del
siglo XVIII. <<
SEI
[4.26]
= principalmente los
británicos Edmund Halley, Brook
Taylor y Colins MacLaurin, también a
principios del siglo XVIII. <<
SEI
[4.27] SEI
Resulta que el obispo George
Berkeley
(1685-1753,
importante
filósofo
empirista
y
apologeta
cristiano; y un destacado adicto al
pleonasmo) hizo una famosa crítica del
cálculo clásico justo en esta línea en un
tratado del siglo XVIII cuyo título de 64
(sí, 64) palabras empieza con «El
Analista…». Sigue un extracto
representativo: «Nada es más fácil que
concebir expresiones o notaciones para
las fluxiones e infinitesimales […]
Pero si quitamos el velo y miramos
debajo, si, dejando a un lado las
expresiones, nos ponemos atentamente
a considerar las cosas mismas que se
supone que son expresadas o indicadas
de ese modo, vamos a descubrir mucha
vacuidad, oscuridad y confusión; es
más, si no yerro, imposibilidades y
contradicciones directas». La invectiva
de Berkeley es en cierto modo la
revancha del cristianismo contra
Galileo y la ciencia moderna (y en
realidad es muy divertido de leer con
sus excentricidades, aunque esto no
tiene nada que ver). Su argumento
general es que las matemáticas del
siglo XVIII, a pesar de sus pretensiones
deductivas, en realidad descansan sobre
la fe no menos que la religión, es decir,
que «[A]quel que puede asimilar una
segunda o tercera fluxión, una segunda
o tercera [derivada], no necesita, a mi
parecer, ser remilgado con aspecto
alguno de la divinidad» (Berkeley en
Works, v. 4, págs. 68-69)· Por otro
lado, Jean le Rond d’Alembert (17171783, gran matemático poscálculo e
intelectual todoterreno, y además uno
de los primeros proponentes de la idea
según la cual «la verdadera metafísica
del cálculo debe hallarse en la idea de
límite») objeta a los infinitesimales, en
los términos estrictamente lógicos de
la LTE, en su famosa Encyclopédie que
coeditó con Diderot en la década de
1760, como en, por ejemplo: «Una
cantidad es algo o nada; si es algo,
todavía no se ha desvanecido; si no es
nada, se ha desvanecido literalmente.
La suposición de que hay un estado
intermedio entre esos dos es una
quimera» (D’Alembert, Encyclopédie.
Traducción semiextractada y editada a
partir de Boyer, pág. 450). <<
[4.28]
La paradoja de la flecha, como la
dicotomía, se discute en el Libro VI de
la Física de Aristóteles; también
aparece en forma fragmentaria en
Vidas y opiniones de Diógenes Laercio.
<<
[4.29] SEI
No hace falta decir que es
algo dudosa la compatibilidad de esta
afirmación con las objeciones de
Aristóteles a la dicotomía, basadas en
series temporales, que vimos en §2b.
Hay modos de reconciliar los dos
argumentos de Aristóteles, pero son
muy complicados, y < 100%
convincentes; y de todos modos se trata
de duros asuntos de erudición
aristotélica muy lejos de nuestro
recorrido. <<
[4.30] SEI
Puede revisar la llamada de
atención de §2a sobre la diferencia
entre aplicar fórmulas y resolver
verdaderamente los problemas, que
aquí es plenamente oportuna. <<
[4.31] SEI
Respecto a la objeción de
D’Alembert a los infinitesimales en la
reciente nota 27, es precisamente esta
tercera posibilidad lo que resta solidez
a su argumento. <<
[4.32] SEI
Este es un bonito ejemplo de
un caso en que un poco de pensamiento
abstracto
madrugador
horizontal
realmente da buen resultado. Una vez
estamos levantados y usando nuestras
palabras, es casi imposible pensar
acerca de lo que significan realmente.
<<
[4.33] SEI
Observe, por favor, que no es
en absoluto lo mismo que la objeción
de Aristóteles a «¿Está la flecha […]
instante t?». Lo que él piensa que es
realmente incoherente es la idea de la
premisa (2) de que el tiempo puede
estar
compuesto
de
instantes
infinitesimales, que es un argumento
sobre la continuidad temporal, bajo
cuya interpretación la paradoja de la
flecha se puede resolver con una
simple fórmula de cálculo. Como
probablemente ha empezado a ver,
Aristóteles consigue de algún modo
estar grandiosa y sobrecogedoramente
equivocado, siempre y en todas partes,
cuando se trata del ∞. <<
[4.34]
(no o) <<
[4.35]
Solución que, aunque 100%
técnica, por lo menos tiene la ventaja
de reconocer que el movimiento-en-uninstante es un concepto que siempre
involucra más de un instante (poco más
que una ligera reformulación de
Sainsbury, pág. 21). <<
[4.36]
Como veremos en §5,
básicamente lo que hace Weierstrass es
hallar una manera de definir los límites
de un modo que elimine lo de «tiende
a» o «se aproxima gradualmente». Se
había demostrado que expresiones
como esas eran vulnerables a
confusiones, al estilo de Zenón, acerca
del espacio y el tiempo (por ejemplo,
«¿se aproxima desde dónde?», «¿cuán
rápido?», etc.), además de ser, en
general, rebuscadas. <<
SEI
[4.37]
Este es el problema, y el motivo
por el que la relación entre los
infinitesimales y la divisibilidad al
estilo de Zenón es de algún modo como
la relación entre la quimioterapia y el
cáncer. La dificultad con cantidades
que son menores que , , ,
,
,…
, pero, aun así, mayores que o es que
no se puede llegar a ellas dividiendo
una y otra vez, del mismo modo que no
se puede llegar a un número transfinito
sumando o multiplicando números
finitos. ∞ y
están exentos de todas
las paradojas de subdivisión infinita y
expansión… aunque, en cierto sentido,
son la misma encarnación de dichas
paradojas. O sea, que todo el asunto es
pero que muy raro. <<
[4.38]
En el sentido de intervalo en el
tiempo, en el espacio o en la recta real;
los tres son terreno de la continuidad.
<<
[5.1]
Si pegamos «pero más» detrás de
cada predicado, los últimos tres
párrafos de §3 b también se pueden
aplicar aquí bastante acertadamente.
<<
[5.2] SEI
Esta dificultad, a pesar de lo
que suelen pensar los que han
estudiado humanidades, no es a causa
de toda la notación de aspecto pesado
que puede intimidarnos cuando
hojeamos un libro de matemáticas
superiores. La notación especial del
análisis en realidad solo es una manera
muy muy compacta de representar
información. No hay tantos símbolos
distintos, y en comparación con el
lenguaje natural es ridículamente fácil
de aprender. El problema no es la
notación: es la extrema abstracción y
generalidad
de
la
información
representada por el simbolismo lo que
hace tan difíciles las matemáticas
superiores. Con un poco de suerte esto
se entenderá, porque es cien por cien
cierto. <<
[5.3] SEI
Es decir, nuevos resultados no
solo
en
las
matemáticas
ya
establecidas,
sino
en
áreas
completamente nuevas de la era
poscálculo, incluyendo las ecuaciones
diferenciales, varios tipos de series
infinitas, geometría diferencial, teoría
de números, teoría de funciones,
geometría proyectiva, cálculo de
variaciones, fracciones continuas, y así
sucesivamente. <<
[5.4] SEI
Observe que hemos vuelto a lo
del árbol. <<
[5.5]
Véase en este caso no solo la
famosa racionalización de D’Alembert
por no tener una definición rigurosa del
concepto de límite, «Simplemente siga
adelante, y la fe vendrá», sino también
esta declaración, hacia 1740, de AlexisClaude Clairaut (1713-1765, gran
fisicomatemático): «[Solía ocurrir que]
la geometría, igual que la lógica, debía
basarse en el razonamiento formal para
rebatir a los quisquillosos. Pero ahora
es al revés. Todo razonamiento
concerniente a lo que el sentido común
conoce de antemano, sirve solo para
ocultar la verdad y cansar al lector y
actualmente se desprecia» (Clairaut
extractado y editado a partir de Kline,
págs. 618-619). <<
[5.6]
El Alto Mando reconoce:
francamente, algunas partes del G. E. II
van a ser brutales, y en conjunto esa
podría ser la parte más dura de todo el
libro, y aquí mismo expresamos
nuestro arrepentimiento. Pero en
realidad es mejor hacerlo todo aquí en
un pasaje denso y sin contexto que
tener que ir deteniéndose y dando
pequeñas definiciones sin fin, y
explicaciones que interrumpan la
descripción del verdadero trabajo de
las personas. Se intentó de las dos
maneras, y Mal1 < Mal2. <<
[5.7] SEI
Este simbolismo universal para
funciones es cortesía del antes
mencionado Leonhard Euler, la gran
figura
predominante
de
las
matemáticas del siglo XVIII. <<
[5.8]
=
lo
que
se
conoce
académicamente
como
cálculo
multivariable, es decir, esencialmente
las matemáticas de las superficies en el
espacio de 3 dimensiones, f(x, y), o de
los sólidos en el espacio de 4
dimensiones, f(x, y, z), etc. <<
[5.9] SEI
Lo que sigue era la manera que
tenía el doctor Goris de explicar las
ecuaciones diferenciales, que resultaba
más clara y significativa que la manera
llena de fórmulas en que suelen
presentarse en los cursos de
matemáticas superiores. <<
[5.10]
Curiosidad gorisiana: el
ideograma japonés original para
función significaba, literalmente, «caja
para números». <<
SEI
[5.11]
Por así decirlo. <<
[5.12]
Larga historia: por favor, recuerde
simplemente que existe algo así. <<
[5.13]
Todo esto se puede encontrar en
el primer capítulo de la famosa obra de
Cauchy Course d’analyse, por ejemplo,
para y ∞: «Una cantidad variable se
hace infinitamente pequeña cuando su
valor numérico decrece de forma
indefinida de tal manera que converge
al límite o» (Cauchy, Cours d’analyse
algébrique. Traducción extractada,
algo editada, a partir de Kline, pág.
951) y «Una cantidad variable se hace
infinitamente grande cuando su valor
numérico crece de forma indefinida de
tal manera que converge al límite ∞»
(pero donde, como indica Kline «∞
significa no una cantidad fija, sino algo
indefinidamente grande»). <<
[5.14]
Otra ventaja de pensar en las
ecuaciones
diferenciales
como
metafunciones es que, como las
sucesiones/series de funciones son el
resultado del desarrollo de las E. D., en
cierto modo tiene sentido suponer que
lo que surja de tales sucesiones/series
será una función. <<
[5.15] SEI
Puede saber o recordar de las
matemáticas superiores que esto no se
parece en nada a la prueba de
convergencia general que se enseña
hoy. La razón es otra semiequivocación
de Cauchy: resulta que se puede
demostrar rigurosamente que su 3C
original solo es una condición
necesaria de convergencia. Una prueba
fiable de convergencia también debe
proporcionar condiciones suficientes
(véase la nota [1.14] y su explicación
acerca de condiciones necesarias y
suficientes), para lo cual resulta que se
necesita una teoría de los números
reales, que no estará disponible hasta la
década de 1870. <<
[5.16] SEI
Respecto a las dos últimas, o
en clase de astronomía, puede que haya
aprendido algo de la ecuación de onda
y de su relación con las funciones de
Bessel, que son soluciones particulares
de la ecuación de onda expresadas en
un tipo especial de sistema de
coordenadas 3D. <<
[5.17]
que
por
supuesto
son,
estrictamente hablando, funciones
trigonométricas, de modo que puede
usted ver por qué las series
trigonométricas son un caso clásico del
tema de series de funciones analizado
antes en el apartado Ecuaciones
diferenciales (b). <<
[5.18]
En realidad no hará ningún daño
volver al G. E. I y repasar el apartado
Series
de
Fourier
otra
vez,
especialmente lo de las series de
Fourier como desarrollos de funciones
periódicas. Por ello, las propias series
trigonométricas
tienden
a
ser
periódicas, en el sentido de que
básicamente repiten una y otra vez la
misma onda, donde «período» se
refiere al tiempo requerido para una
oscilación completa, e y = sen x (alias
onda senoidal) es una función
periódica prototípica. (SEI Si resulta
que usted recuerda el término serie
oscilante, esa es una cosa totalmente
distinta que no tiene nada que ver, y
debería eliminarse de la memoria
durante el resto de este libro). <<
[5.19]
Larga historia, que se desarrolla
más o menos a lo largo de los
siguientes §. <<
[5.20]
No pregunte. <<
[5.21] SEI
Una función monótona, por
otro lado, es una función cuya primera
derivada no cambia de signo +/−,
independientemente de si la derivada
es continua o no. (Es bastante seguro
que no vamos a tener que tratar con
funciones monótonas, aunque el
análisis weierstrassiano tiende a
necesitarlo casi todo). <<
[5.22] SEI
La forma nominativa inglesa
se traduciría directamente como
«monotonicidad» [aunque en español
suele usarse simplemente el término
«monotonía». (N. del t.)]. <<
[5.23]
Aquí quiere decir un punto en el
dominio de f(x). <<
[5.24]
<<
Los detalles siguientes son SEI.
[5.25] SEI
Esta es la misma c de la
ecuación de onda: se define como «la
velocidad de propagación de la onda» o
algo parecido. <<
[5.26] SEI
Por alguna razón, este es un
período de la historia en el que casi
todos los matemáticos importantes son
franceses o suizos. El siguiente siglo lo
van a dominar los alemanes. No hay
una buena explicación de esto en la
literatura. Quizá las matemáticas son
como la geopolítica o los deportes
profesionales, con distintas dinámicas
que siempre están desarrollándose y
decayendo. <<
[5.27]
Lo cual (otra vez, y como el
doctor Goris en persona solía repetir y
enfatizar porque decía que si no
captábamos esto nunca entenderíamos
cómo se relacionaban el P. C. V. y la
ecuación de onda con las series
trigonométricas) es lo mismo que una
curva. <<
[5.28] SEI
1802-1829; él y Évariste
Galois son los dos grandes prodigios
trágicos del siglo; larga, triste historia;
ejerció (Abel) una influencia póstuma
especialmente
fértil
en
Karl
Weierstrass. <<
[5.29] SEI
Curioso añadido al misterio
de la nota 26. Muchos matemáticos
franceses preeminentes de esta época
también eran nobles: LaPlace un
marqués, LaGrange un conde, Cauchy
un barón, y así sucesivamente. Algunos
de estos títulos fueron concedidos por
Napoleón I. En todo caso, el de Fourier
lo fue: su padre era sastre. <<
[5.30]
Breve versión de la historia tras la
f(x)
discontinua
de
Fourier:
aparentemente, cuando un cuerpo
adquiere calor, su temperatura se
distribuye no de manera uniforme, en
el sentido de que partes distintas tienen
temperaturas distintas en momentos
distintos. Es en la distribución del calor
en lo que Fourier está realmente
interesado. <<
[5.31]
Es decir, como área o suma de
áreas. <<
[5.32]
Esta E. D. parcial se conoce
comúnmente como la ecuación de
difusión, la cual, como usted puede
observar, se parece a la ecuación de
onda. Es precisamente dicho parecido
lo que las series de Fourier pueden
explicar, matemáticamente hablando.
<<
[5.33]
Puesto que en el G. E. I
prometimos
apartarnos
de
los
coeficientes de Fourier, las cinco
siguientes líneas de texto están
clasificadas como SEI. <<
[5.34]
Aquí es mejor pensar en las
funciones discontinuas como funciones
que no pueden ser expresadas mediante
una única ecuación de tipo «y = f(x)».
Véase un párrafo más adelante en el
texto principal. <<
[5.35]
Expresión analítica significa
básicamente lo de «y = f(x)». Otra
manera de enunciar lo que dice el texto
principal es que Fourier interpreta una
función denotativamente, es decir,
como un conjunto de correspondencias
específicas entre valores, más que
connotativamente como el nombre de
la regla que genera la correspondencia.
Lo cual, como veremos en el siguiente
§, es una manera muy moderna de
pensar en las funciones. <<
[5.36]
Realmente no hay nada que se
pueda hacer respecto a la frase anterior
excepto disculparse. <<
[5.37] SEI Véase
§1d. <<
[5.38] SEI
Recuerde, por ejemplo, el
truco de Euler con
en §3a, o ya
puestos todo el asunto de la serie de
Grandi. <<
[5.39]
Observación importante: la última
frase de Abel es solo un rodeo para
decir «inducción». <<
[5.40]
Ni tampoco se puede
demostrar dicha equivalencia mediante
cálculos, ya que, por supuesto, tanto
√2 como √3 representan decimales
infinitos. En la nomenclatura del
análisis, no se puede demostrar que el
producto de las sumas de las series
infinitas de esos dos decimales
converja hacia la suma correspondiente
a √6. <<
SEI
[5.41] SEI
Dicho trabajo es de Joseph
Liouville y de Charles Hermite (más
franceses). Respecto a todo el asunto
de
algebraico-o-irracionaltrascendente, véase o recuérdese la
nota de §3a. También hay algo más
acerca de la demostración de Liouville
más adelante en §7c. <<
[5.42]
Otra cita ejemplar en esa línea es
de Eric Temple Bell: «Si Cantor
hubiera sido educado como un ser
humano independiente, nunca habría
adquirido la tímida deferencia respecto
a los hombres de reputación
establecida que hizo desdichada su
vida» (Bell, pág. 560). <<
[5.43]
SEI Se
cita a menudo otro
intercambio de cartas, con todas las
rarezas y cursivas sic: Georg W. →
Georg Jr.: «… Acabo con estas
palabras: tu padre, o más bien tus
padres y todos los demás miembros de
la familia tanto en Alemania como en
Rusia y en Dinamarca tienen sus ojos
puestos en ti como el mayor, y esperan
que seas nada menos que un Theodor
Schaffer [profesor de G. C. Jr.] y, Dios
mediante, después quizás una brillante
estrella en el horizonte de la ciencia».
Georg Jr. → Georg W.: «… Ahora soy
feliz de ver que ya no va a disgustaros
que siga mis propios sentimientos en
esta decisión. Tengo la esperanza de
que estaréis orgullosos de mi algún día,
querido padre, pues mi alma, todo mi
ser vive por mi vocación; sea lo que
sea lo que uno quiere y es capaz de
hacer, sea lo que sea hacia lo que una
voz secreta, desconocida [?!] le llama,
aquello será lo que llevará a cabo con
éxito! (Dauben, GC, págs. 275-277)».
<<
[5.44]
Baste decir que las
definiciones y resultados de Bolzano
acerca de la continuidad que vimos en
§3c se pueden extender, sin más que
unos pequeños ajustes, al concepto de
convergencia de una serie. <<
SEI
[5.45] SEI
del G. E. II, apartado E. D.
(b), interpolación. <<
[5.46]
Esto es 1826. El
contraejemplo específico de Abels es la
SEI
serie sen x −
+
− …,
que resulta ser el desarrollo en serie de
Fourier de y =
en el intervalo
−π < x < π y es, con mucho,
convergente, pero su suma es
discontinua para x = π(2n + 1), donde
n es un entero. <<
[5.47] SEI
Prueba que todavía se usa en
la actualidad, y puede que la haya
estudiado. Si no lo hizo, aquí está para
que pueda ver el verdadero aspecto de
una de esas cosas: supongamos que
cn(x) es una sucesión de funciones en
algún intervalo [a, b]. Si (1) la sucesión
se puede reescribir en la forma
cn(x) = anfn(x), y si (2) la serie ∑an es
uniformemente convergente, y si (3)
fn(x) es una sucesión monótona
decreciente tal que fn−1(x) ≤ fn(x) para
todo n, y si (4) fn(x) es acotada en
[a, b], entonces (5) para todo x en
[a, b], la serie ∑cn es uniformemente
convergente. [Si el requisito (2) de que
∑an sea uniformemente convergente le
parece extraño/circular, sepa que un
truco habitual de las matemáticas puras
es tomar una propiedad de algo en un
caso simple o fácil de demostrar
(siendo ∑an la parte más simple, con
mucho, de la descomposición de cn(x)
en (1)) y usarlo para demostrar que la
misma propiedad se cumple para un
ente mucho más complicado. De hecho,
ese mismo truco es clave para la
inducción matemática, una técnica de
demostración 100% respetable que hará
su aparición en §7]. <<
[5.48] SEI
Por favor, vea o recuerde la
nota 15 de §5a. <<
[5.49] SEI
De nuevo, también conocidas
como puntos excepcionales. <<
[5.50] SEI
= 1837, en un artículo cuyo
encantador título es: «Über die
Darstellung
ganz
willkürlicher
Functionen
durch
Sinus
und
Cosinusreihen», cuya traducción viene
a ser «Sobre la representación de
funciones completamente arbitrarias
mediante series de senos y cosenos».
(Es
impresionante
cómo
los
matemáticos de esta época parece que
saben escribir tanto en francés como en
alemán, según la revista a la que envían
el artículo). <<
[5.51]
En el sentido de que ahora, en el
análisis, una función en realidad no es
ni una cosa ni un procedimiento, sino
más bien solo una correspondencia
entre dos conjuntos, llamados dominio
y recorrido. <<
[5.52]
Deberíamos mencionar que
Fourier, Cauchy y Dirichlet trabajaban
de manera habitual con funciones de la
física matemática, que tienden a ser
comparativamente simples y de buen
comportamiento. <<
[5.53] SEI
Justo aquí se vislumbra de
verdad, por primera vez, cómo el
análisis avanzado da lugar a las
matemáticas transfinitas. <<
[5.54]
Uno duda de si entrar en esto,
pero, de hecho, la versión riemanniana
de la geometría no euclídea —a veces
conocida como «geometría diferencial
general», y que se remonta a 1854 (un
excelente año para Riemann)—
constituye un vector de explicación
completamente distinto de por qué en
el siglo XIX se hacen necesarias las
teorías rigurosas sobre los números
reales y el ∞. Es ligeramente
tangencial, y brutalmente abstracto, y
será mayoritariamente omitido excepto
aquí. De forma muy simplificada, la
geometría de Riemann involucra (a) el
plano complejo de Gauss (es decir, una
malla cartesiana que tiene números
reales en un eje y números imaginarios
en el otro eje) y (b) algo llamado una
esfera de Riemann, que se puede
concebir básicamente como un plano
euclidiano 2D curvado en forma de
bola y puesto encima del plano
complejo. Esta nota no es técnicamente
SEI, pero puede usted detenerse en
cualquier momento. Lo que relaciona
la geometría de Riemann con la antes
mencionada geometría proyectiva de
Desargues es que cada punto de la
esfera de Riemann tiene una «sombra»
en el plano complejo, y las relaciones
trigonométricas creadas por esas
sombras resultan ser terriblemente
fecundas, en términos de Por ejemplo,
una recta en el plano complejo es la
sombra de algo llamado un círculo
máximo en la esfera de Riemann, es
decir, un círculo cuya circunferencia
pasa por el polo norte de la esfera de
Riemann, polo definido, literalmente,
como «punto del ∞». De hecho, la
propia esfera de Riemann se puede
definir como «el plano complejo con
un punto en el ∞», algo conocido
también
como
plano
complejo
ampliado. El 0 es el polo sur de la
esfera de Riemann, e ∞ y 0, en
términos geométrico-diferenciales, son
inversos el uno del otro (porque tomar
el inverso de un número en el plano
complejo es equivalente a darle la
vuelta a la esfera de Riemann: larga
historia). Así que en la geometría de
Riemann, «0 =
» y «∞ = » no solo
son
legales:
son
teoremas.
Detendremos aquí la discusión
específica y esperaremos que tenga
sentido a grandes rasgos. Algo
importante que conviene saber: no es
ningún accidente que el símbolo del
plano complejo ampliado sea «C∞»
mientras que el símbolo más famoso de
Cantor para el conjunto de todos los
números reales (alias el continuo, que
como veremos es básicamente el 2.º
orden matemático de ∞) es «c». Hay
todo tipo de conexiones fascinantes
entre la geometría riemanniana y la
teoría de conjuntos cantoriana, la
mayor parte de las cuales están
desafortunadamente más allá de lo que
nos hemos propuesto explicar. <<
[5.55] SEI
En esta época, todos los
participantes de primera línea en la
creación
de
las
matemáticas
transfinitas están vivos, y la mayoría
matemáticamente en activo. En 1854,
Riemann tiene veintiocho años;
Dedekind, veintitrés; Weierstrass tiene
treinta y nueve; y L. Kronecker, treinta
y uno. El todavía no mencionado Heine
tiene treinta y tres. Cantor tiene nueve
años y está tocando el violín ante la
atenta mirada de Georg W. <<
[5.56] SEI
El largo título de este artículo
empieza
con
«Über
die
Darstellbarkeit…»
(=«Sobre
la
representabilidad…»). En realidad era
más como una segunda tesis doctoral
que una monografía profesional (larga
historia), y los manuscritos circularon
entre los matemáticos hasta que
finalmente Dedekind hizo posible su
publicación tras la muerte de Riemann.
<<
[5.57] SEI
Para los incondicionales y/o
con fuerte preparación, o quizá si solo
quiere usted recrearse algo más en la
simbología del análisis: Riemann
deduce su f(x) tomando una serie
trigométrica estándar e integrando cada
término dos veces, dando: f(x) = C +
C1x +
x2 −
,y
logra demostrar que esta serie
trigonométrica es convergente siempre
y cuando
se comporte en cierto modo especial
(modo del cual, una vez más, no
podemos hablar por carecer de las
herramientas conceptuales adecuadas,
pero no son dudosas ni extrañas, solo
muy técnicas). <<
[5.58]
SEI como se ha definido en
G. E. I. <<
[5.59]
Más premoniciones: la
primera y la última de estas cuestiones
serán lo que el trabajo temprano del
propio Cantor intente contestar, y es
dicho trabajo lo que le lleva al ∞ per
se. <<
SEI
[5.60]
Las partes precedentes
aparecen en las págs. 55 y 59. <<
SEI
[5.61] SEI
N. B. Tenga en cuenta, sin
embargo, que las Hochschulen técnicas
alemanas
eran
instituciones
extremadamente autoritarias desde el
punto de vista actual, y que el cálculo y
el análisis básico eran asignaturas
obligatorias. (Pero los salarios de los
profesores
eran
legendariamente
bajos). <<
[5.62]
El estudiante que sí tomó notas a
escondidas y a quien se debe
principalmente que ciertas teorías de
Weierstrass sobre funciones fueran
conocidas fue un tal Gösta MittagLeffler (1846-1927), quien más tarde
puso en marcha la famosa revista
especializada Acta Mathematica y
publicó el trabajo de Cantor sobre el ∞
cuando la mayoría de las revistas de
matemáticas todavía lo consideraban
una locura. Históricamente, MittagLeffler es considerado como el
segundo
matemático
que
más
correspondencia mantuvo con Cantor,
después de Dedekind. <<
[5.63] SEI
Principalmente, las integrales
elípticas son generalizaciones de
funciones trigonométricas inversas.
Tienden a aparecer en todo tipo de
problemas
físicos,
del
electromagnetismo a la gravedad. Si
las ve usted en una clase de
matemáticas, habitualmente es en
conjunción con Adrien Marie Legendre
(otro de los franceses de principios del
siglo XIX), que fue para las integrales
elípticas lo que Fourier para las series
trigonométricas, y desarrolló las
«integrales elípticas de Legendre de
1.ª, 2.ª y 3 ª especie». (SEI2 Si,
casualmente, sabe que Riemann
también trabajó mucho con las I. E. y
ciertas integrales asociadas en el
cálculo de variaciones, sepa que no
vamos a entrar en nada de esto). <<
[5.64]
Es casi seguro que en el G. E. I se
mencionó que las series de Fourier se
pueden entender como sumas de series
de potencias. <<
[5.65]
Por razones que se harán
evidentes,
esta
definición
tan
tecnificada no es SEI. <<
[5.66]
El Alto Mando reconoce: lo que
sigue va a ser mucho menos
formal/riguroso que la explicación del
propio doctor Goris acerca de la
definición. Buscamos una explicación
que resulte comprensible al máximo en
términos del vocabulario y los
conceptos desarrollados hasta ahora en
el libro. <<
[5.67]
Hablando 100% técnicamente, la
definición de Weierstrass «para cada
… existe … tal que» en realidad está
formulando
una
relación
de
implicación en el cálculo de predicados
de primer orden, que es una lógica de
un tipo más elaborado que usa
cuantificadores como ∀ y ∃. Excepto
por uno o dos comentarios en §7, sin
embargo, este libro no entra en el
cálculo de predicados, de modo que
aquí estamos simbolizando la relación
entre los ε y δ de la definición como
una conjunción lógica. Para nuestros
propósitos de dar demostraciones
ilustrativas eso será suficiente: los
valores «cierto»/«falso» relevantes
resultan ser los mismos. <<
[5.68] SEI
Curiosidad: esta técnica de
Weierstrass resulta tan significativa
que
una
gran
cantidad
de
demostraciones posteriores en el
análisis y la teoría de números usan la
formulación «Para cada ε, existe
un…», para la cual el llamativo
término (en inglés) es epsilontic proof
(«demostración epsilóntica»). <<
[5.69] SEI
Su prueba de convergencia
uniforme, conocida como prueba M de
Weierstrass, todavía se enseña en las
clases de análisis. <<
[5.70]
<<
por ejemplo, una serie de Fourier.
[5.71]
Curiosidad histórica: la
contribución de Weierstrass a este
teorema en realidad es parte de su
intento infructuoso de definir los
números irracionales: véase §6a más
adelante. <<
SEI
[5.72]
Esencialmente, esto consiste en
reformular el concepto de convergencia
hacia un límite en términos de
conjuntos de puntos e intervalos de la
R. R. Ejemplo de Shaughan Lavine: «1
es un punto límite del conjunto
{0, , , , K}. Intuitivamente uno ve
que los elementos del conjunto se
aglomeran junto a 1» (semiextractado
de Lavine, pág. 38). Admitimos que no
es una definición totalmente rigurosa
de punto límite, pero ciertamente es lo
relevante. Observe aquí también que el
punto límite de una sucesión infinita es
un punto tal que cada intervalo a su
alrededor contiene un número infinito
de términos de la sucesión: o sea, que
funciona más o menos del mismo
modo, lo cual resultará relevante en
§7a. <<
[5.73] SEI
Una consecuencia directa del
teorema de Bolzano es algo
habitualmente llamado el teorema de
los valores intermedios (T. V. I.), que
es una pieza básica de la teoría de
funciones y dice esencialmente que si
una f(x) es continua en [a, b] y tal que
f(a) = A y f(b) = B, entonces f(x) toma
todos los valores posibles entre A y B.
Si definimos la función continua como
f(x) = 2x, [a, b] como [0, 1] y [A, B]
como [0, 2], entonces puede usted ver
que un primer ejemplo del T. V. I. es la
demostración de Bolzano en §3c acerca
de la correspondencia uno a uno entre
[0, 1] y [0, 2]. A su vez, esto podría
aclarar por qué el teorema de Bolzano
requiere una teoría de los números
reales, pues «todos los posibles valores
entre A y B» no van a ser una cantidad
que podamos verificar contando. <<
[5.74] SEI
También en lo del G. E. I
acerca de Límites y cotas. <<
[5.75]
Ciertamente, en lo que
respecta al mundo real, es el paradigma
de una función. <<
SEI
[5.76]
Lo que sigue es, de nuevo, muy
informal, y hecho a medida para
trabajar con los conceptos de lógica y
matemáticas que hemos preparado
hasta ahora. (SEI Una respuesta 100%
rigurosa pondría en práctica la
definición weierstrassiana del límite de
una sucesión infinita, que es una forma
algo diferente de demostración
epsilóntica, y hemos decidido no
dedicar otra interpolación a desarrollar
eso. Para lo que pretendemos hacer, la
definición del límite de una función
funcionará perfectamente). <<
[5.77]
En el sentido de que n «va hacia»
el ∞ igual que la sucesión de enteros 1,
2, 3, … (SEI ¿Hemos mencionado antes
en §2 el asombroso parecido entre la
dicotomía revisada y la propiedad de
exhaustación de Eudoxo?). <<
[5.78]
Como quizá ya sabe, este adjetivo
viene de «orden», y número ordinal
significa el 1.er número, el 2.º número,
el 3.er número, etc., a diferencia de los
números cardinales 1, 2, 3, etc. En
otras palabras, la ordinalidad concierne
a dónde está el número en una
secuencia dada más que a qué es. La
distinción cardinal-ordinal resulta tener
una mastodóntica importancia en la
teoría de conjuntos cantoriana, respecto
a lo cual véase como pequeño adelanto
lo que dice Russell: «En su teoría [del
∞], es necesario tratar de manera
separada los cardinales y los ordinales,
los cuales son mucho más distintos en
sus propiedades cuando son transfinitos
que cuando son finitos» (Russell,
Principies of Mathematics, pág. 304).
<<
[5.79] SEI
Esto, por supuesto, es lo
mismo que demostrar que 0 es el límite
de
cuando n = 1, 2, 3, … Usamos la
función
para una máxima
claridad respecto a la dicotomía. <<
[6.1]
El primer matemático en indicar
esto: el profesor Georg Cantor. <<
[6.2] SEI
Extraña curiosidad: casi todos
tos grandes filósofos de la historia
fueron solteros toda su vida. Heidegger
es la única verdadera excepción. En el
caso de tos grandes matemáticos hay
más o menos un 50% de casados, aún
por debajo de la media de la población.
No hay registro de una explicación
concienzuda: puede elaborar usted sus
hipótesis. <<
[6.3] SEI
= «Stetigkeit und irrationale
Zahlen», cuya traducción al inglés está
en la obra de Dedekind Essays on the
Theory of Numbers. Véase la
Bibliografía. (Observemos también
aquí que, a pesar de su profundidad, el
artículo de Dedekind es claro y
accesible y raramente requiere nada
más que matemáticas de bachillerato.
En esto no es como tos materiales de
Cantor, que tienden a ser casi
medusianos en su lenguaje y
simbolismo). <<
[6.4]
Weierstrass, por otro lado, estaba
interesado principalmente en la
continuidad desde la perspectiva de las
funciones, la cual en definitiva depende
de la continuidad aritmética (como
indica Kline al principio de §6a) pero
sigue siendo harina de otro costal. <<
[6.5]
En caso de que parezca circular o
cuestionable que Dedekind use la recta
numérica geométrica para una teoría no
geométrica de la continuidad, sepa que
la R. N. es soto un recurso ilustrativo, y
que más adelante, en Continuidad y
números irracionales, lo abandonará y
hablará
de
«cualquier
sistema
ordenado» de números. Incluso al
introducir la recta, Dedekind subraya
que:
«[S]erá
necesario
indicar
claramente las propiedades puramente
aritméticas correspondientes para
evitar incluso la apariencia de que la
aritmética esté necesitada de ideas
ajenas a ella» Dedekind, pág. 5
(sintaxis sic). <<
[6.6] SEI
Este artículo, aparecido en la
década de 1880, consiste íntegramente
en 171 teoremas y demostraciones + 1
«Comentario Final». Aquí mismo le
ahorramos el título en alemán. La
versión inglesa es la otra mitad del
libro Essays mencionado en la nota 3
anterior. <<
[6.7]
= del alemán Gedankenwelt,
literalmente «mundo del pensamiento».
<<
[6.8]
En el sentido matemático, aunque
en la demostración no está claro si el
«sistema infinito» S de Dedekind está
representado
como
un
ente
estrictamente matemático o como un
ente más general del tipo de una
«forma» platónica, lo cual es otro
problema de este argumento. <<
[6.9]
Quizá recuerde que la
demostración de §2e, basada en
SEI
, para ver que entre dos
puntos racionales siempre hay un
tercero, involucraba distancias en la
recta numérica, lo cual podría parecer
un poco circular en el presente
contexto. En este caso, aquí está una
fórmula
100%
aritmética
para
encontrar el valor medio. Tome dos
números racionales expresados como
fracciones con denominador común y
numeradores sucesivos, por ejemplo,
y
, y doble los cuatro números que
intervienen.
Así
se
crea
automáticamente espacio para un
número entero entre los nuevos
numeradores, puesto que ahora
tenemos
y
, de modo que
podemos insertar el valor medio
<<
.
[6.10] SEI
Un algoritmo que encontrarán
divertido las personas que encuentran
divertido este tipo de cosas: cualquier
número racional expresado en forma
decimal finita o periódica se puede
poner en forma fraccionaria
mediante
(a) la multiplicación del decimal por
10n, donde n = el número de dígitos en
el período del decimal (por ejemplo, el
período de 0,111111… tiene un solo
dígito y es 1; el período de 876,956​756​
756​7567… tiene tres dígitos y son
567), después (b) la sustracción del
decimal original de la cantidad
obtenida en (a), después (c) la división
del resultado por (10"− 1), y después
(d) la simplificación del resultado
eliminando los posibles factores
comunes. Ejemplo: x = 1,24242424…,
luego n − 2; luego 10n = 100.
100x = 124,242424…
−
x =
1,242424…
99x = 123
Así, x =
x=
. <<
, que simplificando da:
[6.11]
El verbo que usa aquí el propio
Dedekind es geschnitten (n. = schnitt),
que parece poder denotar cualquier
cosa desde rebanar hasta partir: una
palabra muy concreta y física, y
bastante más divertida de pronunciar
que «corte». <<
[6.12] SEI
La traducción al inglés de
«Continuidad y números irracionales»
usa «classes» (esp. «clases»), que era
el término matemático original para los
conjuntos. Cantor, Russell y demás
tienden a decir «clase», aunque en
realidad Cantor a veces también usa
palabras que se pueden traducir como
«multiplicidad»,
«variedad»
o
«agregado». Decisión del Alto Mando:
de aquí en adelante solo vamos a usar
«conjunto». <<
[6.13]
SEI Si está regresando desde
capítulos posteriores, observe lo mucho
que se parece esto al material
cantoriano, en §7c y posteriores, acerca
de los órdenes de los conjuntos
infinitos. <<
[6.14]
SEI El verdadero ejemplo de
Dedekind en «C. y N. I.» es más
abstracto y usa el hecho de que si D es
un entero positivo que no es el
cuadrado de ningún entero, entonces
existe un entero positivo λ tal que
λ2 < D < (λ + 1)2, lo cual ahora resulta
ser un teorema básico de la teoría de
números.
Dedekind
quiere
una
demostración totalmente abstracta y
general porque su verdadero objetivo
es: «demostrar que existe una infinidad
de cortes no producidos por números
racionales». Su propia demostración,
sin embargo, resulta demasiado
compleja y con demasiada teoría de
números para nuestros propósitos, así
que solo usaremos √2 y le pediremos
que confíe en que este resultado se
puede ampliar para cubrir todos los
irracionales (que puede). <<
[6.15]
Vea o recuerde la
demostración de la incomensurabilidad
de en las págs. 81-82. <<
SEI
[6.16] SEI
De aquí la definición de
número irracional que daba el doctor
Goris en clase: «schnitt sandwich», que
obviamente tenía mucho éxito entre los
adolescentes. <<
[6.17]
Respecto a la pág. 191: que los
puntos de la recta real pueden ponerse
en correspondencia uno a uno con el
conjunto de todos los números reales es
lo que ahora se conoce como el axioma
de Cantor-Dedekind. <<
[6.18] SEI
En el lenguaje de la lógica,
una disyunción es verdadera si por lo
menos uno de sus términos es
verdadero. <<
[6.19]
Este es el término de Dedekind
para las magnitudes geométricas. <<
[6.20]
glups <<
[6.21] SEI
Una diferencia, relacionada
con esto, entre Eudoxo y Dedekind es
la concepción que tienen de los
conjuntos infinitos de sus respectivas
teorías. Recuerde de §2d que la
propiedad de exhaustación de Eudoxo
involucra conjuntos infinitos en el
sentido de secuencias infinitas de
restos-de-sustracciones, excepto, por
supuesto, que aquí las sustracciones
son a partir de magnitudes geométricas
y el ∞ es solo potencial. Recuerde, por
ejemplo, de la pág. 88, la Propiedad I
del Libro X de los Elementos:
«
p(1 − r)n = 0» que es como el
análisis pre-Dedekind habría tratado
los restos de la exhaustación.
Matemáticamente y metafísicamente,
la visión de Dedekind es exactamente
opuesta a la de Eudoxo. Dedekind
considera
los
puntos/líneas
geométricos de su propia teoría como
únicamente teóricos e ilustrativos: no
importa si se podría construir
realmente una recta numérica completa
o medir las longitudes exactas
necesarias para aislar el punto √2. Lo
que importa —y para Dedekind son
reales, pues después de todo «Los
números son creaciones libres de la
mente humana» y la existencia
matemática es «un resultado inmediato
de las leyes del pensamiento»— son
los conjuntos infinitos A de todos los
x2 < 2 y B de todos los x2 > 2. Son
estos ∞, y no ninguna cantidad o figura
geométrica, los que son fundamentales
para la teoría de Dedekind. <<
[6.22]
El otro gran relato apócrifo sobre
Kronecker concierne a su reacción
cuando Ferdinand Lindemann demostró
en 1882 que π era un irracional
trascendente
(demostración
que
finalmente clavó una estaca en el
corazón del viejo problema griego de la
cuadratura del círculo). Según el relato,
en un congreso, Kronecker se dirigió
espontáneamente a Lindemann y dijo,
muy seriamente: «¿De qué sirve su
adorable demostración sobre π? ¿Por
qué malgastar su tiempo con problemas
como este, si los irracionales ni
siquiera existen?» (semiextractado de
Kline, pág. 1.198). No hay constancia
de la reacción de Lindemann. Perfil
rápido de Leopold Kronecker l’homme:
fechas de nacimiento y muerte ya
dadas. Uno de los muy escasos
matemáticos de primera fila que
también fue un gran hombre de
negocios. Kronecker hace tal fortuna en
operaciones bancarias que a la edad de
treinta años puede retirarse y dedicar
su vida a las matemáticas puras. Se
convierte en profesor en la Universidad
de Berlín, el Harvard de Alemania,
donde también había sido un alumno
estrella. Desde el punto de vista de su
investigación, es principalmente un
algebrista, siendo su especialidad los
cuerpos de números algebraicos, que
son una larga historia. También lo es su
más famoso descubrimiento, la función
delta de Kronecker, que en cierto modo
anticipa las matemáticas binarias de la
digitalización moderna. Un buen
gimnasta y alpinista, Kronecker no
mide más de 1,65 m, es ágil y
muscular, siempre inmaculadamente
peinado, vestido y arreglado. Lo de los
1,65 m no es broma. De modales
corteses, aparentemente, aunque es una
verdadera piraña en las matemáticas y
la política académica. Muy activo y
bien relacionado en toda la comunidad
matemática, el tipo de colega que más
vale no tener como enemigo porque
está en todos los comités y consejos
editoriales posibles. Principal aliado: el
teórico de números Erns Eduard
Kummer. Principal enemigo preCantor: el antes mencionado, alto,
arrugado, flegmático Karl Weierstrass.
Las descripciones de los debates entre
Kronecker y Weierstrass a menudo
evocan la imagen de un chihuahua
rabioso persiguiendo a un dogo.
Motivos de la antipatía: (1) La
especialidad de Weierstrass son las
funciones continuas, que Kronecker
considera ilusorias y perversas; (2)
Kronecker cree que el programa de
Weierstrass de aritmetización del
análisis se queda muy corto. Gran
sueño de Kronecker: basar todo el
análisis en los enteros. La ontología
matemática
ultraconservadora
de
Kronecker se considera ahora como la
precursora del intuicionismo y el
constructivismo, aunque no tuvo otros
adherentes hasta Poincaré y Brouwer,
todo lo cual se desarrolla extensamente
en §7. <<
[6.23] SEI
Al doctor Goris le gustaba
decir que Weierstrass, Dedekind y
Cantor formaban su propia serie
convergente especial, donde por turnos
cada uno proporcionaba a los demás
justo lo que necesitaban para que sus
avances fueran viables. <<
[6.24]
Hay, no hace falta decirlo,
matemáticos de finales del siglo XIX
para los que nada de esto resulta
convincente. Kronecker es solo uno de
ellos. <<
[6.25]
= algo así como «Sobre la
extensión de una proposición de la
teoría de series trigonométricas», que
es el primer artículo importante de
Cantor y ocupará buena parte de los
dos siguientes §. <<
[6.26]
Curiosidad
gorisiana:
Brunswick es más conocido por su
inexplicablemente popular sándwich
Braunschweiger, que es un poco como
paté que se ha dejado solidificar en la
punta del pie de una vieja zapatilla de
gimnasia. En nuestra clase (para
obtener puntos extra), durante la
lección sobre Dedekind y Cantor, todo
el mundo estaba invitado a probar un
poco, encima de una galleta salada. <<
SEI
[6.27]
Algo más relevante para nosotros
es que la teoría de Cantor de los
irracionales simplemente no es tan
buena como la de Dedekind. Esta
última es más simple y más elegante y
(bastante irónicamente) hace mejor uso
de los conjuntos de tipo. <<
[6.28] SEI
Probablemente notará algunas
notables similitudes entre el material
sobre fracciones decimales y lo
explicado en §5e(1) sobre la
aproximación de números racionales
mediante
series
de
potencias
convergentes de otros racionales. En
cualquier caso, concedamos una vez
más que si buscáramos el rigor técnico
más que la comprensión general, todos
estos tipos de conexiones se
seguirían/discutirían a fondo, aunque,
por supuesto, entonces el libro entero
sería mucho más largo y difícil, y el
nivel requerido de preparación-y-
paciencia-del-lector, mucho más alto.
O sea, que es una serie continua de
compromisos. <<
[6.29] SEI
Seguramente es innecesario
insistir una vez más en que una serie es
solo un tipo particular de sucesión. <<
[6.30] SEI
Si ha notado el parecido de
esto con la condición de convergencia
de Cauchy de §5a (véase G. E. II,
Ecuaciones diferenciales (b)), puede
entender por qué Cantor no dice que la
secuencia de a define un número real si
y solo si converge de esa manera, sino
meramente si converge. <<
[6.31]
Naturalmente, esto solo es
cuestión de notación. En el verdadero
«Über […] Reihen», Cantor sigue el
programa de Weierstrass y evita
«tiende
a»/«se
aproxima
a»,
prefiriendo el bueno y viejo pequeño
épsilon; así, técnicamente, el límite de
la secuencia se define mediante la regla
de que para cualquier ε dado, no más
de un número finito de términos
sucesivos de la sucesión pueden dejar
de diferir entre sí en un valor m tal que
m < ε. <<
[6.32] SEI
Es decir, si la sucesión tiene
un comportamiento constante a partir
de cierto punto, y a partir de entonces
todos sus términos tienen exactamente
el mismo valor, la sucesión define
dicho valor. <<
[6.33]
infinitas, de hecho, aunque la
demostración es demasiado elaborada
para que entremos en ella. <<
[6.34]
De nuevo, cuestión de notación.
Lo mismo respecto al final de la frase.
<<
[6.35]
de nuevo, fuera de cuadro:
desarrollarlo costaría varias páginas y
otro glosario de emergencia entero.
Vamos a dedicar un tiempo más que
suficiente a las demostraciones
formales de Cantor sobre ∞ en §7, de
todos modos. <<
[6.36] SEI
Algunos historiadores de las
matemáticas usan «constructivismo»
para referirse también al intuicionismo,
o viceversa, y a veces, operacionalismo
para referirse a ambos —además está
el convencionalismo, que es a la vez
similar y algo distinto—, es decir, que
puede resultar todo extremadamente
complicado y desagradable. Por ello,
de aquí en adelante, vamos a clasificar
las diversas escuelas e ideologías de la
manera más simple que sea posible.
(Por favor, observe también que de
toda la controversia intuicionista no
vamos a discutir nada más que lo
directamente relevante para nuestra
misión. Para los lectores especialmente
interesados
en
el
debate
metamatemático que empieza con
Kronecker y termina con las
demoliciones de fundamentos por
Gödel en la década de 1930, nos
complace recomendar la obra editada
por Paolo Mancuso From Brouwer to
Hilbert, también Introduction to
Metamathematics de Stephen C.
Kleene, y/o Philosophy of Mathematics
and Natural Science de Hermann
Weyl; todos ellos están en la
Bibliografía). <<
[6.37]
Aquí hay una interesante
coincidencia lingüística en la idea
kroneckeroide
de
demostración
constructiva.
Aparte
de
tener
connotaciones literales como «que
involucra una construcción real», la
palabra «constructivo» puede significar
«no destructivo». Como algo positivo
más que negativo, edificante más que
rupturista. El principal tipo de
demostración destructiva resulta ser la
reducción al absurdo; y, ciertamente, el
constructivismo no considera la
reducción al absurdo como un
procedimiento de demostración válido.
La verdadera razón, sin embargo, es
que la reducción al absurdo depende en
términos lógicos de la ley del tercero
excluido, en virtud de la cual (como
recordará de §1c) toda proposición de
tipo matemático es, formalmente
hablando, o bien verdadera, o bien
falsa. Los constructivistas (en especial
el seco y extremadamente excéntrico
Luitzen Brouwer) rechazan la LTE
como
un
axioma
formal,
principalmente porque la LTE no se
puede demostrar constructivamente; es
decir, no existe formulación alguna de
un procedimiento de decisión mediante
el cual se pueda verificar, para
cualquier proposición P, si P es
verdadera o falsa. Además, hay todo
tipo
de
hipótesis
matemáticas
importantes
—por
ejemplo,
la
conjetura
de
Goldbach,
la
irracionalidad de la constante de Euler,
y la hipótesis del continuo del propio
Cantor— que o bien no se pueden
demostrar todavía, o bien se puede
demostrar que son indemostrables sin
la LTE. Etc. [Observe, SEI, que por
estrafalario o fundamentalista que
pueda sonar el constructivismo, no está
desprovisto de influencia y valor. El
énfasis de dicho movimiento en los
procedimientos de decisión fue
importante para el advenimiento de la
lógica matemática y el diseño de
ordenadores, y su rechazo de la LTE es
en parte motivo de que el intuicionismo
se considere como el antecedente de la
lógica multivaluada, incluyendo la
lógica difusa hoy tan vital para la
inteligencia artificial, la genética, los
sistemas no lineales, etc. (SE muy I
respecto a esto último, los lectores con
cierta hipertrofia de preparación
matemática y mucho tiempo disponible
deberían ver la obra de Klir y Yuan
Fuzzy Sets and Fuzzy Logic: Theory
and Applications, cuyos datos también
están en la Bibliografía)]. <<
[6.38]
Aunque, para ser justos, en
realidad no es su terreno. <<
[6.39]
SEI Hay más detalle/contexto
acerca de esa definición más adelante,
en §7a. Por ahora, un buen ejemplo de
un conjunto sería el conjunto de todos
los
números
irracionales,
especialmente tras ver a Dedekind
explicar un procedimiento muy
definido para determinar si cualquier
número dado es irracional o no. <<
[7.1]
Más específicamente en
ecuaciones indeterminadas y formas
ternarias, temas de teoría de números
algebraica en los que Kronecker está
interesado. (¿Hemos mencionado que
Kronecker fue el director de tesis de
Cantor? ¿Y que es habitual que los
jóvenes matemáticos trabajen en
problemas propuestos por su director
de tesis? Véase también la inminente
explicación sobre la continuación por
Cantor de la demostración de Heine).
<<
SEI
[7.2] SEI
El sistema académico alemán
del siglo XIX es bastante indescifrable.
<<
[7.3]
SEI =
un tipo particular de
ecuación diferencial parcial que quizá
recuerde de las matemáticas de
segundo
curso
de
carrera,
probablemente en el contexto del
teorema de Green. <<
[7.4]
Lo cual, como quizá recuerde del
G. E. II, de su apartado Convergencia
Uniforme y secretos asociados,
significa que la f(x) que la serie
representa (= suma) tiene que ser
continua.
(SEI
La
verdadera
demostración de Heine requiere que la
serie y la función sean uniformemente
convergentes y continuas «casi en
cualquier punto», lo cual implica
distinciones tan finas que podemos
ignorarlas sin distorsión alguna). <<
[7.5] SEI
Es decir, el mismo artículo en
el que, como vimos en §6e, presenta su
teoría de los números reales (y cuyo
título probablemente ahora resultará
más comprensible). <<
[7.6]
Véase
el
apartado
Convergencia uniforme y los secretos
asociados, del G. E. II, sección (d) en
lo que respecta a puntos excepcionales,
los cuales, recuerde por favor otra vez,
también
pueden
llamarse
«discontinuidades». (N. B.: En algunas
clases de matemáticas también se usa
el término singularidad, lo cual es a la
vez confuso e intrigante, pues dicho
término también se refiere a los
agujeros negros, que en cierto sentido
es lo que las discontinuidades son). <<
SEI
[7.7]
Es importante recordar, en toda
esta sección, que para nosotros son la
misma cosa. <<
[7.8]
Véase §5e, el texto de la pág. 178 y
la nota 72. <<
[7.9]
C.f. Cantor, justo al principio de
«Sobre la extensión […] series»
afirma: «A todo número le corresponde
un determinado punto de la recta, cuya
coordenada es igual a ese número»
(Cantor, Gessamelte Abhandlungen, p.
97. Traducción extractada a partir de
Dauben, GC, pág. 40). <<
[7.10]
¿Hemos indicado ya en algún
lugar que esas extrañas llaves que
parecen el contorno de una persona,
{ }, son lo que se pone alrededor de las
cosas para indicar que forman un
conjunto matemático? <<
[7.11]
Es decir, que no es integrable
término a término de tal modo que el
resultado sea convergente. <<
[7.12] SEI
Evidentemente aquí es donde
Kronecker fue especialmente de ayuda.
<<
[7.13]
Y
claramente,
si
una
representación
en
serie
acaba
resultando demostrablemente idéntica
a la serie representativa original de la
f(x), entonces esa serie original es la
representación única de la función. Así
es básicamente como funciona el
teorema de unicidad: no es que solo
haya una serie que represente una
función dada, sino más bien que todas
las series que sí la representan son
demostrablemente equivalentes. <<
[7.14] SEI
Si el siguiente par de párrafos
le resultan muy difíciles, por favor, no
se desanime. La verdad es que la ruta
de Cantor hacia la teoría del ∞ es
mucho más dura, matemáticamente,
que la teoría misma. Todo lo que
necesita adquirir usted en realidad es
una cierta comprensión de cómo el
teorema de unicidad conduce a Cantor
a las matemáticas transfinitas. La parte
más compleja terminará enseguida. <<
[7.15]
Véase, por ejemplo, Joseph W.
Dauben sobre la demostración de 1872:
«Cantor subrayó, sin embargo, que los
números en esos varios dominios
[conjuntos derivados] se mantenían
enteramente independientes de esta
identificación geométrica, y el
isomorfismo servía, en realidad, como
una ayuda para pensar en los números
mismos» (ibíd.). Se dará cuenta de que
esta actitud es más o menos idéntica a
la de Dedekind en «Continuidad y
números irracionales». <<
[7.16]
Una cuestión previa: necesitamos
trazar una distinción entre dos
diferentes tipos de teoría de conjuntos
de los que podría usted saber algo. Lo
que se llama teoría de conjuntos de
puntos se refiere a conjuntos cuyos
elementos son números, puntos
espaciales o de la recta real, o varios
grupos/sistemas de estos mismos. La
teoría de conjuntos de puntos es hoy
muy importante para, por ejemplo, la
teoría de funciones y topología
analítica. Por otro lado, la teoría de
conjuntos abstracta se denomina así
porque la naturaleza y/o los elementos
de
sus
conjuntos
no
están
especificados. Es decir, que concierne a
conjuntos de prácticamente cualquier
cosa; es totalmente general y no
específica: por eso se llama
«abstracta». De aquí en adelante,
«teoría de conjuntos» se referirá a la
teoría de conjuntos abstracta, a menos
que se indique lo contrario. Lo
complicado es que Cantor, cuya fama
se debe realmente a ser el autor de la
teoría
de
conjuntos
abstracta,
obviamente puso en marcha (y
básicamente inventó) el tipo de
conjunto de puntos. En realidad, hasta
la década de 1890 no proporciona la
definición de conjunto que ahora
caracteriza la teoría de conjuntos
abstracta: «Una colección, como un
todo, de objetos distintos y definidos
de nuestra intuición o pensamiento,
[los cuales] se llaman los elementos
del conjunto» (traducción extractada a
partir de Edwards, v. 7, pág. 420), pero
todos sus resultados significativos en
las décadas de 1870 y 1880 sobre
conjuntos de puntos también son
válidos para la teoría de conjuntos
abstracta. Además, por favor, observe
finalmente, respecto a la anterior
definición de Cantor en comparación
con lo que vimos en §6f, que su
«definido» significa que para algún
conjunto S y cualquier objeto x, es por
lo menos, en principio, posible
determinar si x es un miembro de S (si
ha estudiado mucha lógica, quizá
recuerde que esa característica de los
sistemas
formales
se
llama
decidibilidad).
En
cambio,
el
«distinto» de su definición significa
que para dos elementos cualesquiera x
e y de S, x ≠ y, lo cual sirve
formalmente para distinguir un
conjunto de una sucesión, puesto que
en las sucesiones un mismo término
puede aparecer una y otra vez. <<
[7.17]
No hace falta decir que todo esto
está muy condensado; no es que
estuviera en su despacho y en un
momento dado tuviera una singular
epifanía en la que se lo ocurrieran
todas esas cosas. <<
[7.18] SEI
Algunas obras académicas de
primera categoría (en inglés) son The
Theory of Sets and Transfinite
Arithmetic de Alexander Abian,
Cantonan Set Theory and Limitation of
Size de Michael Hallett, y Georg
Cantor:
His
Mathematics
and
Philosophy of the Infinite de Joseph W.
Dauben, todos los cuales figuran en la
Bibliografía. La salvedad, sin embargo,
es que en este caso «académico»
significa despiadadamente denso y
técnico. En particular, el libro de
Dauben requiere tantos conocimientos
de matemáticas puras que es difícil
imaginar que cualquier lector capaz de
disfrutarlo pierda su tiempo con el
librito que tiene en sus manos… por lo
cual esta misma nota tiende a
autoanularse, ya que en cierto modo
carece de interés. <<
[7.19] SEI
Estas últimas en relación con
la lógica extensional de George Boole
(1815-1864), del cual es una vergüenza
que no vayamos a hablar. <<
[7.20] SEI
Es más exacto decir que la
parte más importante de su trabajo
original lo realiza entre 1874 y 1884, y
que los artículos de la siguiente década
son principalmente ampliaciones y
revisiones de demostraciones previas,
así como réplicas a objeciones de otros
matemáticos. <<
[7.21]
Por favor, tenga en cuenta que
mientras inventaba estas cosas Cantor
no procedía axiomáticamente: basó la
mayor parte de ello en lo que llamaba
«imágenes», o conceptos en bruto.
Además, a pesar del uso masivo de
símbolos, la mayoría de sus
argumentaciones eran en lenguaje
natural, y no precisamente en un
lenguaje rígidamente claro de calibre
russelliano, tampoco. Lo importante es
que el trabajo original de Cantor es
algo más difuso y complicado que las
matemáticas transfinitas que vamos a
discutir, que usan axiomatizaciones y
codificaciones aportadas por teóricos
de conjuntos poscantorianos como
Ernst Zermelo, Abraham A. Fraenkel y
Thoralf Skolem (no es que los nombres
importen mucho aún en este §). <<
[7.22] SEI
Aunque obviamente todo se
puede encontrar en las publicaciones de
Cantor indicadas en la Bibliografía. <<
[7.23] SEI
Especialmente si tiene usted
la edad adecuada para que le
sometieran a las nuevas matemáticas.
<<
[7.24] SEI
Las disculpas y garantías de la
nota 14 también son pertinentes para el
siguiente párrafo del texto principal.
<<
[7.25] SEI
= término usado por Cantor.
Por lo que parece, en alemán no tiene
las connotaciones postmortem que tiene
para nosotros. <<
[7.26] SEI
La demostración de Cantor de
que P' = Q ∪ R es enormemente
compleja pero totalmente válida; por
favor, haga un acto de fe. <<
[7.27] SEI Observe
que la sucesión de (1)
también tiene puntos suspensivos
exteriores al paréntesis, lo cual
significa que la sucesión continúa más
allá de la progresión con superíndices
finitos. Los puntos suspensivos de (2)
son 100% intraparentéticos porque n
misma es infinita. ¿Se entiende? <<
[7.28]
La notación que sigue es, por
supuesto, SEI, pero por lo menos es
bastante bonita. <<
[7.29] SEI
En verdad hay una analogía de
los números transfinitos mucho mejor
que los enteros, o sea algún otro tipo de
número que en realidad no se puede
nombrar ni contar pero que a pesar de
todo se puede generar de forma
abstracta, por ejemplo, dibujando la
diagonal del cuadrado unidad, o
tomando la raíz cuadrada de 5, o
describiendo unos A y B particulares
dedekindianos y un schnitt intersticial.
Respecto a todo lo cual, por favor, vea
o espere la discusión dos párrafos
después. <<
[7.30] SEI Que
aleph sea una letra hebrea
a veces es muy aprovechado por
algunos historiadores en relación a los
supuestos
orígenes
o
estudios
cabalísticos de Cantor. Explicaciones
más plausibles de que Cantor eligiera
ℵ son que (1) quería un símbolo
completamente nuevo para un tipo de
número completamente nuevo, y/o, (2)
las letras griegas de toda la vida ya
estaban todas ocupadas. <<
[7.31] SEI
Las demostraciones de lo cual
llegarán a partir de §7c. <<
[7.32] SEI
<<
Matemáticamente hablando.
[7.33]
Aquí está hablando del método
del schnitt de Dedekind, el cual, tras un
tiempo trabajando en el Cantor,
prefirió a su propio enfoque, por
razones bastante obvias. <<
[7.34]
Por consideraciones de espacio no
vamos a entretenernos demasiado en
esto, pero subrayemos una vez más
aquí que Cantor es, como Dedekind, un
platónico matemático, es decir, cree
que tanto los conjuntos infinitos como
los números transfinitos existen
realmente, en un sentido metafísico, y
que se «reflejan» en auténticos
infinitos del mundo real, aunque su
teoría acerca de esto último involucra
las mónadas leibnizianas y es mejor no
entrar en ella. Resulta que Cantor
también desarrolla todo tipo de
planteamientos
y
argumentos
teológicos
respecto
al
algunos
concienzudos y poderosos, y otros
meramente excéntricos. Aun así, como
matemático y rétorico, Cantor es lo
bastante listo para argumentar que no
se necesita aceptar ninguna premisa
metafísica particular para admitir a los
conjuntos infinitos o sus números
abstractos en el dominio de los
conceptos matemáticos legítimos.
Véase, por ejemplo, este pasaje de la
obra de Cantor antes mencionada
«Contribuciones…»: «En particular, al
introducir nuevos números, las
matemáticas solo están obligadas a dar
definiciones de ellos, mediante las
cuales se les confiera tal precisión y, si
las circunstancias lo permiten, tal
relación con los antiguos números que,
dados los casos, se puedan distinguir
definitivamente los unos de los otros.
Tan pronto como un número satisface
todas esas condiciones, puede y debe
ser contemplado como existente y real
en matemáticas. Aquí percibo la razón
por la que debe considerarse que los
números racionales, irracionales y
complejos son tan existentes como los
enteros positivos finitos» (Cantor,
Gessamelte Ab., pág. 182). Esta última
frase tan clara es un pequeño guiño a
Kronecker. Como el resto es bastante
críptico, Dauben lo resume así: «Para
los matemáticos, solo se necesitaba una
prueba: tan pronto como se veía que los
elementos de una teoría matemática
cualquiera eran consistentes, entonces
eran matemáticamente aceptables. No
se necesitaba nada más» (Dauben, GC,
pág. 182). <<
[7.35] SEI
Aquí el mejor apoyo es del
seguidor de Cantor Abraham A.
Fraenkel: «El concepto de magnitud
transfinita es insignificante mientras
solo se conozca la existencia de una
única magnitud de ese tipo» (Fraenkel
en Edwards, v. 2, págs. 20-21). <<
[7.36]
En realidad, más «en
conjunción» que «simultáneamente»,
pues al final resulta que ambos
proyectos tienen todo tipo de
relaciones de alto nivel. <<
SEI
[7.37]
Si alguna vez se ha
encontrado con referencias a los
cardinales transfinitos de Cantor, eso
es lo que son: los números cardinales
de conjuntos infinitos. <<
SEI
[7.38] SEI
La paradoja de Galileo se
sustenta de modo directo aunque
encubierto en esta definición. Véase,
por ejemplo, §1d, pág. 47: «Es también
obvio que mientras todo cuadrado
perfecto (o sea 1, 4, 9, 16, 25, …) es un
entero, no todo entero es un cuadrado
perfecto». <<
[7.39] SEI
«Aquí» = principalmente dos
artículos fundacionales en 1874 y 1878,
aunque también dedica mucho tiempo a
concretar la idea en sus artículos
posteriores, más discursivos. Si quiere
saber el título de la monografía de
1874, es «Über eine Eigenschaft des
Inbegriffes aller reellen algebraischen
Zahlen». La traducción sería algo así
como «Sobre una característica del
conjunto de todos los números reales
algebraicos», respecto a lo cual puede
mirar la nota 53 más adelante. <<
[7.40] SEI
En esto, de hecho, consiste
contar una colección cualquiera de n
cosas: es poner las cosas en una
correspondencia uno a uno con el
conjunto de enteros {1, 2, 3,…, n}. La
equivalencia de contar y poner en C1-1
con {todos los enteros} es lo que
convirtió a la teoría de conjuntos en la
base para enseñar aritmética a los
niños, de acuerdo con las nuevas
matemáticas. <<
[7.41] SEI N.
B. En la teoría de conjuntos
cantoriana numerable está relacionado
con contable pero no es sinónimo.
Definición: un conjunto es contable si
y solo si es o bien (a) finito, o bien (b)
numerable. <<
[7.42]
Esto se llama tradicionalmente
aleph-cero. <<
[7.43] SEI
El orden solo empieza a ser
importante
con
los
ordinales
transfinitos de Cantor, que hacen su
aparición en §7g. <<
[7.44]
Observe que estamos
empezando a ser capaces de responder
a la epigráfica cuestión de Russell al
principio de §7. <<
SEI
[7.45]
Decisión del Alto Mando: de aquí
en adelante, cuando hablemos de
«todos los números» trataremos solo
con valores positivos. Esto incluye a
los enteros, pues al fin y al cabo
acabamos de demostrar que la
cardinalidad del conjunto de todos los
enteros = la del conjunto de todos los
enteros positivos. Además, debería ser
obvio que las demostraciones de
Cantor para todos los racionales
positivos, todos los reales positivos,
etc., seguirán siendo válidas si los
conjuntos infinitos relevantes se doblan
para incluir los valores negativos. Si
tiene dudas, entonces observe que
doblar algo es lo mismo que
multiplicarlo por 2, y que 2 es finito, y
que —por los teoremas transfinitos (3)
y (6) de §7b— cualquier ℵ
multiplicado por un n finito seguirá
siendo = ℵ. <<
[7.46] SEI
De nuevo, tenga en cuenta,
por favor, que estamos haciendo estas
demostraciones en el orden que facilita
una exposición más clara y lógica.
N. B. Tenga en cuenta también que hay
algunas distinciones entre cardinales y
ordinales que de momento vamos a
eludir. <<
[7.47]
Lo que Cantor llama
realmente «diagonalización» es su
método para demostrar la no
numerabilidad de los reales, que como
veremos es bastante diferente. <<
SEI
[7.48] SEI
Si esta definición esquemática
le parece insuficiente y quiere usted
una verdadera C1-1 entre los conjuntos
de los racionales y de los enteros,
entonces tome simplemente la fila
ordenada que hemos visto y empareje
su primer elemento con 1, su segundo
elemento con 2, …, y así
sucesivamente. <<
[7.49]
SEI Aquí
quizá pueda usted
anticipar
algunas
complicaciones
familiares respecto a cuál podría ser el
primerísimo número real de la
sucesión, y para ver por qué ninguna de
las anteriores manipulaciones con los
órdenes de las filas funcionará con los
números reales. En este caso, para su
tranquilidad, le informamos ahora de
que el famoso axioma de elección (otro
lío enmarañado, véase §7f) de la teoría
de conjuntos, del profesor Zermelo,
asegura que siempre podemos construir
un conjunto ordenado de números
reales de tal modo que tenga un
auténtico primer elemento. Sería
interesante
que
de
momento
simplemente se creyera esto. <<
[7.50]
Así que el motivo de que se llame
«diagonal» es por lo del primer dígito
en la primera fila, el segundo dígito en
la segunda fila, y la construcción de R
en un ángulo de 45°. <<
[7.51] SEI Véase
el principio de §5e. <<
[7.52]
SEI La demostración de esta
extraña curiosidad, véanse las págs. 9193 de §2e, está claro que ahora se
puede liberar del requisito de que todos
los pañuelos y medios pañuelos y
mitades de medios pañuelos sean
infinitesimalmente pequeños; solo
invocamos
la
demostración
de
Weierstrass en §5e(i) de que
= 0. <<
[7.53] SEI
Desde un punto de vista
histórico, el primer resultado acerca de
la no numerabilidad que Cantor pudo
realmente demostrar fue que el
conjunto de todos los números
trascendentes era no numerable y que
el conjunto total de todos los números
racionales + todos los irracionales
algebraicos
tenía
la
misma
cardinalidad que el de los racionales.
Véase la nota 39 anterior, y el título del
artículo de Cantor de 1874, que ahora
debería resultar más comprensible. <<
[7.54] SEI
= «Lo veo, pero no me lo
creo» (lo cual es un retazo muy
conciso, aunque involuntario, de
antiempirismo). No está claro por qué
le escribe esto en francés a un
destinatario que también era alemán;
podría haber sido un modo de subrayar
la emoción. El alemán académico de
Cantor, también, a menudo cambia al
francés o al griego por ninguna razón
discernible. Quizás era habitual en su
contexto. <<
[7.55]
Esta unicidad es crítica. No se
pueden permitir dos expresiones
decimales distintas para representar un
mismo punto, porque la idea principal
es ver si a cada punto en particular del
cuadrado unidad le corresponde un
punto en particular en el intervalo [o,
1] de la R. R. Ahora debería quedar
100% claro por qué Cantor necesita
estipular que números como
deberán
ser designados solo por 0,4999…, y así
sucesivamente. Si recuerda que
mencionamos esta estipulación en §7c,
ahora sepa que Dedekind se la sugirió a
Cantor en relación a esta demostración
de la dimensión, indicando que la
«correspondencia única» (que era el
término original de Dedekind y de
Cantor para la C1-1) quedaría destruida
si se permitían a la vez 0,4999… y
0,5000… <<
[7.56]
INTERPOLACIÓN TAN SEI
QUE NI SIQUIERA ESTÁ EN el texto
principal Técnicamente es algo más
complicado, pero no mucho más. La
demostración de la dimensión original
de Cantor es, en cierto modo,
innecesariamente intrincada. Supone
definir la representación decimal de un
punto (x, y) como la serie convergente
β1
βn
+ β2
+ β3
+ … +
+ …, y entonces «separar los
términos [de esta serie]» de modo que
para cada miembro se forme una
sucesión
de
«ρ
variables
independientes» (Cantor resumido por
Dauben, GC, pág. 55) en [0, 1],
designadas por α1 α2 α3, α4, …, αρ. La
«separación» y la subsiguiente
correspondencia (así como la operación
recíproca,
de
modo
que
la
correspondencia α ↔ β funcione en
ambos sentidos) se consigue mediante
cuatro ecuaciones, de las cuales la
primera
tiene
este
aspecto:
«α1,n = β(n−1)ρ+1». Lo cual puede hacer
que la C1-1 no sea demasiado obvia. El
problema de la verdadera demostración
(como explicó en 1979 el imponente
doctor Goris) es que la descripción
«a1a2a3b1b2b3» de las coordenadas
(x, y) del plano que hemos dado antes
resulta un poco simple porque parece
que a y b sean dígitos individuales. Lo
que hace realmente la técnica de
Cantor es subdividir x e y en pequeñas
tiras de cifras decimales; la regla es
que cada tira termina en la primera
cifra distinta de cero que se encuentre
(otro motivo, más técnico, por el que
Cantor no puede permitir que los
enteros y los racionales terminen en
0,000…). Así que digamos, por
ejemplo, que x = 0,020093089… y que
y = 0,702064101…, en cuyo caso se
subdividen en: x = 0,02 009 3 08 9…
y = 0,7 02 06 4 1 01… Son estas tiras
las
que
se
combinan
con
alternadamente
para
dar
la
representación decimal única del punto
(x, y) = 0,02 7 009 02 3 06 08 4 …
Y aquí los espacios extra son solo a
efectos ilustrativos; la auténtica
representación decimal de (x, y) es
0,02700902306084… Por supuesto,
esto también es un número real,
concretamente el punto z de [0, 1] que
es igual a 0,0270​090​230​6084… Y lo
ingenioso de jugar con las tiras de este
modo es que si hay algún z' que difiere
de z en una sola cifra n posiciones tras
la coma (de los que por supuesto habrá:
∞ z, de hecho), entonces el (x, y)
relevante también será diferente en la
tira que contenga esa n-ésima cifra, de
modo que la correspondencia relevante
es biunívoca: eso quiere decir que para
cada z hay un único (x, y), y viceversa,
o sea que se trata de una genuina C1-1.
<<
[7.57] SEI
(incluida a insistencia del
editor) = el lascivo término para
poliedros en 4 o más dimensiones. <<
[7.58] SEI
como se ha mencionado en los
§ 5b y 5d. (Y en §5d, por lo menos se
habló un poco del uso en la geometría
riemanniana del ∞ y de puntos
relacionados con el ∞). <<
[7.59]
Esto entra en un área bastante
especializada de la teoría de funciones,
pero básicamente correspondencia no
continua significa que si usted se
mueve continuamente a lo largo de los
puntos de [0, 1] en la R. R., los puntos
correspondientes en el cuadrado unidad
no formarán una curva continua, sino
que quedarán esparcidos por todas
partes. (SEI Respecto al segundo
párrafo de §7d un poco antes, resulta
que la suposición de Riemann et al.
estaba equivocada de un modo
interesante: la dimensión de un
conjunto dado de puntos depende no
solo de cuántas coordenadas por punto
hay, ni tampoco de la cardinalidad de
todo el conjunto de puntos, sino
también del modo particular en que los
puntos están distribuidos. Esto último
es una cuestión de la topología de
conjuntos de puntos, respecto a la cual
todo lo que estamos en situación de
decir en este libro es que es otra rama
más de las matemáticas que no
existiría sin el trabajo de Cantor sobre
el ∞). <<
[7.60] SEI
fecha = 1878; título = «Ein
Beitrag zur Mannigfaltigkeitslehre», o
algo así como «Una contribución a la
teoría
de
multiplicidades/agregados/conjuntos».
<<
[7.61] SEI
Probablemente resulta obvio
que aquí las «ficciones» de Du BoisReymond son específicamente las
representaciones decimales compuestas
de (x, y); pero en el contexto más
amplio de su escrito también está
hablando de los conjuntos infinitos de
puntos de la R. R. y del C. U. que los
decimales
representan.
(N.
B.
Exactamente la misma acusación se
podría haber lanzado contra los A y B
de la teoría del schnitt de Dedekind;
por alguna razón, Dedekind nunca
atrajo la misma hostilidad que Cantor).
<<
[7.62]
Cantor a menudo se refiere a esto
como la primera clase numérica y la
segunda
clase
numérica,
respectivamente. <<
[7.63] SEI
Los libros de texto a menudo
formulan esto como un teorema
abstracto,
por
ejemplo,
«Dado
cualquier conjunto infinito S, es
posible construir otro conjunto infinito
S' con un número cardinal mayor». <<
[7.64] SEI
Este principio se conoce en la
teoría de conjuntos como el axioma del
conjunto potencia (A.C.P.). Una razón
por la que es un axioma es que depende
directamente de las definiciones de
«subconjunto» y «conjunto vacío», tal
como resultará evidente enseguida en
el texto principal. Sin embargo, hay
problemas con el A.C.P.: véase el §7f
interpolativo más adelante. <<
[7.65] SEI
Técnicamente, esto debería
escribirse «P(A) = 2A», donde A
representa el número cardinal de A.
Habiendo declarado esto para que
quede constancia, a partir de ahora lo
escribiremos informalmente, sin más.
<<
[7.66] SEI
Una vez más, técnicamente
sería mejor decir que «∅» es el
símbolo de { }, el cual es el conjunto
vacío… pero ya se entiende. <<
[7.67] SEI
Puede demostrar que P(A) =
20 también en el caso del conjunto
vacío. Si A = ∅, tiene o elementos. Sin
embargo, tiene un subconjunto, o sea
∅, pues el conjunto vacío es un
subconjunto de todo conjunto. O sea,
que en este caso P(A) = 1, que es 20.
<<
[7.68]
Entenderá esto si recuerda que el
contexto
general
de
estas
demostraciones es el intento por parte
de Cantor de obtener conjuntos
infinitos (también conocidos como
clases numéricas) cuya cardinalidad
excediera c. <<
[7.69] SEI
De hecho, la de 1891 es en
realidad una demostración de que este
conjunto potencia es no contable. Pero
recuerde que para que un conjunto sea
contable debe ser o finito o numerable,
y es fácil ver que en este caso el
conjunto relevante no es finito. Como
el conjunto de todos los enteros {1, 2,
3, 4, 5,…} es, él mismo, infinito, basta
tomar cada elemento individual,
ponerlo entre llaves, y darse cuenta de
que {1}, {2), {3), etc., son todos
subconjuntos del conjunto de todos los
enteros. Así que el conjunto de todos
los subconjuntos no puede ser finito en
modo alguno. O sea, que la verdadera
cuestión es si el conjunto potencia es
numerable. <<
[7.70] SEI EXTRACTO DE LA CARTA DEL
EDITOR CON PETICIONES ACERCA DE LA
VERSIÓN
MANUSCRITA
DEL
LIBRO:
«pág. 250, párrafo tras gráfica de la
“Tabla n.º 3”; o sea que, en otras
palabras,
sin
importar
cuántos
subconjuntos de E podamos obtener,
¿siempre podemos crear otros nuevos?
Si es así, ¿quiere usted que lo digamos
tal cual, soltarlo sin más?», de la
respuesta del autor: «No, no queremos
decir algo así, porque sería erróneo. Lo
que muestra la Tabla n.º 3 es que sin
importar
cuántos
infinitos
o
subconjuntos de E pongamos en la
lista, es demostrable que siempre habrá
algunos subconjuntos que no están en
la lista. Esto es, recuerde, lo que “no
numerable” significa: que no puede ser
exhaustivamente listado/puesto en
fila/puesto en una tabla (y, de nuevo, es
por lo que siempre habrá más
irracionales que pañuelos de la muerte
en la demostración del doctor Goris en
§2e: los pañuelos, como los enteros y
los racionales, solo pueden formar un
∞ numerable). Además, la parte de
“siempre podemos crear otros nuevos”
es profunda y seriamente, errónea: no
estamos creando nuevos subconjuntos;
estamos demostrando que existen y
siempre existirán algunos subconjuntos
que ninguna lista o C1-1 con los
enteros podrá capturar. Respecto a
“existir”, cabe reconocer que necesita
un “en cierto modo” o “sea lo que sea
que esto significa” o algo parecido,
pero el lector tendría que ser un
fundamentalista-radical kroneckeriano
para creer que lo que estamos haciendo
en esta demostración es realmente
crear esos nuevos subconjuntos». <<
[7.71]
SEI Esto saca a relucir una
cuestión importante. Puede muy bien
haber notado el gran parecido entre la
demostración en diagonal de la no
numerabilidad
de
P(E)
y
la
demostración en diagonal de la no
numerabilidad de {todos los números
reales} en §7c. Y ahora, dado que tanto
P(E) como {todos los reales} tienen
cardinalidades > ℵ0, puede muy bien
estar preguntándose si el número
cardinal de P(E) es c igual que lo es el
de {todos los números reales}. En cuyo
caso, usted habrá formulado, por sí
mismo, una versión de uno de los
problemas más profundos de la teoría
de conjuntos cantoriana, el cual se
analiza extensamente en §7g. Lo
importante es que está 100% acertado
al preguntarse sobre la relación entre
P(E) y c, pero espere. <<
[7.72] SEI,
es decir, que B es también
P(A), pero para esta demostración es
más fácil si olvida usted todo el asunto
del conjunto potencia. <<
[7.73] SEI
a veces conocida también
como la paradoja de Euclides para
distinguirla de la variante de
Epiménides «Todos los cretenses son
mentirosos» —larga historia—. <<
[7.74]
1906-1978, el absoluto
Príncipe de las Tinieblas de las
matemáticas modernas, ya se ha hecho
referencia a él en §1a y en otras partes.
<<
SEI
[7.75] SEI
Sabemos, por ejemplo, que se
la explicó a David Hilbert, y se
menciona por lo menos en una de las
cartas de Cantor a Dedekind. Observe
ahora, de cara a más adelante, que hay
otra paradoja con la que también se
encontró y tampoco publicó, que hoy se
conoce como la paradoja de BuraliForti y tiene que ver con los ordinales
transfinitos, que como se ha
mencionado también están al llegar.
<<
[7.76] SEI
Lo de Frege y Russell es una
historia larga pero muy apreciada por
los historiadores de las matemáticas, y
muy fácil de encontrar en otra parte.
(N. B. La antinomia de Russell también
se conoce como la paradoja de Russell,
pero resulta cansino decir «paradoja»
una y otra vez). <<
[7.77] SEI
Una vez más, es algo más
complicado. Lo que la antinomia de
Russell explota realmente es un axioma
poco sólido de la teoría de conjuntos
temprana llamado (no es broma) el
principio de abstracción ilimitada
(P. A. I.), que a todos los efectos
afirma
que
toda
característica/condición
concebible
determina un conjunto; es decir, que
dada cualquier propiedad concebible,
existe un conjunto de todas las
entidades que poseen dicha propiedad.
Tres rápidos comentarios acerca del
P. A. I. (1) Observe su intrigante
parecido con el argumento de Platón
del Uno Sobre Muchos de §2a. (2)
Pronto debería ser evidente en el texto
principal por qué el P. A. I. es
defectuoso y da lugar a la antinomia de
Russell. (3) Por favor, retenga
neocorticalmente durante solo unas
páginas el hecho de que el sistema de
axiomas de Zermelo-Fraenkel-Skolem
para la teoría de conjuntos enmienda el
P. A. I. con el principio de abstracción
limitada (P. A. L.), el cual sostiene que
dada cualquier propiedad p y un
conjunto S, podemos formar el
conjunto de todos los elementos de S
que tienen p. <<
[7.78] SEI
El resto del texto principal de
este párrafo lo puede omitir usted si ya
puede ver cómo funciona la paradoja
simplemente a partir de «¿Es N un
conjunto normal?». (SEI2 Russell
también tiene una manera famosa de
presentar su antinomia en lenguaje
natural, a saber: imagine un barbero
que solo afeita a los que no se afeitan a
sí mismos; entonces, ¿se afeita el
barbero a sí mismo?). <<
[7.79] SEI
En esta oposición a Poincaré
se le asocia a menudo con los
especialistas en conjuntos de puntos
finitos Félix Édouard Borel y Henri
Léon Lebesgue, y así en la metafísica
de las matemáticas este trío es a veces
conocido
como
la
Escuela
antiplatónica. <<
[7.80]
algo muy parecido a la
caracterización griega del ∞ como to
apeiron. <<
[7.81] SEI
Aquí está uno que quizá ya
haya usted anticipado: si alguna
propiedad es impredicativa si se aplica
a sí misma —digamos, por ejemplo, la
propiedad de ser expresable en
lenguaje natural, o correctamente
deletreado, o abstracto— entonces
podemos llamar a una propiedad
«predicativa» si no se aplica a sí
misma. Pero entonces, esa propiedad
de ser predicativa, ¿es predicativa o
impredicativa? <<
[7.82] SEI
Sí: ahora estamos volviendo
de nuevo a las cuestiones de existencia
abstracta y denotación planteadas en
§1. <<
[7.83] SEI
Si cree que puede ver al
fantasma del Tercer Hombre de
Aristóteles flotando encima de la teoría
de tipos, no se equivoca. Muchos de los
problemas fundacionales de la teoría de
conjuntos acaban remontándose a la
metafísica griega. <<
[7.84] SEI
N. B. Observe también que los
argumentos de Russell respecto a la
conexión entre la tipología metafísica
de entidades/abstracciones y la
tipología
semántica
de
entidades/enunciados/metaenunciados
son largos y complejos, pero están allí:
no es que lo postule todo a partir de la
nada. <<
[7.85] SEI
Las subsiguientes extensiones
y modificaciones de la teoría de tipos
russelliana, por lógicos como Ramsey
y Tarski, son tan horripilantemente
complicadas y confusas que, si saca
usted el tema, la mayoría de los
matemáticos harán como si ni siquiera
le oyeran. <<
[7.86] SEI
Es decir, el segundo de los 10
Principales Problemas no Resueltos
que Hilbert presentó en el 2.º C. I. M.
en el año 1900 como problemas
cruciales para las matemáticas que
debían resolverse durante el inminente
siglo; otra muy larga historia que
puede encontrar en cualquier buen
compendio de historia de las
matemáticas. (SEI2 Si le enseñaron o ha
leído que en realidad había 23
Problemas de Hilbert, la verdad es que
Hilbert presentó una lista del 1 al 10 en
su discurso de París y del 1 al 23 en la
versión escrita publicada en 1902). <<
[7.87]
Compare
esta
ontología
formalista
con
la
visión
del
intuicionismo de que: «[L]os objetos
matemáticos son entidades mentales
que
no
existen
de
manera
independiente de nuestra capacidad
para proporcionar una demostración de
su existencia en un número finito de
pasos» (Nelson, pág. 229). Puede ver
que ambas visiones no son para nada
disímiles, especialmente en su rechazo
de la idea de que las matemáticas
tengan algo que ver con la realidad
extramental, aunque tras el criterio
intuicionista del «número finito de
pasos» está la intención específica de
proscribir
entidades
como
los
irracionales y los conjuntos infinitos
con los que Poincaré y Brouwer, igual
que Kronecker antes de ellos, tenían
problemas metafísicos (no solo de
procedimiento). (SEI La manera del
doctor Goris de contrastar ambas
escuelas era decir que el intuicionismo
era taimado mientras que el
formalismo era más bien simplemente
excéntrico). <<
[7.88] SEI véase
§1c. <<
[7.89]
Estos improperios ya deberían
estar en un G. E. III a estas alturas. Son
términos de lógica, de la teoría de
modelos. Un sistema es completo si y
solo si todas y cada una de las
proposiciones verdaderas se pueden
deducir como un teorema; es
consistente si no incluye ni implica
contradicción alguna. Hay también un
tercer criterio, antes brevemente
mencionado, llamado decidibilidad,
que concierne a si hay un
procedimiento/algoritmo
para
determinar, para cualquier proposición
bien formada del sistema, si es o no
verdadera (es decir, si es un teorema).
Los tres criterios están obviamente
interconectados, pero también tienen
diferencias importantes, y un sistema
formal deductivamente inmaculado se
supone que satisface las tres… respecto
a lo cual, a grandes rasgos, Gödel
demostró
que
ningún
sistema
significativamente potente podía, por
lo cual se le conoce como el Príncipe
Tenebroso, y por ello las matemáticas
han estado en el aire durante los
últimos setenta años. <<
[7.90] SEI
Fechas: 1871-1953. Artículo
principal: «Investigaciones de los
fundamentos de la teoría de conjuntos»
(1908).
Principal
colaborador:
Abraham Fraenkel, quien es también el
primer biógrafo de Cantor. <<
[7.91]
paradojas de las que ahora
muchos matemáticos profesionales no
se preocupan demasiado durante su
trabajo del día a día; no mucho más de
lo que nosotros nos preocupamos de si
el suelo se hundirá bajo nuestros pies
cuando nos levantemos de la cama. <<
[7.92]
Probablemente
más
que
«independiente» sería mejor decir
«conceptualmente anterior a» o
«subyacente» a las matemáticas per se.
La idea tras la T. A. C. es que como la
teoría de conjuntos es la rama más
abstracta
y
primitiva
de
las
matemáticas, sirve como fundamento
para los conceptos matemáticos más
básicos, como «número», «función»,
«orden», etc. Aunque toda la cuestión
se complica mucho —particularmente
las cuestiones acerca de la relación de
la teoría de conjuntos con la lógica
simbólica y sobre cuál es el verdadero
fundamento de las matemáticas— es,
sin embargo, cierto que tanto Gottlob
Frege como Giuseppe Peano, las dos
figuras más importantes en la
fundamentación de la aritmética,
definen los números y las operaciones
matemáticas básicas en términos de la
teoría de conjuntos. <<
[7.93] SEI
= o bien una función o algún
predicado en lenguaje natural que tenga
sentido para todos los elementos de S
(donde «que tenga sentido» significa
básicamente que el predicado es algo
definitivamente
verificable
como
cierto o falso para cualquier elemento
del conjunto, como «es azul» o «pesa
más de 28,7 gramos» en contraste con
«es adorable» o «tiene gusto de
pollo»). <<
[7.94]
Usar este símbolo en una frase
así, tal cual, es la manera llamativa de
decir «elemento de S». <<
[7.95]
Así, un corolario obvio del P. A. I.
es: los conjuntos infinitos existen. <<
[7.96] SEI
Este es otro punto donde no
está claro exactamente qué lectores
sabrán o recordarán lo que se está
omitiendo. Si no está familiarizado con
los postulados de Peano y le gustaría
estarlo, invierta 45 segundos en lo
siguiente: los postulados de Peano son
los cinco axiomas básicos de la teoría
de números; permiten deducir toda la
sucesión infinita de los enteros
positivos a partir de solo dos conceptos
primitivos, que son (a) «es un entero»,
y (b) «es sucesor de». En lenguaje
natural, los postulados son: (1) 1 es un
entero; (2) Si x es un entero, el sucesor
de x es un entero; (3) 1 no es sucesor de
ningún entero; (4) Si los sucesores de
dos números x e y son iguales, entonces
x = y; (5) Si un conjunto E contiene 1,
y si, para cualquier entero x de E, el
sucesor de x está en E, entonces todo
entero está en E. Por qué exactamente
el postulado (5) es la autoridad
axiomática tras la demostración por
inducción matemática es algo que
queda claro mediante una formulación
alternativa, que sería más o menos así:
(5) Si P es cierta propiedad, y si 1 tiene
P, y si cuando un entero x tiene P, el
sucesor de x tiene P, entonces todos los
enteros tienen P. (SEI2 Curiosidad
gorisiana: Aunque Peano merece un
100% de reconocimiento por introducir
todo tipo de cosas importantes en la
teoría de números y en la teoría de
conjuntos (como los símbolos estándar
∈, ∩ y ∪), sus epónimos postulados son
un caso claro de los caprichos de la
fama matemática, pues axiomas
equivalentes a los postulados (1)-(5)
habían aparecido en la obra de
Dedekind Naturaleza y significado de
los números por lo menos dos años
antes que en la obra de Peano
Arithmetices Principia Nova Methode
Expósita). <<
[7.97] SEI
No nos preocuparemos mucho
de los productos cartesianos (P. C.)
excepto para decir (1) que son un tipo
específico de unión inter-conjuntos que
involucra «pares ordenados», los cuales
en sí mismos son toda una saga; y (2)
que los P. C. son un ejemplo del
importante principio de preservación
de la homogeneidad, en el sentido de
que si dos conjuntos A y B comparten
ciertas características especiales, su
producto cartesiano (A × B) también
tendrá dichas características (por
ejemplo, si A y B son conjuntos de
puntos y comparten la característica de
ser un espacio topológico, su P. C.
también será un espacio topológico).
<<
[7.98] SEI
Aquí «producto cartesiano»
específicamente significa (inspiración
profunda) «el conjunto de solo aquellos
subconjuntos de la unión de todos los
elementos de S tal que cada uno (=
cada
subconjunto)
contiene
exactamente un elemento de cada
conjunto de S». Este tipo de cosa es
solo para que tenga una muestra del
embriagador aroma de la auténtica
T. A. C. <<
[7.99] SEI
Cualquier libro decente sobre
lógica matemática o teoría de
conjuntos incluye un capítulo entero
sobre el A. E. y su relación con otros
seductores conceptos como el axioma
multiplicativo de Russell, el lema de
Zorn, el principio de tricotomía, el
principio maximal de Hausdorff y (no
es broma) el lema del elemento
máximo de Teichmüller-Tukey. <<
[7.100] SEI
un americano (!) al cual
estamos a punto de ver en acción
respecto al tema de la hipótesis del
continuo, justo a continuación. <<
[7.101]
El
historial
de
demostraciones relacionadas con el
A. E. es —sorpresa— una muy larga
historia; lo importante queda resumido
en el siguiente extracto de la obra de
Mendelson de 1979 Introduction to
Mathematical Logic (y donde la
segunda frase es de un tono muy
acalorado para tratarse de un lógico):
«El estatus del axioma de elección se
ha hecho menos controvertido en años
recientes. Para la mayoría de los
matemáticos parece bastante plausible
y tiene tantas aplicaciones importantes
en prácticamente todas las ramas de las
SEI
matemáticas que no aceptarlo parecería
restringir deliberadamente la actividad
práctica del matemático (Mendelson,
pág. 213)». <<
[7.102] SEI
Si quiere ver el axioma de
regularidad simbólicamente desnudo
al 100%, es (∀S)[(S ≠ ∅ → (∃x)((x ∈ S)
& (x ∩ S = ∅))], en el cual los únicos
símbolos no familiares podrían ser los
cuantificadores
del
cálculo
de
predicados «∀S» (que significa «Para
todo S…») y «∃x» (que significa
«Existe por lo menos un x tal que…»;
donde el significado de «existe» es
matemático/teórico-conjuntista [donde,
claro está, se supone que este tipo de
existencia es distinto de otro(s)
tipo(s)]) (extractado de Mendelson,
pág. 213, con modificaciones menores
en el simbolismo). <<
[7.103]
Estas
tienen
que
ver
principalmente
con
cuantas
interpretaciones válidas diferentes
puede tener un sistema de axiomas
(siendo modelo el término elegante
para designar una interpretación
específica de qué representan en
realidad las fórmulas y los símbolos
abstractos). Resulta que la mayoría de
los
axiomáticas
razonablemente
completas tienen ∞ modelos válidos
—a veces incluso un ∞ no numerable
—, lo cual implica enormes dolores de
cabeza, pues sistemas como ZFS o los
postulados de Peano se han elaborado
pensando
en
modelos
bastante
específicos, y no es difícil ver que, con
un ∞ real de posibles modelos, algunos
van a contradecir los que se buscaban.
<<
[7.104] SEI
Las dos principales eran la
paternidad real (biológica) de Jesús, y
si fue Bacon el verdadero autor de las
obras atribuidas a Shakespeare. No se
necesita mucha psicología: se trata de
obsesiones
acerca
de
hechos
incomprobables y que comportan
descrédito. Dada la hostilidad y la
desconfianza que tuvo que soportar
Cantor en su vida profesional, que se
centrara en tales obsesiones parece
comprensible y, a la vez, triste. <<
[7.105] SEI
En algunos textos se llama a
esto el problema del continuo. <<
[7.106]
Los matemáticos que lo llaman
el problema del continuo enuncian la
forma general como: «¿Existe un
conjunto con una cardinalidad más alta
que la de ℵn pero más baja que la de
P(ℵn)?» (semiextractado de Edwards,
v. 2, pág. 208). <<
[7.107] SEI
Es el hecho de que Cantor se
centrara específicamente en c lo que le
dio este nombre a la hipótesis del
continuo. <<
[7.108] SEI
N. B. Tenga en cuenta que lo
que viene ahora es, incluso para
nuestro
rasero,
un
resumen
deplorablemente simplificado de la
teoría de los ordinales de Cantor —una
teoría que es incluso más compleja y
ramificatoria que la de los números
cardinales— y la única razón por la que
pasamos el dedo siquiera es que aún
sería más deplorable pretender que la
H. C. solo tiene que ver con la jerarquía
de los cardinales transfinitos. <<
[7.109] SEI
La teoría horripilantemente
técnica de Cantor acerca de los
ordinales y los tipos de orden de los
conjuntos se desarrolla principalmente
en dos artículos: «Principios de una
teoría de los tipos de orden» (1885) y
«Contribuciones a la fundamentación
de la teoría de los números
transfinitos» (1895). <<
[7.110]
La razón por la que esto podría
resultar confuso al principio es la
misma por la que la frase de nuestra
explicación inicial «de tal modo que el
orden de los elementos de A y B
permanezca inalterado» era simplista:
el tipo de orden no es lo mismo que
mera ordenación, {a, b} y {b, a} tienen
el mismo tipo de orden, por ejemplo.
<<
[7.111] SEI
Otra metáfora a medida del
doctor Goris era que los números
cardinales eran como los personajes en
una de las obras de teatro de la escuela
y los números ordinales eran los
lugares que tenían que ocupar en una
escena. Algo así como el guión de la
obra por un lado, y sus acotaciones por
otro. <<
[7.112] SEI
Podemos ver aquí algunas
claras afinidades con la teoría de
Cantor sobre los irracionales como
límites de sucesiones de números (en
§6e). Esta teoría anterior fue, en ciertos
sentidos, el origen de su trabajo sobre
los ordinales. <<
[7.113]
La todavía sin definir
paradoja
de
Burali-Forti
sale
directamente de esta definición.
Considérese el conjunto de todos los
números ordinales. Todos ellos. Ahora
considere el número ordinal de este
mismo conjunto, el cual por definición
será mayor que cualquier ordinal en el
conjunto; solo que este conjunto se ha
definido como uno que contiene todos
los ordinales. O sea, que de uno u otro
modo hay una contradicción. Esta es
muy fea, y es el verdadero motivo
«profiláctico» que hay tras el axioma
de regularidad. <<
SEI
[7.114]
Pero véase la nota 102 de §7f
respecto a lo que significa el inminente
«∀x», lo cual en retrospectiva significa
que la nota 102 no se debería haber
clasificado como SEI. <<
[7.115]
DEFINITIVAMENTE SEI No
estoy seguro de que sea muy
inteligente mencionar esto, pero por lo
menos algunas veces Cantor usó «ℵ0»
para designar el primer ordinal
transfinito y «ω» para designar el
primer cardinal transfinito. La verdad
estricta es que fue en realidad el
conjunto de todos los ordinales finitos
(que es lo que él realmente llamaba la
«primera clase numérica») lo que
Cantor usó para obtener el primer
cardinal transfinito, cosa que hizo
básicamente porque en su teoría los
números cardinales también eran
definibles como ordinales límite,
concepto que no vamos a discutir
porque requiere un grado de detalle
teórico-conjuntista sobre las relaciones
entre números cardinales y ordinales
para el que este librito no está
equipado. Estamos usando lo que ha
llegado a ser actualmente el
simbolismo estándar, o sea «ℵ»s para
los cardinales transfinitos y «ω» para
los
ordinales
transfinitos;
el
razonamiento para justificarlo es que
este simbolismo es el que tiene más
posibilidades de resultar familiar por lo
menos a algunos lectores. (N. B. Tenga
en cuenta que todas las matemáticas
cantorianas con todos sus intríngulis y
sin
rebajar
excrecencias
están
disponibles en varios excelentes libros
técnicos,
incluyendo
las
antes
mencionadas Georg Cantor, de
Dauben, Theory of Sets, de Abian, y
The Continuum and Other Types of
Serial Order, with an Introduction to
Cantor’s Transfinite Numbers de
Huntington —véase la Bibliografía—).
<<
[7.116] SEI
y que están relacionados con
las épsilons weierstrassianas de §5e
solo en el sentido de que son creadas
por una definición de tipo «existe… tal
que» similar; por ejemplo, el primer
número ordinal k tal que ωk = k se
designa «épsilon o» o «ε0». <<
[7.117]
SEI
en
mencionada
números». <<
§15 de la antes
«Contribuciones…
[7.118]
Estas dos cuestiones se colapsan
en una solamente si o bien (1) la teoría
formal
de
conjuntos
es
una
representación o reflejo fidedigno de la
verdadera realidad del ∞ y de los
conjuntos de tipo ∞, o bien (2) la
teoría formal de conjuntos es esa
verdadera realidad, en el sentido de que
la «existencia» de un conjunto infinito
dado es única y exclusivamente una
cuestión de su compatibilidad lógica
con los axiomas de la teoría. Observe,
por favor, que estas son precisamente
las cuestiones sobre el estatus
metafísico de los entes abstractos que
han afligido a las matemáticas desde
los griegos. <<
[7.119] SEI
Si la teoría de conjuntos y la
teoría de la demostración no fueran tan
increíblemente esotéricas, ya se habría
hecho una película de gran presupuesto
sobre la demostración de Cohen y los
relatos que la rodean, relatos que los
historiadores de las matemáticas
adoran y que se pueden encontrar en
una miríada de fuentes bibliográficas.
Lo que es pertinente para nosotros son
algunos inquietantes paralelismos con
Cantor. Para empezar, Cohen proviene
del análisis funcional y el análisis
armónico, áreas que involucran tanto
ecuaciones diferenciales como series
de Fourier; es decir, que él también
llega a la teoría de conjuntos desde el
análisis puro. La cosa se vuelve todavía
más inquietante. La tesis doctoral de
Cohen (Universidad de Chicago, 1958)
se titula Temas de la teoría de unicidad
de las series trigonométricas. Además,
así como Cantor había inventado
demostraciones teórico-conjuntistas de
tipo «φ» y diagonal completamente
nuevas, asimismo Cohen inventa una
técnica
de
demostración
completamente nueva conocida como
forcing, que es prohibitivamente hipertecnificada, pero en ciertos aspectos se
parece a una especie de inducción
matemática maniquea donde se pide
que los casos «n = 1» y «k» tomen uno
de solo dos valores posibles… Lo cual
quizá no se entienda pero no es para
nada vital ahora mismo: lo que es
hollywoodiense es que Cohen se pasa a
la teoría de conjuntos, inventa y refina
su método de demostración, y
demuestra la independencia de la H. C.,
todo en un solo año. <<
[7.120] SEI Véanse
§1d y 5b. <<
[7.121]
Este tipo de independencia (que
también se puede llamar indecidible)
sin duda es importante. Por lo menos
demuestra que los resultados de Gödel
acerca de la incompletitud (así como la
demostración de Church en 1936 de
que la lógica de predicados de
1.er orden también es indecidible) no
están describiendo solo posibilidades
teóricas, que existen realmente
auténticos teoremas significativos en
las matemáticas que no se pueden
demostrar ni contradecir (extractado de
Bunch, pág. 158). Lo cual a su vez
significa que incluso unas matemáticas
maximalmente abstractas, generales,
completamente formales no van a ser
capaces de representar (o, dependiendo
de sus convicciones metafísicas,
contener)
todas
las
verdades
matemáticas del mundo real. Es este
quebrantamiento de la creencia de que
100% abstracción = 100% verdad de lo
que las matemáticas puras aún no se
han recuperado, ni tampoco está claro
qué significaría aquí «recuperación».
<<
[7.122]
Además,
en
otra
demostración de 1963, Cohen pudo
demostrar que incluso si el axioma de
elección se añade a los axiomas de
ZFS, la hipótesis del continuo en su
forma
general
sigue
sin
ser
demostrable. Así se establece que el
A. E. y la H. C. también son
independientes mutuamente, algo que
impactó de nuevo al mundo
matemático. <<
SEI
[7.123]
Aquí «supuesto» = de un modo
especulativo, preguntándose «¿y si?»
(SEI Curiosidad acerca de los «diversos
equivalentes» de la misma frase: la
obra de Waclaw Sierpinski en 1934
Hypothèse du Continu da una lista de
más
de
ochenta
proposiciones
matemáticas que son equivalentes o
reducibles a la H. C. en su forma
general). <<
[7.124] SEI
Buena parte de la teoría de
conjuntos
contemporánea
parece
incluir discusiones acerca de qué
significan esos términos técnicos y
exactamente cuándo y por qué lo hacen
(= significar lo que significan, si
significan algo (y, si no significan
nada, entonces qué podría significar
ese nada, y así sucesivamente)). <<
[7.125] SEI
De nuevo puede ver cómo
esta visión formalista incorpora
elementos del intuicionismo, el más
obvio de los cuales es la voluntad de
olvidar la LTE. <<
[7.126] SEI
La declaración de Luitzen
E. J. Brouwer acerca de toda la cuestión
de la consistencia y la indecidibilidad
en teoría de conjuntos suena muy
aristotélica: «Nada que tenga valor
matemático se conseguirá de ese modo;
una teoría falsa que no es detenida por
una contradicción es igualmente falsa,
del mismo modo en que una
negligencia criminal no reprendida en
un juicio sigue siendo igualmente
criminal» (Brouwer extractado por
Barrow, pág. 217). <<
[7.127] SEI
Hilbert tampoco tuvo un
final fácil. Brouwer y Russell, por otro
lado, resultaron ser tan longevos que
prácticamente tuvieron que echarlos a
garrotazos. <<
[7.128] SEI
En el momento de escribir
este libro Paul J. Cohen era el Marjorie
Mhoon Fair Professor de ciencia
cuantitativa en Stanford. <<