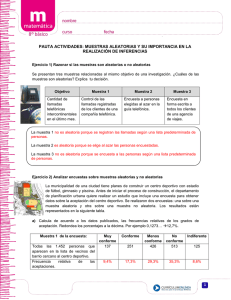
Modelos estocásticos en las finanzas

TRABAJO FIN DE GRADO
Título
Modelos estocásticos en las finanzas
Autor/es
Guillermo Serna Calderón
Director/es
José Manuel Gutiérrez Jiménez
Facultad
Facultad de Ciencias, Estudios Agroalimentarios e Informática
Titulación
Grado en Matemáticas
Departamento
Curso Académico
2012-2013
Modelos estocásticos en las finanzas, trabajo fin de grado
de Guillermo Serna Calderón, dirigido por José Manuel Gutiérrez Jiménez (publicado por
la Universidad de La Rioja), se difunde bajo una Licencia
Creative Commons Reconocimiento-NoComercial-SinObraDerivada 3.0 Unported.
Permisos que vayan más allá de lo cubierto por esta licencia pueden solicitarse a los
titulares del copyright.
©
©
El autor
Universidad de La Rioja, Servicio de Publicaciones, 2013
publicaciones.unirioja.es
E-mail: [email protected]
Facultad
Facultad de Ciencias, Estudios Agroalimentarios e Informática
Titulación
Grado en Matemáticas
Título
Modelos estocásticos en las finanzas
Autor/es
Guillermo Serna Calderón
Tutor/es
José Manuel Gutiérrez Jiménez
Departamento
Departamento de Matemáticas y Computación
Curso académico
2012-2013
Modelos estocásticos en las finanzas
Guillermo Serna
11 de junio de 2013
ii
iii
Resumen
Este trabajo de fin de Grado es una pequeña introducción a los modelos estocásticos en las
finanzas desde un punto de vista práctico, cuyo objetivo es facilitar la adaptación a un máster
de Matemática financiera.
El trabajo está dividido en tres capítulos. En el primer capítulo se estudian las variables
aleatorias, la generación de números aleatorios y hacemos hincapié especial en el método de
Monte Carlo, desarrollando varias ejemplos mediante el programa Wolfram Mathematica 8.
En el segundo capítulo, tratamos los procesos estocásticos dividiéndolos en procesos de estado discreto y procesos de estado continuo. En los procesos de estado continuo se estudia el
proceso de Wiener, que es fundamental en los modelos estocásticos financieros.
En el último capítulo trataremos el modelo de Black y Scholes, que es trascendental en la
valoración de opciones y acabaremos con la ecuación de Black-Scholes y su importancia.
Por último, nótese que este trabajo puede ser completado en un futuro con las integrales y
ecuaciones diferenciales estocásticas.
Abstract
This Final Year Dissertation is a short introduction to stochastic financial models from a
practical standpoint, whose aim is to make easier the adaptation to a master about Mathematical finance.
This work has three chapters. In the first chapter random variables and generation of random numbers are studied, and a special emphasis in Monte Carlo method is made. In this
section several examples are carried out with the computational software program Wolfram
Mathematica 8.
In the second chapter we explain the stochastic processes and these are divided in processes
with discrete state and processes with continuous state. In the processes with continuous
state, we study the Wiener process, that is essential in stochastic financial models. In the
last chapter we speak about the Black-Scholes model, which is fundamental in the valuation
of options and we will finish with the Black-Scholes equation and his importance.
Finally, we would like to emphasize that this work could be completed with stochastic integration and stochastic differential equations.
iv
Introducción
He decidido realizar este trabajo fin de Grado porque quiero hacer un máster sobre Matemática financiera y así poder obtener algunos conocimientos previos antes de realizar el máster.
Además este trabajo podría ser completado en un futuro con el estudio de integrales y ecuaciones diferenciales estocásticas, puesto que por la limitación de tiempo no hemos podido
realizar este estudio.
En este trabajo se pueden ver tanto temas tratados en la carrera como cadenas de Markov
o variables aleatorias, aunque con un enfoque diferente, como temas no tratados durante la
carrera como pueden ser el proceso de Wiener y el modelo de Black y Scholes.
El propósito de este trabajo fin de Grado es realizar una pequeña introducción a los modelos
estocásticos en las finanzas desde un punto de vista práctico. La estructura general del trabajo consiste en desarrollar una teoría y completarla con ejemplos, muchos de estos ejemplos
son teóricos formando así “pequeños teoremas”. También se han realizado muchos ejemplos
con ordenador mediante el programa Wolfram Mathematica 8, y además en muchos de estos
ejemplos podemos ver el código utilizado.
Se ha divido el trabajo en tres capítulos. En el primer capítulo se estudian las variables aleatorias, para ello hemos definido primero los espacios de probabilidad. También hemos definido
los espacios de Hilbert de variables aleatorias. Y para finalizar el capítulo hemos tratado la
generación de números aleatorios y desarrollado con bastantes ejemplos el método de Monte
Carlo, ya que es un método muy usado en las finanzas.
En el segundo capítulo se habla de los procesos estocásticos dividiendo estos en procesos de
estado discreto y procesos de estado continuo. En los procesos de estado continuo se estudia
el proceso de Wiener o movimiento Browniano que es un proceso de vital importancia en el
mundo de las finanzas cuantitativas y que nos será de utilidad para el siguiente capítulo.
Por último, en el tercer capítulo se estudia el modelo de Black y Scholes que es muy usado
en la valoración de opciones. También se trata la fórmula de Itô, herramienta indispensable
en las Matemática financieras. Por último se ha finalizado este trabajo fin de Grado con la
ecuación de Black-Scholes y la importancia de esta fórmula.
Nótese que en los dos primeros capítulos se ha usado [3] como bibliográfica básica y [1, 2, 4,
5, 7, 8, 9] como complementaría. Y para realizar el último capítulo nos hemos basado en [6].
La conclusión que se puede sacar de este trabajo es que es una pequeñísima introducción a
v
vi
los modelos estocásticos en las finanzas y que se dejan muchos temas abiertos como el de las
integrales y las ecuaciones diferenciales estocásticas.
Finalmente quiero agradecer a mi tutor, José Manuel Gutiérrez, por la predisposición que ha
tenido en todo momento con este trabajo, incluso sin que las finanzas sean su especialidad.
Índice general
1. Variables aleatorias
1.1. Introducción . . . . . . . . . . . . . . . .
1.2. Espacio de probabilidad . . . . . . . . .
1.3. Variables aleatorias . . . . . . . . . . . .
1.4. Espacio de Hilbert de variables aleatorias
1.5. Generación de números aleatorios . . . .
1.6. Método de Monte Carlo . . . . . . . . .
2. Procesos estocásticos
2.1. Introducción . . . . . . . . . . . . .
2.2. Procesos de estado discreto . . . . .
2.3. Procesos de estado continuo . . . .
2.4. Generación de procesos estocásticos
3. El modelo de Black y Scholes
3.1. Introducción . . . . . . . . . .
3.2. El modelo de Black y Scholes
3.3. Proceso de Wiener económico
3.4. Valoración de opciones . . . .
3.5. La ecuación de Black-Scholes .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
Bibliografía
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
1
1
1
4
8
12
15
.
.
.
.
27
27
30
39
45
.
.
.
.
.
49
49
50
51
52
54
57
vii
viii
ÍNDICE GENERAL
Capítulo 1
Variables aleatorias
1.1.
Introducción
Una variable aleatoria es una función de valores reales definida en un conjunto de resultados de un experimento aleatorio. Las variables aleatorias son importantes en el estudio de
integrales y ecuaciones diferenciales estocásticas que son de gran utilidad en el mundo de
las finanzas, aunque en este trabajo no llegaremos a abordarlas (para ver información sobre
ecuaciones diferenciales e integrales estocásticas consultar [3]).
En este capítulo después de ver espacios de probabilidad, variables aleatorias y una introducción de espacios de Hilbert de variables aleatorias (fundamental para entender las integrales y
ecuaciones diferenciales estocásticas) hablaremos de la generación computacional de números
aleatorios, por último veremos el método de Monte Carlo como aplicación a la generación
computacional de números aleatorios.
Y con todo esto ya estaremos en condiciones de estudiar los procesos estocásticos del capítulo
2.
1.2.
Espacio de probabilidad
Un espacio de probabilidad es una terna (Ω, F, P ) dónde Ω es el conjunto de posibles resultados del experimento (llamado espacio muestral), F la colección de todos los sucesos o eventos
aleatorios y P : F → [0, 1] es una función que asigna probabilidad a los eventos. Asumimos
que F es una σ-álgebra que satisface las siguientes propiedades.
Si A ∈ F entonces Ac ∈ F.1
∪∞
i=1 Ai ∈ F si A1 , A2 , . . . ∈ F.
1
Cuando escribimos Ac nos referimos al complementario de A.
1
2
CAPÍTULO 1. VARIABLES ALEATORIAS
El par (Ω, F) es un espacio medible, que es un espacio donde podemos definir una medida.
Una medida es una función µ concreta que asigna un valor real o medida a cada elemento de
Ω y cumple
1. µ(A) ≥ µ(∅) = 0 ∀A ∈ F.
2. Si Ai ∈ F es una sucesión contable de conjuntos disjuntos entonces
µ(∪∞
i=1 Ai ) =
∞
X
µ(Ai )
i=1
.
Si µ(F) = 1, llamamos a µ medida de probabilidad y como hemos dicho antes la denotamos
como P y si A ∈ F se tiene que P (Ac ) = 1 − P (A). Sea µ una medida en (Ω, F) tenemos que
Si A ⊂ B entonces µ(A) ≤ µ(B) (si µ(A) < ∞ entonces µ(B − A) = µ(B) − µ(A).
Si A ⊂ ∪∞
n=1 An entonces µ(A) ≤
P∞
n=1
µ(An ).
Los siguientes ejemplos muestran algunos espacios de probabilidad. Para ampliar la información véase [4].)
Ejemplo 1.1. Lanzamiento de una moneda.
Consideremos el experimento aleatorio de lanzar una moneda dos veces. Los posibles sucesos
que podemos tener son ω1 = CC, ω2 = CT , ω3 = T C y ω4 = T T (dónde C es cara y T es
cruz). Así el espacio muestral es Ω = {ω1 , ω2 , ω3 , ω4 }. Sin embargo hay muchos conjuntos F
que satisfacen la propiedad de σ-álgebra, el más pequeño es F = {∅, Ω}. Si queremos que los
sucesos {ω1 }, {ω2 } pertenezcan a F entonces tenemos que la σ-álgebra más pequeña que los
contiene es
F = {∅, {ω1 }, {ω2 }, {ω1 , ω2 }, {ω3 , ω4 }, {ω1 , ω3 , ω4 }, {ω2 , ω3 , ω4 }, Ω}.
Para N resultados diferentes la σ-álgebra más pequeña tendrá 2 elementos, ∅ y Ω, y la más
grande tendrá 2N elementos.
Para este ejemplo, P ({ωi }) = 1/4 i = 1, 2, 3, 4. Usando las propiedades anteriores podemos
hallar la probabilidad del evento {ω1 ó ω3 ó ω4 } que es P ({ω1 , ω3 , ω4 }) = 1 − P ({ω2 }) = 3/4.
(Ω, F, P ) es el espacio de probabilidad para este ejemplo.
Ejemplo 1.2. Medida de Lebesgue.
Consideramos el experimento aleatorio de elegir un número real x del intervalo [0, 1]. Entonces Ω = {x : 0 ≤ x ≤ 1}. Sea (a, b] un intervalo en [0, 1] donde x ∈ (a, b]. Definimos
la σ-álgebra F como el conjunto generado por todos los intervalos de la forma (a, b]. Así
que todos los intervalos de la forma (a, b], uniones de intervalos y sus complementarios están
3
1.2. ESPACIO DE PROBABILIDAD
contenidos en la σ-álgebra F. Esta σ-álgebra se llama la σ-álgebra de Borel. Ahora definimos
la medida de probabilidad P . Sea A = (a, b] ∈ F, entonces P (A) = b − a. Entonces P (A)
es la probabilidad de que un elemento x ∈ [0, 1] este en A. Esta medida de probabilidad se
llama medida de Lebesgue para la σ-álgebra F.
Vemos que gracias a las propiedades de medida, un gran número de conjuntos están en F. Por
1
ejemplo (a, b) ∈ F ya que (a, b) = ∪∞
n=1 (a, b − n ]. Por las Leyes de Morgan las intersecciones
1
contables también están en F, en particular {ω} = {x} esta en F ya que {ω} = ∩∞
n=1 (x− n , x].
1−2n 2−2n
Consideremos el siguiente ejemplo particular, sea B1 ∈ F donde B1 = ∪∞
,2
) enn=1 (2
P∞ 1 2n−1
2
= 3.
tonces P (B1 ) = n=0 ( 2 )
Ejemplo 1.3. Número de observaciones; distribución de Poisson.
Consideremos un experimento donde el número de observaciones de un resultado en el intervalo de tiempo [0, t] es interesante. Suponemos que el número de observaciones del resultado
en algún intervalo de tiempo ∆t tiene probabilidad λ∆t + o(∆t) y la probabilidad es independiente del tiempo (por ejemplo la probabilidad de que un coche pase por un cruce puede
satisfacer esta suposición). Consideremos ahora el número de resultados donde t es grande
en comparación con ∆t y sea ωn igual al suceso donde n resultados ocurren en el intervalo
[0, t]. Entonces es claro que Ω = {ω0 , ω1 , ω2 , . . . }. Sea ahora F = {∅, {ω0 }, {ω1 }, . . . , Ω} la
σ-álgebra generada asumiendo que {ωi } ∈ F para = i = 0, 1, 2, . . . . Ahora vamos a determinar una medida de probabilidad para Ω. Por conveniencia de notación P ({ωn }) = Pn (t) es la
probabilidad de que se produzcan n resultados en el intervalo [0, t]. Usando las suposiciones
hechas es claro que P0 (0) = 1 y que Pn (0) = 0 para n ≥ 1. Además
P0 (t + ∆t) = (1 − λ∆t)P0 (t) + o(∆t)
y
Pn (t + ∆t) = (1 − λ∆)Pn (t) + λ∆tPn−1 (t) + o(∆t),
para n ≥ 1 donde 1 − λ∆t es la probabilidad de no tener resultados en el intervalo ∆t y λ∆t
es la probabilidad de un resultado en el intervalo ∆t. Haciendo ∆t → 0 en ambas expresiones
obtenemos
dP0 (t)
= −λP0 (t), P0 (0) = 1
dt
y
dPn (t)
= −λPn (t) + λPn−1 (t), Pn (0) = 0, n ≥ 1.
dt
n
Resolviendo el sistema obtenemos que P {wn } = Pn (t) = e−λt (λt)
para n = 0, 1, 2, . . . , donde
n!
P {wn } es la probabilidad de n resultados en el tiempo t. Con esta probabilidad de medida
(Ω, F, P ) es un espacio de probabilidad. Para verificar esta medida de probabilidad notemos
que
∞
∞
X
X
(λt)n
P (Ω) =
P ({ωn }) =
e−λt
=1
n!
n=0
n=0
4
CAPÍTULO 1. VARIABLES ALEATORIAS
para cualquier t ≥ 0. Llamamos distribución de Poisson al número de resultados en este
experimento aleatorio.
1.3.
Variables aleatorias
En este apartado vamos a definir las variables aleatorias y algunas de sus propiedades, puesto
que son una pieza clave en los procesos estocástico que veremos en el siguiente capítulo (véase
[1]).
Definición 1.1. Una variable aleatoria X en un espacio de probabilidad (Ω, F, P ) es una
función de Ω en R, X : Ω → R.
Definición 1.2. La función de distribución de una variable aleatoria X es la función FX de
R en [0, 1] dada por
FX (x) = P ({ω ∈ Ω : X(ω ≤ x)}), x ∈ R.
Una variable aleatoria puede ser discreta o continua. Una variable aleatoria es discreta si toma
valores en un subconjunto contable {x1 , x2 , x3 . . . } ⊂ R. Es decir que X(ω) ∈ {x1 , x2 , x3 , . . . }
para cada ω ∈ Ω. La función de masa de probabilidad p de una variable aleatoria X es la
función p : {x1 , x2 , x3 , . . . } → [0, 1] dada por p(x) = P (X = x). Notemos que para una
P
variable aleatoria discreta FX (x) = xi <x p(xi ).
Una variable aleatoria es continua si existe una función a trozos no negativa p(x) tal que
Rx
FX (x) = −∞
p(s)ds. En este caso llamamos a p(x) función de densidad de X. Notemos que
R
P (a ≤ X ≤ b) = FX (b) − FX (a) = ab p(s)ds.
Es útil notar que si X es una variable aleatoria y g : R → R es medible Borel, entonces
Y = g(X) es también una variable aleatoria. En efecto, Y (ω) = g(X(ω)) = g(x) si X(ω) = x.
Además, si p(x) es la función de masa para una variable aleatoria discreta X y la inversa de
g existe entonces P (Y = y = g(x)) = P (X = x) = p(x) = p(g −1 (y)). Así q(y) = p(g −1 (y)) es
la función de masa de Y . Además, si X toma los valores discretos {x1 , x2 , x3 , . . . } entonces
Y toma los valores discretos {y1 , y2 , y3 , . . . } donde yi = g(xi ).
Esperanza
Vamos a definir la esperanza dependiendo de si estamos ante una variable aleatoria discreta
o una variable aleatoria continua (véase [4]).
Definición 1.3. Suponemos que X es una variable aleatoria discreta donde
X(ω) ∈ {x1 , x2 , x3 , . . . }
con ω ∈ Ω. Sea p(x) la función de masa de X, entonces decimos que la esperanza de X es
µ = E(X) =
X
i
xi p(xi ) =
X
i
X(ωi )P ({wi })
5
1.3. VARIABLES ALEATORIAS
donde la suma es convergente.
Sea g : R → R una función, sabemos que g(X) = Y también es una variable aleatoria discreta
y la esperanza de g(X) es
E(g(X)) =
X
g(xi )p(xi ).
i
En particular el k-ésimo momento de X es
E(X k ) =
(xi − µ)k p(xi ) para k = 1, 2, . . .
X
i
y definimos el k-ésimo momento central como
E((X − µ)k ) =
X
(xi − µ)k p(xi ) para k = 1, 2, . . . .
i
Definición 1.4. Suponemos que X es una variable aleatoria continua donde X(x) = x y
con función de densidad p(x). Notemos que p(x)∆x es la probabilidad de aproximación de
que X tome un valor en el intervalo (x − ∆x/2, x + ∆x/2). La esperanza de X puede ser
P
aproximada como E(X) ≈ xp(x)∆x y como ∆x → 0 la esperanza de X es
E(X) =
Z ∞
xp(x)dx.
∞
Si definimos una función g como antes tenemos que la esperanza de g(X) es
E(g(X)) =
Z ∞
g(x)p(x)dx.
−∞
El k-ésimo momento y el k-ésimo momento central son
E(X k ) =
Z ∞
xk p(x)dx
−∞
E((X − µ)k ) =
Z ∞
(x − µ)k p(x)dx.
−∞
Propiedades de la esperanza. Sean X, Y variables aleatorias tenemos que
E(X + Y ) = E(X) + E(Y ).
E(XY ) = E(X)E(Y ) si X e Y son independientes, es decir, X no depende de Y y Y
no depende de X.
E(aX) = aE(X) con a ∈ R.
6
CAPÍTULO 1. VARIABLES ALEATORIAS
Varianza
Definición 1.5. La varianza de X se define como el segundo momento central
Var(X) = E((X − µ)2 ).
Nota 1.1. Notemos que:
E((X − µ)2 ) = E(X 2 ) − µ2 .
Ejemplo 1.4. Distribución de Poisson.
Consideremos el experimento aleatorio del ejemplo 1.3 donde la probabilidad de un resultado
en un intervalo de tiempo ∆t es λ∆t+o(∆). Sea γ = λt y recordemos que ωn es igual al suceso
donde n resultados ocurren en el intervalo [0, t]. Sea X(ωn ) = n la definición de una variable
aleatoria X. La función de masa de X es p(n) = P (ωn ) = (e−γ γ n )/n! para n = 0, 1, 2 . . . y
su función de probabilidad es
FX (x) = e−γ
n
X
γk
para n ≤ x < n + 1
k=0 k!
para n = 0, 1, 2, . . . . La variable aleatoria X es una distribución de Poisson.
Para calcular su media y su varianza necesitamos
E(X) =
∞
X
kp(k) =
∞
X
ke−γ
k=0
k=0
∞
X
γk
γ k−1
= e−γ γ
=γ
k!
k=1 (k − 1)!
y
E(X 2 ) =
∞
X
k 2 p(k) = e−γ γ 2
k=0
∞
X
(
k=1
(k − 1)γ k−2
γ k−2
+
) = γ 2 + γ.
(k − 1)!
(k − 1)!
Por lo tanto E(X) = γ y Var(X) = γ.
Ejemplo 1.5. Distribución Uniforme en [u, v].
La distribución Uniforme es el modelo continuo más simple. Corresponde al caso de que
una variable aleatoria sólo puede tomar valores comprendidos entre dos extremos u y v, de
manera que todos los intervalos de una misma longitud (dentro de [u, v]) tienen la misma
probabilidad. También puede expresarse como el modelo probabilístico correspondiente a
tomar un número al azar dentro de un intervalo [u, v].
Sea X(x) = x la definición de una variable aleatoria X. La función de probabilidad de X es
FX (x) =
Z x
p(s)ds donde p(s) =
−∞


0,

1
,
v−u
Notemos que si a, b ∈ [u, v] entonces P (a ≤ X ≤ b) =
distribución uniforme en [u, v], X ∼ U [u, v].
Para calcular su media y su varianza necesitamos
E(X) =
Z b
a
x
Rb
a
s<u o s>v
u ≤ s ≤ v.
p(s)ds = (b − a)/(v − u). X es una
dx
b+a
=
b−a
2
7
1.3. VARIABLES ALEATORIAS
y
2
E(X ) =
Z b
x2
a
Por lo tanto E(X) =
b+a
2
y Var(X) =
dx
1
= (b2 + ab + a2 ).
b−a
3
1
(b
12
− a)2 . Además E(f (X)) =
Rb
a
dx
f (x) b−a
Variables aleatorias múltiples
Consideremos un experimento aleatorio con espacio muestral Ω, conjunto de eventos aleatorios F y medida de probabilidad P . Sean X1 y X2 dos variables aleatorias definidas en
este espacio de probabilidad. El vector aleatorio X = [X1 , X2 ]T lleva Ω a R2 . Notemos que
si A1 , A2 ∈ F como A1 = {ω ∈ Ω : X1 (ω) ≤ x1 } y A2 = {ω ∈ Ω : X2 (ω) ≤ x2 } entonces
A1 ∩ A2 ∈ F y
P (X1 ≤ x1 , X2 ≤ x2 ) = P (A1 ∩ A2 ).
Definición 1.6. La función de distribución acumulativa de X1 y X2 se denota FX1 X2 (x1 , x2 )
y se define como
FX1 X2 (x1 , x2 ) = P (X1 ≤ x1 , X2 ≤ x2 ) = P (A1 ∩ A2 ).
Además si A1 y A2 son independientes se tiene que
FX1 X2 (x1 , x2 ) = P (A1 ∩ A2 ) = P (A1 )P (A2 ) = FX1 (x1 )FX2 (x2 ).
Si suponemos que X1 , X2 son variables aleatorias discretas que toman los valores (x1,i )(x2,j )
para 1 ≤ i ≤ M, 1 ≤ j ≤ N con N, M ∈ N, tenemos que
pX1 X2 (x1,i , x2,j ) = P (X1 = x1,i , X2 = x2,j ).
Por lo tanto llamamos a pX1 X2 función de masa de X = [X1 , X2 ]T y
X
FX1 X2 (x1 , x2 ) =
X
pX1 X2 (x1,i , x2,j ).
x1,i ≤x1 x2,j ≤x2
Si X1 , X2 son variables aleatorias continuas, pX1 X2 (x1 , x1 ) es la función de densidad de X =
[X1 , X2 ]T si
Z x1 Z x2
FX1 X2 (x1 , x2 ) =
pX1 X2 (s1 , s2 )ds2 ds1 .
−∞
−∞
Además la función de densidad satisface
pX1 |X2 (x1 |x2 )pX2 (x2 ) = pX1 X2 (x1 , x2 )
y
pX2 |X1 (x2 |x1 )pX1 (x1 ) = pX1 X2 (x1 , x2 ).
Definición 1.7. La covarianza de X1 y X2 variables aleatorias se define como
Cov(X1 X2 ) = E((X1 − µ1 )(X2 − µ2 )) = E(X1 X2 ) − E(X1 )E(X2 ).
8
CAPÍTULO 1. VARIABLES ALEATORIAS
Y además se tiene la siguiente propiedad
Var(X1 + X2 ) = Var(X1 ) + Var(X2 ) + 2Cov(X1 X2 ).
Notemos que si X1 , X2 son independientes entonces Cov(X1 X2 ) = 0.
Si X = [X1 , X2 , . . . Xn ]T es un vector de n variables aleatorias cada una definida en el espacio
muestral Ω, entonces µ = E(X) es la media del vector de longitud n y E((X − µ)(X − µ)T )
es la matriz n × n llamada matriz covariante. La función de distribución FX se relaciona con
la función de densidad pX de la siguiente manera
FX (x1 , x2 , . . . , xn ) =
Z x1 Z x2
−∞
−∞
...
Z xn
−∞
pX (s1 , s2 , . . . , sn )dsn , . . . , ds2 d1 .
Ejemplo 1.6. Vector de variables aleatorias cuando lanzamos una moneda.
Supongamos que lanzamos una moneda dos veces y su espacio muestral es Ω = {ω1 , ω2 , ω3 , ω4 }
donde ω1 = CC, ω2 = CT , ω3 = T C y ω4 = T T . La P ({ωi }) = 41 para i = 1, 2, 3, 4. Sea
X1 (ω1 ) = no de caras en wi y X2 (ω2 ) = no de cruces en ωi . Por lo tanto la función de masa
tiene la forma




1/4 x1 = 2, x2 = 0 or x1 = 0, x2 = 2
pX1 X2 (x1 , x2 ) =  1/2
x1 = 1, x2 = 1


0
otro caso.
Para este experimento aleatorio E(X) = µ = [1, 1]T y la matriz covariante es




1/2 −1/2 
(X1 − µ1 )2
(X1 − µ1 )(X2 − µ2 ) 
= E
E((X−µ)(X−µ)T ) = E 
2
−1/2 1/2.
(X1 − µ1 )(X2 − µ2 )
(X2 − µ2 )
Por lo tanto X1 y X2 no son independientes y tienen Cov(X1 X2 ) = − 21 .
1.4.
Espacio de Hilbert de variables aleatorias
Los espacios de Hilbert de variables aleatorias y procesos estocásticos unifican y simplifican
el desarrollo de integrales y ecuaciones diferenciales estocásticas.
Recordemos que un espacio vectorial con una métrica o norma definida se llama espacio
métrico.
Definición 1.8. Si un espacio métrico es completo (toda sucesión de Cauchy es convergente)
entonces el espacio métrico es un espacio de Banach.
Definición 1.9. Un espacio pre-Hilbert sobre R es un par (H, (·, ·)) donde H es un espacio
vectorial y (·, ·) : H × H → R cumple:
(λf + µg, h) = λ(f, h) + µ(f, h) para todo λ, µ ∈ R, f, g, h ∈ H,
1.4. ESPACIO DE HILBERT DE VARIABLES ALEATORIAS
9
(f, f ) ∈ [0, ∞) para todo f ∈ H,
(f, f ) = 0 implica f = 0.
Sea (H, (·, ·)) un espacio pre-Hilbert sobre R. Podemos definir una norma en H de la siguiente
manera:
||f || = (f, f )1/2 , f ∈ H.
(1.1)
La norma definida en (1.1) tiene las siguientes propiedades:
Desigualdad triangular:
||f + g|| ≤ ||f || + ||g||.
Desigualdad de Cauchy-Schwarz:
||(f, g)|| ≤ ||f || ||g||.
Definición 1.10. Si un espacio pre-Hilbert es completo entonces lo llamamos espacio de
Hilbert.
Si un espacio S es pre-Hilbert solemos usar un resultado que dice que S puede ser completado
añadiendo elementos a S hasta formar un espacio de Hilbert H. Además se puede ver que
S ⊂ H y que S es denso en H. Por lo tanto si S se completa en H, entonces dado un f ∈ H
y un > 0 existe un g ∈ S tal que ||f − g|| < .
Sea (Ω, F, P ) un espacio de probabilidad. Sea A ∈ F y sea IA la función indicatriz de A, es
decir IA es la variable aleatoria definida por
IA (w) =




1 si w ∈ A



0 si w ∈
/ A.
(1.2)
Entonces se tiene que
E(IA ) = P (A).
Definición 1.11. Las combinaciones lineales finitas de funciones indicatrices son variables
aleatorias simples.
Nota 1.2. Si X es una variable aleatoria simple, entonces X se puede escribir como X(ω) =
i=1 ci IAi y entonces
Pn
E(X) =
n
X
i=1
ci P (Ai ).
10
CAPÍTULO 1. VARIABLES ALEATORIAS
Sea ahora SRV (espacio pre-Hilbert) el conjunto de variables aleatorias simples definidas en el
espacio de probabilidad, SRV = {X : X es un variable aleatoria simple definida en el espacio
de probabilidad (Ω, F, P )}. El conjunto SRV es un espacio vectorial de variables aleatorias.
Sea X, Y ∈ SRV se define el producto como
n X
n
X
(X, Y ) = E(XY ) = E(
ci IAi dj ABj ) =
i=1 j=1
n X
n
X
ci dj P (Ai ∩ Bj )
i=1 j=1
y la norma de la siguiente manera
1
1
||X||RV = (X, X) 2 = (E|X|) 2 .
Podemos completar SRV en HRV , espacio Hilbert, donde SRV es denso en HRV . Si suponemos
que {Xn }∞
n=1 es una sucesión de Cauchy de variables aleatorias en HRV y como HRV es
completo hay una variable aleatoria X ∈ HRV de manera que ||Xn −X|| → 0 cuando n → ∞.
Además dado un > 0 hay una variable aleatoria Y ∈ SRV de modo que ||X − Y || < .
Definición 1.12. La norma de un espacio Hilbert HRV de variables aleatorias es ||X||RV =
(E(|X|2 ))1/2 .
Ejemplo 1.7. Espacio Hilbert L2 [0, 1].
Sea el mismo espacio de probabilidad que en el ejemplo 1.2. Sea SRV todas las variables
aleatorias simples definidas en F. Si X ∈ SRV la variable aleatoria se define como
X(x) =
n
X
ci IAi (x),
i=1
donde Ai ∈ F e IAi es la función indicadora introducida en (1.2) para cada i.
Sea ahora HRV la complexión de SRV . HRV , espacio de Hilbert, incluye todas las variables
aleatorias que están contenidas en [0, 1]. Tomamos una f : [0, 1] → R continua para ver que
las variables aleatorias continuas están en HRV . Sea xi = (i − 1)/n para i = 1, 2, . . . , n y
definimos
fn (x) =
n
X
f (xi )In,i (x), dónde In,i (x) =



i=1
1, (i − 1)/n ≤ x < i/n
0,
otro caso.
Entonces se puede demostrar que esta sucesión de variables aleatorias simples {fn }∞
n=1 es una
sucesión de Cauchy en HRV . Además como ||f − fn ||RV → 0 cuando n → ∞ tenemos que
fn → f en HRV . Así f es el límite de una sucesión de variables aleatorias simples en HRV y
f ∈ HRV .
El espacio de Hilbert HRV de este ejemplo es conocido como L2 [0, 1], que es, HRV = L2 [0, 1] =
R
{funciones medibles Lebesgue f en [0, 1] tal que 01 |f (x)|2 dx < ∞}. Notemos que para
X, Y ∈ HRV se tiene
(X, Y ) =
Z 1
0
X(x)Y (x)dx y
||X||2RV
=
Z 1
0
|X(x)|2 dx.
11
1.4. ESPACIO DE HILBERT DE VARIABLES ALEATORIAS
Convergencia de sucesiones de variables aleatorias
La convergencia de sucesiones de variables aleatorias es importante para el estudio de ecuaciones diferenciales estocásticas. Consideramos una sucesión de variables aleatorias {Xn }∞
n=1
definidas en un espacio de probabilidad (Ω, F, P ) y la existencia de una variable aleatoria X
a la cual la sucesión se aproxima cuando n → ∞. Es importante caracterizar la manera en
que Xn se aproxima a X cuando n → ∞.
Hay varios tipos de criterios de convergencia que suelen usarse para las variables aleatorias.
Un tipo importante es la convergencia en media cuadrática que es la que usaremos.
Definición 1.13. Sea {Xn }∞
n=1 una sucesión de variables aleatorias y sea X una cierta
variable aleatoria. Diremos que {Xn }∞
n=1 converge a X en media cuadrática si se cumple que
lı́m E(Xn − X)2 = 0.
n→∞
Sin embargo, para {Xn }∞
n=1 ⊂ HRV la convergencia en media cuadrática es equivalente a
||Xn − X||RV → 0 cuando n → ∞. Además como HRV es un espacio de Hilbert la existencia
de la variable aleatoria X ∈ HRV es garantizada si {Xn }∞
n=1 es una sucesión de Cauchy en
HRV .
Definición 1.14. Se dice que la sucesión de variables aleatorias {Xn }∞
n=1 es fuertemente
convergente a X si
lı́m E(|Xn − X|) = 0.
n→∞
Convergencia en media cuadrática implica convergencia fuerte.
Desigualdad de Lyapunov (E(|X|p ))1/p <= (E(|X|r ))1/r para 0 < p < r.
Definición 1.15. Se dice que la sucesión de variables aleatorias {Xn }∞
n=1 converge en probabilidad a X si dado algún > 0 tenemos que
lı́m P (|Xn − X| > ) = 0
n→∞
.
Convergencia en media cuadrática también implica convergencia en probabilidad.
Desigualdad de Chebyshev-Markov P ({ω : |X(ω)| ≥ }) ≤
1
E(|X|p )
p
para , p > 0.
Definición 1.16. La sucesión de variables aleatorias {Xn }∞
n=1 se dice que tiene convergencia
casi segura a X si
P (ω ∈ Ω : n→∞
lı́m |Xn (ω) − X(ω)| = 0}) = 1
.
P∞
Lema 1.1. Si
casi segura a X.
n=1
P (|Xn − X| ≥ ) < ∞ para todo > 0, entonces Xn tiene convergencia
12
CAPÍTULO 1. VARIABLES ALEATORIAS
Ejemplo 1.8. Convergencia casi segura y convergencia en media cuadrática.
Sea X una variable aleatoria que es una distribución uniforme en [0, 1], es decir X ∼ U [0, 1],
definimos la sucesión de variables aleatorias {Xn }∞
n=1 de la siguiente manera




0,
0 ≤ X(ω) ≤


X(ω),
1
n2
Xn (ω) = 
1
n2
< X(ω) ≤ 1
para n = 1, 2, . . . . Entonces
∞
X
P (|Xn − X|) ≥ ) ≤
n=1
∞
X
1
<∞
2
n=1 n
para algún > 0.
Por el lema anterior Xn converge casi seguro a X. Y notemos también que
2
E(|Xn − X| ) =
Z
1
n2
0
x2 dx =
1
→ 0 cuando n → ∞.
3n6
Por lo que Xn tiene convergencia cuadrática a X.
Dos resultados importantes que involucran sucesiones de variables aleatorias son la ley de los
números grandes y el teorema central del límite (véase [5]).
La ley de los grandes números. Sean X1 , X2 , . . . variables aleatorias independientes e
idénticamente distribuidas. Sea µ = E(Xn ) y σ 2 = Var(Xn ) ∈ (0, ∞). Definimos Sn =
Pn
i=1 Xi . Entonces
Sn
Sn
lı́m E(| − µ|2 ) = 0 y n→∞
lı́m
= µ.
n→∞
n
n
Teorema 1.2. Teorema central del límite
Sean X1 , X2 , . . . variables aleatorias independientes e idénticamente distribuidas. Sea µ =
P
E(Xn ) y σ 2 = Var(Xn ) ∈ (0, ∞). Definimos Sn = ni=1 Xi . Entonces
lı́m P ((
n→∞
Sn − nµ
√ ) ≤ z) = φ(z),
σ n
dónde φ(z) es la función de distribución de N (0, 1) para cada número real z.
1.5.
Generación de números aleatorios
Para aproximar soluciones de ecuaciones estocásticas se requiere de grandes números aleatorios, [8]. Los algoritmos para generar sucesiones de variables aleatorias son llamados generadores de números pseudo-aleatorios. Hay muchos tipos de generadores para producir
distribuciones uniformes de números aleatorios en [0, 1]. Un generador muy sencillo es de los
centros de los cuadrados, que consiste en tomar un número inicial de cuatro cifras decimales
1.5. GENERACIÓN DE NÚMEROS ALEATORIOS
13
llamado semilla, por ejemplo γ0 = 0.9876 y elevarlo al cuadrado obteniendo un número de
ocho cifras decimales γ02 = 0.97535376. Ahora elegimos las cuatro cifras decimales centrales
y de esta manera obtenemos γ1 = 0.5353, haciendo lo mismo se obtiene γ2 = 0.6546 y así
vamos obteniendo distribuciones uniformes de números aleatorios en [0, 1].
Nota 1.3. Este método presenta algunos problemas, entre otros la obtención de números
pequeños con mayor frecuencia que números grandes.
Ahora vamos a desarrollar el el generador congruencial lineal (uno de los generadores más
conocidos) que tiene la forma
Xn+1 = (aXn + c)mód(m)
para n = 0, 1, 2, . . .
donde a, c y m son enteros no negativos con m normalmente grande y X0 es un número de
partida. Sea d un entero positivo d mod(m) es el resto cuando dividimos d y m, entonces
0 ≤ d mód(m) ≤ m − 1. Ahora podemos calcular la sucesión Un como
Un =
Xn
m
para n = 0, 1, 2 . . .
donde 0 ≤ Un ≤ 1 para cada n. Los Un son distribuciones uniformes en [0, 1]. Si Xi+p = Xi
llamamos periodo del generador al valor más pequeño de p.
Lema 1.3. El periodo de un generador congruencial lineal es m si y solo si (véase [3])
c y m son primos entre sí,
a ≡ 1(mód(d)) para todo d factor primo de m,
a ≡ 1(mód(4)) si m es múltiplo de 4.
Cuando c = 0 y m es un número primo la longitud del periodo es m − 1 si a satisface que
ak 6≡ 1 mod(m) para k = 1, 2, . . . , m − 2. Un generador popular congruente lineal es
Xn+1 = 16807Xn mód(231 − 1)
para n = 0, 1, 2, . . .
donde a = 75 , c = 0 y m = 231 − 1 es un número primo de Mersenne.
Definición 1.17. Se dice que un número primo p es un número de Mersenne si es una unidad
menor que una potencia de 2, p = 2n − 1 n ∈ N.
Ahora asumimos que tenemos una sucesión {Un } de distribuciones uniformes en [0, 1] y
además suponemos que necesitamos una sucesión {Yn } que esta formada por distribuciones
acordes a una distribución FY que no puede ser una distribución uniforme pero tiene que
14
CAPÍTULO 1. VARIABLES ALEATORIAS
ser monótona creciente. Una forma de calcular la sucesión {Yn } con la sucesión {Un } es fijar
Y = g(U ) por una función g, notemos que g −1 (Y ) = U . Para encontrar g −1 consideramos
−1
FY (y) = P ({g(U ) ≤ y}) = P ({U ≤ g (y)}) =
= g −1 (y)
Si FY (y) =
Ry
−∞
Z g−1 (y)
1ds
0
para 0 ≤ g −1 (y) ≤ 1.
py (s)ds, entonces
Z Yn
−∞
py (s)ds = Un
para n = 1, 2, 3 . . .
se suele usar esta fórmula para calcular Yn ya que los Un son distribuciones uniformes pseudoaleatorias.
Para el método de Monte Carlo que veremos más adelante son necesarios números aleatorios
y aunque podemos crearles usaremos la implementación de Mathematica para ellos, ya que
es más eficiente.
Ejemplo 1.9. Generación de números pseudo-aleatorios.
Un par de ejemplos hechos con Mathematica para generar números pseudo-aleatorios mediante el generador congruencial lineal son
n = Prime[10^6]; a = 10; c = 21;
f[x_] = Mod[a*x + c, n]; NestList[f, 12, 50]
n = 101; a = 9; c = 2;
f[x_] = Mod[a*x + c, n]; NestList[f, 12, 50]
Los dos comandos anteriores nos generan una lista de cincuenta números pseudo-aleatorios
empezando por el doce. Para conseguir distribuciones uniformes en [0, 1] solo tenemos que
dividir cada número por n.
Ejemplo 1.10. Generación de números aleatorios distribuidos exponencialmente.
Suponemos que necesitamos que la sucesión {Yn } esté formada por números aleatorios distribuidos exponencialmente en [0, ∞) entonces tenemos que asumir que la sucesión {Un } esta
formada por números aleatorios distribuidos uniformemente en [0, 1]. En este caso la función
de densidad es de la forma py (s) = e−s para s ≥ 0, como necesitamos encontrar Yn se tiene
que
Z Yn
0
e−s = 1 − e−Yn = Un
Por lo tanto Yn = − log(1 − Un )
para n = 1, 2, 3 . . . .
para n = 1, 2, 3 . . .
15
1.6. MÉTODO DE MONTE CARLO
1.6.
Método de Monte Carlo
El método de Monte Carlo es un método estadístico numérico, usado para aproximar expresiones matemáticas complejas y costosas de evaluar con exactitud. El método de Monte Carlo
fue creado por Nicholas Metropolis Constantino (1915-1999) y Stanislaw Ulam (1909-1986)
(véase figuras 1.1 y 1.2). El método se llamó así en referencia al Casino de Monte Carlo
(Principado de Mónaco) por ser “la capital del juego de azar”, al ser la ruleta un generador
simple de números aleatorios.
Historia del método de Monte Carlo
El método de Monte Carlo surge formalmente en el año 1944, sin embargo, ya existían
prototipos y procesos anteriores que se basaban en los mismos principios.
El empleo del método de Monte Carlo para fines de investigación comenzó con el desarrollo de
la bomba atómica en la Segunda Guerra Mundial en el Laboratorio Nacional de Los Álamos.
Durante el desarrollo de este proyecto, los científicos Von Neumann (1903-1957) y Ulam
perfeccionaron la técnica y la aplicaron a problemas de cálculo de difusión de neutrones
en un material. Alrededor de 1970, los desarrollos teóricos en complejidad computacional
comienzan a proveer mayor precisión y relación para el empleo del método Monte Carlo.
Actualmente el método Monte Carlo a veces es usado para analizar problemas que no tienen
un componente aleatorio explícito; en estos casos un parámetro determinista del problema
se expresa como una distribución aleatoria y se simula dicha distribución. La simulación
de Monte Carlo también fue creada para resolver integrales que no se pueden resolver por
métodos analíticos (aquí es donde nos centraremos), para solucionar estas integrales se usaron
números aleatorios. Posteriormente fue utilizado para cualquier esquema que emplee números
aleatorios, usando variables aleatorias con distribuciones de probabilidad conocidas.
Figura 1.1: Nicholas Metropolis Constantino
Figura 1.2: Stanislaw Ulam
16
CAPÍTULO 1. VARIABLES ALEATORIAS
Cálculo de integrales por el método de Monte Carlo
Podemos estimar la integral de una función continua f con Monte Carlo, [9]. Esta integral
puede verse como el cálculo de la esperanza de la función f cuando se aplica a una variable
aleatoria de distribución uniforme. Supongamos que el intervalo de integración es [0, 1] y sea
X1 , X2 , . . . , Xn una muestra de variables aleatorias independientes con distribución uniforme
en el intervalo [0, 1], entonces
Z
1
f (x) dx = E(f (X)),
0
con X una variable aleatoria uniforme en [0, 1].
De esta manera, gracias a la ley de los Grandes Números esta integral se puede aproximar
por
Z 1
n
1X
f (Xi )
f (x) dx ≈
n i=1
0
Todo el problema se reduce a generar la muestra.
Por otro lado, obsérvese que cualquier integral sobre el intervalo [a, b] se puede transformar
a una integral sobre el intervalo [0, 1] con el siguiente cambio de variable x = a + (b − a)u
Z b
f (x) dx = (b − a)
a
Z 1
f (a + (b + a)u) du ≈
0
n
b−aX
f (a + (b − a)Ui ),
n i=1
con Ui variables aleatorias uniformes en [0, 1].
Estimación del error
Sea X una variable aleatoria con función de distribución F , f una función continua y sea
I = E(f (X)). Sea X1 , X2 , . . . , Xn una muestra de variables aleatorias independientes con
P
función de distribución F y denótese In = n1 ni=1 f (Xi ). Si σ 2 es la varianza de f (X) entonces
σ2
es la varianza de In por ser las Xi variables aleatorias independientes.
n
√ n ) se comporta como
Por el Teorema del Límite Central se sabe que para n grande, Zn = (I−I
σ n
una variable aleatoria normal con media cero y varianza uno por lo que
λσ
P (|I − In | < √ ) = P (|Zn | < λ) ≈ λΦ(λ)
n
2
λ −x /2
1
con Φ(λ) = 2π
dx y λ se selecciona dependiendo de la probabilidad que se desee
0 e
obtener. Por ejemplo si se quiere obtener que la probabilidad sea 0.95 se selecciona λ como
1.96. Por lo que el error que se comete al usar el método de Monte Carlo es aproximadamente
√σ . Si σ ≈ 1, se requiere de n = 104 para tener al menos dos cifras significativas.
n
Este resultado permite establecer un intervalo de confianza de α %. Para ello se selecciona λ
dela forma que Φ(λ) = α2 . De esta manera, con probabilidad α podemos asegurar que el valor
exacto de la esperanza I está en el intervalo
R
λσ
λσ
[In − √ , In + √ ].
n
n
1.6. MÉTODO DE MONTE CARLO
17
El problema para usar el resultado anterior es que hay que conocer el valor de la desviación
típica de f (X). Lo que se hace en la práctica es estimarla por la varianza muestral. Con este
intervalo se determina el tamaño que se requiere que tenga n para tener la precisión deseada.
Por ejemplo si se desea tener un intervalo de confianza del 95 % de longitud 10−2 se debe
escoger n > 4(1.96)2 σf 104 .
Error cuadrático medio
Desde el punto de vista estadístico el método de Monte Carlo genera un estimador insesgado
ya que E(In ) = I. Por otro lado, el error cuadrático medio se define como
E((I − In )2 ) = E(I − E(In ))2 + Var(In ).
Si se desea reducir el error cuadrático medio lo que hay que hacer es reducir σ o incrementar
el tamaño n de la muestra de variables aleatorias. A veces el valor de n es tan grande que es
costoso incrementar la muestra, por lo que se ha optado por generar métodos para reducir la
varianza; estos métodos se conocen con el nombre de reducción de varianza.
Ejemplo 1.11. Integral de Monte Carlo con Mathematica.
R
En este ejemplo vamos a aproximar la integral 010 ecos x dx mediante el método de Monte
Carlo con la implementación que tiene Mathematica para el método y la nuestra, empecemos
por la que tiene Mathematica:
NIntegrate[Exp[Cos[x]], {x, 0, 10}, Method -> "MonteCarlo",
MaxPoints -> 1000]
NIntegrate::maxp: The integral failed to converge after 1100 integrand evaluations. NI
11.9987
NIntegrate[Exp[Cos[x]], {x, 0, 10}, Method -> "MonteCarlo",
MaxPoints -> 100000]
11.9804
ListPlot[Last[
Reap[NIntegrate[Exp[Cos[x]], {x, 0, 10}, Method -> "MonteCarlo",
MaxPoints -> 1000,
EvaluationMonitor :> Sow[{x, Exp[Cos[x]]}]]]], Filling -> 0,
AxesOrigin -> {0, 0}] // Quiet
18
CAPÍTULO 1. VARIABLES ALEATORIAS
Nos damos cuenta de que si escogemos un n que genera un error grande Mathematica nos
avisa. Además hemos pintado la solución gráficamente con LisPlot para ver como se va
aproximando aleatoriamente, ver figura 1.3.
Ahora mostraremos un ejemplo para aproximar y dibujar integrales por Monte Carlo sin usar
la implementación que tiene Mathematica de Monte Carlo:
f[x_] = E^(Cos[x]); a = 0; b = 10;
MonteCarloIntegral[n0_] :=
Module[{i},
n = n0;
X = Table[Random[Real, {a, b}], {i, 1, n}];
f1 = 1/n Sum[f[Part[X, i]], {i, 1, n}];
v = (b - a);
approx = v*f1;
Return[{n, approx} ];]
MonteCarloIntegral[100000]
{100000, 12.1103}
MonteCarloDibujo[n0_] := Module[{n = n0},
MonteCarloIntegral[n];
graph =
Plot[f[x], {x, a, b}, PlotStyle -> Magenta];
Y = f[X];
P = Map[Point, Transpose[{X, Y}]];
dots = Graphics[{Red, PointSize[0.01], P}];
L = Map[Line, Transpose[{Transpose[{X, 0 Y}], Transpose[{X, Y}]}]];
lines = Graphics[{Red, Thickness[0.005], L}];
Show[graph, dots, lines]]
La aproximación nos queda parecida a si la hacemos con el método de Monte Carlo que tiene
ya implementado Mathematica. En la figura 1.4 podemos ver la aproximación de la integral
dibjuada con 100 puntos, ya que si usamos más puntos no se aprecian bien la distintas
aproximaciones.
Ejemplo 1.12. Aproximación con Monte Carlo de π.
Imaginamos un círculo de radio uno inscrito en un cuadrado y suponemos que el centro
del círculo tiene coordenadas (0, 0). Sabemos que el área de este círculo es π y el área del
19
1.6. MÉTODO DE MONTE CARLO
2.5
2.5
2.0
2.0
1.5
1.5
1.0
1.0
0.5
0.5
2
4
6
8
10
Figura 1.3: Aproximación de ecos x con la implementación de Mathematica
2
4
6
8
Figura 1.4: Aproximación de ecos x con la implementación nuestra
cuadrado es 4. Llamamos ρ al cociente del área del círculo con el área del cuadrado, ρ =
0.7853981633974483 (con 16 dígitos).
Una forma de aproximar π es coger puntos dentro del cuadrado y contar cuantos de estos están
dentro del círculo. Suponemos que escogemos el siguiente conjunto de puntos {(−1+ 2i−1
, −1+
32
2j−1 32 32
)}i=1 j=1 de los cuales 812 están dentro del círculo y 212 están fuera. El porcentaje de
32
812
puntos dentro del circulo es ρ = 1024
= 0.79296875. Por lo tanto el área aproximada del
circulo es
área del cícurlo ≈ 4 ∗ ρ = 4 ∗ 0.79296875 = 3.171875.
Y como el círculo es de radio uno esto también es la aproximación de π.
Vamos a hacer una simulación de Monte Carlo para aproximar el valor de π cogiendo n
puntos aleatorios {(xi , yi )}ni=1 dentro del cuadrado unidad y calculando ρ = m
dónde m es el
n
2
2
número de puntos que satisfacen xi + yi ≤ 1. Para ello nos ayudaremos de Mathematica:
MonteCarloPi[n0_] := Module[{d, i},
n = n0;
Pin = Pout = {};
For[i = 1, i <= n, i++,
X = Random[];
Y = Random[];
d = X^2 + Y^2;
If[d <= 1, Pin = Append[Pin, {X, Y}],
Pout = Append[Pout, {X, Y}];];];
m = Length[Pin];
k = Length[Pout];
\[Rho] = m/n;
approx = \[Rho]*4.0;
Return[approx];];
10
20
CAPÍTULO 1. VARIABLES ALEATORIAS
MonteCarloPiConDibujo[n0_] := Module[{},
MonteCarloPi[n0];
Pin = Map[Point, Pin];
DOTSin = Graphics[{Red, PointSize[0.02], Pin}];
Pout = Map[Point, Pout];
DOTSout = Graphics[{Green, PointSize[0.02], Pout}];
circle =
Graphics[{Blue, Thickness[0.01], Circle[{0, 0}, 1, {0, Pi/2}]}];
line = Graphics[{Line[{{1, 0}, {1, 1}, {0, 1}}]}];
Print["La aproximación de \[Pi] es ", approx];
Show[DOTSin, DOTSout, circle, line, Axes -> True,
Ticks -> {Range[0, 1, 0.5], Range[0, 1, 0.5]}, AspectRatio -> 1]]
MonteCarloPiConDibujo[1000]
La aproximación de \[Pi] es 3.176
Y la aproximación de π que hallamos con nuestro programa es 3.176.
Nota 1.4. La función MonteCarloPiConDibujo también nos dibuja la sección del circulo
donde escogemos los puntos para calcular la aproximación como se puede ver en las figuras
1.5 y 1.6.
1.
1.
0.5
0.5
0.5
1.
Figura 1.5: Aproximación de π con 100 puntos
0.5
1.
Figura 1.6: Aproximación de π con 1000 puntos
21
1.6. MÉTODO DE MONTE CARLO
Ejemplo 1.13. Estimación mediante Monte Carlo de la distancia media entre dos puntos.
En este ejemplo estudiamos la estimación de la distancia media entre dos puntos aleatorios
en el intervalo [0, 1] y la de distancia de dos puntos aleatorios en el cuadrado [0, 1] × [0, 1].
Podemos plantear cada uno de estos problemas con integrales. En el primer caso
I=
Z 1Z 1
0
0
|x1 − x2 | dx1 dx2
es la distancia media entre dos puntos aleatorios elegidos en el intervalo [0, 1], mientras que
en el segundo caso
J=
Z 1Z 1Z 1Z 1q
0
0
0
0
(x1 − x2 )2 + (y1 − y2 )2 dx1 dx2 dy1 dy2
que es la distancia media entre dos puntos aleatorios en [0, 1]×[0, 1]. La estimación por Monte
Carlo de estos valores se calcula usando las sumas
In =
n
1X
|x1,i − x2,i |
n i=1
donde x1,i , x2,i son distribuciones uniformes en [0, 1] y
Jn =
n q
1X
(x1,i − x2,i )2 + (y1,i − y2,i )2
n i=1
donde x1,i , x2,i , y1,i , y2,i son distribuciones uniformes en [0, 1]. Las integrales múltiples son tan
fáciles de calcular por Monte Carlo como las integrales simples, ya que una integral múltiple
solo involucra una suma. Además el error es proporcional a √1n en ambos casos, como hemos
visto antes. Una forma de programar el ejemplo con Mathematica sería
nrum = 1000000; arum = nrum; s1 = N[0, 8]; s2
For[i = 1, i <= nrum, i++,
x1 = N[RandomVariate[UniformDistribution[]],
x2 = N[RandomVariate[UniformDistribution[]],
s1 = s1 + f/arum; s2 = s2 + (f^2)/arum]
sd = Sqrt[s2 - s1^2];
Print["n = ", nrum, "
s1 = ", s1 , "
s2 =
", s2 , "
n = 1000000
sd = 0.235511
s1 = 0.333285
s2 = 0.166544
= N[0, 8];
8];
8]; f = Abs[x1 - x2];
s1 = N[0, 8]; s2 = N[0, 8];
For[i = 1, i <= nrum, i++,
x1 = N[RandomVariate[UniformDistribution[]], 8];
x2 = N[RandomVariate[UniformDistribution[]], 8];
y1 = N[RandomVariate[UniformDistribution[]], 8];
sd = ", sd
22
CAPÍTULO 1. VARIABLES ALEATORIAS
y2 = N[RandomVariate[UniformDistribution[]], 8];
f = Sqrt[(x1 - x2)^2 + (y1 - y2)^2]; s1 = s1 + f/arum;
s2 = s2 + (f^2)/arum]
sd = Sqrt[s2 - s1^2];
Print["n = ", nrum, "
s1 = ", s1 , "
s2 = ", s2 , "
n = 1000000
s1 = 0.521155
s2 = 0.332928
sd = ", sd]
sd = 0.247641
Para generar las distribuciones uniformes hemos usado programas implementados en Mathematica. Usando un millón de ejemplos, es decir n = 106 , In = 0.3332928 y Jn = 0.521155.
Para la comparación los valores exactos para I y J con cinco cifras significativas son 0.33333
y 0.52141 respectivamente.
Nota 1.5. Notemos que en el código anterior de Mathematica sd es la desviación típica de
dos puntos aleatorias elegidos en el intervalo [0, 1].
Ejemplo 1.14. Estimación de la longitud media de un conjunto.
Este ejemplo muestra la flexibilidad de las técnicas de Monte Carlo. Sea
S = {000, 001, 002, . . . , 999}
el conjunto los números de tres dígitos. En este ejemplo, vamos a seleccionar conjuntos
aleatorios de S pero con con ciertas propiedades. En particular, para cada conjunto B ⊂ S
se selecciona aleatoriamente de tal manera que los elementos de B difieren cada uno del otro
en al menos dos dígitos. Además, el conjunto B se construye tan grande como sea posible
de modo que para cualquier x ∈ B c hay un y ∈ B de tal forma que x e y tienen dos
dígitos iguales. Sea Ω = {B1 , B2 , B3 , . . . , BN } con N = 1016 (el número total de posibles
conjuntos con estas propiedades es más elevado), una colección de conjuntos seleccionados
aleatoriamente con las propiedades explicadas anteriormente. Definimos la variable aleatoria
X en Ω de manera que X(B) es igual al número de elementos en el conjunto B, de forma
que X : Ω → [50, 100] (podemos ver esta demostración en [2]). Definimos la medida de
probabilidad P por P (Bi ) = N1 para i = 1, 2, . . . , N ; es interesante estimar el número medio
P
de elementos en los conjuntos B ∈ Ω, es decir, E(X) = N1 N
i=1 X(Bi ). Como N es muy grande
no podemos computar todos los conjuntos de Ω. Por lo tanto E(X) puede ser estimado usando
P
que E(X) ≈ M1 M
i=1 X(Bi ) para M < N . El código de Mathematica usado para hallar la
aproximación es el siguiente:
A = Flatten[Table[{i, j, k}, {i, 0, 9}, {j, 0, 9}, {k, 0, 9}], 2];
B := RandomInteger[{1, 1000}, 100];
1.6. MÉTODO DE MONTE CARLO
23
sepuedeponer[vec_, mat_, cont_] :=
Module[{v = vec, m = mat, c = cont, inic = 0}, cot = inic;
For[t = 1, t <= c && cot <= 1, t++, cot = 0;
For[n = 1, n <= 3, n++,
If[Part[v, n] == Part[m, t, n], cot = cot + 1]]]; Return[cot];];
sum = 1; cont1 = 0; cont3 = 0; cuadrado = 0; For[i = 1, i <= 10000, i++,
W = ConstantArray[as, {100, 3}]; a = Part[B, i]; b = Part[A, a];
Part[W, 1] = b; cont2 = 1; cont4 = 0;
For[j = RandomInteger[{1, 1000}], cont2 < 2, j++,
For[t = 1, t <= 3, t++,
If[Part[A, j, t] == Part[W, 1, t], cont1 = cont1 + 1]] If[
cont1 < 2, cont2 = cont2 + 1; Part[W, cont2] = Part[A, j];];
cont1 = 0];
For[j = 1, j <= 500, j++,
If[sepuedeponer[Part[A, j], W, cont2] < 2, cont2 = cont2 + 1;
Part[W, cont2] = Part[A, j]]];
For[j = 1000, j > 500, j--,
If[sepuedeponer[Part[A, j], W, cont2] < 2, cont2 = cont2 + 1;
Part[W, cont2] = Part[A, j]]];
For[t = 1, t <= 100, t++,
If[Part[W, t, 1] != "as", cont3 = cont3 + 1; cont4 = cont4 + 1]];
cuadrado = cuadrado + cont4^2]; media =
N[cont3/10000,2]; Print["E(X) = ", media]; Print["Var(X) = ",
N[cuadrado/10000,2] - media^2]
E(X) = 87.35
Var(X) = 2.65
Como vemos computando M = 1000 conjuntos, E(X) y Var(X) es estimado como E(X) =
8.75 y Var(X) = 2.65.
Ejemplo 1.15. Error del método y error estadístico en la estimación de Monte Carlo.
Este ejemplo ilustra los dos tipos de error involucrados en la estimación de integrales estocásticas o en la aproximación de soluciones de ecuaciones diferenciales estocásticas. Sea
IN =
N
X
i−1
, donde ηi ∼ N (0, 1) para cada i.
3/2 η
i
i=1 N
Se tiene que E(IN2 ) → E(I 2 ) =
1
3
cuando N → ∞. Sin embargo E(IN2 ) puede ser calculado
24
CAPÍTULO 1. VARIABLES ALEATORIAS
Tabla 1.1: Estimaciones de E(I 2 ) para el ejemplo 1.15
Valor de M
101
102
103
104
105
N = 101
0.415569
0.287986
0.269821
0.281819
0.286986
N = 102
0.260003
0.323847
0.322794
0.332764
0.328806
N = 103
0.281216
0.375468
0.330602
0.330221
0.333478
exactamente como
E(IN2 )
=
N
X
(i − 1)2
N (N − 1)(2N − 1)
1
1
1 2N 3 − 3N 2 + N
1
)=
+
=
(
= −
.
3
3
3
N
N
6
6N
3 2N
6N 2
i=1
Por lo tanto el método del error en está aproximación es
1
1
−
2N
6N 2
que es cero cuando N tiende a infinito. El error del método se debe a usar N subintervalos en la
aproximación de la integral estocástica. También, hay un error estadístico en la aproximación
de E(I 2 ) por E(IN2 ) que es debido a usar un número finito de muestras M para estimar E(IN2 ).
Supongamos por lo tanto que IN,m , para m = 1, 2, . . . , M son M muestras de IN usando los
números aleatorios ηi,m para 1 ≤ i ≤ N , 1 ≤ m ≤ M . Así que
E(I 2 ) − E(IN2 ) =
IN,m =
N
X
i−1
η , donde ηi,m ∼ N (0, 1).
3/2 i,m
i=1 N
Entonces
M
M X
N
1 X
1 X
i−1
(IN,m )2 =
(
ηi,m )2 ,
M m=1
M m=1 i=1 N 3/2
√
donde hay un error estadístico proporcional a 1/ M en la estimación de E(IN2 ). Por lo tanto
P
2
cuando estimamos E(I 2 ) usando M
m=1 (IN,m ) /M existen dos errores, uno es el error estadís√
tico que es proporcional a 1/ M donde M es el número de muestras. Notemos que cuando
M → ∞ la aproximación puede no ser satisfactoria si el valor de N no es suficientemente
grande. Observemos los diferentes valores de E(IN2 ) que están en la tabla 1.1. Estos cálculos
están hechos en Mathematica con el siguiente programa:
E(IN2 ) ≈
aproximación[M_, N_] :=
Module[{m = M, n = N, sum1 = 0, sum2 = 0},
For[j = 1, j <= m, j++, sum1 = (sum2^2)/(n^3) + sum1; sum2 = 0;
For[i = 1, i <= n, i++,
sum2 = sum2 + (i - 1)*RandomVariate[NormalDistribution[]]]];
Return[Print["E[I^2]= ", sum1/m]]]
1.6. MÉTODO DE MONTE CARLO
25
Recordemos que E(I 2 ) = 1/3 exactamente. Observemos que cuando M aumenta, el error
estadístico disminuye y el error total se acerca al error del método. Para N grande el error
que se produce es debido principalmente al error estadístico que puede ser alto para pequeños
tamaños de muestra, es decir, valores pequeños de M . La primera columna (N = 10) en la
tabla da valores con error del método grande. La primera fila (M = 10) da valores con error
estadístico grande. Este ejemplo muestra que para obtener valores que se asemejen al real el
error del método y el error estadístico deben ser pequeños.
26
CAPÍTULO 1. VARIABLES ALEATORIAS
Capítulo 2
Procesos estocásticos
2.1.
Introducción
La teoría de los procesos estocásticos se centra en el estudio y modelización de sistemas que
evolucionan a lo largo del tiempo, o del espacio, de acuerdo a unas leyes no determinísticas,
es decir, de carácter aleatorio.
La fórmula habitual de describir la evolución del sistema es mediante sucesiones o conjuntos
de variables aleatorias. De esta manera se puede estudiar cómo evoluciona una variable aleatoria a lo largo del tiempo. Por ejemplo, el número de personas que espera en una ventanilla
en un banco en un instante t de tiempo; el precio de las acciones de una empresa a lo largo
de un año, etc.
La primera idea básica es identificar un proceso estocástico con una sucesión de variables
aleatorias {X(t) : t ∈ T } donde la variable t indica el instante de tiempo o espacio correspondiente. Esta idea se puede generalizar fácilmente, permitiendo que los instantes de tiempo
en los que se definen las variables aleatorias sean continuos. Así, se podrá hablar de una
colección o familia de variables aleatorias {X(t) : t ∈ R}, que da una idea más exacta de los
que es un proceso estocático (véase [3]).
Definición 2.1. Un proceso estocástico es una familia de variables aleatorias {X(t) : t ∈ T },
con T ⊆ R, definidas en un espacio de probabilidad (Ω, F, P ) y relacionadas por un parámetro
t donde t varía en el conjunto T .
Nota 2.1. Normalmente el parámetro t juega el papel del tiempo.
Ejemplo 2.1. Algunos ejemplos de variables aleatorias en procesos estocásticos pueden ser
los siguientes:
X(t): número de personas que esperan un autobús en un instante t.
X(t): precio de una acción de una empresa en un día t del mes (t = 1, 2, . . . , 30).
27
28
CAPÍTULO 2. PROCESOS ESTOCÁSTICOS
X(t): número de parados en el mes t (t = 1, 2, . . . , 12).
Para que un proceso estocástico esté completamente definido hay que determinar las variables
aleatorias, es decir, determinar e identificar la distribución de probabilidad asociada a cada
una de ellas y, es más, la distribución conjunta de todas ellas.
Definición 2.2. Al conjunto T ⊆ R se le denomina conjunto paramétrico y puede ser
continuo o numerable.
Definición 2.3. Se denomina conjunto de estados E, al conjunto de los posibles valores que
pueden tomar las variables aleatorias {X(t)}t∈T .
Por tanto, dependiendo de como sea el conjunto T y el tipo de variable aleatoria X(t) se
puede establecer la siguiente clasificación de los procesos estocásticos:
Si el conjunto T , es continuo, por ejemplo R+ , diremos que X(t) es un proceso estocástico de parámetro continuo.
Si por el contrario T es discreto, por ejemplo N, diremos que nos encontramos frente a
un proceso estocástico de parámetro discreto.
Si para cada instante t la variable aleatoria X(t) es de tipo continuo, diremos que el
proceso estocástico es de estado continuo.
Si para cada instante t la variable aleatoria X(t) es de tipo discreto, diremos que el
proceso estocástico es de estado discreto.
Definición 2.4. Una cadena es un proceso estocástico en el cual el tiempo se mueve en forma
discreta y la variable aleatoria solo toma valores discretos en el espacio de estados.
Ejemplo 2.2. Cadena.
Se lanza una moneda varias veces y suponemos que cada vez que sale cara, un jugador gana
una moneda y si sale cruz pierde una moneda. Podemos definir un proceso estocástico que
modeliza la evolución del juego. Así, si X(n) = Xn es el número de unidades monetarias que
le quedan al jugador después de n lanzamientos, el espacio muestral de Xn es
Ω = {n-tuplas de caras y cruces}
de modo que el número de elementos de Ω es 2n.
Suponemos que tanto la probabilidad de obtener cara como la de obtener cruz es la misma,
1/2.
Vemos que es un proceso discreto donde el conjunto paramétrico es T = {1, 2, . . . , n} y el
posible conjunto de estados es
E = {−n, −n + 1, . . . , −3, −2, −1, 0, 1, 2, 3, . . . , n − 1, n}.
29
2.1. INTRODUCCIÓN
Si n = 6 y fijamos por ejemplo ω = (cara, cara, cruz, cruz, cruz, cruz) tenemos que
X1 (ω) = 1
X2 (ω) = 2
X3 (ω) = 1
X4 (ω) = 0
X5 (ω) = −1 X6 (ω) = −2.
Ahora si fijamos t, por ejemplo en t = 3, se puede calcular la distribución de X3 . El conjunto
de posibles estados de X3 es:
0
−1
−2
1
2
0
−1 −3 −1
de modo que E = {−3, −1, 1, 3} y
1
1
0
3 −1
1
23
3
P {X3 = −1} = 3
2
3
P {X3 = 1} = 3
2
1
P {X3 = 3} = 3
2
P {X3 = −3} =
1
1
8
3
=
8
3
=
8
1
= .
8
=
Podemos definir una nueva variable aleatoria en este caso (t = 3):
Y ≡ número de caras obtenidas (éxitos).
Se puede observar que nuestra nueva variable aleatoria Y es igual a una distribución binomial
1
Y ∼ B(3, p = ),
2
por lo tanto X3 se distribuye como una B(3, p = 21 ). Por lo que hemos identificado un proceso
estocástico. Podemos ver este ejemplo más estudiado en el ejemplo 2.4.
Definición 2.5. Un proceso de saltos puros es un proceso estocástico en el cual los cambios
de estados ocurren de forma aislada y aleatoria pero la variable aleatoria solo toma valores
discretos en el espacio de estados.
Para el caso de los procesos de saltos puros se puede considerar como ejemplo la función
indicatriz, definida en la ecuación (1.2).
Vemos que en la función indicatriz solo hay dos posibles estados 0 y el 1, y si escogemos el
conjunto A aleatoria vemos que podemos pasar de un estado a otro en cualquier punto. La
figura 2.1 muestra un ejemplo de esta función.
30
CAPÍTULO 2. PROCESOS ESTOCÁSTICOS
1.0
0.8
0.6
0.4
0.2
1
2
3
4
5
Figura 2.1: Función indicatriz.
2.2.
Procesos de estado discreto
En el caso de procesos estocásticos con espacio de estados discretos, una secuencia de variables
que indique el valor del proceso en instantes sucesivos suele representarse de la siguiente
manera (X(t0 ) = X0 ):
{X0 = x0 , X1 = x1 , . . . , Xn−1 = xn−1 , Xn = xn }
en la que cada variable Xi , i = 0, . . . , n, tiene una distribución de probabilidad que, en
general, es distinta de las otras variables pero podría tener características comunes.
El principal interés del estudio a realizar en el caso discreto es el cálculo de probabilidades
de ocupación de cada estado a partir de las propiedades de cambio de estado. Si en el
instante n − 1 se está en el estado xn−1 , con qué probabilidad se estará en el estado xn .
Está probabilidad se denotará como
P (Xn = xn |Xn−1 = xn−1 )
A este tipo de probabilidad condicionada se le denomina probabilidad de transición o de
cambio de estado. A las probabilidades del tipo P (Xn = xn ) se les denominan probabilidades
de ocupación de estado.
Otro tipo de probabilidades de interés es de ocupar un cierto estado en el instante n, dado
que en todos los instantes anteriores, desde n = 0 hasta n − 1, sé conoce en que estado estuvo
el proceso. Esto se puede definir como:
P (Xn = xn |X0 = x0 , X1 = x1 , . . . , Xn−1 = xn−1 ).
Nótese que esta probabilidad depende de todo el proceso anterior, mientras que la probabilidad de transición depende únicamente del estado actual que ocupe el proceso.
31
2.2. PROCESOS DE ESTADO DISCRETO
Se dice que un proceso cumple la propiedad de Markov cuando todo la historia pasada del
proceso se puede resumir en la posición actual que ocupa el proceso para poder calcular la
probabilidad de cambiar a otro estado, es decir
P (Xn = xn |X0 = x0 , X1 = x1 , . . . , Xn−1 ) = P (Xn = xn |Xn−1 = xn−1 ).
Aquellas cadenas que cumplen la propiedad de Markov se llaman cadenas de Markov. Otra
manera de denotar a las probabilidades de transición es de la forma siguiente
P (Xn = j|Xn−1 = i) = pij (n).
Una propiedad interesante que puede tener una cadena es que los valores pij (n) no dependan
del valor de n. Es decir, las probabilidades de cambiar de estado son las mismas en cualquier
instante. Esta propiedad indica que las probabilidades de transición son estacionarias.
Cadenas de Markov
Ya hemos definido antes las cadenas de Markov ahora notemos que las probabilidades de transición suelen disponerse en forma de matriz cuadrada, encabezada cada fila y cada columna
con el estado correspondiente, tal y como se recoge a continuación (véase [7]):
E1
E2
...
Em
p11

p
 21
 .
 ..
p12
p22
..
.
...
...
..
.
p1m
p2m
..
.
Em pm1
pm2
...
pmm
E1
E2
..
.









A la matriz anterior se le suele llamar matriz de transición. Puesto que los elementos de
la fila i-ésima representan las probabilidades de pasar del estado Ei al resto de los posibles
estados, la suma de todos ellos vale 1, pues corresponde a la probabilidad del suceso seguro.
La matriz de transición de una cadena de Markov es un caso particular de matrices denominadas estocásticas. Una matriz estocástica es una matriz (no necesariamente cuadrada) cuyos
elementos son no negativos y cumplen que la suma de los elementos de cada fila es igual a 1.
Algunas propiedades de las matrices estocásticas
A continuación presentamos las siguientes propiedades que podrán ser de utilidad:
Si A y B son dos matrices estocásticas para las que está definido el producto AB,
entonces dicho producto es también una matriz estocástica.
Si A es una matriz cuadrada estocástica, entonces un valor propio de la matriz es igual
a 1.
32
CAPÍTULO 2. PROCESOS ESTOCÁSTICOS
Si A es una matriz cuadrada estocástica con todos sus elementos positivos, entonces la
sucesión de matrices An , n = 1, 2, . . . converge hacia una matriz U que tiene todas sus
filas iguales a un vector u, que es el único vector fila propio estocástico de la matriz A
correspondiente al valor propio 1, esto es, solución de la ecuación u(A − I) = 0.
Nota 2.2. La hipótesis de que sean positivos todos los elementos de A en la tercera propiedad
descrita es esencial, ya que de no ser así la sucesión de sus potencias no converge hacia una
matriz con todas sus filas iguales.
Uno de los problemas asociados con las cadenas de Markov es el siguiente: dado que la cadena
se halla inicialmente en el estado Ei (P (X0 ) = i), ¿cuál será la probabilidad de que se halle
en el estado Ej después de n pasos? La respuesta para n = 1 es clara: la probabilidad de
transición pij . Para calcularla cuando n = 2 la respuesta no es tan sencilla, la probabilidad
(2)
de pasar del estado Ei al Ej en dos pasos, probabilidad a la que denotaremos pij es la suma
de las probabilidades de pasar de Ei a Ek y de Ek a Ej cuando k varía desde 1 hasta m, es
decir,
(2)
pij =
m
X
pik pkj
k=1
(2)
y la expresión anterior muestra que pij es el elemento de la fila i y de la columna j de la
matriz A2 . Por lo tanto la probabilidad de pasar en n pasos del estado Ei al Ej , pnij , es el
elemento (ij) de la matriz An .
Si se parte del sistema en un determinado estado, digamos el Ei , se puede representar dicho
hecho diciendo que le instante inicial se está con probabilidad 1 en Ei y con probabilidad
0 en cada uno de los restantes estados, lo que sugiere introducir un vector estocástico mdimensional cuyas componentes son funciones de la variable natural n = 0, 1, 2, 3, . . .
x(n) = (x1 (n), x2 (n), . . . , xm (n))
de forma que xi (0) = 1, xj (0) = 0 para j 6= i, y xk (n) es la probabilidad de que en el
paso n el sistema se encuentre en el estado Ek , k = 1, 2, . . . , m. Es claro que el vector
correspondiente a n = 1 es justamente la fila i-ésima de la matriz A, que no es otra cosa
sino el producto del vector (0, 0, . . . , 0, 1(i) , 0, . . . , 0) por la matriz de transición A, es decir,
el vector (pi1 , pi2 , . . . , pim ), formado por las probabilidades de transición desde el estado Ei a
cada uno de los estados. Así pues,
(x1 (1), x2 (1), . . . , xm (1)) = (0, 0, . . . , 0, 1(i) , 0, . . . , 0)A
y, en general,
(x1 (n), x2 (n), . . . , xm (n)) = (0, 0, . . . , 0, 1(i) , 0, . . . , 0)An
lo que también puede expresarse así:
(x1 (n + 1), x2 (n + 1), . . . , xm (n + 1)) = (x1 (n), x2 (n), . . . , xm (n))A, n = 0, 1, 2, . . .
33
2.2. PROCESOS DE ESTADO DISCRETO
o, en forma más compacta,
x(n + 1) = x(n)A.
Esta última expresión permite ver que las ecuaciones planteadas al intentar estudiar la evolución de una cadena de Markov constituyen un sistema de ecuaciones en diferencias, si bien
con unas restricciones derivadas del hecho de que tanto la matriz A como el vector x(n) son
matrices estocásticas. Esto supone, por ejemplo, que el vector nulo, que obviamente es un
punto de equilibrio del sistema de ecuaciones en diferencias, no debe ser considerado en este
contexto.
Una cadena de Markov se llama regular si existe un número natural n tal que la potencia
n-ésima de su matriz de transición tiene todos sus elementos positivos, en cuyo caso todas
las potencias de la matriz de exponente mayor que n también tienen todos sus elementos positivos. El estudio de la evolución de una cadena de Markov regular resulta particularmente
simple.
Ejemplo 2.3. Cadena de Markov regular.
Una sala de cine burgalesa decide programar semanalmente las películas siguiendo el siguiente
método: si en una semana se proyectó una norteamericana, a la semana siguiente se programará, dos de cada tres veces, una española, y una de cada tres veces, una francesa. Si la
película programada fue francesa, la semana siguiente será norteamericana, francesa o española con iguales probabilidades para cada una. Finalmente, si la película programada fue
española, la semana siguiente se programará española una de cada tres veces y norteamericana dos de cada tres veces. Después de seguir este esquema durante un año ¿se habrá cumplido
con la cuota de pantalla que exige programar al menos un 25 % de películas de producción
nacional?
Tal como está planteada la programación, nos encontramos frente a una cadena de Markov
con tres estados a los que denotaremos E,F y N -correspondiente a la nacionalidad de la
película programada, (E)spañola, (F)rancesa o (N)orteamericana- y matriz de transición:
E

E 1/3

M = F
 1/3
N 2/3
F
N

0 2/3

1/3 1/3 

1/3 0
Aunque la matriz no tiene todos los elementos positivos, su cuadrado, que es la matriz


5/9 2/9 2/9


 4/9 2/9 1/3 


1/3 1/9 5/9
sí que los tiene, por lo que la cadena de Markov es regular y se puede aplicar la tercera
propiedad citada anteriormente. Las sucesivas potencias de la matriz de Markov convergen
34
CAPÍTULO 2. PROCESOS ESTOCÁSTICOS
hacia una matriz con todas sus filas iguales, fila que no es otra que le único vector fila propio
estocástico de dicha matriz correspodiente al valor propio 1. Para calcularlo resolvemos el
sistema de ecuaciones:


1/3 − 1
0
2/3



[u1 , u2 , u3 ]  1/3
1/3 − 1 1/3 
 = [0, 0, 0].
2/3
1/3
−1
Si tomamos u3 como parámetro obtenemos las siguientes soluciones
u1 =
t
5t
, u2 = u3 = t
4
2
de forma que, tomando t > 0 y dividiendo cada una de las tres componentes por la suma de
todas ellas obtenemos el vector propio estocástico
u = [5/11, 2/11, 4/11]
y la matriz límite buscada es:


5/11 2/11 4/11


 5/11 2/11 4/11  .


5/11 2/11 4/11
Del examen de la misma se desprende que, en promedio, se habrán proyectado en el año 5 películas españolas de cada 11, lo que equivale alago más de un 45 % cumpliéndose sobradamente
las cuotas de pantalla.
Cadenas de Markov absorbentes Si en una cadena de Markov es imposible abandonar
un estado una vez que se ha llegado a él, se dice que dicho estado es absorbente. Ello obliga
a que si el estado absorbente es el E1 , las probabilidades de transición verifiquen:
p11 = 1, p1i = 0, i 6= 1.
Una cadena de Markov puede tener más de un estado absorbente. Siempre es posible, renombrándolos si es necesario, lograr que los estados absorbentes sean los primeros en la lista
de estados que tiene la cadena. Al resto de estados, que no son absorbentes se les denomina
transitorios. Nótese que todos los estados de una cadena de Markov regular son transitorios.
Una cadena de Markov se dice que es absorbente si tiene al menos un estado absorbente y
desde cualquier estado es posible alcanzar un estado absorbente en un número finito de pasos.
Los principales problemas que se plantean al considerar la evolución de una cadena de Markov
absorbente son:
Si se empieza en un estado transitorio determinado ¿cuál es la probabilidad de terminar
en un estado absorbente prefijado?
35
2.2. PROCESOS DE ESTADO DISCRETO
¿Cuántas veces, por término medio, se pasará por estados transitorios antes de terminar
en un estado absorbente?
¿Cuántas veces, por término medio, se pasará por un estado transitorio determinado si
se comienza el proceso en otro estado transitorio (que puede ser el mismo)?
Para contestar a estas preguntas, comencemos escribiendo la matriz de transición de la cadena
de Markov absorbente colocando en primer lugar los estados absorbentes. En el caso de que
existan r estados absorbentes entre el total de m estados, la matriz de transición será

















1
0
..
.
0
1
..
.
0
0
...
...
pr+1,1 pr+1,2
..
..
.
.
pm1
pm2
0
0
..
.
0
0
..
.
...
...
1
0
. . . pr+1,r pr+1,r+1
..
..
...
.
.
. . . pmr
pm,r+1
...
...
...
...
...
...
...
0
0
..
.









0 

pr+1,m 



..

.

pmm
Como se ve, la matriz de transición en este caso está formada por cuatro bloques bien
diferenciados


I
O
 r

B A
El primero, Ir , es la matriz cuadrada unidad de dimensión r. La submatriz O es la matriz nula
de r filas y m − r columnas. La submatriz B tiene m − r filas y r columnas y no puede ser la
matriz nula, pues algún elemento de la misma tiene que ser igual a la probabilidad de pasar
de uno de los estados transitorios Er+1 , . . . , Em a algún estado absorbente E1 , E2 , . . . , Er .
Por consiguiente, todos sus elementos son no negativos, menores que 1 y al menos uno no es
positivo. Finalmente, la subamtriz A es cuadrada de dimensión m − r, y todos sus elementos
son no negativos y menores que 1.
Si se denota por I la matriz unidad de dimensión m − r se tiene el siguiente teorema (que no
demostraremos, véase [7]).
Teorema 2.1. La matriz I − A admite inversa y además si se define
X = (I − A)−1 , Z = XB
se tiene que
El elemento xij de X nos da el promedio de veces que el proceso de Markov pasa por el
estado Ej si comenzó en el Ei .
36
CAPÍTULO 2. PROCESOS ESTOCÁSTICOS
La suma de los elementos de la fila i de X,
m−r
X
xij
j=1
nos da el promedio de pasos que necesita el proceso para alcanzar un estado absorbente
partiendo del estado transitorio Ei .
El elemento zij de Z nos da la probabilidad de terminar en el estado absorbente Ej
partiendo del estado transitorio Ei .
Por lo tanto quedan contestadas las preguntas que nos hacíamos anteriormente.
Ejemplo 2.4. Cadena de Markov absorbente.
Dos jugadores J1 y J2 , cada uno con la misma cantidad de monedas de igual valor, deciden
jugar una serie de partidas a cara y cruz, conviniendo que si sale cara el jugador J1 pagará
una moneda a J2 , y si sale cruz recibirá una moneda de J2 , continuando el juego de esta
forma hasta que uno de ellos se arruine. ¿Nos hallamos ante un proceso de Markov?, ¿se
puede calificar la correspondiente cadena de Markov de absorbente?
Obviamente nos basta considerar la evolución de la cantidad de monedas que tenga J1 , pues
ese dato determina lo que tiene J2 en cada etapa del juego. Si, inicialmente cada jugador posee
n monedas, consideremos marcados sobre la semirrecta real positiva los puntos de abscisa
0, 1, 2, . . . , 2n. Puesto que J1 posee n monedas, imaginemos que lo colocamos en el punto de
abscisa n. Ahora, J1 juega la primera partida y tiene una probabilidad igual a 1/2 de ganar
o perder. Si pierde, entrega una moneda y tendrá n − 1, por lo que lo desplazaremos al punto
que tiene dicha abscisa, si gana se encontrará con n + 1 monedas, y lo imaginaremos en el
puntos de abscisa n + 1.
Si J1 alcanza el punto de abscisa 2n el juego termina con la ruina de J2 , si por el contrario,
alcanza el punto 0, J1 se arruina. Estamos en presencia de un proceso de 2n + 1 estados,
E0 , E1 , . . . , E2n , correspondientes a cada de uno de los puntos en que puede hallarse el jugador
J1 . Estamos por lo tanto ante una cadena de Markov absorbente, con dos estados absorbentes
E0 y E2n y los demás transitorios.
Por fijar ideas, si tomamos n = 3 la matriz de transición, una vez colocados los estados
absorbentes E0 y E6 en las dos primeras posiciones, es:

















1
0
0
0
0
0
0

0
1
0
0
0
0
0 


1/2 0
0 1/2 0
0
0 


0
0 1/2 0 1/2 0
0 


0
0
0 1/2 0 1/2 0 


0
0
0
0 1/2 0 1/2 

0 1/2 0
0
0 1/2 0
37
2.2. PROCESOS DE ESTADO DISCRETO
Las matrices X = (I − A)−1 y Z = XB son

X=









5/3
4/3
1
2/3
1/3
4/3
8/3
2
4/3
2/3
1
2
3
2
1
2/3
4/3
2
8/3
4/3
1/3
2/3
1
4/3
5/3






,













Z=
5/6
2/3
1/2
1/3
1/6
1/3
1/3
1/2
2/3
5/6





.




Del examen de X se desprende que, en promedio, el número de tiradas necesarias para acabar
la partida si los dos jugadores comienzan con tres monedas cada uno es nueve, que es la suma
de los elementos de la tercera fila de la matriz. Si uno hubiera comenzado con cuatro monedas
y el otro con dos, el promedio del número de jugadas hasta finalizar es ocho, reduciendo a
cinco si un jugador empieza con una moneda y el otro con cinco. La matriz Z, por otra parte
nos informa de que las probabilidades de ganar de cada uno de los jugadores son iguales
si ambos empiezan con el mismo número de monedas. Si uno comienza con dos y otro con
cuatro, este segundo tiene el doble de probabilidad de ganar que el otro, como vemos en la
cuarta fila de la matriz.
Procesos de saltos puros
En este caso, el proceso sigue siendo discreto en estados pero la gran diferencia es que los
cambios de estado ocurren en cualquier instante en el tiempo (tiempo continuo). Hemos
apuntado anteriormente que un ejemplo típico de procesos de saltos puros es la función
indicatriz. Otros ejemplos de procesos de saltos puros son los siguientes:
Definición 2.6. Un proceso estocástico en tiempo continuo {X(t), t ≥ 0} se dice que es un
proceso de conteo si representa el número de veces que ocurre un suceso hasta el instante de
tiempo t.
En particular, se tiene que X(t) ∈ N, y X(s) ≤ X(t) ∀s < t.
Definición 2.7. Un proceso de conteo se dice que es un proceso de Poisson homogéneo de
intensidad (o tasa) λ > 0, si:
X(0) = 0.
X(t1 ) − X(t0 ), X(t2 ) − X(t1 ), . . . , X(tn ) − X(tn − 1) son variables aleatorias independientes (proceso de incrementos independientes).
X(t + s) − X(s) es el número de sucesos que ocurren entre el instante s y el instante
t + s y además sigue una distribución de Poisson de parámetro λt
38
CAPÍTULO 2. PROCESOS ESTOCÁSTICOS
El proceso de Poisson se utiliza básicamente para modelar los llamados procesos de colas. En
ellos se pueden incluir muchos procesos: coches que llegan al peaje de una autopista, clientes
que llegan a un banco, peticiones que llegan a un servidor de Internet, llamadas que pasan
por una centralita, etc.
Tiene algunas características fundamentales:
Para cada instante t, X(t) seguirá una distribución de Poisson de parámetro λt.
Las diferencias entre los tiempos de llegadas consecutivas siguen una distribución exponencial de parámetro λ, es decir, X(i + 1) − X(i) siguen una exponencial de parámetro
λ.
Ejemplo 2.5. Proceso de Poisson con intensidad λ.
Sea X(t) igual al número de observaciones en el tiempo t. Asumimos que la probabilidad de
una observación en el intervalo de tiempo ∆t es igual a λ∆t + o(∆t). Haciendo referecnia
al ejemplo 1.3 es claro que esto es un proceso estocástico continuo y la probabilidad de n
observaciones en un tiempo t es
P (X(t) = n) = Pn (t) = e−λt
(λt)n
.
n!
El proceso X(t) es un proceso estocástico de parámetro continuo y de estado discreto. Específicamente, X(t) es un proceso de Poisson con intensidad λ > 0. Notemos que X(0) = 0 y
el número de observaciones en cualquier tiempo t es una distribución de Poisson con media
λt. Es decir, para cualquier λ ≥ 0
P (X(t + s) − X(s) = n) = e−λt
(λt)n
.
n!
Ciertamente, el proceso es un proceso de Markov y
P (X(t + ∆t) ≤ m + ∆m|X(t) = m) =
∆m
X
l=0
e−λ∆t
(λ∆t)l
l!
y la distribución de probabilidad en el tiempo t+∆t solo depende de el estado del sistema en el
tiempo t y no de la historia del sistema. Ademas si consideramos que Y (t) = X(t + s) − X(s)
para algún s ≥ 0, entonces Y (t) es también un proceso de Poisson con intensidad λ y
Y (0) = 0. La figura 2.2 muestra el comportamiento aleatorio de los saltos discretos en un
proceso de Poisson. Notemos que el promedio del proceso de Poisson (dibujado con línea
discontinua) sigue de cerca la recta λt . Hemos utilizado el siguiente código para dibujarlo:
xx = 4034218;
nt = 500; nrum = 200; time = 10; lambda = 1;
h = time/nt; tt = Range[0, time, h];
39
2.3. PROCESOS DE ESTADO CONTINUO
10
8
6
4
2
2
4
6
8
10
Figura 2.2: Proceso de Poisson con 200 muestras para la trayectoria y λ = 1.
sm = ConstantArray[0, {nt + 1, 1}]; s2 =
ConstantArray[0, {nt + 1, 1}]; patha =
ConstantArray[0, {nt + 1, 1}]; pathb = ConstantArray[0, {nt + 1, 1}];
For[j = 1, j <= nrum, j++, y = 0; Part[sm, 1] = y; Part[s2, 1] = y*y;
Part[patha, 1] = y; Part[pathb, 1] = y;
For[i = 1, i <= nt, i++, unr = random[xx]; xx = Part[unr, 2];
If[Part[unr, 1] < lambda*h, y = y + 1];
Part[sm, i + 1] = (Part[sm, i + 1] + y/nrum);
Part[s2, i + 1] = (Part[s2, i + 1] + y*y/nrum);
Part[pathb, i + 1] = Part[patha, i + 1]; Part[patha, i + 1] = y]]
a = 16807; b = 2^31 - 1;
random[x_] := (d = IntegerPart[a*x/b]; t = a*x - d*b;
unr = ConstantArray[0, {2, 1}]; Part[unr, 1] = t/b;
Part[unr, 2] = t; Return[unr])
Show[ListPlot[{Flatten[sm]}, Joined -> True, PlotStyle -> Dashed,
Ticks -> {{2, 4, 6, 8, 10}, {2, 4, 6, 8, 10}}],
ListPlot[{patha}, Joined -> True]]
2.3.
Procesos de estado continuo
Ahora consideramos un proceso estocástico continuo {X(t) : t ∈ T } definido en el espacio de
probabilidad (Ω, F, P ) donde T = [0, N ] es un intervalo de tiempo y el proceso está definido
40
CAPÍTULO 2. PROCESOS ESTOCÁSTICOS
en todos los instantes de tiempo del intervalo. Un proceso estocástico de tiempo continuo es
una función X : T ×Ω → R de dos variables t y ω y X puede ser de estado continuo o discreto
como hemos dicho en la introducción. En particular X(t) = X(t, ·) es una variable aleatoria
para cada valor de t ∈ T y X(·, ω) asigna el intervalo T a R. Generalmente el conocimiento
especifico de ω es innecesario, pero ω es importante ya que cada ω ∈ Ω define una trayectoria
diferente. Como consecuencia, lo normal es que la variable ω suela suprimirse, es decir, X(t)
representa una variable aleatoria para cada valor de t y X(·) representa una trayectoria en
todo el intervalo T = [0, N ]
Como ya hemos visto antes el proceso estocástico X es un proceso de Markov si el estado de
el proceso en algún tiempo tn ∈ T determina el estado futuro del proceso. Específicamente
P (X(tn+1 ) ≤ xn+1 |X(tn ) = xn ) = P (X(tn + 1) ≤ xn+1 |X(t1 ) = x1 , . . . , X(tn ) = xn ) donde
t1 < t2 < . . . < tn < tn+1 .
Características de un proceso estocástico
Del mismo modo que en una variable unidimensional X, podemos calcular su media, su varianza y otras características, y en variables n-dimensionales obtenemos un vector de medias,
matriz de covarianzas, etc., en un proceso estocástico podemos obtener algunas características
que describen su comportamiento: medias, varianzas y covarianzas. Puesto que las características del proceso pueden variar a lo largo de t estas características no serán parámetros
sino que serán funciones de t. Así:
Definición 2.8. Llamaremos función de medias del proceso a una función de t que proporciona las medias de las distribuciones marginales para cada instante t
µt = E(X(t)).
Definición 2.9. Llamaremos función de varianzas del proceso a una función de t que proporciona las varianzas de las distribuciones marginales para cada instante t
σt2 = Var(X(t)).
Definición 2.10. Llamaremos función de autocovarianzas del proceso a la función que proporciona la covarianza existente entre dos instante de tiempo cualesquiera:
Cov(t, s) = Cov(s, t) = Cov(X(t), X(s)).
Definición 2.11. Llamaremos función de autocorrelación a la estandarización de la función
de covarianzas:
Cov(t, s)
ρt,s =
σt σs
2.3. PROCESOS DE ESTADO CONTINUO
41
En general, estas dos últimas funciones dependen de dos parámetros (dos instantes). Una
condición de estabilidad que aparece en muchos fenómenos es que la dependencia sólo dependa, valga la redundancia, de la “distancia” entre ellos y no del instante considerado. En
estos casos tendremos:
Cov(t, t + j) = Cov(s, s + j) = γj j = 0, ±1, ±2, . . .
Por otro lado, si estudiamos casos concretos como la evolución de las ventas de una empresa
o la concentración de un contaminante, sólo disponemos de una única realización y aunque el
proceso estocástico exista, al menos conceptualmente, para poder estimar las características
“transversales” del proceso (medias, varianzas, etc..) a partir de la serie es necesario suponer
que estas permanecen estables a lo largo de t. Esta idea nos conduce a lo que se entiende por
condiciones de estacionariedad de un proceso estocástico (o de una serie temporal).
Procesos estocásticos estacionarios
En una primera aproximación, llamaremos estacionarios a aquellos procesos estocásticos que
tengan un comportamiento constante a lo largo del tiempo. Si buscamos el correspondiente
comportamiento de las series temporales asociadas a esos procesos, veremos gráficas que se
mantienen en un nivel constante con unas pautas estables de oscilación.
En la práctica del análisis de series encontraremos series con problemas de estacionariedad
que afecten a cualquiera de sus parámetros básicos, siendo los que más suelen afectar al
proceso de análisis las inconstancias en media y varianza.
Definición 2.12. Diremos que un proceso es estacionario en sentido estricto si al realizar un
mismo desplazamiento en el tiempo de todas las variables de cualquier distribución conjunta
finita, resulta que esta distribución no varía, es decir:
F (X(t1 ), X(t2 ), . . . , X(tr )) = F (X(t1+j ), X(t2+j ), . . . , X(tr+j ))
para todo conjunto de índices (t1 , t2 , . . . , tr ) y todo j.
Esta condición resulta bastante restrictiva y por consiguiente se adoptan otras un poco más
“débiles”.
Definición 2.13. Diremos que un proceso estocástico es estacionario en sentido débil si
mantiene constantes todas sus características lo largo del tiempo, es decir, si para todo t:
µt = µ
σt2 = σ 2
Cov(t, t + j) = Cov(s, s + j) = γj j = 0, ±1, ±2, . . .
42
CAPÍTULO 2. PROCESOS ESTOCÁSTICOS
Nota 2.3. En algunos libros este tipo de estacionariedad recibe el nombre de estacionariedad
en sentido amplio o estacionariedad de segundo orden. Por otro lado, si sólo exigimos que la
función de medias sea constante se dirá que el proceso es estacionario de primer orden o en
media.
A continuación veremos un ejemplo que nos introducirá a los procesos de Wiener.
Ejemplo 2.6. Una aproximación al proceso de Wiener (o movimiento Browniano).
Sean Xi (t) para i = 1, 2, . . . , N N procesos independientes de Poisson con intensidad N . Sea
YN (t) otro proceso estocástico definido por
YN (t) =
N
X
Xi (t) − λt
√
λN
i=1
Por el teorema central del límite, cuando N aumenta YN (t) se aproxima a una variable
aleatoria con distribución normal de media 0 y varianza t.
YN (t) se aproxima a un proceso de Wiener o a un movimiento Browniano W (t) cuando
N aumenta. Un proceso de Wiener {W (t), t ≥ 0} es un proceso estocástico continuo con
incrementos estacionarios independientes de manera que
W (0) = 0 y W (t) − W (s) ∼ N (0, t − n) para todo 0 ≤ s ≤ t.
Así E(W (t)) = 0, Var(W (t) − W (s)) = t − s para todo 0 ≤ s ≤ t y, en particular,
W (t2 ) − W (t1 ) ∼ N (0, t2 − t1 ) y W (t4 ) − W (t3) ∼ N (0, t4 − t3 )
son variables aleatorias gaussianas independientes para 0 ≤ t1 < t2 ≤ t3 < t4 . Notemos que
un proceso de Wiener es un proceso de Markov homogéneo. Además W (t) representa una
variable aleatoria en cada valor de t.
Puede ser interesante ver como una trayectoria de un proceso de Wiener W (t) puede ser
generada por un número finito de puntos. Suponemos que la trayectoria de un proceso de
Wiener es descrita en el intervalo [t0 , tN ] con la sucesión de puntos {ti }N
i=0 donde t0 = 0.
Entonces W (t0 ) = 0 y la trayectoria de un proceso de Wiener en los puntos t0 , t1 , . . . , tN
viene dada por
q
W (ti ) = W (ti−1 ) + ηi−1 ti − ti−1 para i = 1, 2, . . . , N.
donde ηi−1 son N (0, 1) distribuciones normales independientes para i = 1, 2, . . . , N . Los
valores W (ti ), i = 0, 1, . . . , N determinan una trayectoria de Wiener en los puntos {ti }N
i=0 .
Otra manera interesante de generar un proceso de Wiener, la cual usa un número contable
de variables aleatorias con distribuciones normales es la expansión de Karhumen-Loève. La
expansión de Karhumen-Loéve se deriva de la serie de Fourier del proceso de Wiener y tiene
la forma
√
∞
X
2 2T
(2n + 1)πt
ηn sen(
)
W (t) =
2T
0 (2n + 1)π
43
2.3. PROCESOS DE ESTADO CONTINUO
para t ∈ [0, T ], donde ηn ∼ N (0, 1) para n = 0, 1, . . . . De hecho ηn es dada en la fórmula
anterior por
η=
(2n + 1)π Z T
(2n + 1)πt
)dt para n = 0, 1, 2, . . . .
W (t) sen(
1/2
3/2
2 T
2T
0
Veamos que la serie W (t) tiene las propiedades requeridas por el proceso de Wiener, sea
√
N
X
(2n + 1)πt
2 2T
ηn sen(
)
SN (t) =
2T
n=0 (2n + 1)π
la N -ésima suma parcial de la serie. Por la definición de espacio de Hilbert, HRV , del tema
anterior es fácil ver que Sn (t) ∈ HRV para cada t ∈ [0, T ] y que {SN (t)} es sucesión de
Cauchy en el espacio de Hilbert HRV . De hecho, como ηn ∼ N (0, 1) para cada n se tiene que
2
(t)) donde
SN (t) ∼ N (0, σN
2
σN
(t) = t −
observemos que
t=
∞
X
8T
(2n + 1)πt
sen2 (
)
2
2
2T
n=N +1 (2n + 1) π
∞
X
8T
(2n + 1)πt
sen2 (
).
2
2
2T
n=0 (2n + 1) π
Notemos que para cada t ∈ [0, T ] W (t) ∈ HRV . Además W es continua en media cuadrática
pero no posee derivada. Para ver la continuidad de W consideramos
||W (t + ∆t) − W (t)||2RV = E(W (t + ∆t) − W (t))2 = ∆t
√
Por lo que ||W (t + ∆t) − W (t)||RV = ∆t y dado > 0 existe un δ > 0 de modo que
||W (t + ∆t) − W (t)||RV < cuando ∆t < δ. Sin embargo como
||
W (t + ∆t) − W (t) 2
1
||RV =
∆t
∆t
no hay F (t) ∈ HRV tal que
||
W (t + ∆t) − W (t)
− F (t)||2RV → 0 cuando ∆t → 0.
∆t
Puede ser útil tratar el tema de la esperanza de las funciones W (t) para 0 ≤ t ≤ T . Primero
recordemos que
−(x−y)2
1
2|t|
p(t, x, y) =
para x, y ∈ R
e
(2π|t|)1/2
es la función de densidad de variables aleatorias normales con media y varianza |t|. Sea W (t)
un proceso de Wiener en [0, T ]. Claramente para t1 ∈ [0, T ] y G : R → R,
E(G(W (t1 ))) =
Z ∞
∞
G(x1 )p(t1 , x1 , 0)dx1 .
44
CAPÍTULO 2. PROCESOS ESTOCÁSTICOS
Además
P (W (t1 ) ≤ z1 ) =
Z z1
∞
p(t1 , x1 , 0)dx1 .
Ahora consideramos una partición de [0, T ], 0 = t0 ≤ t1 ≤ t2 ≤ . . . ≤ tk ≤ T . Para
G : R2 → R,
E(G(W (t1 ), W (t2 ))) =
Z ∞ Z ∞
−∞
−∞
G(x1 , x2 )p(t1 , x1 , 0)p(t2 − t1 , x2 , x1 )dx1 dx2 .
Además para G : Rk → R,
E(G(W (t1 ), W (t2 ), . . . , W (tk ))) =
Z ∞
...
Z ∞
−∞
−∞
G(x1 , . . . , xk )p(t1 , x1 , 0) . . . p(tk − tk , xk , xk−1 )dx1 . . . dxk .
Las funciones de densidades p(tm −tm−1 , xm , xm−1 ) para m = 1, 2, 3, . . . , k definen un conjunto
finito-dimensional de medidas de probabilidad en Rk . La distribución de probabilidad en esta
partición satisface
Ft1 ,t2 ,...,tk (z1 , z2 , . . . , zk ) = P (W (t1 ) ≤ z1 , . . . , W (tk ) ≤ zk ) =
Z zk Z zk−1
−∞
−∞
...
Z z1
−∞
p(t1 , x1 , 0) . . . p(tk − tk , xk , xk−1 )dx1 . . . dxk .
El proceso estocástico es el proceso de Wiener o movimiento Browniano W (t) sobre cualquier
partición de [0, T ], la distribución finita-dimensional de W (t) se reduce a la expresión anterior.
Finalmente consideramos la función de densidad p(y, t, x, s) para el proceso de Wiener de x
en tiempo s e y en tiempo t. En este caso,
p(y, t, x, s) =
−(x−y)2
1
2|t−s|
e
(2π|t − s|)1/2
claramente p(y, t, x, s) = p(y, x, |t − s|), por lo que el proceso de Wiener es un proceso de
Markov homogéneo continuo.
Ejemplo 2.7. Proceso de Wiener con Mathematica.
Con este programa que vamos a mostrar a continuación podemos dibujar dos procesos de
Wiener, las figuras 2.3 y 2.4 son el resultado del programa. También hemos dibujado la media
y la varianza de uno de ellos, véase figura 2.5.
El código utilizado es
xx = 56430.; n = 500; nrun = 200; tf = 5.; h = tf/n; hs =
Sqrt[h]; tt = Range[0, tf, h];
y3 = ConstantArray[0, {n, 1}]; y4 = ConstantArray[0, {n, 1}]; ya =
ConstantArray[0, {n, 1}]; yv = ConstantArray[0, {n, 1}];
45
2.4. GENERACIÓN DE PROCESOS ESTOCÁSTICOS
sa = 0.; sv = 0.; a = 16807; b = 2^31 - 1;
For[j = 1, j <= nrun, j++,
For[i = 1, i <= (n - 1), i++, d = IntegerPart[a*xx/b];
t = a*xx - d*b; unr = ConstantArray[0, {2, 1}]; Part[unr, 1] = t/b;
Part[unr, 2] = t/b; u1 = Part[unr, 1]; u2 = Part[unr, 2];
hlp = Sqrt[-2.*Log[u1]]; Part[unr, 1] = hlp*Cos[Pi*2.*u2];
Part[unr, 2] = hlp*Sin[Pi*2.*u2]; xx = t; a1 = 0; a2 = 0; b11 = 1;
b12 = 0; b21 = 0; b22 = 1;
Part[y3, i + 1] =
Part[y3, i] + a1*h + hs*b11*Part[unr, 1] + hs*b12*Part[unr, 2];
Part[y4, i + 1] =
Part[y4, i] + a2*h + hs*b21*Part[unr, 1] + hs*b22*Part[unr, 2];
Part[ya, i + 1] = Part[ya, i + 1] + Part[y4, i + 1]/nrun;
Part[yv, i + 1] = Part[yv, i + 1] + (Part[y4, i + 1]^2)/nrun];
sa = sa + Part[y4, n]/nrun; sv = sv + (Part[y4, n]^2)/nrun;]
5
15
4
10
3
2
5
1
100
200
300
400
Figura 2.3: Proceso de Wiener
2.4.
500
100
200
300
400
500
Figura 2.4: Proceso de Wiener
Generación de procesos estocásticos
Se suele usar números pseudo-aleatorios para simular procesos estocásticos. Primero consideramos un proceso estocástico discreto, en particular, una cadena de Markov {Xn } en
0 = t0 < t1 < t2 < . . . < tn = T donde x0 = z0 y Xn es una variable aleatoria discreta para
cada tiempo tn , n = 0, 1, . . . , N . Notemos que Xn ∈ M = {z−m , z−m+1 , . . . , zm }. Suponemos
46
CAPÍTULO 2. PROCESOS ESTOCÁSTICOS
250
200
150
100
50
100
200
300
400
500
Figura 2.5: La media (en azúl) y varianza (en rojo) del proceso de Wiener de la figura 2.4
que la matriz de transición dependiente de t viene dada por

Pn =










(n)
(n)
p−m,−m
p−m,−m+1 . . .
(n)
(n)
p−m+1,−m p−m+1,−m+1 . . .
..
..
..
.
.
.
(n)
(n)
pm−1,−m pm−1,−m+1 . . .
(n)
(n)
...
pm,−m
pm,−m+1
(n)
(n)
p−m,m−1
p−m,m
(n)
(n)
p−m+1,m−1 p−m+1,m
..
..
.
.
(n)
pm−1,m−1
(n)
pm,m−1






,


(n)
pm−1,m 

(n)
pm,m
(n)
donde pi,j = P {Xn+1 = zj |Xn = zi }. Consideremos la siguiente trayectoria {Xn , 0 ≤ n ≤
(0)
N } donde en t0 , X0 = z0 . Para encontrar X1 tenemos que calcular primero p0,j para j =
−m, −m + 1, . . . , m. El siguiente paso es generar un número pseudo-aleatorio de distribución
uniforme en [0, 1], η0 , y calcular un r0 que cumpla que
rX
0 −1
(0)
p0,j < η0 ≤
j=−m
r0
X
(0)
p0,j .
j=−m
(1)
Finalmente igualamos X1 a zr0 . Para encontrar X2 tenemos que calcular primero pr0 ,j para
j = −m, −m + 1, . . . , m. Entonces como antes generamos una distribución uniforme η1 en
[0, 1] y calculamos r1 de modo que
rX
1 −1
j=−m
(0)
pr0 ,j < η1 ≤
r1
X
(0)
pr0 ,j .
j=−m
Entonces igualamos X2 a zr1 . Repitiendo estos pasos N veces obtendremos una ordenación
de {Xk }N
k=0 del proceso estocástico.
Ahora consideramos una trayectoria para una cadena de Markov continua {X(t), t ∈ [0, T ]}.
Generalmente las trayectorias de los procesos continuos son determinadas como un conjunto
discreto de tiempos, es decir, una trayectoria X(t) es calculada en los tiempos t0 , t1 , . . . , tN
2.4. GENERACIÓN DE PROCESOS ESTOCÁSTICOS
47
donde 0 = t0 < t1 < t2 < . . . < tN = T . De esta manera X(t) puede ser aproximado entre
estos puntos, usando por ejemplo interpolación lineal a trozos.
Ejemplo 2.8. Simulación de un proceso de Poisson.
Consideremos un proceso de Poisson X(t) con intensidad λ. Recordemos que el proceso X(t)
es igual al número de observaciones en tiempo t donde la probabilidad de una observación
en tiempo ∆t es igual a λ∆t + o((∆t)2 ). Del ejemplo 1.3, vimos que
P (X(t) = n) = e−λt
(λt)n
n!
Consideremos ahora este proceso continuo en los tiempos discretos tk = kh para k =
0, 1, 2, . . . , N donde h = T /N .Sea
X(tk+1 ) = X(tk ) + ηk para k = 0, 1, . . . , N − 1, donde Xt0 = 0
y los números aleatorios ηk son elegidos de forma que
P (ηk = n) = e−λh
(λh)n
para n = 0, 1, 2, . . . .
n!
Por lo tanto X(tk ) son distribuciones de Poisson con intensidad λ en los tiempos discretos
t0 , t1 , . . . , tN . Notemos que para encontrar ηk dada una distribución uniforme ηk en [0, 1]
utilizamos la siguiente relación
ηX
k −1
j=0
e−λh
ηk
X
(λh)j
(λh)j
< ηk ≤
e−λh
.
j!
j!
j=−0
Ejemplo 2.9. Simulación de la trayectoria de un proceso de Wiener.
Consideremos un proceso de Wiener W (t) en [0, T ]. Como antes simulamos este proceso en
los tiempos continuos tk = kh para k = 0, 1, 2, . . . , N donde h = T /N y sea
X(tk+1 ) = X(tk ) + ηk para k = 0, 1, . . . , N − 1,
donde Xt0 = 0 y ηk son distribuciones uniformes normales con media 0 y varianza h. Cada
trayectoria del proceso continuo se calcula en los tiempos discretos t0 , t1 , . . . , tN . Así W (tk ) =
X(tk ) para k = 0, 1, 2, . . . , N . Para estimar W (t) en algún tiempo t 6= tk para algún k,
podemos usar una interpolación lineal continua como por ejemplo
W (t) ≈ X(tk )
tk+1 − t
t − tk
+ X(tk+1 )
para tk ≤ t ≤ tk+1 .
h
h
Ejemplo de un proceso estocástico real
Los procesos estocásticos son comunes en física, biología, meteorología y finanzas. Un ejemplo
clásico de proceso estocástico físico es el decaimiento que consiste en que átomos de isotopos
48
CAPÍTULO 2. PROCESOS ESTOCÁSTICOS
inestables se transforman en otros isotopos. Supongamos que tenemos inicialmente n0 átomos
en un isotopo radiactivo y suponemos también que λ es la constante de decadencia de los
isotopos. Esto significa que la probabilidad que probabilidad de que un átomo se transforme
en un pequeño intervalo de tiempo ∆t es de λ∆t + O((∆)2 ). Sea N (t) el número de átomos
en un tiempo t y sea pn (t) la probabilidad de que halla n átomos también en un tiempo t.
Entonces podemos obtener que
p0 (t + ∆t) = p0 (t)(1 − λn ∆t),
pn (t + ∆t) = pn+1 (t)λ(n + 1)∆t + pn (t)(1 − λn∆t) + O((∆t)2 ).
Haciendo ∆ → 0 obtenemos

 dpn0 (t)

dt
dpn (t)
dt
= −λn0 pn0 (t)
para pn0 (0) = 1
y
= −λnpn (t) + λ(n + 1)pn+1 (t) con pn (0) = 0 para 0 ≤ n < n0 .
Podemos calcular el número esperado de átomos como
n0
X
n0
dE(N (t)) X
dpn (t)
E(N (t)) =
npn (t) y
=
n
.
dt
dt
n=0
n=0
Y
nX
n0
n0
0 −1
dE(N (t)) X
dpn (t) X
λn(n + 1)pn+1 (t)
n
−λ2 pn (t) +
=
=
dt
dt
n=0
n=0
n=0
=
=
n0
X
n=0
n0
X
−λ2 pn (t) +
nX
0 −1
λ(n − 1)pn+1 (t)
n=1
−λnpn (t) = −λE(N (t)).
n=0
Por lo tanto,
Así E(N (t)) = n0 e−λt
dE(N (t))
= −λE(N (t)) con E(N (t)) = n0 .
dt
es el número esperado de átomos en el tiempo t.
Capítulo 3
El modelo de Black y Scholes
3.1.
Introducción
En este capítulo introducimos el modelo básico de las matemáticas financieras, el modelo
de Black y Scholes, y presentamos la famosa fórmula de valoración de opciones europeas de
compra (call option) y de venta (put option). También hablaremos de la fórmula de Itô, una
herramienta matemática necesaria para las finanzas (véase [6]).
Modelización matemática en finanzas
Suponemos que tenemos un mercado financiero con dos posibilidades de inversión:
Un activo sin riesgo, caja de ahorros o cuenta corriente, llamado bono, que paga un
interés instantáneo de tasa r ≥ 0. Notemos que su evolución sigue la siguiente ecuación
diferencial
dBt
= rdt B0 = 1,
Bt
cuya solución es
Bt = ert .
Un activo de riesgo, aleatorio, que designamos mediante
St = S0 eXt ,
donde {Xt } es un proceso estocástico en un espacio de probabilidad (Ω, F, P ) que
cumple que X0 = 0.
Opciones
En este apartado vamos a introducir una tercera alternativa de inversión denominada opción,
que es un contrato que paga f (ST ) (con f una función) en el instante T a su poseedor.
Notemos que
49
50
CAPÍTULO 3. EL MODELO DE BLACK Y SCHOLES
Al activo S se le llama subyacente.
Si f (x) = (x − k)+ , donde k es el precio acordado en T , tenemos una opción de compra
(call option).
Si f (x) = (k − x)+ tenemos una opción de venta (pull option).
Si T es fijo (tiene que estar estipulado en el contrato) la opción es europea.
Si T puede ser elegido por el poseedor del contrato la opción es americana.
3.2.
El modelo de Black y Scholes
El modelo de Black y Scholes es de tiempo continuo t ∈ [0, T ] y consta de dos activos:
B = (Bt )t∈[0,T ] que evoluciona en forma determinística según la ley
dBt
= rdt, B0 = 1,
Bt
donde r es la tasa de interés por unidad de tiempo y B representa un bono (bond).
El precio de la acción (stock) S = (St )t∈[0,T ] es de evolución aleatoria (o contingente) y
sigue la siguiente ecuación diferencial
dSt
= µdt + σdW, S0 = x,
St
donde
• µ es el retorno medio del activo con riesgo (la media).
• σ la volatidad (capacidad de variación en los precios que tiene un activo respecto
a su media).
• W es un movimiento Browiano.
Ahora tenemos que dar una sentido (aunque sea práctico) a la expresión dW .
Fórmula de Itô
Para valorar opciones debemos desarrollar una herramienta fundamental en las finanzas que
es la fórmula de Itô, la cual es una generalización de la regla de la cadena del cálculo usual
de funciones.
Antes de nada tenemos que conseguir dar sentido y generalizar la igualdad
(dW )2 = dt.
51
3.3. PROCESO DE WIENER ECONÓMICO
Para ello consideramos f : R −→ R una función con derivadas continuas (regular) cuyo
desarrollo de Taylor es
1
f (x) − f (x0 ) = f 0 (x0 )∆x + f 00 (x0 )(∆x)2 + . . .
2
Habitualmente el segundo término se desprecia frente al primero, pero si x = Wt y x0 = Wt0
tenemos que
(∆x)2 = (∆W )2 ∼ ∆t,
y el aporte no se desprecia frente al primer sumando (los otros términos son efectivamente
de mayor orden).
Sea ahora f = f (x, t) una función regular de dos variables, argumentando de manera similar
que antes (aunque no lo veremos) se tiene que
f (Wt , t) − f (W0 , 0) =
Z t
0
fx (Ws , s)dWs +
Z t
0
1Z t
ft (Ws , s)ds +
fxx (Ws , s)ds
2 0
que es la fórmula de Itô. Sintéticamente tenemos
1
df (Wt , t) = fx (Wt , t)dWt + fxx (Wt , t)dt + ft (Wt , t)dt.
2
Nota 3.1. La primera integral (llamada integral estocástica)
se como un límite de sumas del tipo
n−1
X
Rt
0
fx (Ws , s)dWs , debe entender-
fx (Wti )(Wti+1 − Wti ).
i=0
Ejemplo 3.1. Sea f (x) = x2 . Tenemos que
ft = 0, fx = f 0 = 2x, fxx = f 00 = 2.
Por lo tanto resulta que
f (Wt ) − f (W0 ) = Wt2 =
Z t
0
Nota 3.2. No tenemos que confundir
el resultado seria (Wt )2 y no es así.
3.3.
(2Ws )dWs +
Rt
0 (2Ws )dWs
Z t
1Z t
2ds = (2Ws )dWs + t.
2 0
0
con una integral normal ya que de ser así
Proceso de Wiener económico
En 1900, L. Bachelier introdujo un modelo del movimiento Browniano que propone que las
acciones evolucionan como
Lt = L0 + σWt + γt,
52
CAPÍTULO 3. EL MODELO DE BLACK Y SCHOLES
donde Wt es un proceso de Wiener, Lt el precio de la acción en el tiempo t y σ, γ constantes.
Notemos que Lt puede tomar valores negativos.
En 1965 P. Samuelson propone el siguiente modelo
Gt = G0 eσWt +γt ,
para los precios de la acción en un tiempo t. A G se le llama movimiento Browniano o
geométrico. Veamos que esta definición verifica la formula del activo con riesgo S en el
modelo de Black y Scholes. Como G es función de W podemos aplicar la fórmula de Itô.
Considerando
f (x, t) = G0 eσx+γt ,
tenemos que
Gt = f (Wt , t).
Las derivadas parciales de f (x, t) son
fx (x, t) = σf (x, t), fx x(x, t) = σ 2 f (x, t), ft (x, t) = γf (x, t),
por lo que
1
dGt = df (Wt , t) = σGt dWt + σ 2 Gt dt + γGt dt,
2
y dividiendo por Gt se tiene
dGt
1
= (γ + σ 2 )dt + σdWt
Gt
2
= µdt + σdWt ,
con µ = γ + 12 σ 2 .
Es decir el proceso de Wiener económico verifica la definición del activo con riesgo en el
modelo de Black y Scholes.
Como µ = γ + 12 σ 2 la fórmula para S es
1
2
St = S0 eσWt +(µ− 2 σ )t .
3.4.
Valoración de opciones
Antes de nada debemos introducir la definición de portafolio.
Definición 3.1. Un portafolio en un modelo de Black y Scholes es un par de procesos
estocásticos π = (at , bt ) que representa la cantidad de bonos at y la cantidad de acciones bt
de un agente en cada instante t. El valor de un portafolio π en el instante t es
Vtπ = at Bt + bt St .
53
3.4. VALORACIÓN DE OPCIONES
Para calcular el precio V (S0 , T ) de una opción europea que se paga f (St ), Black y Scholes
propusieron construir un portafolio que sea equivalente a poseer la opción. Propusieron que
replique la opción y que sea autofinanciante. Cuando existe el portafolio decimos que el
modelos es completo.
Veamos en detalle lo que queremos decir:
Replique la opción, es decir, en el momento de ejecución de la opción el portafolio iguale
en capital a la opción.
VTπ = aT BT + bT ST = f (ST ).
Sea autofinanciante, es decir, la variación de capital es producto únicamente de las
variaciones de los precios de los activos B y S. Matemáticamente esto se formula de la
siguiente manera
dVtπ = at dBt + bt dSt .
El precio de la opción se define entonces como el precio del portafolio autofinanciante en
t = 0, es decir
V (S0 , T ) = a0 B0 + b0 S0 .
Construcción del portafolio
Black y Scholes demostraron que el portafolio replicante y autosuficiente es único, determinando entonces un precio racional para la opción.
Para encontrarlo, buscamos una función H(x, t) tal que
Vtπ = H(St , t).
La condición de réplica es VTπ = f (ST ), lo que se logra si
H(x, t) = f (x).
Como el portafolio y la opción son equivalentes, el precio de la opción sera el capital necesario
para comprar el portafolio en t = 0, es decir
V (S0 , T ) = H(S0 , 0).
Para determinar H y π = (at , bt ) de manera que
Vtπ = at Bt + bt St H(St , t),
comenzamos calculando el diferencial de V de dos formas distintas para igualar el resultado.
Primero como S es función de W , y H es función de S podemos aplicar la formula de Itô,
resultando
1
1
dVtπ = dH = Hx dS + Hxx dt + Ht dt = (µSHx + σ 2 S 2 Hxx + Ht ) + Hx SσdW.
(3.1)
2
2
54
CAPÍTULO 3. EL MODELO DE BLACK Y SCHOLES
Nota 3.3. Para calcular la ecuación anterior tener en cuenta que (dS)2 = σ 2 S 2 (dW )2 y que
(dW )2 = dt.
Por otra parte como π es autosuficiente y at Bt = Ht − Bt St tenemos que
dVtπ = adB + bdS = raBdt + b(µSdt + σSdW )
= r(H − bS)dt + µbSdt + bSσdW
(3.2)
= (rH + (µ − r)bS)dt + bSσdW.
Igualando los coeficientes de dW en 3.1 y 3.2 obtenemos que
bt = Hx (St , t).
3.5.
La ecuación de Black-Scholes
Utilizando que bt = Hx (St , t) e igualando (3.1) y (3.2) se tiene que
1
rsHx + σ 2 S 2 Hxx + Ht = rH.
2
Además, para que sea réplica, se tiene que H(ST , T ) = f (ST ). Si ambas condiciones se
verifican para todos los valores posibles x que toma el activo, se tiene
1 2 2
σ x Hxx (x, t) + rxHx (x, t) + Ht (x, t) = rH(x, t)
2


H(x, T ) = f (x).



Esto es la ecuación de Black-Scholes. Es una ecuación diferencial en derivadas parciales. La
condición de réplica es la condición inicial o de frontera. La condición que obtuvimos primero:
bt = Hx (St , t),
nos da la cantidad de acciones necesarias para replicar la opción.
La solución de la ecuación diferencial viene dada por
H(x, t) = xΦ(x1 (x, t)) − erT KΦ(x2 (x, t)),
con
T −t
x1 (x, t) =
log xeK
− 1 σ 2 (T − t)
√ 2
,
σ T −t
T −t
log xeK
+ 1 σ 2 (T − t)
√ 2
.
σ T −t
Entonces el valor de la opción que corresponde a t0 es
x2 (x, t) =
V (S0 , T ) = S0 Φ(x1 ) − erT KΦ(x2 )
3.5. LA ECUACIÓN DE BLACK-SCHOLES
con
55
T
log S0Ke − 12 σ 2 (T )
√
x1 =
,
σ T
T
log S0Ke + 12 σ 2 (T )
√
x2 =
.
σ T
Importancia de la fórmula de Black-Scholes
El detalle clave es que la solución no depende de µ, el rendimiento del activo subyacente a la
opción, los parámetros que aparecen son r y σ. Para aplicar la formula se tiene que:
r se obtiene de bonos (preferentemente en la misma moneda) con vencimiento (plazo
de vida de una activo financiero) T .
σ no es observable, se calcula (en general) a partir de precios de opciones, es la volatilidad implícita.
56
CAPÍTULO 3. EL MODELO DE BLACK Y SCHOLES
Bibliografía
[1] R. B. Ash: Real Analysis and Probability, Academic Press, Inc. Londres, 1972.
[2] E. J. Allen: Random selection of 3-digits numbers, Mathematical Spectrum 33
(2000/2001), 8–10.
[3] E. J. Allen: Modeling with Itô stochastic differential equations, Springer, The Netherlands, 2007.
[4] R. Durrett: Probability. Theory Examples, Cambridge University Press, Cambridge,
2010.
[5] G. B. Folland: Real Analysis. Modern techniques and their applications, John Wiley
& Sons, Nueva York, 1984.
[6] E. Mordecki: Modelos matemáticos en finanzas: Valuación de opciones. 1998. Curso de
actualización para egresados. UPAE, Facultad de Ciencias Económicas y Administración,
http://www.cmat.edu.uy/~mordecki/courses/upae/upae-curso.pdf
[7] S. Pérez-Cacho, F. M. Gómez y J. M. Marbán: Modelos matemáticos y procesos
dinámicos: un primer contacto, Servicio Publicaciones Univ. Valladolid, 2002.
[8] L. J. Rodríguez-Aragón: Simulación, Método de Montecarlo. Área de Estadística
e Investigación Operativa, Universidad de Castilla-La Mancha, http://www.uclm.es/
profesorado/licesio/Docencia/mcoi/Tema4_guion.pdf
[9] S. Weinzierl: Introduction to Monte Carlo methods, arXiv:hep-ph/0006269.
57
58
BIBLIOGRAFÍA