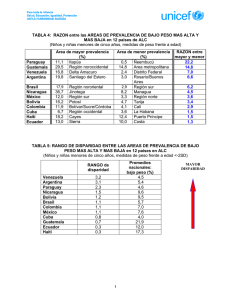
DESARROLLO DE HERRAMIENTAS DE APOYO A LA

Universidad Autónoma de Madrid
Escuela politécnica superior
Proyecto fin de carrera
DESARROLLO DE HERRAMIENTAS
DE APOYO A LA ESTEREOVISIÓN
Ingeniería de Telecomunicación
Alberto Garzón Leo
JULIO 2010
DESARROLLO DE HERRAMIENTAS
DE APOYO A LA ESTEREOVISIÓN
AUTOR: Alberto Garzón Leo
TUTOR: Jesús Bescós Cano
Dpto. de Ingeniería Informática
Escuela Politécnica Superior
Universidad Autónoma de Madrid
JULIO 2010
i
Resumen
Resumen
El contexto de este proyecto es el conjunto de técnicas orientadas a la reconstrucción de
escenas en 3D con el fin de permitir aplicar sobre ellas técnicas tradicionales de análisis 2D
(segmentación, seguimiento, detección, reconocimiento, etc.). El estudio comenzará utilizando
dos cámaras Firewire 1394 situadas en la pasarela de la tercera planta entre los edificios A y B
de la EPS. Posteriormente se ampliará el estudio a cámaras IP y a un mayor número de cámaras.
Su objetivo es un conjunto de herramientas capaces de extraer la información de profundidad
de los objetos en una escena a tiempo real tomada desde varias a vistas para posteriormente ser
añadida a otras técnicas de análisis con el fin de disponer de información imposible de conseguir
con una única cámara.
Palabras Clave
Disparidad, estereovisión, 3D, profundidad, Birchfield, tiempo real.
iii
Desarrollo de herramientas de apoyo a la estereovisión
Abstract
The context of this project is the set of tecniques oriented to the 3D scenes reconstruction
in order to allow to apply over them 2D analysis traditional tecnics (segmentation, tracking,
detection, recognition, etc.). The study will start using two Firewire 1394 cameras placed in
the third floor gateway between the A and B EPS buildings. Lately the study will grow to IP
cameras and a highest number of cameras.
His objective is a set of tools capable to extract the disparity information in real time from
the objects of a scene taked from many views to add it to other analysis techniques in order to
handle information imposible to achieve with a single camera.
Key words
Disparity, stereovision, 3D, depth, Birchfield, real time.
iv
Agradecimientos
A mis padres, que tanto me han apoyado ahora y siempre en todo lo que he hecho o intentado.
En especial va dedicado a vosotros.
A mi hermana, por darme siempre esa visión más optimista al enfrentarme a un problema. No
cambies nunca
A Miriam, por escuchar con interés cada día sobre todas estas cosas y brindarme su confianza.
A mi tutor, Jesús Bescós, por ayudarme en todo lo que necesité.
A los compañeros del laboratorio, en especial a Álvaro, que respondieron y me ayudaron
pacientemente en mis preguntas y problemas de novato.
A Pablo, Guillermo y Bruno, por compartir alegrías y frustraciones durante estos últimos años.
Al resto de gente que debería estar aquí y no está, familiares y amigos. Por saber que estáis ahí.
v
Desarrollo de herramientas de apoyo a la estereovisión
vi
CAPÍTULO 0. AGRADECIMIENTOS
Índice general
Agradecimientos
v
índice de figuras
x
xiii
índice de cuadros
1. Introducción
1
1.1. Motivación del proyecto . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
1
1.1.1. Aplicaciones de un sistema de estereovisión . . . . . . . . . . . . . . . . .
1
1.1.2. Restricciones básicas de un sistema de estereovisión . . . . . . . . . . . . .
2
1.2. Objetivos . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
2
1.3. Estructura de la memoria . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
3
2. Revisión de conceptos básicos
5
2.1. Introducción a la geometría proyectiva . . . . . . . . . . . . . . . . . . . . . . . .
5
2.2. Coordenadas homogéneas . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
6
2.2.1. Representación homogénea de una recta . . . . . . . . . . . . . . . . . . .
6
2.2.2. Representación homogénea de un punto . . . . . . . . . . . . . . . . . . .
6
2.2.3. El punto impropio y la línea del infinito . . . . . . . . . . . . . . . . . . .
6
2.3. El plano proyectivo P 2 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
7
2.4. Transformaciones proyectivas en 2D
. . . . . . . . . . . . . . . . . . . . . . . . .
7
2.5. Transformaciones proyectivas en 3D
. . . . . . . . . . . . . . . . . . . . . . . . .
8
2.6. Análisis de la geometría asociada al proceso de captación . . . . . . . . . . . . . .
9
2.6.1. El modelo pin-hole . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
9
2.6.2. La matriz de proyección . . . . . . . . . . . . . . . . . . . . . . . . . . . .
11
2.7. Análisis de la geometría de visión múltiple . . . . . . . . . . . . . . . . . . . . . .
13
2.7.1. La matriz esencial . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
14
2.7.2. La matriz fundamental . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
15
vii
Desarrollo de herramientas de apoyo a la estereovisión
3. Disparidad
17
3.1. Introducción . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
17
3.2. Rectificación
17
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
3.3. Métodos de cálculo de la disparidad
. . . . . . . . . . . . . . . . . . . . . . . . .
21
3.3.1. Búsqueda por zonas . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
23
3.3.2. Birchfield-Tomasi . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
24
3.4. Relación entre disparidad y profundidad . . . . . . . . . . . . . . . . . . . . . . .
26
4. Sistema, diseño y desarrollo
29
4.1. Sistema físico . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
29
4.1.1. Cámaras Firewire . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
29
4.1.2. Cámaras IP . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
30
4.2. Captura y sincronización . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
31
4.3. Límites
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
32
4.3.1. Precisión . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
33
4.4. Calibración y cálculo de matrices de rectificado . . . . . . . . . . . . . . . . . . .
34
4.5. Rectificado . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
35
4.6. Disparidad . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
36
4.6.1. Birchfield-Tomasi . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
36
4.6.2. Búsqueda por bloques . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
36
4.7. Profundidad . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
36
4.8. Funcionamiento . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
37
5. Experimentos Realizados y Resultados
5.1. Análisis de la velocidad
39
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
39
5.1.1. Pruebas con el método de búsqueda por zonas . . . . . . . . . . . . . . . .
39
5.1.2. Pruebas con el método de Birchfield-Tomasi . . . . . . . . . . . . . . . . .
44
5.2. Analisis de la precisión . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
45
5.2.1. Pruebas con el método de búsqueda por zonas . . . . . . . . . . . . . . . .
47
5.2.2. Pruebas con el método de Birchfield . . . . . . . . . . . . . . . . . . . . .
54
5.3. Comparativa de resultados con el estado del arte . . . . . . . . . . . . . . . . . .
54
viii
ÍNDICE GENERAL
Desarrollo de herramientas de apoyo a la estereovisión
6. Conclusiones y trabajo futuro
57
6.1. Conclusiones sobre los sistemas físicos . . . . . . . . . . . . . . . . . . . . . . . .
57
6.2. Conclusiones sobre la restricción temporal . . . . . . . . . . . . . . . . . . . . . .
58
6.3. Conclusiones sobre la restricción de alineación . . . . . . . . . . . . . . . . . . . .
58
6.4. Conclusiones sobre el cálculo de disparidad mediante búsqueda por bloques . . .
58
6.4.1. Suma de Diferencias Absolutas . . . . . . . . . . . . . . . . . . . . . . . .
58
6.4.2. Suma de Diferencias Cuadráticas . . . . . . . . . . . . . . . . . . . . . . .
59
6.4.3. Correlación Cruzada Normalizada . . . . . . . . . . . . . . . . . . . . . . .
59
6.5. Conclusiones sobre el cálculo de disparidad mediante el método de Birchfield . . .
59
A. Presupuesto
63
B. Pliego de condiciones
65
C. Manual de utilización
69
ÍNDICE GENERAL
ix
Índice de figuras
1.1. Par estereo comercial . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
2
2.1. Proyección de una escena . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
5
2.2. Modelo del plano proyectivo . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
7
2.3. Transformación 3D Euclídea . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
8
2.4. Modelo de una cámara pin-hole . . . . . . . . . . . . . . . . . . . . . . . . . . . .
9
2.5. Geometría epipolar . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
13
3.1. Esquema del proceso de rectificado . . . . . . . . . . . . . . . . . . . . . . . . . .
18
3.2. Variantes en la construcción de la imagen del espacio de disparidad . . . . . . . .
22
3.3. Representación del problema de cálculo de disparidad mediante corte de grafos .
22
3.4. Definición de la región de búsqueda y de las ventanas . . . . . . . . . . . . . . . .
24
3.5. Ejemplo de una secuencia de correspondencias . . . . . . . . . . . . . . . . . . . .
25
3.6. Imagen del espacio de disparidad y posiciones permitidas tras una correspondencia
dada . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
25
3.7. Vista superior del sistema estéreo . . . . . . . . . . . . . . . . . . . . . . . . . . .
26
4.1. Sistema de cámaras Firewire
. . . . . . . . . . . . . . . . . . . . . . . . . . . . .
30
4.2. Sistema de cámaras IP . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
30
4.3. Estado inicial de la sincronización . . . . . . . . . . . . . . . . . . . . . . . . . . .
31
4.4. Estado final de la sincronización . . . . . . . . . . . . . . . . . . . . . . . . . . . .
32
4.5. Ejemplo de imagen usada en la calibración de las cámaras IP . . . . . . . . . . .
34
4.6. Ejemplo de imágenes rectificadas con y sin desplazamiento . . . . . . . . . . . . .
35
4.7. Verificación de la rectificación . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
35
4.8. Ejemplo de funcionamiento del sistema de profundidad . . . . . . . . . . . . . . .
36
5.1. Ejemplo de escena evaluada . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
40
5.2. SAD con ventana de 3x3 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
41
xi
Desarrollo de herramientas de apoyo a la estereovisión
xii
5.3. SAD con ventana de 5x5 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
41
5.4. SSD con ventana de 3x3 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
42
5.5. SSD con ventana de 5x5 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
43
5.6. NCC con ventana de 3x3 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
44
5.7. NCC con ventana de 5x5 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
44
5.8. Imágenes izquierda y derecha del conjunto Cones . . . . . . . . . . . . . . . . . .
45
5.9. Imágenes izquierda y derecha del conjunto Teddy . . . . . . . . . . . . . . . . . .
46
5.10. Disparidad real de Cones . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
46
5.11. Disparidad real de Teddy . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
47
5.12. Resultados con SAD para un tamaño de 3x3, conjunto Cones . . . . . . . . . . .
47
5.13. Resultados con SAD para un tamaño 5x5, conjunto Cones . . . . . . . . . . . . .
48
5.14. Resultados con SAD para un tamaño de 3x3, conjunto Teddy . . . . . . . . . . .
48
5.15. Resultados con SAD para un tamaño de 5x5, conjunto Teddy . . . . . . . . . . .
49
5.16. Resultados con SSD para un tamaño de 3x3, conjunto Cones
. . . . . . . . . . .
50
5.17. Resultados con SSD para un tamaño 5x5, conjunto Cones . . . . . . . . . . . . .
50
5.18. Resultados con SSD para un tamaño de 3x3, conjunto Teddy . . . . . . . . . . .
51
5.19. Resultados con SSD para un tamaño de 5x5, conjunto Teddy . . . . . . . . . . .
51
5.20. Resultados con CNN para un tamaño de 3x3, conjunto Cones . . . . . . . . . . .
52
5.21. Resultados con CNN para un tamaño 5x5, conjunto Cones . . . . . . . . . . . . .
52
5.22. Resultados con CNN para un tamaño de 3x3, conjunto Teddy . . . . . . . . . . .
53
5.23. Resultados con CNN para un tamaño de 5x5, conjunto Teddy . . . . . . . . . . .
53
5.24. Resultados con Birchfield, conjunto Cones . . . . . . . . . . . . . . . . . . . . . .
54
5.25. Resultados con Birchfield, conjunto Teddy . . . . . . . . . . . . . . . . . . . . . .
54
ÍNDICE DE FIGURAS
Índice de cuadros
5.1. SAD 800x600 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
40
5.2. SAD 640x480 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
40
5.3. SAD 320x240 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
40
5.4. SSD 640x480 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
42
5.5. SSD 320x240 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
42
5.6. NCC 640x480 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
43
5.7. NCC 320x240 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
43
5.8. Resultados del método de Birchfield . . . . . . . . . . . . . . . . . . . . . . . . .
45
5.9. Resultados con SAD . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
49
5.10. Resultados con SSD . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
51
5.11. Resultados con CNN . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
53
5.12. Resultados con Birchfield . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
54
xiii
1
Introducción
1.1.
Motivación del proyecto
Un sistema de adquisición de imágenes con una cámara fija relaciona una escena del espacio
tridimensional con los datos captados en una serie o secuencia de imágenes bidimensionales. Sin
embargo, una imagen bidimensional no da una información suficiente en cuanto a la profundidad
de los objetos de la escena, ya que esa información se pierde al proyectarse todos los puntos de
una línea que pase por el centro óptico de la cámara sobre un mismo píxel.
Si en vez de disponer de una única secuencia tenemos las imágenes de un mismo espacio
tomadas de dos o más cámaras o distintos puntos de vista, es posible utilizar esta información
para reconstruir, total o parcialmente, la escena que se ha grabado. Si las cámaras están dispuestas de modo similar a nuestros ojos, es decir, con sus ejes ópticos paralelos, esta técnica se
denomina estereovisión y a las cámaras así situadas se las denomina par estéreo.
La estereovisión surge, no sólo como un paso natural en la evolución de la visión computacional al imitar el sistema visual humano, sino como una forma de poder obtener información
adicional de la escena que con una única secuencia es imposible de conseguir.
1.1.1.
Aplicaciones de un sistema de estereovisión
La información obtenida de un par estéreo permite realizar mapas de entorno de las cámaras,
seguimientos de objetos concretos para aplicaciones de videoseguridad, obtener la posición de
la cámara respecto a objetos que la rodeen o facilitar la navegación por su entorno de un robot
móvil.
Los resultados obtenidos en este proyecto no sólo tienen valor de forma aislada, sino que
introducidos en sistemas de análisis y procesado de imagen ya existentes, como segmentación,
seguimiento, detección o reconocimiento permiten dotarlos de parámetros e información adicional.
1
Desarrollo de herramientas de apoyo a la estereovisión
1.1.2.
Restricciones básicas de un sistema de estereovisión
A lo largo de este proyecto se hará uso de la disparidad. La disparidad no es más que diferencia
de coordenadas de puntos correspondientes en ambas imágenes. Para poder calcular esta medida
es necesario que las sigan una alineación espacial: sus ejes ópticos deben ser paralelos y sus
planos de imagen coplanares. Varias empresas de visión computacional ofrecen pares estereos
cuyo proceso constructivo integrado cumple todas las restricciones de alineación.
Figura 1.1: Par estereo comercial
Este proyecto se llevará a cabo utilizando dos cámaras individuales, lo cual hace imposible
un alineamiento perfecto por razones mecánicas. Por tanto, la restricción de alineamiento deberá
hacerse mediante software, con transformaciones de los planos de imagen. Este proceso se conoce
como rectificación. La des-rectificación posterior hace necesario el uso de interpolación para
rellenar posibles píxeles blancos, incurriendo en errores. Los concepto de disparidad y rectificado,
sus necesidades e implicaciones en el proyecto serán explicadas con más detalle en el capítulo 3
del mismo.
La imposición más importante de un par estéreo es la restricción temporal. Cuando comparemos imágenes capturadas en instantes distintos de tiempo, estaremos incluyendo errores en el
sistema, tanto mayores cuanto mayor sea la velocidad de movimiento de la escena. Para poder
cumplir este requisito se estudiará el nivel de sincronización del sistema de captura; si no cumple
con una diferencia máxima temporal entre la misma imagen de ambas cámaras, se le aplicará
un método de corrección temporal mediante disparadores.
1.2.
Objetivos
El objetivo principal de este proyecto es el desarrollo de un sistema que permita la construcción de un mapa de profundidad, en tiempo real, de una escena grabada por dos cámaras.
Se estudiará primeramente la implementación del sistema sobre dos cámaras con interfaz
Firewire o IEEE 1394 situadas en la pasarela de la tercera planta entre los edificios A y B de la
Escuela Politécnica Superior (EPS). Posteriormente se ampliará el estudio a cámaras IP.
A lo largo del desarrollo del proyecto se han contemplado otros objetivos secundarios, basados principalmente en las posibilidades de obtener un sistema en tiempo real en función de la
sincronización temporal, el alineamiento físico y los métodos de cálculo de la disparidad.
Desarrollo de un sistema de adquisición sincronizada para varias cámaras IP y Firewire.
Estudio de las posibilidades para la rectificación de las imágenes de cada cámara.
2
CAPÍTULO 1. INTRODUCCIÓN
Desarrollo de herramientas de apoyo a la estereovisión
Estudio de los diferentes métodos de cálculo de la disparidad.
1.3.
Estructura de la memoria
La estructura de este PFC se organiza como sigue:
En el capítulo 2 se presenta una revisión a los conceptos básicos de geometría proyectiva
relacionados con el proceso de captación de las imágenes y de la geometría de captación múltiple.
Así mismo se introduce la notación que se utilizará durante todo el proyecto.
En el capítulo 3 se describe un estudio sobre los distintos métodos del cálculo de la disparidad.
El cálculo de un mapa de disparidad se presenta como un paso previo para la obtención de la
profundidad de la escena, ya que disparidad y profundidad siguen una relación inversa y conocida.
El motivo de realizar este paso previo a la obtención de la profundidad se debe a que en el campo
de la disparidad hay muchos métodos e implementaciones ya estudiados.
En el capítulo 4 se explica el desarrollo de los sistemas de captura para los modelos de cámara
presentados anteriormente a partir de los existentes en el grupo de trabajo. Se hará un análisis
crítico del estado de sincronización de las cámaras y una corrección de los tiempos de captura
en caso de ser necesaria.
Así mismo se explicará la necesidad de calibrar las cámaras, ya que es el mecanismo que nos
permite saber en qué forma los objetos del mundo real se proyectan en el plano de imagen, así
como el método utilizado tanto en las cámaras Firewire como en las IP.
Por último, se detalla el sistema de cálculo de la profundidad y su implementación final, así
como su funcionamiento.
En el capítulo 5 se evalúan los resultados obtenidos de las diferentes pruebas realizadas.
En el capítulo 6 se detallan las conclusiones del proyecto y las posibles líneas de trabajo
futuro.
CAPÍTULO 1. INTRODUCCIÓN
3
2
Revisión de conceptos básicos
Este capítulo está centrado en la descripción de los conceptos de geometría proyectiva usados
en el proceso de captación de la imagen y en la modelización matemáticas de las cámaras. Este
estudio se ampliará para abarcar las particularidades de un sistema de captación con múltiples
cámaras
2.1.
Introducción a la geometría proyectiva
Una forma muy intuitiva de acercarse a las leyes que rigen la geometría proyectiva es el
problema del pintor. Si pensamos en los haces de luz que parten de los objetos visibles de una
escena hacia el ojo del pintor y colocamos una pantalla transparente entre ambos obtendremos
una colección de puntos que definen la proyección de la escena. Esto es lo que debe reproducir
el pintor para dar la sensación a los demás de ver lo que él está viendo.
Figura 2.1: Proyección de una escena
Esta geometría nos proporciona un modelo muy útil para el proceso de captación de una
cámara, pues nos relaciona figuras tridimensionales con su proyección sobre un plano bidimensional.
La geometría proyectiva se apoya en dos principios fundamentales:
Dos puntos definen una recta
5
Desarrollo de herramientas de apoyo a la estereovisión
Todo par de rectas se cortan en un punto (cuando dos rectas son paralelas decimos que se
cortan en un punto del infinito).
2.2.
2.2.1.
Coordenadas homogéneas
Representación homogénea de una recta
Como es común en el contexto de la geometría euclidiana, un punto m se representa con un
par de coordenadas (x, y) en R2 . Por ello se suele identificar R2 con un plano. De este modo, si
consideramos R2 como un espacio vectorial en el que (x, y) es un vector, estamos asociando un
punto a un vector.
Una recta en el plano R2 es representada por su ecuación afín ax + by + c = 0. De esta forma
la recta puede ser representada por el vector v = [a, b, c]T en coordenadas homogéneas.
Esta correspondencia entre líneas y vectores no es biunívoca, ya que los vectores [a, b, c]T y
[ka, kb, kc]T con k != 0 representan exactamente la misma recta siendo vectores distintos. Estos
vectores se consideran equivalentes y se definen como vectores homogéneos.
2.2.2.
Representación homogénea de un punto
Un punto m = (x, y)T pertenecerá a la recta [a, b, c]T si se cumple la ecuación ax + by + c =
0. Esto puede expresarse de forma vectorial como [a, b, c]T ! [x, y, 1] = 0, donde [x, y, 1] es la
representación homogénea de m en R2 .
De una forma más genérica puede expresarse M = [X, Y, Z] con (X, Y, Z) ∈ R y Z != 0 como
la expresión homogénea del punto euclidiano m = [x, y], cuya relación viene dada por:
x = X/Z
y = Y /Z
Hay que señalar que a cada M = [X, Y, Z] le corresponde un único m = [x, y]; pero a m le
corresponden los infinitos [kX, kY, kZ], siempre que k sea real y distinto de cero.
2.2.3.
El punto impropio y la línea del infinito
Si consideramos los vectores de dos rectas en coordenadas homogéneas, v = [a, b, c]T y
v’ = [a! , b! , c! ]T , el punto de corte de ambas rectas viene dado por su producto vectorial:
[X, Y, Z] = [a, b, c] × [a! , b! , c! ]
En el ámbito de la geometría euclidiana, dos rectas paralelas no se cortan en ningún punto.
Veamos que ocurre si intentamos calcular el punto de corte de dos rectas paralelas en coordenadas
homogéneas:
[X, Y, Z] = [a, b, c] × [a, b, c! ] = (c! − c)[b, −a, 0]
Si ignoramos el factor de escala (c! −c) y pasamos a coordenadas euclídeas obtenemos el punto
[b/0, −a/0], que no tiene sentido en el ámbito real, excepto sugerir que el punto de intersección
tiene coordenadas infinitamente altas. En general, puntos con coordenadas homogéneas [X, Y, 0]T
no corresponden a ningún punto finito en R2 .
6
CAPÍTULO 2. REVISIÓN DE CONCEPTOS BÁSICOS
Desarrollo de herramientas de apoyo a la estereovisión
Los puntos homogéneos con la coordenada Z = 0 se conocen como puntos impropios o puntos
en el infinito. El conjunto de los puntos impropios, escrito como [X, Y, 0]T pertenecen a la llamada
línea del infinito, definida por l∞ = [0, 0, 1]T ; pudiéndose verificar que [0, 0, 1] · [X, Y, 0]T = 0.
2.3.
El plano proyectivo P 2
Una forma útil de acercarse a P 2 es pensar en un conjunto de líneas que pasen por el origen
en R3 . Cada línea en R3 genera un punto en P 2 (por lo tanto, un punto de P 2 corresponde con
una dirección o recta de R3 ) y cada plano genera una recta. Las líneas de R3 situadas en el plano
X-Y se corresponden con puntos impropios de P 2 , de modo que el propio plano X-Y conforma
la recta del infinitode P 2 .
Figura 2.2: Modelo del plano proyectivo
Se puede observar que cualquier punto perteneciente a la recta [O − m] se proyectará sobre
el propio punto m. Esto es lo mismo que decir que la proyección de k · [X, Y, Z] es igual a la
proyección de [X, Y, Z] para k != 0, y que esta proyección está dada por x = X/Z e y = Y /Z.
En otras palabras, la clase de vectores k · [X, Y, Z] en R3 representa el mismo punto en P 2 .
2.4.
Transformaciones proyectivas en 2D
La geometría proyectiva en 2D es el estudio de las propiedades del plano proyectivo P 2 , que
son invariantes bajo un grupo de transformaciones conocidas como homografías o proyectividades.
Una homografía es una transformación biyectiva del espacio proyectivo que viene dada por
h : P 2 → P 2 de manera tal que una línea recta es transformada como una línea recta. La
homografía queda definida como:
h(m) = m’ = H · m
m, m’ ∈ P 2

 
 

X!
h11 h12 h13
X
 Y !  =  h21 h22 h23  ·  Y 
Z!
h31 h32 h33
Z
donde H es una matriz 3x3 no singular. Hay que aclarar que debido a que las coordenadas
k · [X, Y, Z] definen el mismo punto proyectivo, cualquier par de matrices proporcionales definen
la misma transformación proyectiva.
CAPÍTULO 2. REVISIÓN DE CONCEPTOS BÁSICOS
7
Desarrollo de herramientas de apoyo a la estereovisión
2.5.
Transformaciones proyectivas en 3D
Dentro de las transformaciones 3D únicamente vamos a estudiar la transformación Euclídea.
Este tipo de transformación tiene como característica que conserva la distancia previa entre
puntos transformados; además se usa para representar los cambios de coordenadas sufridos al
variar el sistema de referencia de un sistema. La importancia de esta transformación radica en
que se utilizará más adelante para explicar el modelo pin-hole que usaremos para representar
las cámaras.
Figura 2.3: Transformación 3D Euclídea
Dado el sistema de coordenadas 3D (x, y, z) que se aprecia en la figura 2.3, vemos que ha
sufrido una rotación según cada uno de sus ejes y una traslación, de forma que el nuevo sistema
(x! , y ! , z ! ) surgido de esta transformación euclidiana queda definido como:
 ! 
 
x
x
 y!  = R ·  y  + t
z!
z
Y en coordenadas homogéneas:

X!
'
 Y! 
= R

 Z! 
0T
1



X
(

t 
 Y 

1
Z 
1
R es una matriz 3x3 y t es un vector 3x1 y definen respectivamente la rotación y la translación
del sistema de coordenadas.
La matriz de rotación R puede descomponerse en transformaciones de rotación alrededor de
cada uno de los ejes, dadas por Rx , Ry y Rz :


1
0
0
Rx =  0 cos(ϕx ) sin(ϕx ) 
0 − sin(ϕx ) cos(ϕx )

cos(ϕy ) 0 − sin(ϕy )

0
1
0
Ry = 
sin(ϕy ) 0 cos(ϕy )

8
CAPÍTULO 2. REVISIÓN DE CONCEPTOS BÁSICOS
Desarrollo de herramientas de apoyo a la estereovisión


cos(ϕz ) sin(ϕz ) 0
Rz =  − sin(ϕz ) cos(ϕz ) 0 
0
0
1
Así definimos la rotación total como una rotación alrededor del eje Z, seguida de otra rotación
respecto a Y y otra más respecto a X, lo que matemáticamente podemos expresar como:

R11 R12 R13
R = Rx · Ry · Rz =  R21 R22 R23 
R31 R32 R33

2.6.
Análisis de la geometría asociada al proceso de captación
Para estudiar cómo se relacionan los objetos tridimensionales con la imagen bidimensional
vamos a representar la cámara con el modelo pin-hole. Este modelo es muy utilizado aunque
sencillo, ya que no modela la distorsión que introduce la lente, y está basado en la geometría
proyectiva: un punto cualquiera de la escena es representado en el plano de imagen como la
intersección de la línea que pasa por ese punto y por el centro de proyección con el plano de
imagen.
2.6.1.
El modelo pin-hole
El modelo consiste en un centro óptico C en el cual convergen todos los rayos de proyección
y un plano de imagen situado a una distancia focal f del centro óptico de forma paralela al eje
óptico Zc .
Figura 2.4: Modelo de una cámara pin-hole
La figura 2.4 muestra la proyección de un punto M sobre el plano imagen en m. Como se
puede apreciar, esta proyección consta de varias transformaciones y transiciones entre distintos
sistemas de coordenadas. Los sistemas de referencia que aparecen en la figura son los siguientes:
CAPÍTULO 2. REVISIÓN DE CONCEPTOS BÁSICOS
9
Desarrollo de herramientas de apoyo a la estereovisión
Sistema de coordenadas del mundo: describe la posición del punto 3D M y de la escena
en general. Este sistema debe ser fijado o conocido por el método de calibración. Sus ejes
son X, Y, Z.
Sistema de coordenadas de la cámara: describe la posición del punto 3D Mc respecto de la
cámara. El punto Mc esel mismo que M, pero referido a distinto sistema de coordenadas.
Su origen es el centro óptico y sus ejes son Xc , Yc y Zc , siendo éste último colineal con el
eje óptico.
Sistema de coordenadas de la imagen: describe la posición del punto 2D m respecto al
plano imagen. Normalmente este sistema tiene su origen en c, el centro del plano imagen,
en la intersección del plano con el eje óptico. Sus ejes son u y v.
Sistema de coordenadas de la imagen normalizado: describe la posición del punto 2D mn
respecto al pano imagen, situando el origen en la esquina superior izquierda del plano. El
punto mn es el mismo que m, pero referidos a distintos sistemas de coordenadas. Sus ejes
son un y vn .
El comportamiento de este modelo depende de una serie de parámetros propios de cada
cámara. Estos parámetros se clasifican en extrínsecos (dependientes de la posición externa de
la cámara respecto de la escena) e intrínsecos (dependientes de la construcción interna de la
cámara).
Parámetros extrínsecos: indican la posición relativa de la cámara respecto al sistema de
referencia del mundo.
• Translación: t = [tx , ty , tz ]T es la distancia entre el origen de coordenadas de la cámara
(centro óptico) y el origen de coordenadas del mundo.
• Rotación: R = [ϕx , ϕy , ϕz ] son los ángulos rotados sobre cada uno de los ejes para
alinear el sistema de referencia del mundo con el de la cámara.
Parámatros intrínsecos: marcan en qué forma se transforma el punto 3D Mc en mn . Dependen de la geomtría interna y de la óptica de la cámara. Estos parámetros son:
• Centro del eje óptico c = [u0 , v0 ]: marca el punto de corte del eje óptico con el plano
de imagen, con coordenadas expresadas en píxeles. A este punto también se le llama
punto principal.
• Factores de escalado ku , kv : definen la proporción de tamaño del objeto real respecto
a su proyección sobre el plano imagen. Estos parámetros se descomponen a su vez en:
◦ Factores de conversión milímetros-pixel (du ,dv ): indican la densidad de píxeles
de la cámara, y puede obtenerse dividiendo el tamaño en píxeles del CCD entre
el tamaño en milímetros.
◦ Distancia focal f : expresa la distancia entre el plano imagen y el centro óptico,
en milímetros.
◦ Factor de proporción s: define la relación de tamaño entre la dimensión horizontal
y vertical de un píxel.
La relación entre ellos es: ku = s · du · f y kv = dv · f .
10
CAPÍTULO 2. REVISIÓN DE CONCEPTOS BÁSICOS
Desarrollo de herramientas de apoyo a la estereovisión
2.6.2.
La matriz de proyección
Si consideramos un punto en 3D expresado según sus coordenadas homogéneas, M = [X, Y, Z, T ],
de la misma forma que un punto 2D m= [U, V, S]. Supongamos que tenemos una cámara que
captura la escena y proyecta M sobre m, podemos relacionar ambos puntos a excepción de un
factor de escala, λ:
λ·m=P·M
La matriz P se denomina matriz de proyección y contiene información de los parámetros
intrínsecos y extrínsecos. Para obtener dicha matriz se estudia la relación entre M, expresado en
coordenadas del mundo, y m, expresado en coordenadas normalizadas de la imagen (un y vn )
en la figura 2.3, en función de los parámetros de la cámara. El proceso consta de tres etapas:
1. Transformación escena-cámara: pasamos de las coordenadas del mundo [X, Y, Z] a las
coordenadas de la imagen [Xc , Yc , Zc ] utilizando la matriz de parámetros extrínsecos de la
cámara.
Primero se realiza una rotación alrededor de cada uno de los ejes:

 
  
xr
r11 r12 r13
x
 yr  =  r21 r22 r23  ·  y 
zr
r31 r32 r33
z
(2.1)
Mr = R · M
Después aplicamos una traslación según el vector t:

 
 

xr
tx
xc
 y c  =  y r  +  ty 
zc
zR
tz
(2.2)
Mc = Mr + t
Podemos combinar las ecuaciones 2.1 y 2.2 para expresar directamente el paso de las
coordenadas del mundo a las coordenadas de la cámara:
Mc = R · M + t
Además esta expresión matricial puede expresarse en
la matriz de parámetros extrínsecos [R t]:



Xc
'
(

 Yc 
R t



 Zc  = 0 1 · 
1
(2.3)
coordenadas homogéneas mediante

X
Y 

Z 
1
(2.4)
2. Transformación cámara-imagen: pasamos de las coordenadas 3D de la cámara [xc , yc , zc ] a
las coordenadas 2D del plano de imagen [u, v].
Aplicando lo que sabemos de la geometría de proyección podemos relacionar las coordenadas de ambos sistemas mediante la distancia focal f :
u
v
f
=
=
zc
xc
yc
CAPÍTULO 2. REVISIÓN DE CONCEPTOS BÁSICOS
11
Desarrollo de herramientas de apoyo a la estereovisión
Haciendo uso de estas ecuaciones podemos componer la expresión matricial de la proyección
perspectiva:
' (
'
(
f
u
xc
=
·
v
yc
zc
Expresado en coordenadas homogéneas:


Xc
f 0 0 0
U


 V  =  0 f 0 0  ·  Yc 
 Zc 
0 0 1 0
S
1




(2.5)
3. Transformación imagen-imagen normalizada: convertimos las coordenadas del plano imagen (u,v) en coordenadas normalizadas (un , vn ). Como se ve en la figura 2.4, ambos sistemas de coordenadas pertenecen al mismo plano, por lo tanto para hacer la transformación
sumamos vectorialmente a m la posición relativa de c respecto a cn . Además de ello se
deben aplicar los factores de conversión para pasar las unidades de milímetros a píxeles.
un = du · u + u0
vn = dv · v + v0
Que expresado en coordenadas homogéneas queda de la forma:

 
 

du 0 u0
U
Un
 Vn  =  0 dv v0  ·  V 
Sn
0 0 1
S
(2.6)
Podemos combinar los resultados de la ecuaciones 2.4 y 2.5 para obtener la relación de un
punto 3D Mc con el punto 2D mn , utilizando la matriz de parámetros A.

Xc
du 0 u0
f 0 0 0
Un


 Vn  =  0 dv v0  ·  0 f 0 0  ·  Yc 
 Zc 
Sn
0 0 1
0 0 1 0
1



 

Xc
du · f
0
u0 0
Un
 Yc 

 Vn  =  0
dv · f v0 0  · 
 Zc 
Sn
0
0
1 0
1



 


(2.7)
mn = A · Mc
Finalmente, podemos hallar la expresión general de la matriz de proyección que nos relaciona
un punto 3D M de la escena y su correspondiente mn en el plano imagen multiplicando la matriz
de parámetros intrínsecos A de la ecuación 2.6 y la matriz de parámetros extrínsecos [R t] de la
ecuación 2.3:




r11 r12 r13 tx
du · f
0
u0 0
 r21 r22 r23 ty 

dv · f v0 0  · 
P = 0
 r31 r32 r33 tz 
0
0
1 0
0
0
0 1

 
du · f
Un
λ ·  Vn  =  0
Sn
0
12
0
dv · f
0

 

r11 r12 r13 tx
X
u0 0
 r21 r22 r23 ty   Y
 
v0 0  · 
 r31 r32 r33 tz  ·  Z
1 0
0
0
0 1
1
CAPÍTULO 2. REVISIÓN DE CONCEPTOS BÁSICOS




(2.8)
Desarrollo de herramientas de apoyo a la estereovisión
λ · mn = P · M
2.7.
Análisis de la geometría de visión múltiple
La relación geométrica entre dos proyecciones de un mismo punto físico puede ser expresada
a través de la geometría epipolar.
Figura 2.5: Geometría epipolar
En la figura anterior se muestran dos cámaras "pinhole", los centros de proyección Ci y
Cd y los planos de imagen, las longitudes focales se denotan como fi y fd . A la recta que
une ambos centros de proyección se le llama línea base. Cada cámara identifica un sistema de
referencia 3D con el origen situado en el centro de proyección de la cámara y el eje Z con el eje
óptico. Los vectores Mi = [Xi , Yi , Zi ]T y Md = [Xd , Yd , Zd ]T se refieren al mismo punto 3D, M,
como vectores en los sistemas de referencia de la cámara izquierda y derecha respectivamente.
Los vectores mi = [xi , yi , zi ]T y md = [xd , yd , zd ]T definen las proyecciones del punto M en la
imagen izquierda y derecha respectivamente y están expresados en su correspondiente sistema
de referencia. Para todos los puntos de las imágenes tenemos zi = fi o zd = fd de acuerdo a la
imagen que sea. Así, la relación entre un punto del espacio y su proyección se define según las
fi
fd
ecuaciones de perspectiva, que en forma vectorial quedan: mi = Mi y md =
Md .
Zi
Zd
El nombre de geometría epipolar es debido a que a los puntos en los que corta la recta que
une los centros de proyección con los planos de proyección se les llama epipolos; denotaremos ei
al epipolo izquierdo y ed al epipolo derecho. Por su construcción, los epipolos son la proyección
sobre su plano de imagen del centro de proyección de la otra cámara. Si los planos de imagen
son paralelos a la línea base, los epipolos se encuentran en el infinito.
Los sistemas de referencia de las cámaras izquierda y derecha están relacionados a través de
unos parámetros extrínsecos. Estos definen una transformación rígida en el espacio 3D definida
por un vector de traslación T = Cd − Ci y una matriz de rotación R. Dado un punto M en el
espacio la relación entre Mi y Md es por tanto:
Mi = R · Md + T
(2.9)
Podemos relacionar estos parámetros extrínsecos con los propios de cada una de las cámaras
sabiendo que las matrices de rotación son unitarias:
CAPÍTULO 2. REVISIÓN DE CONCEPTOS BÁSICOS
13
Desarrollo de herramientas de apoyo a la estereovisión
Md = Rd · M + td
Mi = Ri · M + ti
Mi = Ri · RdT (Md − td ) + ti = Ri · RdT · Md + (ti − Ri RdT td )
Si igualamos términos con la ecuación 2.8 obtenemos:
R = Ri · RdT
T = ti − Ri · RdT td = ti − R · td
La importancia del desarrollo de este tipo de geometría radica en el hecho de que para poder
hallar la información de profundidad de un punto es necesario saber dónde se proyecta en ambas
cámaras para poder posteriormente triangular. En principio, la región para buscar el punto
correspondiente al punto mi es toda la imagen derecha, pero si nos fijamos en el plano epipolar,
identificado por M , Oi y Od , vemos que interseca en los planos de imagen en líneas llamadas
líneas epipolares que denotaremos como li y ld . Cada una de estas líneas puede verse como la
proyección sobre su plano de imagen de la recta definida por M y el centro de proyección de la
otra imagen. Si nos fijamos en la recta Oi − M y vemos esta recta como la colección de puntos
k · [X, Y, Z] que son proyectados sobre mi = [X/Z, Y /Z], se puede observar que cada uno de ellos
se proyectará sobre un punto de la línea epipolar ld . Visto de otra manera podemos decir que,
para hallar el punto md correspondiente a mi , sea cual sea el punto M que lo ha proyectado,
tenemos que buscarlo en la línea epipolar ld . A esto se le llama, cualitativamente, restricción
epipolar. De esta forma hemos reducido la búsqueda de correspondencias a un problema en 1D.
A continuación veremos como estimar esta geometría epipolar.
2.7.1.
La matriz esencial
La ecuación del plano epipolar puede escribirse como la coplanariedad de los vectores Mi ,
T y Mi − T , de manera que esta condición de coplanariedad puede escribirse como (Mi − T )T ·
(T × Mi ) = 0. Usando la relación entre Mi y Md y aplicando que el producto vectorial de dos
vectores puede expresarse como el producto de una matriz antisimétrica por un vector tenemos:
(RMd )T · S · Mi = MdT · RT · S · Mi = 0
con


0
−Tz Ty
0
−Tx 
S = [T ]x =  Tz
−Ty Tx
0
con lo que nos queda:
MdT EMi = 0
donde E = RT · S es la matriz esencial. Sabiendo la relación entre entre los puntos y sus proyecciones podemos escribir mTd Emi = 0, que ofrece una expresión cuantitativa de la restricción
epipolar.
La matriz esencial establece por tanto una relación entre la restricción epipolar y los parámetros extrínsecos del sistema estéreo, a través de ella podemos establecer un mapeo entre
los puntos de una imagen y las líneas epipolares de la otra. ld = Emi define la línea epipolar
derecha, lo que resulta en mTd ld = 0, lo que nos demuestra que los puntos equivalentes entre las
imágenes se encuentran en las líneas epipolares. Hay que hacer notar que la matriz esencial nos
da información sobre la geometría epipolar a nivel de coordenadas cámara. Para poder pasar a
14
CAPÍTULO 2. REVISIÓN DE CONCEPTOS BÁSICOS
Desarrollo de herramientas de apoyo a la estereovisión
coordenadas pixel necesitamos haber calibrado las cámaras para conocer sus parámetros intrínsecos. En este sentido, la matriz que relaciona las coordenadas de puntos correspondientes de
ambas imágenes, pero a nivel de píxel, se denomina matriz fundamental.
2.7.2.
La matriz fundamental
Tal y como se explicó anteriormente, podemos hacer uso de la matriz de parámetros intrínsecos para poner en relación un punto 3D en coordenadas cámara con su proyección 2D en
coordenadas píxel normalizadas. Haciendo uso de la ecuación 2.6 podemos escribir:
Mi = A−1
i · mni
Md = A−1
d · mnd
−1
−T
−1
T
T
MdT EMi = (A−1
d · mnd ) E(Ai · mni ) = mnd Ad EAi mni = 0
Lo que se puede reducir a:
mTnd · F · mni = 0
−1
es la matriz fundamental.
donde F = A−T
d EAi
Al igual que la matriz esencial, la matriz fundamental nos relaciones puntos de una de las
imagenes con la recta epipolar en la que se encuentra su conjugado de la otra imagen. La
diferencia radica en que la esencial trabaja con coordenadas de la cámara y la fundamental
directamente con coordenadas píxel.
Una consecuencia muy importante de las propiedades anteriores es que si conocemos la caliración de un sistema estereo (parámetros intrínsecos y extrínsecos), tenemos toda la información
necesaria para obtener la geometría epipolar y hallar todas las correspondencias entre puntos y
rectas epipolares de ambas imágenes.
CAPÍTULO 2. REVISIÓN DE CONCEPTOS BÁSICOS
15
3
Disparidad
3.1.
Introducción
La disparidad medida sobre un par estéreo es la distancia en píxeles que hay entre las
proyecciones del mismo punto en ambas imágenes. En el caso particular de un par estéreo, con
los ejes ópticos de las cámaras paralelos, la disparidad se define como:
d = xi − xd
donde xi y xd son las coordenadas horizontales del punto proyectado en la imagen izquierda y derecha respectivamente. La distancia resulta siempre positiva ya que en las condiciones
descritas, un punto cualquiera en el espacio siempre va a cumplir que xi " xd ; es decir, en la
imagen derecha va a estar situado más a la izquierda que en la imagen izquierda.
La razón de utilizar esta medida es que existen varios métodos implementados para hallar la
disparidad en distintas situaciones, y además, una vez hallada la disparidad, hallar la profundidad
del punto en milímetros es un paso sencillo.
La mayoría de los métodos para obtener el mapa de disparidad de una escena requieren
que ambas imágenes estén rectificadas. Que las imágenes de un par estéreo estén rectificadas
significa que se han modificado para que sus planos de imagen sean coplanares y sus líneas
epipolares, horizontales; resultando los puntos correspondientes en ambas imágenes con la misma
coordenadas vertical. El hecho de exigir que las imágenes estén rectificadas se debe a que la
rectificación es un proceso sencillo y de bajo coste computacional que simplifica muchísimo
los algoritmos posteriores de obtención de disparidad al reducir el área de búsqueda de las
correspondencias de dos dimensiones a una.
3.2.
Rectificación
Como se ha explicado anteriormente, la rectificación consiste en la transformación de las
imágenes mediante software, utilizando los parámetros intrínsecos y extrínsecos de las cámaras,
de forma que las líneas epipolares de ambas imágenes queden alineadas horizontalmente: con
17
Desarrollo de herramientas de apoyo a la estereovisión
ello se consigue que la proyección del mismo punto en ambas imágenes tenga la misma posición
en el eje y.
Figura 3.1: Esquema del proceso de rectificado
El rectificado de imágenes aporta una gran ventaja en la búsqueda de puntos correspondientes, no solo exige un cálculo en 1D, sino que además sabemos que el punto correspondiente a uno
dado va a estar en la misma fila que el punto dado. Por contrapartida, al rectificar una imagen,
no todos los puntos de la imagen destino ocupan un punto exacto en la imagen original. Para
subsanar esto hay que recurrir a la interpolación, incurriendo en errores.
Vamos a utilizar para rectificar el método propuesto por Fusiello et al. [1]. En él se fija que
después de la rectificación las cámaras tienen la misma orientación pero distinta posición en el
espacio. Es decir, los centros ópticos se mantienen invariantes tras la rectificación y la orientación
cambia, ya que rotamos las cámaras para conseguir que los planos de imagen sean coplanares y
contengan a la línea base.
De esta forma, vamos a estudiar la rectificación como una proyección sobre los nuevos planos
de imagen y veremos como relacionar esta nueva proyección con la que ya teníamos. Para poder
realizar esta proyección necesitamos una nueva matriz de parámetros intrínsecos y una nueva
matriz de rotación. Como hemos dicho anteriormente, los centros ópticos se mantienen invariantes, por tanto el vector de traslación será el mismo que el original. Una vez construida esta
nueva proyección la relacionaremos con la antigua para obtener una matriz que nos relacione los
píxeles de la imagen original con los de la rectificada.
Matriz de rotación: al fijar que los planos de imagen de nuestras dos cámaras sean coplanares y que sus ejes ópticos sean paralelos, estamos forzando que los sistemas de coordenadas
de ambas cámaras tengan la misma orientación. Como la rotación para ambas cámaras la
vamos a efectuar desde el sistema de referencia del mundo, ambas matrices de rotación
son iguales.
Vamos a definir tres vectores, r1 , r2 y r3 , que nos marcarán las direcciones de los nuevos
ejes x, y, y z, respectivamente, de los nuevos sistemas de coordenadas de las cámaras.


r1T
Rn =  r2T 
r3T
(3.1)
El nuevo eje x deberá ser paralelo a la línea base que une los centros ópticos. Para calcular
dicha dirección realizamos la diferencia entre los centros ópticos expresados en coordenadas
18
CAPÍTULO 3. DISPARIDAD
Desarrollo de herramientas de apoyo a la estereovisión
de un sistema de referencia común. Se ha tomado como tal el sistema de coordenadas del
mundo por sencillez, ya que para ambas cámaras tenemos sus parámetros extrínsecos, que
nos permiten el cambio de coordenadas facilmente. Si hacemos uso de la ecuación 2.3, y
sabiendo que los centros ópticos tienen coordenadas [0, 0, 0] en el sistema de referencia de
su propia cámara, podemos escribir para la cámara izquierda:
Cci = Ri · Cmi + Ti

0
 0  = Ri · Cmi + Ti
0

Cmi = −Ri−1 · Ti
(3.2)
donde Cci y Cmi son el centro óptico de la cámara izquierda expresado en coordenadas de
la cámara y del mundo, respectivamente; y Ri y Ti los parámetros extrínsecos de la cámara
en cuestión. Esta misma ecuación es aplicable a la cámara derecha, con lo que obtenemos
las coordenadas de ambos centros ópticos, y ya tenemos los datos suficientes para calcular
la matriz de rotación.
• El nuevo eje X paralelo a la línea base: r1 =
(Cmi − Cmd )
' Cmi − Cmd '
• El nuevo eje Y ortogonal al nuevo X (obligatorio) y a k: r2 = k × r1 , donde k es
un vector arbitrario que nos fija la posición del nuevo eje Y perpendicular al eje X.
En este caso hemos fijado k en la dirección del eje Z de Ri . De esta forma, la nueva
matriz de rotación será lo suficientemente parecida a las originales como para que, al
aplicar la rectificación, las imágenes resultantes no queden excesivamente deformadas.
• El nuevo eje Z ortogonal a los nuevos X e Y (obligatorio): r3 = r1 × r2
Con la construcción de la matriz de rotación y con el vector de translación de la proyección
original ya tenemos los parámetros extrínsecos de la nueva proyección sobre el plano de
imagen rectificado.
Matriz de parámetros intrínsecos: vamos a ver a continuación que restricciones deben
cumplir las nuevas matrices de parámetros intrínsecos para que la rectificación se realice
correctamente.
Sean Mi y Md las expresiones del mismo punto M en las coordenadas de sus respectivas
cámaras. Como se vió en el capítulo 2, podemos poner en relación ambas expresiones
utilizando los parámetros extrínsecos de las cámaras, de modo que:
Mi = R · Md + T
donde R = Ri · RdT y T = Ti − Ri · RdT Td = Ti − R · Td .
Si aplicamos RiT y posteriormente Rn a ambos lados de la ecuación anterior obtenemos :
Rn RiT Mi = Rn RdT Md + Rn (RiT Ti − RdT Td )
donde Mi! = Rn RiT Mi y Md! = Rn RdT Md son las expresiones del punto M expresadas en las
coordenadas de sus respectivas cámaras rectificadas. Teniendo en cuenta que RiT Ti − RdT Td
es paralelo al eje x de Rn , podemos reescribir la expresión anterior como:


' Cmi − Cmd '

0
Mi! = Md! + 
0
CAPÍTULO 3. DISPARIDAD
(3.3)
19
Desarrollo de herramientas de apoyo a la estereovisión
Se puede ver por la ecuación anterior que, puntos correspondientes, una vez realizada la
rectificación, tienen la misma coordenada y y z.
Vamos a continuación a proyectar los puntos Mi! y Md! sobre sus respectivos planos de
imagen rectificados utilizando unas matrices de parámetros intrínsecos Ani y And .

Ani

dui · f

=
0
0

x!i
Mi! =  yi! 
zi!
0
dvi · f
0

u0i
v0i 
1
Mi! · Ani
Md! · And


x!d
Md! =  yd! 
zd!
And


dud · f

=
0
0
0
dvd · f
0

dui · f · x!i + u0i · zi!
=  dvi · f · yi! + v0i · zi! 
zi!

u0d
v0d 
1


dud · f · x!d + u0d · zd!
=  dvd · f · yd! + v0d · zd! 
zd!
Una vez realizada la rectificación sabemos que las proyecciones de un mismo punto en
ambas imágenes van a tener la misma coordenada en el eje vertical, por tanto:
dvd · f · yd! + v0d · zd!
dvi · f · yi! + v0i · zi!
=
zi!
zd!
Como sabemos de la ecuación 3.3, yi! = yd! y zi! = zd! , con lo que:
dvi · f · yi! + v0i · zi! = dvd · f · yd! + v0d · zd!
(dvi · f − dvd · f )yi! + (v0i − v0d )zi! = 0
Para que lo anterior se cumpla para todo yi! y zi! , sólo nos queda que:
dvi = dvd
v0i = v0d
(3.4)
Cualquier par de matrices de parámetros intrínsecos que cumplan estas condiciones nos
aseguran una rectificación correcta. En este proyecto se ha elegido fijar las dos matrices
de parámetros intrínsecos a la media de las matrices de intrínsecos antiguas; con esto se
cumplen los requisitos necesarios y nos aseguramos que las nuevas proyecciones no sean
excesivamente distintas de las antiguas.
Rectificación: para poder realizar la rectificación vamos a calcular una transformación que
nos mapee puntos de la imagen original a los puntos de la imagen rectificada. Para ello
vamos primeramente a expresar la ecuación de proyección de la ecuación 2.7 en coordenadas
no homogéneas para la imagen original y para la imagen rectificada, de la cámara izquierda:
λi mi = Ai · (Ri · M + Ti )
λn mn = An · (Rn · M + Tn )
Sabemos que en ambas ecuaciones las coordenadas del mundo son iguales; vamos a relacionarlas a través de ellas:
M = −(Ri−1 · Ti ) + λi (Ai · Ri )−1 · mi
20
CAPÍTULO 3. DISPARIDAD
Desarrollo de herramientas de apoyo a la estereovisión
M = −(Rn−1 · Tn ) + λn (An · Rn )−1 · mn
Combinando las dos anteriores obtenemos que:
mn = λ(An · Rn · Ri−1 · A−1
i )mi
(3.5)
Esta es la matriz Ni = An · Rn · Ri−1 · A−1
i , que utilizaremos para realizar la rectificación de
la imagen izquierda, aplicandola sobre cada píxel de la imagen. Podemos seguir los mismos
pasos y obtener un resultado equivalente para la imagen derecha.
Existe un problema añadido al proceso de rectificación: al no saber cuánto va a rotar los
sistemas de las cámaras, cabe la posibilidad de que al realizar la rectificación varios píxeles
ocupen posiciones fuera de los límites de nuestra imagen. Para solucionar esto, variaremos las
coordenadas de los centros ópticos de las matrices de parámetros intrínsecos según lo siguiente.
Una vez construida la matriz de rectificación como se acaba de explicar, se calcula que posición
ocuparía el punto central de la imagen original en la imagen rectificada para las dos cámaras.
La diferencia entre ambas será lo que variarán los centros ópticos de las matrices de parámetros
intrínsecos. Para no afectar al funcionamiento del sistema de rectificación, la matriz izquierda y
la derecha deberán variar igual en las dos coordenadas del centro óptico: en el vertical para que
las proyecciones de un mismo punto sigan estando en la misma fila en ambas imágenes y en el
horizontal para no variar el valor de la disparidad.
Este método centra la imagen rectificada sobre nuestros límites visibles, pero debido a la
transformación sufrida, una pequeña cantidad de píxeles siguen fuera de la imagen. Ampliando
lígeramente el tamaño de la imagen se consigue que todos los píxeles se encuentren dentro de
ella.
3.3.
Métodos de cálculo de la disparidad
Como se ha explicado anteriormente, la disparidad mide la distancia en píxeles entre el mismo
punto de ambas imágenes. El gran reto de los métodos de cálculo de disparidad es precisamente,
dado un píxel en una imagen, hallar el píxel equivalente en la otra. Este es el llamado problema
de la correspondencia estéreo.
Existen una gran cantidad de métodos que resuelven este problema, y se pueden clasificar
en dos grandes grupos:
Métodos globales: aplican restricciones a la búsqueda del píxel correspondiente en toda
la imagen o en toda la línea epipolar. Son menos sensibles a las zonas conflictivas que
los locales, obteniendo en líneas generales mejores resultados. Los más comunes son los
métodos de Programación Dinámica y los de Corte de Grafos. Por contrapartida, son
mucho más costosos computacionalmente.
• Programación Dinámica: estos métodos reducen la complejidad de cálculo en problemas de optimización descomponiendo el problema en subproblemas menores. Para
esto se construye una representación de las posibles correspondencias para cada punto
construyendo una imagen que se denomina imagen del espacio de disparidad (DSI)
donde se busca un camino que recorra este espacio y minimice un cierto costo.
CAPÍTULO 3. DISPARIDAD
21
Desarrollo de herramientas de apoyo a la estereovisión
Figura 3.2: Variantes en la construcción de la imagen del espacio de disparidad
En la figura anterior, Ii y Id representan una línea epipolar izquierda y su correspondiente derecha. La zona blanca representa las correspondencias permitidas por el
algoritmo. Los diferentes algoritmos varían la construcción y asignación de costos para
luego usar la Programación Dinámica para la minimización del costo global. El mayor problema de este tipo de métodos es que utiliza información de líneas epipolares
correspondientes, perdiendo la información de las líneas adyacentes.
• Corte de Grafos: El corte de grafos se basa en armar un grafo a partir de los datos
de las imágenes y buscar un corte mínimo. Dependiendo como se arma el grafo, el
resultado obtenido es la minimización de una cierta expresión de energía. Este procedimiento se puede considerar análogo al de hallar el mejor camino en una imagen
bidimensional, con Programación Dinámica, pero extendido a un entorno tridimensional.
Figura 3.3: Representación del problema de cálculo de disparidad mediante corte de grafos
En la figura anterior se puede apreciar la forma en la que se arma el grafo, asignando
un nodo por cada disparidad posible de cada píxel. De esta forma, cada nodo está
unido a cuatro nodos de disparidad d, dos en vertical y dos en horizontal, y a dos nodos
de disparidad d-1 y d+1. La supeficie representa el corte del grafo que minimiza alguna
expresión de energía. La diferencia entre los distintos algoritmos y las aplicaciones se
da en la forma en que se asignan los pesos a los arcos del grafo y la expresión de la
energía a minimizar.
Métodos locales: utilizan restricciones en una zona alrededor del punto que se desea evaluar.
Estos métodos presentan mayor velocidad que los anteriores, pero también mayor tasa de
error, sobre todos en las oclusiones (puntos que aparecen en una imagen pero no en otra),
en las zonas fronterizas y en las zonas de baja textura (baja variabilidad en la intensidad
de grises). Pese a estos problemas estos métodos son los más utilizados gracias a sus
22
CAPÍTULO 3. DISPARIDAD
Desarrollo de herramientas de apoyo a la estereovisión
resultados y a la facilidad de implementación. Así mismo estos métodos pueden dividerse
en dos categorías:
• Basados en características: en estos métodos, las imágenes se procesan con un operador que extrae las características deseadas. Después se aplica el proceso de correspondencia a los atributos asociados a las características detectadas. Los bordes y
esquinas presentan buenos resultados, pero el resto de características necesitan un
alto coste computacional en la búsqueda de correspondencias. El gran inconveniente
de este tipo de métodos es que no generan un mapa de disparidad denso, sino aislado
en las zonas de las que ha extraido características.
• Basados en zonas: aquí se utiliza un criterio de semejanza como medida para evaluar
la similitud entre los puntos de ambas imágenes. Dado un píxel de la imagen izquierda
y una ventana alrededor suyo, se busca encontrar una ventana sobre la imagen derecha
que sea la más parecida a la primera, según un criterio de similitud dado. Al encontrar
la ventana de mayor similitud se dice que el píxel central derecho se corresponde con
el píxel central de la ventana izquierda. La disparidad del punto será la diferencia
entre las coordenadas x de ambos puntos.
En este proyecto se han estudiado dos métodos para el cálculo de la disparidad, uno local
basado en zonas y otro basado en Programación Dinámica, el método de Birchfield-Tomasi [2].
El primero fué elegido por ser el más sencillo y, según el criterio de similitud utilizado, de los mas
rápidos. El método de Birchfield-Tomasi se eligió por ser un representante de los métodos globales
con unos resultados bastante buenos y del que existe una implementación de alta eficiencia en
la librería de procesamiento de imagen OpenCV.
3.3.1.
Búsqueda por zonas
En este tipo de métodos es necesario definir tres parámetros:
Región de búsqueda: por geometría epipolar sabemos que la región de búsqueda va a ser
la línea epipolar del punto, pero además, gracias a que las imágenes sobre las que vamos a
calcular la disparidad han sido previamente rectificadas, sabemos que debemos buscar en
los puntos con la misma coordenada y que el original. Ya que el objetivo es desarrollar un
sistema en tiempo real, limitaremos la región a un valor máximo de disparidad centrado
en las mismas coordenadas que el punto original.
Ventanas de cálculo: se han realizado pruebas con ventanas cuadradas centradas en el
píxel que se está evaluando, de tamaños 3x3, 5x5 y 7x7. Éste último fué rechazado tras la
primera prueba debido a un tiempo de cálculo excesivo. Se escogió que fuesen cuadradas
frente a ventanas rectangulares ya que, aunque el píxel correspondiente que buscamos
tiene la misma coordenadas vertical, no por ello los píxeles la misma fila nos aportan más
información de similitud que los de las columnas.
CAPÍTULO 3. DISPARIDAD
23
Desarrollo de herramientas de apoyo a la estereovisión
Figura 3.4: Definición de la región de búsqueda y de las ventanas
Criterio de semejanza: se han escogido las siguientes medidas de similitud por ser las de
mayor simplicidad, y por ello mayor velocidad de procesado: suma de diferencias absolutas
(SAD), suma de diferencias cuadráticas (SSD) y correlación cruzada normalizada (NCC).
SAD =
n
n
)
)
i=−n j=−n
SSD =
n
n
)
)
' Ii (x + i, y + j) − Id (x + i, y + j) '
(Ii (x + i, y + j) − Id (x + i, y + j))2
i=−n j=−n
N CC =
*n
i=−n
*n
j=−n (Ii (x
+ i, y + j) − Ii )(Id (x + i, y + j) − Id )
σI i σI d
donde Ii y σIi se refieren al valor medio y a la desviación estándar de las véntanas de
cálculo.
3.3.2.
Birchfield-Tomasi
El método de Birchfield-Tomasi se basa en la búsqueda de correspondencias y oclusiones
entre líneas epipolares enteras. Para ello busca los emparejamientos por programación dinámica
que minimizan la siguiente función de coste:
γ(M ) = Nocc kocc − Nm kr +
Nm
)
d(xii , xdi )
(3.6)
i=1
donde M es la secuencia a evaluar, kocc la constante de penalización por oclusión, kr la
constante de recompensa por emparejamiento, d(xii , xdi ) la diferencia de intensidad entre píxeles
correspondientes, y Nocc y Nm el número de oclusiones (no de píxeles ocluidos) y el número de
emparejamientos, respectivamente, en M .
24
CAPÍTULO 3. DISPARIDAD
Desarrollo de herramientas de apoyo a la estereovisión
Figura 3.5: Ejemplo de una secuencia de correspondencias
En la imagen, I y D definen líneas epipolares de la imagen izquierda y derecha respectivamente. Las líneas entre ellas marcan la correspondencia entre sus píxeles. En la secuencia de
correspondencias de ejemplo descrita en la imagen anterior
M = ((1, 0), (2, 1), (6, 2), (7, 3), (8, 4), (9, 5), (10, 6), (11, 9), (12, 10)) se pueden observar, de izquierda a derecha, varios elementos utilizados en la función de coste descrita anteriormente:
un píxel ocluido en la línea epipolar izquierda (ya que no tiene correspondiente en la derecha),
dos píxeles correspondientes con un nivel de disparidad de uno, tres píxeles ocluidos en la línea
izquierda, cinco pixeles con sus correspondientes a un nivel de disparidad de cuatro, dos píxeles
ocluidos en la línea derecha, dos píxeles con correspondencia y un nivel de disparidad de dos y
por último dos píxeles ocluidos en la línea derecha.
En la práctica, kocc puede interpretarse como la cantidad de evidencia, expresada en términos
de intensidad de píxel, necesaria para declarar un cambio de disparidad; mientras que kr puede
verse como la máxima diferencia de intensidad de píxel esperada entre correspondencias.
Figura 3.6: Imagen del espacio de disparidad y posiciones permitidas tras una correspondencia
dada
La figura 4.6 a muestra una posible imagen del espacio de disparidad para líneas epipolares
de diez píxeles y una disparidad máxima de 3. En el eje de ordenadas se representa la línea
epipolar de la imagen izquierda y en el de abcisas la derecha. Las posiciones en negro son las
no permitidas, las blancas las permitidas y las marcadas representan una secuencia de emparejamientos. Las figuras 4.6 b y 4.6 c indican las posiciones de correspondencias posibles antes o
después, respectivamente, de una correspondencia conocida (cuadrado rayado).
Una vez procesadas todas las líneas epipolares se realiza un postprocesado para aprovechar
la informacion de dependencia entre una línea epipolar y sus contiguas. Para ello se clasifican los
píxeles en tres categorias no disjuntas (cada una de ellas contiene la anterior) basadas en su nivel
de fiabilidad : escasamente fiable, moderadamente fiable y altamente fiable. Esta categorización
CAPÍTULO 3. DISPARIDAD
25
Desarrollo de herramientas de apoyo a la estereovisión
de fiabilidad se hace en función del número de píxeles contíguos en la misma columna con el
mismo nivel de disparidad. La idea se basa en que si las filas se computan independientemente
y obtenemos valores iguales de disparidad en las columnas, es más probable que el valor sea
correcto.
Un píxel de fiabilidad moderada se propaga por su columna cambiando a su valor de disparidad hasta que se encuentra con un cambio de intensidad o con una región escasamente fiable con
un valor de disparidad menor. La única diferencia entre regiones moderada y altamente fiables
es que las primeras no pueden propagarse si el cambio de disparidad es de un único nivel de
intensidad.
Posteriormente se realiza el mismo procesado en sentido horizontal, y por último se eliminan
las disparidades aisladas y rodeadas por un mismo valor.
3.4.
Relación entre disparidad y profundidad
Como se explicó anteriormente, una de las razones de calcular el mapa de disparidad es que,
una vez conocida la disparidad de un pixel, es inmediato obtener la profundidad del punto que
representa. Hay que hacer notar que la demostración siguiente es válida únicamente si los ejes
ópticos son paralelos y los planos de imagen son coplanares, como se muestra en la figura. En
nuestro caso hemos conseguido esta restricción mediante la rectificación de las imágenes.
Figura 3.7: Vista superior del sistema estéreo
En la figura anterior, Ci y Cd representan los centros ópticos de la cámara izquierda y
derecha, respectivamente, T es la distancia en milímetros que separa ambos centros, f es la
distancia focal, pi y pd las proyecciones del punto P y Z la profundidad del mismo. c0 indica la
coordenada x del punto principal de la imagen.
26
CAPÍTULO 3. DISPARIDAD
Desarrollo de herramientas de apoyo a la estereovisión
Sean xi y xd las coordenadas x de los puntos pi y pd respectivamente. Así, definimos la
disparidad de estos puntos como d = xi − xd . Por semejanza de los triángulos (P, pi , pd ) y
(P, Ci , Cd ) podemos escribir:
T
c0 + T − xi − c0 + xd
=
Z
Z −f
T −d
T
=
Z
Z −f
T
d
En la ecuación anterior, el valor de la disparidad se encuentra expresado en píxeles; para que
tenga sentido, ésta debe convertirse a milímetros utilizando los factores de conversión de la
matriz de parámetros intrínsecos.
Z=f
Z=f
T · du
d
(3.7)
Se puede ver por la ecuación anterior que la disparidad y la profundidad siguen una relación
inversa, y que su relación depende de parámetros obtenidos en el proceso de calibración de las
cámaras.
CAPÍTULO 3. DISPARIDAD
27
4
Sistema, diseño y desarrollo
En este capítulo se va a explicar el desarrollo del objetivo final del proyecto, la obtención de
la profundidad de los objetos de una escena a partir de las imágenes capturadas por un par de
cámaras.
Aunque en un principio el objetivo era desarrollar un sistema válido para los dos tipos de
cámaras citados en capítulos anteriores, en esta tema se explicarán las limitaciones que nos
llevaron a descartar el uso de las cámaras Firewire.
Todo el sistema desarrollado, a excepción de la calibración de las cámaras y la obtención
de las matrices de rectificación, se ha realizado en código C++, haciendo uso de la librería
de procesamiento de imagen OpenCV y de las herramientas integradas en la librería DiVA
desarrollada en el laboratorio VPU.
4.1.
Sistema físico
Como se comentó anteriormente el sistema se va a desarrollar sobre dos soportes distintos,
un par de cámaras Firewire y otras dos cámaras IP. A continuación se va explicar en detalle las
características físicas y ópticas de ambos tipos de cámaras.
4.1.1.
Cámaras Firewire
Las cámaras sobre las que se va a construir este sistema son cámaras fijas que se encuentran
situadas en la pasarela de la tercera planta entre los edificios A y B de la Escuela Politécnica
Superior (EPS). El modelo de las cámaras Firewire es DFW-X710 de SONY y están conectadas
a una red IP del laboratorio VPU.
29
Desarrollo de herramientas de apoyo a la estereovisión
Figura 4.1: Sistema de cámaras Firewire
Especificaciones de las cámaras
Estas cámaras son digitales y soportan hasta 15 imágenes por segundo a una resolución
máxima de 1024x768 píxeles y una profundidad de píxel de 24 bits. La lente montada es el
modelo C815B de COSMICAR, con una montura tipo C y una distancia focal de 8, 5 mm. El
dispositivo CCD que incorporan es de color y de tipo 1/3", con un tamaño de píxel de 4,65x4,65
µm, con lo que los factores de conversión quedan como:
du = dv =
4.1.2.
1
pixeles
= 215,53763
0,00465
mm
Cámaras IP
Este otro tipo de cámaras son móviles y utilizan para su conexión una interfaz GigE. El
modelo es piA1900-32gc de Basler. Se decidió montar dos de estas cámaras sobre un soporte
transversal móvil y de altura e inclinación regulable, de manera que podamos utilizar el par
estéreo fijo enfocando a distintas escenas.
Figura 4.2: Sistema de cámaras IP
30
CAPÍTULO 4. SISTEMA, DISEÑO Y DESARROLLO
Desarrollo de herramientas de apoyo a la estereovisión
Especificaciones de las cámaras
Estas cámaras son digitales y soportan hasta 32 imágenes por segundo a una resolución
máxima de 1900x1200 píxeles y una profundidad de píxel de 24 bits. El CCD utilizado en estas
cámaras es de escaneo progresivo, con un tamaño de píxel de 7,4x7,4 µm, y unos factores de
pixeles
1
= 135,135135
. A estas cámaras se les ha acoplado una
conversión de du = dv =
0,0074
mm
lente Pentax TV con una montura tipo C y una distancia focal de 8, 5 mm.
4.2.
Captura y sincronización
El sistema de captura para ambos tipos de cámara es una modificación de los ya existentes
en el grupo de trabajo integrados dentro de la plataforma DiVA para el control de una única
cámara. El primer paso para el control del par estéreo consiste en la duplicación de los elementos
existentes en los sistemas de cáptura básicos. Dentro de las herramientas proporcionadas por
Matrox se encuentra otra forma de iniciar el proceso de captura distinta a la utilizada en el
sistema de captura básico. Se eligió probar este método ya que envolvía un menor número de
operaciones, lo que favorecería a una primera aproximación a la sincronización de los tiempos
de captura y a un sistema en tiempo real. También fueron necesarias otras modificaciones sobre
el sistema de captura inicial debido a problemas que se encontraron en el manejo interno de las
imágenes.
Esta modificación de las capturadoras nos permite obtener imágenes de ambas cámaras simultáneamente, pero sin información sobre la diferencia de tiempo entre los instantes de captura.
Para obtener información de la sincronización inicial de las cámaras capturamos con ambas
cámaras un elemento que nos permita fijar un instante temporal. Para ello se ha utilizado el
flash de una cámara de fotos, con una duración de destello de 1 ms, y una secuencia de tres
destellos consecutivos, que nos permita hacernos una idea de los momentos de captura.
Figura 4.3: Estado inicial de la sincronización
Como se ve en las imágenes, los tiempos de captura se diferencian dentro de la franja de
exposición del flash, los tiempos de captura se diferencian en más de 1 ms. Esto nos obliga
a buscar un método para forzar la captura en el mismo instante, ya que la precisión en los
tiempos de captura será especialmente importante durante la calibración, como se explicará en
el apartado 4.4.
Los métodos disponibles para la sincronización del tiempo de captura son la instalación de
un sistema de disparo por hardware, la utilización de un disparador software o la adecuación de
los sistemas de captura. La opción de disparo software se descartó ya que la tarjeta capturadora
CAPÍTULO 4. SISTEMA, DISEÑO Y DESARROLLO
31
Desarrollo de herramientas de apoyo a la estereovisión
de la que se disponía durante la elaboración de este proyecto no soportaba esta posibilidad para
ninguno de los dos tipos de cámaras.
Se decidió, antes de añadir al sistema un método hardware de disparo sincronizado para
ambas cámaras, probar las herramientas software que nos proporciona la librería Matrox. Se
decidió cambiar la forma en que se inciaba la captura de los digitalizadores de las cámaras y
utilizar el mismo método de inicio de la capturadora que en el sistema de captura básico. En este
método, se crean de forma manual todos los elementos internos necesarios para el funcionamiento
de las capturadoras y posteriormente se inician ambos sistemas en instrucciones consecutivas.
Este método no nos garantiza a priori ningún nivel de sincronización, por lo que se realizó de
nuevo una medida de la sincronización obtenida. Tras este cambio de obtienen los siguientes
pares de imágenes.
Figura 4.4: Estado final de la sincronización
Así, conseguimos que ambas cámaras capturen con una diferencia temporal inferior a 1 ms,
lo cual es un nivel de sincronización suficiente para nuestro proyecto, ya que no vamos a evaluar
escenarios con velocidades excesivamente elevadas. En caso de ser este punto importante para
estudios posteriores, se deberá inicialmente realizar un estudio exhaustivo de sincronización a
altas velocidades.
4.3.
Límites
Como se vió en el capítulo anterior, la relación entre la disparidad y la profundidad en las
u
condiciones en las que nos encontramos viene dada por: Z = f T ·d
d . La profundidad así calculada
presenta límites máximos y mínimos que es capaz de expresar. Si manejamos disparidades comprendidas entre 0 y dmax , obtenemos estas profundidas máximas y mínimas para cada sistema
de cámaras. El valor máximo que puede tomar dmax es de 255, ya que es el valor máximo que
se puede expresar en imágenes en escala de grises de ocho bits de profundidad. En caso de no
necesitar representación de la disparidad, o de que sea más importante el poder obtener valores
altos de disparidad, es posible el utilizar un tipo de datos distinto que lo soporte.
Cámaras Firewire: Utilizando la ecuación anterior, y tomando como dato que estas cámaras
tienen una separación T = 3, 88 m, obtenemos que:
Zmin =
(1832, 06986 · T )
mm
dmax
Zmin = 27, 87619m
32
Zmax = 1832, 06986 · T mm
Zmax = 7108, 43082m
CAPÍTULO 4. SISTEMA, DISEÑO Y DESARROLLO
Desarrollo de herramientas de apoyo a la estereovisión
Teniendo en cuenta que la escena a la que enfocan las cámaras se encuentra a una distancia
máxima de entre 12 y 14 metros, vemos que nos encontramos fuera del rango de funcionamiento del sistema estereo. Cualquier cálculo de disparidad que intentaramos efectuar
en estas condiciones nos daría como resultado una imagen en la que el sistema de cálculo
redondearía todos los píxeles al máximo valor permitido, 255. Se pensó en la utilización
de un tipo de datos distinto, para aumentar el valor máximo permitido; pero en las circunstancias anteriormente descritas, los puntos correspondientes en ambas imágenes de
la escena tendrían, una vez rectificados, una separación o disparidad entre 500 y 600, es
decir, en la mayor parte de la imagen no se podría calcular la disparidad. Se pensó también
en la inclusión de un desfase de disparidad en una de las imágenes, para que al menos la
mayor parte de las imágenes pudiese ser computada, añadiendo al resultado de disparidad
el desfase añadido inicialmente. Pero este proceso ralentizaría el sistema en exceso, y ya
que nuestro objetivo es obtener un sistema lo más cercano posible al tiempo real. Por ello,
se descartó el uso de las cámaras Firewire y el resto del desarrollo se efectuará únicamente
sobre el par de cámaras IP.
Cámaras IP: La separación de estas cámaras es de T = 156, 33 mm. Este valor ha sido calculado una vez calibrado el par estéreo, con los parámetros extrínsecos de ambas
cámaras.
Zmin =
(1013, 51348 · T )
mm
dmax
Zmax = 1013, 51348 · T mm
Zmin = 621, 343mm
Zmax = 158, 442m
En ambos casos se ha tomado una disparidad máxima teórica de 255. En la práctica, utilizar este
valor ralentiza en gran medida el sistema, por ello es recomensable fijar una disparidad máxima
que se ajuste a la menor distancia entre la escena y las cámaras.
4.3.1.
Precisión
El hecho de no disponer de un sistema contínuo para el cálculo de la profundidad hace
que únicamente tengamos un número finito de profundidas posibles, tantas como la disparidad
máxima. Ello hace que se produzcan errores al asignar a una profundidad de las posibles una
profundidad real. El error cometido máximo se puede expresar como el punto medio entre dos
valores de profundidad permitidos. Vamos a evaluar este error en los valores máximos y mínimos
de disparidad, ya que la diferencia entre dos valores de disparidad consecutivos varía dependiendo
de si son valores altos o bajos de disparidad. Si hacemos uso de la ecuación 3.7 que nos relaciona
disparidad y profundidad podemos ver que el error cometido es:
errormax =
errormin =
Z1 − Z2
1 (d2 − d1 ) · f · T · du
f · T · du
= ·
=
= 44, 892m
2
2
d1 · d2
4
Zdmax −1 − Zdmax
1 (dmax − dmax−1 ) · f · T · du
f · T · du
= ·
=
2
2
dmax · dmax−1
2 · dmax · dmax−1 = 1, 386mm
Así podemos ver que el error será tanto mayor cuanto menor sea el valor de la disparidad,
es decir, cuanto más alejado esté el punto que estemos evaluando, mayor será el error cometido.
De forma teórica, con dmax =255, tendríamos errormin = 1, 386 mm.
CAPÍTULO 4. SISTEMA, DISEÑO Y DESARROLLO
33
Desarrollo de herramientas de apoyo a la estereovisión
4.4.
Calibración y cálculo de matrices de rectificado
Como se vió en el capítulo 2, la importancia de la calibración radica en la necesidad de
expresar en términos de pixel los objetos de una escena. La calibración del sistema estéreo sólo
será necesario realizarla una vez para el par de cámaras Firewire; el par de cámaras IP habrá
que calibrarlo cada vez que las cámaras cambien de posición relativa una respecto de la otra, ya
que sus parámetros extrínsecos habrán cambiado.
Para realizar el sistema de calibración haremos uso de una implementación del método de
Zhang realizada por Javier García Ocón para el VPU de la Universidad Autónoma de Madrid[3].
Hemos resuelto primero el problema de la sincronización ya que en este método de calibración es
especialmente importante. En él se fija el sistema de coodenadas del mundo en una plantilla de
calibración; si las imágenes de la plantilla no están tomadas en el mismo instante, o la plantilla
no se encuentra completamente inmóvil, el sistema de referencia puede estar desplazado en la
calibración de una cámara respecto al de la otra, con lo que los parámetros extrínsecos obtenidos
no podrían ponerse en relación por estar referenciados a distintos sistemas de coordenadas.
Todo el método de calibración utilizado, así como el cálculo de las matrices de rectificación
está desarrollado en código Matlab.
Para la realización de la calibración se necesitan por lo menos tres imágenes de la plantilla
de calibración en distintas posiciones. Esta plantilla debe ocupar la mayor parte del centro de
la imagen, sin acercarse demasiado a los bordes, para evitar efectos de distorsión de las lentes.
Figura 4.5: Ejemplo de imagen usada en la calibración de las cámaras IP
En la implementación que realiza Javier García Ocón son necesarias más de tres imágenes
por cada cámara que se quiera calibrar y la marcación manual de entre 4 y 81 puntos sobre la
plantilla de calibración de cada imagen. Siguiendo los datos obtenidos en su estudio, nos hemos
decantado por la utilización de cinco imágenes por cada cámara y el marcado de nueve puntos
en cada imagen: la utilización de más imágenes o más puntos no mejora el resultado obtenido.
Las salidas de este método para cada cámara son, la matriz de parámetros intrínsecos de la
cámaras y dos matrices de parámetros extrínsecos por cada imagen utilizada. Esto es así ya que,
como se dijo anteriormente, el sistema de referencia del mundo se fija en el centro del tablero
de calibración, por tanto tenemos cinco transformaciones en el espacio distintas. Para nuestros
objetivos nos es válido cualquiera de los cinco, ya que necesitamos conocer la posición de las
cámaras respecto del sistema de coordenadas del mundo, pero nos da igual donde esté situado
y como esté orientado.
Para la calibración de cada par de cámaras se ha realizado un mínimo de tres ejecuciones
sobre los mismos conjuntos de imágenes y se han comparado que los resultados obtenidos sean
suficientemente similares. Se ha hecho esta comprobación para evitar que un marcado erróneo
34
CAPÍTULO 4. SISTEMA, DISEÑO Y DESARROLLO
Desarrollo de herramientas de apoyo a la estereovisión
pudiera producir resultados demasiado alejados del valor real.
Una vez obtenidos los parámetros intrínsecos y extrínsecos de cada cámara, se procede a
aplicar la ecuación 4, 5 para obtener las matrices de rectificado.
4.5.
Rectificado
Como se vió en el capítulo anterior, la rectificación se puede ver como una transformación de
los píxeles de una imagen dada por una matriz de rectificación. Para aplicar esto haremos uso de
la librería OpenCV, y de la función cvWarpPerspective que nos permite aplicar transformaciones
a imágenes. Se ha decidido utilizar este método porque se ha comparado con la aplicación directa
de la fórmula de rectificado y ha resultado ser más rápido y se obtienen los mismos resultados
Tras esto se procederá a la variación de los centros ópticos de las matrices de parámetros
intrínsecos tal y como se explicó en el apartado 3.2.
Figura 4.6: Ejemplo de imágenes rectificadas con y sin desplazamiento
En la figura anterior se puede ver un ejemplo de imagen rectificada con desplazamiento óptico
a la izquierda y sin desplazamiento del centro óptico a la derecha.
Figura 4.7: Verificación de la rectificación
Tras rectificar las imágenes de ambas cámaras vemos como las proyecciones correspondientes
de un mismo punto 3D poseen la misma coordenada y.
CAPÍTULO 4. SISTEMA, DISEÑO Y DESARROLLO
35
Desarrollo de herramientas de apoyo a la estereovisión
4.6.
4.6.1.
Disparidad
Birchfield-Tomasi
Cómo se explicó en el capítulo anterior, para el cálculo de la disparidad según el método de
Birchfield-Tomasi se hará uso de la implementación existente en la librería de procesamiento de
imágenes de OpenCV. La función que realiza esta implementación tiene la siguiente definición:
cvFindStereoCorrespondence(
const CvArr* leftImage, const CvArr* rightImage,
int mode, CvArr* depthImage,
int maxDisparity,
double param1, double param2,
double param3, double param4, double param5);
donde leftImage y rightImage son las imágenes izquierda y derecha respectivamente, rectificadas y en escala de grises con una profundidad de ocho píxeles; mode es el algoritmo de cálculo
de la disparidad, en nuestro caso su valor es CV_DISPARITY_BIRCHFIELD; depthImage es la
disparidad resultante, igualmente en escala de grises de ocho píxeles; maxDisparity es la disparidad máxima que se le permite declarar al algoritmo; param1 define la penalización por oclusión
vista en la ecuación 3, 6; param2 expresa la recompensa por emparejamiento y param3, param4
y param 5 definen las regiones de fiabilidad alta, moderada y escasa, respectivamente. Estos
parámetros de fiabilidad definen que un píxel va a pertenecer a un nivel dado si su fiabilidad es
por lo menos el valor indicado en el parámetro correspondiente. Los valores por defecto son los
indicados en [2]: param1 = 25, param2 = 5, param3 = 12, param4 = 15 y param5 = 25.
4.6.2.
Búsqueda por bloques
La búsqueda por bloques se ha implementado de manera que tanto la disparidad máxima, como el tamaño de la ventana de cálculo y el criterio de semejanza se introduzcan como parámetros
del sistema.
4.7.
Profundidad
Como se vió en el capítulo anterior, la relación entre la disparidad y la profundidad en las
u
condiciones en las que nos encontramos viene dada por: Z = f T ·d
d . Se decidió implementar el
cálculo de la profundidad para puntos aislados marcados manualmente por el usuario sobre el
mapa de disparidad. Tras elegir el punto el sistema devuelve por consola las coordenadas píxel
marcadas y la profundidad del punto 3D al que corresponde.
Figura 4.8: Ejemplo de funcionamiento del sistema de profundidad
36
CAPÍTULO 4. SISTEMA, DISEÑO Y DESARROLLO
Desarrollo de herramientas de apoyo a la estereovisión
4.8.
Funcionamiento
Las capturadoras se encuentran en los archivos GTICapture1394stereo.cpp y GTICaptureGIGE.cpp y deben estar incluidos en la librería libgtibasic.lib, Ésta librería debe estar a su vez
añadida al proyecto que se quiera ejecutar.
Los programas se han separado según se quiera calcular la disparidad mediante el método
de Birchfield o de búsqueda por bloques. Esto se ha hecho así ya que la condensación de ambos
métodos en un único programa resultaría en un sistema demasiado pesado.
Ambos sistemas deben incluir como primer parámetro la ruta del fichero de configuración de
las cámaras.
La ejecución del programa basado en Birchfield requiere la inclusión por parámetros de los
valores de disparidad máxima y los cinco parámetros necesarios para el algoritmo.
Ejemplo: Birchfield D:\u\agl\800x600.dcf 100 25 5 12 15 25
El método basado en bloques requiere el paso por parámetros de la disparidad máxima, el
tamaño de la ventana de cálculo y el criterio de semejanza a utilizar. Éste último se introducirá
como un número, correspondiendo el 1 a Suma de Diferencias Absolutas, el 2 a Suma de Diferencias Cuadráticas y el 3 a Correlación Cruzada Normalizada.
Ejemplo: Bloques D:\u\agl\800x600.dcf 100 3 1
CAPÍTULO 4. SISTEMA, DISEÑO Y DESARROLLO
37
5
Experimentos Realizados y Resultados
Dado que el objetivo final del proyecto es el desarrollo de un sistema de cálculo de profundidad
en tiempo real, los resultados del mismo se evaluarán en función de la precisión del cálculo y del
número de imagenes por segundo obtenidas.
Para la medida de la velocidad se tomará el funcionamiento del sistema completo, sin atenernos a restricciones de la escena, ya que ésta no influye en la medida de la velocidad. Para
estimar la precisión del sistema se ha realizado una modificación en el sistema final para que
tome imágenes desde archivo en vez de desde las cámaras. Las imágenes a utilizar se han obtenido de http://vision.middlebury.edu/stereo/. En esta página se encuentran varios pares de
imágenes con su correspondiente disparidad real, con lo cual se puede evaluar de forma precisa
el error cometido.
5.1.
5.1.1.
Análisis de la velocidad
Pruebas con el método de búsqueda por zonas
Las pruebas se han realizado sobre pares de imágenes de tamaño 640x480 y 320x240 píxeles
para todos los métodos de cálculo. En el caso de Suma de Diferencias Absolutas se ha añadido
un tamaño de imagen de 800x600. Este tamaño no se ha incluído en los otros métodos ya que
daba como resultado velocidades demasiado bajas. Para cada tamaño de imagen se ha probado
con dos tamaños de ventana de cálculo, 3x3 y 5x5 píxeles; y por cada uno de estos tamaños de
ventana se han efectuado cinco pruebas, variando el valor de la disparidad máxima entre 50 y
255. El resultado se ha expresado en las tablas en "frames"por segundo.
La escena evaluada durante las pruebas con el método de búsqueda por bloques es similar a
la presentada a continuación, mientras que para el método de Birchfield se utilizó esta misma
escena como fondo con una figura personal en primer plano.
39
Desarrollo de herramientas de apoyo a la estereovisión
Figura 5.1: Ejemplo de escena evaluada
Suma de Diferencias Absolutas
!!!
!!!!
máxima
!!!Disparidad
!!!
!!!!
Tamaño ventana
!!!
3x3
5x5
50
100
150
200
255
1,22
0,21
0,59
0,12
0,5
0,08
0,41
0,07
0,36
0,06
Cuadro 5.1: SAD 800x600
!!!!
!!!
máxima
!!!Disparidad
!!!
!!!!
Tamaño ventana
!!!
3x3
5x5
50
100
150
200
255
2,15
0,37
1,24
0,21
0,92
0,15
0,77
0,13
0,7
0,1
Cuadro 5.2: SAD 640x480
!!!
!!!!
!!!Disparidad máxima
!!!!
!!!!
Tamaño ventana
!!
3x3
5x5
50
100
150
200
255
8,98
1,68
8,36
1,37
6,15
1,04
5,77
0,97
5,37
0,8
Cuadro 5.3: SAD 320x240
40
CAPÍTULO 5. EXPERIMENTOS REALIZADOS Y RESULTADOS
Desarrollo de herramientas de apoyo a la estereovisión
Los resultados obtenidos con los dos tamaños de ventana de cálculo son los siguientes:
Figura 5.2: SAD con ventana de 3x3
Figura 5.3: SAD con ventana de 5x5
CAPÍTULO 5. EXPERIMENTOS REALIZADOS Y RESULTADOS
41
Desarrollo de herramientas de apoyo a la estereovisión
Suma de Diferencias Cuadráticas
!!!!
!!!
máxima
!!!Disparidad
!!!
!!!!
Tamaño ventana
!!!
3x3
5x5
50
100
150
200
255
0,48
<0,01
0,31
<0,01
0,2
<0,01
0,18
<0,01
0,17
<0,01
Cuadro 5.4: SSD 640x480
!!!
!!!!
!!!Disparidad máxima
!!!!
!!!!
Tamaño ventana
!!
3x3
5x5
50
100
150
200
255
2,43
0,31
2,14
0,26
1,56
0,19
1,43
0,18
1,35
0,16
Cuadro 5.5: SSD 320x240
Los resultados obtenidos para la misma escena que en el caso anterior con los dos tamaños
de ventana de cálculo son los siguientes:
Figura 5.4: SSD con ventana de 3x3
42
CAPÍTULO 5. EXPERIMENTOS REALIZADOS Y RESULTADOS
Desarrollo de herramientas de apoyo a la estereovisión
Figura 5.5: SSD con ventana de 5x5
Correlación Cruzada Normalizada
!!!
!!!!
máxima
!!!Disparidad
!!!
!!!!
Tamaño ventana
!!!
3x3
5x5
50
100
150
200
255
<0,01
<0,01
<0,01
<0,01
<0,01
<0,01
<0,01
<0,01
<0,01
<0,01
Cuadro 5.6: NCC 640x480
!!!!
!!!
máxima
!!!Disparidad
!!!
!!!!
Tamaño ventana
!!!
3x3
5x5
50
100
150
200
255
1,32
0,36
1,03
0,25
0,86
0,14
0,68
0,07
0,47
<0,01
Cuadro 5.7: NCC 320x240
Los resultados obtenidos con los dos tamaños de ventana de cálculo son los siguientes:
CAPÍTULO 5. EXPERIMENTOS REALIZADOS Y RESULTADOS
43
Desarrollo de herramientas de apoyo a la estereovisión
Figura 5.6: NCC con ventana de 3x3
Figura 5.7: NCC con ventana de 5x5
5.1.2.
Pruebas con el método de Birchfield-Tomasi
Las pruebas realizadas con el método de Birchfield se han efectuado utilizando los tres
tamaños de imagen usados en el método de búsqueda por bloques y con los mismos valores de
disparidad. Así mismo se ha procedido a variar los parámetros utilizados en el cálculo, pero estas
variaciones produjeron unas diferencias en el resultados final menores a 0,02 fps. Es por ello que
no se han inluido estas variaciones en los resultados listados a continuación, correspondiendose
éstos a los parámetros especificados por defecto.
44
CAPÍTULO 5. EXPERIMENTOS REALIZADOS Y RESULTADOS
Desarrollo de herramientas de apoyo a la estereovisión
!!!
!!!!
Disparidad máxima
!!!
!!!
!!!!
Tamaño imagen
!!
!
800x600
640x480
320x240
50
100
150
200
255
2,41
3,7
17,44
1,4
2,31
10,42
0,97
1,72
7,55
0,79
1,36
6,54
0,58
1,08
5,7
Cuadro 5.8: Resultados del método de Birchfield
5.2.
Analisis de la precisión
Como se ha comentado anteriormente, para valorar la precisión de los distintos algoritmos de cálculo de la disparidad se van ha utilizar dos pares de imágenes provenientes de
http://vision.middlebury.edu/stereo/ de las que se dispone del valor real de la disparidad. En
las imágenes de disparidad que nos proporcionan, la disparidad está codificada entre los 0.25 y
los 63.75 píxeles; para poder comparar nuestros resultados con los disponibles, ésta disparidad
se recodificará entre 1 y 255 píxeles. Los conjuntos de imágenes utilizados son Cones y Teddy,
de un tamaño de 450x375 pixeles.
Se utilizarán dos medidas de error para evaluar la precisión de los resultados obtenidos: el
porcentaje de píxeles erróneos y el error medio de cada pixel.
Figura 5.8: Imágenes izquierda y derecha del conjunto Cones
CAPÍTULO 5. EXPERIMENTOS REALIZADOS Y RESULTADOS
45
Desarrollo de herramientas de apoyo a la estereovisión
Figura 5.9: Imágenes izquierda y derecha del conjunto Teddy
En las siguientes imágenes se aprecia la imagen de disparidad original a la izquierda y la
recodificada a la derecha.
Figura 5.10: Disparidad real de Cones
46
CAPÍTULO 5. EXPERIMENTOS REALIZADOS Y RESULTADOS
Desarrollo de herramientas de apoyo a la estereovisión
Figura 5.11: Disparidad real de Teddy
A continuación se van a mostrar los resultados obtenidos con cada uno de los algoritmos
utilizados de forma gráfica, comparados con la disparidad real utilizada, y de forma analítica
con tablas con los errores obtenidos.
5.2.1.
Pruebas con el método de búsqueda por zonas
Suma de Diferencias Absolutas
Figura 5.12: Resultados con SAD para un tamaño de 3x3, conjunto Cones
CAPÍTULO 5. EXPERIMENTOS REALIZADOS Y RESULTADOS
47
Desarrollo de herramientas de apoyo a la estereovisión
Figura 5.13: Resultados con SAD para un tamaño 5x5, conjunto Cones
Figura 5.14: Resultados con SAD para un tamaño de 3x3, conjunto Teddy
48
CAPÍTULO 5. EXPERIMENTOS REALIZADOS Y RESULTADOS
Desarrollo de herramientas de apoyo a la estereovisión
Figura 5.15: Resultados con SAD para un tamaño de 5x5, conjunto Teddy
Tamaño 3x3
Tamaño 5x5
% error
Teddy Cones
46,48 40,99
46,33 40,74
Error medio
Teddy Cones
13,57 12,26
12,88 11,38
Cuadro 5.9: Resultados con SAD
CAPÍTULO 5. EXPERIMENTOS REALIZADOS Y RESULTADOS
49
Desarrollo de herramientas de apoyo a la estereovisión
Suma de Diferencias Cuadráticas
Figura 5.16: Resultados con SSD para un tamaño de 3x3, conjunto Cones
Figura 5.17: Resultados con SSD para un tamaño 5x5, conjunto Cones
50
CAPÍTULO 5. EXPERIMENTOS REALIZADOS Y RESULTADOS
Desarrollo de herramientas de apoyo a la estereovisión
Figura 5.18: Resultados con SSD para un tamaño de 3x3, conjunto Teddy
Figura 5.19: Resultados con SSD para un tamaño de 5x5, conjunto Teddy
Tamaño 3x3
Tamaño 5x5
% error
Teddy Cones
45,89 40,59
44,87 39,05
Error medio
Teddy Cones
11,99 11,85
11,14 12,18
Cuadro 5.10: Resultados con SSD
CAPÍTULO 5. EXPERIMENTOS REALIZADOS Y RESULTADOS
51
Desarrollo de herramientas de apoyo a la estereovisión
Correlación Cruzada Normalizada
Figura 5.20: Resultados con CNN para un tamaño de 3x3, conjunto Cones
Figura 5.21: Resultados con CNN para un tamaño 5x5, conjunto Cones
52
CAPÍTULO 5. EXPERIMENTOS REALIZADOS Y RESULTADOS
Desarrollo de herramientas de apoyo a la estereovisión
Figura 5.22: Resultados con CNN para un tamaño de 3x3, conjunto Teddy
Figura 5.23: Resultados con CNN para un tamaño de 5x5, conjunto Teddy
Tamaño 3x3
Tamaño 5x5
% error
Teddy Cones
34,03 35,53
34,07 35,32
Error medio
Teddy Cones
7,83
9,17
7,76
9,99
Cuadro 5.11: Resultados con CNN
CAPÍTULO 5. EXPERIMENTOS REALIZADOS Y RESULTADOS
53
Desarrollo de herramientas de apoyo a la estereovisión
5.2.2.
Pruebas con el método de Birchfield
Figura 5.24: Resultados con Birchfield, conjunto Cones
Figura 5.25: Resultados con Birchfield, conjunto Teddy
Tamaño 3x3
% error
Teddy Cones
21,4 25,55
Error medio
Teddy Cones
5,11
5,98
Cuadro 5.12: Resultados con Birchfield
54
CAPÍTULO 5. EXPERIMENTOS REALIZADOS Y RESULTADOS
Desarrollo de herramientas de apoyo a la estereovisión
5.3.
Comparativa de resultados con el estado del arte
Los resultados obtenidos con los algoritmos de cálculo utilizados difieren mucho del actual
estado del arte. En el sitio web citado anteriormente, http://vision.middlebury.edu/stereo, existe
una relación de los algoritmos que obtienen mejores resultados en conjuntos de imágenes como
los utilizados en este estudio. En el se puede apreciar que los mejores algoritmos dan un 7-8 % de
error en los conjuntos de imágenes aquí utilizados, tomando, dependiendo del algoritmo, entre 20
y 30 segundos por cada par de imágenes. Si bajamos en la lista de resultados proporcionados por
Middlebury, encontramos algoritmos que sí consiguen una velocidad de tiempo real, obteniendo
resultados de entre 13 y 28 % píxeles erróneos, lo cual es consistente con los resultados obtenidos
en este proyecto.
CAPÍTULO 5. EXPERIMENTOS REALIZADOS Y RESULTADOS
55
6
Conclusiones y trabajo futuro
En este capítulo se van a desarrollar las conclusiones a las que se han llegado sobre los
objetivos que se plantearon en la introducción del presente documento. Así mismo se sugieren
posibles líneas de investigación para la mejora de este proyecto y para trabajos futuros.
La bondad de cada uno de los métodos de cálculo de disparidad utilizados se medirá en
función del tiempo de cálculo y de la precisión obtenida.
6.1.
Conclusiones sobre los sistemas físicos
Como se vió en el capítulo 4, de los dos sistemas físicos de los que partíamos, solo es viable
la aplicación del proyecto sobre las cámaras IP, ya que el sistema Firewire necesitaría que la
escena fuese grabada a mucha más distancia de la que es posible. Además de esto, el sistema
formado por cámaras IP presenta mucha flexibilidad, ya que, como se comentó en su momento,
es un sistema móvil y regulable. Ésto es, nos permite grabar distintas escenas, así como modificar
la distancia existente entre las cámaras, con lo que variaríamos entre qué distancias desde las
cámaras el sistema es capaz de calcular la disparidad.
También hay que mencionar la posibilidad de añadir más cámaras al sistema de captura,
y contar con más imágenes para el cálculo de la disparidad. Esto conllevará, por una parte un
incremento notable del tiempo de cálculo, al añadir una línea epipolar más en la que buscar
correspondencias para cada punto. Por otra parte, también dispondremos de más información
para el cálculo de correspondencias, así como la posibilidad de obtener en la nueva imagen
información sobre objetos ocluidos en alguna de las dos imágenes originales, lo cual mejorará la
precisión de el mapa de disparidad, sobre todo en los bordes de los objetos cercanos.
57
Desarrollo de herramientas de apoyo a la estereovisión
6.2.
Conclusiones sobre la restricción temporal
El nivel de sincronización temporal entre los instantes de captura obtenido, mejor a 1ms, es
suficiente para los objetivos de este proyecto, pero no se ha comprobado su funcionamiento frente
a escenas a alta velocidad. Si un estudio sobre el sistema de captura en estas circustancias produce
diferencias en las capturas, se deberá añadir al mismo algún método de disparo sincronizado.
Los método de disparo que podrán utilizarse dependerán de los elementos utilizados. Para
poder usar en método de disparo por software es necesario que la tarjeta capturadora que utiliza
el PC sea compatible con esta característica; para un método de disparo hardware necesitamos
que las cámaras tengan las conexiones necesarias. En nuestro caso, únicamente sería posible la
inclusión de ésta última.
6.3.
Conclusiones sobre la restricción de alineación
La precisión de la alineación epipolar está directamente relacionada con la precisión del
sistema de calibración del que disponemos. Como se puede ver en las conclusiones expuestas en
[3], la precisión del sistema de calibración es fiable, pero mejorable según las líneas de trabajo
futuro propuestas. Entre ellas es destacable la utilización de un detector de esquinas de Harris u
otro proceso de extracción de características fiable, a fin de reducir la aleatoriedad en el proceso
de marcado manual de las esquinas.
Otra línea de mejora concerniente a éste punto sería, partiendo de un sistema de calibración
dado, introducirlo como un paso opcional al iniciar el sistema; de manera que tengamos todas
las herramientas necesarias para la estereovisión integradas. Utilizando el método de calibración
de Javier García Ocón necesitaríamos primeramente pasar el algoritmo a código C++.
6.4.
Conclusiones sobre el cálculo de disparidad mediante búsqueda por bloques
De los resultados obtenidos en el capítulo anterior se pueden extraer varias conclusiones
válidas para los tres algoritmos de cálculo utilizados. La primera de ellas es la escasa velocidad
alcanzada, siendo en el mejor de los casos, inferior a los 10 fps. Estos resultados pueden mejorarse
mediante la inclusión en el algoritmo de una matriz en la que almacenar los resultados de las
operaciones entre las imágenes, de manera que no se realice varias veces la misma operación.
También hay que señalar los problemas que presenta este método para tratar con grandes
superficies, ya sean lisas o presentes brillos o cambios de color. Se puede apreciar este efecto
en el caso mostrado en el capítulo anterior evaluando la puerta y la superficie de pared de la
parte inferior de la imagen. Parte de estos errores vienen dados por la diferencia de intensidad
entre píxeles correspondientes, ya que han sido grabados con distintas cámaras. Esta situación
es subsanada en el método de Correlación Cruzada Normalizada, pero no así en los otros dos.
Para paliar esta situación sería necesaria una igualación de los niveles de gris de las imágenes,
que resultaría en una mejora del resultado, pero en un empeoramiento del tiempo de cálculo.
6.4.1.
Suma de Diferencias Absolutas
De los tres algoritmos de cálculo estudiados dentro del método de búsqueda por bloques,
este es el que obtiene mejor rendimiento temporal, pero menor precisión en el resultado. La
58
CAPÍTULO 6. CONCLUSIONES Y TRABAJO FUTURO
Desarrollo de herramientas de apoyo a la estereovisión
diferencia entre los dos tamaños de ventana de cálculo no es apreciable, ya que mejora ciertas
zonas mientras que empeora otras. Aún así, la utilización de este método es poco recomendable,
ya que genera grandes zonas con una disparidad errónea.
6.4.2.
Suma de Diferencias Cuadráticas
Este algoritmo mejora ligeramente los resultados obtenidos por el anterior, disminuyendo
en gran medida la velocidad final del sistema. Este método genera menos zonas de disparidad
errónea, y más pequeñas, pero el empeoramiento que conlleva en velocidad de cálculo lo hacen
poco adecuado.
6.4.3.
Correlación Cruzada Normalizada
Los resultados obtenidos mediante este algoritmo mejora sensiblemente los obtenidos mediante Suma de Diferencias Cuadráticas, incrementando notablemente el tiempo de cálculo.
Como se ha visto, colocándonos en el equilibrio entre precisión y velocidad de cálculo entre
los métodos de búsqueda por bloque, en caso de necesitar más el primero, nos decantaremos por
el método de Correlación Cruzada Normalizada, que ofrece sin duda los mejores resultados de
los tres. En caso de primar la velocidad de cálculo elegiremos la Suma de Diferencias Absolutas.
6.5.
Conclusiones sobre el cálculo de disparidad mediante el método de Birchfield
La primero que hay que destacar del método de cálculo de disparidad mediante el método de
Birchfield es la aproximación bajo ciertas circunstancias a la velocidad aceptada como tiempo
real, 25 fps. De los métodos probados, es el que mayor velocidad nos proporciona, duplicando los
resultados obtenidos con él método más rápido de búsqueda por bloques. Respecto a la precisión,
los mejores resultados de todos los algoritmos vistos, estando los errores concentrados en la zona
izquierda de la imaagen, en la cual éste algoritmo no puede obtener buenos resultados.
También hay que señalar que varios de los errores de este método pueden subsanarse o
paliarse en cierta medida mediante la variación de forma empírica de los parámetros de cálculo,
pudiendo adaptar el método a la escena que se esté grabando en ese momento.
Comparando este método con los expuestos anteriormente, vemos que nos aporta los mejores
resultados con mayor velocidad, es por ello que la elección de este método para el cálculo de la
disparidad es la más recomendable.
CAPÍTULO 6. CONCLUSIONES Y TRABAJO FUTURO
59
Bibliografía
[1] Alessandro Verri Andrea Fusiello, Emamuele Trucco. A compact algorithm for rectification
of stereo pairs. Springer-Verlag, 2000.
[2] Stan Birchfield y Carlo Tomasi. Depth discontinuities by pixel-to-pixel stereo. International
Journal of Computer Vision, pages 269–293, 1999.
[3] Javier García Ocón. Autocalibración y sincronización de múltiples cámaras PTZ. PhD
thesis, Universidad Autónoma de Madrid, Mayo 2007.
[4] Andrew Zisserman Richard Hartley. Multiple View Geometry in Computer Vision. Cambridge University Press, 2003.
[5] Olivier Faugeras y Quang-Tuan Luong. The geometry of multiples images. MIT Press, 2001.
[6] Olivier Faugeras. Three-dimensional computer vision: a geometric viewpoint. MIT Press,
1993.
[7] Yao Wang, Jörn Osteermann, and Ya-Qin Zhang. Video Processing and comunications.
Prentice-Hall, 2001.
[8] Gary Bradski y Adrian Kaehler. Learning Opencv. O’Reilly Media, 2008.
[9] D. Scharstein and R. Szeliski. High-accuracy stereo depth maps using structured light.
IEEE Computer Society Conference on Computer Vision and Pattern Recognition, 1:195–
202, Junio 2003.
[10] Z. Zhang. A flexible new technique for camera calibration. IEEE Transactions on Pattern
Analysis ans Machine Intelligence, 2000.
61
Desarrollo de herramientas de apoyo a la estereovisión
62
BIBLIOGRAFÍA
A
Presupuesto
1) Ejecución Material
Compra de ordenador personal (Software incluido)
2.200 ¤
Alquiler cámaras IP
880 ¤
Alquiler cámaras Firewire
720 ¤
Alquiler de impresora láser durante 6 meses
280 ¤
Material de oficina
130 ¤
4.210 ¤
Total de ejecución material
2) Gastos generales
478 ¤
sobre Ejecución Material
3) Beneficio Industrial
209 ¤
sobre Ejecución Material
4) Honorarios Proyecto
1800 horas a 15 ¤/ hora
27000 ¤
5) Material fungible
Gastos de impresión
280 ¤
Encuadernación
200 ¤
6) Subtotal del presupuesto
32.377 ¤
Subtotal Presupuesto
7) I.V.A. aplicable
5.180,32 ¤
16 % Subtotal Presupuesto
8) Total presupuesto
37.557,32 ¤
Total Presupuesto
63
Desarrollo de herramientas de apoyo a la estereovisión
Madrid, JULIO 2010
El Ingeniero Jefe de Proyecto
Fdo.: Alberto Garzón Leo
Ingeniero Superior de Telecomunicación
64
APÉNDICE A. PRESUPUESTO
B
Pliego de condiciones
Pliego de condiciones
Este documento contiene las condiciones legales que guiarán la realización, en este proyecto,
de un Desarrollo de herramientas de apoyo a la estereovisión. En lo que sigue, se supondrá que
el proyecto ha sido encargado por una empresa cliente a una empresa consultora con la finalidad
de realizar dicho sistema. Dicha empresa ha debido desarrollar una línea de investigación con
objeto de elaborar el proyecto. Esta línea de investigación, junto con el posterior desarrollo de
los programas está amparada por las condiciones particulares del siguiente pliego.
Supuesto que la utilización industrial de los métodos recogidos en el presente proyecto ha
sido decidida por parte de la empresa cliente o de otras, la obra a realizar se regulará por las
siguientes:
Condiciones generales.
1. La modalidad de contratación será el concurso. La adjudicación se hará, por tanto, a la
proposición más favorable sin atender exclusivamente al valor económico, dependiendo de
las mayores garantías ofrecidas. La empresa que somete el proyecto a concurso se reserva
el derecho a declararlo desierto.
2. El montaje y mecanización completa de los equipos que intervengan será realizado totalmente por la empresa licitadora.
3. En la oferta, se hará constar el precio total por el que se compromete a realizar la obra
y el tanto por ciento de baja que supone este precio en relación con un importe límite si
este se hubiera fijado.
4. La obra se realizará bajo la dirección técnica de un Ingeniero Superior de Telecomunicación,
auxiliado por el número de Ingenieros Técnicos y Programadores que se estime preciso para
el desarrollo de la misma.
5. Aparte del Ingeniero Director, el contratista tendrá derecho a contratar al resto del personal, pudiendo ceder esta prerrogativa a favor del Ingeniero Director, quien no estará
obligado a aceptarla.
65
Desarrollo de herramientas de apoyo a la estereovisión
6. El contratista tiene derecho a sacar copias a su costa de los planos, pliego de condiciones y
presupuestos. El Ingeniero autor del proyecto autorizará con su firma las copias solicitadas
por el contratista después de confrontarlas.
7. Se abonará al contratista la obra que realmente ejecute con sujeción al proyecto que sirvió
de base para la contratación, a las modificaciones autorizadas por la superioridad o a las
órdenes que con arreglo a sus facultades le hayan comunicado por escrito al Ingeniero
Director de obras siempre que dicha obra se haya ajustado a los preceptos de los pliegos
de condiciones, con arreglo a los cuales, se harán las modificaciones y la valoración de las
diversas unidades sin que el importe total pueda exceder de los presupuestos aprobados. Por
consiguiente, el número de unidades que se consignan en el proyecto o en el presupuesto,
no podrá servirle de fundamento para entablar reclamaciones de ninguna clase, salvo en
los casos de rescisión.
8. Tanto en las certificaciones de obras como en la liquidación final, se abonarán los trabajos
realizados por el contratista a los precios de ejecución material que figuran en el presupuesto
para cada unidad de la obra.
9. Si excepcionalmente se hubiera ejecutado algún trabajo que no se ajustase a las condiciones
de la contrata pero que sin embargo es admisible a juicio del Ingeniero Director de obras, se
dará conocimiento a la Dirección, proponiendo a la vez la rebaja de precios que el Ingeniero
estime justa y si la Dirección resolviera aceptar la obra, quedará el contratista obligado a
conformarse con la rebaja acordada.
10. Cuando se juzgue necesario emplear materiales o ejecutar obras que no figuren en el presupuesto de la contrata, se evaluará su importe a los precios asignados a otras obras o
materiales análogos si los hubiere y cuando no, se discutirán entre el Ingeniero Director y
el contratista, sometiéndolos a la aprobación de la Dirección. Los nuevos precios convenidos
por uno u otro procedimiento, se sujetarán siempre al establecido en el punto anterior.
11. Cuando el contratista, con autorización del Ingeniero Director de obras, emplee materiales
de calidad más elevada o de mayores dimensiones de lo estipulado en el proyecto, o sustituya
una clase de fabricación por otra que tenga asignado mayor precio o ejecute con mayores
dimensiones cualquier otra parte de las obras, o en general, introduzca en ellas cualquier
modificación que sea beneficiosa a juicio del Ingeniero Director de obras, no tendrá derecho
sin embargo, sino a lo que le correspondería si hubiera realizado la obra con estricta sujeción
a lo proyectado y contratado.
12. Las cantidades calculadas para obras accesorias, aunque figuren por partida alzada en el
presupuesto final (general), no serán abonadas sino a los precios de la contrata, según las
condiciones de la misma y los proyectos particulares que para ellas se formen, o en su
defecto, por lo que resulte de su medición final.
13. El contratista queda obligado a abonar al Ingeniero autor del proyecto y director de obras
así como a los Ingenieros Técnicos, el importe de sus respectivos honorarios facultativos
por formación del proyecto, dirección técnica y administración en su caso, con arreglo a
las tarifas y honorarios vigentes.
14. Concluida la ejecución de la obra, será reconocida por el Ingeniero Director que a tal efecto
designe la empresa.
15. La garantía definitiva será del 4
16. La forma de pago será por certificaciones mensuales de la obra ejecutada, de acuerdo con
los precios del presupuesto, deducida la baja si la hubiera.
17. La fecha de comienzo de las obras será a partir de los 15 días naturales del replanteo oficial
de las mismas y la definitiva, al año de haber ejecutado la provisional, procediéndose si no
existe reclamación alguna, a la reclamación de la fianza.
66
APÉNDICE B. PLIEGO DE CONDICIONES
Desarrollo de herramientas de apoyo a la estereovisión
18. Si el contratista al efectuar el replanteo, observase algún error en el proyecto, deberá
comunicarlo en el plazo de quince días al Ingeniero Director de obras, pues transcurrido
ese plazo será responsable de la exactitud del proyecto.
19. El contratista está obligado a designar una persona responsable que se entenderá con el
Ingeniero Director de obras, o con el delegado que éste designe, para todo relacionado
con ella. Al ser el Ingeniero Director de obras el que interpreta el proyecto, el contratista
deberá consultarle cualquier duda que surja en su realización.
20. Durante la realización de la obra, se girarán visitas de inspección por personal facultativo
de la empresa cliente, para hacer las comprobaciones que se crean oportunas. Es obligación
del contratista, la conservación de la obra ya ejecutada hasta la recepción de la misma,
por lo que el deterioro parcial o total de ella, aunque sea por agentes atmosféricos u otras
causas, deberá ser reparado o reconstruido por su cuenta.
21. El contratista, deberá realizar la obra en el plazo mencionado a partir de la fecha del
contrato, incurriendo en multa, por retraso de la ejecución siempre que éste no sea debido
a causas de fuerza mayor. A la terminación de la obra, se hará una recepción provisional
previo reconocimiento y examen por la dirección técnica, el depositario de efectos, el interventor y el jefe de servicio o un representante, estampando su conformidad el contratista.
22. Hecha la recepción provisional, se certificará al contratista el resto de la obra, reservándose
la administración el importe de los gastos de conservación de la misma hasta su recepción
definitiva y la fianza durante el tiempo señalado como plazo de garantía. La recepción
definitiva se hará en las mismas condiciones que la provisional, extendiéndose el acta
correspondiente. El Director Técnico propondrá a la Junta Económica la devolución de la
fianza al contratista de acuerdo con las condiciones económicas legales establecidas.
23. Las tarifas para la determinación de honorarios, reguladas por orden de la Presidencia
del Gobierno el 19 de Octubre de 1961, se aplicarán sobre el denominado en la actualidad
"Presupuesto de Ejecución de Contrata anteriormente llamado "Presupuesto de Ejecución
Material"que hoy designa otro concepto.
2
Condiciones particulares.
La empresa consultora, que ha desarrollado el presente proyecto, lo entregará a la empresa
cliente bajo las condiciones generales ya formuladas, debiendo añadirse las siguientes condiciones
particulares:
1. La propiedad intelectual de los procesos descritos y analizados en el presente trabajo,
pertenece por entero a la empresa consultora representada por el Ingeniero Director del
Proyecto.
2. La empresa consultora se reserva el derecho a la utilización total o parcial de los resultados
de la investigación realizada para desarrollar el siguiente proyecto, bien para su publicación
o bien para su uso en trabajos o proyectos posteriores, para la misma empresa cliente o
para otra.
3. Cualquier tipo de reproducción aparte de las reseñadas en las condiciones generales, bien
sea para uso particular de la empresa cliente, o para cualquier otra aplicación, contará
con autorización expresa y por escrito del Ingeniero Director del Proyecto, que actuará en
representación de la empresa consultora.
4. En la autorización se ha de hacer constar la aplicación a que se destinan sus reproducciones
así como su cantidad.
APÉNDICE B. PLIEGO DE CONDICIONES
67
Desarrollo de herramientas de apoyo a la estereovisión
5. En todas las reproducciones se indicará su procedencia, explicitando el nombre del proyecto, nombre del Ingeniero Director y de la empresa consultora.
6. Si el proyecto pasa la etapa de desarrollo, cualquier modificación que se realice sobre él,
deberá ser notificada al Ingeniero Director del Proyecto y a criterio de éste, la empresa
consultora decidirá aceptar o no la modificación propuesta.
7. Si la modificación se acepta, la empresa consultora se hará responsable al mismo nivel que
el proyecto inicial del que resulta el añadirla.
8. Si la modificación no es aceptada, por el contrario, la empresa consultora declinará toda
responsabilidad que se derive de la aplicación o influencia de la misma.
9. Si la empresa cliente decide desarrollar industrialmente uno o varios productos en los que
resulte parcial o totalmente aplicable el estudio de este proyecto, deberá comunicarlo a la
empresa consultora.
10. La empresa consultora no se responsabiliza de los efectos laterales que se puedan producir en el momento en que se utilice la herramienta objeto del presente proyecto para la
realización de otras aplicaciones.
11. La empresa consultora tendrá prioridad respecto a otras en la elaboración de los proyectos
auxiliares que fuese necesario desarrollar para dicha aplicación industrial, siempre que
no haga explícita renuncia a este hecho. En este caso, deberá autorizar expresamente los
proyectos presentados por otros.
12. El Ingeniero Director del presente proyecto, será el responsable de la dirección de la aplicación industrial siempre que la empresa consultora lo estime oportuno. En caso contrario,
la persona designada deberá contar con la autorización del mismo, quien delegará en él las
responsabilidades que ostente.
68
APÉNDICE B. PLIEGO DE CONDICIONES
C
Manual de utilización
1. Colocar el archivo de configuración config.ini y el archivo con las matrices de rectificado
Matrices.txt en la misma carpeta en la que esté el ejecutable.
2. Ejecutar por línea de comandos según el método
-Bloques D:\u\agl\800x600.dcf 100 3 1 Los parámetros se corresponden a el archivo de
configuración de las cámaras, la disparidad máxima, el tamaño de la ventana de cálculo y el
método de obtención de la disparidad (1-SAD, 2-SSD, 3-NCC)
-Birchfield D:\u\agl\800x600.dcf 100 25 5 12 15 25 Los parámetros se corresponden a el
archivo de configuración de las cámaras, la disparidad máxima, y los cinco parámetros de cálculo
del algoritmo de Birchfield.
3. Una vez esté el programa en funcionamiento, al hacer click sobre la imagen de disparidad,
se mostrará por la ventana de comandos las coordenadas pixel del punto marcado, así como su
distancia a las cámaras expresada en milímetros.
69