De yotta a yocto. - UAM-I

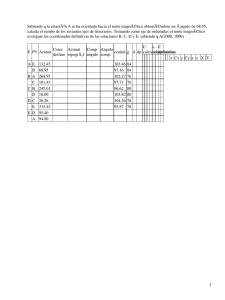
De yotta a yocto.
Caupolicán Muñoz Gamboa,
UAM–Iztapalapa
cientı́ficos y los técnicos, ası́ como las que se requieren en todas las transacciones comerciales. Algunos
de estos patrones son el metro, el kilogramo, el grado centı́grado y el segundo, pero también ha sido necesario disponer de medios para designar las grandes y pequeñas magnitudes derivadas de éstos, como el kilómetro o el miligramo. Tales formas se resumen en la Tabla 1, donde se aprecia la enorme magnitud que representa el yotajoule, ası́ como la pequeña dimensión de un yoctogramo.
Recibido: 07 diciembre 2009.
Aceptado: 15 enero 2010.
Abstract
In this article several aspects of scientific disciplines
and craftsmen are presented. They have the common
denominator of smallness, unusual and surprising.
The IS units are used for this purpose. Tires and
fractals have interesting coincidences.
Resumen
Muchas veces los inventos, las matemáticas, la tecnologı́a, la ciencia y hasta las artesanı́as encuentran cosas en común no sólo en lo novedoso, sino también en
lo grandioso, en lo detallado o en lo minúsculo. En este sentido, en este artı́culo se comentan diversos aspectos de estas disciplinas unidas por el común denominador de las cosas pequeñas y de lo poco perceptible, de lo extraordinario y de lo impresionante, porque entre ellas se encuentran muchos interesantes puntos en común. Al mismo tiempo se consideran las herramientas que se disponen por parte del Sistema Internacional de Unidades (SI) para designar dimensiones que van desde lo muy grande a lo muy pequeño.
Las grandes diferencias que hay entre los extremos
que representan los prefijos de la Tabla 1 son útiles tanto entre las cosas materiales como en las imaginarias. Esto es aunque la realidad y lo concreto suelen verse como un par antagónico del compuesto por la fantası́a y la ficción, lo cual equivale a pensar que las cosas reales (tales como un
simple neumático) y las entelequias producto de
la imaginación (tales como los fractales) no tienen nada que ver entre sı́. Sin embargo, un análisis no muy profundo nos hace llegar a la conclusión de que los mundos real e imaginario pertenecen
al mismo universo y que por ende tienen que tener
vı́nculos sólidos.
Entrando en materia se analiza lo que ocurre con
un simple neumático, objeto cotidiano muy conocido, hasta un fractal, el sorprendente objeto matemático que al ser creado en este universo riguroso tiene todas las caracterı́sticas de un ente artificial. Sin embargo, aunque a primera vista estos dos objetos no tienen nada en común, resulta que pueden encontrarse muchas coincidencias entre ellos, las que se destacan en este artı́culo, considerando especialmente cómo se ingresa en el mundo
del caos, en oposición al que creemos perfectamente
determinado.
Historia de un neumático
El invento de la rueda es uno de los grandes acontecimientos de la humanidad cuya ocurrencia se pierde en los tiempos prehistóricos. No se sabe con seguridad qué tribu, pueblo o civilización fue la primera en tener la genial idea y mucho menos puede identificarse a su inspirado creador, sin embargo, a causa del gran impacto que ha tenido en
el desarrollo de las civilizaciones, pueden determinarse algunas de las etapas más importante de
este descubrimiento porque unas cuantas de sus
más afortunadas mejoras pueden resumirse en las
cuatro siguientes.
Introducción
La ciencia, la tecnologı́a y el comercio han requerido siempre de patrones que sirvan de referencia para las más diversas mediciones que llevan a cabo los
5
6
ContactoS 75, 5–13 (2010)
Tabla 1. Prefijos y sı́mbolos utilizados para designar las grandes y las pequeñas dimensiones
Prefijo Sı́mbolo Valor
yota
Y
1024
zeta
Z
1021
exa
E
1018
peta
P
1015
tera
T
1012
giga
G
109
mega
M
106
kilo
k
103
hecto
h
102
deca
da
10
deci
centi
mili
micro
nano
pico
femto
atto
zepto
yocto
d
c
m
µ
n
p
f
a
z
y
10−1
10−2
10−3
10−6
10−9
10−12
10−15
10−18
10−21
10−24
Ejemplo Equivalencia Comparativo de la escala (aprox.)
yotajoule
1YJ = 1024 J El sol emite en 1 s≈ 400 YJ
zetametro 1Zm = 1021 m Radio de la Vı́a Láctea ≈ 1 Zm
exasegundo
1Es = 1018 s Edad del universo ≈ 0.43 Es
petametro 1Pm = 1015 m 1 año–luz ≈ 9.454 Pm
terametro 1Tm = 1012 m Distancia del Sol a Júpiter ≈ 0.8 Tm
gigasegun
1Gs = 109 s
1 siglo = 100 años ≈ 3.154 Gs
megakelvin 1MK = 106 K* Temperatura del sol ≈ 15 MK
kilogramo
1kg = 103 g
43 tortillas ≈ 1 kg
hectogramo
1hg = 102 g
1 barra de jabón mediana ≈ 1 hg
decalitro
1daL = 10L 1 galón (USA) = 0.3785 daL
La unidad
decı́metro
10dm = 1m Altura promedio de un vaso ≈ 1 dm
centı́metro
102 cm = 1m 1 pulgada = 2.54 cm
milı́metro
103 mm = 1m Grosor de un cerillo de madera ≈ 3 mm
micrómetro 106 µm = 1m Grosor de un hilo de seda ≈ 10 µm
nanómetro
109 nm = 1m Radio del átomo de cloro 4 ≈ 0.1 nm
picogramo
1012 pg = 1g Masa de una bacteria unicelular ≈ 1 pg
femtómetro 1015 fm = 1m Radio de un protón ≈ 1 fm
attosegundo 1018 as = 1s La luz atraviesa un átomo ≈ en 1 as
zeptomol 1021 zmol = 1mol 602 átomos o moléculas ≈ 1 zmol
yoctogramo 1024 yg = 1g Masa del protón o neutrón ≈ 1.7 yg
* Aunque 0◦ C = 273.15 K, se cumple que 1 K = 1◦ C, por lo que 1 MK ≈ 1 millón de grados centı́grados.
La primera de ellas fue con seguridad la idea de lubricar el eje, porque este sencillo procedimiento reduce notablemente el esfuerzo necesario para hacer
avanzar un vehı́culo y también aminora en gran parte el natural deterioro debido a su uso. El segundo perfeccionamiento de la rueda fue posiblemente el uso del rodamiento o cojinete, porque estos dispositivos disminuyen aún más el roce y el desgaste, aumentando con ello su duración en forma considerable y prácticamente indefinida cuando se le proporciona el adecuado mantenimiento. El tercer adelanto importante relacionado con la rueda es, sin duda, el desarrollo de la rueda neumática o neumático, basada en el caucho natural porque hizo posible que el transporte se realizara con gran comodidad y facilitó con ello el desarrollo de los automóviles modernos. Por último, no puede desconocerse que
el movimiento de cualquier vehı́culo se hizo más suave con la incorporación de resortes y más adelante
con amortiguadores, los que pasaron a formar parte integral del sistema de rodamiento y suspensión.
Como puede deducirse fácilmente todos estos avances estuvieron orientados a que el vehı́culo rodara en forma más simple, que tuviera mayor duración, que fuera más cómodo su uso y que ofrecie-
ra menor resistencia al avance para que alcanzara
mayor velocidad.
Las primeras ruedas fueron posiblemente discos o cilindros muy toscos en forma de rodillos angostos
o rodajas de madera (aunque siempre las imaginamos de piedra, de acuerdo con las caricaturas de algunas historietas populares), pero la necesidad de
que fueran más durables y livianas las fue transformando poco a poco hasta la clásica y grácil rueda de carreta colonial con rayos y estructura de madera, aunque con una banda de rodamiento de hierro. Con el tiempo se requirió construirla en una sola estructura metálica con una banda de rodamiento de goma para que fuera posible usarla en los primeros automóviles.
Sin embargo, no hay que olvidar que la rueda moderna no solamente está basada en todos los adelantos
de que hemos hablado, sino que también está construida con caucho sintético de extraordinaria resistencia relleno de aire a presión, que no requiere de
una cámara, es resistente al desgaste, puede ser a
prueba de perforaciones por clavos y otros objetos
punzantes, ası́ como también a veces está construida especialmente para que su movimiento sea silen-
De yotta a yocto. Caupolicán Muñoz Gamboa.
cioso, que tenga mayor agarre al camino o que sirva para avanzar en terrenos lodosos, con nieve o con
hielo, entre muchas otras caracterı́sticas. Adicionalmente, la marcha del neumático se suaviza enormemente con un mecanismo de suspensión compuesto
básicamente de un resorte y un amortiguador (aunque algunos sistemas incluyen otros adelantos) el que
le permite mucha libertad de movimiento.
En un principio, el motor delantero y la tracción trasera de los vehı́culos significaban pérdida de potencia
y de energı́a, pero simplificaban el mecanismo de suspensión. El viejo anhelo de emular a los antiguos coches tirados por caballos, en los cuales tanto la tracción como la dirección estaban adelante, sólo se alcanzó una vez que la suspensión y el movimiento de
las ruedas delanteras permitieron darle suficiente libertad al vehı́culo con una mı́nima pérdida de potencia. Por ello, actualmente casi todos los automóviles utilizan las ruedas delanteras tanto para la dirección como para la tracción.
Por otra parte, el neumático común tiene una circunferencia aproximada de 198 cm (cuando se trata del “rin” 15) y su banda de rodamiento alcanza
una profundidad de unos 9 mm, la que está calculada normalmente para rodar cerca de 60,000 km. Como el desgaste se produce inevitablemente tanto por
el roce normal con el pavimento, como con las frenadas, la banda de rodamiento se va consumiendo lentamente hasta que el neumático debe ser reemplazado por otro nuevo. Suponiendo que el uso y el
desgaste provocado por éste es perfectamente uniforme y que no ha sufrido un deterioro catastrófico que la inutilice, con estas cifras resulta que debe efectuar más de 30 millones de vueltas a lo largo de su vida útil. En consecuencia, en cada vuelta la banda de rodamiento pierde en promedio una
delgadı́sima capa de caucho de sólo 0.3 millonésimas de milı́metro de grosor (0.3 nanómetros), cifra que es inferior a la décima parte del tamaño
de un virus común, lo que nos da una muy buena idea de su extraordinaria duración y resistencia. Esto es algo sobre lo que podrı́amos reflexionar la siguiente vez que abordemos un vehı́culo para
ir a nuestro trabajo, salir de compras o simplemente
escaparnos de vacaciones.
Estas minúsculas dimensiones pueden llegar a ser
inimaginables, pero es interesante comprobar que algunos diestros artesanos pueden lograr maravillas en
los detalles de su obra aunque, por supuesto, no se
aproximen a ellas. Sin embargo, sorprende que pue-
7
dan emular otro tipo de mı́nimas dimensiones tecnológicas como es el caso siguiente.
Alfombras persas y pixeles
Las alfombras orientales han sido a lo largo de la historia objetos no tan solo utilitarios, ya que forman
parte de los enseres tradicionales de antiguos pueblos y tribus nómadas, sino que en ocasiones llegan a ser auténticas obras de arte o son valiosas antigüedades cuyos precios alcanzan valores muy elevados. Su cotización final no sólo depende del hecho de que son artı́culos hechos a mano uno por
uno, de su calidad artı́stica, de los patrones del diseño, de su condición general de conservación y de
su antigüedad, sino que también tienen influencia
en ella el pueblo donde han sido fabricadas e, incluso, los materiales con los que han sido manufacturadas, el prestigio de los artesanos que intervinieron en su construcción, la tribu a la que pertenece y
la densidad de nudos que tiene, entre muchas otras
caracterı́sticas.
Las alfombras anudadas a mano se elaboran nudo
por nudo en una tarea que implica varios artesanos y normalmente varios meses e incluso años de
trabajo, por lo que son muy apreciadas. Los principales centros productores de este tipo de alfombras están en Persia, Turquı́a, Turkmenistán, Afganistán, Pakistán, India, Nepal y China, destacándose en ellos dos tipos de nudos entre los cuales el
turco es el más valorado. Los materiales más finos
que se utilizan son lana de oveja y seda para realizar los nudos, ası́ como pelo de cabra y algodón para el entramado, aunque la lana de la cabra de angora, conocida como mohair, también se usa para el anudado debido a las propiedades naturales
de esta fibra.
Uno de los factores de calidad más reconocidos y
tal vez uno de los más importantes es la densidad
de nudos o el número de nudos por pulgada cuadrada (knots per square inch – kpsi) o la cantidad de nudos por metro cuadrado (npmc) de cada alfombra,
lo cual no es otra cosa que el producto de los nudos por unidad de longitud que hay en cada corrida del entramado multiplicado por el número de corridas que entran en esa misma unidad. Con este
factor, la medición de calidad más aceptada resulta ser la siguiente: menos de 60 kpsi (unos 93 000
npmc) determina una alfombra de baja calidad; hasta 130 kpsi (unos 200 000 npmc) es de buena calidad; hasta 160 kpsi (unos 250 000 npmc) es de calidad media; hasta 290 kpsi (unos 450 000 npmc)
8
la alfombra es de alta calidad; en tanto que al superar estas cantidades se determina una de muy alta
calidad.
Sin embargo, como es de suponer, por encima de estas cifras los ejemplares son muy raros (muchos de
ellos tienen nombre propio, como la famosa Vienna Hunting Carpet, actualmente en el Museo Osterreichisches de Viena y el Tesoro de Hereke, propiedad de la compañı́a japonesa Gandhara Carpet Japan Co. Ltd., de Tokio). Adicionalmente debe destacarse que diversos fabricantes aseguran haber fabricado alfombras de seda anudada sobre un entramado de seda que superan el millón de npmc,
lo cual es algo realmente impresionante.1 Se trata
de especı́menes de extraordinaria calidad que incluso también pueden aparecer en el Libro de Records
de Guinness.
Resolución de un monitor
Por otra parte, en el monitor de la PC que la mayorı́a de nosotros tenemos enfrente, la calidad de
la imagen suele medirse por la resolución, que es
una forma de cuantificar la capacidad de diferenciación de los detalles de una imagen en forma similar a como se hace con los kpsi o los npmc. La resolución es una medida del número de pixeles2 diferentes que pueden distinguirse en ella. Los monitores más pequeños de 14 pulgadas, lo que significa que son más o menos de 28 por 21 cm, pueden ajustarse para disponer de una resolución variable que, para una buena visión de los detalles, va entre 800 por 600 hasta 1024 por 768 pixeles. En realidad es posible ajustarlos para una mayor resolución pero a muchas personas les parece que las letras e iconos se reducen excesivamente. Ambos extremos nos dan para la resolución total del monitor los resultados de 480 000 y 786 432 pixeles en
la pantalla, respectivamente, por lo que estos cálculos nos llevan a concluir que medidos en pixeles por
1 Varias empresas fabricantes de alfombras orientales aseguran haber superado con mucho las cantidades mencionadas en el texto, algunas de las cuales también pueden figurar en el libro de Records de Guinness. Sin embargo, es muy
conveniente aclarar que la densidad de nudos de una alfombra no suele ser uniforme en toda su superficie, por lo que debe hablarse de un promedio y, además, no es la única garantı́a de la calidad de una alfombra.
2 Un pixel (del inglés picture element–elemento de imagen)
es la menor unidad de color que compone una imagen digital. En su formato más simple, llamado RGB (del inglés RedGreen-Blue – rojo verde azul), está compuesto de estos tres
colores básicos. Mediante una codificación normal, que va entre 8 y 24 bits, un monitor permite desplegar una gama de colores (o de niveles de gris para los monitores en blanco y negro) que va desde 256 hasta más de 16 millones.
ContactoS 75, 5–13 (2010)
metro cuadrado (ppmc) estos monitores pueden tener entre 8 y 14 millones de ppmc, cifras que sorprendentemente se aproximan en npmc con las alfombras orientales más finas del mundo.
Es interesante comprobar que a pesar de que nuestra tecnologı́a ha avanzado notablemente y que las
imágenes de nuestros monitores actuales son extraordinariamente fieles y superan con mucho las cifras anteriores, como todos podemos comprobar, los
antiguos artesanos fueron capaces de emprender tareas descomunales como la de realizar una incalculable cantidad de nudo por metro cuadrado. Porque en
el caso de las alfombras que nos ocupa no sólo se trata de una tarea manual en la que cada nudo se amarra individualmente, sino que casi todas ellas son varias veces el tamaño de nuestros monitores, a pesar
de lo cual algunas de las más valiosas compiten notablemente en resolución con ellos.
Por esta razón, si uno ha tenido la curiosidad de observar alfombras orientales (en cualquier tienda especializada) y notar la hermosura de los diseños, la armonı́a de los colores, la calidad de los materiales,
el balance de los patrones, la minuciosidad y el arte con que han sido realizadas, sólo puede maravillarse con la enorme habilidad y paciencia de los artesanos que las han elaborado.
Lo cual no es obstáculo para también apreciar las herramientas que la tecnologı́a nos pone enfrente para disfrutar de una muy buena imagen de alta resolución y con millones de colores en el monitor de la
PC o en una simple fotografı́a digital.
El “copo de nieve”
Y hablando de disponer millones de pixeles en una
pantalla o de anudar pequeños trozos de seda en
un bastidor, por medio de un simple procedimiento es posible desarrollar objetos ficticios muy interesantes como el que se muestra en la Figura 1. Se inicia con un triángulo equilátero, cuyos lados se dividen en tres partes pero el tramo central se sustituye con la punta de un triángulo cuyos lados tienen un tercio de la longitud del triángulo inicial, como puede apreciarse en el primer paso. Esta operación se repite hasta el infinito en cada uno de los nuevos lados, lo que va dando como resultado una intrincada y compleja estructura que semeja un copo de nieve.
Fractales y realidad
El objeto de la Figura 1 es uno de los fractales más
sencillos, que es conocido como el “copo de nieve” de
De yotta a yocto. Caupolicán Muñoz Gamboa.
9
Figura 2. Aumento de la longitud de cada uno de los tres lados del triángulo inicial del fractal de Koch en los primeros
pasos. En cada uno de ellos se incrementa por un factor de 4/3.
Figura 1. Primeros pasos del desarrollo del fractal “copo
de nieve” de Koch.
Koch. Una de las cosas interesantes de este objeto
es que la longitud de su perı́metro crece sin lı́mite,
ya que si se considera que un lado cualquiera del
triángulo inicial tiene una longitud L, la longitud
del primer paso resulta ser 4/3 L, y los que siguen
tendrán una longitud de (4/3)2 L, (4/3)3 L, (4/3)4 L,
etc., tal como se muestra en la Figura 2 para los
primeros pasos, por lo que con cada uno de ellos la
longitud crece indefinidamente hasta el infinito.
Los fractales se obtienen en general por medio de
lo que se conoce como iteración en el plano complejo, lo que no es más que el uso continuo y reiterado de los resultados de una función (procedimiento) como valores de entrada de la misma (esto es, repitiendo el proceso como en el caso del copo de nieve de Koch). Esto significa que una expresión matemática se evalúa con uno o más valores iniciales,
lo que proporciona un primer resultado, con el que
se vuelve a evaluar la función y se obtiene un segundo resultado, con el que se procede nuevamente a evaluar la función y ası́ sucesivamente. En cierta forma este procedimiento es similar al desarrollo del fractal de Koch, en el cual se toma cada uno
de los lados, se divide en tres, se le inserta la punta
de un triángulo a cada uno de ellos, con la figura resultante se procede nuevamente a dividir en tres cada uno de los nuevos lados y se continúa en igual forma hasta el infinito.
Desarrollo de un fractal
Para entender más claramente en qué consiste el proceso de creación de un fractal supóngase que se tiene un plano determinado por sus coordenadas “alto” y “ancho” y que se utiliza una función matemática muy simple para ver como se comporta esta función en dicho plano. Como ejemplo, puede tomarse la función definida por las ecuaciones
A = a2 − b2 + c
B = 2ab + d
En estas ecuaciones a representa el alto y b el ancho,
en tanto que c y d son constantes. Entonces, el proceso se inicia con los datos de las variables, los cuales se conocen como “semilla” y se representan como (a, b), con estas ecuaciones se calculan los nuevos alto A y ancho B, los que a su vez se representan como (A, B). En esta forma las ecuaciones pueden expresarse, por una parte, como ‘el nuevo alto A es igual al alto inicial a multiplicado por el mismo alto inicial a menos el ancho inicial b multiplicado por el mismo ancho inicial b más la constante c’ y,
por la otra, como ‘el nuevo ancho B es igual a 2 veces el alto inicial a multiplicado por el ancho inicial b más la otra constante d.’
Los nuevos valores para ancho y alto, que se han indicado con las letras mayúsculas A y B, son los primeros resultados que se utilizan para evaluar nuevamente las ecuaciones y continuar con el mismo procedimiento en forma sucesiva. Técnicamente, la semilla consistente en el par (a, b), es un punto del
plano complejo con cual se obtiene como resultado un nuevo punto del mismo plano representado
por (A, B) en las ecuaciones. De este modo, con
cada paso se van obteniendo resultados diferentes
en forma sucesiva, lo que produce una secuencia
de puntos del plano los que van definiendo poco a
poco el fractal.
10
Anatomı́a de un fractal
Las distintas secuencias de resultados que se obtienen a partir de diferentes semillas se llaman órbitas, las que pueden tener comportamientos muy diferentes. Cuando en una región se obtienen resultados similares se dice que en esa zona del plano
hay estabilidad. Sin embargo, los resultados tienen
en general comportamientos muy dispares. Por ejemplo, algunos pueden escapar al infinito, otros dirigirse a un punto en particular, ciertos resultados logran
mantenerse en órbitas estables, en tanto que muchos de ellos presentan un comportamiento completamente caótico, siguiendo trayectorias insólitas, como se verá a continuación.
Caso uno.
Por ejemplo, si para el fractal definido por las ecuaciones anteriores la semilla es (0.5, 0), o sea los valores iniciales son a = 0.5 y b = 0 para alto y ancho respectivamente (con las constantes c = −0.25 y
d = 0), se trata de una órbita que después de algunas oscilaciones se dirige al punto (−0.2071, 0), porque el primer resultado es (0, 0); después, en el siguiente paso, se obtiene (−0.25, 0); al repetir la operación una vez más resulta (−0.1875, 0); para continuar con (−0.2148, 0); y seguir aproximándose al
punto (−0.2071, 0) en forma invariable.
Caso dos.
Si, por el contrario, ahora la semilla es −1 y 1 (con
c = −0.75 y d = 0), se tiene una órbita que escapa al
infinito, ya que el primer resultado es (−0.75, −2); la
secuencia sigue con (−4.1875, 3); (7.7852, −25.125);
(−571.4, −391.2); para continuar creciendo sin lı́mite e indefinidamente, como puede observarse en la
Tabla 2.
Caso tres.
Ahora, si la semilla es 0 y 0 (con c = 0 y d = 1), resulta una órbita oscilante que genera primero (0, 1), para después empezar a oscilar entre los valores (−1, 1)
y el par (0, −1) en forma invariable.
Caso cuatro.
Por último, uno de los posibles resultados estables
se obtiene cuando la semilla es −1 y 0 (con c y d =
0), ya que en este caso la serie de resultados consta
siempre del mismo par de valores (1, 0).
El hecho de que algunas semillas muy próximas entre sı́ tengan conductas muy disı́miles genera una estructura de órbitas cuya frontera se denomina fractal. Cuando esta frontera se observa a una escala cualquiera presenta autosimilaridad, lo que quie-
ContactoS 75, 5–13 (2010)
Figura 3. Ejemplo de la autosimilaridad que presenta un
fractal. Un pequeño segmento reproduce el patrón original completo, a una escala menor, pero siempre hasta el infinito.
re decir que la misma estructura (o el mismo ”tipo”de estructura) se manifiesta en todas las escalas, como puede apreciarse en el fractal de la Figura 3. Una pequeña sección reproduce por completo
al fractal aunque en menor escala, por lo que en la figura se han ampliado.
Un ejemplo real de fractal al que siempre se recurre, por ser muy obvio, es la costa de los continentes definida por la orilla que separa la tierra y el mar.
Cuando se mide su longitud con reglas rectas de diferentes largos en mapas con diferentes escalas se observa que mientras más corta es la regla y más grande la ampliación del mapa, también es mayor la longitud medida, lo que se conoce como ”paradoja de la
lı́nea costera”. Si esta serie de resultados se grafican
en una escala logarı́tmica se obtiene una lı́nea recta cuya inclinación se denomina dimensión fractal.
Al respecto, cabe recordar que en geometrı́a el punto tiene dimensión cero; la lı́nea recta, uno; las curvas del plano, dos; en tanto que los volúmenes, tienen dimensión tres. En cambio, la principal caracterı́stica de la dimensión fractal es que nunca toma valores enteros. Por ejemplo, la dimensión fractal del copo de nieve de Koch es ligeramente superior a 1.2618, por lo que es mayor a una recta, pero menor a una superficie.
En los años veinte del siglo pasado Gastón Julia, un
matemático francés, comenzó a estudiar este problema aparentemente académico y poco práctico pero ha resultado que las estructuras fractales sirven
de base para encontrar modelos muy útiles para muchos sistemas naturales de alta complejidad, lo que
ha dado lugar al desarrollo de lo que comúnmente se denomina la ciencia del caos, tema que se analizará a continuación.
Sistemas caóticos
A primera vista el universo es estable, fijo y perfectamente determinado, sin embargo, existen muchos
De yotta a yocto. Caupolicán Muñoz Gamboa.
11
Tabla 2. Secuencias de resultados de los cuatro ejemplos. 1) Convergencia a un punto,
2) crecimiento sin lı́mite, 3) oscilación y 4) resultado estable.
Constantes
Alto y ancho
Semilla
1er. resultado
2o resultado
3er. resultado
4o resultado
Convergencia
Ejemplo
c
−0.25
a
0.5
0
−0.25
−0.1875
−0.2148
−0.2071
1
d
0
b
0
0
0
0
0
0
Ejemplo 2
c
d
−0.75
0
a
b
−1
1
−0.75
−2
−4.1875
3
7.7852
−25.12
−571.4 −391.2
∞
∞
ejemplos de que esta visión no está completa porque
no incluye una serie de situaciones, acontecimientos y fenómenos que no tienen nada de estable, fijo ni determinable. Por ejemplo, el juego de billar parece ser a primera vista un sistema que se comporta en forma perfectamente estable y predecible, pero
resulta que al mismo tiempo puede ser caótico. Para demostrar esta aseveración, supóngase que se tiene una sola bola sobre la mesa, a la cual se le aplica un golpe con el taco respectivo. Los buenos jugadores pueden calcular con mucha precisión la trayectoria que va a seguir, incluso después de que la bola
ha rebotado en una o más bandas, porque en tal habilidad descansa su destreza como jugadores.
Bolas de billar
Este caso se demuestra prácticamente en la Figura 4 a) al observar con cuidado el rebote de una bola
en una banda, porque se ve claramente que el ángulo de choque es igual al ángulo de rebote, por lo
que es más o menos sencillo estimar las trayectorias. Sin embargo, cuando se disponen quince bolas en forma de triángulo al principio del juego, como en la Figura 4 b), ni siquiera con la más potente de las computadoras es posible determinar remotamente lo que ocurrirá con cada una de ellas, cuáles
serán las colisiones que se van a presentar o cuáles
bolas irán a caer en una buchaca.
La diferencia entre ambas situaciones estriba en que en el primer caso se tiene un comportamiento perfectamente definido, llamado determinista, a pesar de que los rebotes en las bandas puedan ser ligeramente diferentes a lo esperado, de que haya imperfecciones en el paño
de la mesa o de que la bola vaya perdiendo velocidad y, por consiguiente, sea más fácil que
se aparte de una trayectoria perfectamente rec-
Ejemplo 3
c
d
0
1
a
b
0
0
0
1
−1
1
0
−1
−1
1
oscila oscila
Ejemplo 4
c
d
0
0
a
b
−1
0
1
0
1
0
1
0
1
0
1
0
ta. La predicción que en este caso un buen jugador está en posibilidades de hacer será más acertada mientras mayor sea su experiencia en
el juego.
Figura 4. Juego de billar en el que se presentan a) trayectoria predecible de la bola, b) trayectorias caóticas que no
es posible predecir y c) efecto de las diferencias del ángulo de choque.
En el segundo caso, en cambio, los sucesos dependen en gran medida de pequeñı́simas diferencias que
pueden existir en la posición de cada bola, las más diminutas irregularidades que puede tener el paño, las
minúsculas variaciones que puede experimentar el
ángulo de choque y de las imperceptibles diferencias que deben producirse en los tiempos de choque
de las bolas entre sı́. Estos hechos se demuestran simplemente jugando una partida, la que es en gran medida un hecho aleatorio que se describe perfectamente como un suceso caótico.
Equilibrio inestable
Otro ejemplo de un sistema aleatorio se tiene al considerar el equilibrio inestable de un objeto cuya base es muy reducida, como un lápiz que se intenta parar apoyado en la punta. Por muchos intentos que se
12
ContactoS 75, 5–13 (2010)
bles desencadenen un proceso aleatorio que domine el comportamiento del sistema y se convierta en el
factor determinante.
Figura 5. Casos del rebote de una pelota sobre a) una
superficie lisa, b) una superficie irregular.
hagan para que permanezca en esta posición siempre caerá en forma espontánea o con la más ligera agitación o movimiento. Lo interesante del asunto es que invariablemente lo hará en alguna dirección cualquiera que no es posible anticipar, porque
ésta depende de la gran inestabilidad del objeto y de
las más mı́nimas variaciones que experimenta el propio agente que lo sacó de su posición.
Rebotes de una pelota
En un tercer caso, una pelota que se lanza desde una
cierta altura describe idealmente una trayectoria parabólica perfecta, siempre y cuando el rebote se produzca en condiciones ideales sobre una superficie pulida, como se muestra en la Figura 5 a). Las parábolas decrecen en forma exponencial y se van haciendo poco a poco más estrechas, hasta que finalmente la bola deja de rebotar. Esta situación se modifica sustancialmente cuando, por ejemplo, la superficie no es completamente lisa o tiene un comportamiento anómalo, situación en la que cada rebote toma una dirección inesperada, como se muestra en la Figura 5 b). Aunque sólo ha variado la rugosidad de la superficie y las alturas máximas de cada parábola disminuyen en forma similar al caso anterior, los rebotes han cambiado notablemente y se
han hecho caóticos.
Los modelos matemáticos que utilizan los cientı́ficos y los ingenieros para explicar o utilizar las virtudes del universo suelen tomar rigurosamente en cuenta sólo a las grandes variables que siempre están
presentes y que pueden determinar casi por completo y en casi toda circunstancia a las situaciones (cuando son modelos deterministas). Sin embargo, con la misma rigurosidad acostumbran (la mayor parte de las veces a propósito, para simplificar
el tratamiento de los problemas) ignorar las variables pequeñas que pasan desapercibidas, que tienen
poca influencia, que se presentan muy esporádicamente o que creen que nunca estarán presentes. Pero puede ocurrir que una o varias de estas varia-
Muchas veces por estas simplificaciones que facilitan los diseños y los cálculos resulta que un puente se desploma, que una máquina experimenta repentinamente fallas imprevistas, que un avión no alcanza la velocidad que se esperaba, que un edificio
se inclina peligrosamente o que los resultados de los
cálculos no tienen nada que ver con la realidad. Porque siempre es más sencillo utilizar modelos deterministas, ya que éstos proporcionan la mayor parte de las respuestas.
Con esta estrategia, sin embargo, hay que confiar
en que los imponderables del caos no lleguen a tener la capacidad suficiente como para hacer que los
pequeños errores, que siempre deben esperarse, crezcan sin proporción.
La perspectiva caótica
Al salir de casa cada mañana tenemos un ejemplo
claro de lo que puede ser una situación que puede estar perfectamente determinada (determinista)
o por el contrario imposible de conocer de antemano (aleatoria), lo que lleva a imaginar que este simple hecho cotidiano puede definir un acontecimiento caótico. Esto es porque al intentar la predicción de un viaje pueden encontrarse dos situaciones extremas: la primera que corresponde al caso en que toda predicción es muy acertada porque,
por ejemplo, ese dı́a no hubo incidentes y el tránsito estuvo muy fluido, circunstancia en la que se aplican perfectamente los modelos deterministas. Por
el contrario, puede suceder que las condiciones del
dı́a sean mucho más complejas que de costumbre las
que producen tal desorden que no es posible aventurar conjeturas plausibles que tengan un éxito razonable, escenario en el cual sólo es posible utilizar modelos aleatorios muy complejos. Las cosas
serı́an muy distintas si siempre supiéramos de antemano cuál es el tipo de modelo que conviene utilizar en la simple rutina diaria de salir de casa con un
rumbo conocido.
Al querer saber de antemano cuál es el mejor modelo aplicable o qué ocurrirá en el futuro próximo, se
está suponiendo lamentablemente que existe la posibilidad de que debe existir un sistema de tipo predictivo que se anticipe a los hechos. Por desgracia
tal hipótesis significa que dicho sistema debe responder antes de que se presente cualquier estı́mulo, lo que conduce a contradicciones teóricas muy
De yotta a yocto. Caupolicán Muñoz Gamboa.
concretas que hacen concluir que no es fı́sicamente
realizable.
Por tales razones puede suponerse que el tipo de modelo establece siempre una plataforma sobre la que
es posible tener una cierta seguridad sobre el comportamiento futuro del sistema, aunque nunca ésta
podrá ser absoluta. Si el modelo no cambia, será posible esperar que la bolsa de valores proporcione buenas ganancias futuras; que el clima seguirá siendo
agradable toda la semana; que el diseño de un puente dará el resultado que se esperaba cuando sea construido; que el camino elegido es el adecuado para el
tiempo que se dispone para recorrerlo; que el combustible que cargamos a un vehı́culo será suficiente para ir y volver en una aventura por terrenos
desolados; que el libro que todavı́a no se imprime
será efectivamente un éxito de ventas cuando salga
al mercado, etc.
Pero todo lo anterior puede ser diferente en cualquier
momento, porque el modelo puede cambiar sorpresivamente en cada uno de los casos del párrafo anterior. La bolsa de valores está sujeta a fuerzas muy sutiles que podrı́an hacerla caer sin previo aviso (como ya ha sucedido); el clima depende de tantas variables que cuando las que se desconocen o no se han tomado en cuenta adquieren preponderancia, no hay
forma de predecirlo; la construcción de una obra de
gran envergadura puede sufrir graves descalabros debido a defectos de los materiales o errores humanos;
una ruta que se desea seguir puede estar interrumpida por múltiples razones circunstanciales; en un viaje de ida y vuelta bien planeado es posible sufrir
pérdidas de combustible (entre otras catástrofes) que
nos impidan regresar; un trabajo editorial puede mal
estimar el entusiasmo del público o una circunstancia
civil o legal podrı́a impedir la distribución del libro, y
ası́ sucesivamente.
Conclusión
En otras palabras, si tenemos un sistema descrito por un modelo estable, determinista y estacionario, el horizonte es perfectamente visible y predecible; pero, si el modelo cambia, deja de ser estacionario o se vuelve aleatorio, el desorden toma
el control haciendo muy difı́cil o imposible ver lo
que sucederá, incluso a corto plazo. Entonces, lo
que era un sistema aparentemente predecible puede también comportarse como un sistema caótico,
circunstancia que ha dado lugar al desarrollo de la
teorı́a del caos.
13
Pensar en el caos significa imaginar exactamente lo
contrario del orden y de lo armónico. Nada parece
más contradictorio para imaginar un modelo del universo, en el cual parece haber una armonı́a y un orden preconcebidos. Sin embargo, ası́ como es inevitable la incorporación del elemento aleatorio a nuestra visión del mundo, también resulta necesario incorporar el concepto del caos cuando se quiere tener una percepción más próxima del mundo real o
un buen modelo del mismo.
En el lenguaje común caos significa la ausencia de orden. En la teorı́a del caos, en cambio, lo que se trata es organizar la anarquı́a en un modelo que permita describirla. Es como si se tratara de ordenar
el desorden o describir lo indescriptible. Lo anterior es posible porque aún en las peores condiciones de desorden puede encontrarse un modelo complejo que describa al menos parcialmente una situación y pueda proporcionarnos una explicación suficientemente satisfactoria, aunque no necesariamente exacta, a cualquier fenómeno por muy complejo que éste sea.
Bibliografı́a
1. Bureau International des Poids et Mesures. The
International System of Units (SI). 8a. Edición.
Parı́s: BIPM Press, 2006.
2. Murray L. Eiland Jr. y Murray Eiland III. Oriental Carpets: A Complete Guide. 4a . Edición. Nueva York: Bulfinch Press, 1998.
3. Kenneth Falconer. Fractal Geometry: Mathematical Foundations and Applications. Nueva York:
John Wiley & Sons, 2003.
4. Edward Ott. Chaos in Dynamical Systems. Nueva
York: Cambridge University Press, 2002.
5. Carl Sagan. Cosmos. Nueva York: Random House, 1980.
6. Kenneth M. Smith, Karl Maramorosch y Max
A. Lauffer. Advances in Virus Research. Vol. 17.
Nueva York: Elsevier, 1972.
7. Arvind Kumar. Chaos, Fractals and Self–
Organization. New Perspectives on Complexity in Nature. Nueva Delhi: National Book
Trust, 2003.
cs