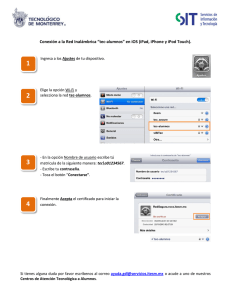
1 Preferencia por un nuevo Detergente: Para un estudio de

Preferencia por un nuevo Detergente: Para un estudio de mercado sobre las preferencias
entre un nuevo detergente Xx y uno standard Mm se consideró una muestra de 1008
consumidores, a los que se preguntó sobre su preferencia, si habían usado previamente Mm,
sobre la dureza del agua utilizada y la temperatura de lavado habitual. Los resultados se recogen
en la siguiente tabla:
Agua
suave
media
Temper
prefiere
MoX
Xx
Mm
Xx
Mm
usuario Previo
alta
baja
nousuario Previo
alta
baja
19
29
57
49
29
27
63
53
23
47
47
55
33
23
66
50
Xx
24
37
42
68
Mm
43
52
30
42
Analiza la tabla de contingencia ajustando un modelo log-lineal que explique la relación entre las
distintas variables.
Ajusta un modelo que explique la preferencia por una u otra marca.
dura
> y <- c(19, 57, 29, 63, 29, 49, 27, 53, 23, 47, 33, 66, 47, 55, 23, 50,
+ 24, 37, 42, 68, 43, 52, 30, 42)
> ly <- length( y )
>
>
>
>
T
P
M
A
<<<<-
gl(2, 1, ly, labels = c("alta", "baja") ) ### Temperatura lavado
gl(2, 2*1, ly, labels=c("si", "no") ) ### usuario Previo
gl( 2, 2*2*1, ly, labels = c("X", "M") ) ### Marca preferida
gl( 3, 2*2*2*1, ly, labels=c("suave", "media", "dura") ) ### Agua lavado
> data.frame( T, P, M, A, y )
T P M
A y
1 alta si X suave 19
2 baja si X suave 57
3 alta no X suave 29
4 baja no X suave 63
5 alta si M suave 29
6 baja si M suave 49
7 alta no M suave 27
8 baja no M suave 53
9 alta si X media 23
10 baja si X media 47
11 alta no X media 33
12 baja no X media 66
13 alta si M media 47
14 baja si M media 55
15 alta no M media 23
16 baja no M media 50
17 alta si X dura 24
18 baja si X dura 37
19 alta no X dura 42
20 baja no X dura 68
21 alta si M dura 43
22 baja si M dura 52
23 alta no M dura 30
24 baja no M dura 42
> tTPMA <- xtabs( y ~ T + P + M + A )
1
> ftable( tTPMA )
A suave media dura
T
P M
alta si X
19
23
24
M
29
47
43
no X
29
33
42
M
27
23
30
baja si X
57
47
37
M
49
55
52
no X
63
66
68
M
53
50
42
Ajuste de modelos log-lineales de orden completo:
> ##################################
> ### modelo completo de orden 1 ###
> m1 <- glm( y ~ A + M + P + T, family=poisson )
>
>
>
>
>
devres <- deviance( m1 ); aic <- AIC( m1 )
gdl <- m1$df.residual
dev.gdl <- devres/gdl
pval.dev <- 1-pchisq( devres, gdl )
cbind( aic, devres, gdl, dev.gdl, pval.dev )
aic
devres gdl dev.gdl
pval.dev
[1,] 187.3437 42.92866 18 2.384925 0.0008190181
> anova( m1, test="Chisq" )
Analysis of Deviance Table
Model: poisson, link: log
Response: y
Terms added sequentially (first to last)
NULL
A
M
P
T
Df Deviance Resid. Df Resid. Dev P(>|Chi|)
23
118.627
2
0.501
21
118.125
0.778
1
0.063
20
118.062
0.801
1
1.921
19
116.141
0.166
1
73.212
18
42.929 1.164e-17
> drop1( m1, test="Chisq" )
Single term deletions
Model:
y ~ A + M + P + T
Df Deviance
AIC
LRT Pr(Chi)
<none>
42.929 187.344
A
2
43.430 183.845
0.501 0.7782
M
1
42.992 185.407
0.063 0.8011
P
1
44.850 187.265
1.921 0.1657
T
1 116.141 258.556 73.212 <2e-16 ***
--Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
2
> ##################################
> ### modelo completo de orden 2 ###
> m2 <- glm( y~A+M+P+T+A*M+A*P+A*T+M*P+M*T+P*T, family=poisson )
>
>
>
>
>
devres <- deviance( m2 ); aic <- AIC( m2 )
gdl <- m2$df.residual
dev.gdl <- devres/gdl
pval.dev <- 1-pchisq( devres, gdl )
cbind( aic, devres, gdl, dev.gdl, pval.dev )
aic
devres gdl dev.gdl pval.dev
[1,] 172.2612 9.846211
9 1.094023 0.3630783
> anova( m2, test="Chisq" )
Analysis of Deviance Table
Model: poisson, link: log
Response: y
Terms added sequentially (first to last)
NULL
A
M
P
T
A:M
A:P
A:T
M:P
M:T
P:T
Df Deviance Resid. Df Resid. Dev P(>|Chi|)
23
118.627
2
0.501
21
118.125
0.778
1
0.063
20
118.062
0.801
1
1.921
19
116.141
0.166
1
73.212
18
42.929 1.164e-17
2
0.395
16
42.533
0.821
2
1.075
14
41.458
0.584
2
6.099
12
35.359
0.047
1
20.463
11
14.896 6.079e-06
1
4.310
10
10.586
0.038
1
0.740
9
9.846
0.390
> drop1( m2, test="Chisq" )
Single term deletions
Model:
y ~ A + M + P + T + A * M + A * P + A * T + M * P + M * T + P *
T
Df Deviance
AIC
LRT
Pr(Chi)
<none>
9.846 172.261
A:M
2
10.062 168.477
0.216
0.89778
A:P
2
10.851 169.266
1.005
0.60502
A:T
2
15.942 174.357
6.096
0.04747 *
M:P
1
29.738 190.153 19.892 8.194e-06 ***
M:T
1
13.585 174.000
3.739
0.05316 .
P:T
1
10.586 171.001
0.740
0.38974
--Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
3
> ##################################
> ### modelo completo de orden 3 ###
>
+
>
>
>
>
>
m3 <- glm( y~A+M+P+T+A*M+A*P+A*T+M*P+M*T+P*T+
A*M*P+A*M*T+A*P*T+M*P*T, family=poisson )
devres <- deviance( m3 ); aic <- AIC( m3 )
gdl <- m3$df.residual
dev.gdl <- devres/gdl
pval.dev <- 1-pchisq( devres, gdl )
cbind( aic, devres, gdl, dev.gdl, pval.dev )
aic
devres gdl
dev.gdl pval.dev
[1,] 177.1523 0.7373169
2 0.3686585 0.6916616
> anova( m3, test="Chisq" )
Analysis of Deviance Table
Model: poisson, link: log
Response: y
Terms added sequentially (first to last)
NULL
A
M
P
T
A:M
A:P
A:T
M:P
M:T
P:T
A:M:P
A:M:T
A:P:T
M:P:T
Df Deviance Resid. Df Resid. Dev P(>|Chi|)
23
118.627
2
0.501
21
118.125
0.778
1
0.063
20
118.062
0.801
1
1.921
19
116.141
0.166
1
73.212
18
42.929 1.164e-17
2
0.395
16
42.533
0.821
2
1.075
14
41.458
0.584
2
6.099
12
35.359
0.047
1
20.463
11
14.896 6.079e-06
1
4.310
10
10.586
0.038
1
0.740
9
9.846
0.390
2
5.328
7
4.518
0.070
2
0.161
5
4.357
0.923
2
1.398
3
2.959
0.497
1
2.222
2
0.737
0.136
> drop1( m3, test="Chisq" )
Single term deletions
Model:
y ~ A + M + P + T + A * M + A * P + A * T + M * P + M * T + P *
T + A * M * P + A * M * T + A * P * T + M * P * T
Df Deviance
AIC
LRT Pr(Chi)
<none>
0.737 177.152
A:M:P
2
5.309 177.724
4.571 0.1017
A:M:T
2
0.899 173.314
0.162 0.9223
A:P:T
2
2.115 174.530
1.377 0.5022
M:P:T
1
2.959 177.374
2.222 0.1361
4
> anova( m1, m2, m3, test="Chisq" )
Analysis of Deviance Table
Model 1: y ~ A + M + P + T
Model 2: y ~ A + M + P + T + A * M + A * P + A * T + M * P + M * T + P *
T
Model 3: y ~ A + M + P + T + A * M + A * P + A * T + M * P + M * T + P *
T + A * M * P + A * M * T + A * P * T + M * P * T
Resid. Df Resid. Dev Df Deviance P(>|Chi|)
1
18
42.929
2
9
9.846 9
33.082 0.0001292
3
2
0.737 7
9.109
0.245
El modelo completo de orden 1, m1, no ajusta bien las frecuencias observadas (se
rechaza la no asociación entre los cuatro factores). El modelo completo de orden 2
proporciona un buen ajuste. Del análisis del modelo m3 se deduce que no parece
necesario incluir ningún efecto de orden 3. A la vista de los resultados del análisis
secuencial de la deviance (anova) y de los tests de eliminación de efectos (drop1) en
el ajuste del modelo completo de orden 2, m2, se puede decir que los efectos AM, AP
y PT no son significativos. Un modelo adecuado es el modelo log-lineal jerárquico
(MP, MT, AT).
> ############################################
> ### efectos seleccionados del ajuste de los modelos de orden completo
> m.MP.MT.AT <- glm( y~A+M+P+T+ M*P + M*T + A*T, family=poisson )
>
>
>
>
>
devres <- deviance( m.MP.MT.AT ); aic <- AIC( m.MP.MT.AT )
gdl <- m.MP.MT.AT$df.residual
dev.gdl <- devres/gdl
pval.dev <- 1-pchisq( devres, gdl )
cbind( aic, devres, gdl, dev.gdl, pval.dev )
aic
devres gdl
dev.gdl pval.dev
[1,] 164.3015 11.88649 14 0.8490348 0.6154184
El modelo (MP, MT, AT) proporciona muy buen ajuste.
> anova( m.MP.MT.AT, test="Chisq" )
Analysis of Deviance Table
Model: poisson, link: log
Response: y
Terms added sequentially (first to last)
NULL
A
M
P
T
M:P
M:T
A:T
Df Deviance Resid. Df Resid. Dev P(>|Chi|)
23
118.627
2
0.501
21
118.125
0.778
1
0.063
20
118.062
0.801
1
1.921
19
116.141
0.166
1
73.212
18
42.929 1.164e-17
1
20.581
17
22.347 5.715e-06
1
4.362
16
17.986
0.037
2
6.099
14
11.886
0.047
La sucesiva adición de efectos, MP, MT y AT produce una mejora (reducción de la
deviance) significativa en el ajuste del modelo.
5
> drop1( m.MP.MT.AT, test="Chisq" )
Single term deletions
Model:
y ~ A + M + P + T + M * P + M * T + A * T
Df Deviance
AIC
LRT
Pr(Chi)
<none>
11.886 164.302
M:P
1
32.468 182.883 20.581 5.715e-06 ***
M:T
1
16.248 166.663
4.362
0.03676 *
A:T
2
17.986 166.401
6.099
0.04738 *
--Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
No es posible la eliminación de ninguno de los efectos de orden 2 del modelo
ajustado, (MP, MT, AT), sin que se produzca una pérdida significativa en el ajuste.
No obstante podríamos pensar que un modelo más sencillo, por ejemplo (A, T, MP),
podría dar un ajuste razonable. Veamos:
>
>
>
>
>
>
>
############################################
m.MP <- glm( y~A+M+P+T+ M*P, family=poisson )
devres <- deviance( m.MP ); aic <- AIC( m.MP )
gdl <- m.MP$df.residual
dev.gdl <- devres/gdl
pval.dev <- 1-pchisq( devres, gdl )
cbind( aic, devres, gdl, dev.gdl, pval.dev )
aic
devres gdl dev.gdl pval.dev
[1,] 168.7622 22.34719 17 1.314541 0.1717329
Podemos observar que este modelo, (A, T, MP), proporciona un buen ajuste (basta
ver su deviance residual), pero si lo comparamos con el modelo anterior, (MP, MT,
AT), la menor complejidad de (A, T, MP) no compensa la pérdida en el ajuste
(observar el mayor valor del AIC del modelo (A, T, MP).
Dado que ambos modelos están anidados podemos mediante anova realizar un test
condicional para valorar la pérdida en el ajuste:
> anova( m.MP, m.MP.MT.AT, test="Chisq" )
Analysis of Deviance Table
Model 1:
Model 2:
Resid.
1
2
y ~ A + M + P + T + M * P
y ~ A + M + P + T + M * P + M * T + A * T
Df Resid. Dev Df Deviance P(>|Chi|)
17
22.347
14
11.886 3
10.461
0.015
La mejora en el ajuste del modelo (MP, MT, AT) respecto del (A, T, MP) es
significativa.
Por consiguiente podemos adoptar como mejor modelo log-lineal: (MP, MT, AT).
P es no está asociada con A y es condicionalmente independiente de T, dado M.
M es condicionalmente independiente de A, dado T, pero está fuertemente asociada
con P y con T.
> ####################################################################
> ### Variable respuesta binaria: Marca preferida: X(la nueva) o M ###
> ### arreglo de los datos: yX=prefieren X; yM=prefieren M;
> yX <- y[M=="X"]; yM <- y[M=="M"]; total <- yX + yM;
> AA <- A[M=="X"]; PP <- P[M=="X"]; TT <- T[M=="X"];
> p.X.obs <- yX/total ### proporción observada de respuesta X
> respuesta <- cbind( yX, yM ) ### para ajuste de logístico en glm
6
> ### m.M: modelo logístico con efectos principales Agua, uso Previo y Temper
> m.M <- glm( respuesta ~ AA + PP + TT, family=binomial )
> summary( m.M )
Call:
glm(formula = respuesta ~ AA + PP + TT, family = binomial)
Deviance Residuals:
Min
1Q
Median
-1.2785 -0.6382 -0.1765
3Q
0.5601
Max
1.5738
Coefficients:
Estimate Std. Error z value Pr(>|z|)
(Intercept) -0.41143
0.15812 -2.602 0.00927 **
AAmedia
-0.07063
0.15664 -0.451 0.65207
AAdura
-0.02111
0.15763 -0.134 0.89346
PPno
0.56702
0.12775
4.439 9.05e-06 ***
TTbaja
0.25665
0.13286
1.932 0.05340 .
--Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
(Dispersion parameter for binomial family taken to be 1)
Null deviance: 32.826
Residual deviance: 8.228
AIC: 75.926
on 11
on 7
degrees of freedom
degrees of freedom
Number of Fisher Scoring iterations: 3
> anova( m.M, test="Chisq" )
Analysis of Deviance Table
Model: binomial, link: logit
Response: respuesta
Terms added sequentially (first to last)
NULL
AA
PP
TT
Df Deviance Resid. Df Resid. Dev P(>|Chi|)
11
32.826
2
0.395
9
32.430
0.821
1
20.463
8
11.967 6.079e-06
1
3.739
7
8.228
0.053
> drop1( m.M, test="Chisq" )
Single term deletions
Model:
respuesta ~ AA + PP + TT
Df Deviance
AIC
LRT
Pr(Chi)
<none>
8.228 75.926
AA
2
8.444 72.142 0.216
0.89763
PP
1
28.120 93.818 19.892 8.192e-06 ***
TT
1
11.967 77.665 3.739
0.05315 .
--Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Aunque el ajuste de este modelo logit , m.M, de efectos principales es bueno (ver
deviance residual), el modelo que excluye el efecto A es mejor, aún dando un peor
ajuste. No obstante el efecto de A podría ser significativo en un modelo con
interacciones.
7
> p.X.pred <- round( m.M$fitted.values, 4 )
> data.frame( AA, PP, TT, total, yM, yX, p.X.obs, p.X.pred )
1
2
3
4
5
6
7
8
9
10
11
12
AA
suave
suave
suave
suave
media
media
media
media
dura
dura
dura
dura
PP
si
si
no
no
si
si
no
no
si
si
no
no
TT total yM yX
p.X.obs p.X.pred
alta
48 29 19 0.3958333
0.3986
baja
106 49 57 0.5377358
0.4614
alta
56 27 29 0.5178571
0.5388
baja
116 53 63 0.5431034
0.6016
alta
70 47 23 0.3285714
0.3818
baja
102 55 47 0.4607843
0.4439
alta
56 23 33 0.5892857
0.5212
baja
116 50 66 0.5689655
0.5846
alta
67 43 24 0.3582090
0.3935
baja
89 52 37 0.4157303
0.4561
alta
72 30 42 0.5833333
0.5336
baja
110 42 68 0.6181818
0.5966
> #####################################################################
> ### modelo log-lineal equivalente al logít de efectos principales ###
> mequiva <- glm( y~A+M+P+T+M*A+M*P+M*T+A*P*T, family=poisson )
> summary( mequiva )
Call:
glm(formula = y ~ A + M + P + T + M * A + M * P + M * T + A *
P * T, family = poisson)
Deviance Residuals:
Min
1Q
-1.098061 -0.494204
Median
-0.002817
3Q
0.403393
Max
1.127415
Coefficients:
Estimate Std. Error z value Pr(>|z|)
(Intercept)
2.95133
0.17285 17.075 < 2e-16 ***
Amedia
0.33422
0.21031
1.589 0.11201
Adura
0.32074
0.21170
1.515 0.12975
MM
0.41143
0.15812
2.602 0.00927 **
Pno
0.45565
0.20912
2.179 0.02934 *
Tbaja
0.93858
0.19050
4.927 8.35e-07 ***
Amedia:MM
0.07063
0.15664
0.451 0.65207
Adura:MM
0.02111
0.15763
0.134 0.89346
MM:Pno
-0.56702
0.12775 -4.439 9.05e-06 ***
MM:Tbaja
-0.25665
0.13286 -1.932 0.05340 .
Amedia:Pno
-0.36741
0.26705 -1.376 0.16888
Adura:Pno
-0.07922
0.26076 -0.304 0.76128
Amedia:Tbaja
-0.41135
0.23336 -1.763 0.07795 .
Adura:Tbaja
-0.50697
0.23775 -2.132 0.03298 *
Pno:Tbaja
-0.10009
0.23906 -0.419 0.67545
Amedia:Pno:Tbaja 0.41580
0.32759
1.269 0.20434
Adura:Pno:Tbaja
0.20387
0.32540
0.627 0.53097
--Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
(Dispersion parameter for poisson family taken to be 1)
Null deviance: 118.627
Residual deviance:
8.228
AIC: 174.64
on 23
on 7
degrees of freedom
degrees of freedom
Number of Fisher Scoring iterations: 4
8
> ### Comprobación:
> pred.eq <- exp( predict( mequiva ) )
> p.X.eq <- round( pred.eq[M=="X"]/total, 4 )
> ###################################################################
> ### La función predict calcula los predictores lineales y su se ###
> ### Cálculo de IC's para la probabilidad de respuesta X, bajo m.M
> fexpit <- function(x) { exp(x)/(1+exp(x)) }
> plin <- predict( m.M, se.fit=TRUE )
> p.X.plin <- round( fexpit( plin$fit ), 4 )
>
>
>
>
>
>
se.plin <- plin$se.fit
alfa <- 0.05; confianza <- 1-alfa;
ic.plin.inf <- plin$fit-qnorm(1-alfa/2)*se.plin
ic.plin.sup <- plin$fit+qnorm(1-alfa/2)*se.plin
ic.p.X.inf <- round( fexpit( ic.plin.inf ), 4)
ic.p.X.sup <- round( fexpit( ic.plin.sup ), 4)
> data.frame(
ic.p.X.sup)
AA
1 suave
2 suave
3 suave
4 suave
5 media
6 media
7 media
8 media
9
dura
10 dura
11 dura
12 dura
AA, PP, TT, total, yM, yX, p.X.obs, p.X.pred, ic.p.X.inf,
PP
si
si
no
no
si
si
no
no
si
si
no
no
TT total yM yX
p.X.obs p.X.pred ic.p.X.inf ic.p.X.sup
alta
48 29 19 0.3958333
0.3986
0.3271
0.4746
baja
106 49 57 0.5377358
0.4614
0.3954
0.5287
alta
56 27 29 0.5178571
0.5388
0.4621
0.6138
baja
116 53 63 0.5431034
0.6016
0.5373
0.6626
alta
70 47 23 0.3285714
0.3818
0.3145
0.4539
baja
102 55 47 0.4607843
0.4439
0.3794
0.5103
alta
56 23 33 0.5892857
0.5212
0.4466
0.5949
baja
116 50 66 0.5689655
0.5846
0.5193
0.6470
alta
67 43 24 0.3582090
0.3935
0.3256
0.4659
baja
89 52 37 0.4157303
0.4561
0.3887
0.5253
alta
72 30 42 0.5833333
0.5336
0.4612
0.6046
baja
110 42 68 0.6181818
0.5966
0.5312
0.6587
9
Modelo logit con interacción AP:
> m.M.int <- glm( respuesta ~ AA + PP + TT + AA*PP, family=binomial )
> summary( m.M.int )
Call:
glm(formula = respuesta ~ AA + PP + TT + AA * PP, family = binomial)
Deviance Residuals:
1
2
-0.76685
0.51160
9
10
0.01582 -0.01335
3
0.37308
11
0.26016
4
-0.26057
12
-0.21502
5
-0.74884
6
0.59853
7
0.82871
8
-0.58125
Coefficients:
Estimate Std. Error z value Pr(>|z|)
(Intercept)
-0.1981
0.1858 -1.066
0.2865
AAmedia
-0.3280
0.2244 -1.461
0.1439
AAdura
-0.3891
0.2308 -1.686
0.0918 .
PPno
0.1698
0.2225
0.763
0.4455
TTbaja
0.2497
0.1333
1.873
0.0611 .
AAmedia:PPno
0.4934
0.3126
1.579
0.1144
AAdura:PPno
0.6918
0.3156
2.192
0.0284 *
--Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
(Dispersion parameter for binomial family taken to be 1)
Null deviance: 32.8256
Residual deviance: 3.1148
AIC: 74.813
on 11
on 5
degrees of freedom
degrees of freedom
Number of Fisher Scoring iterations: 3
> anova( m.M.int, test="Chisq" )
Analysis of Deviance Table
Model: binomial, link: logit
Response: respuesta
Terms added sequentially (first to last)
NULL
AA
PP
TT
AA:PP
Df Deviance Resid. Df Resid. Dev P(>|Chi|)
11
32.826
2
0.395
9
32.430
0.821
1
20.463
8
11.967 6.079e-06
1
3.739
7
8.228
0.053
2
5.113
5
3.115
0.078
> drop1( m.M.int, test="Chisq" )
Single term deletions
Model:
respuesta ~ AA + PP + TT + AA * PP
Df Deviance
AIC
LRT Pr(Chi)
<none>
3.115 74.813
TT
1
6.629 76.327 3.514 0.06085 .
AA:PP
2
8.228 75.926 5.113 0.07757 .
--Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
10
> p.X.int <- m.M.int$fitted.values ### prob de X bajo interacción AP
> difpX <- p.X.pred - p.X.int
> data.frame( AA, PP, TT, total, yM, yX, p.X.obs, p.X.pred, p.X.int, difpX )
1
2
3
4
5
6
7
8
9
10
11
12
AA
suave
suave
suave
suave
media
media
media
media
dura
dura
dura
dura
PP
si
si
no
no
si
si
no
no
si
si
no
no
TT total yM yX
p.X.obs p.X.pred
p.X.int
difpX
alta
48 29 19 0.3958333
0.3986 0.4506474 -0.05204741
baja
106 49 57 0.5377358
0.4614 0.5129144 -0.05151438
alta
56 27 29 0.5178571
0.5388 0.4929312 0.04586879
baja
116 53 63 0.5431034
0.6016 0.5551367 0.04646334
alta
70 47 23 0.3285714
0.3818 0.3714449 0.01035512
baja
102 55 47 0.4607843
0.4439 0.4313614 0.01253864
alta
56 23 33 0.5892857
0.5212 0.5342423 -0.01304231
baja
116 50 66 0.5689655
0.5846 0.5955382 -0.01093820
alta
67 43 24 0.3582090
0.3935 0.3572824 0.03621762
baja
89 52 37 0.4157303
0.4561 0.4164279 0.03967213
alta
72 30 42 0.5833333
0.5336 0.5681687 -0.03456870
baja
110 42 68 0.6181818
0.5966 0.6281078 -0.03150776
Si bien la mejora del ajuste del modelo logit con interacción A*P, m.M.int, respecto
del modelo de efectos principales, m.M, no es significativa (a nivel 0.05) sí es
importante, y el AIC de m.M.int es el menor de los modelos logits ajustados. Así pues
en la explicación de la respuesta, el efecto del factor A se manifiesta principalmente
a través de su interacción con el factor P.
#################################################
> ### plot de probabilidad de respuesta X bajo m.M ###
>
+
+
+
+
>
>
+
>
>
+
>
+
>
>
+
>
plot( 1:length(yX), p.X.obs, ylim=c(0,1), type="b", lty=3, xaxt="n",pch="",
xlab="12 grupos en covariables (Agua, uso Previo, Temperatura)",
ylab="probabilidad de preferir X", cex.main=0.9,
main="Probabilidad de preferencia por la nueva marca de detergente X:
modelo de efectos principales" )
axis( side=1, at=c(1:12), labels=c(1:12) )
text(c(2,6.5,10.5), c(0.15,0.15,0.15),
c("Agua:
suave", "media", "dura"))
segments(c(1:12),ic.p.X.inf, c(1:12),ic.p.X.sup, lwd=2,col="green")
points(c(1,3,5,7,9,11), p.X.pred[c(1,3,5,7,9,11)], pch=16,
col="red", cex=1.5 )
points(c(2,4,6,8,10,12), p.X.pred[c(2,4,6,8,10,12)], pch=15,
col="blue", cex=1.5 )
points( 1:length(yX), p.X.obs ) ### proporciones observadas
text(c(1,2,5,6,9,10), -0.05+p.X.pred[c(1,2,5,6,9,10)], rep("usabaM",6),
cex=0.8 )
points( 1:12, p.X.int, pch=2 ) ### prob de X bajo interacción AP
>
>
>
>
>
>
>
>
>
abline(v=c(4.5,8.5),lty=3)
legend(1,1.05, legend="", col="blue", pch=15, cex=1.5, bty="n")
text(3,0.99, "temperatura baja", cex=0.9 )
legend(1,1, legend="", col="red", pch=16, cex=1.5, bty="n")
text(3,0.94, "temperatura alta", cex=0.9 )
legend(1,0.95, legend="", pch=1, cex=1.5, bty="n")
text(3.4, 0.89, "proporción observada", cex=0.9 )
legend(1,0.9, legend="", pch=2, cex=1.5, bty="n")
text(3.9, 0.84, "prob de X bajo interacción AP", cex=0.9 )
11
1.0
Probabilidad de preferencia por la nueva marca de detergente X:
modelo de efectos principales
temperatura baja
temperatura alta
proporción observada
0.6
0.4
usabaM
usabaM
usabaM
usabaM
usabaM
0.2
usabaM
Agua: suave
media
dura
0.0
probabilidad de preferir X
0.8
prob de X bajo interacción AP
1
2
3
4
5
6
7
8
9
10
11
12
12 grupos en covariables (Agua, uso Previo, Temperatura)
12
Ajuste de modelos con SAS
options pagesize=500;
data deterg;
do A = 1 to 3;
do M =1 to 2;
* M=1 prefiere otra marca; * M=2 la marca de interes;
do P =1 to 2;
* P=1 usuario previo;
do T = 1 to 2;
input FREC @@;
output;
end;
end;
end;
end;
cards;
19 57 29 63
29 49 27 53
23 47 33 66
47 55 23 50
24 37 42 68
43 52 30 42
;
run;
/* proc print data=deterg; var _ALL_; run; */
proc genmod data=deterg; class a m p t;
model frec = a m p t / dist=poi link=log;
title Modelo log-lineal de orden 1 completo;
run;
proc genmod data=deterg; class a m p t;
model frec = a m p t a*m a*p a*t m*p m*t p*t/ dist=poi link=log type1 type3;
title Modelo de orden 2 completo;
run;
proc genmod data=deterg; class a m p t;
model frec = a m p t a*m a*p a*t m*p m*t p*t a*m*p a*m*t a*p*t m*p*t
/ dist=poi link=log type1 type3;
title Modelo de orden 3 completo;
* model frec = a | m | p | t @3/ dist=poi link=log type1 type3;
* Identico modelo, pero el ajuste secuencial de type1 es diferente;
run;
* a partir de los resultados obtenidos en los modelos anteriores;
* Tres modelos log-lineales ¿razonables?;
proc genmod data = deterg; class a m p t;
model frec = a m p t m*p m*t a*t/ dist=poi link=log type1 type3 predicted xvars;
title Modelo (MP, MT, AT);
run;
*****************************************************************************;
* Organizacion de los datos para ajustar un modelo logit usando FREC_M2/TOTAL;
* OJO!!! cuidado con el uso de merge en data D. Hay que asegurarse del orden;
* Comprobar siempre el resultado;
data B; set deterg; frec_M1 = frec; if M = 2 then delete; run;
data C; set deterg; frec_M2 = frec; if M = 1 then delete; run;
data D; set C; merge B; drop M frec;
TOTAL = frec_M1 + frec_M2;
prob_M2 = frec_M2 / TOTAL; * prob_M2: probab. en el M. Saturado (frec.
relativas);
run;
13
proc print data =D; var _ALL_;
title Frecuencias de M segun patron de covariables A P T;
run;
proc genmod data=D; class A P T;
model FREC_M2 / TOTAL = A P T / dist = bin link = logit predicted xvars;
title Modelo logit con todos los efectos principales;
run;
proc genmod data=deterg; class a m p t;
model frec = a m p t m*p m*t m*a a*p*t/ dist=poi link=log;
output out=salida pred=predichos;
title Modelo log-lineal equivalente al logit con todos los efectos principales;
run;
* Una forma complicada de obtener los resultados del ajuste del modelo logit;
* a traves del ajuste del modelo log-lineal equivalente anterior;
data E; set salida;
data F; set E; F_M1 = frec; Pred_M1 = predichos; if M = 2 then delete; run;
data G; set E; F_M2 = frec; Pred_M2 = predichos; if M = 1 then delete; run;
data H; set G; merge F; drop M frec;
TOTAL = F_M1 + F_M2;
FRel_M2 = F_M2 / TOTAL; * prob_M2 probabilidades en el Modelo Saturado;
TotPred = Pred_M1 + Pred_M2;
ppred_M2 = Pred_M2/TotPred; * ppred_M2 probabilidades predichas por el modelo;
run;
proc print data=H;
var A P T F_M1 F_M2 TOTAL FRel_M2 Pred_M1 Pred_M2 TotPred ppred_M2;
title Valores predichos por el log-lineal equivalente al logit;
run;
* ajuste con PROC LOGISTIC del modelo logit con todos los efectos principales;
proc logistic data = H; class A P T / param = REF;
model F_M2 / TOTAL = A P T / covb ;
output out=sal pred=pr_pred lower=inf upper=sup xbeta=xbeta stdxbeta=stdxbeta;
title Modelo logit con todos los efectos principales (PROC LOGISTIC);
run;
proc print data=sal; * observar que coinciden PPRED_M2 y PR_PRED;
var A P T F_M1 F_M2 TOTAL FRel_M2 Pred_M1 Pred_M2 ppred_M2 pr_pred inf sup;
title Probabilidades estimadas de M2 bajo modelo logistico de efectos
principales;
run;
* Modelo logistico sin el efecto A;
proc logistic data = H; class A P T / param = REF;
model F_M2 / TOTAL = P T ;
output out=sal_P_T pred=pr_pred_P_T lower=inf upper=sup xbeta=xbeta
stdxbeta=stdxbeta;
title Modelo logit con los efectos principales P T;
run;
proc print data=sal_P_T;
var A P T F_M1 F_M2 TOTAL FRel_M2 pr_pred_P_T inf sup;
title Probabilidades estimadas de M2 bajo modelo logistico con efectos P T;
run;
14