Guía relato - OCW - Universidad de Murcia

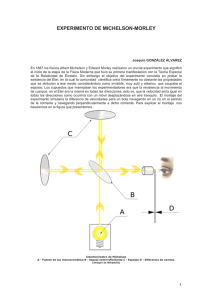
El espacio tiempo de Albert Einstein
José Antonio Pastor González
Departamento de Matemáticas
Universidad de Murcia
1.1
La física a finales del siglo XIX.
Desde el siglo XVII, casi todos los fenómenos dispares de la naturaleza
admitían una explicación coherente y bella a partir de unas pocas leyes
fundamentales. Entre estas leyes se encontraban las leyes de la mecánica de
Newton, la ley de la gravitación de Newton y, por último, la suposición de que
el espacio y el tiempo son conceptos absolutos, nociones que son
independientes del observador y que están ahí presentándose de igual forma
para todos siempre y cuando hagamos correctamente nuestras mediciones.
Recordemos algunas de estas leyes:
- los objetos libres (no sujetos a ninguna fuerza) se mueven en
movimiento rectilíneo y uniforme, es decir, siguen líneas rectas sin
aceleración. Esta ley también se llama ley de la inercia y puede
expresarse diciendo que la inercia de los cuerpos les lleva a seguir un
movimiento rectilíneo y uniforme hasta que una fuerza actúa sobre
ellos.
- la ley de la gravitación expresa que dos cuerpos con masa se atraen con
una fuerza que es proporcional a las masas e inversamente proporcional
al cuadrado de la distancia
- la idea de espacio absoluto como sistema de referencia privilegiado que
nos permite definir el estándar de “inercia” o de “quietud”: por
ejemplo, cuando una esfera rota muy rápido, sufre una dilatación en su
plano ecuatorial y esta dilatación es sencillamente el comportamiento de
la esfera en relación al espacio absoluto que “está quieto”, mientras es
ella la que está rotando. Si pensamos en este experimento con un
universo vacío que contiene sólo a la esfera, el mismo fenómeno
seguiría produciéndose pese a que nada (no hay ninguna referencia
externa) nos permitiría decir que la esfera está rotando: la esfera se
deformaría en su ecuador porque “siente” que rota en relación al
espacio absoluto que está inmóvil y quieto.
- la idea de tiempo absoluto como tiempo que es el mismo para todos los
observadores siempre y cuando los relojes sean idénticos y estén
sincronizados que es algo perfectamente concebible.
La vigencia de estas leyes a lo largo de los siglos y su amplia aceptación se
debió no sólo a su poder explicativo, sino también a su capacidad de
predicción. Entre otras cuestiones, estas leyes (y sus consecuencias) predijeron
las órbitas de los planetas, satélites y cometas, explicaron fenómenos como las
mareas, sentaron las bases para la revolución industrial y científica del siglo
XVIII y, finalmente, permitieron descubrir nuevos planetas en base a
perturbaciones de las órbitas observadas por los astrónomos.
Tras los éxitos obtenidos por la mecánica de Newton, y en paralelo a ésta, se
desarrollaron otras ramas de la física. Concretamente, fueron estudiados
fenómenos como el magnetismo y la electricidad por diversos científicos. En
el siglo XIX, el físico escocés Maxwell recopila, unifica y presenta un conjunto
de ecuaciones que describen, explican y predicen todos los fenómenos
relativos tanto a la electricidad como al magnetismo. La interrelación entre
ambos aspectos de la realidad es tan estrecha que se acuña el término
electromagnetismo para designar con una única palabra a un único fenómeno
que aparentemente, se presentaba bajo dos formas distintas.
Las leyes de Maxwell predicen la existencia de unas ondas (las ondas
electromagnéticas) que se propagan con una cierta velocidad en función de las
características eléctricas y magnéticas del medio. Si el medio es el vacío, esta
velocidad es una constante que llamaremos c. Curiosamente, esta velocidad
coincidía con la velocidad de la luz que se había medido en diversos
experimentos que habían tenido lugar muchos años antes (experimentos de
Bradley, Oersted, etc.). Así pues, Maxwell ratifica la naturaleza ondulatoria de
la luz (había existido una gran controversia desde Newton sobre si la luz era
una onda o un corpúsculo) y la describe como una onda electromagnética que
se propaga en el vacío a velocidad c con independencia del movimiento de la
fuente.
De esta forma, el que la luz es una onda electromagnética se convierte cada
vez más en una evidencia irrefutable. Ahora bien, si la luz es una onda, ¿qué es
lo que está vibrando? Era natural suponer la existencia de un medio a través
del cual se propagaran las ondas de luz de la misma forma que se necesita aire
para que se propague el sonido. La solución a este dilema consistió en
proclamar la existencia de un medio misterioso llamado éter, un medio que lo
rodeaba todo y que inundaba el vacío interestelar. El éter debía tener unas
propiedades muy extrañas: muy ligero, muy incompresible (para que la
velocidad de propagación de la luz fuera tan alta) y muy tenue (para ofrecer
muy poca resistencia al paso de los cuerpos sólidos).
Más aún, se pensó que el éter rellenaba todo el espacio absoluto y que servía
como estándar de “quietud” ya que la velocidad de la luz con respecto al éter
siempre era constante. Es conveniente imaginar el éter como una malla
cuadriculada que rellena el espacio de suerte que la velocidad de los rayos de
luz con respecto a dicha malla es siempre constante: la luz siempre avanza un
número fijo de cuadraditos en un cierto intervalo de tiempo.
A ninguno se nos escapa que la “invención” del éter es bastante artificiosa, así
pues enseguida diversos científicos se propusieron demostrar la existencia de
este medio tan extraño. El primer experimento de entidad con este objetivo
fue diseñado por Michelson y Morley.
1.2
El experimento de Michelson- Morley.
Para entender bien este experimento vamos a recordar primero cuál era la
visión del Universo a finales del siglo XIX. Para los científicos de entonces, se
desconocía la existencia de galaxias (hubo que esperar a los años 20 del siglo
XX para dicho descubrimiento) y se concebía el Universo como un espacio de
dimensiones y forma desconocida que contenía, fundamentalmente, estrellas.
Como las estrellas parecían estar fijas en el cielo nocturno (sus movimientos
eran aparentes y se correspondían con el movimiento de la Tierra) se asimiló
como estándar de “quietud” el sistema de referencia de las estrellas fijas, esto
es, las estrellas que estaban muy lejanas y cuya configuración se mostraba
inalterable con el paso de los años (luego se descubriría que estas estrellas
también se mueven pero, al estar a tanta distancia, dicho movimiento apenas
es apreciable). Así pues, se pensó que en este sistema de referencia de estrellas
fijas el éter también estaba en reposo y que sería posible idear algún método
para detectarlo. ¿Cuál fue dicho método?
En aquella época era bien conocido el movimiento de la Tierra en relación al
Sol y la velocidad de la Tierra en relación al centro de nuestro sistema solar:
ésta es del orden de unos 30.000 kilómetros por hora. Moviéndonos a tales
velocidades era de esperar que un observador situado en la superficie terrestre
fuera capaz de detectar el “viento del éter”, esto es, el desplazamiento de la
Tierra en relación al éter. Es un fenómeno análogo a lo que sentimos cuando,
en un día muy calmado, vamos en moto y notamos un viento fortísimo en la
cara. Esto es porque nuestra velocidad en relación al aire en reposo es muy
alta (tanta como pueda nuestra moto alcanzar) y vamos “rompiendo” el aire
con nuestro movimiento de traslación.
Pero, ¿cómo era posible notar el “viento del éter” si éste era tan ligero y tenue
que ni siquiera influía en la trayectoria de los planetas y estrellas? Bien, quizás
no pudiéramos detectar el “viento del éter” pero sí sabemos medir
perfectamente la velocidad de la luz. Como esta velocidad es siempre
constante en relación al éter, diferentes estados de movimiento en relación al
éter deberían proporcionarnos diferentes medidas para la velocidad de la luz.
Para entender bien esta última afirmación basta pensar de nuevo en el ejemplo
de la moto. Si vamos en moto hacia la Universidad con un aparato que nos
permite medir la velocidad del sonido y rebasamos a un coche que está quieto
y que anuncia la llegada de un circo, entonces podemos medir la velocidad de
las ondas sonoras que salen desde el altavoz del coche. Si vamos en la misma
dirección que las ondas sonoras, éstas se desplazan con respecto a nosotros a
una velocidad menor que 320 metros por segundo (que es la velocidad del
sonido en el aire). Concretamente, la velocidad que medimos es 320-v siendo v
nuestra velocidad con respecto al aire. Si, por el contrario, en lugar de rebasar
el coche nos vamos acercando hacia él entonces la medida sería de 320+v ya
que sumamos a la velocidad de las ondas sonoras nuestra velocidad con
respecto al medio.
La misma idea (salvando las distancias porque es un poquito más complicado)
es la que se aplica en el experimento de Michelson-Morley. En éste la Tierra
hace el papel de la moto, el éter se identifica con el aire y, finalmente, la luz
con el sonido. Era previsible encontrar distintas mediciones de la velocidad de
la luz según la posición en la que se efectuaba la medida: si vamos contra el
“viento del éter” deberíamos medir una velocidad distinta a la que
obtendríamos si vamos a favor de (o en dirección ortogonal a) dicho “viento”
para un mismo rayo de luz que se desplaza con velocidad c en relación al éter.
Nada de esto ocurrió. Siempre se recogían las mismas medidas para la
velocidad de la luz. En otras palabras, la velocidad de la luz parecía ser
constante en cualquier posición de la órbita de la Tierra con independencia del
estado del observador. Este hecho no encajaba con los conocimientos de la
época y la reacción inicial de la comunidad científica fue pensar que los
experimentos estaban mal realizados. Quizás hubo algún error de diseño,
minúsculas fluctuaciones, inesperadas vibraciones, algún detalle que se había
pasado por alto…
Los experimentos se repitieron y se hicieron cada vez más sofisticados y
precisos. Esto motivó que algunos científicos comenzaran a contemplar la
posibilidad de que, quizás, la luz tuviera una naturaleza ondulatoria tan extraña
que no obedeciera a la más simple intuición. Así, Fitzgerald asumió como
válido el experimento y, desarrollando sus consecuencias con unas
matemáticas muy sencillas, llegó a la conclusión de que “la única hipótesis que
puede reconciliarse con este resultado experimental es que la longitud de los
cuerpos materiales cambia, dependiendo de cómo se mueven a través del
éter”.
Esta afirmación, efectuada en la revista Science, es la conocida como
contracción de Lorentz-Fitzgerald y explica (de forma consistente y lógica) los
resultados del experimento de Michelson-Morley. Otros físicos y matemáticos
como Larmor y Poincaré creyeron en el experimento y estudiaron sus
consecuencias. Todos ellos llegaron a unas transformaciones del espacio y el
tiempo no convencionales y aquí debemos detenernos con tranquilidad para
explicar este punto.
El primer concepto a definir es el de sistema de referencia inercial. Un sistema
de referencia (un observador capaz de asignar a cada evento unas coordenadas
espaciales y un tiempo) se dice que es inercial cuando en dicho sistema las
partículas libres siguen una trayectoria rectilínea y uniforme. En otras palabras,
un sistema de referencia se dice que es inercial cuando en él se cumple la ley
de la inercia.
Por ejemplo, en la superficie de la Tierra es imposible hablar de sistemas de
referencia inerciales ya que no existen partículas libres: todas están afectadas
por la gravedad terrestre. Supongamos que fuéramos capaces de apartarnos lo
suficiente de cualquier objeto masivo y que la gravedad fuera prácticamente
nula. Un sistema de referencia inercial sería entonces un laboratorio o un
cohete (por ejemplo) que no estuviera acelerado. En tal laboratorio las
partículas libres se moverían con movimiento rectilíneo y uniforme (esto no
quiere decir que el movimiento de una partícula libre dependa del sistema de
referencia con el que la observamos; lo que sí depende es la trayectoria que
nosotros observamos de dicho movimiento).
Una propiedad interesante de dos sistemas de referencia inerciales es que
ambos deben moverse a velocidad constante uno con respecto al otro. De
hecho, lo que se tiene es una relación de equivalencia y todos los sistemas de
referencia inerciales conforman una clase distinguida: se caracterizan por ser
aquellos en los que las leyes de la mecánica de Newton son válidas
(recordemos la primera ley que hemos enunciado: los objetos libres se mueven
siguiendo una trayectoria rectilínea y uniforme; esto sólo es cierto en un
sistema de referencia inercial).
En cada sistema de referencia inercial podemos hablar de coordenadas. Basta
considerar, por ejemplo, unos ejes cartesianos y podemos asignar a cada punto
del espacio tres coordenadas espaciales y una coordenada temporal. Las
relaciones entre las coordenadas de un sistema y otro están dadas por unas
transformaciones muy sencillas que se conocen como transformaciones de
Galileo (GT). Estas transformaciones dejan invariantes las leyes de la
mecánica de Newton y, de hecho, las leyes de Newton de la mecánica están
enunciadas en relación a esta clase de sistemas de referencia (Newton las
enunció pensando que estaban referidas al espacio absoluto… fue Galileo
quién más tarde demostró que estás leyes eran invariantes para todo sistema
inercial). Cuando se habla de velocidad, de aceleración, de posición, se habla
en relación a las medidas dentro de uno de estos sistemas. Esto es así porque
las leyes de la mecánica adoptan su forma más sencilla en esta clase de
sistemas y la física busca, sobre todo, la máxima simplicidad.
Para dos de estos sistemas, las medidas espaciales, si están bien hechas, no
sufren cambios. Utilizando los ejemplos clásicos de Einstein, si vamos
montados en un tren con una longitud L y pasamos por una estación a una
velocidad v, el jefe de estación que está en el andén medirá también para
nuestro tren una longitud L. Ambos colegimos en la longitud del tren siempre
y cuando hagamos bien nuestras observaciones. Algo análogo se puede
afirmar en relación a las medidas temporales. Los dos estaremos de acuerdo
en este tipo de medidas si las hacemos correctamente.
Por otra parte, el hecho de que las leyes de la mecánica se expresen de la
misma forma en cualquier sistema de referencia inercial nos lleva a la
conclusión de que es imposible distinguir entre dos de tales sistemas
efectuando únicamente experimentos mecánicos. Esto es lo que se conoce
como principio de relatividad de Galileo: se puede jugar un partido de tenis en
una pista que está en tierra firme (en un andén) y en una pista de tierra situada
dentro de un vagón gigante siempre y cuando este se mueva a velocidad
constante. El partido será el mismo y, en ausencia de ventanas, sería imposible
distinguir desde dentro del vagón que nos estamos moviendo.
Toda esta historia sobre los sistemas de referencia inerciales y las relaciones
que transforman sus coordenadas (las GT) están aquí explicadas porque el
resultado del experimento de Michelson-Morley implicaba que las relaciones
entre las coordenadas de dos sistemas de referencia inerciales no podían ser
las GT. Estas transformaciones eran erróneas (si asumimos la corrección del
experimento de Michelson-Morley) y las transformaciones correctas eran las
llamadas transformaciones de Lorentz (LT).
Estas nuevas transformaciones suponían cambios en las medidas espaciales y
temporales hasta el punto de hacerlas relativas: dependían del observador en
cuestión y tanto el que va montado en el tren como el que está en el andén ya
no están de acuerdo en que la longitud del tren sea L. De hecho, las LT
estaban concebidas para hacer constante la velocidad de la luz con
independencia del estado de movimiento del observador y para ello requerían
cambiar las nociones de espacio y tiempo desposeyéndolas de su carácter
absoluto.
Las LT no gozaron de mucha aceptación entre los científicos. Puede
concebirse que las medidas espaciales dependan del estado del observador,
pero las medidas temporales… eso es algo mucho más delicado. El tiempo se
presumía absoluto y su discurrir no podía depender del sistema de referencia.
Eso era algo que no tenía sentido. Las LT fueron desechadas y se siguió
pensando que el experimento de Michelson-Morley era incorrecto.
En este punto debe ser remarcado algo muy notable. Las ecuaciones de
Maxwell que describen con éxito los fenómenos electromagnéticos no están
expresadas en ningún sistema de referencia. En ellas no se hace mención
explícita ni a la velocidad de la fuente de las ondas ni a la velocidad del
observador. Por ello, todos los científicos (incluido Maxwell) interpretaron
que estas ecuaciones estaban expresadas en relación al sistema de referencia
inercial más importante que existe, al sistema de referencia inercial del éter, el
estándar de “quietud”.
Por otra parte, algunos físicos habían observado que las ecuaciones de
Maxwell no permanecían invariantes bajo las GT. Es decir, las leyes de
Maxwell eran unas leyes que, de forma implícita, requerían de la existencia de
un sistema de referencia inercial privilegiado: el sistema del espacio absoluto,
del éter, o del estándar de “quietud”. Tales leyes no admitían una expresión
coherente ni bella en los otros sistemas de referencia inerciales (recordemos
que las leyes de la mecánica sí se conservaban bajo las GT).
No obstante, científicos como Lorentz habían observado que las ecuaciones
de Maxwell sí permanecían invariantes bajo las LT (se dice que las ecuaciones
de Maxwell sí tienen la relatividad del grupo de Lorentz). En otras palabras, si
uno asume como cierto el experimento de Michelson-Morley, si se acepta
como transformación válida entre sistemas de referencia inerciales las LT,
entonces las ecuaciones de Maxwell permanecen invariantes y no es necesario
referirlas a un sistema privilegiado, a ese espacio absoluto, pues son ciertas en
todos los sistemas de referencia inerciales.
Pese a esta curiosidad y coincidencia, las LT fueron finalmente desechadas por
la comunidad científica y no gozaron de la aprobación de los principales
físicos de la época. El experimento de Michelson-Morley debía ser revisado y
perfeccionado y las leyes de Maxwell seguirían siendo ciertas en el sistema de
referencia inercial por excelencia: el del éter.
1.3
La propuesta de Einstein.
En el año 1905 un joven trabajador en la oficina de patentes de Berna que
había estudiado física bajo la dirección de Weber y que no había podido
conseguir su sueño de trabajar en la Universidad propone una solución al
problema creado por el resultado del experimento de Michelson-Morley.
El razonamiento de Einstein asombra por su radicalidad y también por ser la
salida más sencilla y menos forzada de todas las posibles al callejón sin salida
al que había llegado la física en aquellos tiempos. Einstein afirma: 1) si la
medición de la velocidad de la luz es constante en todas las direcciones e
independiente del estado de movimiento del observador; 2) si para mantener
esta constancia es necesario cambiar nuestras nociones de espacio y tiempo de
modo que éstas dependan del estado de movimiento del que efectúa las
medidas y 3) si las leyes del electromagnetismo concuerdan mejor con estas
ideas que con las del espacio absoluto de Newton. Entonces lo que ocurre es
que: 1) no existe éter, ni espacio absoluto (un sistema de referencia
privilegiado), ni tiempo absoluto, y 2) el tiempo y el espacio son relativos,
dependen del estado de movimiento de quien efectúa las medidas.
Las ideas de Einstein pueden resumirse en los dos siguientes postulados:
P1) cualquiera que sea su naturaleza, el espacio y el tiempo deben estar
constituidos de tal forma que la velocidad de la luz siempre sea constante con
independencia del observador y de la fuente
P2) todas las leyes de la física deben ser idénticas en todos los sistemas de
referencia inerciales
Observemos que estamos hablando de postulados, es decir, afirmaciones que
no aspiran a ser probadas, sino que son los pilares básicos sobre los que se
debe construir la física. Si, partiendo de estos postulados y con un
razonamiento lógico, llegamos a un resultado que no se produce en realidad es
porque dichos postulados son erróneos. Hasta el momento, después de más
de cien años de pruebas, no ha habido predicción de la teoría de la relatividad
especial que haya sido refutada por la experiencia.
El postulado P1 explica los resultados del experimento de Michelson-Morley.
El postulado P2 es una generalización del bien conocido principio de
relatividad de Galileo del que ya hemos hablado a todos los ámbitos de la
física, esto es, P2 explica que es imposible distinguir entre dos estados de
referencia inerciales con experimentos físicos, sean de la índole que sean. Por
ello esta teoría se llama teoría de la relatividad (especial), porque no hay un
sistema de referencia inercial privilegiado (no hay éter) y todos estos sistemas
de referencia inerciales son igual de buenos para la formulación de las leyes
físicas.
Algunas consecuencias directas de los postulados de Einstein y que pueden
obtenerse con un poco de sentido común y matemáticas elementales son la
relatividad de la simultaneidad, la contracción de longitudes, la dilatación del
tiempo, etc. No entramos en detalle en estos fenómenos porque requieren
unas cuentas sencillas que abordaremos en pizarra… Lo decisivo es
comprender aquí que las cosas que hemos dado por supuestas desde nuestra
más pura intuición ya no tienen por qué ser ciertas en el escenario de Einstein.
Pareciera que estamos hablando de fenómenos fantásticos cuando en realidad
estas consecuencias han sido testadas experimentalmente. Ahora bien,
podemos preguntar: ¿y cómo no lo habíamos notado previamente? Pues
porque el factor por el que se contraen (resp. dilata) las longitudes (resp. el
tiempo) es del orden de 1.00000001 para velocidades cercanas a los 100
kilómetros por hora, que es una velocidad normal. Dicho factor es tan
próximo a la unidad que resulta imperceptible desde nuestro punto de vista de
personas de la calle. Sin embargo, en experimentos de laboratorio y a
velocidades más altas se han comprobado todos los efectos relativistas que
hemos descrito.
1.4
El formalismo de Minkowski.
Tras la formulación de la teoría especial de la relatividad en 1905 Einstein
esperaba una reacción de la comunidad científica que no se produjo. Su
artículo cayó en la más absoluta indiferencia hasta que, por fin, unos años más
tarde, el propio Max Planck felicitó a Albert por su artículo.
Las razones de este silencio pueden ser varias. En primer lugar, Einstein no
era un científico reputado y las ideas aportadas eran de una radicalidad sin
precedentes, por lo que el escepticismo general fue predominante. Por otra
parte, la imposibilidad de verificar la teoría con experimentos supuso que la
relatividad se mantuviera en el ambiguo terreno de la verdad y la falsedad
durante decenas de años, hasta que se pudieron detectar efectos relativistas en
experimentos de laboratorio. En tercer lugar, otros artículos de Einstein
también aparecieron a lo largo del mismo año (el “annus mirabilis”) que
acapararon la atención de la comunidad mucho más que el germen de la
relatividad especial cuyo título versaba sobre la “electrodinámica de los
cuerpos en movimiento”.
No obstante, y pese a este olvido inicial, en el año 1908 el antiguo profesor de
Matemáticas de Einstein, Hermann Minkowski estudia el artículo de su
discípulo y efectúa una aportación de carácter fundamental en la teoría. En
pocas palabras, podemos decir que Minkowski geometriza la física de Einstein
y le da rigor matemático. La difícil relación de Einstein con sus maestros
queda plasmada en su reacción cuando conoce los trabajos de Minkowski
sobre “su” relatividad. Einstein se muestra reacio a aceptar la visión
matemática de su teoría y la descalifica desechando las aportaciones de
Minkowski por artificiosas, inútiles y apartadas de la intuición física.
Este punto es interesante remarcarlo porque sin la formalización de
Minkowski el propio Einstein no hubiera sido capaz de llegar a extender su
teoría al ámbito de cualquier sistema de referencia, aunque esto sólo se hizo
patente muchos años más tarde en los que Einstein reconoció su error.
Rectificar es de sabios, y Einstein lo era.
Ahora bien, ¿en qué consiste esta formalización? Pensemos en un sistema de
referencia inercial S con coordenadas (t,x) donde t es la coordenada temporal
y x es la espacial (simplificamos asumiendo que sólo existe una dimensión en
el espacio; esto es irrelevante). Se puede demostrar que si S’ es otro sistema de
referencia inercial con coordenadas (t’,x’), entonces el cambio de coordenadas
de un sistema a otro sólo depende de la velocidad relativa entre ambos y tiene
una expresión lineal relativamente sencilla. Este cambio de coordenadas se
conoce como transformación de Lorentz (en honor al físico que las descubrió
para explicar los resultados de Michelson-Morley, aunque no supo interpretar
correctamente la física reflejada en tales ecuaciones).
Con estas transformaciones es muy sencillo demostrar los efectos relativistas
que hemos comentado anteriormente (contracción de longitudes, dilatación
temporal, etc.) así como justificar que la luz siempre tiene velocidad constante
respecto de cualquier observador inercial.
Si representamos en el plano dado por los ejes cartesianos (t,x) las
coordenadas (t’,x’) entonces vemos que los ejes de S’ están inclinados con
respecto a los de S. Un evento (algo que sucede en un punto del espacio en un
determinado momento) tendrá, evidentemente, distintas coordenadas en cada
sistema de referencia porque cada observador asigna a cada evento el espacio
y el tiempo desde su punto de vista.
Si las coordenadas dependen del observador, está claro que éstas no tienen
entidad absoluta. En otras palabras, si efectuamos un experimento, lo
relevante, lo físico en el experimento es lo que ocurre (y mide) todo
observador inercial, y no lo que acontece para uno en concreto que registra en
su particular sistema de coordenadas. Por tanto, sería deseable encontrar
cantidades invariantes que no dependieran de las coordenadas. Tales
cantidades serán candidatas a describir un fenómeno físico real y no un
registro aparente de los hechos según el observador del que se trate.
Pues bien, dados dos eventos A y B con sus coordenadas (ta,xa) (tb,xb)
respecto de un sistema S, resulta que la cantidad (tb-ta)2-(xb-xa)2 no depende
de dicho sistema, es decir, sistema S’ registra para A y B las coordenadas
(ta’,xa’) y (tb’,xb’), entonces resulta que (tb’-ta’)2-(xb’-xa’)2=(tb-ta)2-(xb-xa)2.
Esta cantidad invariante se conoce como intervalo espacio-temporal y tiene un
significado físico muy preciso. De su signo se desprende, por ejemplo, la
causalidad entre los eventos A y B de suerte que si el intervalo es positivo
entonces se dice que ambos eventos están conectados causalmente y que es
posible que uno de ellos influya en el otro. De hecho, se puede ser más
preciso y determinar (de modo absoluto) cuál de los dos sucesos ocurre antes
para todos los sistemas de referencia inerciales y aquí tenemos otro ejemplo de
concepto absoluto: la causalidad, que podemos parafrasear diciendo que las
causas preceden a los efectos para todos los observadores.
Si el intervalo es negativo entonces ninguna señal puede viajar desde A hasta
B sin violar la causalidad y sin exceder la velocidad de la luz. La causalidad es
una hipótesis razonable si queremos tener una visión razonable de las cosas;
por otra parte, el hecho de que nada excede la velocidad de la luz se
demuestra a partir de los postulados de Einstein justificando que, conforme
aceleramos una partícula con masa, entonces cada vez cuesta más trabajo
incrementar su velocidad ya que también su masa se incrementa (con respecto
a las partículas sin masa, éstas son de la misma “naturaleza” que la luz por lo
que se tiene que su velocidad es invariante).
¿Y qué podemos decir cuando el intervalo es nulo? Pues entonces ambos
sucesos están conectados causalmente, pero tal conexión es posible
únicamente con señales luminosas.
Hasta ahora, sólo hemos hablado del signo del intervalo, pero aún es más
importante el hecho de que nos permite, de algún modo impreciso, efectuar
“mediciones” en el espacio-tiempo. El entrecomillado se debe a que estas
medidas no tienen las propiedades habituales que conocemos. Por ejemplo, en
el espacio-tiempo de Minkowski la línea recta que separa dos eventos
(relacionados causalmente con intervalo negativo) es la línea más larga que
une ambos puntos.
En resumidas cuentas, y para cerrar este primer capítulo, lo aportado por
Minkowski es un modelo para el espacio-tiempo, un modelo 4-dimensional en
el que un evento es registrado por un observador (inercial) S y le asigna
coordenadas (t,x,y,z). Estas coordenadas por sí mismas no son mejores que
otras (que las registradas por otro observador inercial S’) pero eso no es lo
importante, porque lo decisivo es que podemos, dentro de la dependencia con
respecto a cada observador, definir objetos absolutos que nos proporcionan
magnitudes y descripciones físicas y reales que son independientes respecto
del observador.