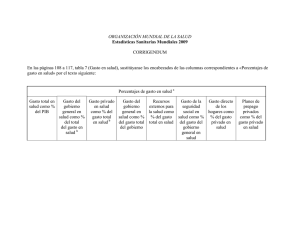
Tablas, barras y líneas: Tres herramientas que propone la didáctica

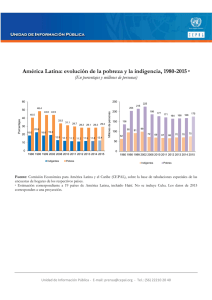
Tablas, barras y líneas:
Tres herramientas que propone la didáctica
realista de la matemática para el trabajo con
porcentajes
Betina Zolkower (Brooklyn College, CUNY, Nueva York, EEUU)
Silvia Pérez
Ana María Bressan
Grupo Patagónico de Didáctica de la Matemática (GPDM)
Escuela de Invierno en Didáctica de la Matemática
Universidad de la República
Salto, Uruguay, Agosto 8-9, 2008
La investigación
Contexto:
Escuela privada bilingüe, de San Carlos de Bariloche (Río
Negro, Argentina)
Sexto grado (23 alumnos)
Nivel socio-económico alto
Docente con 11 de aňos de experiencia en el aula
Preguntas centrales de la investigación:
¿Cómo armoniza la docente las puestas en común en sus
clases de matemática?
¿Qué efectos tiene esta mediación en la apropiación de
ideas/herramientas matemáticas por parte de sus
alumnos?
La didáctica realista de la matemática:
Características principales de esta corriente
(Freudenthal, 1991; Streefland, 1991,
Gravemeijer y otros, 2000; van den-Heuvel Panhuizen, 2003)
La matemática es entendida como el resultado de la actividad de
organización (matematización) de la realidad, incluida la propia matemática.
El sentido común y el lenguaje cotidiano son importantes referentes
para significar y motivar el uso de objetos y procesos matemáticos.
Los contextos y las situaciones realistas (realizables, imaginables) sirven de
punto de partida para la los procesos de matematización progresiva.
Los modelos son centrales en los procesos de enseñanza-aprendizaje en tanto
funcionan como herramientas flexibles de representación, operación y
razonamiento.
La interacción tanto horizontal (entre alumnos) como vertical (docentealumnos) cumple un papel primordial en los procesos de matematización.
En la elaboración de secuencias didácticas se tienen en cuenta relaciones
intra-matemáticas (ideas, ejes) y extra-matemáticas (otras disciplinas).
I.
Tablas, Barras y Líneas
Los modelos en la didáctica realista de la matemática:
(Gravemeijer y otros, 2000; van den Heuvel-Panhuizen, 2003):
Los modelos emergen como herramientas para la matematización de
situaciones problemáticas y favorecen subas en los niveles de matematización
de los alumnos
Ellos deben:
•
estar enraizados en contextos y situaciones realizables o imaginables,
• poseer suficiente flexibilidad como para que puedan ser usados a un nivel
más avanzado o general, y
•
ser re-inventables por los propios alumnos.
Progresivamente, los modelos se van desligando de las situaciones originarias
hasta transformarse en herramientas más potentes que permiten organizar
matemáticamente familias de problemas homólogos a dichas situaciones
(Freudenthal, 1975, Streefland, 1985).
Un problema de porcentajes
Teo contestó correctamente 27 de las 40 preguntas de su
prueba final. Si para pasar de grado necesita responder el
60% de las preguntas correctamente, ¿habrá pasado de
grado?
Tres modelos para trabajar con porcentajes
Teo contestó correctamente 27 de las 40 preguntas de su prueba final. Si
para pasar de grado necesita responder el 60% de las preguntas correctamente, ¿habrá
pasado de grado?
TABLA DE RAZONES
MODELO DE BARRAS
LINEA NUMERICA DOBLE
La tabla de razones:
Un modelo para generar y trabajar con razones equivalentes
(Middleton y van den Heuvel-Panhuizen, 1995)
1) La tabla de razones consiste en un esquema de filas y columnas que define
casilleros para colocar en ellos los números.
2) Las filas se etiquetan indicándose el significado de los números y, si es necesario,
también las unidades que se utilizan. El orden es indistinto en cuanto a qué se coloca
en cada una de las filas.
3) Vista horizontalmente: La razón entre los números de los casilleros de cada
columna es la misma para todas las columnas. Esta razón constante puede entonces
utilizarse para calcular el número que va en un determinado casillero.
4) Vista verticalmente: A su vez, los cocientes que resultan de dividir dos números
cualesquiera de una fila y sus correspondientes en otra fila resultan iguales.
5) Para obtener los números de una columna, los números de otra columna se pueden
multiplicar o dividir. También es posible utilizar la suma y la resta como estrategias
para obtener los números de una columna a partir de otra dada.
6) La tabla de razones aparece primero en la clase como herramienta para resolver
problemas de multiplicación y división y más adelante, para trabajar con fracciones.
7) Esto permite dar sentido tanto a los algoritmos convencionales de la multiplicación y la
división con naturales, fracciones y decimales como a las reglas para trabajar con
proporciones
8) Hay espacio constructivo para que cada alumno utilize las estrategias que él mismo
elija
El modelo de barra (Middleton y otros, 1998)
1) La barra es un modelo de area que hace explícita la relación parte/todo
2) Permite conectar porcentajes, fracciones, decimales, estableciendo razones en
base a el uso de la proporcionalidad directa
3) El que la razón entre los números alineados verticalmente sea la misma, permite
moverse sobre la barra en forma horizontal, pudiéndose asi resolver cada uno
de los tres ‘casos’ de problemas de porcentaje
(i) 24% de 60 = ….
(ii) ¿Qué porcentaje es 36 de 240?
(iii) 72 es el 75% de….
4) A diferencia de la tabla de razones, el orden en el que se colocan los números
es siempre creciente de izquierda a derecha.
El modelo de barra
5) Admite un uso flexible por medio de una gran variedad de estrategias, incluídas:
i) la duplicación y división reiterada por 2 y por 10
ii) el uso de porcentajes, fracciones y decimales de referencia (ej. 50%, ¼, 0,75, etc.)
iii) las estrategias aditivas
iv) las estrategias del 10% y la del 1%
6) Aparece inicialmente en la clase como herramienta para el trabajo con fracciones
7) Se adapta fácilmente al nivel de matematización de cada alumno
8) Su uso frecuente, acompañado de la reflexión acerca de las distintas estrategias utilizadas,
fomenta la esquematización progresiva
10) En tanto herramienta de pensamiento, permite dar sentido al algoritmo convencional para el
cálculo de porcentajes
La línea numérica doble
1) Es un modelo lineal que permite representar y operar con dos magnitudes
directamente proporcionales (ej. distancia/tiempo, paquetes/costo)
2) Permite conectar porcentajes, fracciones, decimales, estableciendo razones en base a
el uso de la proporcionalidad directa
3) Cada punto de la línea representa una relación (razón) que resulta ser la constante
de proporcionalidad
4) A diferencia de la tabla de razones y tal como en el modelo de barra, el orden en el
que se colocan los números es creciente de izquierda a derecha.
5) Admite el uso de las mismas estrategias que el modelo de barra, permitiendo además
el trabajo con porcentajes que superan el 100%
6) Aparece inicialmente en la clase como línea numérica simple abierta, la cual se usa
como herramienta para la resolución de problemas de cálculo elemental
7) Se adapta fácilmente al nivel de matematización de cada alumno y su uso frecuente,
acompañado de la reflexión acerca de las distintas estrategias utilizadas, fomenta la
esquematización progresiva
Características de los tres modelos para el trabajo con porcentajes
1) Permiten mantener a la vista aspectos centrales del contexto o de la
situación
2) Dan lugar a efectuar y registrar pasos intermedios en el camino
hacia la solución buscada
3) Son flexibles en el sentido de que se adaptan fácilmente al nivel de
matematización de cada alumno
4) Sugieren o invitan a la búsqueda de atajos (esquematización
progresiva)
5) Admiten el uso de una gran variedad de estrategias
6) El trabajo simultáneo con más de un modelo permite compararlos,
usándolos como modelos para pensar las relaciones matemáticas
encapsuladas o inscriptas en ellos.
II.
El trabajo con porcentajes
en la clase de 6to grado de Silvia
Secuencia Didáctica de Porcentajes
1) ¿Cuándo y cómo hablamos de porcentajes?
Situaciones cotidianas en las que se habla de porcentajes; relación
entre %, fracciones y probabilidad; carácter relativo de la noción de
porcentaje; porcentajes de referencia (10%, 50%, 25%, 75%, 20%, 1%)
2) ¿Cómo podemos usar el modelo de barra para mostrar cuán
ocupados están los estacionamientos?
Playas de estacionamiento más o menos ocupadas (introducción del
modelo de barra y uso de la tabla de razones); uso de porcentajes
de referencia en estrategias de cálculo
3) ¿Cómo calculo rápido cuánta propina tengo que dejar?
Situaciones cotidianas que involucran porcentajes sobre precios (propinas, descuentos,
aumentos, etc.); uso de distintas estrategias de cálculo mental
4) ¿Cómo se puede usar el modelo de barra para mostrar cuán llenas
están las salas de cine?
Cambia el contexto, el mismo modelo (modelo de/modelo para)
5) ¿Qué significa cuando, al descargar un programa en la computadora, aparece una
ventana con una barra y una información numérica que van cambiando?
Uso de % en la computadora (modelo de barra) (cambia el contexto, el mismo
modelo) (modelo de/modelo para)
6) ¿Cómo podemos averiguar rápidamente distintos porcentajes de 360 usando la
barra?
7) ¿En cuál de los dos negocios me conviene comprar el abrigo?
8) ¿En cuál clase/cine/sala de teatro hubo mayor porcentaje de asistencia?
Problemas en distintos contextos que involucran comparar razones usando la barra
9) Decatlón de problemas puramente numéricos de porcentaje para afianzar el uso
de estrategias eficientes para realizar cálculos mentalmente
10) Cadena de cálculos de % de $350, conexión entre fracciones y los porcentajes
11) ¿Cuántos kilos de agua tenemos en el cuerpo? ¿Qué porcentaje
de agua contienen distintos alimentos? Uso de la barra en forma vertical
12) ¿Qué fracción y qué % representa cada una de las piezas del rompecabezas?
Contexto geométrico y de medida: el rompecabezas cuadrado de Lloyd
13) ¿Cómo se calculan los porcentajes? Institucionalización de las ideas que se
trabajaron durante la secuencia
14) ¿Cómo se calcula un % con la calculadora?
Dos métodos para calcular el porcentaje usando la calculadora: a) con la tecla de % y b)
sin usar esa tecla (o sea, reemplazándola por las operaciones que están implícitas en el
uso de la tecla)
15) ¿Qué nos quieren vender?
16) ¿ Qué porcentajes de descuento están haciéndole a estos pares de zapatos?
Reconocer porcentajes de descuento dado el precio original y el precio rebajado
17) Más actividades de trabajo simultáneo con fracciones, decimales, y
porcentajes
18) Porcentajes o centavos: ¿Qué descuento es mejor?
Dadas dos opciones de descuento, una en porcentaje y otra en centavos, decidir cual de
ellas es más conveniente para el cliente
Algunos momentos en el desarrollo de esta secuencia
¿Cómo usar la barra para mostrar cuán llenas están las salas de cine?
ABRIL/MAYO
Porcentajes en la computadora
(ficha adaptada de “Modelos confiables,” MIC, págs. 18-19)
JUNIO
¿Cómo podemos averiguar rápidamente distintos porcentajes de 360?
JUNIO
Problema: En Stop & Shop todo tiene un descuento del 20% y en Ropa para Todos
…. dos negocios me conviene comprar el
el descuento es del 25%. ¿En cuál de estos
abrigo naval Peacock?
JULIO
Proceso de resolución de problemas: Forma de trabajo
APERTURA
Introducción
la situación
problema
Trabajo
(individual o
grupal)
DESARROLLO
Corte e intercambio
de ideas para resolver
el problema
Trabajo
individual
o grupal)
CIERRE
Discusión del problema, su
solución y las ideas que se
utilizaron para resolverlo
Esta discusión duró
más de 40 minutos
e involucró
activamente a 21 de
los 22 alumnos
presentes ese día
Resolución del problema del abrigo: Etapas de la discusión
Etapas
Apertura
Desarrollo
Cierre
Sub-etapas
Orientación a la conversación
Tratamiento de los datos
Especificación del tema de
conversación
Relación entre la división y el
porcentaje
Interpretación de los resultados
calculados en función del
problema
Enunciación y apreciación del
algoritmo convencional
Estudio de la idea de Julio en la
tabla de razones y en la barra de
porcentajes
Revisión y apreciación de la resta
como estrategia de solución
Recuperación de la idea errónea
de restar
Apertura de nuevo interrogante
(giro meta-cognitivo)
Interrogantes centrales
¿Qué problema estamos tratando de resolver?
¿Con qué números tendría sentido trabajar dado el contexto de este problema?
¿Por qué?
¿Qué ideas surgieron para resolver el problema y cómo usamos cada una de esas
ideas?
¿Dividir por 4 y por 5 o por 25 y por 20? ¿Qué estaríamos averiguando al dividir
los precios iniciales (75 pesos y 69 pesos) por 25 y por 20, respectivamente?
¿Cómo interpretamos los resultados de los cálculos en el contexto del problema a
resolver?
¿Qué idea nos propone Julio?
¿Como podemos usar la tabla de razones y la barra de porcentajes para entender
mejor la idea de Julio?
¿Por qué no sirve la idea de restar los porcentajes de descuento a los precios
iniciales (69 -20 y 75 – 25)? ¿En qué condiciones se podría hacer eso?
¿Cómo podríamos reformular o modificar la idea de restar para dejarla inscripta
en nuestro texto?
¿Qué le pasó a cada uno en relación con las ideas?
Extracto del registro (I)
Docente (D): Voy a poner estas tablas acá al lado chiquitas, para que vean que
esto mismo que está hecho en cuentas se puede hacer también en tabla
(copia las tablas en el afiche al lado de los cálculos de Julio)
69 x 20 = 1,380
1380 ÷ 100 = 13.80
75 x 25 = 1,875
1875 ÷ 100 = 18.75
$
69
0,69
13,80
$
75
0,75
18,75
%
100
1
20
%
100
1
25
Teo: ¡Pero en barras también se podría hacer!
D: ¿En barras también se podría hacer?
Nuria: Sí.
D: Sí, alguien dijo que sí. ¿Se podrá hacer en barra?
Nuria: Sí. 75…
D: ¿Y cómo quedarían las barras, iguales a esta? (Señala las barras ya hechas de los
afiches)
Extracto del registro (II)
Nuria: Dividida en 100
Raul: Sí. ¡La cosa es hacerla!
D: ¿Y se podrá por ahí marcar en la barra sin tener que dividirla en 100?
(Dibuja una nueva barra)
Nuria: Sí, la hacés más chiquita
Teo: Más o menos donde va el 1%
Matias: Igual podés agarrar un lugar ahí en el medio (señalando arriba en el
pizarrón) y hacés por metro
D: ¿Cómo quedaría, a ver?
Raul: ¡Pero te sobresale del pizarrón!
Teo: Podés agarrar una barra más chiquita, y sin medirHablan varios juntos sobre las barras
D: Si quisiera hacer así, no me importa cuánto mide la barra, ¿cómo
quedaría marcada?
Isabel: ¡Hacé una chiquita sin medir y listo!
Extracto del registro (III)
D: La barra de 69 pesos, ¿cómo quedaría marcada?
Isabel: 0.69 arriba, el 1% abajo y listo.
D: Ahí, ahí (mientras escribe el 69, el 1% y el 0.69)
Teo: Y abajo el 1%
D: ¿Y ahora?
Isabel: ¿Y ahora qué tendíamos que hacer?
Nuria: Ah! Multiplicarla por 20 y multiplicarla por 20.
D: Aha. ¿Así? Por 20, está bien. ¿Haría falta dividirla en 100, marcar las
100 divisiones?
Andrea: No.
¿Cómo usa la docente el lenguaje hablado y otros recursos semióticos durante las
puestas en común?
Combina el lenguaje hablado con el lenguaje escrito y el gestual y el uso de diagramas.
Esto le da a las puestas en común un carácter multi-modal.
Hay congruencia entre la forma gramatical de lo que dice y la función
de habla de tales contribuciones. Por ejemplo, casi todas sus preguntas están
realizadas en forma gramatical Interrogativa.
Usa los tiempos verbales presente y presente continuo, y los modos condicional y
Subjuntivo.
Por lo general, usa la primera persona del singular y la del plural.
Contribuye a las conversaciones y discusiones no solamente preguntas abiertas sino
también preguntas polares (si/no).
Sus preguntas rara vez demandan procesos meta-cognitivos a nivel individual
(ej. No dice: Contáme cómo lo pensaste. Explicános cómo lo hiciste).
En cambio, sus preguntas invitan y orientan a la clase a reflexionar acerca de
lo hecho, para repasarlo y avanzar sobre eso, comparando y contrastando ideas
(¿Qué diferencia hay entre ….? ¿Cuál es la que por ahí me serviría?), apreciando ideas
y justificando estas apreciaciones (¿Está bien? ¿Será? ¿Por que?).
Secuencia Didáctica de Porcentajes (continuación)
Decatlón de problemas puramente numéricos de porcentaje para afianzar la
búsqueda y el uso de estrategias eficientes para realizar cálculos mentalmente
Ivana
JULIO
Cadena de cálculos de % de $350
Federico
AGOSTO
¿Cómo se puede calcular un % usando la calculadora?
En resumidas cuentas: ¿Cómo se calculan los porcentajes?
SEPTIEMBRE
¿Cómo se puede calcular un % usando la calculadora?
“En el trabajo con la calculadora había una pregunta sobre por qué
daba lo mismo hacer en la calculadora el 15% de 240 y sumárselo
(apretando 240 x15% +) que hacer 240 x 1.15.
A algunos chicos primero les costó encontrar la relación. Otros trataban de
explicarlo con diagramas que mostraban que cuando apretás la tecla + en la
calculadora después de haber calculado el 15% de 240, eso se
corresponde con el 1 del 1,15 y que el 0,15 era lo mismo que el 15%.
Cuando lo miramos entre todos, les pregunté qué % del total era el
resultado. El 115%, contestaron. Y ya con eso empezaron a levantar la
mano desesperados diciendo que eso era 1,15.
Entonces nos pusimos a jugar con otros ejemplos. ‘Si hago 240x2,15, ¿qué
% estaría averiguando?’ ‘Y si hiciera 240x3,17?’ ‘¿Y si quisiera saber el
159% de 240, con qué multiplicación lo podría reemplazar?’ ‘¿Y el 79% de
1.500?’ Algunos dijeron 1.500 x 7,9. Otros 1.500 x 0,79. Otros
1.500x79/100. Y no podían ser todas esas lo mismo! Para descartar
pasaban los decimales a fracciones 0,79=79/100=79%. ‘Es esa! La
otra no, porque 7,9 es igual a 790/100=790%.’
SEPTIEMBRE
Como estaban tan embalados y copadísimos con esto, les pregunté cómo
se podría reemplazar de otra forma lo que hace la calculadora cuando uno
aprieta la tecla %. Una era multiplicar por el decimal equivalente. ¿Cuál
podría ser otra?
Algunos empezaron a dar ejemplos donde multiplicaban el número por el %
que querían y dividían por 100. Todos estuvieron de acuerdo con eso. Como
parecía que lo tenían tan claro, les pregunté cómo se podría hacer si uno
quisiera calcular un % cualquiera para cualquier número, sin pensar ya en
el 240 o en los ejemplos que habíamos visto.
Salta Raúl de atrás, muy tranquilito como siempre, a decir “Y… un número X
por un número X dividido 100!” Algunos lo miraron diciendo ¡Ah, bueno!
Como si fuera una eminencia. Raúl enseguida se puso colorado y se
encogió de hombros como si lo que dijo hubiera estado mal.
Le pedí que lo repitiera porque sonaba bueno. Al resto de la clase le
pregunté: ¿Cómo anotamos eso que dijo Raúl? ¿estará bien? ‘Para un
número poné X,’ me dictaban. ‘Multiplicado poné un por (x). Ahí otra X pero
no, no es la misma X porque no es el mismo número.
Convinimos en ponerle otra letra, eligieron a. Entonces quedó:
X x a/100 y a es el % que querés saber y X el número, el 100%.”
SEPTIEMBRE
El uso de imágenes como generadoras de actividad matematizadora
¿Qué porcentaje del precio se quita al tener 30 gramos gratis?
¿Cuánto vale el dentífrico sin su descuento?
¿Qué fracción es 30 gramos de 180?
¿Qué figura tiene la caja?
Si usamos 5 gramos por día, ¿cuánto nos duraría?
¿Tiene contenido neto o líquido?
Si hubiese un 50% de descuento, ¿cuál sería el precio?
¿Cuántos kilos tiene?
¿Cuánto mide la caja y cuál es su perímetro? ¿y el área?
¿Siempre te regalan 30 gramos?
¿Cuántos gramos tiene en realidad sin la oferta?
¿Cuánto costaría la caja si fuera la mitad de 210?
¿Qué ingredientes tiene?
¿Cuál es el precio de los 30 gramos?
¿Cuál es el precio de un gramo?
¿Por qué los dentífricos siempre tienen la misma forma?
Si 15 gramos de esta pasta dental salen 0,20$, ¿cuánto sale la pasta dental
sin contar el descuento?
¿Cuánto te dan gratis?
SEPTIEMBRE
¡Bajaron los precios de pares de zapatos!
Raúl
Uso de modelos y estrategias para resolver un problema que involucra comparar razones
Problema: En 6to ‘A’ faltaron 4 de los 32 alumnos. En 6to ‘B’ faltaron 3 de los 25 alumnos. ¿En cuál
de los dos grupos hubo un mayor porcentaje de ausentes?
Cómo averiguar el precio original de un articulo
sabiendo el precio descontado y el porcentaje de descuento
III.
Al año siguiente…
Porcentajes y elecciones locales: Un mismo candidato, ¿tres partidos?
“Estas semanas estuvimos trabajando fuerte con gráficos y sobre las
elecciones para intendente que hubo acá el 18 de mayo. Estuvo muy interesante
cuando miramos materiales referidos a las elecciones que ellos tenían que
recoger y traer. Había gráficos, tablas, artículos, hasta tuvimos las planillas
finales de cuatro mesas (las originales, porque el papá de un nene fue fiscal por
un partido político y las tiene en su poder). Los miraron, los fueron pasando y
después las comentamos. Salieron tantas cosas!!
Primero había algunos conceptos de ciencias sociales que no sabían (voto
en blanco, nulo, recurrido, impugnado); tampoco sabían que el % necesario para
ganar era sobre los votos sin incluir los votos en blanco, razón por la cual empezaron
a expresar que entonces era mejor optar por alguien “porque si no, ayudás a
ganar al que más tiene!” Además, en los gráficos circulares unos mostraban los %
obtenidos por partido y otros por candidato y no coincidían.
Mirando las boletas, que también teníamos, vieron que un mismo señor fue
candidato por tres partidos distintos, y que si juntabas esos tres porcentajes te daba
el total del candidato. “¿Pero vale hacer eso?” dijo una nena, “¿Y a las ideas de
quién va a responder?, preguntó otro.
El debate estuvo muy bueno porque involucró aspectos relacionados con la
legitimidad de ciertas acciones políticas (que son legales).”
MAYO 2008
Porcentajes y elecciones locales:
Una diferencia de 2500 votos: ‘Un montón’ o ‘re-poco’?
“También comparamos los porcentajes, que en algunos aparecía con
más cifras decimales que en otro, de dónde habrán salido (teníamos
los datos del padrón total, la cantidad que efectivamente votó y la
cantidad de votos de cada partido).
Hubo un titular de diario que generó revuelo. Decía "Cascón le
ganó por 2500 votos a Barriga." Ni bien terminé de leerlo, una nena
dice "Ah, un montón" mientras un nene al lado de ella decía ¡"Es re
poco!" ellos mismos se miraron dándose cuenta de que habían
interpretado bien distinto las cosas.
Lo volví a leer y pregunté que si era mucho o poco y sale uno a decir
que si eran como 40.000 los que habían votado que no era mucho y
ahí echó luz sobre el asunto de que no estaba dicho sobre cuántos
votos era la diferencia.
Después cada uno tuvo que escribir tres conclusiones de esa clase y el
trabajo con las elecciones. Algunas son bien interesantes.”
MAYO 2008
Encuestas, angulos centrales y porcentajes
“El otro día hicimos un racconto juntos de distintas formas de averiguar
qué ángulo central le correspondía a un % de un dato de una
encuesta. En realidad sabían que era como averiguar cualquier otro %
pero de 360! Igualmente me pareció oportuno y útil hacerlo.
Nombraron: pensar en una fracción, usar la regla de 3, usar %
"estratégicos o básicos" los llamaron (el 1%, 10%, 50%, 5%, 25%,
75%) y el cálculo tradicional para averiguar un %. Priorizaron estos,
aunque después sugirieron igualmente la tabla de razones (hacés lo
mismo que si vas buscando % básicos) y el modelo de barra que la
nombraron como posible (aunque nadie usa ya eso). También
incluyeron la calculadora en sus dos formas (usando la tecla % o
directamente haciendo los cálculos sin usar la tecla
específica). Terminaron diciendo que era todo lo mismo: puesto en
forma vertical, horizontal o en una tabla es siempre lo mismo.
Fueron saliendo un montón de cosas interesantísimas sobre la
flexibilidad que tienen para pensar distintos usos posibles de un
modelo (que los piensan aunque después no los usan, pero son
capaces de imaginar como seria usarlos).”
JUNIO 2008
Referencias Bibliográficas
Freudenthal, H.: 1991, Revisiting Mathematics Education: China Lectures, Kluwer, Dordrecht.
Gravemeijer, K. y otros: 2000, “Symbolizing, modeling, and instructional design.” En Cobb,
P., Yackel, E. y Mc Clain, K. (Eds.) Symbolizing and Communicating in Mathematics
Classrooms. Lawrence Erlbaum.
Middleton, J., van den Heuvel-Panhuizen, M. y Shew, J.: 1998, “Using bar representations as a
model for connecting concepts of rational number.” Mathematics Teaching in the Middle School,
3 (4), 302-312.
Middleton, J. y van den Heuvel-Panhuizen, M.: 1995, “The ratio table.” Mathematics Teaching in
the Middle School, 1 (4), 282-288.
National Center for Research in Mathematical Sciences Education y el Instituto Freudenthal
(eds.): 1998, Mathematics in Context: A Connected Curriculum for Grades 5-8.
Chicago, Ill: Enciclopedia Britannica.
Streefland, L.: 1991, Fractions in Realistic Mathematics Education: A Paradigm of
Developmental Research. Kluwer. Dordrecht, The Netherlands.
van den Heuvel-Panhuizen, M.: 2003, “The didactical use of models in realistic mathematics
education: An example from a longitudinal trajectory on percentage,” Educational Studies in
Mathematics 54: 9-35.
Grupo Patagónico de Didáctica de la Matemática
www.gpdmatematica.org.ar
[email protected]
[email protected]
[email protected]