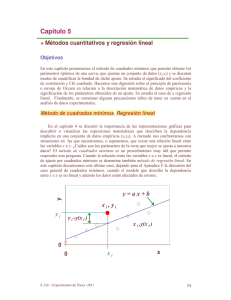
ANÁLISIS DE CORRELACIÓN Y REGRESIÓN LINEAL

ANÁLISIS DE CORRELACIÓN Y REGRESIÓN LINEAL.
REPRESENTACIÓN DE DATOS CON DOS VARIABLES.
Como sabemos los datos los podemos representar de dos maneras primordialmente: una es
mediante tablas o cuadros y la otra es mediante gráficas. En ambas maneras debemos
denotar el nombre de las variables.
REGRESIÓN LINEAL.
El análisis de regresión lineal nos va a permitir apreciar el comportamiento de dos variables a
continuación haremos un recordatorio sobre variables.
Variable.
Es toda característica de algún fenómeno susceptible de medición y que puede tomar
diferentes valores: peso, estatura, ingresos, productividad, etc.
Variable independiente.
Es aquella que puede controlar el investigador y le puede asignar cualquier valor.
Variable dependiente.
Es aquella cuyos valores van a estar determinados del valor que se le asigne a la variable
independiente
DEFINICIÓN DE REGRESIÓN LINEAL.
Se denomina a la estimación de una variable y (variable dependiente) a partir de otra
variable x (variable independiente).
MÉTODO DE MÍNIMOS CUADRADOS.
El ajuste de los datos muéstrales a una recta representativa de la relación de dependencia
entre las dos variables, resulta sencilla mediante la técnica de los mínimos cuadrados. Como
sabemos la ecuación de una recta es y = a + bx en donde a y b son coeficientes constantes
y x e y representan los valores de las variables independiente y dependiente
respectivamente. Utilizando esta fórmula vamos a obtener la recta óptima en la cual las
distancias entre los puntos de la distribución a la recta sean mínimas.
Para hallar la recta de regresión lineal mediante el método de los mínimos cuadrados
utilizaremos las siguientes formulas:
a=
y = a + bx
∑ y − b∑ x
b=
n
n ∑ xy − ∑ x ∑ y
2
n ∑ x 2 − [∑ x ]
Mediante estas dos fórmulas desarrollaremos los cálculos en forma de tabla para obtener el
valor de “a” y “b”
DIAGRAMA DE DISPERSIÓN.
Es la representación gráfica de la nube de puntos de la variable x e y que nos permitirá
visualizar si es posible ajustar a una línea recta que se aproxime a ellos.
Ver la siguiente grafica:
y
y= a +bx
x
CORRELACIÓN ENTRE VARIABLES.
DEFINICIÓN DE CORRELACIÓN. Se denomina correlación al grado de relación de
interdependencia que existe entre dos variables.
El coeficiente de correlación r expresa numéricamente que tan bueno resulta el ajuste de la
recta a los datos, y también representa una medida de que tanto los valores de x y los
valores de y se determinan mutuamente.
El valor de r varía siempre entre -1 y 1, de hecho, r tiene siempre el mismo signo de la
pendiente de la recta, entre más cercanos se encuentren los puntos a la recta, el coeficiente
r se acercara más al valor de -1 ó 1.
Si r=0 no existe correlación entre las variables.
r=
n ∑ xy − ∑ x ∑ y
(n ∑ x 2 − (∑ x ) 2 )(n ∑ y 2 − (∑ y) 2
Ejemplo 1.
En unas pruebas elásticas de rebote de un amortiguador de fricción, se obtuvieron, para
distintas alturas de caída del peso libre (variable independiente x), las alturas de rebote
(variable dependiente y ) que figuran en la tabla adjunta.
a) Determinar la recta de regresión correspondiente mediante el método de mínimos
cuadrados.
b) Obtener el índice de correlación de las variables.
x⋅ y
y2
1.44
2.28
3.61
1.3
5.76
3.12
1.69
3.2
2.1
10.24
6.72
4.41
4
4.3
3.4
18.49
14.62
11.56
5
5.7
2
32.49
11.40
4
6
7
3.8
49
26.60
14.44
7
9
3.3
81
29.70
10.89
∑
32.8
17.8
198.42
94.44
50.68
Puntos
x (dm)
y (mm)
1
1.2
1.9
2
2.4
3
a) Recta de regresión.
Sustituyendo los valores con la fórmula:
b=
n ∑ xy − ∑ x ∑ y 7 (94.44) − (32.8)(17.8)
=
2
2
2
n∑ x − ∑ x
7 (198.42) − 32.8
[ ]
(
)
x2
b=
660.8 − 583.84
76.96
=
= 0.2466
1388.94 − 1075.84 313.1
Para el cálculo de a.
a=
∑ y − b∑ x = 17.8 − (0.2466)(32.8) =
a=
17.8 − 8.088 9.711
=
= 1.38
7
7
n
7
y = a + bx
Recta de regresión:
y= 1.38 + 0.2466x
b) Coeficiente de correlación:
Con los valores de la tabla anterior sustituimos en la siguiente fórmula:
r=
=
=
n ∑ xy − ∑ x ∑ y
(n ∑ x 2 − (∑ x ) 2 )(n ∑ y 2 − (∑ y) 2
7 (94.44 ) − (32.8)(17.8)
2
2
((7 (198.42) − (32.8) )(7 (50.68) − (17.8) )
77.24
(313.1)(37.92 )
r = 0.708
=
77.24
108.96
= 0.708
=