Práctico Nº 1 - Fices

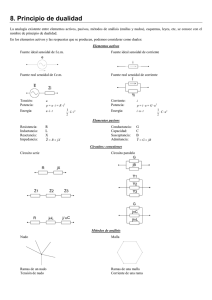
UNIVERSIDAD NACIONAL DE SAN LUIS
FACULTAD DE INGENIERÍA Y CIENCIAS ECONÓMICO-SOCIALES
LABORATORIO DE
MEDICIONES ELECTRÓNICAS
www.fices.unsl.edu.ar/~areaeyc/lme
Profesor Responsable
Ing. Juan Acheriteguy
[email protected]
Responsable Trabajos Prácticos
Ing. José Luis Bossa
[email protected]
2011
Laboratorio de Mediciones Electrónicas - 2011
TRABAJO PRÁCTICO Nº 1
RESPUESTA EN FRECUENCIA DE CIRCUITOS BÁSICOS
1 Objetivos de la Práctica
En esta práctica se pretende que el alumno compruebe el comportamiento en frecuencia de varios circuitos compuestos por generadores de Corriente Alterna (CA),
Amplificadores Operacionales (AOP), resistencias, condensadores y bobinas. Obtener
analíticamente la función de transferencia del filtro y graficar su diagrama de Bode
asintótico y exacto.
Posteriormente podrán compararse las respuestas reales observadas en cada caso
con las obtenidas analíticamente o por medio de simulación con la ayuda de SPICE y
MATLAB.
En esta práctica el alumno deberá obtener con la ayuda de un Osciloscopio Digital
la respuesta en frecuencia de los siguientes casos:
 Filtros pasivos compuestos por resistencias, condensadores y bobinas.
 Filtros activos compuestos por resistencias, condensadores, bobinas y AOP.
2 Estudio Teórico de la Respuesta en Frecuencia
El término respuesta en frecuencia se refiere a la respuesta de un sistema en estado
estable a una entrada senoidal. En los métodos de la respuesta en frecuencia, la frecuencia de la señal de entrada se varía en un cierto rango, para estudiar su respuesta
resultante. Una ventaja del enfoque de la respuesta en frecuencia es que las pruebas
son, en general, sencillas y pueden ser muy precisas con el uso de generadores de señales que se obtienen con facilidad y un equipo de medición preciso. Por lo común las
funciones de transferencias de los componentes complicados se determinan experimentalmente mediante pruebas de la respuesta en frecuencia.
2.1 Respuesta en Frecuencia de un Sistema Lineal e Invariante en el Tiempo
La salida en estado estable para una entrada senoidal en un sistema lineal e invariante con el tiempo como el que se muestra en la Fig. 1 es:
Y (s)
= G (s)
X (s)
La entrada
(1)
x ( t ) es senoidal y se obtiene mediante:
x ( t ) = X ⋅ sen (ωt )
y para un sistema estable, la salida
y ( t ) se obtiene a partir de:
(2)
Laboratorio de Mediciones Electrónicas - 2011
y ( t ) = Y ⋅ sen (ωt + φ )
(3)
Donde,
Y = X G ( jω )
y
 Im ( G ( jω ) ) 

 Re ( G ( jω ) ) 
φ = G ( jω ) = tan −1 
(4)
Un sistema estable, lineal e invariante con el tiempo, sujeto a una entrada senoidal,
tendrá, en estado estable, una salida senoidal de la misma frecuencia que la entrada.
Pero, en general, la amplitud y la fase de la salida serán diferentes de las de la entrada.
Figura 1. Sistema Lineal Invariante con el Tiempo
Por lo tanto, la característica de respuesta en frecuencia de un sistema para una ene
trada senoidal se obtiene directamente de:
Y ( jω )
= G ( jω )
X ( jω )
La función de transferencia senoidal
(5)
G ( jω ) es una cantidad compleja y se reprerepr
senta mediante la magnitud y el ángulo de fase con la frecuencia como parámetro. La
función de transferencia de cualquier sistema lineal se obtiene sustituyendo s por jω
en la función
G ( jω ) .
2.2 Trazas de Bode o Logarítmicas
Una función de transferencia senoidal se puede representar mediante dos gráficas
distintas: una que ofrece la magnitud contra la frecuencia y otra que muestra el ángulo
de fase contra la frecuencia. Las trazas de Bode están formadas por dos gráficas: una es
el logaritmo de la magnitud de una función de transferencia senoidal y la otra es el
ángulo de fase. Ambas se grafican contra la frecuencia en escala logarítmica.
La magnitud logarítmica de
G ( jω ) es 20 ⋅ log G ( jω ) , en donde la base del lol
garitmo es 10 . La unidad que se usa en esta representación de la magnitud es el decibel
[dB] . El ángulo de fase por lo general se representa en grados.
Laboratorio de Mediciones Electrónicas - 2011
Por ejemplo para un sistema de un polo simple con la siguiente función de transferencia:
G (s) =
25
( s + 25)
(6)
Reemplazando s por jω se obtiene:
G ( jω ) =
1
(7)
 jω

+ 1

 25

Entonces se grafican las asíntotas de la ganancia y la fase del sistema. La magnitud
logarítmica del factor de primer orden es:
1
20log
= −20log
jω 25 + 1
Para bajas frecuencias, tales que
aproxima mediante:
−20log
ω2
252
ω2
252
[dB]
+1
ω ≪ 1 T = 1 25 ,
+ 1 = −20log 1 = 0
(8)
la magnitud logarítmica se
[dB]
(9)
Por lo tanto, la curva de magnitud logarítmica para frecuencias bajas es la línea de
0 [ dB] constante. Para altas frecuencias, tales que:
−20log
ω2
25
2
+ 1 = −20log
ω
25
[dB]
(10)
En ω = 1 25 , la magnitud logarítmica es igual a 0 [ dB] ; y en ω = 10 25 , la magni-
tud logarítmica es de −20 [ dB] . Por lo tanto, el valor
−20log ω 25 [ dB] disminuye
en 20 [ dB] por cada década que aumenta ω . La frecuencia donde las dos asíntotas se
cruzan se denomina frecuencia de esquina o de corte.
El ángulo de fase
φ
exacto del factor es:
ω 

 25 
φ = − tan −1 
(11)
A una frecuencia cero, el ángulo de fase es 0o . En la frecuencia de esquina, el ángulo de fase es:
 25 
−1
 = − tan 1 = −45º
 25 
φ = − tan −1 
(12)
Laboratorio de Mediciones Electrónicas - 2011
En el infinito, el ángulo de fase se convierte en −90o . Dado que el ángulo de fase se
obtiene mediante una función de tangente inversa, el ángulo de fase tiene una pendiente simétrica con respecto al punto de inflexión en
φ = −45o .
Figura 2. Trazas de Bode
2.3 Trazas de Bode con MATLAB
El comando bode calcula las magnitudes y los ángulos de fase de la respuesta en
frecuencia de un sistema en tiempo continuo, lineal e invariante con el tiempo. Para el
sistema anterior la programación se puede observar en la Fig. 3.
Figura 3. Función Bode en Matlab
Las trazas de Bode se observan en la Fig. 4.
Laboratorio de Mediciones Electrónicas - 2011
Figura 4. Trazas de Bode
2.4 Desfasaje entre dos señales
Para calcular el desfasaje entre dos señales se visualizarán las dos señales de forma
simultánea en la pantalla del osciloscopio. A continuación se identificarán los dos pasos
por cero (con igual pendiente) de ambas formas de onda y se calculará la diferencia
diferen
de
tiempos ∆t .
Figura 5. Desfasaje de dos señales
Una vez medida la diferencia de tiempos o el retraso de la señal del canal 2 respecto
del canal 1, se calcula el desfasaje entre las dos señales. Teniendo en cuenta que el
tiempo
po correspondiente a un periodo de señal equivale a 360º, el desfase vendrá expreexpr
sado por,
∆Φ = Φ1 − Φ 2 =
2π ⋅ ∆t
360 ⋅ ∆t
[ rad ] =
[º]
T
T
donde T representa el periodo de la señal periódica.
3 Práctica
(13)
Laboratorio de Mediciones Electrónicas - 2011
3.1 Material y Equipo Necesario
 Osciloscopio Digital,
 Generador de Funciones,
 Multímetro,
 Fuente de Alimentación de CC,
 Resistencias varias,
 Capacitores varios.
3.2 Procedimiento
3.2.1 Repuesta en Frecuencia de un Filtro Pasivo de 1er orden
1.
Obtener la función de transferencia del circuito de la Fig. 6 y obtener las trazas
de Bode con Matlab.
2.
Simular el circuito de la Fig. 6 utilizando algún simulador basado en modelos
Spice (ej. OrCAD), encontrar su respuesta en frecuencia y determinar el tipo de
filtro.
3.
Montar el circuito correspondiente a la Fig. 6.
4.
Alimentar el circuito con una señal del tipo
vin ( t ) = V ⋅ sen ( 2π ft ) e
ir va-
riando f .
5.
Colocar las puntas de medida del osciloscopio digital de forma que mida la tensión de entrada y salida del circuito.
6.
Registrar los valores en una tabla para luego graficarlos con Matlab.
7.
Comparar las trazas obtenidas por los tres métodos y escriba su opinión respecto a las mismas.
Figura 6. Filtro pasivo de primer orden práctico
3.2.2 Repuesta en Frecuencia de un Filtro Activo de 2er orden
1.
Obtener la función de transferencia del circuito de la Fig. 7 y obtener las trazas
de Bode con Matlab.
2.
Simular el circuito de la Fig. 7 utilizando algún simulador basado en modelos
Spice (ej. OrCAD) y encontrar su respuesta en frecuencia.
3.
Montar el circuito correspondiente a la Fig.7.
Laboratorio de Mediciones Electrónicas - 2011
1.
Alimentar el circuito con una señal del tipo
vin ( t ) = V ⋅ sen ( 2π ft ) e
ir va-
riando f .
4.
Colocar las puntas de medida del osciloscopio digital de forma que mida la tensión de entrada y salida del circuito.
5.
Registrar los valores en una tabla para luego graficarlos con Matlab.
6.
Comparar las trazas obtenidas por los tres métodos, determinar el tipo de filtro
y escriba su opinión respecto a las mismas.
Figura 7. Filtro Activo de Segundo Orden Práctico
Nota: Para obtener la función de transferencia de un circuito con AOP se puede utilizar el enfoque de impedancias como se puede apreciar en la Fig. 8.
Configuración Inversora
Ei ( s ) = Z1 ( s ) I ( s )
Eo ( s ) = − Z 2 ( s ) I ( s )
Eo ( s )
Z (s)
=− 2
Ei ( s )
Z1 ( s )
Configuración no Inversora


Z1 ( s )
Eo ( s ) = K  Ei ( s ) −
Eo ( s ) 
Z1 ( s ) + Z 2 ( s )



Z1 ( s )
1
Ei ( s ) = 
+  Eo ( s )
 Z1 ( s ) + Z 2 ( s ) K 
como K >> 1 y si Z1
( Z1 + Z2 ) >>1 K , entonces
queda,
 Z (s) 
Eo ( s ) = 1 + 2
 Ei ( s )
 Z1 ( s ) 
Figura 8. Circuitos con Amplificadores Operacionales