Clase 2 - Facultad de Ciencias Exactas

TEORÍA DE LA INFORMACIÓN
Tratamiento probabilístico de la Información
Fuentes de información
continuación
INGENIERÍA DE SISTEMAS
Cursada 2016
Repaso…
Fuente sin memoria
(de orden 0)
Fuente con memoria
(de orden 1 o markoviana)
Conjunto de símbolos S= {s1, s2, …, sN}
S= {s1, s2, …, sN}
Vector de probabilidades de emisión
Matriz (o grafo) de transición o de pasaje
s1
s2
…
si ….
 P( S (t )  s1 )   P( s1 ) 
 P( S (t )  s )   P( s ) 
2 
 2 


  ... 
....
V (t )  
   P( s ) 
 P( S (t )  si )   i 
....
  ... 

 P( S (t )  s ) 
N 
 P( s N )

s1  p1/1

s2 p 2 / 1
M

 
sj  p j / 1

.
 
. 
p1/ 2
p1/ i 
p2 / i 
 

p j / i 
 

p2 / 2 
.
.


p j/2 


Vectores de estado
V (t  1)  M  V (t ) V(0) condición inicial
Estado estacionario
V *  M V *
( M  I ) V *  0
 p(s )*  1
i
i
Teoría de la Información 2016 - Facultad de Ciencias Exactas- UNCPBA
1
Repaso…
Fuente con memoria (de orden 1 o markoviana)
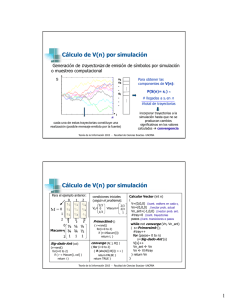
Muestreo computacional
Estado estacionario (para cualquier t ≥ test )
Vector de probabilidad de estado en tn
S
S
t
t
tn
 simular generación de varias trayectorias
(hasta convergencia)
 simular una trayectoria, agregando transiciones
(hasta convergencia)
 # s1 /# transiciones 
 # s /# transiciones 
 2



....
V*  

#
s
/#
transicion
es
i


....


# s /# transiciones 
 N

 # s1 en t n /# trayectori as 
 # s en t /# trayectori as 
n
 2



....
V (t n )  

#
s
en
t
/#
trayectori
as
n
 i

....

# s en t /# trayectori as 
n
 N

Teoría de la Información 2016 - Facultad de Ciencias Exactas- UNCPBA
Repaso…
Fuente sin memoria
Entropía (orden 0)
H ( S )    P( Si )  log P( Si )
i
Fuente con memoria (de orden 1 o markoviana)
Entropía (orden 1)
H1 ( S )   p ( si ) * (  p j / i log p j / i )
i
j
Probabilidad de transición en n pasos
(1° Ec. de Chapman-Kolmogorov)
p j /i
(n)
  pk / i
( m)
. pj/k
( nm)
para m<n
k
Probabilidad de primera transición en n pasos
(2° Ec. de Chapman-Kolmogorov)
n 1
(n)
(n)
( m)
j /i
j /i
j /i
m 1
f
p
 f
. pj/ j
Media de primera transición
Si F j / i  1   j / i 
( nm)
fi / i
n 1
(n)
 pi / i
(n)

n 1
f
m 1
Media de recurrencia

 n. f
Probabilidad de (1°) recurrencia en n pasos
j/i
( n)
Si Fi / i  1  i / i 
( m)
i/i

 n. f
n 1
. pi / i
( nm)
(n)
i/i
Teoría de la Información 2016 - Facultad de Ciencias Exactas- UNCPBA
2
INDICADORES ESTADÍSTICOS
En un proceso estocástico −en particular, una fuente que emite símbolos de un
conjunto {si } en cada instante− se pueden obtener características que describen
su comportamiento, como funciones dependientes del tiempo
• En cada instante t :
Media:
S (t )   si P( S (t )  si )
probabilidades
marginales
i
Desviación:
 (t ) 
 ( s  S (t ) )
i
2
P( S (t )  si )
i
• Entre dos instantes t1 y t2 (tiene sentido el análisis cuando la fuente es markoviana,
si la fuentes no tiene memoria las sucesivas emisiones de símbolos son independientes):
Autocorrelación:
R(t1 , t 2 )  S (t1 ), S (t 2 )   si s j P( S (t1 )  si , S (t 2 )  s j )
i
Autocovarianza:
j
C (t1 , t 2 )  S (t1 ), S (t 2 )  S (t1 ) S (t 2 )
Función coeficiente de autocorrelación:
probabilidades
conjuntas
r (t1 , t 2 )  C (t1 , t 2 ) /  (t1 )  (t 2 )
Teoría de la Información 2016 - Facultad de Ciencias Exactas- UNCPBA
INDICADORES CRUZADOS
Permiten cuantificar el grado de interdependencia o acoplamiento entre dos
procesos estocásticos, por ej. dos fuentes de información:
Correlación cruzada:
RXY (t1 , t 2 )   X (t 1), Y (t 2 ) 
X(t)
Y(t)
Covarianza cruzada:
C XY (t1 , t 2 )   X (t1 ), Y (t 2 )    X (t1 )  Y (t 2 ) 
Función coeficiente de correlación cruzada:
rXY (t1 , t 2 )  C XY (t1 , t 2 ) /  X (t1 )  Y (t 2 )
Teoría de la Información 2016 - Facultad de Ciencias Exactas- UNCPBA
3
INDICADORES CRUZADOS
Cuando el proceso –emisión de la fuente markoviana– es estacionario:
• los vectores de estado son estables a lo largo del tiempo: V*= M.V*
• la media y la desviación son constantes:
S (t )  S , t
 (t )   , t
• la autocorrelación, autocovarianza sólo dependen del intervalo de tiempo
transcurrido y no de los instantes específicos:
R(t1 , t1 )  R(t 2 , t 2 )  R( )
C (t1 , t1 )  C (t 2 , t 2 )  C ( )
r (t1 , t1 )  r (t 2 , t 2 )  r ( ) , t1 , t 2
• Lo mismo sucede con los indicadores cruzados
Teoría de la Información 2016 - Facultad de Ciencias Exactas- UNCPBA
MUESTREO COMPUTACIONAL
para calcular R()
• Si la fuente markoviana es estacionaria, se puede generar una única trayectoria
(mensaje de la fuente) y detectar las emisiones de los sucesivos símbolos,
distanciados  instantes
mensaje
verificar convergencia
del vector
Teoría de la Información 2016 - Facultad de Ciencias Exactas- UNCPBA
4
INDICADORES CRUZADOS
Aplicaciones
• Permiten analizar el grado de relación entre dos fuentes de información (señales,
imágenes, ...)  Valores altos de correlación indican mayor acople
• Se suelen utilizar en problemas de:
 Reconocimiento de patrones
 Registración de imágenes (seguimiento satelital, fusión de imágenes médicas,…)
 Identificación biométrica (por huellas dactilares, por el iris, señal de voz, ...)
 Análisis de procesos económicos, sociales, ambientales, etc.
Teoría de la Información 2016 - Facultad de Ciencias Exactas- UNCPBA
BIBLIOGRAFÍA
Abramson N., Teoría de la Información y Codificación, Ed. Paraninfo, 1981
Cover T., Thomas J., Elements of Information Theory, 2nd ed., John Wiley &
Sons, 2006
Papoulis A., Probability Random Variables and Stochastic Processes,
McGraw-Hill, 1991
Shannon C., Weaver W., Teoría Matemática de la Comunicación, Ed.Forja,
1981
5