La calculadora básica

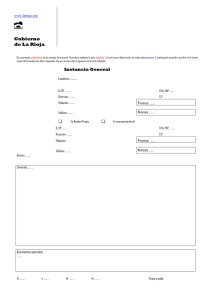
La calculadora básica
Tomás Ortega
LA CALCULADORA BÁSICA
Tomás Ortega
Didáctica de la Matemática. Universidad de Valladolid
[email protected]
La calculadora básica es una potente
herramienta de cálculo matemático que,
sabiendo matemáticas, permite realizar
infinidad de tareas. De los innumerables
modelos que hay en el mercado, aquí se
considera uno de los más sencillos.
Véase la figura.
A la vista de la figura es fácil enumerar los
elementos que la componen:
Figura 6. Calculadora básica
Teclado. Conjunto de teclas que permiten dar las instrucciones, consta de:
-
Una tecla de conexión ON/OFF
-
Diez teclas numéricas: 0, 1, ..., 9.
-
Dos teclas de borrado C y CE.
-
Tres teclas de memoria M+, M- y MR, y algunos modelos tienen “Min”.
-
Cuatro teclas de operaciones aritméticas: +, -, x, :.
-
Una tecla del punto decimal.
-
Una tecla de igualdad.
-
Una tecla de raíz cuadrada.
-
La tecla de % es un adorno en algunos modelos.
-
Algunos modelos suelen tener la tecla de cambio de signo +/-.
Display. Ventana donde aparecen los números que se teclean y los resultados de los cálculos.
Memoria. Parte de la calculadora donde se ejecutan las órdenes y se guardan números:
-
Activa: zona de la memoria destinada a efectuar los cálculos.
-
Pasiva: zona de la memoria destinada a guardar un número.
En la actualidad es una de las mejores herramientas de cálculo y sus características más importantes son
las siguientes:
-
Es de fácil transporte.
-
Tiene un tamaño muy reducido.
-
Es muy barata.
-
Tiene una potencia de cálculo enorme.
1
La calculadora básica
Tomás Ortega
Generalidades
La utilización de la calculadora es muy sencilla. Se conecta pulsando la tecla "ON" y se desconecta con
OFF (algunos modelos se conectan al pulsar una tecla cualquiera y se desconectan tras un período de
inactividad).
1.
Para realizar una operación aritmética (suma, resta, producto o cociente) se teclea el primer
sumando, a continuación la correspondiente tecla de la operación aritmética, después el segundo
número (sumando, sustraendo, factor -multiplicador-, o divisor) y, por fin, tecla "=".
2.
Para hallar una raíz cuadrada se teclea el número y después la tecla
3.
Para hallar un porcentaje se pulsa la tecla "%", después el tanto por ciento, a continuación la
tecla "=", después la cantidad y, finalmente, se pulsa la tecla "=".
4.
Los números decimales (sólo decimales finitos) se escriben pulsando la tecla ".", después de
haber tecleado la parte entera.
.
Cuando el alumno esté en la fase de aprendizaje de las operaciones aritméticas (sea cual
sea la operación) sólo se debe utilizar la calculadora como material de refuerzo: puede
usarla para verificar los resultados que obtiene manualmente y como medio de
aprendizaje de tablas numéricas. Sin embargo, conviene señalar que el uso
indiscriminado de la calculadora es perjudicial porque crea en el alumno una
dependencia tal, que en ocasiones le imposibilita efectuar operaciones muy sencillas,
bien porque no sabe, bien porque le parece que manualmente debe realizar un trabajo
ímprobo. En los siguientes apartados se describe una serie de tareas en las que puede ser
interesante el uso de la calculadora en orden creciente de dificultad. El éxito o fracaso
depende de múltiples factores que, en ocasiones, pueden pasar inadvertidos: el propio
alumno, entorno familiar, profesor, clase, compañeros, momento, etc.
Al comenzar una sesión de trabajo conviene inicializar la memoria (ponerla a cero), esto se hace pulsando
MR y M- o bien MR, la tecla de cambio de signo y M+ (Si tiene la tecla Min se teclea 0 y después Min). Si
no se hace esta puesta a cero, todos los cálculos que se hagan utilizando la memoria aparecerán
incrementados en el valor que figure.
Verificación de resultados
Bajo este título se agrupan actividades elementales que pueden llevar a cabo los niños en el aula y en su
casa para reforzar el aprendizaje del cálculo. Señalamos éstas:
1.
Sumas de dos sumandos menores que 10. Con esta actividad repetitiva el niño puede ir
memorizando las tablas de sumar, para ello conviene que repita oralmente los sumandos y el
resultado.
2.
Sumas de dos sumandos mayores que 10 y sumas con llevadas.
3. Sumas indicadas de varios sumandos. 325+67+1589. Puede comprobar si los
resultados son correctos (fallo de colocación o de suma).
4.
Restas sin llevadas. Adquisición del concepto de resta quitando del minuendo el sustraendo.
5.
Restas El resultado de restar a doce siete es el mismo número que sumado a siete da doce (127=__ 7+__=12)...
2
La calculadora básica
Tomás Ortega
6.
Filas o series de sumas y restas.7+13-5+10+5-15+2.
7.
Verificación de progresiones aritméticas sencillas. 1, 3, 5, 7, ...; 1, 4, 7, 10, ... ¿Son igual de
interesantes esos ejemplos que 2, 4, 6, ...; 3, 6, 9, ...; 4, 8, 12, ...?
8.
Producto de dos factores menores que 10. Ejercicio al que se aplican los mismos comentarios
que para la suma.
9.
Efectuar sumas de sumandos iguales y menores que diez (multiplicando) un número de veces
menor o igual que diez (multiplicador) para asimilar el concepto de multiplicación.
10. Efectuar restas iteradas de un número para entender el concepto de división exacta: dados D y d
encontrar C tal que D=d*C.
11. Obtención del resto: R=D-d*[C]
12. Comprobación de los resultados de divisiones enteras. D=d*C+R.
13. El cálculo mental (o escrito) es muy interesante porque con esta actividad el niño adquiere
destreza operativa y desarrolla la capacidad de retención numérica. Si a la vez que va calculando
mentalmente (o sobre papel) se teclea el ejercicio en la calculadora, manteniendo tapada la línea
de display, al final puede comprobar instantáneamte si su solución coincide con la de la
calculadora.
Verificación de propiedades y cálculos indicados
En este apartado exponemos una series de tareas en las que la calculadora es una
herramienta muy apropiada para comprobar las propiedades y para ordenar los cálculos:
1.
Comprobación de las propiedades asociativa y conmutativa de la suma. 7+6=6+7;
(2+7)+5=2+(7+5);
7-6=-6+7;
(2-7)+5=2+(-7+5);
3.78+0.635=0.635+3.78;
(2+0.76)+5.427=2+(0.76+5.427).
2.
Verificación de las propiedades asociativa y conmutativa del producto. 7*6=6*7,
(2*7)*5=2*(7*5);
7*(-6)=-6*7;
(2*(-7))*5=2*((-7)*5);
3.78*0.635=0.635*3.78;
(2*0.76)+2*5.427=2+(0.76+5.427).
3.
Comprobación de la propiedad distributiva del producto respecto de la suma. 3*2+3*5=3*(2+5);
3*(-2)+3*5=3*(-2+5); 3.7*0.43+3.7*(-2.3)=3.7*(0.43-2.3).
4.
Realizar múltiples ejercicios de "sacar factor común". Hasta con la calculadora es más
complicado efectuar 3*5-3*8+3*7 que 3*(5-8-7), más aún, todavía es más sencillo efectuar (58+7)*3 y con ello el alumno ve la utilidad de la propiedad conmutativa (ídem con números
decimales).
5.
Realizar múltiples ejercicios de reglas aritméticas de signos. 3-(2+5*(3-2*(2+3))-1). (Ídem con
decimales)
6.
Utilización correcta de paréntesis. Además de sacar factor común, se deben evitar ambigüedades
de divisiones y restas: 2-3-5 es distinto de 2-(3-5) (aquí está implícita la distributiva); 2:3:6 es
ambiguo y debe escribirse 2:(3:6) ó (2:3):61. Aunque la utilización correcta de paréntesis no es
motivo de estudio aquí, el abuso de los mismos puede ayudar al niño a realizar bien un ejercicio
determinado pero no a aprender su uso. Ejemplo: 2+(5*8)-7 les ayuda a calcular correctamente
2+5*8-7 (=2+40-7=35); sin embargo, no les enseña a calcularlo y cuando tengan que hacerlo
1
Estas dos ambigüedades de la resta y de la división es debido a que éstas noson operaciones, ya que para
alcanzar este estatus, tienen que tener la propiedad asociativa.
3
La calculadora básica
Tomás Ortega
sin los paréntesis unos alumnos darán la solución correcta, otros escribirán 7*8-7=49 y otros
2+5*1=7.
7.
Comprobación de las operaciones con fracciones utilizando aritmética entera (castillos de
fracciones).
1 9 5
+ :
11 13 3
1 5
3
− :3+
5 7
4
Cálculos diversos
En este apartado enumeramos algunos cálculos en los que la calculadora descrita es el útil adecuado.
También describimos otros en los que sería más apropiado utilizar otra que tuviera teclas de funciones;
sin embargo, lo hacemos con esta para destacar que se trata de una herramienta de cálculo y que, la
deficiencia de la máquina se puede suplir con un conocimiento apropiado de las matemáticas.
1.
Cálculos de descuentos sin utilizar la tecla %. El 20% de descuento de la cantidad A es 0.20*A y
la cantidad a pagar es 0.80*A. El recargo de un 15% es 0.15*A y la cantidad a pagar es 1.15*A.
2.
Reglas de tres simples y compuestas: el computo numérico es muy sencillo una vez que se ha
realizado el esquema correspondiente.
3.
Evaluación de fórmulas matemáticas. El volumen de una esfera es V =
4.
Las soluciones de la ecuación ax2+bx+c=0 son: x =
5.
Buscar números que verifiquen ciertas propiedades: Hallar dos números enteros tales que su
producto sea 759 y su suma 56. Tales números deben de estar cercanos a 28 (56/2) porque
28.28=784, que está cerca de 759; esto nos indica la conveniencia de ensayar productos de dos
números que se obtienen sumando y restando una unidad. Otra técnica apropiada consiste en
descomponer 759 en factores primos e ir examinando la suma.
6.
Obtención de raíces enteras de un polinomio. Las posibles raíces enteras de x4-x3-11x2-x-12 son
±1, ±2, ±3, ±4, ±6, ±12 y de ellas son raíces enteras x=-3 y x=4
7.
Obtención de raíces reales de forma aproximada. P(x)=x4+3x3-2x-1 tiene una raíz entre 0 y 1 ya
que: P(x) es continua, P(0)=-1<0 y P(1)=1>0. Conviene ver el signo de P(0.5), si es positivo la
raíz está entre 0 y 0.5 (se ensaya con x=0.25), si por el contrario P(0.5)<0, la raíz está entre 0.5 y
1 (y se ensaya con x=0.75).
8.
Evitar "overflow"
simplificación).
(rebasamiento)
evaluando
4 3
π ·r .
3
− b ± b 2 − 4ac
2a
números
combinatorios
(Se
evalúa
la
 20  20·19·18·17·16·15
  =
= 19·17·8·15
6·5·4·3·2·1
6
9.
Pasar G grados, M minutos y S segundos a radianes (y el problema recíproco). El mismo
algoritmo sirve para las medidas horarias.
4
La calculadora básica
Tomás Ortega
Rad =
G+
M
S
+
60 3600
180
10. Cálculos estadísticos.
11. Cálculos en progresiones.
12. Cálculos de interpolación.
13. Evaluación de constantes irracionales. (1+1/n)n y la serie 1+1+1/2!+1/3!+1/5!+... permiten
hallar "e". El número π se halla mediante la serie: π/4=1-1/3+1/5-1/7+1/9-1/11+1/13-1/15...
14. Evaluación de funciones trascendentes elementales. ex=1+x+x2/2!+x3/3!+x4/4!+..., log(1+x)=xx2/2+x3/3-x4/4+...,
sen(x)=x-x3/3!+x5/5!-x7/7!+...,
e0.3=1+0.3+0.32/2!+ 0.33/3!+ 0.34/4!+ ...,
log(1+x)=0,2-0,22/2+0,23/3-0,24/4+ ...,
sen(0,2)= 0,2-0,23/3!+0,25/5!-0,27/7!+ …
5