Leccion7.PLASTICOS.FlujoFundidos

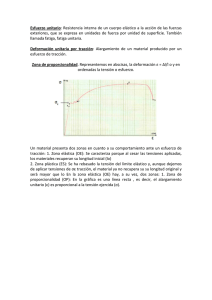
LECCION 7 .- PLASTICOS / FLUJO DE FUNDIDOS. CALCULOS.
1.- Tipos de flujo.
En el procesado de los materiales plásticos pueden presentarse los siguientes tipos de flujo:
(a).- Flujo de presión entre límites.
Ejemplos : Flujo 1 – D en canales circulares o en canales de ranura rectangular delgados de sección
transversal constante, como por ejemplo, los dados de extrusión y los bebederos de los moldes de inyección.
(b).- Flujo de arrastre entre límites móviles.
Ejemplos : Flujo entre la hélice y la camisa en un tornillo de extrusión . Mezclador interno utilizado en el procesado
de las gomas.
(c) .- Flujo de presión sin límites – tensión
Ejemplos : - Moldeo por extrusión-soplado (inflado del parison). Soplado de películas.
(d).- Flujo cortante y de tensión.
Ejemplos: Flujo a través de canales de sección transversal no constante. Flujo de extensión circular entre platos,
como es el caso del moldeo por compresión. Flujo en la espiga y compuerta de los moldes de inyección.
Debido a los diferentes tipos de flujo, los suministradores de materiales proporcionan datos de flujo en condiciones de
corte y de tensión, derivados de métodos de ensayo estandarizados.
2.- Cálculos de flujo de presión. Procedimiento.
La notación que se va a utilizar es la siguiente:
dP
= Gradiente de presión axial.
dz
τ(r) = Distribución radial de la tensión cortante.
•
γ (r) = Distribución radial de la velocidad de deformación por corte.
dV
= Gradiente de velocidad radial.
dr
V(r) = Distribución radial de la velocidad.
Q = Caudal de flujo volumétrico.
Y el procedimiento general para llevar a cabo los cálculos de flujo será el siguiente:
(i).- A partir de consideraciones de equilibrio de fuerzas se relaciona la tensión cortante con el gradiente de presión
 dP 

 dz 
axial, es decir: τ (r ) = f 
(ii).- Usando la ley potencial ( o la que siga el material), se iguala la tensión cortante a la velocidad de deformación
•
por corte, τ ( r ) = η a γ a
(iii).- A partir de consideraciones geométricas hay que relacionar la velocidad de deformación por corte con el
gradiente de velocidad (radial).
(iv).- De los apartados (i) y (iii) se obtiene el gradiente de velocidad en función del gradiente de presión.
(v).- A partir de la distribución de velocidad se calcula el caudal de flujo volumétrico.
El resultado final nos dará Q en términos de
dP
, de tal forma que conocido el gradiente de presión se puede
dz
calcular el caudal de flujo o viceversa.
En el análisis de flujo en canales se realizarán las siguientes suposiciones:
1.- No hay deslizamiento en las paredes.
2.- El fundido es incompresible (Plásticos fundidos se supone que son fluidos incompresibles).
3.- El flujo es estacionario, laminar e independiente del tiempo.
4.- La viscosidad no estará afectada por los cambios de presión a lo largo del canal.
5.- Los efectos de borde son despreciables.
6.- El flujo es isotérmico.
El flujo isotérmico estacionario de fluidos incompresibles a través de tubos horizontales rectos es importante en
numerosos casos de interés práctico.
2.1.- Flujo a lo largo de un canal de sección transversal circular uniforme (Tubo capilar).
Considerando las fuerzas que actuan sobre un elemento de fluido de la figura 2.1.1, en el equilibrio se tendrá :
Figura 2.1.1.- Flujo a través de un canal circular de sección constante.
F2 = F1 + F3

dP
y como:

F1 = π r2  P − dz dz  ,


se obtiene sustituyendo :
F2 = π r2 P

F3 = 2 π r
,
τ dz

dP
π r2 P = π r2  P − dz dz  + 2 π r τ dz
de donde:
τ
=
r dP
2 dz
(2.1.1)
De la ley potencial correspondiente al fluido:
τ = ηa γ
•
a
•
= C  γ 
 
n
Teniendo en cuenta la definición de deformación de cizalladura (Figura 2.1.2) y aplicándola al caso que se está
analizando (Figura 2.1.2), se tiene:
γ=
dz
dr
luego:
•
γ=
dV
d  dz  d  dz  d
=
=
(V ) =




dr
dt  dr  dr  dt  dr
por tanto:
τ
•
n
 dV 

 dr 
n
= C( γ a ) = C 
Figura 2.1.2.- Deformación de cizalladura. Caso particular de flujo en un canal de sección circular
Teniendo en cuenta la relación (2.1.1):
 dV 
C

 dr 
n
=
r dP
2 dz
y ordenando :
 dV 


 dr 
n
=
r dP
2C dz
o bien :
dV
=
dr
Ar
1
n
 1 dP 
donde A = 
 2C dz 
1/ n
(2.1.2)
e integrando:
 n +1 

n 
n 
r
V= A
n +1
+B
(2.1.3)
Para determinar las constantes de integración se imponen las condiciones límites :
 n +1 

n 

n
R
Cuando r = R , V = 0 (Flujo laminar) de donde : B = - A
n +1
luego:
n
V= A
n +1
 n +1 
  nn+1 




− R n  
r


(2.1.4)
A su vez cuando r = 0 , V = V0 (Velocidad máxima) de donde:
 n +1 

n 

n
R
V0 = - A
n +1
 1 dP 
= -- 
 2C dz 
1/ n
 n +1 

n 

n
R
n +1
y finalmente :
 n +1 



 n 
r



V(r) = V0 1 −  

 R


(2.1.5)
En la figura 2.1.3 puede verse el perfil de velocidades para varios valores de n. El caso en que n = 1 corresponde a
fluidos newtonianos.
n = 0.1
n = 0.25
⇒ ≅ 75 % misma velocidad del fluido.
⇒ ≅ 60 % misma velocidad del fluido.
El caudal volumétrico , Q, vendrá dado por :
R

r
Q = ∫ V 2π rdr = 2πV0 ∫ r 1 −  
 R
0
0

R
R
 n +1 


 n 
 3 n +1 
 2



r
n r n  

 dr = 2πV0  −
2 3n + 1  nn+1  



R

0
de donde:
Q = πV0 R2
n +1
3n + 1
(2.1.6)
La velocidad de deformación por corte será:
V0 n + 1 r1/ n
dV
=γa =
R n R 1n
dr
(2.1.7)
V0 n + 1
R n
(2.1.8)
•
y su valor en la pared es ( r = R) :
•
γ aw = y teniendo en cuenta (2.1.6):
V0 (3n + 1)Q
=
R π ( n + 1) R3
•
luego: γ aw =
− (3n + 1)Q −(3n + 1) 4Q
=
4n π R 3
nπ R 3
(2.1.9)
y la tensión cortante en la pared ( r = R) :
n
τ ω = R dP = C  γ aw  = -C  (3n + 13)Q 
2 dz
 
 nπ R 
•
n
(2.1.10)
2.2.- Flujo a lo largo de un canal formado por platos paralelos.
Considerando las fuerzas que actúan sobre un elemento de fluido de la figura 2.2.1, en el equilibrio se tendrá:
Figura 2.2.1.- Flujo entre platos paralelos
El balance de fuerzas nos da:
F2 = F1 + 2F3
y como :

dP

F1 = 2yT  P − dz dz  ,


se obtiene sustituyendo :

F2 =2yTP
F3 = τdzT
,

dP
2yTP = 2yT  P − dz dz  + 2τdzT


de donde:
τ=y
dP
dz
(2.2.1)
De la ley potencial correspondiente al fluido:
•
•
τ = ηa γ a = C( γ a )
n
Teniendo en cuenta la definición de deformación de cizalladura y aplicándola al caso que se está analizando (Figura
2.2.2), se tiene:
γ=
dz
dy
luego:
•
γ=
d  dz  d  dz  d
dV
=
=
(V ) =




dt  dy  dy  dt  dy
dy
por tanto:
 dV 
τ = C( γ a ) = C 

 dy 
•
n
n
Figura 2.2.2.- Deformación de cizalladura en el caso particular de flujo en un canal de platos paralelos.
Teniendo en cuenta la relación (2.2.1) :
 dV
C 
 dy
n

dP
 = y
dz

y ordenando :
 dV

 dy
n

 =

y dP
C dz
o bien :
dV
1/n
= Ay
dy
1/ n
 1 dP 
donde A = 
 C dz 
(2.2.2)
e integrando:
 n +1 

n 
n 
V= A
r
n +1
+B
(2.2.3)
Para determinar las constantes de integración se imponen las condiciones límites :
Cuando y =
h
, V = 0 de donde :
2
 n +1 
  n +1 


n   n   h   n  
V=A
y
− 

n +1 
2


(2.2.4)
y cuando y = 0 , V = V0 , de donde :
 n +1 


n 
n  h 
V0 = - A
 
n +1 2 
con lo que :
 n +1 



2
y
  n  

V = V0 1 − 


  h 


(2.2.5)
El caudal volumétrico , Q, vendrá dado por :
h
h
h
2
∫
Q = 2T Vdy = 2TV0
0
2
∫
0

1 −  2 y 
  h 

 n +1 


 n 
2
 2 n +1 




n


n
h
2
y
 

dy = 2TV  y −
 
0 

2n + 1 2  h 


0

de donde:
 n +1 
 2n + 1 
Q = hTV0 
(2.2.6)
La velocidad de deformación por corte será :
dV
n +1 2 2y 
= --V0
γa =
dy
n h  h 
•
y su valor en la pared es ( y =
1
n
(2.2.7)
h
):
2
•
γ aw = -y la tensión cortante en la pared (y =
2Vo n + 1
2n + 1 2Q
=−
h n
n Th 2
(2.2.8)
h
) :
2
τω
h  dP 
 2n + 1 2Q 
= 
 = −C 
2
2  dz 
 n Th 
n
(2.2.9)
2.3.- Flujo a través de una corona circular (Figura 2.3.1).
Las ecuaciones para este tipo de flujo son las deducidas para el caso de platos paralelos, sin más que hacer:
T = 2π R
Espesor : h
y tomando para h el valor representado en la figura 2.3.1.
Figura 2.3.1.- Flujo a través de una corona circular.
3.- Resumen de las expresiones para flujos bajo presión.
Canal circular uniforme ( Longitud = L , Radio = R)
L  (3n + 1)Q 
∆P = P2 – P1 = 2τwL/R = --2C 
R  nπR 3 
Cambio de presión:
Fluido newtoniano (n = 1, C = η )
Tensión de corte máxima (en la pared):
∆P = --
8η LQ
π R4
R dP
 (3n + 1)Q 
τw =
= -- C 
3
2 dz
 nπR 
•
Máxima velocidad de deformación por corte (en la pared):
γ aw = --
n
n
V n + 1 − (3n + 1)Q
=
R n
nπ R 3
Canal rectangular uniforme ( Longitud =L, anchura = T y altura = h)
Cambio de presión:
Tensión de corte máxima (en la pared):
n
2τ w L
L  (2n + 1)2Q 
∆P = P2 – P1 =
2 = --2C 
R
h  nTh 2 
h  dP 
 2n + 1 2Q 
τw = 
 = −C 
2
2  dz 
 n Th 
•
Máxima velocidad de deformación por corte (en la pared):
γ aw = --
n
2Vo n + 1
2n + 1 2Q
=−
h n
n Th 2
4.- Flujo en canales no uniformes.
4.1.-Introducción
En el flujo a lo largo de canales de sección transversal uniforme solo aparecen tensiones de corte. En muchas
situaciones prácticas incluyendo el flujo de polímeros a través de troqueles y a lo largo de canales, la sección
transversal va disminuyendo. En tal caso también actúan sobre el polímero fundido tensiones de tracción debidas a la
aceleración que se produce a lo largo del canal. Dichas tensiones causan un flujo en tensión, algunas veces
denominado flujo extensional, del material, que se superpone al flujo cortante.
En el soplado de botellas de plástico o en la elaboración de “películas sopladas” de polietileno, el material se deforma
debido a tensiones de tracción.
De una manera similar a la viscosidad cortante, se define una viscosidad a tensión, λ, como sigue:
λ=
Esfuerzo..de..traccion
σ
=
Velocidad .( Rapidez )..de..deformacion :: a..la..traccion
ε
donde:
σ = Tensión de tracción
ε = Velocidad de deformación a la tracción.
Para la mayoría de los polímeros la viscosidad a la tracción es relativamente constante, a diferencia de la viscosidad
cortante que depende de la velocidad de deformación por corte. A bajas tensiones la viscosidad a la tracción es,
usualmente, 2x – 4x la viscosidad cortante, usualmente es λ = 3η . Por tal motivo, las velocidades de deformación a
la tracción son bajas comparadas con las de corte.
La viscosidad cortante η es alta y, por lo tanto, λ más alta aún. Esta es una de las razones por las cuales no pueden
llenarse moldes con el polímero fundido, debido a que para verterlo se necesitan fuerzas de tracción. Un criterio mejor
es el de idear procedimientos que aprovechen las fuerzas cortantes, por ejemplo, bombear el material fundido en un
molde, que es el principio en que se basa el moldeo por inyección.
6
Además, los fluidos tienen una resistencia determinada a la tracción, por lo común del orden de 10
6
comparación con aproximadamente 10
N
, en
m2
N
que tienen los polímeros sólidos. La deformación limitante con
m2
frecuencia tiene una relación de estiramiento de 7:1 (700 %). Si se exceden estas propiedades de resistencia durante su
manufactura, se rompe el material fundido y esto es lo que ocurre algunas veces. Por ejemplo, los huecos que a veces
se encuentran en productos moldeados cuya sección es excesivamente gruesa son el resultado de separaciones que se
producen al enfriarse y contraerse el material. Esto crea fuerzas de tracción en el interior que todavía está fundido.
Esta región se ahueca cuando se sobrepasa su resistencia a la tracción o su límite de extensión (Aparece el fenómeno
de cavitación en él).
También hay un paralelismo con el comportamiento newtoniano y no newtoniano. Si la viscosidad a la tracción es
independiente de la velocidad de deformación, se dice que es troutoniano (que equivale al comportamiento
newtoniano en el corte). Hay dos tipos de comportamiento no troutoniano, el cual sí depende de la velocidad de
deformación: la rigidización por tracción y el suavizamiento (adelgazamiento) por tracción. Estos se muestran en la
figura 4.1.1.
La mayoría de los polímeros fundidos son troutonianos, por ejemplo, polimetilmetacrilato, el poliestireno, el
policarbonato, el nylon, el polietilentereftalato. El polietileno de baja densidad ramificado sufre rigidización por
tracción. Las poliolefinas lineales, por ejemplo, el polietileno de alta densidad y el polipropileno, se suavizan por
tracción. El comportamiento elástico siempre es el de rigidización por tracción
Figura 4.1.1.- Viscosidad a la tracción. Diferentes comportamientos.
El flujo en tensión también ocurre donde existan cambios abruptos en la sección transversal del canal, como es el
caso de la entrada o salida de un dado de extrusión.
En la figura 4.1.2 puede verse la variación de la viscosidad a la tracción, λ, para el polietileno a 20 ºC.
Figura 4.1.2.- Variación de la viscosidad a la tracción , λ, para el polietileno a 20 ºC
4.2.- Flujo isotérmico en canales troncocónicos.
El flujo a lo largo de este tipo de canales esta influenciado por tres factores:
(i).- Efectos cortantes (Sufijo S).
(ii).- Efectos extensionales (Sufijo E).
(iii).- Efectos de entrada (Sufijo O).
Cada uno de ellos contribuirá al modo de comportamiento del fundido y uno de ellos puede ser predominante
dependiendo de la geometría de la situación
Consideremos el canal troncocónico de la figura 4.2.1, en la que también se muestra un elemento infinitesimal.
Figura 4.2.1.- Flujo en un canal troncocónico
Caída de presión debida al corte, PS.
Asumiendo que los diferentes modos de deformación se pueden analizar de forma separada, y considerando el
equilibrio de fuerzas con respecto a las tensiones de corte (Figura 4.2.2), para el elemento infinitesimal de volumen, se
tiene:
F3 = F2 – F1
(4.2.1)
F2 = F1 + F3 ,
F1 = π r 2 ( P − dP )
F3
,
(
)
F2 = π ( r + dr ) P = π r 2 + 2rdr + dr 2 P
2
= (Área lateral)τ cosθ = (2π rdg )τ cosθ = 2π r
dl
τ cosθ= (2π rdl )τ
cos θ
Sustituyendo los valores anteriores en (4.2.1):
π ( r 2 + 2rdr + dr 2 ) P - π r 2 ( P − dP ) = (2π rdl )τ
de donde :
dP =
,
π r 2 dP = (2π rdl )τ
2τ
dl
r
(4.2.2)
 R2 − R1 
 L 
donde: θ = Semiángulo del cono = arctg 
Teniendo en cuenta la ley potencial:
•
τ = C( γ a )n
•
y
 3n + 1  Q
 3
 n  πr
γa = − 
dr
y usando dl =
, la ecuación (4.2.2) puede ponerse en la forma:
tgθ
(Ecuación (2.1.9) haciendo R = r)
2C
dP = −
tgθ
n
 3n + 1  Q  dr
 n  π  r 1+3n
 

(4.2.3)
Figura 4.2.2.- Equilibrio de fuerzas con respecto a las tensiones de corte
Integrando la expresión (4.2.3):
2C  3n + 1  Q 
PS = ∆ P = P2 – P1 = −


tgθ  n  π 
n R2
∫r
dr
1+ 3 n
R1
3n
n
 3n + 1  Q    R1  
2
C
−
1
=
1 −   


3
3n tgθ  n  π R1    R2  


(4.2.4)
Máxima tensión de corte ( a la entrada de la pared ) :
n
 (3n + 1)Q 
R1  dP 
τlw = − C 
 (4.2.5)

 =
3
2
dz
π
n
R


1


Máxima velocidad de deformación (a la entrada de la pared ) :
γalw = −
(3n + 1)Q
nπR13
(4.2.6)
Teniendo en cuenta (4.2.5) la expresión (4.2.4) puede ponerse en la forma:
2τ lw
∆P =
3ntgθ
  R 3 n 
1 −  1  
  R2  
(4.2.7)
Caída de presión debida a la tensión, PE.
Considerando el equilibrio de fuerzas con respecto a la tensión (Figura 4.2.3), se tiene :
πr2dPE = σ π (r + dr ) 2 − π r 2 
πr2dPE = σ π (r 2 + 2rdr + dr 2 ) − π r 2  = σ π (2rdr + dr 2 )  = σ [π 2rdr ]
luego:
dPE = 2σ
dr
r
(4.2.8)
R1
e integrando :
PE =
 dr 
2
σ
∫  r 
R2
(4.2.9)
Figura 4.2.3.- Equilibrio de fuerzas con respecto a la tensión.
Para poder realizar la integración es necesario obtener una relación entre σ y r.
Consideremos un anillo convergente de espesor, h, y radio a dentro del canal troncocónico. En el caso de flujos
convergentes, las líneas de corriente convergen y el elemento de fluido se distorsiona debido al esfuerzo de tracción
que se lleva a cabo, o sea, el material fundido se estira a la vez que se hace más estrecho, al dirigirse hacia la salida.
Por simple geometría se tiene que:
tgθ =
R2 − R1 R2 − r
=
L
l
a2 − a1 a2 − a
=
L
l
tg Φ =
y
luego:
tgθ R2 − r
=
tg Φ a2 − a
y como:
R1 R2 r R2 − r
=
= =
a1 a2 a a2 − a
resulta:
tgθ r
=
tg Φ a
tg Φ =
o bien:
a
tgθ
r
(4.2.10)
Además se cumple que:
dh da
=
h
a
(4.2.11)
La deformación en tensión viene dada por: ε =
dA  dh 
=

A  h 
Como A = 2π ah ( a y h dependientes del tiempo) se tiene :
(4.2.12)
dA = 2π ( adh + hda )
y teniendo en cuenta (4.2.12) :
hda = adh
dA = 2π (2hda ) = 4π hda
resulta:
entonces:
ε=
dA 4π hda 2
=
= da
A
2π ha
a
(4.2.13)
d ε 2 da
=
dt a dt
(4.2.14)
y la velocidad de deformación:
•
ε=
Por otra parte:
da
dl a
dl a
= tg Φ = tgθ = tgθ V
dt
dt r
dt r
donde V es la velocidad del fluido paralelamente al eje del anillo. Sustituyendo el valor anterior de
da
en la
dt
expresión (4.2.14) se tiene:
•
ε=
2 da 2 a
2
=
tgθ V = tgθ V
a dt a r
r
(4.2.15)
De las relaciones (2.1.5) y (2.1.6), particularizando para R = r y r = a, se deduce que:

3n + 1 Q   a 
1−  
V=
n +1 π r 2   r 

n +1
n



(4.2.17)
Con lo que:

2
3n + 1 Q   a 
1−  
ε = tgθ
r
n +1 π r 2   r 
•

n +1
n



La tensión media se obtiene integrando a toda la sección: σπ r 2 =
(4.2.17)
∫
a
0
σ a 2π ada
(4.2.18)
•
y como: σ a = λ ε
σπ r =
2
∫
a
0
•
λ ε 2π ada
(4.2.19)
•
y sustituyendo ε por su valor:
∫
r
σπ r 2 = 0
2λ
3n + 1 2π Q
σπ r 2 =
tgθ
r
n +1 π r2
σπ r 2 =

2
3n + 1 Q   a 
1−  
λ tgθ
r
n +1 π r2   r 

∫
r
0
n +1
n

 2π ada

  a n +1n 
 da
a 1 −  
r




2λ
3n + 1 2π Q (n + 1)r 2
tgθ
r
n + 1 π r 2 2(3n + 1)
o bien: σπ r 2 =
2λ
tgθ Q
r
y finalmente:
 2Q 
σ = λ  3  tgθ
πr 
(4.2.20)
Llevando este valor de la tensión a la expresión (4.2.9):
R1
 dr 
=
PE = ∫ 2σ 
r


R2
∫
R2
R1
dr
 2Q 
Q
2 λ  3  tgθ
= 4λ   tgθ
r
πr 
π 
4 Q
PE = λ   tgθ
3 π 
∫
R2
R1
dr
r4
R2
Q
= 4λ   tgθ
π 
1
1  2  2Q 
 3 − 3  = λ  3  tgθ
 R1 R2  3  π R1 
 −1 
 3r 3 
R1
  R 3 
1 −  1  
  R2  
y teniendo en cuenta (4.2.20):
3
2   R1  
PE = σ 1 1 − 
 
3   R2  


(4.2.21)
Caída de presión a la entrada del troquel, P0.
Cuando el fundido entra en el dado desde un depósito adoptara una conformación de flujo de tal modo que la caída de
presión sea mínima. Dicha forma tiende a ser troncocónica y la caída de presión, puede estimarse considerando un
número infinito de troncos de cono muy cortos.
Consideremos un troquel troncocónico con un radio de salida, R1, de entrada R2 y procedente de un cono de ángulo
2θ .
De la ecuación (4.2.8) se deduce:
PS =
2τ 0
1 − x n 
3ntg (θ0 )
PE =
 4Q 
1
λtgθ 0  3  [1 − x ]
3
 π R1 
y de la (4.2.22):
R 
donde x =  1 
 R2 
3
La caída de presión total, P1, es:
P1 = PS + PE
=
a
+ b tgθ 0
tgθ 0
(4.2.22)
donde:
a=
2τ 0
1 − x n 
3n
y
b=
λ  4Q 

 [1 − x ]
3  π R13 
Para que la caída de presión sea mínima la derivada, con respecto a θ 0 , ha de ser nula:
dP1
−a
= 2
+b
d (tgθ 0 ) tg (θ0 )
dP1
=0
d (tgθ 0 )
⇒
−a
+b = 0
tg 2 (θ 0 )
de donde: tgθ 0 =
a
b
y el valor correspondiente del mínimo de presión es:
P1 =
2τ 1
λ 4Q
2 2
(1 − x n )
(1 − x) =
3
3n
3 π R1
3
a b + a b = 2 ab = 2
λτ 1 4Q
n π R13
(1 − x n )(1 − x)
(4.2.23)
y como:
τ1 = η
4Q
π R13
queda: P1 =
2 2 4Q
3 π R13
λη
n
(1 − x n )(1 − x)
Si se repite el mismo procedimiento para otro corto canal troncocónico, se encuentra que:
( n +1)
P2 = x
2
P1
2
 ( n+1) 2  P
P3 =  x
 1


……………………
2
3
 i =∞ 
( n +1)
( n +1)
( n +1)


2 
2 
P
2
P1 +  x
 ∑ i  = P1 + x
 P1 +  x
 P1 + …… =




 i =1 
  ( n +1) 2
= P1 1 +  x
 
2
3
 +  x ( n+1) 2  +  x ( n +1) 2  + ..........
1
 
 

 = P1
n +1
 
 


1− x 2
(4.2.24)
Sustituyendo P1 por su valor:
 i =∞ 
 ∑ Pi  =
 i =1 
λη
2 2 4Q
3 π R13
(1 − x n )(1 − x)
n
1
1− x
n +1
(4.2.25)
2
Por tanto, la caída total de presión a la entrada, P0, será:
 i =∞ 
P0 = lim  ∑ Pi  =
x→1  i =1

2 2
3
1
 4Q   ηλ  2

 lim f ( x)
2  
 π R1   n  x →1
(4.2.26)
siendo:
(
)
f(x) =  1 − x n (1 − x ) 
1

1
2
1− x
n +1
2
η = Viscosidad correspondiente a la velocidad de deformación existente a la entrada del canal troncocónico.
lim f ( x ) = lim (1 − x n ) (1 − x ) 


x →1
x→1
1
1
2
1− x
(1 − x ) (1 + x + x 2 + ....x n −1 ) (1 − x ) 
= lim
x→1 
(1 + x + x 2 + ....x n −1 ) 
= lim
x→1 
1
1
n +1
1+ x
2
1+ x
n +1
n +1
1
2
n +1
2
1 − x n +1
x→1
2
1+ x 2
(1 − x)(1 + x + x 2 + ..... + x n )
1+ x 2
(1 + x + x 2 + ..... + x n )
2 2  4Q   ηλ 
P0 =



3  π R12   n 
1
lim (1 − x n ) (1 − x )  2 1 + x


=
=
n +1
2
n +1
2
2
2 n
n +1
=
=
=
2 n
n +1
1
4 2  4Q 
ηλ ) 2

2  (
3(n + 1)  π R1 
(4.2.27)
También:
3
1 − x n 


2
τ
π
R
a
3
0
1
tg (θ 0 ) = lim =


 lim 
x→1 b
3n λ  4Q  x →1  1 − x 
2
 2η 
tg (θ0 ) =  
 λ 
1
2
(4.2.28)
 2Q 
tgθ , y particularizándola para r = R1 y haciendo
3 
πr 
Teniendo en cuenta la expresión que nos da σ , σ = λ 
1
 2η  2
tg (θ0 ) =   , queda:
 λ 
1
 2Q 
2ηλ ) 2
3  (
 π R1 
σ =
Combinando esta última expresión con la que da el valor de P0, resulta finalmente:
P0 =
8σ
3(n + 1)
(4.2.29)
4.3.- Flujo en canales en tronco - piramidales de bases rectangulares.
Sea el canal de la figura 4.3.1, cuya longitud es L, Anchura T y altura inicial h1 y final h2.
Figura 4.3.1.- Flujo en canales en tronco - piramidales de bases rectangulares.
Realizando un análisis similar al caso anterior de canales tronco-cónicos, se puede llegar a las siguientes expresiones :
Caída de presión debida al corte.
n
2n
2n
τ lw   h1  
1   h1    (2n + 1)2Q 
1 −    = −C
1 −    
∆P = p2 – p1 =

2ntgθ   h2  
2ntgθ   h2    nTh12 




 h2 − h1 

 2L 
donde θ = Semiángulo del canal = arctg 
Máxima tensión de corte (a la entrada de la pared):
 (2n + 1) 2Q 
τlw = − C 
2 
 n Th1 
n
Máxima velocidad de deformación (a la entrada de la pared):
•
γ alw
(2n + 1) 2Q
= −
n Th12
Caída de presión debida a la tensión.
σ1 
h
1 −  1
PE =
2   h2




2



Caída de presión a la entrada del troquel, P0.
P0 =
1
4  6Q 
 2 (ηλ ) 2
(3n + 1)  Th1 
•
•
,
ε alw
=
γ alw
3
tgθ
5.- Flujo entre platos paralelos para un material newtoniano.
Sea la figura 5.1, donde la velocidad del plato superior con respecto al inferior es Vd . Además se va a suponer que el
gradiente de velocidad es lineal.
Para el elemento infinitesimal que se encuentra representado en la figura se tiene:
dQ = T.dy.Vy
donde T es la anchura
Figura 5.1.- Flujo en canales tronco-piramidales de bases rectangulares.
Como se ha supuesto un gradiente de velocidad lineal se deduce:
Vy = Vd
y
h
donde h es la altura o profundidad.
Sustituyendo el valor de Vy en la expresión del caudal infinitesimal:
dQ = T Vd
y
dy
h
e integrando para toda la sección transversal se obtendrá el caudal volumétrico total :
h
Q=
TVd y
dy
h
0
∫
,
e integrando:
Q=
1
ThVd
2
6.- Cambios de presión debidos al flujo de tensión.
Considerando el flujo newtoniano en un canal troncocónico, el cambio de presión debido a los esfuerzos de tensión
viene dado por la siguiente expresión:
3
2σ 1   R1  
1 −   
∆PT =
3   R2  


donde: σ1= Esfuerzo de tensión a la entrada dentro del polímero fundido.
(6.1)
La expresión equivalente para el cambio de presión debido a los esfuerzos de corte es:
3
2τ 1   R1  
1 −   
∆PS =
3tagθ   R2  


(6.2)
donde: τ1= Esfuerzo cortante a la entrada dentro del polímero fundido.
La relación entre los cambios de presión es:
∆PT σ 1tagθ
=
τ1
∆PS
(6.3)
Por otra parte, para un flujo Q, los esfuerzos de corte y de tracción vienen dados por:
 2Q 
tagθ
3 
 π R1 
σ1 = λ 
con lo que
y
∆PT
λ
=
tag 2θ
∆PS 2η
τ1 =
4Qη
π R13
y como
Considerando un ángulo de 10 º se tiene:
∆PT
= 0.06
∆PS
Considerando un ángulo de 30 º se tiene:
∆PT 2
= ≅ 0.67
∆PS 3
λ = 4η
resulta :
∆PT
= 2tag 2θ
∆PS
(6.4)
Lo que muestra que la caída de presión debida al flujo de tracción es mucho más pequeña que la debida al flujo de
corte. Lo anterior es cierto siempre y cuando el valor de θ no sea grande (canales con una convergencia alta).