1. Considere un reactivo dentro de un frasco que se degrada

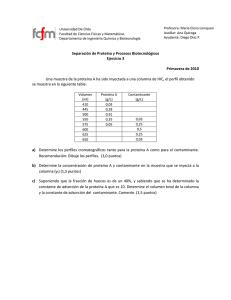
1. Considere un reactivo dentro de un frasco que se degrada siguiendo una reacción de segundo
orden. Los datos experimentales que se muestran a continuación describen su evolución:
t (horas)
c (mg/l)
0
9.0
2
4.0
4
1.9
6
1.2
8
1.45
10
1.0
12
0.5
Determine la constante de degradación de la sustancia.
2. Se construye un embalse pequeño para utilizarlo como sistema de tratamiento de una
sustancia que se degrada de acuerdo a una reacción de primer orden. Con los datos que se
proporcionan a continuación determine
a) Su eficiencia de tratamiento
b) El tiempo de retención que deberá tener para alcanzar una eficiencia del 85 %
Datos:
kd = 0.32 1/día
V = 100,000 m3
G = 0.5 m3/s
La eficiencia de tratamiento  está definida por el cociente entre el material eliminado y el
que entra al sistema
3. Una forma simplificada de simular la evolución de un contaminante no reactivo como el
monóxido de carbono en la atmósfera urbana, es suponer que la atmósfera contigua a la zona
urbana se encuentra bien mezclada, como se enseña en la siguiente figura:
c
j
v
ce
A
L
v
H
Este modelo, denominado modelo de caja, supone que el flujo j [MT-1L-2] de un contaminante
representa una fuente de área uniformemente distribuida en la superficie inferior de la caja,
constituida por emisiones principalmente de origen vehicular. La caja se encuentra limitada
por una altura H y tiene una volumen constante V = HLA en donde se mezcla el contaminante.
El viento sopla con una velocidad v trayendo consigo una concentración ce de contaminante
que ingresa por una de las caras laterales de la caja. Si la zona urbana tiene una concentración
inicial co:
a) Demuestre que la evolución de la concentración del contaminante dentro de la caja está dada
por la siguiente expresión:
vt
c = c0 e- L + (ce +
vt
L
j) (1-e- L )
vH
b) Obtenga la concentración del contaminante en el estado estacionario, si dentro de la zona
urbana se liberan un total de 2 ton/h de CO y el viento sopla con una velocidad de 1.7 m/s
trayendo consigo aire limpio. La caja tiene las siguientes dimensiones:
H = 350 m
A = 10 km
L = 20 km