Estadística para la toma de decisiones.

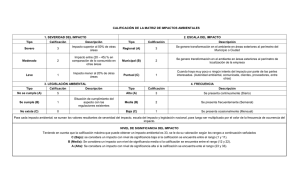
Estadística Inferencial.
Sesión 5. Prueba de hipótesis
Contextualización.
En la práctica, es frecuente tener que tomar decisiones acerca de poblaciones
con base en información de muestreo. Tales decisiones se denominan
decisiones estadísticas.
En esta sesión aprenderemos la definición de una Prueba de hipótesis, sus
componentes así como también los tipos de errores que pueden ser utilizados
estadísticamente.
También se ilustraran las pruebas unilaterales o bilaterales que nos ayudaran a
concluir y dar el resultado de estas pruebas que se aplicarán.
Introducción.
Cuando se deben de tomar decisiones, es útil
hacer suposiciones o conjeturas, acerca de las
poblaciones relacionadas.

¿Cuál es el uso que se le da el conocer el
verdadero valor de un parámetro
poblacional?

¿Cuándo debemos de utilizar las pruebas de
hipótesis?

¿Qué entiendes por un nivel de
significancia?
Fuente: http://www.matematicasypoesia.com.es/Estadist/test-de-hipotesis.jpg
Una prueba de hipótesis se usa para determinar
si una afirmación acerca del valor de un
parámetro poblacional debe o no ser rechazada.
Explicación.
Las hipótesis estadísticas, en general son afirmaciones acerca de las
distribuciones de probabilidad de las poblaciones.
Al proceso de probar si una hipótesis estadística es válida o no se le
llama prueba de hipótesis.
Sus componentes son:

Hipótesis

Tipos de errores

Estadísticos
Explicación.

Hipótesis. (Nula y alternativa)
Cuando se hace una prueba de hipótesis se empieza por hacer una suposición
tentativa acerca del parámetro poblacional. A esta suposición se le llama
hipótesis nula y se denota por Ho.
Esta hipótesis siempre incluye la igualdad, ya sea con =, ≥ ó ≤.
Por ejemplo: si se quiere decir que cierta moneda esta cargada, se formula la
hipótesis de que una moneda no está cargada, esto es, p= 0.5, donde p es la
probabilidad de que ocurra una cara.
Después se define otra hipótesis, llamada hipótesis alternativa que dice lo
contrario de lo que establece la hipótesis nula y esta se denota Ha.
Por ejemplo, si la Ho: p=0.5, posibles hipótesis alternativas son p≠0.5 ó p>0.5.
Explicación.

Tipos de errores:
Si se rechaza una hipótesis nula cuando es cierta, se dice que se ha
cometido un error del tipo I. si, por otro lado, se acepta una hipótesis nula
cuando debe descartarse, se dice que se ha cometido un error del tipo II. En
cualquiera de estos casos, se produce una decisión equivocada o un error
de juicio.
Para que cualquier prueba de hipótesis sea buena, debe diseñarse para
minimizar errores de decisión. No es una cuestión sencilla, ya que una
muestra de cierto tamaño, como un intento de disminuir un tipo de error, se
acompaña, en general, de un aumento en el otro tipo de error.
Explicación.

Nivel de significancia.
Al comprobar una hipótesis, la probabilidad máxima que se estaría
dispuesto a cometer un error del tipo I se llama nivel de significancia de la
prueba. A menudo esta probabilidad se especifica antes de tomar una
muestra, para que los resultados que se obtengan no influyan en la
decisión.
En la práctica se acostumbra que el nivel de significancia sea d 0.05 ó
0.01, aunque se usan otros valores. Por ejemplo: si se elige un nivel de
significancia de 0.05 ó 5%, al diseñar la prueba de hipótesis hay
aproximadamente 5 posibilidades de 100 de que se descarte la hipótesis
cunado debe de aceptarse, esto es, siempre que la hipótesis sea
verdadera tenemos una confianza de 95% de que se tomara la decisión
correcta.
Explicación.

Estadísticos crítico y de prueba.
Estadístico de prueba: un estadístico cuyo valor ayuda a determinar si se rechaza la
hipótesis nula.
Valor crítico: un valor que se compara con el estadístico de prueba para determinar si
se rechaza la hipótesis nula.

Pruebas en las que interviene la distribución normal.
Para ilustrar las ideas anteriores, suponga que, con base en una hipótesis dada, la
distribución de muestre de un estadístico S es una distribución normal con media µs y
una desviación estándar σs. Suponga también que se decide rechazar la hipótesis si S
es demasiado pequeño o demasiado grande.
La distribución de la variable estandarizada Z es la distribución normal estándar (media
0, varianza 1) que se muestra en la siguiente figura, por lo que los valores extremos de
Z llevarían a rechazar la hipótesis.
Explicación.

Fuente: http://www.virtual.unal.edu.co/cursos/sedes/manizales/4030006/images/curvas/4.7.jpg

Como se indica en la figura, es posible tener una confianza de 95% de
que, si la hipótesis fuera verdadera, el puntaje z de un estadístico real
muestral S se encontraría entre -1.96 y 1.96 (puesto que el área debajo
de la curva normal entre estos valores es de 0.95).
Explicación.

Pruebas de una cola y de dos colas.
En la prueba anterior se mostró el interés en los valores extremos del
estadístico S o en su puntaje z correspondiente en ambos lados de la media,
estos es en ambas colas de la distribución, a estas pruebas se les llama
pruebas de dos colas o bilaterales.
No obstante, en ocasiones sólo nos interesa conocer los valores del extremo
de un lado de la media, esto es, en una cola de la distribución, como por
ejemplo, cuando se prueba la hipótesis de que un proceso es mejor que
cualquier otro. Estas pruebas se llaman pruebas de una cola o unilaterales.
Explicación.

La siguiente tabla nos proporciona valores críticos de z de pruebas
unilaterales y bilaterales a varios niveles de significancia:
Nivel
de
significancia α
0.10
0.05
0.01
0.005
0.002
-1.28
-1.645
-2.33
-2.58
-2.88
o 1.28
o 1.645
o 2.33
o 2.58
o 2.88
-1.645
-1.96
-2.58
-2.81
-3.08
y 1.645
y 1.96
y 2.58
y 2.81
y 3.08
Valores Críticos de
z para pruebas de
una cola
Valores Críticos de
z para pruebas de
dos colas
Explicación.

Ilustración de las pruebas unilaterales y bilaterales:
Fuente: http://cienciaseconomicoadministrativas.files.wordpress.com/2011/09/prueba-de-hipotesis.jpg
Conclusión.
Las pruebas de hipótesis son ampliamente
utilizadas tanto en la industria como en la
investigación científica, en esta sesión nos dimos
cuenta que estas pruebas son otra forma de hacer
inferencia sobre los parámetros poblacionales.
En este tipo de problemas se debe de identificar
las hipótesis nulas y alternativa, así como el nivel
de significancia que se utilizara para rechazar o
aceptar estas hipótesis y los estadísticos de
prueba y críticos.
Y para llegar a las conclusiones de aceptación y
rechazo son de gran utilidad las ilustraciones de
las gráficas de pruebas unilaterales y bilaterales.
En la siguiente sesión entraremos de lleno a la
aplicación de las Pruebas de hipótesis para la
media de una población y para la proporción de
una población.
Fuente:
http://origenesamericanos.wikispaces.com/file/view/Pensantes/193856092/298x199/Pensan
tes
Bibliografía.

Anderson, D., Sweeney, D., Williams, T. (2008). Estadística para
administración y economía. (10ª ed.). México: Editorial Cengage
Learning. ISBN: 970-686-278-1

Spiegel, M., Schiller, J., Alu Srinivasan, R. (2010). Probabilidad y
Estadística.(3era.ed.). México: Editorial McGraw-Hill. ISBN-13: 978607-15-0270-4