Solución práctico 5

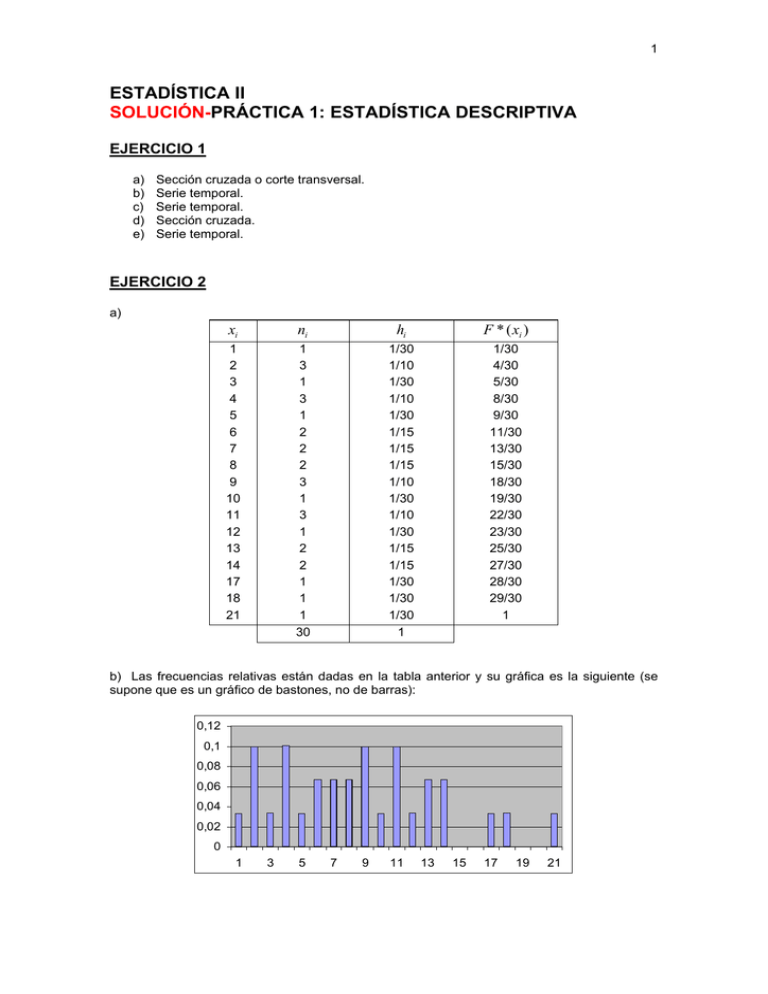
1
ESTADÍSTICA II
SOLUCIÓN-PRÁCTICA 1: ESTADÍSTICA DESCRIPTIVA
EJERCICIO 1
a)
b)
c)
d)
e)
Sección cruzada o corte transversal.
Serie temporal.
Serie temporal.
Sección cruzada.
Serie temporal.
EJERCICIO 2
a)
xi
ni
hi
F * ( xi )
1
2
3
4
5
6
7
8
9
10
11
12
13
14
17
18
21
1
3
1
3
1
2
2
2
3
1
3
1
2
2
1
1
1
30
1/30
1/10
1/30
1/10
1/30
1/15
1/15
1/15
1/10
1/30
1/10
1/30
1/15
1/15
1/30
1/30
1/30
1
1/30
4/30
5/30
8/30
9/30
11/30
13/30
15/30
18/30
19/30
22/30
23/30
25/30
27/30
28/30
29/30
1
b) Las frecuencias relativas están dadas en la tabla anterior y su gráfica es la siguiente (se
supone que es un gráfico de bastones, no de barras):
0,12
0,1
0,08
0,06
0,04
0,02
0
1
3
5
7
9
11
13
15
17
19
21
2
c) Porcentaje de más de 8 años: 50%.
Porcentaje de menos de 13 años: 23/30=76,67%.
d)
F*(xi)
1
1
2 3
4
5 ………….. 14
17 18
21
e)
(xi′−1 , xi′ )
xi
ni
hi
[1, 5)
[5, 9)
[9, 13)
[13, 17)
[17, 21)
[21, 25)
3
7
11
15
19
23
8
7
8
4
2
1
30
8/30
7/30
8/30
4/30
2/30
1/30
1
HISTOGRAMA
8/30
15/30
23/30
27/30
29/30
1
hi
′
xi − xi′−1
2/30
7/120
2/30
1/30
3/120
f * ( xi ) =
F*(xi)
0,267
0,5
0,767
0,9
0,967
1
POLÍGONO DE FRECUENCIAS
f*(x)
1 5
F * ( xi )
F*(x)
9 13 17 21 25
x
Más de 8 años: 1 – F*(8) = 50%
−
Menos de 13 años: F*( 13 )= 76,67%
1
5
9……..
x
3
EJERCICIO 3
m
z=
∑
n
xi +
i =1
∑
n
m
yi
i =1
m+n
m.(
=
∑
xi / m) + n.(
i =1
∑ y / n)
i
i =1
m+n
=
m.x + n.y
m+n
=
m
n
x+
y
m+n
m+n
EJERCICIO 4
500 × 200 + 200 × 800
= 260.
1000
200 × (500 × 0,8) + (800 − 600) × (200 × 0,8)
En tiempo de depresión: xd =
= 280.
200 + (800 − 600)
En tiempo normal el salario promedio es x n =
El nuevo promedio aumenta, porque los que se mandan al seguro de paro son los obreros, que
son los que tienen los salarios más bajos.
Más adelante en el curso veremos que la media es muy sensible a valores extremos, es decir
que algún valor muy alto o muy bajo produce un corrimiento bastante importante de la media, lo
que no ocurre con la mediana (se dice que la mediana es “robusta”).
EJERCICIO 5 (PRIMERA REVISIÓN 1997)
1)
⎧0........si...x < 0
⎪
⎪⎪0,2......si...0 ≤ x < 1
*
FX ( x ) = ⎨0,5......si...1 ≤ x < 2
⎪0,9......si...2 ≤ x < 3
⎪
⎩⎪1.........si...x ≥ 3
2)
xi
FRECUENCIAS RELATIVAS
0
1
2
3
0,2
0,3
0,4
0,1
1
(Asúmase que el gráfico es de bastones, no de barras)
0,5
0,4
0,3
0,2
0,1
0
0
1
2
3
El porcentaje de días en que se vende 0 automóviles, es decir menos de un automóvil, es 0,2.
Por lo tanto el porcentaje de días en que se vende un automóvil o más es 0,8.
4
Nota: No confundir porcentaje o frecuencia relativa con probabilidad: el primero
corresponde al resultado de una muestra, el segundo es un parámetro poblacional.
EJERCICIO 6
Antes: min ( xi ) = 2 .
a) x =
Ahora
min ( xi ) = 1
10
10
1 n
1 10
xi ⇒ 4 = ∑ xi ⇒ 40 = ∑ xi ⇒ 38 = ∑ xi
∑
n i =1
10 i =1
i =1
i=2
⇒ Ahora
10
∑x
i =1
b)
x0,5 = 5
x=4
n=4
i
= 39 ⇒ x =
39
= 3,9
10
x0,5 = 5 porque la cantidad de observaciones antes de la mediana sigue siendo la misma.
EJERCICIO 7
Fábrica A
Fábrica B
x med = 25000
x = 27000
x = 25000
x med = 27000
Observaciones:
Para la fábrica A: si bien el promedio de duración es de 27000 Km, el 50% de las llantas
duraron menos de 25000 km.
Para la fábrica B: si bien el promedio de duración es de 25000 Km, el 50% de las llantas
duraron más de 27000 km.
Recomendaría la compra de la fábrica B (obsérvese los gráficos para comprobar que con
mayor frecuencia la Fábrica B proporciona neumáticos con rendimientos por encima de los
27.000 Km.
EJERCICIO 8 (EXAMEN 2/2000)
X = “Tiempo que transcurre desde la aplicación del insecticida hasta la muerte de un insecto”.
xi′
5
10
30
45
60
F * ( xi′ )
0,5
0,75
0,85
0,95
1
hi
xi
0,5
0,25
0,1
0,1
0,05
1
2,5
7,5
20
37,5
52,5
5
a) La afirmación es falsa. Dos minutos y medio es la marca de clase del primer intervalo,
pero no se puede afirmar que sea el modo.
b) Más de 30 minutos: 0,1 + 0,05 = 0,15
→ La afirmación es verdadera.
c) La afirmación es falsa. Sería verdadera si dijera antes del primer minuto.
5
d)
x=
∑ x h = 2,5(0,5) + 7,5(0,25) + 20(0,1) + 37,5(0,1) + 52,5(0,05)
i i
i =1
⇒ x = 11,5 ⇒ La afirmación es verdadera.
EJERCICIO 9
Las medidas de posición más útiles serían las siguientes.
1) Como el gerente de producción está interesado en el tamaño de envase que tiene que
fabricar en mayor cantidad debe observar en los pedidos aquel que tiene mayor frecuencia,
es decir está interesado en el modo o moda.
2) Para este otro gerente es importante la capacidad de ahorro de dichas regiones, por lo que
resulta conveniente conocer, por ejemplo, el tercer cuartil o el noveno decil de los ingresos
en cada región.
EJERCICIO 10
1)
x0(V,5) = 4000 ⇒ FX* (4000) = 0,5
)
*
y0( M
,5 = 3500 ⇒ FY (3500) = 0,5
*
FY* / (3500) ≤ FY* (4000), por ser F una función no decreciente.
Se cumple que:
⇒ FX* ( 4000) = 0,5 = FY* (3.500) < FY* ( 4.000) ⇒ FX* (4000) < F*Y(4.000)
2) Lo correcto es utilizar el coeficiente de variación, porque varianza y desviación estándar
están afectadas por la unidad de medida de las variables.
EJERCICIO 11
1) Verdadero, ya que sólo depende de la cantidad de observaciones y no tiene en cuenta su
magnitud.
2) Verdadero, sólo se obtiene una aproximación al tomar los puntos medios en los intervalos
3) Falso, el coeficiente de variación no depende de la unidad de medida de la variable.
EJERCICIO 12 (EXAMEN 3/2000)
NOTA: Este ejercicio tiene una leve variación en la tabla respecto del verdadero examen.
PARTE A.1) No, el 81,5% de los establecimientos más pequeños en el número de empleados, producen
el 13,3% del valor agregado industrial acumulado.
6
2) El porcentaje de establecimientos que tienen menos de 2500 empleados es, como se ve
en la tabla, 99,8%. Por lo tanto el 0,2% de los establecimientos tienen 2500 empleados o
más.
3) La participación de estos establecimientos es de 1 – 78,2 = 21,8% del v.a.
4.1) Los establecimientos que tienen hasta 49 empleados generan el 13,3% del v.a., por lo
tanto la respuesta es: 0,133 × 400.000.000 = 53.200.000
4.2)
Intervalo
[y’i-1, y’i)
[1-4]
[5-9]
[10-19]
[20-49]
Marca
yi
h(yi)
n(yi)
2,5
7
14,5
34,5
0,365
0,158
0,153
0,129
36.500
15.800
15.300
12.900
yi.n(yi)
91.250
110.600
221.850
445.050
868.750
La respuesta es entonces 868.750.
PARTE B.1) Algunos de los intervalos originales se colapsaron para formar cinco intervalos.
Intervalo
[y’i-1, y’i)
[1-5)
[5-10)
[10-50)
[50-250)
[250-4000)
Marca
h( y´i )
0,365
0,158
0,282
0,157
0,038
1
F* (y´i)
0,365
0,523
0,805
0,962
1
n(yi)
3
7,5
30
150
2125
yi.h(yi) f*(yi)
1,095 0,09125
1,185
0,0316
8,46
0,00705
23,55 0,00079
80,75
0
115,04
2) La mediana la hallamos mediante la fórmula:
10 − 5
(0.5 – 0.365) = 9,27
0.523 − 0.365
En variable discreta se define la mediana como un valor del recorrido, por lo que en ese caso
ymed = 10. (Obsérvese que la variable número de empleados es discreta).
3) Por lo expuesto en 2) el 50% de los establecimientos tienen hasta 10 empleados.
4) Con idem razonamiento que 2):
5 −1
y0,25 = 1 +
(0,25 – 0) = 3,74.
0.365 − 0
Como en 2) y0,25 debe ser un valor del recorrido, entonces y0,25 = 4.
50 − 10
5) y0,75 = 10 +
(0,75 – 0,523) = 42,19, entonces y0,75 = 43.
0.805 − 0.523
6) El 50% central de las observaciones se encuentran en un intervalo de amplitud 43 – 4 = 39.
7) Lo vemos en la quinta columna: es 115,04. La cantidad estimada de empleados en el total
del país es 115,04 × 100000 = 11.504.000
8) El intervalo modal es el que presenta el valor más alto de la función f*(y). En este caso es el
intervalo [1,5).
ymed = 5 +
7
EJERCICIO 13
Para los cálculos que se solicitan elaboramos el cuadro siguiente:
[y’i-1, y’i)
1000-2000
2000-3000
3000-5000
5000-7000
7000-10000
10000-15000
(yi - y ) 3.h(yi)
(yi-y)^3*h(yi)
-6696231771
-2852103125
-197863281,3
207049479,2
6092097917
36221519531
32774468750
yi
ni ó n(yi)
1500
2500
4000
6000
8500
12500
h(yi)
100
120
150
100
80
50
600
f*(y)
F*(yi)
0,1667
0,2
0,25
0,1667
0,1333
0,0833
1
0,166667
0,366667
0,616667
0,783333
0,916667
1
yi.h(yi)
(yi - y ) 2.h(yi)
0,000167
250
0,000200
500
0,000125 1000
0,000083 1000
0,000044 1133,33
0,000017 1041,67
4925
1955104,17
1176125,00
213906,25
192604,17
1704083,33
4781718,75
10023541,67
(yi - y ) 4.h(yi)
(yi-y)^4*h(yi)
2,29346E+13
6,91635E+12
1,83024E+11
2,22578E+11
2,17793E+13
2,74378E+14
3,26414E+14
1) La distribución de frecuencias relativas en el caso de variables continuas no se grafica. La
función que interesa graficar es f*:
f*(x)
1 2 3
5
7
10
15 y
2) La función de distribución acumulada de frecuencias relativas la tenemos calculada en la
quinta columna en los puntos extremos de intervalo. El gráfico es una poligonal que pasa por
dichos puntos y se completa con: F*(y) = 0 si y < 1000 y F*(y) = 1 si y > 15000.
3)
y = 4925
Intervalo modal = [2000, 3000), según puede observarse en el gráfico de f*.
5000 − 3000
ymed = y0,50 = 3000 +
(0,5 – 0,3667) = 4066,40
0,6167 − 0,3667
4)
S 2y = 10023541,67 y CVy = 0,6428.
5) asy = 1,.033 y ky = 0,248 . Por ello tiene “cola” a la derecha y es más “apuntada” que la
normal.
8
EJERCICIO 14 (EXAMEN SETIEMBRE 97)
A) Como x =
1
n
n
∑x
i
= 5,55
i =1
Entonces para corregir la media debemos cambiar un valor xk = 10 por xk = 15 con lo que nos
queda:
n
x* =
1
( x i − 10 + 15) = 5,55 – 10/100 + 15/100 = 5,60.
n i =1
∑
En el caso de la mediana, ésta no cambia, es decir xmed = x*med ya que estamos cambiando un
valor que está después de ella por otro que también es mayor (recordemos aquí que la
definición del Novales de mediana es aquel valor que deja la mitad de los datos por debajo de
él y la otra mitad por encima).
Piense qué sucedería con la mediana si cambiáramos un valor que está por debajo por otro
que también está por debajo y un valor que está por debajo por otro que está por encima.
Como S2x =
1
n
n
∑ (x − x)
i
i =1
2
⎛1
= ⎜
⎜n
⎝
n
∑x
i =1
⎞
2⎟
i ⎟
2
− x , entonces hay que corregir el segundo momento
⎠
ordinario y la media.
⎛ 152 10 2 ⎞
⎟⎟ + 5,55 2 − 5,60 2 = 16,6925
−
⎝ 100 100 ⎠
(
2
S correg = 16 + ⎜⎜
)
B) Llamemos X = préstamos del año pasado y Y = préstamos del año actual
Entonces, los coeficientes de variación son:
CVx =
CVy =
Sx
x
Sy
y
= 300/650 = 0,4615.
= 350/1000 = 0,35
Por lo tanto, los préstamos de este año mostraron menor variación relativa.
C) En el Ejercicio 9 vimos que la suma de las desviaciones de los datos respecto a la media
siempre da cero. Entonces, para que éstas no se compensen y resulten una medida de la
dispersión, se elevan al cuadrado en el caso de la desviación estándar o se toma valor
absoluto en el caso de la desviación media.
EJERCICIO 15
PARTE A
[xi′−1 , xi′ )
xi
[90, 790)
440
[790, 1490) 1140
[1490, 2190) 1840
[2190, 2540) 2365
TOTAL
ni
hi
F(*xi )
40
36
14
10
100
0,4
0,36
0,14
0,1
1
0,4
0,76
0,9
1
xi hi
176
410,4
257,6
236,5
1080,5
f (*xi )
0,4 / 700
0,36 / 700
0,14 / 700
0,1 / 350
xi2 hi
77.440
467.856
473.984
559.322,5
1.578.602,5
9
x = 1080,5
a)
dólares.
x0 ,5 =
b)
salario promedio anual aproximado de los 100 directores en miles de
0 ,5 − F * (790 )
0 ,5 − 0 , 4
+ 790 =
+ 790 = 984 , 44
*
0 ,36
f (1140 )
700
La mitad de los
directores ganan hasta 984,44 miles de dólares
x 0 , 25 =
c)
x 0 , 75 =
0 , 25 − F * ( 90 )
0 , 25 − 0
+ 90 =
+ 90 = 527 ,5
*
0,4
f ( 440 )
700
0 , 75 − F * ( 790 )
0 , 75 − 0 , 4
+ 790 =
+ 790 = 1470 ,55
*
0 ,36
f (1140 )
700
por lo tanto RI = x0, 75 − x0, 25 = 1470,56 − 527,5 = 943,06
El 50% central de los salarios se encuentran en un intervalo de amplitud 943,06. Es decir, el
50% de los empresarios que se encuentran en el centro de la distribución gana entre 437,5 y
1470,56 miles de dólares.
S2 =
d)
4
∑x
i =1
2
i
h i − x 2 = 1 . 578 . 602 ,5 − (1080 ,5 )
⇒ S = 411 . 122 , 25 ⇒ S =
2
2
S 2 = 641 ,1881549
PARTE B
a) Es el coeficiente de variación debido a que se trata de variables distintas.
641,1881549
= 0,59342
1080,5
6,2
=
= 0,101
61,6
b) CVsalarios =
CVedad
⇒ los salarios son más dispersos que las edades
c) No puede afirmarse que los menores de 61 años y 7 meses tengan salarios menores a
984,44 porque no se conoce la relación entre salario y edad. Por ejemplo, podría suceder que
el más joven gane el salario más alto. Si se supiera que a mayor edad mayor salario, entonces
sería correcto afirmarlo, pero esta información no surge de los datos.
EJERCICIO 16 (NOVALES 1.7)
y=
S2y =
1
n
n
∑
i =1
( y i − y )2 =
1
n
1
n
n
∑
yi =
i =1
1
n
n
∑
(ax i + b) = a
i =1
2
∑ [(ax + b) − (ax + b) ]
n
i
i =1
=
1
n
∑
1
n
xi +
1
n
n
∑ b = ax + b
i =1
n
n
1
∑ [a.( xi − x) ]2 = a2 ∑ ( xi − x)2 = a2S2y
i =1
n
i =1
10
En lo que respecta a la mediana y al modo distinguiremos tres casos:
a) a = 0. Entonces todos los valores son iguales a b y la demostración es trivial.
b) a > 0. En este caso la transformación Y = aX+b es una función que mantiene el orden y
donde F*(yi) = F*(xi) ∀i; por lo tanto, por como fue definida la mediana, ⎨mínimo xi del
recorrido; F*(xi) ≥ 0.50)⎬ o como es definida en el Novales y med = ax med + b . Asimismo en
este caso se mantienen las frecuencias relativas h(yi) = h(xi) y entonces
y mod o = ax mod o + b .
c) a < 0. Aquí nuestra transformación invierte el orden y por lo tanto en algún caso podría
haber un desplazamiento de la mediana ya que si bien se mantienen las frecuencias
relativas, no sucede lo mismo con las frecuencias relativas acumuladas. Es decir podría
suceder que si para algún i se cumple que xi = xmed, entonces ymed podría ser axi+1+b. Para
la definición del Novales la afirmación es cierta. No hay inconveniente para el modo ya que
es el valor de mayor frecuencia.
EJERCICIO 17
a) Para hallar la media y la varianza de los datos elaboramos el siguiente cuadro:
xi
n(xi)
h(xi)
F*(xi)
xi.h(xi)
(xi– x )2.h(xi)
10
11
12
13
14
50
150
100
80
20
400
0,125
0,375
0,25
0,2
0,05
1
0,125
0,5
0,75
0,95
1
1,25
4,125
3
2,6
0,7
11,675
0,3507
0,1709
0,0264
0,3511
0,2703
1,1694
Por lo tanto x = 11.675 y Var(X) = 1,1694.
b) Aplicando el cambio de variable:
Y = 1,23 × X deducimos que Y = 1,23 × x = 14,36 y S y = 1,232 × 1,1694 = 1,7692.
2
c) Aquí efectuamos otro cambio Z = X+1 y entonces: z = x + 1 = 12,675; la Var(Z) = Var (X)
= 1,1694 y para el modo y la mediana sólo hay que sumarle 1 a los correspondientes a X:
xmed = 11 (cuarta columna) y entonces zmed = 12
xmodo = 11 (segunda o tercera columna), luego zmodo = 12.
EJERCICIO 18 (EXAMEN 7/10/96)
Elaboramos el siguiente cuadro que muestra los cálculos para los datos originales y para los
dos posibles acuerdos:
Intervalo
[y’i-1, y’i)
14000-15000
15000-16000
16000-17000
17000-18000
18000-19000
19000-20000
20000-21000
21000-22000
Marca clase
yi
14500
15500
16500
17500
18500
19500
20500
21500
Ni ó n(yi)
5
7
8
6
5
4
3
2
40
h(yi)
0,125
0,175
0,2
0,15
0,125
0,1
0,075
0,05
1
F*(yi) yi.h(yi) (yi - y ) 2.h(yi)
0,125 1812,5 997578,125
0,3
2712,5 582859,375
0,5
3300
136125
0,65
2625
4593,75
0,775 2312,5 172578,125
0,875 1950
473062,5
0,95 1537,5 756046,875
1
1075
871531,25
17325
3994375
11
a)
y = 17325 (ver sexta columna).
b) M ( y ) = 0,8.M (U ) − 2000 ⇒ M (U ) =
M ( y ) + 2000 17.325 + 2000
= 24.156,25
=
0,8
0,8
*
c) Como se observa en la columna de F es:
F * (17.000) = 0,5 ⇒ ymediana = 17.000 ⇒ tmediana = 1,2 ymediana + 3000 = 23.400
d) Esto equivale a hallar el percentil 80 (p80). Para ello busco el primer intervalo donde F*(yi) ≥
0,80: es [19000, 20000). Entonces bajo la suposición razonable de que el ingreso en dicho
intervalo es uniforme puedo calcular fácilmente p80 recordando la fórmula de la ecuación
de una recta:
y − yo
y – y0 = 1
(x – x0)
x1 − x 0
donde:
y = 0,80; y0 = 0,775; y1 = 0,875
x0 = 19000; x1 = 20000
y la incógnita es x = p80.
Despejando nos queda:
0,875
0,80
0,775
20000 − 19000
= 19250.
19000
19250
20000
0,875 − 0,775
e) (F*(18000) = 0,65). Por lo tanto el porcentaje de personas que ganan 18000 o más es de
35%.
p80 = 19000 + (0,80 – 0,775)
f) V ( y ) = V (0,8U − 2000) = 0,82V (U ) ⇒ V (U ) =
g) CVu =
V ( y ) 3.994.375
=
= 6.241.211
0,82
0,64
Su
= 0,1034.
u
h) CVt = 0,1008.
ST2 = 1,2 2 SY2 = 5.751.900 ⇒ CVT =
5.751.900
= 0,1008
1,2 *17.325 + 3.000
EJERCICIO 19
xi
n(xi)
h(xi)
F* ( x i )
xi.h(xi)
0
1
2
3
4
5
6
7
10
11
14
20
13
14
11
7
100
0,1
0,11
0,14
0,2
0,13
0,14
0,11
0,07
1
0,1
0,21
0,35
0,55
0,68
0,82
0,93
1
0
0,11
0,28
0,6
0,52
0,7
0,66
0,49
3,36
(xi - x )2.h(xi)
⎮xi - x ⎮.h(xi)
1,12896
0,612656
0,258944
0,02592
0,053248
0,376544
0,766656
0,927472
4,1504
0,336
0,2596
0,1904
0,072
0,0832
0,2296
0,2904
0,2548
1,716
12
(xi - x )3.h(xi)
(xi - x )4.h(xi)
-3,7933056
-1,44586816
-0,35216384
-0,0093312
0,03407872
0,61753216
2,02397184
3,37599808
0,450912
12,7455068
3,41224886
0,47894282
0,00335923
0,02181038
1,01275274
5,34328566
12,288633
35,3065395
0
1 2
3 4
5 6
7
xi
0 1
2
3 4 5 6
7
1) En la tercera columna de la hoja de cálculo aparece la distribución de frecuencias relativas
graficada arriba con el título h(xi).
2)
La función de distribución de frecuencias relativas acumuladas aparece en la cuarta
columna y se grafica con el título F ( x ) .
*
3) x = 3,36 (la media muestral o promedio es la suma de la quinta columna).
x med = 3 (la mediana es definida como el ⎨mínimo xi del recorrido; F*(xi)≥0.50)⎬). Otra
definición: ver pág. 25 de Novales.
x mod o = 3 (el modo se define como el valor del recorrido que tiene mayor frecuencia
absoluta).
4) S2 = 4,1504; s2 = 4,19232 son la varianza y la cuasi-varianza muestrales. S2 aparece
n
S2 . Existen también otras medidas de dispersión
calculado en la sexta columna; s2 =
n −1
S
como la d.m = 1,716 (desviación media) calculada en la séptima columna y el c.v. =
=
x
0,60633 (coeficiente de variación).
5) a.s. = 0,0533 cuyo cálculo fundamental está hecho en la octava columna. Se definen
x − x med
x − x mod o
= 0,1767 y as2 =
=
también otros coeficientes de asimetría como as1 =
S
S
0,1767.
Por otra parte se calcula en la última columna y en su parte fundamental el coeficiente de
curtosis o apuntamiento k = -0,95037. Recordemos que en la fórmula que aparece en el
página 31 del Novales el término –3 corresponde a la comparación con una distribución
normal ya que ésta tiene su momento centrado de orden 4 igual a
3σ 4 .
13
6) Para la fábrica B los cálculos son los siguientes:
xi
n(xi)
h(xi)
F* ( x i )
xi.h(xi)
0
1
2
3
4
5
6
7
5
8
7
23
18
10
19
10
100
0,05
0,08
0,07
0,23
0,18
0,1
0,19
0,1
1
0,05
0,13
0,2
0,43
0,61
0,71
0,9
1
0
0,08
0,14
0,69
0,72
0,5
1,14
0,7
3,97
(xi - x )2.h(xi)
0,788045
0,705672
0,271663
0,216407
0,000162
0,10609
0,782971
0,91809
3,7891
⎮xi - x ⎮.h(xi)
0,1985
0,2376
0,1379
0,2231
0,0054
0,103
0,3857
0,303
1,5942
(xi - x )3.h(xi) (xi - x )4.h(xi)
-3,12853865
-2,09584584
-0,53517611
-0,20991479
4,86E-06
0,1092727
1,58943113
2,7818127
-1,488954
12,4202984
6,22466214
1,05429694
0,20361735
1,458E-07
0,11255088
3,22654519
8,42889248
31,6708636
x = 3,97; x med = 4 y x mod o = 3 .
S2 = 3,7891; s2 = 3.8274; dm = 1.5942; cv = 0,4903.
as = -0,2019; as1 = -0.0154; as2 = 0,4983.
k = -0,7941.
Observaciones:
Si bien las medidas de posición de la fábrica A son mejores que las de la B en el sentido que
en general “habría” menos defectuosas, todas las medidas de dispersión son peores. Además
en el primer caso la asimetría es positiva, es decir tiene cola a la derecha y en el segundo es al
revés (todo esto tiende a “emparejar las cosas”: téngase en cuenta que as2 proporciona una
idea muy relativa de la asimetría por su propia definición). Como si esto fuera poco, el k de la
fábrica A es menor que el de la B, lo que indica que la gráfica de esta última es más puntiaguda
que la primera y por ello los datos deberían estar menos dispersos.
Por último diremos que si bien las medidas de posición son mejores para la fábrica A que la B,
todos los otros indicadores tienden a disminuir dicha ventaja por lo que la calidad de
producción de ambas se emparejarían. Sin embargo la conclusión final queda en manos del
analista: en este caso Ud.
14
EJERCICIO 20
País
Haití
Guatemala
Nicaragua
El Salvador
Honduras
Bolivia
Brasil
Dominicana R.
Perú
Colombia
México
Ecuador
Panamá
Venezuela
Paraguay
Chile
Costa Rica
Cuba
Argentina
Uruguay
Barbados
Tasa de alfabetización
53
55
57
73
73
78
81
83
85
87
87
88
88
88
90
93
93
94
95
96
99
1) Tasa de alfabetización es una variable cuantitativa continua, pero en este caso las tasas se
toman sin decimales por lo que puede considerarse como discreta (como la edad en años
cumplidos).
2)
5
6
7
8
9
357
338
13577888
0334569
3) Q1 = 78 (primer cuartil)
Q2 = 87 (mediana)
Q3 = 93 (tercer cuartil)
4)
RiQ = 93 − 78 = 15 (recorrido intercuartílico)
1,5.RiQ = 22,5
3.RiQ = 45
Q1 − 1,5.RiQ = 55,5 (barrera interior inferior)
Q3 + 1,5.RiQ = 115,5 (barrera interior superior)
Q1 − 3.RiQ = 23 (barrera exterior inferior)
Q3 + 3.RiQ = 138 (barrera exterior superior)
Valores mínimo y máximo dentro de las barreras: 57 y 99 (bigotes)
Valores atípicos: 53 y 55
Valores atípicos extremos: no hay
15
5) La posición de la mediana y el largo de los bigotes indican asimetría negativa (con cola a la
izquierda), y que las tasas de alfabetización de Haití y Guatemala son atípicas (muy bajas) en
el conjunto de los países americanos.
EJERCICIO 21
1) El PBI per cápita es una variable cuantitativa continua (las categorías de respuesta son
números y entre dos valores cualesquiera siempre es posible, en teoría, encontrar un
país con un PBI per cápita entre aquellos dos).
2)
002
003
004
006
008
010
018
029
066
070
146
149
198
02 05 30 60 75
77
06
81
67
00
00
95
27
55
41
90
60
3) Q1 = 275
Q2 = 867
Q3 = 6627
4) RiQ = 6627 − 275 = 6352
El 50% de los valores centrales del PBI per cápita se encuentran en un intervalo de
amplitud U$$ 6352.
5) 1,5 RiQ = 9528
3RiQ = 19056
Q1 − 3RiQ = −18781
Q1 − 1,5QiQ = −9253
Q3 + 1,5RiQ = 16155
16
Q3 + 3RiQ = 25683
*
0
202
6)
275 867
6627
14990
16155
25683
19860
Países atípicos: sólo Japón, porque escapa a la barrera interior superior.
EJERCICIO 22
1) Falso. Si bien en la muestra no hay parejas con 7 hijos o más, de ello no se debe inferir
que en la población no lo haya. Este es un suceso tal vez poco probable pero no
imposible.
2) n(0) = 200;
n(4) = 20+20+20+20+10 = 90;
n(1) = 100+100 = 200;
n(5) = 10+10+10 = 30;
n(2) = 80+150+70 = 300; n(6) = 10;
El modo muestral es 2. En virtud de los resultados de la muestra es probable que en la
población el modo sea también 2.
3) La cantidad de descendientes varones en la muestra es 310+2×130+3×90+4×30 = 960 y la
de mujeres es 310+2×150+3×90+4×10 = 920, es decir que poco más del 51% son varones
y poco menos del 49% son mujeres y por lo tanto es cierta la afirmación.
4) El promedio de descendientes por pareja es (960 + 920) 1000 = 1,88 , por lo que la afirmación
es falsa.
EJERCICIO 23
1)
COMP
0
1
2
3
4
h(COMP )
∑
COMP 2 .h(COMP )
∑
0
0,24
0,92
2,07
2,88
= 6,11
0,12
0,24
0,23
0,23
0,18
=1
COMP.h(COMP )
∑
0
0,24
0,46
0,68
0,72
= 2,11 ⇒ media de COMP es 2,11
17
S comp = 6,11 − 2,112 = 1,29
h(CRED )
CRED
1
2
3
0,39
0,35
0,26
∑
=1
MODOCRED = 1
2)
COMP / CRED = 3
0
1
2
3
4
hi
1 / 26
3 / 26
6 / 26
8 / 26
8 / 26
∑
=1
(COMP / CRED = 3).hi
0
3 / 26
12 / 26
24 / 26
32 / 26
∑
= 71 / 26 = 2,73
3) Cuando se tiene una tarjeta, lo más frecuente es que se hagan pocas compras con tarjeta, y
a medida que aumenta el número de tarjetas aumenta la proporción de personas que realizan
más compras con tarjeta. Por lo tanto, existe cierta correlación positiva entre las variables, pero
no muy fuerte (la distribución no está concentrada en la diagonal principal de la matriz de la
distribución conjunta).
EJERCICIO 24
1-2-3) Distribución conjunta y marginales
OPINION
1
2
3
4
Marg. De EDAD
20 - 40
0,12
0,07
0,08
0,07
0,34
40 - 60
0,03
0,08
0,12
0,10
0,33
60 - 80
0,03
0,05
0,08
0,17
0,33
Marg. De OPINION
0,18
0,20
0,28
0,34
1
4) Media de EDAD = 30*0,34 + 50*0,33 + 70*0,33 = 49,8
Si se hacen las cuentas con las frecuencias absolutas se obtiene que la media de EDAD es
50. La diferencia se debe a la aproximación con dos decimales.
5) EDAD / OP=1
20 – 40
40 – 60
60 – 80
hi
12 / 18
3 / 18
3 / 18
∑
=1
18
hi
EDAD / OP=3
7 / 20
8 / 20
5 / 20
20 – 40
40 – 60
60 – 80
6) EDAD / OP=2
20 – 40
40 – 60
60 – 80
∑
=1
EDAD / OP=4
hi
20 – 40
40 – 60
60 – 80
7 / 34
10 / 34
17 / 34
∑
hi
8 / 28
12 / 28
8 / 28
∑
=1
=1
7) M (EDAD / OP = 1) = 30.
12
3
3
+ 50. + 70. = 22
18
18
18
8) M (EDAD / OP = 2 ) = 30.
5
8
7
+ 50. + 70. = 48
20
20
20
M (EDAD / OP = 3) = 30.
8
12
8
+ 50.. + 70. = 50
28
28
28
M (EDAD / OP = 4) = 30.
7
10
17
+ 50. + 70. = 55,9
34
34
34
9) El promedio de edades aumenta cuanto mayor el puntaje otorgado por los clientes. Este
resultado indica correlación positiva entre edades y puntajes.
EJERCICIO 25
a)
Y (ALTURA HIJO)
1,85
b) n = 12
12
1,8
1,75
1,7
1,65
1,6
1,5
∑ xi = 20,32
i =1
1,6
1,7
1,8
X (ALTURA PADRE)
12
∑y
i =1
i
= 20,61
1,9
19
12
12
∑ xi2 = 34,4634
∑y
i =1
2
i
i =1
= 35,4223
x = 1,693
S x2 = 0,0046976
S x = 0,0676
y = 1,7175
S y2 = 0,00205209
S y = 0,0453
S xy =
c) rxy =
1 12
1 12
34,925
(
)(
)
x
−
x
y
−
y
=
xi yi − x y =
− (1,693)(1,7175) = 0,0021724
∑
∑
i
i
n i =1
n i =1
12
S xy
SxS y
= 0,70941 . Existe correlación lineal positiva fuerte entre la estatura del padre y
la estatura del hijo mayor.
EJERCICIO 26 (NOVALES 1.14)
Como Y = a.X + b entonces tenemos que:
ρ XY = ρ X.( aX + b ) =
1
n
n
∑
( x i − x )( y i − y )
i =1
S x .S y
=
=
1
n
n
∑
( x i − x )((ax i + b) − (a x + b))
i =1
S x .Sax + b
a S 2x
= Sgn(a) que es
a S 2x
a
=
1
n
n
∑ ( x − x)(x − x)
i
i =1
a S x .S X
⎧+ 1...si...a > 0
⎨
⎩− 1...si...a < 0
EJERCICIO 27 (NOVALES 1.12)
El coeficiente de correlación había sido definido como:
n
1
( x i − x )( y i − y )
n i =1
ρ xy =
S xS y
∑
Por lo tanto, si multiplicamos tanto X como Y por constantes, obtenemos:
n
n
1
1
(αx i − α x )(βy i − β y )
( x i − x )( yi − y )
n
αβ n i =1
=
= Sgn(α).Sgn(β). ρ xy
ραxβy = i =1
α Sx β Sy
S xS y
αβ
∑
Luego:
si Sgn(α) = Sgn(β) entonces ραxβy = ρ xy
si Sgn(α) ≠ Sgn(β) entonces ραxβy = - ρ xy
Si, en cambio, sumamos constantes:
∑
i
=
20
ρα+x
β+y
1 n
∑ [ (α + x i ) − (α + x ) ][. ( β + y i ) − ( β + y )
n i =1
=
SxSy
]
= ρ xy .
Ya que aplicando el Ejercicio 23 para a = 0 resultan: Sα + x = S x y Sβ + y = S y .
Concluimos entonces que al sumar constantes a las variables originales, no se modifica el
coeficiente de correlación, independientemente del signo de dichas constantes.