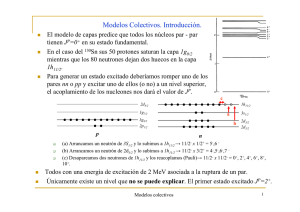
Primera parte y segunda parte

Estudio de los estados
de alto momento angular del 49V
Darío Pablo Rodrigues Ferreira Maltez
Tesis de Licenciatura en Ciencias Físicas
Facultad de Ciencias Exactas y Naturales
Universidad de Buenos Aires
Marzo 2011
TEMA: Estructura Nuclear
ALUMNO: Darío Pablo Rodrigues Ferreira Maltez
LU Nº: 072/01
LUGAR DE TRABAJO: Laboratorio Tandar - Centro Atómico Constituyentes – CNEA
DIRECTOR DEL TRABAJO: Dr. Daniel Hojman
CODIRECTOR: Dra. Silvia Lenzi
FECHA DE INICIACION: Abril 2010
FECHA DE FINALIZACION: Marzo 2011
FECHA DE EXAMEN:
INFORME FINAL APROBADO POR:
Darío Pablo Rodrigues Ferreira Maltez
Jurado: Dr. G. García Bermúdez
Director: Dr. Daniel Hojman
Jurado: Dr. Hugo Sofía
Profesora: Dra. Mirta Alicia Gil
Jurado: Dr. Leszek Szybisz
ii
Estudio de los estados
de alto momento angular del 49V
Darío Pablo Rodrigues Ferreira Maltez
iii
No era ni siquiera un problema, sino haberse
negado desde temprano a las mentiras
colectivas o a la soledad rencorosa del que se
pone a estudiar los isótopos radiactivos o la
presidencia de Bartolomé Mitre.
Rayuela, Julio Cortazar
iv
Agradecimientos
Al Laboratorio Tandar por abrirme las puertas, por los próximos años.
A Daniel Hojman por tanta paciencia, trabajo y disciplina, por su tiempo y por enseñarme a
hacer las cosas bien.
A Silvia Lenzi por confiar en que con sus datos podríamos hacer algo interesante, por hacerme
sentir en Italia, junto a Daniel Napoli, como si estuviera en Argentina.
A Maria Angélica, por todo el trabajo detrás de escena.
A Laura, Daniela, Jimena, Melina, Valeria y Maria José por mostrarme que la amistad puede
ser eterna.
A Dafne por tantas horas de charla y estudio y por hacer de la amistad algo tan simple.
A Cintia Ríos Lado, por haber sido mí amiga, mi referencia.
A Daniel, Pedro y Ochi, por disfrutar hacer física con los dedos.
Al Doc por ser un apasionado de las cosas importantes.
A Hernán y a Ricardo por ser tan buenos tipos.
A María Eugenia por darme un lugar entre sus amigos.
A Alejandro por tantas charlas sin reparos, por compartir la visión de ciertas cosas.
A Iván por ser tan grande.
A Juan Manuel, por su opinión bien pensada de las cosas.
A Micaela, por haber organizado aquel 12 de agosto.
A Sabrina, por ocuparse siempre del festejo de los otros.
A Francis por tantas charlas de café en cualquier parte.
A Santu y a Ariel, por el humor y la música.
A María por su visión femenina y psicológica de las cosas.
A Sandra, por motivarme desde temprano con sus desafíos matemáticos.
A Alejandra, Gustavo C, Carolina y Cinthia, por aquellos primeros años.
A Gustavo D. por sentarse a estudiar conmigo, porque se puede.
A Fernando M. por hacer que pasarme de estación sea una decisión.
A Ana por haber compartido conmigo la profundidad de sus charlas.
A Nicolás, Diego, Romina, Laura O., Eliana y Cristian y a los más nuevos: Tomas, Maxi, y
Adrián.
Al Laboratorio de Metrología de Radioisótopos, por darme un lugar en el grupo.
A Guillermo, Leandro, Ricardo, Rodrigo, Esteban, Norma, Roberto, Marcos y Sebastián, por
tantas risas, por tanto humor. A Celeste, por sus charlas desafiantes.
A Pablo, por enseñarme a dar los primeros pasos en la física experimental, y por ser más mí
amigo que mi jefe. A Christian, por hacerme reír tanto, por la complicidad.
A todos los docentes que me enseñaron algo, a la universidad pública y a los que la defienden.
A la familia Ruiz, por aceptarme.
A mis abuelos, por enorgullecerse de mí.
A mi familia, por darme la oportunidad, por mostrarme el camino y saber esperar a que lo
recorra.
A María Emilia, por ser mi compañera, por incentivarme, por amarme y dejar que la ame, y
principalmente, por estar en mi futuro.
v
Resumen
Se han estudiado los estados de alto momento angular del
evaporación
28
28
49
V mediante la reacción de fusión-
49
Si( Si,xpynzα) V a una energía del haz de 117 MeV. El haz fue provisto por el
acelerador Vivitron del Instituto de Investigaciones Subatómicas (IReS), Estrasburgo, Francia.
La detección de las radiaciones  se realizó mediante el sistema multidetector EUROBALL IV
al que se le acopló un Filtro de Núcleos en Retroceso (RFD).
En base a los datos provistos por este experimento se ha extendido el esquema de niveles del
núcleo hasta una energía de excitación de aproximadamente 13 MeV.
Más de veinte estados de alto momento angular, incluyendo un segundo estado 19/2- predicho
por el Modelo de Capas Nuclear, han sido observados por primera vez en este experimento.
Se ha determinado además la terminación de banda en el estado 27/2-, en concordancia con
cálculos teóricos.
Se llevaron a cabo cálculos teóricos en el marco del Modelo de Capas Nuclear utilizando el
código Antoine con el fin de interpretar los resultados experimentales.
vi
Índice general
Introducción ......................................................................................................................... 1
Modelos del Núcleo ............................................................................................................... 3
2.1 Modelo de Capas Nuclear .................................................................................................. 3
2.1.1 Aproximación del potencial ............................................................................................. 4
2.1.2 Acoplamiento Spin Órbita ............................................................................................... 5
2.1.3 Modelo de Capas Nuclear Deformado .............................................................................. 6
2.2 Modelos colectivos ........................................................................................................... 7
2.2.1 Rotor rígido ................................................................................................................... 7
2.2.2 Modelo de Partícula más Rotor Axial ............................................................................... 8
2.3 Código Antoine ................................................................................................................ 9
Zona de Masa A≈50 ............................................................................................................ 11
3.1 Generalidades ................................................................................................................ 11
3.2 Dificultades de la espectroscopía en la zona de masa A  50 .............................................. 13
3.3 Capas involucradas......................................................................................................... 13
Desarrollo Experimental ..................................................................................................... 15
4.1 Sistema multidetector EUROBALL IV............................................................................. 15
4.2 Filtro de núcleos en retroceso (RFD) ................................................................................. 17
4.3 EUROBALL IV y RFD acoplados .................................................................................... 17
4.4 El experimento .............................................................................................................. 18
4.5 Canales de reacción ........................................................................................................ 19
vii
Análisis de Datos ................................................................................................................ 21
5.1 Corrección Doppler evento por evento ............................................................................. 21
5.2 Reconstrucción de eventos .............................................................................................. 22
5.3 Coincidencias temporales: Cubo simétrico -- y matrices simétricas - ........................... 22
5.4 Correlaciones angulares: Matrices asimétricas - ............................................................. 23
5.5 Espectros en coincidencia ............................................................................................... 24
5.6 Dificultades en los espectros ........................................................................................... 25
Resultados .......................................................................................................................... 27
6.1 Diferencias con el esquema de niveles preexistente ............................................................ 27
6.2 Intensidades y correlaciones angulares .............................................................................. 29
6.3 Nuevo esquema de niveles propuesto ............................................................................... 31
6.4 Momentos angulares y estados Yrast................................................................................ 33
6.5 Estados de paridad positiva ............................................................................................. 34
6.6 Transiciones débiles entre estados de bajo momento angular .............................................. 35
6.7 Transiciones de alta energía ............................................................................................ 37
6.8 Terminación de banda .................................................................................................... 38
6.9 Rotaciones en la línea Yrast ............................................................................................ 39
6.10 Nuevos estados observados ........................................................................................... 40
Cálculos teóricos ................................................................................................................. 43
7.1 Uso del código Antoine ................................................................................................... 43
7.2 Comparación de resultados teóricos y experimentales ......................................................... 44
7.3 Interpretación de los resultados obtenidos .......................................................................... 46
Conclusiones....................................................................................................................... 49
Apéndice ............................................................................................................................ 50
Archivos de entrada del código Antoine ................................................................................. 51
Referencias ......................................................................................................................... 55
viii
Capítulo 1
Introducción
En los últimos 30 años se han realizado una gran cantidad de trabajos en la zona de los núcleos con
masa A50 [For78; Cam91; Len97; Lac01; Bra05; Axi07]. Esta región resulta de interés debido a
que en núcleos relativamente livianos con alto momento angular, se pone de manifiesto la
interacción entre el comportamiento de partícula independiente y el colectivo.
La aparición de sistemas multidetectores de alta eficiencia ha abierto la posibilidad de
estudiar los núcleos de esta zona de la tabla periódica hasta momentos angulares cercanos a los 30ħ.
Con las generaciones anteriores de detectores, los estudios en esta zona se limitaban a estados de
menor momento angular.
Paralelamente, los cálculos basados en el Modelo de Capas Nuclear han dejado de
restringirse a la capa f7/2 como espacio de valencia y pasaron a considerar todas las capas fp,
reproduciendo con buena exactitud los resultados experimentales [Bra05]. Desde el punto de vista
teórico, la espectroscopía de los núcleos de esta zona provee un excelente test para el Modelo de
Capas Nuclear.
Por otro lado, los núcleos cercanos a la mitad de la capa f7/2 cuentan con un significativo
número de partículas para desarrollar deformación. En particular, el estado fundamental del núcleo
del 49V, con tres protones y seis neutrones fuera de la capa doblemente cerrada, presenta una banda
de tipo rotacional. Las propiedades rotacionales de los núcleos de la capa f7/2 son afectadas por la
subyacente estructura microscópica, ya que los nucleones de valencia pueden alinearse
completamente a lo largo del eje rotacional creando estados de terminación de banda.
1
En este trabajo, con el objetivo de estudiar los estados de alto momento angular del núcleo
49
V,
analizamos datos de un experimento realizado con el dispositivo multidetector EUROBALL
acoplado a un filtro de núcleos en retroceso (RFD). Este experimento, llevado a cabo a partir de
reacciones de fusión-evaporación 28Si(28Si,xpynzα) a una energía del haz de 117 MeV, ha permitido
estudiar varios núcleos, entre ellos el
49
V. Como resultado del análisis, proponemos un nuevo
esquema de niveles en el cual se ha duplicado el número de transiciones y estados conocidos hasta
el momento. Realizamos, además, cálculos teóricos basados en el Modelo de Capas Nuclear para
interpretar los resultados experimentales.
Con intensiones de dar una presentación clara de esta tesis, se la ha estructurado de la
siguiente manera: En el Capítulo 2, se desarrolla el marco teórico en que se enmarca el trabajo,
describiendo en forma somera el Modelo de Capas Nuclear y los modelos colectivos. En el Capítulo
3 se mencionan las características generales de la zona de masa A50 junto con las dificultades que
presenta la espectroscopía en esta región. En el Capítulo 4 se da una descripción del dispositivo
experimental utilizado junto a las características principales del experimento. En el Capítulo 5 se
describe el análisis de los datos y en el Capítulo 6 se presentan los resultados obtenidos, donde se
incluye un nuevo esquema de niveles propuesto para el
49
V. En el Capítulo 7 se hace una
comparación entre los resultados obtenidos a partir de cálculos teóricos basados en el Modelo de
Capas Nuclear y los resultados experimentales con la finalidad de interpretar estos últimos.
Finalmente en el Capítulo 8, se enuncian las conclusiones que surgen de este trabajo.
2
Capítulo 2
Modelos del Núcleo
2.1 Modelo de Capas Nuclear
Muchas propiedades de los núcleos pueden ser descriptas considerando que los nucleones se
mueven como partículas independientes. La principal razón para pensar así es que, debido al
principio de exclusión de Pauli y al principio de incerteza, los núcleos no son muy densos. De
hecho, el volumen de todos los nucleones es del orden del 1 % del volumen nuclear.
Por otra parte, el movimiento de los nucleones en el núcleo puede ser considerado como no
perturbado ya que, mediante experimentos de dispersión, se ha estimado que su camino libre medio
es al menos del orden del tamaño del núcleo [Rin80].
Una de las evidencias experimentales más fuertes para la formulación de un Modelo de
Capas Nuclear es la existencia de los llamados números mágicos (2, 8, 20, 28, 50, 82 y 126), donde
los efectos de capa cerrada son análogos a los observados en capas cerradas de electrones en
átomos.
Debe notarse que, a diferencia del fuerte potencial coulombiano central existente en los
átomos, no existe, en principio, tal cosa en los núcleos. Sin embargo, podemos imaginar un
3
potencial de esas características construido por la acción de todos los nucleones. En otras palabras,
el movimiento de estas partículas independientes puede pensarse gobernado por un potencial medio
creado por ellas mismas.
2.1.1 Aproximación del potencial
Vale la pena discutir la forma que debería tener un potencial para este Modelo de Capas Nuclear.
Consideremos un nucleón cerca del centro del núcleo. Por razones de simetría, la fuerza neta
sobre él debería ser nula y, por lo tanto, se tiene que:
 V (r ) 

 0
 r  r 0
Por otro lado, las fuerzas de ligadura nuclear crecen yendo desde la superficie (r=R) hacia el centro
del núcleo, con lo cual:
 V (r ) 
0


 r  r R0
Y, debido al rango finito de las fuerzas nucleares, tenemos que V(r) ≈ 0 para r>R0.
Un potencial que representa bastante bien esas condiciones es el conocido como potencial de
Woods-Saxon:

 r  R0 
V (r )  V0 1  exp 

 a 

1
con R0  r0 A 3 ; V0  50MeV  ; a  0.5 fm; r0  1.2 fm
1
Ya que las autofunciones de este potencial no pueden ser dadas en forma cerrada, lo habitual es
seguir dos aproximaciones cualitativas, a saber:
(i) Oscilador armónico
(ii) Pozo cuadrado
4
Ambas son esféricamente simétricas, pero representan potenciales no físicos ya que tienden a
infinito para r>R0, razón por la cual deben ser tratadas con cuidado.
Para el oscilador armónico, tenemos que los niveles de energía son equidistantes y están dados por:


3
2
 N  0  N    V0
donde N=2(n-1)+l, siendo N el número de cuantos del oscilador, n el número cuántico radial, l el
momento angular y ω0 la frecuencia del oscilador. La degeneración de los niveles está dada por
D(N)=½(N+1).(N+2). Esta degeneración accidental del oscilador armónico es removida por el
potencial del pozo cuadrado. Las energías buscadas, es decir, las correspondientes al potencial de
Woods-Saxon, quedarán entre los límites dados por estos dos potenciales.
Completando el esquema de niveles con nucleones (por analogía con el sistema periódico de
los átomos), vemos que de acuerdo con el principio de exclusión de Pauli, D(N) protones y D(N)
neutrones pueden ser puestos dentro de cada capa (grupo de estados degenerados con igual N) del
oscilador. Esto significa que ambos potenciales reproducen los números mágicos, 2, 8 y 20.
Notemos aquí que este modelo puede explicar la estabilidad de los núcleos 4He, 16O y 40Ca.
2.1.2 Acoplamiento Spin Órbita
Hasta aquí hemos considerado la fuerza nuclear independiente del spin. En el caso atómico, un
término de la forma f(r).l.s da lugar a la ruptura de la degeneración, con la aparición de niveles con
j=l±1/2.
Experimentos de dispersión de protones y neutrones sobre partículas α mostraron que este
modelo es válido también en el caso nuclear. Por lo tanto, resultó ser una idea decisiva incorporar
un término de spin órbita dentro del operador hamiltoniano de partícula independiente.
Aquí, los niveles están caracterizados en el esquema acoplado por los números cuánticos n, l
y j y puede mostrarse que la separación de los niveles doblemente degenerados |slj = l±½> para
f(r) constante es:
E(l )  l  (l  1)  2l  1
Esta ecuación muestra, además, que la separación aumenta conforme aumenta el valor de l, como se
observa en la figura 2.1.
5
Figura 2.1: Esquema de niveles del Modelo de Capas Nuclear incluyendo un término de
acoplamiento spin órbita.
2.1.3 Modelo de Capas Nuclear Deformado
Cuando el núcleo en su estado fundamental presenta deformación axial estable causada por efecto
de capas, los niveles del potencial deformado se llenan con pares de nucleones, llamados pares de
Cooper, que se acoplan a momento angular I=0. Estos nucleones no se mueven en forma
independiente sino que están acoplados con la fuerza de apareamiento que provoca una disminución
de unos pocos MeV en la energía del estado fundamental.
Conforme crece el momento angular del núcleo, pueden distinguirse distintos regímenes:
 Para momentos angulares bajos, la línea Yrast (que une los estados de menor energía para
un dado momento angular) sigue la banda del estado fundamental. La rotación es colectiva y
perpendicular al eje de simetría. Las fuerzas de Coriolis tienden a alinear los momentos
angulares de las partículas acopladas a I=0 con el eje de rotación, pero no aportan suficiente
energía para lograrlo, lo cual implicaría romper un par de Cooper.
6
 Con momentos angulares mayores, la energía alcanza para romper un par de Cooper
disminuyendo las correlaciones de apareamiento y, dado que la fuerza de Coriolis es
proporcional a J, se romperán preferentemente los pares con el mayor J posible.
 Aumentando aún más el momento angular, es mayor el número de pares que se rompe y más
bajas las correlaciones de apareamiento. Las partículas alineadas con el eje de rotación
tienen una distribución de densidad oblada siendo el eje de rotación el de simetría. En estas
condiciones, el núcleo presenta una deformación triaxial.
 Cuando una parte importante de los nucleones se alinean con el eje de rotación, se tiene una
forma esencialmente oblada axial y la rotación deja de ser colectiva. En estas circunstancias
el movimiento es de partícula independiente con un potencial deformado de forma oblada.
 Para momentos angulares muy grandes, se espera otra paso a una forma triaxial antes de la
fisión del núcleo.
Cabe aclarar que no todos los núcleos pasarán necesariamente por todos estas etapas, sino que
dependerá de su deformación.
2.2 Modelos colectivos
Desde el punto de vista energético, para núcleos con un número par de protones y un número par de
neutrones, resulta muy costoso crear una excitación partícula-agujero. Es más eficiente realizar
movimientos colectivos, que pueden ser vibracionales o rotacionales. Los modos vibracionales son
importantes para núcleos cerca de capa cerrada, ya que por tener una configuración esférica, no
pueden rotar. Estas vibraciones pueden estudiarse mediante el Modelo de la Gota Líquida.
A medida que nos alejamos de capa cerrada, la tendencia a la deformación aumenta.
Finalmente la forma esférica se torna inestable aún en el estado fundamental y entonces el núcleo se
deforma, volviéndose importantes los modos rotacionales.
2.2.1 Rotor rígido
El hamiltoniano de un rotor está dado por
2
H
2
7
I k2
k 2
k
donde Ik son las componentes del momento angular I en el sistema rotante y k las componentes
diagonales del tensor de inercia en un sistema de ejes principales.
El momento angular I y su proyección sobre el eje z del sistema laboratorio, son las
constantes de movimiento, pero puede mostrarse que la proyección sobre el eje z del sistema rotante
también lo es. Para el caso axialmente simétrico resulta que 1=2=3 y por lo tanto:
H
2
2
 I 2  I 32 I 32 
2

  E J , K 


2
 
 I ( I  1)  J 2 J 2 




3 

donde J es el momento angular de los nucleones que se anula en el estado fundamental de los
núcleos par-par.
2.2.2 Modelo de Partícula más Rotor Axial
Si pensamos al núcleo como formado por un carozo interno y unos pocos nucleones de valencia
(más adelante mejoraremos estas definiciones), el hamiltoniano que lo representa puede escribirse
como la suma de tres partes, a saber:
1. Una parte intrínseca que describe a los nucleones de valencia: Hint
2. Una parte colectiva que describe al carozo interno: Hcol
3. Una parte que acopla los grados de libertad colectivos con los de partícula independiente.
Desarrollando este modelo, puede demostrarse que, para núcleos deformados con número másico A
impar, los niveles excitados pueden ser entendidos en términos de bandas rotacionales ΔI=1,
construidas sobre un orbital de una partícula independiente.
El Modelo de Partícula más Rotor Axial predice estados excitados basados en los niveles de
partícula independiente predichos por el Modelo de Nilsson para núcleos deformados. Esos estados
de partícula independiente se acoplan junto a una rotación, a un carozo par-par. Incluso para núcleos
triaxiales, la aproximación de axialidad permite una buena estimación de diversos parámetros tales
como factores giromagnéticos y proporciones de mezcla de multipolaridades.
8
2.3 Código Antoine
Se han hecho muchos esfuerzos por mejorar la calidad de los cálculos con el Modelo de Capas
Nuclear [Cau94; Cau05] para la descripción de núcleos de la capa 1f7/2, con especial atención en la
comprensión del origen de sus rotaciones colectivas. Por otro lado se ha trabajado mucho para
incluir en los cálculos la capa 2p [Mar96].
Uno de los códigos utilizados para la realización de los cálculos del Modelo de Capas
Nuclear, es el código Antoine [Cau99; Cau04].
El código Antoine trabaja dividiendo el espacio en tres partes, a saber:
Carozo interno: Constituido por los orbitales que se encuentran completos siempre.
Espacio de Valencia: Constituido por los orbitales que contienen los grados de libertad físicos que
dan lugar a las propiedades relevantes del núcleo. La distribución de las partículas en estos estados
está gobernada por una interacción.
Espacio externo: Constituido por todos los orbitales restantes que estarán siempre vacíos.
El problema a resolver consta de tres pasos:

Definir el espacio de valencia

Derivar una interacción efectiva tal que:
H  E  H efectivo efectivo  E efectivo

Construir y diagonalizar el hamiltoniano.
La interacción efectiva a utilizar dependerá fuertemente de las capas necesarias para definir el
espacio de valencia. En el caso particular de un espacio de valencia definido por las capas fp, una de
las interacciones que mejor responde a los datos experimentales es la GXPF1A [Hon05], resultado
de una modificación sobre la interacción GPXF1 [Hon02]. Esta última fue derivada utilizando
principalmente datos de las energías experimentales de núcleos estables y fue sometida con éxito a
diferentes pruebas mediante el cálculo de energías de ligaduras, de momentos electromagnéticos y
de transiciones de diferentes núcleos de la zona. Se ha considerado además la interacción efectiva
KB3G [Pov01] como referencia, ya que esta interacción ofrece una excelente descripción de los
núcleos livianos de las capas fp. Estas interacciones predicen estructuras similares para núcleos
livianos, pero se observan ciertas diferencias en núcleos ricos en neutrones.
Para el cálculo de los estados de paridad positiva, se utilizó la interacción efectiva SDPF [Pov98].
9
10
Capítulo 3
Zona de Masa A≈50
3.1 Generalidades
La mayoría de los núcleos desde el 40Ca hasta el 56Ni son bien descriptos por el Modelo de Capas
Nuclear en el cual las configuraciones más importantes son [Pov83; Moo83]:
(f7/2)n
y
(f7/2)n-r (f5/2p3/2p1/2)r,
donde (r = 1, 2, ...)
Además, estados de paridad opuesta se originan a partir de excitaciones de las capas sd.
La espectroscopía de los estados de menor energía para un dado momento angular (estados
Yrast) de la mayoría de los núcleos de las capas f siguen lo esperado por el Modelo de Capas,
exhibiendo algún espaciamiento irregular de niveles, a menudo con una marcada discontinuidad en
la terminación de la banda f7/2 de estados con
Jmax=1/2[(Z-20)(28-Z)+(N-20)(28-N)]
11
que, para el 49V, esto corresponde a Jmax=27/2 ћ.
Los núcleos cercanos al
48
Cr, para el cual Jmax=16 corresponde al mayor valor posible,
tienen el máximo número de partículas para desarrollar deformación en la capa f7/2 y por lo tanto
aparece una estructura diferente. Esto trae aparejado el acoplamiento de grados de libertad
colectivos y de partícula independiente, dando lugar a bandas de tipo rotacional [Len96; Len97].
Los estados de bajo momento angular de los núcleos en esta zona siguen aproximadamente
una regla de energías de la forma J(J+1) y presentan grandes probabilidades de transición
cuadrupolar eléctrica B(E2). Estas dos características juntas son indicadores de un movimiento
colectivo.
En esta región se predicen además fenómenos de “backbending” (incremento abrupto en la
pendiente de la curva del momento angular en función de la energía de transición), cambios de
forma y triaxialidad [She90; Fra94]. Sin embargo, la interpretación no es exactamente la misma que
la correspondiente a núcleos más pesados ya que en la zona de masa A ≈ 50, los protones y
neutrones de valencia están llenando la misma capa.
Las propiedades rotacionales de los núcleos de la capa f7/2 son además afectados por la
estructura microscópica subyacente ya que, los nucleones de valencia pueden alinearse
completamente a lo largo del eje de rotación creando un estado de terminación de banda. Una marca
del proceso de terminación de banda puede ser el suave decrecimiento del momento de inercia
mientras el núcleo se aproxima al límite superior de momento angular disponible. Otro indicador
puede ser la aparición de transiciones de alta energía conectando el estado de terminación de banda
con estados de mayor momento angular.
Para mayores valores de momento angular, pero por debajo de Jmax, ocurren irregularidades
en el espaciamiento de niveles. Estos podrían ser tomados como evidencia de un cambio de nivel
con el consecuente “backbending”, o alternativamente, como una disminución de la colectividad y
reaparición del comportamiento de partícula independiente.
Ha sido demostrado [Moo83] que un apropiado aumento de la base en el Modelo de Capas
Nuclear conduce a B(E2) “colectivos” mejorados y niveles de energía de la forma J(J+1).
Por lo tanto, la espectroscopía en la capa f7/2 a altos momentos angulares, en las cercanías de
Jmax, y particularmente cerca de mitad de capa como es el caso del 49V, es importante para entender
la estructura de partícula independiente subyacente en el comportamiento colectivo, proveyendo
una buena prueba para el Modelo de Capas Nuclear y las interacciones efectivas asociadas.
12
3.2 Dificultades de la espectroscopía en la zona de masa A  50
La espectroscopía de alto momento angular en esta zona de la tabla periódica no es una tarea fácil
por las siguientes razones:
a) El momento angular de un núcleo compuesto en una reacción fusión-evaporación está
restringido debido a las masas livianas de los núcleos correspondientes a blancos y
proyectiles.
b) La alta velocidad de los núcleos livianos en retroceso, junto con los efectos de la cinemática
debidos a la evaporación de partículas cargadas, incrementa considerablemente el ancho de
los picos en los espectros de energía por efecto Doppler.
c) Conforme se incrementa el momento angular, la energía de transición se vuelve más alta y
esto conlleva a una disminución en la resolución y la eficiencia de detección.
d) El número de canales que compiten en la evaporación de partículas cargadas se vuelve muy
grande.
Aunque ha habido considerables avances en espectroscopía de altos momentos angulares desde los
primeros estudios realizados en núcleos de la capa f7/2, continua siendo difícil observar tales núcleos
con momentos angulares por encima de los 13 ħ. Esto se debe a que el pequeño tamaño de los
núcleos de la capa f implica altas energías  y bajos momentos angulares [Cam91].
3.3 Capas involucradas
El núcleo de 49V está formado por 23 protones y 26 neutrones.
Se observarán estados de paridad negativa cuando 20 protones y 20 neutrones se encuentren
completando las capas 1s, 1p, 1d y 2s (Ver figura 2.1), mientras los 3 protones y 6 neutrones que
restan se encuentren, dependiendo del estado de excitación, en las capas 1f7/2, 2p3/2, 1f5/2 y 2p1/2. En
este caso, el carozo interno estará dado por los 20 protones y 20 neutrones que no sufrirán
excitaciones, es decir, por las ya mencionadas capas 1s, 1p, 1d y 2s.
Los estados de paridad positiva, en cambio, aparecerán cuando ocurran excitaciones desde
las capas sd, es decir: 1d5/2, 2s y 1d3/2. En este caso, el carozo interno quedará restringido a las capas
1s, 1p3/2 y 1p1/2, totalizando 8 protones y 8 neutrones.
En el primer caso, el espacio de valencia estará dado por las capas fp, mientras que en el
segundo, el espacio de valencia será mayor e incluirá las capas sd.
13
14
Capítulo 4
Desarrollo Experimental
4.1 Sistema multidetector EUROBALL IV
EUROBALL fue una colaboración Europea para la construcción de un espectrómetro de rayos 
para espectroscopía nuclear. Los países involucrados fueron Alemania, Dinamarca, Francia, Italia,
Reino Unido y Suiza.
Figura 4.1: Esquema de EUROBALL IV,
donde se representan los detectores de
tipo Clover (azul oscuro) y los de tipo
Cluster (naranja oscuro) [EHP].
15
Este nuevo dispositivo experimental permitió un gran avance en el estudio de las propiedades de
núcleos atómicos dada su eficiencia significativamente mayor que la de las generaciones de
instrumentos previos.
La fase IV de este dispositivo experimental consistió en (Ver figura 4.1):
 15 detectores de tipo Cluster, compuestos cada uno por 7 cristales de germanio y un
supresor Compton (naranja oscuro, en el centro del esquema)
 26 detectores de tipo Clover, compuesto cada uno por 4 cristales de germanio (azul oscuro
en el centro del esquema)
En esta fase se removieron los 30 detectores de germanio de cristal único que ocupaban los ángulos
delanteros. Esto se hizo para acoplar un filtro de núcleos en retroceso.
Los detectores compuestos, como los de tipo cluster y clover, poseen varias funciones.
Primeramente, permiten disponer de una mayor granularidad que la que se tendría con detectores de
cristal único de volumen igual a la suma de los volúmenes individuales. Esto redunda en una mejor
definición del ángulo de incidencia y por lo tanto, en una mejora en las medidas de las correlaciones
angulares. Por otra parte, es posible reconstruir un evento que involucra una dispersión Compton
(esta reconstrucción recibe el nombre de “add-back” en inglés). Finalmente, los detectores clover,
ubicados en anillos aproximadamente perpendiculares al haz, permiten el estudio de los coeficientes
de polarización lineal, los que, en conjunto con los coeficientes de correlaciones angulares, definen
la multipolaridad de las transiciones fijando los momentos angulares y las paridades de los estados
del núcleo.
La primera fase de EUROBALL comenzó a operar a principios de 1997 en el Laboratorio
Nacional de Legnaro (LNL), Italia.
En noviembre de 1998, EUROBALL fue trasladado al Instituto de Investigaciones
Subatómicas de Estrasburgo, Francia. En esta nueva fase, la cual comenzó a principios de 1999, el
dispositivo fue mejorado al incluir un filtro de BGO interno y un sistema multidetector de silicio
para partículas cargadas (no usado en el presente experimento) [EHP].
16
4.2 Filtro de núcleos en retroceso (RFD)
Se trata de un detector de iones pesados, segmentado en elementos individuales para detectar
residuos de evaporación en coincidencia temporal con la radiación . El mismo permite filtrar
eventos de interés y determinar el vector velocidad del núcleo en retroceso detectado permitiendo la
corrección Doppler para cada radiación  individual, lo cual se traduce en mayor limpieza de los
espectros y una mayor resolución en energía.
El RFD [Mec07] consta de una folia de aluminio delgada que frena a los núcleos en
retroceso. Esta folia posee un agujero central cuyo diámetro es calculado, en cada caso concreto,
para lograr el mejor balance posible entre la menor detección de núcleos provenientes del haz y la
mayor detección de núcleos en retroceso. En líneas generales, por el agujero pasa el 99.9% del haz
y el 50% de los núcleos en retroceso. Los electrones eyectados, cuya cantidad depende del núcleo
que ha interactuado con la folia,
son acelerados y focalizados por lentes electrostáticas en
centelladores plásticos delgados que entregan una señal proporcional al número de electrones. Los
18 centelladores están dispuestos en anillos concéntricos, brindando una excelente medida de la
dirección del núcleo en retroceso y conjuntamente con una medida de tiempo de vuelo (ToF)
determinan su vector velocidad. Al trabajar el RFD en coincidencia temporal con los detectores de
EUROBALL, se puede corregir, evento por evento, el corrimiento Doppler de las radiaciones γ.
4.3 EUROBALL IV y RFD acoplados
En la figura 4.2 presentamos una fotografía del RFD acoplado a EUROBALL IV, todo el
dispositivo experimental se encuentra en línea con el acelerador tandem VIVITRON del IReS, cuyo
haz ingresa por la izquierda.
En la imagen, un hemisferio de EUROBALL IV fue separado para mostrar la cámara con el
blanco. La misma se encuentra frente a los detectores Clover y Cluster, conectada con el tanque del
RFD a la derecha mediante una cámara cónica. A la derecha se observa el tanque del RFD,
reemplazando los detectores cilíndricos de germanio de EUROBALL IV. Puede verse además la
base de algunos de los 18 fotomultiplicadores que sobresalen del tanque del RFD.
17
Figura 4.2: Fotografía del RFD acoplado a EUROBALL IV (extraída de [Mec07])
4.4 El experimento
Se ha hecho incidir un haz de
28
Si a 117 MeV, provisto por el acelerador VIVITRON del IReS,
sobre un blanco constituido por dos folias de 28Si de 200 g/cm2 cada una. La radiación  emitida
por los productos de la reacción fue detectada con el sistema multidetector EUROBALL fase IV
acoplado al filtro de núcleos en retroceso RFD, descriptos más arriba.
Antes de comenzar el experimento con el haz, se realizó la calibración en eficiencia y
energía de los detectores utilizando fuentes radiactivas de 56Co, 60Co y 152Eu. En esta etapa se ajustó
la electrónica y la ganancia de los detectores. Una segunda calibración, utilizando las mismas
fuentes radiactivas, se realizó al finalizar el experimento con el haz, luego de retirar los blancos.
El experimento duró 5 días. Si bien se registraron en cintas magnéticas del tipo DLT todos
los eventos en los cuales se dispararon por lo menos 2 detectores de germanio, para el análisis de
los datos se utilizaron fundamentalmente eventos triples. El número de estos eventos triples ha sido
de unos 410 millones aproximadamente. Los datos fueron adquiridos en 42 bloques de datos. Se ha
pasado de un bloque a otro luego de haber completado una cinta DLT, o cuando se ha procedido a
reajustes del haz, de detectores o de la electrónica asociada.
18
4.5 Canales de reacción
A fin de conocer los canales de reacción a los que dio lugar el experimento, se utilizó el programa
PACE4 [Gav80]. Este programa permite estimar la sección eficaz de producción de los diferentes
núcleos formados a partir de una dada reacción, en nuestro caso:
28
Si +
28
Si a 117 MeV. Los
resultados obtenidos para los principales canales de reacción, en forma porcentual, son presentados
en la figura 4.3:
Fe-52
4%
Fe-53
7%
Ti-46
4%
V-47
9%
V-48
1%
Mn-53
2%
V-49
7%
Mn-52
26%
Cr-49
14%
Mn-51
1%
Cr-50
9%
Mn-50
10%
Cr-52
4%
Cr-51
2%
Figura 4.3: Relación porcentual de los principales núcleos formados en la reacción estudiada.
Como puede observarse en la figura 4.3, núcleos tales como
que el
49
52
Mn y
49
Cr fueron más favorecidos
V en esta reacción. La existencia de al menos 14 núcleos diferentes, con significativa
sección eficaz de producción, introduce complicaciones en el análisis de datos como veremos más
adelante.
19
20
Capítulo 5
Análisis de Datos
5.1 Corrección Doppler evento por evento
Las mediciones llevadas a cabo con las fuentes radiactivas permitieron obtener una calibración para
cada detector. Las mismas se aplicaron a cada uno de los 42 bloques de datos medidos durante el
experimento con el haz. A continuación se estudiaron las derivas temporales de las ganancias de los
detectores y se realizaron los ajustes necesarios para su corrección. A partir de este punto, las
diferencias existentes entre los espectros de cada detector se deben al corrimiento Doppler, el cual
depende principalmente de la posición que cada detector tiene en el sistema multidetector.
El corrimiento Doppler es consecuencia de que los núcleos emiten la radiación  en vuelo,
en este caso con velocidades de aproximadamente el 7 % de la velocidad de la luz. Esta velocidad
es lo suficientemente grande como para que el corrimiento Doppler medido en los detectores esté
lejos de ser despreciable, y lo suficientemente chica como para considerar efecto Doppler clásico.
Es aquí donde se pone de manifiesto la ventaja de utilizar el filtro de núcleos en retroceso (RFD)
descrito en la sección 4.2. El mismo permitió conocer el vector velocidad de cada núcleo en el
momento de la emisión  y esta información, junto con la posición de cada detector, hizo posible la
corrección Doppler evento por evento.
21
Para cuantificar la importancia de realizar la corrección de esta manera, podemos decir que cuando
la corrección Doppler se lleva a cabo considerando una misma velocidad media para todos los
núcleos y como ángulo de emisión de la radiación , el correspondiente a la posición del detector
medido desde el lugar de la reacción, el ancho a mitad de altura de un pico de 1300 keV es
aproximadamente de 17 keV. Si en lugar de tomar como ángulo de emisión el ángulo de cada
detector, se lo determina utilizando un sistema multidetector de partículas para definir la dirección
del núcleo en retroceso, el ancho del pico se reduce a 10 keV. Utilizando el RFD en cambio, puede
determinarse la velocidad de cada núcleo y el ángulo de cada emisión, con esta información la
corrección Doppler de un pico de 1300 keV, reduce su ancho a tan sólo 6 keV.
5.2 Reconstrucción de eventos
La utilización de detectores tipo Clover y tipo Cluster compuestos cada uno de ellos por cuatro y
siete detectores de germanio respectivamente, permite la reconstrucción de los eventos que no
depositan toda su energía por efecto fotoeléctrico en un único detector, sino que parte la depositan
en un detector adyacente, mediante interacción Compton primero y fotoeléctrica después. El criterio
utilizado para la reconstrucción de estos eventos, es asignar al detector en que se depositó mayor
energía, la energía total depositada en ambos detectores. Este criterio está sustentado por
simulaciones hechas con el código Geant 4 [Ago03]. En rigor, también se imponen condiciones en
la posición de los detectores vecinos al que detecta la mayor deposición de energía para realizar la
suma.
5.3 Coincidencias temporales: Cubo simétrico -- y matrices simétricas -
Una vez realizada la corrección Doppler evento por evento, los datos están en condiciones de ser
clasificados según diferentes criterios dando lugar a cubos o matrices.
Una de las clasificaciones utilizada para el análisis de los datos, fue la que dio lugar a un
cubo simétrico --. La misma consistió en contabilizar las coincidencias temporales triples que
tuvieron lugar considerando todos los detectores. De este modo, cada elemento del cubo contiene el
número de eventos de coincidencias temporales triples registrados con las energías que determinan
las coordenadas del elemento en el cubo. Este cubo es simétrico por construcción, ya que el número
22
de eventos guardados en el elemento con coordenadas (Ei, Ej, Ek) o cualquiera de sus
permutaciones, es el mismo.
Otras clasificaciones utilizadas, son las matrices simétricas - que se obtienen de proyectar
el cubo --, pidiendo que uno de los tres eventos en coincidencia temporal sea de una energía
específica. Estas matrices son de gran utilidad a la hora de estudiar todas las transiciones asociadas,
por medio de alguna vía de desexcitación nuclear, con un determinado rayo .
5.4 Correlaciones angulares: Matrices asimétricas -
Los coeficientes de correlación angular (DCO) han sido estimados a partir de la siguiente relación:
DCO 
I1 (en 1 en coincidencia con  2 en  2 )
I1 (en  2 en coincidencia con  2 en 1 )
donde 1 es el rayo  que se está investigando y 2 es el rayo  de multipolaridad conocida. Para su
determinación resulta de utilidad clasificar los datos en matrices de coincidencias - temporales
asimétricas. Las mismas se construyen restringiendo cada uno de los ejes de la matriz a los eventos
detectados en un conjunto específico de detectores. En particular, para el cálculo de los DCO, se
construyó una matriz - asimétrica que contiene las correlaciones entre rayos  detectados en 5
detectores del tipo cluster a ≈ 156º, por un lado, y aquellos detectados en los 26 detectores de tipo
clover ubicados en ángulos de 77º o 103°, por el otro.
En la geometría de EUROBALL, los valores teóricos de DCO correspondientes a
transiciones cuadrupolares puras (ΔI=2) o dipolares puras sin cambio de momento angular, son
cercanos a uno, mientras que, para transiciones dipolares puras con ΔI=1, estos valores son
cercanos a 0.6. Luego, de la relación entre los eventos contabilizados para una determinada
transición en la matriz - asimétrica y su transpuesta, se obtienen los valores de DCO dando
información sobre las multipolaridades de las radiaciones.
23
5.5 Espectros en coincidencia
Para la construcción del esquema de niveles, trabajamos con espectros en coincidencias, los mismos
se obtienen de restringir el cubo -- a aquellos rayos que hayan sido medidos en coincidencia con
otros dos rayos dados. A modo de ejemplo y para exhibir la calidad de estos espectros en
coincidencia, en la figura 5.1, presentamos el que resulta de reducir el cubo -- a aquellos rayos
que se encuentren en coincidencia con rayos de 1021 keV y 1240 keV.
Figura 5.1: Espectro en coincidencia con rayos  de 1021 keV y 1240 keV.
Análogamente, pueden obtenerse espectros en coincidencia imponiendo a una matriz -, la
condición de coincidencia con un determinado rayo .
En estos espectros, el área de cada pico, corregido mediante la curva de eficiencia obtenida
de la calibración de los detectores, es una medida de la intensidad de cada transición, mientras que
el ancho a mitad de altura, es una medida de la resolución del sistema para la energía del pico.
24
5.6 Dificultades en los espectros
La “contaminación” de los espectros es una de las dificultades con que nos enfrentamos al
utilizarlos para la construcción del esquema de niveles ya que, como consecuencia de la
competencia de la emisión de partículas cargadas con la evaporación de neutrones en la región de
masa A ≈ 50, la reacción utilizada (28Si+28Si) dio lugar a numerosos canales de reacción (ver
sección 4.5). Los espectros analizados presentan transiciones provenientes de varios núcleos que no
son, aquí, de nuestro interés como se muestra en la figura 5.2.
La dificultad para discriminar entre los distintos núcleos que aparecen en el espectro debido
a la gran cantidad de canales de reacción abiertos se debe, en parte, a que no se observan los rayos
X de los distintos elementos. Esto es consecuencia de la baja conversión interna producto de los
bajos números atómicos y las altas energías de transición involucradas.
Figura 5.2: Proyección  del cubo --, donde se observan rayos
de los principales núcleos productos de la reacción
Por otro lado, esta región de la tabla periódica no es bien conocida a altos momentos angulares. Por
lo tanto, la identificación de transiciones pertenecientes a los diferentes núcleos presentes en la
reacción es tarea difícil por no contarse con esquemas de niveles con un significativo número de
transiciones.
25
Otra de las dificultades con que nos enfrentamos es la baja eficiencia de detección para rayos  de
alta energía. Este no es un problema menor, teniendo en cuenta la gran cantidad de transiciones que
se observan a energías mayores a 1500 keV. Esto último implicó, además, la adopción de un rango
energético amplio, por lo que los rayos de baja energía aparecen muy comprimidos y más
mezclados.
26
Capítulo 6
Resultados
6.1 Diferencias con el esquema de niveles preexistente
Varios estudios fueron realizados sobre los estados de paridad negativa [Bla73; Saw73; Haa75;
For78] y los de paridad positiva [Haa75; Kha86] del
49
V. El último trabajo al respecto es el de
Cameron y sus colaboradores [Cam91], donde confirmaron las asignaciones previas y extendieron
el esquema hasta el nivel de 8414 keV asignado como 27/2-.
Además de los estados Yrast, Cameron y sus colaboradores observaron otros estados de
paridad negativa a 2672 keV (11/2-) y 6845 keV (23/2-) y confirmaron la asignación de momento
angular y paridad 15/2- al estado de 2728 keV que había sido observado previamente en [For78].
Los estados de paridad positiva basados sobre el estado 3/2+ a 748 keV que habían sido
observados en [Haa75] con asignaciones de momento angular hasta 9/2 ћ, fueron confirmados por
los datos de distribuciones angulares de Cameron y sus colaboradores y establecieron además el
estado de 2741 keV como 11/2+.
El esquema de niveles más completo conocido hasta el momento, es entonces el publicado
por Cameron y sus colaboradores, que presentamos en la figura 6.1.
27
Figura 6.1: Esquema de niveles reportado en el trabajo [Cam91] donde hemos señalado en rojo las
transiciones y niveles no observados en el experimento con EUROBALL
De las 46 transiciones informadas por Cameron y sus colaboradores para el
49
V, 15 no han sido
observadas en el experimento con EUROBALL (señaladas en rojo en la figura 6.1). En cuanto a los
20 estados presentes, 18 de ellos han sido confirmados por este experimento.
Nuestros cálculos de DCO son consistentes con la paridad y el momento angular asignados
hasta el estado 23/2-. Sin embargo, el estado más cercano a 6845 keV (como veremos en la próxima
sección, a 6836 keV) parece corresponder a un valor de momento angular y paridad 25/2-, en
contraposición con la establecido hasta el momento, donde este valor se asignaba a un estado de
7801 keV. Por otra parte, la energía correspondiente al estado 27/2-, no corresponde en nuestro
análisis a 8414 keV sino a 7791 keV. Los estados de paridad positiva basados sobre el 3/2+ fueron
confirmados hasta el estado 11/2+.
28
6.2 Intensidades y correlaciones angulares
En la tabla 6.1 listamos todas las transiciones γ correspondientes al núcleo
49
V observadas en el
experimento con EUROBALL, indicando para cada una de ellas: su energía E y la de su estado
inicial Ei, ambas en keV; su intensidad I, relativa a la transición de 1021 keV normalizada a 1000;
la asignación de momentos angulares y paridades propuesta y el coeficiente de correlación angular
(DCO).
Las intensidades de las transiciones γ pueden ser consideradas como totales, dada la baja
conversión interna en esta región. Sin embargo, las mismas no deben ser consideradas como las
intensidades reales de las transiciones, ya que fueron obtenidas a partir de eventos de coincidencias
triples con efectos de correlaciones angulares. Presentamos estas intensidades con el objeto de
ilustrar, en forma cualitativa y aproximada, los principales caminos de desexcitación del núcleo.
Tabla 6.1: Energías de las transiciones y de sus estados iniciales, intensidades relativas,
asignación de momentos angulares y paridades y coeficientes de correlación angular.
E [keV]
90.4
156.7
366.1
375.6
392.2
416.7
461.9
463.9
501.1
555.1
562.9
574.6
596.7
597.8
608.9
634.0
655.4
656.7
701.4
777.0
779.9
796.5
853.8
873.7
933.8
954.9
1021.0
1036.7
1049.3
1061.7
1063.9
Ei [keV]
90.1
5684.5
7025.3
6836.7
1139.8
3739.8
3739.8
2725.3
11649.3
7580.6
2739.5
2176.5
2858.3
3323.1
6461.5
8360.7
4395.2
747.3
7726.7
6461.5
8360.7
6659.2
1601.3
9234.4
6461.5
7791.6
1021.0
2176.5
1139.8
3323.1
1154.3
I
102
49
24
51
3
567
6
247
26
35
6
5
6
249
69
93
53
5
57
9
12
4
4
115
26
182
1000
10
15
392
29
Ii If
5/2- 7/223/2- 21/225/2- 23/25/2+ 3/2+
19/2- 17/27/2+ 5/2+
15/2- 15/2-
11/2+ 9/2+
9/2+ 7/2+
13/2- 15/217/2- 15/223/2- 21/219/2- 19/23/2+ 5/2-
DCO
0.36(3)
0.53(19)
0.46(3)
1.02(11)
0.53(5)
0.51(12)
1.35(21)
23/2- 23/2-
7/2+ 3/2+
23/2- 21/227/2- 25/211/2- 7/29/2+ 5/2+
5/2+ 5/217/2- 15/29/2- 5/2-
0.58(12)
0.48(2)
0.96(7)
0.52(12)
1072.2
1132.9
1137.8
1139.9
1152.2
1154.5
1162.9
1172
1221.4
1240.4
1339.9
1354.1
1400
1478.3
1510.9
1523.4
1585.3
1601.7
1654.0
(1695)
1703.8
1704.1
1717.3
1718.2
1726.8
1729
1783.3
1787.8
(1833)
(1836)
1874.0
1915
1944.7
1958.2
2042.4
2065.7
2112.5
2124
2177.0
2198.6
2414.9
2592
2630
2721.1
(2729)
2878.2
2919
3094
3163
3284
(3684)
4808
4395.2
5527.8
2739.5
1139.8
6836.7
1154.3
7025.3
7025.3
4079.4
2261.4
4079.4
4079.4
3577
3739.8
1601.3
8360.7
2739.5
1601.3
9234.4
5272
2725.3
2858.3
7580.6
2739.5
8563.1
8563.1
5862.6
5527.8
9414
2858.3
7726.7
11149
5684.5
10521.5
7726.7
6461.5
5852.3
5862.6
2176.5
7726.7
11649.3
13114
7025.3
6461.5
10521.5
8563.1
6659.2
(6834)
10000
7025.3
10521.5
12600
93
70
55
30
310
86
43
6
27
850
68
17
7
216
51
24
10
27
7
5
66
6
15
18
10
11
67
29
4
3
12
37
470
37
37
6
75
12
12
32
37
20
17
12
5
31
2
14
4
10
5
4
19/2- 17/221/2- 19/211/2+ 7/2+
5/2+ 7/225/2- 23/29/2- 7/2-
0.37(3)
21/213/2-
15/2- 11/211/2+
15/2-
9/2+
19/2- 15/27/2+ 5/225/2-
11/2+ 9/2-
0.37(3)
1.09(6)
1.11(6)
15/2- 11/213/2- 9/211/2+ 11/225/2- 25/225/2- 
21/2- 19/2-
0.55(15)
13/2- 11/221/2-
23/2- 19/227/2- 25/223/2-
23/2- 19/221/2- 19/219/2-
9/2+ 7/221/2-
27/2-
19/223/2- 19/227/2- 27/225/2- 23/219/219/2-)
25/2-
19/227/2- 25/227/2-
1.17(12)
0.76(27)
0.99(45)
0.88(13)
0.89(14)
0.62(13)



Las incertezas porcentuales relativas en los valores de intensidad deben considerarse entre 10% y
50% dependiendo de la intensidad de la transición y la complejidad del espectro correspondiente.
En forma similar, las incertezas en las energías de las transiciones se encuentran entre 0.3 y 1.5 keV.
30
6.3 Nuevo esquema de niveles propuesto
El nuevo esquema que presentamos a continuación en la figura 6.2, cuenta con 83 transiciones  de
las cuales 52 han sido observadas por primera vez en este experimento. Hemos encontrado 22
nuevos estados, totalizando 40 estados en todo el esquema, el cual se extiende hasta el nivel de
13114 keV.
Figura 6.2: Esquema de niveles propuesto a partir del experimento realizado con EUROBALL IV
donde el espesor de cada línea es proporcional a la intensidad de la transición.
Las 5 transiciones indicadas con línea punteada y su energía entre paréntesis, no han sido
observadas claramente.
31
El esquema de niveles de la figura 6.2 muestra una gran interconexión entre los estados observados,
con gran precisión en las energías de los mismos. Haciendo uso de la Tabla 6.1, hemos comprobado
un buen balance general de intensidades, dentro de las incertezas del experimento, entre
transiciones que pueblan y despueblan los diferentes estados. La única excepción corresponde al
estado ubicado a 6659.2 keV. Aquí, la intensidad entrante (relativa al rayo de 1021.0 keV) a través
de la transición de 366.1 keV es de 24/1000, mientras que la intensidad total de las transiciones
salientes (2919 keV y 796.5 keV) es de tan sólo 6/1000. Sin embargo, dada la gran fragmentación
de la intensidad que se observa en la despoblación de los estados próximos no es de descartar la
presencia de una o más transiciones no observadas.
Otro aspecto a discutir se relaciona con el estado de 3739.8 keV. Si calculamos la relación de
intensidades entre los rayos de 416.7 keV y 1478.3 keV, utilizando un espectro en coincidencias con
un rayo que se encuentre sobre este nivel, obtenemos el valor 1.78. Si en cambio la misma relación
es calculada a partir de un espectro en coincidencia con el rayo de 1021.0 keV, el valor que
obtenemos para la relación de intensidades es 2.51. Esta diferencia podría explicarse teniendo en
cuenta que los caminos de mayor multiplicidad se vieron favorecidos en este experimento. Esto se
debe a que la condición impuesta para la utilización de un evento fue la detección en coincidencia
de al menos tres detectores. De esta manera, también se podría entender por qué la transición de
1478.3 keV aparezca como menos intensa que las transiciones de 416.7 keV y 1061.7 keV.
En el esquema de niveles, indicamos con línea punteada y su energía entre paréntesis, el
estado de 6834 keV, porque no hemos podido determinar el orden de las transiciones de 1729 keV y
3094 keV, ya que no hay conexiones con otros estados y sus intensidades son muy similares. En
caso de no ser correcto el orden indicado, el estado correspondería a 5469 keV. La situación es un
poco diferente con el estado de 11149 keV ya que la transición de 501.1 keV es sensiblemente
menos intensa que la de 1915 keV.
Por otra parte, los valores de DCO calculados, nos han permitido realizar una asignación
consistente de momentos angulares a 23 de los 40 estados observados.
Si reescribimos el esquema de la figura 6.1, de modo tal de mantener solo aquellas transiciones que
han sido corroboradas por el experimento con EUROBALL, obtenemos el esquema de la figura 6.3.
Presentamos esta figura a fin de poner en evidencia el contraste con el esquema de niveles producto
de este trabajo presentado en la figura 6.2.
32
Figura 6.3: Parte del esquema publicado por Cameron et al. [Cam91]
que ha sido confirmado en el experimento con EUROBALL
6.4 Momentos angulares y estados Yrast
Para una visualización más clara de los valores de DCO, en la figura 6.4 los presentamos en función
de la energía.
Figura 6.4: Gráfico de los coeficientes de correlación angular (DCO)
en función de la energía de la transición para la cual fue estimado.
33
En esta figura indicamos además las rectas correspondientes a DCO = 0.6 y DCO = 1 por ser estos,
como señalamos en la sección 5.4, los valores teóricos correspondientes a transiciones dipolares
puras con ΔI=1, y transiciones cuadrupolares puras (ΔI=2) o dipolares puras sin cambio de
momento angular, respectivamente.
Es mediante esta información que concluimos que las transiciones de 1944.7 keV, 1478.3
keV, 1240.4 keV y 1021.9 keV (indicadas en rojo) que llevan al núcleo desde el estado de momento
angular y paridad 23/2- hasta el estado fundamental de paridad negativa 7/2-, (ver figura 6.2) son
cuadrupolares puras. Mientras que las transiciones de 954.9 keV y 1152.2 keV (indicadas en azul)
que llevan al núcleo desde el estado de momento angular y paridad 27/2- al estado 23/2-,
corresponden a transiciones con ΔI=1. Debido a la predominante intensidad de estos estados
podemos afirmar que son ellos los que conforman los estados Yrast del núcleo.
6.5 Estados de paridad positiva
En la figura 6.5 mostramos el espectro obtenido al tomar coincidencias con rayos de 634.0 keV y
701.4 keV.
Figura 6.5: Espectro en coincidencias con rayos  de 634.0 keV y 701.4 keV.
34
En este espectro observamos, entre otros, rayos que corresponden a transiciones entre estados de
paridad positiva junto a los principales rayos que vinculan a los estados de paridad negativa. Esto
indica la posición en el esquema de niveles de los estados desexcitados por las transiciones de 634.0
keV y 701.4 keV. Observamos además claramente, la transición de 90.4 keV que alimenta al estado
fundamental.
Cuando el núcleo se desexcita pasando por los estados de 8360.7 keV, 7726.7 keV y 7025.3
keV, emitiendo los rayos de 634.0 keV y 701.4 keV, puede luego tomar varios caminos. En términos
generales, hacia la izquierda del esquema pasando por estados de paridad negativa, o hacia la
derecha del esquema, pasando por estados de paridad positiva. En el primer caso, llegará al
fundamental pasando por los estados de 2261.4 keV y 1021 keV, emitiendo rayos de 1240.4 keV y
1021 keV, respectivamente. Por eso aparecen también en el espectro de la figura 5.1. Si en cambio
toma un camino de desexcitación hacia la derecha del esquema, pasará eventualmente por estados
tales como el 5862.6 keV, 4079.4 keV y 2739.5 keV, emitiendo rayos de 1783 keV y 1339.9 keV
que se observan en el espectro de la figura 6.5. Para estos últimos estados se destaca la gran
competencia entre la desexcitación hacia estados de paridad negativa, que son más Yrast, y hacia
estados de paridad positiva, que tienen mayor similitud en su estructura.
6.6 Transiciones débiles entre estados de bajo momento angular
En la figura 6.6 presentamos el espectro en coincidencia con rayos  de 90.4 keV y 1339.9 keV.
Figura 6.6: Espectro en coincidencia con rayos  de 90.4 keV y 1339.9 keV.
35
En esta figura hemos señalado (indicado su energía en forma horizontal), algunas de las transiciones
más débiles. La baja intensidad de las transiciones, observable en esta figura, es una importante
dificultad para la construcción del esquema de niveles. Sin embargo, los espectros que obtuvimos
muestran claramente las coincidencias gracias a la gran estadística del experimento y la calidad de
la reconstrucción de los eventos. La baja población de los estados de paridad positiva puede
entenderse en base a la reacción de fusión-evaporación usada, con un proyectil pesado de alta
energía, con lo cual se pueblan preferentemente los estados Yrast.
Para poder apreciar cada una de estas transiciones débilmente pobladas es necesario tomar espectros
en coincidencia con rayos cercanos a las mismas. A modo de ejemplo, presentamos en la figura 6.7
el espectro en coincidencia con rayos de 1137.8 keV y 1339.9 keV, donde se observa claramente la
transición de 461.9 keV, difícil distinguir en la figura 6.6.
Figura 6.7: Espectro en coincidencias con rayos  de 1137.8 keV y 1339.9 keV.
36
6.7 Transiciones de alta energía
En el esquema de la figura 6.2 encontramos 18 transiciones con energías mayores a los 2 MeV.
Como mencionamos en la sección 3.2, la detección de transiciones de alta energía se ve
dificultada por la disminución en la resolución y la eficiencia de detección.
En la figura 6.8 mostramos el espectro en coincidencia con rayos de 1240.4 keV y 873.7 keV, donde
se ven claramente 5 transiciones de alta energía. No observamos en este espectro la transición de
2919 keV por ser de muy baja intensidad (2/1000 relativa a la de 1021.0 keV).
Figura 6.8: Espectro en coincidencia con rayos  de 1240.4 keV y 873.7 keV.
No aparecen en este espectro, las transiciones entre estados de paridad positiva por debajo del
estado 2739.5 keV, lo cual es consistente con el esquema de niveles propuesto (figura 6.2).
Otro espectro en coincidencia que presenta un importante número de transiciones de alta
energía es el que se obtiene al imponer coincidencias con los rayos  de 416.7 keV y 1958.2 keV.
Presentamos este espectro en la figura 6.9.
Se observan claramente las transiciones de 2592 keV y 2878.2 keV por encontrarse
inmediatamente por encima y por debajo, respectivamente, de la transición de 1958.2 keV utilizada
en la construcción del espectro. También aparece con importante estadística el pico correspondiente
37
a la transición de 3094 keV, la cual, junto con la transición de 1729 keV, conectan los estados de
8563.1 keV y 3739.8 keV como presentamos en el esquema de la figura 6.2.
Figura 6.9: Espectro en coincidencia con rayos  de 416.7 keV y 1958.2 keV.
6.8 Terminación de banda
Como mencionamos en la sección 3.1, el momento angular esperado según el Modelo de Capas
Nuclear para el estado de terminación de banda, es 27/2 ћ. Por otra parte, de lo dicho en la sección
anterior, sabemos cuales son los estados de paridad negativa del núcleo, desde el fundamental 7/2 hasta el 27/2-. Observamos ahora de la figura 6.2 que la transición que llega desde el estado de
12600 keV al estado 27/2- es de una energía significativamente mayor a la de las transiciones que
conforman la banda Yrast (en realidad, es sensiblemente la mayor observada), a saber: 4808 keV.
Esto es un indicador de la terminación de banda, como mencionamos en la sección 3.1.
En la figura 6.10, aunque débilmente, puede observarse la transición de 4808 keV en el
espectro en coincidencia que obtuvimos al imponer sobre el cubo -- que dos de las tres
transiciones detectadas en coincidencias temporal sean las correspondientes a 1021.0 keV y 954.9
keV.
38
Figura 6.10: Espectro en coincidencias con rayos  de 1021.0 keV y 954.9 keV,
donde puede observarse la transición de 4808 keV.
6.9 Rotaciones en la línea Yrast
En la figura 6.11 graficamos el momento angular en función de la energía de transición para la línea
Yrast hasta el estado ubicado a 7791.6 keV. En este gráfico comparamos los valores experimentales
(en azul) con los obtenidos a partir de la fórmula rotacional (ver sección 2.2.1) con parámetros
extraídos a partir de los 2 primeros estados (en rojo). La última transición graficada en la curva
experimental no fue observada en el experimento sino que corresponde a la diferencia entre los
estados ubicados a 7791.6 y 5684.5 keV. Se procedió de esta manera con el fin de no tener en
cuenta los efectos de signatura.
39
Figura 6.11: Gráfico comparativo de los estados Yrast observados en el experimento (azul)
y los correspondientes al modelo rotacional (rojo).
Del gráfico puede observarse que sólo los primeros estados presentan un comportamiento rotacional
relativamente puro. En efecto, la diferencia de energías para las primeras 3 transiciones es similar,
produciéndose luego un gran aumento seguido de una importante disminución.
6.10 Nuevos estados observados
Entre los resultados más importantes de este experimento, relativos al 49V, se encuentran los 22
nuevos estados observados que presentamos en la tabla 6.12
Hemos indicado entre paréntesis, aquellos valores de energía que no han sido observados
claramente y los valores de momento angular sugeridos por consideraciones relativas a la estructura
del esquema pero que no han sido corroborados con valores de DCO.
En particular, el estado de 4395.2 keV asignado como 19/2-, es avalado por tres transiciones
que llegan: 1132.9 keV o parten: 655.4 keV y 1072.2 keV de él (ver figura 6.2). Este estado fue
sugerido a partir de cálculos teóricos basados en el Modelo de Capas Nuclear [Bra05].
40
Tabla 6.2: Energía y momentos angulares tentativos, de los 22 nuevos estados encontrados, junto al
número de transiciones que llegan o parten de cada uno de ellos.
Energía
[keV]
3577
4079.4
4395.2
(5272)
5852.3
5862.6
6461.5
6659.2
(6834)
7025.3
7580.6
7726.7
8360.7
8563.1
9234.4
9414
10000
10521.5
11149
11649.3
12600
13114
Momento
Angular
(13/2+)
(15/2+)
19/2(17/2+)
21/2(19/2+)
23/2-
25/2-
(29/2-)
27/2-
# de
transiciones
2
4
3
1
4
5
6
3
2
7
5
5
4
4
4
1
1
4
2
2
1
1
Los estados de energía 5852.3 keV y 6461.5 keV, asignados como 21/2- y 23/2- respectivamente y
avalados por 7 transiciones observadas por primera vez en este experimento, son también un desafío
para el Modelo de Capas Nuclear que, como veremos en el capítulo 7, supera exitosamente.
41
42
Capítulo 7
Cálculos teóricos
7.1 Uso del código Antoine
Para realizar los cálculos teóricos mediante el Modelo de Capas Nuclear, utilizamos el código
Antoine que hemos mencionado en la sección 2.3.
En acuerdo con lo dicho en la sección 3.3, para el cálculo de los estados de paridad negativa
consideramos un carozo formado por 20 protones y 20 neutrones y un espacio de valencia
determinado por las cuatro capas fp. Las dos interacciones efectivas que mejor describen esta zona
de masa A50 son la KB3G [Pov01] y la GXPF1A [Hon05], como hemos comentado en la sección
2.3. En el caso particular del
49
V, la GXPF1A reproduce con mejor precisión los datos
experimentales.
Para el cálculo de los estados de paridad positiva, debió redefinirse el espacio de valencia,
considerándose uno que incluya, además, las capas sd. En este caso se utilizó la interacción SDFP
[Pov98].
Para que el cálculo resulte factible y que el número de configuraciones posibles del núcleo
no sea extremadamente grande, el código permite asignar a cada capa del espacio de valencia una
importancia, de modo tal de limitar el acceso de los nucleones y, al mismo tiempo, el número de
configuraciones posibles del núcleo. Es así que, eligiendo adecuadamente la importancia de cada
capa, puede cerrarse completa o parcialmente una de ellas o bien dejar sin límites el paso de
nucleones de una a otra. (Para una descripción más detallada ver Apéndice 1).
43
7.2 Comparación de resultados teóricos y experimentales
En la figura 7.1 mostramos una comparación entre los valores experimentales (azul) y teóricos
(rojo) obtenidos con la interacción efectiva GXPF1A para los estados de paridad negativa:
Figura 7.1: Comparación de valores de energía experimentales (azul)
y teóricos (rojo) de los estados de paridad negativa.
La primera columna en azul, corresponde a los estados Yrast de paridad negativa. Podemos
observar como en todos los casos, la columna en rojo correspondiente a los cálculos teóricos
reproduce con muy buena precisión los valores experimentales. El mayor apartamiento lo
observamos para el estado 19/2-, alcanzando los 141 keV.
En la segunda columna azul, observamos un segundo estado 19/2- a una energía de 4395
keV, el mismo es predicho por el Modelo de Capas Nuclear con una energía de 4405 keV, a tan sólo
10 keV de diferencia. La presencia de esta predicción del modelo ya había sido notada previamente
por Brandolini et al. [Bra05] pero el estado no había sido observado.
A continuación, resumimos en la figura 7.2, los valores de energía teóricos obtenidos para
cuatro de los estados de paridad negativa establecidos por primera vez en este experimento. (Ver
tabla 6.2)
44
Figura 7.2: Comparación de valores de energía experimentales (azul) y teóricos (rojo) de cuatro de
los estados de paridad negativa observados por primera vez en este experimento.
En la figura 7.3, presentamos la comparación entre los valores experimentales (azul) y teóricos
(rojo) obtenidos con la interacción SDFP correspondiente a los estados de paridad positiva. El
esquema central es obtenido permitiendo la excitación de un nucleón desde el orbital d3/2 a las capas
fp, mientras que en el esquema de la derecha, la excitación permitida es desde la d3/2 o la s1/2.
Figura 7.3: Comparación de valores de energía experimentales (azul a la izquierda) y teóricos de los
estados de paridad positiva permitiendo excitaciones desde la capa d3/2 (rojo central) y desde la d3/2
y s1/2 (rojo a la derecha).
45
7.3 Interpretación de los resultados obtenidos
El momento angular del estado fundamental, 7/2 ћ, y su cercanía con el estado de momento angular
5/2 ћ es interpretado en términos del modelo de Nilsson como índice de una discreta deformación
del núcleo. De la figura 7.1 observamos que el núcleo presenta una separación de las dos signaturas,
la cual probablemente se encuentre relacionada con efectos de triaxialidad.
En la figura 7.2, hemos asignado el valor de momento angular 29/2 ћ y paridad negativa, al
estado de 10 MeV. Las razones para ello provienen esencialmente de los cálculos teóricos ya que no
nos fue posible determinar el DCO de la transición debido a la baja intensidad de la transición de
3163 keV (razón por la cual su momento angular fue indicado entre paréntesis). Además de la
energía de excitación, también el modo de decaimiento observado está de acuerdo con los cálculos
teóricos que indican un valor de B(M1) casi nulo y un valor de B(E2), que si bien es chico, dado el
gran salto de energía, resulta en una probabilidad significativa de decaer al 25/2-.
Para los estados de paridad positiva, los cálculos permiten la excitación de una sola partícula
(protón o neutrón) desde las capas sd. En la figura 7.3, observamos que al realizar los cálculos
dejando abierta sólo la capa d3/2 (rojo central), la diferencia de energía entre estados es mayor que la
experimental, es decir, la predicción es menos colectiva que el experimento. Sin embargo, si
permitimos que una partícula se excite tanto desde la d3/2 como de la s1/2, la predicción resulta en
mejor concordancia con los valores experimentales (rojo a la derecha).
Para un análisis más detallado de la función de onda, podemos calcular los números de
ocupación de las capas involucradas y la probabilidad de cada configuración utilizando el código
Antoine.
De los cálculos de los números de ocupación para estados de paridad positiva (Tabla 7.1)
observamos como los mismos se forman a partir de la excitación de un protón desde la d3/2 a la fp, y
no sólo a la f7/2 aunque esta es dominante.
Si bien el número de ocupación de la s1/2 es chico, mostrando que el rol de esta capa es
mucho menor que el de la d3/2, es suficiente para hacer más colectiva la función de onda y por lo
tanto más ligada, como hemos observado experimentalmente. En efecto, la banda de paridad
positiva presenta una estructura mucho más regular que la de paridad negativa, con valores de
B(E2) que indican una deformación mayor. Esto puede entonces ser interpretado como una
coexistencia de forma.
46
Tabla 7.1: Números de ocupación para el estado de momento angular 11/2 ћ y paridad positiva
1d5/2 2s1/2 1d3/2 1f7/2 2p3/2 1f5/2 2p1/2 1d5/2 2s1/2 1d3/2 1f7/2 2p3/2 1f5/2 2p1/2
Neutrones
Probabilidad
Protones
%
6
2
4
6
0
0
0
6
2
3
4
0
0
0
27,50%
6
2
4
6
0
0
0
6
2
3
3
1
0
0
5,61%
6
2
4
6
0
0
0
6
2
3
3
0
1
0
1,66%
6
2
4
6
0
0
0
6
1
4
4
0
0
0
2,38%
6
2
4
5
1
0
0
6
2
3
4
0
0
0
8,69%
6
2
4
5
1
0
0
6
2
3
3
1
0
0
3,25%
6
2
4
5
1
0
0
6
1
4
4
0
0
0
1,45%
6
2
4
5
0
1
0
6
2
3
4
0
0
0
3,19%
6
2
4
5
0
1
0
6
2
3
3
0
1
0
1,70%
6
2
4
4
2
0
0
6
2
3
4
0
0
0
3,06%
6
2
4
4
2
0
0
6
2
3
3
1
0
0
1,23%
6
2
4
4
1
1
0
6
2
3
4
0
0
0
1,77%
6
2
4
4
0
2
0
6
2
3
4
0
0
0
2,16%
El momento angular de los estados reportados en la figura 7.3 (13/2+, 15/2+ y 17/2+) están indicados
entre paréntesis, ya que no nos fue posible determinarlos experimentalmente. La asignación se basa
en la información provista por cálculos teóricos, ya que de los mismos se obtienen valores de B(E2)
muy grandes y B(M1) muy chicos. Esto sugiere transiciones cuadrupolares con ΔI=2.
47
48
Capítulo 8
Conclusiones
Hemos estudiado los estados de alto momento angular del 49V en base a los datos provistos por un
experimento llevado a cabo en Estrasburgo, Francia. El mismo consistió en una reacción de fusiónevaporación
28
Si(28Si,xpynzα)49V a una energía del haz de 117 MeV. El haz fue provisto por el
acelerador Vivitron del Instituto de Investigaciones Subatómicas (IReS).
Se utilizó el sistema multidetector EUROBALL IV para la detección de radiaciones  al que
se le acopló un Filtro de Núcleos en Retroceso (RFD).
Valiéndonos de cubos simétricos --, matrices simétricas -, sus proyecciones y espectros
en coincidencia, construimos un nuevo esquema de niveles para el núcleo, con la asignación de
intensidades correspondientes a cada transición. Realizamos cálculos de coeficientes de correlación
angular utilizando matrices asimétricas - y establecimos valores de momento angular para
numerosos estados del núcleo. Confirmamos parte del esquema de niveles preexistente y lo
extendimos de manera considerable. Varios de los nuevos estados que encontramos, habían sido
predichos por el Modelo de Capas Nuclear.
Hemos llevado a cabo además, cálculos teóricos basados en el Modelo de Capas Nuclear
utilizando el código Antoine y los comparamos con los resultados experimentales con el fin de
interpretarlos.
49
Las conclusiones más relevantes que se derivan de nuestro trabajo son:
 El nuevo esquema de niveles cuenta con 83 transiciones  de las cuales 52 han sido
observadas por primera vez en este experimento. Hemos encontrado 22 nuevos estados,
totalizando 40 estados en todo el esquema, el cual se extiende hasta el nivel de 13114 keV.
 De las 46 transiciones y 20 estados del 49V reportados en trabajos anteriores, 15 transiciones
y 2 estados no han sido confirmados en el presente trabajo.
 Hemos determinado la intensidad de las 83 transiciones observadas y asignado, mediante el
cálculo de correlaciones angulares y relaciones de coincidencia, el valor de momento
angular correspondiente a 23 de los 40 estados presentes. Otras 4 asignaciones se basaron en
cálculos teóricos.
 Hemos observado la terminación de banda en el estado 27/2-, de acuerdo a lo predicho por
cálculos teóricos.
 Mediante cálculos teóricos utilizando el código Antoine, reprodujimos con excelente
aproximación los valores experimentales de energía y momento angular de todos los estados
Yrast de paridad negativa.
 Cuatro de los estados de paridad negativa encontrados fuera de la banda Yrast por primera
vez en este experimento, han sido reproducidos mediante el código Antoine.
 Los cálculos teóricos para los estados de paridad positiva, recuperan la estructura del
espaciamiento de niveles observados experimentalmente y corroboramos que las
predicciones se vuelven más colectivas y consecuentemente concordantes con los valores
experimentales, conforme se incrementa la libertad de los nucleones en la banda de valencia.
 A partir de los valores de B(E2) y B(M1) calculados con Antoine, fue posible asignar
tentativamente el momento angular y la paridad de varios estados para los que no fue
posible una asignación basada en datos experimentales.
 Como tarea futura quedaría el estudio de las polarizaciones a partir de los detectores de tipo
Clover. Este análisis hará un significativo aporte a la determinación de las multipolaridades
de las transiciones.
50
Apéndice
Archivos de entrada del código Antoine
Para conocer los valores de energía de los estados de paridad negativa construimos el archivo de
entrada que presentamos en la figura 9.1.
La primera línea de cada bloque indica el tipo de cálculo que se le solicita al código, siendo
4 0 0 la opción correspondiente al cálculo de energías y 12 0 0 la correspondiente al cálculo de
momentos cuadrupolares. La segunda línea de cada bloque asigna un número al archivo de trabajo
del código, 50 en este caso, y la cantidad de estados de distinto momento angular requeridos, 8 en el
primer bloque y 5 en el segundo.
Figura 9.1: Archivo de entrada del código Antoine para estados de paridad negativa
51
Como tercera y cuarta línea, en todos los bloques hemos indicamos:
6 4 307 1103 305 1101 0 0 0 0
0
3 4 307 1103 305 1101 0 0 0 0
0
El 6 de la primera línea indica el número de neutrones fuera de capa cerrada y el 3 con que
comienza la segunda, el de protones. El 4 siguiente, refiere a la cantidad de capas que se
considerarán como espacio de valencia. Indicamos las mismas a continuación usando la siguiente
nomenclatura:
307 → 1f7/2; 1103 → 2p3/2; 305 → 1f5/2 y 1101 → 2p1/2
Las líneas terminan con la posibilidad de dar diferente importancia a cada capa; en este archivo de
entrada no usamos esta posibilidad asignando un 0 a todas ellas. La línea siguiente, es en todos los
bloques 5 1 0, indicado con el 5 que 5/2 es el estado de menor momento angular y el 1 que la
paridad del mismo es negativa.
En los primeros dos bloques, la línea 65 0, refiere a la interacción efectiva que el código
utilizará. Un archivo externo al código, asigna números a las interacciones disponibles. En este
caso, la interacción 65 refiere a la GPXF1A mencionada en la sección 2.3.
En la línea siguiente, enumeramos los diferentes estados de momento angular de los que
queremos conocer su energía, indicando en la línea a continuación, la cantidad de estados de cada
momento angular que deben considerarse.
Por último, en los primeros dos bloques, ingresamos el número de iteraciones, 100 en este
ejemplo, que el código debe realizar seguido de la cota de convergencia, 0.005, pretendida.
La última línea de los dos últimos bloques lleva información sobre la carga efectiva de
neutrones y protones necesaria para el cálculo de las probabilidades del momento del cuadrupolo y
las probabilidades de transición cuadrupolar y los factores giromagnéticos para el cálculos de las
B(M1) y los momentos magnéticos.
En la figura 9.2 presentamos parte de un archivo de entrada utilizado para el cálculo de los
estados de paridad positiva.
52
Figura 9.2: Parte del archivo de entrada del código Antoine utilizado para el cálculo de la
energía de los estados de paridad positiva desde el 3/2 al 17/2
Tanto la primera como la segunda línea, tienen la misma interpretación que antes, las diferencias
aparecen básicamente en la tercera y cuarta línea. Es en estas dos, como dijimos más arriba, donde
indicamos al código la cantidad de neutrones (18) y protones (15) fuera de capa cerrada, es decir, en
el espacio de valencia. Luego, definimos 7 capas, donde las últimas 4 coinciden con las indicadas
en el caso de paridad negativa, pero ahora consideraremos además, las capas sd, a saber:
205 → 1d5/2; 1001 → 2s1/2 y 203 → 1d3/2
A diferencia del archivo de entrada presentado en al figura 9.1, en éste sí asignamos una
importancia a cada capa, en otras palabras, establecimos cierta dificultad de los nucleones para
acceder a ellas: 0 0 6 8 8 8 8 respectivamente.
El 14 al final de la línea indica la cantidad de “saltos” totales que cada tipo de nucleón puede
dar para pasar de una capa a otra. Por ejemplo, para pasar de la 1d5/2 a la 2s1/2 no requiere dar
ningún “salto” porque ambas tienen importancia 0, pero para pasar de la 1d5/2 a la 1d3/2 un salto de
“orden” 6 es necesario. El número máximo de saltos permitidos para protones más neutrones está
dado por el número 2 en la quinta línea del archivo. Esto permite truncar el cálculo. En el presente
caso sólo un salto de dos unidades para una partícula o de 1 unidad para dos partículas es permitido,
lo que se traduce en la posibilidad de excitar una partícula por vez desde la capa d3/2 a las capas fp.
53
54
Referencias
[Ago03] S. Agostinelli et al., Nucl. Inst. and Meth. A 506, 250 (2003)
[Axi07] M. Axiotis, S. M. Lenzi, et al., Phys. Rev. C 76, 014303 (2007)
[Bla73] P. Blasé, R. B. Huber, W. Kutschera, and C. Signorini, Proceedings of the International
Conference on Nuclear Physics, Munich, Vol. 1, p. 211 (1973)
[Bra05] F. Brandolini and C. A. Ur., Phys. Rev. C 71, 054316 (2005)
[Cam91] Cameron et al., Physical Review C Vol. 44 Number 5 (1991)
[Cau94] E. Caurier et al., Phys. Rev. C 50, 225 (1994)
[Cau99] E. Caurier, F. Nowacki, Acta Physica Polonica 30 – 705 (1999)
[Cau04] E. Caurier, shell model code ANTOINE, IReS, Strasbourg (1989-2004)
[Cau05] E. Caurier et al., Rev. Mod. Phys. 77, 427 (2005)
[EHP] Página Web de Euroball: http://npg.dl.ac.uk/euroball-home/
[For78] G. Fortuna, S. Lunardi, M. Morando, and C. Signorini, Nucl. Phys. A 299, 479 (1978)
[Fra94] S. Frauendorf et al., Phys. Rev. C 50, 196 (1994)
[Gav80] A. Gavron. Phys. Rev. C 21, 230 (1980)
[Haa75] B. Haas et al., Phys. Rev. C 11, 1179 (1975)
[Hon02] M. Honma et al., Eur. Phys. J. A 25, 499-502 (2005)
[Hon05] M. Honma et al., Phys. Rev. C 65 061301® (2002)
[Kha86] M. Khaliquazzaman et al., Can. J. Phys. 64, 219 (1986)
[Lac01] M. Lach et al., Eur. Phys. L. A 12, 381-382 (2001)
[Len96] S. M. Lenzi et al., Z. Phys. A 354, 117 (1996)
[Len97] S. M. Lenzi et al., Phys. Rev. C 56, 1313 (1997)
[Mar96] G. Martínez-Pinedo et al., Phys. Rev. C54, R2150 (1996)
[Mec07] W. Meczynski et. al., Nucl. Inst. and Meth. A 580, 1310-1326 (2007)
[Moo83] R. B. Mooy and P. M. W. Glaudemans, Z. Phys. 312, 59 (1983)
[Pov83] A. Poves and A. Zuker, Phys. Rep. 70, 235 (1981)
[Pov98] A. Poves and J. Sánchez Solano, Phys. Rev. C 58, 179 (1998)
[Pov01] A. Poves et al., Nucl. Phys. A 694, 157 (2001)
[Rin80] Peter Ring, Peter Schuck, “The nuclear many-body problem” Springer-Verlag, 1980, Cap. 2
[She90] J.A. Sheikh et al., Phys. Lett. B 240, 11 (1990)
[Saw73] Z. P. Sawa et al., Nucl. Phys. A 205, 257 (1973)
55