Tema 8

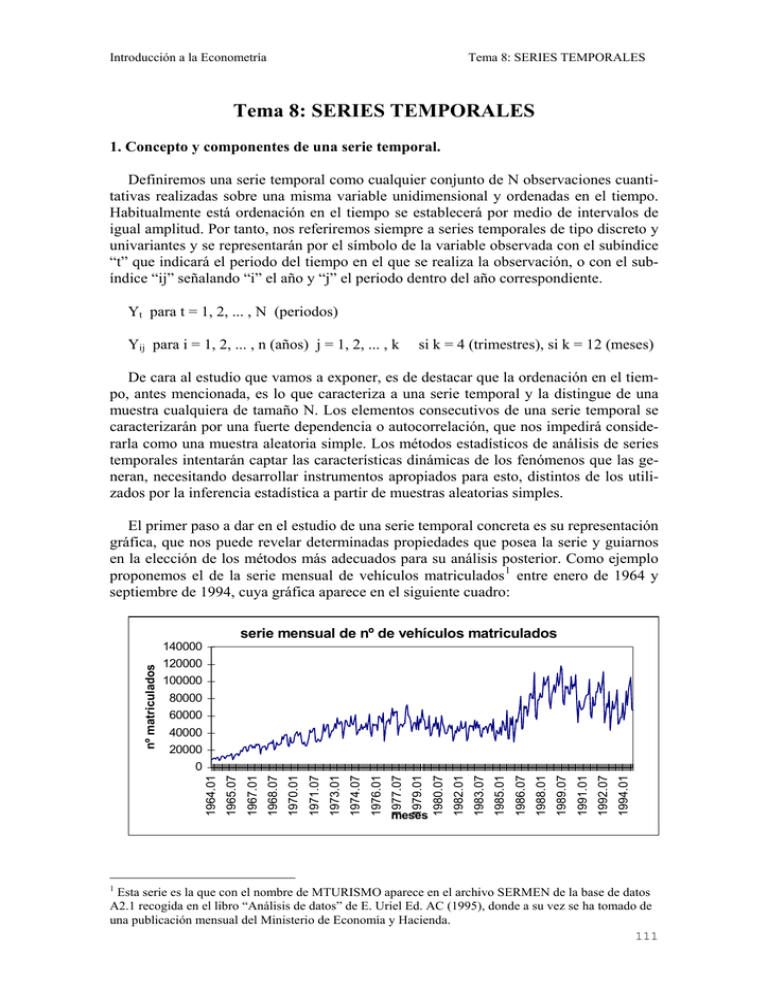
Introducción a la Econometría
Tema 8: SERIES TEMPORALES
Tema 8: SERIES TEMPORALES
1. Concepto y componentes de una serie temporal.
Definiremos una serie temporal como cualquier conjunto de N observaciones cuantitativas realizadas sobre una misma variable unidimensional y ordenadas en el tiempo.
Habitualmente está ordenación en el tiempo se establecerá por medio de intervalos de
igual amplitud. Por tanto, nos referiremos siempre a series temporales de tipo discreto y
univariantes y se representarán por el símbolo de la variable observada con el subíndice
“t” que indicará el periodo del tiempo en el que se realiza la observación, o con el subíndice “ij” señalando “i” el año y “j” el periodo dentro del año correspondiente.
Yt para t = 1, 2, ... , N (periodos)
Yij para i = 1, 2, ... , n (años) j = 1, 2, ... , k
si k = 4 (trimestres), si k = 12 (meses)
De cara al estudio que vamos a exponer, es de destacar que la ordenación en el tiempo, antes mencionada, es lo que caracteriza a una serie temporal y la distingue de una
muestra cualquiera de tamaño N. Los elementos consecutivos de una serie temporal se
caracterizarán por una fuerte dependencia o autocorrelación, que nos impedirá considerarla como una muestra aleatoria simple. Los métodos estadísticos de análisis de series
temporales intentarán captar las características dinámicas de los fenómenos que las generan, necesitando desarrollar instrumentos apropiados para esto, distintos de los utilizados por la inferencia estadística a partir de muestras aleatorias simples.
El primer paso a dar en el estudio de una serie temporal concreta es su representación
gráfica, que nos puede revelar determinadas propiedades que posea la serie y guiarnos
en la elección de los métodos más adecuados para su análisis posterior. Como ejemplo
proponemos el de la serie mensual de vehículos matriculados 1 entre enero de 1964 y
septiembre de 1994, cuya gráfica aparece en el siguiente cuadro:
serie mensual de nº de vehículos matriculados
nº matriculados
140000
120000
100000
80000
60000
40000
20000
1
1994.01
1992.07
1991.01
1989.07
1988.01
1986.07
1985.01
1983.07
1982.01
meses
1980.07
1979.01
1977.07
1976.01
1974.07
1973.01
1971.07
1970.01
1968.07
1967.01
1965.07
1964.01
0
Esta serie es la que con el nombre de MTURISMO aparece en el archivo SERMEN de la base de datos
A2.1 recogida en el libro “Análisis de datos” de E. Uriel Ed. AC (1995), donde a su vez se ha tomado de
una publicación mensual del Ministerio de Economía y Hacienda.
111
Departamento de Estadística e Investigación Operativa II (Métodos de Decisión)
A la vista de esta representación gráfica podemos exponer las principales características de una serie temporal.
Componentes de una serie temporal
Tradicionalmente se ha supuesto que en la formación y determinación de los sucesivos valores observados de una serie ha podido influir cuatro clases de movimientos o
variaciones que reciben el nombre de “componentes no observadas” de la serie, y son:
- Tendencia: Movimiento a largo plazo que señala la evolución general del conjunto
de datos que forman la serie temporal. En la gráfica que nos sirve de ejemplo se puede observar una tendencia creciente del número de automóviles matriculados, debido, principalmente, al crecimiento general de la economía. La representaremos por Tt
ó Tij.
- Ciclo o variación cíclica: Es la componente que capta, si existen, ciertas oscilaciones periódicas, normalmente a medio plazo, sobre la tendencia. A veces, debido a la
amplitud del ciclo o a la poca duración de la serie, es difícil distinguirlo de la tendencia. En la series económicas se supone que recoge las variaciones provocadas por las
sucesivas situaciones de prosperidad o de crisis. En el ejemplo de la serie de matriculaciones se puede observar un primer ciclo, más amplio, desde el inicio en 1964 hasta
1986 con un máximo en 1978, y otro ciclo, más corto, desde 1986 hasta 1993 con un
máximo en 1989. Se representará por Ct ó por Cij .
- Componente estacional o variación estacional: En ella se recogen las variaciones a
corto plazo que, habitualmente, con periodo anual se producen en una serie temporal,
detectándose un comportamiento casi homogéneo de los datos dentro de cada año o
periodo que se considere. En las series económicas las causas de estas variaciones
pueden ser: cambios climáticos, vacaciones, otras costumbres sociales, etc... . En el
ejemplo se puede observar que, en cada año, se inicia con el menor valor, adquiriendo las cifras más altas, relativamente, en los meses de julio y diciembre. La representaremos por St ó por Sij .
- Componente errática o término de error: Recoge todo aquello no explicado por
las anteriores componentes sistemáticas. Se puede representar por una variable aleatoria con media nula, varianza constante y sin autocorrelación. Su símbolo será rt ó rij
.
Las tres primeras componentes tratan de captar movimientos regulares y sistemáticos
que se producen en la evolución de la serie temporal, así que el objeto de su estudio será
la búsqueda de determinadas funciones analíticas, índices u otras formas definidas que
puedan representar a cada componente. Mientras que sobre el término de error se harán
diversas hipótesis acerca de su comportamiento aleatorio.
Los métodos de análisis de series temporales a través de sus componentes se empezaron a desarrollar a partir de 1920 y consideran que los valores observados de la variable se forman por la intervención de los cuatro componentes. Es decir
Yt = F(Tt , Ct , St , rt )
112
Introducción a la Econometría
Tema 8: SERIES TEMPORALES
Estas componentes podrán intervenir bajo uno de los siguientes esquemas, generalmente aceptados:
- Esquema aditivo: Yt = Tt + Ct + St + rt
- Esquema multiplicativo: Yt = Tt · Ct · St · rt
- Esquema mixto: Yt = Tt · Ct · St + rt
Cualquier método de descomposición de una serie temporal tratará de aislar e identificar a sus componentes y deberá advertir previamente bajo que supuesto de esquema de
intervención trabaja. En un esquema multiplicativo o mixto las componentes sistemáticas actúan como factores influyendo el nivel alcanzado por una sobre el alcance de las
otras, de tal forma que bajo este esquema las correcciones de los efectos de las componentes se deberán hacer por cociente. Mientras que bajo un esquema aditivo, en el que
no se producen esas interacciones, la serie temporal se ajustará, en sus componentes,
por diferencias. Nótese que de un esquema multiplicativo se podrá pasar a un esquema
aditivo por medio de una transformación logarítmica de la siguiente forma:
Yt = Tt · Ct · St · rt ⇒ LogYt = LogTt + LogCt + LogSt + Logrt
Con el objeto de mejorar nuestro conocimiento sobre las características de una serie
temporal, o con ciertos fines específicos, se suelen aplicar sobre los valores originales
de la serie ciertas transformaciones matemáticas. Las más importantes son:
- transformación diferencia: ΔYt = Yt - Yt-1 . La serie resultante representará a las variaciones periódicas experimentadas por la variable. Se suele aplicar para eliminar
efectos de una fuerte tendencia. Si los valores que entran en la diferencia no son consecutivos, tendremos: ΔhYt = Yt - Yt-h .
- transformación logarítmica: LogYt . Se aplican logaritmos neperianos a los datos
originales. Se suele utilizar para reducir una creciente variabilidad de los valores respecto a su nivel medio (heterocedasticidad).
- transformación conjunta: ΔLogYt = LogYt - LogYt-1 . Acumula los dos efectos anteriores y su resultado tiene la virtud de ser la aproximación lineal de la tasa de variación:
Y - Yt -1
Y
Y
ΔLogYt = LogYt - LogYt -1 = Log t ≅ t - 1 = t
Yt -1
Yt -1 Yt -1
En muchos casos se utiliza esta transformación para obtener una serie de características estacionarias, sin tendencia creciente o decreciente y sin alteraciones en la dispersión de los valores respecto a su nivel medio (homocedasticidad).
En lo que sigue vamos a trabajar con series en las que no es posible distinguir el ciclo de la tendencia y, por tanto, expondremos únicamente métodos de análisis de la tendencia y de la variación estacional.
113
Departamento de Estadística e Investigación Operativa II (Métodos de Decisión)
2. Estudio de la tendencia.
Supondremos que no existe estacionalidad (por ejemplo, una serie anual) o que ha
sido eliminada y, por tanto, la serie con la que trabajamos está desestacionalizada. Los
dos esquemas posibles son:
- Esquema aditivo o mixto: Yt = Tt + rt
- Esquema multiplicativo: Yt = Tt · rt
Expondremos dos métodos, el de ajuste de una función del tiempo y el que utiliza las
denominadas medias móviles.
Ajuste de una función del tiempo
En este método se identifica la tendencia con una función del tiempo determinada en
la forma pero con parámetros desconocidos que hay que estimar, siendo el procedimiento de los mínimos cuadrados el más utilizado.
La elección de la forma se hará a partir de la gráfica de la serie, estudiando que tipo
de función se ajusta mejor al desarrollo descrito en ella, o a partir de la verificación de
determinados supuestos de crecimiento y evolución de los datos. Únicamente estudiaremos los dos casos más simples, el de tendencia lineal y el de tendencia exponencial.
Tendencia lineal: Tt = β1 + β2·t
En este caso se supone que el crecimiento o decrecimiento de los datos de la serie se
produce con una variación constante. Esto se puede comprobar obteniendo la serie
transformada ΔYt = Yt - Yt-1 , de primeras diferencias, y verificar que el resultado es una
serie estacionaria con valores muy parecidos unos a otros. Si es así, el esquema adecuado sería el aditivo, quedando:
Yt = β1 + β2·t + rt , con t = 1, 2, ... , N
Que supone un modelo de regresión lineal simple donde la variable exógena es el
tiempo y los parámetros se estimarán por M.C.O. resultando:
⎫
⋅ t = b1 ⎪
S
⎪
*
⎬ ⇒ Tt = b1 + b2·t
S
ty
β 2∗ = 2 = b 2 ⎪
⎪⎭
St
β 1∗ = Y −
S ty
2
t
El coeficiente de determinación, R2, nos servirá como medida de la bondad de ajuste
de la tendencia estimada a la evolución temporal de los datos de la serie. En este caso se
podrá calcular de la siguiente forma:
R2 =
114
S 2tY
S 2t ⋅ S 2Y
Introducción a la Econometría
Tema 8: SERIES TEMPORALES
Tendencia exponencial: T t = e
β1 + β 2 ⋅ t
El supuesto, en este caso, es que los datos evolucionan a una tasa de variación constante. Esto se podrá confirmar obteniendo la serie transformada ΔLogYt , que como ya
vimos supone una aproximación lineal de la tasa de variación, y verificar, como en el
caso anterior, que el resultado es una serie estacionaria con valores casi constantes. Si
comprobamos esto, el esquema más apropiado sería el multiplicativo, quedando:
Y t = e β 1 + β 2 ⋅t ⋅ e u t , para t = 1, ... , N donde ut ∼ N[ 0 ; σ2 ] e independientes
Tomando logaritmos neperianos se obtiene el correspondiente modelo de regresión
lineal simple que se podrá estimar por M.C.O.:
LogYt = β1 + β2·t + ut , con t = 1, 2, ... , N
Resultando:
S
⎫
⋅ t = b1 ⎪
β 1∗ = LY − t LY
2
S 2tLY
St
⎪
2
⎬ con R = 2 2
S
S t ⋅ S LY
⎪
=
β 2∗ = t LY
b
2
2
⎪⎭
St
*
y Tt = e
b1 + b 2 ⋅ t
Medias Móviles
El objetivo de la utilización de medias móviles es el alisado o suavizado de la serie.
La obtención de las medias móviles supone el cálculo de medias aritméticas consecutivas, utilizando los datos sucesivos de la serie temporal, todas con el mismo número de
datos pero retirando el primero de la media anterior e incorporando el dato siguiente. El
número de datos que entran en el cálculo de cada media se denomina longitud o tamaño
de las medias móviles y para su elaboración distinguiremos medias móviles de longitud
impar de las de longitud par.
Cuando la longitud de las medias móviles es impar (l = 2h+1) su valor se asigna al
momento de tiempo central “t”, siendo el primer dato el situado en “t-h” y el último el
que corresponde al instante “t+h”, y se dice que la serie de medias móviles está centrada. Veamos, como ejemplo, las fórmulas de cálculo de las tres primeras medias móviles
de longitud 3 (2h+1=3 ⇒ h=1) de una serie cualquiera:
t
1
Yt
Y1
2
Y2
3
Y3
4
5
Y4
Y5
medias móviles
(se pierde)
Y1 + Y2 + Y3
Y2 (3) =
3
Y 2 + Y 3 + Y4
Y3 (3) =
3
Y3 + Y4 + Y5
Y4 (3) =
3
y así sucesivamente ...
115
Departamento de Estadística e Investigación Operativa II (Métodos de Decisión)
Se observa que la serie de medias móviles no se inicia en el primer periodo sino que
se pierde un periodo al principio y se perderá otro al final, pero sus valores resultan directamente situados en los periodos centrales de cálculo (2, 3, 4, ... ). Una expresión general de una media móvil de longitud impar sería la siguiente:
Yt (2h + 1) =
Yt - h + Yt - h + 1 + ... + Yt + Yt + 1 + ... + Yt + h
2h + 1
para t = h+1, h+2, ... , N-h
Donde se observa que no se obtienen datos para los “h” primeros periodos y para los
“h” últimos, perdiéndose en total 2h datos. El resultado será una nueva serie de “N-2h”
valores más suave que la original y, por tanto, más representativa de la tendencia general de los datos al haberse suprimido las alteraciones y variaciones más importantes.
Si la longitud fuese par (l = 2h) los valores de las medias móviles no quedan directamente centrados, dado que no existe periodo central, sino que quedarán situados entre
dos periodos. Para centrar la serie de medias móviles se deberá proceder a un nuevo cálculo de medias móviles de longitud “2” y estos nuevos valores si que resultarían centrados en los periodos de observación de la serie. Lo vemos primero con un ejemplo que
utiliza las primeras observaciones de una serie temporal cualquiera para el cálculo de
medias móviles de longitud 4.
t
1
2
Yt
Y1
Y2
Y2,5 (4) =
(2,5)
3
medias móviles centradas
(se pierde)
(se pierde)
Y1 + Y2 + Y3 + Y4
4
1
1
⋅ Y1 + Y2 + Y3 + Y4 + ⋅ Y5
2
Y3 (4x2) = 2
4
Y3
Y3,5 (4) =
(3,5)
4
5
medias móviles simples
Y2 + Y3 + Y4 + Y5
4
Y4
Y5
y así sucesivamente ...
A la expresión utilizada de la media móvil centrada se llega de la siguiente forma:
Y1 + Y 2 + Y 3 + Y 4 Y 2 + Y 3 + Y 4 + Y 5
+
4
4
=
2
1
1
⋅ Y 1 + Y 2 + Y 3 + Y4 + ⋅ Y5
Y1 + 2Y2 + 2Y3 + 2Y4 + Y5 2
2
=
=
4
8
Y2,5 (4) + Y3,5 (4)
=
Y3 (4x2) =
2
116
Introducción a la Econometría
Tema 8: SERIES TEMPORALES
Siendo, por tanto, la expresión general de una media móvil centrada de longitud par,
igual a 2h, la siguiente:
1
1
⋅ Yt - h + Yt - h + 1 + ... + Yt + Yt + 1 + ... + ⋅ Yt + h
2
Yt (2hx2) = 2
2h
para t = h+1, h+2, ... , N-h
Como en el caso anterior se observa que se han perdido “2h” periodos (los “h” primeros y los “h” últimos) y que el resultado es un conjunto de “N-2h” valores que constituye una serie más alisada que la original y susceptible de representar a la tendencia de
la misma.
La longitud ( l = 2h+1 ó l = 2h) de las medias móviles se deberá corresponder con el
número de periodos que forme el intervalo de tiempo que incluye al conjunto de oscilaciones y variaciones que reiteradamente se repite a lo largo de la serie.
En el siguiente gráfico aparece, junto a la serie original de datos mensuales correspondiente al ejemplo propuesto de vehículos matriculados entre 1964 y 1994, una línea
en tono más claro que representa a la serie de medias móviles centradas de longitud
igual a 12 meses. Obsérvese como esta última línea atenúa bastante las irregularidades
que se perciben en la serie original, pudiéndose tomar sus valores como estimaciones de
la tendencia.
serie mensual y m. moviles(12x2)
Nº Matric.
M.Mov.(12x2)
140000
120000
80000
60000
40000
20000
1994.09
1993.05
1992.01
1990.09
1989.05
1988.01
1986.09
1985.05
1984.01
1982.09
1981.05
1980.01
1978.09
1977.05
1976.01
1974.09
1973.05
1972.01
1970.09
1969.05
1968.01
1966.09
1965.05
0
1964.01
nº autos
100000
meses
117
Departamento de Estadística e Investigación Operativa II (Métodos de Decisión)
3. Estudio de la estacionalidad. Método de desestacionalización.
En este epígrafe nos vamos a limitar a desarrollar un método de desestacionalización
para el caso de existencia de estacionalidad bajo el esquema mixto y sin posibilidad de
distinguir el ciclo de la tendencia. Utilizando la notación con doble subíndice, “i” para
indicar el año y “j” para el periodo o fracción dentro del año, supondremos, por tanto,
que cada observación de la serie temporal se ha formado de la siguiente forma:
Yij = Tij · Sij + rij
con i = 1, ... , n (años) y j = 1, ... , k (fracciones dentro del año)
El método de la razón a la media móvil consiste en determinar para cada periodo o
fracción dentro del año un índice de variación estacional, que represente la variación
media, sobre el valor de tendencia de la serie, debida a ese periodo. La serie se podrá
desestacionalizar dividiendo los datos correspondientes a cada periodo por su índice. El
supuesto que necesitamos, aparte del esquema mixto y la no distinción del componente
cíclico, es que las variaciones estacionales para cada periodo se mantengan estables a lo
largo de los años en que se haya observado la serie.
Los pasos para aplicar este método son los siguientes:
1) Se obtienen las medias móviles centradas de longitud igual a “k”, número de periodos dentro del año (si son meses: k = 12, si son bimestres: k = 6, si son trimestres: k
= 4, si son cuatrimestres: k = 3 y si son semestres: k = 2), perdiéndose un número
igual de observaciones al principio y al final de la serie ( k/2 si k es par o (k-1)/2 si k
es impar). Suponiendo que k es par, se calcularían las siguientes medias móviles:
Yij (k × 2) = MM ij
para (i,j) = (1,k/2+1), ... , (n,k/2)
Es decir, de tener “n” datos de cada periodo o fracción dentro del año y en total,
por tanto, n×k datos, pasamos, al obtener las medias móviles, a tener “n-1” datos para cada periodo y en total (n-1)×k datos.
Las medias móviles calculadas se pueden considerar como estimaciones de los valores de la tendencia: MMij ∼ Tij .
2) Se calculan los índices brutos de variación estacional dividiendo las cifras originales
de la serie entre los valores obtenidos de las medias móviles centradas.
IBVE ij =
Yij
MM ij
= Sij +
rij
MM ij
para (i,j) = (1,k/2+1), ... , (n,k/2)
Se deberá comprobar que, para cada periodo “j”, los “n-1” índices brutos obtenidos no tienen cifras muy dispares, pudiéndose aceptar el supuesto de estabilidad de
las variaciones estacionales a lo largo de los años observados.
118
Introducción a la Econometría
Tema 8: SERIES TEMPORALES
3) Para cada periodo “j” se promedian los “n-1” índices brutos calculados, obteniéndose
“k” índices de variación estacional no normalizados que representamos por S j .
n -1
Sj =
∑ IBVE
i =1
n -1
ij
=
1
⋅
n -1
Yij
n -1
∑ MM
i =1
=
ij
1
⋅
n -1
n -1
∑
Sij +
i =1
1
⋅
n -1
n -1
rij
∑ MM
i =1
ij
El segundo sumando puede considerarse prácticamente nulo, al ser el promedio de
los términos de error de cada periodo, expresados en porcentaje de la media móvil
MMij , a lo largo de los n-1 años, quedándonos los “k” índices no normalizados.
n -1
Sj =
∑ IBVE
i =1
n -1
ij
=
1
⋅
n -1
n -1
∑S
ij
para j = 1, ... ,k
i =1
4) Se normalizan los “k” índices obtenidos con el objetivo de que su media sea igual a 1
ó, lo que es lo mismo, su suma sea igual a k. De forma que las variaciones al alza se
compensen con las variaciones a la baja, respecto a la tendencia de la serie. Para la
normalización se calcula primero la media de los “k” índices.
k
S=
∑S
j
j=1
k
Obteniendo los índices de variación estacional al dividir cada S j entre su media S :
IVE j =
Sj
S
para j = 1, ... ,k
5) Para finalizar el proceso se desestacionaliza la serie original dividiendo cada dato por
su correspondiente índice de variación estacional, es decir, cada Yi1 entre IVE1 , cada Yi2 entre IVE2 , y así hasta cada Yik que se dividirían entre su índice IVEk. Los
valores desestacionalizados serían:
Yij
para i = 1, ... , n y j = 1, ... , k
YijD =
IVE j
Una serie temporal desestacionalizada representa la evolución que hubieran tenido
los datos de la variable si no existieran los factores que influyen en la estacionalidad, es
decir, si en cada periodo del año no se diera ninguna característica que lo diferenciara
de los demás. Supone, por tanto, un instrumento muy valioso para el conocimiento del
comportamiento a medio plazo de los fenómenos económicos que se desarrollan en el
tiempo, al retirar la influencia de los factores estacionales que la modifican a corto plazo.
Un ejemplo del método de desestacionalización expuesto aparece en la resolución
del ejercicio nº 3 que se incluye como apéndice.
119
Departamento de Estadística e Investigación Operativa II (Métodos de Decisión)
4. Tasas de variación en datos temporales.
Dada una magnitud Y que se observa en el tiempo dando lugar a la serie temporal
representada por los valores Yt, para t = 1, 2, ..., N, se denomina tasa de variación a la
medida de la variación relativa experimentada por dicha magnitud desde el periodo “th” hasta el periodo “t”, siendo “h” la amplitud del intervalo de tiempo en que se mide la
variación. Si para su cálculo se emplease un único valor para cada periodo la fórmula
para su obtención sería:
Th1 =
Y
Δ h Yt Yt - Yt-h
=
= t -1
Yt-h
Yt-h
Yt-h
Esta expresión tiene su aproximación lineal por medio de una transformación logarítmica, como ya vimos en el primer epígrafe de este tema. La aproximación será tanto
mejor cuanto menores sean las cifras de las tasas.
Th1 =
Yt - Yt-h
≅ Δ h LogYt = LogYt - LogYt-h
Yt-h
Las tasas de variación constituyen un instrumento fundamental para el estudio y estimación del crecimiento de las magnitudes económicas. Nosotros aquí vamos a exponer las características más elementales de los tipos de tasas que más se utilizan en los
análisis de coyuntura, suponiendo una magnitud económica observada mensualmente.
Como ejemplo vamos a utilizar la serie ficticia de ventas mensuales de la empresa B del
ejercicio nº 3, cuya gráfica es:
ventas mensuales
200
ventas
150
100
50
56
51
46
41
36
31
26
21
16
11
6
1
0
m eses
Tasa de variación intermensual: T11
Es la que nos muestra el crecimiento básico de la serie. Su expresión de cálculo es:
T11 =
120
Yt - Yt-1 Yt
=
-1
Yt-1
Yt-1
Introducción a la Econometría
Tema 8: SERIES TEMPORALES
- Sus valores son muy volátiles al reflejar las variaciones a corto plazo en las que influyen diversos factores que a medio y largo plazo desaparecen o disminuyen sus efectos.
- Amplia las fluctuaciones que se producen a corto plazo, es decir las más erráticas.
- Se suele asignar al mes “t” el valor de la tasa intermensual.
En la siguiente gráfica aparecen las tasas intermensuales correspondientes a la serie
de las cifras de ventas del ejemplo del ejercicio nº 3.
tasas intermensuales
tasas T1,1
0,4
0,2
0
-0,2
-0,4
m eses
Aunque representan el crecimiento original de la serie, su excesiva variabilidad hace
que se busquen otras tasas de variación con amplitud mayor. En el caso de series mensuales serán tasas anuales las que se consideren más apropiadas para representar la evolución del crecimiento de las magnitudes que representan.
Tasa de variación interanual: T121
Representa la variación relativa experimentada por la variable entre dos meses que
distan entre sí un año. Su expresión será:
T121 =
Yt - Yt-12
Y
= t -1
Yt-12
Yt-12
- Suaviza las variaciones estacionales al comparar, siempre, meses con las mismas características.
- Se puede comprobar que amplia las fluctuaciones a medio plazo (de periodo entre 14 y
72 meses), mientras que suaviza las oscilaciones con periodo superior 72 meses.
- La serie de tasas T121 , asignada al último mes “t”, resulta desfasada o retrasada, en sus
oscilaciones, respecto a la serie de crecimientos básicos, por lo que se puede pasar a
“centrarla” asignándola al mes “t-6”.
- Su expresión se puede igualar a una suma ponderada de las tasas intermensuales obtenidas a lo largo del año.
121
Departamento de Estadística e Investigación Operativa II (Métodos de Decisión)
Los valores de estas tasas interanuales calculados con los datos del ejemplo se pueden ver en el siguiente gráfico.
Tasas interanuales
tasas T1,12
0,25
0,2
0,15
0,1
0,05
57
53
49
45
41
37
33
29
25
21
17
13
9
5
1
0
m eses
Tasa de variación interanual de medias móviles: T1212
Representa la tasa de variación de la media de doce meses respecto a la media de los
doce meses anteriores. Su expresión es:
Yt + Yt -1 + ... + Yt -11
T1212 =
-1
Yt -12 + Yt -13 + ... + Yt -23
- Esta tasa amplia, también, las fluctuaciones a medio plazo (de periodo entre 20,4 y 68
meses), mientras que atenúa las oscilaciones con periodo superior 68 meses y las de
menos de 20,4 meses, incluidas las estacionales, como se puede ver en el ejemplo.
- La serie de tasas T1212 , asignada al último mes “t”, resulta desfasada o retrasada, en sus
oscilaciones, respecto a la serie de crecimientos básicos, por lo que se puede pasar a
“centrarla” asignándola al mes “t-11”.
Las tasas T1212 del ejemplo aparecen en el siguiente gráfico.
Tasas interanuales T12,12
0,2
tasas
0,15
0,1
0,05
m eses
122
57
53
49
45
41
37
33
29
25
21
17
13
9
5
1
0
Introducción a la Econometría
Tema 8: SERIES TEMPORALES
Tasas interanuales centradas
Las tasas interanuales definidas se centran con las siguientes expresiones que, siendo
las mismas que las expuestas anteriormente, corrigen la posición del periodo “t” al que
se asigna el valor de la tasa.
Yt + 6 - Yt - 6
Yt - 6
T121 (centrada) =
T1212 (centrada) =
y
Yt + Yt +1 + ... + Yt +11
-1
Yt -1 + Yt -2 + ... + Yt -12
Las gráficas correspondientes a las tasas interanuales centradas del ejemplo son las
que aparecen a continuación.
tasas interanuales centradas
0,25
tasas
0,2
0,15
0,1
0,05
57
53
49
45
41
37
33
29
25
21
17
13
9
5
1
0
m eses
Tasas T12,12 centradas
0,2
0,1
0,05
57
53
49
45
41
37
33
29
25
21
17
13
9
5
0
1
tasas
0,15
m eses
123
Departamento de Estadística e Investigación Operativa II (Métodos de Decisión)
EJERCICIOS DE SERIES TEMPORALES
1. Dada la siguiente serie anual del PIB español, en billones de pesetas const. de 1986:
año: 1985 1986 1987 1988 1989 1990 1991 1992 1993 1994 1995 1996
PIB(bill.
Pts. 86) 31,32 32,32 34,15 35,91 37,61 39,02 39,9
40,18 39,70 40,54 41,66 42,57
1º: Dibuje la gráfica de la serie temporal.
2º: Obtenga las medias móviles centradas 1º) de longitud 3 y 2º) de longitud 4.
3º: Estime la Tendencia lineal que se ajusta a la serie dada.
4º: Añada a la primera gráfica los resultados obtenidos en los apartados anteriores.
2. La empresa A ha obtenido las siguientes cifras de beneficios anuales, en millones de
pesetas, durante el periodo 1988-97:
año:
Bº :
1988
12
1989
15
1990
18
1991
22
1992
26
1993
32
1994
40
1995
49
1996
60
1997
74
1º: Dibuje la gráfica de la serie temporal.
2º: Deduzca, razonadamente, el modelo más adecuado de Tendencia.
3º: Estime el modelo de Tendencia elegido.
3. Calcule los índices constantes de variación estacional para cada mes por el método de
“la razón a la media móvil” y utilícelos para obtener la serie desestacionalizada de
las ventas mensuales de la empresa B, a partir de los datos que aparecen, expresados
en millones de pesetas, en la siguiente tabla.
Ventas mensuales de la empresa B
Año 1
Año 2
Año 3
Año 4
Año 5
124
ENE
31,99
34,85
43
48,7
53,97
FEB
41,28
48,28
56,04
63,87
73,93
MAR
47,23
57,55
65,23
74,66
82,43
ABR
51,45
62,78
74,21
81,17
92,91
MAY
64,17
76,19
88,51
98,3
109,74
JUN
75,84
91,93
103,33
116,67
129,2
JUL
90,72
103,46
120,22
134,27
150,93
AGO
73,27
84,06
99,61
109,36
123,43
SEP
56,78
65,43
74,97
85,87
95,74
OCT
50,86
61,58
68,62
76,99
85,88
NOV
47,88
55,92
62,35
71,54
77,08
DIC
29,76
35,11
39,51
44,33
47,86
Introducción a la Econometría
Tema 8: SERIES TEMPORALES
4. A partir de la serie trimestral del número de vehículos matriculados, en cierta Comunidad Autónoma, que aparece en la siguiente tabla, calcule los índices constantes de
variación estacional de cada trimestre por el método de la “razón a la media móvil” y
desestacionalice la serie. Efectúe una gráfica conjunta de la serie original y de la serie desestacionalizada.
1994
1995
1996
TRIM. 1
28338
36312
49192
TRIM. 2
31694
40931
64285
TRIM. 3
28629
36531
61547
TRIM. 4
38306
45518
75649
5. Dada la siguiente serie temporal:
t:
1
2
3
4
5
6
7
8
9
10
11
12
Yt
2
5
10
4
4
7
12
6
6
9
14
8
1º: Dibuje su gráfica y, a partir de ella, deduzca la longitud que han de tener las medias
móviles para representar de forma más adecuada su tendencia.
2º: Obtenga dichas medias móviles centradas e incorpórelas al gráfico, comentando el
resultado.
6. A partir de la serie cuatrimestral de datos que aparece en la siguiente tabla, calcule
los índices constantes de variación estacional de cada cuatrimestre por el método de
la “razón a la media móvil” y desestacionalice la serie.
CUAT. 1 CUAT. 2 CUAT. 3
1995
6
10
2
1996
9
13
5
1997
12
16
8
(realice los cálculos aproximando con los dos primeros decimales que se obtengan)
125
Departamento de Estadística e Investigación Operativa II (Métodos de Decisión)
Datos de la resolución del ejercicio 3:
Serie de ventas mensuales de la empresa B
Ene
Feb
Mar
Abr
May
Jun
Jul
Ago
Sep
Oct
Nov
Dic
año 1
31,99
41,28
47,23
51,45
64,17
75,84
90,72
73,27
56,78
50,86
47,88
29,76
año 2
34,85
48,28
57,55
62,78
76,19
91,93
103,5
84,06
65,43
61,58
55,92
35,11
año 3
43
56,04
65,23
74,21
88,51
103,3
120,2
99,61
74,97
68,62
62,35
39,51
año 4
48,7
63,87
74,66
81,17
98,3
116,7
134,3
109,4
85,87
76,99
71,54
44,33
año 5
53,97
73,93
82,43
92,91
109,7
129,2
150,9
123,4
95,74
85,88
77,08
47,86
Ene
Feb
Mar
Medias móviles centradas de longitud 12 (12x2)
Abr
May
Jun
año 1
Jul
Ago
Sep
Oct
Nov
Dic
55,22
55,63
56,35
57,26
58,23
59,4
año 2
60,6
61,58
62,39
63,2
63,98
64,54
65,1
65,76
66,41
67,2
68,19
69,18
año 3
70,36
71,7
72,75
73,44
74
74,45
74,87
75,43
76,15
76,84
77,53
78,5
año 4
79,64
80,63
81,49
82,29
83,03
83,61
84,03
84,67
85,41
86,23
87,19
88,19
año 5
89,41
90,69
91,68
92,47
93,07
93,44
Ene
Feb
Mar
Índices brutos de variación estacional
Abr
May
Jun
año 1
Jul
Ago
Sep
Oct
Nov
Dic
1,643
1,317
1,008
0,888
0,822
0,501
año 2
0,575
0,784
0,922
0,993
1,191
1,424
1,589
1,278
0,985
0,916
0,82
0,508
año 3
0,611
0,782
0,897
1,011
1,196
1,388
1,606
1,32
0,984
0,893
0,804
0,503
año 4
0,612
0,792
0,916
0,986
1,184
1,395
1,598
1,292
1,005
0,893
0,82
0,503
año 5
0,604
0,815
0,899
1,005
1,179
1,383
sumas:
2,401
3,173
3,634
3,995
4,75
5,59
6,436
5,207
3,983
3,591
3,267
2,015
0,817
0,504
0,816
0,503
Índices de variación estacional no normalizados
medias:
0,6
0,793
0,909
0,999
1,188
1,398
1,609
1,302
0,996
0,898
Media:
1,001
0,995
0,897
Índices de variación estacional
índices
0,6
0,793
0,908
0,998
1,186
1,396
1,608
1,301
Serie desestacionalizada de ventas mensuales de la empresa B
Ene
Feb
Mar
Abr
May
Jun
Jul
Ago
Sep
Oct
Nov
Dic
año 1
53,33
52,09
52,03
51,56
54,08
54,31
56,44
56,33
57,08
56,71
58,67
59,14
año 2
58,1
60,92
63,4
62,91
64,22
65,83
64,36
64,63
65,77
68,66
68,53
69,78
año 3
71,69
70,71
71,86
74,37
74,6
74
74,79
76,58
75,36
76,51
76,41
78,52
año 4
81,19
80,59
82,24
81,34
82,85
83,55
83,53
84,08
86,32
85,84
87,67
88,1
año 5
89,98
93,28
90,8
93,11
92,49
92,52
93,89
94,89
96,24
95,76
94,46
95,11
126
Introducción a la Econometría
Tema 8: SERIES TEMPORALES
VENTAS MENSUALES Y SERIE DESESTACIONALIZADA
160
140
120
VALORES
100
80
60
40
20
MESES
ventas mensuales
127
Serie Desest.
58
55
52
49
46
43
40
37
34
31
28
25
22
19
16
13
10
7
4
1
0