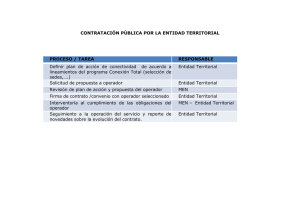
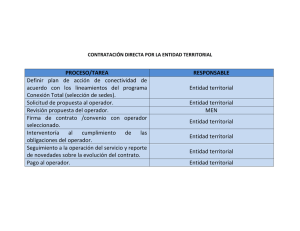
Tarea V de ´Algebra Lineal II

Tarea V de Álgebra Lineal II
Semestre 2016-II
7 de mayo de 2016
Profra: Gabriela Campero Arena
Ayudtes: Tonatiuh Velázquez, Hugo Yáñez y Manuel Zúñiga
I. Descomposición en valores singulares y la pseudoinversa
1. Establezca si las siguientes afirmaciones son verdaderas o falsas, dando una prueba o un contraejemplo:
(i) Los valores singulares de cualquier operador lineal en un espacio vectorial de dimensión finita también son
eigenvalores del operador.
(ii) Los valores singulares de cualquier matriz A son los eigenvalores de A*A.
(iii) Para cualquier matriz A y cualquier escalar c, si σ es un valor singular de A, entonces |c|σ es un valor
singular de cA.
(iv) Los valores singulares de cualquier operador lineal son no negativos.
(v) Si λ es un eigenvalor de una matriz autoadjunta A, entonces λ es un valor singular de A.
(vi) Para cualquier matriz A de m × n y cualquier b ∈ F n , el vector A† b es una solución de Ax = b.
(vii) La pseudoinversa de cualquier operador lineal existe aunque el operador lineal no sea invertible.
2. Sea T : V → W una transformación lineal de rango r, donde V y W son espacios vectoriales de dimensión
finita con producto interno. Para cada uno de los siguientes, encuentre bases ortonormales {v1 , v2 , ..., vn } para
V y {u1 , u2 , ..., um } para W , y los valores singulares no cero σ1 > σ2 > ... > σr de T tal que, para 1 6 i 6 r,
T (vi ) = σi ui . Además, encuentre una fórmula explı́cita para T † :
(a) T : R2 → R3 definida como T (x1 , x2 ) = (x1 , x1 + x2 , x1 − x2 )
(b) T : P2 (R) → P1 (R) donde T (f (x)) = f 00 (x) y el producto interno es el del ejemplo visto
en clase
R 2π
(c) Sea V = W = span({1, sin x, cos x}) con el producto interno definido como < f, g >= 1 f (t)g(t)dt y T se
define como T (f ) = f 0 + 2f .
3. Encuentre una descomposiciónen valores
singulares y la pseudoinversa de cada una de las siguientes matrices.





1 1
1
1
1
1
1
0 1

 1 −1
0 
1  (b) 
(a)  1
1 0 (c)
1
0 −1
−1 −1
1 1
4. Sea T : V → W una transformación lineal de rango r, donde V y W son espacios vectoriales de dimensión
finita con producto interno sobre F con bases ortonormales
{v1 , v2 , ..., vn } para V y {u1 , u2 , ..., um } para W , y
σi ui 1 6 i 6 r
supongamos que σ1 > σ2 > ... > σr son tal que T (vi ) =
0
r < i.
(a) Pruebe que {u1 , u2 , ..., um} es un conjunto de eigenvectores de T T ∗ con correspondientes eigenvalores
σi2 1 6 i 6 r
λ1 , λ2 , ..., λm , donde λi =
0
r 6 i.
(b) Sea A una matriz de m × n con entradas reales o complejas. Pruebe que los valores singulares no cero de A
son las raı́ces cuadradas positivas de los eigenvalores no cero de AA∗ , incluyendo repeticiones.
(c) Pruebe que T T ∗ y T ∗ T tienen los mismos eigenvalores no cero, incluyendo repeticiones.
(d) Establezca y pruebe un resultado análogo a (c) para matrices.
5. Este ejercicio relaciona los valores singulares de un operador lineal (o matriz) que se comporta bien y sus eigenvalores
(a) Sea T un operador lineal normal en un espacio vectorial n-dimensional con producto interno con eigenvalores
λ1 , λ2 , ..., λn . Pruebe que los valores singulares de T son |λ1 |, |λ2 |, ..., |λn |.
(b) Establezca y pruebe un resultado análogo a (a) para matrices
6. Pruebe que si A es una matriz semidefinida positiva, entonces los valores singulares de A son los mismos que los
eigenvalores de A.
7. Pruebe que si A es una matriz definida positiva y A = U ΣV ∗ es una descomposición en valores singulares de A,
entonces U = V .
8. Sean T y U operadores lineales en R2 definidos como, para todo (x1 , x2 ) ∈ R2
T (x1 , x2 ) = (x1 , 0) y U (x1 , x2 ) = (x1 + x2 , 0).
(a) Pruebe que (U T )† 6= T † U † .
(b) Dé ejemplos de matrices A y B tal que AB está definido, pero (AB)† 6= B † A† .
9. Sea A una matriz de m × m. Pruebe los siguientes resultados.
(a) Para cualquier matriz unitaria G de m × m, (GA)† = A† G∗ .
(b) Para cualquier matriz unitaria H de n × n, (AH)† = H ∗ A† .
10. Sea A una matriz con entradas reales. Pruebe los siguientes resultados:
(a) Los valores singulares no cero de A son los mismos que los valores singulares no cero de A∗ , los cuales son
iguales a los valores singulares no cero de At .
(b) (A† )∗ = (A∗ )† .
1
(c) (A† )t = (At )† .
11. Sean V y W espacios vectoriales de dimensión finita con producto interno, y sea T : V → W lineal. Pruebe los
siguientes resultados:
(a) T T † T = T .
(b) T † T T † = T † .
(c) T † T y T T † son autoadjuntos.
(d) Establezca y pruebe resultados análogos a los tres incisos anteriores para matrices.
Las tres primeras propiedades anteriores son llamadas las condiciones de Penrose, y tales condiciones caracterizan a la pseudoinversa de una transformación lineal, como veremos en el siguiente ejercicio.
12. (a) Sean V y W espacios vectoriales de dimensión finita con producto interno. Sean T : V → W y U : W → V
transformaciones lineales tales que T U T = T , U T U = U , y tanto U T como T U son autoadjuntos. Pruebe
que U = T † .
(b) Establezca y pruebe un resultado análogo al primer inciso para matrices.
13. Sean V y W espacios vectoriales de dimensión finita con producto interno, y sea T : V → W lineal, pruebe los
siguientes resultados:
(a) Si T es inyectiva, entonces T T ∗ es invertible y T † = (T ∗ T )−1 T ∗ .
(b) Si T es sobre, entonces T T ∗ es invertible y T † = T ∗ (T T ∗ )−1 .
II. La forma canónica de Jordan I
14. Establezca si las siguientes afirmaciones son verdaderas o falsas, dando una prueba o un contraejemplo:
(i) Los eigenvectores de un operador lineal T también son eigenvectores generalizados de T .
(ii) Es posible que un eigenvector generalizado de un operador lineal T corresponda a un escalar que no es un
eigenvalor de T .
(iii) Cualquier operador lineal sobre un espacio de dimensión finita tiene una forma canónica de Jordan.
(iv) Un ciclo de eigenvectores generalizados es linealmente independiente.
(v) Hay exactamente un ciclo de eigenvectores generalizados correspondiente a cada eigenvalor de un operador
lineal definido en un espacio de dimensión finita.
(vi) Sea T un operador lineal sobre un espacio de dimensión finita cuyo polinomio caracterı́stico se descompone y
sean λ1 , ..., λk los distintos eigenvalores de T . Si para cada i, βi es una base para Kλi , entonces β1 ∪β2 ∪...∪βk
es una base canónica de Jordan para T .
(vii) Para cualquier bloque de Jordan J, la forma canónica de Jordan del operador LJ es J.
(viii) Sea T un operador lineal definido sobre un espacio vectorial de dimensión n y tal que su polinomio caracterı́stico se descompone. Entonces, para cualquier eigenvalor λ de T , Kλ = N ((T − λI)n ).
15. Sean V = M2×2 (R); T : V → V tal que T (A) = 2A + At . Encuentre una base para cada eigenespacio generalizado
de T que consista en la unión de ciclos disjuntos de eigenvectores generalizados. Posteriormente, encuentre una
forma canónica de Jordan para T .
16. Sea T un operador lineal definido sobre un espacio vectorial V y sea γ un ciclo de eigenvectores generalizados
que corresponden al eigenvalor λ. Pruebe que L(γ) es un subespacio T -invariante de V .
17. Sean γ1 , ..., γp ciclos de eigenvectores generalizados de un operador lineal T correspondientes al eigenvalor λ.
Pruebe que si todos los vectores iniciales de los ciclos son distintos, entonces los ciclos son ajenos dos a dos.
18. Sea T : V → W una transformación lineal. Pruebe los siguientes resultados:
(a) N (T ) = N (−T )
(b) ∀k ∈ N (N (T k ) = N ((−T )k )).
(c) Si V = W (de modo que T es un operador lineal sobre V ) y λ es un eigenvalor de T , entonces para cada
k ∈ N se tiene que N ((T − λIV )k ) = N ((λIV − T )k ).
19. Sea U un operador lineal sobre un espacio vectorial de dimensión finita V . Pruebe que:
(a) N (U ) ⊆ N (U 2 ) ⊆ ... ⊆ N (U k ) ⊆ N (U k+1 ) ⊆ ...
(b) Si rango(U m ) = rango(U m+1 ) para algún m ∈ N+ , entonces ∀k ≥ m (rango(U m ) = rango(U k )).
(c) Si rango(U m ) = rango(U m+1 ) para algún m ∈ N+ , entonces ∀k ≥ m (N (U m ) = N (U k )).
(d) Sea T un operador lineal definido sobre V y sea λ un eigenvalor de T . Pruebe que si
rango((T − λI)m ) = rango((T − λI)m+1 ) para algún m ∈ N+ , entonces Kλ = N ((T − λI)m ).
(e) Segundo Test de Diagonalizabilidad. Sea T un operador lineal sobre V cuyo polinomio caracterı́stico se
descompone y sean λ1 , ..., λk los distintos eigenvalores de T . Entonces, T es diagonalizable si y sólo si
rango(T − λi I) = rango((T − λi I)2 ) para 1 ≤ i ≤ k.
20. Sea T un operador lineal sobre un espacio vectorial de dimensión finita V cuyo polinomio caracterı́stico se
descompone.
(a) Pruebe el Teorema 7.5(b).
(b) Sea β una base canónica de Jordan para T y sea λ un eigenvalor de T . Sea β 0 = β ∩ Kλ . Pruebe que β 0 es
base para Kλ .
21. Sea T un operador lineal sobre un espacio vectorial de dimensión finita cuyo polinomio caracterı́stico se descompone y sea λ eingenvalor de T .
(a) Supongamos que γ es una base para Kλ que consiste en la unión de q ciclos disjuntos de eigenvectores
generalizados. Pruebe que q ≤ dim(Eλ ).
2
(b) Sea β una base canónica de Jordan para T y supongamos que J = [T ]β tiene q bloques de Jordan con el
valor λ en sus entradas diagonales. Pruebe que q ≤ dim(Eλ ).
III. La forma canónica de Jordan II
22. Establezca si las siguientes afirmaciones son verdaderas o falsas. En todos los casos, asuma que el polinomio
caracterı́stico de la matriz u operador lineal en cuestión se descompone.
(i) La forma canónica de Jordan de una matriz diagonal es ella misma.
(ii) Sea T un operador lineal sobre un espacio vectorial de dimensión finita. Sea J su forma canónica de Jordan.
Si β es cualquier base para V , entonces la forma canónica de Jordan de [T ]β es J.
(iii) Operadores lineales con el mismo polinomio caracterı́stico son similares.
(iv) Matrices con la misma forma canónica de Jordan son similares.
(v) Toda matriz es similar a su forma canónica de Jordan.
(vi) Todo operador lineal con polinomio caracterı́stico (−1)n (t − λ)n tiene la misma forma canónica de Jordan.
(vii) Todo operador lineal sobre un espacio de dimensión finita tiene una única base canónica de Jordan.
(viii) El diagrama de puntos de un operador lineal sobre un espacio vectorial de dimensión finita es único.
23. Sea T un operador lineal sobre un espacio vectorial de dimensión finita V tal que el polinomio caracterı́stico de T
se descompone. Supongamos que λ1 = 2, λ2 = 4 y λ3 = −3 son los distintos eigenvalores de T y que el diagrama
λ1 = 2
λ2 = 4 λ3 = −3
• • •
• •
• •
de puntos para la restricción de T a cada Kλi es el siguiente:
Encuentre la forma
• •
•
•
•
canónica de Jordan J para T .
24. Sea T un operador lineal sobre un espacio
vectorial
de
dimensión
finita
V
con
forma canónica de Jordan


2 1 0 0 0 0 0
 0 2 1 0 0 0 0 


 0 0 2 0 0 0 0 


 0 0 0 2 1 0 0 


 0 0 0 0 2 0 0 


 0 0 0 0 0 3 0 
0 0 0 0 0 0 3
(a)
(b)
(c)
(d)
(e)
Encuentre el polinomio caracterı́stico de T .
Encuentre el diagrama de puntos correspondiente a cada eigenvalor de T .
¿Para qué eigenvalores λi se cumple que Kλi = Eλi ?
Para cada eigenvalor λi , encuentre el menor entero positivo pi tal que Kλi = N ((T − λi I)pi ).
Calcule los siguientes valores para cada i, donde Ui denota la restricción de T − λi I a Kλi :
(i) rango(Ui ) (ii) rango(Ui2 ) (iii) nulidad(Ui ) (iv) nulidad(Ui2 )
25. Encuentre una forma canónica de Jordan J para T y una base canónica de Jordan βsi:
3 1
(a) T es el operador lineal definido sobre M2×2 (R) definido como T (A) =
· (A − At ).
0 3
(b) V es el espacio vectorial de funciones polinomiales con dos variables reales x y y de grado a lo más 2 tal como
∂
∂
se definió en el ejemplo 4 y T es el operador lineal definido sobre V tal que T (f (x, y)) = ∂x
f (x, y)+ ∂y
f (x, y).
t
26. Sea A ∈ Mn×n (F ) cuyo polinomio caracterı́stico se descompone. Pruebe que A y A tienen la misma forma
canónica de Jordan y concluya que A y At son similares. Sugerencia: Para cualquier eigenvalor λ de A y At y
para cada r ∈ N+ , pruebe que (rango(A − λI)r ) = rango((At − λI)r ).
27. Sean A una matriz de n×n cuyo polinomio caracterı́stico se descompone, γ un ciclo de eigenvectores generalizados
correspondientes al eigenvalor λ y W el subespacio generado por γ. Defina γ 0 como el conjunto ordenado obtenido
de γ al invertir el orden de los vectores en γ.
(a) Pruebe que [TW ]γ 0 = ([TW ]γ )t .
(b) Sea J la forma canónica de Jordan de A. Utilice el inciso anterior para probar que J y J t son similares.
(c) Utilice (b) para probar que A y At son similares.
Definición: Un operador lineal T definido sobre un espacio vectorial V es nilpotente si y sólo si T p = T0 para algún
p ∈ N+ . Una matriz A es nilpotente si Ap = O para algún p ∈ N+ .
28. Pruebe que cualquier matriz cuadrada triangular superior con cada entrada en la diagonal igual a cero es una
matriz nilpotente.
29. Sea T un operador lineal nilpotente sobre un espacio V de dimensión n y supóngase que p es el menor entero
positivo tal que T p = T0 . Pruebe que:
(a) ∀i ∈ N+ (N (Ti ) ⊆ N (T i+1 )).
(b) Existe una sucesión de bases ordenadas β1 , β2 , ..., βp tal que βi es base para N (T i ) y βi ⊆ βi+1 para
1 ≤ i ≤ p − 1.
(c) Sea β = βp base ordenada para N (T p ) = V como en (b). Entonces [T ]β es una matriz triangular superior
con todas sus entradas en la diagonal iguales a cero.
(d) El polinomio caracterı́stico de T es (−1)n tn . Por tanto, el polinomio caracterı́stico de T se descompone y 0
es el único eigenvalor de T .
3
30. Pruebe el recı́proco al ejercicio 29(d): Si T es un operador lineal sobre un espacio vectorial V de dimensión n y
(−1)n tn es el polinomio caracterı́stico de T , entonces T es nilpotente.
31. Encuentre un ejemplo de un operador lineal T sobre un espacio de dimensión finita tal que T no sea nilpotente
pero el 0 sea su único eigenvalor. Caracterice al conjunto de todos los operadores lineales que cumplan esta
condición.
32. Sea T un operador lineal definido sobre un espacio vectorial de dimensión finita V tal que el polinomio caracterı́stico de T se descompone y sean λ1 , ..., λk los distintos eigenvalores de T . Sea S : V → V la función definida
por S(x) = λ1 v1 + λ2 v2 + ... + λk vk , donde para cada i, vi es el único vector en Kλi tal que x = v1 + ... + vk .
Dicha unicidad está garantizada por el Teorema 7.8.
(a) Pruebe que S es un operador diagonalizable sobre V .
(b) Sea U = T − S. Pruebe que U es nilpotente y que conmuta con S, es decir, que SU = U S.
IV. El polinomio mı́nimo
33. Establezca si las siguientes afirmaciones son verdaderas o falsas dando una prueba o un contraejemplo. En todos
los casos asuma que el espacio vectorial en el que se está trabajando es de dimensión finita.
(i) Todo operador lineal T tiene un polinomio p(t) de grado máximo tal que p(T ) = T0 .
(ii) Todo operador lineal tiene un único polinomio mı́nimo.
(iii) El polinomio caracterı́stico de un operador lineal divide al polinomio mı́nimo del mismo.
(iv) El polinomio mı́nimo y el polinomio caracterı́stico de un operador diagonalizable coinciden.
(v) Sean T un operador lineal sobre un espacio V de dimensión n, p(t) el polinomio mı́nimo de T y f (t) el
polinomio caracterı́stico de T . Suponga que f (t) se descompone. Entonces f (t) divide a [p(t)]n .
(vi) El polinomio mı́nimo de un operador lineal siempre tiene el mismo grado que el polinomio caracterı́stico de
dicho operador.
(vii) Un operador lineal es diagonalizable si su polinomio mı́nimo se descompone.
(viii) Sea T un operador lineal sobre un espacio vectorial V tal que V es un subespacio T -cı́clico de él mismo.
Entonces el grado del polinomio mı́nimo de T es la dimensión de V .
(ix) Sea T un operador lineal sobre un espacio vectorial V tal que T tiene n eigenvalores distintos, donde
n = dim(V ). Entonces, el grado del polinomio mı́nimo de T es n.
(x) Sea T un operador lineal definido sobre el espacio V de dimensión finita y sean W1 y W2 subespacios
T -invariantes de V tales que V = W1 ⊕ W2 . Si p1 (t) y p2 (t) son los polinomios mı́nimos de TW1 y TW2
respectivamente, entonces p1 (t)p2 (t) es el polinomio mı́nimo de T .
34. Para cada operador lineal T definido sobre V , encuentre el polinomio mı́nimo de T y diga si dicho operador es
(a) V = P2 (R) y T (g(x)) = g 0 (x) + 2g(x).
diagonalizable.
(b) V = Mn×n (R) y T (A) = At . Sugerencia: Recuerde que T 2 = I.
35. Describa quiénes son todos los operadores lineales T sobre R2 tales que T es diagonalizable y
T 3 − 2T 2 + T = T0 .
36. Pruebe el Teorema 7.13 y su corolario.
37. Sea T un operador lineal sobre un espacio vectorial de dimensión finita y sea p(t) el polinomio mı́nimo de T .
(a) T es invertible si y sólo si p(0) 6= 0.
Pruebe que: (b) Si T es invertible y p(t) = tn + an−1 tn−1 + ... + a1 t + a0 , entonces
T −1 = − a10 (T n−1 + an−1 T n−2 + ... + a2 T + a1 I).
38. Sea T un operador lineal diagonalizable definido sobre un espacio vectorial de dimensión finita. Pruebe que V es
un subespacio T -cı́clico de él mismo si y sólo si cada uno de sus eigenespacios tiene dimensión uno.
39. Sea T un operador lineal sobre un espacio vectorial V de dimensión finita y sea W un subespacio T -invariante
de V . Pruebe que el polinomio mı́nimo de TW divide al polinomio mı́nimo de T .
40. Sea D el operador derivada definido sobre P (R), el espacio de polinomios sobre R. Pruebe que no existe ningún
polinomio g(t) tal que g(D) = T0 , y por tanto D no tiene polinomio mı́nimo.
41. Sea T un operador lineal definido sobre un espacio vectorial de dimensión finita y tal que su polinomio caracterı́stico se descompone. Sean λ1 , λ2 , ..., λk los distintos eigenvalores de T y para cada i, sea pi el orden del bloque
de Jordan más grande correspondiente a λi en alguna forma canónica de Jordan de T . Pruebe que el polinomio
mı́nimo de T es (t − λ1 )p1 (t − λ2 )p2 · · · (t − λk )pk .
Definición: Sea T un operador lineal sobre un espacio vectorial de dimensión finita V y sea x ∈ V \ {0}. Un polinomio
p(t) es llamado T -anulador de x si p(t) es un polinomio mónico de grado mı́nimo tal que p(T )(x) = 0
42. Sea T un operador lineal sobre un espacio vectorial de dimensión finta V y sea x ∈ V \ {0}. Pruebe que:
(a) El vector x tiene un único T -anulador.
(b) El T -anulador de x divide a cualquier polinimio g(t) tal que g(T ) = T0 .
(c) Si p(t) es el T -anulador de x y W es el subespacio T -cı́clico generado por x, entonces p(t) es el polinomio
mı́nimo de TW y dim(W ) = grado(p(t)).
(d) El grado del T -anulador de x es uno si y sólo si x es eigenvector de T .
43. Sea T un operador lineal definido sobre un espacio vectorial V de dimensión finita y sea W1 un subespacio
T -invariante de V . Sea x ∈ V tal que x ∈
/ W1 . Pruebe que:
(a) Existe un único polinomio mónico g1 (t) de grado mı́nimo tal que g1 (T )(x) ∈ W1 .
(b) Si h(t) es un polinomio para el cual h(T )(x) ∈ W1 , entonces g1 (t) divide a h(t).
(c) g1 (t) divide al polinomio mı́nimo y al polinomio caracterı́stico de T .
(d) Sea W2 un subespacio T -invariante de V tal que W2 ⊆ W1 y sea g2 (t) el único polinomio mónico de grado
mı́nimo tal que g2 (T )(x) ∈ W2 . Entonces g1 (t) divide a g2 (t).
4