Ejercicios de Difracción

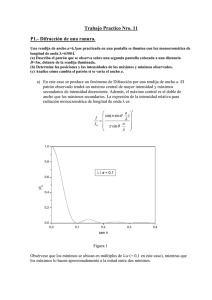
Ejercicios de Difracción.
1.- Una red de difracción tiene
104 líneas uniformemente distribuidas en 0,0254 [m]. Se
ilumina normalmente con luz amarilla de una lámpara de sodio. Esta luz está formada por dos
líneas muy cercanas entre sí (doblete del sodio) de longitudes de onda de 589 y 589,59 [nm].
a) ¿Para qué ángulo se formará el máximo de primer orden para la primera de estas
longitudes?
b) ¿Cuál es la separación angular entre los máximos de primer orden para esas líneas?
c) ¿Cuántas líneas debe tener una red para que esté en el límite de poder separar el doblete
del sodio en el tercer orden del espectro?
Solución
Datos; ܰ = 10ସ líneas, ݊ =
ଵ଴ర ௟í௡௘௔௦
ଶ,ହସ
ቂ
௖௠
ଵ
ቃ → ݀ = ௡ = 2,54 ∙ 10ିସ ሾܿ݉ሿ = 2540 ሾ݊݉ሿ.
ߣଵ = 589 ሾ݊݉ሿ, ߣଶ = 589,59 ሾ݊݉ሿ, ݉௜ = 1
a)
Condiciones de máximo de interferencia:
ହ଼ଽ
݀‫݉ = ߠ݊݁ݏ‬௜ ߣ → ‫ = ߠ݊݁ݏ‬ଶହସ଴ = 0,23 → ߠ = 13,3଴
b)
De la ecuación anterior:
‫= ߠ݊݁ݏ‬
௠೔ ఒ
, como ߠ y ߣ son variables, derivando, se tiene:
ௗ
ܿ‫= ߠ݀ ߠݏ݋‬
௠೔
ௗ
݀ߣ →
ௗఏ
ௗఒ
=
௠೔
ௗ௖௢௦ఏ
Si las longitudes de onda están muy cercanas entre sí podemos escribir ݀ߠ y ݀ߣ como ∆ߠ y
∆ߣ, respectivamente. Luego:
∆ߠ =
c)
ܴ=
௠೔
ௗ௖௢௦ఏ
∆ߣ =
ଵ ∙ሺହ଼ଽ,ହଽିହ଼ଽሻ
ଶହସ଴∙௖௢௦ଵଷ,ଷబ
= 2,39 ∙ 10ିସ ሾ‫݀ܽݎ‬ሿ → ∆ߠ = 0,1370
Se sabe que:
ഥ
ఒ
∆ఒ
= ݉௜ ܰ
Si ߣҧ = 589,3 y ∆ߣ = 0,59 , luego:
ܴ=
ହ଼ଽ,ଷ
଴,ହଽ
= ݉௜ ܰ → ܰ =
ହ଼ଽ,ଷ
଴,ହଽ∙ଷ
= 333 .
Por lo tanto, esta red resuelve el doblete del sodio en el tercer orden del espectro.
2.- Sobre una red de difracción que da un patrón
como el de la figura, incide luz de sodio
(ߣଵ = 589ሾ݊݉ሿ, ߣଶ = 589,59 ሾ݊݉ሿ).
a) ¿Cuántas aberturas tiene la red?
b) Calcule el ancho del máximo central de difracción, si se sabe que la red está a 50 [cm] de la
pantalla que recibe el patrón y que tiene 1 [cm] de ancho.
௟í௡௘௔௦
c) Si se cambiara la red por otra de 2 [cm] por lado y 3000 ቂ
ቃ. ¿Cuál es el poder de
௖௠
resolución para el quinto orden del espectro?
d) ¿Cuál es la separación angular entre el primer y segundo máximo de interferencia?
e) Calcule el ancho del máximo central de interferencia.
Solución
Datos: ߣଵ = 589ሾ݊݉ሿ, ߣଶ = 589,59 ሾ݊݉ሿ, ‫ = ܮ‬50ሾܿ݉ሿ
a) La red de la figura tiene 5 aberturas, porque:
ܰ − 2 = número de máximos secundarios. De la figura: ܰ − 2 = 3 → ܰ = 5
b)
Condición de mínimo de difracción:
ܽ‫݉ = ߠ݊݁ݏ‬ௗ ߣ
(1)
Para ángulos pequeños: ‫ ≈ ߠ݊݁ݏ‬tan ߠ, luego (1) se puede escribir como:
ܽ ‫݉ = ߠ݊ܽݐ‬ௗ ߣ
(2)
Condición de máximo de interferencia:
݀‫݉ = ߠ݊݁ݏ‬௜ ߣ
(3)
Dividiendo (3) por (1), se obtiene:
ௗ௦௘௡ఏ
௔௦௘௡ఏ
௠೔ ఒ
=
→ ܽ =
௠೏ ఒ
Como ܰ = 5 → ݊ = 5 ቂ
ௗ௠೏
(4)
௠೔
௟í௡௘௔௦
ቃ;
௖௠
luego:
ଵ
݀ = ௡ = 0,2 ሾܿ݉ሿ, sustituyendo en (4), se obtiene:
ܽ=
଴,ଶ
ସ
≈ 0,5 ሾ݉݉ሿ .
De la figura:
‫= ߠ݊ܽݐ‬
ܽ
∆௬
௅
∆௬
௅
; introduciendo en (2):
= ݉ௗ ߣ → ∆‫= ݕ‬
∆‫= ݕ‬
ଵ ∙ହ଼ଽ ∙ହ଴ ∙ ଵ଴ళ
଴,ହ ∙ ଵ଴ల
௠೏ ఒ௅
௔
; reemplazando por los valores, se obtiene:
= 5,89 ∙ 10ହ ሾ݊݉ሿ.
Como el ancho del máximo central es 2∆‫ݕ‬, su valor es 11,78 ∙ 10ହ ሾ݊݉ሿ.
௟í௡௘௔௦
ቃ,
௖௠
c) Si se cambia la red por otra de densidad ݊ = 3000 ቂ
݀=
ଵ
ሾܿ݉ሿ
ଷ଴଴଴
=
ଵ଴ళ
ଷ ∙ ଵ଴య
se tiene:
= 0,33 ∙ 10ସ ሾ݊݉ሿ
ܰ = ݈݊ = 3000 ∙ 2 = 6000 ݈í݊݁ܽ‫ݏ‬
ܴ = ݉௜ ܰ = 5 ∙ 6000 = 30000
d) ‫= ܦ‬
∆ߠ =
∆ఏ
∆ఒ
=
௠೔
௠೔
ௗ ௖௢௦ఏ
ௗ௖௢௦ఏ
∆ߣ =
ଵ
଴,ଷଷ∙ ଵ଴ర ∙ଵ
0,59
∆ߠ = 1,74 ∙ 10ିସ ሾ‫݀ܽݎ‬ሿ ≈ 0,01଴
e) Calcular el máximo central de interferencia significa aplicar las condiciones de mínimo de
interferencia para una red de difracción.
݀‫= ߠ݊݁ݏ‬
௠೔ ఒ
ே
௬
; como ‫ ≈ ߠ݊݁ݏ‬tan ߠ = ௅ , luego:
‫=ݕ‬
௠೔ ఒ ୐
ேௗ
= 148,74ሾ݊݉ሿ , y el ancho es 2‫ = ݕ‬297,48 ሾ݊݉ሿ .
3.- La figura representa
un patrón de interferencia-difracción.
a) Diga el número de aberturas que tiene esta red. Explique.
b) Si sobre esta red incide luz de 540 [nm] y se sabe que el ancho de la red es de 2 [cm], calcule
el ancho del máximo central de difracción que se forma en una pantalla colocada a 80 [cm] de
la red.
c) Calcule el ancho del máximo central de interferencia.
d) Diga cuántos máximos de interferencia se forman. Explique.
e) Diga si esta red puede resolver el doblete del sodio (ߣଵ = 589ሾ݊݉ሿ, ߣଶ = 589,59 ሾ݊݉ሿ)
para el máximo de quinto orden. Explique.
Solución
a)
ܰ − 2 = número de máximos secundarios.
De la figura: ܰ − 2 = 4 → ܰ = 6 .
b) Condición de mínimos de difracción:
ܽ‫݉ = ߠ݊݁ݏ‬ௗ ߣ
(1)
Condiciones de máximos de interferencia:
݀‫݉ = ߠ݊݁ݏ‬௜ ߣ
ଵ
(2)
଺
௟í௡௘௔௦
ቃ
௖௠
݀=௡ → ݊=ଶ=3 ቂ
ଵ
݀ = ଷ ≈ 0,33 ሾܿ݉ሿ ≈ 0,33 ∙ 10଻ ሾ݊݉ሿ
‫= ߠ݊ܽݐ ≈ ߠ݊݁ݏ‬
∆௬
௅
(3)
Dividiendo (1) por (2):
௔௦௘௡ఏ
=
ௗ௦௘௡ఏ
௠೏ ఒ
௠೔ ఒ
→ ܽ=
ௗ௠೏
௠೔
=
଴,ଷଷ∙ ଵ଴ళ ∙ଵ
ଷ
= 0,11 ∙ 10଻ ሾ݊݉ሿ .
Introduciendo (3) en (1):
ܽ
∆௬
௅
௠೏ ఒ௅
= ݉ௗ ߣ → ∆‫= ݕ‬
௔
=
ଵ ∙ହସ଴ ∙଼଴ ∙ଵ଴ళ
଴,ଵଵ ∙ ଵ଴ళ
= 392727 ሾ݊݉ሿ = 0,392 ሾ݉݉ሿ , luego:
2 ∆‫ = ݕ‬0,785 ሾ݉݉ሿ .
c) Condiciones de mínimo de interferencia en una red de difracción:
݀‫= ߠ݊ܽݐ‬
௠೔ ఒ
ே
→ ݀
∆௬
௅
=
௠೔ ఒ
ே
De aquí:
∆‫= ݕ‬
௠೔ ఒ
ௗே
‫=ܮ‬
ଵ∙ହସ଴∙଼଴ ∙ଵ଴ళ
଴,ଷଷ ∙ଵ଴ళ ∙଺
= 21818,2 ሾ݊݉ሿ
Por lo tanto: 2∆‫ = ݕ‬43636,4 ሾ݊݉ሿ = 0,043 ሾ݉݉ሿ.
d) Se forman 9 máximos de interferencia: cuatro a cada lado, más el máximo central. Se anulan
los órdenes ±3 y ±6 por coincidir con un mínimo de difracción.
e) ܴ =
ഥ
ఒ
∆ఒ
=
ହ଼ଽ,ଷ
଴,ହଽ
= 999 , el poder separador de la red utilizada es ܴ = ݉௜ ܰ = 5 ∙ 6 = 30.
Luego esta red no resuelve el doblete del sodio para el quinto orden del espectro, ya que
30 < 999.
4.- Una red de difracción
de 2,5 [cm], que tiene 3150 líneas por centímetro es iluminada con
luz de mercurio.
a) ¿Qué dispersión es de esperar en el tercer orden cerca de la línea verde intensa
ߣ = 546ሾ݊݉ሿ.
b) ¿Cuál es el poder separador que se puede esperar de esta red en el quinto orden?
Solución
Datos: ݊ = 3150 ቂ
௟í௡௘௔௦
ቃ
௖௠
, ݀=
ଵ
௡
= 3174,6ሾ݊݉ሿ, ݉௜ = 3 (para inciso a), ݉௜ = 5 (para
inciso b).
a) Sabemos que:
‫=ܦ‬
௠೔
ௗ௖௢௦ఏ
y que ߠ = ‫ି݊݁ݏ‬ଵ ቀ
௠೔
ௗ
ߣቁ = ‫ି݊݁ݏ‬ଵ ቀ
ଷ∙ହସ଺
ଷଵ଻ସ
ቁ = ‫݊݁ݏ‬−1 0,52
Luego ߠ = 31,1଴ y ܿ‫ ݏ݋‬31,3 = 0,85, por lo tanto:
‫=ܦ‬
ଷ
ଷଵ଻ସ∙଴,଼ହ
௥௔ௗ
= 1,1 ∙ 10ଷ ቂ ௡௠ ቃ
௚௥௔ௗ௢௦
ቃ.
௡௠
‫ = ܦ‬6,3 ∙ 10ିଶ ቂ
b) ܰ = ݈݊ = 3150 ∙ 2,5 = 7875
ܴ = ݉௜ ܰ = 5 ∙ 7875 = 39375
De aquí podemos decir que cerca de 546 [nm] se puede distinguir una diferencia de longitudes
de onda ∆ߣ dada por:
ܴ=
ഥ
ఒ
∆ఒ
→ ∆ߣ =
ఒ
ோ
= 0,01ሾ݊݉ሿ .
5.- ¿Cuál es la longitud de onda más larga que se puede observar en el espectro de quinto
orden utilizando una red con 4000 rendijas por cm?
Solución
௟í௡௘௔௦
ቃ,
௖௠
Datos: ݉௜ = 5, ݊ = 4000 ቂ
‫ = ߠ݊݁ݏ‬1
Condiciones de máximo de interferencia:
݀‫݉ = ߠ݊݁ݏ‬௜ ߣ
Pero: ݀ =
ଵ
௡
(1)
௖௠
= ସ଴଴଴
De (1):
ߣ=
ௗ௦௘௡ఏ
௠೔
=
௖௠
ସ଴଴଴ ∙ହ
=
ଵ଴ళ
ଶ∙ ଵ଴ర
ሾ݊݉ሿ → ߣ = 500 ሾ݊݉ሿ .
6.- Se hace incidir, normalmente, luz de sodio de 589 [nm] de longitud de onda sobre una red
de difracción de 4 [cm2] con 4000 líneas por centímetro. Se proyecta el diafragma de
difracción de Fraunhofer sobre una pantalla situada a 1,5 [m], mediante una lente de 1,5 [m]
de distancia focal, situada justo en frente de la red. Calcular:
a) Las posiciones de los dos primeros máximos de intensidad en uno de los lados del máximo
central.
b) El ancho del máximo central de interferencia.
c) La resolución en el primer orden.
Solución
Datos : ݊ = 4000 ቂ
௟í௡௘௔௦
ቃ,
௖௠
݀=
ܰ = ݈݊ = 8000 ሾ݈í݊݁ܽ‫ݏ‬ሿ
ଵ
௡
→ ݀ = 2,5 ∙ 10ି଺ ሾ݉ሿ, ‫ = ݂ = ܮ‬1,5 ሾ݉ሿ,
a)
Condiciones de máximo de interferencia:
݀‫݉ = ߠ݊݁ݏ‬௜ ߣ
(1)
Para ángulos pequeños: ݀‫݉ = ߠ݊ܽݐ‬௜ ߣ (2)
De la figura:
݀
௬భ
௅
= ݉௜ ߣ → ‫ݕ‬ଵ =
௠೔ ఒ௅
ௗ
=
ଵ ∙ହ଼ଽ ∙ଵ଴షవ ∙ଵ,ହ
ଶ,ହ ∙ଵ଴షల
→ ‫ݕ‬1 = 0,353 ሾ݉ሿ
Siguiendo un proceso análogo al anterior, se obtiene:
‫ݕ‬ଶ =
ଶ ∙ହ଼ଽ ∙ଵ଴షవ ∙ଵ,ହ
ଶ,ହ ∙ଵ଴షల
= 0,7078 ሾ݉ሿ.
b) ߠ =
௬
௅
→ ∆‫ = ݕ‬2‫ߠܮ‬௠í௡
(3)
Condiciones de mínimo de interferencia en una red de difracción:
݀‫= ߠ݊݁ݏ‬
௠೔ ఒ
ே
→ ‫= ߠ݊݁ݏ‬
௠೔ ఒ
ேௗ
Para un ángulo pequeño:
ߠ௠í௡ =
௠೔ ఒ
ேௗ
=
ହ଼ଽ ∙ ଵ଴షవ
଼ ∙ ଵ଴య ∙ଶ,ହ ∙ ଵ଴షల
= 2,945 ∙ 10ିହ ሾ‫݀ܽݎ‬ሿ,
Introduciendo los valores en (3), se obtiene:
∆‫ = ݕ‬2 ∙ 1,5 ∙ 2,945 ∙ 10ିହ = 8,84 ∙ 10ିହ ሾ݉ሿ → ∆‫ = ݕ‬88,4 ሾµ݉ሿ.
c) ܴ = ݉௜ ܰ = 8000.
7.- El telescopio del Monte Palomar posee un diámetro aproximado de 5 [m].
Supóngase una
estrella doble situada a cuatro años luz. En condiciones ideales, ¿cuál debería ser la
separación mínima de las dos estrellas del sistema para que sus imágenes puedan ser
resueltas utilizando luz de longitud de onda de 550 [nm]?
Solución
Datos: ‫ = ܦ‬5ሾ݉ሿ, ‫ = ܮ‬4 ሾܽñ‫ ݏ݋‬− ݈‫ݖݑ‬ሿ, ߣ = 550 ሾ݊݉ሿ.
Según el criterio de Rayleigh se tiene:
ߠ௠í௡ = 1,22
ఒ
஽
ହହ଴
= 1,22 ହ ∙ଵ଴వ → ߠ݉í݊ = 1,342 ∙ 10−7 ሾ‫݀ܽݎ‬ሿ .
Si designamos por ‫ ݕ‬a la separación entre las estrellas, se tiene que:
‫ߠ ܮ = ݕ‬௠í௡ ; entonces:
1ሾܽñ‫ ݋‬− ݈‫ݖݑ‬ሿ = 365 ∙ 86400 ሾ‫ݏ‬ሿ, luego:
4 ሾܽñ‫ ݏ݋‬− ݈‫ݖݑ‬ሿ = 365 ∙ 86400 ሾ‫ݏ‬ሿ ∙ 4 ≈ 1,26 ∙ 10଼ ሾ‫ݏ‬ሿ
௠
‫ = ݐ ∙ ܿ = ܮ‬3 ∙ 10଼ ቂ ௦ ቃ ∙ 1,26 ∙ 10଼ ሾ‫ݏ‬ሿ → ‫ = ܮ‬3,78 ∙ 10ଵ଺ ሾ݉ሿ
Luego:
‫ = ݕ‬3,78 ∙ 10ଵ଺ ∙ 1,26 ∙ 10଼ → ‫ = ݕ‬5,07 ∙ 10ଽ ሾ݉ሿ .
8.- Los faros de un pequeño coche se
encuentran separados por una distancia de 112 [cm].
¿A qué distancia máxima pueden resolverse estos faros si el diámetro de las pupilas es de
5 [mm] y la longitud de onda efectiva de la luz es de 550 [nm]?
Solución
ߠ௠í௡ = 1,22
ఒ
ହହ଴
= 1,22 ହ ∙ଵ଴ల → ߠ݉í݊ = 1,342 ∙ 10−4 ሾ‫݀ܽݎ‬ሿ
஽
Por otro lado:
‫ߠ ܮ = ݕ‬௠í௡ → ‫= ܮ‬
௬
ఏ೘í೙
=
ଵଵଶ
ଵ,ଷସଶ ∙ଵ଴షర
9.- Dos fuentes de 700 [nm] de longitud
= 83,46 ∙ 10ସ ሾܿ݉ሿ → ‫ = ܮ‬8,34 ሾ݇݉ሿ .
de onda están separadas por una distancia horizontal
‫ݔ‬. Están a 5 [m] de una rendija vertical de 0,5 [mm] de ancho. ¿Cuál es el menor valor de ‫ݔ‬
que permite que el diafragma de difracción de las fuentes sea resuelta mediante el criterio de
Rayleigh?
Solución
Datos: ߣ = 700 ሾ݊݉ሿ, ‫ = ܮ‬5 ሾ݉ሿ, ‫ = ܦ‬0,5 ሾ݉݉ሿ, ‫ݔ = ݕ‬.
ߠ௠í௡ = 1,22
ఒ
஽
= 1,22
଻଴଴
଴,ହ ∙ ଵ଴షల
≈ 1,708 ∙ 10ି଺ ሾ‫݀ܽݎ‬ሿ
‫ߠ ܮ = ݕ‬௠í௡ = 5 ሾ݉ሿ ∙ 1,708 ∙ 10ି଺ = 8,50 ∙ 10ି଺ ሾ݉ሿ → ‫ = ݕ‬8,5 ሾ݉݉ሿ .
10.- La estrella Mizar de la Osa mayor es un sistema binario formado por dos estrellas de
magnitudes iguales. La separación angular entre las dos estrellas es de 14 segundos de arco.
¿Cuál es el diámetro mínimo de la pupila que permite la resolución de las dos estrellas
utilizando luz de 550 [nm]?
Solución
Datos: ߣ = 550ሾ݊݉ሿ, ߠ௠í௡ = 14 ሾ‫݋ܿݎܽ ݁݀ ݏ݋݀݊ݑ݃݁ݏ‬ሿ, ‫? ¿ = ݕ‬
ߠ௠í௡ = 1,22
ఒ
஽೘í೙
→ ‫ܦ‬௠í௡ = 1,22 ఏ
ఒ
೘í೙
Se sabe que: 1 ݉݅݊‫ = ݋ܿݎܽ ݁݀ ݋ݐݑ‬60 ‫ ≈ ݋ܿݎܽ ݁݀ ݏ݋݀݊ݑ݃݁ݏ‬3 ∙ 10ିସ ሾ‫݀ܽݎ‬ሿ, por lo tanto :
14 ሾ‫݋ܿݎܽ ݁݀ ݏ݋݀݊ݑ݃݁ݏ‬ሿ ≈ 0,7 ∙ 10ିସ ሾ‫݀ܽݎ‬ሿ
Luego:
ହହ଴
‫ܦ‬௠í௡ = 1,22 ଴,଻∙ ଵ଴షర → ‫݉ܦ‬í݊ ≈ 9,58 ሾ݉݉ሿ .