Relaciones métricas en plano
Anuncio

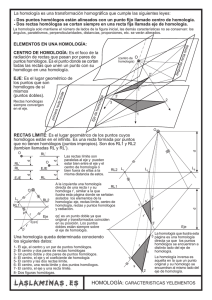
RELACIONES MÉTRICAS EN PLANO CONCEPTO, DEFINICIÓN Y TIPOS Magnitud y cantidad, bajo un punto de vista euclidiano, relación no es sino una clase de conexión que vincula la dimensión entre magnitudes de la misma especie, que implica la división de entes en un cierto nº de partes. Por magnitud entendemos la idea de cualidad que nos permite operar algebraicamente con igualdades y sumas entre elementos geométricos. Toda magnitud definida en un conjunto que cumpla las condiciones de igualdad y suma recibe el nombre de escalar, si además, esos elementos pueden ordenarse linealmente, esto es, entre dos elementos no iguales, puede establecerse la relación de mayor−menor, se deduce que la longitud de un segmento, la amplitud de un ángulo, el área de una superficie son magnitudes escalares ya que son magnitudes escalares ya que las magnitudes que representan pueden ordenarse de forma lineal. La longitud y la amplitud son además contínuas puesto que sus cantidades pueden ser clasificadas en dos diferentes clases ( + y −) con una frontera común (cantidad nula ). Las cantidades correspondientes serán por un nº natural cualquiera. 1º Postulado (el del límite de Weierstrass) : Toda sucesión indefinida de cantidades monótona, creciente y acotado , siendo A una cantidad fija que tiene un límite menor que A. Esta es la base para las mediciones por aproximación. 2º Postulado de Arquímedes: consideramos 2 cantidades absolutas a y b desiguales, tales que la 1ª sea mayor que la 2ª, existe un nº entero n tal que su producto por la 1ª sea siempre igual o mayor que la 2ª (esta es la fase para la adopción de unidades de medidas). 3º Postulados de Cantor del punto límite: Dos sucesiones monótonas convergentes de cantidades ( 1 creciente y otra decreciente ) tales que todo elemento de una sea siempre dos términos homólogos tales que su diferencia sea menor que esta cantidad y por tanto ambas sucesiones tendrán un límite común. Si las cantidades fueran longitudes de segmentos, situados todos ellos sobre una recta cumplirían esta propiedad en la existencia de un punto límite común singular a un punto medio del segmento formado por ambas sucesiones ; otro tanto ocurriría al tratar de magnitudes de ángulos. Esta es la base para los sistemas de medición de cantidades inconmensurables. Las relaciones geométricas son comparaciones o correspondencias establecidas entre elementos geométricos basándose en las magnitudes que los definen. Distinguiremos distintos tipos de relaciones según sean los conceptos de partida para comparar magnitudes (igualdades o proporcionalidad ), según sean los conceptos de congruencia o razón entre sus magnitudes. Según las cantidades de las magnitudes que comparémosla relación de igualdad entre segmentos implica igualdades de cantidades de longitud; sin contar la igualdad de polígonos implica la igualdad de las magnitudes de áreas y la longitud de lado. Podemos distinguir distintos tipos de relación, también a través de los elementos entre los que se establece las distintas comparaciones como relaciones métricas entre polígonos a las relaciones métricas entre un punto y una circunferencia (potencia). IGUALDAD, CONGRUENCIA Y EQUIVALENCIA EN EL PLANO Dos elementos son iguales entre sí, si podemos obtener el uno a partir del otro mediante un movimiento. Equivalencia implica que si existe un carácter coincidente entre dos elementos. Siempre podemos enunciar que 2 elementos equivalentes tienen una cualidad común (la aplicación más concreta es la equivalencia de polígonos) como relación de la cualidad métrica de superficie entre ellos. En un sentido geométrico, igualdad, aplicado a los números de cantidad de medida nos introduce el concepto de congruencia aplicado más concretamente sobre aquellos que mantienen iguales cantidades de medida en l magnitud que los define diferenciándose en el sentido un orden sobre el plano. El concepto de igualdad implica no sólo una misma 1 metricidad sino una concordancia de orden en el plano. Por ejemplo el segmento ab es congruente pero no igual al segmento ba puesto que no mantienen el mismo sentido. Dos figuras son congruentes pero no iguales. No obstante igualdad y congruencia cumplen idénticas propiedades y axiomas. La igualdad de segmentos y ángulos significa igual medida y de sentido pero no necesariamente de posición en el plano. 2 figuras las consideraríamos congruentes cuando todas sus características formales y métricas coinciden, serán iguales si además tienen el mismo sentido en el plano. Por ejemplo: 2 líneas quebradas serán congruentes si mantienen ordenadamente sus lados y ángulos TRANSLACIÓN GEOMÉTRICA: Los vectores equipolentes son iguales en módulo y sentido. A una figura se le aplica un vector de translación y se obtiene la misma figura. Al aplicar un giro hay que tener en cuenta el ángulo y el sentido de giro, todos los vértices se giran en el mismo sentido. HOMOGRAFÍA Si unimos por medio de rectas un punto V exterior a los puntos A, B, C, D de la razón doble, obtenemos un haz de rectas a, b, c, d de vértice V. Si cortamos el haz de rectas A', B', C', D'. A esta operación de unir los puntos de la recta r con V se le denomina proyectar desde V. La operación de cortar el haz de rectas que parte de V con otra recta se le denomina seccionar. En esta operación la razón doble (ABCD) y la determinada en la recta r' es la misma, tiene el mismo valor. En la proyectividad, la razón doble del haz de cuatro puntos es invariante en las operaciones de proyectar y seccionar, es decir, se mantiene la misma razón doble entre los puntos y las rectas en las secciones, cualquiera que sea la recta que corte el haz. TRANSFORMACIONES GEOMÉTRICAS. HOMOLOGÍA Y AFINIDAD Definimos como homología a la correspondencia entre elementos del mismo nombre (punto por punto, recta con recta) de dos figuras planas proyectivas. En una correspondencia biunívoca en el que si un elemento A está en o pasa por otro elemento B, el elemento A' correspondiente al A está en o pasa por B', correspondiente aB La correlación es la correspondencia proyectiva entre elementos de distinto nombre ( punto con recta) de dos figuras planas. La homología: dos secciones planas de la misma radiación determinan dos figuras planas homográficas. En una homografía las figuras se corresponden punto por punto y recta por recta. La homografía de dos secciones de una misma radiación superpuestas en un plano redibe el nombre de homología. En la homología, la intersección de los planos de sección, es la recta llamada eje de homología y el centro de proyección es el centro de homología. Los puntos que se corresponden son puntos homólogos y que están alineados con el centro de homología. Las rectas que se corresponden son rectas homólogas que corresponden puntos homólogo. Estas rectas se encuentran en un punto del eje de homología. Dos figuras son homológicas cuando: • Dos puntos homólogos(A y A') están alineados con un punto fijo V, punto de partida de la radiación y centro de homología. • Las rectas homólogas (r y r') se encuentran en un punto de la recta e ( eje de homología). Una homología quedará definida conociendo: 2 − El centro V, el eje e y un par de puntos homólogos. − El centro V, el eje e y un par de rectas homólogas • Dos triángulos homológicos TEOREMA DE DESARGUES Si dos triángulos ABC y A'B'C' en el mismo plano o en el espacio tienen sus vértices A y A', B y B', C y C' situados dos a dos en tres rectas que concurren en el mismo punto, sus lados AB y A'B', BC y B'C', CA y C'A' se cortan dos a dos en tres puntos P, Q, R que están en una línea recta. Dos triángulos homográficos definen una homología, ya que sus lados homólogos determinan el eje e y las rectas que unen vértices homólogos se cortan en el centro 0, centro de homología. RECTAS LÍMITES Reciben este nombre las rectas l y l'. Son los lugares geométricos de los puntos cuyos homólogos están en el infinito. Son paralelas al eje. El eje de homología es el lugar geométrico de los puntos dobles ya que todas las rectas homólogas se encuentran en un punto del eje e. La transformada de una circunferencia es una cónica. No importa que la circunferencia esté a uno u otro lado del eje. 1.Si la circunferencia está próxima al eje y lejos de la recta límite, la homóloga será una elipse. 2.Si la circunferencia es tangente al eje de la elipse, el resultado será tangente también a ese punto del eje (por ser dobles). 3. Si la circunferencia es tangente a la recta límite, la homóloga tendrá un punto impropio ( en el infinito), por lo que la curva no se cerrara−−−Parábola. 4.Si la circunferencia es secante a la recta límite, la homóloga tendrá dos puntos impropios y la transformada será una hipérbola. 3