Interferencia Intersimbólica (ISI)

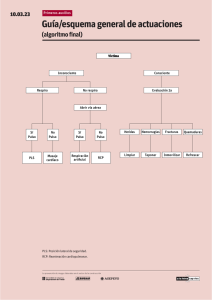
ITERFERECIA ITERSIMBOLICA
Hemos convertido una señal analógica en digital a través del proceso de muestreo, cuantificación
y codificación. Ahora nos disponemos a transmitirla por un canal que usualmente tiene ancho de banda
finito y por lo tanto producirá dispersión de los pulsos transmitidos que interferirán con los pulsos
vecinos (interferencia intersimbólica o ISI por sus siglas en ingles); en el canal también se agrega ruido
que generalmente puede ser modelado como blanco, gausseano. Al final al receptor llegara una señal
con ISI y ruido. El problema que tenemos al frente es diseñar el mejor receptor que permita rescatar la
señal de la mejor forma; esto depende fuertemente de la forma del pulso básico de transmisión p(t).
Por lo complicado del problema lo hemos atacado de la siguiente forma: primero vimos el efecto
del ruido blanco, gausseano aditivo, se buscó el receptor óptimo para minimizar la probabilidad de
error; ahora estudiaremos el problema de la Interferencia Intersimbólica y como atacarlo; finalmente
mezclaremos los dos problemas y diseñaremos, en forma conjunta el transmisor y el receptor óptimos.
Interferencia Intersimbólica (ISI)
Para transmitir una señal digital, no importa que código de línea usemos, se necesita un canal de
ancho de banda infinito. Sin embargo, sabemos que esto no es posible, el canal práctico tiene ancho de
banda finito, por lo tanto los pulsos se "chorrearan" o “dispersarán” y hará que estos entorpezcan la
decisión sobre los bits vecinos. Observe la siguiente gráfica de tres bits seguidos que se han dispersado
porque el canal no tiene ancho de banda infinito. Podría ocurrir, por ejemplo que el tercer bit
(combinación de los voltajes presentes y pasados) al llegar al receptor sea visto como un cero. Que
podemos hacer para evitar esto???
Para entender mejor el concepto de ISI suponga que un pulso transmitido al pasar por toda la
cadena de Transmisor – Canal y Recepción produce un pulso a la puerta del bloque de toma de
decisiones como el siguiente:
Suponga que tbit=1 segundo. De la gráfica se aprecia que el retardo que produce la cadena es de 5
segundos ya que el primer bit se generó entre 0 y 1 segundo y, viendo el pulso p(t), se sabrá cual fue
ese bit a los 6 segundos(donde está el máximo). También se observa que el pulso se dispersa hacia los
lados afectando 2 tbit a la izquierda y 2 tbit a la derecha. Cuando se transmitan varios pulsos seguidos la
situación podría ser como sigue:
Imagine que quiere decidir que voltaje se presenta en 6 segundos. Se aprecia que en t=6 seg. No
solo se tiene el voltaje propio del pulso que corresponde a ese slot de tiempo, sino que dos pulsos a la
“derecha” con 0.4v y -0.2 v , y dos pulsos a la izquierda (0.4 v y -0.2 v). El voltaje total en t=6 es igual
a 1+0.4-0.2-0.2+0.4=1.4 v. La decisión sobre el pulso dirá que es un “1”.
Sin embargo si la combinación de pulsos fuese otra, la suma total de voltajes podía llevar al
sistema de toma de decisiones a cometer error.
Ejemplo: Pulso negativos los que están centrados en 4, 6 y 8 segundos. Positivos el resto
La suma daría -1+0.4+0.2+0.4+0.2=0.2 mayor que cero es decir se decidirá que el pulso
transmitido era un “1” cuando en realidad era un “0”
Paso 1:
Primero tomamos el pulso que se encuentra a -2tb a la izquierda (azul claro). Para t=6seg., toma
el valor de -0.2V. Pero si el pulso fuese el de polaridad opuesta, el valor sería de 0.2V. Luego tomamos
el pulso que está a –tb a la izquierda (verde). Para t=6seg. toma un valor de 0.4V. Si fuese el de
polaridad opuesta, tendría un valor de -0.4V.
Paso 2:
Repetimos el procedimiento del paso 1, pero tomando en consideración los pulsos que estén a +tb
y +2tb del aislado (naranja y morado, respectivamente).
Paso 3:
Elaboramos una tabla que contenga todas las combinaciones de ISI posibles. Dado que el pulso
aislado se ve afectado por cuatro vecinos (dos a su izquierda y dos a su derecha), cada uno con dos
valores posibles, el total de combinaciones será de dieciséis (16):
-2tb
-tb
tb
2tb
ISI
Pro
b
-0.2
-0.2
-0.2
0.4
0.4
0.4
0.4
0.4
-0.4
-0.2V
0.2V
-0.2V
-0.2
-0.2
0.4
-0.4
-0.4
0.4
0.2V
-0.2V
-0.2
-0.2
-0.4
-0.4
0.4
-0.4
0.2V
-0.2V
-0.2
-0.4
-0.4
0.2V
0.2
0.2
0.2
0.2
0.2
0.2
0.2
0.4
0.4
0.4
0.4
-0.4
-0.4
-0.4
0.4
0.4
-0.4
-0.4
0.4
0.4
-0.4
-0.2V
0.2V
-0.2V
0.2V
-0.2V
0.2V
-0.2V
0.2
-0.4
-0.4
0.2V
0.4
0.8
0.4
0
0.4
0
1.2
0.8
0.8
1.2
0
0.4
0
0.4
0.8
0.4
1/16
1/16
1/16
1/16
1/16
1/16
1/16
1/16
1/16
1/16
1/16
1/16
1/16
1/16
1/16
1/16
Finalmente:
Total ISI
0
0.4
-0.4
0.8
-0.8
1.2
-1.2
Probabilidad
4/16
3/16
3/16
2/16
2/16
1/16
1/16
Es a partir de esta tabla que se puede graficar la fdp:
Para el cálculo de la probabilidad de error se deben considerar las combinaciones de la primera
tabla que pudieran provocar la decisión incorrecta. El pulso punteado toma como máximos valores 1
(para el “1”) y -1 (para el “0”). Cuando a estos valores se les sume la ISI podrá ocurrir un error. Por
ejemplo si se transmitió un “1” (1 volt.) y la ISI vale -1.2, al sumar 1-1.2=-0.2. Como el umbral está en
cero se tomará la decisión de que lo transmitido fue un “0” y se comete un error. Si se analizan todos
los casos posibles, existen dos posibilidades de error por interferencia: que se transmita un “1” y la ISI
sea de -1.2V o que se transmita un “0” y la ISI dé 1.2V. Por lo tanto:
1 e  1 e 
P
 + P
=
2  t1  2  t0 
1
1
P (1 + ISI < 0) + P (− 1 + ISI > 0 ) =
2
2
1
1
1 1  1
P (ISI < −1) + P (ISI > 1) = 2 .  =
2
2
 2 16  16
Pe =
Hagamos otro ejemplo para afianzar el mecanismo: Imaginemos que a la salida del receptor, en
una transmisión polar binaria, tb =1 seg. cuando se transmite un “1” se recibe el siguiente pulso
Este pulso solo afecta a los vecinos inmediatos (tb a la izquierda y tb a la derecha). Para calcular
la fdp de la ISI hay que estudiar todas las combinaciones que pueden tomar esos vecinos. Por ejemplo
si el pulso anterior y el posterior provienen de “1s” (11) entonces la situación sería la siguiente
Al pulso que está centrado en 6 le afectarán los siguientes voltajes 0.8 (del pulso anterior) y 0.8
(del pulso posterior). Es evidente que faltan tres combinaciones mas 00,01,10. Es necesario entonces
hacer la siguiente tabla
-tb
0.8
-0.8
-0.8
0.8
Gráficamente la fdp será:
tb
0.8
-0.8
0.8
-0.8
ISI total
1.6
-1.6
0
0
Probabilidad
1/4
1/4
1/4
1/4
Al calcular la Probabilidad de Error por bit debida a la ISI tendremos
1 e  1 e 
P
 + P
=
2  t1  2  t0 
1
1
P(1 + ISI < 0 ) + P(− 1 + ISI > 0 ) =
2
2
1
1
1 1 1
P(ISI < −1) + P(ISI > 1) = 2 .  =
2
2
2 4 4
Pe =
Aún cuando la Interferencia Intersimbólica es crítica al momento de recibir una señal, pudiéramos
disminuir (o eliminar) los errores de decisión a través de ciertos métodos. Es posible prever la forma de
los pulsos a la salida del receptor y de esta manera tratar de que el mismo no produzca ISI.
CRITERIOS DE YQUIST Nyquist desarrollo 3 procedimientos para seleccionar los pulsos de
manera de controlar la ISI. Primer Criterio de yquist:
La
idea
es
buscar
 1 ; t=0

p (t ) = 
0 ; t = ± nt

b
BW =
1
2t b
El pulso p(t) podría ser
un
pulso
recibido
que
tenga
las
siguientes
características:
p (t ) = Af b Sinc (tf b )
P( f ) = A∏ ( ftb )
Pero esto es imposible de lograr. Algo posible se lograría, por ejemplo, flexibilizando el requisito
de ancho de banda; por ejemplo se puede permitir un P(f) que ocupe un ancho de banda mayor que
0.5fb.
En el receptor lo que se hace es muestrear cada tb (seria como convolucionar p(t) con una
sumatoria infinita de impulsos); lo que se desea es que al muestrear cada pulso y sus vecinos, solo
quede el valor del pulso en el instante de muestreo de interés. Por ejemplo suponga que estamos
tomando el valor en t=0
p (t )∑ δ (t − ktb ) = p(0)δ (t )
P( f ) *
1
tb
∑ δ ( f − nfb ) =
1
tb
∑ P( f − nfb ) = 1
Esto implica que al sumar todas las repeticiones de P(f) cada fb estas deben sumar una constante
(que en este caso la colocamos como 1)
Esto recuerda VSB y efectivamente a este tipo de filtros se les llama filtros vestigiales. Para
analizar matemáticamente el efecto, conviene descomponer P(f) en dos componentes como sigue
Matemáticamente:
 f 
P( f ) = ∏   + H1 ( f )
 fb 
p (t ) =
 t 
1
Sinc  + h1 (t )
tb
 tb 
H1(f) es simétrica y par.
∞
h1 (t ) =
∫ H 1 ( f )e
jωt
∞
df = 2 ∫ H 1 ( f )Cos (ωt )df
−∞
0
fb
2
∫ H1 ( f )Cos(ωt )df
h1 (t ) = 2
fb − β
2
fb + β
2
+ 2 ∫ H 1 ( f )Cos (ωt )df
fb
2
 Para la primera Integral :

c.d .v : 
 Para la segunda Integral :

f = fb
f = fb
2
2
−x
+x
Entonces :
β
β
fb
fb
 fb

 fb

h1 (t ) = 2 ∫ H1  − x Cos (2π ( − x))tdx + 2 ∫ H 1  + x Cos (2π ( + x))tdx
2
2
 2

 2

0
0
Por simetría :
H1 (
fb
fb
+ x) = − H 1 ( − x)
2
2
β
fb
fb
 fb





h1 (t ) = 2 ∫ H1  + x  Cos 2πt ( + x)  − Cos 2πt ( − x)  dx
2
2
 2





0
β
 fb

h1 (t ) = −4 ∫ H1  + x [Sen(πf b t ).Sen(2πxt )]dx
 2

0
β
 fb

h1 (t ) = −4Sen(πf b t ) ∫ H 1  + x  Sen(2πxt )dx
 2

0
Para cada ntb el término que se encuentra fuera de la integral se anulará cada ntb. De esta forma,
se evita la interferencia.
Por lo tanto, como
p (t ) =
t 
1
Sinc  + h1 (t )
tb
 tb 
Y esto vale cero para todo t= ntb y toma el valor de 1/ tb para t=0 y esto sin duda evita la interferencia
inter simbólica.
Un ejemplo de un pulso realizable que presenta simetría vestigial es el siguiente:
fbP ( f ) = 1 para f ≤ 0.5 f b − β
fbP ( f ) = 0
para f ≥ 0.5 f b + β
π ( f − 0.5 f b + β )

fbP ( f ) = 0.51 − Cos

2β


La forma de onda temporal quedaría:
p (t ) = Sinc ( f b t )
Cos (2πβt )
1 − (4 β t ) 2
Cuando β=0 queda la forma de onda Sinc
para 0.5 f b − β < f < 0.5 f b + β
Una selección preferida es tomar β=0.5fb. En este caso el pulso en su zona de caída tiene la
siguiente expresión:
π ( f )

2  π ( f )
fbP( f ) = 0.51 − Cos
=
Cos



2
f
f
 b 
b 

para 0 < f < f b
Segundo Criterio de yquist:
Buscando eliminar la ISI y además disminuir el ancho de banda, se define el segundo criterio de
Nyquist. Este criterio se basa en definir los pulsos de manera que exista interferencia controlada entre
un bit y sus vecinos mas cercanos. Conociendo la ley de interferencia uno puede detectar cada bit en el
receptor. Lo que va a ocurrir es que la señal va a ocupar menos ancho de banda pero consumirá mas
potencia.
Por ejemplo, si en vez de enviar la secuencia de bits originales que llamaremos ak, se envia yk=
ak+ ak-1
Esto se le denomina señalamiento duobinario ya que en el mismo ancho de banda se puede
transmitir el doble de bits que antes. Veamos su efecto:
Bit
Original
0
1
0
1
0
0
1
1
ak
-
1
-1
1
-1
-1
1
1
yk
0
0
0
0
-2
0
2
ak=
1
-1
1
-1
-1
1
1
1
yk- ak-1
Generar la secuencia se logra muy fácilmente pasando la secuencia por un filtro pasabajo que
limitará el ancho de banda. Este filtro se construye de la siguiente manera:
La respuesta en frecuencia de este sistema es la siguiente:
Esto se anula en 0.5fb.
En definitiva la secuencia yk tendrá menor ancho de banda que la original sufriendo menos el
efecto de la limitación en ancho de banda del canal. En el receptor se puede rescatar la secuencia
original usando la siguiente relación:
yk- ak-1= ak
Ecualización
Si se usa algún sistema para controlar ISI pero la forma de los pulsos resultantes no es perfecta, se
puede colocar antes del circuito que decide un ecualizador el cual puede tener la estructura de un filtro
transversal. La idea es la siguiente:
Los coeficientes Ck pueden ajustarse para compensar cualquier cambio en el canal.
m= !
POUT [t ] =
∑C
m
PI! [t − (m + ! )TS ] Pero la salida está retardada !Ts segundos
m =− !
m= !
POUT [( K + ! )TS ] =
∑C
m
PI! [( K − m)TS ]
m =− !
1 K =0

POUT [( K + ! )TS ] = 
0 K = ±1,±2,.....,± !
Ejemplo 1:
Usaremos un sistema ecualizador con 3 tomas:
0
1
0
0
1
0
 p I! (0) p I! (−1) p I! (−2) C −1 
=  p I! (1) p I! (0) p I! (−1)   C 0  =
 p I! (2) p I! (1)
p I! (0)   C1 
0 .2
0  C −1 
 1

=  − 0 .3
1
0.2  C 0 
 − 0.1 − 0.3 1   C1 
Esto se resuelve y produce las siguientes soluciones:
C-1=-0.1792
C0=0.8961
C1=0.2509
m =1
POUT [( K + 1)TS ] =
∑C
m
PI! [( K − m)TS ]
m = −1
Ejemplo 2: Se sabe que un pulso recibido tiene el siguiente comprtamiento
PIN(tb)= 0.2= PIN(-tb)
PIN(2tb)= 0= PIN(-2tb)= PIN(3tb)= 0= PIN(-3tb)
PIN(0)= 0.8
Diseñe un ecualizador de 3 tomas para forzar el pulso de salida para que no proporcione ISI:
p 0 (0) = 0 = C −1 p I! (0) + C 0 p I! (−t b ) + C1 p I! (−2t b )
p 0 (t b ) = 1 = C −1 p I! (t b ) + C 0 p I! (0) + C1 p I! (−t b )
p 0 (t b ) = 0 = C −1 p I! (2t b ) + C 0 p I! (t b ) + C1 p I! (0)
0 = C −1 0.8 + C 0 0.2
1 = C −1 0.2 + C 0 0.8 + C1 0.2
0 = C 0 0.2 + C1 0.8
Se despejan y se obtiene: C1=-1/2.8; C0=4/2.8; C-1=-1/2.8
Diseño de filtro Transmisor y Filtro Receptor Optimo Considerando Efecto del
ruido e ISI
Considere el sistema compuesto por Transmisor, Canal y receptor.
El objetivo es conseguir el onjunto Transmisor-Receptor Optimos que logren
a)
Elegir una forma de pulso PR(f) que evite la ISI
H T ( f ) H c ( f ) H R ( f ) = PR ( f )
b)
Lograr que la relación Señal a Ruido a la salida sea máxima para minimizar la
Probabilidad de Error
2
S
!
∫ H T ( f ) H c ( f ) H R ( f )e
=
η
∫ 2 HR( f )
2
jωt 0
df
df
Por otra parte a la salida tendremos una sucesión de pulsos que llamaremos la señal y(t) los cuales
corresponden a una secuencia aleatoria asociada a un pulso de salida pR(t). Estos se relacionan con los
de entrada de la siguiente forma:
Recordemos el uso de la desigualdad de Schwartz en la obtención del Receptor óptimo para el
caso de que el canal solo contamina con ruido
∞
∫−∞ V ( f ).W
*
2
( f )df
2
∞
2
∞
≤ ∫− ∞ V ( f ) df .∫−∞ W ( f ) df
Si : V ( f ) = k .W ( f )
∞
∞
∫−∞ W ( f )
2
∫−∞V ( f ).W
df =
∞
∫−∞ V ( f )
Nuevamente debemos definir quien sería V ( f ) =
η
2
Por lo tanto
H T ( f ) H c ( f ) H R ( f )e jωt 0 =
W *( f ) =
η
2
H R ( f )W * ( f )
H T ( f ) H c ( f )e jωt 0
η
2
W( f ) =
2
η
H T * ( f ) H c * ( f )e − jωt 0
V ( f ) = kW ( f )
η
2
HR( f ) = k
HR( f ) = k
2
η
HR( f ) = k
2
η
2
η
*
H T * ( f ) H c * ( f )e − jωt 0
H T * ( f ) H c * ( f )e − jωt 0
HT ( f ) H c ( f )
Pero también se cumple que
H T ( f ) H c ( f ) H R ( f ) = PR ( f )
2
( f )df
2
df
HR( f )
HT ( f ) H c ( f ) k
2
HT ( f ) =
2
η
H T ( f ) H c ( f ) = PR ( f )
η PR ( f )
2k H c ( f ) 2
PR ( f )
2
2
PR ( f )
HR( f ) =
=
2
2
η PR ( f )
2
HT ( f ) H c ( f )
Hc ( f )
2
2k H c ( f )
2
2
HR( f ) =
2k
η
PR ( f )
Observe que si el canal tiene una Hc(f) mas o menos constante en la banda de la señal tanto el
filtro de transmisión como el filtro de recepción tendrán una respuesta en frecuencia cuya magnitud es
proporcional a la raíz de PR(f)
H T ( f ) = K1 PR ( f )
H R ( f ) = K 2 PR ( f )
Por eso si se toma la decisión de que el pulso sea uno de tipo coseno alzado, a la respuesta en
frecuencia de los filtros se les llama raíz cuadrada de coseno alzado