Aplicación

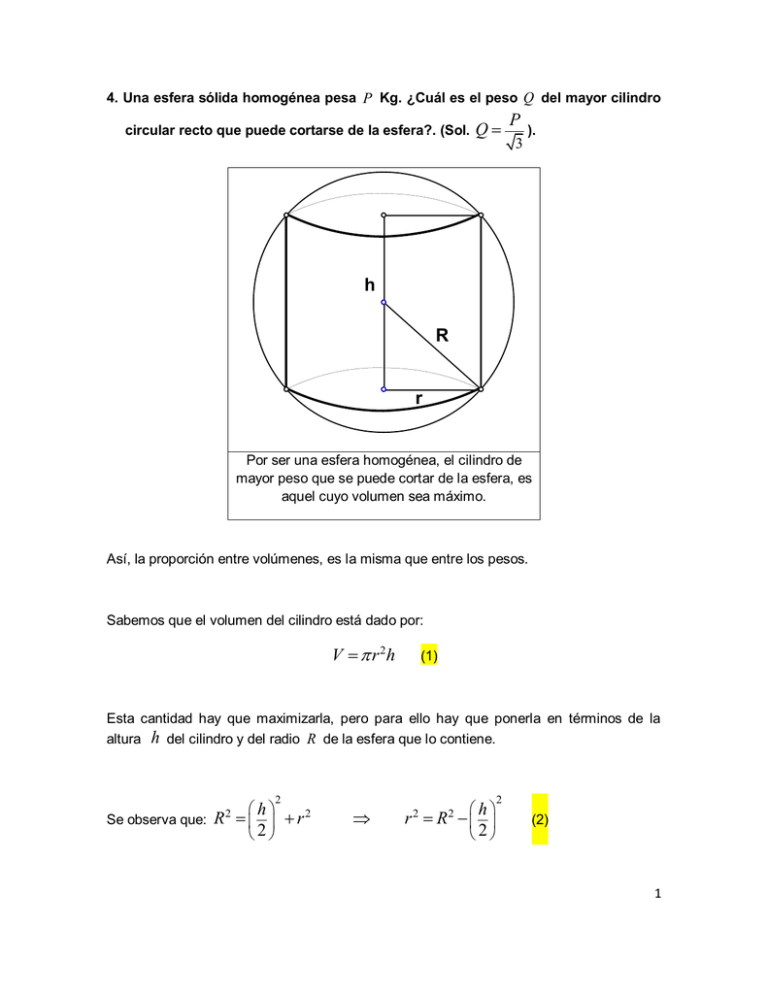
4. Una esfera sólida homogénea pesa P Kg. ¿Cuál es el peso Q del mayor cilindro
circular recto que puede cortarse de la esfera?. (Sol.
Q
P
3
).
h
R
r
Por ser una esfera homogénea, el cilindro de
mayor peso que se puede cortar de la esfera, es
aquel cuyo volumen sea máximo.
Así, la proporción entre volúmenes, es la misma que entre los pesos.
Sabemos que el volumen del cilindro está dado por:
V   r 2h
(1)
Esta cantidad hay que maximizarla, pero para ello hay que ponerla en términos de la
altura h del cilindro y del radio R de la esfera que lo contiene.
2
h
2
Se observa que: R     r
2
2

h
r  R  
2
2
2
2
(2)
1
 2  h 2 
Sustituyendo (2) en (1), nos queda: V (h)    R     h

 2  

De donde:

V '(h)    R 2 

3h2 

4 
(3)
Para obtener el máximo, debemos tener que:
Sustituyendo



(2)
 R 

 3
V    R2  
2
y
V '(h)  0
(4)
en

(1),
h
2R
3
tenemos
(4)
que:
 2R
4

 R3 .(Volumen máximo del cilindro).

 3
3 3

4
 R3
Volumen cilindro 3 3
1
, que es la proporción entre los


4 3
Volumen esfera
3
R
3
Q
1

volúmenes y como es la misma proporción entre los pesos, tenemos que:
, de
P
3
Realizando el cociente:
donde:
Q
P
kg
3
Peso del cilindro circular recto que puede cortarse de la esfera.
2