Cálculo Diferencial e Integral II 9 de octubre de 2013 1

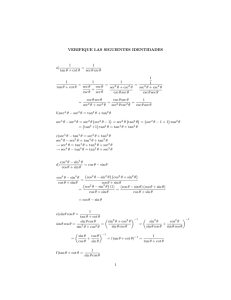
Cálculo Diferencial e Integral II
9 de octubre de 2013
1
Métodos de Integración
Integrales de potencias de las funciones trigonométricas
Teorema 1. Si n es un entero positivo, entonces
Z
Z
senn−1 x cos x n − 1
senn x dx = −
senn−2 x dx
+
n
n
Demostración. Dado que senn x = senn−1 x (sen x), escogiendo u(x) = senn−1 x y v 0 (x) = sen x, se
tiene
u(x) = senn−1 x ⇒ u0 (x)
= (n − 1)R senn−2 x (cos x)
R
v 0 (x) = sen x ⇒ v(x) = v 0 (x) dx = sen x dx = − cos x
Por tanto aplicando la fórmula de integración por partes, se obtiene
Z
Z
Z
n
n−1
n−1
sen x dx = sen
x sen x dx = − sen
x cos x + (n − 1) senn−2 x cos2 x dx
= − senn−1 x cos x+(n−1)
= − sen
Z
n−1
Z
senn−2 x (1 − sen2 x) dx = − senn−1 x cos x+(n−1)
senn−2 x − senn x) dx =
Z
x cos x + (n − 1)
sen
n−2
Z
x dx − (n − 1)
senn x dx
por lo tanto
Z
Z
senn x dx = − senn−1 x cos x + (n − 1)
senn x dx + (n − 1)
Z
sen
n
x dx (1 + n − 1) = − sen
sen
Ejemplo.-Calcular
n
senn−2 x dx − (n − 1)
senn x dx = − senn−1 x cos x + (n − 1)
Z
Z
Z
Z
n−1
Z
x cos x + (n − 1)
− senn−1 x cos x (n − 1)
+
x dx =
n
n
Z
Z
Z
senn x dx
senn−2 x dx
senn−2 x dx
senn−2 x dx
sen2 x dx
Aplicando la fórmula se tiene
Z
Z
− sen x cos x 1
− sen x cos x 1
sen2 x dx =
+
dx =
+ x+C
2
2
2
2
Prof. Esteban Rubén Hurtado Cruz
1 of 3
Cálculo Diferencial e Integral II
9 de octubre de 2013
Teorema 2. Si n es un entero positivo, entonces
Z
Z
cosn−1 x sen x n − 1
cosn x dx =
cosn−2 x dx
+
n
n
Demostración. Dado que cosn x = cosn−1 x (cos x), escogiendo u(x) = cosn−1 x y v 0 (x) = cos x, se
tiene
n−2
u(x) = cosn−1 x ⇒ u0 (x)R = (n − 1) cos
x (− sen x)
R
v 0 (x) = cos x ⇒ v(x) = v 0 (x) dx = cos x dx = sen x
Por tanto aplicando la fórmula de integración por partes, se obtiene
Z
Z
Z
cosn x dx = cosn−1 x cos x dx = cosn−1 x sen x + (n − 1) cosn−2 x sen2 x dx
n−1
= cos
Z
x sen x+(n−1)
cos
n−2
Z
n−1
n−2
n
x (1 − cos x) dx = cos
x sen x+(n−1)
cos
x − cos x) dx =
2
= cosn−1 x sen x + (n − 1)
Z
cosn−2 x dx − (n − 1)
Z
cosn x dx
por lo tanto
Z
cos
Z
n
n−1
x dx = cos
cosn x dx + (n − 1)
Z
Z
x sen x + (n − 1)
Z
cos
n−2
Z
x dx − (n − 1)
cosn x dx = cosn−1 x sen x + (n − 1)
Z
cosn x dx
cosn−2 x dx
Z
cosn x dx (1 + n − 1) = cosn−1 x sen x + (n − 1) cosn−2 x dx
Z
Z
Ejemplo.-Calcular
cosn x dx =
cosn−1 x sen x (n − 1)
+
n
n
Z
cosn−2 x dx
cos3 x dx
Aplicando la fórmula se tiene
Z
Z
cos2 x sen x 2
cos2 x sen x 2
3
+
cos x dx =
+ (sen x) + C
cos x dx =
3
3
2
3
Prof. Esteban Rubén Hurtado Cruz
2 of 3
Cálculo Diferencial e Integral II
9 de octubre de 2013
Teorema 3. Si n es un entero positivo, entonces
Z
ln | sec x| + C
n=1
tann x dx = tann−1 x R
n−2
−
tan
x
dx
n=
6 1
n−1
Z
Ejemplo.-Calcular
tan2 x dx
Aplicando la fórmula se tiene
Z
tan2 x dx =
tan x
−
1
Z
dx = tan x − x + C
Teorema 4. Si n es un entero positivo, entonces
Z
ln | sen x| + C
n
cot x dx = − cotn−1 x R
− cotn−2 x dx
n−1
Z
Ejemplo.-Calcular
n=1
n 6= 1
cot3 x dx
Aplicando la fórmula se tiene
Z
Z
cot2 x
cot2 x
3
cot x dx = −
− cot x dx = −
− ln | sen x| + C
2
2
Teorema 5. Si n es un entero positivo, entonces
Z
ln | sec x + tan x| + C
secn x dx = secn−2 x tan x n−2 R
+ n−1 secn−2 x dx
n−1
Z
Ejemplo.-Calcular
n=1
n 6= 1
sec4 x dx
Aplicando la fórmula se tiene
Z
Z
sec2 x tan x 2
sec2 x tan x 2
sec4 x dx =
+
sec2 x dx =
+ tan x + C
3
3
3
3
Teorema 6. Si n es un entero positivo, entonces
Z
ln | csc x − cot x| + C
n=1
n
R
csc x dx =
cscn−2 x cot x
n−2
n−2
−
+ n−1 csc
x dx n =
6 1
n−1
Z
Ejemplo.-Calcular
csc3 x dx
Aplicando la fórmula se tiene
Z
Z
csc x cot x 1
csc2 x cot x 1
3
csc x dx = −
+
csc x dx = −
+ ln | csc x − cot x| + C
2
2
2
2
Prof. Esteban Rubén Hurtado Cruz
3 of 3