teoría de mecanismos práctica 6 síntesis numérica de

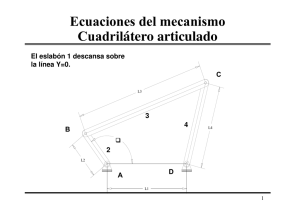
TEORÍA DE MECANISMOS
PRÁCTICA 6
Departamento de Ingeniería Mecánica
Universidad Carlos III de Madrid
Hoja: 1/6
PRÁCTICA 6
SÍNTESIS NUMÉRICA DE MECANISMOS
1. INTRODUCCIÓN
En las clases teóricas, el estudio de los mecanismos planos articulados consistió
en analizar el mecanismo, es decir, determinar el movimiento de todos sus puntos
(trayectorias y formas de ser recorridas), provocadas por las condiciones cinemáticas de
la barra conductora. Se conocen, por tanto, las dimensiones de los eslabones del
mecanismo.
El problema inverso y que hay que abordar, necesariamente, a la hora de diseñar
un mecanismo, se conoce con el nombre de síntesis de mecanismos.
Por medio de la síntesis cinemática de mecanismos se trata de averiguar el
mecanismo físico (dimensiones y disposición de sus elementos) que engendra el
movimiento predeterminado de un punto o de un conjunto de puntos.
En la práctica anterior se prestó especial interés a los métodos de síntesis
estructurales por modificación de cadenas cinemáticas o mecanismos ya conocidos, así
como algún método de síntesis gráfica.
En esta práctica, sin embargo, se van a tratar algunos métodos de síntesis
numéricos aplicados a cuadriláteros articulados, más precisos que los abordados en la
práctica precedente. Los métodos de síntesis numérica seleccionados, para realizar una
comprobación de su utilidad, son:
ƒ La síntesis utilizando la ecuación de Freudenstein, que permite establecer una
relación entre la evolución angular de la barra conductora y la conducida en
un mecanismo de cuatro barras.
ƒ La síntesis de Bloch que, aplicando la técnica de los números complejos,
permite dimensionar un cuadrilátero articulado a partir de la velocidad
angular y la aceleración angular de sus barras.
TEORÍA DE MECANISMOS
PRÁCTICA 6
Departamento de Ingeniería Mecánica
Universidad Carlos III de Madrid
Hoja: 2/6
2. SÍNTESIS NÚMERICA DE FREUDENSTEIN
La síntesis de numérica de Freudenstein es una herramienta muy empleada en la
síntesis de mecanismos de cuatro barras. Aquí, sólo se abordará el problema más
sencillo: el cálculo de las dimensiones de las barras, aunque podría generalizarse para
unas condiciones dadas de velocidad angular y aceleración angular.
Si en un cuadrilátero articulado se establecen las relaciones entre las longitudes
de las barras y los ángulos que forman estas, en el citado mecanismo pueden
representarse las barras como vectores (figura 1).
Figura 1.- Representación vectorial de un mecanismo de cuatro barras.
Siguiendo como referencia la notación utilizada en la figura 1, se observa que,
evidentemente, la suma de las proyecciones de las componentes vectoriales en el eje X
debe ser cero:
L1 ⋅ cos α + L 2 ⋅ cos β − L 3 ⋅ cos φ + L 4 = 0
(1)
Además, la suma de las proyecciones de las componentes vectoriales en el eje Y
también debe ser cero:
L1 ⋅ sen α + L 2 ⋅ sen β − L 3 ⋅ sen φ = 0
( 2)
TEORÍA DE MECANISMOS
PRÁCTICA 6
Departamento de Ingeniería Mecánica
Universidad Carlos III de Madrid
Hoja: 3/6
Si las ecuaciones (1) y (2) se reorganizan y se elevan al cuadrado resulta:
L22 ⋅ cos 2 β = ( L 3 ⋅ cos φ − L1 ⋅ cos α − L 4
L22 ⋅ sen 2 β = ( L 3 ⋅ sen φ − L1 ⋅ sen α
)2
)2
(3 )
( 4)
Si las ecuaciones (3) y (4) se suman, el resultado sería:
L22 = L21 + L23 + L24 − L 3 ⋅ L 4 ⋅ cos φ − L1 ⋅ L 3 ⋅ cos α ⋅ cos φ − L1 ⋅ L 3 ⋅ sen α ⋅ sen φ − L1 ⋅ L 4 ⋅ cos α
(5)
Para simplificar esta ecuación puede realizarse un cambio de variables con la
siguiente asignación de parámetros:
R1 =
L4
L3
R2 =
L4
L1
R3 =
(L
2
4
+ L23 + L21 − L22
2 ⋅L1 ⋅L 3
)
Resultado del cambio de variables de la ecuación (5) es la expresión:
R1 ⋅ cos α − R 2 ⋅ cos φ + R 3 = cos ( α − φ )
(6)
Esta ecuación (6) es conocida como la ecuación de Freudenstein para los
mecanismos de cuatro barras, probablemente la técnica de síntesis más utilizada en los
problemas de diseño donde se requiere el movimiento coordinado entre el eslabón de
entrada y el de salida.
TEORÍA DE MECANISMOS
PRÁCTICA 6
Departamento de Ingeniería Mecánica
Universidad Carlos III de Madrid
Hoja: 4/6
3. SÍNTESIS DE BLOCH
La síntesis de Bloch consiste en satisfacer requisitos cinemáticos aplicando la
técnica de los números complejos. Por este procedimiento, conociendo las velocidades
angulares ( ω2 , ω3 y ω4 ) y las aceleraciones angulares ( ε2 , ε3 y ε4 ) de las barras 2, 3
y 4 de un cuadrilátero articulado como el de la figura 2, se pueden calcular las
dimensiones de las cuatro barras.
B
α4
L3
3
A
L2
4
α3
L4
2
α2
O2
1
α1
L1
O4
Figura 2.- Representación de un cuadrilátero articulado.
En efecto, si se consideran las barras como vectores y se hace uso de la forma
compleja en coordenadas polares, se obtiene:
r r
r
r
L 1 +L 2 +L 3 +L 4 = 0
L 1 ⋅ e j ⋅α1 + L 2 ⋅ e j ⋅α 2 + L 3 ⋅ e j ⋅α 3 + L 4 ⋅ e j ⋅α 4 = 0
(7 )
Si la ecuación (7) se deriva respecto al tiempo, resulta:
L 2 ⋅ω 2 ⋅ e j ⋅α 2 + L 3 ⋅ω 3 ⋅ e j ⋅α 3 + L 4 ⋅ω 4 ⋅ e j ⋅α 4 = 0
(8 )
TEORÍA DE MECANISMOS
PRÁCTICA 6
Departamento de Ingeniería Mecánica
Universidad Carlos III de Madrid
Hoja: 5/6
Si a su vez, la ecuación (8) se deriva respecto al tiempo, se obtiene:
L 2 ⋅ ( ε 2 + j ⋅ω 22 ) ⋅ e j ⋅α 2 + L 3 ⋅ ( ε 3 + j ⋅ω 32 ) ⋅ e j ⋅α 3 + L 4 ⋅ ( ε 4 + j ⋅ω 42 ) ⋅ e j ⋅α 4 = 0
(9 )
Pasando las ecuaciones (7), (8) y (9) a la forma vectorial, se obtiene:
L1
0
0
+L2
+ L 2 ⋅ω 2
+ L 2 ⋅( ε 2 +
j ⋅ω 22
+L3
+ L 3 ⋅ω 3
)
+ L 3 ⋅( ε 3 +
j ⋅ω 32
+L4
+ L 4 ⋅ω 4
)
+ L 4 ⋅ ( ε 4 + j ⋅ω )
2
4
=0 ⎫
⎪
=0 ⎬
= 0 ⎪⎭
(10)
Si las ecuaciones (10) se dividen por “L 1” se podrá calcular “L 2 / L 1”, “L 3 / L 1”
y “L 4 / L 1”. Además, si se considera la longitud de la barra 1 (O2O4) como la unidad
(L 1 = 1), se podrían obtener las longitudes de un cuadrilátero semejante.
También, al hacer el discriminante igual a la unidad (∆ = 1), los vectores que se
obtienen, al resolver el sistema, serán semejantes y aparecerán girados un mismo
ángulo. Resumiendo, el mecanismo será homólogo al de referencia.
Resolviendo el sistema de ecuaciones (10), planteado anteriormente, resulta:
r
r
r
r
L 1 = −(L 2 +L 3 +L 4 )
L 2 = ω 4 ⋅ ( ε 3 + j ⋅ω 32 ) − ω 3 ⋅ ( ε 4 + j ⋅ω 42 ) = ω 4 ⋅ ε 3 − ω 3 ⋅ ε 4 + j ⋅ω 4 ⋅ω 3 ⋅ ( ω 3 − ω 4 )
L 3 = ω 2 ⋅ ( ε 4 + j ⋅ω 42 ) − ω 4 ⋅ ( ε 2 + j ⋅ω 22 ) = ω 2 ⋅ ε 4 − ω 4 ⋅ ε 2 + j ⋅ω 2 ⋅ω 4 ⋅ ( ω 4 − ω 2 )
L 4 = ω 3 ⋅ ( ε 2 + j ⋅ω 22 ) − ω 2 ⋅ ( ε 3 + j ⋅ω 32 ) = ω 3 ⋅ ε 2 − ω 2 ⋅ ε 3 + j ⋅ω 3 ⋅ω 2 ⋅ ( ω 2 − ω 3 )
TEORÍA DE MECANISMOS
PRÁCTICA 6
Departamento de Ingeniería Mecánica
Universidad Carlos III de Madrid
Hoja: 6/6
4. APLICACIÓN PRÁCTICA
1.- Considerando que los ángulos formados en un cuadrilátero articulado de
referencia, siguiendo la notación del representado en la figura 1, son:
ƒ
α = 0º
Î
φ = 30º
ƒ
α = 30º Î
φ = 50º
ƒ
α = 60º Î
φ = 80º
Conociendo, además, que la barra L1 = 100 mm. Se pide:
¾ Calcular, aplicando la ecuación de Freudenstein, las dimensiones de las
otras tres barras.
2.- Considerando que los parámetros geométricos de un cuadrilátero articulado de
referencia, siguiendo la notación del representado en la figura 2, son:
ƒ
α 1 = 180º
ƒ
α 2 = 60º
ƒ
L1 = 80 mm.
ƒ
L2 = 30 mm.
ƒ
L3 = 75 mm.
ƒ
L4 = 65 mm.
Conociendo, además, que cuando el elemento 2 gira con una velocidad angular
constante ω 2 = - 2 rad/s (el sentido positivo es el antihorario), la velocidad angular
y la aceleración angular del resto de elementos del cuadrilátero articulado son:
ƒ ω 3 = 0,476 rad/s.
ƒ ω 4 = - 0,514 rad/s.
ƒ ε 3 = 1,45 rad/s2.
ƒ ε 4 = 2,01 rad/s2.
Se pide:
¾ Comprobar como por medio de la síntesis de Bloch y a partir de los
valores cinemáticos del cuadrilátero dados, es factible representar un
cuadrilátero análogo al de referencia.
¾ Calcular, a partir del cuadrilátero de referencia y el determinado en el
punto anterior, el valor del discriminante.