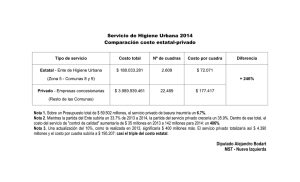
Una aplicación de los residuos cuadráticos al cálculo de sumas

Una aplicación de los residuos cuadráticos al
cálculo de sumas trigonométricas
Iveth V. Martı́nez
Darı́o Herrera
Resumen
Se realiza un estudio del uso de los residuos cuadráticos para la transformación de sumas trigonométricas a expresiones más simples y otra forma de encontrar el número de clase asociado a formas cuadráticas binarias
reducidas a través de las sumas de Gauß y el sı́mbolo de Legendre. Además
se analiza gráficamente el comportamiento de las sumas trigonométricas
al introducir una variable real en el argumento para un número primo fijo.
1.
Introducción
Euler en 1754 presenta unadefinición formal de residuo cuadrático y residuo
no cuadrático al encontrarse con la ecuación cuadrática Diofantina de la forma
x2 − n y los utilizó en la famosa Ley de Reciprocidad Cuadrática. Los residuos
cuadráticos en la actualidad no limita su aplicación en la Ley de Reciprocidad
Cuadrática, presentada por Euler y Gauß , sino que tienen diversas utilidades
en otras áreas de la ciencia como en el caso de la electrónica (en el Diseño de
difusores de sonidos, en difusores de residuos cuadráticos, entre otras) y en la
Matemática para simplificar el cálculo de expresiones con alto grado de complejidad. En este artı́culo analizamos la importancia de los residuos cuadráticos
en la simplificación de los cálculos de sumas trigonométricas, en que el argumento involucra un primo impar, ası́ como otra forma de encontrar de manera
rápida y precisa el valor del número de clases . Iniciamos con algunos conceptos y propiedades básicas que nos faciliten realizar, sistemáticamente, las
transformaciones de una expresióna otra. A la vez nos apoyamos del Algebra
computacional, con el uso del software de aplicación MATHEMATICA, versión
7, para comparar los resultados obtenidos e introducir cambios que nos permita
generar nuevas inferencias.
2.
Nociones básicas
El concepto de residuos cuadráticos tiene su génesis de manera implı́cita en la
solución de las ecuaciones cuadráticas Diofantina, de la forma x2 − n. Estas
29
Factorial!-Revista matemática de la Universidad de Panamá
30
ecuaciones fueron de interés para matemáticos como Fermat al evidenciarse en
su primer teorema que 1 es un residuo cuadrático módulo p. Euler introduce en
1754 la terminologı́a de residuos cuadráticos al afirmar que “Si existe un x tal
que x2 − p es divisible por q, entonces p se dice un residuo o resto cuadrático
de q, ai no existe tal x, p se dice un no resto cuadrático de q”. Lo que equivale
a resolver la ecuación descrita en el párrafo anterior.
En 1772-1783, Bernoulli presenta un ensayo que es considerado un reescrito del
artı́culo de Euler, en donde realiza una recopilación del material sobre residuos
cuadráticos, en especial los teoremas para decidir si -1 es un residuo cuadrático
módulo p o no. Estos resultados intrigaron y desconcertaron a Gauß durante
muchos años y el punto de partida fue una pregunta sencilla: ¿Cómo son los
cuadrados perfectos a un módulo dado? Para tal efecto en el artı́culo 95 de
Disquisitiones Arithmeticae, adopta el lenguaje introducido por Euler, en el
que separa para cualquier módulo, todos los números en dos clases: la clase
que contiene los números que son congruentes a algún cuadrado y la clase que
contiene los números que no pueden ser congruentes a algún cuadrado. Los
números de la primera clase son los residuos cuadráticos y los segundos no
residuos cuadráticos.
Definición 1: Para todo a y p un primo impar tal que (a, p) = 1, recibe el
nombre de residuo cuadrático módulo p si la congruencia x2 ≡ a(modp) tiene
una solución. Si no tiene una solución, entonces a es un residuo no cuadrático.
Ejemplo 1 Mediante una rutina desarrollada en Mathematica, se encuentra los
residuos cuadráticos para cualquier primo p. Ası́ para p = 7, 11 y 19 tenemos
que
In[1]= resp[p ]:=Table[Mod[x2 , p],{x,1,(p-1)/2};res[7] res[11] res[19]
Out[1]={1,4,2} {1,4,9,5,3}{1,4,9,16,17,11,7,5}
Legendre (1808) inventó el sı́mbolo ap para simplificar los cálculos en la Ley
de Reciprocidad Cuadrática, definido de la forma siguiente.
Sea p un primo impar y (a,p) = 1, el sı́mbolo de Legendre se define por
a
1 si a es un residuo cuadrático de p.
=
−1 si a es un residuo cuadrático de p.
p
Vale la pena enunciar algunas propiedades de los residuos cuadráticos que serán
de utilidad a lo largo de este trabajo.
Propiedad 1. Para un primo impar p, los residuos cuadráticos de p son congru2
.
entes módulo p con uno y sólo uno de los enteros 12 , 22 , . . . , p−1
2
Propiedad 2. Si p es un primo impar tal que p ≡ 1(mod4) y C es un conjunto
completo de residuos cuadráticos módulo p, entonces −C ≡ C(modp).
Propiedad 3. (Artı́culo 98 de Disquisitiones Arithmeticae): El producto de dos
residuos cuadráticos de un primo p es un residuo; el producto de un residuo con
un no residuo es un no residuo; finalmente, el producto de dos no residuos es un
residuo cuadrático.
Propiedad 4. Sea p es un número primo, entonces:
VOL.1, NO.1, JULIO 2011
c
Universidad
de Panamá
31
Factorial!-Revista matemática de la Universidad de Panamá
a) Si p ≡ 7(mod8), entonces los conjuntos
2
2n /1 ≤ n ≤ p − 1 y n2 /1 ≤ n ≤ p − 1
son idénticos módulo p.
b) Si p ≡ 3(mod8), entonces los conjuntos
2
2
2n /1 ≤ n ≤ p − 1
y
−n /1 ≤ n ≤ p − 1
son idénticos módulo p.
Los números complejos z soluciones de la ecuación z n = 1, (n = 1,2, ...) se denominan raı́ces de la unidad y vienen dados por zn = e2πk/n , k = 0, 1, 2, ..., n−1.
Cuando k y n son coprimos se denominan raı́ces primitivas n-ésimas de la
unidad.
Residuos cuadráticos y sumas trigonométricas
Sea p un primo impar, consideramos la suma
p−1
2
√ X
T (p) = p
tan
n=1
πn2
p
(1)
Si C es un sistema completo de residuos cuadráticos módulo p. En virtud de la
propiedad 1, la expresión (1) toma la forma
jπ
√ X
(2)
T (p) = p
tan
p
j∈C
ya que p es impar, p ≡ 1(mod4) ó p ≡ 3(mod4) . Si p ≡ 1(mod4), por la
propiedad 2, −C ≡ C(modp) lo que implica que T (p) = 0.
Ejemplo 2 Consideremos p = 13 y los conjunto de residuos cuadráticos C =
{1, 3, 4, 9, 10, 12} y −C = {−1, −3, −4, −9, −10, −12}. Se observa que 1 ≡ −12
, 3 ≡ −10, 4 ≡ −9, 9 ≡ −4, 10 ≡ −3, 12 ≡ −1 (mod13). De (2), obtenemos:
T (13)
√
13
= tan
π
13
+ tan
3π
13
+ tan
4π
13
+ tan
9π
13
T (13)
√
13
= tan
π
13
+ tan
3π
13
+ tan
4π
13
+ tan
−4π
13
+ tan
+ tan
10π
13
+ tan
−3π
13
12π
13
+ tan
−π
13
T (13) = 0
2πi
Sean p ≡ 3(mod4) y ζ = e p , entonces ζ es una raı́z primitia p-ésima de la
unidad. Al hacer uso de la idntidad:
tan(x) = −i
VOL.1, NO.1, JULIO 2011
1 − e−2ix
1 + e2ix
c
Universidad
de Panamá
Factorial!-Revista matemática de la Universidad de Panamá
32
La fórmula (2), toma la forma:
T (p) =
√ X 1 − ζj
p
1 + ζj
(3)
j∈C
En Laradji, A. (2010), se deriva de (3) que T (p) es equivalente a
T (p) =
√ p−1
p−1
X
i pX
(−1)k
ζ 2k
2
j=0
(4)
k=1
Lo sorprendente es que la expresión
S(k, p) =
p−1
X
ζ 2k ,
j=0
para k = 1, 2, . . . , p − 1 es de un tipo particular de sumas incompletas de Gauß,
las cuales se calculan a través de la fórmula:
q
k
√
p
(5)
S(k, p) = i
p
Combinando (4) y (5), obtenemos otra expresión para T (p) en función del sı́mbolo de Legendre:
p−1
pX
k
k+1
T (p) =
(6)
(−1)
2
p
k=1
Esta nueva expresión presenta ventajas, ya que kp = ±1, si k es un residuo
cuadrático o un residuo no cuadrático. Podemos calcular fácilmente T (p) como
un entero impar divisible por p y no por otras potencias de p, de la siguiente
manera:
T (p) = p(q0 (p) − qe (p))
(7)
donde qe (p) y qo (p) representa, respectivamente, la cantidad de residuos cuadrático
pares e impares módulo p.
Ejemplo 3 Analicemos el caso para p = 19 y el conjunto completo de residuos
cuadráticos C, dado en el ejemplo 1.
Tenemos que qo (p) = 6 y qe (p) = 3 y por lo tanto T (p) = 19(6 − 3) = 57.
Comparando este valor con el obtenido en Mathematica, la ecuación T (p) en
(1) para cualquier primo impar, se obtiene:
√
h
h
2 ii
, {k, 0, (q-1)/2}
In[1] = T[a ]:= q ∗ Sum T an N[Pi,10]k
q
In[2] = T[19]
Out[1] = 57.000000
VOL.1, NO.1, JULIO 2011
c
Universidad
de Panamá
Factorial!-Revista matemática de la Universidad de Panamá
33
Con la finalidad de generalizar este estudio, consideremos un primo fijo p un
primo fijo y la función definida para todo x ∈ R por
X
jπx
(8)
T (p, x) =
tan
p
j∈C
A continuación presentamos una rutina en Mathematica para calcular esta nueva
suma para un p fijo.
A partir de esta rutina (función) se puede derivar dos tipos de gráficas, uno
para el caso discreto y el otro para el caso continuo. En el caso discreto cuando
fijamos p = 19 y variamos x de 0 a 42 el valor T [p, y] es 57 ó -57, como se observa
a continuación.
vemos que |T (19, x)| ≤ 57.
Procediendo de manera análoga para el caso continuo, la gráfica viene dada por:
VOL.1, NO.1, JULIO 2011
c
Universidad
de Panamá
Factorial!-Revista matemática de la Universidad de Panamá
34
la expresión (8) es una función periódica y de perı́odo 19, continua y acotada.
De inmediato surge la pregunta, ¿Se mantendrá este comportamiento para otros
primos de la forma 4k + 3?, Procedamos analizar el caso p = 103 y x variando
de 0 hasta 210.
Por (7), y con la siguiente rutina en Mathematica obtenemos los valores de
T (p, x).
Entonces T (103) = 103(23 − 28) = −515. Igual que para el caso anterior;
se puede obtener, respectivamente, la gráfica discreta y continua, las cuales
mostramos a continuación.
VOL.1, NO.1, JULIO 2011
c
Universidad
de Panamá
Factorial!-Revista matemática de la Universidad de Panamá
35
Se observa el mismo comportamiento que el caso p = 19, es decir |T (103, x)| ≤
|T (103)| = 515 y la expresión (8) es una función, (para p = 103) periódica
con perı́odo 103, continua y acotada. ¡Sorprendente! Para todos los primos de
la forma 4k + 3, es posible demostrar que este comportamiento se mantiene.
Ahora describiremos un procedimiento para determinar el signo de T (p), para
tal efecto tengamos presente que:
Si p ≡ 3(mod4) entonces p ≡ 3(mod8) ó p ≡ 7(mod8).
Del artı́culo 98, Gauss, F.(1995), la ecuación (1) se reescribe:
2
√ X
p−1
p
πn
T (p) =
tan
2 n=1
p
La Desigualdad de A. L. Whiteman
2
p−1
X
πn
>0
cot
p
n=1
VOL.1, NO.1, JULIO 2011
c
Universidad
de Panamá
Factorial!-Revista matemática de la Universidad de Panamá
36
Tomando en cuenta la identidad tanθ = cotθ − 2 cot2θ la expresión en el
punto 2, se escribe de la forma
2
p−1
p−1
X
X
2πn2
πn
2
−2
cot
cot
√ T (p) =
p
p
p
n=1
n=1
Ası́, si p ≡ 7(mod8) por la propiedad 4-a, se deduce que T (p) < 0 y el número
de residuos cuadráticos impares es menor que el número de residuos cuadráticos
pares. Si p ≡ 3(mod8) implica que T (p) > 0, (por la propiedad 4-b), y por ende
el número de residuos cuadráticos impares es mayor que el número de residuos
cuadráticos pares.
El número de clases y el sı́mbolo de Legendre
Los restos cuadráticos también se utilizan para hacer un cálculo rápido y preciso
del número de clases de la forma cuadrática binarias reducidas. Presentamos,
primeramente, algunas definiciones útiles para centrarnos en el número de clases
antes señalado.
Una forma cuadrática binaria es un polinomio f (x, y) ∈ Z[x, y], el cual es homogéneo de grado 2. Su forma general es:
f (x, y) = ax2 + bxy + cy 2
El discriminante de la forma cuadrática binaria f (x, y) = ax2 + bxy + cy 2 se
define por D = b2 − 4ac. Si a y c son ambos positivos y D es negativo, diremos
que f es definida positiva. En el caso en que |b| ≤ a < c y si |b| = a ó a = c
entonces b ≥ 0, diremos que f es reducida.
Un entero D es un discriminante fundamental si D ≡ 1(mod4) y es libre
de cuadrado o D ≡ 0(mod4) , D/4 es libre de cuadrado y D ≡ 2(mod4),
ó D ≡ 3(mod4). En particular, si p es primo y p ≡ 3(mod4), −p es un discriminante fundamental.
El número de clases h(D) se define como el número de formas cuadráticas binarias reducidas de discriminante D. En el corolario 2.3 del artı́culo, B.C. Berndt
y A. Zaharescu (2008), prueban que
p−1 1 X
h(−p) = √
2 p
k=1
k
p
cot
kπ
p
A partir de esta última expresión y de los resultados aquı́ mostrados, se tiene
que:

si p ≡ 7(mod8).
 qe (p) − q0 (p)
h(−p) =
 1
si p ≡ 3(mod8).
3 [qe (p) − q0 (p)]
Ejemplo 4 Calculemos h(−11). Como 11 ≡ 3(mod8), tenemos tenemos que:
VOL.1, NO.1, JULIO 2011
c
Universidad
de Panamá
Factorial!-Revista matemática de la Universidad de Panamá
1
(qo (11) − qe (11)) =
3
Este tipo de cálculos se pueden verificar con el
Mathematica
h(−11) =
37
1
(4 − 1) = 1
3
uso de la siguiente rutina en
Esto nos indica que sólo hay una forma cuadrática binaria reducida del discriminante -11, y ası́ todas las formas de discriminante -11 son equivalentes y por
ende representan los mismos enteros.
También obtenemos:
h(−3) = h(−7) = h(−19) = h(−43) = h(−163) = 1
Gauß, en Disquisitiones Arithmeticae, conjeturó nueve discriminantes fundamentales D asociados a la forma cuadrática con h(D) = 1 y en consecuencia
otros tantos cuerpos imaginarios con anillos de enteros donde vale el principio
de factorización única.
Referencias
[1] Apostol, T. M. 1984. Introducción a la Teorı́a Analı́tica de Números. SpringerVerlag, Barcelona. pp. 223-225
[2] Berndt, B.C. &Zaharescu, A. 2004. Finite Trigonometric sums and class
number. Math. Ann 330. 551-575.
[3] Boccara, Nino. 2007. Essentials of Mathematica: with Applications to Mathematics and Physics. Springer, Chicago Illinois.
[4] Burton, D. 1980. Elementary Number Theory. Allyn & Bacon, Boston. pp.
184-189
[5] Chamizo, F. 2010. Formas Cuadráticas Binarias Definidas Positivas.
http://www.uam.es/personal pdi/ciencias/fchamizo/kiosco/files/qua2010.
pdf
[6] Gauß, K. F. 1995. Disquisitiones Arithmeticae. Universidad de Costa Rica,
San José.
[7] Krantz, S. G. 2010. An Episodic History of Matehemathic:
Mathematical Culture Through Problem Solving. TheMathematicalAssociation
of America, USA. pp. 187-189
[8] Laradji, A., Mignotte, M. & Tzanakis, N. 2010. Elementary
VOL.1, NO.1, JULIO 2011
c
Universidad
de Panamá
Factorial!-Revista matemática de la Universidad de Panamá
38
Trigonometric Sums related to Quadratic Residues. Math. N. T. pp 1-9
[9] Lemmermeyer, F. 2000. Reciprocity Laws: From Euler to Eisenstein. SpringerVerlag, New York. pp. 12-25
[10] Leveque, W. J. 1968. Teorı́a Elemental de los Números. Herrero Hermano,
México: Centro Regional de Ayuda Técnica, pp. 69-76
[11] López, R. 2005. Formas Cuadráticas, Grupo de Clases y Factorización de
Enteros. http://smm.org.mx/SMMP/html/modules/Publicaciones/AM/Cm/35/
artExp06.pdf
VOL.1, NO.1, JULIO 2011
c
Universidad
de Panamá