DEDUCCIÓN DE LAS ECUACIONES DE LA RECTA

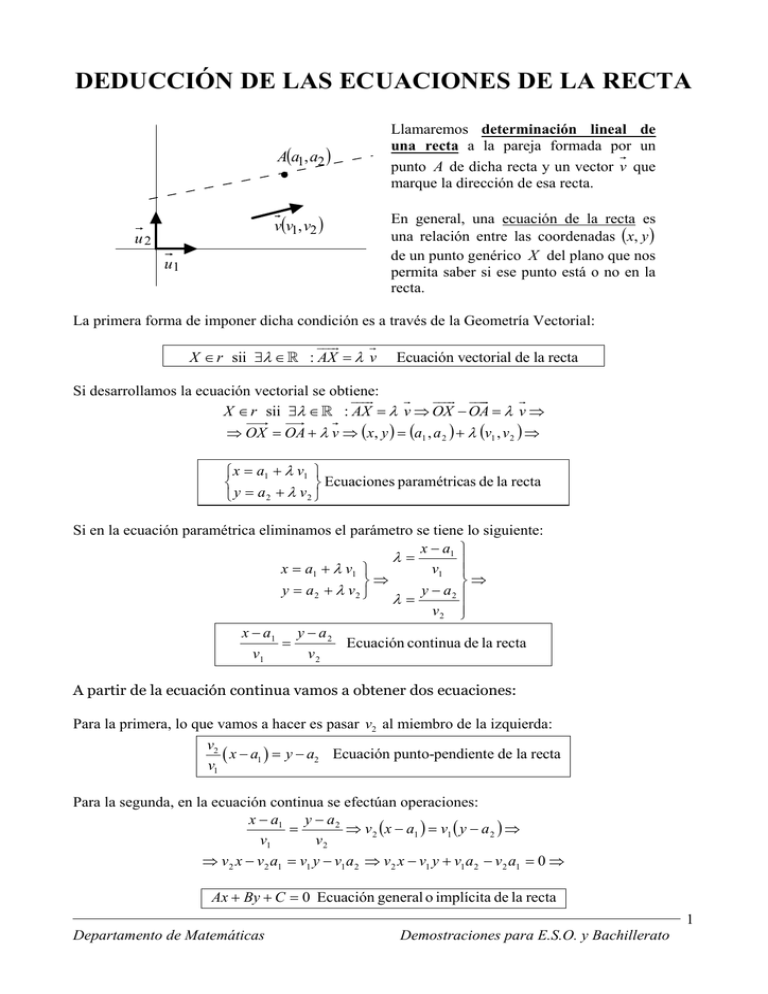
DEDUCCIÓN DE LAS ECUACIONES DE LA RECTA
Aa1,a2 

vv1,v2 
u2
u1
Llamaremos determinación lineal de
una recta a la pareja formada por un
punto A de dicha recta y un vector v que
marque la dirección de esa recta.
En general, una ecuación de la recta es
una relación entre las coordenadas  x, y 
de un punto genérico X del plano que nos
permita saber si ese punto está o no en la
recta.
La primera forma de imponer dicha condición es a través de la Geometría Vectorial:


X  r sii    : AX   v
Ecuación vectorial de la recta
Si desarrollamos la ecuación vectorial se obtiene:

  

X  r sii    : AX   v  OX  OA   v 
 OX  OA   v   x, y   a1 , a 2    v1 , v 2  
 x  a1   v1 

 Ecuaciones paramétricas de la recta
y

a

v

2
2

Si en la ecuación paramétrica eliminamos el parámetro se tiene lo siguiente:
x  a1 

x  a1   v1 
v1 



y  a2   v2 
y  a2 

v 2 
x  a1 y  a 2
Ecuación continua de la recta

v1
v2
A partir de la ecuación continua vamos a obtener dos ecuaciones:
Para la primera, lo que vamos a hacer es pasar v2 al miembro de la izquierda:
v2
 x  a1   y  a2 Ecuación punto-pendiente de la recta
v1
Para la segunda, en la ecuación continua se efectúan operaciones:
x  a1 y  a 2

 v 2  x  a1   v1  y  a 2  
v1
v2
 v2 x  v2 a1  v1 y  v1a 2  v2 x  v1 y  v1 a 2  v2 a1  0 
Ax  By  C  0 Ecuación general o implícita de la recta
1
Departamento de Matemáticas
Demostraciones para E.S.O. y Bachillerato
donde A  v2 , B  v1 y C  v1a 2  v2 a1 .
El vector director de una recta dada en forma general es el vector v   B, A , siendo B y A los
coeficientes de y ý de x . Para sacar un punto basta dar un valor a x (o a y ) y calcular el que falta.
Si en la ecuación general despejamos y , obtenemos:
A
C
x 
B
B
y  mx  n Ecuación explícita de la recta
Ax  By  C  0  y 
donde m  
A
C
y n .
B
B
Al coeficiente m se le llama pendiente de la recta y su valor es
m
v2
v
 2
 v1 v1
y n recibe el nombre de ordenada en el origen, que da la coordenada y del punto de corte de la
recta con el eje OY.
A partir de la ecuación general Ax  By  C  0 , podemos escribir Ax  By  C . Si C  0
tenemos:
Ax By
x
y

1

 1 (si A  0  B)
C C
C C
B
A
Así:
x y
  1 Ecuación canónica o segmentaria de la recta
p n
donde p 
C
es la abscisa en el origen (coordenada x del punto de corte de la recta con el eje
A
OX).
Para calcular la ecuación de la recta que pasa por dos puntos dados, basta tomar como punto uno de
ellos y como vector director el vector que determinan los dos puntos.
Observación: Ecuaciones de los ejes
En rectas paralelas a los ejes alguno de los denominadores de la ecuación continua es cero, por lo
que dicha ecuación adquiere un carácter simbólico; para obtener en estos casos la ecuación general
basta igualar a cero el correspondiente numerador.
2