Trabajo en grupo

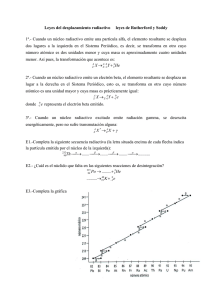
Trabajo en grupo
LECCIÓN 1: Introducción a las Ecuaciones Diferenciales
En los ejercicios 1 a 3 vamos a estudiar el fenómeno de la desintegración radiactiva.
Por experimentación se sabe que ésta se comporta de acuerdo con el siguiente principio:
La tasa a la que una cantidad de un isótopo radiactivo se desintegra es proporcional a la
cantidad de isótopo presente. La constante de proporcionalidad depende únicamente de la
partı́cula radiactiva considerada.
Problema 1 .- Llamando t al tiempo (variable independiente), r(t) a la cantidad de
isótopo radiactivo particular presente en el tiempo t (variable dependiente) y −λ a la tasa
de desintegración (nótese el signo menos para que λ > 0):
(a) Escribe un modelo (una ecuación diferencial) para la desintegración radiactiva de
un isótopo particular.
(b) Si la cantidad de isótopo presente en t = 0 es r0 , escribe el Problema de Condición
Inicial correspondiente a este modelo.
(c) Resuelve el Problema de Condición Inicial usando técnicas analı́ticas.
(d) Utiliza técnicas cualitativas para dibujar la gráfica de la solución del apartado (b).
Problema 2 .- La vida media de un isótopo radiactivo es el tiempo que tarda una
cantidad de material radiactivo en desintegrarse a la mitad de su cantidad original.
(a) La vida media del carbono 14 (C-14) es de 5230 años. Determina la constante λ del
C-14.
(b) ¿ Cuáles son las unidades de las constantes de desintegración de los apartados anteriores?
(c) Para estimar la vida media de un isótopo, podrı́amos comenzar con 1.000 átomos
del isótopo y medir el tiempo que tardan 500 de ellos en desintegrarse; o podrı́amos
comenzar con 10.000 átomos del isótopo y medir lo que tardan en desintegrarse
5.000 de ellos. ¿ Obtendrı́amos la misma respuesta?. Explı́calo.
Problema 3 .- El fechado de carbono es un método para determinar el tiempo transcurrido desde la muerte del material orgánico. Las hipótesis implı́citas en el fechado por
carbono son las siguientes:
1
El C-14 constituye una porción constante del carbono total que la materia viva
ingiere de forma regular, y
una vez que la materia muere, el C-14 presente se desintegra, pero ningún átomo
nuevo es agregado a la materia.
Entonces, al medir la cantidad de C-14 que aún permanece en la materia orgánica y
compararla con la cantidad de C-14 encontrada en la materia viva, puede calcularse el
“tiempo desde la muerte”. Usando la constante de la tasa de desintegración del C-14
encontrada en el ejercicio anterior, calcula el tiempo desde la muerte si
(a) el 88 % del C-14 original aún está presente en la materia.
(b) el 12 % del C-14 original aún está presente en la materia.
(c) el 2 % del C-14 original aún está presente en la materia.
2