2. VARIABLE ALEATORIA CONTINUA

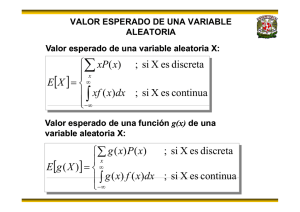
Mientras la función de probabilidad se representa en unos ejes de coordenadas cartesianas por
medio de una serie de barras, de cualquier anchura, discontinuas, la función de distribución se dibuja
a partir de una gráfica escalonada.
F.X
K <0
0
0<K<1
0.6
1<K <2
1
- -
0.3
2<K
O
2
X
2. VARIABLE ALEATORIA CONTINUA
Una variable aleatoria X es continua cuando toma valores en un intervalo (a, b) donde a y b
pueden tender a -oc y +oc respectivamente.
Una variable aleatoria X es absolutamente continua si existe una función g x , FUNCIÓN DE
DENSIDAD, tal que:
<R
X:Q
W
donde:
>
k
F x (k) =
g x (t)dt
Vk e <R
F x sigue siendo la convención para la función de distribución de X.
Ejemplo 7
Suponga la variable aleatoria X, duración de un bombillo.
Q =
Sí
J i = P (Q) partes de Q
S
= {co / X (c¡>) >10}
{X e S ) = {X > 10}
B c R
e
La función de densidad g x cumple las propiedades:
1. g x es continua
50
m. = [0, a ]
2.
gx(x)>0
3.
£
4.
g x
gx(k)dk = l
(x).F^(x)=^0
5. P(Xe/3)=\p
gx('k)dk
Jl r/R
6. g x (k) no indica una probabilidad
7. P(X = k) - 0 por continuidad de X
8. P (a < X < b)
= P (a < X <b) = P(a < X < b) = P(a < X < b)
Así mismo, para la Función de Distribución es posible verificar los siguientes teoremas:
TEOREMAS (PROPIEDADES)
1. Si a < b => P (a < X < b) = F x (b) - F x (a)
2. Si K¡ < K 2 => F x ( K t ) < F x (K2)
3.
LimFx (x) = 0
x—>-a
4.
LimFx (x) = 1
5.
LimFx fx) = F x (a) F x es continúa por la derecha
x—> a
x->
a
+
6. F x es única para cada variable aleatoria.
Ejemplo 8
Sea un experimento en el cual se selecciona aleatoriamente un punto del intervalo [a, b] de la
recta real. Obtener su función de densidad y distribución.
Solución: Aquí g x (x) = H
a<x<b
Se puede encontrar el valor de H teniendo en cuenta la propiedad 3:
51
H
fb
Ja
H dh=l=>H=-—=>g x ( x )"
ri-a
b-a
0
Fx(*) = f ' g,(*)dx
k-a
b-a
1
a<b
k<a
a<k<b
k>b
Ejemplo 9
Un ingeniero observa la variable aleatoria (Y) resistencia a la flexion de un material normal de
acero sometido a la tension. Los datos experimentales permitieron construir la figura que aparece
adelante, con base en ella encontrar:
a. gY(y)
0.1
b. F Y (y)
c. P(Y < 37)
d. P(Y > 45)
e. P(37 < Y < 52)
Solución
a. A partir de los puntos:
(41, 0.1)
(55, 0)
(35, 0)
(41,0.1)
52
55-41
•41
0-0.1
-0.0
[41-35 = x - 3 5 _
1.0-0.1 y-0"
-0.1
• Y = (x-41)
14
y
_(x
35)
í^llU
- x + 55
+ 0.1 =
140
~ 6 60
k-35
60
gy(k) = ' - k + 55
140
35<k<41
41<k<55
en otro caso
0
k < 35
j
35 < k < 41
35
b-
Fy(y)=
4
Í gy(k)dk =
60
y
f
J
35
f
60
J
41
41<k<55
140
55<k
c. P ( Y < 3 7 ) = {33; ^ p d y = 0 0 3 3
El 3.3% de las unidades de acero ensayadas tienen resistencia a la tensión no mayor a 37 kg./pulg 2
55 - y + 55
d. P ( Y > 45) = £45
dy = 0.357
140
La probabilidad de que una unidad de acero presente resistencia a la tensión al menos de 45 kg. /pulg2
es de 0.357
e. P(37 < Y < 52) = F y (52) - FY (37) = FY (52) = 0.9678 - 0.033 = 0.9348
El 93.48% de las unidades de acero alcanzan resistencias a la tensión que oscilan entre 37 y
52 kg./pulg 2 .
53
3. VARIABLES ALEATORIAS MIXTAS
La variable aleatoria puede ser a la vez discreta y continua, es decir asume valores puntuales con
una probabilidad diferente de cero, al igual que valores por intervalos. Este es el caso de ensayo de
equipos, donde X es el tiempo de funcionamiento del equipo, existe una probabilidad de que el artículo
no funcione del todo, falla en el tiempo X = 0; ó también cuando Y es la variable aleatoria que
representa la demora de un motorista al hacer un pare obligatorio, existe una probabilidad de que no
haya tráfico y el motorista no tenga demora X = 0, sí tiene que esperar, lo debe hacer por un tiempo
continuo.
La probabilidad de que una cierta variable aleatoria X tenga un comportamiento probabilistico
entre a y b, a < b, se escribe como sigue:
P ( a < X < b ) = £ gx(x)dx+
£
P(X = x)
Vxe[a,b]
Sea Y una variable aleatoria mixta, su función de distribución es:
Fy (y) = Pi F, (Y) + p 2 F 2 ( Y ) :
F, = Función de distribución escalonada (parte discreta)
F 2 = Función de distribución continua
P! = Probabilidad acumulada de los puntos discretos
p 2 = Probabilidad acumulada de los puntos continuos
Ejemplo 10
Suponga la variable aleatoria, Y, Duración de un componente electrónico, en cientos de horas.
Pi. P(Y = 0) = 1/4 : falla inmediata
g 2 (Y) = e Y
54
p 2 = 3/4
si no falla inmediatamente
F
i(y)=
10
Y<o
11
Y>O
F2(y)=Je"ydy
O
y>0
F Y ( y ) = l / 4 F ^ y ) + 3 / 4 F 2 (y)
4. FUNCIÓN DE UNA VARIABLE ALEATORIA
Sea X una variable aleatoria definida sobre un espacio de probabilidad, H una función
real tal que:
H:
Rx
X
X(w)
> Y
> H(X)=Y
> H(X(w))
Y sí para todo subconjunto C e ÍHY {H(X) e C}= {w | H [X(w)] e C} e
entonces H(X) es una variable aleatoria.
(sigma álgebra),
La descripción de la función de una variable aleatoria puede hacerse por intermedio de las
funciones de probabilidad, densidad y distribución. Estas pueden ser obtenidas conociendo las funciones
equivalentes de la variable aleatoria original, como sigue:
4.1 Sí X es una variable aleatoria discreta con función de probabilidad f x (x), y H(X) = Y una
variable aleatoria definida sobre el recorrido de X. Entonces la función de probabilidad de H(X) es:
f H(X) (H(x)) = f Y (y) = P(Y = y) = P(H(X) = y) = P(X = H ^ y ) ) sí existe H 1
f Y (y)=
I
P(X = xi)
\/{Xi/H(Xi)=y}
Ejemplo 7 7
Sea una variable aleatoria X que toma valores enteros en [-5, 6] con igual probabilidad. Obtener
f Y ( y ) s í H ( X ) = |X|
55
5
R [o, i]
2/12
-4
4
2/12
-3
3
2/12
-2
2
2/12
-1
0
1
1
0
1
2
2
3
3
4
4
5
5
6
6
«v
H
-5
12
fx(x) =
x = -5,-4,-3,-2,-l
0,1, 2, 3, 4, 5,6
0 en otro caso
2/12
1/12
7
6
y = 1,2,3,4,5
f Y (y)= 12 y=o,6
1/12
0
en otro caso
Ejemplo 12
Una persona gana determinada cantidad de dinero (Y) según el número de puntos obtenidos al
lanzar un dado (X). H (X) = Y = 3 x - 10
K
H(l) = -7
-4
1
2
3
4
5
6
fx(x)
-
x = l , 2, 3, 4, 5, 6
0
en otro caso
}
y = 7, -4, -1, 2, 5, x
0
en otro caso
6
-1
2
5
f Y (y) :
P(Y = y) = P(3X - 1 0 = y) = —
6
= P
( X = Y ± ^ ) = P(X
6
Vy
= H-1(y))
4.2 Dada la variable aleatoria X absolutamente continua con función de densidad g x (x), la
función Y -= H(X) puede ser una variable aleatoria:
a. Continua. Se obtiene primero la función de distribución y por derivación se logra la función
de densidad.
56
TEOREMA 1
lea X una variable aleatoria continua con función de densidad g x (x), Y = H(x) una función
estrictamente creciente o decreciente y derivable para todo x en los reales. Entonces
g Y (y) = g x (H- 1 (y))
3(H - 1 (y))
y s K
Ejemplo 13
Sea I la corriente variable distribuida igualmente en el intervalo (9, 11). Sí esta corriente fluye a
través de una resistencia de 2 ohmios. Encontrar la función de densidad de la potencia, siendo ésta P = 212
Solución: Sea I: la corriente variable
Los rangos son k, = (9, 11)
gi(i) =
1
11-9
1
2
K = (162, 242)
Ft(i)-
i-9
11-9
i-9
:
F p ( P ) = P ( P < p ) = P ( 2 1 <p) = P
v
,
=P
V2
/
IF)
V
)k
F,
V
1 *
11-9
V2
(
\
/
A,
8p
1
II
= F,
(P) =
<
I?)*
v
> 2
\l l
/
81
, 2 ,2)
i—\
f ÍP|
K'2
1
V
J
-1/2
í i
V
í5
i l
-9
/
/y
9
=
vzr\
i''
p
V2 /
'
\
f l—A\
I |P 1
í
r
2,
,i.n
8 VP
dp
9<J—
\ 2
<11
162 < p < 242
57
b. Discreta. La función de probabilidad f v (y), se puede calcular así:
f Y (y) = P(Y = y)= [ g x ( x ) d x
Ac7?x
y
sR
A
Ejemplo 14
El porcentaje de material de cierto componente se puede considerar como una variable aleatoria
con la función de densidad
gx(x) = 20x3(l -x)
0<x <1
El precio de venta del compuesto depende del contenido de material y se vende a US$3 el galón
sí está entre 1/3 y 2/3, de otro modo se vende a US$ 2. El costo de producción es de US$ 1.6. Encuentre
la función de probabilidad de la utilidad (U).
Solución:
U=
3 - 1 . 6 = 1.4
3
3
en otro caso
2 - 1 . 6 = 0.4
fU(u) = P(U=u):
J2^3 2 0 x 3 ( l - x ) d x = 0.4156
u = 1.4
£ / 3 g x d x + £ / 3 g x ( x ) d x = 0.584
u = 0.4
en otro caso
TEOREMA 2
Sea X una variable aleatoria continua con función de densidad no monótona g x (x) y H(X)=Y
una función aleatoria de X. Entonces la función de densidad de la función Y se puede obtener como:
(-H-(y))
gY(y) = [gx (H-'íyfl + gxC-H-'íy))]
y e R
Ejemplo 15
Sea X una variable aleatoria con función de densidad g x (x) = 0.5 -1 < x < 1. Y sea la función
aleatoria H(X) = x2. Entonces:
58
F Y (y) = P ( Y < y ) = P ( X 2 < y ) = p(-Vy < x < V y ) = F x ( V y ) - F x ( - V y )
5. OTRAS CARACTERÍSTICAS DE LAS VARIABLES ALEATORIAS
Una variable aleatoria se caracteriza además de las funciones de probabilidad, ó de densidad y
distribución por una serie de medidas que ayudan a describir la tendencia, dispersión, asimetría y
apuntamiento de sus valores, tales pueden ser el valor esperado, la desviación estándar, los cuantiles,
coeficientes de variación, asimetría y apuntamiento.
5.1 Valor Esperado de Variables y Funciones Aleatorias
• Sea X una variable aleatoria. Se define valor esperado de X:
- Cuando X es discreta con función de probabilidad f x (x) a
E(X) =
vx
x f x (x) = (i, existe sí
vx
|x| f x (x) < a
- Sí X es una variable continua con función de densidad g x (x)
E(X)=i
x g x ( x ) d x = |a, existe sí
|x|g x (x)dx <00 existe
• Sea H(X) una función de la variable aleatoria X. Se define valor esperado de H(X):
- Si X es una variable aleatoria discreta con función de probabilidad f x (x) a:
E ( H ( X ) ) = £ H ( x ) f x ( x ) = n, existe sí £ |H(x)| f x ( x ) < a existe
vx
vx
- Si X es una variable continua con función de densidad g x (x)
I (H( X))
1
H(x) g x (x)dx = x = |a., existe sí
J ^ |H(x) | g x ( x ) d x < 00 existe
El valor esperado también conocido como esperanza matemática es considerado como un promedio
antmético a la larga.
• PROPIEDADES DEL VALOR ESPERADO DE X ( Y DE H (X) )
59
1. E(K) = K
K es una constante
H(X)=K
2. E(K*X) = K*E(X)
H(X)=K*X
3. E(K,* X + K2) = K,*E(X) + K2
H(X)= K,* X + K;- 2
5.2 Varianza y Desviación Estándar de una Variable Aleatoria
Sea una variable aleatoria X, se define:
- Varianza de X a: V(X) = E(X - E(X))2 = <x.2
- Desviación Estándar de X a: ^/V(X) = a
La raíz de la varianza, la desviación estándar, indica la variación de la variable aleatoria con
respecto a su valor esperado, denotando el nivel de homogeneidad de los valores.
PROPIEDADES DE LA VARIANZA DE X (Y DE H(X))
1. V(K) = 0
siendo K una constante
H(X)=K
2. V(K*X) = K 2 V(X)
H(X)=K*X
3. V(X + K) = V(X)
H(X)=X + K
4. V(K,* X + K 2 ) = K, 2 V(X)
H(X)= K,* X + K 2
5. V(X) = E(X 2 ) - (E(X))2
Ejemplo 16
En el problema de la partícula, ejemplo 2, el valor esperado, la varianza y la desviación estándar
de la variable se pueden calcular así:
- E(X) = 1/8*0 + 3/8*1 + 3/8*2 + 1/8*3 = 1.5
Se espera que el número de movimientos a la izquierda de tres movimientos efectuados por
una partícula tienda a ser 1.5 = 2
- V(X) = (0 - 1.5)2 * 1/8 + (1 - 1.5)2 * 3/8 + (2 - 1.5)2 * 3/8 + (3 •- 1.5)2 *l/8 = 0.75
- cr =0.866
El número de movimientos a la izquierda de tres movimientos efectuados por una partícula
varía con respecto al número esperado de movimientos en 0.866 s 1
Ejemplo 17
La variable aleatoria X¡ el punto seleccionado de un intervalo, ejemplo 8, tiene valor esperado y
varianza como sigue:
60
E(X) = {B
Ja
-2L-DX=I±*
b-a
2
2
V(X) = A2=JAB ( X - E ( X ) ) 2
GX(X)DX =
^
Ejemplo 18
En el ejemplo 13, obtener el valor esperado y la desviación estándar de P.
.
E(P) = E(2I 2 ) = 2E(I 2 ) = Jg1 2 i 2 * i d i = j9H i 2 d i = 200.67 =
p g p (p)d p
La potencia media generada es de 200.67 vatios.
-
V(P) = E(P 2 )-[E(P)] 2
= 40800.8-(200.67) 2
= 532.35 =>o = 23.07
E ( P 2 ) = E[(2I 2 ) 2 ]=E[4I 4 ]= jj1 ^ g ^ O d i
= 40800.8 = J * 2 p 2 g p (p) d p
La variación de la potencia con respecto a la potencia mcum c» uc ¿J.u / vauus.
Ejemplo 19
Calcular la utilidad esperada por galón y su variación, según el ejemplo 14.
- E(U) = 1.4* 0.4156+ 0.4* 0.5844 = 0.8156 US$
- V(U)=1.42 * 0.4156 + 0.42 * 0.584 - (0.8156)2 = 3.27 = o 2
=> a =1.8 US$. La utilidad es muy heterogénea.
5.3 Otras medidas de Variables Aleatorias
Es de importancia conocer que las variables aleatorias se describen con otras medidas de gran
uso por algunos profesionales, denominadas de posición, las que a continuación se presentan.
• CUANTILES
Se define cuantil, al valor bajo el cual se encuentra una determinada proporción de los valores de
la variable.
Los cuantiles pueden ser:
• Pereentiles, cuando la serie de valores se divide en cien partes, cada una equivalente a un
uno por ciento.
• Cuartiles, sí la serie de valores se clasifica en cuatro partes, cada una relacionada con un
veinticinco por ciento.
• Deciles, cuando el conjunto de valores se reparte en diez partes, cada una relativa a un diez
por ciento.
El cuantil de orden R de una variable aleatoria X, es denotado por x R y definida como el valor de
X que es máximo para R% de los valores de la variable y a la vez el mínimo para los restantes (1-R)%
de valores, se calcula de la siguiente manera:
•
Sí X es discreta. Es aplicable uno de los siguientes métodos:
- P(X < x R ) < R y P(X < x R ) > R.
En este caso la solución para el cuantil no es siempre satisfactoria, por lo tanto se ofrece
aquí una alternativa de respuesta algo más general aunque pueden existir situaciones en los
que tampoco sea adecuada.
- Sea MI R = I n f U / F x (x) > R y MS R = Inf< x / F x (x) > R ¡>.
El intervalo [MIR, MS R ] se llama intervalo cuantilico de orden R y cualquier punto dentro
de él se denomina Cuantil de orden R. En este caso, es común asignarle el valor MS R a x R .
Sí MI R = M S r => x R es el cuantil de orden R y es único.
- Otra alternativa de obtención es
S Í F x ( x M ) < R < F x ( x , ) = > X r = x,
Cuando Fx(xi_1)=R => x R = (Xj_|+ x¡)/2
•
Sí X es continua.
Se resuelve la ecuación F x (XR) = R.
Cuando R = 0.5 entonces Xq 5 — M e : es llamada MEDIANA
• MODA
Representa el valor de la variable aleatoria que más se repite ó el más probable, es decir, el que
maximiza la función de probabilidad o de densidad. Se denota por M d . Si existe se denomina Moda
absoluta.
Una variable aleatoria puede tener dos valores con igual probabilidad de ocurrir, siendo ésta la
máxima, razón por la cual se llama Bimodal, si tiene tres valores con igual probabilidad de ocurrir,
siendo ésta la más alta, se describe como Trimodal, y así sucesivamente.
62
Ejemplo
14
Sea la variable aleatoria discreta X tal que:
X:
0
15
25
40
P(X = x):
0.2
0.3
0.3
0.2
P(X <x):
0.2
0.5
0.8
1.0
El cuartil 1 se obtiene:
MI25 = Inf \ x / F x (x) > 0.25 >-=15
MS25= Inf^ x / F x (x) > 0.25 ^=15
De ahí que el cuartil de orden 1 de X sea 15.
La Mediana se podría conocer mediante la alternativa:
MI50= Inf <¡ x / F x (x) > 0.5 ¡>=15
MS50= Inf \ x / F x (x) > 0.5 ¡>=25.
Entonces se tiene el intervalo [15, 25] llamado intervalo mediano.
La Moda absoluta no existe, puesto que no hay un valor de la variable que sea más probable que
cualquier otro. Como se presentan los valores 15 y 25 con igual probabilidad se denominan modas
relativas de primer orden, así mismo los valores 0 y 40, también con igual probabilidad pero inferior
a la de los valores anteriores, son llamados modas relativas de segundo orden. Además, se puede decir
que la variable aleatoria X es Bimodal puesto que no tiene una moda absoluta, en cambio si posee dos
valores que se constituyen en modas de primer orden.
Ejemplo 21
Sea la variable aleatoria X que representa el tiempo de duración, en horas de un cierto componente
eléctrico con función de densidad g x (x) = 1000 -1 e"(x"100>'1000 x > 100
Determinar: a. E(X)
b. M e
c. Cuartil 3
d. Decil 4
e. M d
a
a.
E(X) = J x g x ( x ) dx = 1100
La duración media del componente es de 1100 horas.
100
b- F x (x0 5) = P(X < x 0 5) = 0.5
7
g x ( x ) d x = e" 1 0 0 / 1 0 0 0 -e^ x ° 5 ~ 1 0 0 ' , / 1 0 0 0 = 0.5 => despejando x 0 5 =602.24
100
63
Lo cual se interpreta diciendo: el 50% de los componentes alcanzan duraciones no mayores
a 602.24 horas. También indica que la mitad de los componentes al menos duran 602.24
horas.
c. F x (x0 75 ) = P(X < x 0 75) = 0.75. Por un procedimiento similar al anterior x 0 75 = 1135.16. Esto
es, el 75% de los componentes tienen, cada uno, duraciones no mayores a 1135.16horas.
d- F x (x0.4) = P(X < x 0 4 ) = 0.4 ^ x 0 4 = 449.315
e. M d = Máximo de la función de densidad g x .
Se puede verificar que el máximo de g x es 100. Lo anterior indica que la duración más probable
ie un componente es 100 horas.
5.4 Desigualdad de Tchebyshev
Permite generar un intervalo de valores de la variable aleatoria dada la probabilidad de que esto
acurra, o también es posible realizar el hallazgo de la probabilidad de que ocurran los valores que
:oma la característica aleatoria incluidos en un intervalo dado. En cualquier caso es necesario disponer
ie la varianza poblacional a 2
TEOREMA 4. Desigualdad de Markov
Sea X una Variable Aleatoria, y H(X) una función no negativa con dominio en los reales, entonces
P(H(X)>e)<E(H(X))
e
Ve>0
Demostración:
Sean A t ={x / H(X) > e }
A 2 ={ x / H(X) < s }
E(H(X)) = j H(x) g x ( x ) dx = { H ( x ) g x ( x ) d x + { H ( x ) g x ( x ) d x
-a
>
Al
{H(x)gx(x)dx
Al
> { sgx(x)dx>8P(H(X)>£)
Al
E(H(X))>P(H(X)>£)
8
64
A2
COROLARIO. Desigualdad de Tchebyshev
Sí X es una variable aleatoria con varianza finita a 2 y H(x) = (X - \xxf
=> P ( ( X - (ax)2 > k2 a 2 ) = P(|X- n x | > k a x ) <
P( |X - |a x | < k a x ) > 1 3
k
e = K2 a 2
, equivalente a la expresión
Nótese que se puede escribir como:
((ax - k CTx < X < ii x + kCTx)> 1
k
j
es útil para cuando k > 1.
Ejemplo 22
Las ventas diarias por cliente en un supermercado son de US$ 5.25 y la variación de las mismas
asciende a US$3.04. Sí K = 3/2 ¿Qué rango de ventas se espera para al menos que porcentaje de clientes?
Solución
X: Ventas diarias por cliente del supermercado.
=
5.25 a x = 3.04
1—y =—
k
9
Entonces (5.25 ± (3 / 2)*3.04): (0.69 < X < 9.81)
Cada uno de los 55.6% de clientes del supermercado realizan compras entre US$0.69 y US$9.81
Ejemplo 23
El número de gusanos por pie3 en cierto suelo tiene un promedio y varianza iguales a 100. Encuentre
un intervalo que incluya 16/25 de los valores muéstrales del número de gusanos, obtenidos de un gran
número de muestras de un pie 3 .
Solución:
16
,
1
1 9
5
— = 1
2r- = > ^ 2- = — => K = —
25
k
k
25
3
16
P(|a - K a < X < u + Ka) > — =>
P ^ 1 0 0 - | * 1 0 < X < 1 0 0 + | * 1 0 j =P(83.3<X<116.6) >0.64
En al menos el 64% de muestras de un pie3 se encuentran entre 83 y 117 gusanos por pie3.
65
5.5 Momentos de una Variable Aleatoria
Sea X es una variable aleatoria. El r-ésimo momento de X consiste en obtener los valores esperados
de X hasta de orden r:
Se conocen varias clases de momentos, a saber:
1. Respecto al origen, denotado por (i r , es definido por:
(j.r = E(X r ), existe sí la esperanza existe.
Así se tiene: Ui = E(X)
2.
a1 =
- |i 2 i = V(x)
Respecto al momento central.
H'r = E((X - E(X))r
H',=0
\¿2 = E(X - E(X))2 = V(x) = a 2
= E(X - E(X))3 llamado medida de asimetría.
(j,'4 = E(X - E(X))4 reconocida como medida de curtosis.
• La simetría de una distribución de probabilidades, véase la próxima figura, es otro rasgo
interesante de una variable aleatoria, utilizando el momento central de tercer orden se puede decir que sí:
f
f
f
/
( 1 ) Asimetría negativ»
X
(2) Simétrica
\
A
X
(3) Asimetría positiva
X
• |i' 3 = 0 : La variable es simétrica respecto a su valor esperado
•
jLt' 3
<
0
: Existe asimetría a la izquierda (asimetría negativa)
• (i'3 > 0 : Existe asimetría a la derecha (asimetría positiva)
NOTA 1.
Adicionalmente se conoce un coeficiente estandarizado de asimetría, definido por: a 3 = (i'3 / CT3
66
• La curtosis es el grado de apuntamiento que tiene una distribución de probabilidad de una determinada
variable aleatoria. Se cuantifica por el momento de orden cuatro con respecto a la media, (i'4.
NOTA 2.
Al igual que con la asimetría, también se define un coeficiente estandarizado de curtosis, dado por:
a 4 = (j,'4 / 4 .
Se puede determinar el tipo de apuntamiento de la distribución, si
• a 4 = 3 : No hay exceso da curtosis, apuntamiento normal
• a 4 < 3 : El apuntamiento es inferior al normal, aplanada
• a 4 > 3 : El apuntamiento es superior al normal, apuntada
1
(1) Platikúrtica
(2) Mesokúitica
(3) l^ptokiirtica
Un momento particular da poca información sobre la distribución de una variable aleatoria, pero
el conjunto de momentos ordinariamente determina la distribución exacta.
3. Momento Factorial de Orden R
Hay otra manera de obtener artificialmente los diferentes momentos de orden r, ésta es llamada
momento factorial definida como:
Mr = E (X (X - 1) (X - 2) ... (X - r+1))
Para r = 1, Iví, = E(X)=
r = 2, M 2 = E(X(X-1)) = E(X2 - X) = E(X2) - E(X) = M 2 - Mi=
- ^
entonces a" = ¡x2 - M-j2 y así sucesivamente.
Ejemplo 24
Con base en el ejemplo 20, indicar cual es la forma de la distribución, y usando el teorema de
Tchebyshev que resultado se espera de X si k= 1.5.
67
-
ji-3 - E(X - E(X))3= Y f x - 2 ° f f x ( x ) = °
Vx
a3 =
-
-
3
2
/ a = 0. (a = 175)
n' 4 = E ( X - E ( X ) ) 4 =
v*
4
a 4 = u'i / a = 2.1 < 3
2Jx-20ffx(x)=64315
De acuerdo a los cálculos realizados, se puede señalar que la distribución de la variable discreta,
tiene una forma asimétrica negativa y es aplanada.
Aplicando la desigualdad de Tchebyshev con k=l .5
P(|X - 20| < 1.5*VÍ75)> 1 -
=
0.56 ^ P ( 0 . 1 6 < X < 39.84) >0.56
La probabilidad de que la variable aleatoria X este entre 0.16 y 39.84 es de al menos 0.56.
Ejemplo 25
Continuando con el ejemplo 21, obtener la asimetría y apuntamiento de la distribución. Aplique
el Teorema de Tchebyshev para un K=2.
-
M'3 = E ( X - E ( X ) ) 3 =
J; 0 0 ( X - 1 1 0 0 ) 3
gx(x)dx = 2*109 > 0
\¿2 = E(X - E(X))2 =1*106= o 2 =>CT=1000=> a 3 = 2 > 0 La asimetría es positiva
-
H'4 = E(X-E(X)) 4 =
(x-1100) 4 g x ( x ) d x = 9*10 12 ^ a 4 = 9 > 3
El apuntamiento es tipo leptocurtico.
Aplicando la desigualdad de Tchebyshev con k=2
P(|X - 1100| < 2*1000) > 1—^- = 0.75 => P ( - 9 0 0 < X < 3100) >0.75
2
Al menos el 75% de los componentes eléctricos tienen duraciones entre 100 y 3100 horas.
5.6 Función G e n e r a d o r a de Momentos
Dada una variable aleatoria X, con función de densidad (ó de probabilidad). Se define con el
nombre de función generadora de momentos a:
E (etx) = M x (t)
68
V t, - b < t < b
b>0
e " g x (x) dx
x : continua
= M(t) =
^
e tx f x ( x )
x : discreta
Vx
existe cuando exista el valor esperado.
Sí existe M x (t), va a ser única y determina completamente la distribución de una variable aleatoria.
La existencia de M(t), permite que M(t) sea continuamente diferenciable, garantizando la
existencia de tales derivadas de orden r en t = 0, las que resultan ser los momentos con respecto al
•rigen de una distribución, de ahí su nombre.
d r M(t)
dt r
n[xretxJ=-
dVx)
dt r
:(M(t)) r =E
Í
*
r
t x
x e gx(x)dx
x : continua
Vx
haciendo t = 0 (M(0)) r = n r = E(X r )
tx
0
M'(t)
)=í>M , (t
0) = E(X) = ji
^ x r= eE(Xe
' f x (x)
x :=discreta
Ejemplo 26
Sea X una variable aleatoria cuya función de densidad es:
x
gx( )
:
íe~x x > 0
0
en otro caso
Determine: a. M(t).
b. E(X).
c. V(X)
Solución:
U
a.
tx
E(e ) = M x (t) = J e
A
b.
E(X) = M x ( t = 0)
c.
E(X 2 ) = M"(t = 0)
Li
tx
x
e~ dx = J e
f\
i
(t_1)x
dx =
1
Mx(t)=
t<1
1- t
(l-t)2
M'i(t):
(1-ty
M^(t = 0) = l
M^(t = 0) = 2
V(X) = 1
69
Ejemplo77
Un jugador de baloncesto lanza la bola hasta que encesta, momento en el cual finaliza
lanzamientos, la probabilidad de encestar es 0.4
Si X es la variable aleatoria que denota el número de ensayos que realiza el jugador.
Halle: a. f x (x)
b. M(t)
c. E(X)
d. V(X)
Solución: Como los lanzamientos se pueden asumir como independientes, entonces
a.
f x (x) = (1 - P) x_1 P = (0.6)x_1 (0.4)
b.
M(t) = X e tx (0.6) x_1 (0.4) = ^ X (0.6e') x = ~ 0.6e'(1 + q e 1 + ( q e ' ) 2 + . . . + ...)
Vx
3
x=l,2...
vx
3
,
- x n = l + x + x + . . . + ...=
AYUDA.ParadeterminarM(t). V
0.4 e
=> M(t) = — 0.6 e l * — 1 l
3
l-0.6e
c.
1
l-0.6e
E(X) = M(t = 0) = 2.5
( M e ' O - O . ó e ^ - O ^ e ' (-0.6 e l ) _
0.4 e l
M'(t) = (1-0.6e 1 ) 2
(l-0.6e1)2
d
M
„(ú
=
=
0-4 e{ (1 - 0.6 e 1 ) 2 - 0.4 e 1 2(1 - 0.6 e { ) (-0.6 e { )
(l-0.6e')4
0-4^(1 + 0 . 6 ^ )
1 3
(l-O.óe )
=>
ffl
=
0.4Q + 0.6)
7
=1Q
(1-0.6)
=> V(X) = 10-(2.5) 2 =3.75 <j = 1.94
TEOREMA 5
Sea X una variable aleatoria con función generadora de momentos M x (t).
Sí Y = a X+ b entonces M Y (t) = etb M x (a t)
Demostración:
M v (etY) = E(et(aX + b)) = E(e taX etb) = etb E(etaX) = etb M x (at)
70
ii
|x|< 1
5.7. Función G e n e r a d o r a de Momentos Factoriales
Sea X una variable aleatoria y v F x (t) una función real tal que:
Sí d ¥ x (0
d tr
gr((i+t)x)
atr
4 y x (t) = E ((1+ t) x )
existe para todo t, entonces
VX 0) = E [ X ( X - 1 ) ( X - 2 )
dtr
( X - ( k - l ) ) ( l + t)x"k I y
(t) se denomina
Función Generadora de Momentos Factoriales de X de orden r.
El argumento contenido en el valor esperado se puede expresar en términos factoriales
X ' f l + tY'"k
——
-—
(X-k)!
de ahí su nombre.
Es de mayor facilidad de aplicación con variables aleatorias discretas, pudiendo obtenerse los
momentos factoriales de la variable y luego encontrar los momentos con respecto al origen. Así, si
(1 + t ) x = e x l n ( 1 , t ) =>
(t) = M x (ln(l + 1 ) ) ¥ x (e v) = M x (t).
5.8. Función característica de una Variable Aleatoria
Sea X una variable aleatoria y 0 X una función real tal que:
0 x ( t ) = E(e ltx ) = E (Cos (tx)) + i E ( Sen (tx))
Característica de X.
V t e R, entonces se dice que 0 X es la Función
6. EJERCICIOS PROPUESTOS
1. Una caja contiene cuatro artículos aceptables, uno defectuoso. Se inspecciona artículo por artículo
hasta cuando se localiza el defectuoso. Sea la variable aleatoria X que denota el número de la
inspección en que se localiza el artículo defectuoso.
a. Determine la función de probabilidad de X.
b. Encuentre la función de distribución de X.
c. Calcule el.valor esperado y la varianza.
d. Deduzca la función generadora de momentos de X.
'/1
2. Sea X una variable aleatoria que representa el peso (en onzas) de un artículo, con función de
densidad
8 < x <9
x-8
9 < x < 10
gx <X> = 1 0 - x
0
en otro caso
El fabricante vende el artículo a $200. Garantiza el reintegro del precio de venta si el peso del
artículo es inferior a 8.25 onzas. El costo de producción es función del peso, C.= 5 * X, otros costos
menores suman $30.
a. Determine la función del costo y de la utilidad.
b. Encuentre la utilidad esperada por el fabricante.
c. ¿Cuál es la variación del costo y de la utilidad?
3. Un artículo tiene los defectos A, B, AB, Ninguno. La probabilidad de A es 0.4, la de B es 0.5 y la
de los dos defectos 0.2.
Sí X es la variable aleatoria que indica número de defectos de un articulo. ¿Cuál es la función de
probabilidad?, ¿De distribución?. Encuentre todas las medidas que caractericen a X.
4. Un proyecto consta de 3 actividades: A,B y C. La actividad B debe ser ejecutada antes que C
pueda comenzar. A se realiza independientemente pero simultáneamente a B y C. Se han estimado
los siguientes tiempos y probabilidades:
ACTIVIDAD
TIEMPO PARA TERMINAR
PROBABILIDAD
A
4
6
0,50
0,50
B
1
3
0,25
0,75
C
2
4
0,80
0,20
a. Obtenga la función de probabilidad del tiempo total para terminar la tarea.
b. ¿Cómo realizaría usted el proyecto? Justifique la respuesta.
c. Calcule e interprete el valor esperado y la varianza del tiempo total.
5. La función de densidad de la variable aleatoria X, diámetro final de un cable eléctrico blindado,
esta dado por