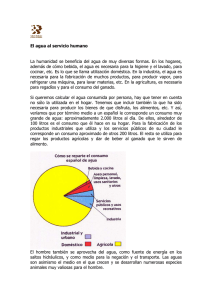
Soluciones

Tarea 7
Soluciones
1. Una inversión de $3500 produce un rendimiento de $420 en un año,
¿qué rendimiento producirá una inversión de $4500 a la misma tasa de interés
durante el mismo tiempo?
Sol. Sea x el porcentaje que no conocemos, entonces tenemos la siguiente
ecuación:
(3500)x = 420
3
420
=
x=
3500
25
Ahora, queremos saber cuando producirá una inversión de 4500 con interés
3
:
25
3
(4500)( ) = 540
25
Por lo tanto una inversión de $4500 producirá un interés de $540.
2.En 1974 la razón entre las especies de insectos descritos hasta entonces y el
. Si entonces se tenı́a la descripción de 950, 000 especies.
total de ellos era 19
60
¿Cuál era el total de especies de insectos?
Sol. Tenemos la siguiente razón:
19
especies descritas
=
total de especies
60
Pero como conocemos la cantidad de especies descritas, solo hay que sustituir:
19
950000
=
x
60
(60)(950000)
= 3, 000, 000
19
El total de especies eran 3,000,000.
x=
1
3. Si se mezclan 200 litros de aceite de maı́z cuyo consto es de $6.85 el litro
con 250 litros de aceite de girasol, se obtiene una mezcla cuyo valor es de
$4.60 el litro.
1. ¿Cuál es el precio del aceite de girasol?
Sol. Tenemos 200lt a $6.85 en total el aceite de maı́z nos cuesta $1370.
Y 450lt a $4.60 el total del costo de la mezcla es de $2070.
Sea x el precio del aceite de girasol, tenemos la siguiente ecuacion:
(450)(4.60) = (200)(6.85) + 250x
2070 = 1370 + 250x
2070 − 1370
= 2.8
x=
250
2. ¿Qué cantidad debe mezclarse de cada uno para obtener 20 litros a
$4.42 el litro?
Sol. Sea x la cantidad de aceite de maı́z y y la cantidad de aceite de
girasol. Y queremos que el costo total de la mezcla sea de (20)(4.42) =
88.4. Tenemos el siguiente sistema de ecuaciones:
6.85x + 2.80y = 88.4
x + y = 20
Uso sustitución:
x = 20 − y
6.85(20 − y) + 2.8y = 88.4
137 − 6.85y + 2.8y = 88.4
4.05y = 48.6
y = 12
x = 20 − y = 20 − 12 = 8
Por lo tanto, deben de mezclarse 8 litros de aceite de maı́z y 12 litros
de aceite de girasol.
2
3. Si se mezclan 50 litros de aceite de maı́z y 40 litros de aceite de girasol,
¿qué precio tiene el litro de la mezcla obtenida?
Sol. Tenemos 50lt a $6.85 y 40lt a $2.8, sea x el precio por litro de la
mezcla, entonces tenemos la siguiente ecuación:
(50)(6.85) + (40)(2.8) = 90x
342.5 + 112 = 90x
454.5
= 5.05
x=
90
Por lo tanto, cada litro de la mezcla cuesta $5.05.
4. Si se mezclan cierta cantidad de litros de aceite de maı́z y de girasol se
obtiene 108 litros de una mezcla cuyo valor es de $642.60. ¿Cuántos de
cada tipo se mezclaron?
Sol. Sea x la cantidad de aceite de maı́z y y la cantidad de aceite de
girasol. Y sabemos que el costo total de la mezcla es $642.60. Tenemos
el siguiente sistema de ecuaciones:
6.85x + 2.80y = 642.60
x + y = 108
Uso sustitución:
x = 108 − y
6.85(108 − y) + 2.8y = 642.60
739.80 − 6.85y + 2.8y = 642.60
4.05y = 97.5
y = 24
x = 108 − y = 108 − 24 = 84
Por lo tanto, deben de mezclarse 84 litros de aceite de maı́z y 24 litros
de aceite de girasol.
3
4. Nueve menos tres cuartos de un número es $63. Encuentra dicho número.
Sol.
3
9 − x = 63
4
3
9 − 63 = x
4
(−54)(4)
x=
3
x = (−18)(4) = −72
El número es −72.
5. Para una fiesta se preparan dos tipos de ponche, 8 litros sin alcohol para
los niños y 11 litros para los adultos que contiene 20 % de alcohol.
1. ¿Cuántos mililitros de ponche sin alcohol debe agregarse para reducir
la cantidad de alcohol al 10 %?
Sol. Primero hay que ver cuantos litros de alcohol hay en la mezcla,
11(0.20) = 2.2
Entonces hay 11 − 2.2 = 8.8 litros de ponche. Nuestra solución tiene
2.2 litros de alcohol, ahora queremos que esta cantidad sea el 10 %,
2.2 10 %
x 90 %
Tenemos,
(2.2)(90)
= 19.8
10
La mezcla debe de tener 19.8 litros de ponche, pero ya teniamos 8.8,
entonces la cantidad que hay que agregar son 19.8 − 8.8 = 11.
Por lo tanto hay que agregar 11000 mililitros de ponche a la mezcla
para reducir la cantidad de alcohol al 10 %.
x=
4
2. ¿Cuántos mililitros hay que agregar para reducir al 8 %? Sol. Ya sabemos que hay 2.2 litros de alcohol en la mezcla y 8.8 litros de ponche.
Queremos que esos 2.2 litros de alcohol sean el 8 %,
2.2 8 %
x 92 %
Y queremos ver cuantos litros de ponche (llamaremos x) se necesitan,
Tenemos la siguiente ecuación,
x=
(2.2)(92)
= 25.3
8
La mezcla debe de tener 25.3 litros de ponche, pero ya teniamos 8.8,
entonces la cantidad que hay que arreglar son 25.3 − 8.8 = 16.5.
Por lo tanto hay que agregar 16500 mililitros de ponche a la mezcla
para reducir la contidad de alcohol al 8 %.
3. Si se agregan 4 litros de ponche con el 15 % de alcohol, ¿qué porcentaje
de alcohol tendrá la mezcla obtenida? Sol.
11lt con 20 %alcohol → 2.2lt alcohol
4lt con 15 %alcohol → 0.6lt alcohol
En total,
15lt con 100x %alcohol → 2.8lt alcohol
Tenemos que,
(15)x = 2.8
2.8
15
⇒ x = 0.186
⇒x=
Por lo tanto el porcentaje de alcohol en la mezcla es de 18.7 %.
4. ¿Cuántos litros de ponche al 15 % hay que agregar para obtener una
mezcla con el 16 % de alcohol?
Sol.
11lt 20 %alcohol → 2.2lt alcohol
5
xlt 15 %alcohol → 0.15xlt alcohol
En total,
11 + xlt 16 %alcohol → 2.2 + 0.15lt alcohol
Resolvemos la ecuación,
(11 + x)0.16 = 2.2 + 0.15x
⇒ 1.76 + 0.16x = 2.2 + 0.15x
⇒ 0.01x = 0.44
⇒ x = 44
Por lo tanto, se tienen que agregar 44lt de ponche al 15 % para obtener
una mezcla al 16 %.
6. Los lados de dos triángulos rectángulos están en razón 61 . Si el más pequeño
tiene base 3 y altura 4:
1. ¿Cuál es el área del triángulo mayor?
Sol. Si la altura del triángulo menor es de 4, encontremos la altura del
triángulo mayor (x):
1
4
=
x
6
Entonces,
(4)(6)
= 24
x=
1
Ahora la base,
3
1
=
x
6
Entonces,
(3)(6)
x=
= 18
1
. Tenemos que el area del triángulo mayor es,
Area =
(18)(24)
= 216
2
6
2. ¿Están las áreas en razón 16 ?
Sol. Las areas estan en razón de
en razón de 16 .
6
216
=
3
108
=
1
.
36
Por lo tanto, no están
7. Al comprar un vestido que tenı́a marcado como precio 124 pesos, se hizo
un descuento de 29.76. ¿Qué porcentaje tenı́a de descuento?
Sol. Tenemos que 124 es el 100 %, entonces encontrar cuanto es 29.76, hacemos una regla de 3,
124 → 100 %
29.76 → x %
Tenemos que,
(29.76)(100)
= 24
124
. Por lo tanto, el descuento fue de 24 %.
x=
8. Un grupo de 14 amigos decidieron ir a un concierto. Dos de ellos no podı́an
pagar el costo del boleto, ası́ que los otros 12 pagaron cada uno, su boleto y
4 pesos más. ¿Cuánto costaba cada boleto?
Sol.
12(x + 4) = 14x
⇒ 12x + 48 = 14x
⇒ 48 = 14x − 12x
⇒ 2x = 48
⇒ x = 24
Cada boleto costaba 24.
9. Tres obreros laboran 8 horas cada jornada. El primero es capaz de realizar
un 90 horas, es decir en 11 41 jornadas. El segundo puede realizar el mismo
trabajo en 15 jornadas y el tercero lo logra en sólo 9 jornadas. ¿Cuántas horas
de trabajo requerrán para realizar el trabajo si lo hacen los tres juntos?
Sol. Vamos a ver cual es el trabajo que realizan entre los 3 en una hora,
1
1
1
4+3+5
12
+
+
= 2 3
=
90 120 72
(3 )(2 )(5)
360
7
Cada jornada tiene 8 horas, entonces en una jornada hacen:
(8)
96
12
=
360
360
Necesitas 3.75 jornadas para que completen un trabajo entre los 3.
10. Cambia a notación decimal los siguientes números racionales:
1
7
= 0.142857
6
13
= 0.461538
46
55
= 0.836
11. Dime si es posible expresar estos números decimales como cociente entre
dos enteros, en caso de que si, dime cuales son.
7.1459
Sea
x = 7.1459
10000x = 71459.1459
10000x − x = 71459.1459 − 7.1459
9999x = 71452
71452
x=
9999
Entonces, 7.1459 =
71452
9999
0.7
Sea
x = 0.7
10x = 7.7
10x − x = 7.7 − 0.7
9x = 7
7
x=
9
Entonces, 0.7 =
7
9
8
25.25 Sea
x = 25.25
100x = 2525.25
100x − x = 2525.25 − 25.25
99x = 2500
2500
x=
99
Entonces, 25.25 =
2500
99
0.12345678 Sea
x = 0.12345678
10x = 1.2345678
10x − x = 1.23456788 − 0.12345678
9x = 1.1111111
90000000x = 11111111
11111111
x=
90000000
Entonces, 0.12345678 =
11111111
90000000
9