ANÁLISIS DE CIRCUITOS 1º Ingeniería en Telecomunicación 2ª

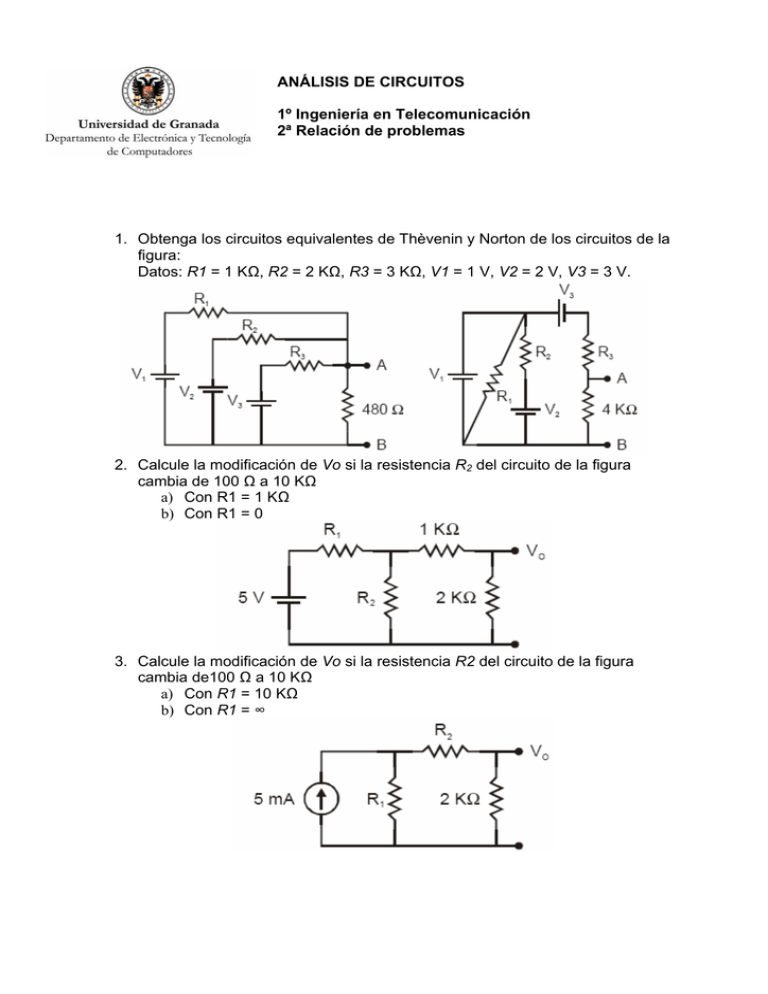
ANÁLISIS DE CIRCUITOS
1º Ingeniería en Telecomunicación
2ª Relación de problemas
1. Obtenga los circuitos equivalentes de Thèvenin y Norton de los circuitos de la
figura:
Datos: R1 = 1 KΩ, R2 = 2 KΩ, R3 = 3 KΩ, V1 = 1 V, V2 = 2 V, V3 = 3 V.
2. Calcule la modificación de Vo si la resistencia R2 del circuito de la figura
cambia de 100 Ω a 10 KΩ
a) Con R1 = 1 KΩ
b) Con R1 = 0
3. Calcule la modificación de Vo si la resistencia R2 del circuito de la figura
cambia de100 Ω a 10 KΩ
a) Con R1 = 10 KΩ
b) Con R1 = ∞
4. Calcule el valor de V’ en el circuito de la figura
5. En el circuito de la figura, calcule el valor de la corriente que circula por R3
pasando todas las fuentes a fuentes de tensión y resolviendo por el método
de las corrientes en las mallas.
R1 =R2 =1 KΩ, R3 = R4 =2 KΩ, V1 =1 V, V2 =3 V, I3 =1 mA
6. Resuelva el problema anterior pasando todas las fuentes a fuentes de tensión
y resolviendo por el método de las tensiones en los nudos.
7. Aplicando el método de las corrientes en las mallas, calcule la corriente I que
circula a través de la resistencia R2 en el circuito de la figura
8. Se conectan dos fuentes de tensión con resistencias internas r1 = r2 = 1&, y valores
nominales V1 = 1 V y V2 = 2 V, respectivamente, tal como muestra la figura.
a) Obtenga la corriente que circula por cada fuente y por RL.
b) Suponiendo que las fuentes del circuito son baterías con carga suficiente para
proporcionar 1 mA durante 100 h, calcule el tiempo que tardaría en
descargarse V2 manteniendo constante la corriente calculada en el apartado
anterior
9. Calcule la condición que deben cumplir las resistencias del circuito de la
figura para que la corriente que circula por R6 sea nula.
10. Se conecta a los terminales de salida de un circuito lineal una resistencia de
100 KΩ obteniendo una tensión de salida de 14 V. Si se conecta una
resistencia de 1 KΩ la salida es de 10 V. Calcule el circuito equivalente de
Thèvenin.
11. Calcule la corriente eléctrica que circula por R5 en el circuito de la figura
12. En el circuito de la figura las entradas pueden estar conectadas a V = 5 V o a
0 V, según la posición de los conmutadores. Si éstos están controlados por
las variables lógicas S0, S1, S2, S3 (de izquierda a derecha) de manera que
cuando S=0 la entrada está a la referencia (0 V) y cuando S =1 está a 5 V.
a) Obtenga la resistencia equivalente de Thèvenin excluyendo la
resistencia 2R de salida.
b) Calcule la tensión de salida con S0=0, S1=0, S2=0 y S3=1
c) Calcule la máxima tensión de salida
13. En el circuito de la figura aparece una fuente de corriente dependiente de
corriente. Obtenga el valor de la tensión Vo
14. En el circuito de la figura existe una fuente de tensión dependiente de tensión.
Sea R= 1 KΩ y Rf = 10 KΩ:
a) Si Av = 200000, Rin = 1 MΩ y Ro =10 Ω, obtenga la relación entre las
tensiones de entrada y salida
b) Repita el cálculo en el límite Ro → 0
c) Calcule de nuevo la relación entre las tensiones de entrada y salida si,
además, Rin → ∞ y Av → ∞
15. Obtenga el equivalente de Thevenin y de Norton del siguiente circuito (por
separado)
16. Obtenga la diferencia de potencial entre los nudos A y B de los circuitos de la
figura, y la resistencia vista desde esos terminales: