problemario1
Anuncio

Problemas de Electrónica Digital
Tema 1 – Fundamentos
UNIVERSIDAD DE VALLADOLID
Departamento de Electricidad y Electrónica
1.- De acuerdo con el teorema de DeMorgan, el complemento de la función X+YZ es
X Y + Z . Ambas funciones toman el valor lógico “1” para XYZ=110. ¿Cómo
pueden la función y su complemento ser “1” para la misma combinación de entrada?
¿Qué está mal aquí?
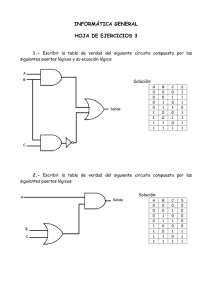
6. - Un circuito lógico tiene 5 entradas y 1 salida. Cuatro de las entradas, A, B, C y D
representan un dígito decimal en BCD. La quinta entrada, E, es de control. Cuando
el control E esté en “0” lógico, la salida estará en “0” lógico si el número decimal es
par y en “1” lógico si es impar. Cuando el control esté en “1”, la salida será “1”
cuando la entrada sea múltiplo de 3 y “0” en caso contrario. Diseñar el circuito.
2.- Un tipo de puerta, disponible comercialmente es la puerta AOI (AND-OR-INVERT).
Consta de una serie de puertas AND en un primer nivel cuyas salidas son las entradas
a una puerta NOR. La salida de la puerta NOR es la salida de la puerta AOI.
7. – A partir de los cronogramas de las entradas A, B y C y de la salida F de un circuito
lógico que aparecen en la figura, determinar cuál es su estructura de puertas.
Demostrar que con una puerta AOI se puede implementar las funciones NAND, NOR
y NOT.
3.- a)
b)
Implementar la función f = ( A + B + C )( D + E )( F + G ) utilizando una
puerta AOI
Implementar la función f = A ⊕ B utilizando sólo dos puertas AOI teniendo
en cuenta los inversores.
4. – Generar las siguientes funciones empleando puertas AOI suponiendo que como
entradas se dispone tanto de las variables como de sus complementos.
f ( X , Y , Z ) = XY + X Y Z
f ( A, B, C , D ) = ∏ (2,3,4,7,10,11,15)
4
5. – Analizar el circuito de la figura y simplificar la función que realiza.
8. – Diseñar un circuito digital capaz de detectar temperaturas comprendidas entre T1 y T2
por un lado y entre T3 y T4 por otro, verificándose:
T1<T2<T3<T4
Suponer que el sistema toma información a partir de 4 sensores capaces de detectar
si la temperatura es mayor que una dada. Implementar el circuito con puertas
NAND. Implementarlo con puertas NOR.
9. – Diseñar un circuito digital capaz de detectar errores en los sensores del sistema
descrito en el ejercicio anterior.
10. – Simplificar utilizando el diagrama de Karnaugh la siguiente función:
f ( A, B, C , D ) = A B C D + BC D + A C + A
1/1
b) La expresión mínima de suma de productos.
11. – En un registro de 4 bits cuyas salidas están disponibles al exterior, se almacena
información en el código BCD.
a)
b)
c)
d)
Realizar la tabla de verdad de un circuito lógico que detecte si el
número contenido en el registro es mayor que 7 o menor que 3.
Minimizar la expresión algebraica de la función obtenida a partir de la
tabla realizada en el apartado anterior.
Realizar la expresión mínima con puertas NAND.
Realizar la expresión mínima con puertas NOR.
12. – Realizar un circuito lógico que tenga por entradas los 4 bits de un número en el
código Gray y por salidas los 4 bits del número correspondiente en binario natural.
Hacer lo mismo para la situación recíproca. Implementar ambos circuitos con
puertas XOR.
13. - La salida de un sistema digital consiste en palabras de 3 bits que han de transmitirse
a otro sistema alejado físicamente. Para proteger la información enviada ante errores
introducidos en la transmisión, se ha determinado añadir un bit de paridad en la
transmisión de cada palabra
Diseñar un circuito combinacional capaz de generar dicho bit de paridad, que ha de
ser “1” cuando el número de “1” en la palabra de información sea par o cero, y “0”
en caso de que el número de “1” sea impar.
Realizar el diseño utilizando exclusivamente 3 puertas XOR de 2 entradas cada una.
14. - En el sistema binario, hay varias maneras de representar un número negativo. Una
de ellas es el complemento a 9. Se genera obteniendo la diferencia a 9 de cada
cifra decimal representada en binario natural. Así, por ejemplo, el complemento a
9 del número 164 será el 835 (8=9-1, 3=9-6, 5=9-4).
17. - Un registro de salidas en paralelo a3 a a0 contiene un dígito codificado en BCD.
Diseñar un sistema combinacional que genere las siguiente funciones binarias.
a) f1: adoptará el estado uno si el dígito contenido en el registro es divisible
por dos y el estado cero en caso contrario.
b) f2: adoptará el estado uno si el dígito contenido en el registro está
comprendido entre 1 y 4 ambos inclusive y el estado cero en caso
contrario.
c) f3: adoptará el estado uno si el dígito contenido en el registro es divisible
por cuatro y el estado cero en caso contrario.
Obtener las expresiones mínimas como suma de productos de f1, f2 y f3 consideradas
como funciones independientes por el método tabular de Karnaugh. Obtener además
las expresiones mínimas de suma de productos de f1, f2 y f3 consideradas como una
multifunción.
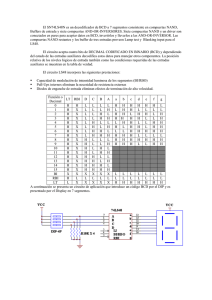
18. – Diseña un convertidor de código utilizando exclusivamente puertas NOR. La
entrada será un número de 4 bits (C3, C2, C1, C0) que representa los dígitos
hexadecimales {0, 1,......9. A, b, C, d, E, F). Las salidas de este circuito controlarán
los LEDs de un display o visualizador de 7 segmentos que muestra el carácter
correspondiente (las letras b y d generalmente se escriben en minúsculas para
distinguirlas de los dígitos 8 y 0 respectivamente).
Nota: El display o dispositivo visualizador de 7 segmentos está formado por 7
LEDs o diodos luminosos. Sus cátodos se conectan a tierra por medio de los pines 3
y 8. Mientras que sus ánodos son las salidas del convertidor de código. Cuando el
ánodo de un LED está también conectado a tierra, éste permanecerá apagado
mientras que si lo conectamos a una tensión positiva se iluminará.
10 9
8
7
6
3, 8 ref
Diseñar un circuito complementador que calcule el complemento a 9 de un número
escrito en código BCD. Implementarlo utilizando el menor número posible de
puertas AND y OR.
a
1e
f
b
2d
g
4c
15. – En un registro de 4 bits se almacena una palabra A3A2A1A0 que representa una cifra
decimal codificada en BCD. Construir un circuito capaz de detectar errores en la
codificación de dicha palabra utilizando el menor número posible de puertas lógicas.
e
c
d
16. – Realizar la síntesis de una función f de cuatro variables a, b, c y d que tome el valor
lógico “1” cuando el número de variables que están en estado uno es superior al de
las que se encuentran en estado cero. Nunca puede haber más de tres variables en
estado “1” simultáneamente. Obtener:
a) La expresión mínima de producto de sumas.
5 pto
6b
7a
9f
1
2
3
4
5
10 g
2/2