Ejercicios d...nometría

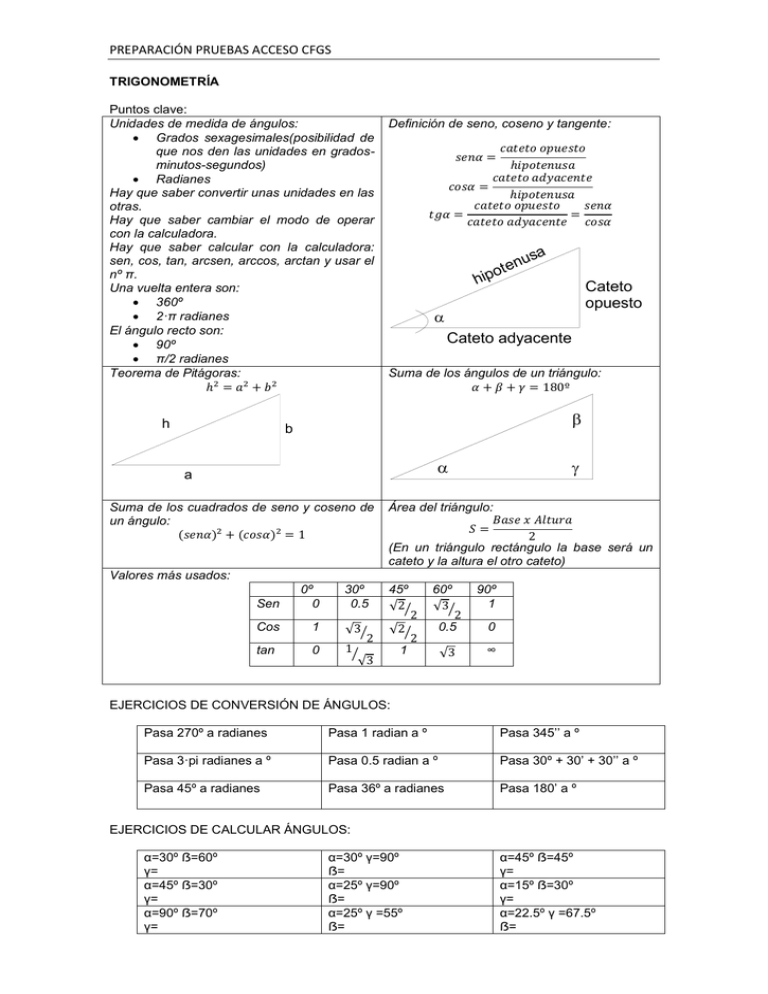
PREPARACIÓN PRUEBAS ACCESO CFGS
TRIGONOMETRÍA
Puntos clave:
Unidades de medida de ángulos:
 Grados sexagesimales(posibilidad de
que nos den las unidades en gradosminutos-segundos)
 Radianes
Hay que saber convertir unas unidades en las
otras.
Hay que saber cambiar el modo de operar
con la calculadora.
Hay que saber calcular con la calculadora:
sen, cos, tan, arcsen, arccos, arctan y usar el
nº π.
Una vuelta entera son:
 360º
 2·π radianes
El ángulo recto son:
 90º
 π/2 radianes
Teorema de Pitágoras:
h
Definición de seno, coseno y tangente:
a
nus
e
t
o
hip
Cateto
opuesto
a
Cateto adyacente
Suma de los ángulos de un triángulo:
b
b
a
a
Suma de los cuadrados de seno y coseno de
un ángulo:
g
Área del triángulo:
(En un triángulo rectángulo la base será un
cateto y la altura el otro cateto)
Valores más usados:
Sen
0º
0
Cos
1
tan
0
30º
0.5
45º
60º
0.5
1
90º
1
0
∞
EJERCICIOS DE CONVERSIÓN DE ÁNGULOS:
Pasa 270º a radianes
Pasa 1 radian a º
Pasa 345’’ a º
Pasa 3·pi radianes a º
Pasa 0.5 radian a º
Pasa 30º + 30’ + 30’’ a º
Pasa 45º a radianes
Pasa 36º a radianes
Pasa 180’ a º
EJERCICIOS DE CALCULAR ÁNGULOS:
α=30º ẞ=60º
γ=
α=45º ẞ=30º
γ=
α=90º ẞ=70º
γ=
α=30º γ=90º
ẞ=
α=25º γ=90º
ẞ=
α=25º γ =55º
ẞ=
α=45º ẞ=45º
γ=
α=15º ẞ=30º
γ=
α=22.5º γ =67.5º
ẞ=
PREPARACIÓN PRUEBAS ACCESO CFGS
EJERCICIOS DE TEOREMA DE PITÁGORAS. CALCULA EL TÉRMINO QUE FALTA:
H=5; B=3
A=7; B=5
H=3; A=6
A=2; B=3.5
H=9; A=8
A=40; B=15
H=5; B=4
A=3.6; B=2.5
H=12; A=9
A=3; B=4
H=8; A=4
A=6; B=6
EJERCICIOS DE SENOS, COSENOS Y TANGENTES DE TRIÁNGULOS RECTÁNGULOS:
H=5; B=3
sen α=
cos α=
tan α=
α=
A=
A=2; B=5
sen α=
cos α=
tan α=
α=
H=
H=5; B=4
sen α=
cos α=
tan α=
α=
α=45º; B=5
sen α=
cos α=
tan α=
H=
A=
H=9; A=8
sen α=
cos α=
tan α=
α=
B=
A=3.6; B=2.5
sen α=
cos α=
tan α=
α=
H=3; α=30º
sen α=
cos α=
tan α=
A=
B=
A=40; α=22.5º
sen α=
cos α=
tan α=
A=
B=
H=12; A=9
sen α=
cos α=
tan α=
α=
EJERCICIOS DE CALCULAR EL ÁREA DEL TRIÁNGULO RECT. A PARTIR DE LOS DATOS:
A=7; B=5
H=5; B=3
H=3; A=6
A=2; B=3.5
α=30º; A=8
α=45º; B=15
α=60º; B=10
α=25º; H=7
α=1.2 rad; A=3
EJERCICIOS FÁCILES PARA PRACTICAR:
Ejercicio:
Tenemos una escalera de 5m de longitud y la hemos apoyado en una pared. El extremo
superior llega a 4.5m de altura. Calcula cuánto mide el espacio horizontal bajo la escalera y
cuál es el ángulo que forma la escalera con la horizontal.
Ejercicio:
Tenemos una cometa con un cable de 50m de longitud y está formando un ángulo con la
horizontal de 65º. Calcula a qué altura está y a qué distancia en horizontal se encuentra.
Ejercicio:
Tenemos un poste del que sabemos que mide 7m de altura. Desde donde nos encontramos
medimos el ángulo que forma entre la horizontal y la visual a la punta del poste y son 15º. ¿A
qué distancia estamos del poste?
Ejercicio:
Subimos por una rampa inclinada con un ángulo constante. Sabemos que cuando recorremos
15m medidos en horizontal, ascendemos 5m en vertical. Calcula cuánto ascenderemos en
vertical si nos desplazamos 80m en horizontal. Calcula cuánto recorremos medido sobre la
rampa inclinada cuando nos hemos movido esos 80m en horizontal. Calcula el ángulo de
inclinación de esa rampa.
PREPARACIÓN PRUEBAS ACCESO CFGS
EJERCICIOS COMO LOS DEL LIBRO DE ORTELLS Y CLEMENTE UN POCO MÁS
DIFÍCILES PARA PRACTICAR:
Ejercicio:
Tenemos a lo lejos una montaña y desde donde estamos medimos con un aparato de
topografía el ángulo que vemos entre la horizontal y la cima y es de 47º. Nos alejamos 1000m
de nuestra posición y volvemos a medir el ángulo, siendo ahora 40º. ¿Qué altura tiene la
montaña?
Ejercicio:
Tenemos a lo lejos una torre de alta tensión y desde donde estamos medimos con un aparato
de topografía el ángulo que vemos entre la horizontal y la cima y es de 35º. Nos acercamos
100m de nuestra posición y volvemos a medir el ángulo, siendo ahora 45º. ¿Qué altura tiene la
torre?
Ejercicio:
Tenemos un triángulo que no es rectángulo y que tiene 1 ángulo α=30º y los lados contiguos
son 3m y 5m. a) ¿Qué superficie tiene el triángulo? b) ¿Cuál es el valor del tercer lado?
Ejercicio:
Tenemos un triángulo que no es rectángulo y que tiene 1 ángulo α=45º y los lados contiguos
son 4m y 7m. a) ¿Qué superficie tiene el triángulo? b) ¿Cuál es el valor del tercer lado?
EXÁMENES REALES:
Ejercicio de la prueba de junio de 2010.
Queremos fijar un poste de 4 m de altura, con un cable que va desde el extremo superior del
poste al suelo. Desde ese punto del suelo se ve el poste bajo un ángulo de 30º.
a) ¿A qué distancia del poste sujetaremos el cable?
b) ¿Cuál es la longitud del cable?
Ejercicio de la prueba de junio de 2011.
Al apoyar una escalera de 3 metros en una pared, su extremo superior alcanza una altura de
2,7 metros. Calcula:
a) El ángulo que forma la escalera y el suelo.
b) La distancia del pie de la escalera a la pared.
Ejercicio de la prueba de junio de 2014.
En una determinada hora, un poste de 5 metros de altura proyecta una sombra que mide 12
metros. Coloca estos datos en el dibujo y:
1. Calcula la distancia, D, desde la parte más alta del
poste al extremo más alejado de su sombra.
2. Calcula el ángulo α formado por la sombra y el
segmento D.
3. En ese mismo momento, se observó que la sombra
proyectada por otro poste próximo medía 7'2 metros.
Calcula la altura del poste.
Ejercicio de la prueba de SEPTIEMBRE de 2011.
En la parte superior de una torre se ha construido un mirador. Si
nos alejamos a 40m de la base de la torre, observamos la altura
de la misma bajo un ángulo de 28º. Desde ese mismo punto
observamos la altura total de la torre y el mirador bajo un ángulo
de 38º. Calcula a) la altura de la torre y b) la altura del mirador.
PREPARACIÓN PRUEBAS ACCESO CFGS
GEOMETRÍA PLANA
Puntos clave:
Sistema de coordenadas cartesianas X, Y:
 Cada punto en el plano se representa
por una coordenada según el eje
horizontal
X
(abscisa)
y
una
coordenada según el eje vertical Y
(ordenada)
 Las coordenadas X positiva son hacia
la derecha y las coordenadas Y
positivas son hacia arriba.
Distancia entre 2 puntos A y B:
A(xA, yA)
B(xB, yB)
y
B (xB, yB)
yB
y
yA
yA
A (xA, yA)
A (xA, yA)
x
x
xA
xA
xB
Punto medio del segmento que une los
puntos A y B:
A(xA, yA)
B(xB, yB)
El punto medio M tiene por coordenadas:
¿Cómo expresar una
dirección en el plano?
Mediante un vector v
con coordenadas x e y.
v (v , v )
La coordenadas de
v(vx, vy) indican la
x
dirección
desde
cualquier punto desplazándose vx en dirección
horizontal y vy en dirección vertical.
y
x
y
Una misma dirección puede ser expresada con
diferentes vectores , por ejemplo u(1,2) y
v(2, 4) tienen la misma dirección. A la hora de
usarlos para dar la dirección de, por ejemplo,
una recta, me servirán indistintamente.
1ª) A partir de un punto A y una dirección V.
Las coordenadas de Cualquier punto P de la
recta r se podrán escribir como suma de las
coordenadas de A y t veces la dirección V.
Ecuación de la recta r:
Hay 4 formas de representarla:
1ª) Ecuación vectorial (Punto-Dirección)
2ª) Ecuación paramétrica
3ª) Ecuación continua
4ª) Ecuación general o implícita
3ª) Si de la anterior pareja de ecuaciones
despejo la t y hago una igualación, me queda
una única ecuación que relaciona las
coordenadas x e y de los puntos de la recta r.
Es:
2ª) De la fórmula anterior, las coordenadas de
cualquier punto M de la recta r serán:
Es decir, que si voy dando valores a t, a partir
de la fórmula voy obteniendo las coordenadas
de diferentes puntos de la recta r. Como ese
punto M es un punto cualquiera, puedo decir
que las ecuaciones de la recta son:
4ª) Si despejo en la anterior ecuación me
queda:
Puedo ver la semejanza con la función de
1er grado y=mx+n
Sería m=
n=
PREPARACIÓN PRUEBAS ACCESO CFGS
Intersección entre 2 rectas:
Si tienen la misma dirección, serán rectas
paralelas y nunca se cortarán.
Si no tienen la misma dirección, entonces al
buscar un punto que pertenezca a las 2 rectas
a la vez, lo que tengo es que resolver un
sistema de 2 ecuaciones con 2 incógnitas.
Vector con la dirección perpendicular a una
recta r: y=mx+n
Sabemos que m=
así que podemos
Distancia punto-recta
Me dan un punto P y la ecuación de una recta r
y se trata de ver cuál es la distancia de ese
punto a esa recta. La idea es:
1º) Calcular el vector perpendicular a la recta.
2º) Escribir la ecuación de la recta que pasa
por P y tiene por dirección la del vector
perpendicular.
3º) Calcular el punto C donde se cortan las 2
rectas.
4º) Calcular la distancia de P a C.
Escalas
Sin necesidad de realizar todos esos cálculos,
si tenemos P=(px, py) y r= Ax+By+C=0 hay una
fórmula que me da directamente la solución:
expresar el vector de la recta v como v=(1,m)
El vector perpendicular será u=
Ejemplo:
Si mido en el plano 2cm y la escala es 1:500,
la medida real será:
Así despejo:
Realidad=500x2cm=1000cm=10m
(Se puede razonar esto con la regla de 3)
Ejemplo:
Si lo que en la realidad mide 5m yo lo dibujo
como 1mm la escala será:
Si le doy al botón 1/x de la calculadora me
sale: 5000, que significa que la escala es
1/5000.
La “escalera” para el cambio de unidades
de longitud:
km
:10
:60
hm
dam
h
m
min.
dm
s
cm
x10
mm
x60
Ejercicios de Escalas:
:100
km2
1.- En un plano a escala 1:500 mido una distanciahm
de 223mm. ¿Cuál es la distancia real en
metros?
dam2
2.- En un plano a escala 1:10000 mido una distancia de 2.6dm.
¿Cuál2 es la distancia real en
m
km?
2
dm¿Cuál
3.- En un plano a escala 1:2000 quiero dibujar un cuadrado de 6m de lado.
ha de ser el
lado en el dibujo en cm?
cm2
2 la
4.- En un plano a escala 1:5000 quiero dibujar una recta dex100
100m de lado. ¿Cuál ha de
ser
mm
longitud en el dibujo en mm?
5.- Si tengo una calle de 150m de largo y la quiero dibujar en el plano y que la línea tenga
1.5cm de largo, ¿qué escala he de utilizar?
6.- Si tengo un campo de fútbol de 110m de largo y quiero dibujarlo en el plano y que la línea
tenga 55mm de longitud ¿qué escala he de emplear?
7.- En un plano a escala 1:50 tengo una piscinakm
que3 mide 8cm x 20cm.
¿Cuál es su superficie
:1000
en el plano y cuál es su superficie real?
hm3
8.- En un plano a escala 1:20000 tengo una parcela rectangular
que3 mide 10cm x 24cm. ¿Cuál
dam
es su superficie en el plano y cuál es su superficie real?
3
m
dm3
cm3
x1000
mm3
PREPARACIÓN PRUEBAS ACCESO CFGS
Ejercicios de dibujar puntos en el plano:
9.- Dibuja en un papel cuadriculado un sistema de ejes cartesianos y ubica los siguientes
puntos (incluye la letra que los caracteriza):
A(6,3); B(-5,5); C(3,4); D(-3,4); E(2,-4); F(-6,-5); G(4,-2); H(-3.-6)
Ejercicios de distancias entre puntos:
10.- Calcula la distancia entre los puntos A(10,5) y B(15,5)
11.- Calcula la distancia entre los puntos A(10,5) y B(10,17)
12.- Calcula la distancia entre los puntos A(0,5) y B(5,0)
Calcula la distancia entre los puntos O(0,0) y A(0,5)
Calcula la distancia entre los puntos O(0,0) y B(5,0)
13.- Calcula la distancia entre los puntos A(2,3) y B(5,7)
14.- Calcula la distancia entre los puntos A(-3,-2) y B(3,1)
15.- Calcula la distancia entre los puntos A(6,3) y B(-5,5)
16.- Calcula la distancia entre los puntos A(-5,5) y B(-3,4)
17.- Calcula la distancia entre los puntos A(2,-4) y B(-6,-5)
Ejercicios de punto medio entre otros dos conocidos:
18.- Calcula el punto medio entre los puntos A(10,5) y B(15,5)
19.- Calcula el punto medio entre los puntos A(10,5) y B(10,17)
20.- Calcula el punto medio entre los puntos A(0,5) y B(5,0)
21.- Calcula el punto medio entre los puntos A(2,3) y B(5,7)
22.- Calcula el punto medio entre los puntos A(-3,-2) y B(3,1)
23.- Calcula el punto medio entre los puntos A(6,3) y B(-5,5)
24.- Calcula el punto medio entre los puntos A(-5,5) y B(-3,4)
25.- Calcula el punto medio entre los puntos A(2,-4) y B(-6,-5)
PREPARACIÓN PRUEBAS ACCESO CFGS
Ejercicios de ecuación de la recta:
26.- Escribe la ecuación de la recta entre los puntos A(2,3) y B(4,5) de las diferentes maneras
posibles.
27.- Escribe la ecuación de la recta entre los puntos A(-2,5) y B(5,-5) de las diferentes maneras
posibles.
28.- Escribe la ecuación de la recta entre los puntos A(0,5) y B(5,0) de las diferentes maneras
posibles.
29.- Escribe la ecuación de la recta entre los puntos A(2,3) y B(4,3) de las diferentes maneras
posibles.
30.- Escribe la ecuación de la recta entre los puntos A(2,3) y B(2,5) de las diferentes maneras
posibles.
31.- Escribe la ecuación de la recta entre los puntos A(-1,-1) y B(1,1) de las diferentes maneras
posibles.
32.- Escribe la ecuación de la recta que pasa por A(-1,1) y tiene dirección v(2,1) de las
diferentes maneras posibles.
33.- Escribe la ecuación de la recta que pasa por A(1,3) y tiene dirección v(0.5,0.5) de las
diferentes maneras posibles.
34.- Escribe la ecuación de la recta que pasa por A(-1,-1) y tiene dirección v(0,1) de las
diferentes maneras posibles.
35.- Calcula la dirección y los puntos de cortes con los ejes de la recta 3y+2x=4.
36.- Calcula la dirección y los puntos de cortes con los ejes de la recta y=2(x-1).
37.- Calcula la dirección y los puntos de cortes con los ejes de la recta 0.5·(y-2)=3·(x-4).
38.- Calcula la dirección y los puntos de cortes con los ejes de la recta y=x+1.
39.- Calcula la dirección y los puntos de cortes con los ejes de la recta y+x=2.
40.- Calcula la dirección y los puntos de cortes con los ejes de la recta 3x-2y=0.
Ejercicios de ecuación de la recta perpendicular a otra recta:
41.- Escribe el vector que da la dirección de la recta entre los puntos A(2,3) y B(4,5) y calcula
su dirección perpendicular.
42.- Escribe el vector que da la dirección de la recta entre los puntos A(-1,1) y B(1,1) y calcula
su dirección perpendicular.
43.- Calcula la dirección perpendicular a la recta y=x+1.
44.- Calcula la dirección perpendicular a la recta 0.5·(y-2)=3·(x-4).
45.- Calcula la dirección perpendicular a la recta y+x=2.
46.- Calcula la dirección perpendicular a la recta 3x-2y=0.
Ejercicios de punto a una distancia de otro a lo largo de una recta:
No vamos a hacer de este tipo.
Ejercicios de distancias punto-recta:
47.- Calcula la distancia entre el punto P(7,8) y las rectas:
a) y=x+1.
b) 0.5·(y-2)=3·(x-4).
c) y+x=2.
d) 3x-2y=0.
e) Pasa por A(-1,1) y tiene dirección v(2,1)
f) Pasa por A(-1,-1) y tiene dirección v(0,1)
g) Pasa por los puntos A(2,3) y B(4,5)
h) Pasa por los puntos A(0,5) y B(5,0)
i) Pasa por los puntos A(2,-4) y B(-6,-5)
Ejercicios de intersecciones entre 2 rectas:
48.-Calcula la intersección entre las rectas:
a) y=x+1.
0.5·(y-2)=3·(x-4).
b) y+x=2.
3x-2y=0.
c) Recta que pasa por A(-1,1) y tiene dirección v(2,1)
Recta que pasa por A(-1,-1) y tiene dirección v(0,1)
PREPARACIÓN PRUEBAS ACCESO CFGS
EXÁMENES REALES:
Ejercicio de la prueba de junio de 2012.
Un mapa cuya escala es 1:20.000 lleva incorporado un sistema de referencia euclídeo cuyas
unidades vienen en cm. En el punto (-2,1) se encuentra situado un pozo y en el punto (6,7) se
encuentra situada una fábrica. Queremos construir una tubería de cemento que, en línea recta,
lleve el agua desde el pozo a la fábrica. Calcula:
a) La longitud de la tubería en el mapa y en la realidad.
b) La ecuación de la recta que sustenta la tubería.
Ejercicio de la prueba de junio de 2013.
En un mapa, que incorpora unos ejes de coordenadas perpendiculares con las unidades en
centímetros, figuran dos poblaciones A y B, situadas respectivamente en los puntos (3, 0) y
(−1, −3).
a) Calcula la distancia en el plano entre las dos poblaciones
b) Calcula la distancia real en km si la escala es 1:50.000
c) Si pudiéramos construir una carretera totalmente recta entre las dos poblaciones, ¿cuál sería
la ecuación que cumpliría en el plano dicha carretera?
Ejercicio de la prueba de julio de 2014.
Los puntos A = (-3,0) y B = (1,3), son dos vértices consecutivos de un cuadrado. Sabiendo que
la abscisa del tercer vértice C es positiva:
a) Calcula, a simple vista, las coordenadas de los otros dos vértices C y D.
b) Halla la ecuación de la recta que pasa por los vértices A y C.
c) Halla el área del cuadrado.
Ejercicios pruebas de acceso a Universidad:
Ejemplo de examen:
Los vértices de un triangulo rectángulo son: O=(0,0); A=(8,0); B=(0,8 )
Obtenga razonadamente el seno de los ángulos A y B. Obtenga razonadamente la ecuación de
la recta que pasa por A y B.
Junio de 2013:
Obtener razonadamente la ecuación de la recta r que pasa por los puntos A = (4, 0) y B = (2, 2)
y Obtener razonadamente la distancia del punto (0, 0) a la recta r.
Junio de 2014:
La base de un triángulo está formada por el segmento que une los puntos A(−3, 1) y B(5, −1) .
El tercer vértice es el punto C(6, 5). a) Obtener de forma razonada la altura del triángulo. b)
Obtener razonadamente el valor del área del triángulo.