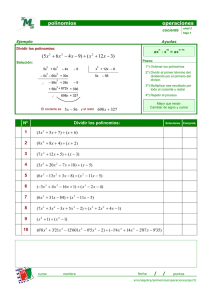
2 OPERACIONES CON POLINOMIOS

OPERACIONES CON POLINOMIOS.
EXPRESIONES ALGEBRAICAS.
Una expresión matemática que usa números o variables o ambos para indicar productos o
cocientes es un término.
2x + 4
y 16x 2 son todos expresiones algebraicas. Las
2
expresiones algebraicas están formadas por sumas, restas, productos, cocientes, potencias y
radicales.
Los términos 2x, 3xy, (a+b),
En una expresión algebraica como 4xy el coeficiente es el numero 4, los factores son x,y.
Los nombres de los términos de una expresión matemática.
Los términos como 2x, 3xy, 6x2 o –5ab son monomios. En griego monos significa uno,
único, así monomio significa único término.
Los términos (x + y), (x2 – y) o (4x2 + y3) son binomios. La palabra binomio. (De bi- y el griego.
νοµός, parte, porción). Expresión compuesta de dos términos algebraicos unidos por los signos más o
menos.
Los términos (2x + 3 + y) o (3ab + 2a –5b + 6b2) son polinomios. La palabra polinomio. (De
poli y el griego. νόµος, varios). Expresión compuesta de dos o más términos algebraicos
unidos por los signos más o menos.
Las expresiones de dos o tres términos reciben los nombres especiales de binomio y
trinomio, respectivamente.
SUMA DE POLINOMIOS.
Para sumar dos polinomios se agrupan los términos semejantes y se suman los coeficientes.
Recordemos que los términos semejantes son aquellos términos que tienen los mismos
factores literales, cada uno con la misma base y exponente.
Son términos semejantes:
6x y 9x
2x2y y 3x2y
–6ab2c4 y 5ab2c4
Ejemplos resueltos.
De manera práctica pueden colocarse los polinomios unos debajo de los otros de modo que
los términos semejantes queden en columna; se hace la reducción de ellos, separándolos unos
de los otros con sus propios signos.
Ejemplo 1
Sumar 6m–2n; –4n+5p; –m –5p
6m –2n
–4n +5p
–m
–5p
5m –6n
Ejemplo 2
Sumar a+2b –3c; –3a +5b; –4b+6c
a +2b –3c
–3a +5b
–4b +6c
–2a +3b +3c
Ejemplo 3
Sumar 3x2+4xy+y2; –4xy + 6x2 –3y2; –6y2–8xy–9x2
3x2 +4xy +y2
+ 6x2 –4xy –3y2
–9x2 –8xy –6y2
0x2
–8xy –8y2
Ejemplo 4
Sumar ax –ay –az; –5ax –7ay +6az; 5az –8ay –3ax
ax –ay –az
–5ax –7ay +6az
–3ax –8ay +5az
–7ax –16ay +10az
RESTA DE POLINOMIOS.
La resta es una operación que tiene por objeto, dada una suma de dos sumandos (minuendo)
y uno de ellos (sustraendo), hallar el otro sumando (resta o diferencia).
Cuando el sustraendo es un polinomio, hay que restar del minuendo cada uno de los términos
del sustraendo, así que a continuación del minuendo escribiremos el sustraendo cambiándole
el signo a todos sus términos.
Ejemplo 1
A 6m–2n restar –4n+5p
Cambiamos los signos al sustraendo.
6m –2n
+4n –5p
6m +2n –5p
Ejemplo 2
A a+2b –3c restar –3a +5b–6c
Cambiamos los signos al sustraendo.
a +2b –3c
+3a –5b +6c
+4a –3b +3c
Ejemplo 3
A 3x2+4xy+y2 restar –4xy + 6x2 –3y2
3x2 +4xy +y2
–6x2 +4xy +3y2
–3x2
+8xy +4y2
Ejemplo 4
A ax –ay –az restar 5az –8ay –3ax
Cambiamos los signos al sustraendo.
ax –ay –az
+3ax +8ay –5az
+4ax –7ay –6az
MULTIPLICACIÓN DE POLINOMIOS.
La multiplicación es una operación que tiene por objeto, dadas dos cantidades llamadas
multiplicando y multiplicador, hallar una tercera cantidad, llamada producto, que sea
respecto del multiplicando, en valor absoluto y signo, lo que el multiplicador es respecto de
la unidad positiva.
El multiplicando y multiplicador son llamados factores del producto.
Al multiplicar dos cantidades hay que considerar el signo de cada una de ellas, para saber cuál será el
signo del producto se tomará en cuenta lo siguiente.
(+)
(+)
( -)
( -)
por
por
por
por
(+) = + que se lee “más por más igual a más”
(-) = - que se lee “más por menos igual a menos”
(+) = - que se lee “menos por más igual a menos”
(-) = + que se lee “menos por menos igual a más”
En conclusión tenemos que:
Al multiplicar signos iguales el producto es positivo
Al multiplicar signos distintos el producto es negativo
Producto de potencias de la misma base.
El resultado es una potencia con la misma base y como exponente la suma de los exponentes de las
potencias que se multiplican.
(bm)(bm)=bm+ n
Ley de los coeficientes.
El coeficiente del producto de dos factores es el producto de los coeficientes de los factores.
REGLA PARA MULTIPLICAR DOS POLINOMIOS.
Se multiplican todos los términos del multiplicando por cada uno de los términos del
multiplicador, teniendo en cuenta la ley de los signos, el producto de potencias de la misma
base y la reducción de términos semejantes.
Ejemplos resueltos.
Ejemplo 1
Multiplicar 6m–2n por –4m+5n
6m –2n
+4m +5n
24m2 –8mn
+30mn –10n2
24m2 +22mn –10n2
Ejemplo 2
Multiplicar a+2b –3c por –3a +5b
a +2b –3c
–3a +5b
–3a2 –6ab +9ac
+5ab
+10b2 –15bc
–3a2 –ab +9ac +10b2 –15bc
Ejemplo 3
Multiplicar 3x2+4xy+y2 por + 6x2 –3y2
3x2 +4xy +y2
+6x2 –3y2
18x4 +24x3y +6x2y2
–9x2y2 –12xy3–3y4
18x4 +24x3y –3x2y2 –12xy3–3y4
Ejemplo 4
Multiplicar ax –ay –az por 5az –8ay –3ax
ax –ay –az
–3ax –8ay +5az
–3a2x2 +3a2xy +3a2xz
–8a2xy
+8a2y2 +8a2yz
2
+5a xz
–5a2yz –5a2z2
–3a2x2 –5a2xy +8a2xz +8a2y2 +3a2yz –5a2z2
DIVISIÓN DE POLINOMIOS.
La división es una operación que tiene por objeto, dado el producto de dos factores dividendo
y uno divisor, hallar el otro factor (cociente).
Ley de los signos.
En la división para saber el signo del resultado se deberá aplicar una regla parecida a la de la
multiplicación tal como se muestra en la siguiente tabla.
(+ ) = +
(+ )
Que se lee “más entre más es igual a más”
(+ ) = −
(− )
Que se lee “más entre menos es igual a menos”
(− ) = −
(+ )
Que se lee “menos entre más es igual a menos”
(− ) = +
(− )
Que se lee “menos entre menos es igual a más”
División de potencias de la misma base.
El resultado es una potencia con la misma base y como exponente la diferencia de los exponentes del
numerador y el denominador.
bm
= b m−n
n
b
Ley de los coeficientes.
El coeficiente del cociente es; el cociente de dividir el coeficiente del dividendo entre el
coeficiente del divisor.
División de monomios.
Para dividir monomios aplicamos la regla de los signos de la división y las leyes de los
exponentes.
Ejemplos.
Dividir 6x entre 2
6x
= 3x
2
Dividir 12m3 entre 3m2
12m 3
= 4m 3−2 = 4m
3m 2
Dividir
–30x4y3 entre 6xy
− 30 x 4 y 3
= −5 x 4−1 y 3−1 = −5 x 3 y 2
6 xy
División de un polinomio entre un monomio.
Para dividir un polinomio entre un monomio se divide cada termino del polinomio entre el
monomio.
Ejemplos.
Dividir 3x2y3–6a2x4 entre –3x2
3 x 2 y 3 − 6a 2 x 4 3 x 2 y 3 6a 2 x 4
=
−
= − x 2− 2 y 3 + 2a 2 x 4− 2 = − y 3 − 2 a 2 x 2
− 3x 2
− 3x 2 − 3x 2
Dividir
4x8+10x6–8x4 entre 2x5
4 x 8 + 10 x 6 − 8 x 4 4 x 8 10 x 6 8 x 4
= 5+
− 5 = 2 x 8−5 + 5 x 6−5 − 4 x 4−5 = 2 x 3 + 5 x − 4 x −1
5
5
2x
2x
2x
2x
Dividir 6m3–3m2n+20mn2 entre –2m
6m 3 − 3m 2 n + 20mn 2 6m 3 3m 2 n 20mn 2
3m 2−1n
3mn
=
−
+
= −3m 3−1 +
− 10m1−1n 2 = −3m 2 +
− 10n 2
− 2m
− 2m − 2 m
− 2m
2
2
División de dos polinomios.
La división de dos polinomios se verifica mediante la siguiente regla:
• Se ordena el dividendo y el divisor con relación a una misma letra.
• Se divide el primer término del dividendo entre el primer término del divisor y
tendremos el primer término del cociente.
• Este primer término del cociente se multiplica por todo el divisor y el producto se
resta del dividendo, para lo cual se le deberá cambiar de signo, escribiendo cada
término debajo de su semejante. Si no existe término semejante en el dividendo se
escribe en el lugar que le corresponda de acuerdo con la ordenación del dividendo y el
divisor.
• Se divide el primer término del resto entre el primer término del divisor y tendremos
el segundo término del cociente. Se repite el paso anterior y así sucesivamente hasta
que el residuo sea cero.
Ejemplos resueltos.
Dividir x2–20+x entre x+5
x–4
x + 5 x 2 + x − 20
–x –5x
–4x –20
+4x +20
0
Dividir x4– 9x2+3+x entre x+3
x3 –3x2 +1
x + 3 x4 − 9x2 + x + 3
–x4–3x3
–3x3–9x2+x+3
+3x3+9x2
+x+3
–x–3
0
5
2
Dividir x +12x +5x entre x2+2x+5
x3+2x2+x
x 2 + 2 x + 5 x 5 + 12 x 2 + 5 x
–x5+2x4+5x3
2x4+5x3+12x2+5x
–2x4 –4x3–10x2
x3 +2x2 +5x
–x3 –2x2 – 5x
0