Principios de la Mec´anica

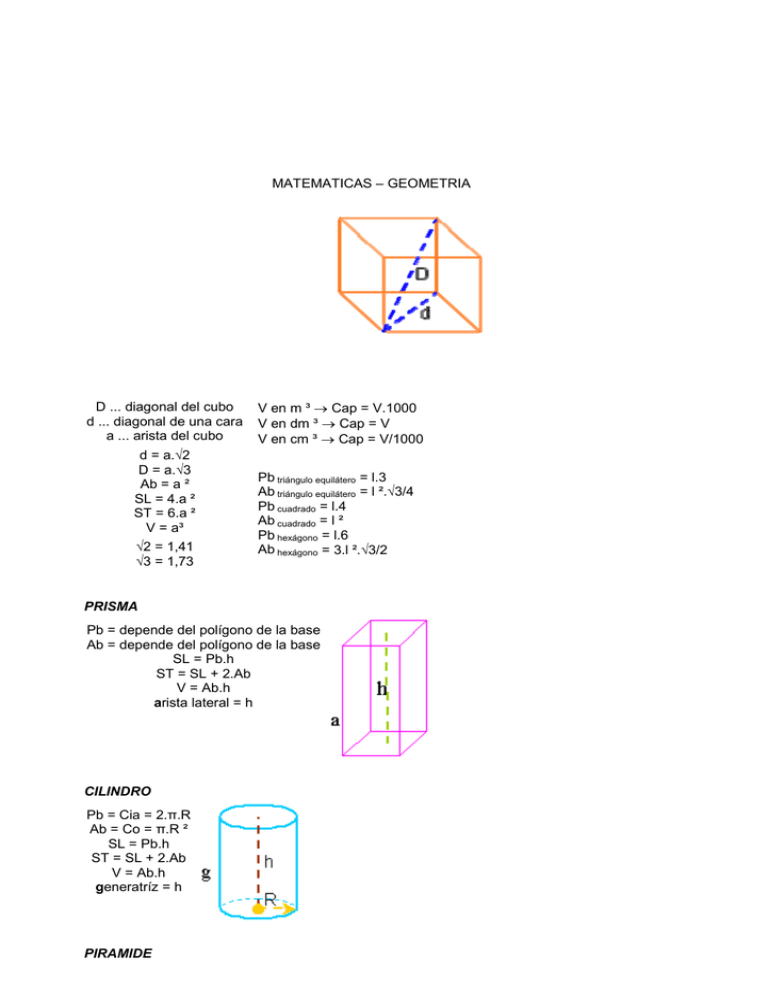
MATEMATICAS – GEOMETRIA
D ... diagonal del cubo
d ... diagonal de una cara
a ... arista del cubo
d = a.√2
D = a.√3
Ab = a ²
SL = 4.a ²
ST = 6.a ²
V = a³
√2 = 1,41
√3 = 1,73
V en m ³ → Cap = V.1000
V en dm ³ → Cap = V
V en cm ³ → Cap = V/1000
Pb triángulo equilátero = l.3
Ab triángulo equilátero = l ².√3/4
Pb cuadrado = l.4
Ab cuadrado = l ²
Pb hexágono = l.6
Ab hexágono = 3.l ².√3/2
PRISMA
Pb = depende del polígono de la base
Ab = depende del polígono de la base
SL = Pb.h
ST = SL + 2.Ab
V = Ab.h
arista lateral = h
CILINDRO
Pb = Cia = 2.π.R
Ab = Co = π.R ²
SL = Pb.h
ST = SL + 2.Ab
V = Ab.h
generatríz = h
PIRAMIDE
h ... altura de la pirámide
Ap ... apotema de la pirámide
a ... arista lateral de la pirámide
ap ... apotema de la base
r ... radio de la base
Pb = depende del polígono de la base
Ab = depende del polígono de la base
SL = Pb.Ap/2
ST = SL + Ab
V = Ab.h/3
Ap ² = h ² + ap ²
a²=h²+r²
CONO
g ... generatríz del cono
h ... altura del cono
R ... radio de la base
Pb = Cia = 2.π.R
Ab = Co = π.R ²
SL = Pb.g/2
ST = SL + Ab
V = Ab.h/3
g²=h²+R²
ESFERA
R²=r²+d²
d ... distancia entre las circunferencias
R ... radio de la circunferencia máxima o de la esfera
r ... radio de cualquier circunferencia menor
π = 3,14
Cia máxima = 2.π.R
Cia menor = 2.π.r
Co máxima = π.R ²
Co menor = π.r ²
A = 4.π.R ²
V = 4.π.R³/3
ap triángulo equilátero = l.√3/6
r triángulo equilátero = l/√3
ap cuadrado = l/2
r cuadrado = l/√2
ap hexágono = l.√3/2
r hexágono = l
1) Dados tres puntos, A, B y C, no alineados, dibujar: la semirrecta de origen C que contiene
al punto B, y la AB´.
2) Dibujar dos semirrectas que tengan el mismo origen y no sean opuestas.
3) ¿Qué figura constituye la unión del conjunto de los puntos de la AB´ y los de la semirrecta
de origen A que no contiene al punto B?
4) Dibujar, sobre una recta, cuatro segmentos consecutivos.
5) ¿Cuál es la figura formada por la intersección del conjunto de puntos de la semirrecta de
origen A que contiene al punto B y de la semirrecta de origen B que no contiene al punto A?
6) Dados los puntos M, P, Q y S de la figura, hallar:
PS´ ∩ QS´
MQ´ ∩ QP´
MQ´ ∩ PS´
MQ´ ∪ PS
MQ ∪ PS
7) Decir cual es el conjunto de los puntos tal que su intersección con XY de por resultado el
XY.
8) Comprobar, en un ejemplo, el carácter transitivo de la relación de mayor entre
segmentos.
9) Comprobar, en un ejemplo, el carácter transitivo de la relación de menor entre
segmentos.
10) ¿Si AB = CD y CD < EF, cómo es EF con respecto a AB?
11) ¿Si AB > MN y MN = EF, cómo es EF con respecto a AB?
12) ¿Si AB > CD, CD = EF y EF no es mayor que MN, cómo es AB con respecto a MN?
13) ¿Si MN = PQ, PQ > RS y RS no es menor que TV, cómo es MN con respecto a TV?
14) Verificar gráficamente en una suma de tres segmentos, la propiedad conmutativa.
15) Verificar gráficamente en una suma de cinco segmentos, la propiedad asociativa.
16) ¿Si AB > CD y MN > PQ, cómo es AB + MN con respecto a CD + PQ?
17) ¿Si RS < CD y AB = MN, cómo es RS + MN con respecto a AB + CD?
18) ¿Si AB < MN, cómo es AB x 6 con respecto a MN x 6?.
19) ¿Si AB + CD + EF = MN, cómo es MN con respecto a AB?
20) Comprobar gráficamente las propiedades de la resta de segmentos.
21) Expresar en símbolos las propiedades de la resta de segmentos.
22) Dibujar un segmento y hallar su duplo, su triplo y su cuádruplo.
23) Si un segmento se divide por tres y a ese resultado se lo multiplica también por tres,
¿qué segmento se obtiene?, comprobarlo gráficamente.
24) Dibujar un segmento, y mediante un hilo dividirlo aproximadamente en dos, tres,cuatro,
y seis partes iguales.
Polígonos Regulares Inscriptos en una Circunferencia
1) El perímetro de un triángulo equilátero inscripto en una Cia mide 72,66 m. Calcular: a) el
lado del triángulo equilátero; b) la superficie del triángulo; c) el radio de la Cia; d) la longitud
de la Cia y e) el área del Co.
Respuesta: l = 24,22 m; S = 253,70 m ²; R = 14 m; Cia = 87,92 m y Co = 615,44 m ².
2) Determinar la superficie, el perímetro, la altura, el radio y la longitud de la Cia del triángulo
equilátero inscripto cuyo lado mide 5 m.
Respuesta: S = 10,81 m ²; P = 15 m; h = 4,32 m; R = 2,89 m y Cia = 18,14 m.
3) La longitud de la Cia de un triángulo equilátero inscripto mide 50,24 m. Hallar el perímetro
de dicho triángulo y el área del Co.
Respuesta: Co = 200,96 m ² y P = 41,52 m.
4) El perímetro de un triángulo equilátero inscripto mide 20,4 m. Encontrar la longitud del
lado, la altura y la superficie del triángulo.
Respuesta: l = 6,8 m; h = 5,88 m y S = 19,99 m ².
5) El lado de un triángulo equilátero inscripto mide 0,692 m. Hallar la longitud de la Cia, el
área del Co, la apotema y la altura de dicho triángulo.
Respuesta: R = 0,4 m; Cia = 2,512 m; Co = 0,5024 m ²; ap = 0,19952 m y h = 0,59858 m.
6) El perímetro de un triángulo equilátero inscripto mide 1,8 m. Hallar el área del Co, la
longitud de la Cia y la altura del triángulo.
Respuesta: l = 0,6 m; R = 0,34 m; Cia = 2,1352 m; Co = 0,362984 m ² y h = 0,519 m.
7) El radio de una Cia mide 1,6 m. Calcular el perímetro, la altura, la apotema y la superficie
del triángulo equilátero inscripto.
Respuesta: l = 2,768 m; P = 8,304 m; h = 2,39432 m; ap = 0,7981 m y S = 3,31373 m ².
8) El diámetro de una Cia mide 1,8 m. Calcular el perímetro, la altura, la apotema y la
superficie del triángulo equilátero inscripto.
Respuesta: R = 0,9 m; l = 1,557 m; P = 4,671 m; h = 1,3468 m; ap = 0,44893 m y S =
0,362984 m ².
9) La longitud de una Cia mide 3,14 m. Calcular el perímetro, la altura y la superficie del
triángulo equilátero inscripto.
Respuesta: R = 0,5 m; l = 0,865 m; P = 2,595 m; h = 0,74822 m y S = 0,3236 m ².
10) El lado de un cuadrado inscripto mide 2,82 m. Calcular el radio de la Cia y el perímetro
del cuadrado.
Respuesta: R = 2 m y P = 11,28 m.
11) Hallar la longitud de la Cia inscripta en un cuadrado de 20 m de perímetro.
Respuesta: Cia = 22,23 m.
12) El lado de un cuadrado inscripto mide 8,46 m. Calcular la medida del radio de la Cia, la
longitud de la Cia, el área del Co, el perímetro y la superficie del cuadrado.
Respuesta: R = 6 m; Cia = 37,68 m; Co = 113,04 m ²; P = 33,84 m y S = 71,57 m ².
13) El radio de una Cia mide 1,4 m. Hallar el perímetro y la superficie del cuadrado inscripto.
Respuesta: l = 1,974 m; P = 7,896 m y S = 3,896676 m ².
14) La longitud de una Cia mide 4,396 m. Calcular el perímetro y la superficie del cuadrado
inscripto.
Respuesta: R = 0,7 m; l = 0,987 m; P = 3,948 m y S = 0,974169 m ².
15) El área de una Cia es de 1,1304 m ². Calcular el perímetro y la superficie del cuadrado
inscripto.
Respuesta: R = 0,6 m; l = 0,846 m; P = 3,384 m y S = 0,715716 m ².
16) El lado de un cuadrado inscripto mide 0,282 m. Calcular la longitud de la Cia y el área
del Co.
Respuesta: R = 0,2 m; Cia = 1,256 m y Co = 0,1256 m ².
17) El perímetro de un cuadrado inscripto mide 1,692 m. Calcular la longitud de la Cia y el
área del Co.
Respuesta: l = 0,423 m; R = 0,3 m; Cia = 1,884 m y Co = 0,2826 m ².
18) La superficie de un cuadrado inscripto mide 0,09 m ². Calcular la longitud de la Cia y el
área del Co.
Respuesta: l = 0,3 m; R = 0,21 m; Cia = 1,3188 m y Co = 0,138474 m ².
19) Calcular el lado y el perímetro de un hexágono regular inscripto en una Cia cuyo radio
mide 8 m.
Respuesta: : l = 8 m y P = 48 m.
20) Calcular el perímetro de un hexágono regular inscripto en una Cia cuya longitud es de
12 m.
Respuesta: P = 11,46 m.
21) La apotema de un hexágono regular inscripto en una Cia mide 3,46 m. Calcular: a) la
longitud del lado del hexágono inscripto y b) la superficie del hexágono.
Respuesta: l = 4 m y S = 41,52 m ².
22) Determinar cuánto mide la apotema de un hexágono regular inscripto en una Cia, la
superficie, el lado, la longitud de la Cia y el área del Co. Sabiendo que su perímetro es igual
a 48 m.
Respuesta: l = 8 m; ap = 6,92 m; S = 166,08 m ²; Cia = 50,24 m y Co = 200,96 m ².
23) El radio de una Cia mide 1,2 m. Hallar el perímetro y la superficie del hexágono
inscripto.
Respuesta: l = 1,2 m; P = 7,2 m y S = 3,7368 m ².
24) El perímetro de un hexágono inscripto mide 14,4 m. Calcular la longitud de la Cia y el
área del Co.
Respuesta: l = 2,4 m; R = 2,4 m; Cia = 15,072 m y Co = 18,0864 m ².
25) La longitud de una Cia mide 2,512 m. Calcular el perímetro, la apotema y la superficie
del hexágono inscripto.
Respuesta: R = 0,4 m; l = 0,4 m; P = 2,4 m; ap = 0,346 m y S = 0,4152 m ².
26) Calcular la superficie de un hexágono inscripto en una Cia de 1,1304 m ² de área.
Respuesta: R = 0,6 m; l = 0,6 m y S = 0,9342 m ².
27) La apotema de un hexágono inscripto mide 2,076 m. Hallar la longitud de la Cia y el área
del Co.
Respuesta: l = 2,4 m; R = 2,4 m; Cia = 15,072 m y Co = 18,0864 m ².
28) El diámetro de una Cia mide 1,8 m. Hallar el perímetro, la apotema y la superficie del
hexágono inscripto.
Respuesta: R = 0,9 m; l = 0,9 m; P = 5,4 m; ap = 0,7785 m y S = 2,10195 m ².
29) Se tiene un patio circular de 5 m de diámetro, dentro del cual se construyó una piscina
hexagonal inscripta. ¿Cuántos m ² de pasto se necesitan para empastar alrededor de la
piscina?.
Respuesta: R = 2,5 m; l = 2,5 m; Co = 19,625 m ²; S = 16,21875 m ² y se necesitan para
empastar alrededor de la piscina 3,40625 m ² de pasto.
30) La apotema de un hexágono regular inscripto en una Cia mide 3,46 m. Calcular la
longitud del lado del cuadrado inscripto. Respuesta: l hexágono = 4 m; R = 4 m y l cuadrado =
5,64 m.
31) Datos
l=5m
32) Datos
P = 15,57 m
33) Datos
P = 72,66 m
34) Datos
P = 20,4 m
35) Datos
S = 32,3607 m ²
36) Datos
S = 2,422 m ²
Incógnitas
R=?
ap = ?
h=?
P=?
S=?
Cia = ?
Co = ?
Incógnitas
ap = ?
h=?
S=?
Cia = ?
Co = ?
Fórmulas
Triángulo equilátero inscripto
Incógnitas
l=?
R=?
ap = ?
h=?
S=?
Cia = ?
Co = ?
Incógnitas
l=?
R=?
ap = ?
h=?
S=?
Cia = ?
Co = ?
Incógnitas
l=?
ap = ?
h=?
P=?
Cia = ?
Co = ?
Fórmulas
Triángulo equilátero inscripto
l = R.√3
Incógnitas
D=?
ap = ?
h=?
P=?
Cia = ?
Co = ?
Fórmulas
Triángulo equilátero inscripto
l = R.√3
l = R.√3
Fórmulas
Triángulo equilátero inscripto
l = R.√3
Fórmulas
Triángulo equilátero inscripto
l = R.√3
Fórmulas
Triángulo equilátero inscripto
l = R.√3
Solución
R = 2,89 m.
ap = 1,441 m.
h = 4,325 m.
P = 15 m.
S = 97,3125 m ².
Cia = 18,1492 m.
Co = 26,225 m ².
Solución
l = 5,19 m.
R = 3 m.
ap = 1,496 m.
h = 4,489 m.
S = 11,649863 m ².
Cia = 18,84 m.
Co = 28,26 m ².
Solución
l = 24,22 m.
R = 14 m.
ap = 6,983 m.
h = 20,95 m.
S = 253,70813 m ².
Cia = 87,92 m.
Co = 615,44 m ².
Solución
l = 6,8 m.
R = 3,93 m.
ap = 1,96 m.
h = 5,882 m.
S = 19,9988 m ².
Cia = 24,6804 m.
Co = 48,49698 m ².
Solución
l = 8,65 m.
R = 5 m.
ap = 2,494 m.
h = 7,482 m.
P = 25,95 m.
Cia = 31,4 m.
Co = 78,5 m ².
Solución
l = 2,37 m.
R = 1,37 m.
D = 2,74 m.
ap = 0,68 m.
h = 2,05 m.
P = 7,11 m.
Cia = 8,60 m.
Co = 5,89 m ².
37) Datos
S = 0,6228 m ²
Incógnitas
l=?
ap = ?
h=?
P=?
Cia = ?
Co = ?
Fórmulas
Triángulo equilátero inscripto
l = R.√3
38) Datos
Cia = 50,24 m
Incógnitas
l=?
R=?
ap = ?
h=?
P=?
S=?
Co = ?
Incógnitas
ap = ?
h=?
P=?
S=?
Co = ?
Fórmulas
Triángulo equilátero inscripto
l = R.√3
Incógnitas
l=?
R=?
ap = ?
h=?
P=?
S=?
Co = ?
Incógnitas
l=?
R=?
ap = ?
h=?
P=?
S=?
Co = ?
Incógnitas
R=?
P=?
S=?
Cia = ?
Co = ?
Incógnitas
S=?
Cia = ?
Co = ?
Fórmulas
Triángulo equilátero inscripto
l = R.√3
Incógnitas
S=?
Cia = ?
Co = ?
Fórmulas
Cuadrado inscripto
l = R.√2
39) Datos
Cia = 25,12 m
40) Datos
Cia = 8,792 m
41) Datos
Cia = 56,62 m
42) Datos
l = 2,82 m
43) Datos
P = 33,84 m
44) Datos
P = 21,432 m
Fórmulas
Triángulo equilátero inscripto
l = R.√3
Fórmulas
Triángulo equilátero inscripto
l = R.√3
Fórmulas
Cuadrado inscripto
l = R.√2
Fórmulas
Cuadrado inscripto
l = R.√2
Solución
l = 1,2 m.
R = 0,69 m.
ap = 0,346 m.
h = 1,038 m.
P = 3,6 m.
Cia = 4,3332 m.
Co = 1,4949 m ².
Solución
l = 13,84 m.
R = 8 m.
ap = 3,99 m.
h = 11,971 m.
P = 41,52 m.
S = 82,843472 m ².
Co = 601,4531 m ².
Solución
l = 6,92 m.
R = 4 m.
ap = 1,995 m.
h = 5,985 m.
P = 20,76 m.
S = 20,710868 m ².
Co = 50,24 m ².
Solución
l = 2,422 m.
R = 1,4 m.
ap = 0,698 m.
h = 2,095 m.
P = 7,266 m.
S = 2,53708 m ².
Co = 6,1544 m ².
Solución
l = 15,59 m.
R = 9,016 m.
ap = 4,495 m.
h = 13,485 m.
P = 46,77 m.
S = 105,12 m ².
Co = 255,25 m ².
Solución
R = 2 m.
P = 11,28 m.
S = 7,9524 m ².
Cia = 12,56 m.
Co = 12,56 m ².
Solución
l = 8,46 m.
R = 6 m.
S = 71,5716 m ².
Cia = 37,68 m.
Co = 113,04 m ².
Solución
l = 5,358 m.
R = 3,8 m.
S = 28,708164 m ².
Cia = 23,864 m.
Co = 45,3416 m ².
45) Datos
P = 20 m
Incógnitas
l=?
R=?
S=?
Cia = ?
Co = ?
Incógnitas
l=?
R=?
ap = ?
D=?
S=?
Cia = ?
Co = ?
Incógnitas
P=?
Cia = ?
Co = ?
Fórmulas
Cuadrado inscripto
l = R.√2
48) Datos
S = 20,358144 m ²
Incógnitas
P=?
Cia = ?
Co = ?
Fórmulas
Cuadrado inscripto
l = R.√2
49) Datos
S = 50,24 m ²
Incógnitas
l=?
R=?
ap = ?
D=?
P=?
Cia = ?
Co = ?
Incógnitas
l=?
R=?
ap = ?
P=?
Cia = ?
Co = ?
Incógnitas
P=?
S=?
Co = ?
Fórmulas
Cuadrado inscripto
l = R.√2
52) Datos
Cia = 94,2 m
Incógnitas
P=?
S=?
Co = ?
Fórmulas
Cuadrado inscripto
l = R.√2
53) Datos
Co = 153,86 m ²
Incógnitas
l=?
R=?
ap = ?
P=?
Fórmulas
Cuadrado inscripto
l = R.√2
46) Datos
P = 60 m
47) Datos
S = 161,0361 m ²
50) Datos
S = 10,24 m ²
51) Datos
Cia = 23,236 m
Fórmulas
Cuadrado inscripto
l = R.√2
Fórmulas
Cuadrado inscripto
l = R.√2
Fórmulas
Cuadrado inscripto
l = R.√2
Fórmulas
Cuadrado inscripto
l = R.√2
Solución
l = 5 m.
R = 3,546 m.
S = 25 m ².
Cia = 22,26888 m.
Co = 39,48272 m ².
Solución
l = 15 m.
R = 10,638 m.
ap = 7,5 m.
D = 21,15 m.
S = 225 m ².
Cia = 66,80664 m.
Co = 355,34451 m ².
Solución
l = 12,69 m.
R = 9 m.
P = 50,76 m.
Cia = 56,52 m.
Co = 254,34 m ².
Solución
l = 4,512 m.
R = 3,2 m.
P = 18,048 m.
Cia = 20,096 m.
Co = 32,1536 m ².
Solución
l = 7,09 m.
R = 5,028 m.
ap = 3,545 m.
D = 9,997 m.
P = 28,36 m.
Cia = 31,57584 m.
Co = 79,38166 m ².
Solución
l = 3,2 m.
R = 2,269 m.
ap = 1,6 m.
P = 12,8 m.
Cia = 14,249 m.
Co = 16,166 m ².
Solución
l = 5,217 m.
R = 3,7 m.
P = 20,868 m.
S = 27,217089 m ².
Co = 42,9866 m ².
Solución
l = 21,15 m.
R = 15 m.
P = 84,6 m.
S = 447,3225 m ².
Co = 706,5 m ².
Solución
l = 9,87 m.
R = 7 m.
ap = 4,935 m.
P = 39,48 m.
54) Datos
R = 1,2 m
S=?
Incógnitas
ap = ?
P=?
S=?
Cia = ?
Co = ?
Fórmulas
Hexágono inscripto
l=R
55) Datos
ap = 8,65 m
Incógnitas
P=?
S=?
Cia = ?
Co = ?
Fórmulas
Hexágono inscripto
l=R
56) Datos
ap = 6,92 m
Incógnitas
S=?
Cia = ?
Co = ?
Fórmulas
Hexágono inscripto
l=R
57) Datos
ap = 5,19 m
Incógnitas
P=?
S=?
Cia = ?
Co = ?
Fórmulas
Hexágono inscripto
l=R
58) Datos
P = 31,4 m
Incógnitas
S=?
Cia = ?
Co = ?
Fórmulas
Hexágono inscripto
l=R
59) Datos
P = 14,4 m
Incógnitas
S=?
Cia = ?
Co = ?
Fórmulas
Hexágono inscripto
l=R
60) Datos
S = 373,68 m ²
Incógnitas
P=?
Cia = ?
Co = ?
Fórmulas
Hexágono inscripto
l=R
61) Datos
S = 12,5598 m ²
Incógnitas
P=?
Cia = ?
Co = ?
Fórmulas
Hexágono inscripto
l=R
62) Datos
S = 41,52 m ²
Incógnitas
ap = ?
P=?
Cia = ?
Co = ?
Fórmulas
Hexágono inscripto
l=R
63) Datos
S = 6,6432 m ²
Incógnitas
l=?
ap = ?
P=?
Cia = ?
Co = ?
Fórmulas
Hexágono inscripto
l=R
S = 97,42 m ².
Solución
l = 1,2 m.
ap = 1,03 m.
P = 7,2 m.
S = 3,73 m ².
Cia = 7,53 m.
Co = 4,52 m ².
Solución
l = R = 10 m.
P = 60 m.
S = 259,5 m ².
Cia = 62,8 m.
Co = 314 m ².
Solución
l = R = 8 m.
S = 166,08 m ².
Cia = 50,24 m.
Co = 200,96 m ².
Solución
l = R = 6 m.
P = 36 m.
S = 93,42 m ².
Cia = 37,68 m.
Co = 113,04 m ².
Solución
l = R = 5,23 m.
S = 70,98 m ².
Cia = 32,84 m.
Co = 85,89 m ².
Solución
l = R = 2,4 m.
S = 14,9472 m ².
Cia = 15,072 m.
Co = 18,0864 m ².
Solución
l = R = 12 m.
P = 72 m.
Cia = 75,36 m.
Co = 452,16 m ².
Solución
l = R = 2,2 m.
P = 13,2 m.
Cia = 13,816 m.
Co = 15,1976 m ².
Solución
l = R = 4 m.
ap = 3,46 m.
P = 24 m.
Cia = 25,12 m.
Co = 50,24 m ².
Solución
l = R = 1,6 m.
ap = 1,384 m.
P = 9,6 m.
Cia = 10,048 m.
Co = 8,0384 m ².
64) Datos
Cia = 12 m
Incógnitas
P=?
S=?
Co = ?
Fórmulas
Hexágono inscripto
l=R
Solución
l = R = 1,91 m.
P = 11,46 m.
S = 9,4668195 m ².
Co = 11,45503 m ²
MATEMATICAS – TRIGONOMETRIA
Funciones trigonométricas
cosec x = 1/sen x
sec x = 1/cos x
tg x = senx/cos x
tg x = 1/cotg x
cotg x = cos x/sen x
Relaciones fundamentales
sen ² x + cos ² x = 1
1 + tg ² x = 1/cos ² x
tg x.cotg x = 1
1 + cotg ² x = 1/sen ² x
Funciones de suma y diferencia de ángulos
sen 2.α = 2.sen α.cos α
cos 2.α = cos² α - sen² α
cos 2.α = 2.cos² α - 1
sen (α/2) = √(1 - cos α)/2
cos (α/2) = √(1 + cos α)/2
sen (α ± β) = sen α.cos β ± cos α.sen β
cos (α ± β) = cos α.cos β + sen α.sen β
Suma y diferencia de funciones
Producto de funciones
TRIGONOMETRIA
Trigonometría, rama de las matemáticas que estudia las relaciones entre los lados y los
ángulos de triángulos, de las propiedades y aplicaciones de las funciones trigonométricas de
ángulos. Las dos ramas fundamentales de la trigonometría son la trigonometría plana, que
se ocupa de figuras contenidas en un plano, y la trigonometría esférica, que se ocupa de
triángulos que forman parte de la superficie de una esfera.
Las primeras aplicaciones de la trigonometría se hicieron en los campos de la navegación,
la geodesia y la astronomía, en las que el principal problema era determinar una distancia
inaccesible,como la distancia entre la Tierra y la Luna, o una distancia que no podía ser
medida de forma directa. Otras aplicaciones de la trigonometría se pueden encontrar en la
física, química y en casi todas las ramas de la ingeniería,sobre todo en el estudio de
fenómenos periódicos, como el sonido o el flujo de corriente alterna.
Trigonometría plana
El concepto trigonométrico de ángulo es fundamental en el estudio de la trigonometría. Un
ángulo trigonométrico se genera con un radio que gira. Los radios OA y OB (figuras 1a, 1b y
1c) se consideran inicialmente coincidentes con OA. El radio OB gira hasta su posición final.
Un ángulo y su magnitud son positivos si se generan con un radio que gira en el sentido
contrario a las agujas del reloj, y negativo si la rotación es en el sentido de las agujas del
reloj. Dos ángulos trigonométricos son iguales si sus rotaciones son de igual magnitud y en
la misma dirección.
Una unidad de medida angular se suele definir como la longitud del arco de circunferencia,
como s en la figura 2, formado cuando los lados del ángulo central (con vértice en el centro
del círculo) cortan a la circunferencia.
Si el arco s (AB) es igual a un cuarto de la circunferencia total C, es decir, s = 3C, de
manera que OA es perpendicular a OB, la unidad angular es el ángulo recto. Si s = 1C, de
manera que los tres puntos A, O y B están todos en la misma línea recta, la unidad angular
es el ángulo llano. Si s = 1/360 C, la unidad angular es un grado. Si s = YC, de manera que
la longitud del arco es igual al radio del círculo, la unidad angular es un radián. Comparando
el valor de C en las distintas unidades, se tiene que
1 ángulo llano = 2 ángulos rectos = 180 grados = p radianes
Cada grado se subdivide en 60 partes iguales llamadas minutos, y cada minuto se divide en
60 partes iguales llamadas segundos. Si se quiere mayor exactitud, se utiliza la parte
decimal de los segundos. Las medidas en radianes menores que la unidad se expresan con
decimales. El símbolo de grado es °, el de minuto es ´ y el de segundos es ". Las medidas
en radianes se expresan o con la abreviatura rad o sin ningún símbolo. Por tanto, 61° 28´
42,14" = 1,073 rad = 1,073
Se sobreentiende que el último valor es en radianes.
Un ángulo trigonométrico se designa por convenio con la letra griega theta (q). Si el ángulo q
está dado en radianes, entonces se puede usar la fórmula s = rq para calcular la longitud del
arco s; si q viene dado en grados, entonces:
s = π.r. θ /180
Funciones trigonométricas
Las funciones trigonométricas son valores sin unidades que dependen de la magnitud de un
ángulo. Se dice que un ángulo situado en un plano de coordenadas rectangulares está en
su posición normal si su vértice coincide con el origen y su lado inicial coincide con la parte
positiva del eje x.
En la figura 3, el punto P está situado en una línea recta que pasa por el origen y que forma
un ángulo q con la parte positiva del eje x. Las coordenadas x e y pueden ser positivas o
negativas según el cuadrante (I, II, III, IV) en que se encuentre el punto P; x será cero si el
punto P está en el eje y o y será cero si P está en el eje x. La distancia r entre el punto y el
origen es siempre positiva e igual a x ²+ y ², aplicando el teorema de Pitágoras.
Las seis funciones trigonométricas más utilizadas se definen de la siguiente manera:
seno (sen) del ángulo θ = sen θ = y/r
coseno (cos) del ángulo θ = cos θ = x/r
tangente (tg) del ángulo θ = tg θ = y/x
cotangente (cotg) del ángulo θ = cotg θ = x/y
secante (sec) del ángulo θ = sec θ = r/x
cosecante (cosec) del ángulo θ = cosec θ = r/y
Como la x y la y son iguales si se añaden 2p radianes al ángulo - es decir, si se añaden
360° - es evidente que sen (q + 2p) = sen q. Lo mismo ocurre con las otras cinco funciones.
Dadas sus respectivas definiciones, tres funciones son las inversas de las otras tres, es
decir,
cotg θ = 1/tg θ ; sec θ = 1/cos θ ; cosec θ = 1/sen θ
Si el punto P, de la definición de función trigonométrica, se encuentra en el eje y, la x es
cero; por tanto, puesto que la división por cero no está definida en el conjunto de los
números reales, la tangente y la secante de esos ángulos, como 90°, 270° y -270° no están
definidas. Si el punto P está en el eje x,la y es 0; en este caso, la cotangente y la cosecante
de esos ángulos, como 0°, 180° y -180° tampoco está definida. Todos los ángulos tienen
seno y coseno, pues r no puede ser igual a 0.
Como r es siempre mayor o igual que la x o la y, los valores del sen q y cos q varían entre -1
y +1. La tg q y la cotg q son ilimitadas, y pueden tener cualquier valor real. La sec q y la
cosec q pueden ser mayor o igual que +1 o menor o igual que -1.
Como se ha podido ver en los anteriores apartados, el valor de las funciones trigonométricas
no depende de la longitud de r, pues las proporciones son sólo función del ángulo.
Si q es uno de los ángulos agudos de un triángulo rectángulo (figura 4), las definiciones de
las funciones trigonométricas dadas más arriba se pueden aplicar a q como se explica a
continuación. Si el vértice A estuviera situado en la intersección de los ejes x e y de la figura
3, si AC descansara sobre la parte positiva del eje x y si B es el punto P de manera que AB
= AP = r, entonces el sen q = y/r = a/c, y así sucesivamente:
sen θ =
cos θ =
tg θ =
cotg θ =
sec θ =
cosec θ =
opuesto
hipotenusa
adyacente
hipotenusa
opuesto
adyacente
adyacente
opuesto
hipotenusa
adyacente
hipotenusa
opuesto
=
=
=
=
=
=
a
c
b
c
a
b
b
a
c
b
c
a
Los valores numéricos de las funciones trigonométricas de ciertos ángulos se pueden
obtener con facilidad. Por ejemplo, en un triángulo rectángulo isósceles, se tiene que q = 45
° y que b = a, y además se sabe,por el Teorema de Pitágoras, que c2= b2+ a2. De aquí se
deduce que c ² = 2.a ² o que c = a ². Por tanto
sen 45° = cos 45° = 1/√2
tg 45° = cotg 45° = 1
sec 45° = cosec 45° = √2
Los valores numéricos de las funciones trigonométricas de un ángulo cualquiera se pueden
hallar de forma aproximada dibujando el ángulo en su posición normal utilizando la regla, el
compás y el transportador de ángulos. Si se miden x, y y r es fácil calcular las proporciones
deseadas. En realidad, basta con calcular los valores del sen q y del cos q para unos
cuantos ángulos específicos, pues los valores de los demás ángulos y las demás funciones
se calculan utilizando las igualdades que se mencionan en el siguiente apartado.
Igualdades trigonométricas
Las siguientes fórmulas, llamadas igualdades o identidades, muestran las relaciones entre
las diversas funciones trigonométricas, que se cumplen para cualquier ángulo q, o pareja de
ángulos q y f:
Utilizando con reiteración una o más fórmulas del grupo V, conocidas como fórmulas de
reducción, es posible calcular el seno de q y el coseno de q, para cualquier valor de q, en
función del seno y del coseno de ángulos entre 0° y 90°. Utilizando las fórmulas de los
grupos I y II, se pueden calcular los valores de la tangente, cotangente, secante y cosecante
de q en función del seno y del coseno. Por tanto, es suficiente tabular los valores del seno y
el coseno de q para valores de q entre 0° y 90°. En la práctica, para evitar cálculos
tediosos,se suelen también tabular las otras cuatro funciones para los mismos valores de q.
Sin embargo, desde la popularización de las calculadoras electrónicas y los ordenadores o
computadoras, las tablas de funciones trigonométricas han caído en desuso.
La variación de los valores de las funciones trigonométricas para diversos ángulos se
pueden representar gráficamente (ver figuras adjuntas). Se puede ver con claridad en estas
curvas que todas las funciones trigonométricas son periódicas, es decir, el valor de cada
una se repite a intervalos regulares llamados periodos. El periodo de todas las funciones,
excepto la tangente y la cotangente, es 360° o 2p radianes. La tangente y la cotangente
tienen un periodo de 180 ° o p radianes.
Funciones inversas
La expresión ´y es el seno de q,´ o y = sen q, es equivalente a la expresión q es el ángulo
cuyo seno es igual a y, lo que se escribe como q = arcsen y, o también como q = sen-1y.
Las otras funciones inversas, arccos y, arctg y, arccotg y, arcsec y, y arccosec y, se definen
del mismo modo. En la expresión y = sen q o q = arcsen y, un valor dado de y genera un
número infinito de valores de q, puesto que sen 30° = sen 150 ° = sen (30° + 360°)...= 1. Por
tanto, si q = arcsen 1, entonces q = 30° + n360° y q = 150° + n360°, para cualquier entero n
positivo, negativo o nulo. El valor 30° se toma como valor principal o fundamental del arcsen
1. Para todas las funciones inversas, suele darse su valor principal. Hay distintas
costumbres, pero la más común es que el valor principal del arcsen y, arccos y, arctg y,
arccosec y, arcsec y y arccotg y, para y positiva es un ángulo entre 0° y 90°. Si y es
negativa, se utilizan los siguientes rangos:
-90° ≤ arcsen y; arctg y < 0°
90° < arccos y; arccotg y ≤ 0°
-180° ≤ arcsec y; arccosec ≤ -90°
El triángulo general
Entre las diversas aplicaciones prácticas de la trigonometría está la de determinar distancias
que no se pueden medir directamente. Estos problemas se resuelven tomando la distancia
buscada como el lado de un triángulo, y midiendo los otros dos lados y los ángulos del
triángulo. Una vez conocidos estos valores basta con utilizar las fórmulas que se muestran a
continuación.
Si A, B y C son los tres ángulos de un triángulo y a, b, c son los tres lados opuestos
respectivamente, es posible demostrar que
Las reglas del coseno y de la tangente tienen otras dos expresiones que se obtienen
rotando las letras a, b, c y A, B, C.
Estas tres relaciones son suficientes para resolver cualquier triángulo, esto es, calcular los
ángulos o lados desconocidos de un triángulo, dados: un lado y dos ángulos, dos lados y su
correspondiente ángulo, dos ángulos y un ángulo opuesto a uno de ellos (que tiene dos
posibles soluciones), o los tres lados.
Trigonometría esférica
La trigonometría esférica, que se usa sobre todo en navegación y astronomía,estudia
triángulos esféricos, es decir, figuras formadas por arcos de circunferencias máximas
contenidos en la superficie de una esfera. El triángulo esférico, al igual que el triángulo
plano, tiene seis elementos, los tres lados a, b, c, y los tres ángulos A, B y C. Sin embargo,
los lados de un triángulo esférico son magnitudes angulares en vez de lineales, y dado que
son arcos de circunferencias máximas de una esfera, su medida viene dada por el ángulo
central correspondiente. Un triángulo esférico queda definido dando tres elementos
cualesquiera de los seis, pues, al igual que en la geometría plana, hay fórmulas que
relacionan las distintas partes de un triángulo que se pueden utilizar para calcular los
elementos desconocidos.
La trigonometría esférica es de gran importancia para la teoría de la proyección
estereográfica y en la geodesia. Es también el fundamento de los cálculos astronómicos.
Por ejemplo, la solución del llamado triángulo astronómico se utiliza para encontrar la latitud
y longitud de un punto, la hora del día, la posición de una estrella y otras magnitudes.
Historia
La historia de la trigonometría se remonta a las primeras matemáticas conocidas,en Egipto y
Babilonia. Los egipcios establecieron la medida de los ángulos en grados, minutos y
segundos. Sin embargo,hasta los tiempos de la Grecia clásica no empezó a haber
trigonometría en las matemáticas. En el siglo II a.C. el astrónomo Hiparco de Nicea compiló
una tabla trigonométrica para resolver triángulos. Comenzando con un ángulo de 71° y
yendo hasta 180 °C con incrementos de 71°, la tabla daba la longitud de la cuerda
delimitada por los lados del ángulo central dado que corta a una circunferencia de radio r.
Esta tabla es similar a la moderna tabla del seno. No se sabe con certeza el valor de r
utilizado por Hiparco, pero sí se sabe que 300 años más tarde el astrónomo Tolomeo utilizó
r = 60, pues los griegos adoptaron el sistema numérico sexagesimal (base 60) de los
babilonios.
Tolomeo incorporó en su gran libro de astronomía, el Almagesto, una tabla de cuerdas con
incrementos angulares de 1°, desde 0° a 180°, con un error menor que 1/3.600 de unidad.
También explicó su método para compilar esta tabla de cuerdas, y a lo largo del libro dio
bastantes ejemplos de cómo utilizar la tabla para calcular los elementos desconocidos de un
triángulo a partir de los conocidos. Tolomeo fue el autor del que hoy se conoce como
teorema de Menelao para resolver triángulos esféricos, y durante muchos siglos su
trigonometría fue la introducción básica para los astrónomos. Quizás al mismo tiempo que
Tolomeo los astrónomos de la India habían desarrollado también un sistema trigonométrico
basado en la función seno en vez de cuerdas como los griegos. Esta función seno, al
contrario que el seno utilizado en la actualidad, no era una proporción, sino la longitud del
lado opuesto a un ángulo en un triángulo rectángulo de hipotenusa dada. Los matemáticos
indios utilizaron diversos valores para ésta en sus tablas.
A finales del siglo VIII los astrónomos árabes habían recibido la herencia de las tradiciones
de Grecia y de la India, y prefirieron trabajar con la función seno. En las últimas décadas del
siglo X ya habían completado la función seno y las otras cinco funciones y habían
descubierto y demostrado varios teoremas fundamentales de la trigonometría tanto para
triángulos planos como esféricos. Varios matemáticos sugirieron el uso del valor r = 1 en vez
de r = 60, lo que produjo los valores modernos de las funciones trigonométricas. Los árabes
también incorporaron el triángulo polar en los triángulos esféricos. Todos estos
descubrimientos se aplicaron a la astronomía y también se utilizaron para medir el tiempo
astronómico y para encontrar la dirección de la Meca, lo que era necesario para las cinco
oraciones diarias requeridas por la ley islámica. Los científicos árabes también compilaron
tablas de gran exactitud. Por ejemplo, las tablas del seno y de la tangente, construidas con
intervalos de 1/60 de grado (1 minuto) tenían un error menor que 1 dividido por 700
millones. Además, el gran astrónomo Nasir al-Dín al-Tusí escribió el Libro de la figura
transversal, el primer estudio de las trigonometrías plana y esférica como ciencias
matemáticas independientes.
El occidente latino se familiarizó con la trigonometría árabe a través de traducciones de
libros de astronomía arábigos, que comenzaron a aparecer en el siglo XII. El primer trabajo
importante en esta materia en Europa fue escrito por el matemático y astrónomo alemán
Johann Müller, llamado Regiomontano. Durante el siguiente siglo, el también astrónomo
alemán Georges Joachim, conocido como Rético, introdujo el concepto moderno de
funciones trigonométricas como proporciones en vez de longitudes de ciertas líneas. El
matemático francés Fran|ois Viète incorporó el triángulo polar en la trigonometría esférica y
encontró fórmulas para expresar las funciones de ángulos múltiples, sen n. θ y cos n. θ, en
función de potencias de sen θ y cos θ.
Los cálculos trigonométricos recibieron un gran empuje gracias al matemático escocés John
Napier, quien inventó los logaritmos a principios del siglo XVII. También encontró reglas
mnemotécnicas para resolver triángulos esféricos, y algunas proporciones (llamadas
analogías de Napier) para resolver triángulos esféricos oblicuos.
Casi exactamente medio siglo después de la publicación de los logaritmos de Napier, Isaac
Newton inventó el cálculo diferencial e integral. Uno de los fundamentos del trabajo de
Newton fue la representación de muchas funciones matemáticas utilizando series infinitas
de potencias de la variable x. Newton encontró la serie para el sen x y series similares para
el cos x y la tg x. Con la invención del cálculo las funciones trigonométricas fueron
incorporadas al análisis, donde todavía hoy desempeñan un importante papel tanto en las
matemáticas puras como en las aplicadas.
Por último, en el siglo XVIII, el matemático suizo Leonhard Euler definió las funciones
trigonométricas utilizando expresiones con exponenciales de números complejos. Esto
convirtió a la trigonometría en sólo una de las muchas aplicaciones de los números
complejos; además, Euler demostró que las propiedades básicas de la trigonometría eran
simplemente producto de la aritmética de los números complejos.
MAS INFORMACION
Grado, en trigonometría, arco igual a 1/360 de la circunferencia de un círculo, o ángulo
central que corresponde a dicho arco. El grado es la unidad corriente de medida de ángulos
y arcos de un círculo. Se divide en 60 minutos, cada uno de los cuales equivale a 1/21.600
de la circunferencia de un círculo; cada minuto se divide en 60 segundos, cada uno de los
cuales equivale a 1/1.296.000. Los grados se indican normalmente con el símbolo °, los
minutos con ´ y los segundos con ", como en 41°18´09", que se lee "41 grados 18 minutos y
9 segundos".
La medida de ángulos en grados es ampliamente usada en ingeniería y en las ciencias
físicas, principalmente en astronomía, navegación y topografía. El método más corriente de
localizar una estrella, o un punto en la superficie de la Tierra, es utilizar su distancia angular
en grados, minutos y segundos a ciertos puntos o líneas de referencia fijadas. Los
posiciones en la superficie de la Tierra se miden en grados de latitud norte o sur del ecuador
y grados de longitud este u oeste del meridiano principal, que normalmente es el meridiano
que pasa por Greenwich en Inglaterra.
Grados de latitud
Si la Tierra fuera una esfera exacta, un grado de latitud sería igual a 1/360 de la
circunferencia de un círculo dibujado sobre la superficie de la Tierra y que pasa por los polos
Norte y Sur. La Tierra, sin embargo, está achatada por los polos, por lo que la longitud de un
grado, determinado astronómicamente, varía del ecuador a los polos. En el ecuador un
grado de latitud son 110.568,18 m, o unos 110,57 km. La longitud de un grado a 45° N o S,
llamado ángulo medio, es 111.131,9 m o alrededor de 111,13 km.
Grados de longitud
El tamaño de un grado de longitud varía desde un valor máximo en el ecuador hasta cero en
los polos Norte y Sur. Esto es debido a que la longitud se mide como el arco de un paralelo
de latitud dada, y los círculos que forman los paralelos disminuyen en radio al incrementar
su distancia al ecuador. En el ecuador, un grado de longitud equivale a 112,09 km, pero a
40° N o S, un grado son 85,99 km. La longitud se puede medir también utilizando horas
hacia el este u oeste del meridiano principal, pues una hora equivale a 15 grados y un
minuto horario a 15 minutos angulares. Así, la longitud de la ciudad de México puede
escribirse como 99° o como 6 horas 36 minutos al oeste de Greenwich.
Otras medidas angulares
En ciertas ramas de las matemáticas avanzadas, en particular aquéllas que incluyen
cálculos, los ángulos se miden habitualmente en radianes (rad). En 360° hay 2p rad, o unos
6,28 rad.
En el ejército, los ángulos se miden generalmente en milésimas, especialmente para la
localización de objetivos de artillería. Una milésima es la medida del ángulo central formado
por un arco que es 1/6.400 del círculo. Una milésima equivale a 0,05625° y,
aproximadamente, 0,001 radianes.
Radián, en matemáticas, la unidad de ángulo plano igual al ángulo central formado por un
arco de longitud igual al radio del círculo. La medida en radianes de un ángulo se expresa
como la razón del arco formado por el ángulo, con su vértice en el centro de un círculo, y el
radio de dicho círculo. Esta razón es constante para un ángulo fijo para cualquier círculo. La
medida en radianes de un ángulo no es la razón de la longitud de la cuerda y el radio, sino
la razón de la longitud del arco y el radio.
La medida en radianes de un ángulo y su medida en grados están relacionadas. La
circunferencia de un círculo está dada por
C = 2pr
donde r es el radio del círculo y π es el número 3,14159. Dado que la circunferencia de un
círculo es exactamente 2 π radios, y que un arco de longitud r tiene un ángulo central de un
radián, se deduce que
2 π radianes = 360 grados
Al dividir 360° por 2 π se puede ver que un radián es aproximadamente 57°17´44,8". En
aplicaciones prácticas, las siguientes aproximaciones son lo suficientemente exactas:
un radián = 57,3 grados
un grado = 0,01745 radianes
El grado y el radián son unidades angulares de distinto tamaño y son intercambiables. Los
ingenieros y técnicos utilizan más los grados, mientras que la medida en radianes se usa
casi exclusivamente en estudios teóricos, como en el cálculo, debido a la mayor simplicidad
de ciertos resultados, en especial para las derivadas y la expansión en series infinitas de las
funciones trigonométricas. Como se puede ver, mientras que el símbolo ° se utiliza para
indicar grados, no se utiliza ningún símbolo para indicar la medida en radianes.
Trigonometría
Grados y radianes
Las unidades de medida de ángulos mas conocidas son los grados, minutos y segundos.
Este tipo de medidas está basada en la división en partes iguales de una circunferencia.
Las equivalencias son las siguientes:
360° = un giro completo alrededor de una circunferencia
180° = 1/2 vuelta alrededor de una circunferencia
90° = 1/4 de vuelta
1° = 1/360 de vuelta, etc.
También se puede definir otra unidad angular, el radian, que en las aplicaciones físicas es
mucho mas practico y directo que trabajar con grados.
La magnitud de un ángulo medido en radianes está dada por la longitud del arco de
circunferencia que subtiende, dividido por el valor del radio. El valor de este ángulo es
independiente del valor del radio; por ejemplo, al dividir una pizza en 10 partes iguales, el
ángulo de cada pedazo permanece igual, independiente si la pizza es chica, normal o
familiar.
De esta forma, se puede calcular fácilmente la longitud de un arco de circunferencia; solo
basta multiplicar el radio por el ángulo en radianes.
Long. arco de circunferencia = [Angulo en radianes] x [Radio de la circunferencia]
Ya que conocemos el perímetro de una circunferencia de radio unitario (2π * r = 2< Imagen
>), entonces el ángulo de una circunferencia completa, medido en radianes es 2pi. Como
además sabemos que este mismo ángulo, medido en grados mide 360°, entonces podemos
definir una equivalencia:
1 radian = 57,29°
a partir de esta igualdad, determinamos que:
90° = π/2 radianes
60° = π/3 radianes
45° = π/4 radianes
30° = π/6 radianes
Geometría - Definiciones
# Recta: es una sucesión de infinitos puntos que se extiende en una misma dirección y en
ambos sentidos.
# Semirrecta - Rayo: es un subconjunto de puntos de una recta. Es una recta o un segmento
de recta que tiene un origen, una dirección y un sentido.
# Segmento: es una porción de una recta.
# Angulo: es la abertura formada por la unión de 2 semirrectas en un mismo punto llamado
vértice; las semirrectas reciben el nombre de lados del ángulo.
Es la figura geométrica formado por 2 rayos que tiene un punto común llamado vértice.
El ángulo se obtiene por la rotación de una semirrecta alrededor de su origen.
La posición original de la semirrecta se denomina lado inicial y la posición final se denomina
lado terminal.
La rotación del ángulo se puede efectuar en 2 sentidos; en el sentido contrario a las
manecillas del reloj, en éste caso el ángulo es positivo y girando en el sentido de las
manecillas del reloj el ángulo es negativo.
# Medición de ángulos
Medir un ángulo es compararlo con otro que se toma por unidad de medida. Para medir los
ángulos existen varios sistemas, siendo los más conocidos el sistema sexagesimal y el
circular.
Sistemas de medidas angulares
# Sistema Sexagesimal: en éste sistema la unidad de medida es el grado sexagesimal que
corresponde a 1/360 que se abrevia 1°; éste a su vez se divide en 60 partes iguales y 1°/60
corresponde a un minuto sexagesimal que se abrevia 1´; éste a su vez se divide en 60
partes iguales y 1´/60 corresponde a un segundo sexagesimal que se abrevia 1".
# Sistema Circular: en éste sistema la unidad de medida es el radian.
¿Qué es el radian?: El radian es un ángulo central que tiene como lados 2 radios de una
circunferencia, cuyo arco es igual al radio de la circunferencia al cual pertenece.
1 radián = 360º/2.π.R = 360º/6,283185307 = 57,29577951º = 57º 17´ 44,8"
Siendo;
π = 3,141592654
R=1
Las unidades de medida que pasaré a estudiar pertenecen al sistema sexagesimal y
circular.
Equivalencia entre los sistemas
α°/360° = αrad/2.π
Ejercicios de aplicación
1- Expresar en grados.
a)
b)
c)
d)
e)
53° 16´ 50" =
170° 36´ 50" =
28° 10´ =
45° 36" =
276° 09´ 07" =
Respuesta: 53,28055556°
Respuesta: 170,6138889°
Respuesta: 28,16666667°
Respuesta: 45,01°
Respuesta: 276,1519444°
2- Expresar en minutos.
a)
b)
c)
d)
16° 29´ 32" =
148° 19´ 37" =
45° 10´ =
82° 18" =
Respuesta: 989,5´
Respuesta: 8899,6´
Respuesta: 2710´
Respuesta: 4920,3´
3- Expresar en segundos.
a)
b)
c)
d)
35° 19´ 43" =
72° 40´ =
180° 19" =
342° 18´ 56" =
Respuesta: 127183"
Respuesta: 261600"
Respuesta: 496819"
Respuesta: 1232336"
4- Expresar en grados, minutos y segundos.
a)
b)
c)
d)
e)
f)
38,466° =
126,03334° =
136,44´ =
362,62´ =
40436" =
68367" =
Respuesta: 38° 27´ 57,6"
Respuesta: 126° 02´
Respuesta: 2° 16´ 26,4"
Respuesta: 6° 02´ 37,2"
Respuesta: 11° 13´ 56"
Respuesta: 18° 59´ 27"
5- Reducir al sistema circular. Para π = 3,14.
a)
b)
c)
d)
e)
f)
g)
42° 29´ 36" =
150° =
36° 18´ =
146° 36" =
184,68´ =
58348" =
270° =
Respuesta: 0,74 rad
Respuesta: 2,61 rad = (5/6).π rad
Respuesta: 0,63 rad
Respuesta: 2,54 rad
Respuesta: 0,05 rad
Respuesta: 0,28 rad
Respuesta: 4,71 rad = (3/2).π rad
6- Reducir al sistema sexagesimal.
a)
b)
c)
d)
e)
f)
g)
h)
1,36 rad =
0,28 rad =
(3/2).π rad =
(3/4).π rad =
(2/5).π rad =
(3/7).π rad =
(5/9).π rad =
(11/12).π rad =
Respuesta: 77° 57´ 42,42"
Respuesta: 16° 03´ 03,44"
Respuesta: 270°
Respuesta: 42° 59´ 37,07"
Respuesta: 72°
Respuesta: 77° 08´ 34,29"
Respuesta: 100°
Respuesta: 165°
Ejercicios de aplicación
Se considera para π = 3,14.
1- Expresar en el sistema circular un ángulo de:
a)
b)
c)
d)
e)
f)
g)
h)
i)
j)
k)
l)
ll)
m)
n)
ñ)
o)
p)
q)
18° =
30° =
36° =
43° =
45° =
60° =
72° =
75° =
80° =
120° =
161° =
540° =
35° 40´ =
42° 27´ 32" =
42° 59´ 37" =
46° 20´ 30" =
55° 84´ =
97° 25´ =
150° 03´ 24" =
Respuesta: (1/10).π rad
Respuesta: (1/6).π rad
Respuesta: (1/5).π rad
Respuesta: 0,75 rad
Respuesta: (1/4).π rad
Respuesta: (1/3).π rad
Respuesta: (2/5).π rad
Respuesta: (5/12).π rad
Respuesta: (4/9).π rad
Respuesta: (2/3).π rad
Respuesta: 2,81 rad
Respuesta: 3.π rad
Respuesta: 0,62 rad
Respuesta: 0,74 rad
Respuesta: 0,75 rad
Respuesta: 0,81 rad
Respuesta: 0,98 rad
Respuesta: 1,70 rad
Respuesta: 2,61 rad
2- Expresar en el sistema sexagesimal un ángulo de:
a)
b)
c)
d)
e)
f)
g)
h)
i)
j)
k)
l)
(1/12).π rad =
(1/8).π rad =
(1/5).π rad =
1 rad =
(3/5).π rad =
(2/3).π rad =
(3/4).π rad =
2,5 rad =
(4/5).π rad =
2,7 rad =
3,6 rad =
(4/3).π rad =
Respuesta: 15°
Respuesta: 22° 30´
Respuesta: 36°
Respuesta: 57° 19´ 29,43"
Respuesta: 108°
Respuesta: 120°
Respuesta: 135°
Respuesta: 143° 18´ 43,5"
Respuesta: 144°
Respuesta: 154° 46´ 37,4"
Respuesta: 206° 22´ 09,94"
Respuesta: 240°
ll)
m)
n)
ñ)
o)
p)
q)
r)
4,18888 rad =
(7/5).π rad =
(5/3).π rad =
(7/4).π rad =
5,55555 rad =
6 rad =
6,17222 rad =
(7/3).π rad =
Respuesta: 240° 07´ 36,76"
Respuesta: 252°
Respuesta: 300°
Respuesta: 315°
Respuesta: 318° 28´ 15,6"
Respuesta: 343° 56´ 56,5"
Respuesta: 353° 49´ 17,5"
Respuesta: 420°
1) Calcular el otro lado del triángulo ABC, empleando el Teorema del coseno y tablas de
valores naturales:
"El cuadrado de un lado de un triángulo es igual a la suma de los cuadrados de los otros dos
lados menos el doble del producto de dichos lados por el coseno del ángulo que forman".
Lado
Lado
Angulo
a - A = 11 cm B = 6 cm c =
42°
b- A= 7m
C= 8m
b = 52° 20´
c - B = 10 cm C = 15 cm a = 123° 40´
C ² = A ² + B ² - 2.A.B.cos c
A ² = B ² + C ² - 2.B.C.cos a
B ² = A ² + C ² - 2.A.C.cos b
aC ² = A ² + B ² - 2.A.B.cos c
C ² = (11 cm) ² + (6 cm) ² - 2.(11 cm).(6 cm).cos 42°
C ² = 121 cm ² + 36 cm ² - 132 cm ².0,7431
C ² = 58,9049 cm ²
C = 7,675 cm
bB ² = A ² + C ² - 2.A.C.cos b
B ² = (7 m) ² + (8 m) ² - 2.(7 m).(8 m).cos 52° 20´
B ² = 49 m ² + 64 m ² - 112 m ².0,6111
B ² = 44,5605 m ²
B = 6,675 m
cA ² = B ² + C ² - 2.B.C.cos a
A ² = (10 cm) ² + (15 cm) ² - 2.(10 cm).(15 cm).cos 123° 40´
A ² = 100 cm ² + 225 cm ² - 300 cm ².(-0,5544)
A ² = 491,3081 cm ²
A = 22,165 cm
2) Resolver las siguientes identidades:
a) tg α + cotg α = 1/(sen α .cos α)
b) (sen α + cos α) ² + (cos α - sen α) ² = 2
sen ² α + 2.sen α.cos α + cos ² α + sen ² α - 2.sen α.cos α + cos ² α = 2
sen ² α + cos ² α + sen ² α + cos ² α = 2
(sen ² α + cos ² α) + (sen ² α + cos ² α) = 2
1+1=2
c) (1 + cos α).(1 - cos α)/cos α = sec α - cos α
d) sen4 α - sen ² α = cos4 α - cos ² α
e) (cos ² α - sen ² β)/(sen ² α .sen ² β) = tg ² (π /2 - α).tg ² (π /2 - β) - 1
f) [sen (α + β) + cos (α - β)]/[sen (α - β) - cos (α + β)] = (sen α + cos α)/(sen α - cos α)
g) cos (α + β).cos (α - β) = cos ² α - sen ² β
h) [tg (α + β) + tg (α - β)]/(1 + tg ² β) = 2.tg α /(1 - tg ² α .tg ² β)
i) 1/(1 + tg ² α) = cos ² α
3) Resolver los siguientes triángulos rectángulos:
ab-
a = 27,6 m
cb = 75 cm
α = 40° 57´ 24"
α = 30° 19´ 47"
a = 33,40 m
c = 42,18 m
d-
b = 4,20 cm
c = 17,15 cm
asen α = a/c ⇒ c = a/sen α ⇒ c = 27,6 m/sen (40° 57´ 24") ⇒ c = 27,6 m/0,655 ⇒ c = 42,11
m
tg α = a/b ⇒ b = a/tg α ⇒ b = 27,6 m/tg (40° 57´ 24") ⇒ b = 27,6 m/0,868 ⇒ b = 31,80 m
α + β + 90° = 180° ⇒ β = 180° - α - 90° ⇒ β = 180° - 40° 57´ 24" - 90° ⇒ β = 49° 2´ 36"
bcos β = a/c ⇒ arccos (a/c) = β ⇒ β = arccos (33,40 m/42,18 m) ⇒ β = arccos 0,79184448 ⇒
β = 37° 38´ 30"
sen α = a/c ⇒ arcsen (a/c) = α ⇒ α = arcsen (33,40 m/42,18 m) ⇒ α = arcsen 0,79184448
⇒ α = 52° 21´ 30"
c ² = a ² + b ² ⇒ b ² = c ² - a ² ⇒ b ² = (42,18 m) ² - (33,40 m) ² ⇒ b ² = 1779,15 m ² - 1115,56
m ² ⇒ b ² = 663,59 m ²
b = 25,76 m
ccos α = b/c ⇒ c = b/cos α ⇒ c = 75 cm/cos (30° 19´ 47") ⇒ c = 75 cm/0,863 ⇒ c = 86,89 cm
tg α = a/b ⇒ a = b.tg α ⇒ a = 75 cm.tg (30° 19´ 47") ⇒ b = 75 cm.0,585 ⇒ b = 43,88 cm
α + β + 90° = 180° ⇒ β = 180° - α - 90° ⇒ β = 180° - 30° 19´ 47" - 90° ⇒ β = 59° 40´ 13"
dcos α = b/c ⇒ arccos (b/c) = α ⇒ α = arccos (4,20 cm/17,15 cm) ⇒ α = arccos 0,24489796
⇒ α = 75° 49´ 27"
sen β = b/c ⇒ arcsen (b/c) = β ⇒ β = arcsen (4,20 cm/17,15 cm) ⇒ β = arcsen 0,24489796
⇒ β = 14° 10´ 33"
c ² = a ² + b ² ⇒ a ² = c ² - b ² ⇒ a ² = (17,15 cm) ² - (4,20 cm) ² ⇒ a ² = 294,12 cm ² - 17,64
cm ² ⇒ a ² = 276,48 cm ²
a = 16,63 cm
4) Resolver los siguientes triángulos:
a-
b-
A = 325 m
a = 30° 45´ 20"
c = 87° 30´
A = 40 cm
B = 38 cm
C = 27 cm
c-
d-
B = 601 m
C = 1000 m
c = 95° 02´ 08"
A = 12,33 cm
C = 24,05 cm
b = 76° 45´ 30"
Teorema del seno: "En todo triángulo sus lados son proporcionales a los senos de los
ángulos opuestos".
A/sen a = B/sen b = C/sen c
aa + b + c = 180° ⇒ b = 180° - a - c ⇒ b = 180° - 30° 45´ 20" - 87° 30´ ⇒ b = 61° 44´ 40"
A/sen a = C/sen c ⇒ C = A.sen c/sen a ⇒ C = (325 m.sen 87° 30´)/(sen 30° 45´ 20") ⇒ C =
(325 m.0,9990)/0,5114
C = 634,935 m
A/sen a = B/sen b ⇒ B = A.sen b/sen a ⇒ B = (325 m.sen 61° 44´ 40")/(sen 30° 45´ 20") ⇒
B = (325 m.0,8808)/0,5114
B = 559,812 m
bA ² = B ² + C ² - 2.B.C.cos a
B ² + C ² - A ² = 2.B.C.cos a
cos a = (B ² + C ² - A ²)/2.B.C
cos a = [(38 cm) ² + (27 cm) ² - (40 cm) ²]/2.(38 cm).(27 cm)
cos a = (1444 cm ² + 729 cm ² - 1600 cm ²)/(2052 cm ²)
cos a = (573 cm ²)/(2052 cm ²)
cos a = 0,2792 ⇒ a = arccos 0,2792 ⇒ a = 73° 47´ 7"
B ² = A ² + C ² - 2.A.C.cos b
A ² + C ² - B ² = 2.A.C.cos b
cos b = (A ² + C ² - B ²)/2.A.C
cos b = [(40 cm) ² + (27 cm) ² - (38 cm) ²]/2.(40 cm).(27 cm)
cos b = (1600 cm ² + 729 cm ² - 1444 cm ²)/(2160 cm ²)
cos b = (885 cm ²)/(2160 cm ²)
cos b = 0,4097 ⇒ b = arccos 0,4097 ⇒ b = 65° 48´ 45"
a + b + c = 180° ⇒ c = 180° - a - b ⇒ c = 180° - 73° 47´ 7" - 65° 48´ 45" ⇒ c = 40° 24´ 8"
cC/sen c = B/sen b ⇒ sen b = (B/C).sen c ⇒ sen b = (601 m/1000 m).sen 95° 02´ 08" ⇒ sen
b = 0,601.0,9961
sen b = 0,5987 ⇒ b = arcsen 0,5987 ⇒ b = 36° 46´ 32"
a + b + c = 180° ⇒ a = 180° - b - c ⇒ a = 180° - 36° 46´ 32" - 95° 02´ 08" ⇒ a = 48° 11´ 20"
A/sen a = C/sen c ⇒ A = C.sen a/sen c ⇒ A = (1000 m.sen 48° 11´ 20")/(sen 95° 02´ 08") ⇒
A = (1000 m.0,7453)/0,9961
A = 748,23 m
dB ² = A ² + C ² - 2.A.C.cos b
B ² = (12,33 cm) ² + (24,05 cm) ² - 2.(12,33 cm).(24,05 cm).cos 76° 45´ 30"
B ² = 152,0289 cm ² + 578,4025 cm ² - 593,073 cm ².0,2291
B ² = 594,582801 cm ²
B =24,38 cm
C/sen c = B/sen b ⇒ sen c = (C/B).sen b ⇒ sen c = (24,05 cm/24,38 cm).sen 76° 45´ 30") ⇒
sen c = 0,9863.0,9734
sen c = 0,9601 ⇒ c = arctg 0,9601 ⇒ c = 0,7650 ⇒ c = 43° 49´ 59"
a + b + c = 180° ⇒ a = 180° - c - b ⇒ a = 180° - 43° 49´ 59" - 76° 45´ 30" ⇒ a = 59° 24´ 31"
MATEMATICAS – POLINOMIOS
Valor numérico de una fracción algebraica:
Valor numérico de una fracción algebraica, para determinados valores de sus
indeterminadas, es el número que resulta al sustituir estas por sus valores respectivos y
realizar las operaciones indicadas. Cuando los dos términos de una fracción son polinomios
en "X", el hecho de que se anulen para un valor determinado "A", significa que son divisibles
por (X - A) y se puede simplificar la fracción descomponiendo sus dos términos en factores.
El valor numérico de la fracción descomponiendo sus dos términos en factores. El valor
numérico de la fracción equivalente obtenida se llama verdadero valor de la fracción dada.
Reducción de fracción algebraica a mínimo común denominador:
Reducir a mínimo común denominador dos o más fracciones algebraicas, es hallar otras
fracciones equivalentes a las primeras que tengan como denominador común. (PASOS)
- Se reducen las fracciones lo más posible.
- Se halla el m.c.m de los denominadores, obteniendo así el denominador común.
- Para hallar el numerador de cada fracción, se divide el m.c.m por el denominador y se
multiplica el cociente obtenido por el numerador correspondiente.
Trinomio cuadrado perfecto:
Un trinomio es un cuadrado perfecto cuando coincide con el desarrollo del cuadrado de un
binomio, es decir:
- Dos de sus términos son cuadrados perfectos.
- El otro término, con signo más o menos, es el doble del producto de las bases de los
cuadrados anteriores.
Binomio diferencia de cuadrados:
Un binomio formado por la sustracción de dos cuadrados perfectos, se puede expresar
como una multiplicación de dos factores, uno de ellos puede expresar como una
multiplicación de dos factores; uno de ellos es la suma de las bases de los cuadrados y el
otro es su diferencia.
POLINOMIOS
Son el resultado de sumar monomios no semejantes. Cada monomio, cada sumando, es un
término del polinomio.
Grado de un polinomio:
- Es el grado del término de mayor grado.
- El término de primer grado se llama término lineal.
- El término de grado cero se denomina término independiente.
Valor numérico de un polinomio:
Para hallar el valor numérico de un polinomio se sustituyen las indeterminadas por sus
valores y se efectúan las operaciones indicadas.
Adición de polinomios:
Para sumar dos polinomios se escriben uno a continuación de otro, intercalando entre
ambos el signo de la adición, y se reducen términos semejantes.
Sustracción de polinomios:
La sustracción de dos polinomios se realiza sumando al minuendo el opuesto del
sustraendo.
Expresiones algebraicas:
Una expresión algebraica es un conjunto de números y letras unidas por los signos de las
operaciones aritméticas.
- Monomio: es cualquier expresión algebraica cuyos elementos no están separados por los
signos +, -.
- Monomios semejantes: Son expresiones monómicas que tienen las mismas letras y los
mismos exponentes.
- Monomios iguales: Son monomios semejantes con coeficientes iguales.
- Monomios opuestos: Son monomios semejantes con coeficientes opuestos.
Operaciones con fracciones algebraicas:
- Adición y sustracción:
La suma y diferencia de dos fracciones que tengan el mismo denominador es otra fracción
cuyo numerador es la suma o la diferencia de los numeradores y cuyo denominador es el
denominador común.
- Multiplicación y división:
Se llama fracción producto a la fracción que tiene como numeradores y denominadores el
producto de los denominadores de las fracciones dadas. Antes de efectuar una
multiplicación de fracciones algebraicas conviene simplificar los factores dividiendo los
numeradores y los denominadores por factores comunes.
- Potenciación y radicación:.
La potencia de una fracción algebraica es igual a la potencia del numerador partida por la
del denominador. La raíz de una fracción algebraica es igual a la raíz del numerador por la
raíz del denominador.
Resolver:
1) Clasificar las siguientes expresiones algebraicas
a) (5 - x ²)/3x
b) x³ + 2x - x1/2
c) y³/2 - 2xy/(x - 3)
d) 2.(x - 3) + 5yz ²x - x ²/4
1/2
e) [2
+ (3x)1/3 - 41/4]/(x - y)
-1
f) 4.x + 3
2) Decir si las siguientes expresiones algebraicas son polinomios o no.
a) 2x + 3x ² -1/2
b) 2x + 3x ² -1/x
c) 3x - 2(x + 4) ²
(-2/3)
d) (3x - 4).x
+4
3) Determinar grado y coeficiente principal de los siguientes polinomios, ordenarlos según
las potencias decrecientes.
a) 4x³ - 1 + 3x ²
b) x5/2 + x6
c) -2x + 3x³ - 2x ²/3
d) -(x - 4)/3 + (4 - x + x³)/2
4) Hallar C(x) y R dividiendo P(x) y Q(x).
a) P(x) = x³ - x ² + 4 y Q(x) = - x³ - x + 1
4
4
b) P(x) = x + a y Q(x) = x ² + a ²
4
c) P(x) = 2y /3 y Q(x) = y ² - y
d) P(x) = z³ - 2z ² - 1 + z y Q(x) = - z + 1
5) Hallar C(x) y R dividiendo P(x) y Q(x) por Ruffini.
a) P(x) = x4/2 + x ² - 1 y Q(x) = x - 2
b) P(x) = - x5 + x³ y Q(x) = x + 1/2
c) P(x) = - x + 3 - x³ - x5 y Q(x) = x + 2
d) P(x) = a.(x³ - a³) y Q(x) = x - a
e) P(x) = (x - 2)³ - 3(x - 2) y Q(x) = 3x - 1 + 2x)
4
f) P(x) = x - x y Q(x) = (3x - 1)/4
g) P(x) = 2x³ y Q(x) = - 3x + 2
6) Decir si P(x) es divisible por Q(x).
a) P(z) = 2z ² - z - 1 y Q(z) = z - 1
4
b) P(t) = t - a ²t ² + t + a y Q(t) = t + a
7) Simplificar
a) (4 ² - 1)/(2.x³ + x ²)
b) (4 - y ²)/(y ² - 2.y)
c) (z ² - z)/(1 - z ²)
d) (x³ - 8)/(2.x ² - 8.x + 8)
1) Dividir aplicando regla de Ruffini:
4
a) (-2.x³ + x - 1):(x + 2) =
4
5
b) (a.x - a ):(x - a) =
c) [(1 + i).x4 - i.x³ + x - 9.(3 - i)]:(x + 3 - i) =
d) (3.x³ - 6.x + 1):(3.x - 9) =
e) (4.z³ + z ²):[z + (1 + i)] =
4
f) (i.x - 2.x ² + i):(x + i) =
g) (-a.x³ + a³.x - 1):(x - a) =
h) (3.x4 + x³/2 - 29.x ²/6 + 16.x/15 - 3/15):(x + 1/3) =
5
i) (x - 2.x³ - x ² + 3):(x - 3) =
j) (3.x8/2 - 7.x6/4 + 9.x4/4 + x - 3):(x - 1) =
k) (2.a4 + 11.a/2 + 3 - a ²/2):(a + 3/2) =
l) 3.x³ - 32.x ²/15 - 24.x/5 + 10):(x - 0,6) =
4
m) (3.y + 2.y³/5 - 27.y ²/25 + 9.y/10 + 1):(y + 0,2) =
2) Hallar el polinomio P(x) tal que:
a) P(x)/(x + a) = x³ - a.x ² + a ².x - a³
b) (x5 - 32)/P(x) = x4 + 2.x³ + 4.x ² + 8.x + 16
c) P(x)/(x + 3) = x³ - 3.x ² + 9.x - 27
d) P(x)/(x - 3) = x³ + 3.x ² + 9.x + 27
3) Dada la expresión:
5
4
S(x) = (x - x - 7.x³ + x ² + k.x)/(x ² - 1)
a) Hallar aplicando sucesivamente la regla de Ruffini el valor de k para que el cociente sea
exacto.
b) Decir para que valores no esta definido S(x).
c) Factorear S(x).
4) Obtener las restantes raíces y factorear el polinomio: P(x) = x5 - 3.x4 - x³ + 11.x ² - 12.x +
4, sabiendo que 2 y -2 son raíces.
MATEMATIAS – PROGRESIONES ARITMETICAS
PRIMERA PARTE
Las progresiones constituyen el ejemplo más sencillo del concepto de sucesión. Desde los
albores de la historia de las matemáticas se han estudiado sus propiedades, y éstas han
sido aplicadas, sobre todo, a la aritmética comercial.
El estudio de las progresiones aritméticas es paralelo al de las geométricas por cuanto las
propiedades de estas últimas emanan de las primeras sin más que convertir las sumas en
productos, diferencias en cocientes, y el producto por un número natural en una potencia de
exponente natural.
El origen de las progresiones, al igual que el de tantas otras ramas de las matemáticas, es
incierto. No obstante, se conservan algunos documentos que atestiguan la presencia de
progresiones varios siglos antes de nuestra era, por lo que no se debe atribuir su paternidad
a ningún matemático concreto.
Es conocido el problema de calcular en cuánto tiempo se doblaría una cantidad de dinero a
un determinado interés compuesto, propuesto por los babilonios (2000 a.C. - 600 a.C.), lo
cual hace pensar que conocían de alguna manera la fórmula del interés compuesto y, por
tanto, las progresiones geométricas.
En el libro IX de Los Elementos de Euclides aparece escrita una fórmula, semejante a la
actual, de la suma de n términos consecutivos de una progresión geométrica. Bhaskara,
matemático hindú del siglo XII, plantea en su más conocida obra, el Lilavati , diversos
problemas sobre progresiones aritméticas y geométricas.
SUCESIONES
Se entenderá por sucesión una colección de números dispuestos uno a continuación de
otro.
Sirvan de ejemplo:
a) -3, 0, 1/5, √2, 7, π, 13...
b) -1, 3, 7, 11, 15...
c) 3, 6, 12, 24, 48...
En el primero no es posible averiguar qué número seguiría a 13 (no se encuentra una regla
que indique la relación entre los términos). En el segundo, a 15 le seguirían 19, 23, 27...
(cada término es cuatro unidades mayor que el anterior). En el tercero, al término quinto,
que es 48, le seguiría 96 (cada término es el doble del anterior).
Cuando se habla de una sucesión cualquiera, la forma más usual de referirse a ella es
escribir a1, a2, a3, a4, ..., an - 2 , an - 1 , an, ... donde los subíndices determinan el lugar que
cada término ocupa dentro de la sucesión, y los puntos suspensivos evitan la necesidad de
escribir todos los números.
Es también frecuente encontrar una sucesión simbolizada por (an)nN, o simplemente (an).
Término general de una sucesión
El término general de una sucesión es una fórmula que permite conocer el valor de un
determinado término si se conoce previamente el lugar que ocupa en la misma. Por
costumbre, al término general de una sucesión se le denota por an y se hablará de término
n-ésimo.
De entre los muchos ejemplos que se podrían citar, valgan los siguientes:
1/2, 3/2, 3/4, 4/5, ... an = n/(n + 1)
4, 4/2, 16/3, 25/4, ... bn = (n + 1) ²/n
1/2, 1, 9/8, 1, 25/32, ... cn = n ²/2n
Ejercicio: determinación de términos de una sucesión
1) ¿cuál es el término sexagésimo de la sucesión 1/2, 3/2, 3/4, 4/5, ...?
Resolución:
- Es claro que el término general es an = n/(n + 1)
- Así, el término a60 será a60 = 60/61
Escribir los seis primeros términos de la sucesión an = 3.2n - 1
Resolución:
a1 = 3.21 - 1 = 3.1 = 3 a4 = 3.23 = 24
a2 = 3.2 = 6 a5 = 3.24 = 48
a3 = 3.2 ² = 12 a6 = 3.25 = 96
La obtención del término general de una sucesión puede entrañar una notable dificultad. No
obstante, se estudiarán a continuación dos clases de sucesiones en las que el hallazgo del
término general es bastante sencillo.
PROGRESIONES ARITMETICAS
Una progresión aritmética es una sucesión en la que cada elemento se obtiene sumando al
anterior un número fijo llamado diferencia, que se representa por la letra d.
Así, si (an) es una progresión aritmética, se verifica que:
an = an - 1 + d
Ejercicio: cómo reconocer una progresión aritmética
Para asegurarse de que una sucesión es una progresión aritmética se ha de comprobar que
la diferencia entre cada término y su anterior es siempre la misma. Además, esta
comprobación elemental determina el valor de la diferencia de la progresión.
¿Es la sucesión 7, 5, 3, 1, -1, -3, -5 ... una progresión aritmética? Si lo es, ¿cuál es la
diferencia?
Resolución:
Se determina si la diferencia entre cada dos términos consecutivos es la misma:
5 - 7 = -2; 3 - 5 = -2; 1 - 3 = -2; -1 - 1 = -2; ...
Es una progresión aritmética de diferencia d = -2.
2) ¿Es 1, 3/2, 2, 5/2, 3, 9/2, ... una progresión aritmética?
Resolución:
3/2 -1 = 1/2, 3 - 5/2 = 1/2, 2 - 3/2 = 1/2, 9/2 - 3 = 3/2, 5/2 - 2 = 1/2
No es una progresión aritmética.
Término general de una progresión aritmética
La fórmula del término general de una progresión aritmética (an) se encuentra sin más que
observar que:
a2 = a1 + d
a3 = a2 + d = (a1 + d) + d = a1 + 2 d
a4 = a3 + d = (a1 + 2.d) + d = a1 + 3 d
a5 = a4 + d = (a1 + 3.d) + d = a1 + 4 d
Nótese que en todos los casos el término correspondiente es la suma de dos cantidades:
- La primera es siempre a1
- La segunda es el producto (n - 1) d.
an = a1 + (n - 1) d
Si la diferencia de una progresión aritmética es positiva, la progresión es creciente; es decir
cada término es mayor que el anterior.
Si la diferencia de una progresión aritmética es cero, la progresión es constante, es decir,
tiene todos sus términos iguales.
Si la diferencia de una progresión aritmética es negativa, la progresión es decreciente, es
decir, cada término es menor que el anterior.
Ejercicio: cálculo del término general de una progresión aritmética
Sea la sucesión 1, 3, 5, 7, 9, ... ¿Cuál es su término general?
Resolución:
Se trata de una progresión aritmética de diferencia d = 2 y primer término a1 = 1. El término
general es, por tanto:
an = 1 + (n - 1).2 = 2 n-1
Calcular a qué altura sobre el suelo se encuentra una persona que vive en un 6.° piso,
sabiendo que los bajos del edificio tienen una altura de 4 m y que entre cada dos pisos
consecutivos hay un desnivel de 2,8 m.
Resolución:
Es claro que si se considera la sucesión de las alturas de los pisos, la diferencia entre cada
vivienda y la anterior es constante e igual a 2,8 m.
Así pues, se está en el caso de una progresión aritmética en la que el primer término es 4
(altura a la que se encuentra el primer piso) y la diferencia es 2,8.
El problema se resuelve calculando el término 6.°:
an = 4 + (n - 1).2,8
a6 = 4 + (6 - 1).2,8 = 18
Términos equidistantes de una progresión aritmética
El interés de las progresiones aritméticas no acaba en el cálculo del término general.
Estudiando más detalladamente algunos modelos de progresiones aritméticas, se pueden
deducir propiedades de enorme interés:
En cada uno de estos tres modelos se han elegido al azar dos parejas distintas de términos,
de forma que la suma de los subíndices es igual en ambos casos. Sumando el valor de los
términos en cada una de las dos parejas, se observa que los resultados coinciden.
Esto conduce a la pregunta de si, elegidas cualesquiera dos parejas de términos cuyas
sumas de subíndices coincidan, también coincidirán las sumas de sus términos
correspondientes.
Dicho en lenguaje matemático, cabe preguntarse si será cierto que el hecho de
ser r + s = u + v, se desprende la igualdad ar + as = au + av .
La respuesta es afirmativa, y este resultado se conoce con el nombre de propiedad de los
términos equidistantes de una progresión aritmética.
Propiedad: Si an es una progresión aritmética de diferencia d y r + s = u + v, entonces ar + as
= au + av.
Demostración:
Estos dos resultados son iguales por ser r + s = u + v.
Ejercicio: cálculo de términos equidistantes en una progresión aritmética
En una progresión artimética se sabe que a1 = -2, a32 = 91, a16 = 43. Encontrar a17.
Resolución:
Puesto que 1 + 32 = 16 + 17 = 33, por la propiedad de los términos equidistantes,
a1 + a32 = a16 + a17
-2 + 91 = 43 + a17 ⇒ a17 = 46
Interpolación de medios aritméticos
Interpolar (de inter , entre y polos, ejes) n números entre otros dos conocidos a y b; consiste
en construir una progresión aritmética a, a1, a2, ... , an, b.
Para resolver este problema basta con conocer la diferencia que ha de tener la progresión,
la cual se deduce sin más que tener en cuenta dos cosas:
1) La sucesión tiene n + 2 términos
2) El primer término es a y el término an + 2 es b.
Aplicando la fórmula del término general de una progresión aritmética, se tiene que:
b = a + [(n + 2) - 1]. d ,
d = (b - a)/(n + 1)
Una vez conocido el valor de la diferencia, a1 se obtiene como la suma de a y d ; a2 es la
suma de a1 y d , y así sucesivamente.
Los números a1, a2, ... , an reciben el nombre de medios aritméticos.
Ejercicio: interpolación de medios aritméticos
Interpolar cinco medios aritméticos entre -18 y 25.
Resolución:
La progresión es: -18, a1, a2, a3, a4, a5, 25.
Aplicando la fórmula obtenida con a = -18 y b = 25.
d = [25 - (-18)]/(5 + 1) = 43/6
a1 = -18 + 43/6 = -65/6
a2 = -65/6 + 43/6 = -22/6 = -11/3
a3 = -11/3 + 43/6 = 21/6 = 7/2
a4 = 7/2 + 43/6 = 64/6 = 32/3
a5 = 32/3 + 43/6 = 107/6
La progresión aritmética que se buscaba es:
-18, -65/6, -11/3, 7/2, 32/3, 107/6, 25, ...
Suma de términos consecutivos de una progresión aritmética
Se denotará por Sn a la suma a1 + a2 + ... + an
Se tiene entonces:
Sn = a1 + a2 + a3 + ... + an - 2 + an - 1 + an
Invirtiendo el orden,
Sn = an + an - 1 + an - 2 + ... + a3 + a2 + a1
y sumando,
2 Sn = (a1 + a2) + (a2 + an - 1) + ... + (an - 1 + a2) + (an + a1)
Ahora bien, por la propiedad de los términos equidistantes se sabe que:
a1 + an = a2 + an - 1 = a3 + an - 2 = ... = an + a1
Por tanto, 2. Sn = n(a1 + an), y despejando:
Sn = (a1 + an).n/2
Esta fórmula no sólo sirve para sumar los primeros términos de una progresión aritmética
sino para sumar cualesquiera n términos consecutivos.
Para sumar, por ejemplo, a5 + a6 ... + a83, es necesario constatar que hay
(83 - 4 = 79) 79 términos (faltan los cuatro primeros).
La suma es:
(a5 + a63).79/2
Es muy conocida la anécdota según la cual a Carl Frederich Gauss (1777-1855), cuando
contaba con diez años de edad, le propusieron en la escuela primaria de su aldea natal que
sumara los 100 primeros números naturales. Ante el asombro del profesor, apenas éste
había acabado de dictar el problema, Gauss dio la solución: 5 050.
Lo que este insigne matemático observó fue que la suma 1 + 100 era igual a
2 + 99, igual a 3 + 98, ... etc. es decir, sólo tuvo que darse cuenta de que contaba con 50
parejas de números, cada una de las cuales sumaba 101. Así, se limitó a multiplicar: 50.101
= 5 050.
Ejercicio: suma de términos de una progresión aritmética
Sumar los veinte primeros términos de la progresión:
-5, 4, 13, 22, 31, 40
Resolución:
S20 = (a1 + a20).d/2
La diferencia es d = 9
a20 = -5 + (20 - 1).9
a20 = -5 + 19·9 = 166
S20 = (-5 + 116).20/2 = 1610
Dada la progresión aritmética 8, 3, -2, -7, -12, ..., sumar los términos comprendidos entre a24
y a36.
Resolución:
La diferencia es d = -5.
a24 = 8 + 23.(-5) = -107
a36 = 8 + 35.(-5) = -167
Entre ambos hay 36 - 23 = 13 términos. La suma pedida es S13 = [(-120) + (-116)].13/2 = 1781
¿Cuántos términos de la progresión -11, -4, 3, 10, ... hay que tomar para que su suma sea
570?
Resolución:
Se sabe que:
a1 = -11, d = 7, an = -11 + (n - 1) 7 = 7 n - 18 y Sn = 570.
Se ha de calcular n:
570 = (-11 + 7.n - 18).n/2
1140 = 7 n ² - 29 n
7 n ² - 29 n - 1140 = 0
Se resuelve la ecuación de 2.° grado:
n = (29 ± √841 + 31920)/14 = (29 ± √32761)/14 = (29 ± 181)/14 =
Como n ha de ser entero y positivo -76/7 no puede ser la solución, luego n = 15
PROGRESIONES GEOMETRICAS (I)
Una progresión geométrica es una sucesión en la que cada elemento se obtiene
multiplicando el anterior por un número fijo llamado razón, y que se representará por la letra
r.
Así, si (an) es una progresión geométrica, se verifica
an = an - 1 .r
Ejercicio: cómo reconocer una progresión geométrica
Para asegurarse de que una sucesión es una progresión geométrica se ha de comprobar
que el cociente entre cada término y su anterior es siempre el mismo. Además esta
comprobación elemental determina el valor de esta razón de la progresión.
¿Es 5, 15, 45, 135, 405 ... una progresión geométrica?
Resolución:
- 15/5 = 45/15 = 135/45 = 405/135 = 3. Es una progresión geométrica de razón 3.
2) ¿Es la sucesión 25, -5, 1, -1/5, 1/25, 1/125 una progresión geométrica?
Resolución:
No es una progresión geométrica
Término general de una progresión geométrica
La fórmula del término general de una progresión geométrica (an) se encuentra sin más que
observar que:
a2 = a1 .r
a3 = a2. r = (a1 .r). r = a1 .r ²
a4 = a3. r = (a1 .r ²). r = a1 .r³
4
a5 = a4. r = (a1 .r³). r = a1 .r
Nótese que, en todos los casos, el término correspondiente es el producto de dos
cantidades:
- La primera es siempre a1
- La segunda es una potencia de base r y exponente un cierto número, que se obtiene
restando una unidad al subíndice.
En definitiva, la expresión del término general es:
an = a1 .rn - 1
Si la razón de una progresión geométrica es mayor que uno, la progresión es creciente, es
decir, cada término es mayor que el anterior.
Si la razón de una progresión geométrica está comprendida entre cero y uno, la progresión
es decreciente, es decir, cada término es menor que el anterior.
Si la razón de una progresión geométrica es igual a uno, la progresión es constante, es
decir, tiene todos los términos iguales.
Si la razón de una progresión geométrica es menor que cero, la progresión es alterna, es
decir, sus términos son alternativamente positivos y negativos
Ejercicio: cálculo del término general de una progresión geométrica
1) Calcular el término general de la progresión 1/3, 1, 3, 9, ...
Resolución:
Se trata de una progresión geométrica de razón r = 3 y primer término
a1 = 1/3
El término general es, por tanto:
an = (1/3).3n - 1
an = 3n - 2
¿Cuál es el término general de la progresión -1, 2, -4, 8, -16, ...?
Resolución:
Es una progresión geométrica en la que el primer término a1 vale -1, y la razón es:
2/(-1) = -4/2 = 8/(-4) = -16/8 = -2
Su término general es, pues:
n-1
an = -1.(-2)
Este tipo de progresiones geométricas recibe el nombre de progresión geométrica alternada.
Nótese la similitud que hasta el momento se da entre las progresiones aritméticas y las
geométricas. Se seguirán comprobando todas las propiedades, sin más que cambiar sumas
por productos.
Términos equidistantes de una progresión geométrica
La analogía observada hasta ahora conduce a la pregunta de si, elegidas cualesquiera dos
parejas de términos cuyas sumas de subíndices coincidan, también coincidirán los
productos de sus términos correspondientes.
Dicho en lenguaje matemático, cabe preguntarse si será cierto que del hecho de ser t + s =
u + v, se desprende la igualdad at. as = au. av .
La respuesta es afirmativa, y este resultado se conoce con el nombre de propiedad de los
términos equidistantes de una progresión geométrica.
Propiedad: Si en una progresión geométrica t + s = u + v, entonces at. as = au. av
Demostración:
Al ser t + s = u + v, estas dos expresiones coinciden.
Ejercicio: cálculo de términos de una progresión geométrica
Encontrar el término a1 de una progresión geométrica de la que se sabe que:
a3 = 9; a9 = 1/81 y a11 = 1/729
Resolución:
Puesto que 3 + 9 = 1 + 11 = 12,
a3. a9 = a1 .a11
9.1/81 = a1.1/729
1/9 = a1.1/729 ⇒ a1 = 9/729
a1 = 81
Interpolación de medios geométricos
Interpolar n medios geométricos entre otros dos conocidos a y b, consiste en construir una
progresión geométrica a, a1, a2, ..., an, b.
Para resolver este problema basta con conocer la razón que ha de tener la progresión, la
cual se deduce sin más que tener en cuenta dos cosas:
1) La sucesión tiene n + 2 términos.
2) El primer término es a y el n + 2 es b.
Aplicando la fórmula del término general de una progresión geométrica se tiene que:
b = a.r
n+2-1
, de donde
Una vez conocido el valor de la razón, a1 se obtiene como el producto de r por a; a2 es el
producto de a1 por r , y así sucesivamente.
Ejercicio: interpolación de medios geométricos
Interpolar cuatro medios geométricos entre 128 y 4.
Resolución:
La progresión es 128, a1, a2, a3, a4, 4.
Aplicando la fórmula obtenida con a = 128 y b = 4:
a1 = 128.(1/2) = 64
a2 = 64.(1/2) = 32
a3 = 32.(1/2) = 16
a4 = 16.(1/2) = 8
La progresión geométrica que se buscaba es:
128, 64, 32, 16, 8, 4, ...
Interpolar tres medios geométricos entre 3 y 48.
Resolución:
Aplicando la fórmula:
Recuérdese que una raíz de índice par tiene dos soluciones, una positiva y una negativa.
Así pues, en este caso, hay dos posibilidades.
Si r = 2, la progresión es 3, 6, 12, 24, 48, ...
Si r = -2, la progresión es: 3, -6, 12, -24, 48, ...
Producto de términos consecutivos de una progresión geométrica
Continuando con la analogía observada, se encuentra la fórmula del producto de términos
de una progresión geométrica.
Se denotará por Pn al producto a1. a2 ..... an.
Se tiene entonces:
Pn = a1 · a2 · a3 ... an - 2 · an - 1 · an
Invirtiendo el orden Pn = an · an - 1 · an - 2 ... a3 · a2 · a1
______________________________
y multiplicando Pn ² = (a1 · an)(a2 · an - 1) ... (an - 1 · a2)(an · a1)
Ahora bien, por la propiedad de los términos equidistantes se sabe que:
a1 · an = a2 · an - 1 = a3 · an - 2 = ... = an · a1
Por tanto Pn ² = (a1 · an)n y despejando:
Para determinar el signo, ha de estudiarse cada caso concreto.
Esta fórmula no sólo sirve para multiplicar los primeros términos de una progresión
geométrica, sino que también es válida para multiplicar cualesquiera n términos
consecutivos, al igual que se hace en las progresiones aritméticas.
Ejercicio: cálculo del producto de términos consecutivos de una progresión
geométrica
1) Multiplicar los veinte primeros términos de la progresión 1/16, 1/8, 1/4, 1/2, ...
Resolución:
Es una progresión geométrica de razón r = 2
Para poder escribir dicho número serían necesarias 34 cifras, lo que da idea de la gran
velocidad de crecimiento que tienen las progresiones geométricas.
Calcular el producto de los siete primeros términos de la progresión
1, -2, 4, -8, ...
Resolución:
Es una progresión geométrica de razón r = -2
n-1
an = 1·(-2)
; a7 = 1·(-2)6 = 64
Para determinar el signo, obsérvese que hay tres términos negativos y al ser este número
impar, el producto de todos ellos es negativo.
21
Así pues, P7 = -2
Suma de varios términos consecutivos de una progresión geométrica
Se denotará por Sn a la suma de n términos consecutivos de una progresión geométrica:
Sn = a1 + a2 + ... + an - 1 + an
Para obtener una fórmula que permita hacer este cálculo de un modo rápido, se multiplican
ambos miembros de la igualdad por la razón:
Sn. r = (a1 + a2 + ... + an - 1 + an). r
Sn. r = a1 · r + a2 · r + ... + an - 1 · r + an · r,
y teniendo en cuenta que al multiplicar un término por la razón se obtiene el término
siguiente,
Sn. r = a2 + a3 + ... + an + an. r
Restando ahora a esta igualdad la primera:
Sn. r = a2 + a3 + ... + an + an. r
Sn = a1 + a2 + ... + an - 1 + an
Sn. r - Sn = - a1 + an. r
Sn (r - 1) = an. r - a1
Despejando Sn.
Sn = an.(r - a1)/(r - 1)
Esta fórmula que da la suma de n términos consecutivos de una progresión geométrica tiene
n-1
:
otra versión igualmente útil si se expresa el término general an como a1 .r
Ejercicio: suma de términos de una progresión geométrica
Sumar los quince primeros de la progresión geométrica 3/2, 9/2, 27/2 ...
Resolución:
- Utilizando la segunda fórmula, basta calcular la razón:
Sabiendo que 3 es el primer término de una progresión geométrica y 1 875 el quinto,
calcular la suma de esos cinco términos.
Resolución:
4
4
4
4
a5 = 1875 = 3·5 = a1· r ⇒ r = 5 ⇒ r = ± 5
Sumar los términos comprendidos entre el tercero y el vigésimo lugar de la progresión
geométrica 8, 4, 2, 1, 1/2, ...
Resolución:
Suma de todos los términos de una progresión geométrica ilimitada decreciente
Una progresión geométrica es decreciente (cada término es menor que el anterior), cuando
su razón está comprendida entre cero y uno. La progresión 8, 4, 2, 1, 1/2, ... es una
progresión decreciente de razón 1/2.
La relevancia de este apartado es que se trata de sumar todos los términos de la progresión
y no una parte de ellos. Obsérvese que en el caso de una progresión creciente (cada
término mayor que el anterior), la suma de todos los términos de la misma será infinito,
independientemente del valor de los términos. No ocurre así para el caso de progresiones
decrecientes.
Partiendo de la fórmula
n
S = a1.(r - 1)/(r - 1)
donde r es un número comprendido entre cero y uno y n el número de términos de la
progresión (infinito), la potencia rn es una cantidad tan pequeña (tiende a cero), que se
puede despreciar. Recuérdese que el resultado de una potencia cuya base está
comprendida entre cero y uno va disminuyendo a medida que aumenta el exponente.
Se tiene entonces:
S = a1.(0 - 1)/(r - 1)
S = - a1/(r - 1)
o bien
S = a1/(r - 1)
PROGRESIONES GEOMETRICAS ( II)
Cómo se suman los términos de una progresión geométrica de razón -1 < r < 1
Si r es un número mayor que -1 y menor que 1, rn se aproxima tanto más a cero cuanto más
n
grande sea n; matemáticamente esto se expresa diciendo que r tiende a cero.
Obsérvese cómo, por ejemplo, (1/2) ² = 1/4 = 0,25
(1/2)³ = 1/8 = 0,125
4
(1/2) = 1/16 = 0,0625
...............................................
(1/2)
20
= 1/1048576 = 0,0000009
Y de igual modo (-1/2) ² = 1/4 = 0,25
(-1/2)³ = 1/8 = -0,125
4
(-1/2) = 1/16 = 0,0625
................................................
(-1/2)
20
= 1/1048576 = 0,0000009
Ejercicio: suma de infinitos términos de una progresión geométrica (| r |< 1)
Calcular la suma de todos los términos de la progresión: 0,3; 0,15; 0,075;...
Resolución:
Se trata de una progresión geométrica decreciente cuyo primer término es 0,3 y razón
0,15/0,3 = 0,5
S = a1/(1 - r) = 0,3/(1- 0,5) = 0,3/0,5 = 0,6
Sumar todos los términos de la progresión geométrica -7, 7/3, -7/9, 7/27...
Resolución:
En un triángulo equilátero de 6 metros de lado, se unen los puntos medios de sus lados,
obteniéndose así otro triángulo inscrito en el primero. Este proceso se repite
indefinidamente. Calcular la suma de las áreas de todos los triángulos formados.
Resolución:
Se trata aquí de sumar todos los términos de una progresión geométrica ilimitada cuya
razón es menor que uno, puesto que las áreas de los triángulos que se van formando son
cada vez menores.
El primer término de la progresión será el área del primer triángulo:
- La razón es 1/4, puesto que el área del segundo triángulo es 1/4 del área del primero.
- Aplicando la fórmula de la suma:
Dado un círculo de radio r, se construye un segundo círculo cuyo diámetro sea el radio del
anterior, un tercero cuyo diámetro sea el radio del segundo y así sucesivamente. ¿Cuál será
la suma de las áreas de todos los círculos así formados?
Resolución:
Como en el caso anterior, se trata de sumar todos los términos de la progresión geométrica
que forman las áreas de los círculos.
Se observa que se trata de una progresión geométrica decreciente de razón 1/4, siendo, por
lo tanto, su suma:
Entre las progresiones aritméticas y las geométricas se pueden apreciar notables
diferencias. Estas últimas «crecen» mucho más deprisa (si la razón es mayor que la unidad)
que las progresiones aritméticas; o «decrecen» de manera tan vertiginosa que incluso es
posible sumar una cantidad infinita de números y obtener un resultado tan inesperado como
sorprendentemente pequeño, cuando la razón, en valor absoluto, es menor que la unidad,
como ya se ha visto.
Sirva como ilustración de cuanto se acaba de decir, la siguiente situación:
Piénsese en dos personas (de economías solventes) que acuerdan que uno dará al otro dos
millones de pesetas el primer día de mes; cuatro millones al día siguiente; seis el tercero, y
así, sumando dos millones diarios hasta completar el mes. Simultáneamente, el segundo
dará al primero una peseta el primer día; dos pesetas, el segundo; cuatro, el tercero, y así
sucesivamente, duplicando la cantidad del día anterior, hasta cumplir el plazo asignado de
treinta días. ¿Quién obtendrá mayores beneficios?
El primero, la última jornada desembolsa
a30 = 2 + (30 - 1) 2 = 60; 60 millones
En todo el mes tiene un gasto de S 30 = (2 + 60).30/2 = 930; 930 millones.
Por su parte, el otro amigo aporta (1 + 2 + 4 + ... + 229) pesetas. Sin más que hacer uso de
la fórmula de la suma de los términos de una progresión geométrica, se tiene que la
cantidad es:
30
(2
- 1)/(2 - 1) pesetas, es decir, ¡1.073.741.823 pesetas!
De otro lado, los números a que dan lugar las progresiones geométricas serían
sencillamente increíbles (de hecho, son increíbles para muchas personas) a poco que se
dudase de la exactitud de las matemáticas.
Piénsese en un folio de 1/20 mm de espesor; es decir, veinte folios bien prensados tendrían
un grosor de 1 mm. Si se dobla el papel por su mitad; se vuelve a doblar otra vez por la
mitad, y se continúa este proceso hasta repetirlo 50 veces, ¿qué grosor tendría el trozo de
papel resultante?
Es claro que en la quincuagésima operación de plegado, se tendría un grosor de
50
2
veces el espesor inicial, es decir,
250/20 mm; o también,
50
2 /200 cm; o bien,
250/20000 m; o mejor aún,
250/2000000 km.
Haciendo las oportunas operaciones; resulta que el grosor del tan citado papel es de
¡¡56 295 500 km!!
Compárese este dato con la distancia media de la Tierra a la Luna, que es de
385 000 km.
MATEMATICA – SISTEMAS DE ECUACIONES, MATRICES Y
DETERMINANTES
Resolución de sistemas de ecuaciones con dos incógnitas
Un sistema está formado por dos semiecuaciones (arriba y abajo), que siempre debemos
ordenar de forma que delante del igual siempre haya las dos letras y detrás el término
independiente. Si ello no ocurre se hace la transposición de términos. Si aparecen
fracciones se resuelven por el método del mínimo común múltiplo.
2 x + 3 y = 7[A semiecuación de arriba]
4 x - 5 y = 3[B semiecuación de abajo]
Sustitución
Pasos a seguir:
1. Se despeja la x de la semiecuación de arriba (siempre positiva)
2. El valor de la x despejada de la semiecuación de arriba se sustituye en la x de la
semiecuación de abajo.
3. Se resuelve la semiecuación de abajo como una ecuación de 1er grado cuya incógnita es
y.
4. El valor de la y obtenida se sustituye por la y de la semiecuación de arriba.
Igualación
Pasos a seguir:
1. Se despeja la x de las dos semiecuaciones (siempre positivas).
2. Como las x despejadas son las mismas se igualan los valores.
3. Se resuelve la ecuación de 1er grado cuya incógnita es y que queda multiplicando en cruz
para suprimir los denominadores..
4. El valor de la y obtenida se sustituye en las dos x despejadas al principio y que por tanto
tendrán el mismo valor.
Reducción
Pasos a seguir:
1. Se multiplica el coeficiente (número de delante) de la x de la semiecuación de abajo por
toda la semiecuación de arriba sin el signo y el coeficiente de la x de arriba por toda la
semiecuación de abajo sin el signo.
2. Quitamos paréntesis mediante la propiedad distributiva.
3. Cambiamos los signos a conveniencia para poder tachar en caso de estar cambiados los
signos pudiendo tachar se deja tal y como estaba.
4. Se tachan las x y se suman miembro a miembro las y, que se despeja y hallamos su valor
5. Para hallar el valor de la x se repiten los pasos con los coeficientes de las y.
Sistemas de ecuaciones
1. Expresiones algebraicas
Expresión algebraica es la forma de las matemáticas que escribimos con letras, números,
potencias y signos.
Al número le llamamos coeficiente, a la letra o letras les llamamos parte literal y al
exponente le llamamos grado.
Valor número de una expresión algebraica. Para hallar el valor numérico de una
expresión algebraica sustituimos las letras por el valor dado y hacemos las operaciones que
se nos indiquen.
Clases de expresiones algebraicas:
1ª- Si una expresión algebraica está formada por un solo término se llama monomio. Ej: 3x ²
2ª- Toda expresión algebraica que esté formada por dos términos se llama binomio. Ej: 2x ²
+ 3xy
3ª- Toda expresión algebraica formada por tres términos se llama trinomio.
5
Ej: 5x ² + 4y - 6x ²y
4ª- Si la expresión algebraica tiene varios términos se llama polinomio.
Polinomio es un conjunto de monomios. Tendremos en cuenta lo siguiente:
1°- Si está ordenado. Para ordenar un polinomio, colocamos los monomios de mayor a
menor, según su grado.
2°- Si está completo. Completar un polinomio es añadir los términos que falten poniendo de
coeficiente 0.
3°- Cuál es su grado. El grado de un polinomio es el mayor exponente de sus términos.
Expresiones algebraicas equivalentes: Dos o más expresiones algebraicas son
equivalentes cuando tienen el mismo valor númerico.
2. Ejercicios operatorios con los monomios y polinomios
Suma o resta de monomios: Para sumar o restar monomios es necesario que sean
semejantes. Monomios semejantes son aquellos que tienen la misma parte literal y el
mismo grado. Ej: 2x³ + 5x³ - 6x³.
Para hacer la operación sumamos los coeficientes y dejamos la misma parte literal. Ej: 2x³ +
5x³ - 6x³ = x³.
Multiplicación de monomios: Para multiplicar monomios no es necesario que sean
semejantes. Para ello se multiplican los coeficientes, se deja la misma parte literal y se
suman los grados. Ej: 3xy.4x ²y³= 12x³y4
División de monomios: Para dividir dos monomios, se dividen los coeficientes, se deja la
misma parte literal y se restan los grados. Ej: 4x5y³:2x ²y= 2x³y2
Suma de polinomios: Para sumar polinomios colocaremos cada monomio debajo de los
que son semejantes y sumaremos sus coeficientes.
Ej:
7x5+0x4+3x³+4x ²-2x
5
4
5x +0x +0x³ -x ² -x
12x5+0x4+3x³ +3x ² - 3x
Multiplicación de polinomios: Para multiplicar polinomios haremos lo mismo que para
multiplicar monomios, multiplicamos los coeficientes y sumamos los grados de las letras que
son iguales.
Si son varios los polinomios que tenemos que multiplicar haremos lo mismo pero pondremos
los que son semejantes debajo unos de otros y los sumaremos al final.
Ej:
P(x) =
2x5+3x4-2x³-x ²+2x
Q(x) =
2x³
8
7
6
5
4
P(x).Q(x) = 4x +6x -4x -2x +4x
División de polinomios: Para dividir un polinomio y un monomio, ordenamos y
completamos los polinomios, dividimos el primer monomio del dividendo por los monomios
del divisor, multiplicamos el cociente por el divisor y se lo restamos del dividendo. Así
sucesivamente.
Para dividir dos polinomios haremos lo mismo que para dividir monomios y polinomios,
teniendo en cuenta que en el divisor nos encontraremos con 2 términos.
Ej:
4x4 -2x³ +6x ² -8x -4
4
-4x
0
2x
2x³-x ²+3x-4
-2x³
+2x³
0
+6x ²
-6x ²
0
-8x
+8x
0 -4
P(x):Q(x) = 2.x³ - x ² + 3.x - 4
R=-4
3. Igualdades notables
1- Cuadrado de la suma de dos números: Es igual al cuadrado del primero más doble
producto del primero por el segundo más cuadrado del segundo.
Ej: (a+b) ²= a ²+2ab+b ²
2- Cuadrado de la diferencia de dos números: Cuadrado del primero menos doble
producto del primero por el segundo más el cuadrado del segundo.
Ej: (a-b) ²= a ²-2ab+b ²
3- Cubo de la suma de dos números: Es igual al cubo del primero más triple del cuadrado
del primero por el segundo más triple del cuadrado del segundo por el primero más cubo del
segundo.
Ej: (a+b)³= a³+3a ²b+3b ²a+b³
4- Cubo de la diferencia de dos números: Es igual al cubo del primero menos triple del
cuadrado del primero por el segundo más triple del cuadrado del segundo por el primero
menos cubo del segundo.
Ej: (a-b)³= a³-3a ²b+3b ²-b³
5- La suma por la diferencia de dos números: Es igual a la diferencia de cuadrados.
Ej: (a+b) (a-b)= a ²-b2
Las ecuaciones
1. Ecuación y función
Ecuación es toda función algebraica igualada a 0 ó a otra igualdad algebraica. A la primera
parte de la igualdad se la llama 1er término y a la segunda se la llama 2° término. Dos
ecuaciones son equivalentes cuando tienen el mismo resultado.
Hay distintos tipos de igualdades:
Una igualdad numérica: 2+5=4+3
Una igualdad algebraica: 2x+3x=6x
Una función: 3x+2=y
Una función es una expresión algebraica igualada a y.
2. Resolución de ecuaciones
Para resolver una ecuación, hallaremos el valor de la incógnita, siendo la incógnita el
número desconocido, expresado normalmente por x.
Pasos para resolver una ecuación:
1°- Se quitan los paréntesis si los hubiere.
2°- Se quitan los denominadores si los hubiere.
3°- Se pasan todas las incógnitas al 1er miembro de la igualdad.
4°- Se reducen los términos semejantes.
5°- Hallamos el valor de la incógnita.
Ej: 5x-7=28+4x ; 5x-4x=28+7 ; x = 35
Ecuaciones con denominadores:
Quitamos los denominadores por el m.c.m. para ello:
1°- Hallamos el m.c.m. de los denominadores.
2°-Ese es el denominador común y lo sustituimos por los denominadores anteriores.
3°- Se divide el m.c.m. entre el denominador antiguo y se multiplica por el denominador.
Ej: x/2 - 4 = x/3 - 3 ; m.c.m.(2 y 3)=6 ; 3x-24 = 2x-18 ; 3x-2x = -18+24 ; x = 6
3. Sistemas de ecuaciones
Si una expresión algebraica la igualamos a otra expresión algebraica y nos encontramos
con dos incógnitas necesitamos otra igualdad de expresiones algebraicas para poderla
resolver.
Una expresión algebraica con dos incógnitas es lo que llamamos sistema de ecuaciones.
Todo sistema de ecuaciones necesita tantas ecuaciones como incógnitas tenga.
Sistema de ecuaciones con dos incógnitas:
Para resolver un sistema de ecuaciones podemos utilizar cuatro métodos:
1°- Método de sustitución.
2°- Método de igualación.
3°- Método de reducción o de sumas y restas.
4°- Método gráfico.
Resolver un sistema por el método de sustitución:
1°- Quitamos los paréntesis (si los hubiere) de las dos ecuaciones.
2°- Quitamos los denominadores (si los hubiere) de las dos ecuaciones.
3°- Pasamos las incógnitas al 1er miembro de la igualdad y los números al 2° miembro.
4°- Reducimos los términos semejantes.
5°- Despejamos una incógnita y la sustituimos en la 2ª ecuación.
6°- Resolvemos la ecuación resultante.
Resolver un sistema por el método de igualación:
1°- Quitar los paréntesis (si los hubiere) de las dos ecuaciones.
2°- Quitar los denominadores (si los hubiere) de las dos ecuaciones.
er
3°- Pasamos las incógnitas al 1 miembro de la igualdad y los números al 2° miembro.
4°- Despejar la misma incógnita en las dos ecuaciones.
5°- Igualar las incógnitas despejadas y resolver la ecuación resultante.
Resolver un sistema por el método de reducción o de sumas y restas:
1°- Quitamos los paréntesis (si los hubiere) de las dos ecuaciones.
2°- Quitamos los denominadores (si los hubiere) de las dos ecuaciones.
er
3°- Pasamos las incógnitas al 1 miembro de la igualdad y los números al 2° miembro.
4°- Igualar los coeficientes de una incógnita y cambiar de signo si son iguales.
5°- Sumar o restar el sistema que ha quedado al multiplicar y resolver la ecuación
resultante.
Sistemas de Ecuaciones
# concepto y representacion
# RESOLUCION DE SISTEMAS
# TIPOS DE SISTEMAS
# TEOREMA ROUCHE-FROBENIUS
# REGLA DE CRAMER
# SISTEMAS HOMOGENEOS
# POR DESCOMPOSICION L U
concepto y representacion
Llamaremos sistema de m ecuaciones con n incognitas a toda expresión:
a11 x1 + a12 x2 +...+ a1n xn = b1
a21 x1 + a22 x2 +...+ a2n xn = b2
.......................
am1 x1 + am2 x2 +...+ am n xn = bm
Donde: aij ∈ K
son los coeficientes
bi ∈ K son los términos independientes
son las incognitas
xi
a) Se puede representar de forma MATRICIAL:
A·X=B
Donde
A = Matriz de los coeficientes
x = Vector solución
B = Vector de Términos Independientes
A* = Resulta de añadir los términos independientes a la matriz A
b) También de forma VECTORIAL :
x1 A1 + x2 A2 + ... + xn An = B (Donde Ai son las columnas de A)
c) Como una APLICACION LINEAL
Sabiendo que toda matriz de dimensión m x n define una aplicación lineal f: Kn Km respecto
n
m
de las bases canónicas de K y K .
Podemos entender un sistema de m ecuaciones y n incognitas, como una aplicación lineal
n
coeficientes de las distintas incognitas ∈ K
SIMPLIFICACION
Si a un sistema de ecuaciones se le añade un numero finito de ecuaciones lineales que son
combinaciones lineales de las dadas, el nuevo sistema es equivalente al inicial.
Del mismo modo si eliminamos una ecuacion que sea c.l. de otra se puede eliminar.
solución del sistema
Si (α 1, α 2,..., α n) satisface las m ecuaciones decimos que α es el vector solución del
sistema.
Según el numero de soluciones un sistema puede ser:
SISTEMA HOMOGENEO:
Si los términos independientes son cero
SISTEMA INCOMPATIBLE:
Si el sistema no tiene solucion
SISTEMA COMPATIBLE
DETERMINADO:
Si el sistema posee una una solucion
INDETERMINADO: Si el sistema posee infinitas soluciones
Si dos sistema tienen las mismas soluciones son EQUIVALENTES
Si Ax = b un sistema de ecuaciones podemos ver la matriz A como asociada a una
aplicación lineal f.
Resolver el sistema es hallar f -1(b) = x + Ker f donde f(x) = b.
Ej.- Obtener una base del espacio vectorial solución del sistema:
x + 0.y + 0.z + 0.t = 0
x + 0y - 1z + at = 0 ⇒ x = 0 ⇒ (x, y, z, t) = (0, y, 0, 0)
t=0
z=0
3x + 0y - 1z + at = 0
bx + 0y + 0z + 1t =
La solución es < (0, 1, 0, 0) > que es base del espacio vectorial formado por las soluciones.
TEOREMA ROUCHE-FROBENIUS
Dado Ax = b un sistema de m ecuaciones con n incognitas, tiene solución si:
rango A = rango A* = n° de
incognitas (n)
S. C.
DETERMINADO
rango A = rango A* < n° de
incognitas (n)
S. C.
INDETERMINADO
rango A < rango A*
S. INCOMPATIBLE
REGLA DE CRAMER
Dado un sistema COMPATIBLE DETERMINADO, tenemos que:
-1
Su expresion matricial es A X = B y al ser rg A = n ⇒ |A| ≠ 0 y además A tiene inversa A .
Así pues:
-1
-1
-1
-1
t
A · A · X = A · B ⇒ I · X = A · B ⇒ X = A · B ⇒ X = ( 1/|A| · A )· B ⇒
⇒ xi = 1/|A| · (A1i b1 + A2i b2 +....+ An i bn)
De donde obtenemos la Regla de Cramer:
det(C1, B, C3,..., Cn)
det(B, C2, C3,..., Cn)
x1 =
,
x2 =
det(C1, C2, C3,..., B)
,.......
xn =
det |A|
det |A|
det |A|
Si el sistema es COMPATIBLE INDETERMINADO podemos resolverlo por Cramer:
- Pasamos una de las incognitas a la matriz de los términos independientes en cada
ecuacion.
- Resolvemos el sistema por Cramer, y nos daran las soluciones en funcion de esa
incognita.
- Expresamos la solución en forma de envoltura lineal.
Ej.- Resolver el sistema
x + y + z = 1 por Cramer
x - y + 3z = 3
Cambiamos z por λ y pasamos λ a la derecha
Resolvemos el sistema por Cramer y obtenemos:
x = -2 λ +2 de modo que la solución es {(-2 λ + 2, -1 + λ, λ) ; λ ∈ R}⇒ {(2, -1, 0) + (-2 λ, λ, λ);
λ ∈ R}
y = -1 + λ
y por ultimo extrayendo λ tenemos que las infinitas soluciones del sistema son:
{ (2, -1, 0) + < (-2, 1, 1) > }
SISTEMAS HOMOGENEOS
Un sistema homogeneo siempre posee, al menos, la solución trivial (x, y, z, t ...) = (0, 0,
0...0).
Por el T.de Rouche podemos afirmar que siempre es compatible, ya que Rg A = Rg A*. Ax =
0
Si rg A = rg A* = n es S.C.Determinado con la solución trivial como única solucion.
Si rg A = rg A* < n es S.C.Indeterminado cuyas soluciones son los valores que anulan la
ecuacion.
Es decir, los valores de las incognitas para los cuales f es cero (Ker f).
Un sistema homogeneo siempre se puede expresar con n ecuaciones con n
incognitas. De modo que si faltan ecuaciones (ecuaciones < incognitas) se añaden
combinaciones lineales y si sobran (ecuaciones > incognitas) entonces se eliminan pq
alguna ecuacion será c.l.
Ej.- Resolver el siguiente sistema homogeneo:
x+y+z=0
2x + 2y +2z = 0
x+y-z=0
3x + 3y + z = 0
Primero eliminamos la segunda ecuacion pq es proporcional a la primera.
Hallamos el determinante de A para saber el rango
Como C1 = C2 el rango es dos. Y al ser homogeneo Rg A = Rg A* = 2 < n.incognitas ⇒
S.C.I
Si resolvemos el sistema por igualacion tenemos x = - y por lo que la solución es { (x, -x, 0) :
∈ R}
O lo que es lo mismo { < (1, -1, 0) > } = Ker (f) si tomamos el sistema como la ap. lineal f.
METODO DE GAUSS
Consiste en transformar un sistema Ax = B en un sistema triangular Ux = c realizando
operaciones elementales de Gauss en la matriz ampliada A *. El sistema triangular obtenido
es equivalente al inicial.
Si al reducir por Gauss llegaramos a un absurdo como 0 = 1 el Sistema inicial era
Incompatible.
Ej.- Resolvemos el sistema anterior por Gauss
x + y +z = 0
x+y-z=0
3x + 3y + z = 0
x + y+ z = 0 ⇒ z = 0 ⇒ x = -y
Solución: < (x, -x, 0) > ; x ∈ R
POR DESCOMPOSICION L U
Dado un sistema AX = B siendo A una matriz cuadrada (incognitas = ecuaciones) podemos
encontrar la descomposicion LU de la matriz A de modo que A = L · U.
A X= B ⇔ LU X= B ⇔ UX = Y
LY=B
La solución se obtiene resolviendo dos sistemas triangulares, se resuelve LY = B y una vez
tenemos el vector Y hallamos X, las componentes de X con las incognitas x, y, z, t...
Este metodo es util para la resolucion se sistemas simultáneos, es decir, que con una sola
descomposicion LU podemos hallar las soluciones de un mismo sistema para cualquier
valor que tomen sus términos independientes (cambiando B).
MATEMATICAS – VECTORES
VECTORES
Nota: En éste trabajo las letras con una raya arriba representan un vector, por ejemplo a es
el vector a.
El presente tema se dedicará al estudio de los conceptos de vectores y números complejos.
Se comenzará con un pequeño estudio de los vectores del plano y sus propiedades
fundamentales, así como de las bases y coordenadas.
Después se hará un somero estudio de los números complejos, enlazándolo con la primera
parte del tema y con la trigonometría vista en capítulos anteriores.
El estudio de los vectores es uno de tantos conocimientos de las matemáticas que
provienen de la física. En esta ciencia se distingue entre magnitudes escalares y
magnitudes vectoriales. Se llaman magnitudes escalares aquellas en que sólo influye su
tamaño. Por el contrario, se consideran magnitudes vectoriales aquellas en las que, de
alguna manera, influyen la dirección y el sentido en que se aplican.
Como ejemplos de magnitudes escalares se pueden citar la masa de un cuerpo, la
temperatura, el volumen, etc.
Cuando se plantea un movimiento no basta con decir cuánto se ha desplazado el móvil, sino
que es preciso decir también en qué dirección y sentido ha tenido lugar el movimiento. No
son los mismos los efectos de un movimiento de 100 km a partir de un punto si se hace
hacia el norte o si se hace en dirección suroeste, ya que se llegaría a distinto lugar.
Aunque el estudio matemático de los vectores tardó mucho en hacerse formalmente, en la
actualidad tiene un gran interés, sobre todo a partir de los estudios de David Hilbert (18621943) y Stefan Banach (1892-1945), que hicieron uso de la teoría de espacios vectoriales,
aplicándolos a las técnicas del análisis matemático.
VECTORES FIJOS
Un vector fijo del plano es un segmento cuyos extremos están dados en un cierto orden (se
suele decir que es un segmento orientado). Se representa por AB, siendo los extremos A y
B
A un segmento AB le corresponden dos vectores fijos distintos: AB y AB.
Se considera como caso singular el vector fijo definido por un segmento cuyos extremos
coinciden. En este caso el vector fijo se reduce a un solo punto.
Los puntos en los que empieza y termina un vector se llaman origen y extremo,
respectivamente.
Módulo, dirección y sentido de un vector fijo
- En un vector fijo se llama módulo del mismo a la longitud del segmento que lo define.
El módulo de un vector fijo AB se representa por |AB| y se leerá «módulo de AB ».
- Se dice que un vector fijo tiene la misma dirección que otro si los segmentos que los
definen pertenecen a rectas paralelas.
- Dados dos vectores fijos AB y CD del plano que tengan la misma dirección, se dice que
tienen el mismo sentido si los segmentos AD y BC (los segmentos que unen el origen de
cada uno con el extremo del otro) tienen un punto en común. En otro caso se dice que los
dos vectores tienen sentido contrario o sentido opuesto.
También se puede decir que dos vectores de la misma dirección tienen el mismo sentido si
la recta definida por sus orígenes deja a los extremos en el mismo semiplano.
Estas dos definiciones son válidas en el caso en que los dos vectores se encuentren en
distinta recta. Si los dos vectores se encontrasen en la misma recta, se buscaría un vector
fijo en una recta paralela que tuviese el mismo sentido que ambos. Si lo hubiese, se diría
que los dos vectores tienen el mismo sentido. En otro caso se diría que los dos vectores
tienen sentido contrario.
Vectores equipolentes
Se dice que dos vectores son equipolentes si tienen el mismo módulo, la misma dirección y
el mismo sentido.
Si AB y CD son equipolentes, el cuadrilátero ABCD es un paralelogramo.
VECTORES LIBRES DEL PLANO
Un vector libre es el conjunto de todos los vectores fijos del plano que son equipolentes a
uno dado.
Como todos los vectores fijos del plano consistentes en un solo punto son equipolentes,
definen un único vector libre, que recibirá el nombre de vector cero, r
Representantes de un vector libre
A uno cualquiera de los vectores que constituyen un vector libre se le denomina
representante del vector libre.
Para representar un vector libre se escribe uno cualquiera de sus representantes, o bien se
escribe una letra con una flecha encima.
Resultado fundamental
Dados un punto P y un vector libre del plano,a, existe un único representante de a con
origen en P. Igualmente se puede encontrar un único representante de a con extremo en el
punto P.
Demostración:
Para construir un representante de a con origen en P se traza una recta paralela al vector a
que contenga al punto P.
En ella, desde P, y con el mismo sentido que a, se mide una distancia igual al módulo de a,
|a|, obteniéndose un punto Q. El vector fijo PQ es un representante de a.
Para hallar un representante de a con extremo en P, se mide la distancia |a| en sentido
contrario, obteniendo el punto Q´. El representante de a es, en este caso, el vector fijo Q´P.
SUMA DE VECTORES
Dados dos vectores libres del plano a y b, se define su suma como el vector libre construido
así:
- Se elige un punto arbitrario del plano, O.
- Con origen en O se busca un representante del vector a. Se llamará P a su extremo.
- Con origen en P se busca el vector PQ, representante de b.
- El vector suma a + b viene representado por el vector fijo, OQ (se une el origen del
representante de a con el extremo del representante de b).
Propiedades de la suma de vectores
Conmutativa: Dados dos vectores del plano a y b, a + b = b + a.
Asociativa: Dados tres vectores a y b y c del plano, (a + b) + c = a + ( b + c).
Elemento neutro: Dado a, un vector cualquiera del plano, a + 0 = 0 + a = a.
Es decir, el vector 0 es el elemento neutro de la operación suma de vectores libres del
plano.
Demostración:
Recuérdese que 0 es el vector del plano formado por todos los vectores fijos cuyo origen
coincide con el extremo.
Se elige un punto fijo del plano, O, y con origen en O se busca el vector OP representante
de a.
Los vectores OO y PP son representantes del vector 0.
Así se tiene:
a + 0 = OP + PP = OP = a y 0 + a = a
Elemento simétrico: Dado un vector a del plano, existe otro vector - a, tal que,
a + (- a) = (- a) + a = 0. El vector - a recibe el nombre de simétrico u opuesto de a.
Demostración:
Bastará con demostrar una de las dos igualdades:
Sea PQ un representante de a. Considérese el vector - a = QP.
a + (- a) = PQ + QP = PP = 0 y (- a) + a = 0
Como consecuencia de todas las propiedades vistas se dice que el conjunto de los vectores
fijos del plano, junto con la suma de vectores, constituye un grupo conmutativo.
Observaciones:
1. Dado un vector a, su opuesto - a tiene el mismo módulo, la misma dirección y sentido
contrario al de a, Basta con ver la construcción de - a.
2. Dados dos vectores a y b, existe un único vector x que verifica a = x + b.
Si existe tal vector, sería: a = b + x ⇒ (- b) + a = (- b) + ( b + x)
Por la propiedad asociativa, (- b) + ( b + x) = [ (- b) + b] + x = 0 + x = x
Así, el único vector que puede verificar tal propiedad es el vector x = (- b) + a.
Falta ver que efectivamente la verifica:
b + x = b + [ (- b) + a] = [b + (- b)] + a = 0 + a = a, que es la igualdad buscada.
El vector (-b) + a recibe el nombre de diferencia entre los vectores a y b, y suele
representarse por a - b.
Nota: En éste trabajo las letras con una raya arriba representan un vector, por ejemplo a es
el vector a.
PRODUCTO DE VECTOR POR NUMERO REAL
Sean a un vector del plano y r un número real. Se define el producto r · a de la siguiente
forma:
a) Si r = 0 ó a = 0, el producto es r· a = 0
b) El caso contrario, es decir, si a ≠ 0 y r ≠ 0, se define:
- El módulo de r · a es | r· a| = |r|.|a|, donde | r| es el valor absoluto de r.
- La dirección de r · a es la misma que la de a.
- El sentido de r · a es el mismo que el de a si r es positivo, y contrario si r es negativo.
Obsérvese que el producto de un vector por un número sólo puede ser nulo en el caso de
serlo alguno de ellos. En dichos casos las propiedades son de comprobación inmediata, por
lo que, en lo que sigue, se supondrá que tanto el número como el vector son no nulos.
Primeras propiedades del producto de números por vectores
1 . Dado un vector a se verifica que 1· a = a.
Demostración:
En efecto, |1· a | = |1| | a| = | a|
Por definición 1· a tiene la misma direción que a.
Como 1 es positivo, el sentido de 1· a es el de a.
Por tener el mismo módulo, la misma dirección y el mismo sentido,los vectores libres a y 1·
a coinciden.
2. Para cualquier vector a, se verifica que (-1)· a = - a
Demostración:
Para verlo conviene recordar que - a tiene el mismo módulo, la misma dirección y sentido
contrario al de a. Si se concluye que (-1)· a cumple esas tres condiciones, se tendrá la
propiedad dada.
|(-1)· a| = |-1| | a| = 1| a| = | a|
La dirección de (-1)· a es la de a.
El sentido de (-1)· a es opuesto al de a, porque -1 es negativo.
Así pues (-1)· a tiene módulo, dirección y sentido iguales a los de - a. Por tanto:
(-1)· a = - a.
3. Sean a y b dos vectores no nulos. Entonces:
Si a y b tienen la misma dirección, existe un número r tal que a = r · b; y res positivo si a y b
tienen el mismo sentido, y negativo en caso contrario.
Además, de a = r.b, se deduce que |a| = |r|.|b| ⇒ |r| = |a|/|b|
A partir de ahora, para diferenciar números de vectores, a los primeros se les llamará, a
menudo, escalares.
Otras propiedades del producto de escalares por vectores
1. Dados dos números reales r y s, y un vector a se tiene:
(r.s) a = r (s. a)
(Debido al extraordinario parecido que tiene esta propiedad con la propiedad asociativa del
producto de números, a veces se la denomina propiedad asociativa.)
2. Propiedad distributiva del producto respecto de la suma de escalares
Dados dos números r y s y un vector a, se cumple la igualdad:
(r + s) a = r a + s a
Demostración:
Se hará únicamente en el caso r, s > 0. Para comprobarlo en los demás casos, bastará con
hacer pequeñas modificaciones teniendo en cuenta los sentidos de los vectores.
Los vectores r a y s a tienen la misma dirección y el mismo sentido. Al sumarlos se suman
los módulos y se mantienen la dirección y el sentido.
Así pues, | r a + s a| = | r a| + | s a| = r| a| + s| a|
Pero |(r + s) a| = (r + s)| a| = r| a| + s| a|
Luego ambos vectores tienen el mismo módulo.
La dirección y el sentido de ambos coinciden con los de a.
Por tener iguales el módulo, la dirección y el sentido ambos vectores libres son iguales.
3. Propiedad distributiva del producto respecto de la suma de vectores
Dados un número real r y dos vectores a y b, se verifica r(a + b) = r a + r b.
Demostración:
- Para demostrarlo se elige un punto P del plano y a partir de él se llevan los vectores a =
PH y r a = PH´
- Se construye el vector b con origen en H, obteniéndose el punto M.
- Prolongando la recta PM y trazando por H ´ una paralela a HM, se obtiene M ´ como punto
de intersección.
- Los dos triángulos P H M y P H´M´ son semejantes por el teorema fundamental de
semejanza de triángulos. Su razón de semejanza es:
PH´/PH = r por ser PH´ = r.a y PH = a.
Así pues, H´M´/HM = r, con lo que H´M´ = r.HM
Puesto que los vectores HM y H´M´ tienen la misma dirección y sentido, se tiene que H´M´ =
r.HM = r.b
De la misma forma PM' = r.PM, de donde se da la igualdad vectorial PM' = r.PM.
- Ya es fácil demostrar el resultado enunciado:
r.(a + b) = r.(PH + HM) = r.PM = PM´
r.a + r.b = PH´ + H´M´ = PM´.
De ahí la igualdad.
Ejercicio de aplicación
Dados un número real x y un vector a, demostrar que (-x) a = x(- a) = -(x a)
Resolución:
Se comprobará que los dos primeros vectores son iguales a -(x a) o, lo que es lo mismo,
que sumados a x a el resultado es el vector 0.
(-x).a + x.a = [(-x) + x ].a = 0.a = 0, luego (-x).a = -(x.a)
De la misma forma, x(- a) + x a = x [(- a) + a] = x· 0, luego x(- a) = -(x a)
MATEMATICAS – LIMITES
LIMITE DE UNA FUNCION
Idea intuitiva de límite de una función en un punto
El límite de una función y = f(x) en un punto x0 es el valor al que tiende la función en puntos
muy próximos a x0.
Idea intuitiva de límite
1. Considérese la función lineal y = 2 x + 1. ¿A qué valor se aproxima la función, cuando x
se aproxima al valor 3?
Resolución:
- Si se quiere estudiar el límite de esta función cuando x tiende a 3, hay que ver los valores
que toma la función en puntos muy próximos a 3.
Para ello se puede hacer la siguiente tabla de valores:
- Se observa que al tomar valores de x muy próximos a 3, ya sean mayores o menores que
él, sus imágenes se aproximan al valor 7. Cuanto mayor es la proximidad de x a 3, mayor es
la proximidad de f(x) a 7.
Esto se expresa diciendo que, cuando x tiende a 3, el límite de la función y = 2 x + 1 es 7, y
se escribe
(2.x + 1) = 7
LIMITES LATERALES
- El límite por la izquierda de una función y = f(x), cuando x → x0, es el valor al que tiende la
función para puntos muy próximos a x0 y menores que x0.
Para expresar el límite por izquierda se escribe
f(x)
- El límite por la derecha de una función y = f(x), cuando x → x0, es el valor al que tiende la
función para puntos muy próximos a x0 y mayores que x0.
Para expresar el límite por derecha se escribe
f(x)
Relación entre el límite y los límites laterales de una función
El límite de una función y = f(x) en un punto x0 existe si y solo si existen los límites laterales
y coinciden:
f(x) = l ⇔
f(x) =
f(x) = l
Si se verifica esto, y l es un número finito, se dice que la función es convergente.
En el ejemplo anterior los límites por la derecha y por la izquierda coinciden:
(2.x + 1) =
(2.x + 1) = 7
PROPIEDADES DE LOS LIMITES DE FUNCIONES
Si una función f(x) tiene límite cuando x → x0,el límite es único.
Esto se puede escribir también así:
Si
f(x) =l´ ⇒ l = l´
f(x) = l y
Ejercicio: cálculo aproximado de límites
Sea la función definida por f(x) =
x ², si x ≠ 2
7, si x = 2
¿Cuál es su límite cuando x tiende a 2?
Resolución:
Para calcular el límite de la función cuando x tiende a 2, puede hacerse una tabla de valores
para puntos de abscisa próximos a 2:
Se observa que cuando x tiende a 2,tanto por la derecha como por la izquierda, la función
tiende al valor 4. Por lo tanto,
f(x) =
f(x) = 4 ⇔
Sea la función f(x) =
f(x) = 4
1, si x < 3
definida en ℜ - {3}
x - 2, si x > 3
¿A qué valor se aproxima la función cuando x se aproxima a 3?
Resolución:
Cuando x se aproxima a 3, tanto por la izquierda como por la derecha, la función se
aproxima al valor 1. Por lo tanto,
f(x) = 1
Obsérvese cómo se pone de relieve que el valor del límite de una función en un punto es
independiente del valor que la función tome en ese punto.
En este ejemplo, el límite de la función en el punto 3 es 1 y sin embargo, la función ni
siquiera está definida en él.
LIMITE DE UNA FUNCION EN UN PUNTO
1. Se dice que una función f(x) converge, en el punto x0,hacia el valor l, o que su límite en x0
es l, y se escribe
f(x) = l, cuando a valores muy próximos a x0 corresponden valores de
la función muy próximos a I.
La definición anterior se puede concretar más:
2. Una función f(x ) converge hacia I en x0,o tiene por límite I en x0,cuando para
todo entorno de I de radio ε, E(I, ε) = (I - ε, I + ε), hay un entorno de x0de radio δ ,
E(x0, δ) = (x0 - δ , x0 + δ),tal que para cualquier x de E(x0, δ),su imagen f(x ) está
en E(I, ε).
O bien:
3. Una función f(x) converge hacia l en x0, o tiene por límite l en x0, cuando para cualquier ε
> 0, existe un δ > 0 tal que si 0 < | x - x0 | < δ ⇒ | f(x) - l | < ε
Límites infinitos
Una función es divergente cuando su límite es + ∞ó -∞.
Se estudiarán los siguientes límites:
1.
f(x) = ±∞
2.
f(x) = l
3.
f(x) = ±∞
Caso 1.
f(x) = -∞
Sea la función f(x) = 1 / x ².
Para calcular el límite de esta función en el punto x0 = 0, hay que estudiar los valores que
toman las imágenes de puntos próximos a 0. De la observación de la gráfica de la función
se deduce que:
Para valores próximos a 0 y menores que 0, la función toma valores cada vez mayores. Esto
significa que
1/x ² = +∞
Para valores próximos a 0 y mayores que 0, la función toma valores cada vez mayores. Esto
significa que
Puesto que
1/x ² = +∞
1/x ² =
1/x ² = +∞, entonces
1/x ² = +∞
En el caso de la función g(x) = -1/x ², el límite de la función cuando x → 0 es -∞.
Para valores próximos a 0 y distintos de 0, tanto por la derecha como por la izquierda, los
valores que toma la función son cada vez menores.
Caso 2.
f(x) = l
Sea la función y = x / (x - 1).
Observando la gráfica de la función, se ve como a medida que x toma valores cada vez
mayores, la función se aproxima más a 1. Por lo tanto, el límite de la función cuando x
tiende a infinito es 1.
x/(x - 1) = 1
De la observación de la gráfica se deduce que a medida que x toma valores cada vez
menores, la función se aproxima más a 1. Por lo tanto, el límite de la función cuando x
tiende a -∞ es también 1.
x/(x - 1) = 1
Caso 3.
f(x) = ±∞
Sea la función f(x) = x + 5.
Observando la gráfica se ve claramente que cuando x tiende a más infinito, la función
también tiende a más infinito. Es decir, a valores cada vez mayores de x,corresponden
valores cada vez mayores de la función. Por lo tanto,
(x + 5) = +∞
Cuando x toma valores cada vez menores, la función también toma valores cada vez
menores. Por lo tanto,
(x + 5) = - ∞
Si se estudian los límites en el infinito de g(x) = -(x + 5), se tiene:
-(x + 5) = - ∞
- (x + 5) = +∞
Es decir, cuando x toma valores cada vez mayores, x → +∞, la función toma valores cada
vez menores, g(x) → -∞.
Y cuando x toma valores cada vez menores, x → +∞, la función toma valores cada vez
mayores, g(x) → +∞.
OPERACIONES CON LIMITES DE FUNCIONES
Sean f y g dos funciones tales que:
f(x) = A y
g(x) = B
Límite de una suma de funciones
El límite de una suma de dos funciones convergentes, es igual a la suma de los límites de
cada una de ellas:
(f + g)(x) =
f(x) +
g(x) = A + B
Límite de una resta de funciones
El límite de una resta de dos funciones convergentes, es igual a la diferencia de los límites
de cada una de ellas:
(f - g)(x) =
f(x) -
g(x) = A - B
Límite de un producto de funciones
El límite de un producto de dos funciones convergentes, es igual al producto de los límites
de cada una de ellas:
(f.g)(x) =
f(x) .
g(x) = A.B
Límite de un cociente de funciones
El límite de un cociente de dos funciones convergentes es igual al cociente de los límites de
cada una de ellas, si el denominador no es nulo:
(f/g)(x) =
f(x) /
g(x) = A/B (siempre que B ≠ 0)
Ejercicio: límites de suma, resta, producto y cociente de funciones
Si f(x) = x ² + 2 y g(x) = 1/x; calcular:
(f + g)(x),
(f - g)(x),
(f.g)(x) y
(f/g)(x)
Resolución:
f(x) = 2 ² + 2 = 11 y
(f + g)(x) =
f(x) +
(f - g)(x) =
f(x) -
g(x) = 1/3
g(x) = 11 + 1/3 = 34/3
g(x) = 11 - 1/3 = 32/3
(f.g)(x) =
f(x) .
g(x) = 11.(1/3) = 11/3
(f/g)(x) =
f(x) /
g(x) = 11/(1/3) = 33
CALCULO DE LIMITES DE FUNCIONES (I)
Cálculo del límite de funciones polinómicas
Una función polinómica es una función del tipo:
f(x) = a0 + a1.x + a2.x ² + ... + an.xn
Para estudiar el cálculo de su límite, se distinguirán dos casos:
A. Límite de una función polinómica en el punto x0 finito
El límite de una función polinómica en un punto x0 es igual al valor que toma la función en
ese punto:
Límite de una función polinómica en el infinito
El límite de una función polinómica en el infinito es +∞ ó -∞,dependiendo de que el
coeficiente del término de mayor grado del polinomio sea positivo o negativo:
a0 + a1.x + a2.x ² + ... + an.xn = + ∞; si an es positivo.
a0 + a1.x + a2.x ² + ... + an.xn = -∞; si an es negativo.
Ejercicio: cálculo de límites de funciones polinómicas
1) Calcular
4.x³ - 3.x - 2
Resolución:
(4.x³ - 3.x - 2) = 4.(-1)³ - 3.(-1) - 2 = -4 + 3 - 2 = -3
2)
3 + x ² - 4.x5 y
8.x³/3 + 5.x/2 - 6
Resolución:
3 + x ² - 4.x5 = -∞
ya que el coeficiente del término de mayor grado es -4.
puesto que el coeficiente del término de mayor grado, 8/3, es
8.x³/3 + 5.x/2 - 6 = +
positivo.
∞
Cálculo de límites de funciones racionales
Una función racional es una función del tipo f(x) = P(x) / Q(x), donde P(x) y Q(x) son
polinomios.
Para estudiar el límite de una función racional, se distinguirán dos casos:
A. Límite de una función racional en el punto x0 finito
Puesto que una función racional es el cociente de dos polinomios, para calcular su límite
puede aplicarse la regla para el cálculo del límite de un cociente de dos funciones:
P(x)/Q(x) =
P(x)/
Q(x)
Tanto el límite del numerador como el del denominador son límites de funciones
polinómicas, cuyo cálculo se explicó en el apartado anterior.
Al efectuar estos límites pueden darse varias situaciones.
A.1. El límite del denominador es distinto de cero:
Q(x) ≠ 0
Se calculan en este caso los límites de P(x) y Q(x) como funciones polinómicas y se halla su
cociente.
A.2. El límite del denominador es cero:
Q(x) = 0
Si el denominador se anula en x0,puede ocurrir que el numerador también se anule en x0, o
que el numerador no se anule en x0.
A.2.1. El límite del numerador también es cero:
Q(x) = 0 y
P(x) = 0
En este caso se obtiene el resultado 0 / 0, que es una indeterminación.
Para resolver esto basta con tener en cuenta que si Q(x0) = 0 y P(x0) = 0, x0 es raíz de los
polinomios P(x) y Q(x), y por tanto el cociente P(x) / Q(x) se puede simplificar.
Una vez hecha la simplificación, bien dividiendo P(x) y Q(x) entre x - x0 ó bien aplicando la
regla de Ruffini, se vuelven a calcular los límites de los polinomios ya simplificados.
A.2.2. El límite del numerador no es cero.
El límite del cociente da como resultado la indeterminación
P(x)/0
Para resolver esta indeterminación es necesario estudiar los límites laterales de la función
f(x) = P(x) / Q(x), en el punto x0.
Si ambos límites laterales son iguales, la función tiene por límite su valor. Si no son iguales,
la función no tiene límite.
Ejercicio: cálculo de límites de funciones racionales (x → x0)
1) Calcular el límite de la función f(x) = (2.x³ - 1)/(3.x ² + 4), cuando x → 1
Resolución:
(2.x³ - 1)/(3.x ² + 4) =
(2.x³ - 1)/
(3.x ² + 4) = 1/7
2) Calcular el límite de la función g(x) = (x³ - 2.x ² - 6.x + 12)/(x ² + 3.x - 10), cuando x → 2
Resolución:
(x³ - 2.x ² - 6.x + 12)/(x ² + 3.x - 10) =
2.2 ² - 6.2 + 12)/(2 ² + 3.2 - 10) = 0/0
(x³ - 2.x ² - 6.x + 12)/
(x ² + 3.x - 10) = (2³ -
Esta indeterminación se resuelve simplificando el cociente. Aplicando la regla de Ruffini, se
obtiene la descomposición de los polinomios P(x) = x³ - 2 x ² - 6 x +12 y
Q(x) = x ² + 3 x -10.
- Descomposición factorial de P(x):
2
1 -2 -6 12
2 0 -12
1
0 -6
0
P(x) = x³ - 2.x ² - 6.x + 12 = (x - 2).(x ² - 6)
- Descomposición factorial de Q(x):
10
2 10
1
3
1
5
2
0
P(x) = x ² + 3.x - 10 = (x - 2).(x + 5)
- El límite del cociente P(x)/ Q(x) es:
(x³ - 2.x ² - 6.x + 12)/(x ² + 3.x - 10) =
+ 5) = -2/7
[(x - 2).(x ² - 6)]/[(x - 2).(x + 5)] =
(x ² - 6)/(x
3) Calcular el límite de la función f(x) = (3.x ² - 4.x)/x, cuando x → 0
Resolución:
(3.x ² - 4.x)/x =
(3.x ² - 4.x)/
x = 0/0, indeterminación.
- Se simplifican numerador y denominador:
(3.x ² - 4.x)/x =
4) Calcular
x.(3.x - 4)/x =
(3.x - 4) = -4
1/(x - 3) ²
Resolución:
1/(x - 3) ² = 1/
(x - 3) ² = 1/0, indeterminación.
- Para resolver la indeterminación se estudian los límites laterales de la función en el punto
x0 = 3.
1/(x - 3) ² =
1/
(x - 3) ² = 1/0 = + ∞
1/(x - 3) ² =
1/
(x - 3) ² = 1/0 = + ∞
Como los límites laterales coinciden,
1/(x - 3) ² = + ∞
Calcular el límite de la función f(x) = 1 / (x - 1), cuando x → 1.
Resolución:
1 / (x - 1) =
1/
(x - 1) = 1/0, indeterminación.
- Se estudian los límites laterales:
1/(x - 1) =
1/
(x - 1) = 1/0 = + ∞
1/(x - 1) =
1/
(x - 1) = 1/0 = - ∞
Como los dos límites laterales no coinciden, la función f(x) = 1/(x - 1) no tiene límite cuando
x tiende a 1.
CONTINUIDAD
Función continua
Una función f es continua en un punto x0 cuando existe el límite de la función en x0 y
coincide con el valor que toma la función en x0.
f(x) = f(x0)
f es continua en x0 ⇔
Para que una función sea continua en x0, se tienen que cumplir tres condiciones:
1. Existir el límite de la función cuando x → x0.
2. Estar definida la función en x0, es decir, existir f(x0).
3. Los dos valores anteriores han de coincidir:
f(x) = f(x0)
Si alguna de las tres condiciones no se cumple, la función es discontinua en x0.
Se dice que una función es continua en un intervalo cuando es continua en todos los puntos
del intervalo.
Ejercicio: estudio de la discontinuidad de una función
1) Probar que la función definida por f(x) =
es discontinua en el punto x0 = 3.
Resolución:
2, si x ≤ 3
-1, si x > 3
Para probar la discontinuidad de la función en x0 = 3 hay que ver cuál de la tres condiciones
de continuidad no se cumple.
En este caso es la primera, ya que no existe el límite de la función cuando x tiende a 3; los
límites laterales no coinciden:
f(x) = -1
f(x) = 2
Por lo tanto, la función es discontinua en x0 = 3.
2) Probar que la función definida por f(x) =
1, si x < 3
x - 2, si x > 3
es discontinua en el punto x0 = 3.
Resolución:
- En este caso existe el límite de la función cuando x tiende a 3, y es 1; los dos límites
laterales coinciden:
f(x) =
1=1
f(x) =
(x - 2) = 3 - 2 = 1
- Sin embargo, la función no está definida en x0 = 3; no existe f (3).
Por tanto, la función es discontinua en x0 = 3.
3) ¿Es la función definida por f(x) =
x ² - 1 , si x ≠ 2
discontinua en el punto x0 = 2?
5, si x = 2
Resolución:
- Existe el límite de la función cuando x tiende a 2, ya que los dos límites laterales coinciden:
f(x) = 2 ² - 1 = 3
f(x) = 2 ² - 1 = 3
- La función está definida para x = 2 y vale 5: f(2) =5.
- Sin embargo, el valor del límite de la función cuando x → 2 no coincide con f (2):
f(x) = 3 ≠ f(2) = 5
Por tanto, la función es discontinua en x0 = 2.
OPERACIONES CON FUNCIONES CONTINUAS
Suma
La suma de dos funciones continuas en un punto es también una función continua en ese
punto.
Demostración:
Sean f y g dos funciones continuas en un punto x0. Esto significa que:
f(x) = f(x0) y
g(x) = g(x0)
Para probar que la función suma f + g es una función continua en x0, es necesario
demostrar que
(f + g)(x) = (f + g)(x0)
Aplicando una de las propiedades de los límites de funciones,
(f + g)(x) =
f(x) +
g(x) = f(x0) + g(x0) = (f + g)(x0)
La demostración es válida para una suma de n funciones continuas en x0.
Resta
La resta de dos funciones continuas en un punto es también una función continua en ese
punto.
Esta demostración, como las que siguen, se hacen de forma similar a la anterior, basándose
en las propiedades de los límites de funciones.
Producto
El producto de dos funciones continuas en un punto es también una función continua en ese
punto.
Producto de una función por un número
El producto de una función continua en un punto, por un número real, es otra función
continua en ese punto.
Cociente
El cociente de dos funciones continuas en un punto es otra función continua en ese punto.
(Siempre que el denominador no se anule).
Composición de funciones
Si f es una función continua en x0 y g es otra función continua en f(x0), la función compuesta
gof es continua en el punto x0.
PROPIEDADES DE LAS FUNCIONES CONTINUAS
Si una función es continua en un punto x0, entonces es convergente en x0, es decir, existe el
límite de la función cuando x tiende a x0.
Si f(x) es continua en x0 ⇔
f(x) = f(x0)
LIMITES
n
m
DEFINICION: Sea f: U ⊂ R → R y aun punto de acumulación de U. Entonces se dice que:
f(X) = l ∈ ℜm
si:
∀ ε > 0, ∃ δ > 0 /x ∈ U, 0 < d(x, a) < δ → d(f(x), f) < ε
Gráficamente podemos verlo así: Siempre existe un Δtal que las imágenes de la parte de la
bola de centro ay radio Δque pertenece a U pertenecen a una bola de radio ε con centro en
f.
Ejemplo:
Demostrar que
d(f(x,y),2) < ε ⇔ d((x,y)(0,0)) < δ
d(f(x,y),2) = |f(x,y) - 2| =
como
(x ² + y ²)½ < δ ⇒ |y| ≤ δ
d(f(x,y),2) ≤ 2.|y| ≤ 2.δ
δ = ε/2
Con lo que queda comprobado.
DEFINICION: Decimos que el límite de f(x) es infinito si:
f(X) =
⇔ ∀ K > 0 ∃ δ > 0/x ∈ U, (0 < (d(x,a)) < δ) → d(f(x),0) > K
Es decir, si por mucho que nos acerquemos a a, la distancia de la función al cero es muy
grande.
n
n
DEFINICION: Si E ⊂ R es un contorno de a∈ R es, llamamos ENTORNO PERFORADO
de aa E - {a} PROPIEDADES:
1) Si f(x) tiene límite en a, este es único.
2) Si f(x),g(x): Rn → Rm tienen límites f1, f2 en a respectivamente, entonces:
[f(x) ± g(x)] = l1 ± l2
3) Si f(x),g(x): Rn → Rm tienen límites f1, f2 en a respectivamente, entonces:
[f(x).g(x)] = l1.l2
4) Si además g(x) ≠ 0 en un entorno perforado de ay l2 ≠ 0, entonces:
[f(x)/g(x)] = l1/l2
OBSERVACION: El principal problema que nos encontramos a al hora de calcular límites es
como acercarnos al punto. Hay muchas maneras(por rectas, parábolas, cúbicas, etc). Pero
como el límite ha de ser siempre el mismo, podemos asegurar que no existe si el límite nos
da diferente para varios modos de acercarse. El caso más sencillo a probar es acercarse al
origen por una recta de pendiente m.
Ejemplo:
Nos acercamos por una trayectoria recta:
y = m.x
El límite depende de la pendiente, luego el límite no existe.
Sin embargo, el hecho de que por un tipo de trayectorias el límite sea el mismo no indica
que el límite exista; solo dice que si existiera debería ser ese.
Ejemplo:
Si f(x) tuviera límite, debería ser cero. Si probamos ahora con otro tipo de trayectorias, como
por ejemplo:
y = x ² - x³
Luego el límite no existe.
n
m
PROPOSICION: Sea f(x): U ⊂ R → R , f(x) = (f1(x), f2(x), ..., fm(x)), y sea l =
f(X),
m
f = (l1, l2, ...,lm)∈ R
Entonces
f(X) = l ⇔
fi(X) = li i = 1,...,m
n
TEOREMA (Del Sandwich): Supongamos que tenemos f,g,h: U ⊂ R → R, y sea a un punto
de acumulación de U. Si existe un entorno E de a tal que g(x)≤ f(x) ≤ h(x)∀x ∈ (E - {a})∩ U y
se verifica que:
g(X) =
h(X) = l
Entonces:
f(X) = l
Ejemplo:
OBSERVACION: Otro método de acercarnos al origen consiste en usar coordenadas
polares, haciendo que r tienda a cero. Muchas veces este sistema es muy cómodo.
Ejemplo:
1)
Luego el límite dependen del ángulo. Por tanto, no existe el límite.
2)
Por el teorema del Sandwich
0 ≤ |r ².cos θ.sen³ θ| ≤ r ²
↓
↓
↓
0
0
0
CONTINUIDAD
DEFINICION: Decimos que f: U ⊂ Rn → Rm es continua en a, punto de acumulación de U, si:
1) Existe f(a)
2) Existe y es finito
3)
f(X)
f(X) = f(a)
PROPIEDADES:
1) Si f,g: Rn → Rm son continuas en a, entonces f ± g es continua en a
2) Si f, g:Rn → R son continuas en a, entonces f.g es continua en a
3) Si además g(a) ≠ 0, entonces f/g es continua en a
n
m
PROPOSICION: f = (f1,...,fm): R → R es continua en a si y solo si f1:Rn → R son continuas
en a para i = 1,...,m.
MATEMATICAS - DERIVADAS
Análisis Matemático - Derivadas
Recta tangente a una curva en un punto
m = Δy/Δx⇒m = tg α
y2´ = f´(x)
pero y2´ en a:
tg α = f´(a) ⇒m = f´(a)
por lo tanto la ecuación de la recta tangente a la curva en el punto a,es:
y1 = f´(a).x + b
Las coordenadas forman el punto de intersección entre la recta (tangente a la curva) y la
curva.
1) Dado el punto P(a; ya), hallar la ecuación de la recta tangente.
a- derivar la función de la curva.
y2´ = f´(x)
b- reemplazar en la derivada x por el valor a.
y2´ = f´(a)
c- el resultado es la pendiente m.
m = f´(a)
d- armar la ecuación de la recta con m y el punto dado.
y1 = m.(x - a) + ya
2) Dadas las ecuaciones de la recta y la curva, verificar que la recta sea tangente a la curva.
a- se debe hallar el punto de intersección entre ambas funciones, esto se logra igualando
las funciones.
y1 = y2 ⇒m.x + b = f(x)
b- despejando x se obtiene el valor de a, ya que x = a.
c- con el valor de x reemplazar en y1 ó y2 para hallar ya.
d- el punto de intersección será:
P(a; ya)
e- derivar la función de la curva.
y2´ = f´(x)
f- reemplazar en la derivada x por el valor a.
y2´ = f´(a)
g- verificar que f´(a) sea igual a m.
y2´ = m
3) Dada una recta cualquiera (y = m3.x + b3), hallar la recta tangente paralela a una curva.
a- la pendiente de esta recta (m3) debe ser igual a la pendiente de la recta tangente (m1).
m3 = m1
b- además, esta pendiente, debe ser igual al valor de la derivada en el punto de
intersección.
m3 = f´(a) ⇒m3 = f´(x)
c- despejar el x = a.
d- con el valor de x reemplazar en y2 para hallar ya.
e- el punto de intersección será:
P(a; ya)
f- armar la ecuación de la recta tangente con m3 y el punto hallado.
y1 = m3.(x - a) + ya
PROPIEDADES DE LAS FUNCIONES DERIVABLES
LEMA (de monotonía).Sea f : I-->R una función. Supongamos que f´(t0)>0 en un punto t0interior. Entonces existe
Δ>0 tal que f(s)<f(t0)<f(t) cuando s∈ (t0-Δ,t0) y t∈ (t0,t0 +Δ), es decir, es creciente en t0.
Análogamente si f´(t0)<0, es decreciente en t0.
Teorema de Rolle.Sea f:[a,b]-->R una función continua en [a,b] y derivable en (a,b). Si f(a) = f(b) entonces
existe c ε (a,b) tal que f´(c) = 0.
Teorema de Cauchy.Sean f:[a,b]-->R y g:[a,b]-->R continuas en [a,b] y derivables en (a,b). Entonces existe c ∈
(a,b) tal que
[ f(b) - f(a) ] g´(c) = [ g(b) - g(a) ] f´(c).
Teorema del valor medio (o de los incrementos finitos).Sea f:[a,b]-->R una función continua en [a,b] y derivable en (a,b). Entonces existe c ε (a,b)
tal que f(b) - f(a) = (b - a) f´(c).
Consecuencias del t.v.m.1.- T. del v.m. sobre monotonía.Sea f:[a,b]-->R una función continua en [a,b] y derivable en (a,b). Entonces
- si f´(t)≥0 para todo t ε (a,b) entonces f es monótona creciente en [a,b].
- si f´(t)≤0 para todo t ε (a,b) entonces f es monótona decreciente en [a,b].
- si f´(t)=0 para todo t ε (a,b) entonces f es constante en [a,b].
2.- Si f y g son funciones continuas en [a,b] y derivables en (a,b) tales que f´(x) = g´(x) para
todo x ∈ (a,b), entonces existe un numero real "c" tal que f(x) = g(x) + c para todo x ∈ [a,b] ;
es decir, las dos funciones f y g se diferencian en una constante.
ESTUDIO LOCAL DE UNA FUNCION
Crecimiento y decrecimiento de una función
Definición:
Sea f : [a, b] -->R, x0∈ (a, b), se dice que f es creciente en x0si existe un entorno de x0, E (x0,
h) tal que
Si x0 - h < x < x0 → f(x) < f(x0)
Si x0 < x < x0 + h → f(x0) < f(x)
Se dice que f es decreciente si (-f) es creciente.
Proposición 1 (monotonía).-
Sea f : (a, b)-->R una función derivable y x0 ∈ (a, b) . Entonces :
si f´(x0)>0, f es creciente en x0.
si f´(x0)<0, f es decreciente en x0.
Observación : La condición es suficiente pero no es necesaria. Ej : f(x) = x³
Proposición 2.Sea f : (a, b)-->R una función, x0∈ (a,b),f derivable en x0 y creciente (decreciente). Entonces
f ´(x0) ≥0 (f´(x0) ≤ 0).
Máximos y mínimos relativos. Condiciones para la determinación de extremos.Definición: Sea f : [a, b] -->R, x0∈ (a, b), se dice que f tiene un máximo / mínimo relativo en,
x0 si existe un entorno de x0, E (x0, h) tal que ∀x ∈ E (x0, h) se tiene que f(x) ≤ f(x0) / f(x) ≥
f(x0).
Condición necesaria.f derivable en x0∈ (a, b) y presenta en x0 un máximo o mínimo, entonces f´(x0)=0.
Condición suficiente.-
Proposición 1.- f : [a, b] -->R continua en I, x0∈ (a, b) y f derivable en el intervalo (x0-Δ,x0 +Δ)
contenido en I salvo quizás x0.
a) si f ´ (x)>0, x ∈ (x0-Δ,x0) (f creciente a la izquierda de x0)
f ´ (x)<0, x ∈ (x0,x0 +Δ) (f decreciente a la derecha de x0)
entonces f presente un máximo relativo en x0.
b) Análogamente para mínimo relativo.
Proposición 2.f : [a, b] -->R, x0∈ (a,b) tal que f ´ (x0)=0 y f " (x0) ≠ 0.
Entonces :
f"(x0)>0 entonces x0es mínimo relativo.
f"(x0)<0 entonces x0 es máximo relativo.
Condición necesaria y suficiente.Sea f : [a, b] -->R continua en [a, b], x0∈ (a, b) tal que f ´(x0)=0.
Supongamos que f admite derivadas sucesivas (finitas) en un intervalo centrado en x0y
n)
supongamos que la primera derivada que no se anula en x0 es f (x0), derivada n-esima de
f.
En estas condiciones :
" La condición necesaria y suficiente para que f presente en x0 un máximo o mínimo relativo
es que "n" sea par. Además si f n) (x0) < 0 ( > 0) será un máximo (mínimo) relativo."
Además si "n" es impar existe un punto de inflexión de tangente horizontal.
Concavidad y convexidad
Definición:
-· Una función f es cóncava en el punto x0cuando la tangente a la gráfica de f en el punto (x0,
f(x0)) queda por debajo de la gráfica de la función.
De otra manera : Una función se dice cóncava hacia arriba si la recta que une dos puntos de
la gráfica queda por encima de la gráfica.
-· Una función f es convexa en el punto x0 cuando la tangente a la gráfica de f en el punto
(x0, f(x0)) queda por encima de la gráfica de la función.
De otra manera : Una función se dice cóncava hacia abajo si la recta que une dos puntos de
la gráfica queda por debajo de la gráfica.
Condición suficiente de concavidad
Si una función f es tal que∀x ∈ (a,b) f"(x) >0 entonces f es cóncava hacia arriba en (a,b)
Si una función f es tal que ∀x ∈ (a,b) f"(x) <0 entonces f es cóncava hacia abajo en (a,b)
Punto de inflexión
Definición: Un punto x0 se dice de inflexión de f si la función en ese punto cambia de
concavidad,es decir, pasa de cóncava a convexa o de convexa a cóncava. Por tanto, en ese
punto (x0, f(x0)) la tangente atraviesa la gráfica.
Condición necesaria .- Si x0 es punto de inflexión entonces f"(x0)= 0
Condición suficiente .- Sea x0 / f"(x0)= 0, entonces si además f"´(x0) ≠ 0, x0 es punto de
inflexión.
Regla de L´Hopital.Sea f,g : [a,b]-->R dos funciones verificando :
i) f,g son derivables en (a,b)
ii) g´(x) ≠ 0 para todo x ∈ (a,b)
lim f´(x)
iii) Existe
= l ∈ R (real o ± ∞)
x → a g´(x)
iv)
lim
f(x)
x→a
Entonces existe lim f(x)
=
lim
g(x)
=0
x→a
y su valor es l
x → a g(x)
Con este resultado se resuelven todos los casos de indeterminación del calculo de limites :
∞
0/0, ∞/∞, ∞ - ∞, 0 * ∞, 1 , ∞° y 0°
Representación de funciones
ESQUEMA A SEGUIR EN LA REPRESENTACION DE FUNCIONES
1.
2.
3.
4.
5.
6.
7.
Propiedades de f obtenidas directamente
Caracterización
Dominio (D) de la función
Recorrido (R) de la función
x ∈ D ⇔ Existe y tal que y = f(x)
y ∈ R ⇔ Existe x tal que y= f(x)
Simetrías:
a) Función par
f(- x) = f(x) Eje de simetría OY
b) Función impar
f(- x) = - f(x) Centro de simetría el origen
Periodicidad
f(x + T) = f(x) T periodo mínimo
Puntos de corte con los ejes:
a) Corte con el eje OX
f(x) = 0 Ninguno, uno o más puntos
b) Corte con el eje OY
f(0) = y Ninguno o un punto
Regiones de existencia de la función:
a) Intervalos de positividad
f(x) > 0 Gráfica por encima del eje OX
b) Intervalos de negatividad
f(x) < 0 Gráfica por debajo del eje OX
Ramas infinitas. Puntos en el infinito:
a) Punto de partida de la gráfica
(- ∞,?) Cuadrantes II o III
b) Punto de llegada de la gráfica
(+ ∞,?) Cuadrantes I o IV
Asíntotas:
lim
f (x) = ± ∞ (a = a, a+, a-)
a) Asíntotas verticales: x = u
x→a
lim
f(x) = k
b) Asíntotas horizontales: y = k
x → ±∞
lim
f(x)/x = m
c) Asíntotas oblicuas: y = mx + n,
8.
9.
10.
Puntos de discontinuidad
x → ±∞
lim
x → ±∞
lim
myn∈ℜ
[f(x) - m.x = b]
m∈ℜ
f(x) ≠ f(a)
x→a
Propiedades de f obtenidas por las derivadas sucesivas
Monotonía:
a) Intervalos de crecimiento
f´>0
b) Intervalos de decrecimiento
f´<0
c) Puntos críticos
f ´(a)=0 y f"(a) > 0 Mínimo
f ´(a)=0 y f"(a) < 0 Máximo
Curvatura:
a) Intervalos de convexidad
f" > 0
b) Intervalos de concavidad
f" < 0
c) Puntos de inflexión
f"(a)=0 y f"´(a) > 0 Cóncavo - convexo
f"(a)=0 y f"´(a) < 0 Convexo - cóncavo
Estudio de función
Sea y = f(x)
1. Dominio :
2. Paridad :
para f(x) = f(-x) es par
para f(x) = -f(-x) es impar
3. Signo :
para f(x) > 0 es positiva → positividad = (, )
para f(x) < 0 es negativa → negatividad = (, )
4. Intersección con eje x : (raíces)
para y = 0
5. Intersección con eje y :
para x = 0
6. Continuidad :
lim f(x) = f(a) es continua → a es un punto crítico y finito
x→a
- de salto: L+ ≠ L- finitos
+
- punto de infinito: L = ∞ó L = ∞
- esencial : L+ ó L- no existe
- evitable :
L=
lim f(x) ≠ f(a) se salva escribiendo y = f(x) para x ≠ a y L para x = a
x→a
Indeterminaciones:
∞- ∞,0 x ∞,1∞, ∞°
0/0 y ∞/∞(aplicar L´hospital)
7. Asíntotas :
- vertical en x = a:
lim f(x) = ∞ → a es un valor finito y punto crítico
x→a
- oblicua en y = m.x + b:
m=
b=
lim f(x) → si m = 0 ó ∞ no tiene asíntota oblicua
x→∞
lim [f(x) - m.x]
x
x→∞
- horizontal en y = b:
AH =
lim f(x)
x→∞
si alguno de los límites no existe no existirá esa asíntota.
8. Crecimiento y decrecimiento :
y´ > 0 crece → crecimiento = (,)
y´ < 0 decrece → decrecimiento = ( ,)
9. Máximos y mínimos :
y´ = 0 dará valores en x
x1 luego hacer y1 = f(x1) mínimo si cambia de decrecimiento a crecimiento
x2 luego hacer y2 = f(x2) máximo si cambia de crecimiento a decrecimiento
m: (x1;y1)
M: (x2;y2)
Si y´ ≠ 0 ⇒no cambia el crecimiento, no tiene máx. ni mín.
10. Concavidad :
y" > 0 ⇒cóncava hacia arriba = (,)
y" < 0 ⇒cóncava hacia abajo = (,)
11. Punto de inflexión :
y" = 0 ⇒x1 = p ⇒y1 = f(p) si cambia la concavidad.
P.I.: (x1;y1)
Si y" ≠ 0 ⇒no cambia la concavidad, no tiene pto. de inflexión.
12. Gráfica :
Recta tangente a una curva
Caso 1:
Sea la curva y = f(x) ∧P (x1;y1) un punto perteneciente a la curva
La recta tangente será: yt = m.x + b
m es la pendiente
b la ordenada al origen
f´(x1) = m
Para generar la ecuación de la recta tangente se puede proceder:
yt = m.(x - x1) + y1
Caso 2:
Sea la curva y = f(x) ∧la recta tangente yt = m.x + b, hallar el punto de tangencia:
f´(x1) = m, despejar x1 y luego hacer y1 =f(x1)
luego:
punto de tangencia P (x1;y1)
MATEMATICAS – ECUACIONES DIFERENCIALES
Ecuaciones diferenciales NO homogéneas (primera parte)
Integrar las siguientes ecuaciones diferenciales. Cuando se indique, hallar la integral
particular que verifica las condiciones iniciales impuestas.
1) y" - 2.y´ - 3.y = e-x/2
Cálculo de las raíces:
La integral homogénea es:
x
-1.x
y* = c1.e³. + c2.e
Cálculo de la integral particular:
y = a.x5.e-x
como
s=1
-x
y = a.x.e
Sus derivadas son:
-x
-x
y´ = a.e - a.x.e
y" = -a.e-x - (a.e-x - a.x.e-x)
-x
-x
-x
y" = -a.e - a.e + a.x.e
-x
-x
y" = -2.a.e + a.x.e
debe verificar:
(-2.a.e-x + a.x.e-x) - 2.(a.e-x - a.x.e-x) - 3.(a.x.e-x) = e-x/2
-x
-x
-x
-x
-x
-x
-2.a.e + a.x.e - 2.a.e + 2.a.x.e - 3.a.x.e = e /2
-2.a.e-x - 2.a.e-x + a.x.e-x + 2.a.x.e-x - 3.a.x.e-x = e-x/2
-x
-x
-4.a.e = e /2
-4.a = 1/2 ⇒ a = -1/8
La integral particular es:
-x
y = -x.e /8
Luego la integral general es:
y = y* + y ⇒ y* = C1.e³.x + C2.e-1.x - x.e-x/8
2) y" - y = x
Cálculo de las raíces:
λ ² - 1 = 0 ⇒ λ ² = 1 ⇒ λ1,2 = ±1
λ1 = 1
λ2 = -1
La integral homogénea es:
y* = c1.e1.x + c2.e-1.x
Cálculo de la integral particular:
5
y = x .(a.x + b)
como
s=0
y = a.x + b
Sus derivadas son:
y´ = a
y" = 0
debe verificar:
(0) - (a.x + b) = x ⇒ -a.x - b = x
a = -1
b=0
La integral particular es:
y = -1.x
Luego la integral general es:
x
-x
y = y* + y ⇒ y* = c1.e + c2.e - x
3) y" - y = e
x
Cálculo de las raíces:
λ ² - 1 = 0 ⇒ λ ² = 1 ⇒ λ1,2 = ±1
λ1 = 1
λ2 = -1
La integral homogénea es:
x
-1.x
y* = c1.e + c2.e
Cálculo de la integral particular:
y = a.x.e
x
Sus derivadas son:
x
x
y´ = a.e + a.x.e
x
x
x
y" = a.e + a.e + a.x.e
y" = 2.a.ex + a.x.ex
Debe verificar:
y" + y = ex
x
x
x
x
2.a.e + a.x.e - a.x.e = e
2.a.ex = ex ⇒ 2.a = 1 ⇒ a = 1/2
La integral particular es:
x
y = x.e /2
La solución general es:
x
-x
x
y = C1.e + C2.e + x.e /2
4) y" + 4.y = 16.x.sin 2.x
Cálculo de las raíces:
La integral homogénea es:
y* = c1.con 2.x + c2.sin 2.x
Cálculo de la integral particular:
y = x.[(a.x + b).cos 2.x + (c.x + d).sen 2.x] = (a.x ² + b.x).cos 2.x + (c.x ² + d.x).sen 2.x
5) y" - 4.y´ + 5.y = 2.e ².x.cos x
Cálculo de las raíces:
λ² - 4.λ + 5 = 0
6) y" + ω0.y = A.sen (ω.t)
con
A>0
ω>0
ω0>0
distinguir:
ω ≠ ω0
ω=ω0
7) y" - y´ - 2.y = x ² + cos x
Cálculo de las raíces:
λ² - λ - 2 = 0
La integral homogénea es:
x
-1.x
y* = c1.e ². + c2.e
Cálculo de la integral particular:
y1 = a.x ² + b.x + c
y2 = d.cos x + e.sen x
Sus derivadas son:
y1´ = 2.a.x + b
y1" = 2.a
y2´ = -d.sin x + e.cos x
y2" = -d.cos x - e.sen x
La primer integral debe verificar:
y"1 - 1.y´1 - 2.y1 = x ²
2.a - 2.a.x - b - 2.(a.x ² + b.x + c) = x ²
2.a - 2.a.x - b - 2.a.x ² - 2.b.x - 2.c = x ²
- 2.a.x ² - 2.a.x - 2.b.x + 2.a - b - 2.c = x ²
- 2.a = 1 ⇒ a = -1/2
- 2.a - 2.b = 0 ⇒ a + b = 0 ⇒ b = -a ⇒ b = -(-1/2) ⇒ b = 1/2
2.a - b - 2.c = 0 ⇒ 2.a - b = 2.c ⇒ 2.(-1/2) - 1/2 = 2.c
-1 - 1/2 = 2.c ⇒ - 3/2 = 2.c ⇒ c = - 3/4
Una primera integral particular es:
y1 = x ²/2 + x/2 - 3./4
La segunda integral debe verificar:
y"2 - y´2 - 2.y2 = cos x
x
x
y´ = a.e + b.x.e
y" = a.ex + a.ex + b.x.ex
y"2 - y´2 - 2.y2 = cos x
-d.cos x - e.sen x - (-d.sen x + e.cos x) - 2.(d.cos x + e.sen x) = cos x
-d.cos x - e.sen x + d.sen x - e.cos x - 2.d.cos x - 2.e.sen x = cos x
-d.cos x - e.cos x - 2.d.cos x - e.sen x + d.sen x - 2.e.sen x = cos x
(-d - e - 2.d).cos x + (-e + d - 2.e).sen x = cos x
-d - e - 2.d = 1 ⇒ - e - 3.d = 1
-e + d - 2.e = 0 ⇒ d - 3.e = 0 ⇒ d = 3.e
- e - 3.(3.e) = 1 ⇒ - e - 9.e = 1 ⇒ -10.e = 1 ⇒ e = -1/10
d = 3.(-1/10) ⇒ d = -3/10
La segunda integral es:
y2 = -3.(cos x)/10 - (sen x)/10
Luego la integral general es:
2.x
y = C1.e
+ C2.e-x - x ²/2 + x/2 - 3/4 - 3.(cos x)/10 - (sen x)/10
8) y" + y = 1 + sin 2.x
y(0) = 1
y´(0) = 0
Cálculo de las raíces:
9) y" + 4.y = 3.cos 2.x - 7.x ²
y(0) = 0
y´(0) = 0
Cálculo de las raíces:
10) y" + 4.y´ + 4.y = x.ex + sin x
Cálculo de las raíces:
λ ² + 4.λ + 4 = 0
(λ + 2) ² = 0
λ1 = λ2 = -2
La integral homogénea es:
y* = c1.e-2.x + c2.e-2.x
Cálculo de la integral particular:
x
x
y1 = a.x.e + b.e
y2 = a.cos x + b.sin x
Sus derivadas son:
x
x
x
y´1 = a.e + a.x.e + b.e
y"1 = a.ex + a.ex + a.x.ex + b.ex ⇒ y"1 = 2.a.ex + a.x.ex + b.ex
y´2 = -a.sin x + b.cos x
y"2 = -a.cos x - b.sin x
La primer integral debe verificar:
y"1 + 4.y´1 + 4.y1 = x.e
x
x
x
x
2.a.e + a.x.e + b.e + 4.(a.ex + a.x.ex + b.ex) + 4.(a.x.ex + b.ex) = x.ex
2.a.ex + a.x.ex + b.ex + 4.a.ex + 4.a.x.ex + 4.b.ex + 4.a.x.ex + 4.b.ex = x.ex
x
x
x
x
x
x
x
x
x
2.a.e + 4.a.e + a.x.e + 4.a.x.e + 4.a.x.e + b.e + 4.b.e + 4.b.e = x.e
6.a.ex + 9.a.x.ex + 9.b.ex = x.ex
6.a + 9.a.x + 9.b = x
9.a = 1 ⇒ a = 1/9
6.a + 9.b = 0 ⇒ 6.(1/9) + 9.b = 0 ⇒ 2/3 + 9.b = 0 ⇒ 9.b = -2/3 ⇒ b = -2/27
Una integral particular es:
y1 = x.ex/9 - 2.ex/27
La segunda integral debe verificar:
y"2 + 4.y´2 + 4.y2 = sin x
-a.cos x - b.sin x + 4.(-a.cos x + b.sin x) + 4.(a.cos x + b.sin x) = sin x
-a.cos x - b.sin x - 4.a.cos x + b.sin x + 4.a.cos x + b.sin x = sin x
(4.b + 3.a).cos x + (-4.a + 3.b).sin x = sin x
4.b + 3.a = 0 ⇒ -4.b = 3.a ⇒ -4.b/3 = a
-4.a + 3.b = 1
La segunda integral es:
y2 = -4.(cos x)/25 + 3.(sen x)/25
Luego la integral general es:
-2.x
y = C1.e
+ C2.x.e-2.x + x.ex/9 - 2.ex/27 - 4.(cos x)/25 + 3.(sen x)/25
11) y" - 2.y´ + 10.y = -e-2.x
y(0) = 0
y´(0) = 0
Cálculo de las raíces:
λ ² - 2.λ + 10 = 0
12) y" + 9.y = 1
y(0) = 0
y´(0) = 1
Cálculo de las raíces:
Ecuaciones diferenciales NO homogéneas (segunda parte)
Integrar las siguientes ecuaciones diferenciales. Cuando se indique, hallar la integral
particular que verifica las condiciones iniciales impuestas.
13) y" + 4.y = -√2; y(0) = 1; y´(0) = 0
14) y" + 2.y = 3/ex + x.(1 - ex)
x
15) y" = 6.e³. - 9.y, y(0) = y´(0) = 0
-3.x
16) y" + 3.y´ = 3.e
, y(0) = y´(0) = 0
17) 3.y" - 12.y´ + 12.y = e ².x, y(0) = y´(0) = 0
18) y" + √3.y = x ²; y(0) = 0; y´(0) = 1
Cálculo de las raíces:
La integral homogénea es:
Cálculo de la integral particular:
y = a.x ² + b.x + c
Sus derivadas son:
y´ = 2.a.x + b
y" = 2.a
debe verificar:
y" + √3.y = x ² ⇒ 2.a + √3.(a.x ² + b.x + c) = x ²
La integral particular es:
Luego la integral general es:
Para el punto dado:
19) 3.y" - 5.y´ = 20.x³ - 216.x/5 - 1
20) y" + y = x + ex, y(0) = 0, y´(0) = 0
21) y" - y = 2.x³ + e-x + 1
Cálculo de las raíces:
λ ² - 1 = 0 ⇒ λ ² = 1 ⇒ λ1,2 = ±1
La integral homogénea es:
-3.x
y* = c1.e
+ c2.ex
Cálculo de la integral particular:
y1 = a.x³ + b.x ² + c.x + d
-x
y2 = c3.x.e
Sus derivadas son:
y´1 = 3.a.x ² + 2.b.x + c ⇒ y"1 = 6.a.x + 2.b
y´2 = c3.e-x - c3.x.e-x ⇒ y"2 = -2.c3.e-x + c3.x.e-x
debe verificar:
y"1 + y1 = 2.x³ + 1
6.a.x + 2.b - (a.x³ + b.x ² + c.x + d) = 2.x³ + 1
6.a.x + 2.b - a.x³ - b.x ² - c.x - d = 2.x³ + 1
- a.x³ - b.x ² + 6.a.x - c.x + 2.b - d = 2.x³ + 1
- a.x³ - b.x ² + (6.a - c).x + 2.b - d = 2.x³ + 1
-a = 2 ⇒ a = -2
-b = 0 ⇒ b = 0
6.a - c = 0 ⇒ 6.a = c ⇒ 6.(-2) = c ⇒ c = -12
2.b - d = 1 ⇒ 2.0 - d = 1 ⇒ - d = 1 ⇒ d = -1
y"2 + y2 = e-x
-x
-x
-x
-x
-2.C3.e + C3.x.e - C3.x.e = e
-2.C3.e-x = e-x
-2.C3 = 1
C3 = -1/2
La integral particular es:
y1 = -2.x³ - 12.x - 1
y2 = x.e-x/2
Luego la integral general es:
-x
x
-x
yp = y* + y1 + y2 = C1.e + C2.e - 2.x³ - 12.x - 1 - x.e /2
22) y" + y´ = 2 + 3.x.e-x, y(0) = 2, y´(0) = 1
23) y" + y = x.cos x
24) y" + 4.y = sen x + sen 2.x
Cálculo de las raíces:
λ ² + 4 = 0 ⇒ λ ² = -4
La integral homogénea es:
y* = c1.cos 2.x + c2.sen 2.x
Cálculo de la integral particular:
y1 = a.sen x + b.cos x
y2 = c.x.sen 2.x + d.x.cos 2.x
Sus derivadas son:
y´1 = a.cos x - b.sen x
y"1 = -a.sen x - b.cos x
y´2 = c.sen 2.x + 2.c.x.cos 2.x + d.cos 2.x - 2.d.x.sen 2.x
y"2 = 4.c.cos 2.x - 4.c.x.sen 2.x - 4.d.sen 2.x - 4.d.x.cos 2.x
debe verificar:
La integral particular es:
y1 = (sen x)/3
y2 = x.(cos 2.x)/4
Luego la integral general es:
yp = y* + y1 + y2 = C1.cos 2.x + C2.sen 2.x + (sen x)/3 + x.(cos 2.x)/4
MATEMATICAS - FUNCIONES
FUNCIONES DE VARIAS VARIABLES
IDEA INTUITIVA: Hasta el momento hemos trabajado con función de una sola variable, es
decir, que van de R a R. Ahora vamos a trabajar con funciones escalares, que reciben un
vector de Rn y devuelven un valor de R, y con funciones vectoriales que reciben un vector
n
m
de R y devuelven uno de R . La dificultad de estas funciones reside en que no tienen
representación gráfica posible, a excepción de las funciones de R ² en R, que se pueden
representar como superficies tridimensionales. Además, los cálculos de límites se complican
mucho llegando a ser imposibles. Por ello nos ocuparemos casi siempre de las más
sencillas de este tipo de funciones, aunque toda la teoría se referirá a funciones de n
variables.
CONCEPTOS BASICOS
n
n
DEFINICION: Sea f:R → R una aplicación que a cada x ∈ R le asigna f(x) ∈ R. Entonces
n
f:R → R es una función escalar de varias variables.
x = (x1,...xn) ∈ Rn
f(x) = f(x1,...xn) = t ∈ R
NOTACION: En el caso de que n = 2, haremos:
x1 = x, x2 = y
Y en el caso de que n = 3
x1 = x, x2 = y, x3 = z
n
n
DEFINICION: Sea f:R → R. Llamamos DOMINIO de la función al conjunto de puntos de R
en el que está definida f:Rn → R
Ejemplo:
f(x,y) = [ln (x ² + y ² - 25)]/(x + y ²)
dom(f) = {(x, y) ∈ ℜ ² / x ² + y ² > 25, x ≠ -y ²}
OBSERVACION: Sea f:R ² → R. Llamamos GRAFICA de f al conjunto {(x, y, z) ∈ R³ / z =
f(x, y) ⊂ R³}. A dicha gráfica la llamaremos superficie:
Ejemplo:
Llamamos CURVAS DE NIVEL a los puntos de la forma {(x, y) ∈ ℜ ² / f(x, y) = constante}.
Son los puntos obtenidos al intersectar la superficie generada por f con un plano z =
constante, y proyectarla en el plano.
OBSERVACION: Sea f:R³ → R. Llamamos SUPERFICIES DE NIVEL de f a los conjuntos
de la forma conjunto {(x, y, z) ∈ ℜ³ / f(x, y, z) = constante}.
n
m
n
DEFINICION: Sea f:R → R una aplicación que a cada x ∈ R le asigna un vector f(x) = Y ∈
m
n
m
R . Entonces f:R → R es una función vectorial de varias variables.
x = (x1,...xn) ∈ Rn
f(x) = [f1(x), f2(x), ..., fm(x)] ∈ Rm, fi: Rn → R
Y a las f1:Rn → R se las llama funciones coordenadas.
Ejemplo:
f(x, y) = [(x + y)/(x - y), sen (x + y), cos (x.y)] f: R ² → R³
n
m
DEFINICION: Sea f:R → R . Llamamos DOMINIO de la función a la intersección de los
dominios de las funciones coordenadas de f.
SUPERFICIES EN R³
M.x ² + N.y ² + P.z ² = R
M, N, P
Lugar geométrico obtenido
Con R > 0
Todos positivos
Elipsoide
Todos positivos e iguales
Esfera
Todos negativos
No existe lugar geométrico
2 positivos y uno negativo
Hiperboloide de una hoja
2 negativos y uno positivo
Hiperboloide de dos hojas
1 cero y dos positivos
Cilindro Elíptico
1 cero y dos positivos iguales Cilindro Circular
1 cero y 2 negativos
No existe lugar geométrico
1 cero, 1 positivo y 1 negativo
Cilindro Hiperbólico
2 ceros y 1 positivo
Dos planos paralelos
2 ceros y 1 negativo
No existe lugar geométrico
M.x ² + N.y ² + P.z ² = R
M, N, P
Lugar geométrico obtenido
Con R = 0
Todos del mismo signo
Un punto P(0,0,0)
2 positivos y 1 negativo
Cono recto
1 cero y 2 del mismo signo
Eje coordenado
1 cero y 2 de distinto signo
Dos planos que se cortan
2 cero
Plano coordenado
M.x ² + N.y ² = S.R
MyN
Lugar geométrico Obtenido
Con S > 0
Del mismo signo
Paraboloide Elíptico
Del mismo signo iguales
Paraboloide Circular
Signos Opuestos
Paraboloide Hiperbólico
Uno es Cero
Cilindro Parabólico
Con S = 0
Uno es Cero
Plano Coordenado
Del mismo signo
Eje Coordenado
Signos Opuestos
Planos que se cortan
MATEMATICAS – INTEGRALES
INTEGRACION POR SUSTITUCION
F(x) = ∫f(x).g(x).dx ⇒F(x) = ∫u.du ⇔ u = g(x) ⇔ du = f(x).dx
INTEGRACION POR PARTES
La integral de un producto de un factor finito por un factor diferencial es igual al factor
finito por una integral del factor diferencial, menos la integral de la integral hallada
por la diferencial del factor finito.
F(x) = ∫u.dv ⇒ F(x) = u.v - ∫v.du
F(x) = ∫f(x).g5(x).dx ⇔ F(x) = f(x).g(x) - ∫g(x).f´(x).dx
u = f(x) ⇔ du = f´(x).dx
dv = g5(x).dx ⇔ v = g(x)
Método abreviado
f(x)
f¹(x)
f ²(x)
5
g (x)
g4(x)
g³(x)
g ²(x)
g¹(x)
f³(x)
4
f (x) = 0
F(x) = f(x).g4(x) - f¹(x). g³(x) + f ²(x). g ²(x) - ³(x).g¹(x)
INTEGRACION DEL COCIENTE DE DOS POLINOMIOS
F(x) = ∫f(x)/g(x).dx
1) si f(x) y g(x) son polinomios y el grado de f(x) es igual o mayor que el de g(x), se dividen:
f(x) = g(x).c(x) + R
F(x) = ∫c(x).dx + ∫ R/g(x).dx
2) si f(x) y g(x) son polinomios y el grado de f(x) es menor que el de g(x), se factorean:
a)
f(x) = (x + a)
g(x) = (x + b).(x + c)
F(x) = ∫ (x + a) / (x + b).(x + c) dx ⇒F(x) = [(a - b) /(c - b)].ln (x + b) + [(a - c) /(b - c)].ln (x + c)
b)
f(x) = (x + a)
g(x) = (x + b) ²
F(x) = ∫ (x + a) / (x + b) ² dx
u = x + b ⇒x = u - b
du = dx
x+a=u-b+a
F(x) = ∫ du/u + (a - b).∫ du/u ² = ln u - (a - b)/u
INTEGRACION POR SUSTITUCION TRIGONOMETRICA
a)
x = b.sen t ⇒t = arcsen (x/b)
dx = b.cos t .dt
a.dx
F(x)
=∫
= a. ∫
= a.
b.cos t .dt
cos t .dt
=
a.b
.
√ b ² - x ∫ √ b ² - (b sen t) a.b.∫ √b ² - b ².sen t
²
²
²
cos t .dt
= a. ∫ dt = a.t = a.arcsen (x/b)
cos t
=
b
∫
cos t .dt
√ 1 - sen t
²
cos t
.dt
= a.
∫
√ cos t
²
b)
x = √b. t ⇒t = x/√b
dx = √b.dt
F(x) =
a.dx
= a.
√b.dt
∫
=
dt
∫ b + (√b.t) a.√b.∫ b + b.t
b+x
²
²
²
INTEGRALES TRIGONOMETRICAS
a.√b
=
b
∫
dt
1+t
²
=
a.√b.arctg
t
b
=
a.√b.arctg
(x/√b)
b
n
m
F(x) = ∫sen x.cos x.dx
siendo m ó n impar, por ej.:
F(x) = ∫sen ² x .cos³ x .dx ⇒F(x) = ∫sen ² x .cos ² x .cos x .dx ⇒F(x) = ∫(1 - sen ² x) .sen ² x
.cos x .dx ⇒
F(x) = ∫(sen ² x - sen4 x).cos x .dx F(x) = ∫sen ² x .cos x .dx - ∫sen4 x.cos x .dx
u = sen x
du = cos x .dx
F(x) = ∫u ².du - ∫u4.du ⇒F(x) = u³/3 - u5/5 ⇒F(x) = (sen³ x)/3 - (sen5 x)/5
METODOS DE INTEGRACION
En este tema se continúa con los métodos de integración iniciados en el capítulo anterior, en
el que a partir del concepto de primitiva y de las derivadas de las funciones elementales se
obtenían las integrales inmediatas, bien de forma directa, bien por cambio de variable.
Se estudiarán las técnicas más elementales para reducir a inmediatas aquellas integrales
que no lo sean: integración por partes, integrales de cocientes de polinomios por
descomposición en fracciones simples y fórmulas de reducción.
Todos los métodos de integración tienen por objetivo transformar una integral dada, no
inmediata, en otra, o suma de varias, cuyo cálculo resulte más sencillo.
La integración por partes consiste en descomponer una integral en una suma de un
producto de funciones más una integral que, pretendidamente, es más sencilla que la de
partida.
La descomposición en fracciones simples de un cociente de polinomios transforma éste en
una suma de fracciones cuyas integrales pueden solucionarse con facilidad.
Por último, las fórmulas de reducción permiten, en algunos casos, resolver integrales que
dependen de un número natural n si se conoce el valor de la integral que depende del
número anterior o ante-anterior. Así, por ejemplo,a partir de ∫ sen° x dx = ∫ 1 dx = x y ∫ sen x
4
dx = - cos x, va a ser posible calcular las integrales de sen ² x, sen³ x, sen x,etc.
INTEGRACION POR PARTES
Este método permite resolver un gran número de integrales no inmediatas.
1. Sean u y v dos funciones dependientes de la variable x; es decir, u = f(x), v = g(x).
2. La fórmula de la derivada de un producto de dos funciones, aplicada a f(x).g(x), permite
escribir,
d(f(x).g(x)) = g(x).f´(x)dx + f(x).g´(x)dx
3. Integrando los dos miembros,
∫ d[f(x).g(x)] =∫ g(x).f´(x).dx + ∫ f(x).g´(x).dx
De la misma manera que ∫ dx = x, también ∫ d[f(x).g(x)] = f(x).g(x)
Por tanto, f(x).g(x) = ∫ g(x).f´(x).dx + ∫ f(x).g´(x).dx. De aquí se obtiene que:
∫ f(x).g´(x).dx = f(x).g(x) - ∫ g(x).f´(x).dx
Esta no es la fórmula usual de la integración por partes. Puesto que u =f(x), du = f´(x)dx, y al
ser v = g(x), dv = g´(x)dx. Llevando estos resultados a la igualdad anterior,
∫ u.dv = u.v - ∫ v.du
Cómo se resuelve una integral por partes
Este método consiste en identificar u con una parte de la integral y dv con el resto, con la
pretensión de que al aplicar la fórmula obtenida, la integral del segundo miembro sea más
sencilla de obtener que la primera. No hay, y éste es el mayor problema de este
procedimiento, una regla fija para hacer las identificaciones más convenientes. La resolución
de un buen número de problemas es el mejor camino para adquirir la técnica necesaria.
No obstante, se suelen identificar con u las funciones de la forma xm si m es positivo; si m es
m
negativo,es preferible identificar con dv a x .dx. También suelen identificarse con u las
x
funciones ln x, arc sen x, arc tg x y con dv, e .dx, sen x dx, cos x dx, etc.
Antes de empezar a practicar este método se ha de tener presente que al hacer la
identificación de dv,ésta debe contener siempre a dx.
Ejercicio: integración por partes
1) Calcular ∫ ln x dx
Resolución:
Este es uno de los casos más sencillos; la integral consta de una sola función, ln x.
Haciendo u = ln x, y diferenciando, du = dx/x
Necesariamente, dv = dx. Integrando ambos miembros, ∫ dv =∫ dx. Es decir, v = x.
Aplicando la fórmula, ∫ ln x dx = x.ln x - ∫ x.(1/x).dx = x.ln x - x + C
2) Calcular ∫ sen ² x dx
Resolución:
Se puede resolver efectuando cambios distintos:
a) La identificación, en este caso, puede ser u = sen x y dv = sen x dx
De u = sen x se deduce, diferenciando, que du = cos x dx.
De dv = sen x dx, integrando, ∫ dv = ∫ sen x dx, es decir, v = - cos x
Aplicando la fórmula, ∫ u.dv = u.v - ∫ v.du,
∫ sen ² x dx = sen x . (- cos x) - ∫ (- cos x).cos x dx = - sen x . cos x + ∫ cos ² x dx
Puesto que cos ² x =1 - sen ² x,
∫ sen ² x dx = - sen x .cos x + ∫ (1 - sen ² x).dx = - sen x .cos x + ∫ dx - ∫ sen ² x dx
∫ sen ² x dx = - sen x .cos x + x - ∫ sen ² x dx
Al volver a obtener en el segundo miembro la integral de partida puede llegarse a la
conclusión de no haber avanzado en el propósito de calcular la integral. No es así en este
caso, pasando al primer miembro
- ∫ sen ² x dx, se obtiene
2.∫ sen ² x dx = x - sen x .cos x. Y pasando al segundo miembro,
∫ sen ² x.dx = (x - sen x.cos x)/2 + C
b) Esta integral admite también la identificación u = sen ² x, dv = dx
Diferenciando u, du = 2 sen x cos x dx = sen 2 x.dx
Integrando dv, ∫ dv = ∫ dx ⇒ v = x.
Aplicando la fórmula de integración por partes, ∫ sen ² x dx = sen ² x .x - ∫ x.sen 2.x dx (1)
Y aquí es necesario volver a integrar por partes ∫ x.sen 2.x dx
Si u = x, du = dx.
Si dv = sen 2.x dx, v = ∫ sen 2.x dx = ½ .∫ 2.sen 2.x dx = - ½.cos 2.x
∫ x.sen 2.x dx = - ½.cos 2.x -∫ - ½.cos 2.x dx = - ½.x.cos 2.x + ½.∫ cos 2.x dx =
= - ½.x.cos 2.x + ½.½.∫ 2.cos 2.x dx = - ½.x.cos 2.x + ¼.sen 2.x
Volviendo a la igualdad (1)
∫ sen ² x.dx = x.sen ² x + (x.cos 2.x)/2 - (sen 2.x)/4 + C
No hay que dejarse engañar por la apariencia de que los resultados que se han obtenido
son distintos; en realidad son iguales. Si en la segunda expresión se sustituye cos 2 x por su
valor, cos ² x - sen ² x, y sen 2 x por el suyo, 2 sen x.cos x, se obtiene:
x.sen ² x + (x/2).(cos ² x - sen ² x) - (1/4).2.sen x.cos x =
= x.sen ² x + (x/2).cos ² x - (x/2).sen ² x - (1/2).sen x.cos x =
= (x/2).cos ² x + (x/2).sen ² x - (1/2).sen x.cos x =
= (x/2).(sen ² x + cos ² x) - (1/2).sen x.cos x =
= (x/2).1 - (1/2).sen x.cos x =
= (x - sen x.cos x)/2
3) Resolver ∫ arc sen x.dx
Resolución:
La identificación obligada es u = arc sen x; así du =
dv = dx, de donde v = ∫ dx = x
Aplicando la fórmula,
∫ arc sen x dx = x.arc sen x - ∫ x.
dx =
∫ arc sen x dx = x.arc sen x - ∫ x.(1 - x²)-1/2 dx
∫ arc sen x dx = x.arc sen x - (-1/2). ∫ -2.x.(1 - x²)-1/2 dx =
4) Calcular ∫ x.√1 + x.dx
Resolución:
Llamando u = x, du = dx;
5) Hallar ∫ x ².ex.dx
Resolución:
Se hace la identificación u = x ²; diferenciando, du = 2 x.dx
dv = ex.dx, integrando, v = ∫ ex.dx = ex
Aplicando la fórmula,
∫ x ².ex.dx = x ².ex - ∫ ex.2.x.dx = x ².ex - 2.∫ x.ex.dx (1)
Se vuelve a integrar por partes ∫ x.ex.dx
x
x
x
u = x, du = dx; dv = e .dx, v = ∫ e .dx = e
Así,
dx
∫ x ².ex.dx = x.ex - ∫ ex.dx = x.ex - ex = ex.(x - 1)
Llevando este resultado a (1),
∫ x ².ex.dx = x ².ex - 2.ex.(x - 1) = ex.[x ² - 2.(x - 1)] = ex.(x ² - 2.x + 2) + C
INTEGRALES DE FUNCIONES RACIONALES
Se trata de resolver integrales de la forma ∫ P(x)/Q(x).dx en las que p(x) y q(x) son
polinomios.
Integrales racionales inmediatas
Son aquellas que se convierten en suma de integrales inmediatas sin más que dividir p(x)
entre q(x). Para ello es preciso que el grado de p(x) sea mayor o igual que el grado de q(x).
Se sabe que en una división D = d·c + r. Dividiendo ambos miembros entre el divisor, d ,
D/d = d.c/d + r/d = c + r/d
En general, para polinomios, si p(x) es el dividendo, q(x) el divisor, c(x) el cociente y r(x) el
resto,
p(x)/q(x) = c(x) + r(x)/q(x)
Por consiguiente,
∫ P(x)/Q(x).dx = ∫ [c(x) + r(x)/q(x)].dx = ∫ c(x).dx + ∫ r(x)/Q(x).dx
Ejercicio: cálculo de integrales de funciones racionales
1) Calcular ∫ [x ²/(x ² + 1)].dx
Resolución:
Se divide x ² entre x ² + 1. El cociente es 1 y el resto - 1.
∫ [x ²/(x ² + 1)].dx = ∫ [1 - 1/(x ² + 1)].dx = ∫ dx - ∫ dx /(x ² + 1) = x - arctg x + C
2) Hallar ∫ [(x ² - 5.x + 4)/(x + 1)].dx
Resolución:
Se dividen los polinomios.
x ² - 5 x + 4 = (x + 1) (x - 6) + 10
El cociente es x - 6 y el resto 10.
∫ [(x ² - 5.x + 4)/(x + 1)].dx = ∫ [(x - 6) + 10/(x + 1)].dx = ∫ x.dx - 6.∫ dx + 10.∫ dx/(x + 1) = x ²/2
- 6.x + 10.(ln |x + 1|) + C
Hay, no obstante, integrales racionales que no se convierten tan fácilmente en inmediatas.
Para resolverlas es preciso hacer uso de la descomposición en fracciones simples.
INTEGRALES DE COCIENTES
Una fracción simple es cualquier fracción propia de polinomios (el grado del numerador es
estrictamente menor que el grado del denominador), cuyo denominador sea de la forma (ax
+ b)n ó (ax ² + bx + c)n si el polinomio ax ² + bx + c no tiene raíces reales, y n es un número
natural. Así,
3/(x + 4); (5.x - 2)/(x ² + x + 3); (x - 3)/(2.x + 1)³
son fracciones simples. Al hacer el estudio de integrales de la forma ∫ P(x)/Q(x).dx, se
supondrá que el grado del numerador, p(x), es estrictamente menor que el grado del
denominador, pues si el grado del numerador fuese mayor o igual al grado del denominador,
se dividiría p(x) entre q(x), obteniéndose un cociente c(x) y un resto r(x), en cuyo caso la
integral ∫ P(x)/Q(x).dx se convierte en ∫ [c(x) + r(x)/q(x)].dx.
La integral ∫ c(x).dx es inmediata por tratarse de un polinomio y la integral ∫ r(x)/Q(x).dx es
del caso supuesto, ya que el grado del resto, r(x), en una división de polinomios, es
estrictamente menor que el grado del divisor q(x).
Método de integración por descomposición en fracciones simples
Para resolver este tipo de integrales
∫ r(x)/Q(x).dx
se procede del siguiente modo:
1. Se descompone factorialmente el polinomio q(x), es decir, se hallan las raíces de la
ecuación q(x) = 0.
2. Se descompone la fracción p(x)/q(x) en suma de fracciones simples como se verá en los
ejemplos.
3. Se integran los sumandos que resulten.
Ahora bien, al resolver la ecuación q(x) = 0 es posible encontrar resultados distintos y éstos
se pueden clasificar en tres casos:
_ obtención de raíces simples (ninguna raíz está repetida).
_ obtención de raíces múltiples (al menos hay una raíz repetida).
_ obtención de raíces imaginarias (números complejos).
Hay que estudiar, pues, cada uno de los casos.
A) Se obtienen raíces reales simples.
Si x1, x2, ..., xn son las raíces simples de q(x),se tiene:
∫ [p(x)/q(x)].dx =
∫ [p(x)/q(x)].dx =
A1, A2, ...., Anson constantes que se tienen que determinar. Como se aprecia, las integrales
que resultan son inmediatas.
Ejercicio: cálculo de integrales
1) Calcular la integral ∫ [(x³ - 3.x ² + 1)/(x ² - 1)].dx
Resolución:
Al ser el grado del numerador, 3, mayor que el del denominador, 2, se dividen los polinomios
y se obtiene:
x³ - 3 x ² + 1 = (x ² - 1) (x - 3) + (x - 2)
∫ [(x³ - 3.x ² + 1)/(x ² - 1)].dx = ∫ [x - 3 + (x - 2)/(x ² - 1)].dx = ∫ x.dx - 3.∫ dx + ∫ [(x - 2)/(x ² 1)].dx = x ²/2 - 3.x + ∫ [(x - 2)/(x ² - 1)].dx =
Las raíces de x ² - 1 son: x ² - 1 = 0 ⇒x ² = 1 ⇒ x = ±1
Tiene, por tanto, dos raíces simples distintas, 1 y - 1.
Se descompone (x - 2)/(x ² - 1) en fracciones simples:
(x - 2)/(x ² - 1) = A/(x - 1) + B/(x + 1) = [A.(x + 1) + B.(x - 1)]/(x ² - 1)
Puesto que los denominadores son iguales, los numeradores también han de serlo:
x - 2 = A(x + 1) + B(x - 1).
Para determinar A y B, se dan valores a x:
si x = 1, 1 - 2 = A(1 + 1) + B(1 - 1), - 1 = 2 A, A =- 1/2
si x = -1, - 1 - 2 = A(- 1 + 1) + B(- 1 - 1), - 3 = -2 B, B = 3/2
Debe hacerse notar que, aunque a x se le pueden dar valores arbitrarios,en este caso se
han elegido aquellos que anulan uno de los sumandos para simplificar los cálculos. Este
será un procedimiento muy generalizado. Así pues:
(x - 2)/(x ² - 1) = (-1/2)/(x - 1) + (3/2)/(x + 1), por lo que
∫ [(x - 2)/(x ² - 1)].dx = ∫[(-1/2)/(x - 1)].dx + ∫[(3/2)/(x + 1)].dx = -(1/2).ln |x - 1| + (3/2).ln |x + 1|
Finalmente, ∫ [(x³ - 3.x ² + 1)/(x ² - 1)].dx = x ²/2 - 3.x - (1/2).ln |x - 1| + (3/2).ln |x + 1| + C
B) Se obtienen raíces reales múltiples.
Si a es una raíz múltiple de multiplicidad n (está repetida n veces), la descomposición en
n
fracciones simples de p(x)/(x - a) es
A1, A2, A3, ..., An vuelven a ser constantes a determinar. De nuevo, las integrales de la forma
∫ Ai/(x - a)i.dx son inmediatas.
Ejemplo: cálculo de integrales
1) Calcular ∫ [(x ² + 3.x - 5)/(x³ - 3.x + 2)].dx
Resolución:
Como el grado del numerador, 2, es menor que el del denominador, 3, no se dividen los
polinomios.
Las raíces del polinomio x³ - 3 x + 2 se obtienen aplicando la regla de Ruffini:
x³ - 3 x + 2 = (x - 1) ² (x + 2)
El polinomio tiene una raíz simple, - 2, y una raíz múltiple, 1, de multiplicidad dos.
La descomposición en fracciones simples de la fracción es:
Como en el caso anterior, se igualan los numeradores y se dan valores arbitrarios a x para
determinar A, B y C.
x ² + 3 x - 5 = A(x - 1) (x + 2 ) + B(x + 2 ) + C(x - 1) ²
Si x = 1 → -1 = 3.B ⇒B = -1/3.
Si x = -2 → -7 = 9.C ⇒C = -7/9.
Si x = 0 → -5 = -2.A + 2.B + C = -2.A - 2/3 - 7/9 ⇒A = 16/9.
Por tanto,
∫ [(x ² + 3.x - 5)/(x³ - 3.x + 2)].dx = ∫[(16/9)/(x - 1)].dx + ∫[(-1/3)/(x - 1) ²].dx + ∫[(-7/9)/(x +
2)].dx =
= (16/9).∫ dx/(x - 1) - (1/3).∫ dx/(x - 1) ² - (7/9).∫ dx/(x + 2) =
= (16/9).ln |x - 1| - (1/3).[(x - 1)-1/(-1)] - (7/9).ln |x + 2| + C =
= (16/9).ln |x - 1| - (7/9).ln |x + 2| + (1/3)/(x - 1) + C
C) Se obtienen raíces imaginarias
Si un polinomio con coeficientes reales tiene una raíz imaginaria x = α + i. β, su conjugada
también es raíz del polinomio, x = α - i. β . Si se multiplica x - (α + i. β) por x - (α - i. β), se
obtiene:
(x - α - i. β).(x - α + i. β) = (x - α) ² + β ²
(el número imaginario i verifica i ² = - 1).
Cada par de raíces imaginarias conjugadas determina una fracción simple de la forma
, por lo que se hace necesario aprender la técnica de resolución de integrales
de la forma
.dx.
1. Se suma y se resta al numerador A α y se descompone en las dos integrales siguientes:
Estas dos integrales son inmediatas aplicándoles un cambio de variable:
2. Al ser [(x - α) ² + β ]´ = 2.(x - α),
Puesto que la derivada de (x - α)/ β es 1/ β,
4. Concluyendo:
Obsérvese que C1 + C2 = C
Para este tercer caso sólo se estudiarán las integrales en las que las raíces imaginarias del
denominador sean simples.
MATEMATICAS – PROBABILIDADES Y ESTADISTICAS
INTERVALO DE CONFIANZA
1) Para la media μ de una población normal:
Li/s = x ± zα/2.σ/√n
Tener en cuenta que una confianza del 95% significa:
α/2 = 0,95
p=1-q
p = x/n
2) Para la media X :
Li/s = x ± t(n - 1)(1 - α/2).S/√n
t(α,v) se busca en tabla
2
3) Para la varianza S :
2
X
(α,v)
se busca en tabla
4) Para el desvío estándar S:
5) Para muestras grandes:
Un intervalo de confianza 100(1 - α)% para la proporción p de una población, de muestras
grandes, es:
p ± zα/2√p.q/n
Dónde p = x/n, n tamaño muestral, x es el número observado de éxitos, y q = 1 - p.
Este intervalo se puede emplear siempre que n.p ≥ 5 y n.q ≥ 5.
Ejemplo:
El gerente financiero de una gran cadena de tiendas seleccionó una muestra aleatoria de
200 de sus clientes que utilizan tarjetas de crédito, y encontró que 136 habían incurrido en
cargos por intereses durante el año anterior debido a falta de pago de sus saldos.
a) Calcule un intervalo de confianza de 95% para la verdadera proporción de clientes que
utilizan tarjetas de crédito, quienes han incurrido en cargos por intereses durante el año
anterior.
b) Si la longitud deseada del intervalo de 90% es 0,05, ¿qué tamaño muestral es necesario
para asegurar esto?
c) Calcule el intervalo de confianza de 82% para la verdadera proporción.
n = 200
x = 136
a) Para 1 - α/2 = 0,95
p = x/n
p = 136/200 = 0,68
p=1-q⇒q=1-p
q = 1 - 0,68 = 0,32
Li/s = p ± z(1 - α/2).√p.q/n
Li/s = 0,68 ± z( 0,95).√0,68.0,32/200
De tabla z(0,95) = 1,645
Li/s = 0,68 ± 1,645.0,33
Li/s = 0,68 ± 0,054
(0,626; 0,734)
b)
n = [z(1 - α/2) ².p.q]/L ²
n = 1,645 ².0,5.0,5/(0,25 ²)
Sin sondeo previo tomar p = q = 0,5
n = 10,82 clientes
c) Para el 82%
Li/s = p ± z(1 - α/2).√p.q/n
α = 0,82
1 - α = 0,18
α/2 = 0,09
1 - α/2 = 0,91
De tabla e interpolando z(1 - α/2) = 1,3425
Li/s = 0,68 ± z(0,91).√0,68.0,32/200
De tabla z(0,91) = 1,645
Li/s = 0,68 ± 1,3425.0,33
Li/s = 0,68 ± 0,0443
(0,6357; 0,7243)
Autor: Ricardo Santiago Netto
Fuente: "Probabilidad y estadísticas para ingeniería y ciencias". Jay L. Devore. 1998.
DISTRIBUCION DE LA MEDIA DE UN MUESTREO
Sea X1, X2, ..., Xn una muestra aleatoria de una distribución con valor medio μ y desviación
estándar σ. Entonces:
1. E(X) = μx = μ
2. V(X) = σx ² = σ ²/n y σx = σ/√n
Además, con T0 = X1 + X2 + ... + Xn (la muestra total), E(T0) = n.μ, V(T0) = n.σ ², y σ.T0 =
√n.σ.
N: número de muestras.
n: número de muestras en el subconjunto extraído del conjunto madre de N muestras.
μx = μx
σx ² = σ ²/n
σx = σ/√n
A medida que aumentan las muestras, la variabilidad disminuye.
Sea X1, X2, ..., Xn una muestra aleatoria de una distribución normal con valor medio μ y
desviación estándar σ. Entonces, para cualquier n, X está normalmente distribuida (con
media μ y desviación estándar σ/√n), como es T0 (con media n.μ desviación estándar √n.σ).
TEOREMA DEL LIMITE CENTRAL
Teorema:
Sea X1, X2, ..., Xn una muestra aleatoria de una distribución con media μ y varianza σ ².
Entonces, si n es suficientemente grande, X tiene aproximadamente una distribución normal
con μx = μ y σx ² = σ ²/n, y T0 tiene también aproximadamente una distribución normal con
μT0 = n.μ, σ ²T0 = n.σ ². Cuanto mas grande sea el valor de n, mejor será la aproximación.
El Teorema del Límite Central garantiza una distribución normal cuando n es
suficientemente grande
Si n > 30, se puede usar el TLC.
Si la distribución madre es normal, la distribución de la media muestral también es normal,
independientemente del tamaño.
x ≈ N(μx; σx) ⇒ x ≈ N(μx; σx)
Ejemplo 1:
Si se sabe que la dureza Rockwell de pernos de cierto tipo tiene un valor medio de 50 y
desviación estándar de 1,5.
a) Si la distribución es normal, ¿cuál es la probabilidad de que la dureza muestral media
para una muestra aleatoria de 9 pernos sea por lo menos 52?
b) ¿Cuál es la probabilidad (aproximada) de que la dureza muestral media para una muestra
aleatoria de 40 pernos sea al menos 52?
x = 50
σ = 1,5
x ≈ N(50; 1,5)
a)
n=9
x = 52
x ≈ N(50; 1,5.√9)
z = (x - μ)/(σ/√n)
La probabilidad de que la media muestral sea superior a 52 es:
P(x ≥ 52) =
⇒ P(z ≥ 4) = 0
Con el valor de z obtenido de tablas:
P(x1 ≤ x ≤ x2) =
⇒ P(z1 ≤ z ≤ z2) = φ(z)
Tener en cuenta que los valores para:
φ(z) = P(z ≤ z1)
b)
n = 40
Con el valor de z obtenido de tablas:
⇒ P(z ≥ 8,4327) = 0
P(x ≥ 52) =
Autor: Ricardo Santiago Netto
Fuente: "Probabilidad y estadísticas para ingeniería y ciencias". Jay L. Devore. 1998.
Inferencia Estadística
¿Qué es una Hipótesis?
Hipótesis: Es un suposición acerca del valor de un parámetro de una población con el
propósito de discutir su validez.
Ejemplo de hipótesis acerca de un parámetro de una población son:
- El sueldo promedio de un profesional asciende a $2,625.
- El veinte por ciento de los consumidores utiliza aceite de oliva
¿Qué es una prueba de hipótesis?
Prueba de hipótesis: es un procedimiento, basado en la evidencia de la muestra y en la
teoría de las probabilidades, usado para determinar si la hipótesis es una afirmación
razonable y debería no ser rechazada o si no es razonable debería ser rechazada
Prueba de Hipótesis
Paso 1: Establecer la hipótesis nula y la
alternativa
↓
Paso 2: Seleccionar el nivel de significación
↓
Paso 3: Identificar el estadístico de prueba
↓
Paso 4: Formular una regla de decisión
↓
Paso 5: Tomar una muestra, llegar a una
decisión
↓
No realizar la hipótesis
↓
Rechazar la nula y aceptar la
alternativa
Definiciones
Hipótesis nula H0: Una afirmación acerca del valor de un parámetro de la población.
Hipótesis Alternativa H1: Una afirmación que es aceptada si la muestra provee la evidencia
de que la hipótesis nula es falsa.
Nivel de significación: La probabilidad de rechazar la hipótesis nula cuando en realidad es
verdadera.
Error tipo I: Rechazar la nula cuando en realida es verdadera
Error tipo II: Aceptar la hipótesis nula cuando en realidad es falsa.
Estadístico de prueba: Es un valor, determinado a partir de la información de la muestra,
usado para decidir si rechazar o no la hipótesis nula.
Valor crítico:El punto que divide la región entre el lugar en el que la hipótesis nula es
rechazada y y la región donde la hipótesis nula es no rechazada.
Hipótesis nula unilateral a derecha
Distribución de muestreo para la estadística z
Una cola - nivel de significación 0.05
Hipótesis nula bilateral
Distribución de muestreo para la estadística z
A dos colas - nivel de significación 0,05
Prueba de hipótesis para la media de una Población, muestras grandes desviación
estándar población conocida
Cuando se plantean hipótesis par la media de la población , a partir de muestras grandes y
la desviación estándar poblacional es conocida, el estadísitco de prueba está dado por:
z = (X - μ)/(σ/√n)
Características de la distribución t-Student
Tiene las siguientes propiedades:
- Es continua, campanular, y simétrica como la distribución z.
- Existe una familia de distribuciones t con media cero, pero con diferentes desviaciones
estándar.
- La distribución t es más aplanada y de colas más larga que la z.
- Tiende a la z para tamaños grandes de muestra.
Caso 1:Prueba de hipótesis para la media de una Población
Supongamos que una máquina empacadora de harina produce bolsas con un contenido de
50 kg. Para controlar el funcionamiento de la máquina se tomó una muestra de 20 bolsas de
harina y el peso medio resultó ser de 42 kg. con un desvío standard de 11 kgs. ¿Está la
máquina trabajando correctamente ? ( α = 0.10)
En este caso, se debe considerar que la máquina está trabajando correctamente si produce
empaques que no excedan demasiado el peso promedio, ni por encima ni por debajo de 50
kgs, así que se trata claramente de una prueba bilateral.
Caso 1: Prueba de hipótesis para la media de una población, tamaño muestral
pequeño y desviación estándar desconocida
La estadística t para el caso de una sola muestra es:
t = (X - μ)/(s/√n)
Resolución
Hipótesis. H0: μ = 50; H1: μ ≠ 50.
Nivel de significación. α = 0.10.
Estadística de prueba.
tn - 1 = (X - μ)/(sn - 1/√n)
Región crítica. Puesto que P(t19 < -1.729 ∪ t19 > +1.729) = 0.10, se rechazará H0 si t < 1.729 ó t > +1.729.
Cálculos. n = 20, = 42, = 5 y
t19 = (42 - 50)/(11/√20) = -8/2,460 = - 3,25
Decisión. Dado que el valor del estadístico de prueba cae netamente en la región
crítica izquierda, H0 es rechazada a favor de H1.
Valor P
• Valor p: probabilidad de observar un valor de prueba más extremo que el valor
observado, dado que la hipótesi nula es verdadera.
• Si el valor p es más chico que el nivel de significación la hipótesis nula es rechazada.
• Si el valor p es más grande que el nivel de significación la hipótesis nula no es
rechazada.
Prueba de hipótesis para dos medias
• Si un número grande de muestras aleatorias e independientes de dos poblaciones
normales es seleccionada, la distribución de la diferencias entre las medias de ambas
también es normal.
•
Caso 2: Prueba de diferencia entre medias con muestras independientes
Un investigador estaba interesado en comparar el efecto de 2 hormonas (A y B) de
crecimiento sobre la longitud total alcanzada por una leguminosa. Para ello se tomó una
muestra de 20 plantas, asignando al azar 10 a cada hormona. Los resultados en cm. fueron
los siguientes:
Hormona A:
Hormona B:
10 10 13 12 10 8 12 11 16 15
15 11 16 17 18 9 14 12 15 16
a) Determinar si hay diferencias significativas entre los crecimientos producidos por ambas
hormonas a un nivel del 5%.
b) Realizar el mismo análisis que en a), pero suponiendo que cada una de las parejas, en el
orden dado, tienen la misma ascendencia genética.
Ver Tutorial 1
Resolución
Prueba t para dos muestras suponiendo varianzas iguales
Caso 3: Muestras relacionadas
En un estudio para predecir a partir del perímetro torácico el peso de novillos de raza
británica sin balanza, se compararon las evaluaciones hechas mediante una cinta métrica
de origen norteamericano con los obtenidos mediante el pesado por método nacional. Las
observaciones para cada animal fueron las siguientes:
a) ¿Qué tipo de análisis sería correcto realizar? ¿Por qué? ¿Por qué cree que el
experimento se diseñó de esa manera? ¿Cómo se debería haber hecho el experimento para
que lo correcto fuera otro análisis?
b) ¿Cuáles son las hipótesis que se postulan? ¿Qué significa cada una de ellas?
c) Utilizando un nivel de significación del 5%, ¿cuál es la región de rechazo para el
estadístico de prueba?
d) ¿A qué conclusión se llega? ¿En qué se basa dicha conclusión?
e) ¿Qué error se puede estar cometiendo al arribar a la conclusión anterior? ¿En qué
consiste dicho error en términos de este problema?
f) Construya un intervalo del 95% de confianza para estimar la diferencia promedio entre los
dos preparados.
g) ¿Era de esperar que el intervalo cubriera o no el valor 0? ¿Por qué?
Ver Tutorial 2
Ver Tutorial 3
Ver Tutorial 4
Prueba t para medias de dos muestras emparejadas
Prueba t para dos muestras suponiendo varianzas iguales
Prueba t para dos muestras suponiendo varianzas desiguales
Ver Tutorial 5
Prueba z para medias de dos muestras
Análisis de variancia - Caso de una sola variable. Varias Muestras
Una compañía de alimentos envasados desea probar 4 nuevos diseños de empaques para
un nuevo cereal para desayunos. Se seleccionaron 10 negocios con igual volumen de
ventas como unidades experimentales. A cada negocio se le consignó al azar un diseño de
empaque. Tres diseños de empaques se asignaron al azar a 3 negocios y el otro diseño
fue asignado a dos negocios. Todas las otras condiciones ajenas al empaque, como precio
, cantidad de estantes y localización de los mismos y esfuerzos especiales de promoción,
se mantuvieron constantes (homogéneos) para todos los negocios del experimento. Las
ventas, según número de casos, fueron registradas para el período de estudio y los
resultados se presentan en la siguiente tabla:
Número de ventas por negocio para cada uno de los 4 diseños
Diseño de empaques
Negocios, repetición
2
1
12
18
3
33
3
11
2
14
12
13
39
3
13
3
19
17
21
57
3
19
4
24
30
24
Total
3
Total Nº de negocios Media
1
78
3
26
207
12
17,25
Análisis de varianza de un factor
Análisis de Datos Categóricos
En el análisis de datos, especialmente del área biológica (Cs. Naturales, Medicina,
Farmacología, etc.) a menudo nos encontramos con mediciones de respuestas que son de
naturaleza categórica. Éstas respuestas reflejan información de categorías más que
mediciones en escala de intervalos o razón.
Extenderemos los principios básicos de la prueba de hipótesis a situaciones que implican
variables categóricas.
Trataremos información que se obtiene del recuento del número de casos que se presentan
al estudiar caracteristicas cualitativas
Para el desarrollo de los contenidos correspondientes a esta presentación se ha
considerado un hilo conductor según se presenta en el mapa conceptual.
La distribución χ² que hemos visto en los capítulos sobre Estimación de Parámetros y de
Pruebas de hipótesis con relación a variancias muestrales, tiene un gran campo de
aplicación en el análisis de variables de naturaleza categórica,
Introducción
Si consideramos la situación más sencilla de esta unidad donde cada observación de una
muestra se clasifica como pertenecientes a un número finito de categorías:
Ejemplo 1
Se observaron 80 nacimientos de un cruzamiento de cerdos de los cuales 42 fueron rojizos,
12 negros y 26 blancos. Las leyes de la herencia implican que estas tres categorías
presentan un modelo genético 9:3:4, es decir que deben tener probabilidades 9/16; 3/16 y
4/16 de aparecer en cada cruzamiento. ¿Son los datos consistentes con el modelo teórico
propuesto?
Ejemplo 2
En la frontera fitosanitaria de la Patagonia se revisaron cargamentos de frutas de distinta
procedencia para evaluar la posibilidad de introducción de mosca de las frutas (Ceratitis
capitata), una plaga importante de los frutales, en áreas no infestadas. La información de
cargamentos con presencia de la plaga se resume en la siguiente tabla:
Presencia de la plaga
Región de procedencia del cargamento
Cuyo
NOA
NEA
22
67
32
5
33
10
Con mosca
Sin mosca
¿Existe alguna dependencia entre la región de procedencia y la presencia de la plaga?
Ejemplo 3
Una medicación nueva para tratar cierta enfermedad de vacunos se comparó con la
medicación de mayor uso. Para esto se tomó al azar un grupo de 300 animales que
padecían la enfermedad; a la mitad de éstos, tomados al azar, se los trató con la nueva
medicación y a los otros 150, con la medicación tradicional. Luego de un tiempo se
analizaron nuevamente los animales con el siguiente resultado:
Estado de los animales luego del tratamiento
Empeoró Sin efecto Mejoró Totales
Tratamiento
Nuevo
Tradicional
16
20
30
42
104
88
150
150
Totales
36
72
192
300
¿Considera que estos medicamentos se comportan de manera similar?
Distribución χ²-cuadrado
Para resolver estos problemas utilizaremos la distribución χ²-cuadrado.
La aplicaremos básicamente:
χ²cuadrado
Bondad de Ajuste
Pruebas con probabilidades de cada categoría
completamente especificada
Bondad de ajuste a una variable discreta
Bondad de ajuste a una variable continua
Tablas de
contingencia
Pruebas de Homogeneidad
Pruebas de Independencia
Propiedades χ²-cuadrado
Antes de dar una descripción más detallada de estas pruebas repasemos algunas
propiedades de esta distribución:
No toma valores negativos
Tiene una distribución diferente para cada número de grados de libertad
Pruebas de Bondad del Ajuste
(Inferencias acerca del Experimento Multinomial)
Se desea contrastar una distribución de frecuencias observada en una muestra con una
distribución de frecuencias teórica
Verificar si responde a un determinado modelo o situación preconcebida.
Es una generalización del experimento binomial.
Para aplicar la prueba se necesita una tabla donde se encuentren registradas las
frecuencias observadas y las frecuencias teóricas o esperadas según el modelo. El
estadístico que se utiliza en estas pruebas es el siguiente:
donde k es el número de categorías y oi y ei son las frecuencia observada y esperada en la
i-ésima categoría, respectivamente.
Características de la multinomial
Consta de n ensayos independientes e idénticos.
El resultado de cada ensayo cae en una de las k categorías posibles (medidas en escala
nominal) de la única variable, donde k>2.
Hay una probabilidad asociada a cada categoria, la cual es constante de un ensayo a otro
Las categorias son exhaustivas y excluyentes, por lo cual la suma de sus probabilidades es
1
Se obtienen frecuencias observadas para cada categoría, siendo su suma igual a n.
El número esperado de intentos que resulten en la categoría i es E(Ni)= n*πi,, donde πi es
la probabilidad de que cualquier observación en particular pertenezca a la categoría i
Prueba de hipotesis para el experimento multinomial
Hipotesis nula
H0: π1, π 2, ... , π k poseen valores especificados (iguales o no)
Hipotesis
alternativa
Ha: alguna probabilidad de las celdas. Difiere de los valores especificados
en H0
Estadistico de
prueba
donde o y e representan las Frecuencias observadas y esperadas para
cada celda
Región de rechazo
Esta determinada por la distribución χ² , con un determinado α y k - 1
grados de libertad
Supuesto
Las frecuencias esperadas no pueden ser en ningún caso inferiores a 5
Prueba de hipotesis para el experimento multinomial
Bajo la hipótesis nula los ni deben estar razonablemente cerca de n*πi
Cuando los valores de πi difieran marcadamente de lo especificado en la hipótesis nula, los
valores observados diferirán de los esperados.
El procedimiento de prueba implica medir las discrepancias entre ni y n*πi, rechazando la
hipótesis nula cuando la discrepancia sea suficientemente grande
Hay solo k -1 valores de celda determinadas libremente y por lo tanto k -1 grados de
libertad.
Dado que grandes discrepancias entre valores observados y esperados conducen a gran
valor de ji-cuadrado el rechazo de H0 es apropiado cuando χ² ≥ χ²α, k -1(unilateral a la
derecha)
Veamos un ejemplo utilizado en genética acerca de los experimentos clásicos conducidos
por Mendel resuelto en la guía teórica.
Mendel tenía arvejas con dos tipos de tegumento, rugoso y liso y, según su hipótesis, en
cruzamientos realizados entre ciertos tipos de plantas, el esperaba que aparecieran en la
descendencia de dichos cruzamientos, arvejas de tegumento liso y rugoso en la proporción
3:1, es decir, 3 semillas de tegumento liso por cada semilla de tegumento rugoso.
Supongamos que en un experimento en el cual se obtiene una descendencia compuesta por
400 semillas, un genetista encuentra 285 semillas de tegumento liso y 125, de tegumento
rugoso. ¿Sería razonable, con α = 0.05, pensar que esa proporción observada no está
demasiado alejada de la proporción 3:1 dictada por la ley de Mendel?
Hipótesis. H0: la proporción es 3:1; H1: la proporción no es 3:1.
Nivel de significación. α = 0.05.
Estadística de la prueba. que se distribuye compuesto que, para esta prueba k = 2 y, por
consiguiente, υ = 2 - 1 = 1.
Regla de decisión. Rechazamos H0 si, y solo si, el valor de χ2 calculado es mayor que
3.84. En caso contrario, se acepta H0.
Cálculos.
Tegumento
Liso
Rugoso
Total
oi
ei
285 400.(3/4) = 300
115 400.(1/4) = 100
400
400
oi - ei (oi - ei)²/ei
15
15
0,75
2,25
-
3,00
• Decisión. Puesto que 3.0 < 3.84 no puede rechazarse H0 con α = 0.05. Los datos de la
muestra no constituyen una prueba suficiente como para dudar de que las proporciones
verdaderas son 3:1.
Aún cuando hemos desarrollado la prueba χ²-cuadrado para situaciones donde k>2, también
se puede utilizar cuando k = 2.
La hipótesis nula en este caso se puede expresar como H0: π1= π10.
Estas hipótesis también se pueden probar utilizando una prueba z de dos colas con
estadísticos de prueba
De manera sorprendente, los dos procedimientos de prueba son completamente
equivalentes. Esto es porque se puede demostrar que Z²= χ² y (zα/2)= χ²1 α de modo que χ² ≥
χ²α, k -1 si y sólo si Z ≥ zα/2.
Tablas de contingencia con dos criterios de clasificación
En una tabla de contingencia la información está representada por conteos o frecuencias
organizadas en i-filas y j-columnas (dos criterios de clasificación). Se presentan dos
situaciones:
Hay i-poblaciones de interés ubicadas cada una en una fila de la tabla y en cada población
se describen j-categorías o atributos. Se toma una muestra de cada población y las
frecuencias se anotan en la celda de la tabla.
Hay una sola población de interés, y cada individuo es clasificado respecto a dos factores
diferentes (i-categorías de un factor j-categorías de otro). Se toma una sola muestra y se
anota el número de individuos en cada categoría de ambos factores.
Características de las tablas de contingencia
Consta de n ensayos independientes e identicos
Hay 2 variables en juego y se representa una tabla de doble entrada
El resultado de cada ensayo cae en una de las celdas, las cuales resultan de las
combinaciones posibles de categorias (medidas en escala nominal) de ambas variables
Hay una probabilidad asociada a cada celda, la cual es constante de un ensayo a otro
La probabilidad asociada a cada celda resulta del producto de sus probabilidades
marginales
La suma de las probabilidades asociadas a cada celda es 1
Se obtienen frecuencias observadas para cada categoria, siendo su suma igual a n
Caso 1: Prueba de homogeneidad
Ocurre cuando una de las 2 variables es controlada por el investigador, de modo que los
totales por fila o por columna estan predeterminados
El analisis es idéntico al de las tablas de contingencia para independencia
La hipotesis nula que se plantea en este caso consiste en sostener que la distribución de
proporciones entre las categorias de la variable no controlada (por fila o por columna) es la
misma para cada categoria de la variable controlada
Otra manera de abordar el mismo problema es preguntarse si las muestras provienen de la
misma población
Prueba de hipótesis para prueba de homogeneidad
Hipótesis. H0: las i-muestras son extraídas de la misma población. H1: son extraídas de
diferentes poblaciones.
H0: π1j= π2j= π3j= ...= πij
H1: H0 no es verdadera
Nivel de significación. α = 0.05.
Estadística de la prueba. que se distribuye aproximadamente como. Aquí υ = (i - 1)·(j - 1)
Regla de decisión. Rechazamos H0 si, y solo si, el valor de χ² calculado es mayor que χ²
α,(i-1)*(j-1). En caso contrario, se acepta H0.
El esperado es estimado en cada celda
Ejemplo para prueba de homogeneidad
Objetivo: establecer si las preferencias acerca del envase de dulce de leche son similares
para hombres y mujeres
Envase
lata
plastico
carton
vidrio
varones 27 (19,5) 30 (29,5) 19 (22,5) 24 (28,5)
mujeres 12 (19,5) 29 (29,5) 26 (22,5) 33 (28,5)
Total
39
59
45
57
Total
100
100
200
h0: las preferencias (%) acerca del envase de dulce de leche no difieren entre hombres y
mujeres
ha: las preferencias (%) acerca del envase de dulce de leche difieren entre hombres y
mujeres
Estadistico χ²*: 8,296 χ² tabla (α = 0,05; gl = 3): 7,81
Valor p: 0,0402
Conclusión: se rechaza h0: las preferencias acerca del envase de dulce de leche difieren
entre hombres y mujeres
Caso 2: Prueba de independencia
Este tipo de prueba se aplica cuando existe interés en determinar si dos atributos
categóricos presentan algún tipo de asociación entre ellos o, por el contrario, son
independientes.
Este tipo de información se suele presentar en tablas de doble entrada.
El estadístico que se utiliza en estas pruebas es el mismo que el empleado en las pruebas
de bondad del ajuste y homogeneidad.
Se estudia la relación entre dos factores diferentes de la misma población
A diferencia de las pruebas de homogeneidad donde en general los totales de filas están
fijos por anticipado, en las pruebas de independencia solo el tamaño muestral es fijo. Por lo
tanto los totales de filas como de columnas son variables aleatorias
Hipotesis nula
H0: πij = πi.* π.j las variables son independientes
Hipotesis
alternativa
Ha: πij ≠ πi.* π.j las variables no son independientes
Estadistico de
prueba
χ² = ∑ (O - E)²/E
donde O y E representan las Frecuencias observadas y esperadas para
cada celda
egión de rechazo
Esta determinada por la distribución χ² , con un determinado α y
(i -1)(j -1) grados de libertad
Ejemplo para prueba de independencia
Una muestra de 500 estudiantes ingresantes en una universidad participó en un estudio
diseñada con el fin de evaluar el grado de conocimiento en matemáticas. La siguiente tabla
muestra los estudiantes clasificados según su formación secundaria (escuelas técnicas,
bachiller y otras) y el nivel de conocimiento en matemáticas (bueno=aprobó el examen;
deficiente = no aprobó el examen):
Bueno Deficiente
Técnicas
Bachiller
Otras
20
15
25
60
150
230
¿Confirman estos datos que la aptitud en matemáticas depende de la orientación de los
estudios secundarios?
H0: La aptitud en matemáticas es independiente de la orientación del secundario
H1: La aptitud en matemáticas es dependiente de la orientación del secundario
Estadistico χ²*: 15,289 χ² tabla (α = 0,05; gl = 2): 5.99
Valor p: 0,00047845
Conclusión: se rechaza h0: La aptitud en matemáticas es independiente de la orientación del
secundario, por lo tanto las variables son dependientes.
Precauciones en la interpretación de resultados
Los grados de libertad dependen de la cantidad de categorías de las variables y no del
número de casos, de modo que el valor de tabla no se modifica al aumentar el número de
casos
Utilizando muestras grandes, se dice poca cosa al decir que una relación es significativa,
ya que es relativamente fácil establecer significación, aún en el caso de que la relación
existente sea muy superficial.
Ejercicios: Probabilidad condicional. Con reposición y sin reposición. Simples o
marginales, conjuntas. Regla de la independencia.
Ver resumen teórico
1) De un paquete de 20 cigarrillos se marcan 5 con una cruz. Se los coloca en una caja y se
escoge uno al azar. ¿Cuál es la probabilidad de que tenga una cruz?
Solución:
n = 20
L: lote
C: cruz
P = {L,C} = {20,5}
P(C) = C/L
P(C) = 5/20
P(C) = 0,25
2) Halle la probabilidad de obtener exactamente una espada en 4 extracciones de una
baraja española de 40 cartas, cuando las extracciones se hacen:
a) con reemplazamiento.
b) sin reemplazamiento.
Solución:
n = 20
E: espada
P(E) = 10/40 = ¼
P(E) = 30/40 = ¾
Las posibilidades son:
1
2
3
4
E
E
E
E
E
E
E
E
E
E
E
E
E
E
E
E
a)
P(Ë) = P(E).P(E).P(E).P(E) + P(E).P(E).P(E).P(E) + P(E).P(E).P(E).P(E) +
P(E).P(E).P(E).P(E)
P(Ë) = 4.P(E).P(E)³
P(Ë) = 4.¼.(¾)³
P(Ë) = 108/256
P(Ë) = 27/64
b)
P(Ë) = (10/40).(30/39).(29/38).(28/37) + (30/40).(29/39).(28/38).(10/37) +
(30/40).(10/39).(29/38).(28/37) + (30/40).(29/39).(10/38).(28/37)
P(Ë) = 4.243600/2193360 = 9744400
P(Ë) = 4060/9139
3) En un pueblo se consumen dos tipos de bebidas alcohólicas: A y G. El 30% de las
personas consume al menos la bebida A, el 60% consume al menos la bebida G y se sabe
que el 5% consume ambas bebidas.
a) ¿Cuál es la probabilidad de que elegida una persona al azar tome bebidas alcohólicas?
b) ¿Qué probabilidad hay de que una persona elegida al azar no consuma bebidas
alcohólicas?
c) ¿Cuál es la probabilidad de que elegida una persona al azar tome la bebida A solamente?
d) Si elegimos dos personas al azar, ¿cuál es la probabilidad de que ambas tomen bebidas
alcohólicas?
e) Se elige una persona al azar y resulta ser consumidora de bebidas alcohólicas, ¿cuál es
la probabilidad de que tome A?
f) Idem anterior pero determinando la probabilidad de que tome la bebida G.
Solución:
A: bebida A.
G: bebida G.
A: no toman bebida A.
G: no toman bebida G.
T: toman bebidas.
T: no toman bebidas.
Armamos la tabla:
A
G
G
A
0,05 0,55 0,60
0,25 0,15 0,40
0,30 0,70
1
a)
P(T) = P(A) + P(G) + P(A ∪ G)
P(T) = 0,25 + 0,55 + 0,05
P(T) = 0,85
b)
P(T) = P(A ∪ G)
P(T) = 0,15
c)
P(A) = 0,25
d)
P(T1/T2) = P(T1).P(T2)
P(T1/T2) = 0,85.0,85
P(T1/T2) = 0,7225
e)
P(T ∩ A) = P(T).P(A/T)
P(A/T) = P(T ∩ A)/P(T)
P(A/T) = 0,30/0,85
P(A/T) = 0,35294
f)
P(T ∩ G) = P(T).P(G/T)
P(G/T) = P(T ∩ G)/P(T)
P(G/T) = 0,60/0,85
P(G/T) = 0,70588
4) Una ciudad X es afectada por 2 tipos de contaminación: aire y agua, mientras que la
ciudad Y sólo presenta contaminación del aire. Se ha puesto en marcha un plan para
controlar estas fuentes de contaminación.
Se estima que la probabilidad de que la contaminación del aire sea controlada exitosamente
en la ciudad X es el cuádruple de dicha probabilidad en la ciudad Y, y que si la
contaminación del aire es controlada en la ciudad Y, la contaminación del aire en la ciudad X
será controlada con un 90% de probabilidad. El control de la contaminación del agua en la
ciudad X es independiente del control de la contaminación del aire en ambas ciudades. En
la ciudad X, la probabilidad de que la contaminación sea controlada totalmente (es decir,
ambas fuentes) es de 0,32. Controlar la contaminación del agua en la ciudad X es sólo la
mitad de probable que hacerlo con la contaminación del aire en esa misma ciudad.
Determinar:
a) La probabilidad de que la contaminación del aire sea controlada en ambas ciudades.
b) La probabilidad de que la contaminación (en sus dos formas, en ambas ciudades) sea
completamente controlada.
c) La probabilidad de que por lo menos una ciudad se encuentre libre de toda fuente de de
contaminación.
Respuesta:
a) 0,18
b) 0,072
c) 0,448
5) Se lanzan 2 dados en perfectas condiciones de azar 15 veces, y en todas se obtiene un
puntaje total de 9. Se lanzan por 16° vez: ¿Cuál es la probabilidad de obtener un puntaje
total de 6?
Respuesta: 5/36
6) Si la probabilidad de hacer blanco, disparando una vez en una polígono de tiro, es de 0,4
para el hombre y de 0,5 para la mujer, hallar la probabilidad de que tras un disparo de cada
uno (independientes entre sí) se obtenga:
a) un blanco exactamente.
b) al menos un blanco.
c) dos aciertos.
d) dos errores.
Respuesta:
a) 0,5
b) 0,7
c) 0,2
d) 0,3
7) Sean tres tiradores A, B y C, con probabilidades de acertar un tiro al blanco de 0,3, 0,4 y
0,6 respectivamente. Si los tres efectúan un solo disparo simultáneamente, calcular:
a) La probabilidad de tener en total un solo acierto.
b) La probabilidad de tener en total un solo acierto, sabiendo que hubo uno.
Respuesta:
a) 0,436
b) 0,524
8) Sean A y B dos sucesos tales que P(A) = 0,375, P(B) = 0,908 y P(A ∪ B) = 0,989. Hallar:
a) P(A/B)
b) P(B/A)
Solución:
P(A ∪ B) = P(A) + P(B) - P(A ∩ B)
P(A ∩ B) = P(A) + P(B) - P(A ∪ B)
P(A ∩ B) = 0,375 + 0,908 - 0,989
P(A ∩ B) = 0,294
a)
P(A ∩ B) = P(B).P(A/B)
P(A/B) = P(A ∩ B)/P(B)
P(A/B) = 0,294/0,908
P(A/B) = 0,32379
b)
P(B/A) = P(A ∩ B)/P(A)
P(B/A) = 0,294/0,375
P(B/A) = 0,784
9) Halle la probabilidad de obtener exactamente 3 caras en 5 tiradas de una moneda.
Solución:
C: cara.
C: seca.
P(C) = 0,5
P(C) = 0,5
Esto también implica obtener dos secas en 5 tiradas, las combinaciones posibles son:
1
2
3
4
5
6
7
8
9
10
0,5
C
C
C
C
C
C
C
C
C
C
0,5
C
C
C
C
C
C
C
C
C
C
0,5
C
C
C
C
C
C
C
C
C
C
0,5
C
C
C
C
C
C
C
C
C
C
0,5
C
C
C
C
C
C
C
C
C
C
P(A) =10. [P(C)]³.[P(C)] ²
P(A) = 10.0,5³.0,5 ²
P(A) = 10.(½)5
P(A) = 10/32
10) El total de la población infantil de un país se distribuye en tres regiones de la siguiente
manera: en la región A se encuentra el 50% de la población, en la región B el 30% y en la
región C el 20%. Se sabe que la probabilidad de encontrar un niño con caries en cada una
de dichas regiones es, respectivamente, 0,4, 0,5 y 0,6.
Si se toma al azar un niño de la población, calcular:
a) la probabilidad de que tenga caries.
b) la probabilidad de que sea de la región B.
c) la probabilidad de que, teniendo caries, provenga de la región B.
Solución:
X: caries.
A = 50%
B = 30%
C = 20%
P(A) = 0,5
P(B) = 0,3
P(C) = 0,2
P(XA) = 0,4
P(XB) = 0,5
P(XC) = 0,6
a)
P(X) = P(A).P(XA) + P(B).P(XB) + P(C).P(XC)
P(X) = 0,5.0,4 + 0,3.0,5 + 0,2.0,6
P(X) = 0,2 + 0,15 + 0,12
P(X) = 0,47
b)
P(B) = 0,3
c)
P(B/X) = P(B ∩ X)/P(X)
P(B/X) = P(B).P(XB)/P(X)
P(B/X) = 0,3.0,5/0,47
P(B/X) = 0,31915
FISICA – DINAMICA
DINAMICA
Estudia el movimiento de los objetos y de su respuesta a las fuerzas. Las descripciones del
movimiento comienzan con una definición cuidadosa de magnitudes como el
desplazamiento, el tiempo, la velocidad, la aceleración, la masa y la fuerza.
Isaac Newton demostró que la velocidad de los objetos que caen aumenta continuamente
durante su caída. Esta aceleración es la misma para objetos pesados o ligeros, siempre que
no se tenga en cuenta la resistencia del aire (rozamiento). Newton mejoró este análisis al
definir la fuerza y la masa, y relacionarlas con la aceleración.
Para los objetos que se desplazan a velocidades próximas a la velocidad de la luz, las leyes
de Newton han sido sustituidas por la teoría de la relatividad de Albert Einstein. Para las
partículas atómicas y subatómicas, las leyes de Newton han sido sustituidas por la teoría
cuántica. Pero para los fenómenos de la vida diaria, las tres leyes del movimiento de
Newton siguen siendo la piedra angular de la dinámica (el estudio de las causas del cambio
en el movimiento).
Las leyes del movimiento de Newton
Con la formulación de las tres leyes del movimiento, Isaac Newton estableció las bases de
la dinámica.
Primera ley de Newton (Equilibrio)
Un cuerpo permanece en reposo o en movimiento rectilíneo uniforme (M.R.U. = velocidad
constante) si la fuerza resultante es nula (ver condición de equilibrio).
El que la fuerza ejercida sobre un objeto sea cero no significa necesariamente que su
velocidad sea cero. Si no está sometido a ninguna fuerza (incluido el rozamiento), un objeto
en movimiento seguirá desplazándose a velocidad constante.
Para que haya equilibrio, las componentes horizontales de las fuerzas que actúan sobre un
objeto deben cancelarse mutuamente, y lo mismo debe ocurrir con las componentes
verticales. Esta condición es necesaria para el equilibrio, pero no es suficiente. Por ejemplo,
si una persona coloca un libro de pie sobre una mesa y lo empuja igual de fuerte con una
mano en un sentido y con la otra en el sentido opuesto, el libro permanecerá en reposo si
las manos están una frente a otra. (El resultado total es que el libro se comprime). Pero si
una mano está cerca de la parte superior del libro y la otra mano cerca de la parte inferior, el
libro caerá sobre la mesa. Para que haya equilibrio también es necesario que la suma de los
momentos en torno a cualquier eje sea cero. Los momentos dextrógiros (a derechas) en
torno a todo eje deben cancelarse con los momentos levógiros (a izquierdas) en torno a ese
eje. Puede demostrarse que si los momentos se cancelan para un eje determinado, se
cancelan para todos los ejes. Para calcular la fuerza total, hay que sumar las fuerzas como
vectores.
a) Condición de equilibrio en el plano: la sumatoria de todas las fuerzas aplicadas y no
aplicadas debe ser nula y, la sumatoria de los momentos de todas las fuerzas con
respecto a cualquier punto debe ser nula.
Σ Fx = 0
Σ Fy = 0
Σ MF = 0
b) Condición de equilibrio en el espacio: la sumatoria de todas las fuerzas aplicadas y no
aplicadas debe ser nula y, la sumatoria de los momentos de todas las fuerzas con
respecto a los tres ejes de referencia debe ser nula.
Σ Fx = 0
Equilibrio de
fuerzas
Σ Fy =
0
Σ Fz = 0
Equilibrio
de
momentos
Σ My = 0
Σ Mx = 0
Σ Mz = 0
Segunda ley de Newton (masa)
Para entender cómo y por qué se aceleran los objetos, hay que definir la fuerza y la masa.
Una fuerza neta ejercida sobre un objeto lo acelerará, es decir, cambiará su velocidad. La
aceleración será proporcional a la magnitud de la fuerza total y tendrá la misma dirección y
sentido que ésta. La constante de proporcionalidad es la masa m del objeto. La masa es la
medida de la cantidad de sustancia de un cuerpo y es universal.
Cuando a un cuerpo de masa m se le aplica una fuerza F se produce una aceleración a.
F = m.a [ N ] [ Kg ]
Unidades: En el Sistema Internacional de unidades (SI), la aceleración a se mide en metros
por segundo cuadrado, la masa m se mide en kilogramos, y la fuerza F en newtons.
Se define por el efecto que produce la aceleración en la fuerza a la cual se aplica. Un
newton se define como la fuerza necesaria para suministrar a una masa de 1 kg una
aceleración de 1 metro por segundo cada segundo.
Un objeto con más masa requerirá una fuerza mayor para una aceleración dada que uno
con menos masa. Lo asombroso es que la masa, que mide la inercia de un objeto (su
resistencia a cambiar la velocidad), también mide la atracción gravitacional que ejerce sobre
otros objetos. Resulta sorprendente, y tiene consecuencias profundas, que la propiedad
inercial y la propiedad gravitacional estén determinadas por una misma cosa. Este
fenómeno supone que es imposible distinguir si un punto determinado está en un campo
gravitatorio o en un sistema de referencia acelerado. Albert Einstein hizo de esto una de las
piedras angulares de su teoría general de la relatividad, que es la teoría de la gravitación
actualmente aceptada.
Se deduce que:
1 kg = 9,81 N
En particular para la fuerza peso:
P = m.g
Tercera ley de Newton (acción y reacción)
Cuando a un cuerpo se le aplica una fuerza (acción o reacción), este devuelve una
fuerza de igual magnitud, igual dirección y de sentido contrario (reacción o acción).
Por ejemplo, en una pista de patinaje sobre hielo, si un adulto empuja suavemente a un
niño,no sólo existe la fuerza que el adulto ejerce sobre el niño, sino que el niño ejerce una
fuerza igual pero de sentido opuesto sobre el adulto. Sin embargo, como la masa del adulto
es mayor, su aceleración será menor.
La tercera ley de Newton también implica la conservación del momento lineal, el producto de
la masa por la velocidad. En un sistema aislado, sobre el que no actúan fuerzas externas, el
momento debe ser constante. En el ejemplo del adulto y el niño en la pista de patinaje, sus
velocidades iniciales son cero, por lo que el momento inicial del sistema es cero. Durante la
interacción operan fuerzas internas entre el adulto y el niño, pero la suma de las fuerzas
externas es cero. Por tanto, el momento del sistema tiene que seguir siendo nulo. Después
de que el adulto empuje al niño, el producto de la masa grande y la velocidad pequeña del
adulto debe ser igual al de la masa pequeña y la velocidad grande del niño. Los momentos
respectivos son iguales en magnitud pero de sentido opuesto, por lo que su suma es cero.
Otra magnitud que se conserva es el momento angular o cinético. El momento angular de
un objeto en rotación depende de su velocidad angular, su masa y su distancia al eje.
Cuando un patinador da vueltas cada vez más rápido sobre el hielo, prácticamente sin
rozamiento, el momento angular se conserva a pesar de que la velocidad aumenta. Al
principio del giro, el patinador tiene los brazos extendidos. Parte de la masa del patinador
tiene por tanto un radio de giro grande. Cuando el patinador baja los brazos, reduciendo su
distancia del eje de rotación, la velocidad angular debe aumentar para mantener constante
el momento angular.
Un libro colocado sobre una mesa es atraído hacia abajo por la atracción gravitacional de la
Tierra y es empujado hacia arriba por la repulsión molecular de la mesa. Como se ve se
cumplen todas las leyes de Newton.
Cuarta ley de Newton (gravitación)
Fg = G.m1.m2 / r ²
La fuerza entre dos partículas de masas m1 y m2 y, que están separadas por una distancia
r, es una atracción que actúa a lo largo de la línea que une las partículas, en donde G es la
constante universal que tiene el mismo valor para todos los pares de partículas.
En 1798 Sir Henry Cavendish realizó la primera medición experimental de la constante G
utilizando para ello una balanza de torsión. El valor aceptado actualmente es:
G = 6,67.10-11 N.m²/kg²
Fuerza elástica:
Una fuerza puede deformar un resorte, como alargarlo o acortarlo. Cuanto mayor sea la
fuerza, mayor será la deformación del resorte (Δx), en muchos resortes, y dentro de un
rango de fuerzas limitado, es proporcional a la fuerza:
Fe = -k. Δx
k: Constante que depende del material y dimensiones del resorte.
Δx: Variación del resorte con respecto a su longitud normal.
Fuerza normal:
Fuerza normal al plano e igual pero de sentido contrario a la componente normal al plano,
de la fuerza peso.
N = cos α.m.g
Fuerza de rozamiento:
Fuerza aplicada y contraria al movimiento y que depende de la calidad de la superficie del
cuerpo y de la superficie sobre la cual se desliza.
Fr = μ.N
μ :Coeficiente de rozamiento.
Fuerza de rozamiento estática: fuerza mínima a vencer para poner en movimiento un
cuerpo.
Fuerza de rozamiento cinética: fuerza retardadora que comienza junto con el movimiento de
un cuerpo.
En el caso de deslizamiento en seco, cuando no existe lubricación, la fuerza de rozamiento
es casi independiente de la velocidad. La fuerza de rozamiento tampoco depende del área
aparente de contacto entre un objeto y la superficie sobre la cual se desliza. El área real de
contacto (la superficie en la que las rugosidades microscópicas del objeto y de la superficie
de deslizamiento se tocan realmente) es relativamente pequeña. Cuando un objeto se
mueve por encima de la superficie de deslizamiento, las minúsculas rugosidades del objeto
y la superficie chocan entre sí, y se necesita fuerza para hacer que se sigan moviendo. El
área real de contacto depende de la fuerza perpendicular entre el objeto y la superficie de
deslizamiento. Frecuentemente, esta fuerza no es sino el peso del objeto que se desliza. Si
se empuja el objeto formando un ángulo con la horizontal, la componente vertical de la
fuerza dirigida hacia abajo se sumará al peso del objeto. La fuerza de rozamiento es
proporcional a la fuerza perpendicular total.
Centro de gravedad
En cuanto al tamaño o peso del objeto en movimiento, no se presentan problemas
matemáticos si el objeto es muy pequeño en relación con las distancias consideradas. Si el
objeto es grande, se emplea un punto llamado centro de masas, cuyo movimiento puede
considerarse característico de todo el objeto. Si el objeto gira, muchas veces conviene
describir su rotación en torno a un eje que pasa por el centro de masas.
El centro de gravedad o baricentro o centro de masas, es un punto donde puede
suponerse encontrada todo el área,peso o masa de un cuerpo y tener ante un sistema
externo de fuerzas un comportamiento equivalente al cuerpo real.
PRESION
Las fórmulas espantan, generalmente porque hay que pensar mucho y porque cuesta
entenderlas. Los invitamos a hacer un pequeño esfuerzo para entender una. Es una tarea
que vale la pena:
La letra P indica presión y se define como la fuerza (F) aplicada sobre una determinada
superficie (S). En realidad no se trata de una ley, es solo una definición.
Si no sabés como leer una fórmula puede aprender fácilmente. Observá que si el valor de la
superficie crece, la presión disminuye. Pero si el valor de la superficie decrece, la presión
aumenta. Los valores de P y S se comportan como niños en los extremos de un sube y baja;
cuando uno sube, el otro baja y viceversa.
Por último la presión se mide, por ejemplo, en Kg/cm ². Vemos en acción esta fórmula en
muchos casos en el mundo cotidiano.
Contacto
Cuando usted empuja algo, la fuerza que está haciendo se distribuye en toda la superficie
de contacto entre su mano y el objeto.
Cuanto más superficie de contacto haya, menor será la presión. Empujar apoyando ambas
manos disminuye la presión sobre las misma y sobre el propio objeto.
Por ejemplo, si cierra el puño y prueba presionar contra una pared, sentirá mayor dolor que
al empujar con la palma. Esto no es solo porque la palma es blanda y el puño expone los
huesos, sino que también se debe a que el puño hace contacto en una menor superficie y
concentra más la fuerza aplicada. Por esta razón los que practican las artes marciales
hacen flexiones con los nudillos en lugar de usar la mano entera. El mismo peso se
distribuye de maneras distintas en ambos casos; más concentrado en el puño, más disperso
en la mano.
Todos los golpes duros de las artes marciales buscan disminuir la superficie de contacto
para concentrar la fuerza; así se pega con el metatarso (pie),nudillos, punta de los dedos,
etc.
Calzado
¿Qué sucede si una dama con tacos altos quiere caminar sobre un terreno fangoso?
Seguramente se hundirá, es que todo su peso se concentra en la pequeña superficie de
apoyo que le brinda ese par de zapatos.
Para evitar hundirse, debe aumentar la superficie de apoyo. Recuerde que aumentando esa
variable disminuye la presión (como en el sube y baja). Por esta razón tanto las raquetas
(zapatos) para nieve como los esquís buscan aumentar la superficie de contacto para
disminuir la presión de apoyo y así no hundirse en la nieve.
Pero a veces se persigue el fin opuesto. Pensando en los tacos altos se puede ver que unos
zapatos así servirían si lo que se busca es justamente hundirse en el terreno. Es el caso de
los botines de fútbol. También es el caso de los zapatos de alpinista, hechos con puntas
filosas en la base que se aferran al resbaloso hielo. Esas puntas reducen al mínimo la
superficie de contacto aumentando al máximo la presión. El resultado es un gran agarre en
el hielo.
Puntas agudas
Cuando tomamos un tenedor, no pensamos que lo que hace que el mismo pinche es
justamente la menor superficie de apoyo de sus puntas. Toda la fuerza se concentra en
esos cuatro puntos. Un clavo concentra toda la fuerza del golpe dado en su cabeza sobre su
punta, al igual que las tachuelas. La cabeza chata de las chinches permite hacer fuerza
sobre ella y concentrarla en un solo punto, el de apoyo. El principio es similar al de los
clavos, pero la amplia superficie de la cabeza permite hacer fuerza con los propio dedos sin
lastimarse. En el caso de los alfileres, como están destinados para atravesar cosas blandas
como tela,a lo sumo papel, la fuerza requerida no es muy grande, y alcanza una pequeña
cabeza para evitar que el alfiler se clave en el dedo que empuja. El filo del cuchillo presenta
el mismo principio de disminución de la superficie para aumentar la presión.
Podemos pensar en muchos otros objetos del estilo, como ser espadas, flechas,
escarbadientes, arpones, el aparato bucal de los mosquitos para picar, las estacas y más.
Analicemos dos casos interesantes
Arados: Los arados, sean arrastrados por animales o máquinas, tienen un gran peso y una
mínima superficie de apoyo en sus cuchillas porque la idea es justamente que se
introduzcan en tierra para removerla.
Patines para hielo: La cuchilla de estos patines parece contradecir el principio que venimos
viendo. ¿No se usan acaso zapatos afilados para agarrarse en el hielo? Es verdad, pero nos
falta considerar dos pequeñas cosas.
La primera es que se trata de un filo, no de una aguja. El filo tiene libertad de moverse
longitudinalmente pero no a los lados (como el caso del cuchillo), así que el agarre del patín
sobre el hielo evitará que se deslice de costado. Y segundo, hay algo que decir sobre el
hielo. Cuando este es presionado, se derrite momentáneamente. Disminuyendo la superficie
de apoyo del patinador en solo dos cuchillas, se aumenta mucho la presión sobre el
hielo,obligando al mismo que se encuentra bajo las cuchillas a derretirse un poco. Esto lo
torna sumamente resbaladizo y le permite deslizarse suavemente. Cuando la cuchilla se
retira del lugar el agua formada rápidamente vuelve a congelarse dado que regresa a su
presión normal.
Transporte
El peso de un automóvil (que es una fuerza) se distribuye en una superficie de apoyo que no
es toda la rueda,sino solo la parte en contacto con el suelo. Las ruedas vienen a ser como
los calzados de los automóviles.
El número elevado de ruedas en un transporte pesado busca disminuir la presión sobre el
pavimento. También se puede reforzar ese efecto aumentando el tamaño de las mismas, lo
que aumenta la superficie de contacto, o haciéndolas más anchas (patonas). En estos casos
entran los ómnibus, camiones y vehículos todo terreno.
Si decimos que las ruedas son los zapatos de los transportes, ¿Qué clase de rueda se
parecería al esquí? El esquí busca aumentar la superficie para disminuir la presión y no
hundirse en la nieve. El equivalente en "ruedas" es la llamada oruga. Se trata de una cinta
sinfín con numerosas y pequeñas ruedas en el interior que distribuyen el peso sobre esa
cinta. Las orugas son tan útiles para transportes en la nieve como en el barro o terrenos
pantanosos; hablamos de los camiones de la Antártida,de tanques de guerra o máquinas
para la construcción.
Las cadenas que se agregan a los vehículos para circular en caminos helados, no mejoran
el asunto de la presión pero sí el del agarre. Equivaldría a hablar de zapatos de alpinista.
¿Existe algún transporte que busque minimizar el apoyo para ejercer una fuerte presión
sobre la base? Parecería ridículo que exista algo así pues se hundiría y no podría avanzar.
Si juntamos dos metales, estos deslizarán entre sí. Pero si entre ambos la presión se hace
muy fuerte, habrá adherencia, y la misma es la base de cualquier transporte, por ejemplo
entre la goma y el asfalto. Una rueda que no se adhiera al camino no serviría como
transporte.
Pero para construir algo así debería haber carreteras cubiertas de metal, los vehículos
tendrían ruedas metálicas y deberían pesar mucho para lograr la adherencia rueda
carretera.
Resolver:
1) Una fuerza de 10 kgf actúa sobre una masa que se desplaza con una velocidad de 20
cm/s y al cabo de 5 s le hace adquirir una velocidad de 8 cm/s, ¿cuál es la masa del
cuerpo?.
Ver solución al final de ésta página
2) Si la tensión en el cable de un ascensor es de 2800 N, el peso del ascensor es de 300 kgf
y transporta a una persona de 80 kgf de peso. Calcular:
a) ¿Qué aceleración tiene?.
b) ¿El ascensor sube o baja?.
Ver solución al final de ésta página
3) Calcular para el sistema de la figura su aceleración y la tensión en la cuerda si m1 = 12
kg, m2 = 8 kg y α = 30°.
Ver solución al final de ésta página
4) Con los datos del problema anterior calcular α para que el sistema tenga una aceleración
de 3 m/s ².
Ver solución al final de ésta página
Desarrollo:
1) Datos:
F = 10 kgf = 10 kgf.(9,80665 m/s ²)/ 1 kgf = 98,0665 N
v1 = 20 cm/s = 20 cm/s.(1 m/100 cm) = 0,2 m/s
v2 = 8 cm/s = 8 cm/s.(1 m/100 cm) = 0,08 m/s
t=5s
De acuerdo a los datos la fuerza le produce a la masa una desaceleración.
F = -98,0665 N
Primero, empleando ecuaciones de cinemática, calculamos la aceleración (negativa)
producida por la fuerza.
v2 - v1 = a.t ⇒ a = (v2 - v1)/t ⇒ a = (0,08 m/s - 0,2 m/s)/5 s ⇒ a = -0,024 m/s ²
Luego:
F = m.a ⇒ m = F/a ⇒ m = -98,0665 N/(-0,024 m/s ²) ⇒ m = 4086,1 kg
2) Datos:
T = 2800 N
PA = 300 kgf = 300 kgf.(9,80665 m/s ²)/ 1 kgf = 2942 N
PP = 80 kgf = 80 kgf.(9,80665 m/s ²)/ 1 kgf = 784,5 N
Se adopta g = 10 m/s ²
a) La condición de equilibrio es:
∑F = 0
Pero como hay movimiento:
∑F = m.a
La masa es:
m = (PA + PP)/g ⇒ m = (2942 N + 784,5 N)/10 m/s ² ⇒ m = 372,65 kg
Las fuerzas sobre el eje (tomando el eje positivo hacia arriba) son:
T - PA - PP = m.a ⇒ a = (T - PA - PP)/m ⇒ a = (2800 N - 2942 N - 784,5 N)/372,65 kg ⇒ a = 2,49 m/s ²
b) Como la aceleración del sistema es negativa el ascensor desciende.
3) Datos:
m1 = 12 kg
m2 = 8 kg
α = 30°
Se adopta g = 10 m/s ²
Los gráficos correspondientes a las masas puntuales son:
Nos interesa particularmente el movimiento a lo largo del eje "x", la condición de equilibrio
es:
∑ Fx = 0
Pero como hay movimiento:
∑ Fx = m.a
La ecuación en el eje "x" es:
P2x - T = m2.a ⇒ T = P2.sen 30° - m2.a (para la masa 2)
T = m1.a (para la masa 1)
Igualando:
m1.a = P2.sen 30° - m2.a ⇒ m1.a + m2.a = P2.sen 30° ⇒ (m1 + m2).a = P2.sen 30° ⇒ a =
P2.sen 30°/(m1 + m2)
a = 8 kg.(10 m/s ²).0,5/(12 kg + 8 kg) ⇒ a = 40 N/20 kg ⇒ a = 2 m/s ²
Luego:
T = m1.a ⇒ T = 12 kg.2 m/s ² ⇒ T = 24 N
4) Datos:
m1 = 12 kg
m2 = 8 kg
a = 3 m/s ²
Se adopta g = 10 m/s ²
Los gráficos son los mismos del ejercicio n° 3.
Para el caso:
∑ Fx = m.a
P2x - T = m2.a ⇒ T = P2.sen α - m2.a (para la masa 2)
T = m1.a (para la masa 1)
Igualando:
m1.a = P2.sen α - m2.a ⇒ m1.a + m2.a = P2.sen α ⇒ (m1 + m2).a/P2 = sen α
sen α = (12 kg + 8 kg).(3 m/s ²)/(8 kg.10 m/s ²) ⇒ sen α = 0,75
α = arcsen 0,75 ⇒ α = 48° 35´ 25"
FISICA – ELECTRODINAMICA
CARGAS ELECTRICAS
Las cargas en los conductores pueden moverse con cierta libertad. La corriente eléctrica
constituye un movimiento continuado de las cargas libres. La cantidad de carga que circula
por un conductor en la unidad de tiempo es la intensidad de corriente. Los responsables de
mantener la corriente en un circuito eléctrico son los generadores eléctricos, los cuales
suministran al circuito la energía precisa para ello. Dos leyes de naturaleza experimental
descubiertas por Georg Simon Ohm y James Prescott Joule respectivamente aportan
algunas relaciones que facilitan el estudio científico de la corriente eléctrica.
La característica esencial de los conductores, sean éstos sólidos, líquidos o gaseosos,
consiste en que disponen de partículas cargadas que pueden moverse con bastante libertad
bajo la acción de campos eléctricos. Cuando un conductor descargado se pone en contacto
con un cuerpo cargado se produce un desplazamiento de la carga del uno a otro por efecto
de las fuerzas eléctricas. Si ambos están aislados,el movimiento de las cargas libres durará
unos instantes entre tanto el sistema de cargas encuentra una configuración de equilibrio en
la cual las fuerzas eléctricas que se ejercen sobre cada una de las cargas se compensan
mutuamente. Esto es lo que sucede cuando un hilo metálico se conecta por uno de sus
extremos a uno solo de los bornes de una pila. Sin embargo, cuando se conecta el otro
extremo del conductor al segundo borne, se produce un movimiento continuado de cargas
en el conductor. Se tiene en tal caso una corriente eléctrica. La parte de la física que se
ocupa del estudio de este tipo de movimiento de las cargas eléctricas a través de un
conductor recibe el nombre de electrocinética.
LA CORRIENTE ELECTRICA
Movimiento de cargas y corriente eléctrica
La presencia de un campo eléctrico permanente en el seno de un conductor es la causa del
movimiento continuado de las cargas libres. En términos de potencial puede decirse que
para que se mantenga una corriente eléctrica es necesario que exista una diferencia de
potencial constante entre los extremos del conductor. Si ésta disminuye por efecto de la
circulación de las cargas, el campo eléctrico llega a hacerse nulo y cesa el movimiento. Esta
es la situación que corresponde a esos desplazamientos de carga que se producen cuando
un conductor aislado se carga o descarga eléctricamente.
Debido a su facilidad de manejo, en electrocinética para describir las propiedades del campo
en el interior de un conductor se recurre a la noción de diferencia de potencial,también
denominada tensión eléctrica porque de ella depende el movimiento de las cargas libres de
un punto a otro. El sentido de la corriente eléctrica depende no sólo del signo de la
diferencia de potencial, sino también del signo de los elementos portadores de carga o
cargas móviles presentes en el conductor.
En un conductor metálico los portadores de carga son los electrones (-), por lo que su
desplazamiento se producirá del extremo del conductor a menor potencial hacia el extremo
a mayor potencias, o en términos de signos desde el polo negativo hacia el positivo. En una
disolución salina los portadores de carga son iones tanto positivos como negativos; cuando
se somete dicha disolución a una diferencia de potencial constante, como la producida entre
los bornes de una pila, se generarán movimientos de carga de sentidos opuestos; las cargas
positivas se desplazarán por la disolución del extremo de mayor potencial al de menor
potencial,o lo que es lo mismo, del polo positivo de la pila al polo negativo, y las negativas
en sentido contrario. Algo semejante sucede en un medio gaseoso ionizado como el que se
produce en el interior de un tubo fluorescente o de neón sometido a una diferencia de
potencial intensa.
Benjamin Franklin fue el primero en asignar un sentido de circulación a la corriente eléctrica
en los conductores metálicos. El supuso que era la electricidad positiva la que, como un
fluido sutil, se desplazaba por el interior del conductor. Según dicha suposición, la corriente
eléctrica circularía del polo positivo al negativo. Más de un siglo después la moderna teoría
atómica revelaba que los electrones son los portadores de carga en los metales, de modo
que el sentido real de la corriente resulta ser justamente el opuesto al avanzado por
Franklin. Por razones históricas y dado que en la electrocinética el sentido de circulación de
la corriente no tiene mayor trascendencia, se sigue aceptando como sentido convencional el
postulado por Franklin. Sin embargo, en otras partes de la física, como la electrónica, la
distinción entre ambos resulta importante.
La intensidad de la corriente eléctrica
Junto a la idea de movimiento de partículas, la noción de corriente eléctrica lleva asociada la
de transporte de carga eléctrica de un punto a otro. La importancia de dicho transporte en
términos de cantidad se expresa mediante la magnitud intensidad de corriente eléctrica que
se define como la carga total que circula por el conductor en la unidad de tiempo. En forma
de ecuación se puede escribir como:
I = q/t
(10.1)
La unidad de intensidad de corriente en el SI recibe el nombre de ampere (A) por el
científico André Marie Ampere y equivale a un transporte de carga que se produzca a razón
de 1 coulomb (C) en cada segundo (s),1 A = 1 C/s. En un metal, en donde la corriente
eléctrica es debida únicamente al movimiento de electrones, sólo el transporte de carga
negativa contribuye al valor de la intensidad. En las disoluciones iónicas, al ser conducida la
corriente tanto por iones positivos como negativos, se produce una doble contribución de
ambos tipos de carga a la intensidad de corriente eléctrica.
Voltímetro y amperímetro
El galvanómetro, cuyo nombre honra a Galvani, aprovecha el efecto magnético de la
corriente eléctrica. Consta, en esencia, de un imán entre cuyos polos se dispone una bobina
que puede girar sobre un eje dispuesto perpendicularmente al plano del imán. Una aguja
solidaria con el bastidor de la bobina hace visible, sobre una escala graduada, el posible
movimiento de aquélla. Este movimiento se halla impedido en ausencia de corriente por dos
muelles recuperadores o resortes en espiral Cuando se hace pasar una corriente por la
bobina, aparece una fuerza magnética entre la bobina y el imán que desvía la aguja de su
posición inicial tanto más cuanto mayor es la intensidad de corriente.
Un amperímetro se utiliza para medir intensidades y consiste, básicamente, en un
galvanómetro con un shunt o resistencia en paralelo con la bobina, de magnitud lo
suficientemente pequeña como para conseguir que prácticamente toda, la corriente se
desvíe por ella y que el aparato de Medida perturbe lo menos posible las condiciones del
circuito. Los amperímetros se conectan en serie con el circuito, es decir, se intercalan entre
los puntos en donde se desea medir la intensidad.
Un voltímetro se utiliza para medir diferencias de potencial entre dos puntos cualesquiera y
viene a ser un galvanómetro con una importante resistencia asociada en serie con él. El
conjunto se conecta en paralelo o derivación entre los puntos cuya diferencia de potencial
se desea medir. Si la resistencia total del voltímetro es mucho mayor que la del circuito,
entre tales puntos la corriente se derivará en su mayor parte por el tramo que ofrece menor
resistencia a su paso y sólo una fracción de ella atravesará el voltímetro. Con ello se logra
que la perturbación que introduce en el circuito el aparato de medida sea despreciable.
Aplicación del concepto de intensidad de corriente
Por una bombilla de 40 W conectada a la red de 220 V circula una corriente de intensidad
aproximadamente igual a 0,2 A. ¿Durante cuánto tiempo ha de estar conectada la bombilla
para que a través de ella haya pasado una carga de 4,5 C? ¿Cuántos electrones habrán
circulado por la bombilla en ese intervalo?. La expresión que define la magnitud intensidad
de corriente viene dada por:
I = q/t ⇒ t = q/i
sustituyendo se tiene:
t = 4,5 C/0,2 A ⇒ t = 22,5 s
Para averiguar el número de electrones que han circulado por la bombilla es preciso saber
18
que 1 coulomb equivale a 6,27x10 veces la carga del electrón. Si en el intervalo de tiempo
considerado han circulado 4,5 C, el número de electrones resulta ser: número de e- =4,5
18 19 C.6,27.10 e /C = 2,8.10 e
GENERADORES ELECTRICOS
El movimiento de los electrones por un conductor metálico como consecuencia de una
diferencia de potencial entre sus extremos puede compararse con el flujo de agua entre
depósitos situados a diferente altura y conectados mediante una tubería. Cuando se llena el
depósito superior el agua desciende, pero dicho movimiento dura sólo en tanto se mantiene
una diferencia entre los niveles de agua en ambos depósitos. Para mantener el agua en
continua circulación es necesario intercalar una bomba que eleve de nuevo el agua desde el
depósito inferior al superior. El papel de la bomba en dicho circuito hidráulico es el de
comunicar a la masa de agua que lo atraviesa la energía suficiente como para salvar la
diferencia de altura entre los dos depósitos, lo que equivale de hecho a mantener constante
la diferencia de niveles del agua entre ambos depósitos aun a pesar del flujo continuo que
los atraviese.
Para mantener una corriente eléctrica en un conductor es preciso que exista una diferencia
de potencial constante entre sus extremos; hace falta, pues, un dispositivo que juegue un
papel análogo al de la bomba en el circuito hidráulico. Dicho dispositivo recibe el nombre de
generador.Una asociación de conductores con un generador constituye un circuito eléctrico
en donde puede tener lugar un movimiento continuado de cargas. El generador mantiene
constante la diferencia de potencial entre dos puntos del circuito, o dicho en otros términos,
genera un campo eléctrico en el conductor que es el responsable de la corriente.
Fuerza electromotriz de un generador
La fuerza electromotriz es la magnitud que caracteriza el comportamiento del generador en
un circuito eléctrico. En el caso de una bomba hidráulica la potencia mecánica representa la
energía que suministra al circuito por unidad de tiempo. En los circuitos eléctricos se define
la fuerza electromotriz de un generador y se representa mediante la letra ε, como la energía
que cede el generador al circuito por cada unidad de carga que lo atraviesa y que se invierte
en incrementar su energía potencial eléctrica. Cada carga al pasar por el generador recibe
una dosis de energía que podrá gastar después en su recorrido a lo largo del circuito. Con
frecuencia, se emplean las iniciales f.e.m. para designar esta magnitud, que siendo una
energía se la denomina impropiamente fuerza. Según su definición la f.e.m. se expresará en
unidades de energía partido por unidades de carga. Este es también el caso de las
magnitudes potencial y diferencia de potencial. Por tal motivo su unidad en el SI es el volt.
Tipos de generadores
El tipo de generadores más conocido es el generador químico, al cual pertenece la pila
eléctrica o pila seca. Transforma energía producida en ciertas reacciones químicas en
energía eléctrica capaz de mantener una diferencia de potencial constante entre sus polos o
bornes. Una pila cinc-carbón, como las que se emplean para alimentar un aparato de radio
portátil, está formada por dos elementos o electrodos de diferentes sustancias. Uno es de
cinc y tiene forma de envoltura cilíndrica, el otro es una barrita de carbón. Entre ambos
existe una pasta intermedia o electrolito que contribuye al proceso de generación de tensión.
La reacción química que se produce en el electrodo de cinc libera electrones, con lo que
éste se convierte en un polo negativo (cátodo); la que se produce en el electrodo de carbón
da lugar a una disminución de electrones, resultando de signo positivo (ánodo). La tensión
producida por una pila es constante y al aplicarla sobre un circuito eléctrico produce una
corriente continua. Este tipo de corriente se caracteriza porque el sentido del movimiento de
los portadores de carga se mantiene constante.
La pila de combustible es otro tipo de generador químico de uso frecuente en el suministro
de energía eléctrica a naves espaciales. Recibe este nombre porque las sustancias que
participan en las correspondientes reacciones químicas son, en parte, introducidas desde el
exterior como si de un combustible se tratara. Una pila de combustible típica es la que se
basa en las reacciones hidrógeno-oxígeno que se producen con pérdida de electrones en un
electrodo y ganancia en el otro, dando lugar a una diferencia de potencial capaz de producir
una corriente eléctrica exterior.
Un termopar es un generador termoeléctrico que transforma calor en electricidad. Se
produce cuando dos hilos conductores unidos entre sí por sus extremos respectivos se
someten a una diferencia de temperatura, sumergiendo una de las soldaduras en hielo
fundente y aplicando a la otra la llama de un mechero. Entre ambos puntos se genera una
diferencia de potencial que aumenta con la temperatura y puede detectarse con un aparato
de medidas eléctricas. Dicho efecto generador de electricidad conocido como efecto
Seebeck se emplea principalmente en la medida de temperaturas.
La célula fotovoltaica es un generador que transforma la energía luminosa en energía
eléctrica. Se basa en la, capacidad de los semiconductores para conducir la electricidad en
un sentido dado, pero no en el opuesto. Al incidir la luz sobre la célula, arranca algunos
electrones de sus átomos, electrones que se acumulan en una región determinada a
expensas de la pérdida de electrones en la región opuesta. Estas dos regiones constituyen
los polos negativo y positivo, respectivamente, de la célula cuya diferencia de potencial se
mantendrá constante en tanto no varíe la intensidad luminosa que alcanza su superficie.
El generador electromagnético se basa en el fenómeno de la inducción electromagnética.
Cuando un conductor cerrado se hace girar en el seno del campo magnético producido por
un imán se genera en su interior una diferencia de potencial capaz de producir una corriente
eléctrica. Es el tipo de generador denominado alternador que se emplea en las grandes
plantas de producción de energía eléctrica. En ellas, diferentes formas de energía, cuya
naturaleza depende del tipo de central, se invierten en mover grandes bobinas de
conductores, haciéndolas girar en el seno de campos magnéticos. De este modo se
producen tensiones eléctricas entre sus bornes cuya polaridad positiva/negativa, se invierte
alternativamente con el tiempo a razón de cincuenta veces en cada segundo. Cuando esta
tensión se aplica a un circuito eléctrico, produce en él una corriente alterna que se
caracteriza por una inversión alternativa, con idéntica frecuencia, del sentido del movimiento
de los portadores de carga.
LA LEY DE OHM
Diferencia de potencial e intensidad de corriente
En un conductor el movimiento de cargas eléctricas es consecuencia de la existencia de una
tensión eléctrica entre sus extremos. Por ello la intensidad de corriente que circula por el
conductor y la tensión o diferencia de potencial deben estar relacionadas. Otros fenómenos
de la física presentan una cierta semejanza con la conducción eléctrica; así el flujo de calor
entre dos puntos depende de la diferencia de temperaturas entre ellos y la velocidad de
caída de un cuerpo por un plano inclinado es función de la diferencia de alturas. Ese tipo de
analogías, y en particular la relativa a la conducción del calor, sirvió de punto de partida al
físico alemán Georg Simon Ohm (1787-1854) para investigar la conducción eléctrica en los
metales. En 1826 llegó a establecer que en los conductores metálicos el cociente entre la
diferencia de potencial entre sus extremos y la intensidad de corriente que lo atraviesa es
una cantidad constante, o en otros términos, que ambas magnitudes son directamente
proporcionales. Esta relación de proporcionalidad directa entre tensión e intensidad recibe el
nombre de ley de Ohm. Representando, como es habitual en electrocinética,la tensión
eléctrica por V y no por Δ V, la ley de Ohm se puede escribir en la forma:
I = G.V
(10.2)
donde G es una constante característica de cada conductor que recibe el nombre de
conductancia.
Curva característica de un conductor y concepto de resistencia
Se denomina curva característica I-V de un conductor a la línea que se obtiene cuando se
representa gráficamente la variación de la intensidad de corriente I que atraviesa un
conductor con la diferencia de potencial o tensión V aplicada entre sus extremos. Su forma
es característica de cada conductor,de ahí su nombre. La determinación experimental de
una curva característica se efectúa mediante un montaje que permita aplicar a los extremos
de un conductor cualquiera una tensión variable y que a la vez haga posible la medida tanto
de la tensión aplicada como de la intensidad de corriente que constituye la respuesta del
conductor. Algunas curvas características I-V son lineales, lo que equivale a decir que en
sus conductores correspondientes ambas magnitudes eléctricas son directamente
proporcionales. Esto es lo que viene a establecer la ley de Ohm para los conductores
metálicos.
En la curva característica I-V de un conductor metálico la pendiente de la gráfica coincide
con la constante de G que, de acuerdo con su definición, constituye una medida de la
aptitud para la conducción eléctrica del cuerpo considerado. Cuanto mayor sea G, mayor
será la inclinación de la característica I-V y, por tanto, mayor la intensidad que circulará por
el conductor para una misma diferencia de potencial. La inversa de la conductancia G se
denomina resistencia eléctrica y se representa por la letra R:
R = 1/G
Desde un punto de vista físico, la resistencia R de un conductor constituye una medida de la
oposición que presenta éste al paso de la corriente eléctrica. En los metales los electrones
han de moverse a través de los átomos de la estructura cristalina del propio metal. Tales
obstáculos al movimiento libre de las cargas contribuyen, en su conjunto, al valor de la
resistencia R. La expresión (10.2) puede escribirse, haciendo intervenir a la resistencia, en
la forma:
V = I.R
(10.3)
que constituye la expresión más conocida de la ley de Ohm. A partir de la ecuación anterior
se define el ohm (Ω) como unidad de resistencia eléctrica en la forma:
1 ohm (Ω) = 1 volt (V)/1 ampere (A)
El hecho experimentalmente observado de que no todos los conductores posean
características I-V rectilíneas indica que no todos cumplen la ley de Ohm. Es ésta, por tanto,
una ley de carácter restringido que sólo puede aplicarse a cierto tipo de conductores
llamados óhmicos. En los no óhmicos la resistencia no tiene un valor constante, sino que
éste depende de la tensión que se aplique entre los extremos del conductor.
Resistividad y conductividad
Experimentos con hilos metálicos de diferentes longitudes y grosores llevaron a Ohm a
establecer el concepto de resistencia al observar que la intensidad I de corriente era
inversamente proporcional a la longitud l del conductor y directamente proporcional a su
sección S o grosor. Cuando este descubrimiento se combina con la relación de
proporcionalidad inversa entre R e I resulta la relación:
R = ρ .l/s
(10.4)
donde ρ es una constante característica del tipo de metal que constituye el hilo conductor
considerado. Dicha constante se denomina resistividad y equivale a una resistencia
específica referida a una longitud y sección unidad. Se expresa en ohm x metro (Ω.m). La
inversa de la resistividad recibe el nombre de conductividad y se representa por la letra σ (σ
= 1/ ρ) . Se expresa en Ω-1.m-1 y caracteriza el comportamiento de un material como
7
-1
-1
conductor eléctrico. En los metales, σ toma valores del orden de 10 Ω .m y en los
-14
aisladores típicos como el vidrio o la parafina alcanza 10 en el primer material y 107 Ω-1.m1
en el segundo. Los materiales semiconductores presentan valores de σ intermedios.
El significado energético de la ley de Ohm
Dado que la diferencia de potencial V constituye una energía por unidad de carga, la ley de
Ohm puede ser interpretada en términos de energía. Las colisiones de los electrones en los
metales con los nudos de la red cristalina llevan consigo una disipación de energía eléctrica.
Dicho fenómeno es el responsable de la pérdida o caída de potencial V que se detecta, en
mayor o menor medida, entre los extremos de un conductor, e indica que cada unidad de
carga pierde energía al pasar de uno a otro punto a razón de V julios por cada coulomb de
carga que lo atraviese.
Si se aplica el principio general de conservación de la energía a los fenómenos eléctricos, la
ley de Ohm, definida por la expresión (10.3), puede ser considerada como una ecuación de
conservación en donde el primer miembro representa la energía perdida en el circuito por
cada unidad de carga en movimiento y el segundo la energía cedida al exterior por cada
coulomb que circula entre los puntos considerados.
Comprobación experimental de la ley de ohm
Cuando entre los extremos de un conductor se establece una diferencia de potencial V,
aparece en él una corriente eléctrica de intensidad i que lo atraviesa. Dado que I es
consecuencia de V, debe existir una relación entre sus valores respectivos. Para
conductores metálicos dicha relación es lineal o de proporcionalidad directa y constituye la
ley de Ohm. La comprobación experimental de la ley de Ohm pueda efectuarse con la ayuda
de los siguientes medios: una fuente de f.e.m. cuya tensión de salida pueda graduarse a
voluntad, una resistencia metálica que hará las veces de conductor, problema cuyo
comportamiento se desea estudiar, un voltímetro,un amperímetro y cables de conexión.
Con la ayuda de un montaje determinado se modifica la tensión de salida de la fuente
actuando sobre el mando circular o potenciómetro. Para cada posición del potenciómetro se
efectúan sendas lecturas en el voltímetro y el amperímetro. Se ordenan las parejas de
valores I/V correspondientes en una tabla y a continuación se representan en una gráfica.
Dentro del error experimental,los puntos de la gráfica se ajustarán a una recta que pasa por
el origen, indicando así una relación de proporcionalidad directa entre intensidad y tensión.
La obtención de tal relación lineal constituirá una comprobación de la ley de Ohm.
LA SUPERCONDUCTIVIDAD
La superconductividad es una propiedad que presentan algunos materiales sometidos a
ciertas condiciones especiales, de conducir la electricidad sin oponer ninguna resistencia y,
por tanto, sin disipar energía por efecto Joule. Aun cuando el fenómeno de la
superconductividad fue descubierto por Onnes en 1911, hasta hace sólo unos años
resultaba necesario, para conseguir tal propiedad, someter a ciertos metales a temperaturas
próximas al cero absoluto (- 273 °C). Investigaciones recientes han conseguido sintetizar
materiales de tipo cerámica capaces de convertirse en superconductores a temperaturas
mucho más altas. La desenfrenada carrera científica que se ha desatado en este campo
permite albergar la esperanza de conseguir, a corto plazo, materiales superconductores a
temperaturas muy próximas a la ambiente.
La importancia de este logro científico puede resultar decisiva en un buen número de
aplicaciones técnicas. Cabe destacar la posibilidad de fabricar electroimanes a base de
superconductores con un costa reducido, lo cual abarataría la construcción de algunos
sofisticados aparatos de diagnóstico médico que emplean potentes imanes, facilitaría la
producción de la energía del futuro y permitiría construir medios de transporte terrestre
ultrarrápidos y económicos basados en la sustentación o levitación magnética. Un tren
experimental alemán de estas características ha conseguido una velocidad de 406 km/h.
Este tipo de trenes, al desplazarse sin entrar en contacto con el suelo, evitan los efectos
indeseables del rozamiento y equivalen a aviones que se muevan en vuelo rasante.
POTENCIA
Potencia y energía de un generador
La energía eléctrica We que suministra un generador al circuito eléctrico depende de la
cantidad de carga que lo atraviese. Dado que la fuerza electromotriz de un generador
representa la energía que suministra al circuito por cada unidad de carga que lo atraviesa,
se podrá escribir:
Energía total suministrada = Energía x carga / carga
es decir:
We = q. ε
Pero de acuerdo con la definición de intensidad eléctrica,la carga eléctrica q se puede
escribir como el producto de la intensidad por el tiempo (10.1); luego la energía eléctrica
suministrada por el generador al circuito en un tiempo t vendrá dada por la expresión:
We = ε .i.t
(10.5)
La potencia P de un generador representa la energía eléctrica que cede al circuito por
unidad de tiempo:
P = We/t
(10.6)
Combinando las anteriores ecuaciones resulta para P la expresión:
P = ε .i
(10.7)
Al igual que la potencia mecánica, la potencia eléctrica se expresa en watts (W).
Efectos caloríficos de la corriente eléctrica. Ley de Joule
El calentamiento de los conductores por el paso de la corriente eléctrica fue uno de los
primeros efectos observados por los científicos estudiosos de los fenómenos eléctricos,sin
embargo, habría de pasar algún tiempo antes de que se conociera la magnitud de tal efecto
calorífico y los factores de los que depende. James Prescott Joule (1818-1889) se interesó
desde joven en la medida de temperaturas de motores eléctricos,lo que le permitió hacia
1840 encontrar la ley que rige la producción de calor por el paso de una corriente eléctrica a
través de un conductor. La ley de Joule establece que la cantidad de calor producida es
directamente proporcional a la resistencia R del conductor, al cuadrado de la intensidad de
corriente I que lo atraviesa y al tiempo t. Es decir:
Q = I ².R.t
(10.8)
El efecto calorífico, también llamado efecto Joule, puede ser explicado a partir del
mecanismo de conducción de los electrones en un metal. La energía disipada en los
choques internos aumenta la agitación térmica del material, lo que da lugar a un aumento de
la temperatura y a la consiguiente producción de calor. La ley de Joule, por su parte, puede
ser enfocada como una consecuencia de la interpretación energética de la ley de Ohm. Si
I.R representa la energía disipada por cada unidad de carga, la energía total que se disipa
en el conductor en forma de calor, cuando haya sido atravesado por una carga q, será:
Q = q.I.R
Pero dado que q = I.t, se tiene finalmente:
Q = I ².R.t
que es precisamente la ley de Joule. La potencia calorífica representa el calor producido en
un conductor en la unidad de tiempo. Su expresión se deduce a partir de la ley de Joule en
la forma:
P = Q/t = i ².R.t/t = i ².R
(10.9)
Puesto que el calor es una forma de energía, se expresa en joules (J) y la potencia calorífica
en watts (W). Cuando se combinan las ecuaciones (10.9) y (10.3) resulta otra expresión
para la potencia eléctrica consumida en un conductor:
P = I.R.I = I.V
(10.10)
Fuerza electromotriz y diferencia de potencial
La noción de fuerza electromotriz de un generador como energía que comunica el circuito
por cada unidad de carga que lo atraviesa, está referida a un generador ideal o puro. En tal
caso toda la energía que produce el generador la cede íntegramente al circuito, por lo cual
la fuerza electromotriz ε coincide exactamente con la diferencia de potencial V constante
que mantiene entre sus bornes:
ε=V
(10.11)
En realidad, una pila, una batería o un alternador son en sí mismos elementos conductores
que forman parte del circuito por donde pasa la corriente y en mayor o menor medida
oponen, como tales, una cierta resistencia al movimiento de las cargas. Ello significa que el
generador, al formar parte del circuito, se calienta y disipa, por tanto, una cierta cantidad de
calor. La idea de balance de energía a la que equivale la interpretación de la ley de Ohm en
términos energéticos puede entonces extenderse al caso de un generador con el propósito
de encontrar la relación entre ε y V en esta nueva situación. Aplicando la conservación de la
energía por unidad de carga a los extremos del generador, se tiene:
Energía disponible por unidad de carga = Energía producida por el generador por unidad de
carga - Energía disipada por efecto Joule por unidad de carga
que en forma de símbolos resulta ser:
V = ε - i.r
(10.12)
Esta ecuación se conoce como ley de Ohm generalizada a un generador y permite
determinar la diferencia de potencial que es capaz de mantener entre sus bornes un
generador real, esto es, con resistencia interna r no despreciable.
Aplicación de la ley de joule
La ley de Joule permite calcular la energía disipada en forma de calor en un conductor. Su
expresión matemática es Q = I ².R.t, siendo R la resistencia en ohms, I la intensidad de
corriente en amperios y t el tiempo en segundos. Para elevar la temperatura del agua en 1
°C se necesitan 4,2 J por cada gramo. Se trata de determinar, aplicando la ley de Joule,el
valor de la resistencia eléctrica que debe tener un calentador eléctrico para que, conectado
a un enchufe de 220 V,sea capaz de elevar la temperatura de un litro de agua de 15 °C a 80
°C en cinco minutos. La energía calorífica necesaria para elevar la temperatura del agua de
15 °C a 80 °C será:
Q = 1 kg.(80 °C - 15 °c).4,2 J/kg °C = 2,73.105.J
pues un litro de agua corresponde a un kilogramo de masa y 4,2 representa el calor en
joules por gramo y grado centígrado (calor específico). Dado que se dispone del valor de la
tensión, pero no de la Intensidad, será necesario transformar la ley de Joule de modo que
en la fórmula correspondiente aparezca aquélla y no ésta. Recurriendo a la ley de Ohm V =
i.R se tiene:
Q = (V/R) ².R.t = V ².t/R
Despejando R y sustituyendo los valores conocidos resulta:
5
R = V ².t/Q = (220 V) ².300 s/2,73.10 J = 53,2.Ω
Aplicación del concepto de potencia eléctrica
En una bombilla ordinaria puede leerse la inscripción 60 W-220 V. Con estos datos se trata
de determinar: a) la intensidad de corriente que pasa por la bombilla cuando está conectada
a la red. b) El valor en Ω de su resistencia eléctrica. c) La energía eléctrica expresada en
joules y en kW-h que consume al cabo de dos horas de estar encendida.
La potencia eléctrica P consumida en una resistencia puede expresarse bien en la forma P
= I.V siendo I la intensidad de corriente , V la caída de potencial entre sus extremos, bien en
la forma P = I ². R que combina la anterior ecuación con la ley de Ohm V = I.R.
a) El valor de la intensidad se obtiene a partir de la primera ecuación sustituyendo los datos
que aparecen grabados en la bombilla:
P = i.V
i = P/V = 60 W/220 V ≅ 0,27 A
b) El valor de la resistencia puede calcularse, bien utilizando la segunda expresión de la
potencia, bien a partir de la ley de Ohm:
V = i.R
R = V/i = V ²/P = (220 V) ²/60 W ≅ 807Ω
c) El valor de la energía eléctrica consumida en joules resulta de aplicar la noción de
potencia como energía por unidad de tiempo:
P = We/t ⇒ We = P.t
Dado que cada hora consta de 3 600 segundos, resulta:
5
We = 60.2.3600 = 4,32.10 .J
-
Recordando que 1 W = 10 ³ kW, el resultado en kW-h vendrá dado por:
We = 60.10-³.kW.2.h = 0,12.kW.h
Circuitos de corriente continua
Un circuito eléctrico está formado por la asociación de una serie de elementos conductores
que hacen posible el mantenimiento por su interior de una corriente eléctrica. Si los
generadores producen una diferencia de potencial constante entre sus bornes o polos, la
corriente producida será continua. Tal es el caso de las pilas y de las baterías.
En los circuitos de corriente continua pueden distinguirse básicamente dos tipos de
elementos, los generadores y los receptores. Los primeros aportan al circuito la energía
necesaria para mantener la corriente eléctrica, los segundos consumen energía eléctrica y,
o bien la disipan en forma de calor,como es el caso de las resistencias, o bien la convierten
en otra forma de energía, como sucede en los motores.
Una pila en un circuito eléctrico se representa mediante el símbolo:
que refleja la polaridad del generador. Una resistencia se representa por el
símbolo:
Para simplificar el estudio, se supone que las magnitudes o parámetros característicos de
estos elementos se concentran en los puntos del circuito donde se representan. Así,la
resistencia de los cables de conexión o se desprecia o se supone concentrada en un punto
como si se tratara de un elemento de circuito más. El estudio cuantitativo de los circuitos
eléctricos de corriente continua se efectúa como una aplicación de dos principios básicos:
El principio de conservación de la energía referido a la unidad de carga eléctrica, según el
cual en todo el circuito, o en cualquier tramo de él, la energía que pierde la corriente
eléctrica es igual a la energía cedida por el circuito al exterior. Es, en esencia, la ley de Ohm
generalizada e interpretada como balance de energías.
El principio de no acumulación de cargas, que indica que las cargas no pueden acumularse.
Eso significa que si no hay bifurcaciones, la intensidad de corriente es la misma en todo el
circuito, y si las hay, la intensidad de corriente que entra en un nudo o punto de bifurcación
ha de ser igual a la suma de las que salen de él.
Tales principios se conocen también como leyes de Kirchhoff.
Asociación de resistencias
Existen dos modos fundamentales de conectar o asociar las resistencias entre sí, en serie y
en paralelo o derivación. En la asociación en serie las resistencias se conectan una tras otra
de modo que por todas ellas pasa la misma intensidad de corriente. En la asociación en
paralelo la conexión se efectúa uniendo los dos extremos de cada una de ellas a un mismo
par de puntos. En este caso la diferencia de potencial entre los extremos de cualquiera de
las resistencias asociadas es la misma, pero, de acuerdo con el principio de no acumulación
de cargas, la intensidad total que llega al nudo o punto de bifurcación se reparte entre ellas.
Se denomina resistencia equivalente de una asociación de resistencias a aquella resistencia
única por la que podría sustituirse la asociación sin alterar la intensidad que circula por el
circuito. En el caso de una asociación en serie de tres resistencias, la fórmula de la
resistencia equivalente Re se obtiene como sigue. De acuerdo con la ley de Ohm aplicada a
cada una de ellas, se tiene:
V1 = I.R1 ; V2 = I.R2 ; V3 = I.R3
donde V1, V2 y V3 son las tensiones entre sus extremos respectivos e I la intensidad de
corriente que las atraviesa, igual para todas ellas. De acuerdo con el principio de
conservación de energía referido a la unidad de carga, la cantidad total de energía que
pierde la unidad de carga al atravesar las tres resistencias será igual a la suma de las
cantidades que pierde en cada resistencia, es decir:
V = V1 + V2 + V3 = IR1 + IR2 + IR3 = I.(R1 + R2 + R3)
Si la ley de Ohm se aplica a la asociación en su conjunto, se tiene: V = I.Re
Comparando ambas ecuaciones resulta:
e
= R1 + R2 + R3
(10.13)
Ecuación que puede generalizarse a cualquier número de resistencias.
Si la asociación fuera en paralelo, al llegar al nudo la corriente se reparte entre las diferentes
resistencias y, de acuerdo con el principio de no acumulación de cargas, se cumplirá, en
este caso, la relación
I = I1 + I2 + I3
con V1 = V2 = V3 = V
Aplicando la ley de Ohm a cada resistencia, resulta ahora:
V = I1.R1 ; V = I2.R2 ; V = I3.R3
Para la asociación en su conjunto se tendrá:
V = I.Re
Si se sustituyen los valores de I,I1, I2 e I3 en la ecuación de las intensidades se obtiene:
V/Re = V/R1 + V/R2 + V/R3
es decir:
1/Re = 1/R1 + 1/R2 + 1/R3
(10.14)
En este caso es la suma de los inversos la que da lugar,no a la resistencia equivalente, sino
a su inverso. Por tal motivo en este tipo de asociación el valor de la Re,resulta ser inferior al
de la más pequeña de las resistencias asociadas.
Análisis de circuitos
En el estudio del comportamiento de cualquiera de las partes o de los elementos de un
circuito, se precisa conocer cuál es la intensidad de corriente que circula por él. La
determinación de la intensidad o intensidades de corriente que circulan por todos y cada uno
de los elementos de un circuito dado recibe el nombre de análisis de circuito.
En el caso de circuitos simples con un solo generador, o con 1arios asociados en serie, es
posible llevar a término el análisis de circuitos aplicando de forma general los principios
anteriormente considerados, así como las fórmulas de asociación de resistencias. Sin
embargo, cuando existen 1arios generadores distribuidos por diferentes bifurcaciones o
ramas el problema del análisis se complica y es preciso recurrir a procedimientos más
potentes y también más laboriosos.
Ejemplo del análisis de un circuito eléctrico: Con cuatro bombillas de 2, 3, 4 y 6 Ω de
resistencia eléctrica y una pila de 4,5 1 se monta un circuito como el de la figura. Se trata
de: a) Analizar el circuito. b) Determinar la diferencia de potencial entre los puntos A y B. c)
Calcular la energía que cede la pila al circuito en un minuto.
a) Analizar un circuito eléctrico significa determinar la intensidad, o intensidades, de
corriente que circulan por él. En circuitos con un solo generador (o con 1arios asociados en
serie) el procedimiento consta de las siguientes etapas:
1. Determinar la resistencia equivalente de todo el circuito. Ello equivale a convertirlo en otro
equivalente simplificado del tipo representado en la figura adjunta. En el presente caso se
trata de una asociación mixta serie-paralelo:
Re (serie) = R3 + R4 = 2 Ω + 4 Ω = 6 Ω
Re (paralelo) = R1.R2/(R1 + R2) = 6 Ω.3 Ω/(6 Ω + 3 Ω) = 2 Ω
pues
1/Re = 1/R1 + 1/R2
Re (total) = Re (serie) + Re(paralelo) = 6 Ω + 2 Ω
2. Aplicar la ley de Ohm al circuito equivalente simplificado:
ε = i.Re (total) ⇒ i = ε /Re(total)
i = 4,5 V/8 Ω ≅ 0,6 A
3. Si, como en el caso presente, el circuito presenta derivaciones, calcular las intensidades
que circulan por cada una de las ramas. De acuerdo con el principio de no acumulación de
las cargas:
I = I1 + I2 es decir I1 + I2 = 0,6 A
Dado que en toda asociación en paralelo los puntos de confluencia o nodos son los mismos,
la tensión entre ellos es la misma y, por tanto, aplicando la ley de Ohm, resulta:
1 = R1.I1 = R2.I2 es decir 3 Ω.I1 = 6 Ω.I2
Resolviendo el sistema de ecuaciones:
I1 + I2 = 0,6 A
3Ω.I1 = 6Ω.I2
resulta:
I1 = 0,4 A e I2 = 0,2 A
b) Una 1ez el circuito ha sido analizado es posible responder a cualquier otra pregunta
sobre el mismo. La diferencia de potencial entre A y B se calcula efectuando un balance de
energía por unidad de carga. Cuando una carga unidad procedente de B pasa por la pila
recibe ε joules de energía y al pasar por la resistencia R3 pierde I.R3, luego el balance total
será:
VB - VA = ε - l.R3
es decir: V BA = 4,5 V - 2 Ω.0,6 A = 3,3 V
c) La energía que cede el generador al circuito en un tiempo t viene dada, de acuerdo con el
concepto de potencia, por el producto de la potencia del generador por el tiempo:
Ee = P.t = ε .I.t = 4,5 V.0,6 A.60 s = 162 J
ELECTRODINAMICA
Resolver:
1) Se requiere una fuerza de 0,01 N para sostener una carga de 12 μ C,calcule la intensidad
del campo eléctrico.
Resolución:
-2
datos: F = 0,01 N = 10 N
-5
q = 12 μ C = 1,2.10 C
-2
-5
E = F/q ⇒E = 10 N/1,2.10 C ⇒E = 833,33 N/C
2) ¿Cuánto trabajo se requiere para transportar una carga de 12 C de un punto a otro
cuando la diferencia de potencial entre ellos es de 500 V?.
Resolución:
datos: q = 12 C
V = 500 V
V = L/q ⇒L = V.q ⇒L = 500 V.12 C ⇒L = 6000 J
3) Se requiere un trabajo de 600 J para transportar una carga de 60 C desde una terminal a
otra de una batería. ¿Cuál es la diferencia de potencial entre los terminales?.
Resolución:
datos: q = 60 C
L = 600 J
V = L/q ⇒V = 600 J/60 C ⇒V = 10 V
4) En una batería la diferencia de potencial entre bornes es de 6,3 V. ¿Cuánto trabajo se
requiere para transportar 12 C entre terminales?.
Resolución:
datos: q = 12 C
V = 6,3 V
V = L/q ⇒L = V.q ⇒L = 6,3 V.12 C ⇒L = 75,6 J
5)
a) ¿Cuál es la intensidad del campo eléctrico en un punto colocado a la mitad entre una
carga positiva de 100 μ C y una negativa de 50 μ C separadas 20 cm?.
b) ¿Y si ambas fueran negativas de 50 μ C?.
Resolución:
-4
datos: q1 = 100 μ C = 10 C
-5
q2 = -50 μ C = -5.10 C
r = 20 cm = 2.10-1 m
-1
-1
rm = r/2 ⇒rm = 2.10 m/2 ⇒ rm = 10 m
a) F1 = k0.q1.q/rm ² y F2 = k0.q2.q/rm ²
E = F/q ⇒E = (F1 + F2)/q ⇒E = (k0.q1.q/rm ² + k0.q2.q/rm ²)/q⇒E = q.k0.(q1 + q2)/q.rm ² ⇒E =
k0.(q1 + q2)/rm ²
9
-4
-5
-1
9
-5
-2
E = 9.10 (Nm ²/C ²).(10 C - 5.10 C)/(10 m) ² ⇒E = 9.10 (Nm ²/C ²).5.10 C/10 m ² ⇒E
= 4,5.107 N/C
-5
b) si q1 = q2 = -5.10 C
E = k0.(q1 + q2)/rm ² ⇒E = k0.2.q1/rm ² ⇒E = 9.109 (Nm ²/C ²).2.(- 5.10-5 C)/(10-1 m) ²
9
-4
-2
7
E = -9.10 (Nm ²/C ²).10 C/10 m ² ⇒E = -9.10 N/C
6) Tres capacitores de 2, 3 y 6 μ F se conectan en serie a una fuente de 10 V.
a) Encuentre el número de μ C de carga de cada uno.
b) Calcule la caída de tensión en cada capacitor.
Resolución:
datos: C1 = 2 μ F
C2 = 3 μ F
C3 = 6 μ F
V = 10 V
a) C = q/V ⇒q = C.V
q1 = C1.V ⇒q1 = 2 μ F.10 V ⇒ q1 = 20 μ C
q2 = C2.V ⇒q2 = 3 μ F.10 V ⇒ q2 = 30 μ C
q3 = C3.V ⇒q3 = 6 μ F.10 V ⇒q3 = 60 μ C
b) 1/C = 1/C1 + 1/ C2 + 1/C3 ⇒1/C = 1/2 μ F + 1/3 μ F + 1/6 μ F ⇒1/C = (3 μ F + 2 μ F + 1 μ
F)/6 μ F ²
1/C = 6 μ F/6 μ F ² ⇒1/C =1/ μ F ⇒ C = 1 μ F
q = C.V ⇒q = 1 μ F.10 V ⇒ q = 10 μ C
V = q/C
V1 = q/C1 ⇒V1 = 10 μ C/2 μ F ⇒ V1 = 5 V
V2 = q/C2 ⇒V2 = 10 μ C/3 μ F ⇒ V2 = 3,33 V
V3 = q/C3 ⇒V3 = 10 μ C/6 μ F ⇒ V3 = 1,66 V
7) Encuentre la capacitancia, expresada en μ F de un capacitor que tiene 240 μ C con una
batería de 120 V.
Resolución:
datos: q = 240 μ C
V = 120 V
C = q/V ⇒C = 240 μ C/120 V ⇒ C = 2 μ F
8) Encuentre la capacitancia, expresada en Faradios, de un capacitor que fue construido
pegando una hoja de papel de estaño en ambos lados de una de papel de parafina de área
625 cm ² y de espesor s = 0,0025 cm.
Resolución:
-2
datos: A = 625 cm ² = 6,25.10 m ²
-5
s = 0,0025 cm = 2,5.10 m
C = Κ.ε0.A/s ⇒C = 2,1.8,85415.10-12 (C ²/Nm ²). 6,25.10-2 m ²/2,5.10-5 m ⇒C = 4,65.10-8 C
²/Nm
C = 4,65.10-8 F
9) Un capacitor de placas paralelas separadas una distancia s = 0,02 m está sometido a una
tensión de 200 V.
a) Encuentre la intensidad del campo eléctrico entre placas, expresada en V/cm y en N/C.
b) Encuentre la aceleración de un protón (H+) en ese campo, sabiendo que mH+ =3,32.10-27
kg y qH+ = 1,06.10-13 C.
Resolución:
datos: s = 0,02 m
V = 200 V
+
-27
mH = 3,32.10 kg
qH+ = 1,06.10-13 C
a) E = -V/s ⇒E = 200 V/0,02 m ⇒E = 10000 V/m
E = 10000 (V/m).1 m/100 cm ⇒E = 100 V/cm
E = 10000 V/m ⇒E = 10000 (N.m/C)/m ⇒E = 10000 N/C
b) E = F/q ⇒F = q.E y F = m.a
q.E = m.a ⇒a = q.E/m ⇒a = 1,06.10
-13
C.10000 (N/C)/3,32.10-27 kg ⇒ a = 3,193.1017 m/s ²
Resolver:
1) Por un conductor pasa una corriente de 120 C en 3 minutos. ¿Cuál es la intensidad de la
corriente en A y mA?.
Respuesta: 0,66 A y 660 mA
2) Por un conductor circula una corriente eléctrica de 10 A durante 10 minutos. ¿Cuál es la
carga eléctrica correspondiente?.
Respuesta: 6000 C
3) En el caso del problema anterior, ¿cuantas ues(q) y cuantos electrones circularon por el
conductor?.
Respuesta: 18.1012 ues(q) y 36.1022 electrones
4) ¿Cuál es la caída de tensión que se produce en un conductor cuando circula por él una
corriente de 25 A y su resistencia es de 12 Ω?.
Respuesta: 300 V
5) Una corriente de 20 A circula por un conductor de 50 m de longitud y 0,1 mm ² de
sección, ¿cuál es la tensión si el conductor es de aluminio?.
Respuesta: 256 V
6) Calcular la intensidad de una corriente sabiendo que la carga eléctrica es de 3000 C y el
tiempo que dura el pasaje es de 5 minutos.
Respuesta: 10 A
7) Por un conductor circulan durante ¼ de hora 54.1022 electrones,calcular la intensidad de
esa corriente.
Respuesta: 10 A
8) Por un conductor circula una corriente eléctrica de 10 A durante 10 minutos. ¿Cuál es la
carga eléctrica correspondiente?.
Respuesta: 6000 C
9) En el caso del problema anterior ¿cuántas ues(q) y cuántos electrones circularon por el
conductor?.
Respuesta: 18.1012 ues(q) y 36.1022 e
10) Por un conductor de 8 Ωde resistencia circula una corriente de 6 A, ¿cuál es la tensión
de esa corriente?.
Respuesta: 480 V
11) La intensidad de una corriente es de 25 A, si la tensión es de 220 V, ¿cuál es la
resistencia del conductor?.
Respuesta: 8,8 Ω
12) ¿Cuál es la diferencia de potencial que debe aplicarse a un conductor de 110 Ωde
resistencia para que la intensidad sea de 4 A?.
Respuesta: 440 V
13) ¿Cuál es la caída de tensión que se produce en un conductor cuando circula por él una
corriente de 25 A y su resistencia es de 12 Ω?.
Respuesta: 300 V
14) ¿Qué cantidad de electricidad en Coulomb habrá pasado por un conductor en ½ hora, si
la intensidad de la corriente es de 15 A?.
Respuesta: 27000 C
15) En el caso del problema anterior ¿cuántas ues(q) y cuántos electrones circularon por el
conductor?.
Respuesta: 81.1012 ues(q) y 164.1022
FISICA – HIDRODINAMICA
DINAMICA DE FLUIDOS O HIDRODINAMICA
Esta rama de la mecánica de fluidos se ocupa de las leyes de los fluidos en movimiento;
estas leyes son enormemente complejas, y aunque la hidrodinámica tiene una importancia
práctica mayor que la hidrostática,sólo podemos tratar aquí algunos conceptos básicos.
Euler fue el primero en reconocer que las leyes dinámicas para los fluidos sólo pueden
expresarse de forma relativamente sencilla si se supone que el fluido es incompresible e
ideal, es decir, si se pueden despreciar los efectos del rozamiento y la viscosidad. Sin
embargo, como esto nunca es así en el caso de los fluidos reales en movimiento, los
resultados de dicho análisis sólo pueden servir como estimación para flujos en los que los
efectos de la viscosidad son pequeños.
a) Flujos incompresibles y sin rozamiento
Estos flujos cumplen el llamado teorema de Bernoulli, que afirma que la energía mecánica
total de un flujo incompresible y no viscoso (sin rozamiento) es constante a lo largo de una
línea de corriente. Las líneas de corriente son líneas de flujo imaginarias que siempre son
paralelas a la dirección del flujo en cada punto, y en el caso de flujo uniforme coinciden con
la trayectoria de las partículas individuales de fluido. El teorema de Bernoulli implica una
relación entre los efectos de la presión, la velocidad y la gravedad, e indica que la velocidad
aumenta cuando la presión disminuye. Este principio es importante para predecir la fuerza
de sustentación de un ala en vuelo.
Ecuación de continuidad: (para flujo estacionario e incompresible, sin fuentes ni sumideros,
por evaluarse a lo largo de una línea de corriente).
1) Ley de conservación de la masa en la dinámica de los fluidos:
A1.v1 = A2.v2 = constante.
Recordar que p = F/A ⇒F = p.A
Flujo de volúmen: (caudal).
Φ = A .v [m ³/s]
Ecuación de Bernoulli: (principio de conservación de la energía) para flujo ideal (sin
fricción).
p1 + δ.v1 ²/2 + δ.g.h1 = p2 + δ.v2 ²/2 + δ.g.h2 = constante
p1/δ + v1 ²/2 + g.h1 = p2/δ + v2 ²/2 + g.h2
p/ δ = energía de presión por unidad de masa.
g.h = energía potencial por unidad de masa.
v ²/2 = energía cinética por unidad de masa.
Ecuación de Bernoulli para flujo en reposo: v1 = v2 = 0
p1 + δ.g.h1 = p2 + δ.g.h2
b) Flujos viscosos: movimiento laminar y turbulento
Los primeros experimentos cuidadosamente documentados del rozamiento en flujos de baja
velocidad a través de tuberías fueron realizados independientemente por Poiseuille y por
Gotthilf Heinrich Ludwig Hagen. El primer intento de incluir los efectos de la viscosidad en
las ecuaciones matemáticas se debió a Navier e, independientemente, a Sir George Gabriel
Stokes, quien perfeccionó las ecuaciones básicas para los fluidos viscosos incompresibles.
Actualmente se las conoce como ecuaciones de Navier-Stokes, y son tan complejas que
sólo se pueden aplicar a flujos sencillos. Uno de ellos es el de un fluido real que circula a
través de una tubería recta.
El teorema de Bernoulli no se puede aplicar aquí,porque parte de la energía mecánica total
se disipa como consecuencia del rozamiento viscoso, lo que provoca una caída de presión a
lo largo de la tubería. Las ecuaciones sugieren que, dados una tubería y un fluido
determinados, esta caída de presión debería ser proporcional a la velocidad de flujo. Los
experimentos demostraron que esto sólo era cierto para velocidades bajas; para
velocidades mayores, la caída de presión era más bien proporcional al cuadrado de la
velocidad.
Este problema se resolvió cuando Reynolds demostró la existencia de dos tipos de flujo
viscoso en tuberías. A velocidades bajas, las partículas del fluido siguen las líneas de
corriente (flujo laminar), y los resultados experimentales coinciden con las predicciones
analíticas. A velocidades más elevadas, surgen fluctuaciones en la velocidad del flujo, o
remolinos (flujo turbulento), en una forma que ni siquiera en la actualidad se puede predecir
completamente.
Reynolds también determinó que la transición del flujo laminar al turbulento era función de
un único parámetro, que desde entonces se conoce como número de Reynolds. Si el
número de Reynolds (que carece de dimensiones y es el producto de la velocidad, la
densidad del fluido y el diámetro de la tubería dividido entre la viscosidad del fluido) es
menor de 2.000, el flujo a través de la tubería es siempre laminar; cuando los valores son
mayores a 3000 el flujo es turbulento. El concepto de número de Reynolds es esencial para
gran parte de la moderna mecánica de fluidos.
Los flujos turbulentos no se pueden evaluar exclusivamente a partir de las predicciones
calculadas, y su análisis depende de una combinación de datos experimentales y modelos
matemáticos; gran parte de la investigación moderna en mecánica de fluidos está dedicada
a una mejor formulación de la turbulencia. Puede observarse la transición del flujo laminar al
turbulento y la complejidad del flujo turbulento cuando el humo de un cigarrillo asciende en
aire muy tranquilo. Al principio, sube con un movimiento laminar a lo largo de líneas de
corriente, pero al cabo de cierta distancia se hace inestable y se forma un sistema de
remolinos entrelazados.
Ecuación de Bernoulli para flujo real (con fricción)
p1/δ + v1 ²/2 + g.h1 = p2/δ + v2 ²/2 + g.h2 + H0
H0 = perdida de energía por rozamiento desde 1 hasta 2.
c) Flujos de la capa límite
Los flujos pueden separarse en dos regiones principales. La región próxima a la superficie
está formada por una delgada capa límite donde se concentran los efectos viscosos y en la
que puede simplificarse mucho el modelo matemático. Fuera de esta capa límite, se pueden
despreciar los efectos de la viscosidad, y pueden emplearse las ecuaciones matemáticas
más sencillas para flujos no viscosos.
La teoría de la capa límite ha hecho posible gran parte del desarrollo de las alas de los
aviones modernos y del diseño de turbinas de gas y compresores.
d) Flujos compresibles
El interés por los flujos compresibles comenzó con el desarrollo de turbinas de vapor por el
británico Parsons y el sueco Laval. En esos mecanismos se descubrió por primera vez el
flujo rápido de vapor a través de tubos, y la necesidad de un diseño eficiente de turbinas
llevó a una mejora del análisis de los flujos compresibles. El interés por los flujos de alta
velocidad sobre superficies surgió de forma temprana en los estudios de balística,donde se
necesitaba comprender el movimiento de los proyectiles.
Uno de los principios básicos del flujo compresible es que la densidad de un gas cambia
cuando el gas se ve sometido a grandes cambios de velocidad y presión. Al mismo tiempo,
su temperatura también cambia, lo que lleva a problemas de análisis más complejos. El
comportamiento de flujo de un gas compresible depende de si la velocidad de flujo es mayor
o menor que la velocidad del sonido.
El sonido es la propagación de una pequeña perturbación, u onda de presión, dentro de un
fluido. Para un gas, la velocidad del sonido es proporcional a la raíz cuadrada de su
temperatura absoluta. La velocidad del sonido en el aire a 20 °C (293 Kelvin en la escala
absoluta), es de unos 344 metros por segundo. Si la velocidad de flujo es menor que la
velocidad del sonido (flujo subsónico),las ondas de presión pueden transmitirse a través de
todo el fluido y así adaptar el flujo que se dirige hacia un objeto. Por tanto, el flujo subsónico
que se dirige hacia el ala de un avión se ajustará con cierta distancia de antelación para fluir
suavemente sobre la superficie. En el flujo supersónico, las ondas de presión no pueden
viajar corriente arriba para adaptar el flujo. Por ello, el aire que se dirige hacia el ala de un
avión en vuelo supersónico no está preparado para la perturbación que va a causar el ala y
tiene que cambiar de dirección repentinamente en la proximidad del ala, lo que conlleva una
compresión intensa u onda de choque. El ruido asociado con el paso de esta onda de
choque sobre los observadores situados en tierra constituye el estampido sónico de los
aviones supersónicos. Frecuentemente se identifican los flujos supersónicos por su número
de Mach, que es el cociente entre la velocidad de flujo y la velocidad del sonido. Por tanto,
los flujos supersónicos tienen un número de Mach superior a 1.
Viscosidad
Propiedad de un fluido que tiende a oponerse a su flujo cuando se le aplica una fuerza. Los
fluidos de alta viscosidad presentan una cierta resistencia a fluir; los fluidos de baja
viscosidad fluyen con facilidad. La fuerza con la que una capa de fluido en movimiento
arrastra consigo a las capas adyacentes de fluido determina su viscosidad, que se mide con
un recipiente (viscosímetro) que tiene un orificio de tamaño conocido en el fondo. La
velocidad con la que el fluido sale por el orificio es una medida de su viscosidad.
La viscosidad de un fluido disminuye con la reducción de densidad que tiene lugar al
aumentar la temperatura. En un fluido menos denso hay menos moléculas por unidad de
volumen que puedan transferir impulso desde la capa en movimiento hasta la capa
estacionaria. Esto, a su vez, afecta a la velocidad de las distintas capas. El momento se
transfiere con más dificultad entre las capas, y la viscosidad disminuye. En algunos líquidos,
el aumento de la velocidad molecular compensa la reducción de la densidad. Los aceites de
silicona, por ejemplo, cambian muy poco su tendencia a fluir cuando cambia la temperatura,
por lo que son muy útiles como lubricantes cuando una máquina está sometida a grandes
cambios de temperatura.
TENSION SUPERFICIAL
El efecto de las fuerzas intermoleculares es de tirar las moléculas hacia el interior de la
superficie de un liquido, manteniéndolas unidas y formando una superficie lisa. La tensión
superficial mide las fuerzas internas que hay que vencer para poder expandir el área
superficial de un liquido. La energía necesaria para crear una mueva área superficial,
trasladando las moléculas de la masa liquida a la superficie de la misma, es lo que se llama
tensión superficial. A mayor tensión superficial, mayor es la energía necesaria para
transformar las moléculas interiores del liquido a moléculas superficiales. El agua tiene una
alta tensión superficial, por los puentes de hidrogeno.
1.- Para hacer el primer experimento necesitas una aguja de coser bien seca, un Tenedor y
un Vaso lleno con agua de la canilla hasta un centímetro de su borde superior. Coloca la
Aguja sobre los dientes del Tenedor y, con estos en posición horizontal, sumergirlos con
cuidado y lentamente en el Vaso con agua. Cuando la Aguja toque el agua retira con
cuidado tenedor del vaso sin tocar la aguja. La Aguja flotará aún después de retirado el
Tenedor. Si observas de cerca la superficie del agua verás como esta parece hundirse por
el peso de la Aguja.
2.- Para realizar el segundo experimento necesitas un Vaso, un Plato hondo, Agua y
algunas Monedas. Apoya el Vaso en el Plato hondo. Seca con un repasador los bordes del
mismo. Llena el Vaso con Agua hasta el ras sin que se derrame en el Plato ni una gota.
Luego, con cuidado y por el borde del Vaso, introducir en el Vaso las monedas de a una
hasta que el Agua del Vaso desborde. Observarás, que antes de que desborde el Agua,
esta puede llenar el Vaso algunos milímetros más debido al fenómeno de la Tensión
Superficial.
3.- Para realizar el tercer Experimento necesitas una Brocha de Pintor y un Recipiente con
Agua. Si observas primero la Brocha cuando las cerdas están secas apreciarás que las
mismas aparecen más bien separadas.
Al sumergir la Brocha en el Recipiente con Agua observarás que las cerdas tienden a
juntarse debido a la Tensión Superficial.
BALANCES MACROSCOPICOS
BALANCE DE MASA
∂/∂t ∫v ρ.dv = ρ2.<v2>.A2 - ρ1.<v1>.A1
BALANCE DE CANTIDAD DE MOVIMIENTO
∂/∂t ∫v ρ.v.dv = -Δ.(ρ.<v ²>.A + p.A) + F + p
Estado estacionario:
F = Δ(ρ .<v ²>.A + p.A)
Si
Perfiles planos turbulentos:
∂/∂t ∫v ρ.v.dv = -Δ.(<v>.G + p.A) + F + p
BALANCE DE ENERGIA TOTAL
Estado estacionario:
Perfiles planos turbulentos:
<v³>/<v> = <v ²> = <v> ²
BALANCE DE ENERGIA MECANICA
Wf: pérdidas por fricción.
Estado estacionario:
W/G.g: Energía/masa
Expresado en metros:
Altura desarrollada: Δ(< v ² >/2.g) = Hb
Altura geométrica: Δz = Hg
Altura de presión: Δ(p/ ρ .g) = Hp
Potencia de la bomba: Pb = HT.Q. ρ .g/ η
FISICA – INERCIA
Resolver:
1) ¿Cuál será la aceleración de la gravedad en un lugar donde el péndulo cumple una
oscilación en 1,2 s, si su longitud es de 0,357 m?.
Respuesta: 9,8024 m/s ².
2) En un mismo lugar, dos péndulos oscilan empleando 2 y 4 s, respectivamente, ¿cuántas
veces es más largo el segundo que el primero?.
Respuesta: 4 veces.
3) Un reloj de péndulo que está en La Plata es llevado hasta Tierra del Fuego, si la
aceleración de la gravedad en La Plata es de 9,79 m/s ² y en Tierra del Fuego es de 9,82
m/s ², ¿atrasa o adelanta?, ¿cuánto?.
Respuesta: atrasa 0,081 s.
4) Calcular la aceleración de la gravedad en un lugar donde un péndulo de 2 m posee un
período de
2,84 s.
Respuesta: 9,77 m/s ².
Responder:
1) ¿Qué entiende por volante?.
2) En las rotaciones, ¿se cumple el principio de inercia?, ¿cómo lo enuncia?.
3) ¿Qué es la cupla de arranque y frenado?.
4) ¿Qué es período, frecuencia y amplitud en el movimiento pendular?.
5) ¿Cuáles son las leyes del péndulo?, exprese su enunciado.
6) ¿Qué es péndulo de torsión?.
7) ¿Cuál es el tiempo de oscilación del péndulo?
FISICA - ELECTROMAGNETISMO
OPTICA
Rama de la física que se ocupa de la propagación y el comportamiento de la luz. En un
sentido amplio, la luz es la zona del espectro de radiación electromagnética que se extiende
desde los rayos X hasta las microondas, e incluye la energía radiante que produce la
sensación de visión. El estudio de la óptica se divide en dos ramas, la óptica geométrica y la
óptica física.
Naturaleza de la luz
La energía radiante tiene una naturaleza dual, y obedece a leyes que pueden explicarse a
partir de una corriente de partículas o paquetes de energía, los llamados fotones, o a partir
de un tren de ondas transversales (Movimiento ondulatorio). El concepto de fotón se emplea
para explicar las interacciones de la luz con la materia que producen un cambio en la forma
de energía, como ocurre con el efecto fotoeléctrico o la luminiscencia. El concepto de onda
suele emplearse para explicar la propagación de la luz y algunos de los fenómenos de
formación de imágenes. En las ondas de luz, como en todas las ondas electromagnéticas,
existen campos eléctricos y magnéticos en cada punto del espacio, que fluctúan con
rapidez. Como estos campos tienen, además de una magnitud,una dirección determinada,
son cantidades vectoriales. Los campos eléctrico y magnético son perpendiculares entre sí y
también perpendiculares a la dirección de propagación de la onda. La onda luminosa más
sencilla es una onda senoidal pura, llamada así porque una gráfica de la intensidad del
campo eléctrico o magnético trazada en cualquier momento a lo largo de la dirección de
propagación sería la gráfica de un seno.
La luz visible es sólo una pequeña parte del espectro electromagnético. En el espectro
visible, las diferencias en longitud de onda se manifiestan como diferencias de color. El
rango visible va desde, aproximadamente, 350 nanómetros (violeta) hasta unos 750
nanómetros (rojo), un nanómetro, nm, es una milmillonésima de metro. La luz blanca es una
mezcla de todas las longitudes de onda visibles.
La velocidad de la luz en las sustancias materiales es menor que en el vacío, y varía para
las distintas longitudes de onda; este efecto se denomina dispersión. La relación entre la
velocidad de la luz en el vacío y la velocidad de una longitud de onda determinada en una
sustancia se conoce como índice de refracción de la sustancia para dicha longitud de onda.
El índice de refracción del aire es 1,00029 y apenas varía con la longitud de onda. En la
mayoría de las aplicaciones resulta suficientemente preciso considerar que es igual a 1.
Las leyes de reflexión y refracción de la luz suelen deducirse empleando la teoría
ondulatoria de la luz introducida. El principio de Huygens afirma que todo punto en un frente
de ondas inicial puede considerarse como una fuente de ondas esféricas secundarias que
se extienden en todas las direcciones con la misma velocidad, frecuencia y longitud de onda
que el frente de ondas del que proceden. Con ello puede definirse un nuevo frente de onda
que envuelve las ondas secundarias. Como la luz avanza en ángulo recto a este frente de
ondas, el principio de Huygens puede emplearse para deducir los cambios de dirección de
la luz.
Cuando las ondas secundarias llegan a otro medio u objeto, cada punto del límite entre los
medios se convierte en una fuente de dos conjuntos de ondas. El conjunto reflejado vuelve
al primer medio, y el conjunto refractado entra en el segundo medio. El comportamiento de
los rayos reflejados y refractados puede explicarse por el principio de Huygens. Es más
sencillo, y a veces suficiente, representar la propagación de la luz mediante rayos en vez de
ondas. El rayo es la línea de avance, o dirección de propagación, de la energía radiante. En
la óptica geométrica se prescinde de la teoría ondulatoria de la luz y se supone que la luz no
se difracta. La trayectoria de los rayos a través de un sistema óptico se determina aplicando
las leyes de reflexión y refracción.
Optica física
Esta rama de la óptica se ocupa de aspectos del comportamiento de la luz tales como su
emisión, composición o absorción, así como de la polarización, la interferencia y la
difracción.
Polarización de la luz
Los átomos de una fuente de luz ordinaria emiten pulsos de radiación de duración muy
corta. Cada pulso procedente de un único átomo es un tren de ondas prácticamente
monocromático (con una única longitud de onda). El vector eléctrico correspondiente a esa
onda no gira en torno a la dirección de propagación de la onda, sino que mantiene el mismo
ángulo, o acimut, respecto a dicha dirección. El ángulo inicial puede tener cualquier valor.
Cuando hay un número elevado de átomos emitiendo luz, los ángulos están distribuidos de
forma aleatoria, las propiedades del haz de luz son las mismas en todas direcciones, y se
dice que la luz no está polarizada. Si los vectores eléctricos de todas las ondas tienen el
mismo ángulo acimutal (lo que significa que todas las ondas transversales están en el
mismo plano), se dice que la luz está polarizada en un plano, o polarizada linealmente.
Cualquier onda electromagnética puede considerarse como la suma de dos conjuntos de
ondas: uno en el que el vector eléctrico vibra formando ángulo recto con el plano de
incidencia y otro en el que vibra de forma paralela a dicho plano. Entre las vibraciones de
ambas componentes puede existir una diferencia de fase, que puede permanecer constante
o variar de forma constante. Cuando la luz está linealmente polarizada, por ejemplo, esta
diferencia de fase se hace 0 o 180°. Si la relación de fase es aleatoria, pero una de las
componentes es más intensa que la otra, la luz está en parte polarizada. Cuando la luz es
dispersada por partículas de polvo, por ejemplo, la luz que se dispersa en un ángulo de 90°
con la trayectoria original del haz está polarizada en un plano, lo que explica por qué la luz
procedente del cenit está marcadamente polarizada.
Para ángulos de incidencia distintos de 0 o 90°, la proporción de luz reflejada en el límite
entre dos medios no es igual para ambas componentes de la luz. La componente que vibra
de forma paralela al plano de incidencia resulta menos reflejada. Cuando la luz incide sobre
un medio no absorbente con el denominado ángulo de Brewster, la parte reflejada de la
componente que vibra de forma paralela al plano de incidencia se hace nula. Con ese
ángulo de incidencia, el rayo reflejado es perpendicular al rayo refractado; la tangente de
dicho ángulo de incidencia es igual al cociente entre los índices de refracción del segundo
medio y el primero.
Algunas sustancias son anisotrópicas, es decir, muestran propiedades distintas según la
dirección del eje a lo largo del cual se midan. En esos materiales, la velocidad de la luz
depende de la dirección en que ésta se propaga a través de ellos. Algunos cristales son
birrefringentes, es decir, presentan doble refracción. A no ser que la luz se propague de
forma paralela a uno de los ejes de simetría del cristal (un eje óptico del cristal), la luz se
separa en dos partes que avanzan con velocidades diferentes. Un cristal uniáxico tiene uno
de estos ejes. La componente cuyo vector eléctrico vibra en un plano que contiene el eje
óptico es el llamado rayo ordinario; su velocidad es la misma en todas las direcciones del
cristal, y cumple la ley de refracción de Snell. La componente que vibra formando un ángulo
recto con el plano que contiene el eje óptico constituye el rayo extraordinario, y la velocidad
de este rayo depende de su dirección en el cristal. Si el rayo ordinario se propaga a mayor
velocidad que el rayo extraordinario, la birrefringencia es positiva; en caso contrario la
birrefringencia es negativa.
Cuando un cristal es biáxico, la velocidad depende de la dirección de propagación para
todas las componentes. Se pueden cortar y tallar los materiales birrefringentes para
introducir diferencias de fase específicas entre dos grupos de ondas polarizadas, para
separarlos o para analizar el estado de polarización de cualquier luz incidente. Un
polarizador sólo transmite una componente de la vibración, ya sea reflejando la otra
mediante combinaciones de prismas adecuadamente tallados o absorbiéndola. El fenómeno
por el que un material absorbe preferentemente una componente de la vibración se
denomina dicroísmo. El material conocido como Polaroid presenta dicroísmo; está formado
por numerosos cristales dicroicos de pequeño tamaño incrustados en plástico, con todos
sus ejes orientados de forma paralela. Si la luz incidente es no polarizada, el Polaroid
absorbe aproximadamente la mitad de la luz. Los reflejos de grandes superficies planas,
como un lago o una carretera mojada, están compuestos por luz parcialmente polarizada, y
un Polaroid con la orientación adecuada puede absorberlos en más de la mitad. Este es el
principio de las gafas o anteojos de sol Polaroid.
Los llamados analizadores pueden ser físicamente idénticos a los polarizadores. Si se
cruzan un polarizador y un analizador situados consecutivamente, de forma que el
analizador esté orientado para permitir la transmisión de las vibraciones situadas en un
plano perpendicular a las que transmite el polarizador, se bloqueará toda la luz procedente
del polarizador.
Las sustancias ópticamente activas giran el plano de polarización de la luz linealmente
polarizada. Un cristal de azúcar o una solución de azúcar, pueden ser ópticamente activos.
Si se coloca una solución de azúcar entre un polarizador y un analizador cruzados tal como
se ha descrito antes, parte de la luz puede atravesar el sistema. El ángulo que debe girarse
el analizador para que no pase nada de luz permite conocer la concentración de la solución.
El polarímetro se basa en este principio.
Algunas sustancias (como el vidrio y el plástico) que no presentan doble refracción en
condiciones normales pueden hacerlo al ser sometidas a una tensión. Si estos materiales
bajo tensión se sitúan entre un polarizador y un analizador, las zonas coloreadas claras y
oscuras que aparecen proporcionan información sobre las tensiones. La tecnología de la
fotoelasticidad se basa en la doble refracción producida por tensiones.
También puede introducirse birrefrigencia en materiales normalmente homogéneos
mediante campos magnéticos y eléctricos. Cuando se somete un líquido a un campo
magnético fuerte, puede presentar doble refracción. Este fenómeno se conoce como efecto
Kerr. Si se coloca un material apropiado entre un polarizador y un analizador cruzados,
puede transmitirse o no la luz según si el campo eléctrico en el material está conectado o
desconectado. Este sistema puede actuar como un conmutador o modulador de luz
extremadamente rápido.
Interferencia y difracción
Cuando dos haces de luz se cruzan pueden interferir, lo que afecta a la distribución de
intensidades resultante. La coherencia de dos haces expresa hasta qué punto están en fase
sus ondas. Si la relación de fase cambia de forma rápida y aleatoria, los haces son
incoherentes. Si dos trenes de ondas son coherentes y el máximo de una onda coincide con
el máximo de otra, ambas ondas se combinan produciendo en ese punto una intensidad
mayor que si los dos haces no fueran coherentes. Si son coherentes y el máximo de una
onda coincide con el mínimo de la otra, ambas ondas se anularán entre sí parcial o
totalmente, con lo que la intensidad disminuirá. Cuando las ondas son coherentes, puede
formarse un diagrama de interferencia formado por franjas oscuras y claras. Para producir
un diagrama de interferencia constante,ambos trenes de onda deben estar polarizados en el
mismo plano. Los átomos de una fuente de luz ordinaria irradian luz de forma independiente,
por lo que una fuente extensa de luz suele emitir radiación incoherente. Para obtener luz
coherente de una fuente así, se selecciona una parte reducida de la luz mediante un
pequeño orificio o rendija. Si esta parte vuelve a separarse mediante una doble rendija, un
doble espejo o un doble prisma y se hace que ambas partes recorran trayectorias de
longitud ligeramente diferente antes de combinarlas de nuevo, se produce un diagrama de
interferencias. Los dispositivos empleados para ello se denominan interferómetros; se
emplean para medir ángulos pequeños,como los diámetros aparentes de las estrellas, o
distancias pequeñas, como las desviaciones de una superficie óptica respecto a la forma
deseada. Las distancias se miden en relación a la longitud de onda de la luz empleada. El
primero en mostrar un diagrama de interferencias fue Thomas Young, en el experimento
ilustrado en la figura 8. Un haz de luz que había pasado previamente por un orificio,
iluminaba una superficie opaca con dos orificios. La luz que pasaba por ambos orificios
formaba un diagrama de franjas circulares sucesivamente claras y oscuras en una pantalla.
En la ilustración están dibujadas las ondulaciones para mostrar que en puntos como A, C o
E (intersección de dos líneas continuas), las ondas de ambos orificios llegan en fase y se
combinan aumentando la intensidad. En otros puntos, como B o D (intersección de una línea
continua con una línea de puntos), las ondas están desfasadas 180° y se anulan
mutuamente.
Las ondas de luz reflejadas por las dos superficies de una capa transparente
extremadamente fina situada sobre una superficie lisa pueden interferir entre sí. Las
irisaciones de una fina capa de aceite sobre el agua se deben a la interferencia, y
demuestran la importancia del cociente entre el espesor de la capa y la longitud de onda de
la luz. Puede emplearse una capa o varias capas de materiales diferentes para aumentar o
disminuir la reflectividad de una superficie. Los separadores de haz dicroicos son conjuntos
de capas de distintos materiales, cuyo espesor se fija de forma que una banda de longitudes
de onda sea reflejada y otra sea transmitida. Un filtro interferencial construido con estas
capas transmite una banda de longitudes de onda extremadamente estrecha y refleja el
resto de las longitudes. La forma de la superficie de un elemento óptico puede comprobarse
presionándolo contra un patrón y observando el diagrama de franjas que se forma debido a
la capa delgada de aire que queda entre ambas superficies.
La luz que incide sobre el borde de un obstáculo es desviada, o difractada, y el obstáculo no
genera una sombra geométrica nítida. Los puntos situados en el borde del obstáculo actúan
como fuente de ondas coherentes, y se forma un diagrama de interferencias denominado
diagrama de difracción. La forma del borde del obstáculo no se reproduce con exactitud,
porque parte del frente de ondas queda cortado.
Como la luz pasa por una abertura finita al atravesar una lente, siempre se forma un
diagrama de difracción alrededor de la imagen de un objeto. Si el objeto es extremadamente
pequeño, el diagrama de difracción aparece como una serie de círculos concéntricos claros
y oscuros alrededor de un disco central, llamado disco de Airy. Esto ocurre incluso con una
lente libre de aberraciones. Si dos partículas están tan próximas que los dos diagramas se
solapan y los anillos brillantes de una de ellas coinciden con los anillos oscuros de la
segunda, no es posible resolver (distinguir) ambas partículas.
En óptica, el análisis de Fourier permite representar un objeto como una suma de ondas
senoidales sencillas,llamadas componentes. A veces se analizan los sistemas ópticos
escogiendo un objeto cuyas componentes de Fourier se conocen y analizando las
componentes de Fourier de la imagen. Estos procedimientos determinan la llamada función
de transferencia óptica. En ocasiones, el empleo de este tipo de técnicas permite extraer
información de imágenes de baja calidad. También se han aplicado teorías estadísticas al
análisis de las imágenes formadas.
Una red de difracción está formada por varios miles de rendijas de igual anchura y
separadas por espacios iguales (se consiguen rayando el vidrio o el metal con una punta de
diamante finísima). Cada rendija produce un diagrama de difracción, y todos estos
diagramas interfieren entre sí. Para cada longitud de onda se forma una franja brillante en
un lugar distinto. Si se hace incidir luz blanca sobre la red, se forma un espectro continuo.
En instrumentos como monocromadores, espectrógrafos o espectrofotómetros se emplean
prismas y redes de difracción para proporcionar luz prácticamente monocromática o para
analizar las longitudes de onda presentes en la luz incidente.
Emisión estimulada
Los átomos de una fuente de luz corriente (como una bombilla incandescente, una lámpara
fluorescente o una lámpara de neón) producen luz por emisión espontánea, y la radiación
que emiten es incoherente. Si un número suficiente de átomos absorben energía de manera
que resultan excitados y acceden a estados de mayor energía en la forma adecuada,puede
producirse la emisión estimulada. La luz de una determinada longitud de onda puede
provocar la producción de más luz con la misma fase y dirección que la onda original, por lo
que la radiación será coherente. La emisión estimulada amplifica la radiación con una
longitud de onda determinada, y la luz generada presenta una desviación del haz muy baja.
El material excitado puede ser un gas, un sólido o un líquido, pero su forma (o la forma de
su recipiente) debe ser tal que forme un interferómetro en el que la longitud de onda que se
amplifica se refleje numerosas veces en un sentido y otro. Una pequeña parte de la
radiación excitada se transmite a través de uno de los espejos del interferómetro. Este
dispositivo se denomina láser, que en inglés corresponde al acrónimo de "amplificación de
luz por emisión estimulada de radiación". El proceso de suministrar energía a un número
elevado de átomos para llevarlos a un estado adecuado de energía superior se denomina
bombeo. El bombeo puede ser óptico o eléctrico. Como un láser puede emitir pulsos de
energía extremadamente alta con una desviación de haz muy pequeña, es posible detectar,
por ejemplo, luz láser enviada a la Luna y reflejada de vuelta a la Tierra, lo que permite
medir con precisión la distancia Tierra-Luna. El haz intenso y estrecho del láser ha
encontrado aplicaciones prácticas en cirugía y en el corte de metales.
Gabor fue el primero en observar que si se pudiera registrar el diagrama de difracción de un
objeto y conservar también la información sobre la fase, la imagen del objeto podría
reconstruirse iluminando con luz coherente el diagrama de difracción registrado. Si se
iluminara el diagrama de interferencia con una longitud de onda mayor que la empleada
para producirlo, aparecería un aumento de tamaño. Como la fase absoluta de una onda
luminosa no puede detectarse directamente, era necesario proporcionar un haz de
referencia coherente con el haz que iluminaba el objeto,para que interfiriera con el diagrama
de difracción y proporcionara información sobre la fase. Antes del desarrollo del láser, el
proyecto de Gabor estaba limitado por la falta de fuentes de luz coherente lo bastante
intensas.
Un holograma es un registro fotográfico de la interferencia entre un haz de referencia y el
diagrama de difracción del objeto. Para generar un holograma, la luz procedente de un único
láser se divide en dos haces. El haz de referencia ilumina la placa fotográfica (por ejemplo, a
través de una lente y un espejo) y el segundo haz ilumina el objeto. El haz de referencia y la
luz reflejada por el objeto forman un diagrama de difracción sobre la placa fotográfica. Si
una vez revelado el holograma se ilumina con luz coherente, no necesariamente de la
misma longitud de onda que la empleada para crearlo, puede obtenerse una imagen
tridimensional del objeto. Es posible producir hologramas de un objeto teórico mediante
ordenadores o computadoras, y después pueden reconstruirse las imágenes de esos
objetos.
Los haces láser intensos y coherentes permiten estudiar nuevos efectos ópticos producidos
por la interacción de determinadas sustancias con campos eléctricos, y que dependen del
cuadrado o de la tercera potencia de la intensidad de campo. Esta rama de la óptica se
denomina óptica no lineal, y las interacciones que estudia afectan al índice de refracción de
las sustancias. El efecto Kerr antes mencionado pertenece a este grupo de fenómenos.
Se ha observado la generación armónica de luz. Por ejemplo, la luz láser infrarroja con
longitud de onda de 1,06 micrómetros puede convertirse en luz verde con longitud de onda
de 0,53 micrómetros (es decir, justo la mitad) mediante un cristal de niobato de sodio y
bario. Es posible producir fuentes de luz coherente ampliamente sintonizables en la zona de
la luz visible y el infrarrojo cercano bombeando medios adecuados con luz o con radiación
de menor longitud de onda. Se puede lograr que un cristal de niobato de litio presente
fluorescencia roja, amarilla y verde bombeándolo con luz láser azul verdosa con una
longitud de onda de 488 nanómetros. Algunos fenómenos de difusión pueden ser
estimulados con un único láser para producir pulsos de luz intensos en una amplia gama de
longitudes de onda monocromáticas. Los efectos ópticos no lineales se aplican en el
desarrollo de moduladores eficaces de banda ancha para sistemas de comunicación.
Espectro
Serie de colores semejante a un arco iris (por este orden: violeta, azul, verde, amarillo,
anaranjado y rojo) que se produce al dividir una luz compuesta como la luz blanca en sus
colores constituyentes. El arco iris es un espectro natural producido por fenómenos
meteorológicos. Puede lograrse un efecto similar haciendo pasar luz solar a través de un
prisma de vidrio.
Cuando un rayo de luz pasa de un medio transparente como el aire a otro medio
transparente, por ejemplo vidrio o agua, el rayo se desvía; al volver a salir al aire vuelve a
desviarse. Esta desviación se denomina refracción; la magnitud de la refracción depende de
la longitud de onda de la luz. La luz violeta, por ejemplo, se desvía más que la luz roja al
pasar del aire al vidrio o del vidrio al aire. Así, una mezcla de luces roja y violeta se dispersa
al pasar por un prisma en forma de cuña y se divide en dos colores.
Los aparatos para observar visualmente un espectro se denominan espectroscopios; los
que sirven para observar y registrar un espectro fotográficamente se llaman espectrógrafos;
los empleados para medir la intensidad de las diferentes partes del espectro se denominan
espectrofotómetros. La ciencia que utiliza los espectroscopios, espectrógrafos y
espectrofotómetros para estudiar los espectros se conoce como espectroscopia. Para
medidas espectroscópicas extremadamente precisas se emplean interferómetros. En el
siglo XIX, los científicos descubrieron que más allá del extremo violeta del espectro podía
detectarse una radiación invisible para el ojo humano pero con una marcada acción
fotoquímica; se la denominó radiación ultravioleta. Igualmente, más allá del extremo rojo del
espectro se detectó radiación infrarroja que aunque era invisible transmitía energía, como
demostraba su capacidad para hacer subir un termómetro. Como consecuencia, se redefinió
el término espectro para que abarcara esas radiaciones invisibles, y desde entonces se ha
ampliado para incluir las ondas de radio más allá del infrarrojo y los rayos X y rayos gamma
más allá del ultravioleta.
En la actualidad, el término espectro se aplica frecuentemente en un sentido más amplio a
cualquier distribución ordenada producida por el análisis de un fenómeno complejo. Un
sonido complejo, como por ejemplo un ruido, puede analizarse como un espectro acústico
formado por tonos puros de diferentes frecuencias. Igualmente, una mezcla compleja de
elementos o isótopos con distinta masa atómica puede ser separada en una secuencia
ordenada según su masa atómica y denominada espectro de masas.
La espectroscopia no sólo ha proporcionado un método importante y sensible para el
análisis químico, sino que ha sido el principal instrumento para descubrimientos en campos
aparentemente no relacionados, como la astrofísica o la teoría atómica. En general, los
cambios en el movimiento de los electrones exteriores de los átomos dan lugar a espectros
en la región visible, infrarroja y ultravioleta. Los cambios en el movimiento de los electrones
interiores de los átomos pesados producen espectros de rayos X. Los cambios en la
configuración del núcleo de un átomo producen espectros de rayos gamma. Los cambios en
la configuración de las moléculas producen espectros visibles e infrarrojos.
Los distintos colores de luz tienen en común el ser radiaciones electromagnéticas que se
desplazan con la misma velocidad, aproximadamente 300.000 kilómetros por segundo. Se
diferencian en su frecuencia y longitud de onda (la frecuencia es igual a la velocidad de la
luz dividida entre la longitud de onda). Dos rayos de luz con la misma longitud de onda
tienen la misma frecuencia y el mismo color. La longitud de onda de la luz es tan corta que
suele expresarse en nanómetros (nm), que equivalen a una milmillonésima de metro, o una
millonésima de milímetro. La longitud de onda de la luz violeta varía entre unos 400 y 450
nm, y la de la luz roja entre unos 620 y 760 nm.
Oscilación
En física, química e ingeniería, movimiento repetido de un lado a otro en torno a una
posición central, o posición de equilibrio. El recorrido que consiste en ir desde una posición
extrema a la otra y volver a la primera,pasando dos veces por la posición central, se
denomina ciclo. El número de ciclos por segundo, o hercios (Hz), se conoce como
frecuencia de la oscilación.
Cuando se pone en movimiento un péndulo o se puntea la cuerda de una guitarra, el
péndulo y la cuerda acaban deteniéndose si no actúan sobre ellos otras fuerzas. La fuerza
que hace que dejen de oscilar se denomina amortiguadora. Con frecuencia, estas fuerzas
son fuerzas de rozamiento, pero en un sistema oscilante pueden existir otras fuerzas
amortiguadoras, por ejemplo eléctricas o magnéticas.
Frecuencia natural
Cualquier objeto oscilante tiene una ´frecuencia natural´, que es la frecuencia con la que
tiende a vibrar si no se le perturba. Por ejemplo, la frecuencia natural de un péndulo de 1 m
de longitud es de 0,5 Hz, lo que significa que el péndulo va y vuelve una vez cada 2
segundos. Si se le da un ligero impulso al péndulo cada 2 segundos, la amplitud de la
oscilación aumenta gradualmente hasta hacerse muy grande. El fenómeno por el que una
fuerza relativamente pequeña aplicada de forma repetida hace que la amplitud de un
sistema oscilante se haga muy grande se denomina resonancia. Muchos problemas graves
de vibración en ingeniería son debidos a la resonancia. Por ejemplo, si la frecuencia natural
de la carrocería de un automóvil es la misma que el ritmo del motor cuando gira a una
velocidad determinada, la carrocería puede empezar a vibrar o a dar fuertes sacudidas. Esta
vibración puede evitarse al montar el motor sobre un material amortiguador, por ejemplo
hule o goma, para aislarlo de la carrocería.
Flameo
Un tipo peligroso de vibración es la oscilación repentina y violenta conocida como flameo.
Este fenómeno se produce sobre todo en las superficies de control de los aviones, pero
también ocurre en los cables eléctricos cubiertos de escarcha cuando la velocidad del viento
es elevada. Uno de los casos de flameo más espectaculares provocó en 1940 el
hundimiento de un puente en Tacoma, Estados Unidos. La causa fue un viento huracanado
cuya velocidad potenció la vibración del puente.
En el flameo, la amplitud de vibración de una estructura puede aumentar tan rápidamente
como para que ésta se desintegre casi de forma instantánea. Por eso, impedir el flameo es
muy importante a la hora de diseñar puentes y aviones. En el caso de los aviones, el
análisis de flameo suele complementarse con pruebas realizadas con una maqueta del
avión en un túnel aerodinámico.
Frecuencia
Término empleado en física para indicar el número de veces que se repite en un segundo
cualquier fenómeno periódico. La frecuencia es muy importante en muchas áreas de la
física, como la mecánica o el estudio de las ondas de sonido.
Las frecuencias de los objetos oscilantes abarcan una amplísima gama de valores. Los
temblores de los terremotos pueden tener una frecuencia inferior a 1, mientras que las
veloces oscilaciones electromagnéticas de los rayos gamma pueden tener frecuencias de
1020 o más. En casi todas las formas de vibración mecánica existe una relación entre la
frecuencia y las dimensiones físicas del objeto que vibra. Por ejemplo, el tiempo que
necesita un péndulo para realizar una oscilación completa depende en parte de la longitud
del péndulo; la frecuencia de vibración de la cuerda de un instrumento musical está
determinada en parte por la longitud de la cuerda. En general, cuanto más corto es el objeto,
mayor es la frecuencia de vibración.
En todas las clases de movimiento ondulatorio, la frecuencia de la onda suele darse
indicando el número de crestas de onda que pasan por un punto determinado cada
segundo. La velocidad de la onda y su frecuencia y longitud de onda están relacionadas
entre sí. La longitud de onda (la distancia entre dos crestas consecutivas) es inversamente
proporcional a la frecuencia y directamente proporcional a la velocidad. En términos
matemáticos, esta relación se expresa por la ecuación v = l f, donde v es la velocidad, f es la
frecuencia y l (la letra griega lambda) es la longitud de onda. A partir de esta ecuación
puede hallarse cualquiera de las tres cantidades si se conocen las otras dos.
La frecuencia se expresa en hercios (Hz); una frecuencia de 1 Hz significa que existe 1 ciclo
u oscilación por segundo. Heinrich Rudolf Hertz fue el primero en demostrar la naturaleza de
la propagación de las ondas electromagnéticas. Las unidades como kilohercios (kHz) (miles
de ciclos por segundo), megahercios (MHz) (millones de ciclos por segundo) y gigahercios
(GHz) (miles de millones de ciclos por segundo) se usan para describir fenómenos de alta
frecuencia como las ondas de radio. Estas ondas y otros tipos de radiación electromagnética
pueden caracterizarse por sus longitudes de onda o por sus frecuencias. Las ondas
electromagnéticas de frecuencias extremadamente elevadas, como la luz o los rayos X,
suelen describirse mediante sus longitudes de onda, que frecuentemente se expresan en
nanómetros (un nanómetro,abreviado nm, es una milmillonésima de metro). Una onda
electromagnética con una longitud de onda de 1 nm tiene una frecuencia de
aproximadamente 300 millones de GHz.
Resolver:
1) Frente a una lente convergente de 20 cm de distancia focal y sobre su eje se coloca un
objeto, calcular la distancia objeto-lente para que la distancia imagen-lente sea el doble.
Respuesta: 30 cm
2) Repetir el ejercicio anterior para el caso que la imagen sea virtual.
Respuesta: 10 cm
3) Construir la de un objeto OH que está frente a una lente convergente, entre el foco y la
lente. Analizar sus características.
4) Un objeto OH está frente a una lente divergente, entre el foco y el infinito, encontrar la
imagen y analizar sus características.
5) Un objeto está situado a 0,6 m de una lente convergente cuya distancia focal es de 0,3 m.
¿A qué distancia se forma la imagen?.
Respuesta: 0,6 m
6) Delante de una lente divergente cuya distancia focal es 0,8 m, hay un objeto a 0,6 m. ¿A
qué distancia está la imagen?.
Respuesta: -12/35 m
7) Exprese en dioptrías la potencia de una lente divergente de distancia focal -80 cm.
Respuesta: -5/4
8) Dibujar la imagen de un objeto cuya distancia a una lente convergente es mayor que F.
Trace la figura que indique las propiedades de la imagen.
9) Un objeto está a 20 cm de una lente convergente cuya distancia focal es de 30 cm. ¿A
qué distancia se forma la imagen?. Trace previamente la figura que corresponda.
Respuesta: -60 cm
OPTICA
LA REVOLUCION DE LA ILUMINACION
El mundo se iluminará de forma diferente dentro de algunos años. Los ingenieros de los
Sandia National Laboratories y de otros organismos de investigación están trabajando en un
proyecto que establecerá las bases científicas y tecnológicas para la sustitución de las
actuales bombillas incandescentes y tubos fluorescentes por diodos semiconductores
emisores de luz.
Los LEDs serán los protagonistas de la denominada "iluminación de estado sólido", una
revolución comparable a la que experimentó la electrónica hace 50 años,cuando las
lámparas y los tubos de vacío fueron reemplazados por semiconductores. Y tal como ocurrió
en la revolución microelectrónica, la iluminación de estado sólido podría proporcionar
nuevas aplicaciones que aún desconocemos.
Como explica James Gee, uno de los líderes del proyecto, los LEDs ya se encuentran en
juguetes, electrónica de consumo,luces de tráfico, grandes pantallas exteriores, etc. Se trata
de dispositivos que deben ser duraderos, compactos y operar a baja temperatura. En
algunas aplicaciones los LEDs también ahorran dinero, ya que consumen menos energía.
Así,en las señales de tráfico, consumen sólo una décima parte de lo que gastan las
bombillas tradicionales, lo que permite que se paguen por sí mismos en el plazo aproximado
de un año.
A medida que la tecnología avance, se espera que la iluminación de estado sólido supere de
forma amplia a otras fuentes de luz, tanto en coste como en rendimiento.
Los LEDs, que ahora pueden servir también como fuente de luz blanca, son 10 veces más
eficientes que las bombillas incandescentes y dos veces más que los fluorescentes. Así, el
reemplazo de estos sistemas tradicionales por LEDs de nuevo diseño colaborará en la
reducción del consumo mundial de energía.
La iluminación es en la actualidad responsable del 20 por ciento del consumo eléctrico. En
una nación industrializada,el uso de la tecnología de estado sólido para esta tarea reduciría
el consumo en un 10 por ciento.
Los LEDs fueron desarrollados en 1962 por la compañía General Electric. En 1968
empezaron a ser incorporados en diversos productos. Sin embargo, hasta 1985 sólo eran
utilizados en aplicaciones de escasa señal. A partir de esta fecha, su potencia se vio
aumentada y se abrieron nuevas vías de utilización. En 1993 se desarrolló un LED de luz
azul, después paulatinamente mejorado. Hoy en día, existen LEDs eficientes para luz de
colores diversos, del rojo al azul, pasando por el verde, lo que permite generar luz blanca
para iluminación.
El principal problema es que las fuentes de luz basadas en LEDs son caras (en dos órdenes
de magnitud respecto a las bombillas comerciales), y no serán prácticas hasta que su coste
se reduzca o aumente su eficiencia. Este es precisamente el objetivo del LEDsproject.
LA BOMBILLA FRIA
Las bombillas de filamentos de tungsteno, las más utilizadas en todo el mundo como fuente
de luz, queman nuestras manos si las tocamos. Son famosas por generar más calor que luz,
un despilfarro de energía que científicos de los Sandia National Laboratories pretenden
evitar con un nuevo diseño que convierte la mayor parte de la radiación infrarroja
desperdiciada en frecuencias de luz visible.
Para conseguirlo, han preparado un filamento de tungsteno fabricado con un patrón
cristalino interno. Con él, la eficiencia de la bombilla eléctrica incandescente pasa de un 5
por ciento a más de un 60 por ciento.
Este invento podría reducir en gran medida el consumo energético en todo el mundo, y
paliar las deficiencias de iluminación de muchos hogares. Pero la tecnología también
promete mayores eficiencias en aplicaciones térmico-fotovoltaicas. Los sistemas
fotovoltaicos funcionan mejor cuando se les suministra energía procedente de generadores
de calor que emiten en longitudes de onda óptimas.
Shawn Lin y Jim Fleming son los responsables de este avance. Se han basado en los
trabajos sobre cristales fotónicos de silicio realizados por Eli Yablonovitch, de la UCLA, hace
más de una década. Su capacidad de transmitir rayos de luz a frecuencias elegidas y
desviar sus trayectorias sin pérdida de energía los hace muy interesantes. Pero también lo
es su habilidad de detener otras frecuencias, evitando su paso a través de ellos.
La fabricación de los cristales tridimensionales con tungsteno permite soportar altas
temperaturas y aprovechar las emisiones de luz en el rango visible. En cuanto a las
radiaciones infrarrojas, éstas se ven suprimidas y la energía térmica de excitación es
redirigida hacia el espectro visible, aumentando su rendimiento.
Lo más curioso es que la lógica del proceso aún no ha sido explicada. Podría ocurrir que la
luz variara su velocidad al propagarse a través de tales estructuras, pero aún deben
efectuarse nuevos estudios teóricos que lo confirmen.
EL RAYO MANIPULADOR
Varios científicos han creado un rayo de luz ultravioleta, parecido a un láser y altamente
enfocado, mediante un dispositivo que cabe sobre una mesa. Creen que esta fuente de luz
podrá utilizarse para medir y manipular objetos a una escala de pocos nanómetros. El rayo
promete romper algunas de las barreras del progreso tecnológico.
El tamaño ha sido uno de los principales obstáculos que los investigadores han encontrado
a la hora de desarrollar, o incluso ver, los diminutos componentes de la próxima generación
de ordenadores o máquinas nanoscópicas. Son más pequeños que la longitud de onda de la
luz utilizada para iluminarlos.
Es cierto que los microscopios electrónicos y otros sistemas similares pueden ver
estructuras muy pequeñas, pero muchas mediciones esenciales requieren microscopios
ópticos, que están limitados por la longitud de onda de sus fuentes de luz.
Para solucionar esto, Margaret Murnane y Henry Kapteyn, de la University of Colorado, han
desarrollado una nueva fuente de luz de longitud de onda muy corta. La luz ultravioleta,
cuya longitud de onda es de sólo unas decenas de nanómetros, puede pulsar más
lentamente que cualquier otro sistema y tiene un foco muy ajustado, difícil de conseguir por
otros medios.
La ciencia de la nanotecnología podrá ahora seguir avanzando a mayor velocidad, gracias a
la disponibilidad de una herramienta que permite hace mediciones e interacciones a nivel de
una sola molécula.
La luz ultravioleta del dispositivo se produce mediante un proceso llamado HHG (high
harmonic generation). Se dispara un láser de luz visible sobre un gas, creando un fuerte
campo magnético. El campo ioniza el gas, separando los electrones de sus átomos. Los
electrones recolisionarán entonces con los átomos ionizados, y oscilarán dentro del campo
magnético. Como resultado de ello, saldrá del sistema un chorro de fotones bien
sincronizados, en la longitud de onda de la luz ultravioleta. El rayo está tan enfocado que su
diámetro es el más pequeño del mundo, de 20 a 30 veces más pequeño que el más común
de los láseres de helio-neón, y cientos de veces más intenso. Un rayo producido de esta
forma que empezara con un diámetro de un centímetro en la superficie de la Tierra, sólo se
habrá expandido hasta los 30 metros cuando llegue a la distancia de la Luna. Un láser
convencional habría alcanzado un diámetro de al menos un kilómetro.
La luz obtenida mediante el nuevo método servirá para observar el comportamiento de las
moléculas, y ayudará pronto a los ingenieros a alinear y probar algunos sistemas de
fabricación. Asimismo, permitirá crear hologramas biológicos de alta resolución.
LUZ DE BURBUJAS DE GAS
Una burbuja de gas excitada por ultrasonidos convierte una pequeña fracción de la energía
sónica en luz. Este fenómeno, denominado sonoluminiscencia, ha venido observándose
desde hace décadas. Ahora, químicos de la University of Illinois han conseguido por primera
vez medir las reacciones químicas y la emisión de luz de una única burbuja de agua
excitada por ondas de sonido.
Ken Suslick y Yuri Didenko, autores del trabajo, conocen bien el fenómeno. Cuando se
aplican ultrasonidos a un líquido, se produce un proceso llamado cavitación, que implica la
formación, crecimiento, compresión y colapso de burbujas microscópicas. Estas pequeñas
oscilaciones pueden causar un intenso calor y presión, similares a las condiciones
producidas a gran escala por las explosiones u ondas de choque. Esta excitación puede
ocasionar también la emisión de cortos destellos de luz.
El uso de ultrasonidos para inducir reacciones químicas de alta energía podría tener
interesantes aplicaciones industriales y médicas. Pero, antes, los científicos necesitar
cuantificar la energía y las partículas moleculares liberadas dentro de una única burbuja
aislada.
El experimento de Illinois mostró que a medida que las burbujas pulsantes de agua
colapsan, crean temperaturas lo bastante altas como para romper las moléculas.
En este proceso, menos de una millonésima de energía sónica es convertida en luz. Mil
veces más energía se va en la formación de átomos, fragmentos moleculares e iones. La
mayor parte de la energía sónica es convertida en energía mecánica, causando ondas de
choque y movimiento en el líquido que rodea a la burbuja de gas.
La cavitación, que dirige el colapso implosivo de estas burbujas, crea temperaturas
parecidas a las que se encuentran en la superficie del Sol y presiones como las del fondo
del océano. Este fenómeno ofrece un medio de concentrar la energía difusa del sonido en
una forma químicamente útil.
Se estiman diversas aplicaciones, como la eliminación del azufre de la gasolina, la mejora
de las reacciones químicas utilizadas para fabricar fármacos, etc.
LA FUENTE ELECTROLUMINISCENTE MAS PEQUEÑA
Utilizando emisiones de fotones procedentes de moléculas individuales de plata,
investigadores del Georgia Institute of Technology han creado la que se supone es la fuente
de luz electroluminiscente más diminuta del mundo.
El trabajo es también la primera demostración de la existencia de electroluminiscencia de
moléculas individuales, una investigación que podría llevarnos a nuevos tipos de
interconexiones ópticas a escala nanométrica, microscopia óptica de alta resolución,
litografía nanométrica y otras aplicaciones donde se requieren fuentes de luz muy
pequeñas. Dado que se sabe que las moléculas individuales emiten un único fotón a un
tiempo, la técnica podría usarse como base para un sistema de procesamiento de
información cuántica de alta eficiencia, y para criptografía.
Aunque el efecto fue detectado por primera vez en moléculas de plata compuestas por 2-8
átomos, los investigadores ya han demostrado la existencia de electroluminiscencia en
grupos de cobre, lo que sugiere que el efecto podría aplicarse a otros metales.
Robert Dickson y sus colegas explican que empezaron con películas delgadas de óxido de
plata que no son electroluminiscentes. Exponiendo la película a una corriente eléctrica de
aproximadamente un amperio, "activaron" algunas de las moléculas del óxido de plata, que
aparecieron entonces dentro de regiones "descoloridas" en la película. Cuando se aplicaron
electrodos a esta última y se aplicó una corriente alterna, una fina línea de grupos de plata
empezó a emitir en colores que variaban dependiendo de su tamaño. El sistema operó a
temperatura ambiente.
Observando de cerca el proceso, se puede ver claramente que las emisiones proceden de
moléculas individuales. Parpadean y presentan patrones de emisión dipolares.
La electroluminiscencia aparece cuando un electrón se recombina con una molécula
cargada positivamente, de la cual se ha extraído un único electrón. En primer lugar se retira
el electrón, para crear la carga positiva. Después, se inyecta otro rápidamente en un estado
diferente de la misma molécula. La diferencia de cargas provocará una recombinación y la
emisión de un fotón.
Aunque la aplicación de corriente continua produce electroluminiscencia en los grupos
activados de plata, un voltaje de corriente alterna de alta frecuencia (sobre los 150 MHz)
produce una respuesta hasta 10.000 veces mayor. Esto prolonga la vida útil de los grupos
emisores y reduce la cantidad de corriente necesaria para producir luz.
La electroluminiscencia tiene muchas aplicaciones, pero los investigadores prefieren primero
entender bien el proceso básico: cuál es la naturaleza de la emisión, cómo ocurre ésta, etc.
ESPEJOS COMBINADOS
Cuatro ojos, mejor que uno. El interferómetro VLT, situado en el observatorio Paranal del
European Southern Observatory, ha superado las pruebas preliminares durante las cuales
se combinaron por parejas los rayos de luz procedentes de sus cuatro grandes telescopios,
cada uno de ellos de 8,2 metros de diámetro (UT).
Los ensayos se efectuaron durante las noches del 15 al 16 de septiembre y del 16 al 17 del
mismo mes. Los ingenieros creen que todo salió conforme a lo previsto, y que estamos ante
un paso adelante hacia la pronta disponibilidad de un instrumento sin parangón para la
observación astronómica.
No es nada fácil asegurar que el cuarteto de telescopios, llamados ANTU, KUEYEN,
MELIPAL y YEPUN, cada uno de ellos un gigante masivo equipado con espejos activos
controlados por ordenador, pueda trabajar conjuntamente, enviando sus rayos de luz hacia
un punto focal común. Pero esto es precisamente lo que se ha conseguido: emparejar los
cuatro telescopios, coordinando sus rayos de luz, lo que permitirá futuras observaciones de
alta precisión y sensibilidad.
Cada uno de los telescopios es por sí solo una formidable herramienta de observación. Pero
es difícil construir espejos o grupos de espejos de diámetros totales mucho mayores que los
del VLTI. Por eso, se prefiere utilizar la técnica interferométrica, que permite la combinación
de la luz recogida por varios instrumentos, como si ésta procediera de uno solo de mucho
mayor diámetro (y por tanto, con mayor capacidad de captación).
Aún estamos lejos de utilizar el VLTI de forma rutinaria y obtener imágenes interferométricas
muy claras, pero las pruebas, que trataban de ensayar los sistemas, confirman que ello será
pronto posible. De momento, sirvieron para demostrar directamente la capacidad de
resolución en 2D del VLTI, lo cual se consiguió después de múltiples mediciones de una
estrella distante. Durante los próximos seis meses están previstas pruebas técnicas
semejantes, algunas de los cuales se efectuarán junto al instrumento interferométrico MIDI,
que se instalará pronto en Paranal.
Las tareas de combinación de la luz procedente de los cuatro telescopios son complicadas
por cuanto es necesario apuntar a cada uno de ellos hacia el mismo objetivo con una
precisión absoluta, garantizando un seguimiento exacto a pesar del movimiento de rotación
de la Tierra. Los cuatro rayos de luz son dirigidos hacia un punto focal, donde ahora mismo
se halla el instrumento VINCI.
FISICA – RESISTENCIA DE LOS MATERIALES
FUERZA ELASTICA
Resortes: Los resortes reales se comportan según la siguiente ecuación, conocida como la
Ley de Hooke: las tensiones son proporcionales a las elongaciones. Los materiales que
responden a esta ley son perfectamente elásticos.
F = k.Δx
k: magnitud de la fuerza por unidad de elongación, que depende de cada resorte [N/m].
Δx = xf - xo [m]
Tensión o esfuerzo: es la relación entre una carga y la superficie sobre la que actúa. Se
considera como tal a la reacción que opone el material de un cuerpo frente a una solicitación
externa (de tensión, compresión, cortante) que tiende a producir un cambio en su tamaño o
forma.
σ = F/A ⇒ σ = ε .E
E: módulo de elasticidad del material. [N/m ²; kg/cm ²]
A: sección del material [m ²; cm ²]
Elongaciones: un cuerpo sometido a la acción de fuerzas externas sufre alargamientos o
acortamientos en una dirección dada que reciben el nombre de deformaciones.
Deformación específica:
ε = Δl/l Δl: elongación
l: longitud origina
acortamiento ε < 0
alargamiento ε > 0
Dentro del límite de proporcionalidad (σ p), el módulo de elasticidad de un material dado es
constante, dependiendo solo de la naturaleza del material.
De 0 hasta a,se llama recta de Hooke. Sin embargo hasta b inclusive, cuando descargamos
la pieza recupera su longitud original (entre 0 y b, el material es elástico).
Modulo de Young: es la constancia de la relación entre tensiones y deformación específica.
E = σ / ε = constante
Esta relación es la expresión analítica de la ley de Hooke.
Elasticidad: una deformación se llama elástica cuando desaparece completamente
(recuperable) una vez que cesa la causa que la produjo.
Plasticidad: una deformación plástica es aquella que no desaparece (irreversible) con la
anulación de la causa. La plasticidad de los materiales esta dada por su capacidad de poder
deformarse sin por ello sufrir fractura. Un material es tanto más dúctil cuanto más extendido
es su diagrama σ - ε en el sentido del eje ε .
A medida que aumenta la resistencia de los materiales disminuye la deformación específica
y por lo tanto su ductilidad. Se dice entonces que el material va ganando en fragilidad.
La maleabilidad como propiedad de los materiales, específicamente metálicos, constituye en
realidad una fase de la ductilidad.
Tenacidad: es la capacidad de un material para absorber simultáneamente esfuerzos y
deformaciones de consideración sin llegar a la fractura.
Rigidez: es la capacidad de resistir una deformación elástica por efecto de una tensión.
Fluencia: en los materiales tenaces el período plástico comienza teóricamente a partir del
punto a (límite de proporcionalidad), que constituye el final del período de proporcionalidad
(recta de Hooke). En realidad,el material suele ser elástico, un poco más allá de dicho
punto, hasta el punto b (límite de elasticidad).
MOVIMIENTO ARMONICO
La ecuación general del movimiento armónico simple es:
X = A.cos (ω .t + θ 0)
puede escribirse en la forma equivalente:
X = B.sin ω .t + C.cos ω .t
a) Determínense las expresiones de las amplitudes de B y C en función de la amplitud A y
del ángulo de fase inicial θ 0.
b)
X = A.cos (ω .t + θ 0)
X = B.sin ω .t + C.cos ω .t
X = A.(cos ω .t . cos θ 0- sin ω .t . sin θ 0)
X = -A.sin ω .t . sin θ 0 + A.cos ω .t . cos θ 0
B = -A.sin θ 0
C = A.cos θ 0
a) 2. Un cuerpo de 0,25 kg. De masa está sometido a una fuerza elástica restauradora, con
constante de recuperación k =25N/m.
b) Dibújense la gráfica de la energía potencial elástica U en función del desplazamiento x en
un intervalo de x comprendido entre -0,3m y + 0,3 m. Tómense 1 cm = 1J en el eje vertical y
1 cm = 0,05m en el eje horizontal.
El cuerpo inicia su oscilación con energía potencial inicial de 0,6J y energía cinética inicial
de 0,2 J. A partir de la gráfica, respóndanse las cuestiones siguientes:
U = k.x ²/2
x
U
0
0
±0,05
0,031
± 0,10
0,125
±0,15
0,281
± 0,20
0,500
± 0,25
0,781
± 0,30
1,125
c) ¿Cuál es la amplitud de la oscilación?.
A=?
ET = ω ².A ²/2
ω ² = k/m
ω ² = 25/0,25 = 100
A = √2.(0,8)/100 = 0,12 m
d) ¿Cuál es la energía potencial cuando el valor de desplazamiento es la mitad que el de la
amplitud?.
Ep = k.x ²/2
x = 0,6 m
Ep = 25.0,6/2 = 4 J
e) ¿Para que valor del desplazamiento son iguales la energía cinética y potencial?
Ep = k.x ²/2 ⇒ 0,6 = 25.x ²/2 ⇒ x =± 0,219 m
f) ¿Cuál es la rapidez del cuerpo en el punto medio de su trayectoria?.
Calcúlense:
Ec = m.v ²/2 ⇒ v = ±√2.0,2/0,25 = ±1,26 m/s
g) El período T1.
T = 1/f = 0
2.π.f = √k/m
ƒ = √k/m/2.π = √25/0,25/2.π
f = 1,59 Hz
T = 0,628 s
h) La frecuencia f1 y
f = 1,59 Hz
i) La frecuencia angular ω .
ω=?
k = m. ω ²
ω = √k/m = √25/0,25
ω = 10 rad/s
j) ¿Cuál es el ángulo de fase inicial θ 0si la amplitud A = 15 cm, el desplazamiento inicial x0 =
7,5 cm y la velocidad inicial Vo es negativa?.
La posición del móvil que describe un M.A.S. en función del tiempo viene dada por la
ecuación:
X = A.cos.(ω .t + θ o)
entonces no da que:
X = A.cos. θ o
por lo que para este caso como son las condiciones iniciales (t = 0) se deduce que:
ω .t 0
nos da pro consiguiente:
7,5 = 15.cos θ 0 ⇒ θ0 = arc cos (7,5/15) = 1,047 rad
2) Un cuerpo está vibrando con movimiento armónico simple de 15 cm de amplitud y 4Hz de
frecuencia, calcúlense:
a) Los valores máximos de la aceleración y de la velocidad.
A = 15 cm
F = 4 Hz
a máximo = ?
V máximo = ?
a = -A. ω ².cos ω .t
a máximo = A. ω ²
a máximo = 15.25 ²
a máximo = 9375 cm/s ² = 93,75 m/s ²
ω = 2.π.f
ω = 2.π.4
ω = 25
V máximo = ω .A ⇒25.0,15 = 3,76 m/s
b) La aceleración y la velocidad cuando el desplazamiento es 9 cm, y.
a = ? y la V = ? cuando x = 9 cm
a = - ω ².x
a = -25 ².9
a = -56,84 m/s ²
V = ± 3,02 m/s
c) El tiempo necesario para desplazarse desde la posición de equilibrio a un punto situado a
12 cm de la misma.
x = A.cos ω .t
12/15 = cos 25.t
cos 25.t =0,8
-1
25.t = cos 0,8
25.t = 0,64
t = 0,025 s
3) Un cuerpo de 10gr. De masa se mueve con movimiento armónico simple de 24 cm. De
amplitud y 4s. de período: El desplazamiento es + 24 cm. Para t = 0. Calcúlense:
a) La posición del cuerpo cuando t = 0,5 s.
m = 10 g
A = 24 cm
T=4s
x = 24 cm para t = 0
t = 0,5 s ⇒x = ?
x = A.cos 2.π.f.t
x = 24.cos (2.π.0,5/4)
x = 16,97 cm
b) La magnitud y dirección de la fuerza que actúa sobre el cuerpo cuando t = 0,5s.
F = -k.x
F = -m. ω ².x
ω = 2.π.f
F = -10.(2.π./4) ².19,97
-1
F = 418,71 g. cm
la dirección está hacia abajo, porque al no completarse todavía el período (X = 16,97), la
fuerza lleva a la masa hacia abajo hasta su máxima amplitud.
c) El tiempo mínimo necesario para que el cuerpo se mueva desde la posición inicial al
punto en que x = -12 cm, y
Δt = ?
x = A.cos ω .t
x/A = cos ω .t
arc cos (x/A) = ω .t
Δt = [arccos (-12/24)]/(2.π /4)
Δt = 1,33 s
d) La velocidad de dicho cuerpo cuando x = -12 cm.
V ⇒ x = 12 cm
V = -A. ω .cos ω .t
V = -24.(2 π /4).cos (1,33.π /2)
-1
V = -18,67 cm.s
4) El movimiento del pistón del motor de un automóvil es aproximadamente armónico
simple.
a) Si la carrera de un pistón (dos veces la amplitud) es 10 cm y el motor gira a
3600 rev/mm., calcúlese la aceleración del pistón al final de la carrera.
2.A = 10 cm
A = 5 cm = 0,05 m
f = 3600 (rev/min).(1 min/60 s) = 60 Hz
a máximo = k.x/m
a máximo = (2.π.f) ².A
a máximo = (2.π.60) ².0,05
a máximo = 7106 m.s ²
b) Si el pistón tiene una masa de 0,5 kg, ¿qué fuerza resultante ha de ejercerse sobre él en
ese punto?.
m = 0,5 kg
F = m.a
F = 0,5.7106
F = 3553 N
c) ¿Cuál es la velocidad del pistón, en kilómetros por hora, en el punto medio de su
carrera?.
V = ? en el punto medio, la velocidad es máxima.
V máximo = ω .A
ω = 2 π.f
V máximo = (2 π.f).A
V máximo = (2 π.60).0,05
V máximo = 18,85 m/s = 67,9 km/h
5) Un cuerpo de 2 kg. De masa está suspendido de un resorte de masa despreciable, y se
produce un alargamiento de 20 cm.
m = 2 kg
x = 20 cm
a) ¿Cuál es la constante de recuperación del resorte?.
F = -k.x
m.g/x = k
k = 2.9,8/0,2 = 98 N/m
b) ¿Cuál es el período de oscilación del cuerpo si se tira hacia abajo y se abandona así
mismo?.
k = m. ω ²
ω = √k/m = 7 rad/s
ω = 2.π.f
f = ω /2.π = 1,11 Hz
T = 1/f = 0,89 s
c) ¿Cuál sería el período de un cuerpo de 4 kg de masa pendiente del mismo resorte?.
m = 4 kg
-1
ω = 4,94 rad.s
T = 1,26 s
6) La escala de una balanza de resorte que registra de 0 a 180N tiene 9 cm de longitud. Se
observa que un cuerpo suspendido de la balanza oscila verticalmente a 1,5 Hz. ¿Cuál es la
masa del cuerpo?. Despréciese la masa del resorte.
F = 180 N
f = 1,5 Hz
F = -k.x
k = -F/x
Por lo que si sustituímos en la ecuación se tiene que:
k = |-2000 N/m|
k = m.ω ²
ω = 2.π.ƒ
ω = 2.π.1,5
ω = 9,42 rad/s
Sustituyendo:
m = k/ω ²
m = (2000 N/m)/(9,42 rad/s) ²
m = 22,53 kg
FISICA – TERMODINAMICA
EL CALOR
Cantidades de calor
Aun cuando no sea posible determinar el contenido total de energía calorífica de un
cuerpo, puede medirse la cantidad que se toma o se cede al ponerlo en contacto con
otro a diferente temperatura. Esta cantidad de energía en tránsito de los cuerpos de
mayor temperatura a los de menor temperatura es precisamente lo que se entiende en
física por calor.
La ecuación calorimétrica
La experiencia pone de manifiesto que la cantidad de calor tomada (o cedida) por un
cuerpo es directamente proporcional a su masa y al aumento (o disminución) de
temperatura que experimenta. La expresión matemática de esta relación es la ecuación
calorimétrica.
(8.6)
Q = ce.m.(Tf - Ti)
donde Q representa el calor cedido o absorbido, la masa del cuerpo y Tf y Ti las
temperaturas final e inicial respectivamente. Q será positivo si la temperatura final es
mayor que la inicial (Tf> Ti) y negativo en el caso contrario (Tf< Ti). La letra c representa
la constante de proporcionalidad correspondiente y su valor es característico del tipo de
sustancia que constituye el cuerpo en cuestión. Dicha constante se denomina calor
específico. Su significado puede deducirse de la ecuación (8.6). Si se despeja c,de ella
resulta:
ce = Q/ m.(Tf - Ti)
El calor específico de una sustancia equivale, por tanto, a una cantidad de calor por
unidad de masa y de temperatura; o en otros términos, es el calor que debe
suministrarse a la unidad de masa de una sustancia dada para elevar su temperatura un
grado.
Unidades de calor
La ecuación calorimétrica (8.6) sirve para determinar cantidades de calor si se conoce la
masa del cuerpo, su calor específico y la diferencia de temperatura, pero además
permite definir la caloría como unidad de calor. Si por convenio se toma el agua líquida
como sustancia de referencia asignando a su calor específico un valor unidad, la caloría
resulta de hacer uno el resto de las variables que intervienen en dicha ecuación.
Una caloría es la cantidad de calor necesaria para elevar en un grado centígrado (1 °C)
la temperatura de un gramo de agua. Esta definición, que tiene su origen en la época en
la que la teoría del calórico estaba en plena vigencia, se puede hacer más precisa si se
considera el hecho de que el calor específico del agua varía con la temperatura. En tal
caso la elevación de un grado centígrado a la que hace referencia la anterior definición
ha de producirse entre 14,5 y 15,5 °C a la presión atmosférica.
Una vez identificado el calor como una forma de energía y no como un fluido singular, la
distinción entre unidades de calor y unidades de energía perdió significado. Así, la
unidad de calor en el SI coincide con la de energía y es el joule (J), habiendo quedado la
caloría reducida a una unidad práctica que se ha mantenido por razones históricas,pero
que va siendo progresivamente desplazada por el joule.
Calor específico y capacidad calorífica
La ecuación calorimétrica puede escribirse también en la forma:
(8.7)
Q = C.(Tf - Ti)
expresando así que en un cuerpo dado la cantidad de calor cedido o absorbido es
directamente proporcional a la variación de temperatura. La nueva constante de
proporcionalidad C recibe el nombre de capacidad calorífica
C = Q/(T Tf - Ti)
y representa la cantidad de calor que cede o toma el cuerpo al variar su temperatura en
un grado. A diferencia del calor específico, la capacidad calorífica es una característica
de cada cuerpo y se expresa en el SI en J/K. Su relación con el calor específico resulta
de comparar las ecuaciones (8.6) y (8.7) en las que ambas magnitudes están presentes:
(8.8)
C = m.ce
De acuerdo con esta relación, la capacidad calorífica de un cuerpo depende de su masa
y de la naturaleza de la sustancia que lo compone.
Ejemplo de la determinación del calor específico: El calor específico de un cuerpo
puede determinarse mediante el calorímetro. Dado que éste es un atributo físico
característico de cada sustancia, la comparación del valor obtenido con los de una tabla
estándar de calores específicos puede ayudar a la identificación de la sustancia que
compone el cuerpo en cuestión.
Se pretende identificar el metal del que está formada una medalla. Para ello se determina su
masa mediante una balanza que arroja el valor de 25 g. A continuación se calienta al « baño
María »,hasta alcanzar una temperatura de 85 °C y se introduce en el interior de un
calorímetro que contiene 50 g de agua a 16,5 °C de temperatura. Al cabo de un cierto
tiempo y tras utilizar varias veces el agitador, la columna del termómetro del calorímetro deja
de subir señalando una temperatura de equilibrio de 19,5 °C. ¿De qué metal puede
tratarse?
Si se aplica la ecuación de conservación de la energía expresada en la forma, calor tomado
= - calor cedido, resulta:
Q1 = - Q2
m1.ce1.(T - T1) = - m2.ce2.(T - T2)
considerando en este caso el subíndice 1 referido al agua y el 2 referido a la moneda.
Sustituyendo valores en la ecuación anterior, se,tiene:
50 g.1 (cal/g.°C).(19,5 °C - 16,5 °C) = - 25 g. ce2.(19,5 °C - 85 °C)
Operando y despejando ce2 resulta:
150 (cal/g.°C) = 1 637,5. ce2
ce2 = 0,09 cal/g.°C
Si se compara el resultado con una tabla de calores específicos de metales, se concluye
que puede tratarse de cobre. Otras propiedades físicas como el color, por ejemplo,
confirmarán el resultado.
Medida del calor
De acuerdo con el principio de conservación de la energía, suponiendo que no existen
pérdidas, cuando dos cuerpos a diferentes temperaturas se ponen en contacto, el calor
tomado por uno de ellos ha de ser igual en cantidad al calor cedido por el otro. Para todo
proceso de transferencia calorífica que se realice entre dos cuerpos puede escribirse
entonces la ecuación:
Q1 = - Q2
en donde el signo - indica que en un cuerpo el calor se cede, mientras que en el otro se
toma. Recurriendo a la ecuación calorimétrica, la igualdad anterior puede escribirse en la
forma:
m1.ce1.(Te - T1) = - m2.ce2.(Te(8.9)
T2)
donde el subíndice 1 hace referencia al cuerpo frío y el subíndice 2 al caliente. La
temperatura Teen el equilibrio será superior a T1 e inferior a T2. La anterior ecuación
indica que si se conocen los valores del calor específico, midiendo temperaturas y
masas, es posible determinar cantidades de calor. El aparato que se utiliza para ello se
denomina calorímetro. Un calorímetro ordinario consta de un recipiente de vidrio aislado
térmicamente del exterior por un material apropiado. Una tapa cierra el conjunto y dos
pequeños orificios realizados sobre ella dan paso al termómetro y al agitador, los cuales
se sumergen en un líquido llamado calorimétrico, que es generalmente agua.
Cuando un cuerpo a diferente temperatura que la del agua se sumerge en ella y se cierra
el calorímetro, se produce una cesión de calor entre ambos hasta que se alcanza el
equilibrio térmico. El termómetro permite leer las temperaturas inicial y final del agua y
con un ligero movimiento del agitador se consigue una temperatura uniforme.
Conociendo el calor específico y la masa del agua utilizada, mediante la ecuación
calorimétrica se puede determinar la cantidad de calor cedida o absorbida por el agua.
En este tipo de medidas han de tomarse las debidas precauciones para que el
intercambio de calor en el calorímetro se realice en condiciones de suficiente aislamiento
térmico. Si las pérdidas son considerables no será posible aplicar la ecuación de
conservación Q1 = - Q2 y si ésta se utiliza los resultados estarán afectados de un
importante error.
La ecuación (8.9) puede aplicarse únicamente a aquellos casos en los cuales el
calentamiento o el enfriamiento del cuerpo problema no lleva consigo cambios de estado
físico (de sólido a líquido o viceversa, por ejemplo). A partir de ella y con la ayuda del
calorímetro es posible determinar también el calor específico del cuerpo si se conocen
las temperaturas T1, T2 y Te, las masas m1y m2 y el calor específico del agua.
CALOR Y TRABAJO
Relación entre calor y trabajo
Si calor y trabajo son ambos formas de energía en tránsito de unos cuerpos o sistemas a
otros, deben estar relacionadas entre sí. La comprobación de este tipo de relación fue
uno de los objetivos experimentales perseguidos con insistencia por el físico inglés
James Prescott Joule (1818-1889). Aun cuando efectuó diferentes experimentos en
busca de dicha relación, el más conocido consistió en determinar el calor producido
dentro de un calorímetro a consecuencia del rozamiento con el agua del calorímetro de
un sistema de paletas giratorias y compararlo posteriormente con el trabajo necesario
para moverlas.
La energía mecánica puesta en juego era controlada en el experimento de Joule
haciendo caer unas pesas cuya energía potencial inicial podía calcularse fácilmente de
modo que el trabajo W, como variación de la energía mecánica, vendría dado por:
W = Δ Ep = m.g.h
siendo m la masa de las pesas, h la altura desde la que caen y g la aceleración de la
gravedad. Por su parte, el calor liberado por la agitación del agua que producían las
aspas en movimiento daba lugar a un aumento de la temperatura del calorímetro y la
aplicación de la ecuación calorimétrica:
Q = m c (Tf- Ti)
permitía determinar el valor de Q y compararlo con el de W. Tras una serie de
experiencias en las que mejoró progresivamente sus resultados, llegó a encontrar que el
trabajo realizado sobre el sistema y el calor liberado en el calorímetro guardaban
siempre una relación constante y aproximadamente igual a 4,2. Es decir, por cada 4,2
joules de trabajo realizado se le comunicaba al calorímetro una cantidad de calor igual a
una caloría. Ese valor denominado equivalente mecánico del calor se conoce hoy con
más precisión y es considerado como 4,184 joules/calorías. La relación numérica entre
calor Q y trabajo W puede,entonces, escribirse en la forma:
W (joules) = 4,18.Q (calorías)
La consolidación de la noción de calor como una forma más de energía, hizo del
equivalente mecánico un simple factor de conversión entre unidades diferentes de una
misma magnitud física, la energía; algo parecido al número que permite convertir una
longitud expresada en pulgadas en la misma longitud expresada en centímetros.
Máquinas térmicas
Junto a la conversión de trabajo en calor puesta de manifiesto en las experiencias de
Joule, la transformación efectuada en sentido inverso es físicamente realizable. Los
motores de explosión que mueven, en general, los vehículos automóviles y la máquina
de vapor de las antiguas locomotoras de carbón, son dispositivos capaces de llevar a
cabo la transformación del calor en trabajo mecánico. Este tipo de dispositivos reciben el
nombre genérico de máquinas térmicas.
En todas las máquinas térmicas el sistema absorbe calor de un foco caliente; parte de él
lo transforma en trabajo y el resto lo cede al medio exterior que se encuentra a menor
temperatura. Este hecho constituye una regla general de toda máquina térmica y da
lugar a la definición de un parámetro característico de cada máquina que se denomina
rendimiento y se define como el cociente entre el trabajo efectuado y el calor empleado
para conseguirlo. Expresado en tantos por ciento toma la forma:
η (%) = W.100/Q
Ninguna máquina térmica alcanza un rendimiento del cien por cien. Esta limitación no es
de tipo técnico, de modo que no podrá ser eliminada cuando el desarrollo tecnológico
alcance un nivel superior al actual; se trata, sin embargo, de una ley general de la
naturaleza que imposibilita la transformación íntegra de calor en trabajo. Por tal motivo
las transformaciones energéticas que terminan en calor suponen una degradación de la
energía, toda vez que la total reconversión del calor en trabajo útil no está permitida por
las leyes naturales.
Ejemplo de la relación calor-trabajo: En una experiencia como la de Joule se ha utilizado un
peso de 10 kg que se ha elevado a una altura de 2 m. Si el calorímetro completo incluyendo
las aspas equivale a una masa de agua de 1,5 kg y la temperatura inicial es de 15 °C,
determínese la temperatura final que alcanzará el agua, admitiendo que todo el trabajo
mecánico se convierte en calor dentro del calorímetro. (Considérese el calor específico del
agua c = 4,18.10³ J/kg.K). De acuerdo con el principio de conservación de la energía, el
trabajo mecánico se convierte íntegramente en calor:
W=Q
Siendo en este caso W = m g h y Q = m´ ce.(Tf - Ti).
Igualando ambas expresiones y despejando Tf se tiene:
m g h = m´ ce.(Tf - Ti)
Tf = (m.g.h + m´.ce.Ti)/m´.ce
y sustituyendo resulta finalmente:
Tf (K) = [10 g.9,8 m/s ².2 m + 1,5 g.4,18.10³ (cal/g.°C).(15 K + 273 K)]/1,5 g.4,18.10³
(cal/g.°C)
Tf (K) =
es decir:
tf (°C) = 288 - 273 = 15 °C
EL CALOR
El calor es una manifestación de la energía provocada por el movimiento molecular. Al
calentarse un cuerpo, aumenta la energía cinética de las moléculas, produciéndose choques
más o menos violentos, según la cantidad de calor entregada.
El calor es susceptible de medir; lo que se efectúa teniendo en cuenta dos magnitudes
fundamentales: intensidad de calor y cantidad de calor.
1- La intensidad de calor está relacionada con la velocidad del movimiento molecular
estableciéndose para medirla una práctica que da una idea del grado o nivel del calor que
tiene un cuerpo determinado. Arbitrariamente se fijan parámetros comparativos que
permiten determinar dicho nivel de calor, al que se denomina temperatura. Se dice que un
cuerpo con gran velocidad molecular tiene más temperatura o más nivel de calor que otro.
2- La cantidad de calor de un cuerpo representa la suma de las energías térmicas de todas
las moléculas que lo componen. Es decir que mientras la intensidad de calor o temperatura
indica el grado de movimiento molecular o el nivel de calor de un cuerpo, esta magnitud
señala su contenido total de calor.
Se demuestra que la cantidad de calor de un cuerpo es función de la masa del cuerpo y de
su temperatura, o lo que es lo mismo, del número de moléculas que lo componen y de su
nivel de intensidad térmica o velocidad molecular.
Para determinar la cantidad de calor se ha establecido un valor característico, que depende
de las particularidades de cada cuerpo, que se denomina calor específico. Se define
como calor específico a la cantidad de calor necesario para elevar en 1 °C la
temperatura de la unidad de masa de una sustancia.
El calor específico,si bien depende de la temperatura en forma muy leve, puede suponerse
constante para cada sustancia en particular, a los fines de su aplicación práctica. Como
unidad se usa el agua a presión atmosférica normal, considerándose una temperatura
normal de 15 °C que está dentro del entorno de las aplicaciones prácticas.
De esa manera, el calor específico igual a 1, sería la cantidad de calor necesaria para elevar
la temperatura de 1 kg de agua en 1 °C (14,5 a 15,5) a presión atmosférica normal. A esta
cantidad de calor se la denomina (kcal) kilocaloría,y sería entonces la unidad de cantidad
de calor.
Para ello, la unidad de calor específico valdrá:
Ce = kcal/Kg.°C
El SIMELA o Sistema Métrico Legal Argentino, ha establecido como unidad de calor el
Joule . La equivalencia es la siguiente:
1 Kcal = 4185,5 joule
Calor sensible y calor latente
Cuando definimos la unidad de calor, mencionamos que el agregado de dicha energía
provocaba un aumento de la temperatura, a ese estado calórico cuya variación de nivel
puede determinarse mediante un termómetro, que es sensible a ella, se denomina calor
sensible.
Se representa por la fórmula:
Q = m.ce.(t°f - t°i)
Q es la cantidad de calor entregada o recibida por un cuerpo (Kcal)
m es la masa del cuerpo (Kg)
Ce es el calor específico de la sustancia (Kcal/Kg.°C)
T ° i es la temperatura inicial del cuerpo (°C)
T ° f es la temperatura final del cuerpo (°C)
Ejemplo 1: Calentar 1 kg de agua de 10 a 100 °C. ¿Qué cantidad de calor sensible se le ha
agregado?
Si
Q = m.ce.(t°f - t°i) ⇒ Q = 1 kg.(1 kcal/kg.°C).(100 °C - 10 °C) ⇒ Q = 90 kcal
Sin embargo, sucede que cuando se esta materializando un cambio de estado físico, se
verifica que el agregado o sustracción de calor no origina variación de temperatura. En
efecto, por ejemplo, si se tiene agua en ebullición, durante todo el proceso que esta dura, la
temperatura se mantiene constante en los 100 °C, aunque se le agregue calor
continuamente.
A ese calor que agregado a una sustancia no origina cambio de nivel térmico o temperatura,
se lo denomina calor latente, o sea, como su nombre lo indica, ese calor se encuentra
latente, y se consume en la acción de transformación física.
Q = m.c vl
Donde:
C vl es el calor latente de vaporización (kcal/kg)
El calor latente de vaporización del agua (100 °C) es 539 kcal/kg
El calor latente de fusión del agua (0 °C) es 80 kcal/kg
Ver Gráfico
Propagación del calor
Todo cuerpo con una determinada cantidad de calor, tiene la propiedad de cederlo a otro
cuerpo, siempre que éste se encuentre a menor temperatura.
Es decir, existe un flujo térmico que consiste en la cesión del calor de los puntos de mayor
temperatura. De esa manera, entonces, la energía térmica se transfiere del nivel térmico o
temperatura más alto al más bajo, hasta alcanzar un estado de equilibrio o igual
temperatura.
Los fenómenos que intervienen en la transmisión del calor son tres:
1. Convección
2. Radiación
3. Conducción
1 - Conducción
La transmisión del calor por conducción es típica de los sólidos. Se origina por la agitación
molecular provocada por el calor que se transmite progresivamente, sin modificar la
distancia relativa de las moléculas.
La velocidad con que el material deja pasar el calor por conducción,depende de su
conductividad que es una propiedad que tiene cada material.
Hay materiales que conducen más que otros. Los metales son mucho más conductores del
calor que, por ejemplo, los materiales de cerramiento de una construcción.
La conducción del calor se establece por un coeficiente λ de la conductividad térmica, que
es un valor determinado para cada elemento en particular.
Ejemplo 2: Hallar la cantidad de canto rodado necesario para un acumulador solar que
recibe 10000 Kcal/día si se quiere alcanzar una T ° f = 75 °C y partiendo de una T ° i = 20 °C
(Ce = 0.29 Cal/g.°C).
Q = 10000 Kcal = 10000000 Cal
T ° f = 75 °C
T ° i = 20 °C
Ce = 0.29 Cal/g.°C
m= ?
Si:
Q = m.ce.(tf - ti)
m = Q/[ce.(tf - ti)]
m = 10000000 cal/[(0,29 cal/g.°C).(75 °C - 20 °C)]
m = 10000000 cal/[(0,29 cal/g.°C).55 °C]
m = 626959,24 g
m = 626,96 kg
Ejemplo 3:
a - Qué cantidad de calor será necesaria para calentar el agua de una pileta que contiene
25000 litros de agua, si se desea aumentar su temperatura de 20 °C a 30 °C?
m = 25000 l = 25000 Kg
T ° i = 20 °C
T ° f = 35 °C
Ce = 1 Kcal/kg.°C
Q = m.Ce.Δ T ° ⇒ Q = 25000 Kg.(1 Kcal/Kg.°C). (30 °C - 20 °C)
Q = 25000 Kg.1 (Kcal/Kg.°C). 10 °C ⇒ Q = 250000 Kcal
b - Qué tiempo se necesitará para entregar estas calorias al agua si se emplea gas natural?
Poder calorífico del gas = 8000 Kcal/h.
8000 Kcal ⇒ 1 h
250000 Kcal ⇒ t = 250000 Kcal.1 h/8000 Kcal ⇒ t = 31.25 h
Ejemplo 4: Si mezclamos 1 l de agua a 92 °C con 0.5 l de agua 20 °C, qué temperatura
alcanzará la mezcla?
m1.ce.(-tf + ti1) = m2.ce.(tf - ti2)
-m1.ce.tf + m1.ce.ti1 = m2.ce.tf - m2.ce.ti2
m2.ce.ti2 + m1.ce.ti1 = m2.ce.tf + m1.ce.tf
ce.(m2.ti2 + m1.ti1) = (m2 + m1).ce.tf
(m2.ti2 + m1.ti1)/(m2 + m1) = tf
(1 l.92 °C + 0,5 l.20 °C)/(1 l + 0,5 l) = tf
tf = 102 l.°C/1,5 l
tf = 68 °C
Unidades de Energía
Unidades de Potencia
1 kgm = 9,8 J
1 cal = 4,18 J
1 Kcal = 427 kgm
1 C.V. = 735 W
1kgm/s = 9,8 W
-
Convección
La forma de transmisión de calor por convección es propia de los fluidos, por ejemplo, en
nuestro caso el aire o el agua. Por efecto de la variación de su peso debido a un aumento o
disminución de temperatura, se establece en ellos una circulación permanente y continua.
Ese movimiento del fluido produce, entonces, la transferencia del calor por convección,que
se orienta desde los puntos calientes a los fríos.
Se utiliza para su determinación un coeficiente Hc que tiene en cuenta la convección y cierta
radiación, y se denomina coeficiente de transmitancia.
Q = Hc.A.Δ T °
Radiación
La forma de transmisión del calor por radiación se produce en el vacío igual que la radiación
de la luz en forma de ondas electromagnéticas. De esa manera el proceso de transferencia
de calor por radiación no esta vinculado a soporte o vehículo material alguno, no pudiendo
ser explicado como en los casos anteriores en términos de moléculas que chocan o se
desplazan.
Se define entonces la radiación térmica como la transmisión de calor de un cuerpo a otro
sin contacto directo, en forma de energía radiante.
Entonces un cuerpo caliente transforma una parte de su contenido de calor en energía
radiante sobre su superficie, la cual se emite en forma de ondas, que al ser absorbidas por
otro cuerpo, se manifiesta en forma de calor. Se desprende de ello que para que la energía
radiante pueda ser convertida en calor es necesario que sea absorbida por una sustancia.
Todos los cuerpos absorben y además emiten energía radiante, dependiendo de la
temperatura a que se encuentren y de sus características físicas.
El cuerpo negro es un cuerpo ideal que emite y absorbe el máximo el calor por radiación.
Por ello cuando un cuerpo esta constituido por superficies oscuras, emite y absorbe el calor
por radiación en gran proporción, ocurriendo todo lo contrario cuando se trata de cuerpos de
superficies blancas o brillantes.
Los cuerpos calientes emiten mayor cantidad de calor que los fríos, habiendo un continuo
intercambio de energía radiante entre las sustancias que se encuentran a distintas
temperaturas.
La fórmula para su cálculo es:
R = r.A.(T °/100)4.T °
r : constante de radiación
T ° : temperatura en grados kelvin
T °1 > T °2
En el siguiente ejemplo se indican las tres formas de trasmisión de calor. Supóngase que en
un local se ubica un recipiente que contiene agua caliente. Se origina una trasferencia de
calor del agua caliente al aire del local, debido a la diferencia de temperatura.
Si se analiza el proceso de trasferencia a través de la pared del recipiente se observa que
en una primera etapa el calor fluye del agua caliente a la cara interior de la pared por
convección, originándose el movimiento de la misma debido que al enfriarse aumenta su
densidad y desciende. Luego el calor se trasmite por conducción a través de la pared, y
por último se entrega al local por convección al aire produciendose la circulación del mismo
debido a que al calentarse disminuye su densidad y asciende, y por radiación a los distintos
elementos del entorno que rodean al recipiente. El aire es prácticamente diatérmico,o sea
no absorbe en forma directa el calor por radiación.
Coeficiente de transmitancia total K
Para los cálculos de la transferencia de calor de una pared o elemento de la construcción se
utiliza un coeficiente de transferencia de calor total, que tiene en cuenta los fenómenos
indicados precedentemente y permite simplificar dichos cálculos.
Se define al coeficiente de transmitancia total K como la cantidad de calor en kcal, que se
transmite totalmente en una hora a través de un m ² de superficie, existiendo una diferencia
de temperatura de 1° C entre el ambiente interno y externo.
Q = K.A.(T °1 - T °2)
Siendo:
Q : Cantidad de calor que se transmite (kcal/h)
K : Coeficiente de transmitancia térmica (kcal/h.m ².°C). Según tablas.
A : Area (m ²).
T °1 : Temperatura del aire en la cara más caliente (°C).
T °2 : Temperatura del aire en la cara más fria (°C).
Los coeficientes K para las construcciones normales están tabulados por la Norma IRAM
11.601, pero para muros especiales o de características especiales deben calcularse.
Determinación del coeficiente de transmitancia total K
Para el cálculo de transmitancia total K, se emplea la siguiente fórmula:
Se denomina resistencia total Rt a la inversa de K, es decir:
Rt = 1/K
A su vez, las inversas de α, se denominan resistencias superficiales.
R si = 1/ α i y R se = 1/ α e
λ: coeficiente de conductibilidad térmica(kcal/m.h.°C).
α i: coeficiente superficial interior (kcal/h.m ².°C).
α e: coeficiente superficial exterior (kcal/h.m ².°C).
K: coeficiente de transmitancia térmica total(kcal/h.m ².°C).
R t: resistencia a la transmitancia térmica total (m ³.h.°C/kcal).
R si: resistencia superficial interior (m ³.h.°C/kcal).
R se: resistencia superficial exterior (m ³.h.°C/kcal).
e: espesor de los materiales (m).
De esa manera, la ecuación será:
Rt = 1/λ = Rsi + e1/λ1 + e2/λ2 + ... + Rc + Rse
Donde Rc es la resistencia que opone al pasaje de calor en caso de cámaras de aire.
Ejemplo 5 : Calcular la resistencia térmica total de un muro, formado por mampostería de
12 cm de espesor, una cámara de aire de 2 cm y un panderete de mampostería de 5 cm
interior.
Rt = 1/λ = Rsi + e1/λ1 + e2/λ2 + Rc + Rse
Rt = 0,61 m ².h.°C/kcal
O sea:
k = 1/Rt
k = 1/(0,61 m ².h.°C/kcal)
k = 1,64 kcal/m ².h.°C
En este mismo ejemplo ¿qué pasaría si en lugar de la cámara de aire se utilizara lana de
vidrio de 2 cm de espesor?
Rt = 1/λ = Rsi + e1/λ1 + e2/λ2 + e3/λ3 + Rse
Se aprecia, entonces, que mejora notablemente la resistencia térmica del muro aplicándole
aislante térmico.
Ejemplo 6 : Calcular la cantidad de calor que fluye a través de una lámina de aluminio de 2
mm de espesor, si la diferencia de temperatura es de 20 °C.
H = (K/e).A.Δ T ° ⇒H = ((0,49 cal/s.cm.°C)/0,2 cm).20 °C ⇒H = 49 cal/s
Ejemplo 7 : Se tiene un recipiente cúbico de vidrio de 1 m ² de superficie en sus 6 caras,
calcular la temperatura final si entrega 80 Kcal/h y su temperatura inicial es de 20 °C.
Q = m.ce.(tf - ti)
tf = Q/m.ce + ti
Lado = √A/6
Volumen = Lado³ = 0,068 m ³
tf = (80 kcal/h)/[(68 kg).(1 kcal/kg.°C.h)] + 20 °C
tf = 21,18 °C
Ejemplo 8 : Según Normas IRAM el K de un ladrillo en una pared de 30 cm de espesor es
de 1,62 kcal/m ². h.°C, entonses hallar λ para una mampostería de 1 m ² y luego el flujo de
calor para una variación térmica de 1 °C.
k = λ/e
λ = e.k
k = (1,64 kcal/m ².h.°C).(1000 cal/1 kcal).(1 m ²/10000 cm ²).(1 h/3600 s)
k = 0,000045 cal/cm ².s.°C
λ = 30 cm.0,000045 cal/cm ².s.°C
λ = 0,00135 cal/cm.s.°C
A = 1 m ² = 10000 cm ²
H = A.λ.Δt/e
H = 10000 cm ².(0,00135 cal/cm.s.°C).(1 °C/30 cm
H = 0,45 cal/s
Ejemplo 9 : Se tiene un termotanque de 0,5 m de diámetro, 1,2 m de altura y una aislación
térmica de espuma de poliestireno de 2 cm de espesor; calcular:
a) La cantidad de calor necesaria para elevar su temperatura en 20 °C.
b) Si se desea mantener una temperatura interior de 60 °C y la temperatura media exterior
es de 20 °C, calcular las pérdidas de calor hacia el exterior.
c) Calcular el rendimiento del equipo.
d) Calcular el gas consumido anualmente para cubrir las pérdidas.
S = π.d.h + π.d ²/4
S = 3,14.50 cm.120 cm + 3,14.(50 cm) ²/4
S = 20802,5 cm ²
V = π.h.d ²/4
V = 3,14.120 cm.(50 cm) ²/4
V = 235500 cm ³
m = 235,5 kg
a)
Q = m.ce.(tf - ti)
Q = 235,5 kg.(1 kcal/kg.°C).20 °C
Q = 4710 kcal
b)
H = A.λ.Δt/e
H = (20802,5 cm ²/2 cm).(0,00002 cal/cm ².s.°C).40 °C
H = 8,321 cal/s
H = 29,96 kcal/h
c)
Rendimiento
R = Q agua/Q gas
R = 4710 kcal.100%/9300 kcal
R = 50,65 %
d)
H año = (29,96 kcal/h).(8760 h/año)
H año = 262449,6 kcal/año
Calorías perdidas = H año/R
H año/R = (262449,6 kcal/año)/50,65 %
H año/R = 129518,9 kcal/año
Gas perdido = Calorías perdidas/calorias del gas/m ³
Gp = (129518,9 kcal/año)/(9300 kcal/m ³)
Gp = 13,93 m ³/año
Ejemplo 10: ¿Qué cantidad de calor se perderá de un recipiente que contiene 500 cm ³ de
agua a 70 °C durante 45´?. Si la temperatura ambiente es de 18 °C y el recipiente esta
recubierto de poliestireno expandido de 9,52 mm de espesor. λ = 0,03 kcal/h.m.°C
A = π.d.h + π.d ²/4
A = 3,14.7,6 cm.19,5 cm + 3,14.(7,6 cm) ²/4
A = 556,03 cm ²
A = 0,055603 m ²
Δt = tf - ti
Δt = 70 °C - 18 °C
Δt = 52 °C
H = A.λ.Δt/e
H = (0,055603 m ²/0,00952 m).(0,03 cal/m ².h.°C).52
°C
H = 9,11 kcal/h
H* = (9,11 kcal/h).0,75 h
H* = 6,83 kcal
Hallar la temperatura final a los 45 minutos.
Δ T ° = -Q/m.Ce (es negativa debido a que pierde T °)
Δt = ti - te = -Q/m.ce
ti = te - Q/m.ce
ti = 70 °C - 6,83 kcal/[(0,5 kg).(1 kcal/kg.°C)]
ti = 56,33 °C
Ejemplo 11: Se tiene una resistencia eléctrica a la cual se le han medido las siguientes
características:
U = 220 v I = 1,75 A cos φ = 0,95
Se sabe que P = U.I. cos φ, que Δ T ° producira esta resistencia eléctrica cuando calienta
500 cm ³ de agua durante 120 segundos.
P = 220 v . 1,75 A.. 0,95 ⇒ P = 365,75 w
E = P/t
E = 365,75 W.120 s.1 h/3600 s
E = 12,192 W.h
Sabiendo que 860 kcal = 1 kw
E = 12,192 W.h.(860 kcal/1 kW).(1 kW/1000 W)
E = 10,485 kcal
Δt = Q/m.ce
Δt = 10,485 kcal/[(0,5 kg).(1 kcal/kg.°C)]
Δt = 20,97 °C
Hallar el costo:
Costo = Valor (kW.h).E
Costo = (0,15 $/kW.h)/0,012192 kW.h
Costo = $ 0,0018
Hallar la temperatura final para a) 45 min y b) 20 min.
H = A.λ.Δt/e
H = (0,055603 m ²/0,00952 m).(0,03 cal/m ².h.°C).52 °C
H = 7,97 kcal/h
a)
H1 = (7,97 kcal/h).0,75 h
H1 = 5,98 kcal
Δt1 = H1/m.ce
Δt1 = (5,98 kcal)/[(0,5 kg).(1 kcal/kg.°C)]
Δt1 = 11,96 °C
t1 = 60,04 °C
b)
H2 = (7,97 kcal/h).0,33 h
H2 = 2,63 kcal
Δt2 = H2/m.ce
Δt2 = (2,63 kcal)/[(0,5 kg).(1 kcal/kg.°C)]
Δt2 = 5,26 °C
t2 = 66,74 °C
Hallar la temperatura final para: c) 10 min; d) 30 min; e) 40 min; f) 50 min y g) 60min, y luego
graficar la temperatura en función del tiempo.
c)
H3 = (7,97 kcal/h).0,17 h
H3 = 1,35 kcal
Δt3 = H3/m.ce
Δt3 = (1,35 kcal)/[(0,5 kg).(1 kcal/kg.°C)]
Δt3 = 2,71 °C
t3 = 67,29 °C
d)
H4 = (7,97 kcal/h).0,50 h
H4 = 3,99 kcal
Δt4 = H4/m.ce
Δt4 = (3,99 kcal)/[(0,5 kg).(1 kcal/kg.°C)]
Δt4 = 7,98 °C
t4 = 62,02 °C
e)
H5 = (7,97 kcal/h).0,66 h
H5 = 5,31 kcal
Δt5 = H5/m.ce
Δt5 = (5,31 kcal)/[(0,5 kg).(1 kcal/kg.°C)]
Δt5 = 10,62 °C
t5 = 59,38 °C
f)
H6 = (7,97 kcal/h).0,83 h
H6 = 6,64 kcal
Δt6 = H6/m.ce
Δt6 = (6,64 kcal)/[(0,5 kg).(1 kcal/kg.°C)]
Δt6 = 13,28 °C
t6 = 56,72 °C
g)
H7 = (7,97 kcal/h).1 h
H7 = 7,97 kcal
Δt7 = H7/m.ce
Δt7 = (7,97 kcal)/[(0,5 kg).(1 kcal/kg.°C)]
Δt7 = 15,94 °C
t7 = 54,06 °C
Ver Gráfico
Ejemplo 12: Hallar la pérdida por convección en el siguiente caso:
T ° i = 70 °C
T °e = 10 °C
T °s = 25 °C
S=1m²
t=1h
Q = 45,05 kcal
CICLOS TERMODINAMICOS
Resulta útil tratar los procesos termodinámicos basándose en ciclos: procesos que
devuelven un sistema a su estado original después de una serie de fases, de manera que
todas las variables termodinámicas relevantes vuelven a tomar sus valores originales. En un
ciclo completo, la energía interna de un sistema no puede cambiar, puesto que sólo
depende de dichas variables. Por tanto, el calor total neto transferido al sistema debe ser
igual al trabajo total neto realizado por el sistema.
Un motor térmico de eficiencia perfecta realizaría un ciclo ideal en el que todo el calor se
convertiría en trabajo mecánico. El ciclo de Carnot, es un ciclo termodinámico que
constituye el ciclo básico de todos los motores térmicos,y demuestra que no puede existir
ese motor perfecto. Cualquier motor térmico pierde parte del calor suministrado. El segundo
principio de la termodinámica impone un límite superior a la eficiencia de un motor, límite
que siempre es menor del 100%. La eficiencia límite se alcanza en lo que se conoce como
ciclo de Carnot.
Ciclo Otto
En el punto a la mezcla de nafta y aire ya está en el cilindro.
ab: contracción adiabática.
cd: expansión adiabática.
bc: calentamiento isocórico.
ad: enfriamiento isocórico.
R: relación de compresión.
Cp: calor específico a presión constante
Cv: calor específico a volumen constante
γ = Cp/Cv (Sears 419 - Tabla 18.1)
(γ - 1)
η = 1 - 1/R
Para un R = 8, y un γ = 1,4 (aire), η = 0,56
Ciclo diesel
El gasoil se inyecta durante la carrera ab.
ab: contracción adiabática.
cd: expansión adiabáticas.
ad: enfriamiento isocórico.
bc: expansión y calentamiento isobárica.
R: relación de compresión.
Cp: calor específico a presión constante
Cv: calor específico a volumen constante
γ = Cp/Cv (Sears 419 - Tabla 18.1)
η = 1 - 1/R( γ - 1)
Para un R = 15-20, y un γ = 1,4 (aire), η = 0,65-0,70
Ciclo de Carnot
Una máquina de Carnot es perfecta, es decir, convierte la máxima energía térmica posible
en trabajo mecánico. Carnot demostró que la eficiencia máxima de cualquier máquina
depende de la diferencia entre las temperaturas máxima y mínima alcanzadas durante un
ciclo. Cuanto mayor es esa diferencia, más eficiente es la máquina. Por ejemplo, un motor
de automóvil sería más eficiente si el combustible se quemara a mayor temperatura o los
gases de escape salieran a menor temperatura.
ab y cd: contracciones y expansiones isotérmicas.
bc y ad: contracciones y expansiones adiabáticas.
η = W/QH ⇒ η= (QH - QC)/QH ⇒ η = 1 - QC/ QH
QH = W ab = n.R.TH.ln Vb/Va
QC = W cd = n.R.TC.ln Vc/Vd
QC/QH = TC/TH
η = 1 - TC/TH
Ciclo de refrigeración
Los sistemas de compresión emplean cuatro elementos en el ciclo de refrigeración:
compresor, condensador, válvula de expansión y evaporador.
En el evaporador, el refrigerante se evapora y absorbe calor del espacio que está enfriando
y de su contenido.
A continuación, el vapor pasa a un compresor movido por un motor que incrementa su
presión, lo que aumenta su temperatura (entrega trabajo al sistema).
El gas sobrecalentado a alta presión se transforma posteriormente en líquido en un
condensador refrigerado por aire o agua.
Después del condensador, el líquido pasa por una válvula de expansión, donde su presión y
temperatura se reducen hasta alcanzar las condiciones que existen en el evaporador.
QH = QC - L ⇒L = QC-QH
η = - QC /L ⇒ - QC/(QC-QH)
Sistemas de absorción
Algunos refrigeradores domésticos funcionan mediante el principio de absorción. En ellos,
una llama de gas calienta una disolución concentrada de amoníaco en agua en un recipiente
llamado generador, y el amoníaco se desprende en forma de vapor y pasa a un
condensador. Allí se licúa y fluye hacia el evaporador, igual que en el sistema de
compresión. Sin embargo, en lugar de pasar a un compresor al salir del evaporador, el
amoníaco gaseoso se reabsorbe en la solución diluida y parcialmente enfriada procedente
del generador, para formar de nuevo una disolución concentrada de amoníaco. Este
proceso de reabsorción se produce en un recipiente llamado absorbedor, desde donde el
líquido concentrado fluye de vuelta al generador para completar el ciclo.
FISICA – TRABAJO Y ENERGIA
TRABAJO
Una fuerza constante genera trabajo cuando, aplicada a un cuerpo, lo desplaza a lo
largo de una determinada distancia.
Mientras se realiza trabajo sobre el cuerpo, se produce una transferencia de energía al
mismo, por lo que puede decirse que el trabajo es energía en movimiento. Por otra parte, si
una fuerza constante no produce movimiento, no se realiza trabajo. Por ejemplo, el sostener
un libro con el brazo extendido no implica trabajo alguno sobre el libro, independientemente
del esfuerzo necesario. El trabajo se expresa en Joules (J).
Cuando la fuerza tiene la dirección de movimiento.
L = F.d
L: Trabajo realizado por la fuerza.
Cuando la fuerza aplicada tiene una inclinación α con respecto al movimiento.
L = F.cos α .d
Todas las fuerzas perpendiculares al movimiento no realizan trabajo.
La fuerza puede no ser mecánica,como ocurre en el levantamiento de un cuerpo o en la
aceleración de un avión de reacción; también puede ser una fuerza electrostática,
electrodinámica o de tensión superficial.
Energía
La magnitud denominada energía enlaza todas las ramas de la física. En el ámbito de la
física, debe suministrarse energía para realizar trabajo. La energía se expresa en joules (J).
Existen muchas formas de energía: energía potencial eléctrica y magnética, energía
cinética, energía acumulada en resortes estirados, gases comprimidos o enlaces
moleculares,energía térmica e incluso la propia masa.
Energía cinética
Cuando una fuerza aumenta la velocidad de un cuerpo también se realiza trabajo, como
ocurre por ejemplo en la aceleración de un avión por el empuje de sus reactores. Cuando un
cuerpo se desplaza con movimiento variado desarrolla energía cinética.
Ec = ½.m.v ²
L = F.d
L = Ec
F.d = ½.m.v ²
Ec: Energía cinética.
El trabajo realizado por la fuerza resultante que actúa sobre una partícula es igual a la
variación de la energía cinética de dicha partícula.
Δ Ec = Ec2 - Ec1
L = Ec2 - Ec1
F.d = ½.m.(v ²2 - v ²1)
Δ Ec: Variación de la energía cinética.
Energía potencial
Cuando se levanta un objeto desde el suelo hasta la superficie de una mesa, por ejemplo,
se realiza trabajo al tener que vencer la fuerza de la gravedad,dirigida hacia abajo; la
energía comunicada al cuerpo por este trabajo aumenta su energía potencial. Si se realiza
trabajo para elevar un objeto a una altura superior, se almacena energía en forma de
energía potencial gravitatoria.
Cuando un cuerpo varía su altura desarrolla energía potencial.
Ep = m.g.h ⇔ L = F.d ⇔ L = Ep
P.d = m.g.h
Ep: Energía potencial.
El trabajo realizado por la fuerza peso es igual a la variación de la energía potencial.
Δ Ep = Ep2 - Ep1
L = Ep2 - Ep1
P.d = m.g.(h2 - h1)
Δ Ep: Variación de la energía potencial.
En todas las transformaciones entre un tipo de energía y otro se conserva la energía total, y
se conoce como teorema de la energía mecánica (Δ EM). Por ejemplo, si se ejerce trabajo
sobre una pelota de goma para levantarla, se aumenta su energía potencial gravitatoria. Si
se deja caer la pelota, esta energía potencial gravitatoria se convierte en energía cinética.
Cuando la pelota choca contra el suelo, se deforma y se produce fricción entre las
moléculas de su material. Esta fricción se transforma en calor o energía térmica.
Fuerzas conservativas
Para un cuerpo de masa m que se mueve del punto 1 al 2 y luego del punto 2 al 1.
Una fuerza es conservativa si el trabajo efectuado por ella sobre una partícula que se
mueve en cualquier viaje de ida y vuelta es 0.
Δ EM = 0
Δ EM : Variación de la energía mecánica.
Trabajo de fuerzas conservativas:
L = Δ EM
Δ EM = Δ Ec + Δ Ep
L = Δ Ec + Δ Ep
Fuerzas no conservativas
Para un cuerpo de masa m que se mueve del punto 1 al 2 y luego del punto 2 al 1.
Una fuerza es no conservativa si el trabajo efectuado por ella sobre una partícula que
se mueve en cualquier viaje de ida y vuelta es distinto de 0.
Δ EM ≠ 0
Δ EM = HO
Δ EM: Variación de la energía mecánica.
HO : Trabajo de la fuerza de rozamiento.
Trabajo de fuerzas no conservativas:
L = Δ EM + HO
L = Δ Ec + Δ Ep + HO
Siendo: HO = Fr.d
Potencia
La potencia desarrollada por una fuerza aplicada a un cuerpo es el trabajo realizado por
ésta durante el tiempo de aplicación. La potencia se expresa en watt (W).
P=L/t
P = F.d / t
v=d/t
P = F.v
También:
P = (Δ Ec + Δ Ep + HO)/t
Si no hay fuerza de rozamiento
P = (Δ Ec +Δ Ep)/t
Si no cambio su altura
P = (Δ Ec)/t
P: potencia
Caballo de vapor: Unidad tradicional para expresar la potencia mecánica, es decir, el trabajo
mecánico que puede realizar un motor por unidad de tiempo; suele abreviarse por CV. En el
Sistema Internacional de unidades, la unidad de potencia es el vatio; 1 caballo de vapor
equivale a 736 vatios. Su valor original era, por definición, 75 kilográmetros por segundo.
Resolver:
1) Transformar 250 kgf.m a Joul y kW.h.
Ver solución al final de ésta página
2) ¿Cuántos kgf.m y Joul representan 25 kW.h?.
Ver solución al final de ésta página
3) Indicar cuántos Joul y kW.h son 125478 kgm.
Ver solución al final de ésta página
4) Indicar el trabajo necesario para deslizar un cuerpo a 2 m de su posición inicial mediante
una fuerza de 10 N.
Ver solución al final de ésta página
5) ¿Qué trabajo realiza un hombre para elevar una bolsa de 70 kgf a una altura de 2,5 m?.
Expresarlo en:
a) kgf.m
b) Joule
c) kW.h
Ver solución al final de ésta página
6) Un cuerpo cae libremente y tarda 3 s en tocar tierra. Si su peso es de 4 N, ¿qué trabajo
deberá efectuarse para elevarlo hasta el lugar desde donde cayo?. Expresarlo en:
a) Joule.
b) kgm.
Ver solución al final de ésta página
Responder:
1) ¿Qué es el trabajo mecánico?.
2) ¿En que unidades se mide el trabajo?.
3) ¿Cuáles son sus equivalencias?.
4) Si se levanta un cuerpo desde el suelo, ¿hay trabajo?.
5) ¿Las máquinas simples, realizan trabajo?.
Resultados:
1)
1 kgf.m →
9,807 J
250 kgf.m → x = 250 kgf.m × 9,807 J/1 kgf.m
x = 2451,75 J
1 W = 1 J/s
1kW = 1.000 J/s
1kW.h = 1.000 J.3.600 s/s
1kW.h = 3.600.000 J s/s
1 J = 1kW.h/3.600.000
1 kgf.m →
9,807 J/3.600.000
250 kgf.m → x = 250 kgf.m × 9,807 J/3.600.000 kgf.m
x = 6,81.10-4 kW.h
2)
1 kW.h →
3.600.000 J
25 kW.h → x = 25 kW × 3.600.000 J/1 kW.h
x = 9.107 J
1 kW.h →
3.600.000 kgf.m/9.807
25 kW.h → x = 25 kW.h × 9,807 × 3.600.000 J/1 kW.h
x = 9.177.118 kgf.m
3)
1 kgf.m →
9,807 J
125.478 kgf.m → x = 125.478 kgf.m × 9,807 J/1 kgf.m
x = 1.230.563 J
1 kgf.m →
9,807 J/3.600.000
125.478 kgf.m → x = 125.478 kgf.m × 9,807 J/3.600.000 kgf.m
x = 0,3418 kW.h
4)
L = F × d ⇒ L = 10 N × 2 m ⇒ L = 20 J
5)
a) L = F × d ⇒ L = 70 kgf × 2,5 m ⇒ L = 175 kgf.m
b) L = 175 kgf.m × 9,807 J/kgf.m ⇒ L = 1716,225 J
a) L = 175 kgf.m × 9,807 J/3.600.000 kgf.m ⇒ L = 0,000477 kW.h
6)
L = F.d
En éste caso se trata de la fuerza peso, por lo tanto:
L = P.d
y al ser un movimiento vertical la distancia es la altura:
L = P.h
Mediante cinemática calculamos la altura para caída libre.
h = ½.g.t ²
h = ½ × 9,807 (m/s ²) × (3 s) ² ⇒ h = ½ × 9,807 (m/s ²) × 9 s ² ⇒ h = 44,1315 m
Luego:
a) L = P × h ⇒ L = 4 N × 44,1315 m ⇒ L = 176,526 J
b) L = 176,526 J/(9,807 kgf.m × J) ⇒ L = 18 kgf.m
UNIDADES Y MEDIDAS
M.K.S.⇒ Técnico
Técnico ⇒ M.K.S.
M.K.S. ⇒ Otros
Masa
m
kg = 0,06852 slug
slug = 14,59 kg
kg =2,205 lb
Longitud
e
m = 3,28pie
pie = 0,3048 m
m = 39,3 plg
Tiempo
t
s=s
s=s
s=s
Velocidad
v = e/t
m/s = 3,28pie/s
pie/s = 0,3048 m/s
m/s = 2,237 mi/h
m/s ² = 3,28pie/s ²
pie/s ² = 0,3048
m/s ²
m/s ² = 8503,2 mi/h ²
Aceleración a = F/m = v/t
Fuerza
Peso
F = m.a
N = 0,102 kg
kg = 9,807 N
N = 0,2248 lbf
Trabajo
Energía
L = F.e
J = 0,000948BTU
BTU = 1055 J
J = 0,2389 cal
Potencia
P = L/t
W = 3,413 BTU/h
BTU/h = 0,293 W
W =0,00134 hp
Pa = 0,000145 lbf/plg
Pa =0,0000102 kg/cm
lbf/plg ² = 6895 Pa
²
²
Presión
p = F/A
Densidad
δ = m/V
kg/m ³ = 0,00194
slug/pie³
slug/pie³ = 515,4
kg/m ³
kg/m ³ = 0,0003613
lb/plg³
Peso
específico
ρ = P/V =
δ.m/V
N/m ³ = 0,002888
kg/pie³
kg/pie³ = 346,27
N/m ³
N/m ³ =0,00000167
kg/plg³
Momento
M = F.d
N.m = 0,3347 kg.pie
kg.pie= 2,988 N.m
N.m = 0,102 kg.m
Unidad/Sistema
C.G.S
M.K.S
Técnico otros 1
otros 2
Masa
gr.
Kg
slug
Lb
Longitud
cm.
m
m
pulg.
pie
Tiempo
s
s
s
s
s
Velocidad
cm/s
m/s
m/s
pulg/s
pie/s
Aceleración
cm/s ²
m/s ²
m/s ²
pulg/s ²
pie/s ²
Fuerza
dina
N
Kgf
Lbf
Presión
dina/cm ² Pa = N/m ² Kgf/m ² Lbf/pulg ² atmósfera o lbf/pie ²
Trabajo
ergio
(J) Joule
B.T.U
Potencia
ergio/s
Watt (J/s)
H.P
C.V
cal/s
Momento
dina.cm
N.m
Kgm
Lbf.pulg
Lbf.pie
cal
QUIMICA – COMPUESTOS QUIMICOS
LA ENERGIA EN LAS REACCIONES QUIMICAS
El estudio de las reacciones químicas desde un punto de vista energético mejora la
descripción de los procesos químicos. La entalpía o contenido energético cambia al pasar
de los reactivos a los productos y, junto con la entropía o grado de desorden, determina el
que una reacción se produzca o no espontáneamente. La variación de entalpía en una
reacción química no depende del camino seguido por la reacción, sino sólo de los estados
inicial y final.
Las reacciones químicas son procesos de transformación o cambio de unas sustancias en
otras. En ciertas ocasiones, el interés de este tipo de procesos se centra en la obtención de
nuevos productos útiles para la medicina o para la industria; en otras, se persigue la
obtención de energía; tal es el caso, por ejemplo, de la combustión de la gasolina o del
carbón. En general, las reacciones químicas llevan consigo cambios materiales y también
cambios energéticos.
El estudio de los procesos químicos requiere,por tanto, algo más que cálculos sobre cuánta
cantidad de productos se forma a partir de una cantidad dada de reactivos. La
determinación de la cantidad de energía puesta en juego en una reacción o la explicación de
su carácter espontáneo constituyen algunas de las cuestiones o aspectos energéticos de las
reacciones químicas.
ENERGIA Y PROCESOS QUIMICOS
Conceptos fundamentales
Toda reacción química lleva asociada una variación observable de energía que puede
manifestarse en forma luminosa, eléctrica, mecánica o calorífica, siendo esta última, con
mucho, la más frecuente. Para estudiar un proceso químico desde un punto de vista
energético, se suele considerar separadamente el conjunto de sustancias en
transformación, denominado genéricamente sistema , del resto, que recibe el nombre de
medio o entorno . De acuerdo con lo anterior, las reacciones químicas implican una
transferencia de energía que en unas ocasiones se lleva a cabo del sistema al medio y en
otras en sentido inverso. Si la reacción lleva consigo un desprendimiento de calor del
sistema al medio, se denomina exotérmica . Por el contrario, si el proceso químico implica la
absorción de una cierta cantidad de calor del medio por parte del sistema, se denomina
endotérmica .
Todas las reacciones de combustión son exotérmicas; así, la reacción de combustión del
hidrógeno libera gran cantidad de calor:
H2 + ½O2 → H2 O + calor
Por el contrario, la reacción de descomposición del carbonato de calcio es endotérmica pues
requiere la aportación al sistema de una cierta cantidad de energía calorífica del medio:
CaCO3 + calor → CO2 + CaO
La cantidad de calor desprendido o absorbido en una reacción química, referida a las
cantidades de sustancias, en número de moles, que figuran en la correspondiente ecuación
química ajustada, se denomina calor de reacción . Se expresa en kilocalorías (kcal) o en
kilojulios (kJ) y suele situarse en el segundo miembro de la ecuación; en el caso de que se
trate de una reacción endotérmica irá precedido de un signo menos.
Los calores de reacción dependen de las condiciones de presión, temperatura y estado
físico (sólido, líquido o gaseoso) del sistema; por ello, cuando se pretendan hacer cálculos
de energía deben especificarse en la ecuación química dichas condiciones.
Así la reacción de formación del agua se escribirá en forma completa como:
H2 (g; 1 atmósfera) + ½O2 (g; 1 atmósfera) → 298 K → H2 O (g; 1 atmósfera) + 241,8 kJ
Dado que las diferentes sustancias son gaseosas, se ha hecho explícita la presión. En
ocasiones, se sobreentiende que los calores de reacción están referidos a unas condiciones
estándar de presión y temperatura, por lo general 1 atmósfera y 298 K, señalándose
únicamente el estado físico. La ecuación química resultante de añadir toda esta información
recibe el nombre de ecuación termoquímica .
El contenido energético de las sustancias químicas
Si en los procesos químicos se producen cesiones o absorciones de energía del sistema al
medio, cabe pensar que tanto los reactivos como los productos almacenan una determinada
cantidad de energía, siendo la diferencia entre ambas la que entra en juego en la reacción
química. A tal cantidad de energía almacenada por cada una de las sustancias se le
denomina contenido energético o entalpía y se representa mediante la letra H.
De acuerdo con esto, en las reacciones endotérmicas el contenido energético de los
productos es superior al de los reactivos; el sistema ha pasado de un estado inicial menos
energético a otro final más energético, y para ello ha sido preciso la absorción de la
correspondiente cantidad de energía del medio. En las reacciones exotérmicas sucede, por
el contrario, que el contenido energético de los productos es inferior al de los reactivos, de
modo que el estado final del sistema es menos energético que el estado inicial; el sistema
ha perdido energía cediéndosela al medio. En aquellas reacciones en las cuales las
condiciones de presión y temperatura se mantienen constantes, la diferencia Δ H de
contenido energético del sistema entre los estados final e inicial, o lo que es lo mismo, la
energía puesta en juego en el proceso, coincide con el calor de reacción que aparece de
forma explícita en la ecuación termoquímica. En las reacciones endotérmicas la variación de
entalpía es positiva, Δ H > 0, mientras que en las exotérmicas es negativa, Δ H < 0.
Cabe preguntarse cuál es, finalmente, la razón por la que en las reacciones químicas se
producen estos cambios de energía. La respuesta se encuentra en la propia naturaleza de
los procesos químicos. Una reacción química implica una ruptura de enlaces y una posterior
recomposición de los átomos resultantes en moléculas diferentes, formadas por nuevos
enlaces.
No todos los enlaces son igual de fuertes, es decir, la energía necesaria para romperlos
(energía de enlace) es, en general, diferente, de ahí que toda reorganización implique una
variación del contenido energético del sistema. Si los enlaces de los productos son, en
conjunto, más débiles que los de los reactivos, podrá haber producción de energía y la
reacción será exotérmica. Si por el contrario, los enlaces de los productos son más fuertes
que los de los reactivos, habrá sido necesario un aporte de energía y la reacción será
entonces endotérmica.
LA ESPONTANEIDAD DE LAS REACCIONES
El principio de mínima energía
Como en toda la naturaleza, también en las reacciones químicas opera el principio de
mínima energía según el cual los sistemas materiales tienden a evolucionar en el sentido en
el que disminuye su energía potencial. Una bola rueda por un plano inclinado hasta
encontrar la posición más baja, que es la de menor energía; un muelle comprimido se
expande para conseguir una condición de mínima deformación y, por tanto, de mínima
energía acumulada, y una reacción química evoluciona hacia estados de menor contenido
energético.
Sucede, en ocasiones, que siendo el contenido energético de los productos inferior al de los
reactivos, el sistema en cuestión no evoluciona espontáneamente como cabría esperar
según el principio de mínima energía. En una parte de los casos, esto es debido a que se
precisa una cierta cantidad de energía, por lo general pequeña, para poner en marcha la
reacción, de la misma manera que es preciso dar un impulso inicial a un bloque de madera
para que descienda por un plano inclinado. Esta dosis de energía inicial se denomina
energía de activación y se emplea en la ruptura de los primeros enlaces, que suministrará
energía propia suficiente como para mantener la reacción por sí misma.
El principio de máximo desorden
De acuerdo con el principio de mínima energía,considerado aisladamente, ninguna reacción
endotérmica podría ser espontánea, pues en este tipo de reacciones la energía del sistema
aumenta. Sin embargo, existen en la naturaleza reacciones y procesos que, siendo
endotérmicos, se producen espontáneamente. Ello indica que, junto con la energía, otro
factor debe condicionar el carácter espontáneo de una reacción química. Ese factor
adicional es el grado de desorden , también denominado entropía (S) .
La entropía depende de factores tales como el número de partículas en juego o el estado
físico de las sustancias. Así el estado gaseoso es más desordenado que el líquido o que el
sólido y corresponde, por lo tanto, a una mayor entropía.
Junto con la tendencia a alcanzar el estado de mínima energía, los sistemas químicos
tienden de forma natural a alcanzar el estado de máximo desorden y son ambos factores los
que controlan conjuntamente el carácter espontáneo de las reacciones químicas.
Un balance entre energía y desorden
El hecho observado de que la espontaneidad de las reacciones químicas dependa no sólo
de la energía sino también del desorden, puede explicarse a partir de la siguiente ecuación
entre magnitudes físicas:
Δ G = Δ H - T Δ S (23.1)
donde H es el contenido energético o entalpía, T es la temperatura absoluta, S es la
entropía y G la llamada energía libre de Gibbs . Esta magnitud G a la que contribuyen tanto
la entalpía como la entropía, es la que determina el carácter espontáneo de una reacción
química. En todos los procesos espontáneos la energía libre del sistema disminuye, es
decir, el valor final de G es menor que el inicial y, por tanto, Δ G es negativa. De acuerdo
con la anterior ecuación, tal disminución (Δ G < 0) podrá ser debida a una disminución del
contenido energético H ( Δ H < 0), a un aumento del desorden (Δ S > 0) o a ambos.
El resultado final de ese balance entre energía y desorden es entonces el responsable de la
espontaneidad de la reacción. Si T.Δ Ses mayor que Δ H aunque el proceso sea
endotérmico (Δ H > 0) será espontáneo (Δ G < 0). Tal es el caso de la reacción:
N2O4 (g) → 2.NO2 (g)
que no es espontánea a 258 K y sí lo es a 358 K, porque, a esa temperatura, el término de
desorden T.δ S predomina sobre el de energía Δ H, con lo que Δ G resulta negativo. Este
ejemplo muestra la importancia que tiene el factor temperatura a la hora de establecer si
una reacción química es o no espontánea.
Toda reacción exotérmica (Δ H < 0) en la que tenga lugar un aumento de entropía (Δ S > 0)
es espontánea (Δ G < 0). La reacción de descomposición del agua oxigenada constituye un
ejemplo:
2.H2 O2 (g; 1 atmósfera) → 298 K → 2.H2 O (g; 1 atmósfera) + O2 (g; 1 atmósfera) + 211 kJ
En este proceso aumenta el número de partículas (a igualdad de estado gaseoso de
reactivos y productos) por lo que aumenta el desorden; pero además, desprende calor (Δ H
< 0). Ambas circunstancias contribuyen a que la energía libre disminuya y así, el proceso
tiene lugar espontáneamente.
Además de las consideradas anteriormente,existen otras posibilidades para ese balance
definido por la ecuación (23.1). La tabla adjunta las resume esquemáticamente.
APLICACION: EVOLUCION DE UNA REACCION QUIMICA
La reacción de síntesis del amoníaco:
3.H2 (g) + N2 (g) → 2.NH3 (g)
viene acompañada, en las condiciones de 298 K de temperatura y una atmósfera de
presión, por los siguientes cambios en las variables termodinámicas H y S:
Δ H = -22,1 kcal
-
Δ S =-47,4.10 ³ kcal/k
Discútase en qué condiciones la reacción se efectuará espontáneamente.
Dado que Δ H es negativa hay una pérdida de contenido energético por parte del sistema, o
lo que es lo mismo, la reacción es exotérmica. Por su parte la entropía disminuye como
corresponde a una disminución en el número de moléculas que pasa de ser cuatro para los
reactivos a dos para el producto.
Para averiguar si a la temperatura considerada la reacción evoluciona espontáneamente
será preciso determinar Δ G y particularmente su signo:
-
Δ G = Δ H - T.Δ S = -22,1 - [298 - (-47,4) .10 ³] = 8,0 kcal
La Δ G resulta negativa, por tanto la reacción es espontánea. Un aumento de temperatura
no favorece la reacción; en efecto, al aumentar la temperatura el segundo término se hace
más positivo y por tanto Δ G resulta menos negativo.
LA LEY DE HESS
Calor de formación y calor de reacción
El calor de formación Δ Hf de una sustancia química representa la energía liberada o
consumida durante la formación de dicha sustancia, en condiciones normales, a partir de los
elementos que la constituyen. Si en tales condiciones se consideran nulos los contenidos
energéticos H de los elementos, el calor de formación Δ Hf de un compuesto coincide con su
contenido energético o entalpía. Si se compara la definición de calor de formación con la de
calor de reacción se observa que el calor de formación es un tipo particular de calor de
reacción (el correspondiente a reacciones de formación o de síntesis de un compuesto).
La determinación de calores de reacción puede efectuarse de un modo experimental si la
reacción correspondiente se lleva a cabo de forma aislada y controlada en el interior de un
calorímetro. Sin embargo, en ocasiones, esto no es posible porque tienen lugar varias
reacciones simultáneamente,y no una sola. En tales casos es posible determinarlos de una
forma indirecta, recurriendo a una propiedad de la entalpía; el hecho de que H sea una
función de estado , esto es, que dependa exclusivamente de los estados inicial y final del
sistema, permite calcular calores de reacción a partir del conocimiento de procesos
intermedios.
Ley de Hess
El calor de formación Δ H1 del monóxido de carbono, CO:
C (grafito, s) + ½.O2 (g) → CO (g) ΔH1
no puede determinarse directamente porque en las condiciones en que se produce, parte
del CO se transforma en CO2 . Sin embargo, sí que es posible medir directamente, con la
ayuda del calorímetro, los calores de reacción de los siguientes procesos:
CO (g) + ½.O2 (g) → CO2 (g)
ΔH2 = 282,6 kJ/mol
C (grafito, s) + O2 (g) → CO2 (g)
ΔH3 = -392,9 kJ/mol
El conjunto de estas tres reacciones puede escribirse en la forma:
Dado que el efecto térmico de una reacción no depende del camino, sino sólo de los
estados inicial y final, se podrá escribir:
Δ H3 = Δ H1 + Δ H2
y por tanto:
Δ H1 = Δ H3 - Δ H2 = -392,9 + 282,6 = 110,3 kJ/mol
Dicho de otro modo cuando una reacción, C + ½.O2 → CO, escribirse como la suma
algebraica (suma con signos) de otras reacciones:
C + O2
CO2
→
CO2
(ΔH2 )
→ C + ½.O2 (-ΔH3 )
C + ½.O2 →
CO
(ΔH1 )
su calor de reacción es la suma algebraica de los calores de tales reacciones
(Δ H1 = Δ H2 - Δ H3 ). O en otros términos: el calor de la reacción de un determinado
proceso químico es siempre el mismo, cualquiera que sea el camino seguido por la
reacción, o sus etapas intermedias.
El contenido de este enunciado recibe el nombre de Ley de Hess . De acuerdo con esa
misma ley, los calores de reacción pueden calcularse a partir de los calores de formación de
reactivos y productos.
El siguiente diagrama representa los procesos de formación y reacción de reactivos y
productos, y sus relaciones en términos energéticos:
Aplicando la ley de Hess a los dos diferentes caminos que conectan reactivos y productos e
igualando ambos términos resulta:
Δ H = -Δ Hf (reactivos) + 0 + Δ Hf (productos)
es decir:
Δ H = Δ Hf (productos) - Δ Hf (reactivos)
Por tanto, el calor de reacción de un proceso químico resulta ser igual a la diferencia entre
los calores de formación de los productos y los calores de formación de los reactivos:
Δ H =(suma calores de formación de productos) - (suma calores de formación de reactivos)
CALOR DE REACCION Y ENERGIA DE ENLACE
La energía de enlace es la cantidad de energía que se libera en la formación de un enlace
entre átomos cuando reaccionan en estado gaseoso. Constituye una medida de la fuerza
del enlace covalente; así, por ejemplo, a un enlace sencillo carbono-carbono le corresponde
una energía de enlace de -83,1 kcal/mol; a uno doble -147 kcal/mol y a uno triple -194
kcal/mol. Desde el punto de vista de la termoquímica,se puede interpretar como la variación
de entalpía H correspondiente a una reacción del tipo:
A (g) + B (g) → A - B (g)
efectuada en condiciones de 1 atmósfera de presión y 298 K de temperatura, siendo A y B
los átomos considerados. La energía de enlace Δ H(A - B) es siempre negativa, pues en la
unión disminuye el contenido energético del sistema, haciéndose más estable.
La aplicación de la ley de Hess permite determinar el calor de reacción a partir de las
energías de enlace y viceversa. Como ejemplo de la primera posibilidad puede considerarse
el cálculo del calor de reacción del proceso:
H-C≡C-H +
H2
→ H3 C-CH3
acetileno
hidrógeno
etano
en el cual se rompen dos enlaces H — H y un enlace C ≡C y aparecen un enlace
C —C y cuatro enlaces H —C nuevos. El balance global de estas operaciones parciales en
términos de variación del contenido energético será:
Δ Hf = Δ H(C — C) + 4Δ H(C— H) - [Δ H(C ≡ C) + 2Δ H(H— H)]
A partir de las energías de enlace correspondientes, supuestas conocidas, se calcula
entonces el calor de reacción.
Como ejemplo de la segunda posibilidad, se presenta el cálculo de la energía de enlace H
—Cl a partir del calor de formación Δ Hf del HCI y de las energías de los enlaces H —H y Cl
— Cl (supuestas conocidas).
La formación del HCI puede efectuarse por los siguientes caminos:
De acuerdo con la ley de Hess:
Δ H1 = Δ H2 + Δ H3
en donde,
Δ H1 = 2.Δ H.(H — Cl)
Δ H2 = Δ H.(H — H) + Δ H.(Cl — CI)
Δ H3 = 2. δ Hf
por tanto:
ΔH (H-Cl) = ½[ΔH (H-H) + ΔH (Cl-Cl) + 2.Δ.Hf ]
LA MATERIA EN LAS REACCIONES QUIMICAS
Las reacciones químicas son procesos de cambio de unas sustancias en otras. De acuerdo
con la teoría atómica de la materia se explican como el resultado de un reagrupamiento de
átomos para dar nuevas moléculas. Las sustancias que participan en una reacción química
y las proporciones en que lo hacen, quedan expresadas en la ecuación química
correspondiente, que sirve de base para la realización de diferentes tipos de cálculos
químicos.
La naturaleza es dinámica. Tanto la materia viva como la inerte sufren continuamente
procesos de transformación, de los cuales los más importantes son los que afectan a su
constitución. La formación de las rocas, la erosión química de las aguas, el nacimiento de
una planta o la respiración de un mamífero son procesos observables que suponen cambios
de unas sustancias en otras. Todos ellos, más allá de sus diferencias, tienen algo en común:
implican transformaciones a escala molecular, que son las responsables de los cambios
materiales observables a simple vista.
LAS REACCIONES QUIMICAS
Conceptos fundamentales
Una molécula de una determinada sustancia pura constituye el representante elemental de
dicha sustancia, es decir, la cantidad más pequeña de ella que posee todas sus
propiedades químicas. Cuando una sustancia dada, bajo ciertas condiciones, se transforma
en otra u otras con diferentes propiedades, se ha de pensar que algo ha ocurrido a nivel
molecular.
De forma espontánea unas veces y provocada otras, los átomos, que en número y
proporciones fijas forman unas moléculas determinadas, pueden desligarse unos de otros
por rotura de sus enlaces y reunirse nuevamente de diferente manera, dando lugar, por
tanto, a nuevas moléculas. El efecto conjunto de estas transformaciones moleculares se
traducirá en un cambio observable de sustancia o cambio químico. Dicho proceso de
transformación recibe el nombre de reacción química. Con frecuencia, sustancias formadas
por iones participan en las reacciones químicas. En tales casos, las moléculas de la
descripción anterior deben ser consideradas realmente como agregados iónicos.
En las reacciones químicas la sustancia o sustancias iniciales se denominan reactivos y las
finales productos;el proceso de transformación se representa mediante las llamadas
ecuaciones químicas en la forma:
reactivos → (reacción química) → productos
Tanto los reactivos como los productos se escriben mediante sus fórmulas
correspondientes. La flecha indica el sentido de la transformación. Si es posible conviene
indicar en la ecuación química el estado físico de reactivos y productos, el cual se suele
expresar mediante las siguientes abreviaturas situadas a continuación de la fórmula
química:
(s)sólido, (l) líquido, (g) gas, (aq) solución acuosa
Cada uno de los símbolos químicos que aparecen en la ecuación no sólo constituye la
abreviatura del nombre del elemento correspondiente, sino que además representa un
átomo de dicho elemento. Análogamente sucede con la fórmula de un compuesto, la cual
designa a dicho compuesto y muestra los átomos (o los iones) que componen su molécula
(o su agregado iónico elemental) así como la relación numérica entre ellos.
Esta forma simbólica de escribir las reacciones químicas constituye, por tanto, la descripción
de las transformaciones a nivel molecular que aquéllas implican. La representación visual de
tales procesos puede efectuarse recurriendo a modelos o construcciones mediante esferas
que reproducen la estructura aproximada de la molécula o del agregado iónico en cuestión.
En este tipo de modelos, cada esfera, con su correspondiente color, representa un átomo o
un ion y el conjunto describe la forma exterior de la molécula o del agregado iónico.
Tipos de reacciones químicas
El reagrupamiento que experimentan los átomos de los reactivos en una transformación
química puede ser de diferentes tipos. He aquí algunos de ellos:
a) Reacciones de síntesis. Se caracterizan porque los productos son sustancias más
complejas, desde un punto de vista químico, que los reactivos. La formación de un
compuesto a partir de sus elementos correspondientes es el tipo de reacción de síntesis
más sencilla. Así, el cobre, a suficiente temperatura, se combina con el azufre para formar
sulfuro de cobre (I) según la reacción:
2.Cu (s) + S (s) → calor → Cu2S (s) sulfuro de cobre (I)
b) Reacciones de descomposición. Al contrario que en las reacciones de síntesis, los
productos son en este caso sustancias más sencillas que los reactivos. Así, cuando el
carbonato de cobre se calienta fuertemente se descompone según la reacción:
CuCO3 (s) → calor → CuO (s) + CO2 (s)
c) Reacciones de desplazamiento. Tienen lugar cuando siendo uno de los reactivos una
sustancia simple o elemento, actúa sobre un compuesto desplazando a uno de sus
elementos y ocupando el lugar de éste en la correspondiente molécula. Así las reacciones
de ataque de los metales por los ácidos llevan consigo la sustitución del hidrógeno del ácido
por el metal correspondiente. Tal es el caso de la acción del ácido clorhídrico sobre
limaduras de hierro que tiene lugar en la forma:
Fe (s) + 2.HCl (aq) → FeCl2 (s) + H2 (g)
d) Reacciones de doble descomposición. Se producen entre dos compuestos y equivalen a
un intercambio o sustitución mutua de elementos que da lugar a dos nuevas sustancias
químicamente análogas a las primeras. Así el sodio desplaza a la plata en el nitrato de
plata,pero es a su vez desplazado por aquélla en el cloruro de sodio:
NaCl + AgNO3 → NaNO3 + AgCl
MASA Y VOLUMEN EN LAS REACCIONES
La conservación de la masa
Toda reacción química establece una relación cualitativa entre reactivos y productos, pues
expresa la naturaleza de éstos en función de la de aquéllos. Pero, además,fija las
proporciones o cantidades medibles en las que unos y otros intervienen. El fundamento de
esta relación cuantitativa entre las diferentes sustancias que participan en una reacción
dada fue establecido en la última mitad del siglo XVIII por el químico francés Antoine
Laurent Lavoisier (1743-1794). La aplicación de la balanza y de la medida de masas al
estudio de multitud de reacciones químicas le permitió descubrir que en cualquier proceso
químico la suma de las masas de las sustancias que intervienen (reactivos) es idéntica a la
de las sustancias que se originan como consecuencia de la reacción (productos). Es decir,
en toda reacción química la masa no se crea ni se destruye, sólo cambia de unas sustancias
a otras.
La teoría atómica dio una sencilla interpretación a esta ley de conservación. Si los átomos
no son alterados esencialmente en las reacciones químicas,sino únicamente las moléculas,
el número de átomos de cada elemento que constituye los reactivos ha de coincidir
exactamente con el correspondiente de los productos, por lo que la masa total en juego se
mantendrá constante en la reacción. La ley de conservación de la masa de Lavoisier
constituyó una pieza fundamental en el desarrollo y consolidación de la química como
ciencia.
Las proporciones en masa en las combinaciones químicas
El estudio de las cantidades en las que diferentes sustancias participan en una reacción
química fue objeto de la atención de los primeros químicos. Junto con Lavoisier, Proust
(1754-1826), John Dalton (1766-1844) y Richter (1824-1898) enunciaron diferentes leyes
que en conjunto se conocen como leyes ponderales o relativas al peso. La utilización del
concepto de peso en química sería sustituida más adelante por el de masa, de modo que
las leyes ponderales hacen referencia a las proporciones en masa características de las
combinaciones químicas. Dichas leyes fueron enunciadas en su mayoría, antes de que se
dispusiese de un modelo atómico sobre la constitución de la materia y contribuyeron
notablemente a la formulación por John Dalton de dicho modelo.
La ley de Proust o de las proporciones definidas o constantes: Cuando dos o más elementos
se combinan para formar un compuesto lo hacen en una relación ponderal (o de masas) fija
y definida.
Esta ley indica que la composición de una combinación es siempre la misma y que, por lo
tanto, el porcentaje o proporción en la que intervienen los diferentes elementos es constante
y característica de la sustancia compuesta considerada. Así en el amoníaco (NH3) la
proporción en masa nitrógeno/hidrógeno es de 4,67:1 cualquiera que sea la muestra que se
considere.
La ley de Dalton o de las proporciones múltiples: Cuando dos elementos se unen para
formar más de un compuesto, las cantidades de un mismo elemento que se combinan con
una cantidad fija del otro,guardan entre sí una relación que corresponde a números enteros
sencillos.
Para ilustrar el significado de esta ley puede considerarse el caso de los óxidos de carbono;
distintas experiencias de síntesis indican que es posible conseguir dos combinaciones
diferentes de carbono y oxígeno. En una de ellas las masas de oxígeno y carbono que se
combinan están en una relación de 4 a 3, es decir,
O/C = 4/3; se trata del monóxido de carbono (CO). En la otra, dicha relación es de 8 a 3,
O/C = 8/3; se trata en este caso del dióxido de carbono (CO2). Ambos cocientes representan
la cantidad de oxígeno que se combina por unidad de masa de carbono para formar los
óxidos. De acuerdo con la ley, tales cantidades guardan entre sí una relación entera
sencilla: 8/3 ÷ 4/3 = 2.
La ley de Richter o de las proporciones recíprocas: Las masas de dos elementos diferentes
que se combinan con una misma cantidad de un tercer elemento, guardan la misma relación
que las masas de aquellos elementos cuando se combinan entre sí.
Considerando los compuestos Cl2O y H2O las cantidades de cloro e hidrógeno que se
combinan con 16,0 g de oxígeno son 72,0 y 2,0 g respectivamente. Lo que indica la ley de
Richter es que cuando Cl y H se combinan para formar HCI lo hacen en la proporción de
72,0/2.
Las leyes ponderales pueden interpretarse de una forma sencilla recurriendo a las fórmulas
químicas, al concepto de masa atómica y al modelo atómico de Dalton que se esconde
detrás de estos conceptos. Así la ley de Proust es consecuencia de que la composición en
cuanto al tipo de átomos y a su número en una fórmula dada sea siempre la misma. La ley
de Dalton refleja la existencia de las diferentes valencias químicas de un elemento que se
traducen en subíndices definidos en las fórmulas de sus combinaciones con otro elemento
dado. La ley de Richter puede considerarse como una consecuencia de la de Proust y de las
propiedades aritméticas de las proporciones.
Las proporciones en volumen en las combinaciones químicas
La importancia de la medida en el desarrollo de la química alcanzó también a los volúmenes
de las sustancias gaseosas en las reacciones químicas. El químico francés Gay Lussac
estudió con detalle algunas reacciones químicas entre gases tales como la síntesis del
vapor de agua y del amoníaco a partir de sus elementos correspondientes. En todos los
casos las proporciones de los volúmenes de las sustancias guardaban una cierta
regularidad que la expresó en forma de ley.
La ley de Gay Lussac de los volúmenes de combinación: En cualquier reacción química, los
volúmenes de las sustancias gaseosas que intervienen en ella, medidos en las mismas
condiciones de presión y temperatura, guardan entre sí una relación que corresponde a
números enteros sencillos.
Así, dos volúmenes de hidrógeno se combinan con uno de oxígeno para dar uno de vapor
de agua. Un volumen de cloro se combina con otro de hidrógeno para dar dos de cloruro de
hidrógeno. Un volumen de nitrógeno se combina con tres de hidrógeno para dar dos de
amoníaco.
Los experimentos de Gay Lussac indicaban que el volumen de la combinación gaseosa
resultante era igual o menor que la suma de los volúmenes de las sustancias gaseosas
reaccionantes; por lo tanto, los volúmenes de combinación no podían, en general, sumarse.
La ley de Gay Lussac enunciada en 1808 se limitaba a describir los resultados de los
experimentos de un modo resumido, pero no los explicaba. La explicación a dicha ley sería
efectuada tres años más tarde por el físico italiano Amadeo Avogadro (1776-1856).
La ley de Avogadro: En las mismas condiciones de presión y temperatura, volúmenes
iguales de gases diferentes contienen igual número de moléculas.
Avogadro era conocedor del trabajo de Gay Lussac y particularmente de su descubrimiento
de que el volumen de un gas aumenta con la temperatura en una proporción que es la
misma para todos los gases (1.ª ley de Gay Lussac). Este resultado le sugirió que, si la
composición de la molécula de la sustancia gaseosa no influía en la relación entre volumen
y temperatura, dicha relación debería depender del número de moléculas existente; es decir,
a igualdad de presión y temperatura el volumen de un gas debería ser proporcional al
número de moléculas contenidas en él. Además, Avogadro especificó que las moléculas de
los elementos gaseosos debían ser diatómicas (H2, O2, Cl2, etc.). Esta idea entraba en
conflicto con la sostenida erróneamente por Dalton, pero junto con la anterior, explicaba la
ley de los volúmenes de combinación. De acuerdo con ella los resultados de las
experiencias de Gay Lussac representados por medio de ecuaciones químicas toman la
forma:
2.H2(g) + O2(g) → 2.H2O(g)
2.vol + 1.vol → 2.vol
N2 + 3.H2 → 2.NH3
1.vol + 3.vol → 2.vol
Cl2 + H2 → 2.HCI
1.vol + 1.vol → 2.vol
y muestran por qué las proporciones en volumen corresponden a números sencillos.
Empleando algunas ecuaciones de la física puede demostrarse que un mol de cualquier
gas, es decir, 6,029.1023 moléculas, medido en condiciones normales de presión y
temperatura (0 °C y 1 atmósfera de presión), ocupa un volumen de 22,4 litros. Esta cantidad
recibe el nombre de volumen molar y permite expresar, sólo para sustancias gaseosas,una
misma cantidad de sustancia en moles, su volumen correspondiente en litros o su masa en
gramos.
MASA Y ENERGIA
En 1789 Lavoisier escribía: «Debemos considerar como un axioma incontestable que en
todas las operaciones del Arte y la Naturaleza, nada se crea; la misma cantidad de materia
existe antes y después del experímento... y no ocurre otra cosa que cambios y
modificaciones en la combinación de estos elementos. »
El principio de la conservación de la masa en las reacciones químicas ha sido puesto en
duda en diferentes ocasiones desde que fuera formulado por Lavoisier, sin embargo, hasta
la llegada de la teoría de la relatividad de Albert Einstein en 1905 esa intuición vaga de
algunos científicos no se vería materializada en un resultado positivo. De acuerdo con Albert
Einstein «si un cuerpo cede la energía Δ E en forma de radiación,su masa disminuye en Δ
E/ c ². La masa de un cuerpo es una medida de su contenido energético; si la energía
8
cambia en Δ E,la masa del cuerpo cambia en el mismo sentido en Δ E/(3.10 ) ²». Su famosa
ecuación:
Δ E = m.c ²
8
siendo c = 3.10 m/s la velocidad de la luz, indica que en todo cambio de materia, y también
en los procesos químicos,la absorción o la liberación de energía debe ir acompañada de un
aumento o una disminución de la masa del sistema.
Lo que sucede, sin embargo, es que debido a la enorme magnitud de la constante c ² las
variaciones de energía que se producen en las reacciones químicas se corresponden con
cambios de masa ínfimos que no pueden ser detectados ni por las balanzas analíticas más
precisas. Se hace así buena la afirmación de Hans Landolt, uno de los químicos que
pusieron a prueba la ley de Lavoisier, quien en 1909 afirmaba: «La prueba experimental de
la ley de conservación de la masa puede considerarse completa. Si existe alguna desviación
será menor de la milésima de gramo.» La ley de Lavoisier sigue, por tanto, siendo válida, al
menos en términos prácticos, en el dominio de la química.
En las reacciones nucleares, sin embargo, las energías liberadas son mayores y la ley de
conservación de la masa se funde con la de conservación de la energía en un solo principio.
La ley de Lavoisier generalizada con la importante aportación de Albert Einstein, puede
escribirse en la forma:
Σ(masa + energía/c ²) = constante
que indica que, en un sistema cerrado, la suma de las masas incrementada en el término
equivalente de energía se mantiene constante.
APLICACION: CALCULOS ESTEQUIOMETRICOS (II)
Cuando se vierte ácido clorhídrico sobre limaduras de cinc, se produce la siguiente reacción
con desprendimiento de hidrógeno gaseoso:
Zn (s) + HCl (aq) → ZnCl2 (s) + H2 (g)
Determinar qué volumen de hidrógeno, medido en condiciones normales, se recogerá
cuando son atacados 30 g de Zn. ¿Cuántas moléculas de hidrógeno estarán contenidas en
dicho volumen?
Para ajustar la reacción bastará en este caso multiplicar por 2 el HCI:
Zn + 2.HCl → ZnCl2 + H2
De ella se deduce que por cada mol de átomos de Zn se producirá un mol de moléculas de
H2, pues la relación entre sus respectivos coeficientes es de 1:1. Pero un mol de átomos de
Zn tiene una masa igual a un átomo-gramo de dicho metal,esto es, a 65,4 g. Asimismo, un
mol de H2 ocupa 22,4 I en condiciones normales, luego estableciendo la siguiente relación
de proporcionalidad:
65,4 g de Zn/22,4 l de H2 = 30 g de Zn/x
resulta:
x = 30.22,4/65,4 = 10,3 l de H2
Recordando ahora que un mol de cualquier sustancia contiene 6,02 · 1023 moléculas, la
segunda parte del problema se resuelve recurriendo ahora a la proporcionalidad entre
volumen y número de moles:
23
22,4 l de H2/6,02.10
moléculas = 10,3 l de H2/x
23
x = 10,3.6,02.10 /22,4 = 2,76.1023 moléculas
ECUACIONES QUIMICAS
El balance de materia en las reacciones químicas
Partiendo de la ley de conservación de la masa y de su relación con la teoría atómica de la
materia permiten enfocar el estudio de las reacciones químicas como si se tratara de un
balance entre átomos de una misma especie.
Para que dicho balance cuadre, se han de introducir, con frecuencia, algunos coeficientes
numéricos que permiten igualar el número de átomos de cada elemento a uno y otro lado de
la flecha. Cuando esto se consigue se dice que la reacción química está ajustada, lo que
significa que puede ser considerada, en sentido estricto, como una igualdad o ecuación
química.
Dado que las masas de los diferentes átomos son conocidas, las ecuaciones ajustadas se
convierten, en primer término, en relaciones entre las masas de sustancias que intervienen
en la reacción. Ello hace posible la realización de cálculos químicos precisos sobre la base
que proporcionan las ecuaciones químicas ajustadas, sus símbolos y sus coeficientes
numéricos. Así, la reacción de descomposición del óxido de cobre (II) una vez ajustada es:
2.CuO (s) → calor → 2.Cu (s) + O2 (g)
e indica que por cada dos moléculas de óxido de cobre (II) se forman dos átomos de cobre y
una molécula de oxígeno. Tratando dicha ecuación química como si de una ecuación
matemática se tratara, es posible multiplicar ambos miembros por un mismo número N sin
que se altere la igualdad, es decir:
2.N.CuO (s) → calor → 2.N.Cu (s) + N.O2 (g)
Si N representa el número de Avogadro NAo número de partículas que componen un mol,
entonces la ecuación anterior puede interpretarse en términos de moles; dos moles de CuO
se descomponen en dos moles de Cu y un mol de O2. Por tanto los coeficientes de una
ecuación química ajustada representan también la proporción en número de moles, de
reactivos y productos que participan en la reacción.
Cuando las sustancias son gaseosas, de acuerdo con la hipótesis de Avogadro, cada mol
equivale a un volumen de sustancia de 22,4 litros medidos en condiciones normales de
presión y temperatura. Ello significa que, junto con cálculos de masas, es posible efectuar
cálculos de volúmenes en aquellos casos en que intervengan sustancias gaseosas.
El ajuste de las ecuaciones químicas
El conocimiento de cuestiones tales como qué productos cabe esperar a partir de unos
reactivos determinados, qué reactivos darán lugar a ciertos productos o incluso si una
reacción dada es o no posible, son cuestiones que se aprenden con la práctica. Sin
embargo, conocidos los reactivos y los productos, el ajuste de la reacción correspondiente
constituye una mera consecuencia de la ley de Lavoisier de conservación de la masa.
Además ésta es una operación previa a la realización de muchos de los problemas de
química básica.
Uno de los procedimientos habituales empleados para ajustar una reacción química puede
describirse en los siguientes términos:
1. Se escribe la reacción química en la forma habitual:
reactivos → productos
2. Se cuenta el número de átomos de cada elemento en uno y otro miembro de la ecuación.
Si son iguales para cada uno de los elementos presentes, la ecuación está ajustada.
3. Si no es así, será preciso multiplicar las fórmulas de los reactivos y productos por ciertos
coeficientes tales que produzcan la igualdad numérica deseada. La búsqueda de este
conjunto de coeficientes puede hacerse mediante tanteos. No obstante, este procedimiento
de ensayo y error no siempre es efectivo y puede ser sustituido por otro más sistemático,
que equivale a plantear un sistema de ecuaciones con dichos coeficientes como incógnitas.
Tornando como ejemplo de referencia la reacción de combustión del propano:
C3H8 + O2 → CO2 + H2O
estos serían los pasos a seguir:
a) Se fijan unos coeficientes genéricos a, b,c, d:
a.C3H8 + b.O2 → c.CO2 + d.H2O
b) Se impone la ley de conservación de la masa a nivel atómico, para lo cual se iguala, para
cada elemento diferente, el producto de su subíndice por su coeficiente,en ambos miembros
de la ecuación química:
Para el C
Para el H
Para el O
3a = c
8a = 2d
2b = 2c + d
c) Se resuelve el sistema. Si, como en el ejemplo, el número de coeficientes es superior en
una unidad al de elementos, entonces se iguala cualquiera de ellos a uno. Si una vez
resuelto el sistema, los coeficientes resultantes fueran fraccionarios, se convierten en
enteros multiplicando todos ellos por su mínimo común denominador:
a=1
b=5
c=3
d=4
d) Se sustituyen los valores en la ecuación de partida y se comprueba que el ajuste es
correcto mediante el correspondiente recuento de átomos de cada elemento en uno y otro
miembro de la ecuación química:
C3H8 + 5.O2 → 3.CO2 + 4.H2O
Listado de los 64 compuestos inorgánicos ácidos mas comunes
Fórmula
H2O
H2O2
B2O3
Br2O
Br2O3
Br2O5
Clase
Nomenclatura
Oxido ácido o anhídrido
Oxido ácido o anhídrido
Oxido ácido o anhídrido
Oxido ácido o anhídrido
Agua
Peróxido de hidrógeno
Bórico
Hipobromoso
Bromoso
Brómico
Br2O7
Cl2O
Cl2O3
Cl2O5
Cl2O7
CO
CO2
CrO2
CrO3
I2 O
I2 O3
I2 O5
I2 O7
Mn2O7
MnO2
MnO3
N2O3
N2O5
P2O3
P2O5
SO
SO2
SO3
Oxido ácido o anhídrido
Oxido ácido o anhídrido
Oxido ácido o anhídrido
Oxido ácido o anhídrido
Oxido ácido o anhídrido
Oxido ácido o anhídrido
Oxido ácido o anhídrido
Oxido ácido o anhídrido
Oxido ácido o anhídrido
Oxido ácido o anhídrido
Oxido ácido o anhídrido
Oxido ácido o anhídrido
Oxido ácido o anhídrido
Oxido ácido o anhídrido
Oxido ácido o anhídrido
Oxido ácido o anhídrido
Oxido ácido o anhídrido
Oxido ácido o anhídrido
Oxido ácido o anhídrido
Oxido ácido o anhídrido
Oxido ácido o anhídrido
Oxido ácido o anhídrido
Oxido ácido o anhídrido
Perbrómico
Hipocloroso
Cloroso
Clórico
Perclórico
Monóxido de carbono
Dióxido de carbono
Cromoso
Crómico
Hipoyodoso
Yodoso
Yódico
Periódico
Permangánico
Manganoso
Mangánico
Nitroso
Nítrico
Fosforoso
Fosfórico
Monóxido de azufre
Dióxido de azufre
Trióxido de azufre
H2CO3
H2CrO3
H2CrO4
H2MnO3
H2MnO4
H2S
H2SO3
H2SO4
H3BO3
H3PO3
H3PO4
H4P2O5
H4P2O7
HBr
HBrO
HBrO2
HBrO3
HBrO4
HCl
HClO
HClO2
HClO3
HClO4
Acido u oxoácido
Acido u oxoácido
Acido u oxoácido
Acido u oxoácido
Acido u oxoácido
Acido u hidrácido
Acido u oxoácido
Acido u oxoácido
Acido u oxoácido
Acido u oxoácido
Acido u oxoácido
Acido u oxoácido
Acido u oxoácido
Acido u hidrácido
Acido u oxoácido
Acido u oxoácido
Acido u oxoácido
Acido u oxoácido
Acido u hidrácido
Acido u oxoácido
Acido u oxoácido
Acido u oxoácido
Acido u oxoácido
Carbónico
Cromoso
Crómico
Manganoso
Mangánico
Sulfhídrico
Sulfuroso
Sulfúrico
Bórico
Ortofosforoso
Ortofosfórico o Fosfórico
Pirofosforoso
Pirofosofórico
Bromhídrico
Hipobromoso
Bromoso
Brómico
Perbrómico
Clorhídrico
Hipocloroso
Cloroso
Clórico
Perclórico
HF
HI
HIO
HIO2
HIO3
HIO4
HMnO4
HNO2
HNO3
HPO2
HPO3
Acido u hidrácido
Acido u hidrácido
Acido u oxoácido
Acido u oxoácido
Acido u oxoácido
Acido u oxoácido
Acido u oxoácido
Acido u oxoácido
Acido u oxoácido
Acido u oxoácido
Acido u oxoácido
Fluorhídrico
Yodhídrico
Hipoyodoso
Yodoso
Yódico
Periódico
Permangánico
Nitroso
Nítrico
Metafosforoso
Metafosfórico
Listado de los 60 compuestos inorgánicos básicos mas comunes
Fórmula
Clase
Nomenclatura
Ag2O
Al2O3
Au2O
Au2O3
BaO
BeO
Bi2O3
Bi2O5
CaO
Cr2O3
CrO
Cu2O
CuO
Fe2O3
FeO
Hg2O
HgO
K2O
Li2O
MaO
Mn2O3
MnO
Na2O
Ni2O3
NiO
PbO
PbO2
SnO
SnO2
ZnO
Oxido básico
Oxido básico
Oxido básico
Oxido básico
Oxido básico
Oxido básico
Oxido básico
Oxido básico
Oxido básico
Oxido básico
Oxido básico
Oxido básico
Oxido básico
Oxido básico
Oxido básico
Oxido básico
Oxido básico
Oxido básico
Oxido básico
Oxido básico
Oxido básico
Oxido básico
Oxido básico
Oxido básico
Oxido básico
Oxido básico
Oxido básico
Oxido básico
Oxido básico
Oxido básico
De plata
De aluminio
Auroso
Aúrico
De bario
De berilio
Bismutoso
Bismútico
De calcio
Crómico
Cromoso
Cuproso
Cúprico
Férrico
Ferroso
Mercurioso
Mercúrico
De potasio
De litio
De magnesio
Mangánico
Manganoso
De sodio
Niquélico
Niqueloso
Plumboso
Plúmbico
Stanoso
Stánico
De cinc
Ag(OH)
Al(OH)3
Au(OH)
Au(OH)3
Ba(OH)2
Be(OH)2
Bi(OH)3
Bi(OH)5
Ca(OH)2
Cr(OH)2
Cr(OH)3
Cu(OH)
Cu(OH)2
Fe(OH)2
Fe(OH)3
Hg(OH)
Hg(OH)2
K(OH)
Li(OH)
Ma(OH)2
Mn(OH)2
Mn(OH)3
Na(OH)
Ni(OH)2
Ni(OH)3
Pb(OH)2
Pb(OH)4
Sn(OH)2
Sn(OH)4
Zn(OH)2
Hidróxido
Hidróxido
Hidróxido
Hidróxido
Hidróxido
Hidróxido
Hidróxido
Hidróxido
Hidróxido
Hidróxido
Hidróxido
Hidróxido
Hidróxido
Hidróxido
Hidróxido
Hidróxido
Hidróxido
Hidróxido
Hidróxido
Hidróxido
Hidróxido
Hidróxido
Hidróxido
Hidróxido
Hidróxido
Hidróxido
Hidróxido
Hidróxido
Hidróxido
Hidróxido
De plata
De aluminio
Auroso
Aúrico
De bario
De berilio
Bismutoso
Bismútico
De calcio
Cromoso
Crómico
Cuproso
Cúprico
Ferroso
Férrico
Mercurioso
Mercúrico
De potasio
De litio
De magnesio
Manganoso
Mangánico
De sodio
Niqueloso
Niquélico
Plumboso
Plúmbico
Stanoso
Stánico
De cinc
QUIMICA - ENLACES QUIMICOS
ENLACES QUIMICOS
Introducción
Cuándo hacemos leche en polvo, o cuando le echamos azúcar al té, ¿desaparece la leche o
el azúcar? Claro que no, uno respondería que estos se están disolviendo en el agua. Pero
en realidad, ¿Qué sucede? ¿Por qué sucede? Son hechos tan comunes que se nos olvida
hacernos estas preguntas. En realidad lo que sucede es que la leche y el azúcar son
solutos, que serán disueltos en un solvente como el agua. Pero ¿qué es lo que en realidad
sucede? ¿Qué son los solutos y los solventes? Bueno estas preguntas serán respondidas
en este informe.
Este informe habla de enlaces y soluciones, pero, para entenderlos hay que empezar por
conocer el significado de estas palabras, para luego poder pasar a un lenguaje más técnico.
Enlace significa unión, un enlace químico es la unión de dos o más átomos que se han
unido con un solo fin, alcanzar la estabilidad, tratar de parecerse al gas noble más cercano,
para la mayoría de los elementos alcanzar ocho electrones en su último nivel. Las
soluciones son mezclas homogéneas, no se distinguen sus componentes como separados,
entre al menos dos reactantes un soluto, que es él que será disuelto, y un solvente, que es
él que disolverá al soluto.
¿Qué mantiene unidos a los Atomos?
Un concepto básico en química es el estudio de cómo los átomos forman compuestos. La
mayoría de los elementos que conocemos existen en la naturaleza formando agrupaciones
de átomos iguales o de distintos tipos, enlazados entre sí.
Todos los compuestos están constituidos por dos o más átomos de un o más elementos
diferentes, unidos entre sí por enlaces ya sean estos iónicos o covalentes.
Tipos De Enlace
Si los átomos enlazados son elementos metálicos, el enlace se llama metálico. Los
electrones son compartidos por los átomos, pero pueden moverse a través del sólido
proporcionando conductividad térmica y eléctrica, brillo, maleabilidad y ductilidad.
Si los átomos enlazados son no metales e idénticos (como en N2 o en O2), los electrones
son compartidos por igual por los dos átomos, y el enlace se llama covalente apolar. Si los
átomos son no metales pero distintos (como en el óxido nítrico, NO), los electrones son
compartidos en forma desigual y el enlace se llama covalente polar -polar porque la
molécula tiene un polo eléctrico positivo y otro negativo, y covalente porque los átomos
comparten los electrones, aunque sea en forma desigual. Estas sustancias no conducen la
electricidad, ni tienen brillo, ductilidad o maleabilidad.
Cuando una molécula de una sustancia contiene átomos de metales y no metales, los
electrones son atraídos con más fuerza por los no metales, que se transforman en iones con
carga negativa; los metales, a su vez, se convierten en iones con carga positiva. Entonces,
los iones de diferente signo se atraen electrostáticamente, formando enlaces iónicos. Las
sustancias iónicas conducen la electricidad cuando están en estado líquido o en
disoluciones acuosas, pero no en estado cristalino, porque los iones individuales son
demasiado grandes para moverse libremente a través del cristal.
Cuando los electrones son compartidos simétricamente, el enlace puede ser metálico o
covalente apolar; si son compartidos asimétricamente, el enlace es covalente polar; la
transferencia de electrones proporciona enlace iónico. Generalmente, la tendencia a una
distribución desigual de los electrones entre un par de átomos aumenta cuanto más
separados están en la tabla periódica.
Para la formación de iones estables y enlace covalente, la norma más común es que cada
átomo consiga tener el mismo número de electrones que el elemento de los gases nobles grupo 18- más cercano a él en la tabla periódica. Los metales de los grupos 1 (o IA) y 11 (o
IB) de la tabla periódica tienden a perder un electrón para formar iones con una carga
positiva; los de los grupos 2 (o IIA) y 12 (o IIB) tienden a perder dos electrones para formar
iones con dos cargas positivas, y de la misma forma los de los grupos 3 (o IIIB) y 13 (o IIIA)
tienden a formar iones con tres cargas positivas. Por la misma razón, los halógenos, grupo
17 (o VIIA), tienden a ganar un electrón para formar iones con una carga negativa, y los
elementos del grupo 16 (o VIA) a formar iones con dos cargas negativas. Sin embargo,
conforme aumenta la carga neta de un ion, éste tiene menos estabilidad, así que las cargas
aparentemente mayores serían minimizadas compartiendo los electrones covalentemente.
El enlace covalente se forma cuando ambos átomos carecen del número de electrones del
gas noble más cercano. El átomo de cloro, por ejemplo, tiene un electrón menos que el
átomo de argón (17 frente a 18). Cuando dos átomos de cloro forman un enlace covalente
compartiendo dos electrones (uno de cada átomo), ambos consiguen el número 18 del
argón (Cl~~Cl). Es común representar un par de electrones compartido por medio de un
guión entre los átomos individuales: Cl~~Cl se escribe Cl-Cl.
Otros Elementos De Un Enlace
Iones
Los átomos están constituidos por el núcleo y la corteza y que el número de cargas positivas
del primero es igual al número de electrones de la corteza; de ahí su electronegatividad. Si
la corteza electrónica de un átomo neutro pierde o gana electrones se forman los llamados
iones.
Los iones son átomos o grupos atómicos que tienen un número de electrones excesivo o
deficiente para compensar la carga positiva del núcleo.
En el primer caso los iones tienen carga negativa y reciben el nombre de aniones, y en el
segundo están cargados positivamente y se llaman cationes.
Elementos electropositivos y electronegativos
Se llaman elementos electropositivos aquellos que tienen tendencia a perder electrones
transformándose en cationes; a ese grupo pertenecen los metales.
Elementos electronegativos son los que toman con facilidad electrones transformándose en
aniones; a este grupo pertenecen los metaloides.
Los elementos más electropositivos están situados en la parte izquierda del sistema
periódico; son los llamados elementos alcalinos. A medida que se avanza en cada período
hacia la derecha va disminuyendo el carácter electropositivo, llegándose, finalmente, a los
halógenos de fuerte carácter electronegativo.
Electrones de valencia
La unión entre los átomos se realiza mediante los electrones de la última capa exterior, que
reciben el nombre de electrones de valencia.
La unión consiste en que uno o más electrones de valencia de algunos de los átomos se
introduce en la esfera electrónica del otro.
Los gases nobles, poseen ocho electrones en su última capa, salvo el helio que tiene dos.
Esta configuración electrónica les comunica inactividad química y una gran estabilidad.
Todos los átomos tienen tendencia a transformar su sistema electrónico y adquirir el que
poseen los gases nobles, porque ésta es la estructura más estable.
Valencia electroquímica
Se llama valencia electroquímica al número de electrones que ha perdido o ganado un
átomo para transformarse en ion. Si dicho número de electrones perdidos o ganados es 1,
2, 3, etc. Se dice que el ion es monovalente, bivalente, trivalente, etc.
Tipo de
enlace
Tipo de
estructura
Ejemplo de
estructura
Enlace iónico
Red
iónica
Ejemplo: KCl
Cloruro de
potasio, KCl
Enlace
covalente
Moléculas
simples
Metano, CH4
Ejemplo: CH4
Moléculas
gigantes
Ejemplo: C
Diamante, C
Enlace metálico
Red
metálica
Ejemplo: Ag
Plata, Ag
Propiedades
características
Sólidos cristalinos.
Puntos de fusión elevados.
Puntos de ebullición elevados.
Solubles en agua.
Conducen la electricidad fundidos o
en disolución.
No conducen la electricidad en
estado sólido.
Fundamentalmente líquidos y gases.
Puntos de fusión bajos.
Puntos de ebullición bajos.
Insolubles en agua.
No conducen la electricidad.
Sólidos.
Puntos de fusión elevados.
Puntos de ebullición elevados.
La solubilidad y conductividad varían
de una sustancia a otra.
Sólidos cristalinos.
Puntos de fusión elevados.
Puntos de ebullición elevados.
Inolubles en agua.
Dúctiles y maleables.
Esta Tabla Ejemplifica Los Tipos De Enlace
Valencia
En la mayoría de los átomos, muchos de los electrones son atraídos con tal fuerza por sus
propios núcleos que no pueden interaccionar de forma apreciable con otros núcleos. Sólo
los electrones del ´exterior´ de un átomo pueden interaccionar con dos o más núcleos. A
éstos se les llama electrones de valencia.
El número de electrones de valencia de un átomo es igual al número de su familia (o grupo)
en la tabla periódica, usando sólo la antigua numeración romana. Así, tenemos un electrón
de valencia para los elementos de los grupos 1 (o IA) y 11 (o IB); dos electrones de valencia
para los elementos de los grupos 2 (o IIA) y 12 (o IIB), y cuatro para los elementos de los
grupos 4 (o IVB) y 14 (o IVA). Todos los átomos de los gases nobles excepto el helio (o sea:
neón, argón, criptón, xenón y radón) tienen ocho electrones de valencia. Los elementos de
las familias (grupos) cercanas a los gases nobles tienden a reaccionar para adquirir la
configuración de ocho electrones de valencia de los gases nobles. Esto se conoce como la
regla del octeto de Lewis, que fue enunciada por el químico estadounidense Gilbert Newton
Lewis.
El helio es el único que tiene una configuración de dos electrones de valencia. Los
elementos cercanos al helio tienden a adquirir una configuración de valencia de dos: el
hidrógeno ganando un electrón, el litio perdiéndolo, y el berilio perdiendo dos electrones. El
hidrógeno suele compartir su único electrón con un electrón de otro átomo formando un
enlace simple, como en el cloruro de hidrógeno, H-Cl. El cloro, que originalmente tiene siete
electrones de valencia, pasa a tener ocho. Esos electrones de valencia pueden
representarse como:
o
. Las estructuras de N2 y CO2 se pueden expresar ahora
como :N:::N: o IN≡NI y
. Estas estructuras de Lewis muestran la configuración de
ocho electrones de valencia de los gases nobles para cada átomo. Probablemente el 80%
de los compuestos covalentes pueden ser representados razonablemente por las
estructuras electrónicas de Lewis. El resto, en especial aquellos que contienen elementos
de la parte central de la tabla periódica, no puede ser descrito normalmente en términos de
estructuras de gases nobles.
Soluciones
Todas las soluciones están formadas por al menos un soluto y un solvente. Las soluciones
son mezclas homogéneas entre solutos y solventes. El soluto es el que se disuelve en el
solvente. El solvente debe encontrarse siempre en mayor cantidad, excepto el agua.
Conductibilidad
Ningún solvente puro conduce la corriente eléctrica. Y ningún soluto puro conduce la
corriente eléctrica, a menos que este en estado líquido. Pero una solución puede conducir la
corriente. Para que esto suceda, la solución debe estar formada por un soluto electrolito (es
decir, compuestos formado por enlaces iónicos no orgánicos) y por un solvente polar como
el agua, lo cual forma una solución electrolítica.
Las soluciones de NaCl (sal común) o CuSO4 (sulfato cúprico) en agua conducen la
electricidad a toda su intensidad. Pero, el acido acetico o vinagre común (CH3-CO-OH) al
disolverse en agua produce iones los cuales pueden conducir la electricidad, pero solo
levemente.
Resonancia
Una extensión interesante de la estructura de Lewis, llamada resonancia, se encuentra por
ejemplo en los iones nitrato, NO3-. Cada N tiene originalmente cinco electrones de valencia,
cada O tiene seis, y uno más por la carga negativa, suman un total de 24 (5 + (3 x 6) + 1)
electrones para cuatro átomos. Esto proporciona un promedio de seis electrones por átomo,
por tanto, si se aplica la regla del octeto de Lewis, debe producirse un enlace covalente. Se
sabe que el átomo de nitrógeno ocupa una posición central rodeado por los tres átomos de
oxígeno, lo que proporcionaría una estructura de Lewis aceptable, excepto porque existen
tres estructuras posibles. En realidad, sólo se observa una estructura. Cada estructura de
resonancia de Lewis sugiere que debe haber dos enlaces simples y uno doble. Sin
embargo, los experimentos han demostrado que los enlaces son idénticos en todos los
sentidos, con propiedades intermedias entre las observadas para los enlaces simples y los
dobles en otros compuestos. La teoría moderna sugiere que una estructura de electrones
compartidos localizados, tipo Lewis, proporcionaría la forma y simetría general de la
molécula más un grupo de electrones deslocalizados (representados por puntos) que son
compartidos por toda la molécula.
Definiciones
Enlace químico: fuerza entre los átomos que los mantiene unidos en las moléculas. Cuando
dos o más átomos se acercan lo suficiente, puede producirse una fuerza de atracción entre
los electrones de los átomos individuales y el núcleo de otro u otros átomos. Si esta fuerza
es lo suficientemente grande para mantener unidos los átomos, se dice que se ha formado
un enlace químico. Todos los enlaces químicos resultan de la atracción simultánea de uno o
más electrones por más de un núcleo.
Enlace iónico: concepto de enlace químico. Enlace iónico. Estructuras cristalinas de los
compuestos iónicos. Límites de estabilidad. Energía de red. Ciclo de Born-Haber.
Propiedades generales de los compuestos iónicos.
Enlace covalente: introducción. Teoría de Lewis. Teoría del enlace de valencia. Carácter
dirigido del enlace covalente. Orbitales híbridos. Resonancia. Teoría de repulsión de pares
de electrones de la capa de valencia. Teoría de orbitales moleculares. Moléculas diatómicas
homo y heteronucleares. Transición entre el enlace iónico y covalente: electronegatividad y
polarización.
Enlace metálico: propiedades generales de los metales. Estructuras de los metales. Teoría
de enlace. Conductores aislantes y semiconductores.
Enlaces intermoleculares: evidencias. Enlaces por fuerzas de van del waals: orientación,
inducción y dispersión. Enlaces de hidrógeno. Propiedades de los compuestos covalentes.
Tipos de enlace
En la unión o enlace de los átomos pueden presentarse los siguientes casos:
1.
2.
3.
4.
Enlace iónico, si hay atracción electrostática.
Enlace covalente, si comparten los electrones.
Enlace covalente coordinado, cuando el par de electrones es aportado solamente
por uno de ellos.
Enlace metálico, so los electrones de valencia pertenece en común a todos los
átomos.
Conclusiones
Bueno, como hemos visto al hacer jugo o endulzar al té se producen una serie de
reacciones químicas que nunca hubiéramos imaginado. Los enlaces, las soluciones, la
fractura de enlaces y la formación de otros, ¿quien lo hubiera imaginado? Pero ahora que
sabemos todo esto, cuando nos sentemos a tomarnos un té ya no se nos olvidara pensar en
esto.
Metalurgia
Metalurgia: obtención de metales a partir del mineral.
Ganga: mineral sin valor industrial que acompaña al metal.
Métodos mecánicos
(concentra el
mineral)
Preparación del
mineral
Métodos Químicos
(mineral
concentrado)
Trituración, molienda, pulverizado
Tamización
Levigación (oro)
Flotación (sulfuros)
Tostación
Calcinación
Reducción
Electrólisis
Electrometalúrgicos
(mineral
concentrado)
Electrotérmicos
⇒ de sulfuro a óxido con corriente
de aire
⇒ de CO3= a óxido en ausencia de
aire
⇒ óxidos + C = CO2 + metal
Húmeda (Na)
Seca (Na, K, Mg, Al)
Hornos de arco voltáico 2800 3000°C es una reducción
Hematita ⇒Fe2O3
Limonita ⇒ Fe2O3 + 3.H2O
Minerales Magnetita⇒ Fe2O3.FeO
Siderita ⇒ FeCO3
Pirita ⇒ FeS
Producción de arrabio
Los materiales básicos empleados para fabricar arrabio son mineral de hierro, coque y
fundente (caliza).
Se utiliza principalmente Fe2O3 (hematita)
Si ganga ácida SiO2 ⇒fundente básico Al2O3, MgO, CaO
Fundente
Si ganga básica MgO, CaO ⇒ fundente ácido SiO2
Siderurgia
Si ganga neutra ⇒fundente neutro CrO
Coque ⇒combustible y reductor
Aire insuflado desde abajo hacia arriba
El coque se quema como combustible para calentar el horno, y al arder libera monóxido de
carbono, que se combina con los óxidos de hierro del mineral y los reduce a hierro metálico.
La ecuación de la reacción química fundamental de un alto horno es:
Parte baja
C↓ + O2 ⇒ CO2
Fe2O3↓ + C↓ ⇒ 2.Fe↓ + 3.CO
Fe↓ + C↓ ⇒ FSiO2↓ + CaO↓ ⇒ CaSiO3↓(escoria) e3C↓ (cementita)
Parte alta
C↓ + CO2 ⇒2.CO
Fe2O3↓ + 3.CO ⇒2.Fe↓ + 3.CO2
Reacciones:
El revestimiento del alto horno puede ser ácido o básico, dependiendo de la ganga.
La escoria flota sobre el metal fundido.
Sentido de avance
↓ Mineral + coque + fundente
Aire caliente + CO2 + CO
Fundente: mineral que neutraliza la ganga, dando escoria que debe tener bajo punto de
fusión y densidad menor que el metal fundido . El fundente de la carga del horno se
emplea como fuente adicional de monóxido de carbono y como sustancia fundente. Este
material se combina con la sílice presente en el mineral (que no se funde a las temperaturas
del horno) para formar silicato cálcico (escoria), cuyo punto de fusión es menor. Sin la caliza
se formaría silicato de hierro, con lo que se perdería hierro metálico. La escoria flota sobre el
metal fundido en la parte inferior del horno (superior del crisol).
El arrabio producido en los altos hornos tiene la siguiente composición: un 92% de hierro, un
3 o 4% de carbono, entre 0,5 y 3% de silicio, del 0,25% al 2,5% de manganeso, del 0,04 al
2% de fósforo y algunas partículas de azufre.
Arrabio
Fundición gris ⇒ enfriamiento lento, puede maquinarse, contiene carbono libre
Fundición blanca ⇒ enfriamiento rápido, no puede maquinarse, contiene cementita
Un alto horno típico está formado por una cápsula cilíndrica de acero forrada con un material
no metálico y resistente al calor, como asbesto o ladrillos refractarios. El diámetro de la
cápsula disminuye hacia arriba y hacia abajo, y es máximo en un punto situado
aproximadamente a una cuarta parte de su altura total. La parte inferior del horno está
dotada de varias aperturas tubulares llamadas toberas, por donde se fuerza el paso del aire.
Cerca del fondo se encuentra un orificio por el que fluye el arrabio fundido cuando se sangra
(o vacía) el alto horno. Encima de ese orificio, pero debajo de las toberas, hay otro agujero
para retirar la escoria. La parte superior del horno, cuya altura es de unos 30 m, contiene
respiraderos para los gases de escape, y un par de tolvas redondas, cerradas por válvulas
en forma de campana, por las que se introduce la carga en el horno. Los materiales se
llevan hasta las tolvas en pequeñas vagonetas o cucharas que se suben por un elevador
inclinado situado en el exterior del horno.
Ver esquema de un Alto Horno
Los altos hornos funcionan de forma continua. La materia prima que se va a introducir en el
horno se divide en un determinado número de pequeñas cargas que se introducen a
intervalos. La escoria que flota sobre el metal fundido se retira una vez cada dos horas, y el
hierro se sangra cinco veces al día.
El aire insuflado en el alto horno se precalienta a una temperatura situada entre los 550 y los
900 °C. El calentamiento se realiza en las llamadas estufas, cilindros que contienen
estructuras de ladrillo refractario. El ladrillo se calienta durante varias horas quemando gas
de alto horno. Posteriormente los gases de escape que salen de la parte superior del horno.
Después se apaga la llama y se hace pasar el aire a presión por la estufa. El peso del aire
empleado en un alto horno supera el peso total de las demás materias primas.
Estrangulando el flujo de gas de los respiraderos del horno es posible aumentar la presión
del interior del horno hasta 1,7 atmósferas o más. La técnica de presurización permite una
mejor combustión del coque y una mayor producción de hierro. En muchos altos hornos
puede lograrse un aumento de la producción de un 25%. En instalaciones experimentales
también se ha demostrado que la producción se incrementa enriqueciendo el aire con
oxígeno.
El proceso de sangrado consiste en retirar a golpes un tapón de arcilla del orificio del hierro
cercano al fondo del horno y dejar que el metal fundido fluya por un canal cubierto de arcilla
y caiga a un depósito metálico forrado de ladrillo, que puede ser una cuchara o una
vagoneta capaz de contener hasta 100 toneladas de metal. Cualquier escoria o sobrante
que salga del horno junto con el metal se elimina antes de llegar al recipiente. A
continuación, el contenedor lleno de arrabio fundido se transporta a la fábrica siderúrgica.
Los altos hornos modernos funcionan en combinación con hornos de oxígeno básicos, y a
veces con hornos de crisol abierto, más antiguos, como parte de una única planta
siderúrgica. En esas plantas, los hornos siderúrgicos se cargan con arrabio fundido. El metal
fundido procedente de diversos altos hornos puede mezclarse en una gran cuchara antes de
convertirlo en acero con el fin de minimizar el efecto de posibles irregularidades de alguno
de los hornos.
Otros métodos de refinado del hierro
Aunque casi todo el hierro y acero que se fabrica en el mundo se obtiene a partir de arrabio
producido en altos hornos, hay otras formas de refinación del hierro que se han practicado
de forma limitada. Una de ellas es el denominado método directo para fabricar hierro y acero
a partir del mineral, sin producir arrabio. En este proceso se mezclan mineral de hierro y
coque en un horno de calcinación rotatorio y se calientan a una temperatura de unos 950
°C. El coque caliente desprende monóxido de carbono, igual que en un alto horno, y reduce
los óxidos del mineral a hierro metálico. Sin embargo, no tienen lugar las reacciones
secundarias que ocurren en un alto horno, y el horno de calcinación produce la llamada
esponja de hierro, de mucha mayor pureza que el arrabio. También puede producirse hierro
prácticamente puro mediante electrólisis haciendo pasar una corriente eléctrica a través de
una solución de cloruro ferroso. Ni el proceso directo ni el electrolítico tienen importancia
comercial significativa.
Horno de Reverbero
Fe3C + O2 ⇒ 3.Fe + CO2
Aire caliente en contracorriente
Convertidor
Bessemer
Aire a presión
Se oxidan sustancias acompañantes (Si, Mn,
P, S)
Fundición y chatarra
Reducción de la
fundición
Siemens Martin
Arco voltáico
Proceso de crisol abierto
Cualquier proceso de producción de acero a partir de arrabio consiste en quemar el exceso
de carbono y otras impurezas presentes en el hierro. Una dificultad para la fabricación del
acero es su elevado punto de fusión, 1.400 °C, que impide utilizar combustibles y hornos
convencionales. Para superar la dificultad se desarrolló el horno de crisol abierto, que
funciona a altas temperaturas gracias al precalentado regenerativo del combustible gaseoso
y el aire empleados para la combustión. En el precalentado regenerativo los gases que
escapan del horno se hacen pasar por una serie de cámaras llenas de ladrillos, a los que
ceden la mayor parte de su calor. A continuación se invierte el flujo a través del horno, y el
combustible y el aire pasan a través de las cámaras y son calentados por los ladrillos. Con
este método, los hornos de crisol abierto alcanzan temperaturas de hasta 1.650 °C.
El horno propiamente dicho suele ser un crisol de ladrillo plano y rectangular de unos 6 x 10
m, con un techo de unos 2,5 m de altura. Una serie de puertas da a una planta de trabajo
situada delante del crisol. Todo el crisol y la planta de trabajo están situados a una altura
determinada por encima del suelo, y el espacio situado bajo el crisol lo ocupan las cámaras
de regeneración de calor del horno. Un horno del tamaño indicado produce unas 100
toneladas de acero cada 11 horas.
El horno se carga con una mezcla de arrabio (fundido o frío), chatarra de acero y mineral de
hierro, que proporciona oxígeno adicional. Se añade caliza como fundente y espatoflúor
para hacer que la escoria sea más fluida. Las proporciones de la carga varían mucho, pero
una carga típica podría consistir en 60.000 kg. de chatarra de acero, 11.000 kg. de arrabio
frío, 45.000 kg. de arrabio fundido, 12.000 kg. de caliza, 1.000 kg. de mineral de hierro y 200
kg. de espatoflúor. Una vez cargado el horno, se enciende, y las llamas oscilan de un lado a
otro del crisol a medida que el operario invierte su dirección para regenerar el calor.
Desde el punto de vista químico la acción del horno de crisol abierto consiste en reducir por
oxidación el contenido de carbono de la carga y eliminar impurezas como silicio,
fósforo,manganeso y azufre, que se combinan con la caliza y forman la escoria. Estas
reacciones tienen lugar mientras el metal del horno se encuentra a la temperatura de fusión,
y el horno se mantiene entre 1.550 y 1.650 °C durante varias horas hasta que el metal
fundido tenga el contenido de carbono deseado. Un operario experto puede juzgar el
contenido de carbono del metal a partir de su aspecto, pero por lo general se prueba la
fundición extrayendo una pequeña cantidad de metal del horno, enfriándola y sometiéndola
a examen físico o análisis químico. Cuando el contenido en carbono de la fundición alcanza
el nivel deseado, se sangra el horno a través de un agujero situado en la parte trasera. El
acero fundido fluye por un canal corto hasta una gran cuchara situada a ras de suelo, por
debajo del horno. Desde la cuchara se vierte el acero en moldes de hierro colado para
formar lingotes, que suelen tener una sección cuadrada de unos 50 cm y una longitud de 1,5
m. Estos lingotes (la materia prima para todas las formas de fabricación del acero) pesan
algo menos de 3 toneladas. En fechas recientes se han puesto en práctica métodos para
procesar el acero de forma continua sin tener que pasar por el proceso de fabricación de
lingotes.
Proceso básico de oxígeno
El proceso más antiguo para fabricar acero en grandes cantidades, es el proceso Bessemer,
que empleaba un horno de gran altura en forma de pera, denominado convertidor
Bessemer, que podía inclinarse en sentido lateral para la carga y el vertido. Al hacer pasar
grandes cantidades de aire a través del metal fundido, el oxígeno del aire se combinaba
químicamente con las impurezas y las eliminaba.
En el proceso básico de oxígeno, el acero también se refina en un horno en forma de pera
que se puede inclinar en sentido lateral. Sin embargo, el aire se sustituye por un chorro de
alta presión de oxígeno casi puro. Cuando el horno se ha cargado y colocado en posición
vertical, se hace descender en su interior una lanza de oxígeno. La punta de la lanza,
refrigerada por agua, suele estar situada a unos 2 m por encima de la carga, aunque esta
distancia puede variarse de acuerdo las necesidades. A continuación se inyectan en el
horno miles de metros cúbicos de oxígeno a velocidades supersónicas. El oxígeno se
combina con el carbono y otros elementos no deseados e inicia una reacción de agitación
que quema con rapidez las impurezas del arrabio y lo transforma en acero. El proceso de
refinado tarda 50 minutos o menos, y es posible fabricar unas 275 toneladas de acero en
una hora.
Acero de horno eléctrico
En algunos hornos el calor para fundir y refinar el acero procede de la electricidad y no de la
combustión de gas. Como las condiciones de refinado de estos hornos se pueden regular
más estrictamente que las de los hornos de crisol abierto o los hornos básicos de oxígeno,
los hornos eléctricos son sobre todo útiles para producir acero inoxidable y otros aceros de
aleación que deben ser fabricados según unas especificaciones muy exigentes. El refinado
se produce en una cámara hermética, donde la temperatura y otras condiciones se
controlan de forma estricta mediante dispositivos automáticos. En las primeras fases de este
proceso de refinado se inyecta oxígeno de alta pureza a través de una lanza, lo que
aumenta la temperatura del horno y disminuye el tiempo necesario para producir el acero.
La cantidad de oxígeno que entra en el horno puede regularse con precisión en todo
momento, lo que evita reacciones de oxidación no deseadas.
En la mayoría de los casos, la carga está formada casi exclusivamente por material de
chatarra. Antes de poder utilizarla, la chatarra debe ser analizada y clasificada, porque su
contenido en aleaciones afecta a la composición del metal refinado. También se añaden
otros materiales, como pequeñas cantidades de mineral de hierro y cal seca, para contribuir
a eliminar el carbono y otras impurezas. Los elementos adicionales para la aleación se
introducen con la carga o después, cuando se vierte a la cuchara el acero refinado.
Resistencia
Conducción
⇒ Contacto
directo
⇒ Fabricación de abrasivos
Convección
⇒ Corriente de
aire
⇒ Tratamientos térmicos
Radiación
Hornos
eléctricos
Arco
voltáico
Indirecto
Directo
Solera
conductora
Arco
Resistencia
Inducción
⇒ Fusión de metales y
tratamientos térmicos
⇒ Para no férreos y aceros hasta kg
⇒ Un electrodo es el metal hasta 50 Ton
⇒ Un electrodo es el crisol hasta 50 Ton
⇒ La corriente atraviesa el metal
Baja frecuencia
Alta frecuencia
Rinden un 10 % más que los de arco
Frecuencia de
red
Una vez cargado el horno se hacen descender unos electrodos hasta la superficie del metal.
La corriente eléctrica fluye por uno de los electrodos, forma un arco voltaico hasta la carga
metálica,recorre el metal y vuelve a formar un arco hasta el siguiente electrodo. La
resistencia del metal al flujo de corriente genera calor, que (junto con el producido por el
arco voltaico) funde el metal con rapidez. Hay otros tipos de horno eléctrico donde se
emplea una espiral para generar calor.
Procesos de acabado
Colada: Pasaje del metal fundido desde el horno a las lingoteras, por medio de la cuchara.
Lingotes: Para almacenar y transportar.
Laminado: De lingotes a tochos y de tochos a perfiles o láminas.
El acero se vende en una gran variedad de formas y tamaños, como varillas,tubos, raíles o
rieles de ferrocarril, perfiles en H o en T o canales. Estas formas se obtienen en las
instalaciones siderúrgicas laminando los lingotes calientes o modelándolos de algún otro
modo. El acabado del acero mejora también su calidad al refinar su estructura cristalina y
aumentar su resistencia.
El proceso básico de elaboración del acero se conoce como laminado en caliente. En este
proceso, el lingote colado se calienta al rojo vivo en un horno denominado foso de
termodifusión y a continuación se hace pasar entre una serie de rodillos metálicos colocados
en pares que lo aplastan hasta darle la forma y tamaño deseados. La distancia entre los
rodillos va disminuyendo a medida que se reduce el espesor del acero.
El primer par de rodillos por el que pasa el lingote se conoce como tren de desbaste o de
eliminación de asperezas, y las barras cuadradas que produce se denominan tochos.
Después del tren de desbaste, el acero pasa a trenes de laminado en bruto y a los trenes de
acabado que lo reducen a la sección transversal correcta. Los rodillos para producir rieles
de ferrocarril o perfiles en H, en T o en L tienen estrías para proporcionar la forma
adecuada.
Los procesos modernos de fabricación requieren gran cantidad de chapa de acero delgada.
Los trenes o rodillos de laminado continuo producen tiras y láminas con anchuras de hasta
2,5 m. Estos laminadores procesan con rapidez la chapa de acero antes de que se enfríe y
no pueda ser trabajada. Las planchas de acero caliente de más de 10 cm de espesor se
pasan por una serie de cilindros que reducen progresivamente su espesor hasta unos 0,1
cm y aumentan su longitud de 4 a 370 metros. Los trenes de laminado continuo están
equipados con una serie de accesorios como rodillos de borde, aparatos de decapado o
eliminación y dispositivos para enrollar de modo automático la chapa cuando llega al final
del tren. Los rodillos de borde son grupos de rodillos verticales situados a ambos lados de la
lámina para mantener su anchura. Los aparatos de decapado eliminan la costra que se
forma en la superficie de la lámina apartándola mecánicamente, retirándola mediante un
chorro de aire o doblando de forma abrupta la chapa en algún punto del recorrido. Las
bobinas de chapa terminadas se colocan sobre una cinta transportadora y se llevan a otro
lugar para ser recocidas y cortadas en chapas individuales. Una forma más eficiente para
producir chapa de acero delgada es hacer pasar por los rodillos planchas de menor espesor.
Con los métodos convencionales de fundición sigue siendo necesario pasar los lingotes por
un tren de desbastado para producir planchas lo bastante delgadas para el tren de laminado
continuo.
Los sistemas de colado ininterrumpido, en cambio, producen una plancha continua de acero
con un espesor inferior a 5 cm, lo que elimina la necesidad de trenes de desbaste y
laminado en bruto.
Tubos
Los tubos más baratos se moldean doblando una tira plana de acero caliente en forma
cilíndrica y soldando los bordes para cerrar el tubo. En los tubos más pequeños, los bordes
de la tira suelen superponerse y se pasan entre un par de rodillos curvados según el
diámetro externo del tubo. La presión de los rodillos es suficiente para soldar los bordes. Los
tubos sin soldaduras se fabrican a partir de barras sólidas haciéndolas pasar entre un par de
rodillos inclinados entre los que está situada una barra metálica con punta,llamada mandril,
que perfora las barras y forma el interior del tubo mientras los rodillos forman el exterior.
Hojalata
El producto de acero recubierto más importante es la hojalata estañada que se emplea para
la fabricación de latas y envases. El material de las latas contiene más de un 99% de acero.
En algunas instalaciones, las láminas de acero se pasan por un baño de estaño fundido
(después de laminarlas primero en caliente y luego en frío) para estañarlas. El método de
recubrimiento más común es el proceso electrolítico. La chapa de acero se desenrolla poco
a poco de la bobina y se le aplica una solución química. Al mismo tiempo se hace pasar una
corriente eléctrica a través de un trozo de estaño puro situado en esa misma solución, lo
que hace que el estaño se disuelva poco a poco y se deposite sobre el acero. Con este
sistema, medio kilogramo de estaño basta para recubrir 20 metros cuadrados de acero. En
la hojalata delgada, la chapa recibe un segundo laminado en frío antes de recubrirla de
estaño, lo que aumenta la resistencia de la chapa además de su delgadez. Las latas hechas
de hojalata delgada tienen una resistencia similar a las ordinarias, pero contienen menos
acero, con lo que se reduce su peso y su coste. También pueden fabricarse envases ligeros
adhiriendo una delgadísima lámina de acero estañado sobre papel o cartón.
Otros procesos de fabricación de acero son la forja, la fundición y el uso de troqueles.
Hierro forjado
El proceso antiguo para fabricar la aleación resistente y maleable conocida como hierro
forjado se diferencia con claridad de otras formas de fabricación de acero. Debido a que el
proceso, conocido como pudelización, exigía un mayor trabajo manual, era imposible
producir hierro forjado en grandes cantidades. El desarrollo de nuevos sistemas con
convertidores Bessemer y hornos de crisol abierto permitieron producir un volumen mayor
de hierro forjado.
Sin embargo, el hierro forjado ya no se fabrica habitualmente con fines comerciales, ya que
puede sustituirse en casi todas las aplicaciones con acero de bajo contenido en carbono,
con menor costo de producción y calidad más uniforme.
El horno de pudelización empleado en el proceso antiguo tiene un techo abovedado de poca
altura y un crisol cóncavo en el que se coloca el metal en bruto, separado por una pared de
la cámara de combustión donde se quema carbón bituminoso. La llama de la cámara de
combustión asciende por encima de la pared,incide en el techo abovedado y reverbera
sobre el contenido del crisol. Cuando el horno ha adquirido un calor moderado,el operario
que maneja el horno recubre el crisol y las paredes con una pasta de óxido de hierro, por lo
general hematitas. A continuación, el horno se carga con unos 250 kg. de arrabio y se cierra
la puerta. Al cabo de unos 30 minutos, el arrabio se ha fundido, y el operario añade a la
carga más óxido de hierro o residuos de laminado, mezclándolos con el hierro con una barra
de hierro curvada. El silicio y la mayor parte del manganeso contenidos en el hierro se
oxidan, y se elimina parte del azufre y el fósforo. A continuación se eleva un poco la
temperatura del horno, y el carbono empieza a quemarse formando óxidos de carbono
gaseosos. A medida que se desprende gas la escoria aumenta de volumen y el nivel de la
carga sube. Al quemarse el carbono, la temperatura de fusión aumenta, y la carga se vuelve
cada vez más pastosa y vuelve a su nivel anterior. A medida que se incrementa la pureza
del hierro, el operario remueve la carga con la barra para garantizar una composición
uniforme y una cohesión adecuada de las partículas. La masa resultante, pastosa y
esponjosa, se divide en pedazos o bolas de unos 80 o 90 kg. Las bolas se retiran del horno
con unas tenazas y se colocan directamente en una prensa que expulsa de la bola la mayor
parte de la escoria de silicio mezclada y suelda entre sí los granos de hierro puro. A
continuación se corta el hierro en piezas planas que se apilan unas sobre otras, se calientan
hasta la temperatura de soldadura y se laminan para formar una sola pieza. A veces se
repite el proceso de laminado para mejorar la calidad del producto.
La técnica moderna para fabricar hierro forjado emplea hierro fundido procedente de un
convertidor Bessemer y escoria fundida, que suele prepararse fundiendo mineral de hierro,
residuos de laminado y arena en un horno de crisol abierto. Cuando el hierro fundido, que
lleva disuelta una gran cantidad de gas,se vierte en la cuchara que contiene la escoria
fundida, el metal se solidifica de modo casi instantáneo y libera el gas disuelto. La fuerza
ejercida por el gas hace estallar el metal en partículas diminutas que son más pesadas que
la escoria y se acumulan en el fondo de la cuchara, donde se aglomeran formando una
masa esponjosa similar a las bolas producidas en un horno de pudelización. Cuando se
vierte la escoria de la parte superior de la cuchara se retira la bola de hierro y es sometida al
mismo tratamiento que el producto del horno de pudelización.
Clasificación del acero
Aceros al carbono
Más del 90% de todos los aceros son aceros al carbono. Estos aceros contienen diversas
cantidades de carbono y menos del 1,65% de manganeso, el 0,60% de silicio y el 0,60% de
cobre. Entre los productos fabricados con aceros al carbono figuran máquinas, carrocerías
de automóvil, la mayor parte de las estructuras de construcción de acero, cascos de buques,
somieres u horquillas o pasadores para el pelo.
Aceros de aleación
Estos aceros contienen una proporción determinada de vanadio,molibdeno y otros
elementos, además de cantidades mayores de manganeso, silicio y cobre que los aceros al
carbono normales. Estos aceros se emplean, por ejemplo, para fabricar engranajes y ejes
de motores, patines o cuchillos de corte.
Aceros de baja aleación ultrarresistentes
Esta familia es la más reciente de las cinco grandes clases de acero. Los aceros de baja
aleación son más baratos que los aceros de aleación convencional ya que contienen
cantidades menores de los costosos elementos de aleación. Sin embargo, reciben un
tratamiento especial que les da una resistencia mucho mayor que la del acero al carbono.
Por ejemplo, los vagones de mercancías fabricados con aceros de baja aleación pueden
transportar cargas más grandes porque sus paredes son más delgadas que lo que sería
necesario en caso de emplear acero al carbono. Además, como los vagones de acero de
baja aleación pesan menos, las cargas pueden ser más pesadas. En la actualidad se
construyen muchos edificios con estructuras de aceros de baja aleación. Las vigas pueden
ser más delgadas sin disminuir su resistencia, logrando un mayor espacio interior en los
edificios.
Aceros inoxidables
Los aceros inoxidables contienen cromo, níquel y otros elementos de aleación, que los
mantienen brillantes y resistentes a la herrumbre y oxidación a pesar de la acción de la
humedad o de ácidos y gases corrosivos. Algunos aceros inoxidables son muy duros; otros
son muy resistentes y mantienen esa resistencia durante largos periodos a temperaturas
muy rigurosas. Debido a sus superficies brillantes los arquitectos los emplean muchas veces
con fines decorativos. El acero inoxidable se emplea para las tuberías y tanques de
refinerías de petróleo o plantas químicas, para los fuselajes de los aviones o para cápsulas
espaciales. También se usa para fabricar instrumentos y equipos quirúrgicos, o para fijar o
sustituir huesos rotos, ya que resiste a la acción de los fluidos corporales. En cocinas y
zonas de preparación de alimentos los utensilios son a menudo de acero inoxidable, ya que
no oscurece los alimentos y pueden limpiarse con facilidad.
Aceros de herramientas
Estos aceros se emplean para fabricar muchos tipos de herramientas y cabezales de corte y
modelado de máquinas empleadas en diversas operaciones de fabricación. Contienen
wolframio,molibdeno y otros elementos de aleación, que les proporcionan mayor resistencia,
dureza y durabilidad.
Aleaciones
Ni
> Resistencia
< Oxidación
Cr
> Resistencia
> Dureza
Cr-Ni
>> Resistencia
< Oxidación > Dureza
Si > 0,3%
> Elasticidad
Mg
Neutraliza al azufre
Al 1%
18% Cr- 8% Ni - Inox
2% Cr- 5% Ni
Resortes
para temple
para nitruración
p/alto desgaste
Mb
> Resistencia tracción
para temple
V
< Fragilidad
Resortes y herramientas
W
> Dureza
Herramientas
Co-W
>> Dureza
Herramientas
Ti
< Oxidación
B 0,001%
para temple (50 más Mb)
Aceros rápidos: para altas velocidades (600 °C sin perder filo)
Estructura del acero
Las propiedades físicas de los aceros y su comportamiento a distintas temperaturas
dependen sobre todo de la cantidad de carbono y de su distribución en el hierro. Antes del
tratamiento térmico,la mayor parte de los aceros son una mezcla de tres sustancias: ferrita,
perlita y cementita. La ferrita, blanda y dúctil,es hierro con pequeñas cantidades de carbono
y otros elementos en solución. La cementita, un compuesto de hierro con el 7% de carbono
aproximadamente, es de gran dureza y muy quebradiza. La perlita es una profunda mezcla
de ferrita y cementita, con una composición específica y una estructura característica, y sus
propiedades físicas son intermedias entre las de sus dos componentes. La resistencia y
dureza de un acero que no ha sido tratado térmicamente depende de las proporciones de
estos tres ingredientes. Cuanto mayor es el contenido en carbono de un acero, menor es la
cantidad de ferrita y mayor la de perlita: cuando el acero tiene un 0,8% de carbono, está por
completo compuesto de perlita. El acero con cantidades de carbono aún mayores es una
mezcla de perlita y cementita. Al elevarse la temperatura del acero,la ferrita y la perlita se
transforman en una forma alotrópica de aleación de hierro y carbono conocida como
austenita, que tiene la propiedad de disolver todo el carbono libre presente en el metal. Si el
acero se enfría despacio, la austenita vuelve a convertirse en ferrita y perlita, pero si el
enfriamiento es repentino la austenita se convierte en martensita, una modificación
alotrópica de gran dureza similar a la ferrita pero con carbono en solución sólida.
Tratamiento térmico del acero
El proceso básico para endurecer el acero mediante tratamiento térmico consiste en
calentar el metal hasta una temperatura a la que se forma austenita, generalmente entre los
750 y 850 °C,y después enfriarlo con rapidez sumergiéndolo en agua o aceite. Estos
tratamientos de endurecimiento, que forman martensita, crean grandes tensiones internas
en el metal, que se eliminan mediante el temple o el recocido, que consiste en volver a
calentar el acero hasta una temperatura menor. El temple reduce la dureza y resistencia y
aumenta la ductilidad y la tenacidad.
El objetivo fundamental del proceso de tratamiento térmico es controlar la cantidad, tamaño,
forma y distribución de las partículas de cementita contenidas en la ferrita, que a su vez
determinan las propiedades físicas del acero.
Hay muchas variaciones del proceso básico. Los ingenieros metalúrgicos han descubierto
que el cambio de austenita a martensita se produce en la última fase del enfriamiento, y que
la transformación se ve acompañada de un cambio de volumen que puede agrietar el metal
si el enfriamiento es demasiado rápido. Se han desarrollado tres procesos relativamente
nuevos para evitar el agrietamiento. En el templado prolongado, el acero se retira del baño
de enfriamiento cuando ha alcanzado la temperatura en la que empieza a formarse la
martensita, a continuación se enfría despacio en el aire. En el martemplado, el acero se
retira del baño en el mismo momento que el templado prolongado y se coloca en un baño de
temperatura constante hasta que alcanza una temperatura uniforme en toda su sección
transversal. Después se deja enfriar el acero en aire a lo largo del rango de temperaturas de
formación de la martensita, que en la mayoría de los aceros va desde unos 300 °C hasta la
temperatura ambiente. En el austemplado, el acero se enfría en un baño de metal o sal
mantenido de forma constante a la temperatura en que se produce el cambio estructural
deseado, y se conserva en ese baño hasta que el cambio es completo, antes de pasar al
enfriado final.
Hay también otros métodos de tratamiento térmico para endurecer el acero. En la
cementación, las superficies de las piezas de acero terminadas se endurecen al calentarlas
con compuestos de carbono o nitrógeno. Estos compuestos reaccionan con el acero y
aumentan su contenido de carbono o forman nitruros en su capa superficial. En la
carburización la pieza se calienta cuando se mantiene rodeada de carbón vegetal, coque o
de gases de carbono como metano o monóxido de carbono. La cianurización consiste en
endurecer el metal en un baño de sales de cianuro fundidas para formar carburos y nitruros.
La nitrurización se emplea para endurecer aceros de composición especial mediante su
calentamiento en amoníaco gaseoso para formar nitruros de aleación.
TRABAJO DEL ENLACE QUIMICO
3. DESARROLLO
Los átomos se unen entre sí para formar moléculas mediante fuerzas de enlace. Los tipos
fundamentales de enlace son el iónico, el covalente y el metálico.
3.1 ENLACE IONICO
El enlace iónico consiste en la atracción electrostática entre átomos con cargas eléctricas de
signo contrario. Este tipo de enlace se establece entre átomos de elementos poco
electronegativos con los de elementos muy electronegativos. Es necesario que uno de los
elementos pueda ganar electrones y el otro perderlo,y como se ha dicho anteriormente este
tipo de enlace se suele producir entre un no metal (electronegativo) y un metal
(electropositivo).
Un ejemplo de sustancia con enlace iónico es el cloruro sódico. En su formación tiene lugar
la transferencia de un electrón del átomo de sodio al átomo de cloro. Las configuraciones
electrónicas de estos elementos después del proceso de ionización son muy importantes, ya
que lo dos han conseguido la configuración externa correspondiente a los gases nobles,
ganando los átomos en estabilidad. Se produce una transferencia electrónica,cuyo déficit se
cubre sobradamente con la energía que se libera al agruparse los iones formados en una
red cristalina que, en el caso del cloruro sódico, es una red cúbica en la que en los vértices
del paralelepípedo fundamental alternan iones Cl- y Na+. De esta forma cada ion Cl- queda
rodeado de seis iones Na+ y recíprocamente. Se llama índice de coordinación al número de
iones de signo contrario que rodean a uno determinado en un red cristalina. En el caso del
NaCl, el índice de coordinación es 6 para ambos
Propiedades de los compuestos iónicos
Las sustancias iónicas están constituidas por iones ordenados en el retículo cristalino; las
fuerzas que mantienen esta ordenación son fuerzas de Coulomb, muy intensas. Esto hace
que las sustancias iónicas sean sólidos cristalinos con puntos de fusión elevados. En efecto,
para fundir un cristal iónico hay que deshacer la red cristalina, separar los iones. El aporte
de energía necesario para la fusión, en forma de energía térmica, ha de igualar al de
energía reticular, que es la energía desprendida en la formación de un mol de compuesto
iónico sólido a partir de los correspondientes iones en estado gaseoso. Esto hace que haya
una relación entre energía reticular y punto de fusión, siendo éste tanto más elevado cuanto
mayor es el valor de aquella.
Por otra parte, la aparición de fuerzas repulsivas muy intensas cuando dos iones se
aproximan a distancias inferiores a la distancia reticular (distancia en la que quedan en la
red dos iones de signo contrario), hace que los cristales iónicos sean muy poco
compresibles. Hay sustancias cuyas moléculas, si bien son eléctricamente neutras,
mantienen una separación de cargas. Esto se debe a que no hay coincidencia entre el
centro de gravedad de las cargas positivas y el de las negativas: la molécula es un dipolo,
es decir, un conjunto de dos cargas iguales en valor absoluto pero de distinto signo,
separadas a una cierta distancia. Los dipolos se caracterizan por su momento; producto del
valor absoluto de una de las cargas por la distancia que las separa. Un de estas sustancias
polares es, por ejemplo el agua.
Cuando un compuesto iónico se introduce en un disolvente polar, los iones de la superficie
de cristal provocan a su alrededor una orientación de las moléculas dipolares, que enfrentan
hacia cada ion sus extremos con carga opuesta a la del mismo. En este proceso de
orientación se libera una energía que, si supera a la energía reticular, arranca al ion de la
red. Una vez arrancado, el ion se rodea de moléculas de disolvente: queda solvatado. Las
moléculas de disolvente alrededor de los iones se comportan como capas protectoras que
impiden la reagrupación de los mismos. Todo esto hace que, en general, los compuestos
iónicos sean solubles en disolventes polares, aunque dependiendo siempre la solubilidad
del valor de la energía reticular y del momento dipolar del disolvente. Así, un compuesto
como el NaCl, es muy soluble en disolventes como el agua, y un compuesto como el sulfato
de bario, con alta energía reticular, no es soluble en los disolventes de momento dipolar muy
elevado.
3.2 ENLACE COVALENTE
Gilbert Newton Lewis expuso la teoría de que todos los elementos tienen tendencia a
conseguir configuración electrónica de gas noble (8 electrones en la última capa).
Elementos situados a la derecha de la tabla periódica (no metales) consiguen dicha
configuración por captura de electrones; elementos situados a la izquierda y en el centro de
la tabla (metales), la consiguen por pérdida de electrones. De esta forma la combinación de
un metal con un no metal se hace por enlace iónico; pero la combinación de no metales
entre sí no puede tener lugar mediante este proceso de transferencia de electrones; por lo
que Lewis supuso que debían compartirlos.
Es posible también la formación de enlaces múltiples, o sea, la compartición de más de un
par de electrones por una pareja de átomos. En otros casos, el par compartido es aportado
por sólo uno de los átomos, formándose entonces un enlace que se llama coordinado o
dativo. Se han encontrado compuestos covalentes en donde no se cumple la regla. Por
ejemplo, en BCl3, el átomo de boro tiene seis electrones en la última capa, y en SF6,el
átomo de azufre consigue hasta doce electrones. Esto hace que actualmente se piense que
lo característico del enlace covalente es la formación de pares electrónicos compartidos,
independientemente de su número.
Fuerzas intermoleculares
A diferencia que sucede con los compuestos iónicos, en las sustancias covalentes existen
moléculas individualizadas. Entre estas moléculas se dan fuerzas de cohesión o de Van der
Waals, que debido a su debilidad, no pueden considerarse ya como fuerzas de enlace. Hay
varios tipos de interacciones: Fuerzas de orientación (aparecen entre moléculas con
momento dipolar diferente), fuerzas de inducción (ion o dipolo permanente producen en una
molécula apolar una separación de cargas por el fenómeno de inducción electrostática) y
fuerzas de dispersión (aparecen en tres moléculas apolares).
Propiedades de los compuestos covalentes
Las fuerzas de Van der Waals pueden llegar a mantener ordenaciones cristalinas, pero los
puntos de fusión de las sustancias covalentes son siempre bajos, ya que la agitación
térmica domina, ya a temperaturas bajas, sobre las débiles fuerzas de cohesión. La mayor
parte de las sustancias covalentes, a temperatura ambiente, son gases o líquidos de punto
de ebullición bajo (ejem.: agua). En cuanto a la solubilidad, puede decirse que, en general,
las sustancias covalentes son solubles en disolventes apolares y no lo son en disolventes
polares. Se conocen algunos sólidos covalentes prácticamente infusibles e insolubles, que
son excepción al comportamiento general descrito. Un ejemplo de ellos es el diamante. La
gran estabilidad de estas redes cristalinas se debe a que los átomos que las forman están
unidos entre sí mediante enlaces covalentes. Para deshacer la red es necesario romper
estos enlaces, los cual consume enormes cantidades de energía
3.3 ELECTROVALENCIA Y COVALENCIA
Teniendo presenta las teorías de los enlaces iónicos y covalentes, es posible deducir la
valencia de un elemento cualquiera a partir de su configuración electrónica.
· La electrovalencia, valencia en la formación de compuestos iónicos, es el número de
electrones que el átomo tiene que ganar o perder para conseguir la configuración de los
gases nobles.
· La covalencia, número de enlaces covalentes que puede formar un átomo, es el número de
electrones desapareados que tiene dicho átomo. Hay que tener presente que un átomo
puede desaparecer sus electrones al máximo siempre que para ello no haya de pasar
ningún electrón a un nivel energético superior.
3.4 ENLACE METALICO
Los elementos metálicos sin combinar forman redes cristalinas con elevado índice de
coordinación. Hay tres tipos de red cristalina metálica: cúbica centrada en las caras, con
coordinación doce; cúbica centrada en el cuerpo, con coordinación ocho, y hexagonal
compacta, con coordinación doce. Sin embargo, el número de electrones de valencia de
cualquier átomo metálico es pequeño, en todo caso inferior al número de átomos que
rodean a un dado, por lo cual no es posible suponer el establecimiento de tantos enlaces
covalentes.
En el enlace metálico, los átomos se transforman en iones y electrones, en lugar de pasar a
un átomo adyacente, se desplazan alrededor de muchos átomos. Intuitivamente, la red
cristalina metálica puede considerarse formada por una serie de átomos alrededor de los
cuales los electrones sueltos forman una nube que mantiene unido al conjunto.
3.5 POLARIDAD DE LOS ENLACES
En el caso de moléculas heteronucleares, uno de los átomos tendrá mayor
electronegatividad que el otro y, en consecuencia, atraerá mas fuertemente hacia sí al par
electrónico compartido. El resultado es un desplazamiento de la carga negativa hacia el
átomo más electronegativo, quedando entonces el otro con un ligero exceso de carga
positiva. Por ejemplo, en la molécula de HCl la mayor electronegatividad del cloro hace que
sobre éste aparezca una fracción de carga negativa, mientras que sobre el hidrógeno
aparece una positiva de igual valor absoluto. Resulta así una molécula polar, con un enlace
intermedio entre el covalente y el iónico.
1. EXPOSICION DE OBJETIVOS
Los objetivos de éste trabajo son exponer de una forma clara y concisa los diferentes tipos
de enlaces químicos tradicionales, ya que no se ha tomado en cuanto teorías más
modernas ni otros enlaces como el de hidrógeno, etc. Se tratará escuetamente de explicar
los conceptos y propiedades de los distintos enlaces, así como de algunos postulados en
relación con éste tema.
2. INTRODUCCION
Un enlace es la unión entre los átomos de un compuesto. La unión o enlace entre los
átomos tiene su origen en la estructura electrónica de los mismos. La actividad química de
los elementos radica en su tendencia a adquirir, mediante su unión con otros átomos, la
configuración de gas noble (ocho electrones en la capa más externa, salvo el helio que sólo
tiene dos), que es muy estable. Es corriente distinguir tres tipos principales de enlaces
químicos: iónico, covalente y metálico; de los cuales se hablará más extensamente
después. Aunque dichos enlaces tienen propiedades bien definidas, la clasificación no es
rigurosa, existiendo una transición gradual de uno a otro, lo que permite considerar tipos de
enlace intermedios. Gracias a estos enlaces se forman los compuestos químicos, por
ejemplo la sal.
La sal común es un sustancia bien conocida. Es utilizada para conservar y aderezar
alimentos. Nuestra sangre posee casi la misma proporción de sal que el agua del mar, y es
fundamental para mantener muchas de nuestras funciones vitales. Está formada por un no
metal, el cloro y un metal alcalino, el sodio. Ambos en estado puro son extremadamente
peligrosos para el hombre, sin embargo, forman juntas una sustancia, la sal común, que es
inocua en pequeñas cantidades. Se dice por tanto que han formado un compuesto químico,
una sustancia muy diferente de los elementos que la componen.
Muchas de las sustancias que conocemos están formadas por uniones de distintos
elementos. El azúcar, por ejemplo, está formado por oxígeno, hidrógeno y carbono. Estos
átomos que pierden o ganan electrones para unirse se transforman en iones, átomos con
carga eléctrica. Estos iones se unen para formar compuestos químicos, y la forma de unirse
entre ellos se denomina enlace químico, del cual se va a hablar en este trabajo.
Principios de la Mecánica
Este capı́tulo desarrolla algunos principios fundamentales sobre los que
se basa la teorı́a de la mecánica clásica, en la que se centra este curso. Conocer dicho punto de partida, ası́ como las limitaciones de la teorı́a empleada,
resulta imprescindible para una asimilación adecuada de la materia.
1.1.
La Mecánica como Teorı́a Cientı́fica
Definición: La mecánica es una teorı́a cientı́fica que estudia el movimiento de los cuerpos y sus causas, o bien el equilibrio, es decir, la falta de
movimiento.
Se trata de una teorı́a cientı́fica porque pretende interpretar fenómenos
fı́sicos que se observan experimentalmente. Para ello la mecánica parte de
unos postulados o principios fundamentales, sobre los que se basa una teorı́a
a través de modelos matemáticos, dando ası́ una interpretación coherente a
las observaciones experimentales. En la actualidad existen diversas teorı́as
de la mecanica, y a lo largo del tiempo han existido muchas más que han
quedado obsoletas bien por no ser prácticas en su aplicación, o bien por no
adecuarse sus predicciones a la realidad fı́sica observada.
Para juzgar las teorı́as cientı́ficas, y en concreto la mecánica, no tiene
sentido emplear criterios de veracidad absoluta. A pesar de que la mecánica tenga un elevado contenido de modelos matematicos, habiendo sido a
lo largo de la historia una de las motivaciones principales para el desarrollo
de las matemáticas, no es la elegancia ni el rigor formal de estos modelos
matemáticos un criterio adecuado para valorar una teorı́a de la mecánica.
Cada teorı́a (y sus principios subyacentes) es tan buena como la interpretación que realiza de las observaciones experimentales de la realidad fı́sica.
1.1
1.2
Capı́tulo 1. PRINCIPIOS DE LA MECÁNICA
Si las predicciones teóricas se corresponden adecuadamente con las observaciones experimentales, la teorı́a será adecuada, independientemente de su
elegancia matematica. Por el contrario, si los resultados no se corresponden con las observaciones, llegaremos a la conclusión de que se precisa otra
teorı́a distinta para el fenómeno en cuestión.
Ası́, las tres teorı́as principales de la mecánica existentes en la actualidad
son:
La Mecánica Clásica, cuyo desarrollo moderno se considera generalmente iniciado por Newton (1686: Philosophiae Naturalis Principia Mathematica ) y continuado hasta nuestros dı́as por diversos matemáticos y cientı́ficos: Juan, Daniel y Jacobo Bernouilli, L. Euler, J.
D’Alembert, J.L. Lagrange, W. Hamilton, etc. Los modelos newtonianos, enunciados por Isaac Newton, y desarrollados algo más tarde por
Euler, fueron los primeros que lograron explicar satisfactoriamente al
mismo tiempo el movimiento de los cuerpos celestes (observaciones
de Kepler y otros sobre el movimiento de los planetas) y el de los
cuerpos a escala humana (observaciones de Galileo sobre la caı́da de
los cuerpos).
La Mecánica Relativista, que suple la inexactitud de la mecánica clásica para velocidades próximas a la de la luz (teorı́a de la relatividad
restringida) o para campos gravitatorios muy intensos (teorı́a de la relatividad generalizada). Ha sido propuesta por Albert Einstein en este
mismo siglo, e involucra una complejidad matemática notablemente
mayor.
La Mecánica Cuántica, que surge de las observaciones de las partı́culas
elementales, en las que intervienen acciones —productos de energı́a
por tiempo— tan pequeñas que son comparables a la constante de
Planck (Et h). En estos casos se aplica el principio de indeterminación de Heisenberg, que establece la imposibilidad de medir de manera
precisa la posición y velocidad de la partı́cula al mismo tiempo, valores que conocemos tan sólo de manera probabilista. También ha sido
propuesta este mismo siglo (Congreso de Solvay de Bruselas en 1927),
por un grupo de cientı́ficos entre los que destacan L. de Broglie, E.
Schrödinger y P. Dirac.
A pesar de las nuevas teorı́as de la mecánica surgidas recientemente,
se puede afirmar que la mecánica clásica constituye una teorı́a coherente, capaz de proporcionar interpretaciones suficientemente precisas para la
mayorı́a de los fenómenos que observamos.
Aptdo. 1.1. La Mecánica como Teorı́a Cientı́fica
1.3
La teorı́a de la relatividad es de un orden más general que la mecánica clásica. Cuando la velocidad es pequeña en relación con la de la luz
y los campos gravitatorios no son muy intensos, sus predicciones corresponden con las de la mecánica clasica. Sin embargo, es capaz interpretar
correctamente otros fenómenos que la mecánica clásica no explica de manera adecuada1 . Serı́a posible por tanto estudiar el movimiento de los objetos
cotidianos como un automovil o un balón, por ejemplo, mediante la teorı́a
de la relatividad. Sin embargo, los modelos y los desarrollos matemáticos
resultarı́an de una complejidad extraordinaria, por lo que este método es
prácticamente inviable.
La mecanica clásica, a pesar de lo que su nombre parece indicar, no
constituye una teorı́a muerta ni agotada en su desarrollo. En nuestros dı́as
se continúa investigando, especialmente en campos como la mecánica de
medios continuos, o en los métodos cualitativos para el estudio de sistemas dinámicos complejos (estabilidad de sistemas dinámicos no lineales y
movimientos de tipo caótico).
La Mecánica de Medios Continuos es un subconjunto especializado de
la mecánica clásica. En ella se estudia el movimiento y la deformación de los
medios continuos (es decir, aquéllos que no se pueden representar mediante
idealizaciones discretas con un número finito de grados de libertad, como el
punto material o el sólido rı́gido). Los modelos más simples de la mecánica
de medios continuos son la teorı́a de la elasticidad lineal y la de los fluidos
newtonianos, permitiendo estudiar respectivamente la deformación de los
sólidos elásticos y las estructuras en régimen lineal y el flujo de los fluidos.
Recientemente, se han propuesto modelos más generales para comportamientos no lineales, ası́ como métodos y algoritmos muy potentes para su
resolución numérica mediante el ordenador (método de los elementos finitos). Es necesario también una investigación experimental constante para
conocer las propiedades mecánicas de los nuevos materiales (o incluso de
los tradicionales, ya que algunos como el hormigón o los suelos son todavı́a
insuficientemente conocidos).
La Dinámica de sistemas no lineales complejos permite estudiar el comportamiento de sistemas que no pueden ser caracterizados de manera de1
Un ejemplo lo constituye el corrimiento del perihelio (punto de la órbita más cercano
al Sol) observado para algunos planetas, especialmente el de Mercurio, el planeta más
cercano al Sol y cuya órbita es la más excéntrica (salvo la de Plutón). En efecto, se
observa un avance de su perihelio de unos 574 segundos de arco por siglo, y considerando
el efecto gravitacional de los restantes planetas, la dinámica clásica sólo predice unos 531
segundos por siglo. Los restantes 43 segundos son obtenidos de manera muy precisa por
la teorı́a de la relatividad, lo que constituye una contundente confirmación de la misma.
1.4
Capı́tulo 1. PRINCIPIOS DE LA MECÁNICA
terminista. La aparente falta absoluta de orden en su respuesta es debida
a menudo a una sensibilidad extrema a la variación de las condiciones iniciales u otros parámetros del sistema, lo que conduce a la denominación de
sistemas caoticos . Estos sistemas precisan ser analizados mediante métodos cualitativos, propuestos a final del siglo pasado por H. Poincaré y
Liapounov, en lugar de los métodos cuantitativos y deterministas habituales. También en este caso el ordenador es una herramienta de gran utilidad.
Este curso está basado en la Mecánica Clásica, desarrollada a partir de
los principios y teoremas newtonianos. Esta se aplicará fundamentalmente
a sistemas discretos formados por partı́culas o masas puntuales, sólidos rı́gidos, resortes, etc., aunque se hará alguna incursión en medios deformables,
como por ejemplo los cables. La mecánica de medios continuos se tratará en
otras asignaturas de cursos posteriores, como la resistencia de materiales,
elasticidad y plasticidad, la geotecnia, el calculo de estructuras, la hidráulica, etc. Sin embargo los conceptos básicos para todas estas asignaturas son
los mismos que se estudian en este curso de mecánica.
Como se ha dicho, en la mecanica juegan un papel importante las matemáticas, ya que se basa en modelos matemáticos que interpreten las observaciones experimentales. El aparato matemático en algunos casos puede
resultar de cierta complejidad. Es importante no perder de vista, sin embargo, el sentido fı́sico de los conceptos: Las matemáticas no son un fin en sı́,
sino un medio para interpretar conceptos y fenómenos fı́sicos. Aunque los
modelos matemáticos empleados aquı́ puedan ser más generales (y más
complejos por tanto) que los estudiados en cursos anteriores, no conviene
que oscurezcan nunca la interpretación fı́sica intuitiva de los conceptos.
Uno de los postulados esenciales de la mecánica es la causalidad determinista, lo que ha permitido superar interpretaciones mágicas o religiosas
existentes antaño para algunos fenómenos, como el movimiento de los astros
y otros fenómenos del firmamento celeste. Aún en nuestros dı́as existen personas que creen en dicho tipo de interpretaciones (por ejemplo los astrólogos
y sus seguidores), fruto por lo general de la ignorancia o del miedo a la verdad cientı́fica. Sin embargo, conviene admitir que, en ciertas situaciones, el
postulado de la causalidad determinista en sentido estricto es cuestionable,
siendo necesario acudir a métodos probabilistas para describir los fenómenos (como en la mecánica estadı́stica, basada en la causalidad probabilista)
o a métodos cualitativos de analisis (por ejemplo en los sistemas caóticos,
en los que no es posible predecir el movimiento como ecuaciones horarias,
ya que cualquier pequeña perturbación inicial lo modifica). En cualquier
caso, es conveniente evitar un exceso de celo en la aplicación de los modelos deterministas de la mecánica, ya que no debemos olvidar que nuestra
Aptdo. 1.2. Sistemas de Referencia; Espacio y Tiempo
1.5
percepción de la realidad fı́sica es necesariamente subjetiva.
Por otra parte, se postula también la capacidad de definir un conjunto
de causas suficientemente reducido para explicar los fenómenos. Las causas muy alejadas en el espacio o en el tiempo no tienen efecto sobre las
observaciones de fenómenos presentes. Esto también es cuestionable para
interpretaciones muy generales: No es posible prescindir de la estructura del
cosmos en el instante posterior a la primera gran explosión (big-bang) para
explicar la existencia de las galaxias, estrellas y planetas actuales; asimismo parece que algunos fenómenos cosmológicos no se pueden interpretar
sin recurrir a la materia oscura existente en el universo, de naturaleza aún
desconocida (agujeros negros, neutrinos,. . . ).
1.2.
Sistemas de Referencia; Espacio y Tiempo
Los fenómenos mecánicos se describen mediante sistemas de referencia , basados en los conceptos de espacio y tiempo. Por su importancia
conviene enunciar los postulados que asume la mecanica clásica para estos
conceptos.
El espacio, y por tanto su métrica, tiene las propiedades siguientes.
2
1. Independencia de los objetos en él inmersos. (La métrica del espacio
no se ve afectada por los mismos.)
2. Constancia a lo largo del tiempo.
3. Homogeneidad: es igual en todos los puntos, no existiendo puntos
privilegiados.
4. Isotropı́a: es igual en todas las direcciones, no existiendo direcciones
privilegiadas.
El espacio se caracteriza por una métrica Euclı́dea3 , lo que lo convierte
en un espacio puntual Euclı́deo en 3 dimensiones, R3 .
El tiempo se caracteriza a su vez por las siguientes propiedades.
1. Homogeneidad, al no existir instantes privilegiados.
2
No se debe confundir el término sistema mecanico (conjunto de partı́culas o cuerpos
cuyo movimiento se desea estudiar) con sistema de referencia (triedro de ejes, coordenadas
o parametros que sirven para describir dicho movimiento).
3
La distancia entre dos puntos definidos pop
r sus coordenadas cartesianas rectangulares
(x1 , y1 , z1 ) y (x2 , y2 , z2 ) viene dada por d = (x2 − x1 )2 + (y2 − y1 )2 + (z2 − z1 )2
1.6
Capı́tulo 1. PRINCIPIOS DE LA MECÁNICA
2. Fluye constantemente en un sentido, por lo que no se puede retroceder
ni volver al pasado (desgraciadamente para algunos). Asimismo, los
fenómenos futuros no pueden condicionar los presentes. No se cumple
por tanto la isotropı́a, existiendo un único sentido en el que puede
discurrir el tiempo.
3. Simultaneidad absoluta: Los fenómenos considerados simultáneos para dos observadores en sendos sistemas de referencia, lo son asimismo
para cualquier otro observador ligado a cualquier otro sistema de referencia.
En mecanica clásica, el tiempo se considera una variable de naturaleza
distinta de las variables espaciales, y la métrica euclı́dea no está influenciada
por él.
Algunos de estos postulados básicos no son aceptados por la mecánica
relativista. La teorı́a de la relatividad restringida establece una referencia
en cuatro dimensiones espacio-tiempo. La teorı́a de la relatividad general
establece un espacio curvado, con métrica Riemanniana no Euclı́dea, debido
a la presencia de masas que condicionan dicha métrica. De esta forma el
espacio no serı́a independiente de los objetos en él inmersos.
1.3.
Principio de la Relatividad de Galileo
El principio de la relatividad galileana4 establece que:
‘Dos sistemas de referencia en movimiento relativo de traslación
rectilı́nea uniforme son equivalentes desde el punto de vista mecánico; es decir, los experimentos mecánicos se desarrollan de
igual manera en ambos, y las leyes de la mecánica son las mismas.’
Uno de los ejemplos puestos por Galileo es el de un observador viajando
en un barco que navega plácidamente sobre un rı́o, en contraste con un
observador fijo en la orilla. Ambos interpretan de la misma manera la caı́da
de un cuerpo hacia el suelo en su propio sistema, que como sabemos sigue
un movimiento vertical uniformemente acelerado.
4
Galileo Galilei, Discursos y demostraciones en torno a dos ciencias nuevas relacionadas con la mecánica, 1602. Galileo, que vivió entre 1564 y 1642, realizó contribuciones
importantes a la mecánica y a la astronomı́a, estudiando por primera vez los cielos mediante el telescopio que diseñó él mismo. Fue condenado como hereje por la inquisición
católica, que no aceptaba su teorı́a según la cual la tierra gira alrededor del sol.
Aptdo. 1.3. Principio de la Relatividad de Galileo
1.7
Transformación de Galileo5 .— Sea un sistema móvil (O 0 x0 y 0 z 0 ), que se
traslada respecto a otro fijo (Oxyz) con velocidad v, manteniéndose paralelos los ejes de ambos. Puesto que podemos elegir las direcciones del triedro
✻
✻
y
y0
v
✟
✟ ✟
✟✟
✙
✟
✟
O
x ✲
x0 ✲
✟✟ 0
✟
✟ ✟
✲
O
✟ ✟ z0
✙
z
(O 0 x0 y 0 z 0 )
(Oxyz)
Figura 1.1: Sistemas de referencia en movimiento relativo rectilı́neo y uniforme, con velocidad v en la dirección de Ox
de referencia, elegimos la dirección Ox según la dirección de la velocidad de
traslación (recordemos que el espacio es es isótropo, por lo que es lı́cito elegir
una orientación arbitraria para los ejes, sin pérdida de generalidad).
Consideraremos también que Inicialmente (para t = 0) O y O0 coinciden.
Sean (x, y, z) las coordenadas de un punto en el sistema fijo, (x0 , y 0 , z 0 )
en el móvil y v el módulo de la velocidad. Las ecuaciones de transformación
para las coordenadas son:
x0 = x − vt
y 0= y
z0 = z
(1.1)
Derivando sucesivamente6 , obtenemos las velocidades y aceleraciones en
5
En el apartado 6.3.5 se ofrece una generalización de esta transformación y se discute
la relación de las simetrı́as que expresa (invariancias cuando se produce la transformación)
con las constantes del movimiento y los principios de conservación.
6
En lo sucesivo se empleará la notación de uno o dos puntos superpuestos para indicar
def
def
derivadas (totales) respecto al tiempo: ẋ = dx/dt, ẍ = d2 x/dt2 . También emplearemos
la notación mediante negritas para identificar vectores o tensores: a ≡ {ai }, I ≡ [Ikl ].
1.8
Capı́tulo 1. PRINCIPIOS DE LA MECÁNICA
ambos sistemas:
ẋ0 = ẋ − v
ẏ 0 = ẏ
ż 0 = ż
ẍ0 = ẍ
ÿ 0 = ÿ
z̈ 0 = z̈
Se observa por tanto que las derivadas segundas (aceleraciones) coinciden. Esto nos permite intuir —admitiendo como postulado el principio
de la relatividad galileana— que las leyes de la dinámica están basadas
en las derivadas segundas respecto al tiempo, única forma de que las leyes
sean invariantes cumpliéndose dicho principio. En efecto, según sabemos, el
estado de un sistema formado por un partı́cula en movimiento según una
dirección fija se caracteriza en un instante dado por su posición y su velocidad (x, ẋ). La evolución del movimiento viene gobernada por la ecuación
dinámica (F = mẍ).
1.4.
Las Leyes de Newton
Formuladas por Isaac Newton en su obra Philosophiae Naturalis Principia Matematica (1686), constituyen el primer intento de formular una
base axiomática para una teorı́a cientı́fica de la mecánica. Debe aclararse
que no fueron formuladas por Newton de forma precisa como se suelen recoger hoy en dı́a en los libros de texto. También debe advertirse que en sentido
riguroso no recogen de forma completa toda la axiomática necesaria para
la mecanica clasica, siendo necesario incorporar aportaciones adicionales de
Euler, Cauchy y otros. A pesar de esto, la publicación de los principia
constituye un hito monumental de enorme valor, sobre el que se cimienta
la mecanica clasica.
Para aclarar el modelo axiomatico de Newton citaremos aquı́ textualmente de los Principia 7 . Newton parte en primer lugar de cuatro definiciones:
‘DEFINICION PRIMERA. La cantidad de materia es la medida de la misma originada de su densidad y volumen conjuntamente.’
‘DEFINICION II. La cantidad de movimiento es la medida
del mismo obtenida de la velocidad y de la cantidad de materia
conjuntamente.’
‘DEFINICION III. La fuerza ı́nsita de la materia es una
capacidad de resistir por la que cualquier cuerpo, por cuanto
7
Las citas han sido extraı́das de Isaac Newton, Principios Matemáticos de la Filosofı́a
Natural (2 tomos), traducción española de Eloy Rada, Alianza Editorial, 1987.
Aptdo. 1.4. Las Leyes de Newton
1.9
de él depende, perservera en su estado de reposo o movimiento
uniforme y rectilı́neo.’
‘DEFINICION IV. La fuerza impresa es la acción ejercida
sobre un cuerpo para cambiar su estado de reposo o movimiento
uniforme y rectilı́neo.’
La definición primera (cantidad de materia de un cuerpo) equivale a lo
que conocemos por masa. La tercera caracteriza las denominadas fuerzas de
inercia, mientras que la cuarta se refiere a las fuerzas propiamente dichas.
Realizadas estas definiciones, Newton enuncia sus conocidas tres leyes
o principios fundamentales:
‘LEY PRIMERA. Todo cuerpo persevera en su estado de reposo
o movimiento rectilı́neo y uniforme a no ser en tanto que sea
obligado por fuerzas impresas a cambiar su estado.’
Esta ley constituye el llamado principio de la inercia. Admitiendo también el principio de Galileo, nos permite definir los llamados sistemas inerciales, como aquellos en los que se cumple dicho principio. Las leyes de la
mecánica se formulan en un sistema inercial de referencia. Por el principio
de Galileo, admitiendo que existe al menos un tal sistema inercial, existirán
infinitos sistemas inerciales en los que se cumplen las mismas leyes mecánicas y en concreto la ley primera de Newton: todos aquellos relacionados
entre sı́ mediante transformaciones de Galileo (1.1), es decir, que se mueven
con velocidad rectilı́nea y uniforme respecto al primero.
Este principio nos permite también definir, como condiciones iniciales
del movimiento, las que caracterizan a un movimiento estacionario o consdef
tante: la posición r y la velocidad v = ṙ .
Conviene observar también que Newton emplea el término cuerpo
para referirse en realidad a una partı́cula, o punto material, caracterizada
por la posición y velocidad de un solo punto8 .
‘LEY II. El cambio de movimiento es proporcional a la fuerza
motriz impresa y ocurre según la lı́nea recta a lo largo de la cual
aquella fuerza se imprime.’
Esta ley indica claramente una relación lineal ( proporcional ) entre
fuerzas y variaciones de la cantidad de movimiento, de tipo vectorial ( según
8
El tratamiento de los sólidos rı́gidos, ası́ como el de sistemas generales formados
por varias partı́culas, requiere de diversos principios y teoremas adicionales que fueron
propuestos por L. Euler. De esto se tratará en los capı́tulos 6 y 8.
1.10
Capı́tulo 1. PRINCIPIOS DE LA MECÁNICA
la lı́nea recta ). Se denomina en ocasiones ley fundamental de la dinámica,
permitiendo obtener las ecuaciones básicas de la misma. Expresada como
ecuación, equivale a:
∆ (mv) = F
| {∆
z }t .
| {z }
cant. de
movto.
impulsión
Pasando al lı́mite, para un incremento infinitesimal de tiempo, obtenemos la relación diferencial siguiente:
d(mv) = F dt.
def
O bien, llamando cantidad de movimiento a p = mv,
ṗ =
dp
= F.
dt
Admitiremos en principio que la masa de un cuerpo se conserva. Ası́ pues,
se llega a la conocida expresión que define la ley del movimiento de una
partı́cula:
F = ma,
(1.2)
def
donde a = v̇ = dv/dt. Cabe realizar en relación con esta fórmula las
siguientes
Observaciones:
– La aceleración, derivada segunda del vector posición, es asimismo un
vector. La ecuación (1.2) tiene por tanto carácter vectorial, lo que
identifica a las fuerzas como vectores, e implı́citamente supone la aditividad vectorial para las mismas (ley del paralelogramo de fuerzas).
– La expresión (1.2) da lugar a ecuaciones diferenciales de segundo orden, ya que intervienen derivadas segundas de la incógnita r respecto
al tiempo.
‘LEY III. Con toda acción ocurre siempre una reacción igual y
contraria. O sea, las acciones mutuas de los cuerpos siempre son
iguales y dirigidas en direcciones opuestas.’
Se trata del llamado principio de acción y reacción. Todas las fuerzas
deben de tener contrapartida, siendo imposible ejercer una fuerza desde el
vacı́o, sin apoyo. Es siempre necesario apoyarse en algún cuerpo o medio
material que absorba la reacción (modificando a su vez el movimiento de
este otro cuerpo, según la segunda ley).
Aptdo. 1.5. Conceptos de Masa y Fuerza
1.11
Ejemplo 1.1: Fuerza ejercida desde la superficie de la Tierra. Todo cuerpo
cercano a la tierra, tanto en estado de movimiento (caı́da libre) o en reposo
sobre el suelo, recibe una fuerza (denominada peso) ejercida por la tierra,
que lo mueve en el primer caso o lo mantiene inmovil en el segundo. El
cuerpo a su vez ejerce sobre la tierra una fuerza igual y contraria, aunque
esta última, debido a la gran masa de la tierra, produce un efecto muy
pequeño sobre nuestro planeta.
Ejemplo 1.2: Movimiento de un cohete en el vacı́o. Una fuerza no se puede
ejercer sobre el vacı́o, necesitando siempre aplicarse sobre otro cuerpo (que
a su vez producirá una reacción igual sobre el primero). Para moverse —o
más bien acelerar o frenar, es decir, variar el movimiento— en el vacı́o,
un cohete o sonda espacial necesita apoyarse sobre algún medio. Esto se
consigue mediante masa expulsada por la tobera, medio en el cual se apoya
el cohete, a través de la expulsión de los gases del combustible quemado,
propulsión iónica, plasma, u otros medios. De este tema se tratará en el
capı́tulo 6.6.
1.5.
Conceptos de Masa y Fuerza; Discusión de
las Leyes de Newton
Las leyes de Newton reposan sobre las definiciones básicas de masa y
fuerza. Sin embargo, examinando dichas leyes con espı́ritu crı́tico, es fácil
ver que las definiciones realizadas por Newton de estos conceptos adolecen
de algunas deficiencias.
La definición de fuerza (definición IV, pág. 1.9) es claramente circular
con la primera ley. En efecto, se podrı́a entender ésta como una definición
de fuerza, obviando la definición anterior dada por Newton. Aún aceptando
esto, tampoco se puede considerar esta ley como una definición precisa
de fuerza, ya que no proporciona una manera de medir su valor de forma
cuantitativa. En realidad tan sólo se podrı́a deducir de la primera ley cuándo
la fuerza es nula o cuándo no lo es. La segunda ley sin embargo sı́ se puede
interpretar como una definición cuantitativa de fuerza, pero ésto la privarı́a
a su vez de su consideración como principio.
En cuanto a la definicion de masa (definición I, pág 1.8), Newton la
refiere a la densidad (ρ) y volumen (V ) que integran un cuerpo (M = ρV ).
¿Cuál serı́a entonces la definicion de densidad? Es difı́cil aceptar que la
densidad sea un concepto más fundamental que el de masa.
Un procedimiento aparentemente más riguroso para definir la masa es
1.12
Capı́tulo 1. PRINCIPIOS DE LA MECÁNICA
el debido a E. Mach9 (1858-1916), que resumimos a continuación.
Sean dos partı́culas, a y b, formando un sistema binario aislado. Expresando la segunda ley de Newton para la partı́cula a:
ma aa = F ab ,
donde F ab es la fuerza ejercida sobre a por b. Análogamente para b,
mb ab = F ba = −F ab ,
por la 3.a ley de Newton. Ası́,
ma aa = −mb ab ,
y empleando los módulos de las aceleraciones aa y ab ,
mb
a
= − .a
ma
ab
Suponiendo la masa ma como valor de referencia o definición de unidad de masa, este procedimiento nos permite medir la masa de cualquier
partı́cula b a partir de la medicion de las aceleraciones ab y aa .
Aunque aquı́, por clarificar la explicación, se ha llegado a esta definición
partiendo de las leyes de Newton, serı́a posible considerarla como definición
básica de masa, para comprobar posteriormente que, efectivamente, es consistente con las leyes de Newton.
De esta forma, con el espı́ritu crı́tico mencionado, cabrı́a considerar las
leyes primera y segunda de Newton como definiciones de fuerza, con lo que
la única ley que expresa un postulado básico de la mecánica serı́a la ley
tercera. Según Mach por tanto, es la ley tercera de Newton (principio de
acción y reacción) la que reviste mayor importancia en la axiomática de la
mecanica clásica.
En relación con esta última ley, puede ser objeto de cierta polémica la
consecuencia implı́cita de existencia de acciones a distancia, es decir acciones que se propagan de manera instantánea (con velocidad infinita). En
efecto, si se suponen dos cuerpos alejados entre sı́ con fuerzas de interacción centrales (dirigidas según la recta que las une), y uno de ellos sufre
un cambio de posición, la ley de acción y reacción obligarı́a a que la fuerza de reacción sobre la otra partı́cula modificase su dirección de manera
9
E. Mach, The science of mechanics, traducción al inglés, Open Court, 1902.
Aptdo. 1.5. Conceptos de Masa y Fuerza
1.13
instantanea10 .
En la realidad fı́sica parece que no existen tales interacciones instantáneas; respondiendo a ello la teorı́a de la relatividad restringida establece un
lı́mite a la velocidad de propagacion de las interacciones, que es la velocidad
de la luz en el vacı́o (c). Esto origina una cierta inexactitud de la mecánica
clásica, error que sin embargo es muy pequeño para las fuerzas gravitatorias
o elásticas en objetos cotidianos.
Conviene observar también que de la tercera ley se pueden hacer dos
enunciados. En su forma débil, ciñéndose estrictamente al enunciado Newtoniano, establece que las fuerzas son iguales en magnitud y dirección y de
sentido opuesto. Sin embargo, no presupone que tengan la misma dirección
que la recta que une a las dos partı́culas sobre las que actúan. En el caso
en que sı́ se verifique esta última hipótesis más restrictiva, se dice que se
cumple el principio de acción y reacción en su forma fuerte, siendo las fuerzas centrales. En numerosos casos prácticos se verifican ambos enunciados
del principio de accion y reacción, como son las fuerzas gravitatorias, elásticas, o electrostáticas. Sin embargo, existen fenómenos importantes en los
que no se verifica en ninguna de sus dos formas. Estos casos corresponden
a fuerzas que dependen de la velocidad, ligadas por lo general a campos
que se propagan con velocidad finita, como son las fuerzas electrodinámicas
debidas a cargas en movimiento.
En resumen, podemos clasificar las fuerzas citadas esquemáticamente
como sigue.
Fuerzas centrales: Están asociadas a campos que suponen una acción
a distancia, propagandose por tanto de manera instantánea. Se trata
de fuerzas dirigidas hacia las partı́culas que las originan, cumpliendo
la tercera ley de Newton en su forma fuerte. En mecánica clásica se
admite esta hipótesis como adecuada para algunos de los tipos más
usuales de fuerzas:
• Fuerzas gravitatorias. La hipótesis de fuerza central e instantánea se considera adecuada para las mediciones en escalas usuales.
Sin embargo, para mediciones a escalas astronómicas o cosmológicas se trata de una hipótesis cuestionable. Serı́a más correcto
10
Históricamente ha existido siempre, antes y después de Newton, una contestación a
la posibilidad de tales acciones a distancia. Antiguamente se defendı́a que todo el espacio
estaba lleno de una sustancia invisible, llamada É ter, vehı́culo transmisor de las fuerzas.
Este concepto sobrevivió a Newton, alcanzando su mayor predicamento dos siglos después
para explicar el campo electromagnético, siendo la Teorı́a de la Relatividad la que acabó
de desterrarlo.
1.14
Capı́tulo 1. PRINCIPIOS DE LA MECÁNICA
✟✟
✙
✟✟
F ba
b
✠
F
b
ba
F ab
F ab
✒
✯
✟✟
✟✟
a
a
a) Fuerzas centrales
b) Fuerzas no centrales
Figura 1.2: Las fuerzas centrales están dirigidas según la recta que une los
cuerpos, mientras que las fuerzas no centrales no verifican esta hipotesis,
aún siendo iguales en magnitud y dirección y de sentido opuesto.
interpretarlas mediante ondas de gravedad, que se propagan con
la velocidad de la luz.
• Fuerzas electrostáticas o magnetostáticas, de atracción o repulsión debidas a cargas eléctricas o magnéticas en reposo. Al igual
que en el caso gravitatorio, de forma rigurosa para escalas astronómicas puede ser necesario considerar la transmisión de dichas
fuerzas a través de ondas electromagnéticas.
• Fuerzas elasticas, ejercidas entre las partı́culas en contacto de un
medio continuo. Por lo general, podrı́a admitirse que son manifestaciones macroscópicas de las fuerzas electrostáticas entre las
moléculas.
Fuerzas no centrales: ocurren, por lo general, cuando las interacciones
dependen de la velocidad, estando asociadas a campos que se propagan con velocidad finita:
• Fuerzas Electromagnéticas; cuando son debidas a cargas móviles
pueden no cumplir tampoco el principio de acción y reacción en
su forma débil.
Debe quedar claro que en este curso admitiremos la hipótesis de fuerzas
centrales, por lo que será válido el principio de acción y reacción en su
forma fuerte.
La definición de masa según el procedimiento de Mach arriba descrito
no proporciona sin embargo un método viable para medirla. Serı́a prácticamente imposible aislar completamente un sistema binario y al mismo
Aptdo. 1.6. La Ley de la Gravitación Universal
1.15
tiempo realizar mediciones. Una forma más practica de medir la masa, aunque de forma indirecta, es con una balanza de resorte. En ésta lo que se
mide directamente es el peso, o atracción gravitatoria hacia el centro de la
Tierra. Basta dividir el peso (w) por la aceleración de la gravedad en la
superficie de la Tierra (g) para obtener la masa11 :
w = mg
1.6.
w
m= .
g
La Ley de la Gravitación Universal
Newton fue el primero en explicar el movimiento, tanto de los cuerpos
celestes —proporcionando la explicación matemática de las leyes observadas por Kepler para el movimiento de los planetas en órbitas elı́pticas—,
como de los terrestres —la famosa caı́da de la manzana—, a partir de una
única ley para las fuerzas: la ley de la gravitación universal. Anteriormente,
los estudios y teorı́as de la mecánica habı́an buscado explicaciones separadas para ambos fenómenos. Kepler habı́a deducido del análisis minucioso
de las observaciones experimentales que los planetas describı́an elipses con
foco en el Sol, ası́ como la constancia de la velocidad areolar y el perı́odo de
estos movimientos orbitales (aptdo. 5.5). A su vez, Galileo habı́a caracterizado el movimiento de caı́da uniformemente acelerado de los graves, por
—según la leyenda— experimentos desde la torre inclinada de Pisa. Todas
estas descripciones eran empı́ricas, sin una justificación basada en modelos
matematicos coherentes.
La ley de la gravitación universal propuesta por Newton establece que
entre dos cuerpos12 cualesquiera se produce una fuerza gravitatoria de
atracción, proporcional al producto de las masas respectivas y al inverso
del cuadrado de la distancia entre los mismos. La expresión de esta fuerza,
en módulo, es
Mm
F =G 2 ,
r
11
No debe originar confusión la existencia de dos unidades con el mismo nombre para
caracterizar magnitudes distintas: el kg de masa, y el kg de fuerza o kilopondio (kp),
definido como el peso de 1 kg de masa en la superficie de la tierra, considerando un valor
medio constante de la aceleración de la gravedad (1 kg fuerza ' 9,81 N). Ello permite
hablar —afortunadamente para los tenderos, fruteros, pescaderos y demás gremios poco
interesados en la filosofı́a de la mecánica durante su quehacer cotidiano— simplemente
de kg, sin necesitar especificar si se trata de masa o de peso, ya que en la superficie
de la tierra ambos son equivalentes, al menos en una primera aproximación en que g se
suponga constante.
12
Debe entenderse cuerpo en el sentido de partı́cula, tal y como emplea Newton este
término (pág. 1.9).
1.16
Capı́tulo 1. PRINCIPIOS DE LA MECÁNICA
y en forma vectorial
Mm
r,
(1.3)
r3
donde F representa la fuerza ejercida por la masa M sobre m, y r es el
vector que las une, con origen en M y extremo en m.
En la mecanica clasica, la fuerza gravitatoria es una acción a distancia
que, de manera muy aproximada, podemos suponer se transmite de forma
instantánea, sin necesitar de ningún medio material para ello. Ası́, cada masa M crea un campo de fuerzas gravitatorio, campo vectorial caracterizado
en cada punto por una intensidad i:
F = −G
def
i = −G
M
r;
r3
La fuerza ejercida sobre un cuerpo de masa m será el producto de ésta por
la intensidad del campo,
F = mi = −G
Mm
r.
r3
✻
m ✉
✒
✠
r
✟✟
✙
✟✟
✟
M
✟
i=
F
Figura 1.3: Atracción gravitatoria entre dos masas M y m, situadas a distancia r
m
✲
✟
La teorı́a de la relatividad general elimina las fuerzas gravitatorias; para
ello, interpreta el efecto de las masas como una modificación a la métrica
espacio-tiempo, que resulta ser Riemanniana en lugar de Euclı́dea. Ası́, en
esta nueva métrica, las trayectorias de las partı́culas corresponden a las
geodésicas del espacio-tiempo, que vendrı́an a ser las ecuaciones horarias
del movimiento13 .
13
En la mecánica clásica la trayectoria seguida por una partı́cula sometida a la acción
gravitatoria de otra es una cónica, como se verá en el capı́tulo 5. Podrı́amos plantearnos,
Aptdo. 1.6. La Ley de la Gravitación Universal
1.6.1.
1.17
Masa Gravitatoria y Masa Inerte.
En principio, el concepto de masa que interviene en la ley de la gravitación no tendrı́a porqué coincidir con la masa empleada para la ley II de
Newton; en el primer caso sirve para definir la fuerza gravitatoria, mientras
que en el segundo define la fuerza de inercia. Podemos distinguirlas por
tanto denominándolas mg (masa gravitatoria) y mi (masa inerte).
Existe, sin embargo, una observación experimental: en la superficie de
la tierra todos los cuerpos caen en el vacı́o hacia el suelo con la misma
aceleración (g). Sea un cuerpo cualquiera en la superficie de la tierra; su
peso es
Mg mg
w=G
,
R2
donde Mg y mg son las masas respectivas (gravitatorias) de la Tierra y
del cuerpo, R es el radio de la tierra (suponemos el cuerpo a una altura
h pequeña, por lo que R + h ≈ R), y G es la constante de la gravitación
universal.
Empleando la segunda ley de Newton, se puede relacionar el peso con la
aceleración que experimenta el cuerpo:
w = mi g,
siendo mi la masa (inercial) del mismo. Igualando ambas expresiones de w
se obtiene:
mi
Mg G
=
.
mg
gR2
| {z }
constante
Ası́, el cociente mi /mg permanece constante. Ya que G es una constante
cuyo valor puede ser cualquiera, es posible elegir el mismo de forma que
este cociente sea la unidad. De esta forma, ambas masas tendrı́an siempre
igual valor:
mi ≡ mg .
Para ello, el valor de la constante de la gravitación universal ha de ser
G=
gR2
.
M
en la teorı́a de la relatividad general, qué trayectoria seguirı́a un cuerpo en un universo
homogéneo, pero en cualquier caso no resulta ser una cónica. En un caso sencillo, con una
única masa aislada, la métrica de Schwarzschild creada por ésta conduce a órbitas que no
se cierran, lo que puede explicar algunos fenómenos bien conocidos como el corrimiento
del perihelio de Mercurio.
1.18
Capı́tulo 1. PRINCIPIOS DE LA MECÁNICA
Consideraciones sobre el universo.— Supongamos que el universo
tiene un tamaño finito, y que, de forma aproximada, se puede idealizar
como una esfera, con una distribución de masa de densidad media ρ. Sea
un cuerpo de masa m, situado a una distancia R del centro de dicha esfera;
este experimentarı́a una fuerza atractiva hacia el centro del universo de
valor:
’
“
4
mG
4
F = πR3 ρ
= πρmGR.
3
R2
3
| {z }
masa esfera
Ası́, todos los cuerpos del universo experimentarán una aceleración hacia el
centro de aquél de valor creciente proporcionalmente a su distancia R. Si
esto fuese ası́, desde un punto distinto del centro del universo se observarı́a
un movimiento diferente de las estrellas y galaxias según las distintas direcciones de observación; en la dirección del radio creciente, la aceleración serı́a
mayor, mientras que en la opuesta disminuirı́a. Sin embargo, esto no parece
concordar con las observaciones experimentales medidas desde la Tierra.
¿Cómo se puede explicar esto, admitiendo que el universo es finito?
Una posible explicación serı́a una teorı́a antropocéntrica , según la que
el planeta Tierra tendrı́a el inmenso privilegio de estar situado justo en
el centro del universo. De esta forma, nuestras observaciones deberı́an ser
iguales en cualquier dirección, ya que todas serı́an radiales. Sin embargo,
fuera de creencias pseudo-religiosas, la teorı́a antropocéntrica parece poco
probable. Más bien, la observación anterior podrı́a explicarse por una de
las siguientes dos hipótesis:
1. El universo es homogéneo, isótropo e infinito. Sin embargo, esta suposición es incompatible con la teorı́a, generalmente aceptada en la
actualidad, del Big-Bang como origen del universo. Esta primera
explosión primigenia ocurrió al parecer hace unos diez mil millones
de años, lo que establece un lı́mite para el tamaño del universo.
2. El universo es finito, pero con una métrica no euclı́dea, en la que todos
los puntos pueden considerarse el centro de los demás. Esta última
hipótesis es la que parece mas plausible, quedando por discutir el tipo
de métrica, para lo cual existen a su vez distintas teorı́as.
E. Mach interpretó la acción gravitatoria del resto del universo como
responsable de la inercia de los cuerpos. Ası́, serı́a la masa del universo lejano la encargada de mantener un cuerpo con velocidad uniforme y rectilı́nea
o en reposo ante la ausencia de otras fuerzas cercanas. Esto podrı́a ser una
Aptdo. 1.6. La Ley de la Gravitación Universal
1.19
bonita teorı́a, pero Mach lo dejó planteado tan sólo como una especulación,
que carece de una justificación rigurosa.
Tipos de fuerzas en el universo.— Las fuerzas gravitatorias no son
las únicas que existen en el universo fı́sico. De forma esquemática se pueden
distinguir cuatro tipos fundamentales de fuerzas, siendo las demás manifestaciones macroscópicas de éstas.
1. Fuerzas gravitatorias. Aunque en la mecanica clásica se consideran
como acciones a distancia, de propagación instantánea, en la realidad
parece que se propagan con velocidad finita. Esta propagación se realiza mediante las llamadas ondas gravitatorias. En la interpretación
dual onda/corpúsculo equivalen a las partı́culas llamadas Gravitones14 .
2. Fuerzas electromagnéticas. Están gobernadas por las ecuaciones de
Maxwell del campo electromagnético. Se propagan mediante las Ondas electromagnéticas, que incluyen la luz, ondas de radio, etc. Las
partı́culas equivalentes son los Fotones.
3. Fuerzas nucleares fuertes. Son las fuerzas que unen a las partı́culas en
el núcleo atómico. Intervienen únicamente en la mecánica cuántica.
Están asociadas a las partı́culas denominadas Gluones.
4. Fuerzas nucleares débiles. Son las fuerzas que intervienen en la desintegración nuclear. Asimismo intervienen en la mecánica cuántica, y
las partı́culas asociadas son los Bosones.
La publicación por Newton de los Principia con la teorı́a de la gravitación universal supuso en su tiempo un avance importante para la mecánica
y para las matemáticas, al interpretar de forma coherente y unificada dos
tipos de fenómenos que antes se consideraban obedecientes a leyes distintas: el movimiento de los objetos terrestres y el de los objetos celestes. De
manera similar, se busca hoy en dı́a, por parte de los fı́sicos teóricos y matemáticos, una teorı́a unificada que permita explicar, a partir de una causa
común, los cuatro tipos de fuerzas que se observan en el universo. Sin embargo, es de prever que esta teorı́a, aún en el improbable caso de poderse
obtener, serı́a mucho más compleja y engorrosa de utilizar que la mecánica
clásica o los métodos newtonianos. Por ello, aún en la hipótesis de que se
14
Aunque se han establecido diversos experimentos para detectar las ondas gravitatorias, aún no se han llegado a medir de forma fehaciente, debido a su intensidad extremadamente baja.
1.20
Capı́tulo 1. PRINCIPIOS DE LA MECÁNICA
logre algún avance importante en esta lı́nea, es improbable que tenga repercusiones prácticas en la mecanica aplicada a la ingenierı́a, campo que
nos ocupa y en el cual la mecanica clásica seguirá teniendo plena vigencia.
Capı́tulo 2
Dinámica de la Partı́cula
La partı́cula, o punto material, es la idealización más simple de la mecánica, definiéndose como un punto dotado de masa. Por lo general se puede
emplear este modelo cuando las dimensiones de un cuerpo sean lo suficientemente pequeñas como para suponer toda su masa concentrada en un
punto.
Sin embargo, el criterio del tamaño pequeño no es siempre suficiente
para establecer la validez de esta idealización. El modelo del punto material puede ser inadecuado en algunas situaciones, aunque las dimensiones
del cuerpo sean pequeñas. Para ilustrar esta afirmación, supongamos como
ejemplo la caı́da de una bolita pequeña por un plano inclinado bajo dos
hipótesis distintas:
✟
✟✟
ω = v/R
✟ ✟
✉✟ ✟
✟✟
✟ ✟
✟
✛ ✟✟
v ✟✉✟✟
✙
✟✟ ✟
h
✟
✟✟
✟✟
✟
✟
✟
✟✟
✟✟
✉✟ ✟
✟
v ✟✉✟ ✟
✟
✟✟✟
✙
1) Rodando sin deslizar
2) Deslizando
Figura 2.1: Bolita cayendo por un plano inclinado, en las hipotesis de rodadura perfecta o deslizamiento sin rodadura
1) Rodando sin deslizar.— Planteamos la conservación de la energı́a al bajar una altura h. Para ello se tiene en cuenta la energı́a cinética
2.1
h
2.2
Capı́tulo 2. DINÁMICA DE LA PARTı́CULA
correspondiente a una esfera rodando, sumando el término correspondiente
a la traslación del centro de masa, y el de rotación como sólido rı́gido:
1
12
v ‘2
mgh = mv 2 + mR2
2
2 5
R
r
p
10
v=
gh = 1,195
gh
7
2) Deslizando.— En esta hipótesis sólo hay energı́a cinética de traslación:
1
mgh = mv 2
2
p
p
v = 2gh = 1,414 gh
En este segundo caso, que serı́a el correspondiente a la idealización como
partı́cula, la velocidad de caı́da resulta ser un 18,32 % mayor. Esta diferencia
se manifiesta independientemente del tamaño de la bolita, por pequeña que
ésta sea. Baste este ejemplo para hacer notar que el concepto de partı́cula
es una idealización, no necesariamente válida en todos los casos aunque el
cuerpo sea pequeño.
Sin embargo, el modelo del punto material es una idealización sumamente útil, ya que en muchos casos se pueden estudiar independientemente
el movimiento de traslación de un cuerpo (traslación del centro de masas),
y el movimiento de rotación del mismo (alrededor del centro de masas).
También es útil para aplicar los métodos de la mecanica a partes elementales de sistemas mayores (partı́culas de un sistema, elementos diferenciales
de volumen en un medio continuo, etc.). Ası́, en este capı́tulo se exponen los
teoremas generales y se desarrollan los métodos de cálculo que más tarde
se generalizaran a sistemas de varias partı́culas.
2.1.
Principios y Teoremas Generales
2.1.1.
Cantidad de Movimiento
Se llama cantidad de movimiento1 de una partı́cula a
def
p = mv.
1
En Inglés se emplea el término linear momentum o simplemente momentum , por
lo que algunos autores emplean el término momento lineal (traducción literal del inglés)
en lugar de cantidad de movimiento.
Aptdo. 2.1. Principios y Teoremas Generales
2.3
El principio de la cantidad de movimiento se deduce como consecuencia
directa de la segunda ley de Newton (apto 1.4):
d
F = (mv) = ṗ.
dt
(2.1)
En el caso usual de que la masa de la partı́cula no varı́e2 , se obtiene la
expresión clásica de la ley fundamental de la dinamica (1.2), Fuerza =
masa × aceleración:
F = ma = mr̈.
(2.2)
Conviene recordar que, en esta expresion, F representa la resultante de
todas las fuerzas aplicadas sobre la partı́cula. Se deben incluir, mediante
suma vectorial, tanto las fuerzas activas como las reacciones de apoyo o
reacciones del medio.
Cuando la fuerza total se anula, se obtiene el correspondiente teorema
de conservación:
si F = 0, p = cte.
(2.3)
Por lo tanto, el movimiento de una partı́cula aislada es tal que se conserva
su cantidad de movimiento; es decir, su velocidad se mantiene constante,
describiendo un movimiento rectilı́neo uniforme.
2.1.2.
Momento Cinético
Sea una partı́cula m, dotada de una velocidad v y situada en un punto
P . El momento cinético3 respecto a un punto fijo O, H O 4 , se define como el
momento de la cantidad de movimiento respecto a dicho punto. Tomando
O como origen del sistema de referencia (inercial) Oxyz,
def
HO = r
mv;
derivando respecto del tiempo:
dH O
= ṙ mv + r
dt
=0+r
| {zF}
mv̇
MO
2
Estrictamente hablando, la masa de una partı́cula es siempre invariable; al hablar de
casos en los que m sea variable, nos referimos a cuerpos que pierdan o ganen partı́culas
de masa (ver capı́tulo 6.6).
3
En las traducciones literales de la terminologı́a anglosajona se emplea el término
momento angular.
4
Otros autores emplean notaciones distintas para referirse al momento cinético: OK
(M. Roy, Fernández Palacios), LO (Marion, Goldstein, Griffiths)
2.4
Capı́tulo 2. DINÁMICA DE LA PARTı́CULA
✻
P
✉m
✒
❇
❇
❇v
❇
❇❇
z
r = OP
HO
✐P
P
PP
P
Figura 2.2: Momento cinético de una partı́cula respecto al
punto O.
y
✲
✟
✟
O
✟✟
✟
✟✟ x
✙
def
siendo M O = r F el momento de la fuerza F respecto a O. Resulta por
tanto la ecuación:
dH O
MO =
.
(2.4)
dt
El correspondiente teorema de conservación que se deduce de (2.4) es:
si M O = 0,
H O = cte.
(2.5)
Esta conservacion se verificará en el caso de la partı́cula aislada, y también
en el caso de fuerzas centrales que se describe más abajo.
Momento áxico.—
✚
✚
✚
✚
✚
✚
✚
✿
✘✘
✚
✘✘ ✘
✚
✘
✘
✚ ✘✘
O✘
HO
❜✚✘✘
✚
✚
He
Figura 2.3: Momento áxico respecto a un eje (O, e)
❃
✚✚
✚
e
✚
✚
✚
Sea un eje de dirección fija e, pasando por el punto O. Se define como momento áxico respecto de este eje la proyección del momento cinético
respecto de un punto cualquiera del eje sobre la dirección del mismo. Empleando la notación
def
Me = M O · e,
def
He = H O · e,
Aptdo. 2.1. Principios y Teoremas Generales
2.5
multiplicando escalarmente ambos miembros de (2.4) por e se deduce directamente la igualdad:
dHe
Me =
.
dt
Esta fórmula se puede aplicar entre otros casos al movimiento plano de
rotación alrededor de un eje fijo.
Fuerzas centrales.—
Se denominan centrales a las fuerzas que pasan constantemente por un
punto dado, centro de las fuerzas. Es evidente que respecto de este punto
el momento de las fuerzas es nulo, por lo que aplicando (2.5) se deduce que
el momento cinético se conserva:
H O = cte.
Se obtienen inmediatamente 2 caracterı́sticas importantes del movimiento:
1. La trayectoria es plana;
ya que al ser H O = r mv, r es constantemente perpendicular a una
dirección H O fija, definiendo por tanto un plano.
2. La velocidad areolar es constante;
puesto que el área barrida por unidad de tiempo (figura 2.4) es:
dS
=
dt
2
1
|r
dr|
dt
F + dF
✏✏
O
✏✏
✏
✏✏
✏
✏
✏
❜ ✏
2.1.3.
r
1
= |r
2
✏
✏✏
✏✏
F
0
1
|H O |
2m
cte.
Figura 2.4: Fuerzas centrales,
P
✏✏✏ ✄✗
✏
✮✏
dr ✄✄
✄
✛
v| =
✄ P
dirigidas hacia un centro de
fuerzas O. El área barrida en
el intervalo infinitesimal dt es
dS = OP P 0 = 12 |r dr|.
Energı́a Cinética
Sea una partı́cula de masa m, que se mueve según una trayectoria Γ,
bajo la acción de fuerzas con resultante F (recordemos que ésta incluye
todas las fuerzas, activas y pasivas). El trabajo elemental realizado por
2.6
Capı́tulo 2. DINÁMICA DE LA PARTı́CULA
❜ 2
Γ
✶
m ✉
❅
dr
❅
F
❘❅
Figura 2.5: Trabajo realizado por F al recorrer la
curva Γ entre 1 y 2.
❜ 1
F en un desplazamiento infinitesimal dr se define por el producto escalar
siguiente5
def
dW = F · dr;
considerando que F = m dv/dt y dr = vdt,
’
“
1 2
dW = mv · dv = d mv
2
(2.6)
El trabajo realizado al recorrer Γ entre los dos puntos extremos 1 y 2 resulta
de la integral curvilı́nea:
Œ2
1 2Œ Œ
=
F · dr = mv Œ.
2
Γ
1
Z
W12
Se define como energı́a cinética T de la partı́cula:
def 1
T = mv 2 ;
2
ası́, la expresión anterior equivale a
W12 = T2 − T1
(2.7)
Podemos enunciar entonces:
‘El trabajo realizado por la resultante de las fuerzas sobre una
partı́cula es igual al incremento de su energı́a cinética.’
Este resultado se suele llamar también el teorema de las fuerzas vivas.
5
La notación empleada, dW , no indica aquı́ una diferencial exacta de una determinada función W , sino únicamente un incremento infinitesimal de trabajo producido por
F a lo largo de dr. Tan sólo resulta ser una diferencial exacta cuando las fuerzas son
conservativas.
Aptdo. 2.1. Principios y Teoremas Generales
2.7
Caso de fuerzas conservativas.—
Se denomina campo de fuerzas conservativas aquél en el que el trabajo
realizado por la fuerza, para recorrer el camino entre dos puntos dados, es
independiente de la trayectoria seguida Γ para ir de uno al otro. Ası́ para
distintos caminos Γ1 , Γ2 , Γ3 que tengan en común el origen (1) y el final
(2),
❜
Γ1
2
Γ3
Γ2
Figura 2.6: Trayectorias distintas en un
campo conservativo para ir de 1 a 2.
❜
1
Z
Z
F · dr =
Γ1
Z
F · dr =
Γ2
F · dr.
Γ3
Es fácil ver que esta condición es equivalente a que el trabajo realizado para
recorrer cualquier trayectoria cerrada sea nulo. En efecto, sea una curva
cerrada cualquiera Γ, a la que pertenecen los puntos 1 y 2. Ésta puede
descomponerse en dos curvas abiertas con extremos en 1 y 2: Γ = Γ+ Γ− ,
1
2
−
teniendo Γ+
1 el sentido de 1 a 2 y Γ 2 el sentido de 2 a 1. La integral curvilı́nea
sobre Γ es pues
Z
Z
Z
I
Z
F · dr +
F · dr =
F · dr −
F · dr = 0. (2.8)
F · dr =
Γ
Γ+
1
Γ−
2
Γ+
1
Γ+
2
como querı́amos demostrar.
No son conservativas las fuerzas debidas a resistencias pasivas, como el
rozamiento o las fuerzas de tipo viscoso. En éstas el integrando (F · dr)
es siempre negativo, puesto que la fuerza de resistencia (F ) se opone al
movimiento (dr), por lo que la integral (2.8) no se puede anular nunca. Se
produce necesariamente una disipación de energı́a, no pudiendo recobrarse
el nivel energético inicial después de un trayecto cerrado.
Un teorema básico del cálculo vectorial establece que la condición necesaria y suficiente para que un campo vectorial F tenga circulación nula para
cualquier curva cerrada es que sea un campo de gradientes. Recordemos en
2.8
Capı́tulo 2. DINÁMICA DE LA PARTı́CULA
primer lugar la definición de gradiente de un campo escalar; en un sistema de coordenadas cartesianas ortonormal con versores {ei } ≡ {i, j , k} la
expresión es6
def
grad V =
3
X
∂V
ei =
∂x
i
i=1
∂V
i+
∂x
∂V
∂V
j+ k
∂y
∂z
La afirmación anterior quiere decir que existirá un campo escalar V (r),
función de la posición, tal que:
F = − grad V.
Al campo escalar V se le denomina potencial de las fuerzas, energı́a potencial, o simplemente potencial.
Una tercera forma de caracterizar un campo F como conservativo, admitiendo las exigencias adicionales de que F tenga derivada continua y que
el dominio sea simplemente conexo, es que sea irrotacional. Esta condición
es equivalente a su vez a las dos anteriores. Recordemos la definición de
rotacional de un campo vectorial7 :
3
X
def
rot F =
’
=
∂Fj
e
∂xi k
“
’
∂Fy
∂Fx
i+
−
∂z
∂z
ijk
i,j,k=1
∂Fz
−
∂y
∂Fz
∂x
“
’
j+
∂Fy
−
∂x
∂Fx
∂y
“
k
Por lo que la condicion para que el campo F sea conservativo es
rot F = 0.
(2.9)
En este caso, la función potencial V (r) de la que proviene F debe ser al
menos C 2 .
Al expresarse F como un gradiente, el trabajo elemental resulta ser una
diferencial exacta:
F · dr = − grad V · dr = −dV
6
En cuanto a notación, emplearemos indistintamente los ı́ndices o los nombres propios de vectores (i ≡ e1 , j ≡ e2 , k ≡ e3 ) y coordenadas (x ≡ x1 , y ≡ x2 , z ≡ x3 ). Asimismo, a veces emplearemos también notacioP
nes alternativas para el gradiente, grad V =
dV /dr = rV , empleando el operador r = 3i=1 ∂/∂xi ei = ∂/∂x i + ∂/∂y j + ∂/∂z k.
7
Empleando el operador r, el rotacional se puede expresar también mediante la notación rot F = r F .
Aptdo. 2.1. Principios y Teoremas Generales
2.9
Si integramos para obtener el trabajo realizado entre dos puntos 1 y 2, y
empleando el principio de la energı́a cinética (2.7):
Z 2
W12 =
F · dr = V1 − V2
1
= T2 − T1 ,
es decir, se conserva la suma de la energı́a cinética más la potencial:
T1 + V1 = T2 + V2 .
o bien, definiendo como energı́a total 8 a la suma de energı́a cinética y potencial,
def
E = T + V,
se obtiene la siguiente expresión para el teorema de conservación de la
energı́a:
si F = − grad V (conservativa), E = T + V = cte.
(2.10)
En lo anterior se ha supuesto que el potencial V (r) es constante. Pudiera
darse el caso de que F provenga de una función potencial no constante, es
decir que dependa explı́citamente del tiempo, V (r, t):
∂V
∂V
,
con
= 0.
∂r
∂t
En este caso, no se conservarı́a la energı́a total E, puesto que el trabajo
elemental ya no serı́a una diferencial exacta del potencial:
F =−
∂V
∂V
dV = · dr + dt,
∂r
∂t
∂V
F · dr = − · dr = −dV.
∂r
Estarı́amos, pues, ante un campo de fuerzas no conservativas a pesar de
que provengan de un potencial.
Integración de la ecuación fundamental de la dinámica.— Parte
de lo expuesto arriba se puede interpretar como distintos procedimientos
de integración de la ecuación fundamental de la dinámica (2.2). Señalemos
tres procedimientos generales para ello, que permiten obtener los teoremas
de conservación (2.3), (2.5) y (2.10) como casos particulares.
8
Se sobreentiende que ésta es únicamente la energı́a mecánica , excluyendo a otros
tipos de energı́a como la calorı́fica, quı́mica, . . .
2.10
Capı́tulo 2. DINÁMICA DE LA PARTı́CULA
a) Integración directa en el tiempo.— Integrando entre dos instantes t1 y t2 ,
Z t2
Z t2
Z t2
F dt =
mr̈ dt =
dp = p|21
t1
t1
t1
se obtiene la ecuación del balance de la cantidad de movimiento,
Z
t2
t1
F dt = p|12 .
Como caso particular de esta ecuación de balance se desprende el teorema
de conservación de la cantidad de movimiento (2.3)
b) Integración directa según la trayectoria.— Realizando ahora
la integral curvilı́nea entre dos puntos de la trayectoria r 1 y r 2 ,
Œ2
“
Z 2 ’
Z 2
Z 2
Œ
1
1
d mv 2
= mv 2 Œ Œ
F · dr =
mr̈ · dr =
2
2
1
1
1
1
de donde se obtiene la ecuación del balance de la energı́a,
Z
2
1
Œ
Œ2
1
F · dr = mv 2 ŒŒ .
2
1
Análogamente, para el caso de fuerzas conservativas (F = −gradV ), se
desprende el teorema de conservación (2.10).
c) Integración del momento en el tiempo.— Integrando el momento de F entre dos instantes t1 y t2 ,
Z t2
Z t2
Z t2
d
(r mṙ ) dt = H O |2 1
r F dt =
r mr̈ dt =
| {z }
dt
t1
t1
t1
HO
se obtiene la ecuacion del balance del momento cinético,
Z
t2
t1
r
F dt = H O |12 .
Si las fuerzas son centrales o se trata de una partı́cula aislada, análogamente
a los dos casos anteriores se desprende el teorema de conservación (2.5).
Aptdo. 2.2. Expresiones de Velocidad y Aceleración
2.2.
2.11
Expresiones de Velocidad y Aceleración
Antes de proseguir en la aplicación de los principios y teoremas generales
expuestos para ejemplos concretos de dinámica de la partı́cula, conviene
detenerse en el desarrollo de las expresiones de la velocidad y aceleración
que habrán de emplearse.
Según las caracterı́sticas geométricas de cada problema, será conveniente en
cada caso escoger uno u otro sistema de coordenadas. La elección obvia en
el caso más general será un sistema de coordenadas cartesianas ortonormal;
sin embargo en ocasiones es ventajoso emplear otras coordenadas, como las
coordenadas cilı́ndricas (o polares en el caso plano), esféricas, o el triedro
intrı́nseco a la trayectoria.
En cada uno de estos casos, el aspecto que nos ocupa es obtener las componentes de los vectores velocidad, ṙ = dr/dt y aceleración, r̈ = d2 r/dt2 .
2.2.1.
Coordenadas Cartesianas.
El triedro Oxyz está asociado a los versores (i, j, k) según cada dirección coordenada (figura 2.7). Puesto que los versores del triedro son constantes, para obtener la velocidad y aceleración basta derivar directamente
las coordenadas:
r = xi + yj + zk
ṙ = ẋi + ẏ j + żk
r̈ = ẍi + ÿj + z̈k
✻k
✟
✟
✟✟
i ✟
✙
✟
O ❜ j
✟
y
r
r
✒
Figura 2.7: Coordenadas cartesianas
z
✲
❛✟
✟
x
2.12
Capı́tulo 2. DINÁMICA DE LA PARTı́CULA
2.2.2.
Coordenadas Cilı́ndricas / Polares.
En este caso, las coordenadas que definen la posición son (ρ, θ, z), siendo
ρ la distancia desde un punto fijo O, θ el ángulo que forma la proyección
del radio vector sobre un plano fijo con una dirección dada del mismo, y z
la altura del punto sobre dicho plano (figura 2.8).
✻
z
✻
k
r
✿
Figura 2.8: Coordenadas cilı́ndricas
uθ
r ✼ us
ρ
y
O
x ✟✟
✟
✙
✟
✟
✟
✟❜
✿ ρ
θ
✲
El triedro de vectores unitarios asociado (o base fı́sica) es (uρ , uθ , k).
El versor uρ queda definido como un vector unitario en la dirección de la
proyección de r sobre el plano; k es el versor perpendicular al mismo, y uθ es
perpendicular a los dos anteriores. En este triedro tanto uρ como uθ varı́an
de punto a punto, constituyendo un sistema de coordenadas curvilı́neas.
La posición de un punto queda definida mediante
r = ρuρ + zk
(2.11)
expresión que engloba también a las coordenadas polares para el movimiento plano, sin más que hacer z = 0.
Es inmediato establecer las relaciones con las coordenadas cartesianas,
tomando el plano de referencia Oxy de forma que se comparte la coordenada
z:
x = ρ cos θ
y = ρ sen θ
Mientras que entre los versores de ambos triedros la relación es
uρ = cos θi + sen θj
uθ = − sen θi + cos θj
Aptdo. 2.2. Expresiones de Velocidad y Aceleración
2.13
Derivando estas expresiones respecto del tiempo se obtiene
u̇ρ = −θ̇ sen θi + θ̇ cos θj
= θ̇uθ
u̇θ = −θ̇ cos θi − θ̇ sen θj
= −θ̇uρ
k̇ = 0
Empleando estas igualdades y derivando el vector posición (2.11) se
obtiene la velocidad,
ṙ = ρ̇uρ + ρθ̇uθ + żk;
repitiendo la operación, se obtiene la aceleración:
r̈ = (ρ̈ − ρθ̇ 2 )uρ + (2ρ̇θ̇ + ρθ̈)uθ + z̈k.
2.2.3.
Coordenadas Esféricas.
La posición de un punto queda ahora referida a las dos coordenadas
angulares en una esfera de radio r: la longitud ϕ y la latitud θ (figura 2.9).
✻
z
uθ ❖
r
✟✟
x ✟✟
✟✟
✙
O ❜ ■θ
✟
ϕ
✿
✣
s
✣
ur
✿
uϕ
Figura 2.9: Coordenadas esféricas
y
✲
El triedro fı́sico es ahora (uϕ , uθ , ur ). La lı́nea coordenada de longitud ϕ
constante define el meridiano, al cual es tangente el versor uθ . Asimismo la
lı́nea de latitud θ constante define un paralelo, al cual es tangente el versor
uϕ . Por último, el versor ur lleva la dirección y sentido del radio vector r.
Proyectando sobre las direcciones del triedro cartesiano se obtienen las
2.14
Capı́tulo 2. DINÁMICA DE LA PARTı́CULA
relaciones con los versores del mismo:
ur = cos θ cos ϕ i + cos θ sen ϕ j + sen θ k
uθ = − sen θ cos ϕ i − sen θ sen ϕ j + cos θ k
uϕ = uθ
ur = − sen ϕ i + cos ϕ j
En este caso los tres versores son variables, función del punto. Para obtener sus derivadas temporales, expresaremos primero sus derivadas parciales
respecto de las coordenadas:
∂ur
= 0;
∂r
∂uθ
= 0;
∂r
∂uϕ
= 0;
∂r
∂ur
= u ;θ
∂θ
∂uθ
= −u ; r
∂θ
∂uϕ
= 0;
∂θ
∂ur
= cos θ u ϕ
∂ϕ
∂uθ
= − sen θ u ϕ
∂ϕ
∂uϕ
= sen θ u θ − cos θ ur
∂ϕ
Empleando estas relaciones, se obtiene
u̇r =
∂ur
∂ur
∂ur
ṙ +
θ̇ +
ϕ̇
∂r
∂θ
∂ϕ
= θ̇ uθ + ϕ̇ cos θ uϕ
u̇θ = −ϕ̇ sen θ uϕ − θ̇ ur
u̇ϕ = ϕ̇ sen θ uθ − ϕ̇ cos θ ur
Por último, utilizamos estas expresiones en las derivadas temporales de r,
para obtener:
ṙ = ṙur + rθ̇uθ + rϕ̇ cos θuϕ
r̈ = (r̈ − rϕ̇2 cos2 θ − rθ̇ 2 )ur + (2ṙθ̇ + rϕ̇2 sen θ cos θ + rθ̈)uθ
+ (2ṙϕ̇ cos θ − 2rθ̇ ϕ̇ sen θ + rϕ̈ cos θ)uϕ
2.2.4.
Triedro Intrı́nseco.
La propia curva definida por la trayectoria dinámica, r(t), permite definir un triedro denominado intrı́nseco , que a menudo resulta de gran
utilidad para describir el movimiento. Se resumen aquı́ algunas definiciones
y propiedades fundamentales de dicho triedro. Para un mayor detalle puede
consultarse algún texto de geometrı́a diferencial9 .
9
D.J. Struik: Geometrı́a Diferencial Clásica, Aguilar 1973; J.A. Fernández Palacios:
Mecánica Teórica de los Sistemas de Sólidos Rı́gidos, (Anejo 1A), 1989.
Aptdo. 2.2. Expresiones de Velocidad y Aceleración
2.15
Vectores y planos del triedro.— Los versores que constituyen el triedro intrı́nseco están definidos por la trayectoria misma. Ésta puede considerarse parametrizada bien por el tiempo (r(t), con derivada √
ṙ = dr/dt),
bien por la longitud del arco de curva s, sabiendo que ds = dr · dr. El
sentido positivo del arco coincide con el avance real sobre la curva a lo largo
del tiempo.
ṙ
❙♦
❙
❙t
✓
✼
❙♦
❙
✓ b
❙s✓
✙✟
✟
n
Figura 2.10: Vectores del triedro intrı́nseco
def
– tangente t = dr/ds, vector unitario con igual dirección y sentido que
la velocidad ṙ .
– normal principal n, vector unitario normal a la curva (dr · n = 0),
y perteneciente al plano osculador (plano definido por dos tangentes
sucesivas a la curva, t y t + dt). Su dirección y sentido lo tomaremos
por tanto según dt, es decir, hacia el lado concavo de la misma.
def
– binormal b = t n, perpendicular por tanto a la curva (dr · b = 0),
y también a la normal principal (n · b = 0).
Los versores n y b definen el plano normal, cualquier recta contenida en
este plano es normal a la curva. Por otra parte, el plano osculador queda
definido por (t, n), siendo la binormal perpendicular al mismo.
Fórmulas de Frenet.— Al ser un versor de modulo unidad, la derivada
del vector tangente es normal al mismo:
d
dt
(|t{·zt}) = 2t · = 0.
ds
ds
(2.12)
=1
Por la definición hecha de n, la derivada dt/ds lleva la dirección de n, y el
módulo se denomina curvatura :
Œ Œ
def ŒŒ dt ŒŒ
κ = Œ Œ.
ds
2.16
Capı́tulo 2. DINÁMICA DE LA PARTı́CULA
Se puede interpretar de forma intuitiva razonando que cuanto más se doble la curva (por unidad de arco), mayor es su curvatura κ. Dada la definición realizada de n, por la que su sentido es siempre hacia el lado cóncavo,
dicha curvatura resulta siempre positiva. Asimismo, se define el radio de
def
curvatura como su inversa: R = 1/κ. Ası́,
dt
1
= κn = n
ds
R
(1.a fórmula de Frenet).
(2.13)
Veamos ahora la variación de la binormal b. Si la curva es plana, el plano
osculador es fijo y db/ds = 0. En un caso general, esta derivada constituye
una medida del alabeo de la curva que denominaremos torsión. En cuanto
a la dirección de esta derivada, razonamos en primer lugar, por los mismos
argumentos esgrimidos en (2.12), que es normal al propio b. Por otra parte,
d
(b · t) =
ds|{z}
=0
dt
db
db
· t + b · = · t + b · (κ n) = 0.
| {z }
ds
ds
ds
=0
Deducimos pues que db/ds = 0 es normal a b y a t, es decir, lleva la dirección
de n, mientras que su módulo lo llamaremos torsión τ . Estableciendo de
forma convencional el signo negativo en esta relación, puede escribirse
db
1
= −τ n = − n
ds
T
(2.a fórmula de Frenet).
(2.14)
def
(El radio de torsión resulta, analogamente al de curvatura, T = 1/τ .)
Por último, derivando la normal principal,
d
d
n = (b t) = (−τ n)
ds
ds
t+b
(κ n),
es decir:
dn
= τ b −κt
ds
(3.a fórmula de Frenet).
(2.15)
Expresiones de la velocidad y aceleración.— Empleando las fórmulas de Frenet es inmediato deducir las siguientes expresiones para velocidad
y aceleración:
ds
ṙ = t = v t,
dt
Aptdo. 2.3. Movimiento de una Partı́cula Libre
2.17
relación que expresa simplemente que la velocidad es tangente a la trayectoria. Derivando de nuevo,
r̈ = v̇ t + v
dt ds
= v̇ t +
ds dt
v2
n
R
Se identifican en esta expresión claramente dos términos de la aceleración:
v̇ t
v2
n
R
2.3.
aceleracion tangencial
aceleración normal (centrı́peta)
Movimiento de una Partı́cula Libre
El principio de la cantidad de movimiento o 2.a ley de Newton (2.2)
proporciona una ecuacion vectorial, que equivale a 3 ecuaciones escalares.
Llamando (X, Y, Z ) a las componentes cartesianas de la fuerza F ,
F = m r̈
X = mẍ
Y = mÿ
Z = mz̈
Integrando estas 3 ecuaciones, será posible obtener las 3 incógnitas (x, y, z)
que definen la posición de la partı́cula en cada instante. Las dificultades
que puedan surgir para esta integración resultarán de las expresiones de
(X, Y, Z ) que por lo general no tienen porqué ser constantes. Consideraremos
como aplicación dos casos particulares relacionados con
el movimiento de proyectiles.
2.3.1.
Proyectil Pesado en el Vacı́o.
Admitimos en este caso que no existen resistencias del medio, por lo
que la única fuerza actuante sobre la partı́cula es la gravedad terrestre, que
suponemos definida por el campo gravitatorio simplificado (−mgk). Las
ecuaciones son:
mẍ = 0; mÿ = 0; mz̈ = −mg.
Si tomamos unos ejes en los que el plano vertical Oxz contenga a la velocidad inicial v 0 , es fácil comprobar que el movimiento se desarrollará dentro
del mismo plano vertical:
ẏ = ÿ = 0
y = 0.
2.18
Capı́tulo 2. DINÁMICA DE LA PARTı́CULA
✻z
❜
v✒
ϕ
Figura 2.11: trayectoria
parabólica de un proyectil pesado en el vacı́o
v 0 ✁✕
✁
✁
x
✲
ϕ0
O✁
Denominando ϕ0 el ángulo de la velocidad en el lanzamiento con la
horizontal (figura 2.11) las ecuaciones en x y z se integran de manera trivial:
ẋ = v0 cos ϕ0 ,
ż = −gt + v0 sen ϕ0 ;
(2.16)
1
(2.17)
z = − gt 2 + v0 sen ϕ0 t.
2
Las expresiones (2.17) son las llamadas ecuaciones horarias de la trayectoria, es decir, las ecuaciones que permiten obtener la posición en función del
tiempo.
La trayectoria descrita por la partı́cula queda definida por las ecuaciones
horarias de forma paramétrica, mediante el parámetro t. Se puede obtener
la ecuación implı́cita de la trayectoria eliminando el parámetro t de las
ecuaciones horarias: despejando t en (2.171 ) y sustituyendo en la expresión
(2.172 ) de z:
1
x2
z = −g
+ x tg ϕ0 ,
(2.18)
2 (v0 cos ϕ0 )2
ecuación que representa una parábola de eje vertical (movimiento parabólico).
El alcance horizontal se obtiene haciendo z = 0 en (2.18),
x= v0 cos ϕ0 t,
L = sen(2ϕ0 )
v 02
,
g
de donde se deduce inmediatamente que el alcance máximo se produce para
ϕ0 = π/4, valiendo Lmax = v02 /g. Por otra parte, para distancias inferiores,
existen dos soluciones posibles de tiro para obtener un mismo alcance: tiro
directo y por elevación:
š
L
1>
= sen 2ϕ0
2 soluciones ϕ1 < π/4 (tiro directo),
Lmax
ϕ2 > π/4 (tiro por elevación).
Aptdo. 2.3. Movimiento de una Partı́cula Libre
2.19
El tiro por elevación es el caracterı́stico de los morteros, mientras que el
tiro directo es el normal de los proyectiles denominados balı́sticos.
✻
L/L
Figura 2.12: Alcance del tiro parabólico en función del
ángulo inicial ϕ0 : L =
max
❜
1
❜
❜
ϕ1
ϕ2
π/4
v02
2g
ϕ0
✲
sen 2ϕ0 . Para distancias
inferiores al alcance maximo
(Lmax = v 02 /g, para ϕ0 =
π/4), existen dos posibilidades, el tiro directo (ϕ0 = ϕ1 ),
y por elevación (ϕ0 = ϕ2 ).
La envolvente de las posibles parábolas de tiro para v0 dada, es decir
para una energı́a dada, es otra parabola, denominada parábola de seguridad.
Para determinarla, expresamos la condición de que la trayectoria (2.18) pase
z
✻
Figura 2.13: Parábola de seguridad,
envolvente de las
diversas trayectorias (1, 2, 3) para
una energı́a
de
lanzamiento dada
1
2
3
x
✲
por un punto (a, b) dado:
1
a2
b = −g
+ a tg ϕ0 ;
2 (v0 cos ϕ0 )2
haciendo tg ϕ0 = u, obtenemos la ecuacion:
u2 −
2
2v0 2
2
bv
u + 1 + 0 2 = 0;
ag
a g
para que tenga solución real en u, ha de ser b < v 20/2g − ga2 /2v 20. Por tanto,
la ecuación de la parábola de seguridad es
z=
v02 gx 2
−
.
2g
2v02
2.20
Capı́tulo 2. DINÁMICA DE LA PARTı́CULA
La altura máxima en una trayectoria se obtiene haciendo ż = 0 en
(2.16):
v0 sen ϕ0
0 = −gt + v0 sen ϕ0
t=
,
g
y entrando con este valor de t en (2.17),
zmax =
1 v02 sen2 ϕ0
.
2
g
Es obvio que la máxima altura de todas las trayectorias posibles se obtiene
para ϕ0 = π/2, es decir para tiro vertical:
zmax =
1v 20
.
2 g
Mediante consideraciones energéticas se podrı́an haber obtenido algunos
de estos mismos resultados de forma muy sencilla. Por ejemplo, la altura
máxima para un tiro vertical resulta de igualar la energı́a total en el punto
de altura máxima con la inicial:
1 2
mv + 0 = 0 + mgzmax
2 0
zmax =
1 0v 2
.
2 g
Asimismo, para una trayectoria inclinada, podemos obtener la velocidad en
el punto de máxima altura igualando la energı́a con la del instante inicial:
’
“
1 2
12
1 0v 2 sen2 ϕ0
mv + 0 = mv + mg
2 0
2
2
g
De donde v = v0 cos ϕ0 , deduccion que podrı́amos haber realizado también
al considerar que, al ser ż = 0 en ese instante, la velocidad no tiene componente vertical, reduciéndose a la velocidad horizontal que es constante.
2.3.2.
Proyectil Pesado en Medio Resistente
Complicamos ahora el problema anterior al considerar una resistencia
del medio, cuya dirección es la de la velocidad y cuya magnitud depende del
módulo de la misma de forma monotonamente creciente (es decir, a mayor
velocidad, mayor resistencia):
v
R = −R(v) .
v
La función de resistencia R(v) tiene por lo general una caracterización compleja, habiendo de determinarse mediante ensayos aerodinámicos en túneles de viento o simulaciones en el ordenador. Como simplificación se suele
Aptdo. 2.3. Movimiento de una Partı́cula Libre
2.21
aceptar la aproximación como una función proporcional al cuadrado de la
velocidad, R(v) = αv 2 , o para velocidades muy bajas, proporcional a la
velocidad, R(v) = αv.
En un caso general, llamando (Rx , Ry , Rz ) a las componentes cartesianas
de R, las ecuaciones son:
mẍ = Rx ;
mÿ = Ry ;
mz̈ = Rz − mg.
(2.19)
En primer lugar, demostraremos que la trayectoria es plana, manteniéndose
dentro de un plano vertical. En efecto, puesto que R k v,
R
Rx = − ẋ;
v
R
Ry = − ẏ ;
v
R
Rz = − ż
v
Eliminando Rx y Ry con las ecuaciones (2.19) resulta
ẍ
ÿ
R
= =− .
ẋ
ẏ
mv
Integrando cada miembro de esta ecuación en variables separadas se obtiene
log ẏ = log C ẋ
ẏ = C ẋ
y = C x + D,
ecuación que define un plano vertical.
A continuación expondremos un método de solución general, para una
resistencia R(v) cualquiera. Para ello, expresemos las ecuaciones en las direcciones tangencial y normal a la trayectoria:
dv
m = −mg sen ϕ − R(v)
dt
v2
m = mg cos ϕ
ρ
(2.20)
(2.21)
donde ρ es el radio de curvatura de la misma. La relación de éste con los
incrementos infinitesimales de arco (ds) y ángulo girado (dϕ) es
1
dϕ
=− ,
ρ
ds
donde se toma convencionalmente el signo negativo, lo que equivale a establecer que ϕ decrece al crecer s, siendo ρ siempre positivo.
Queremos obtener la ecuación que relaciona el módulo de la velocidad
con el ángulo de la trayectoria, v(ϕ), llamada hodógrafa . Para ello, eliminamos ρ de la ecuación (2.21), quedando:
−mv 2
dϕ
= mg cos ϕ
ds
(2.22)