Antenas loop comparadas mediante 4NEC2 y ecuaciones

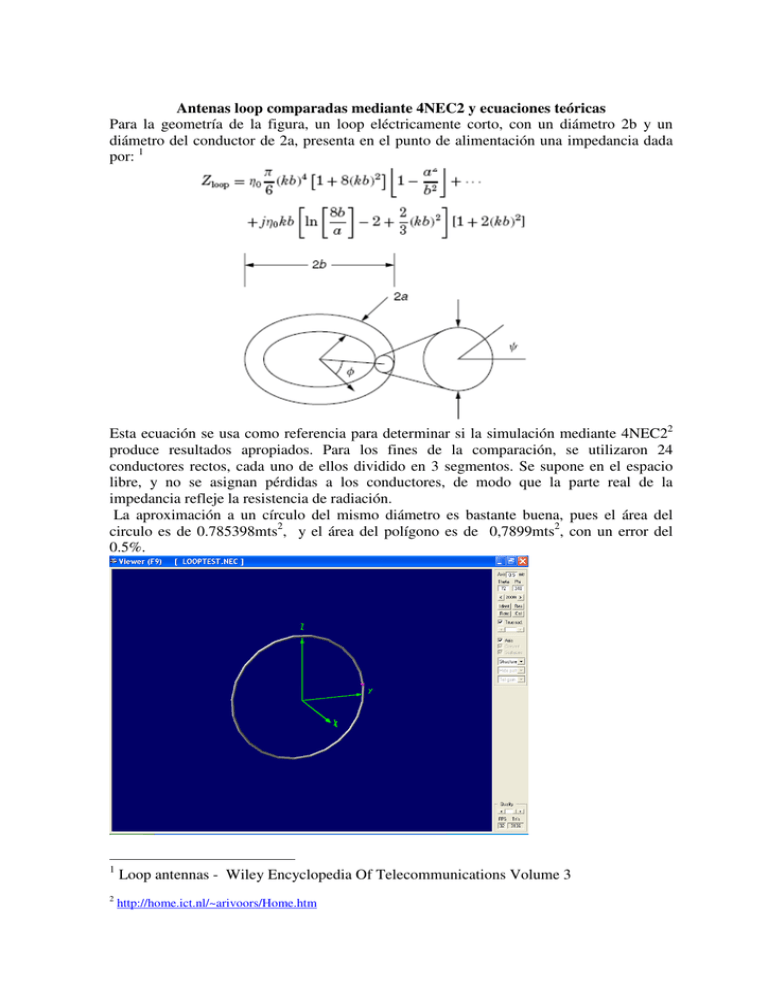
Antenas loop comparadas mediante 4NEC2 y ecuaciones teóricas
Para la geometría de la figura, un loop eléctricamente corto, con un diámetro 2b y un
diámetro del conductor de 2a, presenta en el punto de alimentación una impedancia dada
por: 1
Esta ecuación se usa como referencia para determinar si la simulación mediante 4NEC22
produce resultados apropiados. Para los fines de la comparación, se utilizaron 24
conductores rectos, cada uno de ellos dividido en 3 segmentos. Se supone en el espacio
libre, y no se asignan pérdidas a los conductores, de modo que la parte real de la
impedancia refleje la resistencia de radiación.
La aproximación a un círculo del mismo diámetro es bastante buena, pues el área del
circulo es de 0.785398mts2, y el área del polígono es de 0,7899mts2, con un error del
0.5%.
1
Loop antennas - Wiley Encyclopedia Of Telecommunications Volume 3
2
http://home.ict.nl/~arivoors/Home.htm
El largo eléctrico del loop es de 0.074 longitudes de onda, por lo que se encuentra en el
rango en que la suposición de corriente constante no introduce errores. Por encima de 0.1
de longitud de onda comienza a apreciarse la diferencia entre el modelo real y el de
corriente constante. En los casos de antenas de radioaficionados, la resistencia de
radiación tiende a ser levemente mayor que la predicha por los programas de cálculo para
este tipo de antenas. Esto no es particularmente importante para comparar con 4NEC2,
pero si para otros tipos de calculo.
La elección de las dimensiones y frecuencia del modelo se basan simplemente en la
disponibilidad del archivo para su simulación.
Se hicieron pruebas con tres diámetros de conductor de 1mm, 2.5mm, y 10mm, cuyos
resultados se muestran en la siguiente tabla:
Frecuencia
7.1 MHz.
7.1 MHz.
7.1 MHz.
7.1 MHz.
7.1 MHz.
7.1 MHz.
Diam. del
loop
2 mts.
2 mts.
2 mts.
2 mts.
2 mts.
2 mts.
Diam.
conductor
2.5 mm.
2.5 mm.
1 mm.
1 mm.
10 mm
10 mm
Real de
Z
0.00651
0.00629
0.00651
0.00629
0.00651
0.00629
Imag. de
Z
+154.47
+150.73
+181.07
+176.4
+115.16
+111.91
Método de
cálculo
NEC
ecuación
NEC
Ecuación
NEC
ecuación
Según estos resultados, la resistencia de radiación de ambos métodos solo difiere en un
3.5%, siendo mayor el valor obtenido mediante 4NEC2. Si se supone la resistencia de
radiación directamente asociada al área del loop, la diferencia debería haber sido 1%
mayor, con lo que la diferencia se reduce al 2.5%. Estos resultados no dependen del
diámetro del conductor.
En cuanto a la parte imaginaria, la diferencia es del orden del 2.5%, siempre mayor en
4NEC2. Aquí también debería aplicarse idéntico criterio al caso de la resistencia de
radiación, pues la inductancia crece con el área del loop, son lo que la diferencia se reduce
al 1.5%.
Esta comparación muestra que la simulación mediante 4nec2 produce resultados
consistentes y con una exactitud mucho mas allá de los medios accesibles a los
radioaficionados para su verificación.
Para aquellos que deseen repetir las comparaciones, incluyo el archivo de las
simulaciones:
CM Loop para pruebas
CE
GW
1
3
GW
2
3
GW
3
3
GW
4
3
GW
5
3
GW
6
3
GW
7
3
GW
8
3
GW
9
3
GW
10
3
GW
11
3
GW
12
3
GW
13
3
GW
14
3
GW
15
3
GW
16
3
GW
17
3
GW
18
3
GW
19
3
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0.5
0.0658262 0
0.4659258 0.1929928 0
0.4000996 0.3070072 0
0.3070072 0.4000996 0
0.1929928 0.4659258 0
0.0658262 0.5
0
-0.065826 0.5
0
-0.192993 0.4659258 0
-0.307007 0.4000996 0
-0.4001 0.3070072 0
-0.465926 0.1929928 0
-0.5
0.0658262 0
-0.5
-0.065826 0
-0.465926 -0.192993 0
-0.4001 -0.307007 0
-0.307007 -0.4001 0
-0.192993 -0.465926 0
-0.065826 -0.5
0
0.0658262 -0.5
0
0.4659258 0.1929928 1e-2
0.4000996 0.3070072 1e-2
0.3070072 0.4000996 1e-2
0.1929928 0.4659258 1e-2
0.0658262 0.5
1e-2
-0.065826 0.5
1e-2
-0.192993 0.4659258 1e-2
-0.307007 0.4000996 1e-2
-0.4001 0.3070072 1e-2
-0.465926 0.1929928 1e-2
-0.5
0.0658262 1e-2
-0.5
-0.065826 1e-2
-0.465926 -0.192993 1e-2
-0.4001 -0.307007 1e-2
-0.307007 -0.4001 1e-2
-0.192993 -0.465926 1e-2
-0.065826 -0.5
1e-2
0.0658262 -0.5
1e-2
0.1929928 -0.465926 1e-2
GW
GW
GW
GW
GW
GE
GN
EK
EX
FR
RP
EN
20
21
22
23
24
0
-1
3
3
3
3
3
0
0
0
0
0
0.1929928 -0.465926
0.3070072 -0.4001
0.4000996 -0.307007
0.4659258 -0.192993
0.5
-0.065826
0
0
0
0
0
0.3070072 -0.4001 1e-2
0.4000996 -0.307007 1e-2
0.4659258 -0.192993 1e-2
0.5
-0.065826 1e-2
0.5
0.0658262 1e-2
0
0
0
1
5
73
1
0
1
1
0
1000
0
0.1
0
5
0
6.9
-180
Mediante simulación con 4NEC2, se obtuvieron los siguientes resultados, suponiendo el
radio del conductor de 25mm y el radio del loop de 1mt. Se utilizaron 16 segmentos para
modelar el loop principal, y 8 para el loop de acoplamiento. La eficiencia es de 22.7%, con
una ROE de 1.05 en resonancia. La resonancia se obtiene con 79.6pF.
El diagrama de la antena se puede observar a continuación, con el condensador de sintonía
ubicado en la parte superior, y y el loop de acoplamiento en la parte inferior.
El grafico de ROE muestra que la resonancia esta en 7.099MHz, con un ancho de banda
de 9KHz para 1,5 de ROE, por lo que es apto para usar en SSB.
A continuación se muestra el diagrama de radiación, que se ve mas “achatado” que el
clásico del dipolo.
Para los fines de comparar los diagramas, a continuación se muestra el del dipolo, ubicado
a 1,5mts de altura, para que su ubicación coincida con el centro del loop. En este caso, la
eficiencia es del 11.27%, por la cercanía respecto de tierra y las consecuentes pérdidas que
ocasiona.
Como no se hizo ninguna adaptación para el caso del dipolo, la ROE no es 1, pero el
ancho de banda es mucho mas amplio que el del loop.
Por último, mediante el uso del software de cálculo de KI6GD, disponible en Internet, se
obtiene:
Magnetic Loop Antenna Specifications
Loop Circumference
6.28 meters
Conductor Diameter 25.00 mm
Frequency
7.10 mHz
Bandwidth
9.9 kHz
Capacitor Value
87.7 pF
Capacitor Voltage
4.0 kV
Conductor Wavelength
0.156 lamda
Efficiency
63.8 %
Inductance
4.923 µH
Inductive Reactance 219.6 ohms
Loop Area
10.3 meters²
Loop Diameter
2.0 meters
Loop Q Value
715.1 Qres
Radiation Resistance 0.098 ohms
Resistance Loss
0.056 ohms
No contempla las pérdidas por la cercanía con la tierra. Para ello se utiliza el programa (
bajo DOS) rjeloop1.exe, que también se puede encontrar en Internet, con el que se
obtienen los siguientes resultados:
S.
P.
D.
H.
F.
T.
Shape of loop ................................... CIRCLE
Perimeter or circumference of main loop, metres . 6.28
Diameter of loop conductor, mm .................. 25.0
Height of lowest part of loop above earth, metres
0.5
Frequency of operation, megahertz ............... 7.100
Transmitter output power, watts ................. 100.0
Electrical length of loop ...
Inductance of main loop .....
Coupling loop diameter ......
Turns ratio on coupling xfmr.
Tuning capacitor setting ....
Current in main loop ........
Voltage across capacitor ....
0.149 wavelengths at operating freq.
5.60 micro-henrys
0.43 metres to match to 50-ohm feeder
9.4 to 1 .. .. .. .. ..
83.1 pico-farads at resonance
13.3 amperes rms, opposite capacitor
4531 peak volts
Q when transmitting .........
442
Transmitting bandwidth ......
16.1 kilo-hertz between 3dB points
Radiation resistance ........ 0.0963 ohms distributed around loop
Conductor RF loss resistance 0.0558 ..
..
.. ..
Ground proximity losses ..... 0.4138 ..
..
.. ..
Transmission efficiency .....
17.02 percent of power input
Loss relative to ideal loop .
7.7 dB = 1.3 "S"-points
Se puede ver que las pérdidas dependen fundamentalmente de la proximidad con la tierra,
pues la resistencia equivalente de las pérdidas por la tierra es 8 veces más grande que la de
las pérdidas en el conductor. Dicho de otro modo, es más importante elevar la antena que
aumentar el diámetro del loop, para pasar del 22% al 63% de eficiencia, sin aumentar el
diámetro.