Metales: Modelo de electrones libres

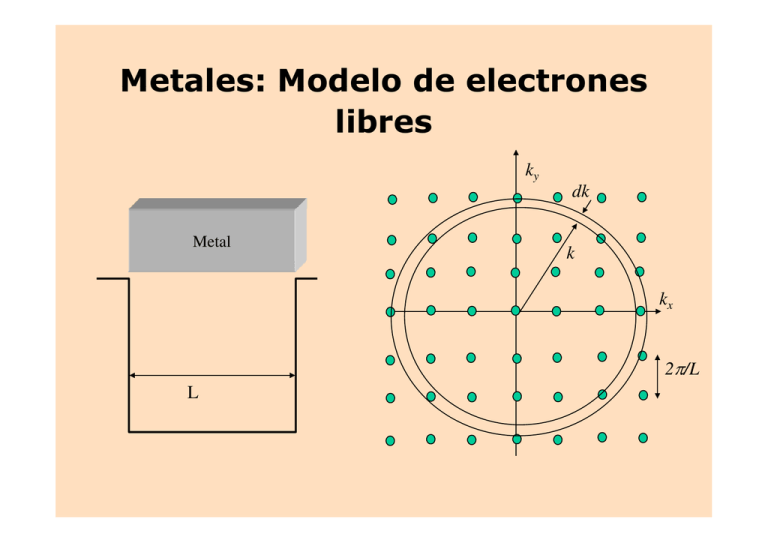
Metales: Modelo de electrones
libres
ky
Metal
dk
k
kx
2π/L
L
Cov. +
Covalente vdW
unión metálica
vdW
Metales
Los electrones se mueven libremente a
través del material
Modelo : Gas de electrones libres
Potencial cristalino
Drude (1900)
Sommerfeld (1927)
Considero un
gas clásico para
estudiar
conductividad
Aplicó la estadística de
Fermi Dirac
Fermi-Dirac
Potencial del modelo
Na: 1s2 2s2 2p6 3s1
Sodio metálico
L
densidad
electrónica
l t ó i
(e/cm3) ?
Z: valencia
A: masa atómica (gr/mol)
ρm = densidad (gr/cm3)
Otra forma de expresar la densidad:
rs(Na)
(N ) = 22.08
08 A
rionico(Na
(N +) = 00.98A
98A
Modelo de Sommerfeld
Para un gas de Ne electrones :
Si despreciamos la interacción e-e, resolvemos el problema de 1
electrón:
Ll
Llenamos
los
l niveles
i l de
d energía
í con los
l Ne electrones
l
Ej.: 1D
L
Condiciones de contorno
=k=nπ/L
n=1,2,…
Números cuánticos: n = 1, 2, 3, 4,….
ms = + ½ , - ½ (↑ , ↓ )
Lleno los niveles con los N electrones
Ej.: N = 6
nF: n correspondiente al último nivel ocupado
En general, si N es par se tiene: nF = N/2
en un cristal
N ≈1023
Definimos la Energía de Fermi como la energía del ultimo nivel
ocupado
p
La energía de Fermi es función de N/L (densidad electrónica del gas)
Para el gas en 3D
ni=1,2,3,..
F
Estas condiciones de contorno no son adecuadas para
estudiar
t di las
l propiedades
i d d de
d bulk
b lk de
d un material
t i l
Condiciones periódicas de contorno (Born-von Karman)
Lz
Ly
Las soluciones son:
Lx
Las funciones de onda
son autofunciones
del operador momento
Poseen momento lineal definido
Valores posibles de k ?
ni
entero
Ne electrones:
Energía
g de
Fermi
ky
Velocidad
de Fermi
kF
kx
estados ocupados
2π/Ly
2π/Lx
Superficie de Fermi
= εF
superficie en el espacio
k (esfera)
Separa los estados
ocupados de los vacios
La energía total del estado fundamental del gas se calcula:
Para una muestra macroscópica, los valores permitidos de k llenan
densamente el espacio
densidad de estados
g(k)
(k) o g(E)
( )
g
g
1d
g
2d
3d
Calor específico de los metales
La energía interna de un gas clásico de N e- es:
E(T) = 3/2 N KB T
(1/2 KB T por grado de libertad)
Cv(clas) = ∂E/∂T = 3/2 N KB
Si N = NA (6.023
(6 023 1023),
) ell calor
l específico
ífi molar
l es:
cv(clas) = 3/2 NA KB = 3/2 R
Este término debería sumarse a la contribución proveniente de las
vibraciones
ib i
de
d la
l red.
d Ell cv de
d un metall a temperatura ambiente
bi
sería
cv = 3/2 R + 3 R = 9/2 R
Recordemos que ocurre en aisladores:
A bajas temperaturas
C v = α T3
C v / T = α T2
En un metal ?
cv = cv fonones+ 3/2 R ?
T Tamb
T=T
cv = 3 R + 3/2 R = 9/2 R ?
La contribución
L
ib ió de
d los
l electrones
l
de
d conducción
d ió all calor
l especifico
ifi
de un metal es pequeña a temperatura ambiente, comparada con la
contribución proveniente de las vibraciones de la red (fonones)
A muy bajas temperaturas :
Tratamiento cuántico - Gas de Sommerfeld
La energía total del estado fundamental del gas :
E(T)
donde
Cv = ∂E/∂T
Cómo calculamos la energía
interna E(T) ?
Distribución de
Fermi-Dirac
T=0
T≠0
EF = lim μ
T
0
Estimación de la contribución electrónica al Cv
g(ε)
No e- excitados
V
≈ g(EF) KB T
Energía de excitación ≈ KB T
E
V
≈ g(EF) (KB T)2
cv≈ g(EF) KB2 T
Su muestra que para un gas de e- en 3D :
3n
3n
g( F) =
g(E
=
2 EF
2 KBTF
cv≈ g(EF) KB2 T = 3/2 n KB T/TF
c(clas) = 3/2 n KB
T=Tamb
cv
≈ T/TF ≈ 10-2
c(clas)
La contribución de los electrones de conducción al calor especifico
de un metal a Tamb es ~ 1% del valor clásico
Para un metal
P
t la
bajas temperaturas
Cv = Cve + Cvpph
= γ T + α T3
C v / T = γ + α T2
γ es proporcional a
g(EF)
Limite clásico ????