12 15. Historia muda: 16. En la siguiente figura aparece la mitad y

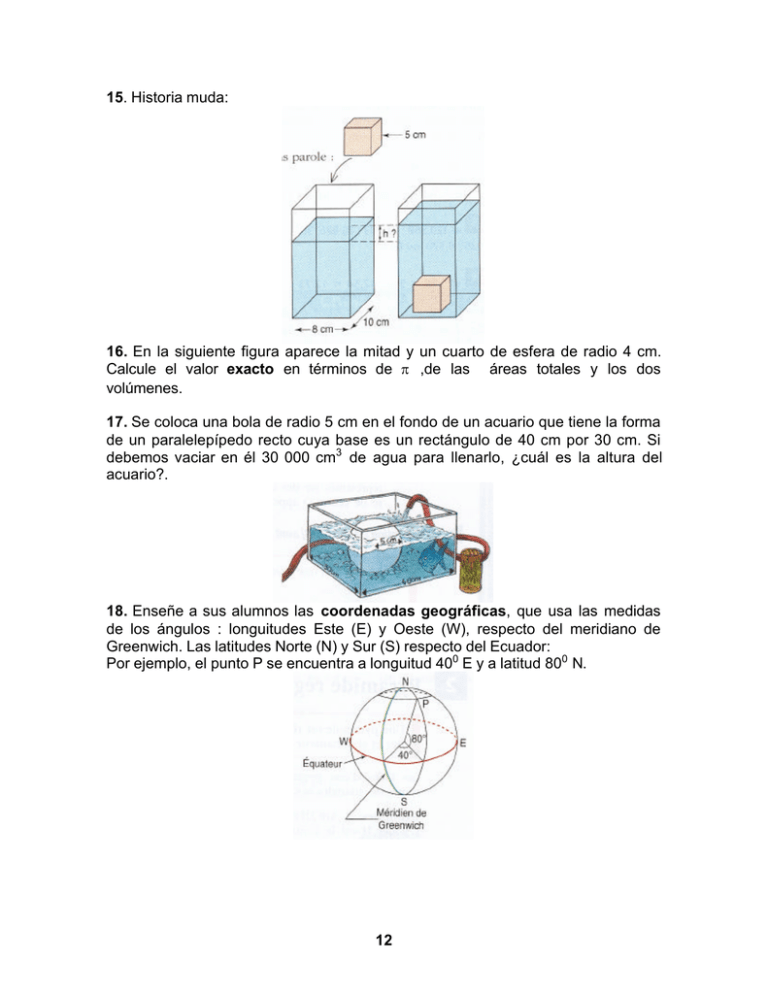
15. Historia muda:
16. En la siguiente figura aparece la mitad y un cuarto de esfera de radio 4 cm.
Calcule el valor exacto en términos de π ,de las áreas totales y los dos
volúmenes.
17. Se coloca una bola de radio 5 cm en el fondo de un acuario que tiene la forma
de un paralelepípedo recto cuya base es un rectángulo de 40 cm por 30 cm. Si
debemos vaciar en él 30 000 cm3 de agua para llenarlo, ¿cuál es la altura del
acuario?.
18. Enseñe a sus alumnos las coordenadas geográficas, que usa las medidas
de los ángulos : longuitudes Este (E) y Oeste (W), respecto del meridiano de
Greenwich. Las latitudes Norte (N) y Sur (S) respecto del Ecuador:
Por ejemplo, el punto P se encuentra a longuitud 400 E y a latitud 800 N.
12
19.
• En la siguiente figura el punto M está en la intersección del meridiano de
Greenwich y el Ecuador. Precisar las coordenadas geográficas de los puntos
A, B, C, D, E y F
•
•
•
Un marino señala que está ubicado en la posición 40 W y 500 N. Con la ayuda
de un mapa, diga si este marino está en el oceáno Atlántico o en el océano
Indico?
La misma pregunta para un barco que está 1050 W y 400 S.
Averigue las coordenadas geográficas de su ciudad.
20. La siguiente figura representa una esfera de centro O y radio 2 cm. Si es
posible, hallar las longuitudes, en cm, de OA, CB, OF, OE.
21. La siguiente figura representa una esfera de radio 1 mm. Se sabe que la
distancia AC (sobre la esfera !!!) es 1,2 mm. CAlcular el valor exacto de AB
22. Calcular el volumen de los dos sólidos que aparecen mas abajo, con una
precisión de 0, 1 cm3 .
13
23. Seccionamos un cono de radio basal 0,9 m y de altura SO = 2,1 m por un
plano perpendicular al trazo SO en el punto H, tal que SH = 1,4 m. Calcular el
radio de la sección circular.
24. ABCDEFG es un pruisma recto de base triangular
•
•
Si se secciona por un plano perpendicular a AE, ¿cuál es la sección obtenida?
La misma pregunta, pero ahora el plano es paralelo al plano ACGE
25. Se introduce una bola de acero de 1,5 cm de radio en una caja en forma de un
prisma de base cuadrada, con arista 4 cm, y que contiene agua. ¿qué altura
alcanza el agua, con una presición de 0,1 cm ?
26. Considere el siguiente sólido:
14
•
•
ABCDEFGH es un paralelepípedo recto de base cuadrada con AB=1,5 cm y
de altura AE=x cm.
SEFGH esc una pirámide regular de altura 4 cm.
a) Expresar el volumen V del sólido en función de x. ¿Este volumen es
proporcional a x?.
b) Considere un cilindro cuya base es un disco de área 3 cm2 y altura x. Exprese
el volumen V ' del cilindro en función de x.
c) ¿Para qué valor de x V = V ' ?.
27. Un punto M sobre la superficie de la Tierra, asimilado a una esfera de 6 370
Km de radio, está sobre un paralelo correspondiente a la latitus 500. H es el centro
de la circunferencia correspondiente a ese paralelo.
a) ¿Cuál es la naturaleza del triángulo OHM? ¿Cuál es la longitud (en Km) del
radio HM del paralelo ?
b) ¿Cuál es la longitud de ese paralelo?.
28. Se derriten 5 esferas de hielo de 2 cm de diámetro en una copa cónica como
la representada mas abajo. Se sabe que OB = 6 cm y OC = 4 cm.
a) ¿Cuál es el valor exacto del volumen V de la copa?
20π
b) muestre que el volumen total del hielo es
cm3.
3
c) Tras el deterretimiento del hielo, el volumen de agua que resulta se obtiene
multiplicando por 0,9 el volumen del hielo. ¿Cuál es el valor exacto del volumen W
del agua en la copa, como resultado del derretimiento?
d) Pruebe que V = 8W.
e) Calcular la altura CI del agua el la copa tras el derretimiento.
29. ¿Cuál es la naturaleza de los sólidos DICHJG, DHEFG, IHEFG, IHJG?
15
30. ¿Es verdad que los patrones abajo representados son de sólidos? . Si así
fuese, precise su naturaleza.
31. ABCDEFGH es un cubo de arista 5 cm. Diseñe un patrón para la pirámide
BFCA.
32. Calcule los volúmenes de los siguientes sólidos:
33. La siguiente pirámide de base cuadrada y caras triángulos isósceles, tiene por
altura SI y SH es la altura de uno de los triángulos laterales. Calcule el volumen
de esta pirámide en los siguientes casos:
a) AB=8 cm y SH = 5 cm
b) AB= 8 cm y SB = 8 cm
16
34. ¿Para qué valor de x el volumen del sólido mas abajo descrito es igual a 80
cm3 (todas las medidas están en cm)
35. Abajo presentamos un cono y su patrón. ¿Puede calcular la altura SH?
36. Con una presición de 0,1 cm3, calcular el volumen del sólido forma por una
semi esfera y un cono:
37. Seccionamos el siguiente sólido formado por un cilindro de altura 4 cm y por
dos semiesferas de radio 1 cm, por un plano que pasa por el centro de las esferas.
Dibujar la sección resultante indicando sus dimensiones,
38. Un reswervorio de agua de forma cónica con vértice S y base un disco de
centro O y diámetro AB = 5 m con ángulo ∠ OSA = 220
a) Hallar el volumen del reservorio
b) Calcular el tiempo que demora en llenarse si llave de agua expelo 35 litros por
minuto.
17
39. SABCD es una pirámide regular de base cuadrada con 24 m de arista y altura
SH = 12 m.
a) Calcular el volumen V 1 en m3 de esta pirámide.
b) Al interior de la pirámide se construye una sala de forma semi esfera con centro
en H y radio 8 m. Calcular el volumen V 2 de esta sala en m3
d) Sehace una maqueta a escala 1:20. Calcular el volumen V3 de la pirámide
reducida.
18