Reglas de equivalencia de las inecuaciones
Anuncio

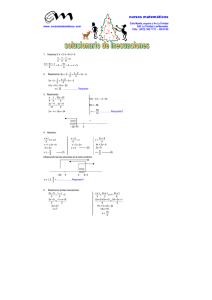
Departamento de Matemáticas REGLAS DE EQUIVALENCIA. INECUACIONES De la suma “si se suma o resta la misma cantidad a una desigualdad se obtiene otra equivalente a la primera” x <a ⇔ x+A<a+A x <a ⇔ x−B< a−B Ejemplo: x + 3 < 5 ⇔ x + 3 − 3 < 5 − 3 ⇔ x < 2 Se suele decir que lo que en un miembro está sumando pasa al otro restando, y viceversa, lo que en un miembro está restando pasa al otro sumando. Del producto: “si se multiplica o divide a los dos miembros de una desigualdad por la misma cantidad POSITIVA se obtiene otra equivalente a la primera” ax < b ⇔ A ⋅ ax < A ⋅ b ⇔ ax b < A A si A > 0 4x + 1 4x + 1 ⇔ 5 ⋅ 3x > 5 ⋅ ⇔ 15x > 4x + 1 5 5 Se suele decir que lo que en un miembro está multiplicando pasa al otro dividiendo, y viceversa, lo que en un miembro está dividiendo pasa al otro multiplicando. ax b ax < b ⇔ A ⋅ ax > A ⋅ b ⇔ > si A < 0 A A “si se multiplica o divide a los dos miembros de una desigualdad por la misma cantidad NEGATIVA se obtiene otra equivalente a la primera CON EL SENTIDO INVERSO DE LA DESIGUALDAD ” −2x 4x − 6 Ejemplo: −2x > 4x − 6 ⇔ < ⇔ x < −2x + 3 −2 −2 Observación: para expresar de modo sencillo la solución de la inecuación conviene que la incógnita esté en el primer miembro, ¿cómo se intercambian los miembros de una inecuación? Ejemplo: 3x > x<a⇔a>x “si se intercambian los miembros de una desigualdad de debe invertir el sentido de la misma” Ejemplo: 2 > 3x ⇔ 3x < 2