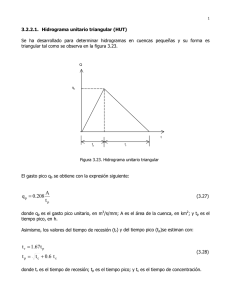
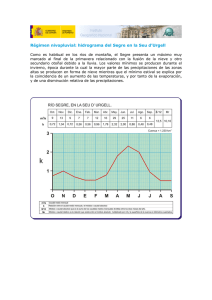
CICLO HIDROLÓGICO PROBLEMA 1 En la Figura 1 se muestra una

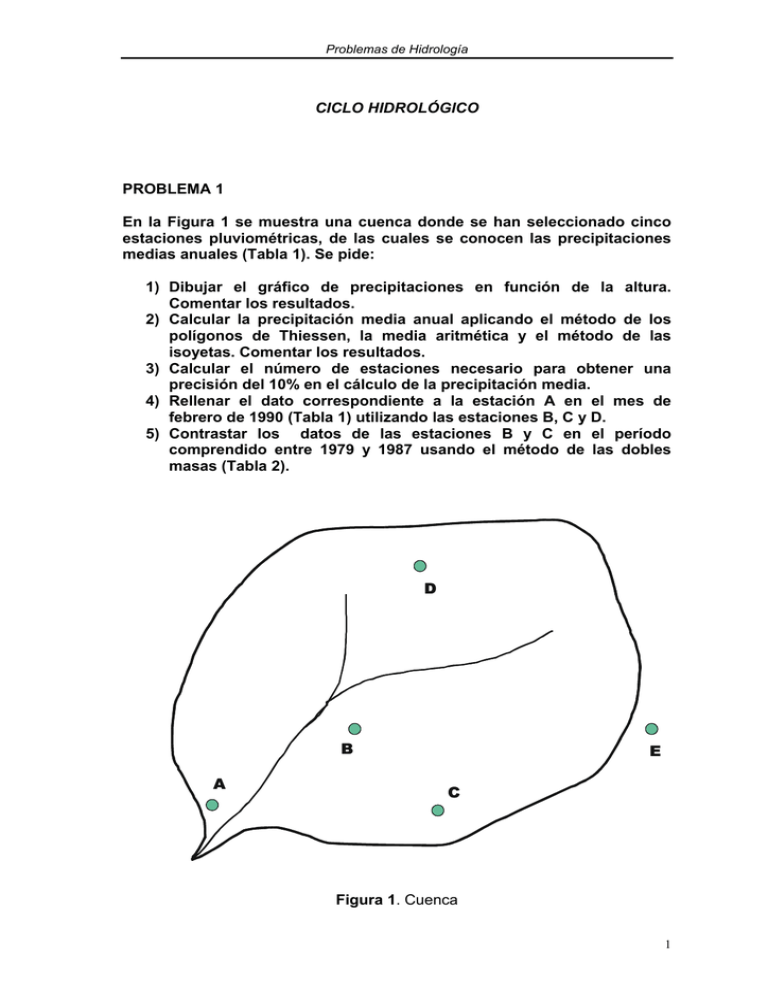
Problemas de Hidrología
CICLO HIDROLÓGICO
PROBLEMA 1
En la Figura 1 se muestra una cuenca donde se han seleccionado cinco
estaciones pluviométricas, de las cuales se conocen las precipitaciones
medias anuales (Tabla 1). Se pide:
1) Dibujar el gráfico de precipitaciones en función de la altura.
Comentar los resultados.
2) Calcular la precipitación media anual aplicando el método de los
polígonos de Thiessen, la media aritmética y el método de las
isoyetas. Comentar los resultados.
3) Calcular el número de estaciones necesario para obtener una
precisión del 10% en el cálculo de la precipitación media.
4) Rellenar el dato correspondiente a la estación A en el mes de
febrero de 1990 (Tabla 1) utilizando las estaciones B, C y D.
5) Contrastar los datos de las estaciones B y C en el período
comprendido entre 1979 y 1987 usando el método de las dobles
masas (Tabla 2).
D
B
A
E
C
Figura 1. Cuenca
1
Problemas de Hidrología
Tabla 1. Precipitaciones año 1990.
ESTACIÓN
ALTITUD (m) P febr. (mm)
P jul. (mm)
PMA
38
16.9
997.4
A
460
54.9
4.9
1905.6
B
500
98.9
12.6
1663.8
C
905
124.9
6
1401
D
1249
90.5
19.4
1423.6
E
P febr.: precipitación total en el mes de febrero, P jul.: precipitación total en el
mes de julio, PMA : Precipitación media anual en mm.
Tabla 2. Precipitaciones anuales totales en las estaciones B y C (mm).
AÑO
1979
1980
1981
1982
1983
1984
1985
1986
1987
ESTACION B
2077.4
1631.9
1754.2
1815.8
1610.6
2424.9
1937.2
1806.8
1802
ESTACIÓN C
2306.4
1649
1871.2
1878.1
1964.7
3412.7
2588.1
1645.1
1558.2
1) Si se representan los valores de lo Módulos Pluviométricos anuales medios de
las cinco estaciones con respecto a la altitud (Tabla 1) se obtiene el gráfico
siguiente:
2000
B
1800
PREC. (mm)
C
1600
D
E
1400
1200
A
1000
0
200
400
600
800
1000
1200
1400
ALTURA (m)
Figura 1.1. Representación de la Precipitación con respecto a la Altitud.
2
Problemas de Hidrología
De la Figura 1.1. se deduce que las precipitaciones medias anuales aumentan
conforme la altitud es mayor, aunque dicho incremento no se cumple para
altitudes superiores a los 430 m. Ello puede ser consecuencia a que no sólo la
altitud influye sobre el valor de la precipitación, sino que la distancia al mar
condiciona también dicho valor.
2) Para calcular la precipitación media en la cuenca se pueden aplicar los métodos
de los polígonos de Thiessen, de las isoyetas, una combinación de ambos
métodos, o bien, una media aritmética. En nuestro caso vamos a aplicar el
método simple de la media aritmética, el de los polígonos de Thiessen y el de las
isoyetas.
a) Media aritmética
Se dispone de cinco estaciones, por lo que su media es:
Pma =
1
⋅ (997.4 + 1905.6 + 1663.8 + 1423.6 + 1401) = 1478.28 mm
5
b) Polígonos de Thiessen
Se unen mediante una línea de trazos las estaciones con las que se encuentran
más próximas, tal y como se representa en la siguiente figura
D
B
A
E
C
Figura 1.2. Método de los Polígonos de Thiessen. Unión de estaciones mediante
líneas.
3
Problemas de Hidrología
A continuación se trazan las mediatrices de los segmentos anteriores, de tal
forma que dichas mediatrices van delimitando las zonas de influencia de cada
estación.
D
B
E
A
C
Figura 1.3. Método de los Polígonos de Thiessen. Mediatrices (trazo continuo).
D
B
A
E
C
Figura 1.4. Método de los Polígonos de Thiessen. Zona de influencia de cada
estación.
4
Problemas de Hidrología
A cada estación le corresponde un área de influencia donde se supone que la
precipitación ha sido homogénea. Dicha área está delimitada por las mediatrices
y por el contorno de la cuenca, tal y como se puede apreciar en la Figura 1.4. Se
trata de planimetrar cada área (por ejemplo, la zona rayada para la estación D) y
realizar la media ponderada calculando el porcentaje de cada área con respecto
al total de la superficie de la cuenca. De este modo, se obtiene para las cinco
áreas de influencia:
PTh =
A 1 ⋅ P1 + A 2 ⋅ P2 + ..... + A 5 ⋅ P5
A 1 + A 2 + .... + A 5
PTh = 0.174 ⋅ 997.4 + 0.218 ⋅ 1905.6 + 0.152 ⋅ 1663.8 + 0.304 ⋅ 1423.6 + 0.152 ⋅ 1401
PTh = 1487.37 mm
c) Isoyetas
En este caso se trazan líneas de igual precipitación interpolando a partir de los
Módulos Pluviométricos anuales medios medidos en cada estación (ver Figura
1.5).
D
2000
1800
1600
A
1400
B
E
C
1200
1000
Figura 1.5. Método de las Isoyetas. Trazado de las líneas de igual precipitación.
5
Problemas de Hidrología
Una vez trazadas las isoyetas se planimetra la superficie comprendida entre
isoyetas consecutivas con el propósito de asignarle a dicha área la precipitación
media cuyas isoyetas limita, tal y como se muestra en la Figura 1.6.
D
2000
1800
1600
A
B
E
C
1400
1200
1000
ISOYETAS
Figura 1.6. Método de las Isoyetas. Área comprendida entre isoyetas.
La precipitación media obtenida aplicando este método consiste en asignar a
cada isoyeta un área de influencia o a cada área comprendida entre dos isoyetas
consecutivas una precipitación media de los valores que tienen ambas. En
nuestro caso se obtiene:
PIs =
A1 ⋅
(P1 + P2 )
2
(P2 + P3 )
+ ..... + A n −1 ⋅
2
A 1 + A 2 + .... + A n −1
+ A2 ⋅
(Pn −1 + Pn )
2
1
⋅ [0.086 ⋅ (1000 ) + 0.152 ⋅ (1000 + 1200) + 0.195 ⋅ (1200 + 1400) + 0.152 ⋅(1400 +
2
1
1600 )] + ⋅ [0.13 ⋅ (1600 + 1800) + 0.13 ⋅ (1800 + 2000) + 0.152 ⋅ (2000)] = 1510.8 mm
2
PIs =
Los resultados obtenidos aplicando los tres métodos proporcionan valores
similares a pesar de las diferencias cuantitativas de los Módulos Pluviométricos
que presentan las estaciones. La ubicación de éstas, y el área de influencia,
también ha influido en los resultados obtenidos.
6
Problemas de Hidrología
3) Para calcular el número de estaciones necesarias para obtener una precisión del
10% en el cálculo de la precipitación media aplicaremos las siguientes
expresiones:
C 
N= v
 ε 
2
siendo N el número de estaciones y ε es el tanto por cien de error para estimar la
lluvia media,
m
Cv =
100 ⋅ σ m −1
P
P=
;
m
1
∑ Pi
m i =1
;
σ m −1 =
∑ (P
i =1
i
− P)
2
m −1
Sustituyendo valores:
P=
1
⋅ (997.4 + 1905.6 + 1663.8 + 1423.6 + 1401) = 1478.28 mm
5
m
σ m −1 =
∑ (P
i =1
i
− P)
2
m −1
= 338.09 mm
En consecuencia,
Cv =
100 ⋅ σ m −1 100 ⋅ 338.09
=
= 22.87
P
1478.28
y
2
2
C 
 22.87 
N= v  =
 = 5.23 ≈ 6 estaciones
 10 
 ε 
4) Para estimar y rellenar el dato que falta en el mes de febrero hay que tener en
cuenta los módulos pluviométricos anuales medios de cada una de las tres
estaciones. Como éstos difieren entre sí en mas de un 10%, aplicaremos una
expresión ponderada:
N
N 
1 N
PA =  PB A + PC A + PD A 
3  NB
NC
ND 
1
997.4
997.4
997.4 
PA =  54.9 ⋅
+ 98.9 ⋅
+ 124.9 ⋅
 = 58.98 mm
3
1905.6
1663.8
1401 
7
Problemas de Hidrología
5) El método de la doble masa consiste en representar los valores acumulados de
las precipitaciones en un sistema de ejes cartesiano y comprobar si dichos datos
representados se encuentran en una recta o si, por el contrario, se alejan de ella
Tabla 1.1. Valores acumulados de precipitaciones
AÑO
1979
1980
1981
1982
1983
1984
1985
1986
1987
ESTACION B
2077.4
1631.9
1754.2
1815.8
1610.6
2424.9
1937.2
1806.8
1802
ESTACIÓN C
2306.4
1649
1871.2
1878.1
1964.7
3412.7
2588.1
1645.1
1558.2
PREC. ACUM. B
2077.4
3709.3
5463.5
7279.3
8889.9
11314.8
13252
15058.8
16860.8
PREC. ACUM. C
2306.4
3955.4
5826.6
7704.7
9669.4
13082.1
15670.2
17315.3
18873.5
Representando
20000
Estación C
16000
12000
8000
4000
0
0
4000
8000
12000
16000
Estación B
Figura 1.7. Contraste de estaciones.
De la Figura 1.7 se deduce que las estaciones están bien contrastadas y que a
partir de una de ellas se pueden extrapolar datos incompletos en la otra.
8
Problemas de Hidrología
PROBLEMA 2
Dadas las precipitaciones máximas diarias registradas en una estación
(Tabla 1), se pide calcular la precipitación diaria máxima para los períodos
de retorno de 10 y 50 años.
Tabla 1. Precipitaciones máximas diarias (mm).
AÑO 1961
PREC. 31.6
AÑO 1970
PREC. 77.2
1962
38.7
1971
65
1963
29.7
1972
50
1964
31.2
1973
45
1965
60.5
1974
72.8
1966
31.5
1975
57.3
1967
46
1976
31.2
1968
57.5
1977
56
1969
37.8
1978
40.5
Para resolver el problema hay que seguir los siguientes pasos:
a) Ordenar de mayor a menor todos los datos
b) Asignar a cada valor un número ordinal que representa el número de veces que
dicho valor se ha igualado o superado
c) A cada valor asignarle la probabilidad o frecuencia relativa
P=
m
n +1
donde m es el número ordinal y n el número de datos totales correspondientes a
los n años.
d) La inversa de la frecuencia relativa será el período de retorno
e) Dibujar en un gráfico, semilogarítmico en abscisas, las precipitaciones máximas
en función de los períodos de retorno o recurrencia
En la Tabla 2.1 se presentan los pasos anteriores
Tabla 2.1. Cálculo del período de retorno.
m
Prec.
1
2
3
4
5
6
7
8
9
77.2
72.8
65
60.5
57.5
57.3
56
50
46
m
n +1
0.052
0.105
0.157
0.21
0.26
0.31
0.368
0.421
0.473
P=
1
P
m
Prec.
19
9.5
6.33
4.75
3.8
3.16
2.71
2.375
2.11
10
11
12
13
14
15
16
17
18
45
40.5
38.7
37.8
31.6
31.5
31.2
31.2
29.7
T=
m
n +1
0.526
0.578
0.631
0.684
0.736
0.789
0.842
0.894
0.947
P=
1
P
1.9
1.72
1.58
1.46
1.357
1.26
1.187
1.11
1.05
T=
9
Problemas de Hidrología
En la Tabla 2.1 se puede comprobar que el valor 31.2 mm de precipitación se repite.
Para elaborar dicha tabla hay que escribir todos los valores y, en aquellos que se repitan,
asignarle la probabilidad más alta (período de retorno menor).
En la Figura 2.1 se ha representado, en escala semilogarítmica, la precipitación máxima
diaria con respecto al período de retorno. Posteriormente, se ha dibujado la recta de
regresión y, a partir de ella, se han obtenido los valores de la precipitación máxima
diaria para los períodos de retorno de 10 y 50 años.
100
90
80
Pd
70
60
50
40
30
1
10
50
100
T
Figura 2.1. Precipitación máxima diaria con respecto al período de Retorno
Para un período de retorno de 10 años se ha obtenido un valor de
Pd = 69 mm
valor que resulta más bajo que los valores de 77.2 mm y 72.8 mm de los períodos de
retorno de 19 y 9.5 años, respectivamente. Ello es debido a la recta de regresión que no
pasa por todos los puntos dibujados. Por ello, cuantos más datos se tengan de series
históricas mejores resultados se obtendrán.
Para un período de retorno de 50 años se ha obtenido un valor de
Pd = 95 mm
10
Problemas de Hidrología
PROBLEMA 3
Tomando los datos anuales de una estación genérica A (43º 18’ 15” N, 08º
22’ 42”) (Tabla 1) se pide, calcular la ETP utilizando los métodos de
Thornthwaite y Turc y Penman en el año 1983 y suponiendo que la cuenca
está constituida por un 40% de bosque de pináceas, un 20% de bosque de
frondosas, un 25% de praderas y cultivos (albedo 0,24), un 7,5% de labor
intensa (zonas urbanizadas) y un 7,5% de matorral sin arbolado (albedo
0,16).
Tabla 1. Datos anuales.
MES
Octubre
Noviembre
Diciembre
Enero
Febrero
Marzo
Abril
Mayo
Junio
Julio
Agosto
Septiembre
T medias
(ºC)
14.9
14.2
10
9.5
7.9
11.2
11.1
12.4
16.9
18.9
19.2
18.3
HUMEDAD
(%)
77
82
75
73
80
76
74
78
71
81
80
76
VEL. VIENTO
(km/d)
165
199
259
218
222
194
277
257
218
189
177
190
HORAS DE SOL
(%)
50
28
32
42
25
36
29
34
46
30
33
50
Método de Thornthwaite
Se calcula la ETP a partir del índice de calor mensual y anual, y la temperatura T
i = (T 5)
1.514
Índice de calor mensual
12
I = ∑i
Índice de calor anual
1
(
ETP = K ⋅ 16 ⋅ 10 ⋅ T
)
I
a
ETP en mm/mes
donde
a = 675 ⋅ 10 −9 I 3 − 771 ⋅ 10 −7 I 2 + 1792 ⋅ 10 −5 I + 0.49239
K=
N d
⋅
12 30
11
Problemas de Hidrología
siendo d el número de días del mes y N el número máximo de horas de sol que depende
de la latitud y del mes.
Para calcular N se ha interpolado los valores correspondientes a los 40º y 45º para cada
mes de la Tabla 3.1, ya que la posición de la estación es de 43º 18’ 15”.
Tabla 3.1. Número máximo diario de horas de sol según latitud Norte en h/d.
Lat. Ene. Feb. Mar. Abr. May. Jun.
0º 12.1 12.1 12.1 12.1 12.1 12.1
5º 11.9 12.0 12.1 12.2 12.4 12.4
10º 11.6 11.8 12.1 12.3 12.6 12.7
15º 11.4 11.6 12.1 12.4 12.8 13.0
20º 11.1 11.4 12.0 12.6 13.1 13.3
25º 10.8 11.3 12.0 12.8 13.4 13.7
30º 10.5 11.1 12.0 12.9 13.7 14.1
35º 10.2 10.9 12.0 13.1 14.1 14.6
40º 9.7 10.6 12.0 13.3 14.4 15.0
45º 9.2 10.4 11.9 13.6 14.9 15.6
50º 8.6 10.1 11.9 13.8 15.5 16.3
9.6
11.8 14.2
16.4 17.5
55º 7.7
9.1
11.8 14.6
17.2 18.7
60º 6.8
Jul. Ago. Sept. Oct. Nov. Dic.
12.1
12.3
12.6
12.9
13.2
13.6
13.9
14.3
14.7
15.3
15.9
17.0
18.0
12.1
12.3
12.4
12.6
12.8
13.0
13.2
13.5
13.7
14.1
14.5
15.1
15.6
12.1
12.1
12.2
12.2
12.3
12.3
12.4
12.4
12.5
12.5
12.6
12.7
12.7
12.1
12.0
11.9
11.8
11.7
11.6
11.5
11.3
11.2
11.0
10.8
10.4
10.1
12.1
11.9
11.7
11.4
11.2
10.9
10.7
10.3
10.0
9.5
9.1
8.4
7.6
12.1
11.8
11.5
11.2
10.9
10.6
10.2
9.8
9.4
8.8
8.1
7.2
6.3
En la Tabla 3.2 se muestran los distintos valores obtenidos de los diferentes parámetros
para calcular la ETP mensual.
Tabla 3.2. Cálculo de la ETP mediante el método de Thornthwaite
MES
Octubre
Noviembre
Diciembre
Enero
Febrero
Marzo
Abril
Mayo
Junio
Julio
Agosto
Septiembre
12
T (ºC)
14.9
14.2
10
9.5
7.9
11.2
11.1
12.4
16.9
18.9
19.2
18.3
i
5.22
4.85
2.85
2.64
1.99
3.39
3.34
3.95
6.32
7.48
7.66
7.13
I
56.82
56.82
56.82
56.82
56.82
56.82
56.82
56.82
56.82
56.82
56.82
56.82
N
11.07
9.67
9
9.37
10.47
11.93
13.5
14.74
15.4
15.1
13.97
12.5
a
1.38
1.38
1.38
1.38
1.38
1.38
1.38
1.38
1.38
1.38
1.38
1.38
K
0.953
0.806
0.775
0.806
0.814
1.027
1.125
1.27
1.28
1.3
1.203
1.041
ETP (mm/mes)
57.67
45.64
27.05
26.21
20.52
41.91
45.35
59.63
92.17
109.25
103.3
83.66
Problemas de Hidrología
Método de Turc
Para estimar la ETP mediante el método de Turc es necesario conocer la humedad
relativa media mensual, la temperatura, posición de la estación y las horas reales de
insolación.
La ETP se calcula aplicando la siguiente expresión:
 T 
ETP = 0.4 ⋅ 
 ⋅ (R i + 50 ) ⋅ g(ε )
 T + 15 
donde T es la temperatura media diaria en ºC y g(ε) es una función de la humedad
relativa ε cuya expresión es
1 ⇒ ε ≥ 50%

g(ε ) =  50 − ε 
1 + 70  ⇒ ε < 50%


y Ri viene dado por
n

R i = R a ⋅  0.18 + 0.62 ⋅ 
N

donde Ra es la intensidad teórica de radiación incidente sobre una superficie horizontal,
suponiendo que no existe atmósfera en cal/cm2.d. Su valor depende del mes y la latitud,
n el número real de horas de insolación y N el número máximo de horas de insolación
(Tabla 3.1).
Tabla 3.3. Intensidad teórica de radiación incidente en cal/cm2.d
Lat. Ene. Feb. Mar. Abr. May. Jun. Jul. Ago. Sept. Oct. Nov. Dic.
0º
5º
10º
15º
20º
25º
30º
35º
40º
45º
50º
55º
60º
858
809
759
701
642
575
508
436
364
293
222
155
88
888
855
821
777
732
678
624
559
495
427
360
288
215
890
882
873
854
834
799
764
719
673
616
560
496
432
862
878
894
898
902
891
880
856
833
798
764
720
676
816
851
885
908
930
940
950
947
944
932
920
900
880
790
832
873
904
934
954
972
979
985
984
983
977
970
804
842
879
905
930
942
955
957
958
948
938
923
908
833
857
880
891
902
896
891
874
858
829
800
764
728
875
874
872
858
843
815
788
749
710
658
607
547
487
880
855
830
793
755
708
658
597
536
470
404
333
262
860
814
767
712
656
593
528
459
390
317
246
179
111
842
789
735
673
610
539
469
395
323
251
180
118
56
En nuestro caso al ser la humedad relativa superior al 50% la función g(ε) es igual a 1.
Los valores de N ya han sido interpolados en la Tabla 3.1 en el apartado anterior. El
13
Problemas de Hidrología
valor Ra se calculará a partir de la Tabla 3.3 interpolando entre la latitud 40º y 45º para
cada mes.
Con todos estos datos se ha elaborado la Tabla 3.4 donde se muestran los valores de los
diferentes parámetros estimados y conocidos.
Tabla 3.4. Cálculo de la ETP mediante el método de Turc
MES
Octubre
Noviembre
Diciembre
Enero
Febrero
Marzo
Abril
Mayo
Junio
Julio
Agosto
Septiembre
T (ºC)
14.9
14.2
10
9.5
7.9
11.2
11.1
12.4
16.9
18.9
19.2
18.3
Ra
492.44
341.82
275.48
317.14
450.12
635.38
809.9
937.78
984.34
951.4
838.86
675.68
N
11.07
9.67
9
9.37
10.47
11.93
13.5
14.74
15.4
15.1
13.97
12.5
n/N
0.50
0.28
0.32
0.42
0.25
0.36
0.29
0.34
0.46
0.30
0.33
0.50
ε
77
82
75
73
80
76
74
78
71
81
80
76
g(ε)
1
1
1
1
1
1
1
1
1
1
1
1
ETP (mm/mes)
58.06
33.23
24.67
29.41
27.7
52.35
58.07
75.39
107.63
88.8
83.67
83.76
En este caso en el enunciado del problema se aportan directamente los valores de la
relación n/N en tanto por cien. En la Tabla 3.4 aparecen en tanto por uno.
Método de Penman
Para estimar la ETP por el método de Penman se necesitan, además de la posición de la
estación, la humedad relativa, el número de horas reales de insolación, velocidad del
viento, temperatura y tipo de superficie. La expresión que se aplica es:
ETP = E ⋅ f ⋅ d
siendo f un coeficiente reductor que depende del mes (Tabla 3.5), d el número de días
del mes y E la evapotranspiración en mm/d y cuya expresión viene dada por:
∆
R n + Ea
γ
E=
∆
+1
γ
con ∆ (pendiente de la curva de vapor saturante) obtenida interpolando a partir de la
Tabla 3.6.
14
Problemas de Hidrología
Tabla 3.5. Coeficiente reductor.
MES
Enero
Febrero
Marzo
Abril
Mayo
Junio
Julio
Agosto
Septiembre
Octubre
Noviembre
Diciembre
f
0.6
0.6
0.7
0.7
0.8
0.8
0.8
0.8
0.7
0.7
0.6
0.6
Tabla 3.6. Relación ∆/(∆+γ). T en ºC.
T
∆/(∆+γ)
T
∆/(∆+γ)
T
∆/(∆+γ)
T
∆/(∆+γ)
0.
0.5
1.
1.5
2.
2.5
3.
3.5
4.
4.5
5.
5.5
6.
6.5
7.
7.5
0.401
0.409
0.418
0.426
0.432
0.440
0.448
0.445
0.462
0.470
0.478
0.485
0.493
0.500
0.508
0.515
8.
8.5
9.
9.5
10.
10.5
11.
11.5
12.
12.5
13.
13.5
14.
14.5
15.
15.5
0.522
0.530
0.537
0.544
0.552
0.559
0.566
0.573
0.580
0.587
0.593
0.600
0.607
0.614
0.621
0.627
16.
16.5
17.
17.5
18.
18.5
19.
19.5
20.
20.5
21.
21.5
22.
22.5
23.
23.5
0.633
0.640
0.646
0.652
0.658
0.664
0.670
0.676
0.682
0.688
0.694
0.699
0.705
0.710
0.715
0.720
24.
24.5
25.
25.5
26.
26.5
27.
27.5
28.
28.5
29.
29.5
30.
0.725
0.730
0.735
0.740
0.745
0.750
0.755
0.760
0.764
0.768
0.772
0.776
0.780
Rn es la radiación neta, expresada en mm de agua que puede evaporar en un día:
R n = R N cl
donde cl es el calor de vaporización (Tabla 3.7) y RN es la radiación neta en cal/cm2/d:
R N = R i ⋅ (1 − α ) − R e
Ri se calcula a partir de
15
Problemas de Hidrología
n

R i = R a ⋅  0.18 + 0.55 ⋅ 
N

donde Ra se ha calculado previamente en el apartado anterior y n/N es conocido.
α es el albedo y se estima a partir de los datos del enunciado y de la Tabla 3.8 y Re
(radicación emitida) se calcula con la siguiente expresión:
(
)

n 

R e = 1440 ⋅ 0.826·10 -10 ⋅ Ta4 0.56 − 0.092 ⋅ e d ⋅ 1 − 0.9 ⋅ 1 −  
 N 

con la presión de vapor
ed = ea ⋅
ε
100
siendo la tensión de saturación ea dada en función de la temperatura (Tabla 3.9).
Tabla 3.7. Calor de vaporización necesario para evaporar 1 mm de agua por cada
cm2 de superficie (en calorías).
T(ºC)
0
1
2
3
4
5
6
7
cl
59.6
59.6
59.5
59.5
59.4
59.3
59.3
59.2
T(ºC)
8
9
10
11
12
13
14
15
cl
59.1
59.1
59.
59.
58.9
58.9
58.8
58.8
T(ºC)
16
17
18
19
20
21
22
23
cl
58.7
58.7
58.6
58.6
58.5
58.5
58.4
58.3
T(ºC)
24
25
26
27
28
29
30
cl
58.3
58.2
58.2
58.2
58.1
58.1
58.
Tabla 3.8. Valores de albedo para distintas superficies evaporantes.
Superficie evaporante
Agua libre a T < 30 ºC
Agua libre a T > 30 ºC
Arcillas húmedas
Arcillas secas
Arenas claras
Arenas oscuras
Arenas ribereñas
Bosques de pináceas
Bosques de frondosas
Cereales
16
α
0.02-0.06
0.06-0.4
0.02-0.08
0.16
0.34-0.4
0.35
0.43
0.1-0.14
0.18
0.1-0.25
Superficie evaporante
Césped verde
Césped seco
Hielo
Lechugas
Limos
Nieve
Patatas
Rocas
Sabanas
Zonas urbanizadas
α
0.26
0.19
0.36-0.5
0.22
0.16-0.23
0.4-0.9
0.19
0.12-0.15
0.05-0.22
0.15-0.25
Problemas de Hidrología
Tabla 3.9. Tensión de vapor saturante (en mm de Hg) a la temperatura T (en ºC).
T
ea
T
ea
T
ea
T
ea
0.
0.5
1.
1.5
2.
2.5
3.
3.5
4.
4.5
5.
5.5
6.
6.5
7.
7.5
4.6
4.8
4.9
5.1
5.3
5.5
5.7
5.9
6.1
6.3
6.5
6.8
7.0
7.3
7.5
7.8
8.
8.5
9.
9.5
10.
10.5
11.
11.5
12.
12.5
13.
13.5
14.
14.5
15.
15.5
8.0
8.3
8.6
8.9
9.2
9.5
9.8
10.2
10.5
10.9
11.2
11.6
12.0
12.4
12.8
13.2
16.
16.5
17.
17.5
18.
18.5
19.
19.5
20.
20.5
21.
21.5
22.
22.5
23.
23.5
13.6
14.1
14.5
15.0
15.5
16.0
16.5
17.0
17.5
18.1
18.7
19.2
19.8
20.4
21.1
21.7
24.
24.5
25.
25.5
26.
26.5
27.
27.5
28.
28.5
29.
29.5
30.
22.4
23.0
23.8
24.5
25.3
26.0
26.7
27.5
28.3
29.2
30.0
30.9
31.8
Por último Ea viene dado en mm/d en función del déficit higrométrico y la velocidad del
viento V2 (m/s):
E a = 0.35 ⋅ (0.5 + 0.54 ⋅ V2 ) ⋅ (e a − e d )
El albedo se estima a partir de la media ponderada siguiente (Tabla 3.10):
Tabla 3.10. Albedo.
ALBEDO
Bosque Pináceas
Bosque frondosas
Praderas y cultivos
Labor intensa
Matorral
(%)
40
20
25
7.5
7.5
α
0.12
0.18
0.24
0.2
0.16
SUMA
TOTAL
0.048
0.036
0.06
0.015
0.012
0.173
En la Tabla 3.11 se estima la radiación emitida a partir de la presión de vapor y el
número de horas reales de insolación.
En la Tabla 3.12 se calcula la radiación incidente a partir de las horas de insolación y en
la Tabla 3.13 la radiación neta teniendo en cuenta el calor latente de vaporización y el
albedo.
Por último ,Ea se calcula en la Tabla 3.14 y en la Tabla 3.15 el valor de la ETP.
17
Problemas de Hidrología
Tabla 3.11. Radiación emitida.
MES
Octubre
Noviembre
Diciembre
Enero
Febrero
Marzo
Abril
Mayo
Junio
Julio
Agosto
Septiembre
T (ºC)
14.9
14.2
10
9.5
7.9
11.2
11.1
12.4
16.9
18.9
19.2
18.3
ea
12.72
12.16
9.2
8.9
7.96
9.96
9.88
10.82
14.42
16.4
16.7
15.8
ε
77
82
75
73
80
76
74
78
71
81
80
76
ed
9.79
9.97
6.9
6.49
6.36
7.56
7.31
8.43
10.23
13.28
13.36
12
n/N
0.50
0.28
0.32
0.42
0.25
0.36
0.29
0.34
0.46
0.30
0.33
0.50
Re
122.24
73.47
108.16
117.68
78.7
100.67
86.99
93.55
114.43
71.56
76.76
113.52
Tabla 3.12. Radiación incidente.
MES
Octubre
Noviembre
Diciembre
Enero
Febrero
Marzo
Abril
Mayo
Junio
Julio
Agosto
Septiembre
T (ºC)
14.9
14.2
10
9.5
7.9
11.2
11.1
12.4
16.9
18.9
19.2
18.3
Ra
492.44
341.82
275.48
317.14
450.12
635.38
809.9
937.78
984.34
951.4
838.86
675.68
n/N
0.50
0.28
0.32
0.42
0.25
0.36
0.29
0.34
0.46
0.30
0.33
0.50
Ri
224.06
114.16
98.07
130.34
142.91
240.17
274.96
344.16
426.21
328.23
303.24
307.43
Comparando la Tabla 3.11 con la Tabla 3.12 se puede comprobar que los meses de
Enero y Diciembre la radiación incidente multiplicada por (1-α) es inferior a la reflejada
por lo que la radiación neta ha de ser nula puesto que no se puede reflejar radiación si
no hay radiación incidente; es decir, se refleja aquella radiación que incide.
Por ello, en la Tabla 3.13 los valores de la radiación neta en dichos meses es nula,
puesto que
onda corta
onda l arg a
R N = R i − R reflejada − R reflejada
18
≤0
Problemas de Hidrología
Tabla 3.13. Radiación neta
MES
Octubre
Noviembre
Diciembre
Enero
Febrero
Marzo
Abril
Mayo
Junio
Julio
Agosto
Septiembre
T
14.9
14.2
10
9.5
7.9
11.2
11.1
12.4
16.9
18.9
19.2
18.3
c1
58.8
58.8
59
59.05
59.1
59
59
58.9
58.7
58.6
58.58
58.6
Ri
224.06
114.16
98.07
130.34
142.91
240.17
274.96
344.16
426.21
328.23
303.24
307.43
α
0.173
0.173
0.173
0.173
0.173
0.173
0.173
0.173
0.173
0.173
0.173
0.173
Ri(1-α)
185.3
94.41
81.1
107.79
118.18
198.62
227.39
284.62
352.47
271.44
250.78
254.24
Re
122.24
73.47
108.16
117.68
78.7
100.67
86.99
93.55
114.43
71.56
76.76
113.52
RN
63.05
20.9
0
0
39.48
97.95
140.4
191.07
238.04
199.8
174.01
140.7
Rn
1.07
0.35
0
0
0.66
1.66
2.37
3.24
4.05
3.41
2.97
2.4
Tabla 3.14. Cálculo de Ea
MES
Octubre
Noviembre
Diciembre
Enero
Febrero
Marzo
Abril
Mayo
Junio
Julio
Agosto
Septiembre
T (ºC)
14.9
14.2
10
9.5
7.9
11.2
11.1
12.4
16.9
18.9
19.2
18.3
ea
12.72
12.16
9.2
8.9
7.96
9.96
9.88
10.82
14.42
16.4
16.7
15.8
ed
9.79
9.97
6.9
6.49
6.36
7.56
7.31
8.43
10.23
13.28
13.36
12
V2
165
199
259
218
222
194
277
257
218
189
177
190
Ea
1.57
1.33
1.69
1.56
1.04
1.43
2
1.75
2.72
1.82
1.87
2.23
Comparando los resultados obtenidos con los distintos métodos, el método que tiene en
cuenta más parámetros hidrometeorológicos es el de Penman, por lo que es el que
proporciona datos más acordes con la realidad, aunque, lógicamente, la aplicación de un
método u otro dependerá de las posibilidades de medición de todos los parámetros
necesarios.
El método de Thornthwaite es el método que necesita menos parámetros para estimar la
ETP y el de Penman el que más parámetros precisa.
19
Problemas de Hidrología
Tabla 3.15. Cálculo de la ETP (mm/mes).
MES
T (ºC)
14.9
Octubre
Noviembre 14.2
10
Diciembre
9.5
Enero
7.9
Febrero
11.2
Marzo
11.1
Abril
12.4
Mayo
16.9
Junio
18.9
Julio
19.2
Agosto
Septiembre 18.3
20
∆ /γ
1.63
1.56
1.23
1.2
1.09
1.31
1.3
1.41
1.81
2.02
2.04
1.95
Rn
1.07
0.35
0
0
0.66
1.66
2.37
3.24
4.05
3.41
2.97
2.4
Ea
1.57
1.33
1.69
1.56
1.04
1.43
2
1.75
2.72
1.82
1.87
2.23
E
1.26
0.73
0.75
0.70
0.84
1.56
2.20
2.62
3.57
2.88
2.60
2.34
f
0.7
0.6
0.6
0.6
0.6
0.7
0.7
0.8
0.8
0.8
0.8
0.7
d
31
30
31
31
28
31
30
31
30
31
31
30
ETP
27.34
13.19
14.09
13.18
14.14
33.86
46.39
65.01
85.84
71.51
64.68
49.18
Problemas de Hidrología
PROBLEMA 4
Con los datos de precipitaciones que se incluyen en la Tabla 1, se pide
calcular la escorrentía superficial con el método del Número de Curva
para los aguaceros producidos entre el 17 y el 24 de Abril, el 7 y el 8 de
Octubre, el 20 de Octubre y el 3 de Noviembre y el 9 y el 13 de Diciembre
de 1990, sabiendo que los datos han sido tomados en la estación
termopluviométrica de Alvedro (Coruña), y la vegetación de la cuenca
está dividida en tres partes iguales aproximadamente de: cultivos y
praderas (tomar los datos correspondientes a praderas permanentes),
matorrales (sin cultivo) y arbolado (bosque natural normal). Cada parte
tiene un 10% de suelo caracterizado por arenas con poco limo, un 60% de
arenas finas, un 15% de arenas muy finas y un 15% de arcillas. Comparar
los valores de Pn en función de P para los cuatro aguaceros. Comentar los
resultados. Para el aguacero del 17 al 24 de Abril, se pide realizar el
cálculo de la precipitación neta diaria.
Tabla 1. Precipitaciones diarias para distintos aguaceros.
AGUACERO
1
2
3
4
DÍAS
17 abril
18 abril
19 abril
20 abril
21 abril
22 abril
23 abril
24 abril
7 octubre
8 octubre
20 octubre
21 octubre
22 octubre
23 octubre
24 octubre
25 octubre
26 octubre
27 octubre
28 octubre
29 octubre
30 octubre
31 octubre
1 noviembre
2 noviembre
3 noviembre
9 diciembre
10 diciembre
11 diciembre
12 diciembre
13 diciembre
PRECIPITACIÓN (mm)
6.5
4.6
12.9
3.5
7.6
13.9
5.5
3.5
16.6
4.5
13.4
12.2
7.5
16.3
15.6
17.5
15.4
20.5
13.2
16.5
20.4
20.6
16.5
14.2
3.2
2.5
27.6
3
4.5
2.2
21
Problemas de Hidrología
Nota: Para todos los aguaceros se tendrá en cuenta que la lluvia en los
cinco días anteriores ha sido inferior a 25 mm.
En primer lugar se evalúa el valor del Número de curva teniendo en cuenta las Tablas
4.1 y 4.2.
Tabla 4.1. Valores de N (no corregidos).
Uso de la tierra y
cobertura
Tratamiento
del suelo
Sin cultivo
Cultivos en surco
Surcos rectos
Surcos rectos
Surcos rectos
Contorneo
Contorneo
Terrazas
Terrazas
Cereales
Surcos rectos
Surcos rectos
Contorneo
Contorneo
Terrazas
Terrazas
Leguminosas o praderas Surcos rectos
con rotación
Surcos rectos
Contorneo
Contorneo
Terrazas
Terrazas
Pastizales
Contorneo
Contorneo
Pradera permanente
Bosques naturales:
Muy ralo
Ralo
Normal
Espeso
Muy espeso
Caminos:
De terracería
Con superficie dura
22
Pendiente
del terreno
->1%
<1%
>1%
<1%
>1%
<1%
>1%
<1%
>1%
<1%
>1%
<1%
>1%
<1%
>1%
<1%
>1%
<1%
>1%
<1%
>1%
<1%
<1%
Tipo de suelo
A
77
72
67
70
65
66
62
65
63
63
61
61
59
66
58
64
55
63
51
68
39
47
6
30
B
86
81
78
79
75
74
71
76
75
74
73
72
70
77
72
75
69
73
67
79
61
67
35
58
C
91
88
85
84
82
80
78
84
83
82
81
79
78
85
81
83
78
80
76
86
74
81
70
71
D
94
91
89
88
86
82
81
88
87
85
84
82
81
89
85
85
83
83
80
89
80
88
79
78
56
46
36
26
15
75
68
60
52
44
86
78
70
62
54
91
84
77
69
61
72
74
82
84
87
90
89
92
Problemas de Hidrología
Tabla 4.2. Tipos de suelos en función de la textura.
Tipo de
suelo
A
B
C
D
Textura del suelo
Arenas con poco limo y arcilla; suelos muy permeables
Arenas finas y limos
Arenas muy finas, limos, suelos con alto contenido en arcilla
Arcillas en grandes cantidades; suelos poco profundos con
subhorizontes de roca sana; suelos muy impermeables
Se trata de calcular una media ponderada de los números de curva asignados a cada tipo
de vegetación y suelo con los porcentajes dados en el enunciado. En la Tabla 4.3 se
muestran los valores seleccionados de la tabla 4.1 para el cálculo de N.
Tabla 4.3. Selección de los Número de Curva.
SUELO
Arenas con poco limo (A) 10%
Arenas finas (B) 60%
Arenas muy finas (C) 15%
Arcillas (D) 15%
VEGETACIÓN
BOSQUE
SIN CULTIVO PRADERA
NATURAL 33%
33%
33%
36
77
30
60
86
58
70
91
71
77
94
78
El valor de N ponderado será:
N = 0.1 ⋅ (36 + 77 + 30) ⋅ 0.33 + 0.6 ⋅ (60 + 86 + 58) ⋅ 0.33 + 0.15 ⋅ (70 + 91 + 71) ⋅ 0.33 +
0.15 ⋅ (77 + 94 + 78) ⋅ 0.33 = 69.61
Debido a que la lluvia los cinco días anteriores a cada aguacero fue inferior a los 25 mm
el valor de N se corrige de acuerdo con la corrección A de la Tabla 4.4
Tabla 4.4. Valores de N corregidos.
N
0
10
20
30
40
50
60
70
80
90
100
N con corrección A
0
4
9
15
22
31
40
51
63
78
100
N con corrección B
0
22
37
50
60
70
78
85
91
96
100
23
Problemas de Hidrología
El valor de N está comprendido entre 60 y 70, por lo que interpolando se obtiene el
valor de la Tabla 4.5.
Tabla 4.5. Valores de N corregidos para cada aguacero.
PRECIPITACIÓN LOS 5
DÍAS ANTERIORES
P5 < 25 mm
P5 < 25 mm
P5 < 25 mm
P5 < 25 mm
AGUACERO
1
2
3
4
CORRECCIÓN
A
A
A
A
N
CORREGIDO
50.57
50.57
50.57
50.57
Una vez calculado N se estima el umbral de escorrentía según:
P0 =
508
508
− 5.08 =
− 5.08 = 4.965 cm = 49.65 mm
N
50.57
que será el mismo para los cuatro aguaceros ya que el N es el mismo. Para calcular el
coeficiente de escorrentía para cada aguacero se estima la precipitación total de cada
uno de ellos.
Tabla 4.6. Precipitación acumulada Aguacero 1.
AGUACERO
1
FECHA
17 ABRIL
18 ABRIL
19 ABRIL
20 ABRIL
21 ABRIL
22 ABRIL
23 ABRIL
24 ABRIL
P (mm)
6.5
4.6
12.9
3.5
7.6
13.9
5.5
3.5
P ACUMULADO (mm)
6.5
11.1
24
27.5
35.1
49
54.5
58
Tabla 4.7. Precipitación acumulada Aguacero 2.
AGUACERO
2
24
FECHA
7 OCTUBRE
8 OCTUBRE
P (mm)
16.6
4.5
P ACUMULADO (mm)
16.6
21.1
Problemas de Hidrología
Tabla 4.8. Precipitación acumulada Aguacero 3.
AGUACERO
3
FECHA
20 OCTUBRE
21 OCTUBRE
22 OCTUBRE
23 OCTUBRE
24 OCTUBRE
25 OCTUBRE
26 OCTUBRE
27 OCTUBRE
28 OCTUBRE
29 OCTUBRE
30 OCTUBRE
31 OCTUBRE
1 NOVIEMBRE
2 NOVIEMBRE
3 NOVIEMBRE
P (mm)
13.4
12.2
7.5
16.3
15.6
17.5
15.4
20.5
13.2
16.5
20.4
20.6
16.5
14.2
3.2
P ACUMULADO (mm)
13.4
25.6
33.1
49.4
65
82.5
97.9
118.4
131.6
148.1
168.5
189.1
205.6
219.8
223
Tabla 4.9. Precipitación acumulada Aguacero 4.
AGUACERO
4
FECHA
9 DICIEMBRE
10 DICIEMBRE
11 DICIEMBRE
12 DICIEMBRE
13 DICIEMBRE
P (mm)
2.5
27.6
3
4.5
2.2
P ACUMULADO (mm)
2.5
30.1
33.1
37.6
39.8
Para calcular el coeficiente de escorrentía se aplican las siguientes fórmulas:
Pn =
(P − P0 )2
P + 4P0
C=
Pn
P
En la Tabla 4.10 se muestran los cálculos realizados. En aquellos aguaceros cuyo valor
total de precipitación es inferior al umbral de escorrentía el coeficiente es nulo ya que
no se ha producido la suficiente lluvia para alcanzar el valor a partir del cual se
comienza a generar la escorrentía superficial.
25
Problemas de Hidrología
Tabla 4.10. Coeficientes de escorrentía para cada aguacero
AGUACERO
1
2
3
4
N
50.57
50.57
50.57
50.57
P0 (mm)
49.65
49.65
49.65
49.65
P (mm)
58
21.1
223
39.8
Pn (mm)
0.27
71.26
-
C
0.004
0.32
-
Para el primer aguacero, si se quiere calcular el coeficiente de escorrentía diario, se
aplicará la misma metodología. En la Tabla 4.11 se muestran los resultados diarios del
coeficiente de escorrentía. Se puede apreciar que hasta que la lluvia acumulada no
supera el umbral de escorrentía no se produce ésta, lo cual ocurre a partir del 23 de
Abril.
Tabla 4.11. Coeficientes de escorrentía para cada aguacero
FECHA
17 ABRIL
18 ABRIL
19 ABRIL
20 ABRIL
21 ABRIL
22 ABRIL
23 ABRIL
24 ABRIL
26
P0 (mm)
49.65
49.65
49.65
49.65
49.65
49.65
49.65
49.65
P (mm)
6.5
11.1
24
27.5
35.1
49
54.5
58
Pn (mm)
0.093
0.271
C
0.0017
0.0046
Problemas de Hidrología
PROBLEMA 5
Un aguacero de 10 cm de lluvia ha producido una Escorrentía Superficial
de 5.8 cm, medida al aforar el río al que vierte la cuenca. Se conoce el
hidrograma de la lluvia, se pide estimar el índice de infiltración φ sin tener
en cuenta la Interceptación, la Detención Superficial y la
Evapotranspiración.
Tabla 1. Precipitación en cada hora
Tiempo (h)
Precipitación en cada
hora (cm)
1
2
3
4
5
6
7
8
0.4
0.9
1.5
2.3
1.8
1.6
1.0
0.5
Al no existir Retención Superficial ni Evapotranspiración todo aquello que no se infiltra
escurre superficialmente. En esta caso sabiendo que la precipitación total es 10 cm (0.4
+ 0.9 + 1.5 + 2.3 + 1.8 + 1.6 + 1.0 + 0.5 = 10 cm) y la escorrentía superficial es 5.8 cm,
la infiltración será:
Inf = 10 − 5.8 = 4.2 cm
Como el aguacero ha durado 8 h, el índice de infiltración es:
φ=
4.2
= 0.525 cm / h
8
Al ser este valor mayor que 0.4 cm/h y 0.5 cm/h, el tiempo de duración de la lluvia
eficaz es, en realidad, 6 horas y sustrayendo ambas cantidades de la infiltración total, se
obtiene:
Inf = 10 − 5.8 − 0.4 − 0.5 = 3.3 cm
y el índice o tasa de infiltración será:
φ=
3.3
= 0.55 cm / h
6
que sigue siendo mayor que 0.4 cm/h y 0.5 cm/h.
A partir de estos datos se puede construir la evolución del aguacero y de la escorrentía
superficial como sigue (Tabla 5.1). En dicha tabla los valores de la escorrentía se han
obtenido restando a la precipitación en cada tiempo el valor de 0.55:
0.9 – 0.55 = 0.35 cm, por ejemplo.
27
Problemas de Hidrología
Tabla 5.1. Precipitación y escorrentía superficial en cada hora
Tiempo (h)
Precipitación en cada hora
(cm)
Escorrentía sup. (cm)
1
2
3
4
5
6
7
8
0.4
0.9
1.5
2.3
1.8
1.6
1.0
0.5
0.
0.35
0.95
1.75
1.25
1.05
0.45
0.
La escorrentía superficial será:
0.35 + 0.95 + 1.75 + 1.25 + 1.05 + 0.45 = 5.8 cm
valor que coincide con el dado en el enunciado. En consecuencia, el valor estimado del
índice de infiltración es correcto. En la Figura 5.1 se muestra la evolución temporal del
aguacero y del índice de infiltración.
2.5
prec (cm) y esc (cm)
2.0
1.5
escorrentía
superficial
1.0
0.55 cm/h
0.5
0.0
0
1
2
3
4
5
6
7
8
9
Tiempo (h)
Figura 5.1. Evolución de la Precipitación y Escorrentía Superficial.
28
Problemas de Hidrología
PROBLEMA 6
Deducir la expresión del tiempo de anegamiento Ta, del volumen de
escorrentía superficial VE y del volumen de infiltración, VI para un
aguacero de duración D e intensidad I a partir de la curva de capacidad de
infiltración exponencial de Horton
CI = CI ∞ + (CI 0 − CI ∞ ) e - Kt
Calcular los valores de Ta, VE y VI para
a) Un aguacero nº 1 de intensidad 10 mm/h y duración 20 horas
b) Un aguacero nº 2 de intensidad 50 mm/h y duración 12 horas
c) Un aguacero nº 3 de intensidad 30 mm/h y duración 6 horas
NOTA: Se adoptarán los valores de CI0 = 100 mm/h; CI∝ = 10 mm/h y K =
0.1 horas-1.
Se pueden dar tres situaciones:
a) I < CI∝ para cualquier duración.
En este caso todo lo precipitado se infiltra y no existe escorrentía superficial ni
tiempo de anegamiento. El volumen de agua infiltrada será:
VI = I ⋅ D
b) I > CI∝ pero D < Ta.
En este caso el aguacero dura menos que el tiempo a partir del cual se genera
escorrentía superficial por lo que tampoco se produce ésta. El volumen infiltrado
es:
VI = I ⋅ D
c) I > CI∝ pero D > Ta.
En este último caso si se produce la escorrentía superficial. El tiempo de
anegamiento vendrá dado a partir de despejar Ta en la siguiente expresión:
I = CI = CI ∞ + (CI 0 − CI ∞ ) e
- KTa
obteniéndose,
29
Problemas de Hidrología
Ta =
 CI − CI ∞
1
⋅ ln 0
K  I − CI ∞



El volumen infiltrado se obtiene integrando la expresión de la capacidad de
infiltración entre el inicio del aguacero y el tiempo D:
VI = ∫ I ⋅ dt + ∫ [CI ∞ + (CI 0 − CI ∞ ) ⋅ exp(− K ⋅ t )] ⋅ dt
Ta
D
0
Ta
Integrando, se obtiene
VI = I ⋅ Ta + CI ∞ ⋅ (D − Ta ) −
(CI 0 − CI ∞ )
K
⋅ [exp(− K ⋅ D ) − exp(− K ⋅ Ta )]
La escorrentía generada será la diferencia del agua caída entre el tiempo Ta y D
y lo infiltrado en dicho intervalo:
VE = ∫ I ⋅ dt − ∫ [CI ∞ + (CI 0 − CI ∞ ) ⋅ exp(− K ⋅ t )] ⋅ dt
D
D
Ta
Ta
Integrando, se obtiene
(CI 0 − CI ∞ )


VE = I ⋅ (D − Ta ) − CI ∞ ⋅ (D − Ta ) −
⋅ [exp(− K ⋅ D ) − exp(− K ⋅ Ta )]
K


Para los distintos valores del enunciado se obtienen los siguientes resultados:
a) Un aguacero nº 1 de intensidad 10 mm/h y duración 20 horas.
En este caso I = CI∝, por lo que no se produce escorrentía superficial. El
volumen infiltrado valdrá:
VI = I ⋅ D = 10 ⋅ 20 = 200 mm
b) Un aguacero nº 2 de intensidad 50 mm/h y duración 12 horas
En este caso I > CI∝. El tiempo de anegamiento calculado aplicando la expresión
anterior es:
Ta =
 CI − CI ∞
1
⋅ ln 0
K  I − CI ∞
 1
 100 − 10 
 =
⋅ ln
 = 8 .1 h
 0.1  50 − 10 
Al ser D > Ta, se producirá escorrentía superficial. El valor del volumen
infiltrado y el volumen de escorrentía es:
VI = 50 ⋅ 8.1 + 10 ⋅ (12 − 8.1) −
30
(100 − 10) ⋅ [exp(− 0.1 ⋅ 12) − exp(− 0.1 ⋅ 8.1)]
0.1
Problemas de Hidrología
VI = 573.29 mm
(100 − 10) ⋅ [exp(− 0.1 ⋅ 12) − exp(− 0.1 ⋅ 8.1)]

VE = 50 ⋅ (12 − 8.1) − 10 ⋅ (12 − 8.1) −

0.1

VE = 26.52 mm
c) Un aguacero nº 3 de intensidad 30 mm/h y duración 6 horas
En este último caso I > CI∝. El tiempo de anegamiento calculado aplicando la
expresión anterior es:
Ta =
 CI − CI ∞
1
⋅ ln 0
K  I − CI ∞
 1
 100 − 10 
 =
⋅ ln
 = 15 h
 0.1  30 − 10 
Al ser D < Ta, no se producirá escorrentía superficial. El valor del volumen
infiltrado es
VI = I ⋅ D = 30 ⋅ 6 = 180 mm
En la Figura 6.1 se representan los tres casos y la curva de capacidad de
infiltración.
Cap. Infil. Int. (mm/h)
100
Capacidad de infiltración
Aguacero 1
Aguacero 2
Aguacero 3
80
60
VE
40
20
0
0
5
Ta
10
15
20
Tiempo (h)
Figura 6.1. Evolución temporal de la Capacidad de infiltración e Intensidad de
precipitación.
31
Problemas de Hidrología
PROBLEMA 7
Calcular el balance hidrológico en el año hidrológico 1982/1983 con los
datos dados a continuación tomando la ETP calculada mediante el
método de Turc en el problema 3. La Intercepción se calculará a partir de
la siguiente fórmula:
INT = 0.1*P
La reserva de agua es 100 mm. Realizar otros dos balances hidrológicos
con 50 mm y 150 mm de reserva de agua.
Tabla 1. Precipitación total mensual (mm)
OCT. NOV. DIC. ENE. FEB MAR ABR. MAY JUN. JUL. AGO. SEP.
46. 85.4 183. 45. 107. 63. 182. 125. 22.
60.
57. 35.5
Para calcular el balance hidrológico con los distintos valores de la reserva de agua
utilizable en el suelo se pueden dar dos situaciones:
1) Que la reserva de agua inicial sea nula (suelo seco)
2) Que la reserva de agua inicial sea la máxima (máxima agua retenida)
A partir de estas dos situaciones los balances hidrológicos variarán fundamentalmente al
principio. En las tablas que a continuación se presentan se han tenido en cuenta ambas
situaciones iniciales para cada uno de los valores de la RAU (reserva de agua
utilizable).
En la Tabla 7.1 se muestra el balance hidrológico en el suelo para un valor de RAU de
50 mm con el suelo inicialmente seco. Para calcular el balance hidrológico se sustrae a
la precipitación el valor de la interceptación, siendo ese valor el que alcanza el suelo.
A continuación se detrae el valor de la ETP (valores obtenidos en el problema 3). Para
el caso del mes de octubre se puede apreciar que el valor neto es negativo (-16.66 mm),
lo que implica que, al no existir más agua (ni en el suelo ni precipitada) hay un déficit,
por lo que el valor de la ETR (Evapotranspiración Real) no coincide con la ETP,
calculándose su valor como:
ETR = ETP- Déficit = 58.06 – 16.66 = 41.4 mm
En el siguiente mes, Noviembre, el balance neto de la lluvia (detrayendo la
interceptación y evapotranspiración potencial) es positivo (43.63 mm) produciéndose un
superávit que va a llenar los poros del suelo sin alcanzar el máximo de la RAU (50
mm).
32
Problemas de Hidrología
Tabla 7.1. RAU = 50 mm. Inicialmente las reservas son nulas.
P
INT
P-INT
ETP
P-INTETP
RAU
EXC
DEF
ETR
OCT.
46
4.6
41.4
58.06
NOV.
85.4
8.54
76.86
33.23
DIC.
183
18.3
164.7
24.67
ENE.
45
4.5
40.5
29.41
FEB.
107
10.7
96.3
27.7
MAR.
63
6.3
56.7
52.35
ABR.
182
18.2
163.8
58.07
MAY.
125
12.5
112.5
75.39
JUN.
22
2.2
19.8
107.63
JUL.
60
6
54
88.8
AGO.
57
5.7
51.3
83.67
SEP.
35.5
3.55
31.95
83.76
TOT.
1010.9
101.09
909.81
722.81
-16.66
43.63
140.03
11.09
68.6
4.35
105.73
37.11
-87.83
-34.8
-32.37
-51.81
0
0
16.66
41.4
43.63
0
0
33.23
50
133.66
0
24.67
50
11.09
0
29.41
50
68.6
0
27.7
50
4.35
0
52.35
50
105.73
0
58.07
50
37.11
0
75.39
0
0
37.83
69.8
0
0
34.8
54
0
0
32.37
51.3
0
0
51.81
31.95
360.54
173.47
549.27
TOT.
1010.9
101.09
909.81
722.81
Tabla 7.2. RAU = 50 mm. Inicialmente RAU = 50 mm.
P
INT
P-INT
ETP
P-INTETP
RAU
EXC
DEF
ETR
OCT.
46
4.6
41.4
58.06
NOV.
85.4
8.54
76.86
33.23
DIC.
183
18.3
164.7
24.67
ENE.
45
4.5
40.5
29.41
FEB.
107
10.7
96.3
27.7
MAR.
63
6.3
56.7
52.35
ABR.
182
18.2
163.8
58.07
MAY.
125
12.5
112.5
75.39
JUN.
22
2.2
19.8
107.63
JUL.
60
6
54
88.8
AGO.
57
5.7
51.3
83.67
SEP.
35.5
3.55
31.95
83.76
-16.66
43.63
140.03
11.09
68.6
4.35
105.73
37.11
-87.83
-34.8
-32.37
-51.81
33.34
0
0
58.06
50
26.97
0
33.23
50
140.03
0
24.67
50
11.09
0
29.41
50
68.6
0
27.7
50
4.35
0
52.35
50
105.73
0
58.07
50
37.11
0
75.39
0
0
37.83
69.8
0
0
34.8
54
0
0
32.37
51.3
0
0
51.81
31.95
393.98
156.81
565.93
33
Problemas de Hidrología
En el mes de Diciembre el superávit producido (140.03 mm) se distribuye en completar
la capacidad máxima de retención del suelo (50 – 43.63 = 6.37 mm) y el sobrante
(140.03 – 6.37 = 133.66 mm), que es el excedente, será la escorrentía (hipodérmica,
superficial y subterránea). Habrá parte que drene (agua gravitacional) a través de la
porosidad drenable para, posteriormente constituir escorrentía hipodérmica y
subterránea. El resto escurrirá superficialmente.
Los siguientes meses (enero, febrero, marzo, abril y mayo) se sigue produciendo
superávit, pero como el suelo no puede retener más agua, dicho superávit alimenta
directamente el flujo de escorrentía (superficial, hipodérmica y subterránea). En los
meses con superávit la ETR coincide con la ETP.
En el mes de junio se produce déficit, en lugar de superávit se vuelve a producir un
balance negativo (87.83 mm). Ahora bien como, el suelo tiene retenida una cantidad de
agua igual a 50 mm, que es agua evapotranspirable, dicho balance mengua en 50 mm
quedando 87.83 – 50 = 37.83 mm que es el déficit producido. En consecuencia, la ETR
no coincide con la ETP, valiendo
ETR = ETP – Déficit = 107.63 – 37.83 = 69.8 mm
vaciándose el suelo quedando la RAU con valor nulo. A partir de ese momento, los
balances negativos proporcionan el valor del déficit que figura en las distintas casilla de
la Tabla en los meses de Julio, Agosto y Septiembre.
Para el caso de que inicialmente el suelo tenga agua en condiciones de máxima
retención (mes de Octubre) el valor del balance es positivo con un superávit de 50 –
16.66 = 33.34 mm, coincidiendo la ETR con la ETP. El mes siguiente el superávit
producido (43.63 mm) sirven para rellenar de nuevo hasta los 50 mm la RAU (50 –
33.34 = 16.66) y el resto ( 44.63 – 16.66 = 26.97 mm) para generar escorrentía
(excedente). A partir del mes de diciembre el cuadro es similar al presentado en la Tabla
7.1.
Para el caso de RAU = 100 mm y RAU = 150 mm se procedería de igual manera. En las
Tablas 7.3, 7.4, 7.5 y 7.6 se muestran los resultados de los distintos balances
hidrológicos.
Hay que hacer constar que los valores totales proporcionados en las últimas columnas
son las sumas totales de la precipitación, interceptación, ETP, ETR, excedente de los
doce meses del año hidrológico. Si se observa el valor de la ETR para los distintos casos
de RAU con valores de 50, 100 y 150 mm, respectivamente, y con las mismas
condiciones iniciales, se puede comprobar que aquella aumenta la misma cantidad que
el aumento en el valor en la RAU. Así, por ejemplo, la ETR total para una RAU de 50,
100 y 150 mm con condiciones inicialmente secas, resultan 549.27 (Tabla 7.1), 599.27
(Tabla 7.3) y 649.27 mm (Tabla 7.5), respectivamente, que coincide con el aumento de
la RAU (50 y 100 mm, respectivamente). Por el contrario, el déficit va disminuyendo en
50 mm cada vez que se aumenta la RAU en dicha cantidad: 173.47 (Tabla 7.1), 123.47
(Tabla 7.3) y 73.47 mm (Tabla 7.5), respectivamente; y 156.81 (Tabla 7.2), 106.81
(Tabla 7.4) y 56.81 mm (Tabla 7.6), respectivamente.
34
Problemas de Hidrología
Tabla 7.3. RAU = 100 mm. Inicialmente las reservas son nulas.
P
INT
P-INT
ETP
P-INTETP
RAU
EXC
DEF
ETR
OCT.
46
4.6
41.4
58.06
NOV.
85.4
8.54
76.86
33.23
DIC.
183
18.3
164.7
24.67
ENE.
45
4.5
40.5
29.41
FEB.
107
10.7
96.3
27.7
MAR.
63
6.3
56.7
52.35
ABR.
182
18.2
163.8
58.07
MAY.
125
12.5
112.5
75.39
JUN.
22
2.2
19.8
107.63
JUL.
60
6
54
88.8
AGO.
57
5.7
51.3
83.67
SEP.
35.5
3.55
31.95
83.76
TOT.
1010.9
101.09
909.81
722.81
-16.66
43.63
140.03
11.09
68.6
4.35
105.73
37.11
-87.83
-34.8
-32.37
-51.81
0
0
16.66
41.4
43.63
0
0
33.23
100
83.66
0
24.67
100
11.09
0
29.41
100
68.6
0
27.7
100
4.35
0
52.35
100
105.73
0
58.07
100
37.11
0
75.39
12.17
0
0
107.63
0
0
22.63
66.17
0
0
32.37
51.3
0
0
51.81
31.95
310.54
123.47
599.27
TOT.
1010.9
101.09
909.81
722.81
Tabla 7.4. RAU = 100 mm. Inicialmente RAU = 100 mm.
P
INT
P-INT
ETP
P-INTETP
RAU
EXC
DEF
ETR
OCT.
46
4.6
41.4
58.06
NOV.
85.4
8.54
76.86
33.23
DIC.
183
18.3
164.7
24.67
ENE.
45
4.5
40.5
29.41
FEB.
107
10.7
96.3
27.7
MAR.
63
6.3
56.7
52.35
ABR.
182
18.2
163.8
58.07
MAY.
125
12.5
112.5
75.39
JUN.
22
2.2
19.8
107.63
JUL.
60
6
54
88.8
AGO.
57
5.7
51.3
83.67
SEP.
35.5
3.55
31.95
83.76
-16.66
43.63
140.03
11.09
68.6
4.35
105.73
37.11
-87.83
-34.8
-32.37
-51.81
83.34
0
0
58.06
100
26.97
0
33.23
100
140.03
0
24.67
100
11.09
0
29.41
100
68.6
0
27.7
100
4.35
0
52.35
100
105.73
0
58.07
100
37.11
0
75.39
12.17
0
0
107.63
0
0
22.63
66.17
0
0
32.37
51.3
0
0
51.81
31.95
393.88
106.81
615.93
35
Problemas de Hidrología
Tabla 7.5. RAU = 150 mm. Inicialmente las reservas son nulas.
P
INT
P-INT
ETP
P-INTETP
RAU
EXC
DEF
ETR
OCT.
46
4.6
41.4
58.06
NOV.
85.4
8.54
76.86
33.23
DIC.
183
18.3
164.7
24.67
ENE.
45
4.5
40.5
29.41
FEB.
107
10.7
96.3
27.7
MAR.
63
6.3
56.7
52.35
ABR.
182
18.2
163.8
58.07
MAY.
125
12.5
112.5
75.39
JUN.
22
2.2
19.8
107.63
JUL.
60
6
54
88.8
AGO.
57
5.7
51.3
83.67
SEP.
35.5
3.55
31.95
83.76
TOT.
1010.9
101.09
909.81
722.81
-16.66
43.63
140.03
11.09
68.6
4.35
105.73
37.11
-87.83
-34.8
-32.37
-51.81
0
0
16.66
41.4
43.63
0
0
33.23
150
33.66
0
24.67
150
11.09
0
29.41
150
68.6
0
27.7
150
4.35
0
52.35
150
105.73
0
58.07
150
37.11
0
75.39
62.17
0
0
107.63
27.37
0
0
88.8
0
0
5
78.67
0
0
51.81
31.95
260.54
73.47
649.27
TOT.
1010.9
101.09
909.81
722.81
Tabla 7.6. RAU = 150 mm. Inicialmente RAU = 150 mm.
P
INT
P-INT
ETP
P-INTETP
RAU
EXC
DEF
ETR
36
OCT.
46
4.6
41.4
58.06
NOV.
85.4
8.54
76.86
33.23
DIC.
183
18.3
164.7
24.67
ENE.
45
4.5
40.5
29.41
FEB.
107
10.7
96.3
27.7
MAR.
63
6.3
56.7
52.35
ABR.
182
18.2
163.8
58.07
MAY.
125
12.5
112.5
75.39
JUN.
22
2.2
19.8
107.63
JUL.
60
6
54
88.8
AGO.
57
5.7
51.3
83.67
SEP.
35.5
3.55
31.95
83.76
-16.66
43.63
140.03
11.09
68.6
4.35
105.73
37.11
-87.83
-34.8
-32.37
-51.81
133.34
0
0
58.06
150
26.97
0
33.23
150
140.03
0
24.67
150
11.09
0
29.41
150
68.6
0
27.7
150
4.35
0
52.35
150
105.73
0
58.07
150
37.11
0
75.39
62.17
0
0
107.63
27.37
0
0
88.8
0
0
5
78.67
0
0
51.81
31.95
393.98
56.81
665.93
Problemas de Hidrología
HIDROGRAMAS
PROBLEMA 8
Dada una cuenca rectangular de 40 km2 de área y 2 h de tiempo de
concentración, se pide deducir y calcular los hidrogramas para aguaceros
de 10 mm/h de intensidad neta de lluvia y duraciones de 1, 2 y 4 horas
A = 40 Km2. ; TC = 2 h. ; In = 10 mm/h
Q = In A = 10 mm/h * 40 km2
Q = 4 .105 m3/h. En el punto de desagüe:
Para ta = 1 h. => 2. 105
Para ta = 2 h. => 4. 105
Para ta > 2 h. => 4. 105
Figura 8.1. Cuenca.
Los hidrogramas correspondientes son:
Q (m3/h)
Q (m3/h)
ta = 4 h
Tc = 2 h
4 10
5
2 10
5
Tc = ta = 2 h
ta = 1 h
1
Q (m3/h)
Tc = 2 h
5
5
4 10
2
3
Tiempo (h)
tb = ta + Tc = 1 + 2 = 3 h;
4 10
2
4
Tiempo (h)
tb = ta + Tc = 2 + 2 = 4 h;
2
4
6
Tiempo (h)
tb = ta + Tc = 4 + 2 = 6 h
Figura 8.2. Hidrogramas.
37
Problemas de Hidrología
PROBLEMA 9
Dado el hidrograma unitario sintético de Snyder de 2 h que figura en el
gráfico adjunto, se pide hallar y calcular el hidrograma compuesto cuyo
hietograma neto se muestra en dicha figura.
q (m3/h/cm)
In (mm/h)
15
10
40
5
3
8 Tiempo (h)
2
4
6
Tiempo (h)
Figura 1. Hidrograma y hietograma
El tiempo base del hidrograma unitario es tb = 8 h, por lo que el tiempo de
concentración de la cuenca Tc será:
Tc = t b − t a = 8 − 2 = 6 h
El hidrograma unitario cumple el primer Principio del Hidrograma Unitario:
ta ≤
Tc
3 ó 5
En este caso cumple la condición menos restrictiva:
ta ≤
Tc
3
2≤
6
3
sustituyendo,
Para calcular el hidrograma compuesto habrá que componer los hidrogramas
desplazados 2 horas obtenidos de multiplicar el unitario por la lluvia caída cada 2 horas.
Para las 2 primeras horas, la lluvia caída es: P = I n ⋅ 2 h = 10 ⋅ 2 = 20 mm = 2 cm
Para las dos siguientes: P = I n ⋅ 2 h = 5 ⋅ 2 = 10 mm = 1 cm
38
Problemas de Hidrología
Para las dos últimas: P = I n ⋅ 2 h = 15 ⋅ 2 = 30 mm = 3 cm
Los hidrogramas unitarios multiplicados por la lluvia caída en cada intervalo del
hietograma son:
Hietograma
In
Hidr. Unit. 2 h
Hidr. para 2 cm de lluvia
Hidr. para 1 cm de lluvia
desplazado 2 h
Hidr. Unit. 2 h desplazado
4h
Hidr. para 3 cm de lluvia
desplazado 4 h
140
Tiempo (h)
120
80
3
Q (m /h)
100
60
40
20
0
0
2
4
6
8
10
12
14
Tiempo (h)
Figura 9.1. Hidrogramas producidos por las distintas lluvias.
El hidrograma compuesto suma de los tres anteriores se obtiene de forma sencilla al
tratarse de segmentos rectilíneos. En la siguiente tabla se muestran los valores
numéricos de los tres hidrogramas y del hidrograma compuesto o total.
Tabla 9.1. Composición numérica de hidrogramas.
Hidrograma
Tiempo Hidrograma
producido por desplazado 2 h de
(h)
2 cm de lluvia
1 cm de lluvia
0
1
2
3
4
5
6
7
8
9
10
11
12
0
26.66
53.33
80
64
48
32
16
0
0
13.33
26.66
40
32
24
16
8
0
Hidrograma
desplazado 4 h de
3 cm de lluvia
Hidrograma
total
Q (m3/h)
0
40
80
120
96
72
48
24
0
0
26.66
53.33
93.33
90.66
128
144
160
112
80
48
24
0
39
Problemas de Hidrología
En la figura adjunta se muestra la representación de los tres hidrogramas y el
hidrograma compuesto obtenido correspondiente a los valores que figuran en la tabla
anterior.
In
Hietograma
180
Hidr. 2 cm de lluvia
Hidr. 1 cm de lluvia
desplazado 2 h
Hidr. 3 cm de lluvia
desplazado 4 h
Hidr. compuesto
Tiempo (h)
160
140
3
Q (m /h)
120
100
80
60
40
20
0
0
2
4
6
8
10
Tiempo (h)
Figura 9.2. Hidrograma compuesto.
40
12
14
Problemas de Hidrología
PROBLEMA 10
Dados los datos de la tabla adjunta dibujar el hidrograma correspondiente
y separar las componentes del mismo con los métodos que se conozcan.
El área de la cuenca es 1200 km2.
Tabla 1. Hidrograma
TIEMPO (d)
22/1/01
23/1/01
24/1/01
25/1/01
26/1/01
27/1/01
28/1/01
29/1/01
30/1/01
31/1/01
1/2/01
2/2/01
3/2/01
4/2/01
5/2/01
6/2/01
7/2/01
8/2/01
9/2/01
10/2/01
11/2/01
12/2/01
13/2/01
Q (m3/s)
3.398
3.186
3.163
3.194
3.357
5.803
16.913
43.57
55
42.669
37.103
17.895
9.662
6.438
4.963
3.119
3.033
2.461
2.277
2.273
2.22
2.083
2.025
El hidrograma correspondiente a la Tabla anterior figura en el gráfico adjunto (Figura
10.1).
Para separar las componentes del hidrograma en Escorrentía Superficial, Hipodérmica y
Subterránea se siguen cuatro métodos diferentes. Los tres primeros distinguen
exclusivamente entre Escorrentía Superficial y Subterránea, incluyendo la Escorrentía
Hipodérmica en las anteriores.
a) Método del flujo subterráneo constante. En este caso se supone que existe un
flujo de base constante correspondiente a la Escorrentía Subterránea. Se traza
una recta paralela al eje de abcisas desde el punto en que comienza la curva de
41
Problemas de Hidrología
concentración. La Escorrentía Superficial corresponderá a la superficie existente
entre el hidrograma y dicha recta (Figura 10.2)
Hidrograma
60
50
3
Caudal (m /s)
40
30
20
10
0
25/1/01
29/1/01
2/2/01
6/2/01
--
Tiempo (días)
Figura 10.1. Hidrograma.
Hidrograma
Escorrentía Subterránea
60
50
3
Caudal (m /s)
40
30
20
Escorrentía Superficial
10
0
25/1/01
29/1/01
2/2/01
6/2/01
--
Tiempo (día)
Figura 10.2. Método del flujo subterráneo constante.
42
Problemas de Hidrología
b) Método de Linsley. Se calcula el tiempo transcurrido entre la punta del
hidrograma y el instante en que se acaba la Escorrentía Superficial:
N = 0.827 ⋅ A 0.2 = 0.827 ⋅ 1200 0.2 = 3.4 dias
N días
60
50
Hidrograma
Método de Linsley
3
Caudal (m /s)
40
30
Escorrentía Superficial
20
10
prolongación
de la curva
Escorrentía Subterránea
0
25/1/01
29/1/01
2/2/01
6/2/01
--
Tiempo (dia)
Figura 10.3. Método de Linsley.
Se prolonga la curva de crecimiento hasta el punto A, que es el tiempo
correspondiente al caudal punta, y a partir de dicho punto se traza la vertical
desplazada 3.4 días (en la figura no se ha representado dicho punto de corte al no
ser un día entero). El punto de corte de dicha vertical es el tiempo a partir del
cual no existe Escorrentía Superficial (Caudal de 14.6018 m3/s). Los valores
entre este caudal y el caudal del tiempo punta 3.317 m3/s están interpolados
(Figura 10.3).
c) Método de aproximación de la curva de agotamiento (Figura 10.4). Se determina
la curva de agotamiento calculando la pendiente de la recta del hidrograma
representado en escala semilogarítmica:
Q = Q 0 ⋅ e − αt
Eligiendo los caudales para los días 6/02/2001 y 13/02/2001 se calcula el
coeficiente de agotamiento α y el caudal Q0:
ln(Q) = ln(Q 0 ) − α ⋅ t
particularizando para ambos días:
43
Problemas de Hidrología
log Q
100
10
Recta de agotamiento
log(Q) = log(Q0)-α.log(e).t
1
26/1/01
31/1/01
5/2/01
10/2/01
--
Tiempo (día)
Figura 10.4. Método de la curva de agotamiento.
Hidrograma
Método de la curva
de agotamiento
60
50
Escorrentía Superficial
3
Caudal (m /s)
40
30
Curva aproximada de
unión del punto A y la
curva de agotamiento
20
Punto de comienzo
de crecida A
10
Punto de inflexión E
Curva de
agotamiento
0
25/1/01
29/1/01
2/2/01
6/2/01
10/2/01
Tiempo (día)
Figura 10.5. Método de la curva de agotamiento. Determinación de escorrentías.
ln(3.119) = ln(Q 0 ) − α ⋅ 16
se obtiene:
44
;
ln(2.025) = ln(Q 0 ) − α ⋅ 23
Problemas de Hidrología
α = 0.0617
;
Q 0 = 8.371
por lo que
Q = 8.371 ⋅ e −0.0617 t
representando la curva de agotamiento hasta el punto de inflexión E y uniendo
este punto con el punto A de crecida se obtiene el Hidrograma de Escorrentía
Subterránea (Figura 10.5).
En la siguiente tabla se muestran los resultados numéricos para cada uno de los
tres métodos anteriores:
Tabla 10.1. Resultados numéricos.
Hidrograma
Met. Hid. Subt. Cte.
Mét. Linsley
Mét. C. Agota.
Tiempo
Q
Hidr. Esc.
Hidr.
Hidr. Hidr. Hidr.
Hidr.
3
(d)
(m /s)
Subt.
Esc Sup. E. Sub. E. Sup. E. Sub. E. Sup.
22/1/01
23/1/01
24/1/01
25/1/01
26/1/01
27/1/01
28/1/01
29/1/01
30/1/01
31/1/01
1/2/01
2/2/01
3/2/01
4/2/01
5/2/01
6/2/01
7/2/01
8/2/01
9/2/01
10/2/01
11/2/01
12/2/01
13/2/01
3.398
3.186
3.163
3.194
3.357
5.803
16.913
43.57
55
42.669
37.103
17.895
9.662
6.438
4.963
3.119
3.033
2.461
2.277
2.273
2.22
2.083
2.025
3.357
3.357
3.357
3.357
3.357
3.357
3.357
3.357
3.357
3.357
3.357
3.357
3.357
3.357
3.357
3.357
≈0
≈0
≈0
≈0
0
2.446
13.556
40.213
51.643
39.312
33.746
14.538
6.305
3.081
1.606
≈0
≈0
≈0
≈0
≈0
≈0
≈0
≈0
3.398
3.186
3.163
3.194
3.357
3.347
3.337
3.327
3.317
6.636
9.955
13.274
9.662
6.438
4.963
3.119
3.033
2.461
0
0
0
0
0
2.456
13.576
40.243
51.683
36.033
27.148
4.621
0
0
0
0
0
0
3.398
3.186
3.163
3.194
3.357
3.447
3.538
3.628
3.719
3.81
3.9
3.991
3.752
3.528
3.317
3.118
2.932
2.756
2.591
2.436
2.290
2.153
2.024
0
0
0
0
0
2.355
13.374
39.941
51.280
38.859
33.202
13.903
5.909
2.909
1.645
≈0
≈0
≈0
≈0
≈0
≈0
≈0
≈0
d) Método de Barnes. Permite obtener las tres escorrentías (Superficial,
Hipodérmica y Subterránea). Se representa el hidrograma original en escala
semilogarítmica en el eje de ordenadas (Figura 10.6). La curva de agotamiento
se convierte en una recta que se prolonga hasta el tiempo punta. Dicho punto se
une con el tiempo de crecida mediante una recta (tiempo correspondiente al
26/01/2001). El hidrograma obtenido es el de Escorrentía Subterránea. La
45
Problemas de Hidrología
diferencia entre el original y éste origina el hidrograma de Escorrentía
Hipodérmica y Superficial.
log Q
100
tiempo punta
10
Hidrograma de Escorrentía
Subterránea
Recta de agotamiento
log(Q) = log(Q0)-α.log(e).t
1
26/1/01
31/1/01
5/2/01
10/2/01
--
Tiempo (día)
Figura 10.6. Método de Barnes. Separación de la componente subterránea.
Hidr. de Escorrentía Superficial
e Hipodérmica
60
50
3
Caudal (m /s)
40
30
20
10
0
25/1/01
29/1/01
2/2/01
6/2/01
10/2/01
Tiempo (día)
Figura 10.7. Método de Barnes. Hidrograma de escorrentías superficial e hipodérmica.
Hay que hacer constar que para restar ambos hidrogramas se restan los valores
originales y no los logaritmos decimales de caudales, tal y como se muestra en la
46
Problemas de Hidrología
tabla siguiente. En dicha tabla los valores de los caudales en el Hidrograma de
Escorrentía Subterránea del 26/01/2001 al 30/01/2001 están interpolados.
Tabla 10.2. Resultados numéricos del hidrograma de Escorrentía Superficial e
Hipodérmica.
TIEMPO (d) Hidr. Original. Q (m3/s) Hidr. Esc. Subt.
22/1/01
23/1/01
24/1/01
25/1/01
26/1/01
27/1/01
28/1/01
29/1/01
30/1/01
31/1/01
1/2/01
2/2/01
3/2/01
4/2/01
5/2/01
6/2/01
7/2/01
8/2/01
9/2/01
10/2/01
11/2/01
12/2/01
13/2/01
3.398
3.186
3.163
3.194
3.357
5.803
16.913
43.57
55
42.669
37.103
17.895
9.662
6.438
4.963
3.119
3.033
2.461
2.277
2.273
2.22
2.083
2.025
3.398
3.186
3.163
3.194
3.357
3.718
4.08
4.441
4.803
4.516
4.245
3.991
3.752
3.528
3.317
3.118
2.932
2.756
2.591
2.436
2.290
2.153
2.024
Diferencia
0
0
0
0
0
2.084
12.832
39.128
50.196
38.152
32.857
13.903
5.509
2.909
1.645
≈0
≈0
≈0
≈0
≈0
≈0
≈0
≈0
Para obtener el de Escorrentía Superficial se procedería de igual forma,
representando el hidrograma en escala semilogarítmica, prolongando la recta de
agotamiento hasta el tiempo punta y uniendo éste mediante una recta con el
tiempo de crecida. Restando ambas figuras se obtendría el Hidrograma de
Escorrentía Superficial.
En este caso la recta de agotamiento tomando los caudales correspondiente al
4/02/2001 y al 5/02/2001 se tiene la expresión siguiente:
ln(2.909) = ln(Q 0 ) − α ⋅ 14
ln(1.645) = ln(Q 0 ) − α ⋅ 15
resolviendo,
α = 0.570
47
Problemas de Hidrología
Q 0 = 8508.11
por lo que
Q = 8508.11 ⋅ e −0.570 t
y representado tanto en escala semilogarítmica como normal se puede apreciar
que el valor en el tiempo punta supera al del propio Hidrograma, lo que significa
que no se puede aplicar el método de Barnes en este caso. No existe la
Escorrentía Hipodérmica y la obtenida en la figura anterior es directamente la
Escorrentía Superficial.
Hidr. de Escorrentía Superficial
e Hipodérmica
Recta de agotamiento
Log Q
100
10
1
25/1/01
29/1/01
2/2/01
6/2/01
Tiempo (dia)
Figura 10.8. Método de Barnes. Separación de las Escorrentías Superficial e
Hipodérmica.
En consecuencia, los valores de los caudales correspondientes al Hidrograma de
Escorrentía Superficial son los que figuran en la cuarta columna de la anterior
Tabla, cuyo encabezamiento se titula “Diferencia” (Tabla 10.2).
En la Figura 10.9 se muestra el hidrograma anterior pero en ejes normales. Se
puede ver que se acentúan las diferencias en el valor máximo.
En la figura siguiente (Figura 10.10) se muestran los hidrogramas de escorrentía
superficial de forma conjunta, obtenidos con los cuatro métodos.
Como se puede apreciar, en este caso, los resultados obtenidos con los diferentes
métodos son similares a excepción de los obtenidos con el método de Linsley, donde el
hidrograma de escorrentía superficial es algo menor.
48
Problemas de Hidrología
Hidr. Escorrentía Superficial
e Hipodérmica
Curva de agotamiento
70
60
Caudal en el tiempo punta menor que
el dado por la curva de agotamiento
3
Caudal (m /s)
50
40
30
20
10
25/1/01
29/1/01
2/2/01
6/2/01
Tiempo (dia)
Figura 10.9. Método de Barnes. Separación de las Escorrentías Superficial e
Hipodérmica en ejes normales.
Hidr. Esc. Sup. Método
de flujo subt. constante
Hidr. Esc. Sup. Método
de Linsley
Hidr. Esc. Sup. Método de
la curva de agotamiento
Hidr. Esc. Sup. Método
de Barnes
60
50
3
Q (m /s)
40
30
20
10
0
24/1/01 27/1/01 30/1/01
2/2/01
5/2/01
8/2/01
Tiempo (día)
Figura 10.10. Comparación de Escorrentías Superficiales obtenidas con los diferentes
métodos.
Los hidrogramas de Escorrentía Subterránea calculadas para cada método se muestran
en la siguiente figura (Figura 10.11).
49
Problemas de Hidrología
Hidr. Esc. Subt. Método
de flujo subt. constante
Hidr. Esc. Subt. Método
de Linsley
Hidr. Esc. Subt. Método de
la curva de agotamiento
Hidr. Esc. Subt. Método
de Barnes
14
13
12
11
3
Q (m /s)
10
9
8
7
6
5
4
3
2
25/1/01 29/1/01
2/2/01
6/2/01
10/2/01
--
Tiempo (día)
Figura 10.11. Comparación de Escorrentías Subterráneas obtenidas con los diferentes
métodos.
50
Problemas de Hidrología
PROBLEMA 11
Dada una cuenca de área 100 km2, y tiempo de concentración 6 h, se pide:
a) Determinar y dibujar el hidrograma unitario sintético de 2 h de
duración según el método de S.C.S. (Hidrograma adimensional).
b) Determinar el hidrograma compuesto de la avenida producida por
un aguacero cuyo hietograma neto es el siguiente:
In (mm/h)
20
15
10
2
4
Tiempo (h)
6
Figura 1. Hietograma.
NOTA: Se determinarán 7 ordenadas como mínimo del hidrograma
unitario.
a) Al ser el tiempo de concentración Tc = 6 h , el hidrograma unitario de ta = 2 h
pedido cumple la condición menos restrictiva del primer Principio del
Hidrograma Unitario:
ta ≤
Tc
3
2≤
6
3
sustituyendo,
Una vez comprobado el cumplimiento de las condiciones del método del
Hidrograma Unitario hay que hallar el valor del caudal y tiempo punta. Para ello
se emplean las siguientes expresiones:
51
Problemas de Hidrología
tp =
ta
+ 0.6 ⋅ Tc
2
Q p = 2.08 ⋅
A
tp
donde Tc es el tiempo de concentración de la cuenca, ta es el tiempo de duración
del aguacero, tp es el tiempo punta en horas, A es el área de la cuenca en km2 y
Qp es el caudal unitario punta en m3/s/cm.
Sustituyendo,
tp =
2
+ 0.6 ⋅ 6 = 4.6 h
2
Q p = 2.08 ⋅
100
= 45.21 m 3 / s / cm
4.6
Multiplicando estos valores por los valores adimensionales del Hidrograma del
S.C.S se obtienen los valores dados en la siguiente tabla.
Tabla 11.1. Hidrograma unitario.
Hidrograma adimensional
t/tp
q/Qp
0
0.2
0.4
0.6
0.8
1
1.2
1.4
1.6
1.8
2
2.2
2.4
2.6
2.8
3
3.5
4
4.5
5
0
0.1
0.31
0.66
0.93
1
0.93
0.78
0.56
0.39
0.28
0.21
0.15
0.11
0.08
0.05
0.02
0.01
0.005
0
Hidrograma Unitario 2h
t (h)
q (m3/s/cm)
0
0.92
1.84
2.76
3.68
4.6
5.52
6.44
7.36
8.28
9.2
10.12
11.04
11.96
12.88
13.8
16.1
18.4
20.7
23
0
4.521
14.017
29.843
42.052
45.217
42.052
35.269
25.321
17.634
12.660
9.495
6.782
4.973
3.617
2.260
0.904
0.452
0.226
0
La representación del hidrograma Unitario se muestra en el gráfico adjunto.
52
Problemas de Hidrología
50
Hidrograma unitario de 2 h
30
3
Caudal (m /s/cm)
40
20
10
0
0
5
10
15
20
25
Tiempo (h)
Figura 11.1. Hidrograma Unitario de 2 h de duración.
b) Inicialmente se comprueba si cumple con el Primer Principio del Hidrograma
Unitario. El tiempo de concentración es 6 h y la duración del aguacero es
también 6 h. En este caso,
ta >
Tc
5
6>
6
5
sustituyendo,
o también la condición menos restrictiva:
ta >
Tc
3
6>
6
3
sustituyendo,
lo que implica que el hidrograma compuesto se calculará a partir de la suma de
los hidrogramas unitarios multiplicados por la precipitación neta cada 2 h.
En este caso la lluvia neta caída cada 2 h es el área del hietograma:
53
Problemas de Hidrología
Las primeras 2 h: 2 h ⋅ 10 mm / h = 20 mm = 2 cm
Las dos siguientes: 2 h ⋅ 20 mm / h = 40 mm = 4 cm
Las dos últimas: 2 h ⋅ 15 mm / h = 30 mm = 3 cm
Por lo tanto, el hidrograma unitario se multiplicará por 2, 4 y 3 cm,
respectivamente, obteniéndose tres hidrogramas desplazados cada 2 h, como
muestra la figura adjunta
Hidrograma Unitario 2 h
Hidrograma para 2 cm de lluvia
Hidrograma para 4 cm de lluvia
desplazado 2 h
Hidrograma para 3 cm de lluvia
desplazado 4 h
200
180
160
120
3
caudal (m /s)
140
100
80
60
40
20
0
0
5
10
15
20
25
30
tiempo (h)
Figura 11.2. Hidrogramas producidos por los distintos volúmenes de caídos.
El hidrograma compuesto es la suma de los tres anteriores tal y como se muestra
en la Figura 11.3.
Para calcular los valores numéricos se han hallado las ordenadas del hidrograma
unitario cada 2 h interpolando a partir de los valores en los tiempos conocidos
(Tabla 11.2).
El hidrograma compuesto calculado numéricamente se halla multiplicando por
2, 4 y 3 cm el hidrograma unitario anterior y sumando los tres hidrogramas
desplazados convenientemente.
En la Tabla 11.3 se muestran los resultados numéricos obtenidos.
54
Problemas de Hidrología
Hietograma
In
350
Tiempo (h)
Hidr. para 2 cm de lluvia
Hidr. para 4 cm de lluvia
desplazado 2 h
Hidr. para 3 cm de lluvia
desplazado 4 h
Hidrograma total
300
3
Caudal (m /s)
250
200
150
100
50
0
0
3
6
9
12
15
18
21
24
27
30
Tiempo (h)
Figura 11.3. Hidrograma compuesto.
Tabla 11.2. Hidrograma unitario Interpolado cada 2 h.
Hidrograma Unitario 2 h
t (h)
q (m3/s/cm)
0
0.92
1.84
2.76
3.68
4.6
5.52
6.44
7.36
8.28
9.2
10.12
11.04
11.96
12.88
13.8
16.1
18.4
20.7
23
0
4.521
14.017
29.843
42.052
45.217
42.052
35.269
25.321
17.634
12.660
9.495
6.782
4.973
3.617
2.260
0.904
0.452
0.226
0
Hidr. Unit. 2h interpolado
t (h)
q (m3/s/cm)
0
2
4
6
8
10
12
14
16
18
20
22
24
0
16.769
43.153
38.513
19.974
9.908
4.9141
2.142
0.963
0.530
0.294
0.098
0
55
Problemas de Hidrología
Tabla 11.3. Resultados numéricos. Hidrograma compuesto.
t (h)
H.U. x 2cm
0
2
4
6
8
10
12
14
16
18
20
22
24
0
33.539
86.306
77.026
39.948
19.816
9.829
4.285
1.926
1.061
0.589
0.196
0
26
28
56
H.U. x 4 cm H.U. x 3 cm
0
67.078
172.612
154.053
79.897
39.633
19.659
8.571
3.853
2.123
1.179
0.393
0
0
50.309
129.459
115.540
59.922
29.725
14.744
6.428
2.889
1.592
0.884
0.294
0
Hidr. Total
0
33.539
153.384
299.947
323.460
215.254
109.386
53.670
25.243
11.343
5.603
2.968
1.277
0.294
0
Problemas de Hidrología
PROBLEMA 12
Dado el hidrograma unitario de un aguacero de cuatro horas de duración,
se pide:
a) Hallar el hidrograma unitario de un aguacero de 2 horas de duración
utilizando el método del Hidrograma en S.
b) A partir del hidrograma unitario de un aguacero de 2 horas de duración
hallar el hidrograma unitario de 12 h.
Tabla 1. Hidrograma unitario de 4 h
Tiempo (h)
q (m3/s/cm)
0
0
4
12
8
75
12
132
16
180
20
210
24
183
Tiempo (h)
q (m3/s/cm)
28
156
32
135
36
124
40
96
44
87
48
66
52
54
Tiempo (h)
q (m3/s/cm)
56
42
60
33
64
24
68
18
72
12
76
6
80
0
a) Para utilizar el método del Hidrograma en S se deben calcular las ordenadas del
hidrograma de intensidad unidad. En este problema se proporcionan las
ordenadas del hidrograma de volumen unidad (m3/s/cm), por lo que el
hidrograma unitario de intensidad unitaria q* se hallará de la siguiente forma:
Si el hietograma correspondiente al hidrograma de volumen unidad de duración
ta es el que se muestra (Figura 12.1), la intensidad correspondiente a ese
volumen unidad será 1/ta. De esta manera:
Vol = 1 cm = t a ⋅
1
ta
Si definimos la intensidad unitaria como 1 mm/h, para definir el hidrograma
unitario (q*) producido por una lluvia de intensidad unitaria (1 mm/h) a partir del
hidrograma unitario (q) de volumen unidad (1 cm) habrá que dividir este último
por la intensidad (1/ta cm/h ó 10/ta mm/h):
q* =
t
q
= q ⋅ a (m 3 / s / mm / h )
(10 t a )
10
En la Tabla 12.1 se calcula el hidrograma unitario producido por una lluvia de
intensidad unidad (1 mm/h) y duración ta = 4 h.
57
Problemas de Hidrología
In (cm/h)
1/ta
1 cm
ta
Tiempo (h)
Figura 12.1. Hietograma.
Tabla 12.1. Transformación de las ordenadas unitarias
Tiempo (h) q (m3/s/cm) 4 h q* (m3/s/mm/h) 4 h
0
0
0
4
12
4.8
8
75
30
12
132
52.8
16
180
72
20
210
84
24
183
73.2
28
156
62.4
32
135
54
36
124
49.6
40
96
38.4
44
87
34.8
48
66
26.4
52
54
21.6
56
42
16.8
60
33
13.2
64
24
9.6
68
18
7.2
72
12
4.8
76
6
2.4
80
0
0
En la figura siguiente se muestran los hidrogramas unitarios de intensidad
unitaria y volumen unitario, respectivamente. También se han representado los
hietogramas correspondientes que originan ambos hidrogramas.
58
Problemas de Hidrología
In
Hietograma
Volumen 1 cm
1/ta
Hietograma
ta Intensidad neta unitaria
Hidrograma unitario de 4 h
(volumen unidad: 1 cm)
Hidrograma unitario de 4 h
(intensidad unidad: 1 mm/h)
210
3
*
3
q (m /s/cm) / q (m /s/mm/h)
1
280
140
70
0
0
20
40
60
80
100
Tiempo (h)
Figura 12.2. Hidrogramas unitarios (volumen unidad e intensidad unidad).
Hay que hacer notar que la duración de la lluvia que originan ambos
hidrogramas es la misma (ta = 4 h), lo único que varía es la intensidad neta que
en un caso es 1 mm/h y en el otro (volumen unidad) es 1/ta.
Una vez calculadas las ordenadas del hidrograma unitario de intensidad 1 mm/h,
se halla el hidrograma en S a partir de sumar infinitos hidrogramas desplazados
ta (4 h) horas producidos por una lluvia indefinida de intensidad unidad.
En la Tabla 12.2 se muestra los resultados numéricos. Para obtener el
hidrograma en S se van hallando los valores acumulados en cada tiempo.
A partir de la hora 76 el valor ya es constante (658). Para hallar el hidrograma
unitario de duración 2 h (cuarta columna de la siguiente tabla) se desplaza el
hidrograma en S 2 horas (tercera columna) y se resta del hidrograma en S
original (segunda columna). Para hacerlo numéricamente hallaremos las
ordenadas cada 2 h interpolando de la figura del Hidrograma en S. Estos
resultados se muestran en la Tabla 12.3.
Para obtener el hidrograma unitario (de volumen unidad: 1 cm) se tendrá que
hacer la conversión inversa:
q = q* ⋅
10
(m 3 / s / cm)
t *a
donde t *a = 2 h .
59
Problemas de Hidrología
Tabla 12.2. Obtención del Hidrograma en S
Tiempo
(h)
q* (m3/s/mm/h)
4h
Valor
acum.
Hidrograma
en S
0
4
8
12
16
20
24
28
32
36
40
44
48
52
56
60
64
68
72
76
80
0
4.8
30
52.8
72
84
73.2
62.4
54
49.6
38.4
34.8
26.4
21.6
16.8
13.2
9.6
7.2
4.8
2.4
0
0
0 + 4.8 = 4.8
4.8 + 30 = 34.8
34.8 + 52.8 = 87.6
87.6 + 72 = 159.6
159.6 + 84 = 243.6
243.6 + 73.2 = 316.8
316.8 + 62.4 = 379.2
379.2 + 54 = 433.2
433.2 + 49.6 = 482.8
482.8 + 38.4 = 521.2
521.2 + 34.8 = 556
556 + 26.4 = 582.4
582.4 + 21.6 = 604
604 + 16.8 = 620.8
620.8 + 13.2 = 634
634 + 9.6 = 643.6
643.6 + 7.2 = 650.8
650.8 + 4.8 = 655.6
655.6 + 2.4 = 658
658 + 0 = 658
0
4.8
34.8
87.6
159.6
243.6
316.8
379.2
433.2
482.8
521.2
556
582.4
604
620.8
634
643.6
650.8
655.6
658
658
In (mm/h)
1
700
Hietograma
t
600
Hidrograma en S
400
3
Q (m /s)
500
300
200
100
0
0
20
40
60
Tiempo (h)
Figura 12.3. Hidrograma en S.
60
80
Problemas de Hidrología
Tabla 12.3. Obtención de ordenadas unitarias con el Hidrograma en S.
Tiempo
(h)
0
2
4
6
8
10
12
14
16
18
20
22
24
26
28
30
32
34
36
38
40
42
44
46
48
50
52
54
56
58
60
62
64
66
68
70
72
74
76
78
80
Hidrograma
en S
0
1.6
4.8
16.8
34.8
58.6
87.6
122
159.6
202
243.6
282
316.8
349
379.2
407
433.2
459
482.8
503
521.2
539.5
556
570
582.4
593.8
604
613
620.8
628
634
639.2
643.6
647.5
650.8
653.5
655.6
657.1
658
658
658
Hidrograma en S
desplazado 2 h
0
1.6
4.8
16.8
34.8
58.6
87.6
122
159.6
202
243.6
282
316.8
349
379.2
407
433.2
459
482.8
503
521.2
539.5
556
570
582.4
593.8
604
613
620.8
628
634
639.2
643.6
647.5
650.8
653.5
655.6
657.1
658
658
q* (m3/s/mm/h)
2h
0
1.6
3.2
12
18
23.8
29
34.4
37.6
42.4
41.6
38.4
34.8
32.2
30.2
27.8
26.2
25.8
23.8
20.2
18.2
18.3
16.5
14
12.4
11.4
10.2
9
7.8
7.2
6
5.2
4.4
3.9
3.3
2.7
2.1
1.5
0.9
0
61
Problemas de Hidrología
En la siguiente figura se muestra el hidrograma unitario obtenido de la diferencia
entre el Hidrograma en S desplazado 2 h y el original.
In (mm/h)
700
t
600
400
3
Q (m /s)
500
300
Hidrograma en S
Hidrograma en S desplazado 2 h
Hidrograma unitario 2 h
*
(intensidad unidad) (q )
200
100
0
0
20
40
60
80
Tiempo (h)
Figura 12.4. Hidrograma S desplazado. Obtención del Hidrograma unitario.
En la Tabla 12.4 se muestran los valores numéricos del hidrograma unitario
(volumen unidad) de 2 h (q), después de hacer la conversión descrita
anteriormente.
En las figuras adjuntas (Figura 12.5 y 12.6) se muestran los hidrogramas
unitarios (intensidad neta unidad) de 2 y 4 h, respectivamente, y los hidrogramas
unitarios (volumen unidad) de 2 y 4 h, respectivamente.
Se puede comprobar que los hidrogramas unitarios de volumen de lluvia unidad
de 2 y 4 h se diferencian en el tiempo y caudal punta y el tiempo base. En el
hidrograma de 4 h el tiempo base es 80 h, el tiempo punta es 20 h y el caudal
punta es 210 m3/s/cm. En el hidrograma de 2 h, el tiempo base es 78 h, el tiempo
punta 18 h y el caudal punta 212 m3/s/cm.
Se puede comprobar que el tiempo punta de uno y otro están desplazados por un
tiempo de 2 h, justamente la diferencia de duración de ambos aguaceros.
62
Problemas de Hidrología
Tabla 12.4. Obtención del Hidrograma Unitario (volumen unidad) de 2 h.
Tiempo (h)
0
2
4
6
8
10
12
14
16
18
20
22
24
26
28
30
32
34
36
38
40
42
44
46
48
50
52
54
56
58
60
62
64
66
68
70
72
74
76
78
80
q* (m3/s/mm/h) 2 h
0
1.6
3.2
12
18
23.8
29
34.4
37.6
42.4
41.6
38.4
34.8
32.2
30.2
27.8
26.2
25.8
23.8
20.2
18.2
18.3
16.5
14
12.4
11.4
10.2
9
7.8
7.2
6
5.2
4.4
3.9
3.3
2.7
2.1
1.5
0.9
0
q (m3/s/cm) 2 h
0
8
16
60
90
119
145
172
188
212
208
192
174
161
151
139
131
129
119
101
91
91.5
82.5
70
62
57
51
45
39
36
30
26
22
19.5
16.5
13.5
10.5
7.5
4.5
0
63
Problemas de Hidrología
100
Hidrograma unitario
(intensidad unitaria) 4 h
Hidrograma unitario
(intensidad unitaria) 2 h
60
40
*
3
q (m /s/mm/h)
80
20
0
0
10
20
30
40
50
60
70
80
90
Tiempo (h)
Figura 12.5. Comparación de Hidrogramas Unitarios de intensidad unidad.
250
Hidrograma unitario
(volumen unidad) 4 h
Hidroagrama unitario
(volumen unidad) 2 h
150
3
q (m s/cm)
200
100
50
0
0
10
20
30
40
50
60
70
80
90
Tiempo (h)
.
Figura 12.6. Comparación de Hidrogramas Unitarios de volumen unidad.
b) Para hallar el hidrograma unitario (volumen unidad) de 12 h de duración a partir
del de 2 h, sumaremos 6 hidrogramas unitarios de 2 h (ya que 12 h / 2 h = 6)
desplazados cada 2 h y el hidrograma resultado lo dividiremos por 6 cm.
En la figura siguiente (Figura 12.7) se muestra el procedimiento de cálculo
seguido: Se desplaza el hidrograma unitario de 2 h 6 veces y se suman. En la
parte superior de la figura se ha representado el hietograma correspondiente a
64
Problemas de Hidrología
cada hidrograma unitario de 2 h. En consecuencia, el volumen del hidrograma
total es de 6 cm. Para convertirlo en unitario se dividen las ordenadas por 6.
In (mm/h)
1 cm
1200
Hidr. unit. (vol. 1 cm) 2 h
Hidr. unit. (vol. 1 cm) 2 h
desplazado 2 h
Hidr. unit. (vol. 1 cm) 2 h
desplazado 4 h
Hidr. unit. (vol. 1 cm) 2 h
desplazado 6 h
Hidr. unit. (vol. 1 cm) 2 h
desplazado 8 h
Hidr. unit. (vol. 1 cm) 2 h
desplazado 10 h
Hidr. compuesto
Tiempo (h)
1000
3
Q (m /s)
800
600
400
200
0
0
20
40
60
80
100
Tiempo (h)
Figura 12.7. Hidrograma compuesto.
In (mm/h)
1/12
1 cm
Tiempo (h)
1200
Hidrogram unitario 12 h
(volumen unidad)
Hidrograma compuesto (suma
de los 6 unitarios de 2 h)
1000
600
3
q (m /s/cm)
800
400
200
0
0
20
40
60
80
100
Tiempo (h)
Figura 12.8. Hidrograma unitario de 12 h.
En la Tabla 12.5 se muestra el procedimiento de cálculo. La última columna
representa el hidrograma unitario de 12 h. Se puede comprobar que el tiempo
base de este hidrograma es 88 h. Para el cálculo del tiempo base, calcularemos
65
Problemas de Hidrología
previamente el tiempo de concentración a partir del hidrograma unitario de 2 h ó
del de 4 h.
Tabla 12.5. Obtención de Hidrograma de 12 h.
T (h)
q 2h
0
2
4
6
8
10
12
14
16
18
20
22
24
26
28
30
32
34
36
38
40
42
44
46
48
50
52
54
56
58
60
62
64
66
68
70
72
74
76
78
80
82
84
86
88
0
8
16
60
90
119
145
172
188
212
208
192
174
161
151
139
131
129
119
101
91
91.5
82.5
70
62
57
51
45
39
36
30
26
22
19.5
16.5
13.5
10.5
7.5
4.5
0
66
Hidrogramas unitarios desplazados 2, 4, 6,
8 y 10 h, respectivamente
q2h
q2h
q2h
q2h
q2h
0
8
16
60
90
119
145
172
188
212
208
192
174
161
151
139
131
129
119
101
91
91.5
82.5
70
62
57
51
45
39
36
30
26
22
19.5
16.5
13.5
10.5
7.5
4.5
0
0
8
16
60
90
119
145
172
188
212
208
192
174
161
151
139
131
129
119
101
91
91.5
82.5
70
62
57
51
45
39
36
30
26
22
19.5
16.5
13.5
10.5
7.5
4.5
0
0
8
16
60
90
119
145
172
188
212
208
192
174
161
151
139
131
129
119
101
91
91.5
82.5
70
62
57
51
45
39
36
30
26
22
19.5
16.5
13.5
10.5
7.5
4.5
0
0
8
16
60
90
119
145
172
188
212
208
192
174
161
151
139
131
129
119
101
91
91.5
82.5
70
62
57
51
45
39
36
30
26
22
19.5
16.5
13.5
10.5
7.5
4.5
0
0
8
16
60
90
119
145
172
188
212
208
192
174
161
151
139
131
129
119
101
91
91.5
82.5
70
62
57
51
45
39
36
30
26
22
19.5
16.5
13.5
10.5
7.5
4.5
0
suma
q 12 h
0
8
24
84
174
293
438
602
774
926
1044
1117
1146
1135
1098
1025
948
885
830
770
710
662.5
614
555
498
454
414
367.5
324
290
258
227
198
172.5
150
127.5
108
89.5
72
52.5
36
22.5
12
4.5
0
0
1.33
4
14
29
48.83
73
100.33
129
154.33
174
186.16
191
189.16
183
170.83
158
147.5
138.33
128.33
118.33
110.41
102.33
92.5
83
75.66
69
61.25
54
48.33
43
37.83
33
28.75
25
21.25
18
14.91
12
8.75
6
3.75
2
0.75
0
Problemas de Hidrología
El hidrograma unitario de 4 h tiene un tiempo base de 80 h. La expresión del
tiempo base tb en este caso es:
t b = t a + Tc
donde ta es el tiempo de duración del aguacero (en este caso 4 h) y Tc es el
tiempo de concentración. En consecuencia,
Tc = 80 – 4 = 76 h
Así, el tiempo base del hidrograma unitario de 12 h será:
tb = 76 + 12 = 88 h
67
Problemas de Hidrología
PROBLEMA 13
Deducir un hidrograma unitario a partir del hidrograma neto de caudales
registrado en la tabla adjunta, sabiendo que el tiempo de concentración
es Tc = 6 h y el hietograma neto el registrado en la figura.
Tabla 1. Hidrograma de caudales
T (h)
Q (m3/s)
1
0.25
2
1
3
3.25
4
6.75
5
9.75
6
10
7
6
8
2
9
0
I (mm/h)
10
5
1
2
3
Tiempo (h)
Figura 1. Hietograma
El tiempo base del hidrograma dado es 9 h y el tiempo de concentración es 6 h, lo que
implica que el tiempo de duración del aguacero es
t a = t b − Tc = 9 − 6 = 3 h
que coincide con el tiempo del aguacero cuyo hietograma es el expuesto en el
enunciado.
Veamos, ahora si cumple el primer Principio del Hidrograma Unitario, ya que si lo
cumple, el hidrograma unitario pedido tendrá el mismo tiempo base que el hidrograma
dado y lo único que habrá que hacer es dividir las ordenadas por el volumen de
precipitación caída. En nuestro caso
6
T

Condición más restrictiva: (t a = 3) >  c = = 1.2 
 5 5

6

T
Condición menos restrictiva: (t a = 3) >  c = = 2 

 3 3
68
Problemas de Hidrología
es decir, el tiempo de duración del aguacero es superior a la quinta y tercera parte del
tiempo de concentración, por lo que no cumple el primer Principio del Hidrograma
Unitario. Ello implica que es un hidrograma compuesto obtenido a partir de la
composición de varios hidrogramas unitarios. Elegiremos el hidrograma unitario de
duración 1 h (que es inferior a 1.2) por lo que cumple la condición más restrictiva del
primer Principio, además de que, para ese intervalo de tiempo, el valor de la intensidad
es constante. Se necesitan, en consecuencia 3 hidrogramas unitarios, cuyo tiempo base
es:
t b = t a + Tc = 1 + 6 = 7 h
Si aplicamos el método de composición tendremos:
Q0 = 0
Q1 = q 1 I1 ∆t 1 = q 1 P1
Q 2 = q 1 I 2 ∆t 2 + q 2 I1 ∆t 1 = q 1 P2 + q 2 P1
Q 3 = q 1 I 3 ∆t 3 + q 2 I 2 ∆t 2 + q 3 I1 ∆t 1 = q 1 P3 + q 2 P2 + q 3 P1
Q 4 = q 2 I 3 ∆t 3 + q 3 I 2 ∆t 2 + q 4 I1 ∆t 1 = q 2 P3 + q 3 P2 + q 4 P1
Q 5 = q 3 I 3 ∆t 3 + q 4 I 2 ∆t 2 + q 5 I1 ∆t 1 = q 3 P3 + q 4 P2 + q 5 P1
Q 6 = q 4 I 3 ∆t 3 + q 5 I 2 ∆t 2 + q 6 I1 ∆t 1 = q 4 P3 + q 5 P2 + q 6 P1
Q 7 = q 5 I 3 ∆t 3 + q 6 I 2 ∆t 2 = q 5 P3 + q 6 P2
Q 8 = q 6 I 3 ∆t 3 = q 6 P3
Q9 = 0
donde Q son las ordenadas del hidrograma compuesto (m3/s), Ii es la intensidad neta en
el tiempo i (hora i), Pi es la precipitación neta en el tiempo i y qj es la ordenada del
hidrograma unitario en el tiempo j (hora j) (m3/s/cm). Este sistema se expresa
matricialmente:
 Q1   P1
Q   P
 2  2
Q 3   P3
  
Q 4  =  0
Q 5   0
  
Q 6   0
Q   0
 7 
Q 8   0
0
0
0
0
P1
0
0
0
P2
P1
0
0
P3
P2
P1
0
0
P3
P2
P1
0
0
0
0
P3
0
P2
P3
0
0
0
0
0
0   q 1 
0  q 2 

0  q 3 
⋅ 
0  q 4 

P1  q 5 
 
P2  q 6 

P3 
con Q0 = Q9 = 0. La expresión simplificada:
Q = P⋅q
69
Problemas de Hidrología
donde Q es el vector de caudales, P es la matriz de precipitaciones y q es el vector de
caudales unitarios. Para resolver el sistema premultiplicamos por la matriz traspuesta de
precipitaciones para obtener una matriz cuadrada y poderla invertir. Se obtiene,
t
t
P ⋅Q = P ⋅P⋅q
−1
t
 t 
 P ⋅ P  ⋅ P ⋅ Q = q


Los valores de las precipitaciones netas son:
Para la primera hora, la lluvia caída es: P1 = I1 ⋅ 1 h = 5 ⋅ 1 = 5 mm = 0.5 cm
Para la siguiente: P2 = I 2 ⋅ 1 h = 5 ⋅ 1 = 5 mm = 0.5 cm
Para las dos últimas: P3 = I 3 ⋅ 1 h = 10 ⋅ 1 = 10 mm = 1 cm
Si sustituimos estos valores en el sistema anterior se obtiene
0
0
0
0
0.25 0.5 0
 1  0.5 0.5 0
0
0
0   q 1 
 

3.25  1 0.5 0.5 0
0
0  q 2 

 

1 0.5 0.5 0
0  q 3 
6.75 =  0
⋅ 
9.75  0
0
1 0.5 0.5 0  q 4 

 

0
0
1 0.5 0.5 q 5 
 10   0
 
 6  0
0
0
0
1 0.5 q 6 

 

0
0
0
0
1 
 2   0
Premultiplicando por la traspuesta, se obtiene
0
0
0   q1 
 3.875   1.5 0.75 0.5
 8.875  0.75 1.5 0.75 0.5
0
0  q 2 

 
 14.75   0.5 0.75 1.5 0.75 0.5
0  q 3 

=
⋅ 
0.5 0.75 1.5 0.75 0.5  q 4 
 18.25   0
15.875  0
0
0.5 0.75 1.5 0.75 q 5 

 
  
0
0
0.5 0.75 1.5  q 6 
 10   0
y resolviendo el sistema de 6x6, se llega
q0 = 0.0 m3/s/cm
q1 = 0.5 m3/s/cm
q2 = 1.5 m3/s/cm
q3 = 4.0 m3/s/cm
70
Problemas de Hidrología
q4 = 6.5 m3/s/cm
q5 = 5.0 m3/s/cm
q6 = 2.0 m3/s/cm
q7 = 0.0 m3/s/cm
En la figura adjunta se muestran el hidrograma compuesto y los tres hidrogramas cuya
suma es igual al compuesto. En la siguiente figura se muestra el hidrograma unitario de
1 h de duración. La combinación de este hidrograma multiplicado por la lluvia neta
caída y desplazado 1 y 2 horas da como resultado el hidrograma compuesto.
I
Hidr. producido por 0.5 cm
de lluvia
Hidr. producido por 0.5 cm
de lluvia desplazado 1 h
Hidr. producido por 1 cm
de lluvia desplazado 2 h
Hidr. total
Hietograma
12
Tiempo (h)
10
6
4
2
0
-1
0
1
2
3
4
5
6
7
8
9
10
Tiempo (h)
Figura 13.1. Hidrograma compuesto.
Hidrograma unitario de 1 h
8
7
6
5
3
q (m /s)
3
Q (m /s)
8
4
3
2
1
0
0
1
2
3
4
5
6
7
8
9
Tiempo (h)
Figura 13.2. Hidrograma Unitario de 1 h.
71
Problemas de Hidrología
Hidr. unitario 1 h
Hidr. unitario 1 h desplazado 1 h
Hidr. unitario 1 h desplazado 2 h
9
8
7
q4
3
q (m /s/cm)
6
5
q5
4
q3
3
2
q6
q2
1
q1
0
0
1
2
3
4
5
6
7
8
9
Tiempo (h)
Figura 13.3. Hidrograma Unitarios desplazados.
72
10
Problemas de Hidrología
PROBLEMA 14
Deducir la expresión del hidrograma unitario instantáneo. (hidrograma
correspondiente a un aguacero de duración infinitesimal dt y altura de
lluvia 1 cm). A partir del hidrograma unitario instantáneo, deducir el
hidrograma unitario de duración D.
Si una cuenca recibe una entrada unitaria (1 cm) de lluvia aplicada instantáneamente en
el tiempo t*, la respuesta de dicho impulso unitario está definida por una función u(t-t*)
en un tiempo t posterior, donde t-t* es el tiempo de retardo (ver figura).
In (t), Q(t)
Impulso unitario
*
u(t-t )
Función impulso respuesta
1
t
Tiempo t
*
Figura 14.1. Pulso y respuesta.
Si la intensidad neta de una lluvia ocurrida en t* en un intervalo infinitesimal dt* es I(t*),
la altura de precipitación será I t * ⋅ dt * , cuyo valor será 1 cm; lluvia que entrará en la
cuenca originando un hidrograma de escorrentía directa como respuesta. El valor de la
respuesta se obtendrá integrando:
( )
t
( ) (
)
Q(t ) = ∫ I t * ⋅ u t − t * ⋅ dt *
0
que es la integral de convolución.
La entrada de pulso unitario es una entrada unitaria (1 cm) que ocurre con una duración
D = ∆t. La intensidad de precipitación será 1/∆t para conseguir que la precipitación sea
1 cm.
En consecuencia, la función respuesta será
73
Problemas de Hidrología
Q (t ) =
t
(
)
1
u t − t * ⋅ dt *
∆t ∫0
Si hacemos el cambio de variable l = t – t*, dl = -dt*. Los límites: Para t* = 0, l = t; y
para t* = t, l = 0,
Q (t ) =
t
(
0
)
t
1
1
1
u t − t * ⋅ dt * = − ∫ u (l ) ⋅ dl =
u (l ) ⋅ dl
∫
∆t 0
∆t t
∆t ∫0
In (cm/h)
1/∆t
1 cm
∆t
Tiempo (h)
Figura 14.2. Hietograma.
Si el intervalo no es infinitesimal si no que es discreto de duración ∆t, la respuesta,
aplicando el Principio de Superposición del Hidrograma unitario, será:
Q (t ) =
1 
 u (l ) ⋅ dl −
∆t  ∫0
t
 1 t
(
)
u
l
⋅
dl
=
∫0
∫ u(l) ⋅ dl
 ∆t t − ∆t
t − ∆t
El valor de la integral dependerá del valor de la función u(l). Si estos valores
corresponden a una función discreta, se puede linealizar y, por tanto, aplicar la regla del
trapecio,
t
 u (t ) + u (t − ∆t ) 
 ⋅ ∆t
2

∫ u (l) ⋅ dl = 
t − ∆t
 u (t ) + u (t − ∆t ) 
donde 
 es el hidrograma unitario de duración ∆t. La aproximación
2

lineal de la integral se puede hacer siempre y cuando ∆t sea muy pequeño. Una vez
74
Problemas de Hidrología
obtenido este hidrograma unitario de duración ∆t, para hallar el hidrograma unitario de
duración D > ∆t, se procedería con otro método, como el del Hidrograma en S, a partir
de dicho hidrograma unitario de duración ∆t.
75
Problemas de Hidrología
PROBLEMA 15
Dada la cuenca geométrica de la figura adjunta con un flujo canalizado de
1 m/s y un flujo superficial de 0.5 m/s, se pide:
a) Deducir el tiempo de concentración de la cuenca Tc.
b) Dibujar 10 isocronas.
c) Deducir el hidrograma para un aguacero de duración Tc/10 e
intensidad neta de 3.6 mm/h.
d) Deducir el hidrograma para un aguacero de duración infinita e
intensidad neta de 3.6 mm/h.
1000 m
V = 0.5 m/s
1000 m
V = 1 m/s
Figura 1. Cuenca
Nota: No tener en cuenta el factor de uniformidad ni el coeficiente
reductor por área.
a) Para hallar el tiempo de concentración habrá que seleccionar el punto más
alejado del punto de desagüe de la cuenca. En este caso, al ser la cuenca
rectangular, el punto más alejado cuyo recorrido hasta llegar al punto de desagüe
observando las líneas de corriente serán los puntos de las esquinas A ó B (ver
Figura 15.1).
El tiempo de concentración será:
Tc =
76
500 m
0.5 m / s
+
1000 m
1 m/s
= 2000 s
Problemas de Hidrología
1000 m
A
B
V = 0.5 m/s
1000 m
V = 1 m/s
Figura 15.1. Recorrido del punto más alejado.
b) Las isocronas son líneas de igual tiempo de escurrimiento, de forma que
cualquier gota de agua precipitada a lo largo de ella tarda el mismo tiempo en
alcanzar el punto de desagüe de la cuenca.
Del dibujo se deduce que un punto A situado a 500 m del cauce tarda en
alcanzar éste:
T=
500 m
0.5 m / s
= 1000 s
el mismo tiempo que tarda en recorrer una gota caída en el extremo opuesto al
punto de desagüe la longitud del río:
T=
1000 m
1 m/s
= 1000 s
por lo que la isocrona de 1000 s será la representada en la Figura 15.2.
Como el tiempo de concentración es 2000 s se dibujarán 10 isocronas
correspondientes a 200, 400, 600, 800, 1000, 1200, 1400, 1600, 1800, 2000 s
(incremento de tiempo ∆t = Tc 10 = 200 s ). En la figura siguiente se muestran
las 10 isocronas.
77
Problemas de Hidrología
1000 m
T = 1000 s
1000 m
Figura 15.2. Isocrona de 1000 segundos.
ISOCRONAS
1000 m
1800
1600
1000 m
1400
1200
800 400
200
600
1000
Figura 15.3. Representación de las 10 isocronas.
c) El área existente entre las isocronas se puede calcular fácilmente al ser figuras
geométricas trapezoidales y triangulares. Las áreas calculadas se muestran en la
siguiente tabla (Tabla 15.1).
78
Problemas de Hidrología
Tabla 15.1. Áreas comprendidas entre isocronas.
ISOCRONAS
0 – 200 s
200 – 400 s
400 – 600 s
600 – 800 s
800 – 1000 s
1000 – 1200 s
1200 – 1400 s
1400 – 1600 s
1600 – 1800 s
1800 – 2000 s
ÁREA (m2)
20000
60000
100000
140000
180000
180000
140000
100000
60000
20000
La expresión del cálculo del caudal que se obtiene a partir de un aguacero de
intensidad neta In y duración D es:
Qi =
1
⋅ In ⋅ Ai
3.6
donde In es la intensidad neta uniforme (en mm/h) producida sobre la cuenca, Ai
es el área (en km2) comprendida entre dos isocronas cuyo intervalo de
separación temporal es D y Qi es el caudal (en m3/s) producido en el punto de
desagüe cada intervalo D. En nuestro caso la duración del aguacero es
D = Tc 10 = 200 s e In = 3.6 mm/h. En la tabla siguiente se muestran los
cálculos realizados para obtener el hidrograma.
Tabla 15.2. Caudales
Tiempo (s)
200
400
600
800
1000
1200
1400
1600
1800
2000
Qi = In Ai /3.6
3.6 0.02/3.6 = 0.02
3.6 0.06/3.6 = 0.06
3.6 0.1/3.6 = 0.1
3.6 0.14/3.6 = 0.14
3.6 0.18/3.6 = 0.18
3.6 0.18/3.6 = 0.18
3.6 0.14/3.6 = 0.14
3.6 0.1/3.6 = 0.1
3.6 0.06/3.6 = 0.06
3.6 0.02/3.6 = 0.02
El agua caída los primeros 200 s producen un caudal de 0.02 m3/s. En ese
momento cesa la lluvia y al cabo de otros 200 s (tiempo 400 s) llega al punto de
desagüe el agua caída en el área comprendida entre la isocrona 200 s y 400 s, y
79
Problemas de Hidrología
así sucesivamente hasta llegar a 2000 s que es el tiempo de concentración. En la
figura adjunta se muestra el hidrograma producido y el histograma (Figura 15.4).
In (mm/h)
hidrograma producido por una
lluvia de 3.6 mm/h de intensidad
neta y duración 200 s
3.6
0.20
Tiempo (s)
200
0.18
0.16
0.14
3
Q (m /s)
0.12
0.10
0.08
0.06
0.04
0.02
0.00
0
400
800
1200
1600
2000
2400
Tiempo (s)
Figura 15.4. Hidrograma e Hietograma
d) Para obtener el hidrograma producido por una lluvia de duración infinita se
calculará el hidrograma con valores acumulados tal y como se realiza para
obtener el hidrograma en S, sólo que en este caso la intensidad neta es 3.6 mm/h
en lugar de 1 mm/h. En la tabla adjunta se muestran los cálculos realizados para
la obtención de dicho hidrograma.
Tabla 15.3. Cálculos para obtener el hidrograma.
Tiempo
(s)
0
200
400
600
800
1000
1200
1400
1600
1800
2000
2200
80
Hidrograma
Q (m3/s)
0
0.02
0.06
0.1
0.14
0.18
0.18
0.14
0.1
0.06
0.02
0
Valor acumulado
Hidrograma
0
0.02
0.08
0.18
0.32
0.5
0.68
0.82
0.92
0.98
1
1
Problemas de Hidrología
Se puede observar que a partir del tiempo 2000 s, que es el tiempo de
concentración el valor del caudal es constante (igual a 1 m3/s). En la siguiente
figura se muestra el hidrograma obtenido y el hietograma.
In (mm/h)
3.6
1.2
Tiempo (s)
1.0
3
Q (m /s)
0.8
0.6
Hidrograma
0.4
0.2
0.0
0
400
800
1200
1600
2000
tiempo (s)
Figura 15.5. Hidrograma e Hietograma producido.
81
Problemas de Hidrología
PROBLEMA 16
Dada la cuenca geométrica de la figura adjunta con las líneas de flujo
convergiendo al punto de desagüe , se pide:
a) Deducir el tiempo de concentración de la cuenca Tc.
b) Dibujar 4 isocronas.
c) Deducir el hidrograma para un aguacero de duración Tc/5 e
intensidad neta de 3.6 mm/h.
d) Deducir el hidrograma para un aguacero de duración infinita e
intensidad neta de 3.6 mm/h.
300 m
V = 1 m/s
400 m
V = 0.75 m/s
Figura 1. Cuenca
a) Para deducir el tiempo de concentración se calcula el tiempo que tarda en llegar
la gota que cae en el punto más alejado de la cuenca al punto de desagüe:
Tc = 400/1 = 400 seg. = 300/0.75
b) Para dibujar las cuatro isocronas se calcula el valor de éstas, que corresponderán
al dividir el tiempo de concentración entre 5:
Isocronas 400/5= cada 80 seg.
En la Figura 16.1 se muestran las isocronas obtenidas.
82
Problemas de Hidrología
300 m
V = 1 m/s
400 m
400 s 240 s 80 s
160 s 320 s
V = 0.75 m/s
Figura 16.1. Isocronas.
c) Para obtener el hidrograma generado por un aguacero de la intensidad dada se ha
de aplicar la fórmula
Qi =
1
⋅ In ⋅ Ai
3.6
En la Tabla 16.1 se muestran los cálculos realizados. En dicha tabla la columna
correspondiente al título de ÁREAS se ha obtenido restando las superficies de
cada triángulo con el anterior para hallar las superficies comprendidas entre
isocronas.
Tabla 16.1. Cálculos para obtener el hidrograma.
ALTURA (m)
80
160
240
320
400
BASE (m)
60 x 2
120 x 2
180 x 2
240 x 2
300 x 2
AREA TRIAN. (m2)
4800
19200
63200
76800
120000
ÁREAS (m2)
4800
14400
24000
33600
43200
Q (m3/s)
0.0048
0.0144
0.024
0.0336
0.0432
En la Figura 16.2 se muestra el hidrograma correspondiente al aguacero
producido.
d) En este caso la duración del aguacero es infinito, por lo que al punto de desagüe
le va a ir llegando el agua caída en todas las superficies de la cuenca, es decir se
va a acumular la cantidad de agua, aumentando el caudal hasta que se alcance un
estacionario cuando el tiempo transcurrido sea el de concentración de la cuenca.
En la Tabla 16.2 se muestran los cálculos realizados. En las Figuras 16.3 y 16.4
se muestra el hidrograma obtenido.
83
Problemas de Hidrología
Tabla 16.2. Cálculos para obtener el hidrograma generado por una lluvia de larga
duración.
ALTURA (m)
80
160
240
320
400
ÁREAS (m2)
4800
14400
24000
33600
43200
BASE (m)
60 x 2
120 x 2
180 x 2
240 x 2
300 x 2
Q (m3/s)
0.0048
0.0144
0.024
0.0336
0.0432
Q (m3/s) ACUM.
0.0048
0.0192
0.0432
0.0768
0.12
Q
0.0432
0.00336
0.024
0.0144
0.0048
80 160 240 320 400 480
t (s)
Figura 16.2. Hidrograma producido por una lluvia de duración 80 s.
0.14
0.12
0.08
3
Q (m /s)
0.10
0.06
0.04
0.02
0.00
0
100
200
300
400
500
600
T (seg)
Figura 16.3. Hidrograma producido por una lluvia de duración infinita.
84
Problemas de Hidrología
Q
0.0768
0.0432
0.0192
0.0048
80 160 240 320 400
t (s)
Figura 16.4. Hidrograma producido por una lluvia de duración infinita. Detalle.
85
Problemas de Hidrología
PROBLEMA 17
Dado de Hidrograma unitario de un aguacero de 4 horas de duración se
pide calcular:
a) El hidrograma en S
b) El hidrograma unitario de un aguacero de 12 horas para la misma
cuenca
c) Tiempo de concentración de la cuenca
Tabla 1. Hidrograma Unitario de 4 h
Tiempo (h)
q (m3/s/cm)
Tiempo (h)
q (m3/s/cm)
0
0
20
130
2
8
24
90
4
20
26
66
6
45
28
52
8
80
32
27
10
100
34
19
12
130
36
15
16
150
40
5
18
143
44
0
Al ser un hidrograma unitario de 4 horas de duración sólo tendremos en cuenta las
ordenadas cada cuatro horas.
a) Hidrograma en S
Para calcula el Hidrograma en S hay que hacer la conversión de las ordenadas
unitarias m3/s/cm a ordenadas m3/s/mm/h mediante la conversión:
(
) (
t
) 10
q * m 3 s mm h = q m 3 s cm ⋅
a
donde ta = 4 h. En la siguiente tabla se muestra los valores numéricos del
Hidrograma en S.
Tabla 17.1. Cálculo del Hidrograma en S.
Tiempo (h)
0
4
8
12
16
20
24
28
32
36
40
44
48
86
q (m3/s/cm)
0
20
80
130
150
130
90
52
27
15
5
0
-
q* (m3/s/mm/h)
0
8
32
52
60
52
36
20.8
10.8
6
2
0
0
Valor acum.
0
0+8=8
8 + 32 = 40
40 + 52 = 92
92 + 60 = 152
152 + 52 = 204
204 + 36 = 240
240 + 20.8 = 268.8
268.8 + 10.8 = 271.6
271.6 + 6 = 277.6
277.6 + 2 = 279.6
279.6 + 0 = 279.6
279.6
Hidr. en S
0
8
40
92
152
204
240
268.8
271.6
277.6
279.6
279.6
279.6
Problemas de Hidrología
b) Hidrograma unitario de un aguacero de 12 horas de duración.
En este caso se desplaza el hidrograma en S anterior 12 horas y se resta del
original. El hidrograma obtenido está dado en m3/s/mm/h. Para obtener el
Hidrograma unitario (volumen unidad) de un aguacero de 12 horas de duración
se aplica la conversión:
(
)
(
) 10
t
q m 3 s cm = q * m 3 s mm h ⋅
a'
donde ta’ = 12 h.
En la siguiente tabla se muestran los resultados obtenidos.
Tabla 17.2. Cálculo del Hidrograma Unitario de 12 h.
Tiempo (h)
Hidr. en S
0
4
8
12
16
20
24
28
32
36
40
44
48
52
56
0
8
40
92
152
204
240
268.8
271.6
277.6
279.6
279.6
279.6
279.6
279.6
Hidr. en S desplazado
12 h
0
8
40
92
152
204
240
268.8
271.6
277.6
279.6
279.6
q* (m3/s/mm/h)
12 h
0
8
40
92
144
164
148
108.8
67.6
37.6
18.8
8
2
0
0
q (m3/s/cm)
12 h
0
6.7
33.3
76.7
120
136.7
123.3
90.7
56.3
31.3
15.7
6.7
1.7
0
0
En los siguientes gráficos se muestran los diferentes hidrogramas obtenidos:
- Hidrograma unitario q 4 h (Figura 17.1).
- Hidrograma unitario q* 4 h (Figura 17.1).
- Hidrograma en S (Figura 17.2).
- Hidrograma en S desplazado (Figura 17.2).
- Hidrograma unitario q 12 h (Figura 17.3).
- Hidrograma unitario q* 12 h (Figura 17.3).
87
Problemas de Hidrología
160
Hidrograma unitario
3
q(m /s/cm) 4 h
Hidrograma unitario
*
3
q (m s/mm/h) 4 h
140
Caudal unitario
120
100
80
60
40
20
0
0
4
8
12 16 20 24 28 32 36 40 44 48 52
Tiempo (h)
Figura 17.1. Hidrogramas Unitarios de 4 h.
3
Hidrograma en S (m /s/mm/h)
Hidrograma en S desplazado 12 h
*
3
Hidrograma unitario q (m /s/mm/h) 12 h
300
250
Caudales
200
150
100
50
0
0
4
8 12 16 20 24 28 32 36 40 44 48 52 56 60
Tiempo (h)
Figura 17.2. Hidrogramas en S.
88
Problemas de Hidrología
Hidrograma unitario
*
3
q (mm /s/mm/h) 12 h
Hidrograma unitario
3
q(m /s/cm) 12 h
180
160
Caudales unitarios
140
120
100
80
60
40
20
0
0
4
8
12 16 20 24 28 32 36 40 44 48 52
Tiempo (h)
Figura 17.3. Hidrogramas Unitarios de 12 h.
c) Tiempo de concentración de la cuenca.
El tiempo de concentración de la cuenca es:
Tc = tb – ta = 44 – 4 = 40 h
Tanto el hidrograma unitario de un aguacero de 4 h de duración como el
hidrograma unitario de un aguacero de 12 h de duración cumplen el Primer
Principio del hidrograma unitario:
4≤
Tc
3
y
12 ≤
Tc
3
ya que
Tc 40
=
= 13.3 h
3
3
89
Problemas de Hidrología
AFOROS Y AVENIDAS
PROBLEMA 18
Calcular el caudal en una estación de aforo siendo las medidas de
velocidades en la sección, a profundidad 0.2 y 0.8 del calado, las
contenidas en el cuadro siguiente (Marín, 2001). En la figura adjunta se
muestra el sistema de referencia.
Tabla 1. Medidas
Medida
número
1
2
3
4
5
6
7
8
9
10
11
12
13
14
Distancia
origen (m)
0
2
4.5
6.8
10
15
20
25.5
30.2
38.5
45.2
50.6
57.6
62.6
0 origen
Ancho
(m)
1
2.25
2.4
2.75
4.1
5
5.25
5.1
6.5
7.5
6.05
6.2
6
2.5
Calado
(m)
0
0.5
1.4
2.4
1.9
2.7
3.1
2.6
3
2.4
1.8
0.9
0.3
0
Distancia
0.2 calado
Calado
0.8 calado
Ancho
Figura 1. Esquema
90
Velocidad a Velocidad a
0.2 d (m/s)
0.8 d (m/s)
0
0
0.3
0.12
0.8
0.35
1.12
0.45
1.2
0.51
1.4
0.62
1.55
0.67
1.45
0.63
1.62
0.72
1.2
0.43
1.97
0.37
0.82
0.28
0.25
0.11
0
0
Problemas de Hidrología
Para hallar el caudal se calcula una media ponderada de los caudales parciales con las
superficies asociadas a cada franja. La velocidad en una franja es la media aritmética de
las velocidades de 0.2 y 0.8 d. Para calcular el área se aproxima la superficie de cada
franja a rectángulos. Posteriormente se multiplicará cada velocidad media por cada
superficie parcial para obtener un caudal en cada franja. La suma total de los caudales
parciales es el caudal total buscado. En la tabla siguiente se muestran los valores
obtenidos.
Tabla 18.1. Cálculos.
Medida Ancho Calado
número
(m)
(m)
1
1
0
2
2.25
0.5
3
2.4
1.4
4
2.75
2.4
5
4.1
1.9
6
5
2.7
7
5.25
3.1
8
5.1
2.6
9
6.5
3
10
7.5
2.4
11
6.05
1.8
12
6.2
0.9
13
6
0.3
14
2.5
0
Totales
Área Velocidad a Velocidad a Velocidad Caudal
(m2) 0.2 d (m/s) 0.8 d (m/s) media (m/s) (m3/s)
0
0
0
0
0
1.125
0.3
0.12
0.21
0.2
3.36
0.8
0.35
0.58
1.9
6.6
1.12
0.45
0.79
5.2
7.79
1.2
0.51
0.86
6.7
13.5
1.4
0.62
1.01
13.6
16.27
1.55
0.67
1.11
18.1
13.26
1.45
0.63
1.04
13.8
19.5
1.62
0.72
1.17
22.8
18
1.2
0.43
0.82
14.7
10.89
1.97
0.37
0.72
7.8
5.58
0.82
0.28
0.55
3.1
1.8
0.25
0.11
0.18
0.3
0
0
0
0
0
117.7
108.2
El caudal resultante es 108.2 m3/s que corresponde a una velocidad media de
v=
108.2
= 0.92 m / s
117.7
91
Problemas de Hidrología
PROBLEMA 19
Determinar los caudales característicos y dibujar la curva de caudales
clasificados del año hidrológico 1989/1990 a partir de los datos de la tabla
adjunta. Se pide también deducir la expresión analítica de Coutagne y la
curva de caudales adimensionalizada. ¿Cuántos días podría operar una
central hidroeléctrica cuyo caudal mínimo de funcionamiento es Qmin = 1
m3/s y el caudal máximo admisible es Qmax = 12 m3/s.
Tabla 1. Datos
Día
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
Oct Nov
0.8
1.36
0.8
1.36
0.8
3.04
0.8
3.6
0.8
3.6
0.8
5.84
0.8
10
0.8
8.92
0.8
8.2
0.8
7.48
0.8
5.56
0.8
5.56
0.8
4.72
0.8
4.44
0.8
4.44
0.72 4.16
0.72 4.16
0.72
6.4
0.8 10.56
0.8
6.76
0.72 6.76
1.08 11.12
2.48 9.64
3.32 9.28
3.04 9.28
2.76 8.92
2.48 7.84
2.2
7.48
2.2
7.12
1.92 6.12
1.64
Dic
5.84
5.84
5.56
4.72
4.16
4.16
3.88
3.88
3.88
3.88
4.16
5
10.56
8.2
17.46
29.8
47.82
41.9
37.98
29
81.9
106.7
77.28
47.82
41.9
42.88
35.4
30.6
26.84
23.96
21.8
En
19.32
16.22
15.6
14.48
13.92
13.36
13.92
13.36
12.8
11.68
11.12
10.56
10
9.64
9.28
8.92
8.56
8.2
7.84
7.48
7.48
7.12
6.76
7.12
7.48
10
14.48
23.96
20.56
29.8
30.6
Feb
32.2
40.92
41.9
35.4
30.6
28.28
24.68
24.68
23.96
23.24
26.12
37
31.4
27.56
25.4
23.24
21.18
19.94
18.7
18.08
17.46
15.6
14.48
13.92
13.36
12.24
11.68
11.12
Mar
10
9.64
9.28
8.92
8.56
8.56
8.56
8.56
8.56
7.84
7.84
8.2
8.2
8.2
7.84
7.48
7.12
6.76
6.76
6.4
6.4
6.4
6.12
6.12
5.84
5.56
5.56
5.56
5.56
5.28
5.28
Abr
5.28
5.56
5.56
5.28
5.56
6.12
6.76
6.12
5.84
5.84
5.56
5.56
5.56
5.56
5.56
6.12
6.12
5.84
5.84
5.84
6.4
6.4
6.4
6.76
6.76
6.4
6.12
5.84
5.56
5.28
May
5.28
5.28
5
5
4.72
4.72
4.44
4.44
5
5
4.72
4.72
5
5.28
5
4.72
4.44
4.44
4.44
4.44
4.44
4.44
4.44
4.16
4.16
3.88
3.88
3.88
3.88
3.88
3.6
Jun
3.32
3.32
3.32
3.32
3.04
3.04
3.04
3.04
3.04
2.76
2.76
2.48
2.48
2.48
2.48
2.48
2.48
2.48
2.48
2.2
2.2
2.48
2.48
2.48
2.48
2.48
2.48
2.48
2.48
2.48
Jul
2.2
2.2
2.2
2.2
2.2
2.2
2.2
2.2
1.92
1.64
1.64
1.64
1.64
1.36
1.36
1.08
1.08
1.08
1.08
0.8
0.8
0.8
0.8
0.8
0.8
0.8
0.8
0.8
0.8
0.8
0.8
Ag
0.8
0.8
0.72
0.72
0.72
0.72
0.72
0.72
0.72
0.72
0.72
0.72
0.72
0.72
0.72
0.72
0.72
0.72
0.72
0.72
0.72
0.72
0.72
0.72
0.72
0.72
0.72
0.72
0.72
0.64
0.64
Sep
0.64
0.64
0.64
0.64
0.64
0.64
0.64
0.64
0.64
0.64
0.64
0.64
0.64
0.64
0.64
0.64
0.64
0.64
0.64
0.64
0.64
0.64
0.64
0.64
0.64
0.64
0.56
0.56
0.64
0.64
En primer lugar se ordenan los caudales de mayor a menor y contamos las veces que se
repiten dichos caudales a lo largo del año. En la tabla adjunta se muestran los valores de
los caudales con la frecuencia absoluta que se ha producido en el año dado. Se han
seleccionado unos intervalos de valores para agrupar los caudales de forma más
sencilla. En la primera figura se muestra la representación de dichos caudales con
respecto a la frecuencia absoluta (número de veces que se ha repetido dicho valor).
92
Problemas de Hidrología
Tabla 19.1. Datos ordenados.
Caudal Número de días Caudal Número de días Caudal Número de días
(m3/s) que se alcanza o (m3/s) que se alcanza o (m3/s) que se alcanza o
supera
supera
supera
106.7
1
20.56
37
6.76
115
81.9
2
19.94
38
6.4
123
77.28
3
19.32
39
6.12
131
47.82
5
18.7
40
5.84
141
42.88
6
18.08
41
5.56
157
41.9
9
17.46
43
5.28
164
40.92
10
16.22
44
5
171
37.98
11
15.6
46
4.72
178
37
12
14.48
49
4.44
189
35.4
14
13.92
52
4.16
196
32.2
15
13.36
55
3.88
205
31.4
16
12.8
56
3.6
208
30.6
19
12.24
57
3.32
213
29.8
21
11.68
59
3.04
220
29
22
11.12
62
2.76
223
28.28
23
10.56
65
2.48
242
27.56
24
10
69
2.2
254
26.84
25
9.64
72
1.92
256
26.12
26
9.28
76
1.64
261
25.4
27
8.92
80
1.36
265
24.68
29
8.56
86
1.08
270
23.96
32
8.2
92
0.8
301
23.24
34
7.84
97
0.72
332
21.8
35
7.48
103
0.64
363
21.18
36
7.12
107
0.56
365
Los caudales característicos que se pueden obtener de la figura o de la tabla anterior son
los siguientes:
•
•
•
•
•
•
•
•
Caudal medio (Q): 7.74 m3/s
Caudal máximo absoluto (QC): 106.7 m3/s
Caudal máximo característico (igualado o superado en 10 días) (QMC): 40.92 m3/s
Caudal superado o igualado en 90 días (Q90): 8.32 m3/s (valor interpolado a partir de
la tabla)
Caudal semipermanente (Qs): 4.58 m3/s
Caudal igualado o superado en 270 días (Q270): 1.08 m3/s
Caudal mínimo característico (Qmc): 0.66 m3/s (valor interpolado a partir de la tabla)
Caudal del día más seco (Qc): 0.56 m3/s
La curva de Coutagne tiene la siguiente expresión:
93
Problemas de Hidrología
q = Q mc +
(Q − Q mc ) ⋅ (1 + n )
T
n
⋅ (T − t )
n
donde q es el caudal igualado o superado durante t días en el curso de un período de
observación de T días, y n es el coeficiente de irregularidad:
n + 1 Q s − Q mc
=
Q − Q mc
2n
Sustituyendo los valores:
n + 1 Q s − Q mc
=
= 0.55367
Q − Q mc
2n
y resolviendo: n = 2.77
La expresión de la curva para T = 365 días es:
q = 0.66 + 2.13 ⋅ 10 −6 (365 − t )
2.77
120
Curva de caudales clasificados
100
3
Q (m /s)
80
60
40
20
0
0
40
80
120 160 200 240 280 320 360 400
Días
Figura 19.1. Curva de caudales clasificados.
La curva de Coutagne se ajusta bien con respecto a la de caudales clasificados para
caudales inferiores, caudales producidos a partir de 40 días.
En cuanto a los días que puede operar la central hidroeléctrica en el año, a partir de la
figura se obtiene el número de días que se iguala o supera el caudal mínimo de 1 m3/s y
94
Problemas de Hidrología
el caudal máximo de 12 m3/s, que son 278 y 57 días, respectivamente. Por tanto, la
central podrá operar 278 – 57 = 221 días al año (Figura 19.4).
Por último, se muestra también la curva de caudales clasificados adimensionalizada: %
de tiempo en el eje de abcisas (% con respecto a 365 días) y Q/Qmed en el eje de
ordenadas, donde Qmed es el caudal medio anual. En la Tabla 19.2 se muestran los
valores numéricos de la curva adimensionalizada de caudales clasificados.
30
Curva de Coutagne
25
3
Q (m /s)
20
15
10
5
0
0
50
100
150
200
250
300
350
400
Días
Figura 19.2. Curva de Coutagne.
16
Curva adimensionalizada de
caudales clasificados
14
12
Q/7.74
10
8
6
4
2
0
0
20
40
60
80
100
120
t/365 (%)
Figura 19.3. Curva adimensionalizada de caudales clasificados.
95
Problemas de Hidrología
Tabla 19.2. Valores numéricos de la curva adimensionalizada de caudales clasificados.
Q/7.74
tiempo/365
Q/7.74
tiempo/365
Q/7.74
tiempo/365
Caudal
(%)
Caudal
(%)
Caudal
(%)
Medio: 7.74 Período:365 Medio: 7.74 Período:365 Medio: 7.74 Período:365
0.27
0.54
0.82
1.36
1.64
2.46
2.73
3.01
3.28
3.83
4.10
4.38
5.20
5.75
6.02
6.30
6.57
6.84
7.12
7.39
7.94
8.76
9.31
9.58
9.86
3
Q (m /s)
13.78
10.58
9.98
6.17
5.54
5.41
5.28
4.90
4.78
4.57
4.16
4.05
3.95
3.85
3.74
3.65
3.56
3.46
3.37
3.28
3.18
3.09
3.00
2.81
2.73
2.65
2.57
2.49
2.41
2.331
2.25
2.09
2.01
1.87
1.79
1.72
1.65
1.58
1.50
1.43
1.36
1.29
1.24
1.19
1.15
1.10
1.05
1.01
0.96
0.91
14
13
12
11
10
9
8
7
6
5
4
3
2
1
0
10.13
10.41
10.68
10.95
11.23
11.78
12.05
12.60
13.42
14.24
15.06
15.34
15.61
16.16
16.98
17.80
18.90
19.72
20.82
21.91
23.56
25.20
26.57
28.21
29.31
0.87
0.82
0.79
0.75
0.71
0.68
0.64
0.60
0.57
0.53
0.50
0.46
0.42
0.39
0.35
0.32
0.28
0.24
0.21
0.17
0.13
0.10
0.09
0.08
0.07
Curva de caudales clasificados
57 d
278 d
0
40
80
120 160 200 240 280 320 360 400
Días
Figura 19.4. Valores de caudales para distintos tiempos.
96
31.50
33.69
35.89
38.63
43.01
44.93
46.84
48.76
51.78
53.69
56.16
56.98
58.35
60.27
61.09
66.30
69.58
70.13
71.50
72.60
73.97
82.46
90.95
99.45
100
Problemas de Hidrología
PROBLEMA 20
Para la medición del caudal en un arroyo se ha recurrido al aforo químico
de inyección instantánea de un trazador. En este caso se inyectó una
solución concentrada de cloruro sódico (100 g en 15 litros de agua). En
una sección situada aguas abajo se extraen muestras a intervalos
regulares de tiempo, cuyas concentraciones se muestran en la siguiente
tabla. Se pide calcular el caudal y la longitud de mezcla sabiendo que el
arroyo tiene 2 m de ancho, 0.5 m de profundidad y el coeficiente de Chezy
es 17.
Tabla 1. Datos
Tiempo (s)
0
15
30
45
60
75
90
105
120
135
150
Concentración (gr/l)
0
0.3
1.7
2.5
2.4
2.1
1.6
1.1
0.5
0.3
0.1
En la Figura 20.1 se representa la evolución temporal de las concentraciones obtenidas
en una sección situada aguas abajo correspondiente a la tabla del enunciado. Haciendo
un balance de masa el caudal viene expresado por:
Q=
M
T
∫ C ⋅ dt
≈
M
∑ C i ∆t i
i
o
donde M es la masa vertida en el río y representa el área que delimita la curva de la
figura.
Para aplicar la anterior fórmula se ha construido una tabla (Tabla 20.1) en la que se dan
los resultados del cálculo de la integral mediante la aproximación de la superficie con
figuras geométricas sencillas (triángulos y trapecios).
97
Problemas de Hidrología
Tabla 20.1. Cálculo de la masa
Tiempo (s) Concentración (gr/l) Concentración media en Cmed x ∆t
el intervalo Cmed
0
0
15
0.3
0.15
2.25
30
1.7
1
15
45
2.5
2.1
31.5
60
2.4
2.45
36.75
75
2.1
2.25
33.75
90
1.6
1.85
27.75
105
1.1
1.35
20.25
120
0.5
0.8
12
135
0.3
0.4
6
150
0.1
0.2
3
165
0
0.05
0.75
3.0
Concentración
Concentración (gr/l)
2.5
2.0
1.5
1.0
0.5
0.0
0
20
40
60
80
100
120
140
160
180
Tiempo (s)
Figura 20.1. Evolución temporal de la concentración.
El valor total:
∑C
i
En consecuencia,
98
i
⋅ ∆t i = 189 gr ⋅ s / l
Problemas de Hidrología
Q=
M
T
∫ C ⋅ dt
≈
M
100
=
= 0.53 l / s
∑ C i ∆t i 189
i
o
La longitud de mezcla viene dada por la expresión:
L = 0.13 ⋅
B2 C
⋅ ⋅ (0.7 ⋅ C + 6 )
H g
donde B es la anchura del arroyo en metros, H la profundidad en metros, g la
aceleración de la gravedad y C el coeficiente de Chezy. En nuestro caso L vale:
L = 0.13 ⋅
2 2 17
⋅
⋅ (0.7 ⋅ 17 + 6) = 32.26 m
0.5 9.81
99
Problemas de Hidrología
PROBLEMA 21
Calcular el caudal máximo para períodos de retorno de 25, 50, 75, 100 y
500 años utilizando los métodos estadísticos de Gumbel, Log-Pearson y
log-Normal y el método empírico de Gete, sabiendo que el área de la
cuenca es 248 Km2. Comparar los resultados obtenidos. Calcular el
intervalo de confianza del 95% para la avenida de T = 500 años.
NOTA: En la tabla adjunta se presentan los dos caudales máximos para
cada año hidrológico. Considerar los 32 datos para el cálculo de los
parámetros de la distribución.
Tabla 1. Caudales máximos
Año hidrológico
1970-71
1971-72
1972-73
1973-74
1974-75
1975-76
1976-77
1977-78
1978-79
1979-80
1980-81
1981-82
1982-83
1983-84
1984-85
1985-86
Caudal 1 (m3/s)
61.0
260.6
111.0
96.0
105.0
52.85
77.0
307.0
172.0
40.0
156.0
55.3
65.18
58.83
63.06
56.0
Caudal 2 (m3/s)
58.0
249.5
52.0
85.2
66.0
48.65
78.0
210.0
114.0
40.1
79.51
43.35
49,2
50.31
38.94
56.0
a) La expresión del caudal por el método empírico de Gete es:
Q T = (4 + 16 ⋅ log T ) ⋅ A 0.5
donde
A es el área en km2
T el período de retorno en años
QT el caudal de la avenida en m3/s para el período de retorno T
Sustituyendo los valores se obtiene la siguiente tabla (Tabla 21.1).
100
Problemas de Hidrología
Tabla 21.1. Método de Gete.
Período de retorno T (años)
25
50
75
100
500
Cálculo
(4 + 16 ⋅ log 25) ⋅ 248 0.5
(4 + 16 ⋅ log 50) ⋅ 248 0.5
(4 + 16 ⋅ log 75) ⋅ 248 0.5
(4 + 16 ⋅ log 100) ⋅ 248 0.5
(4 + 16 ⋅ log 500) ⋅ 248 0.5
QT (m3/s)
415.22
491
535.4
566
743.04
b) La expresión del cálculo del caudal de avenida por el método de Gumbel es:
Q T = Q med + K ⋅ σ
donde Qmed es la media de los caudales, K es el factor de frecuencia y σ es la desviación
típica:
Q med =
σ=
1
⋅ ∑ Qi
N i
1
2
⋅ ∑ (Q i − Q med )
N −1 i
siendo N el tamaño de la muestra. En nuestro caso N = 32. En consecuencia, la media y
desviación típica de los 32 caudales es:
Q med =
σ=
1
⋅ ∑ Q i = 95.48
N i
1
2
⋅ ∑ (Q i − Q med ) = 70.41
N −1 i
Para calcular el factor de frecuencia, calcularemos la función de distribución y la
variable de Gumbel yT:
Pr ob[Q ≥ Q T ] = 1 − exp[− exp(− y T )]
o bien
QT = a −
  T 
1
⋅ Ln Ln

α
  T − 1 
con
101
Problemas de Hidrología
y T = α ⋅ (Q T − a )
donde α y a son dos parámetros de distribución cuya expresión es
σ*
α=
σ
a = Q med −
yN
α
donde σ* y yN son dos parámetros que dependen del tamaño N de la muestra. En nuestro
caso al ser N = 32, se obtiene
σ * = 1.1193
y N = 0.538
de la Tabla 21.2.
Tabla 21.2. Valores de los parámetros en función del tamaño de muestra.
N
14
15
16
17
18
19
20
21
22
23
24
25
26
yN
0.5100
0.5128
0.5154
0.5176
0.5198
0.5202
0.5236
0.5252
0.5268
0.5283
0.5296
0.5309
0.5320
σ*
1.0094
1.0206
1.0306
1.0396
1.0480
1.0544
1.0628
1.0696
1.0754
1.0811
1.0864
1.0915
1.0961
N
32
36
37
38
39
40
41
42
43
44
45
46
47
yN
0.538
0.541
0.5418
0.5424
0.5430
0.5436
0.5442
0.5448
0.5453
0.5458
0.5463
0.5468
0.5473
Sustituyendo,
σ * 1.1193
α=
=
= 0.01589
σ
70.41
a = Q med −
102
yN
0.538
= 95.48 −
= 61.64
α
0.01589
σ*
1.1193
1.1313
1.1339
1.1363
1.1388
1.1413
1.1436
1.1458
1.1480
1.1499
1.1519
1.1538
1.1557
Problemas de Hidrología
El factor de frecuencia viene dado por
K=
yT − y N
σ*
Se puede calcular cada caudal QT a partir de la expresión de la función de distribución
anteriormente dada
QT = a −
  T 
  T 
1
1
⋅ Ln Ln
⋅ Ln Ln
 = 61.64 −

α
0.01589
  T − 1 
  T − 1 
En la tabla siguiente se dan los caudales obtenidos para cada período de retorno, al
sustituir su valor en la ecuación anterior.
Tabla 21.3. Valores de Q mediante Gumbel para los distintos períodos de retorno.
Período de retorno T (años)
25
50
75
100
500
QT (m3/s)
262.9
307.2
332.9
351.14
452.67
Para calcular el intervalos de confianza del 95% se sabe que
Pr ob[ Q − Q T ≤ Q ic ] = 95%
donde Qic es el semiancho del intervalo de confianza β% que viene dado por
Q ic = f (β) ⋅ S e
donde f(β) = f(95%) = 1.96 es una función que depende de β, y Se es el error probable
que se calcula a partir de
1 + 1.3 ⋅ K + 1.1 ⋅ K 2 
Se = σ ⋅ 

N


Al ser el factor de frecuencia K
K=
y T − y N Q T − Q med
=
σ
σ*
y sustituyendo el valor de QT para T = 500 años, se obtiene
103
Problemas de Hidrología
K=
Q T − Q med 452.67 − 95.48
=
= 5.07
σ
70.41
por lo que
1 + 1.3 ⋅ 5.07 + 1.1 ⋅ 5.07 2 
1 + 1.3 ⋅ K + 1.1 ⋅ K 2 
Se = σ ⋅ 
70
.
41
=
⋅
 = 74.58


N
32




y
Q ic = f (β) ⋅ S e = 1.96 ⋅ 74.58 = 146.18
Así,
Q T − Q ic < Q < Q T + Q ic ⇒ 452.67 − 146.18 < Q < 452.67 + 146.18
306.49 < Q < 598.85
que es el intervalo de confianza
c) En el método de Log-Pearson la variable es el logarítmo del caudal:
z = log Q
z T = z med + K z ⋅ σ z
con
z med =
σz =
1
⋅ ∑ zi
N i
1
2
⋅ ∑ (z i − z med )
N −1 i
K z = f (C s , T )
Kz está tabulado en función del coeficiente de asimetría Cs y del período de retorno T,
N ⋅ ∑ (z i − z med )
3
Cs =
i
(N − 1) ⋅ (N − 2) ⋅ σ 3z
Sustituyendo se obtiene,
zmed = 1.897 ; σz = 0.25 ; Cs = 1.00055
104
Problemas de Hidrología
En consecuencia,
z T = z med + K z ⋅ σ z = 1.897 + K z ⋅ 0.25
Teniendo en cuenta los valores de Kz dados en función de Cs y T de la Tabla 21.4 se
calcula el caudal para los distintos períodos de retorno. En los períodos de retorno que
no se tengan datos el valor se obtendrá interpolando.
Tabla 21.4. Valores de Kz en función de Cs y de T.
Cs = 1.2
Cs = 1.0
Cs = 0.8
Cs = 0.6
Cs = 0.4
Cs = 0.2
Cs = 0.0
Cs = -0.2
Cs = -0.4
Cs = -0.6
Cs = -0.8
Cs = -1.0
Cs = -1.4
Cs = -1.8
T = 25 años
2.087
2.043
1.998
1.939
1.880
1.818
1.751
1.680
1.606
1.528
1.448
1.366
1.198
1.035
T = 50 años
2.626
2.542
2.453
2.359
2.261
2.159
2.054
1.945
1.834
1.720
1.606
1.492
1.270
1.069
T = 100 años
3.149
3.022
2.891
2.755
2.615
2.472
2.326
2.178
2.029
1.880
1.733
1.588
1.318
1.087
T = 200 años
3.661
3.489
3.312
3.132
2.949
2.763
2.576
2.388
2.201
2.016
1.837
1.664
1.351
1.097
T = 1000 años
4.820
4.540
4.250
3.960
3.670
3.380
3.090
2.810
2.540
2.275
2.035
1.880
1.465
1.130
En la tabla siguiente se muestran los resultados para cada período de retorno. Los
caudales se han calculado sabiendo que
Q T = 10 z T
Tabla 21.5. Cálculo de Q mediante log-Pearson para los distintos períodos de retorno.
Período de retorno T (años)
25
50
75
100
500
Cs
1.00055
1.00055
1.00055
1.00055
1.00055
Kz
2.043
2.542
2.782
3.022
3.883
zT
2.407
2.532
2.592
2.652
2.867
QT (m3/s)
255.7
340.8
391.29
449.26
737.47
d) El método Log-Normal es un caso particular del método de Log-Pearson en el cual
Cs = 0. En este caso los resultados obtenidos son:
105
Problemas de Hidrología
Tabla 21.5. Cálculo de Q mediante log-Normal.
Período de retorno T (años)
25
50
75
100
500
Cs
0
0
0
0
0
Kz
1.751
2.054
2.19
2.326
2.59
zT
2.335
2.410
2.444
2.478
2.544
QT (m3/s)
216.14
257.33
278.29
300.95
350.52
Comparando los anteriores resultados se puede comprobar que el método empírico de
Gete proporciona valores de caudales mayores que el resto de los métodos estadísticos
empleados.
106
Problemas de Hidrología
PROBLEMA 22
Calcular el caudal máximo para períodos de retorno de 10, 25, 50, 100 y
500 años utilizando el método de la Instrucción de Carreteras sabiendo
que la longitud del cauce del río Mandeo es 35 Km, el desnivel del mismo
es 450 m y el área de la cuenca es 248 Km2. La cuenca está constituida
por un 40% de suelo de tipo B y un 60% de suelo de tipo C y el uso de la
tierra es un 55% de pradera buena (> 3) y un 45% de masa forestal media.
El coeficiente corrector local del umbral de escorrentía es 1.5 y los
valores ya corregidos de Pd para los diferentes períodos de retorno están
en la tabla adjunta:
Tabla 1. Precipitaciones máximas diarias.
T (años)
Pd (mm)
10
87.9
25
100.6
50
110.1
100
119.5
500
141.2
Los pasos a seguir para el cálculo de una avenida por el método empleado en la
Instrucción de Carreteras son los siguientes:
a) Evaluar el tiempo de concentración Tc:
 L 
Tc = 0.3 ⋅  0.25 
J 
0.76
donde L es la longitud del cauce principal en km, J es su pendiente. Así, se obtiene
 L 
J=
= 0.0128 ; Tc = 0.3 ⋅  0.25 
J 
35 2 − 0.45 2
0.45
0.76
35


= 0.3 ⋅ 
0.25 
 0.0128 
0.76
= 10.22 h
Al ser Tc > 6 la cuenca es grande por lo que habrá que aplicar el factor de uniformidad
al caudal obtenido. El factor de reducción por área de la precipitación máxima diaria no
se aplica ya que en el enunciado nos dan las precipitaciones máximas diarias ya
corregidas.
b) Calcular la intensidad diaria Id:
Id =
Pd
24
En la Tabla 22.1 se muestran los cálculos de la intensidad diaria máxima para los
distintos períodos de retorno.
107
Problemas de Hidrología
Tabla 22.1. Cálculo de Id.
T (años)
Pd (mm)
Id (mm/h)
10
87.9
3.66
25
100.6
4.19
50
110.1
4.58
100
119.5
4.97
500
141.2
5.88
c) Calcular la relación I1/Id a partir del mapa de isolíneas. En nuestro caso la
cuenca del río Mandeo está comprendida entre la isolínea 8 y 9. Tomaremos I1/Id
= 8.5 (Figura 22.1).
I1/Id = 8
I1/Id = 9
Figura 22.1. Isolíneas en la zona Norte.
d) Calcular la intensidad horaria I a partir de la expresión:
I
I = I d ⋅  1
 Id



 280.1 − Tc0.1 


0.4


sustituyendo para cada período de retorno se obtiene
Tabla 22.2. Cálculo de I.
T (años)
Id (mm/h)
I (mm/h)
10
3.66
7.5
25
4.19
8.58
50
4.58
9.39
100
4.97
10.19
500
5.88
12.05
e) Calcular el umbral de escorrentía. El valor del umbral de escorrentía P0 se
obtendrá ponderándolo con el área y las características de la vegetación y suelo.
De las tablas se obtienen los umbrales correspondientes:
108
Problemas de Hidrología
Tabla 22.3. Cálculo del umbral de escorrentía.
Suelo B
33
34
Pradera buena pendiente mayor 3
Masa forestal media
Suelo C
18
22
El valor del umbral de escorrentía será:
P0 = 0.4 ⋅ 0.55 ⋅ 33 + 0.6 ⋅ 0.55 ⋅ 18 + 34 ⋅ 0.4 ⋅ 0.45 + 22 ⋅ 0.6 ⋅ 0.45 = 25.26
valor que hay que mayorar consultando el mapa de mayoración. El factor de
mayoración dado en el enunciado es 1.5; por lo que,
P0 = 1.5 ⋅ 25.26 = 37.89
f) Calcular el coeficiente de escorrentía el cual viene dado mediante la fórmula
siguiente:
c=
(Pd − P0 ) ⋅ (Pd + 23 ⋅ P0 )
(Pd + 11 ⋅ P0 )2
sustituyendo,
Tabla 22.4. Cálculo del coeficiente de escorrentía.
T (años)
Pd (mm)
c
10
87.9
0.18
25
100.6
0.22
50
110.1
0.25
100
119.5
0.28
500
141.2
0.33
g) Calcular el caudal de la avenida mediante la expresión:
Q=
1
⋅c⋅I⋅A
3.6
donde la intensidad está en mm/h y el área A en km2, y el caudal en m3/s. El área de
la cuenca es 248 km2.
Teniendo en cuenta todos los parámetros anteriormente calculados se llega a los
resultados que se muestran en la siguiente tabla (Tabla 22.5):
109
Problemas de Hidrología
Tabla 22.5. Cálculo del caudal de avenida.
T (años)
I (mm/h)
c
Q (m3/s)
10
7.5
0.18
97
25
8.58
0.22
134.59
50
9.39
0.25
165.15
100
10.19
0.28
197.39
500
12.05
0.33
278.92
Sabiendo que el factor de uniformidad es:
f = 1+
Tc1.25
10.221.25
=
1
+
= 1.56
Tc1.25 + 14
10.221.25 + 14
En consecuencia, el caudal corregido se obtiene multiplicando los caudales
anteriores por el factor de uniformidad:
Tabla 22.6. Cálculo del caudal de avenida corregido.
T (años)
Q (m3/s)
Q (m3/s) corregido
110
10
97
151.32
25
134.59
209.96
50
165.15
257.63
100
197.39
307.92
500
278.92
435.11
Problemas de Hidrología
PROBLEMA 23
En una cuenca de 400 Km2 de área y tiempo de concentración 24 h se
quiere encauzar el río principal. Para ello se dispone de las curvas
Intensidad-duración-frecuencia que se ajustan a la expresión siguiente:
I=
6.93 ⋅ T 0.189
(D + 0.5)0.878
donde I es la intensidad en cm/h, T es el período de retorno en años y D
es la duración del aguacero en horas.
Se sabe que los coeficientes de escorrentía para los períodos de retorno
de 10, 150 y 500 años son 0.4, 0.6 y 0.95, respectivamente. Se pide el
hidrograma de la avenida producido por un aguacero de 4 h de duración
para los períodos de retorno de 10, 150 y 500 años. Se supondrá que los
factores de uniformidad y de reducción por área valen 1.
La curva Intensidad-duración-frecuencia se representa en la figura siguiente:
18
16
Período de retorno: 10 años
Período de retorno: 150 años
Período de retorno: 500 años
14
I (cm/h)
12
10
8
6
4
2
0
0
5
10
15
20
25
Duración (h)
Figura 23.1. Curva de Intensidad-Duración-frecuencia.
Sabiendo que el aguacero ha tenido una duración de 4 h , por lo que entrando en las
curvas para los diferentes períodos de retorno o aplicando la fórmula dada se obtiene la
intensidad del aguacero.
111
Problemas de Hidrología
El tiempo de concentración de la cuenca es 24 h, por lo que el aguacero de 4 h de
duración cumple el primer Principio del Hidrograma Unitario:
ta ≤
Tc
5
4≤
24
5
sustituyendo,
Tabla 23.1. Intensidad.
T (años)
Cálculo
6.93 ⋅ T
6.93 ⋅ 10 0.189
=
(D + 0.5)0.878 (4 + 0.5)0.878
Intensidad (cm/h)
0.189
10
150
500
6.93 ⋅ T 0.189
(D + 0.5)0.878
6.93 ⋅ T 0.189
(D + 0.5)0.878
=
=
6.93 ⋅ 150 0.189
(4 + 0.5)0.878
6.93 ⋅ 500 0.189
(4 + 0.5)0.878
2.85
4.76
5.98
para calcular el hidrograma de la avenida vale con calcular el hidrograma unitario y
multiplicarlo por la precipitación neta caída, ya que el tiempo base no cambia. Vamos a
aplicar dos métodos para obtener dicho hidrograma: el método racional y el método del
hidrograma unitario.
a) El método racional. Se supone que la cuenca se comporta como un canal
rectangular. El caudal de avenida viene dado por la siguiente expresión:
Q max =
1
⋅c⋅I⋅A
3.6
donde I es la intensidad en mm/h, A el área en km2, el coeficiente de escorrentía y
Q el caudal en m3/s.
Los caudales obtenidos para los distintos períodos de retorno se muestran en la
Tabla 23.2. Al ser el la duración del aguacero (4 h) inferior al tiempo de
concentración (24 h) el caudal que se obtendrá será proporcional a la relación de
tiempos. El hidrograma a partir del tiempo de duración del aguacero hasta el tiempo
de concentración tendrá una meseta, y a partir de dicho tiempo disminuirá. En la
Tabla 23.3 se calculan los valores de los caudales y en la Figura 23.2 se muestran
los hidrogramas para cada período de retorno.
112
Problemas de Hidrología
Tabla 23.2. Caudales máximos.
T (años)
Caudal máx. (m3/s)
Cálculo
1
⋅ c ⋅ I ⋅ A = 0.4 ⋅ 28.5 mm / h ⋅ 400 km 2
3.6
1
⋅ c ⋅ I ⋅ A = 0.6 ⋅ 47.6 mm / h ⋅ 400 km 2
3.6
1
⋅ c ⋅ I ⋅ A = 0.95 ⋅ 59.8 mm / h ⋅ 400 km 2
3.6
10
150
500
1270.66
3179.82
6321.19
Tabla 23.3. Caudales calculados.
T (años)
10
Cálculo del Caudal (m3/s)
t
4
Q = Q max ⋅ a = 1270.66 ⋅
= 211.77
Tc
24
Caudal (m3/s)
211.77
150
Q = Q max ⋅
ta
4
= 3179.82 ⋅
= 529.97
Tc
24
529.97
500
Q = Q max ⋅
ta
4
= 6321.19 ⋅
= 1053.53
Tc
24
1053.53
I
Período de retorno 10 años
Período de retorno 150 años
Período de retorno 500 años
1200
ta
1000
3
Q (m /s)
800
600
400
200
Tc
0
0
4
8
12
16
20
24
28
32
Tiempo (h)
Figura 23.2. Hidrogramas.
Al ser el tiempo de concentración (24 h) superior a 6 h, la cuenca se considera
grande (según la Instrucción de Carreteras 5.2-IC), por lo que habría que aplicar
113
Problemas de Hidrología
los coeficientes de corrección correspondientes. En este caso valen la unidad
según el enunciado del problema.
El tiempo base del hidrograma será:
t b = Tc + t a = 24 + 4 = 28 h
b) El método del Hidrograma unitario del S.C.S. Al carecer de datos de aforos
aplicaremos este método. El tiempo del aguacero son 4 h y el de concentración
24 h, por tanto el tiempo punta y el caudal punta unitario será:
tp =
ta
4
+ 0.6 ⋅ Tc = + 0.6 ⋅ 24 = 16.4 h
2
2
Q p = 2.08 ⋅
A
400
= 2.08 ⋅
= 50.73 m 3 / s / cm
tp
16.4
La lluvia neta para cada período de retorno se calcula a partir de la intensidad
neta. En la tabla adjunta se muestran los cálculos realizados:
Tabla 23.4. Cálculo de la lluvia neta.
T
(años)
10
150
500
Intensidad
(cm/h)
Coef. de escorrentía
c
In = c I
(cm/h)
Pn = In ta
(cm)
2.85
4.76
5.98
0.4
0.6
0.95
1.14
2.86
5.68
4.57
11.44
22.75
El hidrograma unitario de 4 h para cada período de retorno se calcula en la siguiente
tabla, así como las ordenadas de los diferentes hidrogramas producidos por las distintas
lluvias netas correspondientes a cada período de retorno. El tiempo base de los tres
hidrogramas es el mismo, lo que varía es el caudal punta.
En dicha tabla se han multiplicado las coordenadas del eje de abcisas y de ordenadas
por los valores del tiempo punta y del caudal punta, respectivamente, obteniéndose así
un Hidrograma Unitario (volumen unidad e igual a 1 cm) de 4 h.
Para obtener el hidrograma correspondiente a una lluvia neta de volumen no unitario, se
multiplicarán las ordenadas obtenidas del Hidrograma Unitario de 4 h por el volumen
caído.
En el caso de que el tiempo de duración del aguacero hubiese sido distinto a 4 h habría
que haber obtenido el hidrograma de dicha lluvia a partir de la composición de
hidrogramas unitarios desplazados 4 h.
114
Problemas de Hidrología
Tabla 23.5. Cálculo de los hidrogramas de volumen no unitario.
Hidrograma
adimensional
t/tp
q/Qp
0
0.2
0.4
0.6
0.8
1
1.2
1.4
1.6
1.8
2
2.2
2.4
2.6
2.8
3
3.5
4
4.5
5
Hidrograma unitario Hidrogramas para 4.57, 11.44 y 22.75
4h
cm de lluvia, respectivamente. Q = q Pn
3
t (h)
q (m /s/cm)
Q (m3/s)
Q (m3/s)
Q (m3/s)
0
0.1
0.31
0.66
0.93
1
0.93
0.78
0.56
0.39
0.28
0.21
0.15
0.11
0.08
0.05
0.02
0.01
0.005
0
0
3.28
6.56
9.84
13.12
16.4
19.68
22.96
26.24
29.52
32.8
36.08
39.36
42.64
45.92
49.2
57.4
65.6
73.8
82
0
5.073
15.7263
33.4818
47.1789
50.73
47.1789
39.5694
28.4088
19.7847
14.2044
10.6533
7.6095
5.5803
4.0584
2.5365
1.0146
0.5073
0.25365
0
0
23.18361
71.869191
153.011826
215.607573
231.8361
215.607573
180.832158
129.828216
90.416079
64.914108
48.685581
34.775415
25.501971
18.546888
11.591805
4.636722
2.318361
1.1591805
0
0
58.03512
179.908872
383.031792
539.726616
580.3512
539.726616
452.673936
324.996672
226.336968
162.498336
121.873752
87.05268
63.838632
46.428096
29.01756
11.607024
5.803512
2.901756
0
0
115.41075
357.773325
761.71095
1073.31998
1154.1075
1073.31998
900.20385
646.3002
450.101925
323.1501
242.362575
173.116125
126.951825
92.3286
57.705375
23.08215
11.541075
5.7705375
0
En la figura siguiente se representan los hidrogramas correspondientes a los
hidrogramas de las avenidas para los distintos períodos de retorno.
I
Período de retorno 10 años
Período de retorno 150 años
Período de retorno 500 años
1400
ta
1200
800
3
Q (m /s)
1000
600
400
200
0
0
20
40
60
80
100
Tiempo (h)
Figura 23.3. Hidrogramas producidos para distintos períodos de retorno.
115
Problemas de Hidrología
PROBLEMA 24
Calcular el hidrograma de la avenida por el método de Puls, conociendo el
caudal y el volumen del embalse en función del nivel de agua en el
mismo, suponiendo que el hidrograma de entrada de agua al embalse se
produce cuando el embalse está a una cota de 300.2 m. Evaluar la
magnitud del despunte y el retraso en el pico de la avenida producido por
el embalse.
Tabla 1. Flujos y capacidades del embalse
NIVEL
(m)
299.5
300.2
300.7
301.2
301.7
302.2
302.7
CAPACIDAD
(Mm3)
4.8
5.5
6.0
6.6
7.2
7.9
8.8
FLUJO SALIDA
(m3/s)
0
0
15
40
75
115
160
Tabla 2. Hidrograma de entrada
T (h)
I (m3/s)
0
5
3
20
6
9 12
52 60 53
15
43
18
32
21
22
24
16
27
5
El método de Puls consiste en integrar mediante diferencias el balance de masa en el
embalse en un determinado tiempo. La ecuación que se obtiene es la siguiente:
(I1 + I 2 ) ⋅ ∆t + S
2


1
−
Q1 ⋅ ∆t  
Q ⋅ ∆t 
= S 2 + 2

2  
2 
donde I1 e I2 es el caudal de entrada en el embalse al principio y al final del intervalo ∆t,
Q1 y Q2 es el caudal de salida del embalse al principio y al final del intervalo ∆t, S1 y S2
es el volumen del agua en el embalse al principio y al final del intervalo ∆t.
Q ⋅ ∆t 

En primer lugar representaremos las curvas de S +
y caudal de salida Q con
2 

respecto al nivel del agua en el embalse h. Para ello se dispone de la tabla del
enunciado. El incremento de tiempo que se va a tomar es ∆t = 3 h ya que los valores del
hidrograma de entrada se dan cada 3 h.
116
Problemas de Hidrología
∆t = 3 h = 0.0108 ⋅ 10 6 s = 0.0108 Ms
Q ⋅ ∆t 

Con este incremento de tiempo se van a ir obteniendo los valores S +
con
2 

respecto al nivel de la lámina libre del embalse. En las siguientes figuras se muestran el
Q ⋅ ∆t 

con respecto a dicha lámina, respectivamente.
caudal de salida y S +
2 

Tabla 24.1. Caudal de salida y volumen.
NIVEL
(m)
CAPACIDAD
S (Mm3)
Q
(m3/s)
Q ⋅ ∆t 

S + 2 
299.5
300.2
300.7
301.2
301.7
302.2
302.7
4.8
5.5
6.0
6.6
7.2
7.9
8.8
0
0
15
40
75
115
160
4.8
5.5
6.081
6.816
7.605
8.521
9.664
180
Caudal de salida
160
140
100
3
Q (m /s)
120
80
60
40
20
0
299.5
300.0
300.5
301.0
301.5
302.0
302.5
303.0
Nivel (m)
Figura 24.1. Caudal de salida con respecto al nivel.
117
Problemas de Hidrología
11
(S+Q∆t/2)
10
3
(S+Q∆t/2) (Mm )
9
8
7
6
5
4
299.5
300.0
300.5
301.0
301.5
302.0
302.5
303.0
Nivel (m)
Figura 24.2. Volumen con respecto al nivel.
Una vez representadas las funciones anteriores, la secuencia de cálculo es como se
describe a continuación: Se parte de un nivel inicial de 300.2 m que corresponde a un
volumen de 5.5 Mm3 y un caudal de salida del embalse de 0 m3/s, por lo que,
Q ⋅ ∆t 
0 ⋅ 0.0108

= 5.5 Mm 3
S − 2  = 5.5 −
2

1
Del hidrograma de entrada se obtiene
(I1 + I 2 )
2
⋅ ∆t =
5 + 20
⋅ 0.0108 = 0.135 Mm 3
2
En consecuencia,
(I1 + I 2 )
Q ⋅ ∆t 
Q ⋅ ∆t 


= 0.135 + 5.5 = 5.635
⋅ ∆t + S −
S + 2  =
2
2  1


2
valor que llevado a la gráfica (ver figuras adjuntas) corresponde a un nivel de h2 =
300.32 m (Figura 24.3) Para este nivel el caudal de salida es Q2 = 2 m3/s (Figura 24.4).
Por otra parte,
Q ⋅ ∆t 
Q ⋅ ∆t 


3
S − 2  = S + 2  − Q 2 ⋅ ∆t = 5.635 − 2 ⋅ 0.0108 = 5.6134 Mm
2

2 
118
Problemas de Hidrología
y con este nuevo valor se procedería de igual forma para el cálculo de Q3:
(I 2 + I 3 )
Q ⋅ ∆t 
Q ⋅ ∆t 
20 + 52


=
⋅ 0.0108 + 5.6134 = 6.002 Mm 3
⋅ ∆t + S −

S + 2  =
2
2 2
2


3
11
(S+Q∆t/2)
10
3
(S+Q∆t/2) (Mm )
9
8
7
6
5.635
5
4
299.5
300.32
300.0
300.5
301.0
301.5
302.0
302.5
303.0
Nivel (m)
Figura 24.3. Estimación del nivel para un volumen dado.
180
Caudal de salida
160
140
100
3
Q (m /s)
120
80
60
40
20
2
0
299.5
300.32
300.0
300.5
301.0
301.5
302.0
302.5
303.0
Nivel (m)
Figura 24.4. Estimación del caudal de salida para un nivel dado.
119
Problemas de Hidrología
En la tabla siguiente se resume el proceso seguido de los cálculos realizados:
Tabla 24.2. Método de Puls.
(h)
(m3/s)
I n + I n +1
2
0
3
6
9
12
15
18
21
24
27
5
20
52
60
53
43
32
22
16
5
12.5
36
56
56.5
48
37.5
27
19
10.5
Tiempo Entr. I
I n + I n +1
⋅ ∆t
2
0.135
0.38
0.60
0.61
0.51
0.40
0.29
0.20
0.11
Q ⋅ ∆t 

S − 2 
n

(Mm3)
Q ⋅ ∆t 

S + 2 
 n +1

5.5
5.6134
5.8938
6.2156
6.3895
6.4435
6.4089
6.3247
6.2221
NIVEL
Q
(Mm3)
(m)
(m3/s)
5.635
6.002
6.4986
6.8258
6.9079
6.8485
6.7005
6.5299
6.3355
300.2
300.32
300.636
300.95
301.21
301.26
301.21
301.12
301.
300.88
0
2
10.01
26.2
40.4
43
40.7
34.8
28.5
23
En las figuras siguientes se muestran los hidrogramas de las avenidas de entrada y salida
al embalse. Se puede comprobar el desfase y despunte existente entre ambos:
Desfase: 6 h
Despunte: 60 – 43.0 = 17.0 m3/s
En la última figura se muestra la evolución temporal del nivel.
Hidrograma de entrada
Hidrograma de salida
Desfase
60
Despunte
40
3
Caudal (m /s)
50
30
20
10
0
0
5
10
15
20
25
30
Tiempo (h)
Figura 24.5. Hidrogramas de entrada y salida.
120
Problemas de Hidrología
301.4
301.2
Nivel (m)
301.0
300.8
300.6
300.4
300.2
0
5
10
15
20
25
30
Tiempo (h)
Figura 24.6. Evolución temporal del nivel.
En la Figura 24.5 se puede comprobar que el máximo del hidrograma de salida coincide
con el punto de corte de ambos hidrogramas.
121
Problemas de Hidrología
PROBLEMA 25
En un tramo de río se observó un hidrograma de entrada y otro de salida
cuyos valores numéricos se dan en la siguiente tabla. Estimar los valores
de K y x aplicables a dicho tramo mediante el método de Muskingum.
Tabla 1. Hidrogramas
0 6 12 18
Tiempo (h)
Hidr. entrada (m3/s) 5 20 50 50
Hidr. salida (m3/s) 5 6 12 29
24
32
38
30
22
35
36
15
29
42
10
23
48
7
17
54 60 66
5
5
5
13 9 7
El principio que se aplica para el cálculo de K y x es la de la conservación de la masa
que en el método de Muskingum es
(I1 + I 2 ) ⋅ ∆t − (Q1 + Q 2 ) ⋅ ∆t = ∆S = S 2 − S1
2
2
ó
(I1 − Q1 ) + (I 2 − Q 2 )
2
⋅ ∆t = ∆S = S 2 − S1
donde I1, Q1 y S1 son la entrada, salida y volumen de agua en el tramo del río al inicio
del intervalo de tiempo ∆t, respectivamente. I2, Q2 y S2 son la entrada, salida y volumen
de agua en el tramo del río al final del intervalo de tiempo ∆t, respectivamente.
S se expresa
S = K ⋅ [x ⋅ I + (1 − x ) ⋅ Q]
Aplicando un incremento de tiempo de 6 h, los cálculos se muestran en forma de tabla
(Tabla 25.1). El incremento del almacenamiento se calculan en las columnas 6 y 7,
respectivamente. Los valores (I1 – Q1) y (I2 – Q2) se calculan en la columna 4. En la
columna 5 se calcula su media; de esta manera el primer valor (7) es la media de 0 y 14;
el segundo valor (26) es la media de 14 y 38 y así sucesivamente.
En las columnas 8, 9 y 10 se calculan los valores de S mediante la expresión de
Muskingum dada anteriormente para tres valores distintos de x. Posteriormente se
representan y confrontan los valores de S obtenidos con las distintas x con los valores
de S obtenidos del balance de entradas y salidas.
La solución más exacta será aquella cuyos puntos estén más próximos a una recta, es
decir que la correlación sea la más aceptable. A partir de la recta obtenida se puede
deducir el valor de K, ya que será precisamente la pendiente de la misma.
122
Problemas de Hidrología
Tabla 25.1. Método de .Muskingum.
S = K ⋅ [x ⋅ I + (1 − x ) ⋅ Q]
Tiempo
I
(h)
(m3/s)
0
5
6
20
12
50
18
50
24
32
30
22
36
15
42
10
48
7
54
5
60
5
66
5
Q
(m3/s)
5
6
12
29
38
35
29
23
17
13
9
7
I–Q
0
14
38
21
-6
-13
-14
-13
-10
-8
-4
-2
Media ∆t x S = Σ ∆S
(I – Q) Media (m3/s h)
0
7
42
42
26
156
198
29.5
177
375
7.5
45
420
-9.5
-57
363
-13.5
-81
282
-13.5
-81
201
-11.5
-69
132
-9
-54
78
-6
-36
42
-3
-18
24
x=
0.35
5
10.9
25.3
36.4
35.9
30.5
24.1
18.5
13.5
10.2
7.6
6.3
x=
0.3
5
10.2
23.4
35.3
36.2
31.1
24.8
19.1
14
10.6
7.8
6.4
x=
0.25
5
9.5
21.5
34.3
36.5
31.8
25.5
19.8
14.5
11
8
6.5
En las siguientes figuras se puede comprobar que el valor x = 0.25 es el que más
aproxima los puntos a una recta. Así pués, tomaremos este valor como válido. La
pendiente de la recta nos proporcionará el valor de K:
K=
400
= 13.3 h
30
x = 0.35
40
35
3
(I.x+(1-x).Q) (m /s)
30
25
20
15
10
5
0
0
100
200
300
400
500
3
Almacenamiento (m /s.h)
Figura 25.1. Curva para x = 0.35.
123
Problemas de Hidrología
40
x = 0.3
35
3
(I.x+(1-x).Q) (m /s)
30
25
20
15
10
5
0
0
100
200
300
400
500
3
Almacenamiento (m /s.h)
Figura 25.2. Curva para x = 0.3.
40
x = 0.25
35
3
(I.x+(1-x).Q) (m /s)
30
25
20
15
10
5
0
0
100
200
300
400
500
3
Almacenamiento (m /s.h)
Figura 25.3. Curva para x = 0.25.
También se ha representado el hidrograma de la avenida de entrada y el de salida en la
última figura (Figura 25.4).
124
Problemas de Hidrología
Hidrograma de entrada
Hidrograma de salida
Desfase
60
50
Despunte (atenuación)
3
Q (m /s)
40
30
20
10
0
0
10
20
30
40
50
60
70
80
Tiempo (h)
Figura 25.4. Hidrogramas de entrada y salida.
De la Figura 25.4 se puede observar que el máximo del hidrograma de salida no
coincide con el punto de corte de ambos hidrogramas, ya que la solución de x es
aproximada.
125
Problemas de Hidrología
PROBLEMA 26
En un tramo de un río se observó el hidrograma de una avenida donde K =
12 h y x = 0.2. Si inicialmente el caudal de salida de dicho tramo es 10
m3/s se pide el hidrograma de caudales de salida
Tabla 1. Hidrograma de entrada
Tiempo (h)
Hidr. Entrada (m3/s)
0
10
6
20
12
50
18
60
24
55
30
45
36
35
42
27
48
20
54
15
A partir de la ecuación de Muskingum se obtiene el hidrograma de salida de un tramo
de río con la siguiente expresión:
Q n = C 0 ⋅ I n + C1 ⋅ I n −1 + C 2 ⋅ Q n −1
donde Qn e In son los valores de los caudales en el tiempo n de salida y de entrada,
respectivamente; Qn-1 e In-1 son los valores de los caudales en el tiempo anterior,
respectivamente. C0, C1 y C2 vienen dados por las siguientes expresiones:
C0 =
− K ⋅ x + 0.5 ⋅ ∆t
K − K ⋅ x + 0.5 ⋅ ∆t
C1 =
K ⋅ x + 0.5 ⋅ ∆t
K − K ⋅ x + 0.5 ⋅ ∆t
C2 =
K − K ⋅ x − 0.5 ⋅ ∆t
K − K ⋅ x + 0.5 ⋅ ∆t
Como K = 12 h y 2 ⋅ K ⋅ x = 2 ⋅ 12 ⋅ 0.2 = 4.8 h , el incremento de tiempo a elegir debería
estar comprendido entre ambos valores: 12 > ∆t > 4.8. Por ello elegiremos ∆t = 6 h.
Sustituyendo los datos se pueden obtener C0, C1 y C2:
C0 =
− K ⋅ x + 0.5 ⋅ ∆t
− 12 ⋅ 0.2 + 0.5 ⋅ 6
=
= 0.048
K − K ⋅ x + 0.5 ⋅ ∆t 12 − 12 ⋅ 0.2 + 0.5 ⋅ 6
C1 =
12 ⋅ 0.2 + 0.5 ⋅ 6
K ⋅ x + 0.5 ⋅ ∆t
=
= 0.429
K − K ⋅ x + 0.5 ⋅ ∆t 12 − 12 ⋅ 0.2 + 0.5 ⋅ 6
C2 =
K − K ⋅ x − 0.5 ⋅ ∆t 12 − 12 ⋅ 0.2 − 0.5 ⋅ 6
=
= 0.523
K − K ⋅ x + 0.5 ⋅ ∆t 12 − 12 ⋅ 0.2 + 0.5 ⋅ 6
Para el primer intervalo,
126
Problemas de Hidrología
I1 = 10 ⇒ C1 ⋅ I1 = 4.29
I 2 = 20 ⇒ C 0 ⋅ I 2 = 0.96
Q1 = 10 ⇒ C 2 ⋅ Q1 = 5.23
por lo que
Q 2 = C 0 ⋅ I 2 + C1 ⋅ I1 + C 2 ⋅ Q1 = 10.48 m 3 / s
Para los siguientes valores se procedería de igual forma. En la siguiente tabla se
muestran los resultados obtenidos.
Tabla 26.1. Resultados obtenidos.
Tiempo (h)
0
6
12
18
24
30
36
42
48
54
I (m3/s)
10
20
50
60
55
45
35
27
20
15
0.048 In
0.96
2.4
2.88
2.64
2.16
1.68
1.3
0.96
0.72
0.429 In-1
4.29
8.58
21.45
25.74
23.6
19.3
15.02
11.58
8.58
0.523 Qn-1
5.23
5.48
8.61
17.23
23.85
25.95
24.55
21.38
17.74
Q (m3/s)
10
10.48
16.46
32.94
45.61
49.61
46.93
40.87
33.92
27.04
En la siguiente figura se muestran los hidrogramas de entrada y de salida (Figura 26.1).
En dicha figura se puede ver que el valor máximo del hidrograma de salida no coincide
con el punto de corte de ambos hidrogramas. El método aplicado es un método
aproximado lo que origina que el desfase no coincida con dicho punto de corte de
ambos hidrogramas.
127
Problemas de Hidrología
Hidrograma de entrada
Hidrograma de salida
Desfase
70
60
Despunte (atenuación)
40
3
Q (m /s)
50
30
20
10
0
0
10
20
30
40
50
Tiempo (h)
Figura 26.1. Hidrogramas de entrada y salida.
128
60
Problemas de Hidrología
HIDROLOGÍA SUBTERRÁNEA
PROBLEMA 27
Se pretende realizar una excavación de 8 m de profundidad (ver figura),
para lo cual se quiere bajar el nivel freático por debajo de la cota de la
excavación a un mes vista. Para ello se quieren perforar dos tipos de
configuraciones de pozos (A y B), a partir de los cuales bombear. Se pide:
a) El caudal necesario que se ha de bombear en cada pozo en la
configuración de pozos A.
b) El caudal necesario que se ha de bombear en cada pozo en la
configuración de pozos B
c) El caudal necesario que se ha de bombear en cada pozo en las
configuraciones A y B conjuntas.
d) Obtener la expresión del descenso en los pozos A y B por
superposición de los efectos producidos por los bombeos en
los demás pozos.
NOTA: K = 100 m/d, Ss = 0.0001 m-1.
5m
100 m
3m
1m
B
Alzado
A
100 m
10 m
B
50 m
Planta
A
Figura 1. Esquema de la excavación.
129
Problemas de Hidrología
a) Tanto en la configuración A como en la B, el nivel en el punto más alejado de los
sondeos tiene que quedar por debajo de 3 m, lo que implica que en el propio pozo el
nivel ha de quedar a nivel inferior. En el caso de la configuración A el punto más
alejado de ambos sondeos son los puntos C y C’ de la figura adjunta.
Figura 27.1. Representación del bombeo. Alzado.
1m
A
51 m
100 m
C
C’
50 m
Planta
A
Figura 27.2. Representación del bombeo. Planta.
La distancia es:
d = 512 + 25 2 = 56.79 m
Para obtener el caudal que hay que bombear en cada pozo A durante un mes para bajar
el nivel por debajo de la excavación obligaremos a que el descenso producido en C o C’
sea 3 m. El descenso producido en C (o C’) será la suma de los descensos producidos
por el bombeo en ambos pozos (principio de superposición).
130
Problemas de Hidrología
En nuestro caso, como la función u es:
u=
S ⋅ b ⋅ r2
S ⋅ r2
S⋅ r2
0.0001 ⋅ 56.79 2
= s
= s
=
= 2.6 ⋅ 10 −5 ≤ 0.03
4⋅T⋅t 4⋅K ⋅b⋅t 4⋅K ⋅t
4 ⋅ 100 ⋅ 30
se puede aplicar la aproximación de Jacob en la fórmula de Theis:
s=
Q
 2.25 ⋅ T ⋅ t 
⋅ ln

4πT  S ⋅ r 2 
El descenso total se calcula sumando los descensos parciales producidos por cada pozo:
Q
Q
Q
 2.25 ⋅ T ⋅ t 
 2.25 ⋅ T ⋅ t 
 2.25 ⋅ T ⋅ t 
⋅ ln
⋅ ln
⋅ ln
+
 = 2⋅

2
2
4πT  S ⋅ r
4πT  S ⋅ r 2 
 4πT  S ⋅ r

sT = ∑ si =
i
donde r = 56.79 m, T = K b = 100*100 m2/d, S = Ss b = 0.0001*100, t = 30 días.
Como en C (ó C’) el descenso ha de ser sT = 3 m,
3 = 2⋅
Q
Q
 2.25 ⋅ T ⋅ t 
 2.25 ⋅ 100 ⋅ 30 
⋅ ln
⋅ ln
 = 2⋅
2
4
2 
4πT  S ⋅ r
4π10

 0.0001 ⋅ 56.79 
donde, despejando Q = 220 l/s para cada pozo.
b) En el caso de la segunda configuración el valor de la distancia al punto más alejado
es (ver Figura 27.3):
d = 50 2 + 35 2 = 61.03 m
El valor de u es:
u=
S ⋅ r2
S⋅ r2
0.0001 ⋅ 61.03 2
= s
=
= 3.1 ⋅ 10 −5 ≤ 0.03
4⋅T⋅t 4⋅K ⋅t
4 ⋅ 100 ⋅ 30
por lo que se puede aplicar la aproximación de Jacob a la fórmula de Theis. Haciendo el
mismo razonamiento que en el caso anterior,
sT = ∑ si = 2 ⋅
i
Q
Q
 2.25 ⋅ T ⋅ t 
 2.25 ⋅ 100 ⋅ 30 
⋅ ln
⋅ ln
=3
 = 2⋅
2
4
2 
4πT  S ⋅ r
4π10

 0.0001 ⋅ 61.03 
despejando, Q = 222.5 l/s por cada pozo. Se necesita más caudal de extracción en la
segunda configuración que en la primera.
131
Problemas de Hidrología
C
d
B
100 m
10 m
B
50 m
Planta
C’
Figura 27.3. Representación del bombeo. Planta. Posición B.
c) En el caso de utilizar ambas configuraciones conjuntamente, el punto más lejano de
los cuatro pozos es el punto central del rectángulo (punto C) (ver figura).
A
1m
C
B
100 m
10 m
B
50 m
Planta
A
Figura 27.4. Representación conjunta.
132
Problemas de Hidrología
En este caso la distancia AC = 51 m y la distancia BC = 35 m. Los valores de u son:
Ss ⋅ r 2
0.0001 ⋅ 512
u=
=
= 2.1 ⋅ 10 −5 ≤ 0.03
4⋅K ⋅t
4 ⋅ 100 ⋅ 30
u=
Ss ⋅ r 2
0.0001 ⋅ 35 2
=
= 10 −5 ≤ 0.03
4⋅K ⋅t
4 ⋅ 100 ⋅ 30
En consecuencia se puede aplicar la aproximación de Jacob. El descenso en C es la
suma de los descensos producidos por cada bombeo:
sT = ∑ si = 2 ⋅
i
 2.25 ⋅ T ⋅ t 
 2.25 ⋅ T ⋅ t 
Q
Q
 + 2 ⋅
=3
⋅ ln
⋅ ln
2
4πT  S ⋅ r1 
4πT  S ⋅ r22 
es decir,
3 = 2⋅
Q
Q
 2.25 ⋅ 100 ⋅ 30 
 2.25 ⋅ 100 ⋅ 30 
⋅ ln
+ 2⋅
⋅ ln
=3
4
2 
4
2 
4π10
4π10
 0.0001 ⋅ 51 
 0.0001 ⋅ 35 
despejando, Q = 103 l/s para cada uno de los cuatro pozos.
d) Para obtener la expresión de los descensos en los pozos A y B por el efecto
producido conjuntamente por todos los pozos se aplicará el principio de superposición.
Para el caso del pozo A el descenso total sAT será:
s AT = ∑ s i = s AA + s AB + s AB + s A = s AA + 2 ⋅ s AB + s A
i
donde sAA es el descenso producido por el pozo simétrico A por el bombeo de caudal, sA
es el descenso producido en el propio pozo A por bombear un caudal Q y sAB es el
descenso producido en A por el bombeo en los pozos B.:
s AA =
 2.25 ⋅ T ⋅ t 
Q
Q
 2.25 ⋅ 100 ⋅ 30 
 =
⋅ ln
⋅ ln
2
4
2 
4πT  S ⋅ rAA  4π10
 0.0001 ⋅ 102 
sA =
 2.25 ⋅ T ⋅ t 
 2.25 ⋅ 100 ⋅ 30 
Q
Q
 =

⋅ ln
⋅ ln
2
4
2 
4πT  S ⋅ rA  4π10
⋅
0
.
0001
r
A 

s AB =
 2.25 ⋅ T ⋅ t 
 2.25 ⋅ 100 ⋅ 30
Q
Q
 =
⋅ ln
⋅ ln
2
4
2
2
4πT  S ⋅ rAB  4π10
 0.0001 ⋅ 51 + 35
(
)



donde rA es el radio del pozo A, rAB es la distancia entre el pozo A y el B y rAA es la
distancia entre los pozos A. La expresión queda,
133
Problemas de Hidrología
s AT =
 2.25 ⋅ 100 ⋅ 30
Q   2.25 ⋅ 100 ⋅ 30 
⋅ ln
+ 2 ⋅ ln
2 
2
2
4πT   0.0001 ⋅ 102 
 0.0001 ⋅ 51 + 35
(
)
 2.25 ⋅ 100 ⋅ 30 


 + ln
2 
⋅
0
.
0001
r

A 


Para el caso del pozo B el descenso total sBT será:
s BT = ∑ s i = s BB + s BA + s BA + s B = s BB + 2 ⋅ s BA + s B
i
donde sBB es el descenso producido por el pozo simétrico B por el bombeo de caudal, sB
es el descenso producido en el propio pozo B por bombear un caudal Q y sBA es el
descenso producido en B por el bombeo en los pozos A.:
s BB =
 2.25 ⋅ T ⋅ t 
Q
Q
 2.25 ⋅ 100 ⋅ 30 
 =
⋅ ln
⋅ ln
2
4
2 
4πT  S ⋅ rBB  4π10
 0.0001 ⋅ 70 
sB =
 2.25 ⋅ T ⋅ t 
 2.25 ⋅ 100 ⋅ 30 
Q
Q
 =

⋅ ln
⋅ ln
2
4
2 
4πT  S ⋅ rB  4π10
⋅
0
.
0001
r
B 

s BA =
 2.25 ⋅ T ⋅ t 
 2.25 ⋅ 100 ⋅ 30
Q
Q
 =
⋅ ln
⋅ ln
2
4
2
2
4πT  S ⋅ rBA  4π10
 0.0001 ⋅ 51 + 35
(
)



donde rB es el radio del pozo B, rBA es la distancia entre el pozo A y el B (= rAB) y rBB es
la distancia entre los pozos B. La expresión queda,
s BT =
134
 2.25 ⋅ 100 ⋅ 30
Q   2.25 ⋅ 100 ⋅ 30 
⋅ ln
+ 2 ⋅ ln
2 
2
2
4πT   0.0001 ⋅ 70 
 0.0001 ⋅ 51 + 35
(
)
 2.25 ⋅ 100 ⋅ 30 


 + ln
2 

 0.0001 ⋅ rB 
Problemas de Hidrología
PROBLEMA 28
Deducir a partir de la ecuación de Thiem la ecuación de Goodman (1965)
para el cálculo del caudal que fluye hacia un túnel por unidad de longitud,
q, sabiendo que el radio del túnel es r, la profundidad del túnel por debajo
del nivel freático es H0 y la conductividad hidráulica es K.
Aplicar dicha ecuación al cálculo del caudal en un túnel de r = 2.5 m, H0 =
200 m y K = 10 m/d.
La ecuación de Thiem es la solución del descenso producido en régimen permanente en
un pozo situado en un terreno de extensión infinita cuando se bombea un caudal
constante Q. Se supone el medio homogéneo e isótropo:
H0 − h =
Q
R
⋅ ln 
2πT  r 
donde H0 es el nivel fijo existente en el caso de que no existiese el pozo, R es el radio de
influencia a partir del cual el nivel es invariable e igual a H0, h es el nivel producido por
el bombeo a una distancia r del centro del pozo (ver figura).
Q
R
r
H0
h
Figura 28.1. Esquema de pozo.
En el caso de un túnel el problema a resolver equivale al de un pozo vertical completo
que bombea en un acuífero con un límite (túnel) situado a una distancia H0 que está
siendo recargado con un caudal igual que el que fluye al túnel, consiguiéndose el
135
Problemas de Hidrología
régimen estacionario. En este caso el límite se sustituye con un pozo imagen que
introduce un caudal Q a una distancia de 2H0 (igual que si el límite fuese un río).
En la figura adjunta se representa el túnel (Figura 28.2) y el problema equivalente a
resolver (Figura 28.3).
s
H0
r
Figura 28.2. Esquema de túnel.
La fórmula de Thiem se puede expresar en logaritmos decimales:
H 0 − h = 2.3 ⋅
Q
Q
R
⋅ log 
2πT
r
Q
H0
Figura 28.3. Esquema de funcionamiento análogo.
136
Problemas de Hidrología
Aplicando la teoría de las imágenes, el descenso en el propio túnel es
s = 2 .3 ⋅
 R 
 R r 
Q
Q
Q
Q
 2H 0 
R
 = 2.3 ⋅
 = 2.3 ⋅
⋅ log
⋅ log
⋅ log
⋅ log  − 2.3 ⋅

2πT
2πT
2πT
2πT
r
 r 
 2H 0 
 R 2H 0 
como T = k b y b en este caso es la longitud del túnel,
s = 2.3 ⋅
q
Q
Q
 2H 0 
 2H 0 
 2H 0 
⋅ log
⋅ log
⋅ log
 = 2.3 ⋅
 = 2.3 ⋅

2πK ⋅ b
2πK
2πT
 r 
 r 
 r 
siendo q el caudal por unidad de longitud del túnel (Q/b). Despejando y sabiendo que el
descenso es s = H0 – h ≈ H0, se obtiene
q=
2πK
⋅ H0
2H 0 

2.3 ⋅ log
r 

que es la ecuación de Goodman.
Para el caso en que r = 2.5 m, H0 = 200 m y K = 10 m/d, sustituyendo se obtiene
q=
2π10
2πK
⋅ H0 =
⋅ 200 = 2476.04 m 2 d
2
⋅
200
2H
2.3 ⋅ log
2.3 ⋅ log 0 
2 .5
r 

(
)
137
Problemas de Hidrología
PROBLEMA 29
Para la construcción de un depósito enterrado circular es necesario
realizar una excavación circular de 50 m de diámetro y 5 m de
profundidad. Para trabajar en seco se precisa rebajar el nivel freático 3 m
por debajo de su cota natural situada a 2 m de profundidad. Para ello se
propone bombear en un pozo existente de 0.4 m de diámetro situado a 50
m del centro de la excavación. Este pozo es totalmente penetrante. El
acuífero tiene un espesor saturado de 50 m. Como paso previo se decide
realizar un ensayo de bombeo bombeando un caudal de 20 l/s y midiendo
los descensos en un piezómetro de observación perforado a 20 m de
distancia del pozo de bombeo. En este piezómetro se registraron los
descensos a distintos tiempos (ver Tabla).
Tabla 1. Descensos medidos en el punto de observación
Tiempo (h)
10
14
18
22
26
30
34
38
100
Descenso (m)
1.735
1.92
2.059
2.169
2.261
2.34
2.409
2.47
3.002
Se pide:
a) Dibujar los datos de los descensos medidos en el piezómetro de
observación en un gráfico semilogarítmico y razonar porqué los
datos se ajustan a una línea recta.
b) Determinar a partir de dicho gráfico, suponiendo válida la
aproximación de Jacob, la transmisividad y el coeficiente de
almacenamiento del acuífero.
c) Determinar a partir de qué tiempo es aplicable la aproximación de
Jacob.
d) Determinar el caudal que es necesario bombear en el pozo de
bombeo para garantizar que la excavación quede en seco al cabo
de 30 días de iniciar el bombeo.
e) Calcular el descenso producido en el propio pozo de bombeo cuyo
radio es de 0.2 m al cabo de 30 días, sabiendo que la eficiencia del
pozo es de 0.8 (la eficiencia es la relación entre el descenso teórico
y el real).
a) La representación de los descensos en un gráfico semilogarítmico se muestran
en la figura adjunta.
La explicación de que la representación obtenida es una recta es debido a que la
solución de Jacob establece que los descensos s son proporcionales al logaritmo
del tiempo. La relación entre el logaritmo neperiano y el decimal es una
constante de 2.3, por ello la representación de los descensos en ejes logarítmicos
neperianos daría también una recta. La pendiente de dicha recta es:
138
Problemas de Hidrología
Q
4πT
en el caso de que en el eje de abcisas se representasen los logaritmos neperianos.
En el caso de que el eje de abcisas sea de logaritmos decimales, la pendiente
sería,
2.3 ⋅
Q
4πT
3.2
3.0
descensos (m)
2.8
2.6
2.4
2.2
2.0
1.8
1.6
10
100
log (t)
Figura 29.1. Representación de los descensos.
b) Para calcular la transmisividad y el coeficiente de almacenamiento, conociendo
el valor del descenso en dos tiempos cualquiera y suponiendo válida la
aproximación de Jacob se tiene,
s1 =
Q
Q
 2.25 ⋅ T ⋅ t 1 
 2.25 ⋅ T ⋅ t 1 
⋅ ln
⋅ log
 = 2.3 ⋅

2
2
4πT  S ⋅ r
4πT

 S⋅ r

s2 =
Q
Q
 2.25 ⋅ T ⋅ t 2 
 2.25 ⋅ T ⋅ t 2 
⋅ log
⋅ ln
 = 2.3 ⋅

2
2
4πT  S ⋅ r
4πT

 S⋅ r

restando ambas,
139
Problemas de Hidrología
s 2 - s1 =
t 
t 
Q
Q
⋅ log 2 
⋅ ln 2  = 2.3 ⋅
4πT  t 1 
4πT
 t1 
Tomando los tiempos t2 = 100 h y t1 = 10 h y sabiendo que el caudal bombeado
es Q = 20 l/s = 1728 m3/d, se deduce,
3.002 − 1.735 = 2.3 ⋅
1728
1728
 100 
⋅ log
 = 2.3 ⋅
4πT
4πT
 10 
y despejando, T = 249.62 m2/d. Sabiendo que el espesor saturado es b = 50 m, la
permeabilidad es K = T/b = 249.62 / 50 = 5 m/d.
Q
Pozo de observación
20 m
Figura 29.2. Esquema de bombeo.
Para calcular S se sustituye el valor del descenso en un tiempo cualquiera y se
despeja. Escogemos el tiempo t2 = 100 h = 4.16 d,
s2 =
Q
1728
 2.25 ⋅ T ⋅ t 2 
 2.25 ⋅ 249.62 ⋅ 4.16 
⋅ ln
⋅ ln
=
 = 3.002
2
4πT  S ⋅ r
S ⋅ 20 2

 4π ⋅ 249.62 
de donde S = 0.025.
c) La aproximación de Jacob es aplicable siempre que u < 0.03, es decir,
u=
S⋅ r2
=≤ 0.03
4⋅T⋅t
Para los valores de T y S calculados y r = 20 m, el tiempo a partir del cual la
ecuación de Jacob es válida se deduce de
140
Problemas de Hidrología
u=
S⋅ r2
0.025 ⋅ 20 2
≤ 0.03
=
4 ⋅ T ⋅ t 4 ⋅ 249.62 ⋅ t
obteniéndose t > 0.33 d ó t > 8 h, por lo que los datos están en el rango donde es
válida la aproximación de Jacob.
d) Para conseguir que la excavación quede en seco al cabo de 30 días, se debe
bombear un caudal Qe que garantice que el descenso en el punto más desfavorable
sea de 3 m (ver figura). El punto más desfavorable es el punto de la excavación más
alejado del pozo de bombeo. Este punto está situado en el extremo del diámetro de
la excavación que pasa por el pozo de bombeo resultando por tanto que la distancia
re es igual a 75 m.
Entrando en la ecuación de Jacob con t = 30 días e imponiendo un descenso de 3 m,
se obtiene el caudal Qe
50 m
50 m
d = 0.4 m
5m
3m
Figura 29.3. Representación del nivel y excavación cuando se bombea.
se =
Qe
Qe
 2.25 ⋅ T ⋅ t 
 2.25 ⋅ 249.62 ⋅ 30 
⋅ ln
⋅ ln
=
=3
2
2
4πT  S ⋅ r
 4π ⋅ 249.62  0.025 ⋅ 75

Operando se obtiene Qe = 22.75 l/s (1966.25 m3/d).
141
Problemas de Hidrología
e) Para calcular el descenso en el pozo de bombeo se aplica ecuación de Jacob con
r = 0.2. El descenso teórico es
sp =
Qp
1966.25
 2.25 ⋅ 249.62 ⋅ 30 
 2.25 ⋅ T ⋅ t 
⋅ ln
⋅ ln
 = 10.43 m
=
2
2
4πT  S ⋅ r

 4π ⋅ 249.62  0.025 ⋅ 0.2
El descenso real es 10.43/0.8 = 13.04 m.
142
Problemas de Hidrología
PROBLEMA 30
En el plano de la figura se recogen los niveles piezométricos medidos en
una serie de pozos y piezómetros perforados en un acuífero formado por
los materiales de alteración de esquistos. A partir de estos datos y
sabiendo las cotas del arroyo próximo, se pide:
a) Dibujar el mapa de isopiezas con equidistancia de 2 m entre los
valores 240 y 260.
b) Razonar a qué pueden ser debidas la diferencias existentes en el
espaciamiento de las isopiezas e identificar las zonas de mayor y
menor permeabilidad.
c) Dibujar las líneas de corriente que pasan por los puntos A, B, C y D.
d) En uno de los sondeos disponibles de 0.4 m de diámetro se realizó
un ensayo hidráulico de bombeo, bombeándose un caudal
constante de Q = 1 l/s. Sabiendo que al cabo de 10 minutos el
descenso del nivel fue de 2.04 m y que al cabo de 100 minutos el
descenso había aumentado hasta 4.1 m, se pide determinar la
transmisividad del acuífero. Deducir el valor de la conductividad
hidráulica K sabiendo que el espesor saturado es de 10 m.
e) Calcular el tiempo de tránsito desde el punto C hasta el arroyo
suponiendo que la porosidad del acuífero es 0.2 y que la
conductividad hidráulica K es la obtenida en el apartado anterior.
B
A
258.7
262
C
254.5
256
256
252.4
252.5
250
246
100 m
245
250.4
248
252
MAPA DE
ISOPIEZAS
D
244
248
245.7
244
242
239
242
Cotas del Arroyo
240.3
240
238
Arroyo
244
Nivel piezométrico (m.s.n.m.)
Figura 1. Mapa de pozos y piezómetros
143
Problemas de Hidrología
a) y c) El mapa de isopiezas se muestra en la Figura adjunta. Las isopiezas indican
la existencia de flujo hacia el arroyo. Nótese que el arroyo no es un límite de
nivel constante y por ello las isopiezas no son paralelas a la traza del arroyo. Por
el mismo motivo, tampoco son ortogonales al arroyo las líneas de corriente que
pasan por los puntos A, B, C y D.
B
A
C
D
260
258.7
262
254.5
252.5
250
246
245
250.4
248
252
250 100 m
256
256
252.4
MAPA DE
ISOPIEZAS
245.7
244
242
239
244
248
242
Cotas del Arroyo
240.3
240
238
Arroyo
244
Nivel piezométrico (m.s.n.m.)
Figura 30.1. Mapa de isopiezas.
b) Se observa cómo aguas abajo de los puntos A, B, C y D existe una zona donde
las isopiezas están más juntas y por tanto en esta zona el gradiente piezométrico
es mayor alcanzando valores del orden de 0.12 (ver Figura 30.2).
En la zona situada a la derecha y cerca del arroyo, el gradiente es menor (del
orden de 0.05), lo que significa una mayor transmisividad, suponiendo el flujo
en régimen permanente.
Las posibles explicaciones de este comportamiento son que en la primera zona la
transmisividad es menor que en el resto del acuífero. Esta menor transmisividad
puede ser debida a dos motivos:
1. un menor espesor saturado,
2. una menor conductividad hidráulica (posiblemente asociada a la
existencia de un menor espesor de materiales cuaternarios).
d) Se conocen los descensos a dos tiempos, t1 y t2. Si s1 y s2 son los descensos en
estos dos tiempos, aplicando la ecuación de Jacob para el caudal Q = 1 l/s = 86.4
m3/d se obtiene
144
Problemas de Hidrología
B
C
Fuerte
A gradiente de nivel (0.12)
Baja transmisividad
258.7
262
256
252.5
250
100 m
250.4
248
252
MAPA DE
ISOPIEZAS
254.5
256
252.4
D
245
245.7
244
242
239
244
246
Menor
gradiente
piezométrico (0.05)
242
248
Mayor
permeabilidad240
Cotas del Arroyo
240.3
238
Arroyo
244
Nivel piezométrico (m.s.n.m.)
Figura 30.2. Zonas de mayor y menor permeabilidad.
s1 =
Q
Q
 2.25 ⋅ T ⋅ t 1 
 2.25 ⋅ T ⋅ t 1 
⋅ ln
⋅ log
 = 2.3 ⋅

2
2
4πT  S ⋅ r
4πT

 S⋅ r

s2 =
Q
Q
 2.25 ⋅ T ⋅ t 2 
 2.25 ⋅ T ⋅ t 2 
⋅ ln
⋅ log
 = 2.3 ⋅

2
2
4πT  S ⋅ r
4πT

 S⋅ r

restando ambas expresiones,
s 2 - s 1 = 2 .3 ⋅
t 
Q
⋅ log 2 
4πT
 t1 
Puesto que t2 es 10 veces t1, el término del logaritmo de t2 /t1 es reduce a 1. Por
tanto, se obtiene
s 2 - s 1 = 2 .3 ⋅
t 
Q
86.4
86.4
 100 
⋅ log
⋅ log 2  = 2.3 ⋅
 = 2 .3 ⋅
4πT
4πT
4πT
 10 
 t1 
luego,
4.1 − 2.04 = 2.3 ⋅
86.4
4πT
145
Problemas de Hidrología
De esta ecuación se puede obtener la transmisividad, T = 7.68 m2/d. Por tanto, la
conductividad hidráulica K es igual a K = T/b = 0.768 m/d.
e) A partir de la línea de corriente que pasa por el punto C se calculan las
longitudes, Li correspondientes a cada tramo entre isopiezas cuyo espaciamiento
es , ∆h = 2 m y siendo φ la porosidad igual a 0.2.
Para calcular el tiempo de tránsito se aplica la ecuación de Darcy:
q = −K ⋅
dh
= v⋅φ
dx
siendo v la velocidad real. Aproximando la anterior ecuación mediante
diferencias incrementales
K⋅
∆h
∆x
= v⋅φ =
⋅φ
∆x
∆t
donde ∆h es positivo. Despejando el incremento de tiempo ∆t
∆t =
φ ⋅ ∆x 2
K ⋅ ∆h
En nuestro caso ∆x = L. El tiempo de tránsito se calcula sumando todos los
incrementos de tiempo parciales de los 11 tramos (12 isopiezas, ver figura del
apartado a).
Tabla 30.1. Tiempo de tránsito.
Tramo
1
2
3
4
5
6
7
8
9
10
11
Total
146
longitud
cuadrado
Conductividad
Li (m)
Li2
K (m/d)
30.30
30.30
18.18
21.21
15.15
15.15
15.15
18.18
45.45
48.48
81.82
918.27
918.27
330.58
449.95
229.57
229.57
229.57
330.58
2066.12
2350.78
6694.21
0.768
0.768
0.768
0.768
0.768
0.768
0.768
0.768
0.768
0.768
0.768
Tiempo parcial
φ ⋅ L2i
(días)
∆t =
K ⋅ ∆h
119.57
119.57
43.04
58.59
29.89
29.89
29.89
43.04
269.03
306.09
871.64
1920 días (5.26 años)
Problemas de Hidrología
El valor que se obtiene es T = 5.26 años
Ahora bien, hay una zona donde la permeabilidad puede ser menor, por ello los
cálculos se han rehecho considerando que en la zona menos permeable la
conductividad hidráulica es el valor obtenido en el apartado d) dividido por un
factor de 2.4: K = 0.768/2.4 = 0.32 m/d, ya que la relación de gradientes es
aproximadamente 2.4. En régimen permanente, con el espesor saturado
constante, se cumple
q = − K 1 ⋅ ∇h 1 = − K 2 ⋅ ∇h 2
Sustituyendo,
K 1 ⋅ 0.12 = K 2 ⋅ 0.05
es decir,
K1 =
K2
2 .4
En la tabla siguiente se muestran los valores obtenidos. Hay 9 isopiezas más
juntas (zona de mayor gradiente) y 3 isopiezas más espaciadas (zona de menor
gradiente).
Tabla 30.2. Tiempo de tránsito. Opción 2ª.
Tramo
1
2
3
4
5
6
7
8
9
10
11
Total
longitud
cuadrado
Conductividad
Li (m)
Li2
K (m/d)
30.30
30.30
18.18
21.21
15.15
15.15
15.15
18.18
45.45
48.48
81.82
918.27
918.27
330.58
449.95
229.57
229.57
229.57
330.58
2066.12
2350.78
6694.21
0.32
0.32
0.32
0.32
0.32
0.32
0.32
0.32
0.768
0.768
0.768
Tiempo parcial
φ ⋅ L2i
(días)
∆t =
K ⋅ ∆h
286.95
286.95
103.30
140.6
71.74
71.74
71.74
103.30
269.03
306.09
871.64
2583 días (7 años)
En este caso el tiempo de tránsito es de 7 años.
147
Problemas de Hidrología
PROBLEMA 31
Para realizar una excavación de 40 x 60 m y 10 m de profundidad es
necesario rebajar el nivel freático que se encuentra a 5 m de profundidad.
En la zona existe un acuífero libre de 50 m de espesor inicial; su
conductividad hidráulica es de 5 m/d y la porosidad drenable es 0.1.
Se pide:
a) Calcular la transmisividad del acuífero.
b) Calcular la difusividad hidráulica del acuífero.
c) Calcular el caudal que es necesario bombear de forma permanente
en ambos pozos (ambos al mismo caudal) para mantener la
excavación en seco al cabo de 30 días.
d) Calcular el caudal que es necesario bombear de forma permanente
en ambos pozos (ambos al mismo caudal) para mantener la
excavación en seco al cabo de 60 días.
e) Calcular el volumen total bombeado del acuífero en hm3 al cabo de
6 meses en los dos supuestos anteriores (apartados c y d). Indicar
las ventajas e inconvenientes de cada uno de los dos supuestos.
Pozos de Bombeo
Acuífero 20
A
B
20
20
10
40
Excavación
a) La transmisividad es el producto de la conductividad, 5 m/d, y el espesor
saturado inicial, 50 m, es decir T = K b = 250 m2/d.
148
Problemas de Hidrología
b) La difusividad hidráulica del acuífero D es el cociente entre la transmisividad T
y el coeficiente de almacenamiento, S. Para un acuífero libre S coincide con la
porosidad drenable, es decir, S = 0.1, por tanto, D = T/S = 2500 m2/d.
c) Para rebajar el nivel freático 5 m, bombeando en los pozos A y B, es necesario
bombear un caudal Q tal que el descenso total (la suma de los descensos
producidos por ambos bombeos) sea al menos 5 m en el punto más desfavorable
de la excavación (punto C ó C’). El punto más desfavorable es el punto de la
esquina inferior, que es el más alejado.
Pozos de Bombeo
A
Acuífero 20 m
B
20 m
d1
20 m
d2
10 m
d1
40 m
Excavación
C’
C
Figura 31.1. Esquema de pozos y excavación.
Las distancias d1 y d2 desde A y B a C (ó C’) son
d 1 = 20 2 + 50 2 = 53.85 m
d 2 = 40 2 + 50 2 = 64.03 m
El descenso total se calcula mediante la fórmula de Jacob:
sT =
 2.25 ⋅ T ⋅ t 
 2.25 ⋅ T ⋅ t 
Q
Q
 +

⋅ ln
⋅ ln
2
4πT  S ⋅ d 1  4πT  S ⋅ d 22 
Sustituyendo, T = 250 m2/d, S = 0.1, t = 30 días, se obtiene
149
Problemas de Hidrología
5=
Q
Q
 2.25 ⋅ 250 ⋅ 30 
 2.25 ⋅ 250 ⋅ 30 
⋅ ln
+
⋅ ln

2 
4π ⋅ 250  0.1 ⋅ 53.85  4π ⋅ 250  0.1 ⋅ 64.03 2 
El caudal por pozo que se deduce es 23.39 l/s, es decir el caudal total es 46.8 l/s
equivalentes a 4042 m3/d.
Para el cálculo del descenso se ha aplicado la fórmula de Jacob ya que la función
u es inferior a 0.03 para las distancias d1 y d2:
d 12 ⋅ S 53.85 2 ⋅ 0.1
u=
=
= 0.009 ≤ 0.03
4 ⋅ T ⋅ t 4 ⋅ 250 ⋅ 30
u=
d 22 ⋅ S 64.03 2 ⋅ 0.1
=
= 0.013 ≤ 0.03
4 ⋅ T ⋅ t 4 ⋅ 250 ⋅ 30
d) Para rebajar el nivel freático 5 m al cabo de 60 de días bombeando en los pozos
A y B, es necesario bombear un caudal Q tal que el descenso total en el punto C
(ó C’) sea al menos 5 m. El cálculo sería igual que en el apartado anterior pero
con un tiempo de 60 días en lugar de 30 días:
sT =
 2.25 ⋅ T ⋅ t 
 2.25 ⋅ T ⋅ t 
Q
Q

 +
⋅ ln
⋅ ln
2
4πT  S ⋅ d 1  4πT  S ⋅ d 22 
Sustituyendo, T = 250 m2/d, S = 0.1, t = 60 días, se obtiene
5=
Q
Q
 2.25 ⋅ 250 ⋅ 60 
 2.25 ⋅ 250 ⋅ 60 
⋅ ln
+
⋅ ln

2 
4π ⋅ 250  0.1 ⋅ 53.85  4π ⋅ 250  0.1 ⋅ 64.03 2 
El caudal por pozo deducido es 19.83 l/s, es decir el caudal total es 39.7 l/s
equivalentes a 3426.8 m3/d.
En este caso también se aplica la fórmula de Jacob ya que se cumple
u=
d 12 ⋅ S 53.85 2 ⋅ 0.1
=
= 0.0045 ≤ 0.03
4 ⋅ T ⋅ t 4 ⋅ 250 ⋅ 60
u=
d 22 ⋅ S 64.03 2 ⋅ 0.1
=
= 0.0065 ≤ 0.03
4 ⋅ T ⋅ t 4 ⋅ 250 ⋅ 60
e) El volumen bombeado al cabo de 6 meses (180 días) en el caso del apartado c)
es:
Vol = Q ⋅ t = 4042 ⋅ 180 = 727560 m 3 = 0.72 hm 3
En el caso del apartado d):
150
Problemas de Hidrología
Vol = Q ⋅ t = 3426.8 ⋅ 180 = 616824 m 3 = 0.61 hm 3
Se deduce que la primera opción (secar la excavación al cabo de 30 días),
requiere un mayor caudal de bombeo y conlleva un mayor volumen de
extracción de agua. La segunda opción requiere menos bombeo y menor
volumen bombeado, pero tiene el inconveniente de que hay que esperar 30 días
más que en la primera opción para que la excavación quede en seco.
151
Problemas de Hidrología
REGULACIÓN
PROBLEMA 32
En la Tabla se dan los caudales medios mensuales en una cuenca.
Calcular la capacidad mínima y el volumen inicial que debe tener un
embalse que regule las aportaciones de la cuenca para garantizar una
demanda media mensual de 30 m3/s.
NOTA: Aplicar el método analítico para resolverlo.
Tabla 1. Aportaciones.
MES
APOR. (m3/s)
MES
APOR. (m3/s)
Enero
60
Julio
50
Febrero
45
Agosto
80
Marzo
35
Septiembre
105
Abril
25
Mayo
15
Junio
22
Octubre
90
Noviembre
80
Diciembre
70
En la tabla siguiente se muestran los valores de aportaciones y demandas y la diferencia
de ambas, ordenando los meses considerando el año hidrológico. A partir de estos
valores se pueden deducir los meses en los cuales se produce déficit.
Tabla 32.1. Cálculos.
Mes
Octubre
Noviembre
Diciembre
Enero
Febrero
Marzo
Abril
Mayo
Junio
Julio
Agosto
Septiembre
152
Aportaciones (m3/s)
90
80
70
60
45
35
25
15
22
50
80
105
Demanda (m3/s)
30
30
30
30
30
30
30
30
30
30
30
30
Diferencia
60
50
40
30
15
5
-5
-15
-8
20
50
75
Problemas de Hidrología
El déficit total será la suma de los valores de los caudales negativos (-5, -15, -8)
multiplicados por el número de días de cada mes (abril, mayo y junio):
Déficit = (5 x 30 + 15 x 31 + 8 x 30) x 86400 = 73.872 hm3
La capacidad mínima a embalsar será el déficit acumulado. La suma acumulada de la
diferencia de aportaciones y demanda de los meses anteriores a abril superan el déficit
total,
60 x 31 + 50 x 30 + 40 x 31 + 30 x 31 + 15 x 28 + 5 x 31 = 527.472 hm3
por lo que la cantidad de agua inicial embalsada a 1 de octubre (inicio del año
hidrológico) puede ser nula, además de que en octubre la diferencia de aportaciones y
demandas es positiva (60 m3/s).
El volumen del embalse, como mínimo tendrá que tener una capacidad de Emin = 73.872
hm3, para poder almacenar dicha cantidad los meses de octubre a marzo y hacer frente
al déficit producido los tres meses siguientes.
153
Problemas de Hidrología
PROBLEMA 33
El río Zújar es un afluente del río Guadiana. Para regar 40000 ha se
dispone de un embalse de capacidad E = 50 hm3. A partir de los datos de
las aportaciones mensuales de los años hidrológicos 80/81 y 81/82 (ver
Tabla) se pide determinar:
a) La magnitud de los déficits y vertidos.
b) La garantía de suministro.
c) La garantía de regulación.
Se supondrá que inicialmente el embalse está vacío y que la dotación
para riego es de 5000 m3/ha/año.
Tabla 1. Aportaciones.
AÑO 80/81
APORT. (Hm3)
AÑO 80/81
APORT. (Hm3)
AÑO 81/82
APORT. (Hm3)
AÑO 81/82
APORT. (Hm3)
OCT.
0.06
ABRIL
14.78
OCT.
0.56
ABRIL
13.94
NOV.
21.4
MAYO
10.27
NOV.
0.35
MAYO
2.38
DIC.
2.88
JUNIO
2.48
DIC.
92.13
JUNIO
0.73
ENERO
2.61
JULIO
0
ENERO
123.69
JULIO
0
FEBR.
3.67
AGOSTO
1.64
FEBR.
36.35
AGOSTO
0.61
MARZO
4.45
SEPT.
2.64
MARZO
14.74
SEPT.
3.14
Para calcular la magnitud de los déficits y vertidos calcularemos la demanda
correspondiente total:
Demanda total = 5000 m3/ha/año x 40000 ha x 2 años = 400 hm3
Tabla 33.1. Cálculo de la demanda mensual.
Mes
Octubre
Noviembre
Diciembre
Enero
Febrero
Marzo
Abril
Mayo
Junio
Julio
Agosto
Septiembre
154
Nº de días
31
30
31
31
28
31
30
31
30
31
31
30
Cálculo
31 x 400/730
30 x 400/730
31 x 400/730
31 x 400/730
28 x 400/730
31 x 400/730
30 x 400/730
31 x 400/730
30 x 400/730
31 x 400/730
31 x 400/730
30 x 400/730
Demanda mensual (hm3)
16.986
16.438
16.986
16.986
15.342
16.986
16.438
16.986
16.438
16.986
16.986
16.438
Problemas de Hidrología
En la Tabla 33.1 se ha tenido en cuenta los números de días de cada mes, calculando la
demanda correspondiente proporcionalmente:
Demanda del mes i = Nº de días del mes x 400/(2 x 365)
En la siguiente tabla se muestran los valores de déficits, vertidos, volumen de agua
almacenado en el embalse al final del mes y volumen regulado.
Tabla 33.2. Cálculo del volumen regulado.
Mes
Octubre 80/81
Noviembre 80/81
Diciembre 80/81
Enero 80/81
Febrero 80/81
Marzo 80/81
Abril 80/81
Mayo 80/81
Junio 80/81
Julio 80/81
Agosto 80/81
Septiembre 80/81
Octubre 81/82
Noviembre 81/82
Diciembre 81/82
Enero 81/82
Febrero 81/82
Marzo 81/82
Abril 81/82
Mayo 81/82
Junio 81/82
Julio 81/82
Agosto 81/82
Septiembre 81/82
TOTAL
Aport.
(hm3)
0.06
21.4
2.88
2.61
3.67
4.45
14.78
10.27
2.48
0
1.64
2.64
0.56
0.35
92.13
123.69
36.35
14.74
13.94
2.38
0.73
0
0.61
3.14
Demanda
(hm3)
16.986
16.438
16.986
16.986
15.342
16.986
16.438
16.986
16.438
16.986
16.986
16.438
16.984
16.438
16.986
16.986
15.342
16.986
16.438
16.986
16.438
16.986
16.986
16.438
400
Déficit
(hm3)
16.926
0
9.144
14.376
11.672
12.536
1.658
6.716
13.958
16.986
15.346
13.798
16.424
16.088
0
0
0
0
0
0
0
2.044
16.376
13.298
197.346
Vertido
(hm3)
0
0
0
0
0
0
0
0
0
0
0
0
0
0
25.144
106.704
21.008
0
0
0
0
0
0
0
152.856
Volumen
embalsado
0
4.962
0
0
0
0
0
0
0
0
0
0
0
0
50
50
50
47.754
45.256
30.65
14.942
0
0
0
Volumen
regulado
0.06
16.438
7.842
2.61
3.67
4.45
14.78
10.27
2.48
0
1.64
2.64
0.56
0.35
16.986
16.986
15.342
16.986
16.438
16.986
16.438
14.942
0.61
3.14
202.644
Para el cálculo de los volúmenes regulados en cada mes hay que tener en cuenta el
volumen almacenado en el embalse al final del mes anterior, ya que lo que se resuelve
es la ecuación de balance de masa:
E n = E n −1 + A n − D n
si
En < 50 hm3
155
Problemas de Hidrología
donde En y En-1 es el volumen de agua almacenado al final del mes n y n-1,
respectivamente; An y Dn son la aportación y demanda producida en dicho mes n.
La garantía de regulación es:
Gr =
Volumen regulado
Demanda Total
=
202.644
= 0.50 = 50%
400
Para calcular la garantía de suministro se calculan los días en lo cuales no se ha
producido déficit. Los meses donde no se ha producido déficit son: Noviembre del año
80/81, Diciembre, Enero, Febrero, Marzo, Abril, Mayo y Junio del año 81/82. El
número total de días es:
30 + 31 + 31 + 28 + 31 + 30 + 31 + 30 = 242 días
En consecuencia, la garantía de suministro es:
Gs =
156
Tiempo sin déficit
Tiempo Total
=
242
= 0.33 = 33%
730
Problemas de Hidrología
PROBLEMA 34
Para abastecer a una población urbana se ha construido un embalse A de
capacidad EA = 50 hm3 en un río determinado. La demanda media mensual
es de 15 hm3 y las aportaciones mensuales en dos años hidrológicos
característicos son las que se detallan en la Tabla 1.
Tabla 1. Aportaciones al embalse A.
AÑO 1
APORT. (Hm3)
AÑO 1
APORT. (Hm3)
AÑO 2
APORT. (Hm3)
AÑO 2
APORT. (Hm3)
OCT.
5
ABRIL
30
OCT.
15
ABRIL
25
NOV.
10
MAYO
20
NOV.
12
MAYO
10
DIC.
15
JUNIO
0
DIC.
10
JUNIO
5
ENERO
30
JULIO
0
ENERO
20
JULIO
0
FEBR.
40
AGOSTO
0
FEBR.
25
AGOSTO
3
MARZO
45
SEPT.
20
MARZO
30
SEPT.
24
Para regar una importante plantación se dispone de un embalse B de
capacidad EB = 50 hm3 en otro río distinto del anterior, que inicialmente se
encuentra al 50% de su capacidad. A partir de los datos de las
aportaciones mensuales de los años hidrológicos característicos 1 y 2
(ver Tabla 2) se ha podido comprobar que la demanda media mensual de
17 hm3 no se garantiza adecuadamente. Por ello, se ha pensado reutilizar
las aguas residuales provenientes de la población urbana, las cuales
representan el 70 % de la demanda, y canalizar los vertidos del embalse A
hasta la zona de regadío. Tanto el agua reutilizada como la proveniente
del vertido del embalse A servirá, en caso de que se necesite, para reducir
el déficit y evitar vaciar el embalse B, y no para llenarlo. Se pide:
a) Calcular el volumen inicial de llenado del embalse A para satisfacer al
100 % la demanda de la población urbana.
b) Calcular la garantía de regulación y suministro cuando sólo se utiliza
el embalse B para satisfacer la demanda de regadío.
c) Calcular la garantía de regulación y suministro cuando se utilizan las
aguas residuales de la población urbana y los vertidos canalizados del
embalse A.
Tabla 2. Aportaciones al embalse B.
AÑO 1
APORT. (Hm3)
AÑO 1
APORT. (Hm3)
AÑO 2
APORT. (Hm3)
AÑO 2
APORT. (Hm3)
OCT.
0
ABRIL
15
OCT.
15
ABRIL
5
NOV.
21
MAYO
10
NOV.
72
MAYO
1
DIC.
3
JUNIO
2
DIC.
60
JUNIO
0
ENERO
2
JULIO
1
ENERO
36
JULIO
0
FEBR.
4
AGOSTO
3
FEBR.
15
AGOSTO
3
MARZO
5
SEPT.
1
MARZO
14
SEPT.
3
157
Problemas de Hidrología
a) En este caso se realiza un estudio de regulación únicamente con el primer río y
suponiendo que el embalse inicialmente está vacío. En la tabla adjunta se detallan
los déficits, vertidos, volúmenes embalsados al final de un determinado mes y el
volumen regulado.
Al igual que en el problema anterior, para el cálculo de los volúmenes regulados en
cada mes hay que tener en cuenta el volumen almacenado en el embalse al final del
mes anterior, ya que lo que se resuelve es la ecuación de balance de masa:
E n = E n −1 + A n − D n
si
En < C
donde En y En-1 es el volumen de agua almacenado al final del mes n y n-1,
respectivamente; An y Dn son la aportación y demanda producida en dicho mes y C
es la capacidad máxima del embalse.
En caso de que la suma de las aportaciones y del volumen embalsado al final del
mes anterior menos la demanda sea superior a la capacidad máxima del embalse,
éste quedará lleno:
En = C
Tabla 34.1. Cálculo de volúmenes. Embalse A.
Mes
Octubre año 1
Noviembre año 1
Diciembre año 1
Enero año 1
Febrero año 1
Marzo año 1
Abril año 1
Mayo año 1
Junio año 1
Julio año 1
Agosto año 1
Septiembre año 1
Octubre año 2
Noviembre año 2
Diciembre año 2
Enero año 2
Febrero año 2
Marzo año 2
Abril año 2
Mayo año 2
Junio año 2
Julio año 2
Agosto año 2
Septiembre año 2
TOTAL
158
Aport.
(hm3)
5
10
15
30
40
45
30
20
0
0
0
20
15
12
10
20
25
30
25
10
5
0
3
24
Demanda
(hm3)
15
15
15
15
15
15
15
15
15
15
15
15
15
15
15
15
15
15
15
15
15
15
15
15
360
Déficit
(hm3)
10
5
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
15
Vertido
(hm3)
0
0
0
0
0
20
15
5
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
40
Volumen
embalsado
0
0
0
15
40
50
50
50
35
20
5
10
10
7
2
7
17
32
42
37
27
12
0
9
Volumen
regulado
5
10
15
15
15
15
15
15
15
15
15
15
15
15
15
15
15
15
15
15
15
15
15
15
345
Problemas de Hidrología
La garantía de regulación es:
Gr =
Volumen regulado
Demanda Total
=
345
= 0.95 = 95%
360
El volumen inicial de llenado, al comienzo del año hidrológico 1 tendrá que ser el
valor del déficit acumulado 15 hm3. Si inicialmente el embalse tiene 15 hm3, no
existirá déficit.
b) En el caso del segundo río, con el embalse B para satisfacer el regadío, se obtienen
los vertidos, déficits, volúmenes embalsados y regulados que se detallan en la tabla
siguiente.
En este caso el embalse se encuentra al 50 % de su capacidad, es decir 25 hm3, lo
que implica que disponemos de ese volumen de agua adicionalmente.
Tabla 34.2. Cálculo de volúmenes. Embalse B.
Mes
Octubre año 1
Noviembre año 1
Diciembre año 1
Enero año 1
Febrero año 1
Marzo año 1
Abril año 1
Mayo año 1
Junio año 1
Julio año 1
Agosto año 1
Septiembre año 1
Octubre año 2
Noviembre año 2
Diciembre año 2
Enero año 2
Febrero año 2
Marzo año 2
Abril año 2
Mayo año 2
Junio año 2
Julio año 2
Agosto año 2
Septiembre año 2
TOTAL
Aport.
(hm3)
0
21
3
2
4
5
15
10
2
1
3
1
15
72
60
36
15
14
5
1
0
0
3
3
Demanda
(hm3)
17
17
17
17
17
17
17
17
17
17
17
17
17
17
17
17
17
17
17
17
17
17
17
17
408
Déficit
(hm3)
0
0
2
15
13
12
2
7
15
16
14
16
2
0
0
0
0
0
0
0
0
17
14
14
159
Vertido
(hm3)
0
0
0
0
0
0
0
0
0
0
0
0
0
5
43
19
0
0
0
0
0
0
0
0
67
Volumen
embalsado
8
12
0
0
0
0
0
0
0
0
0
0
0
50
50
50
48
45
33
17
0
0
0
0
Volumen
regulado
17
17
15
2
4
5
15
10
2
1
3
1
15
17
17
17
17
17
17
17
17
0
3
3
249
En estas condiciones la garantía de regulación es:
159
Problemas de Hidrología
Gr =
Volumen regulado
Demanda Total
=
249
= 0.61 = 61%
408
teniendo en cuenta que el tiempo total en el que se ha producido déficit es
31 + 31 + 28 + 31 + 30 + 31 + 30 + 31 + 31 + 30 + 31 + 31 + 31 + 30 = 427 días
la garantía de suministro vale:
Gs =
Tiempo sin déficit
Tiempo Total
=
730 − 427
= 0.41 = 41%
730
c) Si se reutilizan las aguas residuales (0.7 x Demanda de abastecimiento = 10.5 hm3)
y los vertidos del embalse A se obtiene los valores de la tabla adjunta. Hay que
tener en cuenta que tanto el agua reutilizada como la procedente del vertido del
embalse A no sirven para llenar el embalse B, pero se utilizan antes que vaciar
dicho embalse.
Tabla 34.3. Cálculo de volúmenes.
Mes
Oct. 1
Nov. 1
Dic. 1
En. 1
Feb. 1
Mar. 1
Abr. 1
May. 1
Jun. 1
Jul. 1
Ago. 1
Sept. 1
Oct. 2
Nov. 2
Dic. 2
En. 2
Feb. 2
Mar. 2
Abr. 2
May. 2
Jun. 2
Jul. 2
Ago. 2
Sept. 2
TOT.
Aport. Demanda
(hm3)
(hm3)
0
17
21
17
3
17
2
17
4
17
5
17
15
17
10
17
2
17
1
17
3
17
1
17
15
17
72
17
60
17
36
17
15
17
14
17
5
17
1
17
0
17
0
17
3
17
3
17
408
0.7 x dem
población
10.5
10.5
10.5
10.5
10.5
10.5
10.5
10.5
10.5
10.5
10.5
10.5
10.5
10.5
10.5
10.5
10.5
10.5
10.5
10.5
10.5
10.5
10.5
10.5
252
La garantía de regulación es:
160
Vertido
Embalse B
0
0
0
0
0
0
0
0
0
0
0
0
0
5
43
19
0
0
0
0
0
0
0
0
67
Déficit
(hm3)
0
0
0
0
0
0
0
0
0
0
1.5
5.5
0
0
0
0
0
0
0
0
0
0
0
0
8.5
Vertido Volumen
A (hm3) embalsado
0
18.5
0
22.5
0
19
0
14.5
0
12
20
12
15
12
5
12
0
7.5
0
2
0
0
0
0
0
0
0
50
0
50
0
50
0
50
0
50
0
48.5
0
43
0
36.5
0
30
0
26.5
0
23
40
Volumen
regulado
17
17
17
17
17
17
17
17
17
17
15.5
11.5
17
17
17
17
17
17
17
17
17
17
17
17
401
Problemas de Hidrología
Gr =
Volumen regulado
Demanda Total
=
401
= 0.98 = 98%
408
Teniendo en cuenta que el tiempo en que el sistema ha permanecido con déficit es
31 + 30 = 61 días la garantía de suministro vale:
Gs =
Tiempo sin déficit
Tiempo Total
=
730 − 61
= 0.91 = 91%
730
es decir, se mejora sustancialmente la garantía del sistema. Se han reutilizado 401 –
249 = 152 hm3.
161