5. Dinámica de la pala Introducción I Rotor articulado. Velocidades I

Rotor articulado
Planos de referencia
Solución estacionaria
Rotor articulado
Planos de referencia
Solución estacionaria
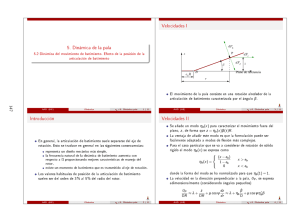
Rotor articulado. Velocidades I
Ã=¼= 2
­r
5. Dinámica de la pala
V1 cos®rsinÃ
V1 cos®rcosÃ
5.1 Dinámica del movimiento de batimiento
V1 cos®r
yr
xr
V1 cos®r
Ã=¼
Ã
Ã=0
r ¯_
¯
V1 cos®rcosÃ
Ã=3 ¼=2
139
AAD (HE)
Rotor articulado
Dinámica
Planos de referencia
Batim. Dinámica pala
1 / 31
Solución estacionaria
Introducción I
1
2
AAD (HE)
Rotor articulado
Dinámica
Planos de referencia
Rotor articulado. Velocidades II
Velocidades adimensionales relativas al elemento de pala (suponiendo
β ≪ 1):
Rotor articulado
Planos de referencia
UT
ΩR
= x cos β + µ sin ψ
UP
ΩR
= λ cos β + x
≈ x + µ sin ψ
≈ λ +x
3
β̇
+ µ cos ψ sin β
Ω
β̇
+ µβ cos ψ
Ω
UR
= µ cos ψ cos β
ΩR
≈ µ cos ψ
Solución estacionaria
AAD (HE)
Batim. Dinámica pala
3 / 31
Solución estacionaria
Dinámica
Batim. Dinámica pala
2 / 31
AAD (HE)
Dinámica
Batim. Dinámica pala
4 / 31
Rotor articulado
Planos de referencia
Solución estacionaria
Rotor articulado. Fuerzas I
Planos de referencia
Solución estacionaria
Rotor articulado. Fuerzas III
­
Equilibrio de momentos con respecto la articulación de batimiento,
∑ MB = 0
dFb
P
z
¯
r cos¯ ¼ r
∫ R
dFc
r
B
Rotor articulado
0
dFI
m r β̈ dr +
2
∫ R
mr
(0∫ R
0
Plano de referencia
∫ R
Ω β dr −
rdFb = 0
)( 0
) ∫R
m r 2 dr β̈ + Ω2 β = rdFb
2 2
0
1
β̈ + Ω β =
Ib
2
∫ R
0
rdFb
∫
donde Ib = 0R m r 2 dr es el momento de inercia de la pala. Para una
distribución uniforme de masa, m(r ) = m0 el momento sería
Ib = m0 R 3 /3 = mb R 2 /3 donde mb = m0 R es la masa de la pala.
dFb fuerza aerodinámica: dFb ≈ dL
dFc fuerza centrífuga dFc = m r Ω2 dr
dFI fuerza de aceleración: dFI = m r β̈ dr
Se desprecian los efectos de la gravedad y de la velocidad radial.
140
AAD (HE)
Rotor articulado
Dinámica
Planos de referencia
Batim. Dinámica pala
5 / 31
Solución estacionaria
Rotor articulado. Fuerzas II
AAD (HE)
Rotor articulado
Dinámica
Planos de referencia
Batim. Dinámica pala
7 / 31
Solución estacionaria
Rotor articulado. Fuerzas IV
La fuerza aerodinámica se puede expresar como (suponiendo U ≈ UT
y aerodinámica lineal):
El objetivo del problema es determinar la dependencia funcional β (ψ).
Por tanto se suele realizar generalmente el cambio de variable,
dβ dβ dψ
=
= Ωβ ′
dt ( d ψ) dt
d dβ
β̈ =
= Ω2 β ′′
dt dt
β̇ =
1
dFb ≈ dL = ρ U 2 cdrCl (α)
2
(
)
1 2
UP
≈ ρ UT cdrClα θ −
2
UT
(
)
1
≈ ρ cdrClα θ UT2 − UP UT
2
[ (
1
2
≈ρ cR (ΩR ) Clα
θ (x + µ sin ψ)2
2
(
)
)]
β̇
− λ + x + µβ cos ψ (x + µ sin ψ) dx
Ω
≈ρ cR (ΩR )2 Clα d F̄b
AAD (HE)
Dinámica
Batim. Dinámica pala
6 / 31
AAD (HE)
Dinámica
Batim. Dinámica pala
8 / 31
Rotor articulado
Planos de referencia
Solución estacionaria
Rotor articulado. Fuerzas V
Planos de referencia
Momento aerodinámico
∫ R
1
M̄b =
rdFb
Ib Ω2 0
∫
ρ c (ΩR )2 R 2 Clα 1
β ′′ + β =
x d F̄b
Ib Ω2
0
β ′′ + β = γ M̄b
∫ 1
x
0
2
y M̄b =
141
∫1
0
AAD (HE)
Rotor articulado
ρ cR 4 Clα
Ib
=
donde:
θ0 es el paso colectivo.
θ1 es la torsión geométrica de la pala.
θ1s sin ψ + θ1c cos ψ es el paso cíclico.
x d F̄b .
Batim. Dinámica pala
9 / 31
Solución estacionaria
AAD (HE)
Rotor articulado
Dinámica
Planos de referencia
Batim. Dinámica pala
11 / 31
Solución estacionaria
Rotor articulado. Fuerzas VIII
Valores característicos del número de Lock son 5-10. Este valor
depende de la densidad del aire y, por tanto, de la altitud.
La dinámica de batimiento es análoga a la de un sistema masa-muelle
sometido a una excitación exterior.
Desde el punto de vista de la respuesta libre del sistema (sin excitación
exterior)
Se considera que el ujo es uniforme: λ = cte
Bajo estas suposiciones, el momento de batimiento aerodinámico se
puede expresar como:
(
Mb = γ Mθ θc + Mθ
frecuencia propia: ω̄b = 1 (adimensional) y ω = Ω. Acciones exteriores
con una variación por vuelta del rotor excitará al modo de batimiento
en la frecuencia natural.
Dinámica
)
)
β̇
θ (x + µ sin ψ) − λ + x + µβ cos ψ (x + µ sin ψ) dx .
Ω
θ (x ) = θ0 + θ1s sin ψ + θ1c cos ψ + θ1 x
Rotor articulado. Fuerzas VI
AAD (HE)
(
2
θ (x ) = θc + θ1 x
fuerzas aerodinámicas
fuerzas de inercia
Dinámica
Planos de referencia
(
Obtenemos su expresión para un caso particular.
Se considera la siguiente distribución de paso
donde γ es el número de Lock:
γ=
Solución estacionaria
Rotor articulado. Fuerzas VII
Por tanto, la EDO del movimiento de batimiento se puede escribir
como:
β ′′ + β =
Rotor articulado
Batim. Dinámica pala
10 / 31
AAD (HE)
1
θ1 + Mλ λ + Mβ β + Mβ ′ β ′
Dinámica
)
Batim. Dinámica pala
12 / 31
Rotor articulado
Planos de referencia
Solución estacionaria
Rotor articulado. Fuerzas IX
Rotor articulado
Planos de referencia
Solución estacionaria
Rotor articulado. Fuerzas XI
Desarrollando los términos se obtiene:
1 1
1
+ µ sin ψ + µ 2 sin2 ψ
8 3
4
1 1
1
Mθ1 = + µ sin ψ + µ 2 sin2 ψ
10 4
6
1 1
Mλ = − − µ sin ψ
6 4
1
1
Mβ = − µ cos ψ − µ 2 cos ψ sin ψ
6
4
1 1
Mβ ′ = − − µ sin ψ
8 6
Mθc =
La acción exterior que alimenta la dinámica del batimiento contiene
variaciones en una vuelta y por tanto excita al sistema en la frecuencia
propia (tanto la excitación como la respuesta se pueden expresar en
términos de una serie de Fourier).
Las acciones aerodinámicas contienen un término β ′ que proporciona
amortiguamiento al sistema dinámico.
De esta manera: la frecuencia propia del sistema cambia ligeramente, y
la amplitud no tenderá a innito dando lugar a una respuesta acotada.
estos términos corresponden a los momentos de batimiento debidos a
variaciones del ángulo de ataque.
142
AAD (HE)
Rotor articulado
Dinámica
Planos de referencia
Batim. Dinámica pala
13 / 31
Solución estacionaria
Rotor articulado. Fuerzas X
Dinámica
Planos de referencia
Batim. Dinámica pala
15 / 31
Solución estacionaria
Plano de puntas I
En concreto:
Mθ
AAD (HE)
Rotor articulado
representa el momento de batimiento debido al cambio de ángulo
de ataque consecuencia del cambio de paso debido al control (θ0 , θ1s ,
θ1c ).
θ1 representa el momento de batimiento debido al cambio de ángulo
de ataque consecuencia del cambio de paso geométrico de la pala.
λ representa el momento de batimiento debido al cambio de ángulo
de ataque consecuencia de la velocidad inducida.
β representa el momento de batimiento debido al cambio de ángulo
de ataque consecuencia de la variación del ángulo de batimiento.
β ′ representa el momento de batimiento debido al cambio de ángulo
de ataque consecuencia de la variación de la velocidad de batimiento.
c
M
M
M
M
Expresamos el batimiento en términos de una serie de Fourier
∞
∑ βns sin nψ + βnc cos nψ
n=1
β (ψ) ≈ β0 + β1s sin ψ + β1c cos ψ + . . .
β (ψ) = β0 +
Los tres primeros términos de la serie representan
β0 : conicidad. Las puntas de la pala describen un círculo cuyo plano se
sitúa paralelo al plano de referencia. La pala describe un cono de
ángulo β0 .
zr
¯0
¯0
Ã= ¼
AAD (HE)
Dinámica
Batim. Dinámica pala
14 / 31
AAD (HE)
Plano de referencia
Dinámica
xr
Ã= 0
Batim. Dinámica pala
16 / 31
Rotor articulado
Planos de referencia
Solución estacionaria
Plano de puntas II
describen un círculo inclinado longitudinalmente, de forma que la parte
delantera apunta hacia abajo y la trasera hacia arriba.
β1s : coeciente de batimiento lateral. Las puntas de las palas
describen un círculo inclinado lateralmente, de forma que la parte del
lado de avance apunta hacia arriba y la parte que retrocede hacia abajo.
zr
Plano de referencia
¯1 c
xr
Ã= 3 ¼= 2 Plano de referencia
Es el sistema más habitual para controlar el paso de las palas.
¯1 s
yr
Ã= ¼= 2
¯1 s
Visto desde el lado retroceso
143
AAD (HE)
Rotor articulado
Solución estacionaria
zr
Ã= 0
¯1 c
Planos de referencia
Control del paso: plato distribuidor
β1c : coeciente de batimiento longitudinal. Las puntas de las palas
Ã= ¼
Rotor articulado
Visto desde la parte trasera
Dinámica
Planos de referencia
Batim. Dinámica pala
17 / 31
Solución estacionaria
Plano de puntas III
AAD (HE)
Rotor articulado
Dinámica
Planos de referencia
Batim. Dinámica pala
19 / 31
Solución estacionaria
Plano de control I
El paso se puede representar mediante la siguiente serie de Fourier:
Plano de puntas: la combinación de los tres batimientos se traduce
en que las puntas de las palas recorren un plano inclinado hacia
adelante y hacia arriba en el lado de avance. La pala describe un cono
inclinado en el espacio.
El plano de puntas representa el plano con respecto del cual la
tracción prácticamente es perpendicular.
Este plano es empleado en el análisis de actuaciones. Hasta ahora ha
sido el plano en el que se ha trabajado.
AAD (HE)
Dinámica
Batim. Dinámica pala
18 / 31
θ = θ0 +
∞
∑ θns sin nψ + θnc cos nψ
n =1
θ ≈ θ0 + θ1s sin ψ + θ1c cos ψ + . . .
La variación de paso proviene de dos fuentes
dinámica torsional de la pala. Los momentos de torsión son bajos en la
la pala, y en primera aproximación será despreciada la dinámica
torsional asociada a la elasticidad de la pala.
sistema de control del helicóptero. Los cambios en la sustentación
debidos a cambios en el paso son grandes porque el ángulo de ataque
efectivo cambia directamente. Por tanto, el control de las fuerzas en el
rotor es muy efectivo si se realiza a través de cambios en el paso.
AAD (HE)
Dinámica
Batim. Dinámica pala
20 / 31
Rotor articulado
Planos de referencia
Solución estacionaria
Plano de control II
Rotor articulado
Planos de referencia
Solución estacionaria
Plano de control IV
Los tres primeros términos de la serie representan
θ0 : paso colectivo. Controla el valor medio de las fuerzas
sustentadoras de la pala.
Plano de control: siempre existirá un plano con respecto del cual el
paso se puede expresar como θ = θ0 es decir no existe variación en
una vuelta y el paso es constante. Este plano recibe el nombre de
plano de control.
µ0
Plano de referencia
Plano de control
Visto desde lado de avance
Dinámica
Planos de referencia
Batim. Dinámica pala
21 / 31
Solución estacionaria
Plano de control III
AAD (HE)
Rotor articulado
Dinámica
Planos de referencia
Batim. Dinámica pala
23 / 31
Solución estacionaria
Equivalencia batimiento-paso I
θ1c y θ1s paso cíclico. Representa una variación por vuelta del paso.
Controla la orientación del vector de tracción modicando la
orientación del plano de puntas.
θ1s : paso cíclico longitudinal.
Ã= 3
¼=
Proporciona control longitudinal del
Ã= ¼
2
helicóptero.
µ 1s
Proporciona control lateral del helicóptero.
µ1 s
l
e contro
Plano d
Visto desde lado de avance
AAD (HE)
{µ 1 c
Plano de referencia
Plano d
zr
e contro
Plan
l
Visto desde atrás
Dinámica
1c
Ã= 0
1c
s
Ã= ¼
=2
µ
µ
1s
Plano de referencia
¯1
¯ 1c
µ
Batim. Dinámica pala
22 / 31
o de
xr
s
¯1 c
Ã= 0
pun
ta
zr
ol
ontr
µ1 s
Plan
Pla
ec
no d
Plano de referencia
Ã= ¼
Visto desde el lado de avance
AAD (HE)
¯1 s{µ 1 c
θ1c : paso cíclico lateral.
¯1 c+µ 1 s
144
AAD (HE)
Rotor articulado
Dinámica
o de
{µ 1 c
Ã= 3¼=2
cont
rol
o de
Plan
tas
pun
¯1 s
yr
Plano de referencia
Ã= ¼=2
Visto desde atras
Batim. Dinámica pala
24 / 31
Rotor articulado
Planos de referencia
Solución estacionaria
Solución estacionaria I
Rotor articulado
Planos de referencia
Solución estacionaria
Solución estacionaria III
La solución estacionaria será de la forma
Despejando los coecientes del plano de puntas
β (ψ) = β0 + β1s sin ψ + β1c cos ψ
β0 = γ
Al buscar la solución estacionaria como funciones armónicas de ψ el
término β ′′ + β de la EDO se reduce a:
θ1c − β1s =
β ′′ + β = β0
θ1s + β1c + θ1s
La EDO se reescribe como:
β ′′ + β = β0 = γ [Mθ (θ0 + θ1s sin ψ + θ1c cos ψ) + Mθ1 θ1 + Mλ λ +
µ2
=
1 − 12 µ 2
[
θ0 (
8
1+µ
2
)
(
)
5
µ
λ
1 + µ 2 + θ1s −
+
10
6
6
6
θ1
4
3 µβ0
1 + 12 µ 2
(
)
− 83 µ θ0 + 34 θ1 − 34 λ
1 − 12 µ 2
]
145
+ Mβ (β0 + β1s sin ψ + β1c cos ψ) +
]
+Mβ ′ (−β1c sin ψ + β1s cos ψ)
AAD (HE)
Rotor articulado
Dinámica
Planos de referencia
Batim. Dinámica pala
25 / 31
Solución estacionaria
Solución estacionaria II
2
)
θ1
(
)
]
5
µ
λ
β0 = γ
1+µ +
1 + µ 2 + θ1s −
8
10
6
6
6
(
)
2
θ
1
1
µ
µ
0 = 1c 1 + µ 2 − β1s − β0 − β1s
8
2
8
6
16
(
)
θ
3
µ
µ
µ
1
µ2
0 = 1s 1 + µ 2 + θ0 + θ1 − λ + β1c − β1c
8
2
3
4
4
8
16
AAD (HE)
θ0 (
Dinámica
Planos de referencia
Batim. Dinámica pala
27 / 31
Solución estacionaria
Solución estacionaria IV
Agrupando los términos sin dependencia azimutal, los términos sin ψ y
los términos cos ψ (pues son funciones independientes) se obtienen
tres ecuaciones para β0 , β1s y β1c :
[
AAD (HE)
Rotor articulado
Dinámica
Batim. Dinámica pala
26 / 31
Estas expresiones permiten obtener la orientación del plano de puntas
con respecto al plano de control. A partir de las ecuaciones del
equilibrado del helicóptero (por ejemplo el momento de alabeo y de
cabeceo proporcionarían β1s y β1c ) y dada una condición de vuelo se
puede obtener la orientación del plano de puntas y a partir de las
anteriores expresiones se puede determinar la orientación del plano de
control. Por tanto se puede determinar el control de paso cíclico para
esa condición de vuelo.
β0 y β1c suelen tomar valores de unos pocos grados, mientras que β1s
suele ser bastante más pequeño.
El efecto de la gravedad es una disminución de 0,1 − 0,2o en β0 .
AAD (HE)
Dinámica
Batim. Dinámica pala
28 / 31
Rotor articulado
Planos de referencia
Solución estacionaria
Solución estacionaria V
Rotor articulado
Planos de referencia
Expresiones trigonométricas empleadas
Solución en vuelo axial
β0 = γ
θ1c − β1s = 0
[
θ0
8
+
θ1
10
−
λ
6
sin2 ψ =
]
cos2 ψ =
cos nψ cos mψ =
θ1s + β1c = 0
Implica que el plano de puntas y el de control se sitúan paralelos. El
plano de puntas corresponde a un cono sin inclinación ni lateral ni
longitudinal.
146
AAD (HE)
Rotor articulado
Dinámica
Planos de referencia
Batim. Dinámica pala
29 / 31
Solución estacionaria
Solución estacionaria VI
Rotor en el vacío (sin fuerzas aerodinámicas) β = β1c cos ψ + β1s sin ψ
(solución de β ′′ + β = 0). Signica que el plano de puntas adquiere
una orientación en el espacio arbitraria pero ja ya que β1c y β1s están
indeterminados (no son función del control). En otras palabras ya que
no hay fuerzas aerodinámicas no hay medios por los que el el paso de
la pala pueda producir momentos sobre el disco.
Rotor en aire (con fuerzas aerodinámicas) tiene la capacidad de
producir un momento debido al paso y por tanto controlar su
orientación en el espacio. Si la inuencia aerodinámica sólo fuera a
través de este momento, el rotor respondería al momento del paso con
una velocidad de inclinación constante. Sin embargo, el momento
asociado a la velocidad de batimiento amortigua este movimiento.
AAD (HE)
Solución estacionaria
Dinámica
Batim. Dinámica pala
30 / 31
sin nψ sin mψ =
cos nψ sin mψ =
AAD (HE)
1 − cos 2ψ
2
1 + cos 2ψ
2
cos (n + m)ψ + cos (n − m)ψ
2
cos (n − m)ψ − cos (n + m)ψ
2
sin (n + m)ψ − sin (n − m)ψ
2
Dinámica
Batim. Dinámica pala
31 / 31