Document

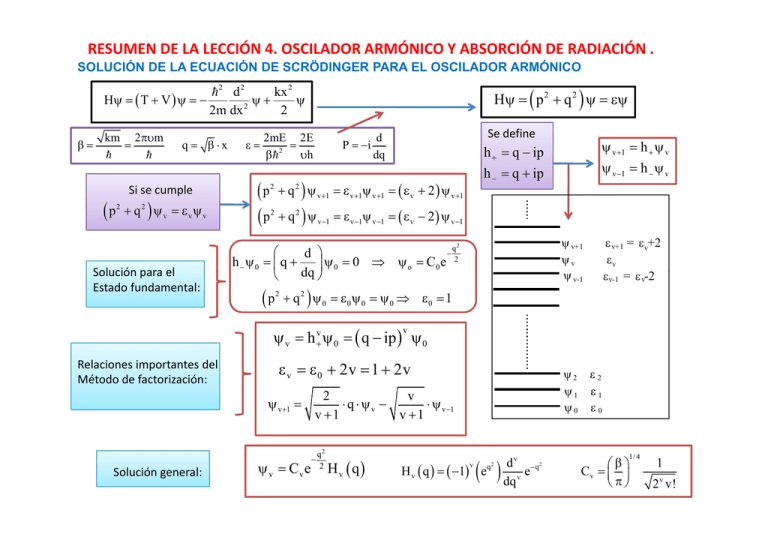
RESUMEN DE LA LECCIÓN 4. OSCILADOR ARMÓNICO Y ABSORCIÓN DE RADIACIÓN .
SOLUCIÓN DE LA ECUACIÓN DE SCRÖDINGER PARA EL OSCILADOR ARMÓNICO
Hψ = ( p 2 + q 2 ) ψ = εψ
kx 2
=2 d 2
Hψ = ( T + V ) ψ = −
ψ+
ψ
2m dx 2
2
β=
km 2πυm
=
=
=
(p
q = β ⋅x
Si se cumple
2
+ q2 ) ψ v = εvψ v
ε=
2mE 2E
=
β=2
υh
(p
(p
2
2
P = −i
Se define
d
dq
+ q 2 ) ψ v +1 = ε v +1ψ v +1 = ( ε v + 2 ) ψ v +1
+ q 2 ) ψ v −1 = ε v −1ψ v −1 = ( ε v − 2 ) ψ v −1
ψ v+1
ψv
ψ v-1
q
−
⎛
d ⎞
h − ψ 0 = ⎜ q + ⎟ ψ 0 = 0 ⇒ ψ o = C0 e 2
dq ⎠
⎝
2
Solución para el
Solución
para el
Estado fundamental:
(p
ψ v +1 = h + ψ v
ψ v −1 = h − ψ v
h + = q − iip
h − = q + ip
2
+ q 2 ) ψ 0 = ε0 ψ 0 = ψ 0 ⇒ ε0 = 1
ε v+1 = εv+2
εv
εv-1 = ε v-2
ψ v = h +v ψ 0 = ( q − iip ) ψ 0
v
Relaciones importantes del Método de factorización:
ε v = ε 0 + 2v = 1 + 2v
ψ v +1 =
Solución general:
ψ v = Cve
ψ2
ψ1
ψ0
2
v
⋅ q ⋅ ψv −
⋅ ψ v −1
v +1
v +1
−
q2
2
Hv (q )
( )
H v ( q ) = ( −1) e
v
q2
d v − q2
e
dq v
ε2
ε1
ε0
⎛β⎞
Cv = ⎜ ⎟
⎝π⎠
1/ 4
1
2 v v!
OSCILADOR ARMÓNICO
A-B
⎛1
⎞
E v = hυ ⎜ + v ⎟
⎝2
⎠
ΔE = E v +1 − E v = hυ < k B T
Cualquier unión entre átomos o moléculas actúa de Cualquier
unión entre átomos o moléculas actúa de
acumulador de energía y se comporta como un oscilador armónico
‐Energía térmica (choques)
‐Enlaces covalentes e iónicos (Región IR)
‐Absorción‐emisión de radiación
Molécula como péndulo o muelle que almacena energía ‐Conversión interna de energía
‐Puentes de hidrógeno (IR lejano)
‐Clusters o molécula de van der Walls (microondas)
OSCILADORES ACOPLADOS: ENERGÍA DE DISPERSIÓN DE LONDON.
μ = ex = αE
μ
μ
E
E London = −
R
x
x1
x2
3hυ1υ2 α1α 2
2R 6 ( υ1 + υ2 )
α (polarizabilidad) tiene unidades de volumen (c.g.s.). Es proporcional al volumen de una molécula, y es una propiedad casi aditiva.
fuerzas de van der Walls :
p
p
‐Dipolo‐dipolo, ‐ Dipolo‐dipolo inducido
‐Dispersión.
ABSORCIÓN DE RADIACIÓN ELECTROMAGNÉTICA
μ nm = e ∫ ψ m rψ n dτ
hυ = Em ‐ En, es condición necesaria, aunque no suficiente, para que se produzca la absorción. Energía
electrónica
Energía
de vibración
Energía
de rotación
Permite obtener las reglas de selección espectroscópicas
Permite obtener las reglas de selección espectroscópicas.
En IR; Δv = ±1. Momento dipolar de transición:
Proporcional a la probabilidad de la transición.
Si μnm = 0, la transición no se da.
El momento dipolar debe modificarse durante la transición.
‐UV‐visible (electrónica). Siempre hay cambio. Energía
cinética
‐IR (vibración). El modo de vibración debe modificar el momento dipolar. ‐Microondas (Rotación). La rotación de la molécula d b
debe modificar el momento dipolar. difi
l
t di l
UV-Visible
Microondas
Por debajo de
Radio ondas
‐Traslación. El momento dipolar nunca se modifica en la transición, luego no existe absorción ni emisión.
IR
kT
Las reglas de selección dependen del valor de μnm