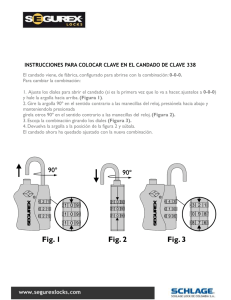
Determinar densidad corriente campo elctrico y potencial dentro

Determinar densidad corriente campo eléctrico y potencial dentro una
argolla
Problema 1
Se tiene una argolla muy delgada, de radio interior a y exterior b, a la que se ha
cortado un trozo, de ángulo . La argolla está hecha de un material de
conductividad g, y sus extremos están terminados en dos placas muy delgadas
hechas de conductor ideal, las que son mantenidas a una diferencia de potencial V0,
por medio de una batería.
a)
Determine la densidad de corriente
, el campo eléctrico
, y el potencial
, dentro de la argolla. Suponga que el potencial electrostático depende
solamente de la coordenada angular
.
b)
Determine el campo magnético
, producido por la distribución de corriente
, en el centro de la argolla.
Figure 11.18:
Solución Problema 1
a)
,
Podemos suponer, de acuerdo a la indicación, que el potencial
y por lo tanto la corriente fluye en la dirección contraria a los punteros del
reloj (aquí suponemos que V(0) = 0, y
Laplace se convierte simplemente en
). La ecuación de
cuya solución, con las condiciones de borde indicadas, es
Por lo tanto, el campo eléctrico y la corriente son:
Como la argolla es muy delgada (espesor
por el de una corriente superficial Js,
), podemos representar su efecto
b)
El campo magnético en el punto de coordenadas
mediante la expresión
se puede evaluar
Para evaluar esta expresión tomamos primero el numerador,
entonces
Finalmente,
http://www.loseskakeados.com