+ (2
Anuncio

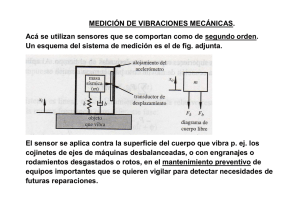
2.7 DINÁMICA DE SISTEMAS DE SEGUNDO ORDEN La ecuación diferencial general para los instrumentos de segundo orden es: a2 d2y/dt2 + a1 dy/dt + a0 y = x(t) (1) Donde: x(t) es la entrada al sensor, la magnitud a medir o controlar y(t) es la salida o respuesta. En todos los análisis se usan en lugar de: a0, a1 y a2 , otros 3 parámetros: K, n y porque como veremos tienen una mejor interpretación física; ellos se definen así: Sensibilidad estática: K = 1/ a0 Frecuencia natural ó propia del sensor: n = (a0 / a2) -1/2 Razón de amortiguamiento: a1 / 2(a0 a2) ½ [ Obs.: es la letra griega Dseda que es equivalente a nuestra: Z ] De aquellas definiciones resulta: (a2 /a0) = (1/n2) (a1 /a0) = (2n) Entonces dividiendo la ec. (1) por a0 y reemplazando queda: (1/n2) d2y/dt2 + (2n) dy/dt + y = Kx (2) 2.7.1 Respuestas de un sensor de segundo orden a una entrada tipo: escalón unitario u(t) En la tabla adjunta se resumen las respuestas: y(t)/K , o soluciones de la ec. diferencial cuando x(t) = u(t) Se puede observar que: - la salida del sensor cambia según que el valor de la razón de amortiguamiento: sea menor, igual o mayor que 1, - en los 3 casos, la salida presenta dos términos: uno permanente o estable y otro transitorio (decreciente por efecto de la exponencial negativa) - cuando “t” tiende a infinito, la salida tiende a la unidad, o sea es igual a la entrada y por tanto no hay error dinámico. - Si es menor que 1 se dice que el sensor es subamortiguado, la salida se aproxima al valor final 1 con oscilaciones o sea “y” toma valores mayores y menores que 1. Esto es porque la parte transitoria de la rta. puede tener valores positivos y negativos según el signo del factor “sen”. - Si es mayor que 1 el sensor es sobreamortiguado, la salida tiende al valor final siempre desde un mismo lado (con valores menores que 1) - Si = 1 se dice que hay amortiguamiento crítico, esto porque cambia el tipo de respuesta. En la gráfica siguiente se representan los 3 tipos de respuesta a una entrada escalón según el valor de . En la gráfica siguiente se aprecia el efecto de los valores de en el caso subamortiguado: cuanto menor es la amortiguación mayores son las oscilaciones alrededor del valor final. En abscisas va: (n t), y en ordenadas: y(t) / K Para la curva correspondiente a = 0.1 se indican: - Mp es el sobrepaso o rebasamiento (overshoot), - tr es el tiempo de elevación o de subida (rise time) desde el 10 % hasta el 90 % del valor final, - ts es el tiempo de asentamiento. 2.7.2 Respuesta de un sensor de segundo orden a una entrada sinusoidal, tipo: A sen t Cuando se estudia el efecto en la salida de una entrada de frecuencia variable, se dice que es la “respuesta en frecuencia” del sensor. Por simplicidad se ha omitido la parte transitoria de la salida, estudiando sólo la respuesta estable o permanente: ENTRADA: A sen t SALIDA: y(t) dada por la expresión: Con dada por la expresión: La amplitud de la señal de salida es la amplitud de la respuesta ideal: KA, dividida por una expresión que ahora depende de dos parámetros: la razón de amortiguación y el cociente n de la frecuencia de entrada (o sea de la magnitud a medir o controlar) dividida por la frecuencia propia del sensor: En las 2 gráficas siguientes se representan: a) en abscisas la razón de frecuencias: ( n) y b) en ordenadas: T= y/KA, (o TRANSMISIBILITY) Ambas en escalas logarítmicas Como la amortiguación se hizovariar entre 0.01 y10, lo que genera es una familia de curvas. Es fácil ver en la fórmula que si n y = 0 entonces se anula el denominador y aparece una asíntota vertical en n =1. Como nunca es cero en la realidad, lo que se observa son “picos” de amplitud de señal de salida, lo que se denomina resonancia. Observando esta primera gráfica: para un buen uso del sensor, lo deseable es trabajar en la zona próxima a la recta horizontal por 1 para tener mínimo error dinámico, para lo cual el valor óptimo de la razón de amortiguamiento es: = 0.707 y que permite llegar a valores de n = 0.6 aprox. En la gráfica siguiente se representa el ángulo de fase en función de n