Composicion de funciones

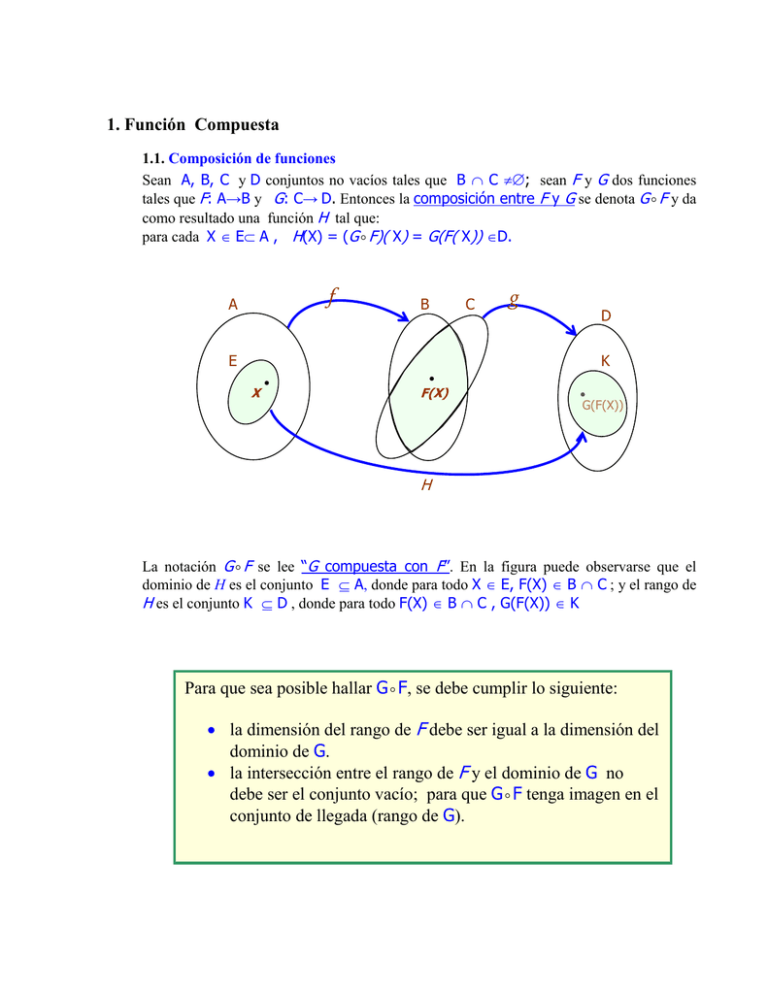
1. Función Compuesta
1.1. Composición de funciones
Sean A, B, C y D conjuntos no vacíos tales que B  C ; sean F y G dos funciones
tales que F: A→B y G: C→ D. Entonces la composición entre F y G se denota G  F y da
como resultado una función H tal que:
para cada X  E A , H(X) = (G  F)( X) = G(F( X)) D.
f
A
B
E
C
g
D
K
X
F(X)
G(F(X))
H
La notación G  F se lee “G compuesta con F”. En la figura puede observarse que el
dominio de H es el conjunto E  A, donde para todo X  E, F(X)  B  C ; y el rango de
H es el conjunto K  D , donde para todo F(X)  B  C , G(F(X))  K
Para que sea posible hallar G  F, se debe cumplir lo siguiente:
 la dimensión del rango de F debe ser igual a la dimensión del
dominio de G.
 la intersección entre el rango de F y el dominio de G no
debe ser el conjunto vacío; para que G  F tenga imagen en el
conjunto de llegada (rango de G).
La composición de funciones no cumple con la propiedad conmutativa.
No obstante, si cumple con la propiedad asociativa:
(H  (G  F)) (X) = H(G  F(X))
= H(G(F(X)))
((H  G)  F))(X) = (H  G)( F(X)) = H(G(F(X))),
y
(H  (G  F)) (X) = ((H  G)  F))(X) = (H  G  F)(X).
1.2. Continuidad de una función compuesta
Sea F: A→B una función continua en X0  A , y sea G : C→D tal que B C  una
función continua en F(X0)  B C . Sea H = G  F.
F
A
G
B
D
C
E
G(F(X0))
F(X0)
X0



H
Como F es continua en X0 entonces lim F(X)  F(X 0 ) ,
X X0
>0
existe un
lo que indica que dado un
 > 0 tal que:
F( X )  F( X 0 )  
cuando
X  X0   .
Así mismo, Como G es continua en F(X0) entonces:
lim
F ( X ) F ( X 0 )
G(F(X))  G( F(X 0 )) ,
lo que indica que dado un  > 0 existe un  > 0 tal que :
G( F( X ))  G( F( X 0 ))   cuando F( X )  F( X 0 )   .
De donde G( F( X ))  G( F( X 0 ))   cuando X  X 0   , lo que es equivalente a
decir que
lim G(F(X))  G( F(X 0 ))
X X0
y permite afirmar que la función H = G  F es continua en X0.
De la composición de dos funciones continuas en X0, resulta otra
función que también es continua en X0.
1.3. Diferencial de la función compuesta. Regla de la cadena
Casos de estudio




gf
gf
gf
gf
,
,
,
,
con
con
con
con
f
f
f
f
:→
:  → p
: n → p
: n → p
y
y
y
y
g:
g:
g:
g:
 → :
p → :
p → :
p → m:
A) Caso g  f , con f :  →  y g:  → :
Sean f y g dos funciones reales de una variable; tales que f es diferenciable en un
elemento x0 de su dominio y g es diferenciable en el elemento f(x0) que pertenece al
dominio de g. La derivada en x0 de la función g  f se calcula a través de:
g
f  ' (x0 ) 
Haciendo
g
lim
t 0
u = f(x0)
y
f  (x0  t)   g f  (x0 ) lim g  f(x0  t)  g  f(x0 )

t 0
t
t
v = f(x0  t)  f(x0 ) ,
o lo que es equivalente,
f(x0  t)  v  f(x0 )  v  u
queda:
g
f  ´ (x0 ) 
lim g  v  u   g  u 
t 0
t
que puede rescribirse así:
g
f  ´ (x0 ) 
=
lim g  v  u   g  u   v  lim g  v  u   g  u   v 
   t 0
 
t 0
t
v
v
t
lim g v  u   g u   f(x0  t)  f(x0 ) 


t 0
v
t


Tomando en cuenta que cuando t  0, v  0, y que u = f(x0) :
g
f  ´ (x0 ) 
lim g  f ( x0 )  v   g  f ( x0 ) lim  f(x0  t)  f(x0 ) 
 , de donde :
v 0
t  0 
v
t

g
f  ´ (x0 )  g ´( f ( x0 )) f ´( x0 )
El resultado obtenido recibe el nombre de “regla de la cadena” y permite determinar
la derivada en x0 de la función compuesta g  f. Este resultado es de uso frecuente en
situaciones como la que se muestra a continuación:
Si g(x) = xn, entonces g´(x) = n xn-1; luego si (g  f)(x) = g(f(x)) = ( f(x))n, entonces:
(g  f)´(x) = (( f(x)) n)´ = n (f(x))
n-1
f´(x).
B) Caso g  F , con F :  → p y g: p → :
En principio, para facilitar la comprensión en éste caso, se toma
F :  → 2 y g: 2 → . Considere que
 f ( t )  x 
F( t )   1    
 f 2 ( t )  y 
es una función diferenciable en el elemento t0 de su dominio, y g(x,y) = z es una función
diferenciable en el elemento F(t0 ).
 x0   f 1 ( t 0 ) 
   
  F( t 0 )
 y0   f 2 ( t 0 ) 
Dado que F :  → 2 y que g: 2 → , y que la intersección del rango de F con el
dominio de g no es vacía ( ya que F(t0) pertenece al dominio de g ), entonces:
z = z(t) = g(f1(t),f2(t)) = (g  F)(t) .
donde g  F :  → .
F
g
 x
 
 y
t
z
gF
Como g es diferenciable en (x0,y0), puede afirmarse, sobre la base de la definición del
diferencial total de una función, que:
z=
z
z
x 
y
x ( x0 , y0 )
y ( x0 , y0 )
1
, resulta:
t
Sea  t = t – t0  0 . Multiplicando la igualdad anterior por
 z z
x z
y

=
t x ( x , y ) t y ( x , y ) t
0
0
0
0
En virtud que cuando t  t0, (x, y)  (x0,y0) y  t 0, entonces:
 z
y 
z
x z
= lim 

t 0 t
t 0 x
t y ( x0 , y0 ) t 
 ( x0 , y 0 )
lim
y dado que:
z dz

t  0  t
dt
 z´(t 0 ) ,
lim
t0
x dx

t 0  t
dt
 x´(t 0 )
lim
y dy

t 0  t
dt
 y´(t 0 ) ,
y lim
t0
t0
Sustituyendo queda:
z
dx
z
dy
dz

=
dt t0  x ( x 0 , y 0 ) dt t 0  y ( x 0 , y 0 ) dt t 0
o en forma equivalente:
z´(t0) = zx(x0,y0)x´(t0) + zy(x0,y0)y´(t0).
Si lo anterior se hace para t
y (x, y) cualquiera de los dominios de F
x
 
respectivamente, con    F( t ) , se obtiene que:
 y
dz
=
dt
 z dx
 x dt

 z dy
 y dt
z´ = zx x´+ zy y´.
Por otra parte, dado que:
z(t) = (g  F)(t) ;
z = g(x,y) ;
x = f1(t),
y = f2(t), y que
(x0,y0) = (f1(t0), f2(t0)) = F(t0)
y
g
y en virtud que :
z´(t0) = zx(x0,y0)x´(t0) + zy(x0,y0)y´(t0)
entonces :
g  F ´( t0 )  g f ( t ) ( F( t0 )) f1´( t0 )  g f ( t ) ( F( t0 )) f 2´( t0 )
1
2
o también:
g
df1
g
d( g  F )

=
 f1 F( t ) dt t 0  f 2
dt
t0
0
F( t 0
df 2
dt
)
t0
que, escrito en forma de producto matricial, queda:
 df1 
 



g

g
d( g  F )
  dt 
= 
dt
 f1 f 2  F ( t 0 )  df2 
t0
 dt t0
Como g es diferenciable en F(t0) y F es diferenciable en t0, entonces:
 df1 


 g g 

 = d F ( t0 ) g ;
d t0 F =  dt 
 df2 
 f1 f 2  F ( t0 )


 dt t0
Por otro lado, en virtud que g  F :  → , al existir
d( g  F )
, puede afirmarse que
dt
t0
g  F es diferenciable en t = t0; luego:
d( g  F )
= d t0 ( g  F ) .
dt
t0
Sustituyendo, queda:
d t0 ( g  F ) = d F ( t0 ) g d t0 F .
Observe que d t0 ( g  F ) es una matriz de una fila con una columna, ya que
g  F :  → .
Todo lo anteriormente escrito es válido para F y g tales que F :  → p es una función de
variable t diferenciable en un elemento t0 de su dominio y g: p →  es una función de
variables x1,x2,x3,…,xp diferenciable en el elemento F(t0). Es decir, dadas las
funciones:
 f1( t ) 


 f2 ( t )
=
F( t )  
 


 f ( t )
p


 x1 
 
 x2 
  
 
x 
 p
g(x1,x2,x3,…,xp) = y
 f 1 ( t 0 )   x10


 f 2 ( t 0 )   x 20
diferenciables en t0 y F( t 0 )  

   


 f ( t )  x
p
0

  p0



 respectivamente, entonces, dada



(g  F)(t) = g( f1(t), f2(t), …, fp(t)),
puede afirmarse que :
d (g  F)
dt
t
g
f1
F ( t0
df1
g

dt t 0 f 2
)
 g

 f
 1
g
f 2
F ( t0
df2
dt
)

=
0

t0
g
f p
df p
F ( t0 )
 df1

 dt
 df2
g 
 dt
f p 
F ( t0 )  
 df p

 dt
o en forma equivalente:
d t0 ( g  F ) = d F ( t0 ) g d t0 F
dt








t 0
=
t0
siendo ésta última matriz de una fila y una columna (note que
resaltar que si F :  → p
g  F :  → ). Cabe
y g: p → , diferenciables en
respectivamente, g  F es diferenciable en t0; ya que como g  F
t0 y F(t0)
:  →  (la existencia
de la derivada de ésta función en t0 es suficiente para afirmar que es diferenciable en t0) .
También:
dy
dt t0
y
=
x1 ( x
10
,x20 ,,x p0
dx1
y

dt t0 x2 ( x
)
10
,x20 ,,x p0
dx2
y

dt t0
x p
)
dxp
( x10 ,x20 ,,x p0 )
dt
t0
y´( t 0 ) = yx1 ( x10 , x20 ,, xp0 )x1´( t0 )  yx2 ( x10 , x20 ,, xp0 )x2´( t0 )   yx p ( x10 , x20 ,, xp0 )xp´( t0 )
y para
t y ( x1 , x2 ,, x p ) cualesquiera de los dominios de F y g respectivamente, con
( x1 , x2 ,, x p )  F( t ) , puede afirmarse que:
y dx1 y dx2
y dxp
dy

 
=
dt
x1 dt x2 dt
x p dt
y´ =
yx1 x1´  yx2 x2´   yx p xp´