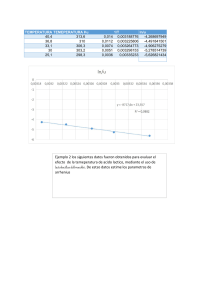
Dependencia con la temperatura

Dependencia de (k vs. T):
k ≡ f (T )
Expresiones empíricas para el estudio de la dependencia de
k con la temperatura:
Ecuación de Arrhenius:
k = Ae
− Ea / RT
Svante Arrhenius
(1859-1927)
Premio Nobel, 1903
A: factor exponencial (depende de la temperatura)
R: constante de los gases (R=8.314472 J mol-1 K-1)
Ea: energía de activación
1
k = Ae − Ea / RT
Aplicando logaritmos:
Ea constante
Ea
ln(k ) = ln( A) −
RT
Ea varía con T
Derivando respecto a 1/T:
d ln(k )
Ea
=−
d (1 / T )
R
Gráfico de Arrhenius
Gráficos de Arrhenius no lineales:
k = A´T m e − E0 / RT
A´, m, E0 : parámetros independiente de T
E0
2
Gráficos de Arrhenius no lineales: k
ln ( k ) = ln ( A´) + m ln (T ) −
= A´T m e
− E 0 / RT
E0
RT
ln ( k ) m E0
E + mRT
= +
= 0
2
dT
T RT
RT 2
d ln ( k )
d (1/ T )
=−
Ea
R
≡
d ln ( k )
Ea
=−
d (T )
RT 2
Ea = E0 + mRT
“Energía de Activación”
Barrera de Reacción:
E1 − E−1 = ΔU
3
Constante de Equilibrio:
k1
⎯⎯
→Y + Z
A + B ←⎯
⎯
k−1
υ1 = υ−1
k1 [ A][ B ] = k−1 [Y ][ Z ]
⎛ [Y ][ Z ] ⎞
Kc = ⎜
⎜ [ A][ B ] ⎟⎟
⎝
⎠eq
∴
d ln ( k1 )
E
= − 12
d (T )
RT
ΔU
⎛ ∂ ln K c ⎞
⎜
⎟ =−
RT 2
⎝ ∂T ⎠ P
Kc =
k1
k −1
d ln ( k−1 )
E
= − −12
d (T )
RT
E1 − E−1 = ΔU
Energía de las Moléculas,
Distribución Estadística:
Maxwell-Boltzman (Clásica)
f (E) =
≅e
-E´/kB T
1
Ae
E / k BT
kB (Constante de Boltzman)
=1.38 x 10-23 J.grado-1
Bose-Einstein
(Cuántica)
1
f ( E ) = E / k BT
Ae
−1
Fermi-Dirac
(Cuántica)
1
f ( E ) = E / k BT
Ae
+1
4
“Energía de Activación”
Barrera de Reacción
Mecánica Estadística:
Velocidad de Reacción TST:
υ = ν ⎡⎣ AB ≠ ⎤⎦
[AB≠] : número de especies con suficiente energía para superar la barrera
(concentración de complejo activado)
ν: frecuencia con que AB≠ se descompone en productos
Energía de una vibración:
Ecuacion de Planck: E=hν
Términos Clásicos: E=kBT
Para calcular [AB≠] se emplea la
hipótesis del equilibrio:
A + B ↔ AB≠ → C
hν = k BT
Ke =
k T
ν= B
h
[AB ]
≠
[A][B]
[AB≠]=Ke[A][B]
υ=
k BT
⋅ K e [ A][B ]
h
5
Según la mecánica estadística, para la reacción general:
aA + bB + " → " + yY + zZ
" qYy ⋅ qZz − RT0
Ke = a b e
q A ⋅ qB "
E
donde:
q: funciones de partición totales, por unidad de volúmen. (q = qe qv qr qt)
E0: cambio de energía (a 0 K) correspondiente a la reacción de a moles de A
con b moles de B.
∴ Para el cuasi-equilibrio: A + B ↔ AB≠
E
− 0
q≠
Ke =
e RT
q A ⋅ qB "
E
Substituyendo
Ke =
− 0
q≠
e RT
q A ⋅ qB "
υ=
en
k BT
⋅ K e [ A][B ]
h
E
− 0
k BT
q≠
⋅
υ=
e RT [A][B ]
h q A ⋅ qB "
E
− 0
k BT
q≠
⋅
k=
e RT
h q A ⋅ qB "
TST
6
Formulación Termodinámica:
Constante de equilibrio en términos termodinámicos:
≠
K e = e −Δ G
0
/ RT
Δ≠G0: variación de energía libre estándar de
Gibbs cuando el complejo activado se forma a
partir de los reaccionantes
Δ≠ G 0 = Δ≠ H 0 − TΔ≠ S 0
≠
Ke = e− Δ S
0
Δ≠S0: variación de entropía estándar
Δ≠H0: entalpía de activación estándar
/ R − Δ≠ H 0 / RT
e
k=
υ=
k BT
⋅ K e [ A][B ]
h
kT −Δ≠ S 0 / R −Δ≠ H 0 / RT
e
e
h
Ejercicio:
Calcular k (298 K) para la reacción A + B → AB, sabiendo que para una
molécula lineal el momento de inercia viene dado por (qe=1):
2
I = d AB
m A mB
m A + mB
m(A)=1 au
m(B)=16 au
d(A-B)*=2Å
E0=1.2 kJ/mol
kB=1.38x10-23J.K-1
h=6.63x10-34 J.s
7