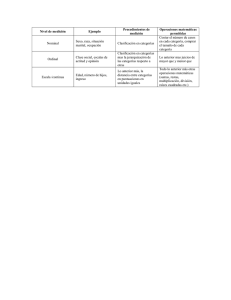
ESCALAS DE MEDICIÓN ............................. Como la estadística

ESCALAS DE MEDICIÓN
.............................
Como la estadística analiza los datos y éstos son el resultado de las mediciones, necesitamos ocupar cierto tiempo para estudiar las escalas de medición. Este tema es de suma
importancia, pues el tipo de escala de medición utilizado para reunir los datos ayuda a
determinar el tipo de prueba de inferencia estadística a emplearse en el análisis de los
datos. Desde un punto de vista teórico, una escala de medición puede tener uno o más de
los siguientes atributos matemáticos: magnitud, un intervalo igual entre unidades
adyacentes y un cero absoluto. Existen cuatro clases de escalas que aparecen de manera
común en las ciencias del comportamiento: nominal, ordinal, de intervalo y razón o proporción. Ellas difieren en el número de atributos matemáticos que poseen.
Escalas nominales
Una escala nominal representa el nivel mínimo de medición y se utiliza con frecuencia para
variables de naturaleza cualitativa y no cuantitativa. Algunos ejemplos de variables
cualitativas son las marcas de zapatos deportivos, tipos de fruta, de música, los días de la
semana, nacionalidad, creencia religiosa y color de los ojos. Al utilizar una escala nominal,
la variable se divide en sus diversas categorías. Estas categorías comprenden las
"unidades" de la escala y los objetos se "miden" al determinar la categoría a la cual pertenecen. Así, la medición con una escala nominal equivale, en realidad, a clasificar los objetos y a darles el nombre (de ahí lo de escala nominal) de la categoría a la cual
pertenecen.
Por ejemplo, si a usted le gusta correr, es probable que esté interesado en las diversas
marcas de zapatos deportivos que se encuentren disponibles en el mercado, como Brooks,
Nike, Adidas, Saucony y New Balance, por mencionar sólo algunas. Los zapatos deportivos
son importantes porque, al correr, cada zapato tiene un contacto con el piso de unas 800
veces por milla. En una carrera de 5 millas, tendrá un contacto de 4000 veces. Si usted
pesa 125 libras, tendría un impacto total de 300 toneladas sobre cada pie durante una
carrera de 5 millas. Eso sí que es un peso. No es de sorprender que los corredores sean
particularmente cuidadosos acerca de la elección de sus tenis.
La variable "marca de zapatos deportivos" es de tipo cualitativa. Se mide en una escala
nominal. Las diversas marcas representan sólo algunas de las posibles categorías (unidades) de esta escala. Si tuviéramos un grupo de zapatos deportivos y quisiéramos
medirlos mediante esta escala, consideraríamos cada uno y determinaríamos su marca. Es
importante observar que las unidades de una escala nominal son categorías, por lo que no
existe una relación de magnitud entre ellas. Así, no existe una relación cuantitativa entre las
categorías de Nike y Brooks. Nike no "es más marca de zapatos deportivos" que Brooks.
Simplemente, son marcas distintas. Esto puede quedar más claro si tuviéramos que lla mar
a las categorías zapatos deportivos 1 y zapatos deportivos 2, en vez de Nike y Brooks. En
este caso, los números 1 y 2 son sólo nombres y no poseen una relación de magnitud entre
ellos.
Una propiedad fundamental de las escalas nominales es la equivalencia. Esto quiere decir
que todos los miembros de una clase dada son iguales desde el punto de vista de la
variable de clasificación. Así, todas las parejas de tenis Nike son consideradas como
iguales desde el punto de vista de "marca de zapatos deportivos", a pesar de que puede
haber varios modelos distintos de tenis Nike.
Una operación que se realiza con frecuencia junto con la medición nominal es la de contar
las instancias dentro de cada clase. Por ejemplo, si tuviéramos varios zapatos deportivos y
determinamos la marca de cada uno, estaríamos realizando una medición nominal.
Además, tal vez nos interese contar el número de zapatos que pertenecen a cada
categoría. Así, podríamos tener 20 zapatos Nike, 19 Saucony y 6 New Balance en total.
Estas frecuencias nos permiten comparar el número de tenis dentro de cada categoría. Esta
comparación cuantitativa de las cantidades, dentro de cada categoría, no debe confundirse
con la afirmación hecha arriba, en el sentido de que no existe una relación de magnitud
entre las unidades de una escala nominal. Podemos comparar de manera cuantitativa las
cantidades de zapatos Nike con las de zapatos Saucony, pero Nike no es "más marca de
zapatos" de lo que es Saucony. Así, una escala nominal no tiene los atributos matemáti cos
de magni tud, intervalos iguales o cero absoluto. Sólo permite la clasificación de los objetos
en categorías mutuamente excluyentes.
Escalas ordinales
La escala ordinal representa el siguiente nivel de medición, el cual es relativamente bajo de
acuerdo con la propiedad de magnitud. Con esta escala, ordenamos los objetos medidos
según si poseen más, menos o la misma cantidad de la variable medida. AsÍ, una escala
ordinal permite determinar si A> B, A = B o A < B.
Un ejemplo de una escala ordinal es el orden de los primeros cinco participantes en un
concurso de oratoria, de acuerdo con su facilidad de palabra. Entre los oradores, la persona
con el rango 1 fue considerada mejor que la persona que posee el rango 2, quien a su vez
fue mejor que la de rango 3. La persona de rango 3 fue estimada como mejor orador que la
de rango 4, la cual fue considerada mejor que la persona del rango 5. Es importante
observar que aunque esta escala permite las comparaciones mejor que, igual a, o menor
que, no dice nada sobre la magnitud de la diferencia entre las unidades adyacentes
pertenecientes a dicha escala. En este ejemplo, la diferencia de facilidad de palabra entre
las personas de rango 1 y 2 podría ser grande y la que existe entre los individuos de rango
2 y 3 podría ser pequeña. Así, una escala ordinal no tiene la propiedad de intervalos iguales
entre las unidades adyacentes. Además, como todo lo que tenemos son órdenes relativos,
la escala no dice nada acerca del nivel absoluto de la variable. Así, los oradores de los
cinco primeros lugares podrían tener un gran nivel de facilidad de palabra o uno bajo. Esta
información no se puede obtener de una escala ordinal.
Otros ejemplos de escala ordinal son la clasificación de los corredores participantes en el
Maratón de Boston de acuerdo con su orden de llegada, la clasificación de los equipos de
fútbol americano colegial con base en las calificaciones de la Associated Press, el orden de
los profesores según su capacidad de enseñanza y el orden de los estudiantes de acuerdo
con su nivel de motivación.
Escalas de intervalos
La escala de intervalos representa un nivel superior de medición con respecto al de la
escala ordinal. Posee las propiedades de magnitud e igualdad de intervalo entre las unidades adyacentes, pero no tiene un cero absoluto. AsÍ, la escala de intervalos posee las
propiedades de la escala ordinal y tiene intervalos iguales entre las unidades adyacentes.
Estos intervalos indican que existen cantidades iguales de la variable medida entre las
unidades adyacentes sobre la escala.La escala Celsius, para medir la temperatura, es un
buen ejemplo de la escala de intervalos. Tiene la propiedad de intervalos iguales entre las
unidades adyacentes pero no tiene un punto absoluto. La propiedad de intervalos iguales
aparece por el hecho de que un cambio dado de calor producirá el mismo efecto en la
lectura de temperatura en la escala, sin importar en qué parte de esta escala ocurra dicho
cambio. Así, la cantidad adicional de calor que provocará un cambio en la lectura de la
temperatura de 2° a 3° Celsius también producirá un cambio en la lectura de 51° a 52° o de
105° a 106° Celsius. Esto ilustra el hecho de que las cantidades iguales de calor quedan
indicadas entre las unidades adyacentes en toda la escala.
Como en una escala de intervalos existen cantidades iguales de la variable entre las
unidades adyacentes de la escala en cuestión, las diferencias equivalentes entre los números de la escala representan diferencias de la misma magnitud en la variable. Así,
podemos decir que la diferencia de calor es la misma entre 78° y 75° Celsius que entre 24°
y 21° de la misma escala. Esto también implica, desde un punto de vista lógico, que las
grandes diferencias entre los números de la escala representan, también, diferencias
grandes entre la magnitud de la variable medida, y que diferencias pequeñas entre los
números de la escala representan pequeñas diferencias en la magnitud de la variable
medida. Así, la diferencia de calor entre 80° y 65° es mayor que la diferencia entre 18° y 15°
Celsius, y la diferencia de calor entre 93° y 91 ° es menor que la diferencia entre 48° y 40°
Ce1sius. En vista del análisis anterior, podemos ver que además de determinar si A = B, A
> B o A < B, una escala de intervalo s nos permite determinar si A - B = C – D, A – B > C D, o A – B < C - D.
Escalas de razón o proporción
El siguiente y máximo nivel de medición es la escala de razón. Tiene todas las propiedades
de una escala de intervalos y, además, posee un cero absoluto. Sin éste no se pueden
calcular las proporciones con las lecturas de la escala. Como este tipo de escala tiene un
cero absoluto, se pueden utilizar las proporciones (de ahí el nombre escala de
proporciones).
Un buen ejemplo para ilustrar la diferencia entre la escala de intervalos y la de proporciones
consiste en comparar la escala Celsius de temperatura con la escala Kelvin. El menor punto
de la escala Kelvin es el cero absoluto (la ausencia completa de calor). El cero de la escala
Celsius es la temperatura a la cual se congela el agua. Es un cero arbitrario, que en
realidad ocurre a los 273° Kelvin. La escala Celsius es de intervalos y la escala Kelvin es de
proporciones. La diferencia de calor entre 8° y 9° es igual a la diferencia entre 99° y 100°
sin importar que la escala sea Celsius o Kelvin. Sin embargo, no podemos calcular
proporciones con la escala Celsius. Una lectura de 20° Celsius no es el doble de caliente
que 10° Celsius. Esto se puede comprobar al convertir las lecturas Celsius al calor real que
representan. En términos del calor real, 20° Celsius es en reali dad 293°K (273° + 20°), y
10° Celsius es en realidad 283°K (273° + 10°). Es obvio que 293° no es el doble de 283°.
Como la escala Kelvin tiene un cero absoluto, una lectura de 20° en esta escala es el doble
de caliente que 10°. Así, se pueden utilizar proporciones con la escala Kelvin.
Otros ejemplos de variables medidas con escalas de proporciones son el tiempo de
reacción, la longitud, el peso, la edad y la frecuencia de cualquier evento, como el numero
de tenis Nike contenidos en el montón de zapatos deportivos ya analizado con anteriori dad.
Con una escala de este tipo, usted puede construir proporciones y realizar las demás
operaciones matemáticas asociadas por lo general a los números (es decir, suma, resta;
multiplicación y división). Las cuatro escalas de medición y sus características se resumen
en la figura 2.1.
ESCALAS DE MEDICIÓN
EN LAS CIENCIAS DEL COMPORTAMIENTO
En las ciencias del comportamiento, muchas de las escalas utilizadas se consideran con
frecuencia: como si fuesen de intervalos, sin establecer con claridad que la escala, en realidad, posee intervalos iguales entre unidades adyacentes. La medición del IQ; las variables
emocionales como la ansiedad y la depresión; las variables de la personalidad como la
autosuficiencia, la introversión, la extroversión y la dominancia; las variables de eficiencia o
logros terminales. Con todas estas variables es claro que las escalas no son de
proporciones. Por ejemplo, con el IQ, si una persona ha obtenido un cero en la escala de
inteligencia para adultos de Wechsler (WAIS), no podríamos decir que tiene inteli gencia
nula. Se supone que se encontrarían algunas preguntas que podría contestar el individuo
en cuestión, de modo que tendría un IQ superior a cero. Así, la prueba WAIS no tiene un
punto cero absoluto y las proporciones no son adecuadas. Por lo tanto, no es correcto decir
que una persona con un IQ de 160 es el doble de inteligente que alguien con un IQ de 80.
Por otro lado, parece que podemos hacer algo más que sólo especificar un ordenamiento
de los individuos. Una persona que posee un IQ de 100, tiene una inteligencia más cercana
a alguien con un IQ de 110 que otra con un IQ de 60. Esto parece ser una escala de
intervalos, pero es difícil establecer que la escala realmente posea intervalos iguales entre
las unidades adyacentes. Muchos investigadores consideran tales variables como si fuesen
medidas en escalas de intervalos, en particular cuando el instrumento de medición es
bastante estándar, como es el caso del WAIS. Es mucho más discutible considerar como
escalas de intervalos las escalas poco estándar y que miden variables psicológicas. Este
tema surge en particular en la estadística inferencial, donde el nivel de las escalas puede
influir sobre la elección de la prueba a realizar en el análisis de datos. Existen dos posturas
al respecto. La primera afirma que el uso de ciertas pruebas, como la t de Student y el
análisis de la varianza, deben limitarse a los datos que pertenecen a escalas de intervalos y
de proporciones. La segunda postura no está de acuerdo y afirma que estas pruebas
también se pueden utilizar con datos nominales y ordinales. Este tema, empero, es
demasiado complejo para ser considerado ahora. *
DEFINICIÓN
•
.Los límites reales de una variable continua son aquellos valores que están por arriba
y por debajo de los valores registrados, a una distancia que es igual a la mitad de la
unidad de medida mínima en la escala.
Por ejemplo, si la variable es el peso, la menor unidad es 1 libra, y registramos 180 libras,
los límites reales están arriba y abajo de 180 en 1/2 libra. Así, los límites reales son 179.5 y
180.5 libras.* Si la unidad mínima fuese 0.1 libras y no 1 libra y registramos 180.0 libras,
entonces los límites reales serían 180+- ½ (0.1), es decir, 179.95 y 180.05.
Cifras significativas
En la estadística analizamos datos; este análisis implica muchos cálculos matemáticos. Con
mucha frecuencia, tenemos un residuo decimal, por ejemplo, después de realizar una
división. Cuando esto ocurre, necesitamos decidir la cantidad de cifras decimales que
utilizaremos para el residuo.
.
En las ciencias físicas, por lo general, se utiliza el mismo número de cifras significativas que
tienen los datos en bruto. Por ejemplo, si medimos el peso de cinco sujetos hasta tres cifras
significativas (173, 156, 162, 165 Y 175 libras), y queremos calcular el promedio de estos
pesos, nuestra respuesta debe contener sólo tres cifras significativas. Así, La respuesta
de166.2 se redondea a tres cifras significativas, dando un resultado final de 166 libras. Por
varias razones, este procedimiento no se ha seguido en las ciencias del comportamiento,
sino que se ha establecido una tradición en la cual la mayor parte de los valores finales se
dan con dos o tres cifras decimales, sin importar el número de cifras significativas de los
datos en bruto. Como éste es un texto para su uso en las ciencias del comportamiento,
hemos optado por seguir esta tradición. Así, en este libro daremos la mayor parte de
nuestras respuestas finales hasta con dos cifras decimales. En ciertas ocasiones habrá
excepciones. Por ejemplo, los coeficientes de correlación y de regresión tienen tres cifras
decimales y los valores de probabilidad se dan, a menudo, hasta con cuatro cifras
decimales, lo que es consistente con la tradición. Es una práctica común realizar todos los
cálculos intermedios con dos o más cifras decimales de las que tendrá la respuesta final.
Así, cuando se pida que esta última tenga dos cifras decimales, usted deberá realizar los
cálculos intermedios con al menos cuatro cifras decimales y redondear la respuesta final a
dos cifras.
Redondeo
Dado que estaremos dando nuestras respuestas finales con dos y en ciertas ocasiones
hasta con tres o cuatro cifras decimales, necesitamos decidir cómo determinar el valor del
último dígito. Por fortuna, las siguientes reglas de redondeo son bastante sencillas y
directas:
1. Divida el número que desee redondear en dos partes: la respuesta potencial y el residuo.
2. Coloque un punto decimal al frente del primer dígito del residuo, creando con ello un iduo
decimal. 3. Si el residuo decimal es mayor que 1/2' sume 1 al último dígito de la respuesta.
.Si el residuo decimal es menor que 1/2' deje el último dígito de la respuesta sin cambio.
5. Si el residuo decimal es igual a 1/2' sume 1 al último dígito de la respuesta si es un dígito
impar, pero si es par, déjelo sin cambio.
Para realizar este redondeo, el número se separa en dos partes: la respuesta potencial y el
residuo. Como estamos redondeando a dos cifras decimales, la respuesta po tencial termina
en la segunda cifra decimal. El resto del número constituye el residuo. Para el primer
número, 34.01350, 34.01 constituye la respuesta potencial y .350 el resi duo. Como .350 es
menor que 1/2' el último dígito de la respuesta potencial permanece sin cambio y la
respuesta final es 34.01. Para el segundo número, 34.01761, el residuo decimal (.761) es
mayor que 1/2' Por lo tanto, debemos sumar 1 al último dígito, por lo que la respuesta
correcta es 34.02. Para los dos números siguientes, el residuo decimal es igual a 1/2' El
número 45.04500 se convierte en 45.04 debido a que el último dígito de la respuesta
potencial es par. El número 45.05500 se convierte en 45.06 debido a que el último dígito es
impar.