Transformación de coordenadas

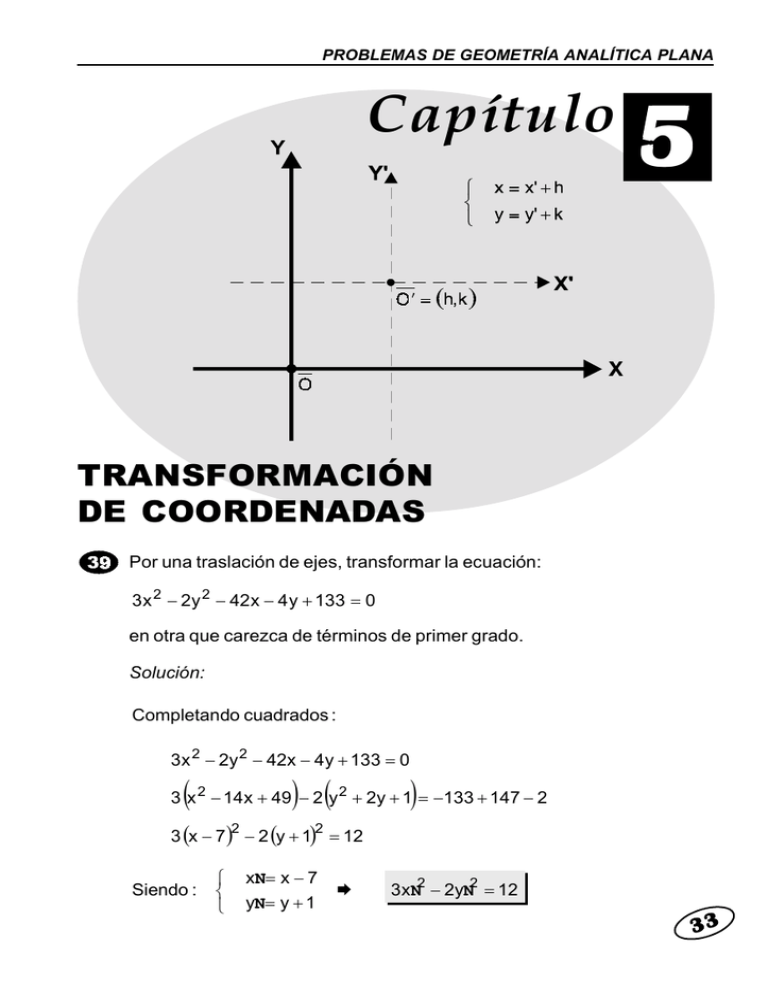
PROBLEMAS DE GEOMETRÍA ANALÍTICA PLANA
Capítulo
5
TRANSFORMACIÓN
DE COORDENADAS
Por una traslación de ejes, transformar la ecuación:
3 x 2 − 2y 2 − 42 x − 4 y + 133 = 0
en otra que carezca de términos de primer grado.
Solución:
Completando cuadrados :
3x 2 − 2y 2 − 42x − 4y + 133 = 0
) (
(
)
3 x 2 − 14x + 49 − 2 y 2 + 2y + 1 = −133 + 147 − 2
3 (x − 7 )2 − 2 (y + 1)2 = 12
Siendo :



xN= x − 7
yN= y + 1
!
3xN2 − 2yN2 = 12
33
Capítulo 5. TRANSFORMACIÓN DE COORDENADAS
Simplificar la ecuación:
72 x 2 + 36 y 2 − 48 x + 36 y − 55 = 0
por una traslación de los ejes coordenados.
Solución:
Completando cuadrados :
72x 2 + 36y 2 − 48x + 36y − 55 = 0
(
)
1
2

72  x 2 − x +  + 36 y 2 + y + 1 = 55 + 8 + 9
9
3


2
2
1
1


72  x −  + 36  y +  = 72
2
3


2
2
1
1


2x −  + y +  = 2
3
2










Siendo :
xN= x −
1
3
2xN2 + yN2 = 2
!
1
yN= y +
2
Por una traslación de ejes, simplificar la ecuación:
x 2 − 2y 2 + 8 x + 4 y − 3 = 0
Solución:
Completando cuadrados en la expresión, se tiene :
(x
2
) (
)
− 8x + 16 − 2 y 2 − 2y + 1 = 3 + 16 − 2
(x − 4 )2 − 2 (y − 1)2 = 17
Siendo :
34



xN= x − 4
yN= y − 1
!
xN2 − 2yN2 = 17
PROBLEMAS DE GEOMETRÍA ANALÍTICA PLANA
Por medio de una traslación de ejes, eliminar los términos de primer grado
de la ecuación: 2xy − x − y + 4 = 0
Solución:
2x y − x − y + 4 = 0
!



x = xN+ h
y = yN+ k
"
→
→
#
# en " :
2 (xN+ h)(yN+ k ) − (xN+ h) − (yN+ k )
2 xNyN+ 2 k xN+ 2 k yN+ 2 hk − xN− h − yN− k + 4
2 x Ny N+ (2 k − 1)xN+ (2 h − 1)yN+ 2 hk − h − k + 4 = 0



De donde :
Luego en
2 k− 1 = 0
2 h− 1 = 0
!
→
h=k =
1
2
!
4 x Ny N+ 7 = 0
!
!:
 1 1 1 1
2 x Ny N+ 2     − − + 4 = 0
 2  2  2 2
Por una rotación de los ejes coordenados, transformar la ecuación:
16 x 2 + 24 xy + 9 y 2 + 25 x = 0
en otra que carezca del término en xy.
Solución:
16x 2 + 24xy + 9y 2 + 25x = 0 →
Luego :
x = xN cosθ − yN sen θ
y = xN sen θ + yN cos θ
"

 →

#
35
Capítulo 5. TRANSFORMACIÓN DE COORDENADAS
# en " :
Ahora
( 16 cos θ + 24 senθ cos θ + 9 sen θ) xN +
+ ( 16 sen θ − 24 sen θ cos θ + 9 cos θ) yN +
+ ( 24 cos θ − 32 sen θ cos θ − 24 sen θ + 18 sen θ cos θ) xNyN+
2
2
2
2
2
2
2
2
+ 25 xNcos θ − 25 yNsen θ = 0
→
⊗
Luego para eliminar el término xN e yN.
! 24 cos 2 θ − 32 sen θ cos θ − 24 sen2 θ + 18 sen θ cos θ = 0
24 cos 2 θ − 24 sen2 θ − 14 sen θ cos θ = 0
(
)
24 cos 2 θ − sen2 θ − 14 sen θ cos θ = 0
24 cos 2θ − 7 × 2 sen θ cos θ = 0
24 cos 2θ − 7 sen 2θ = 0
Dividiendo × cos 2θ :
! 24 − 7 tg 2θ = 0 ! tg 2θ =
24
7
Luego de la figura :
! cos 2θ =
7
25
Además :
!
1 − cos 2θ
senθ =
=
2
1 + cos 2θ
! cosθ =
=
2
36
7
25 =
2
9
25
!
senθ =
3
5
7
25 =
2
16
25
!
cosθ =
4
5
1−
1+
PROBLEMAS DE GEOMETRÍA ANALÍTICA PLANA
⊗:
En
(4 cos θ + 3 sen θ) 2 xN2 + (4 sen θ + 3 cos θ) yN2 + 25 xNcos θ − 25 yNsenθ = 0
!
2
3
4
4 2
3 2  3
 4
 4 ⋅ + 3 ⋅  xN +  4 ⋅ + 3 ⋅  yN + 25 ⋅ xN− 25 ⋅ yN= 0
5
5
5
5
 5
 5
25 xN2 + 20 xN− 15 yN= 0
5xN2 + 4xN− 3yN= 0
!
Simplificar la ecuación:
x 2 − 10 xy + y 2 − 10 x + 2y + 13 = 0
por transformación de coordenadas.
Solución:
x 2 − 10xy + y 2 − 10x + 2y + 13 = 0
Luego :



x = xN+ h
y = yN+ k
→
→
"
#
# en " :
xN2 + 2 hx N+ h2 − 10xNyN− 10 k xN− 10 h yN− 10 hk + yN2 + 2 ky N+ k 2 −
− 10xN− 10 h+ 2yN+ 2 k + 13 = 0
xN2 + yN2 + (2h − 10k − 10 ) xN+ (2 + 2 k − 10 h) yN+
+ k 2 − 10 hk − 10 h + 2 k + 13 = 0
→
⊗
Para eliminar los términos xN e yN; debe cumplirse que



2 h− 10 k − 10 = 0
2 + 2 k − 10 h = 0
! h = 0 ; k = −1
37
Capítulo 5. TRANSFORMACIÓN DE COORDENADAS
En
⊗:
! xN2 + yN2 − 10xNyN+ 1 − 2 + 13 = 0
xN2 + yN2 − 10xNyN+ 12 = 0 ......!
Pero :
xN= xNNcos θ − yNNsen θ
yN= xNNsenθ + yNNcos θ

 ......$

$ en ! :
! xNN2 cos2 θ − 2 xNNyNNsenθ cos θ + yNN2 sen2 θ + xNN2 sen2 θ +
+ 2 xNNyNNsen θ cos θ + yNN2 cos2 θ − 10 + xNN2 senθ cos θ −
− 10 xNNyNNcos2 θ + 10 x NNyNNsen θ + 10 yNN2 sen θ cos θ + 12 = 0
!
(cos θ + sen θ − 10senθ cosθ) xNN +
(sen θ + cos θ + 10senθ cosθ) yNN +
+ (2 senθ cos θ − 2 senθ cos θ − 10 cos θ + 10 sen θ) xNNyNN+ 12 = 0
2
2
2
2
2
2
2
!
2
(1− 10 senθ cos θ) xNN2 + (1+ 10 senθ cos θ) yNN2 +
)
(
+ − 10 cos2 θ + 10 sen2 θ xNN
yNN+ 12 = 0 ...... ⊕
Ahora
el término
xNN
yNN:
Ahorapara
paraeliminar
eliminar
el término
x´´y´´:
! − 10 cos2 θ + 10 sen2 θ = 0
(
)
− 10 cos2 θ − sen2 θ = 0
! cos2 θ − sen2 θ = 0 ! cos 2θ = 0
38
PROBLEMAS DE GEOMETRÍA ANALÍTICA PLANA
Además :
! sen θ =
1 − cos 2θ
=
2
1
2
=
2
2
! cos θ =
1 + cos 2θ
=
2
1
2
=
2
2
Reemplazan do en
⊕:

2
2  2 
2
2  2
⋅
⋅
! 1 − 10 ⋅
xNN + 1 + 10 ⋅
yNN + 12 = 0

2
2 
2
2 


(1 − 5) xNN2 + (1 + 5) yNN2 + 12 = 0
2
2
− 4 xNN
+ 6 yNN
+ 12 = 0
Dividiendo × 2 :
!
2
−6 = 0
2xNN2 − 3 yNN
Un punto P se mueve de tal modo que la diferencia de sus distancias a los
dos puntos
A = (1,4 ) y B = (− 2,1) es siempre igual a 3. Hallar la
ecuación del lugar geométrico y simplificarla por transformación de
coordenadas.
Solución:
Sea P = (x, y ) el punto que se mueve.
De la condición :
!
AP − B P = 3
(x − 1)2 + (y − 4)2 − (x + 2)2 + (y − 1)2
=3
39
Capítulo 5. TRANSFORMACIÓN DE COORDENADAS
Efectuando operaciones se tiene :
! 20 x − 4 y − 8 x y + 9 = 0
→
"
Pero :
!
x = xN+ h
y = yN+ k



→
#
Luego :
!
(20 − 8 k ) xN− (4 + 8 h) yN− 8xNyN+ 20 h− 4 k − 8 h k + 19 = 0
Ahora para eliminar los términos xN e yN:
!
20 − 8 k = 0
4 + 8h = 0

1
5
 ! h= ; k=−
2
2

# en ! :
 1
5
 1  5 
! − 8xNyN+ 10  −  − 4   − 8  −   + 19 = 0
2
2


 
 2  2 
− 8xNyN− 10 − 10 + 10 + 19 = 0
! − 8xNyN− 9 = 0
40
→
!