Convección forzada dentro de un tubo Solución exacta de la

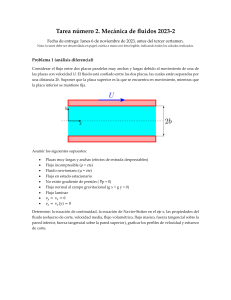
Convección forzada dentro de un tubo
Solución exacta de la ecuación de balance de energía térmica1
Dr. Bernardo Hernández Morales
Considera el flujo de un fluido incompresible2 , en estado estable, dentro de un tubo
circular de radio R, como se muestra en la figura:
El tubo está a una temperatura distinta de la del fluido, por lo que ocurre transferencia
de calor.
Objetivo:
Determinar expresiones para el coeficiente de transferencia de calor y para el número de
Nusselt.
Alcance:
Ocurre transporte de momentum y transporte de energía térmica simultáneamente. Sin
embargo, debido a que se trata de convección forzada, es posible desacoplar ambos fenómenos.
Solo se considera flujo laminar, de un fluido incompresible.
Estrategia:
La definición formal del coeficiente de transferencia de calor es:
h=
qk |pared
qk |pared
=
∆T
TR − T
donde
qk |pared
∂T (r) = −k
∂r pared
introduciendo cambios de variable y notando que en la pared r = R:
k
∂
TR − T (r)
h=−
R ∂(r/R)
TR − T r=R
1
Basado en: G.H. Poirier D.R. Geiger. Transport Phenomena in Materials Processing. TMS.
Pennsylvania, 1994. Pp. 219-223.
2
ρ = constante; β = 0.
1
Formulación matemática:
Modelo matemático generalizado
La ecuación general de energía (sin considerar disipación viscosa de energía térmica3 ) es:
ρCp
DT
= ∇ · k∇T
Dt
donde
∂T −
DT
=
+→
v · ∇T
Dt
∂t
es la derivada total.
Simplificaciones:
•Flujo másico unidimensional (dirección z)
•Estado estable
•Flujo laminar
•Propiedades termofísicas constantes
•Flujo completamente desarrollado (hidrodinámica y térmicamente)
•Flujo de energía por conducción despreciable en la dirección del flujo másico4
•Densidad de flujo de calor uniforme en la pared
Modelo matemático específico
∂T
k 1 ∂
∂T
vz
=
r
∂z
ρCp r ∂r
∂r
Para flujo laminar completamente desarrollado de un fluido incompresible:
r 2 vz = 2vz 1 −
R
Entonces
2vz 1 −
r 2 ∂T
R
Sujeta a las condiciones de frontera:
k 1 ∂
∂T
=
r
∂z
ρCp r ∂r
∂r
C.F.1
en r = 0
C.F.2
en r = R
3
∂T
=0
∂r
T = TR
Para el caso de flujo laminar se requiere que la velocidad el fluido sea baja, lo que resulta en un valor
muy pequeño del término de disipación viscosa de enrgía térmica.
4
Este término sólo aplica par materiales de número de Prandtl muy bajo (metales líquidos) bajo condiciones de flujo de muy baja velocidad.
2
Para un perfil de temperatura completamete desarrollado:
TR − T (r)
= f (r/R), es decir, no es función de z
TR − T
de donde es posible mostrar que
∂TR
∂T
∂T
=
=
∂z
∂z
∂z
Entonces, la ecuación de energía puede resolverse separando variables y aplicando C.F.1:
∂T
2vz
∂z
∂T
r 2 ∂r
k
∂T
dr =
r 1−
∂ r
R
ρCp ∂T
∂r
=0
r=0
∂r
1 r 2
k ∂T ∂T r
=
2vz
1−
∂z 2
2 R
ρCp ∂r r
r
Integrando de nuevo y aplicando C.F.2, se obtiene el perfil de temperaturas:
vz ρCp ∂T 4
TR − T (r) =
3R − 4r2 R2 + r4
2
8R k ∂z
Aplicando teorema de valor medio:
R
vz (TR − T )2πrdr
TR − T = 0 R
vz 2πrdr
0
Para evaluar el coeficiente de transferencia de calor se procede como sigue:
∂
TR − T (r)
k
h=−
R ∂(r/R)
TR − T r=R
Realizando estas operaciones y substituyendo se obtiene:
h = 2.18
k
R
Utilizando la definición del número de Nusselt:
Nu =
hLc
hD
=
k
k
se tiene
Nu = 4.36
Soluciones para otros problemas de flujo laminar completamente desarollado se dan en
la Tabla 7.1 de Poirier y Geiger.
3