TEOREMA DE GAUSS.

TEOREMA DE GAUSS.
→
−
→
−
→
−
−
15. Hallar el flujo del campo →
a = x2 i + y 2 j + z 2 k a través de la superficie
p
z = 1 − x2 + y 2 , 0 ≤ z ≤ 1.
a) Directamente.
b) Aplicando el teorema de Gauss.
Solución
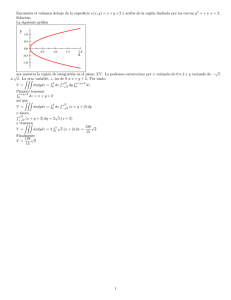
Llamaremos S a la superficie dada y D a su proyección sobre el plano XY (ver figura).
z
S
y
D
x
p
A partir de la fórmula explı́cita z = 1 − x2 + y 2 , obtenemos el vector normal exterior a
la superficie:
∂z
∂z −x
−y
→
−
n = − ,− ,1 = p
,p
,1 .
∂x ∂y
x2 + y 2
x2 + y 2
Como el flujo del campo corresponde a la integral de superficie, por definición tenemos que:
ZZ
ZZ
p
→
−
→
a dS =
(x2 , y 2 , (1 − x2 + y 2 )2 ) · −
n dxdy
D
S
ZZ h
i
p
−x3
y3
p
=
−p
+ (1 − x2 + y 2 )2 dxdy.
x2 + y 2
x2 + y 2
D
Teniendo en cuenta que D es el cı́rculo x2 + y 2 ≤ 1, resolveremos la integral mediante un
cambio a coordenadas polares. Ası́,
ZZ
S
−
→
a dS =
Z
1
Z
2π
u·
du
0
0
h −u3 cos3 v
u
−
i
u3 sen3 v
π
+ (1 − u)2 dv = .
u
6
Para poder aplicar el teorema de Gauss, la superficie debe ser cerrada. Por lo tanto, consideraremos la superficie formada por la unión de S y D y llamamos V al sólido que limita
dicha superficie. De este modo,
ZZ
ZZZ
→
−
→
a dS =
div −
a dxdydz,
S∪D
V
1
con lo que
ZZ
−
→
a dS =
ZZZ
S
Ahora bien,
ZZZ
→
div −
a dxdydz
→
div −
a dxdydz −
ZZ
V
D
√
ZZ
=
V
Z
1−
x2 +y 2
(2x + 2y + 2z) dz
dxdy
0
Z ZD
[(2x + 2y)(1 −
=
−
→
a dS.
p
p
x2 + y 2 ) + (1 − x2 + y 2 )2 ] dxdy.
D
Si hacemos en esta última integral un cambio a coordenadas polares, resulta:
Z 2π
Z 1
π
[(2u cos v + 2u sen v)(1 − u) + (1 − u)2 ] dv = .
u du
I=
6
0
0
→
−
Por último, teniendo en cuenta que el vector n = (0, 0, −1) es normal unitario exterior a
la superficie D, resulta:
ZZ
ZZ
→
−
a dS =
(x2 , y 2 , 0) · (0, 0, −1) dxdy = 0.
D
D
En definitiva,
ZZ
−
→
a dS =
ZZZ
S
−
div →
a dxdydz −
V
ZZ
π
−
→
a dS = .
6
D
16. Comprobar la fórmula de Gauss para calcular
ZZ
x3 dydz + y 3 dxdz + z 3 dxdy,
S
donde S es la superficie exterior de una pirámide formada por los planos x+y+z = a,
x = 0, y = 0, z = 0.
Solución
La superficie dada está compuesta por las cuatro caras del tetraedro de la figura, S =
S1 ∪ S2 ∪ S3 ∪ S4 (donde S4 , que es la cara no contenida en ningún plano coordenado, no
se muestra para mayor claridad del dibujo).
z
a
SH2L
SH3L
a
SH1L
a
x
2
y
Si aplicamos el teorema de Gauss, resulta:
ZZ
ZZZ
ZZZ
→
−
F dS =
div F dxdydz =
(3x2 + 3y 2 + 3z 2 ) dxdydz.
S
V
V
Teniendo en cuenta que la proyección del sólido V sobre el plano XY es el triángulo limitado
por los ejes coordenados y la recta x + y = 1, entonces la integral triple se descompone de
la forma siguiente:
ZZZ
Z a Z a−x Z a−x−y
2
2
2
(3x2 + 3y 2 + 3z 2 ) dxdydz.
dy
dx
(3x + 3y + 3z ) dxdydz =
0
0
V
0
3a5
Al resolver las sucesivas integrales llegamos al resultado I =
. Para resolver la integral
20
directamente, sin aplicar la fórmula de Gauss, debemos descomponerla en suma de integrales
sobre cada una de las caras que limitan la pirámide. Ası́ pues:
→ =
- La superficie S se define por la ecuación z = 0 y su vector normal exterior es −
n
1
1
(0, 0, −1). Por tanto,
−
→
F dS =
ZZ
ZZ
(x3 , y 3 , 0) · (0, 0, −1) dS = 0.
S1
S1
→=
- La superficie S2 viene dada por la ecuación x = 0 y el vector normal exterior es −
n
2
(−1, 0, 0); entonces
ZZ
ZZ
→
−
F dS =
(0, y 3 , z 3 ) · (−1, 0, 0) dS = 0.
S2
S2
→ = (0, −1, 0), de
- La superficie S3 viene definida por y = 0, con vector normal exterior −
n
3
donde
ZZ
ZZ
→
−
F dS =
(x3 , 0, z 3 ) · (0, −1, 0) dS = 0.
S3
S3
- La superficie S4 se define por la ecuación z = a − x − y, cuando (x, y) ∈ S1 , y tiene por
→ = (1, 1, 1). Por definición,
vector normal exterior a −
n
4
ZZ
ZZ
→
−
(x3 , y 3 , (a − x − y)3 ) · (1, 1, 1) dS
F dS =
S4
Z
=
S1
a
Z
a−x
[x3 + y 3 + (a − x − y)3 ] dy =
dx
0
0
3a5
.
20
Sumando los valores correspondientes a cada superficie llegamos al mismo resultado obtenido con la fórmula de Gauss.
→
−
→
−
→
−
→
17. Calcular el flujo del campo vectorial −
a = 4xz i + xyz j + 3z k a través de la cara
exterior de la superficie
S : x2 + y 2 = z 2 (0 ≤ z ≤ 4).
a) Directamente.
3
b) Aplicando el teorema de Gauss.
Solución
p
Parametrizamos la superficie S mediante la fórmula explı́cita z = x2 + y 2 , con (x, y) ∈ D,
donde D = {(x, y) : x2 + y 2 ≤ 16}. De este modo, un vector normal exterior a S viene dado
por
∂z ∂z
x
y
→
−
,
, −1 = p
,p
, −1 .
n =
∂x ∂y
x2 + y 2
x2 + y 2
Por tanto,
ZZ
→
−
F =
a dS
S
ZZ
p
p
p
y
x
,p
, −1 dxdy
=
(4x x2 + y 2 , xy x2 + y 2 , 3 x2 + y 2 ) · p
x2 + y 2
x2 + y 2
D
ZZ
p
=
(4x2 + xy 2 − 3 x2 + y 2 ) dxdy.
D
Resolveremos esta integral mediante un cambio a coordenadas polares, x = u cos v, y =
u sen v, (0 ≤ u ≤ 4, 0 ≤ v ≤ 2π). De este modo,
Z 2π Z 4
F =
dv
(4u3 cos2 v + u4 cos v sen2 v − 3u2 ) du = 128π.
0
0
Para aplicar el teorema de Gauss, consideramos la superficie cerrada S ∪ S 0 , donde S 0 es la
“tapa”del cono, es decir, el cı́rculo x2 + y 2 ≤ 16 contenido en el plano z = 4. De este modo,
ZZZ
ZZ
Z 4
ZZ
→
−
→
a dS =
div −
a dxdydz =
dxdy √
(4z + xz + 3) dz
S∪S 0
V
ZZ h
=
x2 +y 2
D
2
32 − 2(x2 + y 2 ) + 8x −
D
i
p
x(x + y 2 )
+ 12 − 3 x2 + y 2 dxdy.
2
Resolvemos esta última integral mediante un cambio a coordenadas polares, y llegamos al
resultado
ZZ
→
−
a dS = 64π.
S∪S 0
0
Por otra parte, como S se define mediante la fórmula explı́cita z = 4, su vector normal
→
exterior es −
n = (0, 0, 1), de modo que
ZZ
ZZ
→
−
a dS =
(16x, 4xy, 12) · (0, 0, 1) dxdy = 12 · área (D) = 192π.
S0
D
En definitiva,
ZZ
S
−
→
a dS =
ZZZ
−
div →
a dxdydz −
ZZ
S0
V
resultado que coincide con el obtenido de forma directa.
4
−
→
a dS = 128π,
→
−
18. Sea F (x, y, z) = (y, z, xz). Evaluar
−
→
F , donde Ω es el sólido x2 + y 2 ≤ z ≤ 1.
ZZ
∂Ω
Solución
Por el teorema de la divergencia,
ZZ
ZZZ
ZZZ
→
−
F =
div F dxdydz =
x dxdydz.
∂Ω
Ω
Ω
Pasando a coordenadas cilı́ndricas:
x = u cos v, y = u sen v, z = z,
la región Ω se escribe como
0 ≤ u ≤ 1, 0 ≤ v ≤ 2π, u2 ≤ z ≤ 1.
La integral queda ahora:
ZZZ
Z
x dxdydz =
Ω
1
u2 du
0
Z
Z
1
cos v dv
0
5
2π
dz = 0.
u2